Wind Speed Profile Statistics from Acoustic Soundings at a Black Sea Coastal Site

Abstract

More than seven years of remote sensing data with high spatial and temporal resolution were investigated in this study. The 20-min moving averaged wind profiles form the acoustic sounding with Scintec MFAS sodar were derived every 10 min. The profiles covered from 30 to 600 m height with vertical resolution of 10 m. The wind speed probability and the Weibull distribution parameters were calculated by the maximum likelihood method at each level and then the profiles of the Weibull scale and shape parameters were analyzed. Diurnal wind speed at heights above 200 m has shown a well-expressed increase in the averaged values during the night hours, while during the day lower wind speeds were observed. The reversal height was explored from spatially and temporally homogenized diurnal wind speed data with applied quadratic functions for better interpretation of the results. In addition, analyses by type of air masses (land or sea air mass) were performed. One of the outcomes of the study was assessment of the internal boundary layer height, which was estimated to 50–80 m at the location of the sodar. The obtained information forms the basis for climatological insights on the vertical structure of the coastal boundary layer and is unique long-term data set important not only for Bulgaria but for coastal meteorology in general.

1. Introduction

A significant progress has been made over the last years with the technological development of the ground-based instruments for remote sensing measurements of atmospheric characteristics and they have been established as reliable and indispensable tools in a number of innovative scientific methods for the study of the Planetary Boundary Layer (PBL) [1,2,3,4,5,6,7,8,9,10]. On the other hand, the complexity of the observed coastal processes includes the air masses transformation when passing the sharp change in the physical characteristics of the surface and the formation of an Internal Boundary Layer (IBL). The unique sodar data set of this study provides the challenge to investigate the IBL development at the site, which is a new achievement. The IBL height grows with the distance from the shore when marine airflow comes over land [11,12,13]. The interest in this phenomenon is related to the fact that many cities and industrial facilities are located near or on the shores of the seas, oceans or large lakes, and the low height of the IBL creates conditions for fumigation or increased air pollution level, compared to regions with a homogeneous surface [14].

The wind profiles and Weibull distribution parameters profiles are also influenced by the air mass transformation processes and depends on the distance to the shoreline in the direction of the airflow. In this case, studies show that there is a relationship between the height of the maximum in the profile of the shape parameter and the height of the IBL [4,15,16], but no theoretical connections have been found for this dependence.

The two-parameter Weibull distribution is one of the most commonly used and preferred distributions for the assessment of wind energy potential and it is reviewed in a number of scientific studies [17,18,19,20,21]. The vertical profiles of the shape parameter as well as the diurnal wind speed variation are used to determine the so-called “reversal height”—the height at which the shape of the diurnal wind speed variation is reversed [17,22,23,24]. Above a flat and homogeneous surface, the reversal height coincides with the height of the maximum in the shape parameter profile. During the night, the dynamics of the air masses is influenced by the relatively cooler ground and the formation of a Stable Boundary Layer (SBL) theoretically determines a linear increase in wind speeds with height in the adjacent atmospheric layer. On the other hand, the changed thermodynamic state of the atmosphere during the day, under the influence of the relatively warmer ground, theoretically determines higher wind speeds close to it and significantly less variation in height due to the presence of a neutral or unstable stratified atmospheric layer. The height of these two theoretical profiles (defining the variation of wind speed in height for two different thermodynamic states of the atmosphere—neutral or unsustainable during the day and stable stratification in the evening) intersect is called “reversal height” and characterizes the quasi-static state of the diurnal wind speed variation in different thermodynamic atmospheric conditions determined by the direct influence of the ground surface on the adjacent atmospheric layer during the day and night. Above this layer, the atmosphere is distanced from the direct influence of the surface. The height at which no change is observed in the diurnal wind speed variation (in this paper, its square function is a straight line) and divides a diurnal speed variation with opposite curvatures (protrude from concave) is defined as “reversal height”.

In summary, it can be noted that in the literature, there are many short-term studies dedicated to the coastal boundary layer using acoustic remote sounding in different places around the world for short periods [25,26,27,28,29,30,31] and they have proved the great capabilities of the sodar measurements for the study the wind structure of the PBL. The novelty and the contribution to science of this paper consist in the statistical analyzes of sodar long-term wind speed data, which brings new information for the vertical structure of the atmosphere in coastal regions, and particularly for the Bulgarian Black Sea coast. Except for theoretical research, the created database can be used for wind and turbulence regime studies, such as extreme wind events, numerical models evaluation, air pollution, assessment of the wind resource, etc.

2. Study Area and Remote Sensing Equipment

Meteorological Observatory (MO) Ahtopol is the southernmost coastal synoptic station from the operational meteorological network of National Institute of Meteorology and Hydrology (NIMH) and is situated in southeastern Bulgarian Black Sea coast at about 2 km from the town of Ahtopol (Figure 1). The study area is under the influence of the Continental-Mediterranean climate zone in Bulgaria and has been identified into the Black Sea coastal Strandzha climate region, which is a part of the Black Sea climatic sub-region [32]. Well expressed breeze circulation in the warm half of the year is typical for this climate region, whereas during the cold season lower frequency and smaller temporal and spatial scales of coast circulations are registered [33]. MO Ahtopol is located on a flat grassy terrain at 30 m height above sea level and at about 400 m inland. The shore near the observatory is steep about 10 m high and the coastline has an approximate direction from NNW to SSE (Figure 1).

Wind profile measurements in this study are obtained from acoustic sounding of the coastal PBL with a mono-static Doppler multi-frequency remote sensing system—SCINTEC Flat Array Sodar MFAS with working frequency range of 1650–2750 Hz and multi-beam operation of 9 emission/reception angles (0°, ±9.3°, ±15.6°, ±22.1°, ±29°). The spatial resolution of 10 m and range from 150 m to 1000 m in the vertical direction are laid out in instrument specifications with wind speed measurement accuracy of 0.1–0.3 ms⁻¹ and 2–3 Deg for the wind direction [34]. The first measurement level is 30 m and the maximum vertical range for these study reaches 600 m.

The sodar is mounted at an approximate height of 4.5 m above the ground on the roof of the administrative building of the MO Ahtopol (Figure 1) and data records were made every 10 min with moving averaging period of 20 min.

3. Data Analysis and Overview

The wind speed profiles analysis in this paper have covered a period of more than seven years of acoustic atmospheric sounding in the MO Ahtopol from 20 Jul 2008 to 31 Jan 2016. During that period, the measurements were limited at night hours in the summer months of 2008 and 2009 and the remote technical support was practically hampered by the lack of Internet access in the observatory until 2011. After December 2009 there were no restrictions set for the operation hours. In addition, the continuous sodar operating mode was interrupted by frequent accidents of the main power supply on the territory of the MO Ahtopol.

The data availability during the different months of the study period is presented in

Table 1. Monthly data availability (%) and maximum effective height (m) reached by the sodar for the study period. Circles show availability above 70% when green, between 40% and 70% when yellow, and below 40% when red. The range is presented graphically with small charts of 4 bars, where one filled bar denotes a range of 450 m, 2 filled bars—a range over 540 m, 3 filled bars—a range over 640 m and 4 filled bars—a range over 740 m.

where the range of availability above 70% is given in green, between 40 % and 70% in yellow, and below 40% in red. The exact availability is given with the number in %.

The maximum of the actual (effective) sodar range in Table 1 is presented as height (m) and graphically with small charts of 4 bars, where one filled bar denotes a range of 450 m, 2 filled bars—a range over 540 m, 3 filled bars—a range over 640 m and 4 filled bars—a range over 740 m.

The maximum of the vertical range during the different months has been determined by both the availability of turbulent temperature inhomogeneous in the sounded atmosphere layer above the sodar which can return the backscatter signals to the antenna receiver and the updates of the sodar software which have been provided periodically from the manufacturer over the years. The available remote sensing data (Table 1) with high spatial and temporal resolution from 2485 days of the possible 2752 days have been analyzed. The profiles selection that are presented in this paper is related to the data availability check at a height of 110 m above the ground (level at which the sodar data availability is relatively high) and continuity of the profiles after this height (no data interruption is allowed in the involved profiles after 110 m).

The conditions set for the data selection have limited the analysis to 2357 days and aims to avoid the accumulation of a large number of short profiles that have not exceeded 110 m in height, while allowing profiles that have not started from the lowest sodar vertical range to be involved in the analyzes (profiles beginning from 30 m to 40 m above the ground are often seen). The statistical analyzes of wind speed profiles comprise: Analysis I—Wind speed distribution in height; Analysis II—Weibull scale and shape parameters profiles; Analysis III—Average diurnal variation of wind speed at different heights. These three types of analysis are performed for all air masses and separately for marine and land air masses.

The sodar data recordings were performed in local time until 26 Oct 2014 (i.e., during the cold half of the year-GMT + 2, and during the warm one- GMT + 3). After this period, the sodar worked only in winter time mode (i.e., GMT + 2). Most of the performed here analyzes are independent of the time zone (Analysis I, Analysis II), but for the purposes of Analysis III the data were adjusted to GMT + 2. Although a period of more than seven years was analyzed, it is impossible to deduce homogeneous 24-h wind speed profiles data (up to 110–140 m high) or the resulting diurnal data is insignificant in some of the analyzes. Difficulty in conducting Analysis III is due to the presence of local coastal circulation (wind direction changes over a given day not only during the warm half of the year [33]), as well as the insufficient availability of continuous sounding data of marine and land air masses over time and space during the distinct periods (interruptions caused by the night operating mode limitations as well as by the accidents occurrence with the mains electricity).

For the purposes of wind speed distribution analysis (Analysis I) the values of each involved profile under reviewed periods (total, summer, and winter) and for the different types of air masses (all, sea, and land) are processed sorting them by height (every 10 m) and by wind speed intervals from 0 to 40 ms⁻¹ as follows:

• Calm interval—at wind speed values ≥ 0 ms⁻¹, but <0.5 ms⁻¹
• 1 ms⁻¹ interval—at wind speed values ≥ 0.5 ms⁻¹, but <1.5 ms⁻¹
• 2 ms⁻¹ interval—at wind speed values ≥ 1.5 ms⁻¹, but <2.5 ms⁻¹
• …
• 40 ms⁻¹ interval—at wind speed values ≥39.5 ms⁻¹;

The wind speed distributions in height from the selected profiles have allowed at each vertical level the histograms to be generated and their probability distributions to be determined. In Analysis II, the two-parameter Weibull distribution for the wind speed at each measurement level has been applied using the maximum likelihood method [35]:

$$f\left(u;c,k\right)=f\left(x\right)=\left\{\begin{array}{c}\frac{k}{c}{\left(\frac{u}{c}\right)}^{k-1}{e}^{-{\left(u/c\right)}^k},u\ge 0\\ \\ 0,u<0\end{array}\right.$$

(1)

$$k={\left(\frac{{{\displaystyle \sum }}_{i=1}^N{u}_i^k\ln u_i}{{{\displaystyle \sum }}_{i=1}^N{u}_i^k}-\frac{1}{N}{\displaystyle \sum }_{i=1}^N\mathit{ln}{u}_i \right)}^{-1}$$

(2)

$$c={\left(\frac{1}{N}{\displaystyle \sum }_{i=1}^N{u}_i^k \right)}^{1/k}$$

(3)

The probability density function (pdf) also known as the Weibull distribution is described in Equation (1). The two distribution parameters are given in the Equations (2) and (3), respectively, for a shape parameter “k” and the scale parameter “c”. The shape parameter “k” has a non-dimensional value and defines the shape of the probability density distribution curve. The scale parameter “c” assumes the dimensionality of the variable (in the present analysis-(ms⁻¹)) and represents the 63.2th percentile of the distribution [36,37]. These equations have been applied to each level of measurement and as results vertical profiles of the shape “k” and scale “c” parameters with 10-metre resolution have been obtained.

The vertical profiles of the shape parameter “k” from Analysis II, as well as the diurnal wind speed variation from Analysis III, have been used to determine the so-called “reversal height”.

4. Results

4.1. All Air Masses

Wind speed histograms with fitted Weibull distributions and statistics for different measurement levels (minimum, maximum and average wind speeds and the values of the two parameters of the corresponding Weibull distribution) for the study period in the MO Ahtopol are shown in Figure 2. A total of 327,009 time series with selected profiles are included in this analysis, which represents 82.2% data availability over the reviewed total period. The data availability at each presented height is graphically indicated by the pink bar on the right of each histogram. It can be seen that the number of the involved measurements in the output of the statistical graphs in Figure 2 have sharply decreased in height due to the lower number of profiles reaching the respective measurement level. The highest level of the pink bar of 99.8% data availability from all processed time series is observed at 100 m above the ground, while at 600 m is only 3.4%, which is equal to just over 11,100 profiles reaching this height. A shift of the maximum to higher wind speeds is seen at the histograms as the height increases, which is characteristic of the wind speed height variation. The extent of “stretch” or “concise” of the Weibull distribution graph is determined by the shape parameter “k”. The distribution graph is more stretched with higher value of “k”. The existence of the information presented in Figure 2 from 30 m to 600 m above the ground at every 10 m height has allowed the graph of the variation of the wind speed probability distribution in height for the whole study period to be presented in Figure 3.

The color bar in Figure 3 shows the variance of the probability distribution in height. Its color range is limited to 10% to achieve better visualization of the results (values of the probability distributions above 10% are colored in the same color bending 10%). The area with maximum values of the wind speed probability distribution is clearly visible at the presented graph (Figure 3), where up to 180 m it is highest for winds speed up to 3 ms⁻¹, at 300 m the highest probability is observed for the winds in the range of 3 to 6 ms⁻¹, and at 600 m it is highest for the winds at speeds of 10 to 13 ms⁻¹.

From the green bars showing the change in the number of profiles availability reaching a certain height it is seen that it is sharply decreasing after 200 m above the ground, with a maximum of data in the layer from 70 to 110 m. The data availability at the first level of sodar measurements (30 m above the ground) is about 5% lower than the layer at which the maximum data is observed.

Profiles of the shape and the scale parameters in Figure 4 (respectively left and right charts) are derived from the applied two-parameter Weibull distribution to the retrieved wind speed histograms from 30 to 600 m above the ground at every 10 m height.

The color bars on the right side of the graphs show the percentage of the data availability with height. An almost linear change of the values in height is observed in the scale parameter profile (right), while two weak peaks at 50 and 80 m above the ground are distinguished, followed by a major peak at a height of 270–300 m and a slightly sharper change in profile values at a height of 500 m. As mentioned above, the dimensionality of this profile is the same as the wind speed (ms⁻¹) and its values are proportional to the average wind speed values [20,38]. The values of the profile close to the ground start at nearly 2 ms⁻¹, at a height of 300 m they reach approximately 6–7 ms⁻¹, and at 600 m from the ground the values of the scale parameter are close to 12 ms⁻¹. Relatively small peaks at a height of 50 and 80 m above the ground are observed in the shape parameter profile (Figure 4a) with values close to 1.05, a pronounced peak at 260 m with values around 1.65, relatively sharp change in the values at 500 m and at a height of 600 m the value is nearly 2.45. Lower peaks can be associated with the height of IBL or surface layer [4,16].

The graphs of the diurnal wind speed data availability variations from the acoustic sounding of the atmosphere (b—color bar indicates percentage availability) and the diurnal wind speed variations in height determined by the corresponding data availability (a—the color bar indicates the wind speed value in ms⁻¹) are shown in Figure 5. The inhomogeneity of the data, both on the vertical (in height) and the horizontal (on the twenty-four-hour time scale) is observed on the right graph. The vertical inhomogeneous of the data is determined by the different effective sodar range over the various days of the considered period. There is a well-expressed laminar layout of the data availability in height, which is largely determined by the continuity condition after the 110 m height of the involved profiles in the analysis. The highest data availability (over 80%) is observed in the first 180 m, and at a height of 300 m the availability is close to 50%.

After a height of 500 m the data availability does not exceed 10%. Data at 30 m height is characterized by the lowest availability in the layer up to 180 m, due to the fact that a large number of profiles involved in this analysis do not start at the lowest sodar measurement level. In the horizontal direction (the diurnal variations) the homogeneity of the data is relatively more evenly distributed, but due to changes in the sodar’s continuous operation mode until Oct 2009, there is a highest availability of data throughout the day. The missing data cause different number values available for averaging the wind speed variations in height at the left graph in Figure 5. Low wind speed values are observed in the layer defined approximately from the first 90 m above the ground. The increase of the wind speeds in height is well expressed during the night hours, while during the day low wind speeds are also observed in the higher layers. The minimum values in the averaged diurnal wind speed are around 5 ms⁻¹ close to the surface and the maximum speeds of 14 ms⁻¹ are reached at altitudes above 400 m.

Due to the time and space inhomogeneity of data distribution (Figure 5b), a different number of individual values, both in height and at specified 10-min intervals of the day, are involved in the calculation of the averaged diurnal wind speed variations which are presented with dashed lines from 30 m to 110 m with step of 10 m height in different colors in Figure 6a.

Quadratic functions (lines with the same color for the specified heights) are applied to describe the diurnal change of wind speed at the observation levels. For clarity, the variation of the same quadratic functions is presented in Figure 6b. The height at which straight or close to a straight line is observed (no diurnal variation) separates the wind regime close to the ground from the one aloft. An almost straight line is observed at a level of 50 m (green color) above the ground. The curve at 60 m is also almost straight line. The curve at 70 m shows near ground regime with maximal wind speed around noon. Thus, it is difficult to attribute just one level for the value of “reversal height”, and the reason is that all data are averaged including marine and land air masses and all seasons. The height of 50 m can be related to the characteristic height of a formed IBL at 500 m from the shore, and the height of 90 m may be related to the wind regime over the land.

The results of the data homogenization processes in both up to 180 m height and 10-min time series are shown in Figure 7. Due to the process of temporal homogenization (determining uninterrupted diurnal data), the number of days is reduced from 2457 to 1538 days (Figure 7a). The highest data availability (less than 60%) is observed in the layer between 60 and 120 m, and it is rapidly decreasing in altitudes (over 330 m it is below 1%). Continuous twenty-four-hour time series are also recorded at 600 m height, but their availability is less than 0.2%, and the color bar (percent availability scale) does not cover such low values. Sufficient data availability is observed in the layer from 30 to 180 m, for which layer a further process of spatial homogenization (in height) is applied. The final outcome from the data homogenization by time and up to 180 m (Figure 7b) results in a total of 456 days, which are just under 20% of the whole study period.

Diurnal wind speed variations of these 456 days at levels from 30 to 110 m at 10 m height with corresponding applied quadratic functions are shown in the graphs in Figure 8. No wind speed variations at 40 m level (red dashed line, red lines, and red equations) are seen in the graphs. Below this level a slightly protrude shape of the quadratic function curve (brown color) is observed (at 30 m). The applied quadratic functions curves are with concave forms at all other levels above 40 m, and taking into account that a spatially and temporally homogenized data is used in these results (Figure 7b) the “reversal height” can be defined at 40 m height.

4.2. Land and Sea Air Masse

The analysis of marine air masses derived during the whole reviewed period is determined by winds with a direction in the range of 0–120 Deg. The number of profiles in this wind direction interval is just over 47,700 and represents 12% of the total period considered. The number of days with registered marine air masses is 821 out of 2357 days, where the 110 m condition and continuity of data after this height are met. The analysis of land air masses is determined by wind direction range of 170–290 Deg. The number of registered land profiles is just over 45,500 and represents nearly 11% of the study period, which is and covers 561 days.

The diurnal data availability of marine and land air masses is shown in Figure 9 (left and right graphics, respectively).

In comparison with Figure 5b it can be seen that during the whole study period, the night air masses are predominantly from the land, and the daytime from the sea. That specific spatially and temporally inhomogeneous distribution of the two defined main types of air masses has been the reason Analysis III to be invalidated in these cases. The sea air masses data homogenization over time scale has remained at most 11 days (from 821 days) at certain altitudes, and after the next homogenization up to a height of 110 m that number is reduced to only 8 days (too insufficient to retrieve representative results for marine air masses). Due to similar reasons, homogenization of land air masses data up to 110 m has been impossible. On the other hand, the inhomogeneous data distribution during the day indicates the breeze cells characteristic time scales at south-eastern Bulgarian Black Sea coast [33,39,40,41].

The results from the applied two-parameter Weibull distribution in height are presented in Figure 10 for marine (a and b) and land (c and d) air masses with graphs of shape (a and c) and scale (b and d) parameters profiles. With the shape parameter of the marine air masses, similar peaks are observed in the values at almost the same heights as in Figure 4—two small peaks at a height of 50 and 80 m and one pronounced peak at 270–280 m above the ground. The small peaks could again be associated with IBL height, while the 270–280 m peak with the mean height of the upper edge of the breeze cells core with maximum speed in the wind field (an indication of the maximum wind zone in the quasi-stationary period of the sea breeze) [33]. Higher values of this parameter are observed at land air masses with a marked peak of 50 m reaching values of 1.70, followed by a sharp decrease in the profile values up to 110 m, and then raising again to form a pronounced peak with a value close to 2.1 at 270–290 m, which height is close to those have been previously reviewed (260 m at all air masses in Figure 4a, and 270–280 m at marine air masses in Figure 10a). After this pronounced peak, the land air masses shape profile values grow almost linearly reaching 3.4 at 600 m height, with a very low peak observed at 430 m height. In the marine air masses scale parameter profile (Figure 10b) a slower increase of the values in height compared to that in Figure 4b is observed as well as a small peak at 80–90 m height and a significantly more pronounced peak at 230–250 m. The land air masses scale parameter profile (Figure 10d) has the highest values of those considered so far, starting with 3 ms⁻¹ and growing almost linear. At 300 m height the value is close to 10 ms⁻¹, at 500 m–14 ms⁻¹ and at 600 m over 18 ms⁻¹. Peaks are also observed with it, but due to the relatively rapid increase in height, they are not clearly expressed. Two peaks are observed close to the ground at 50 and 80 m height and one at about 290–300 m.

The analysis of applied quadratic functions to the averaged diurnal variation of wind speed from inhomogeneous data (Figure 11, marine air masses—a; land air masses—b) for the two main types of air masses at different heights indicates the reversal height in land air masses at about 40 m, while in the marine air masses it is at 100 m height.

5. Discussion

The study reveals for a first time details in the vertical structure of the wind field within the PBL in a Black Sea coastal area. The period of eight years is among the long-term remote sensing data sets in Europe. The results show reversal height of 40 m for all and for land air masses and about 100 m for marine air masses. At the reversal height the wind speed is characterized with small diurnal changes, which is important for wind energy and other tall constructions sensitive to the variability and strength of the wind. It can be noted that the analysis shows that the wind speed at the reversal height within marine air masses is about 7 ms⁻¹, within land air masses is about 5 ms⁻¹ and for all wind directions is about 4 ms⁻¹.

The height of the IBL at 400 m inland from the coast is assessed to be 50–80 m, a range defined by the definition of marine air masses as those from 0–120 degrees and consequently different fetch over land for air from these directions. As discussed in [13,42], the IBL height is important for air pollution assessments and forecast, as it defines much smaller volume for dilution compared to that at homogeneous areas. When building industry near the coast, the IBL height defines whether the emissions may lead to fumigation and across which area. The IBL characteristics determine the climate and weather comfort for recreation and tourism at coastal sites. The peak in the profiles of the Weibull distribution scale parameter of marine air masses at about 260–300 m is related to the height of maximal wind speed in sea breeze situations. The profiles of the scale and shape parameters of the Weibull distribution for the marine and land air masses are in agreement with the findings of [16,17] investigating this important for wind energy applications topic over land and sea.

6. Conclusions

The current study period is about seven years and allows the start of climatic research of the vertical structure of the coastal boundary layer. With reliable sodar or Doppler lidar remote sensing longer periods of data can be reached.

The statistical analysis through the Weibull distribution have provided additional unique information on the vertical wind structure of the coastal area. The results of the Weibull parameter profiles for the whole considered period (Figure 4) reveal peaks close to the ground at 50 and 80 m, at about 250 and 400 m in the case of inhomogeneous data, which can be related to the IBL height, the height of the core with maximum wind speed in the breeze cells and the height of a stable PBL. The pronounced peaks in the shape parameter profile of the Weibull’s distribution were also investigated by diurnal wind speed variation in height, where characteristic heights of 40, 50, and 90 m are associated with the reversal height depending on wind direction and the spatially and temporally data homogenization.

A summary of some characteristics of the data samples, parameter values, and the profiles peculiarities are outlined in

Table 2. Analysis over a 7-year measurement period.

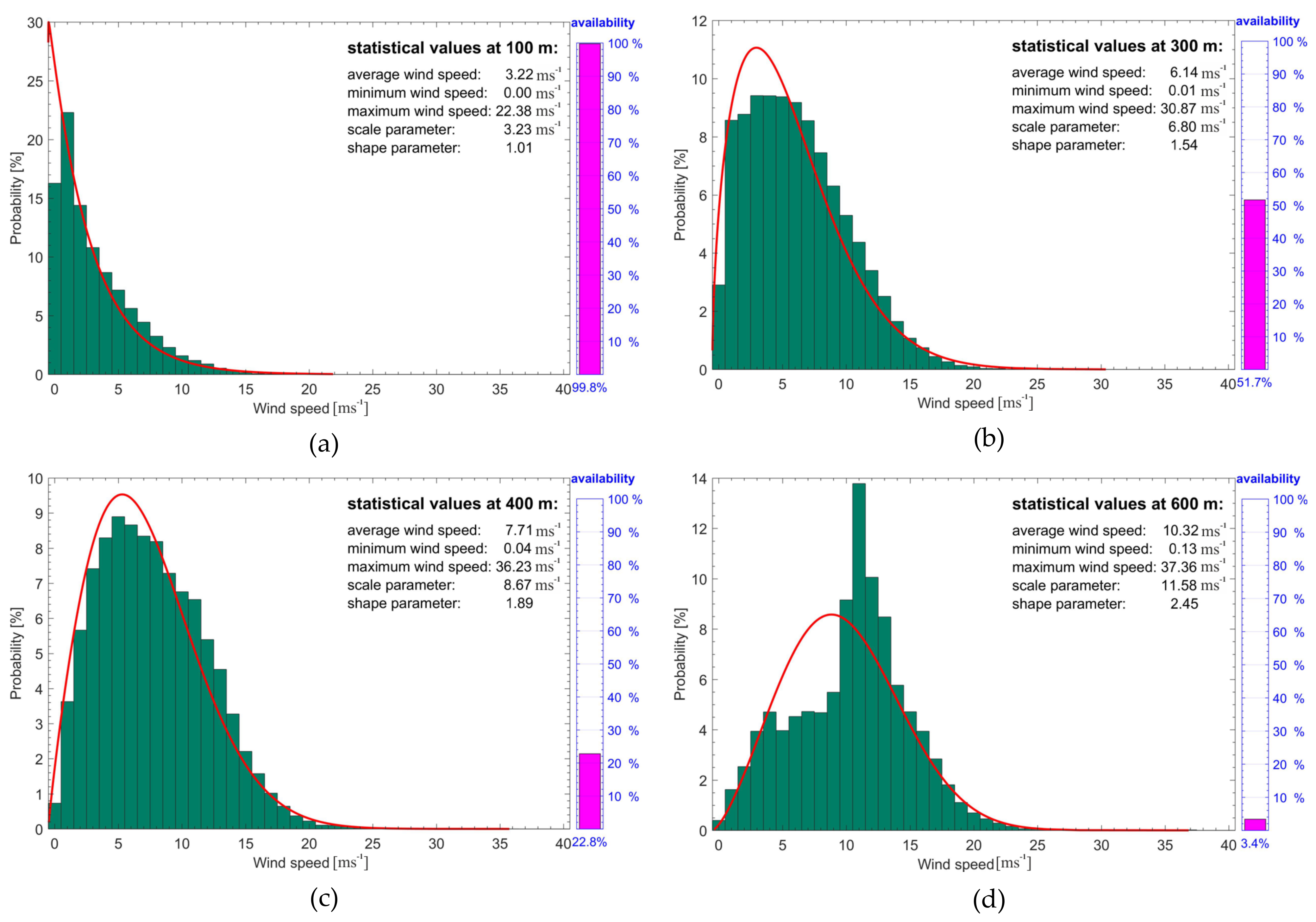
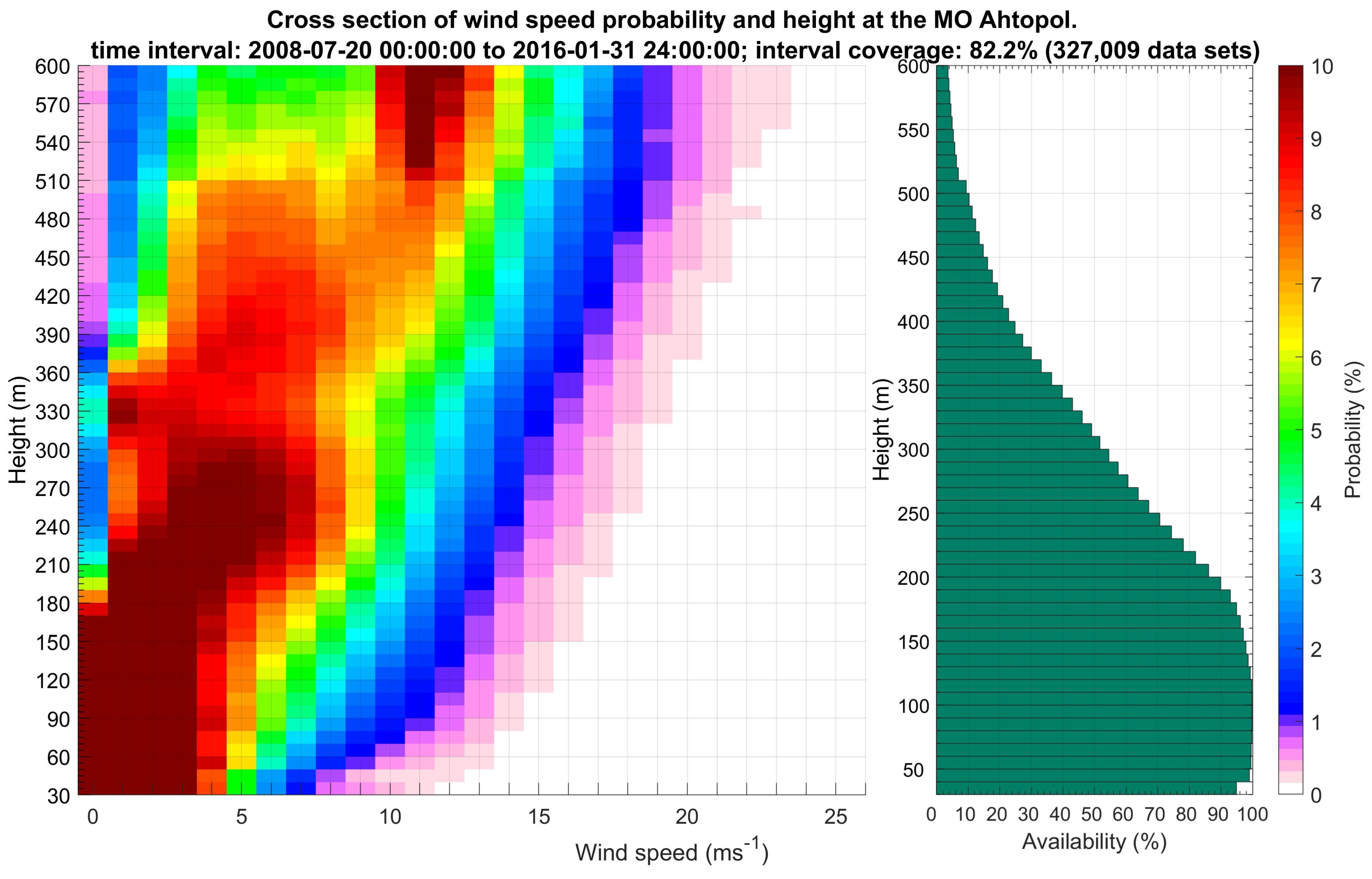
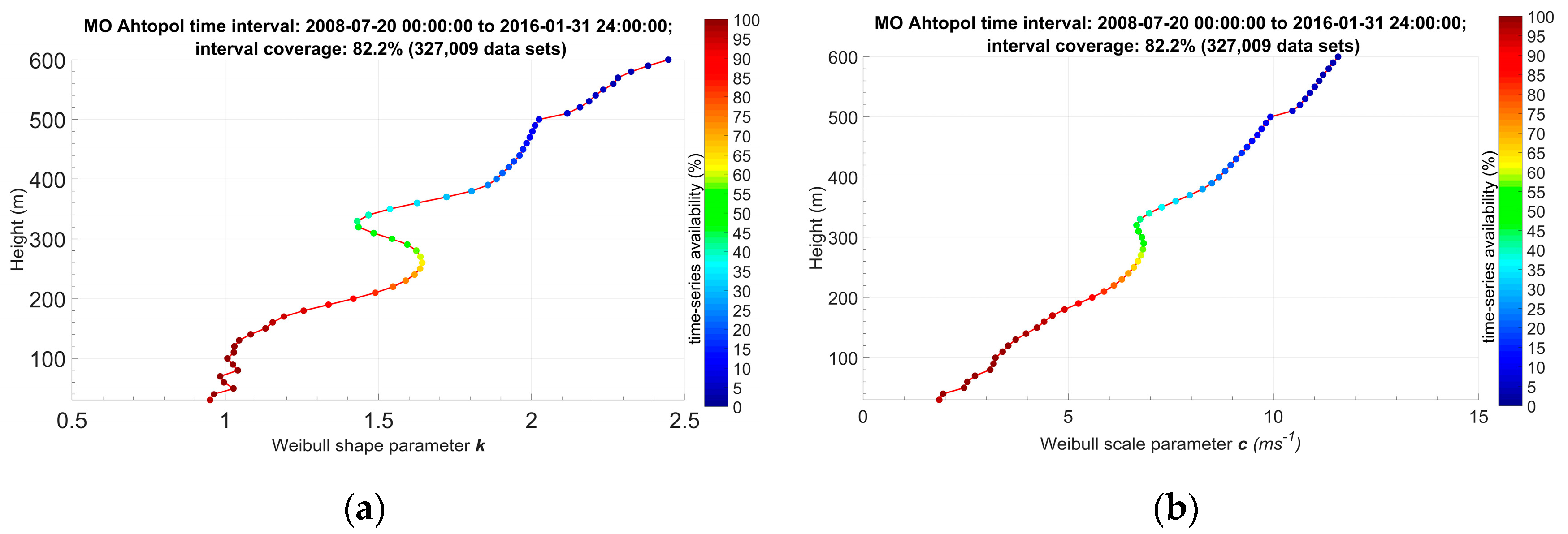
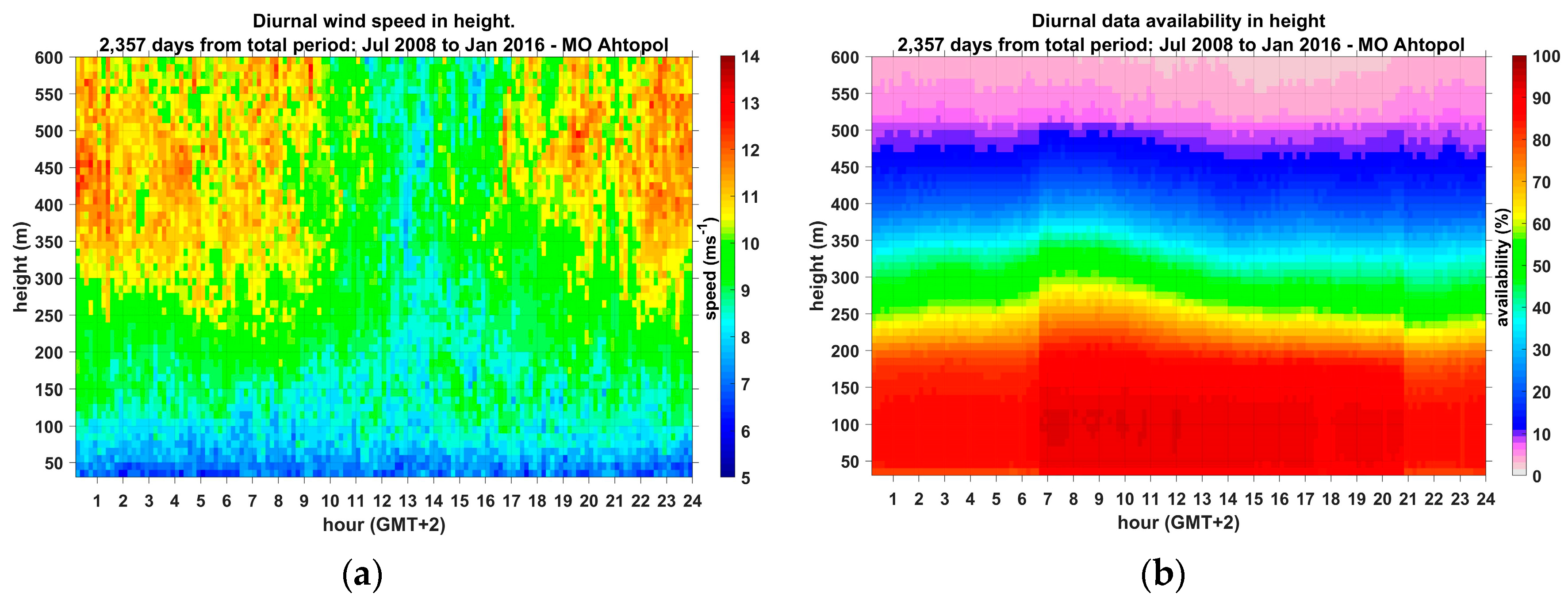
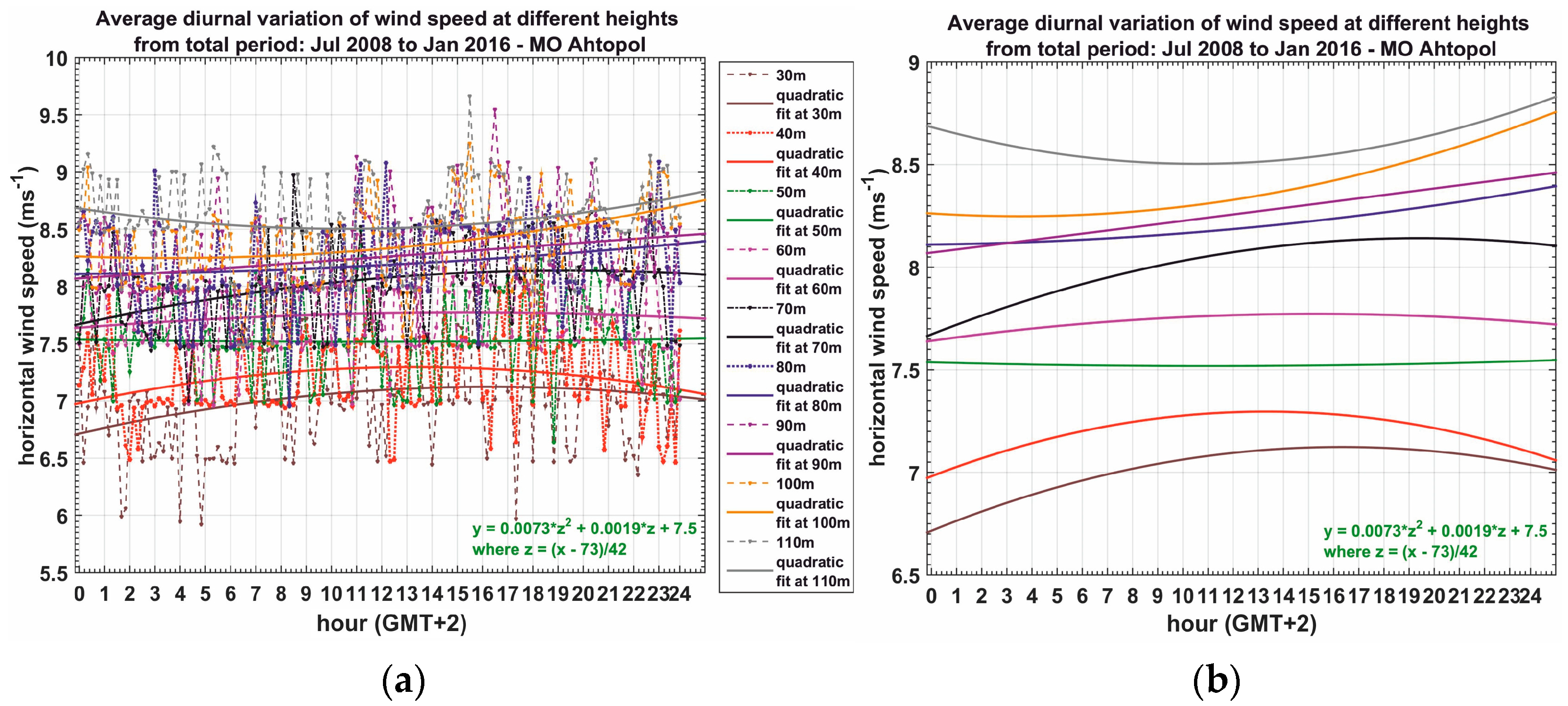
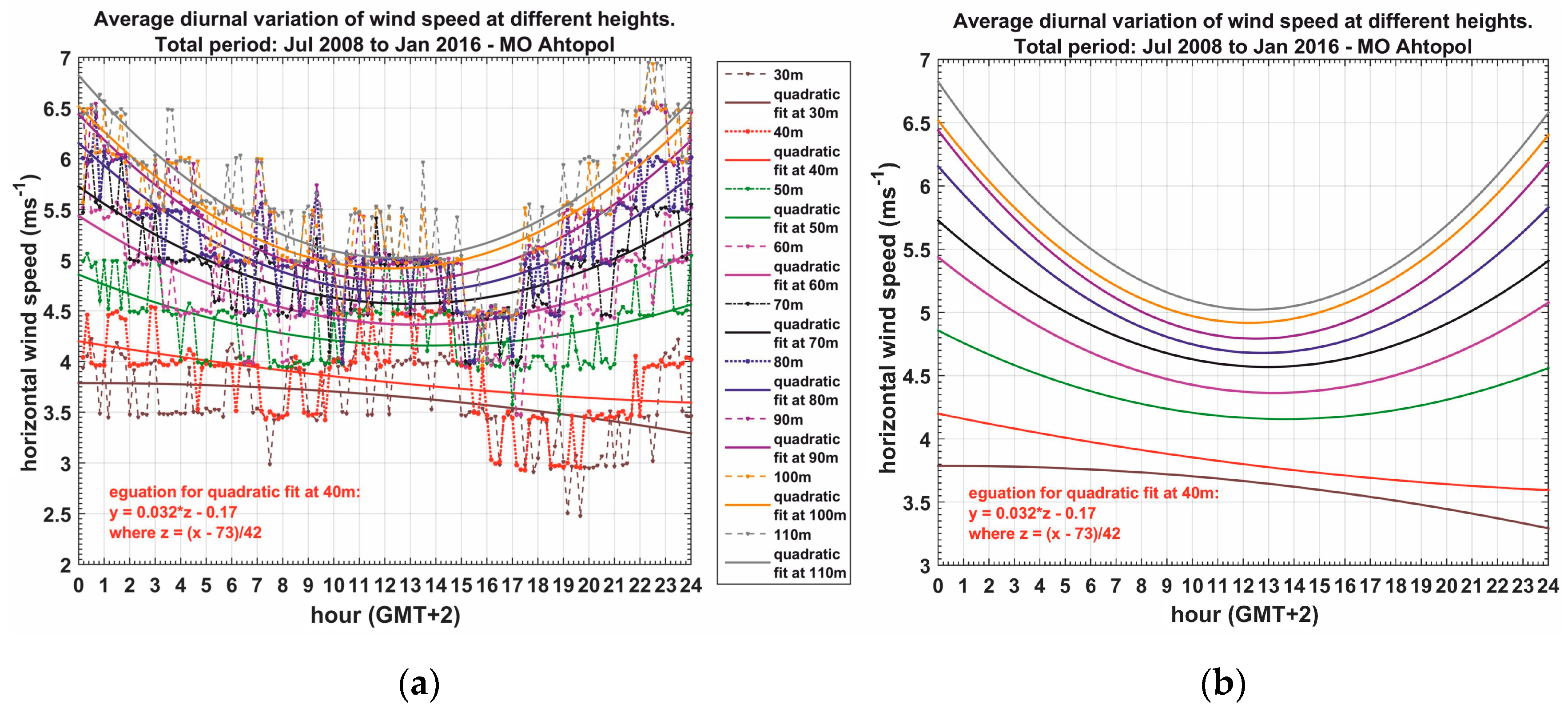
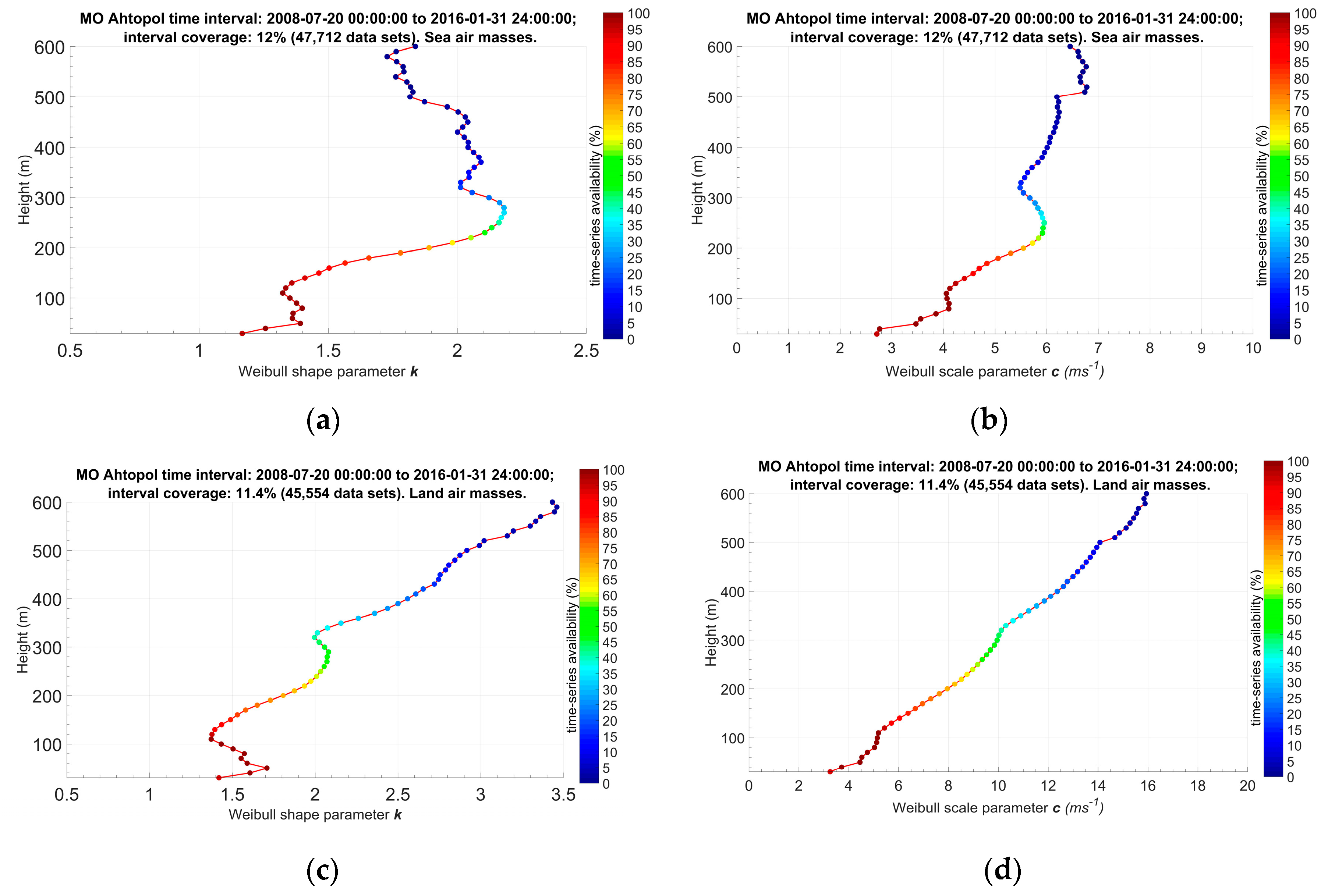
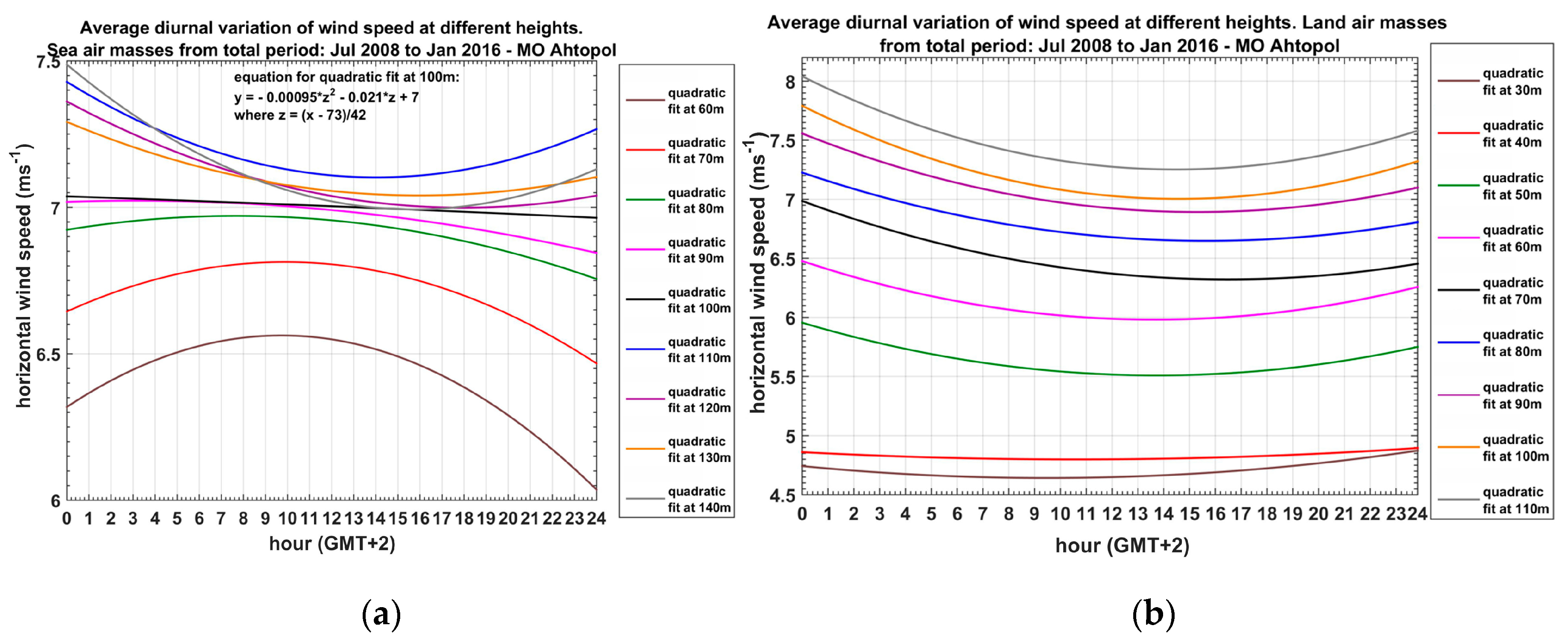
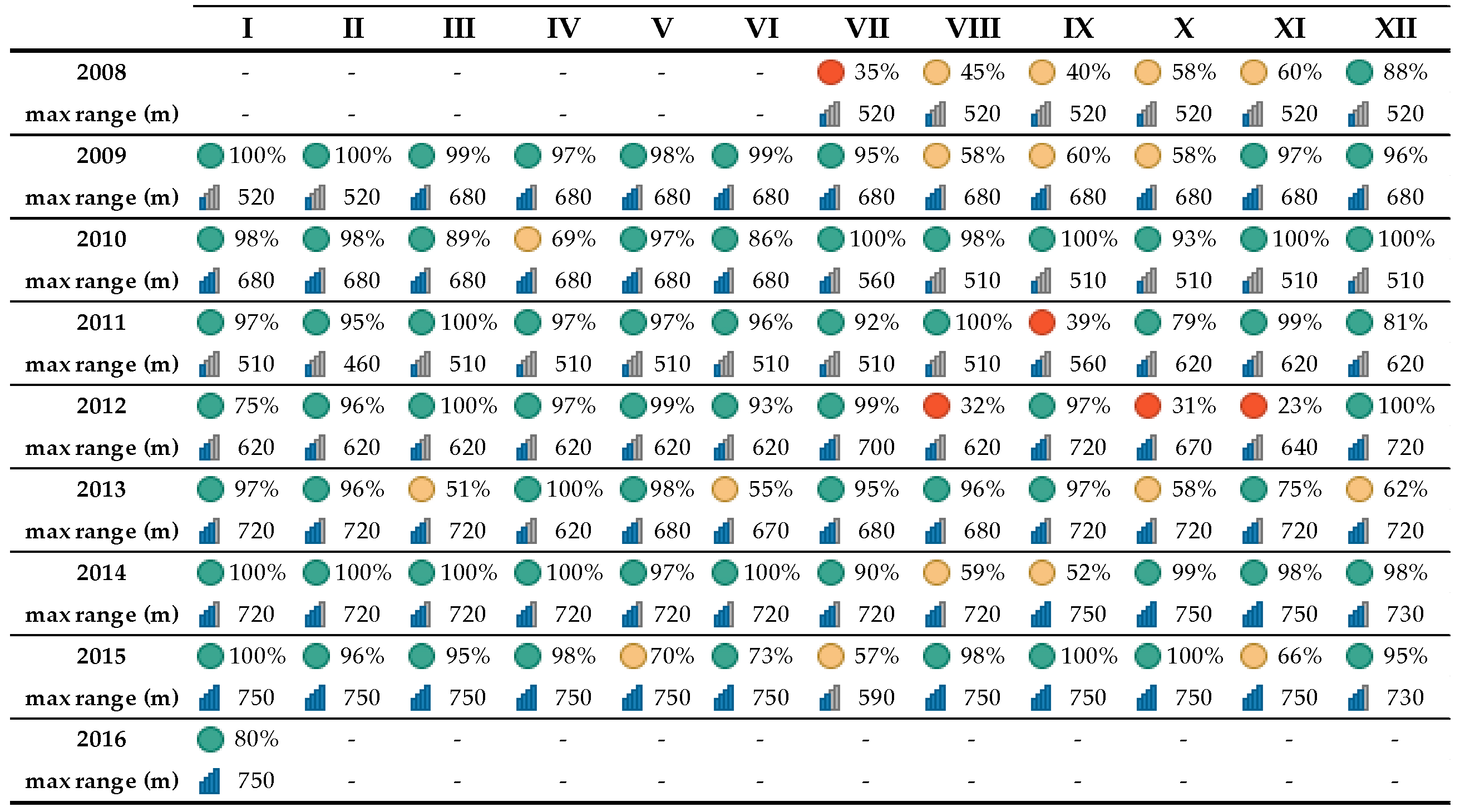
Characteristics of Data Samples, Meteorological Parameters and Profiles		Type of Air Masses (Column)/Jul 2008–Jan 2016/
		All Air Masses (1)	Marine Air Masses (2)	Land Air Masses (3)
Number of days with data		2357	821	561
Number of profiles involved in the study		327,009	47 712	45,554
Representation of the total period (%)		82.2	12	11.4
Height (m) with maximum in scale parameter profile of the Weibull distribution		50	80–90	50
		80	230–250	80
		270–300	520	290–300
			560
Height (m) with maximum in shape parameter profile of the Weibull distribution		50	50	50
		80	80	80
		260	270–280	270–290
		390–400	370	430
			450
			510
			550–560
Reversal height (m) of diurnal wind speed	inhomogeneous data	90	100	40
	homogeneous data	40

.

7. Future Work

The rich sodar data set will be used in future for various mesometeorological model evaluation studies, such as closed sea breeze cells, other specific cases of different interaction of local and synoptic driving forces, wind energy and air pollution assessments. The experience and ideas born from sodar measurements analysis will be explored with different types of ground-based remote sensing instruments at coastal and urban sites within international collaboration.