Mapping Nighttime and All-Day Radiative Cooling Potential in Europe and the Influence of Solar Reflectivity
Abstract
:1. Introduction
2. Methods
2.1. Data Acquisition
2.2. Radiative Cooling Calculation
2.3. Training and Test Datasets
2.4. Interpolation Kriging Model
2.5. Assessment Metrics of the Model
3. Results and Discussion
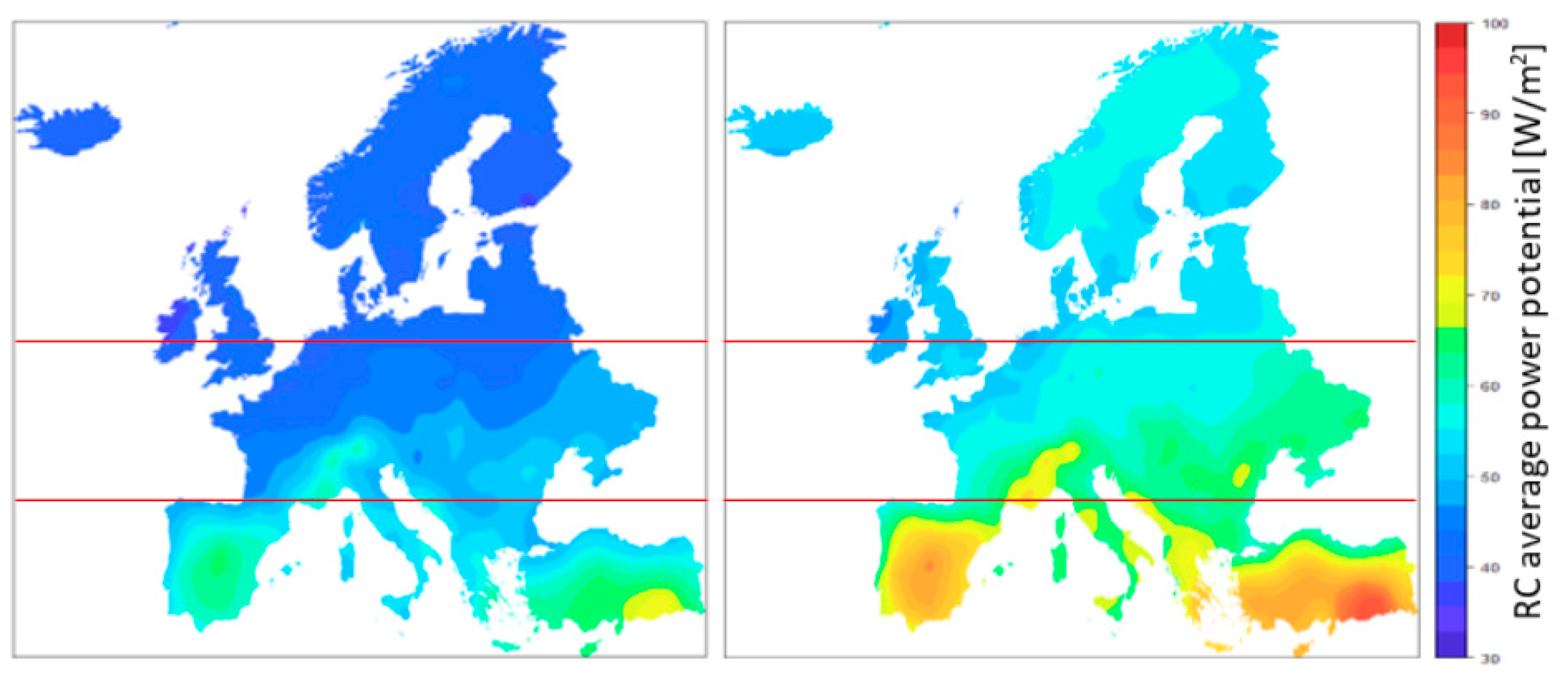
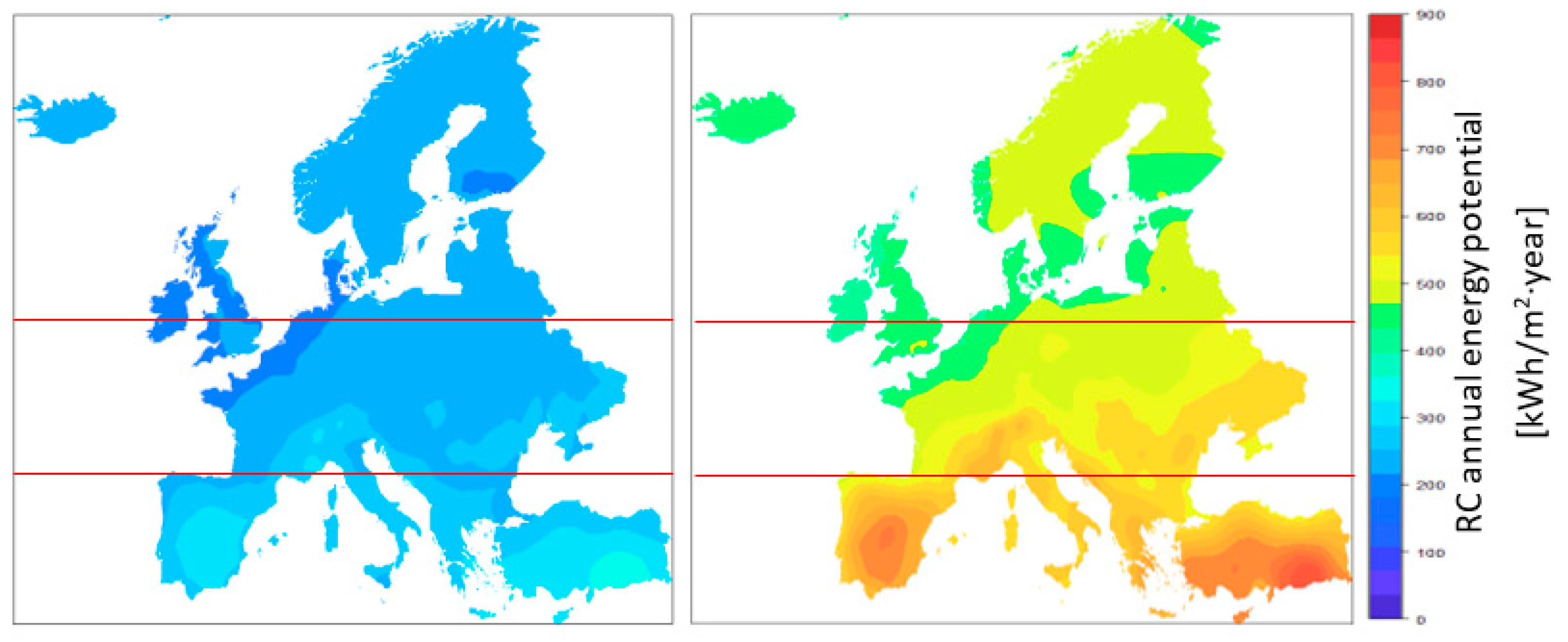
3.1. Nighttime and All-Day Comparison
3.2. Influence of the Solar Reflectivity on the Performance of a Radiative Surface
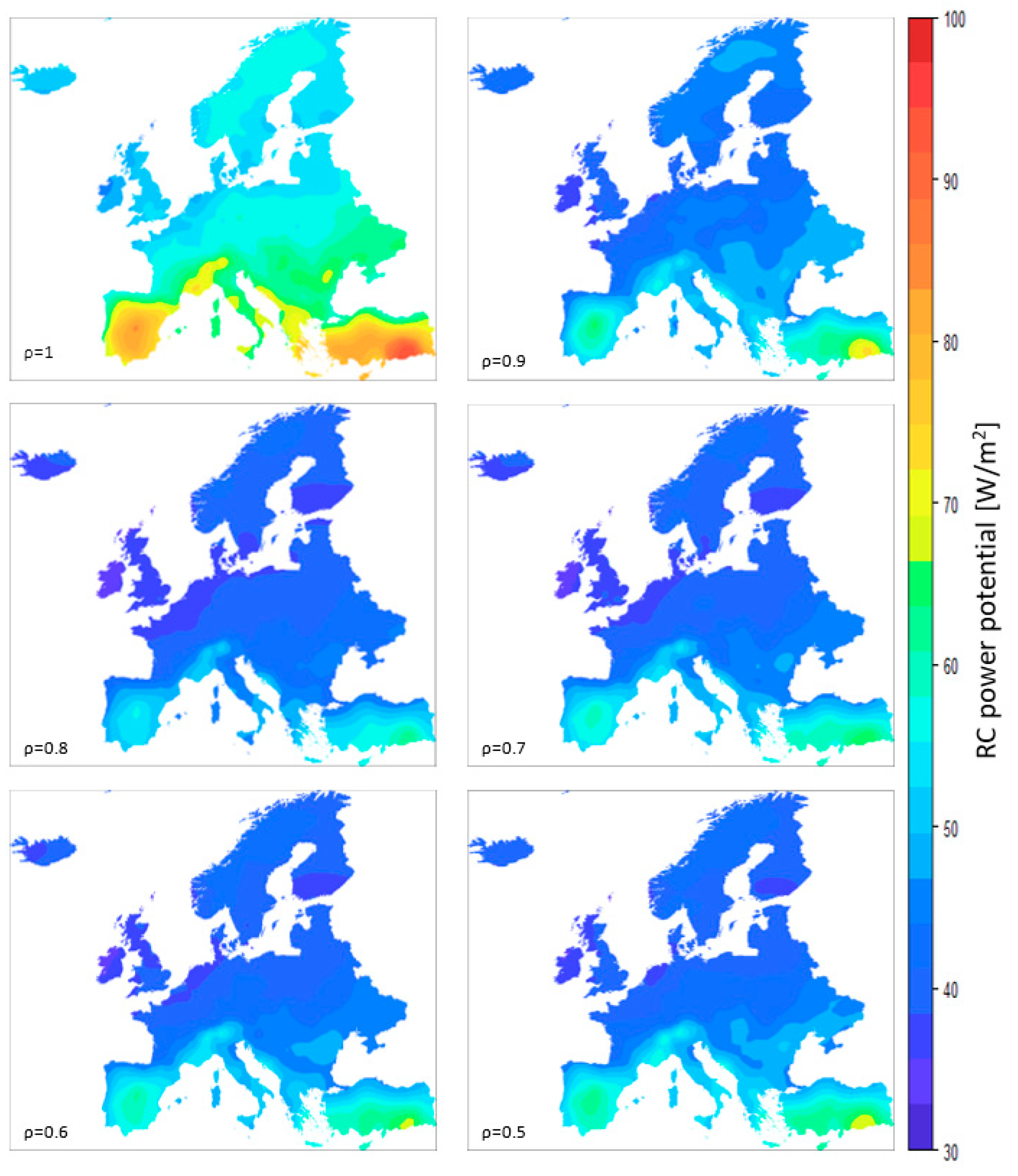
3.2.1. Average Power Potential
3.2.2. RC Activity
3.2.3. Annual Energy Potential
4. Conclusions
- Kriging is a good methodology to predict radiative cooling values from known climatological data. The models presented high values of R2 and low values of RMSE.
- With the implementation of new materials, all-day radiative cooling can be achieved. For solar reflectivity equal to 1, the shift from nocturnal to all-day radiative cooling can improve the average potential power from 47.30 to 60.17 W/m2, with peak values of 94.01 W/m2. The average annual energy increases from 245.76 to 559.47 kWh/m2·year.
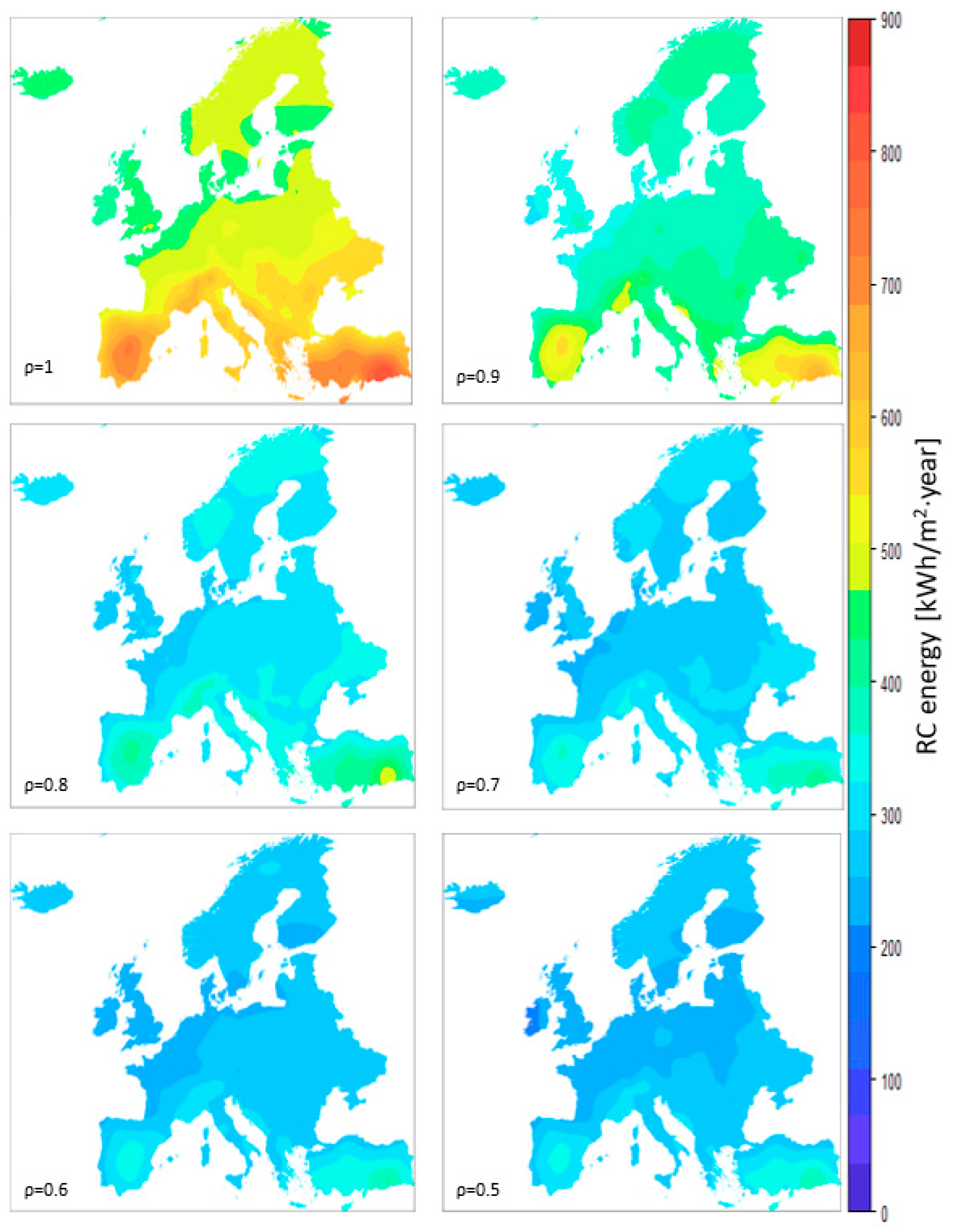
- The areas with the greatest potential of implementation are the regions of southern Europe. These regions present high values of power and energy potential.
- Compared to the other regions, the north holds more hours of available radiative cooling.
- The best performance, in all the three regions defined, is achieved when solar reflectivity is equal to one. In order to minimize the solar radiation absorbed by the surface, the reflectivity values in the solar range must be close to 1.
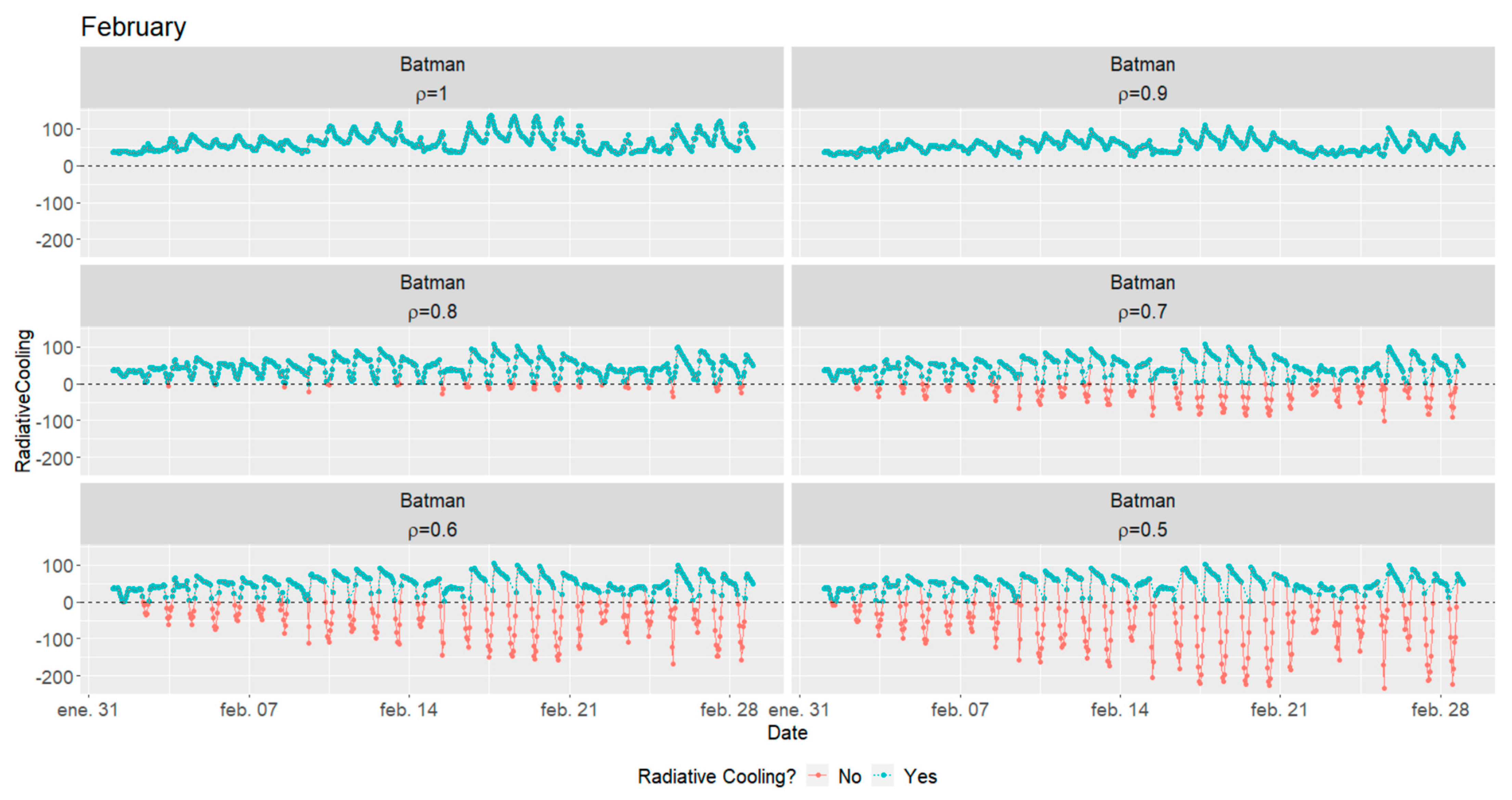
- For solar reflectivity values below 0.5, the behavior of the surface can be assimilated to a nighttime radiative cooler.
- Annual energy and RC activity decreases with reflectivity, while average power potential presents higher values in the 0.6–0.5 range for reflectivity, rather than in the 0.8–0.7 range. This is a result of calculating the average powers using only the observations where RC is achieved, and not for all the observations; for low solar reflectivity values, RC observations correspond mainly to nighttime values where high-power values are obtained. On the contrary, for solar reflectivity values between 0.8 and 0.7, the same nocturnal RC values are achieved, as well as a higher number of low-power daytime observations, thus reducing the average power. Finally, when the solar reflectivity is equal to 0.9, diurnal observations present higher powers, thus increasing the average power.
- For low values of solar reflectivity, maps tend to show homogeneous patterns.
- Small variations in solar reflectivity have greater impacts on the potential at higher reflectivity values than lower ones: in the range of 1–0.8, the reduction of average power potential is 29.19% and the annual energy is 38.83%.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bahadori, M.N. Passive Cooling Systems in Iranian Architecture. Sci. Am. 1978, 238, 144–155. [Google Scholar] [CrossRef]
- Johnson, T.E. Radiation Cooling of Structures with Infrared Transparent Wind Screens. Sol. Energy 1975, 17, 173–178. [Google Scholar] [CrossRef]
- Catalanotti, S.; Cuomo, V.; Piro, G.; Ruggi, D.; Silvestrini, V.; Troise, G. The Radiative Cooling of Selective Surfaces. Sol. Energy 1975, 17, 83–89. [Google Scholar] [CrossRef]
- Vall, S.; Johannes, K.; David, D.; Castell, A. A New Flat-Plate Radiative Cooling and Solar Collector Numerical Model: Evaluation and Metamodeling. Energy 2020, 202, 117750. [Google Scholar] [CrossRef]
- Sodha, M.S.; Singh, U.; Tiwari, G.N. A Thermal Model of a Roof Pond System with Moveable Insulation for Heating a Building. Build. Environ. 1982, 17, 135–144. [Google Scholar] [CrossRef]
- Raman, A.P.; Anoma, M.A.; Zhu, L.; Rephaeli, E.; Fan, S. Passive Radiative Cooling below Ambient Air Temperature under Direct Sunlight. Nature 2014, 515, 540–544. [Google Scholar] [CrossRef]
- Cunha, N.F.; AL-Rjoub, A.; Rebouta, L.; Vieira, L.G.; Lanceros-Mendez, S. Multilayer Passive Radiative Selective Cooling Coating Based on Al/SiO2/SiNx/SiO2/TiO2/SiO2 Prepared by Dc Magnetron Sputtering. Thin Solid Film. 2020, 694, 137736. [Google Scholar] [CrossRef]
- Kecebas, M.A.; Menguc, M.P.; Kosar, A.; Sendur, K. Passive Radiative Cooling Design with Broadband Optical Thin-Film Filters. J. Quant. Spectrosc. Radiat. Transf. 2017, 198, 179–186. [Google Scholar] [CrossRef]
- Mandal, J.; Fu, Y.; Overvig, A.C.; Jia, M.; Sun, K.; Shi, N.N.; Zhou, H.; Xiao, X.; Yu, N.; Yang, Y. Hierarchically Porous Polymer Coatings for Highly Efficient Passive Daytime Radiative Cooling. Science 2018, 362, 315–319. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Peng, L.; Liu, D.; Cheng, H. Design and Fabrication of the Ultrathin Metallic Film Based Infrared Selective Radiator. Sol. Energy Mater. Sol. Cells 2019, 193, 7–12. [Google Scholar] [CrossRef]
- Zhang, J.; Zhou, Z.; Quan, J.; Zhang, D.; Sui, J.; Yu, J.; Liu, J. A Flexible Film to Block Solar Radiation for Daytime Radiative Cooling. Sol. Energy Mater. Sol. Cells 2021, 225, 111029. [Google Scholar] [CrossRef]
- Bao, H.; Yan, C.; Wang, B.; Fang, X.; Zhao, C.Y.; Ruan, X. Double-Layer Nanoparticle-Based Coatings for Efficient Terrestrial Radiative Cooling. Sol. Energy Mater. Sol. Cells 2017, 168, 78–84. [Google Scholar] [CrossRef]
- Hossain, M.M.; Jia, B.; Gu, M. A Metamaterial Emitter for Highly Efficient Radiative Cooling. Adv. Opt. Mater. 2015, 3, 1047–1051. [Google Scholar] [CrossRef]
- Zhai, Y.; Ma, Y.; David, S.N.; Zhao, D.; Lou, R.; Tan, G.; Yang, R.; Yin, X. Scalable-Manufactured Randomized Glass-Polymer Hybrid Metamaterial for Daytime Radiative Cooling. Science 2017, 355, 1062–1066. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cho, J.-W.; Lee, T.-I.; Kim, D.-S.; Park, K.-H.; Kim, Y.-S.; Kim, S.-K. Visible to Near-Infrared Thermal Radiation from Nanostructured Tungsten Anntennas. J. Opt. 2018, 20, 09LT01. [Google Scholar] [CrossRef]
- Wu, D.; Liu, C.; Xu, Z.; Liu, Y.; Yu, Z.; Yu, L.; Chen, L.; Li, R.; Ma, R.; Ye, H. The Design of Ultra-Broadband Selective near-Perfect Absorber Based on Photonic Structures to Achieve near-Ideal Daytime Radiative Cooling. Mater. Des. 2018, 139, 104–111. [Google Scholar] [CrossRef]
- Rephaeli, E.; Raman, A.; Fan, S. Ultrabroadband Photonic Structures to Achieve High-Performance Daytime Radiative Cooling. Nano Lett. 2013, 13, 1457–1461. [Google Scholar] [CrossRef]
- Zhu, L.; Raman, A.P.; Fan, S. Radiative Cooling of Solar Absorbers Using a Visibly Transparent Photonic Crystal Thermal Blackbody. Proc. Natl. Acad. Sci. USA 2015, 112, 12282–12287. [Google Scholar] [CrossRef] [Green Version]
- Gao, M.; Han, X.; Chen, F.; Zhou, W.; Liu, P.; Shan, Y.; Chen, Y.; Li, J.; Zhang, R.; Wang, S.; et al. Approach to Fabricating High-Performance Cooler with near-Ideal Emissive Spectrum for above-Ambient Air Temperature Radiative Cooling. Sol. Energy Mater. Sol. Cells 2019, 200, 110013. [Google Scholar] [CrossRef]
- Vall, S.; Castell, A.; Medrano, M. Energy Savings Potential of a Novel Radiative Cooling and Solar Thermal Collection Concept in Buildings for Various World Climates. Energy Technol. 2018, 6, 2200–2209. [Google Scholar] [CrossRef]
- Feng, J.; Santamouris, M.; Shah, K.W.; Ranzi, G. Thermal Analysis in Daytime Radiative Cooling. IOP Conf. Ser. Mater. Sci. Eng. 2019, 609, 072064. [Google Scholar] [CrossRef]
- Bijarniya, J.P.; Sarkar, J.; Maiti, P. Environmental Effect on the Performance of Passive Daytime Photonic Radiative Cooling and Building Energy-Saving Potential. J. Clean. Prod. 2020, 274, 123119. [Google Scholar] [CrossRef]
- Carlosena, L.; Ruiz-Pardo, Á.; Feng, J.; Irulegi, O.; Hernández-Minguillón, R.J.; Santamouris, M. On the Energy Potential of Daytime Radiative Cooling for Urban Heat Island Mitigation. Sol. Energy 2020, 208, 430–444. [Google Scholar] [CrossRef]
- Argiriou, A.; Santamouris, M.; Balaras, C.; Jeter, S. Potential of Radiative Cooling in Southern Europe. Int. J. Sol. Energy 1992, 13, 189–203. [Google Scholar] [CrossRef]
- Chang, K.; Zhang, Q. Modeling of Downward Longwave Radiation and Radiative Cooling Potential in China. J. Renew. Sustain. Energy 2019, 11, 066501. [Google Scholar] [CrossRef]
- Li, M.; Peterson, H.B.; Coimbra, C.F.M. Radiative Cooling Resource Maps for the Contiguous United States. J. Renew. Sustain. Energy 2019, 11, 036501. [Google Scholar] [CrossRef]
- Aubinet, M. Longwave Sky Radiation Parametrizations. Sol. Energy 1994, 53, 147–154. [Google Scholar] [CrossRef]
- Hengl, T. A Practical Guide to Geostatistical Mapping. 2019, p. 15. Available online: http://spatial-analyst.net/book/system/files/Hengl_2009_GEOSTATe2c1w.pdf (accessed on 19 August 2021).

| RC Power (Nighttime) | RC Power (All-Day) | ||||||
|---|---|---|---|---|---|---|---|
| Latitude Range | min (W/m2) | avg (W/m2) | max (W/m2) | min (W/m2) | avg (W/m2) | max (W/m2) | |
| Center | 43.46 N–53.55 N | 37.95 | 46.48 | 60.11 | 46.43 | 58.69 | 73.08 |
| North | 53.55 N–71.15 N | 35.14 | 41.51 | 45.31 | 43.82 | 53.77 | 57.81 |
| South | 34.60 N–43.46 N | 46.67 | 57.36 | 71.34 | 56.36 | 72.33 | 94.01 |
| Europe | 34.60 N–71.15 N | 35.14 | 47.30 | 71.34 | 43.82 | 60.17 | 94.01 |
| Energy (Nighttime) | Energy (All-Day) | ||||||
|---|---|---|---|---|---|---|---|
| Latitude Range | min (kWh/m2·Year) | avg (kWh/m2·Year) | max (kWh/m2·Year) | min (kWh/m2·Year) | avg (kWh/m2·Year) | max (kWh/m2·Year) | |
| Center | 43.46 N–53.55 N | 194.22 | 238.00 | 296.31 | 406.74 | 545.83 | 639.71 |
| North | 53.55 N–71.15 N | 194.15 | 229.99 | 250.19 | 384.08 | 485.70 | 506.40 |
| South | 34.60 N–43.46 N | 231.12 | 283.07 | 352.59 | 493.88 | 688.64 | 822.66 |
| Europe | 34.60 N–71.15 N | 194.15 | 245.76 | 352.59 | 384.08 | 559.47 | 822.66 |
| Power | Energy | |||
|---|---|---|---|---|
| Nocturnal | All-Day | Nocturnal | All-Day | |
| RMSE | 2.28 (W/m2) | 2.46 (W/m2) | 12.38 (kWh/m2·year) | 21.58 (kWh/m2·year) |
| R2 | 0.89 (-) | 0.91 (-) | 0.83 (-) | 0.91 (-) |
| Solar Reflectivity | ||||||||
|---|---|---|---|---|---|---|---|---|
| Latitude Range | 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | ||
| Center | 43.46 N–53.55 N | min | 46.43 | 36.31 | 34.20 | 34.65 | 35.09 | 35.82 |
| avg | 58.69 | 45.27 | 41.31 | 42.40 | 43.34 | 44.12 | ||
| max | 73.08 | 56.17 | 51.62 | 53.81 | 55.98 | 57.87 | ||
| North | 53.55 N–71.15 N | min | 43.82 | 35.70 | 33.78 | 33.55 | 33.88 | 34.09 |
| avg | 53.77 | 43.76 | 39.31 | 39.59 | 39.95 | 40.23 | ||
| max | 57.81 | 48.00 | 42.19 | 42.25 | 42.90 | 43.38 | ||
| South | 34.60 N–43.46 N | min | 56.36 | 42.23 | 40.80 | 42.43 | 43.67 | 44.41 |
| avg | 72.33 | 54.33 | 49.84 | 52.51 | 53.72 | 55.05 | ||
| max | 94.01 | 72.76 | 62.24 | 66.05 | 67.16 | 69.14 | ||
| Europe | 34.60 N–71.15 N | min | 43.82 | 35.70 | 33.76 | 33.55 | 33.88 | 34.09 |
| avg | 60.18 | 46.87 | 42.61 | 43.79 | 44.59 | 45.32 | ||
| max | 94.01 | 72.56 | 62.34 | 66.05 | 67.16 | 69.14 | ||
| Reflectivity | R2 (-) | RMSE (W/m2) |
|---|---|---|
| 1 | 0.91 | 2.46 |
| 0.9 | 0.84 | 2.40 |
| 0.8 | 0.87 | 1.90 |
| 0.7 | 0.87 | 2.16 |
| 0.6 | 0.90 | 2.02 |
| 0.5 | 0.88 | 2.32 |
| Solar Reflectivity | ||||||||
|---|---|---|---|---|---|---|---|---|
| Latitude Range | 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | ||
| Center | 43.46 N–53.55 N | min | 100 | 100 | 79.04 | 68.52 | 63.76 | 61.29 |
| avg | 100 | 99.89 | 85.68 | 74.93 | 69.42 | 65.93 | ||
| max | 100 | 98.55 | 89.41 | 78.36 | 73.07 | 69.55 | ||
| North | 53.55 N–71.15 N | min | 100 | 99.72 | 84.34 | 76.60 | 70.87 | 67.07 |
| avg | 100 | 99.96 | 90.42 | 80.53 | 75.21 | 71.66 | ||
| max | 100 | 99.99 | 94.48 | 84.12 | 78.33 | 74.53 | ||
| South | 34.60 N–43.46 N | min | 100 | 99.03 | 72.35 | 64.03 | 60.55 | 58.43 |
| avg | 100 | 99.78 | 82.50 | 70.25 | 65.08 | 62.07 | ||
| max | 100 | 99.96 | 90.32 | 73.37 | 67.73 | 64.50 | ||
| Europe | 34.60 N–71.15 N | min | 100 | 98.55 | 72.35 | 64.03 | 60.55 | 58.43 |
| avg | 100 | 99.89 | 86.58 | 75.78 | 70.41 | 67.07 | ||
| max | 100 | 100 | 94.48 | 84.12 | 78.33 | 74.53 | ||
| Reflectivity | R2 (-) | RMSE (-) |
|---|---|---|
| 0.9 | 0.25 | 0.19 |
| 0.8 | 0.84 | 1.49 |
| 0.7 | 0.87 | 1.43 |
| 0.6 | 0.88 | 1.24 |
| 0.5 | 0.91 | 1.05 |
| Solar Reflectivity | ||||||||
|---|---|---|---|---|---|---|---|---|
| latitude Range | 1 | 0.9 | 0.8 | 0.7 | 0.6 | 0.5 | ||
| Center | 43.46 N–53.55 N | min | 406.74 | 312.63 | 254.79 | 228.15 | 220.30 | 213.05 |
| avg | 514.16 | 396.23 | 309.89 | 278.54 | 263.55 | 254.74 | ||
| max | 639.71 | 493.03 | 378.74 | 333.92 | 322.46 | 317.90 | ||
| North | 53.55 N–71.15 N | min | 384.08 | 313.42 | 258.55 | 232.97 | 221.06 | 213.08 |
| avg | 470.99 | 383.47 | 311.62 | 280.07 | 264.03 | 253.50 | ||
| max | 506.40 | 422.26 | 346.71 | 309.46 | 291.11 | 278.34 | ||
| South | 34.60 N–43.46 N | min | 493.88 | 368.86 | 281.38 | 266.07 | 246.96 | 240.26 |
| avg | 633.56 | 475.55 | 360.98 | 323.36 | 306.98 | 299.93 | ||
| max | 822.66 | 642.35 | 492.60 | 413.61 | 397.85 | 388.09 | ||
| Europe | 34.60 N–71.15 N | min | 384.08 | 312.63 | 254.79 | 228.15 | 220.30 | 213.05 |
| avg | 527.10 | 410.35 | 322.43 | 289.55 | 273.87 | 264.87 | ||
| max | 822.66 | 642.35 | 492.60 | 413.61 | 397.85 | 388.09 | ||
| Reflectivity | R2 (-) | RMSE (kWh/m2·year) |
|---|---|---|
| 1 | 0.91 | 21.58 |
| 0.9 | 0.83 | 21.34 |
| 0.8 | 0.81 | 16.24 |
| 0.7 | 0.74 | 16.04 |
| 0.6 | 0.81 | 13.30 |
| 0.5 | 0.78 | 13.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vilà, R.; Medrano, M.; Castell, A. Mapping Nighttime and All-Day Radiative Cooling Potential in Europe and the Influence of Solar Reflectivity. Atmosphere 2021, 12, 1119. https://doi.org/10.3390/atmos12091119
Vilà R, Medrano M, Castell A. Mapping Nighttime and All-Day Radiative Cooling Potential in Europe and the Influence of Solar Reflectivity. Atmosphere. 2021; 12(9):1119. https://doi.org/10.3390/atmos12091119
Chicago/Turabian StyleVilà, Roger, Marc Medrano, and Albert Castell. 2021. "Mapping Nighttime and All-Day Radiative Cooling Potential in Europe and the Influence of Solar Reflectivity" Atmosphere 12, no. 9: 1119. https://doi.org/10.3390/atmos12091119
APA StyleVilà, R., Medrano, M., & Castell, A. (2021). Mapping Nighttime and All-Day Radiative Cooling Potential in Europe and the Influence of Solar Reflectivity. Atmosphere, 12(9), 1119. https://doi.org/10.3390/atmos12091119







