An Empirical Atmospheric Density Calibration Model Based on Long Short-Term Memory Neural Network
Abstract
:1. Introduction
2. Data and Methods
2.1. NRLMSISE-00 Model
2.2. The “True” Density
2.3. LSTM Neural Network
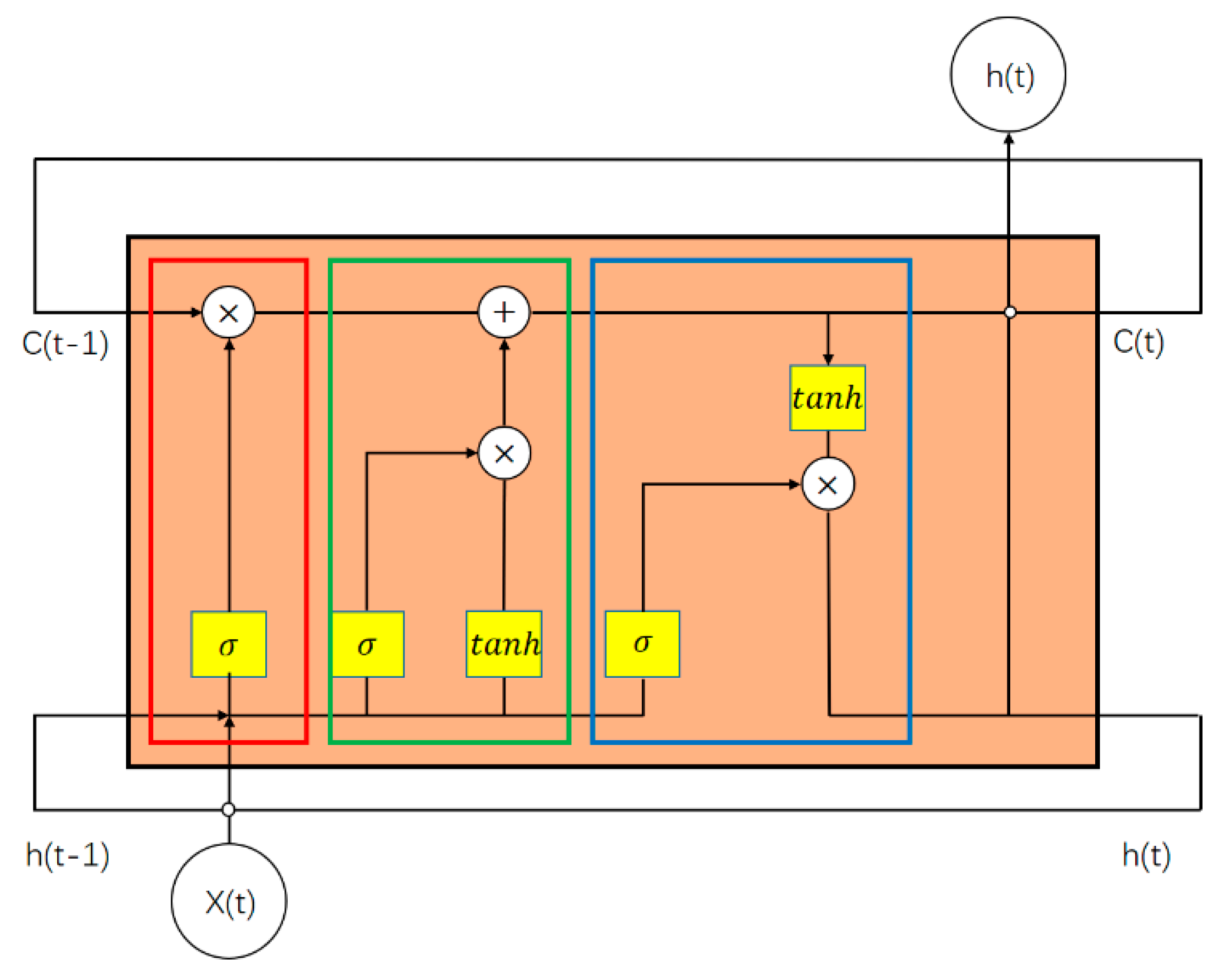
2.3.1. LSTM Cells
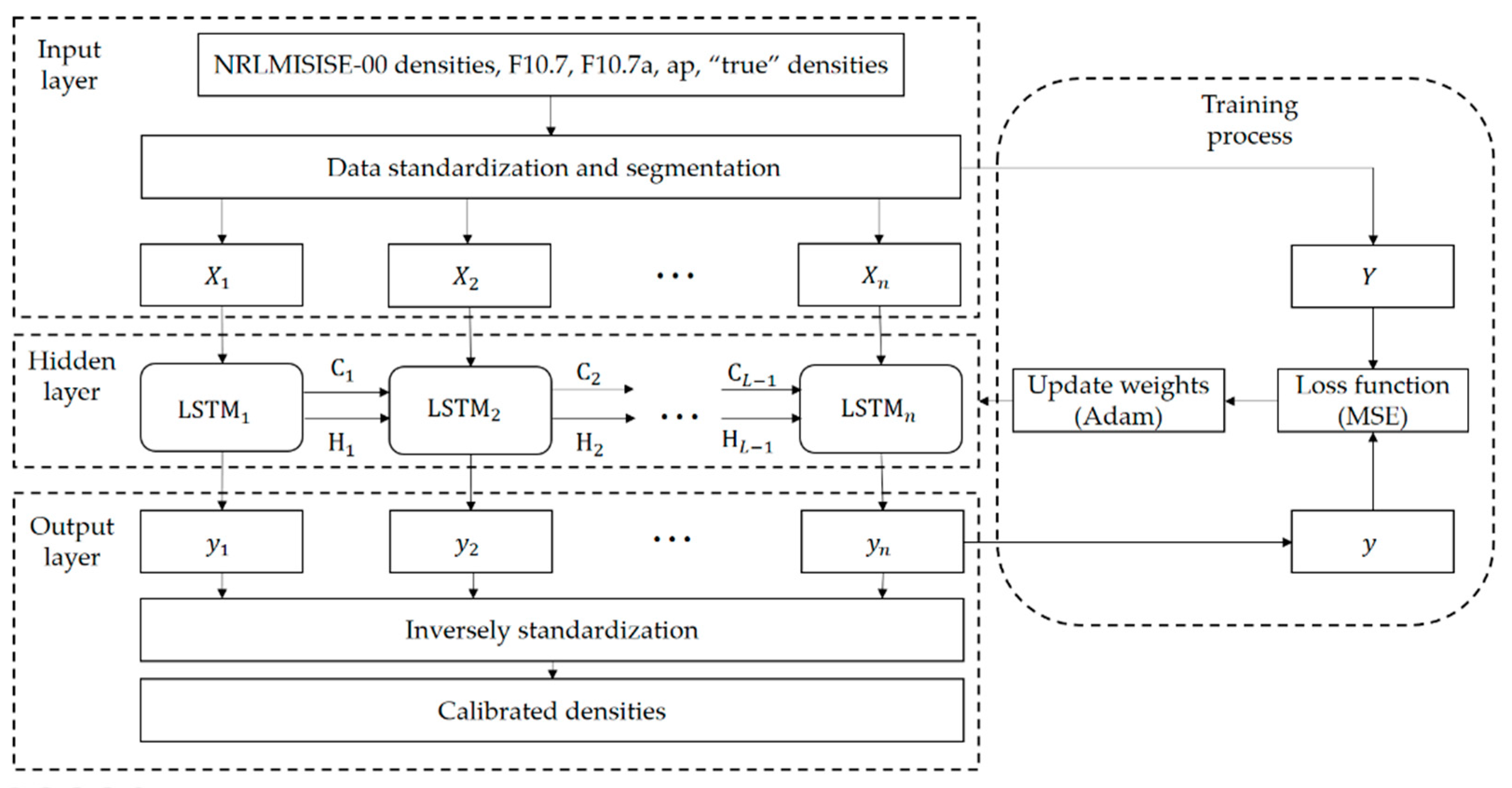
2.3.2. LSTM-NRL Model
2.4. Test Experiment Design
- Test 1: the purpose is to determine the time delay and sample rate. The time delay and the sample rate of the LSTM-NRL model are tuned. In the tuning, the data on 31 January 2007 is used as the test data. The parameter tuning results are presented in Section 3.1.
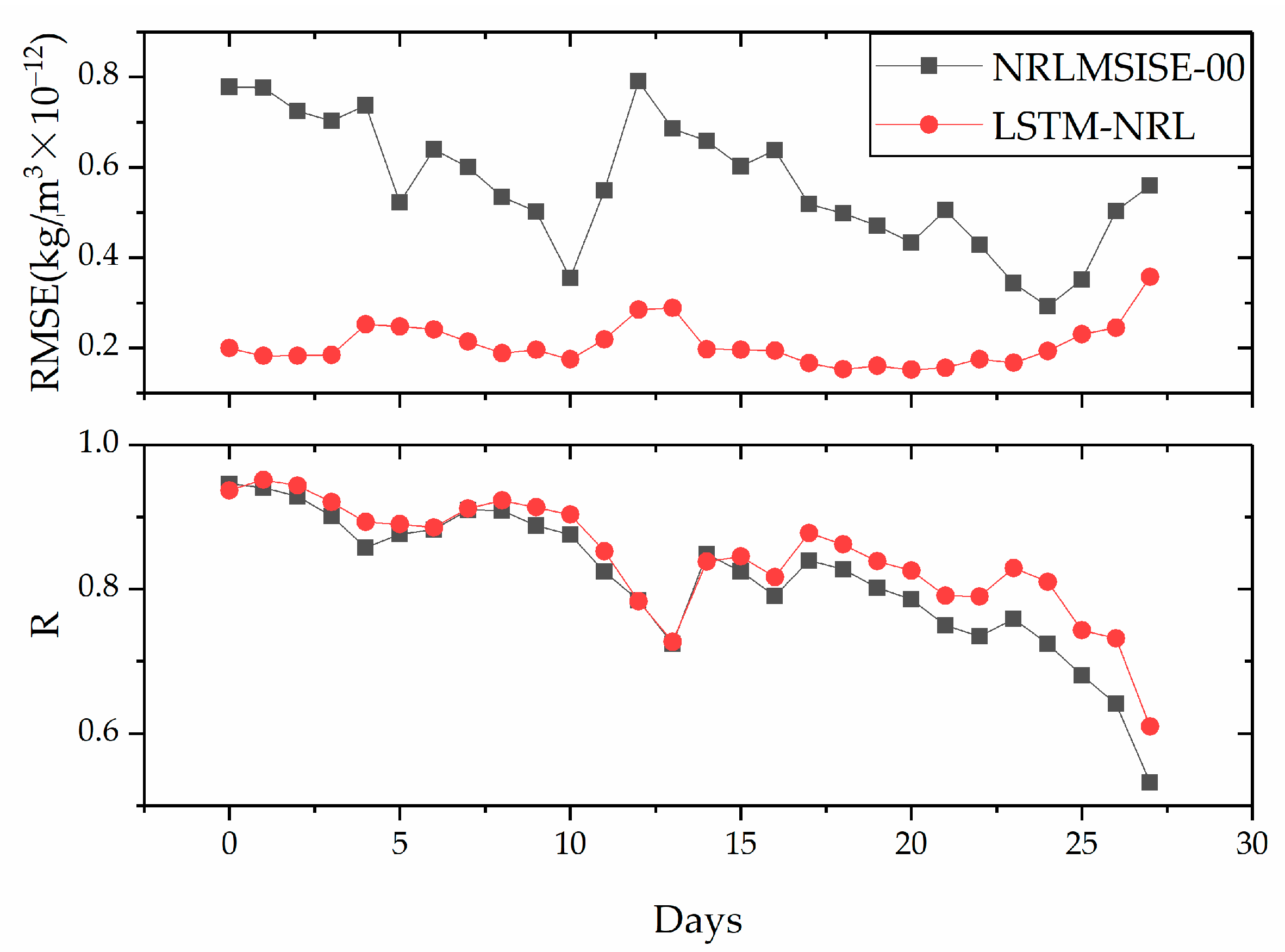
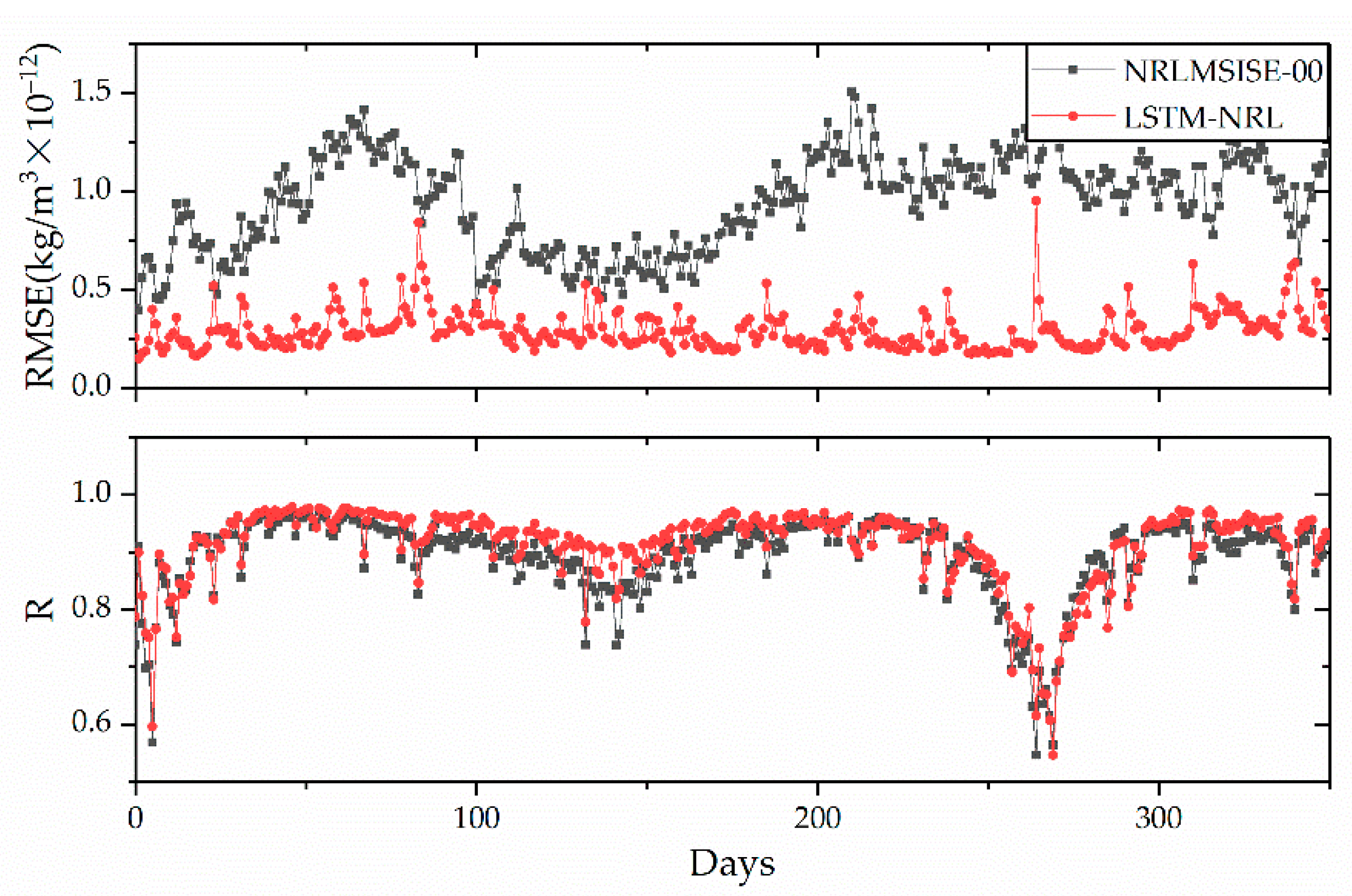
- Test 2 and Test 3: the purpose is to evaluate the performance of LSTM-NRL over different time spans after the training window. Test 2 uses the data sets in a month 1–28 February 2007 as test data, and Test 3 uses the data in a year from 1 March 2007 to 29 February 2008.
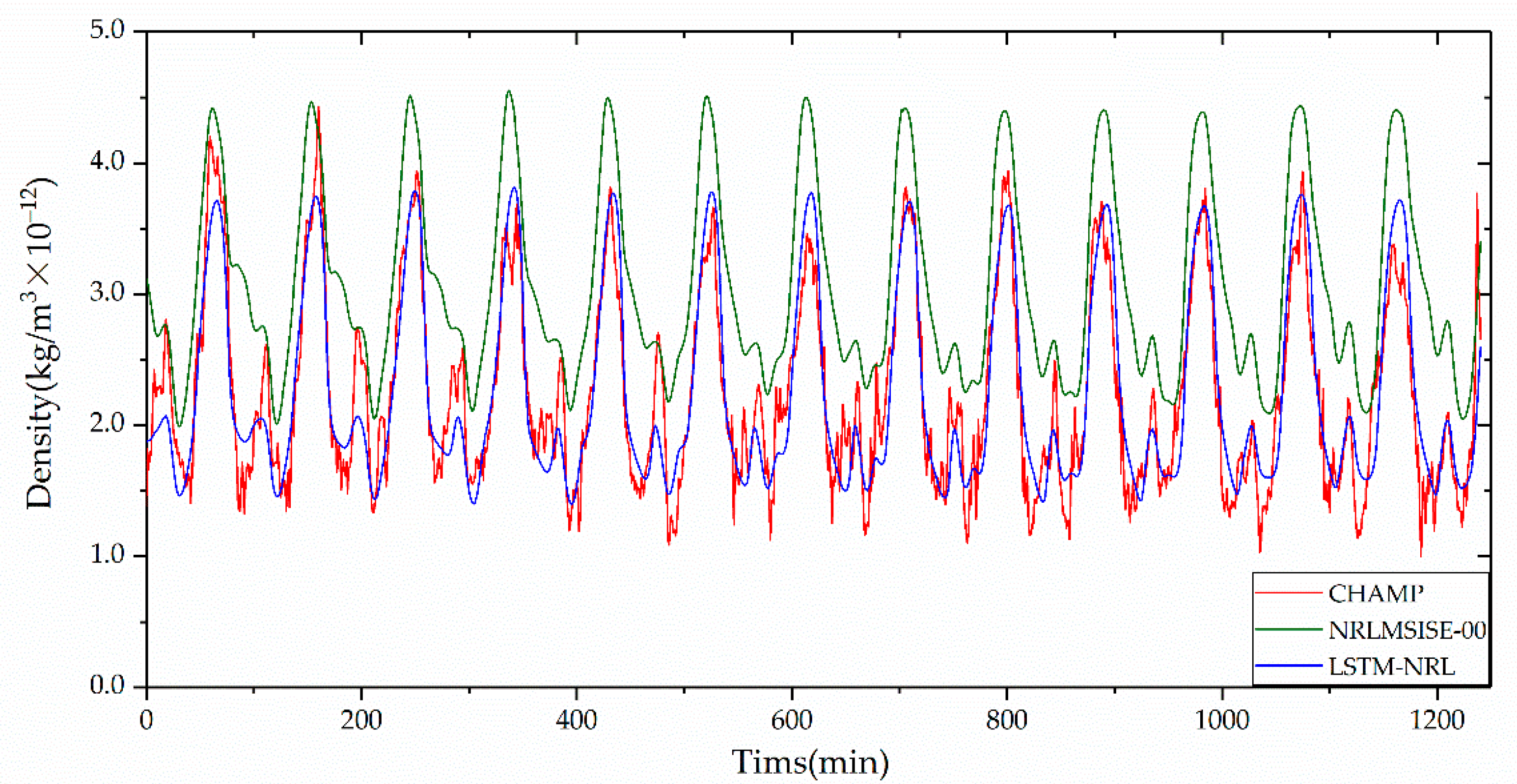
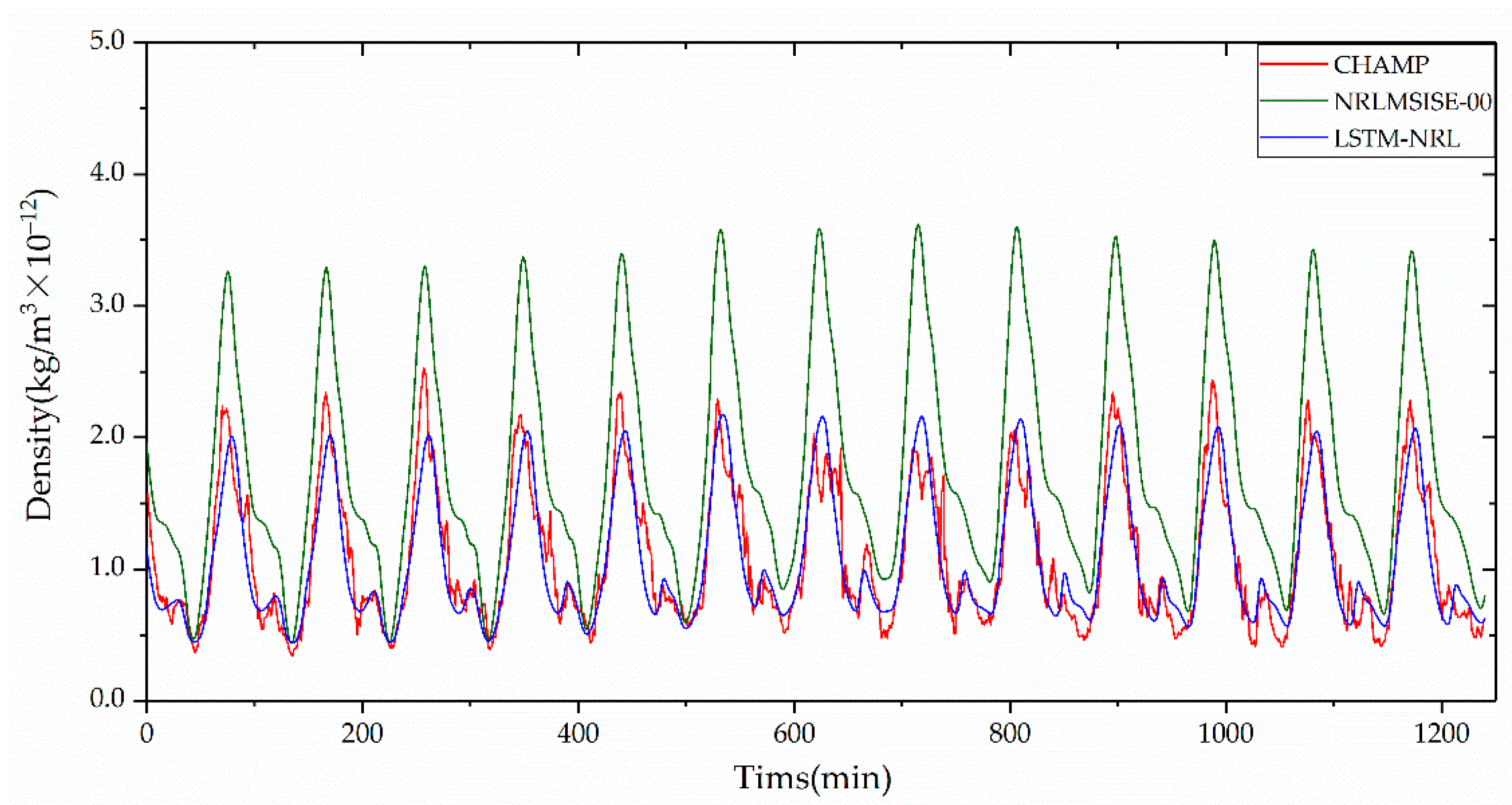
- Test 4 and Test 5: the purpose is to evaluate the performance of the LSTM-NRL model at different solar and geomagnetic activity level. Test 4 chooses 2 days, a day of high solar and geomagnetic activity on 30 January 2007 (day 30 of 2007) and a day of low solar and geomagnetic activity on 19 August 2007 (d231), as test sets to observe the performance of the LSTM-NRL model. It is noted that the 2 days in Test 4 are chosen to compare with the calibration performance of other researchers under typical high or low solar and geomagnetic activity [22,24]. To further verify the LSTM-NRL model performance during period of high or low solar and geomagnetic activity, Test 5 chooses other 3 days with high solar and geomagnetic activity (Test 5-high, day 118, 195, and 345 of 2007), and 3 days with low (Test 5-low, day 103, 204, and 322 of 2007) as test sets.
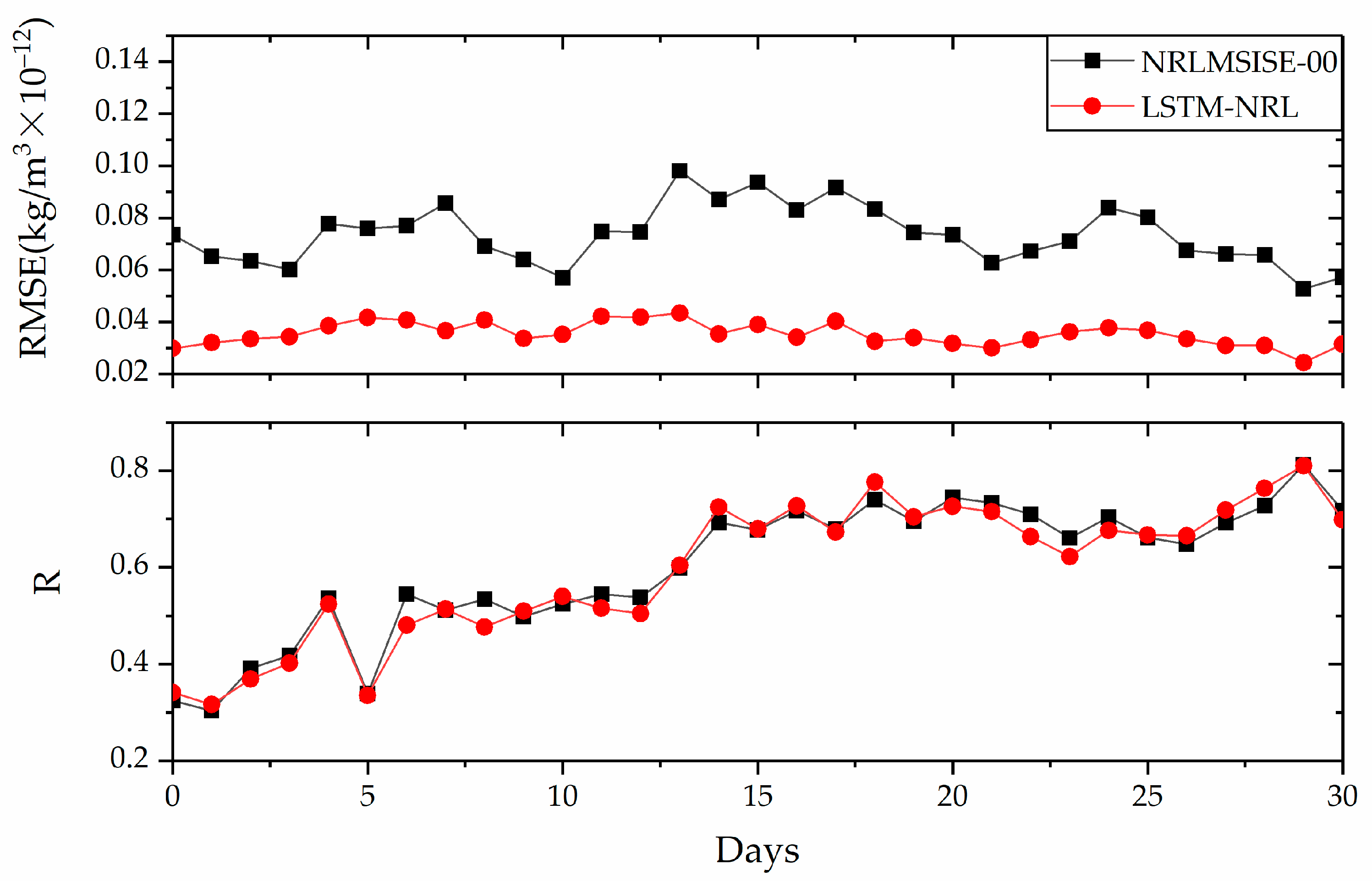
- Test 6: the purpose is to assess the LSTM-NRL’s performance over most of CHAMP satellite’s operation life. The data in 6 full years from 2003 to 2008 is chosen as test sets, during which the orbital altitude of the satellite has changed significantly.
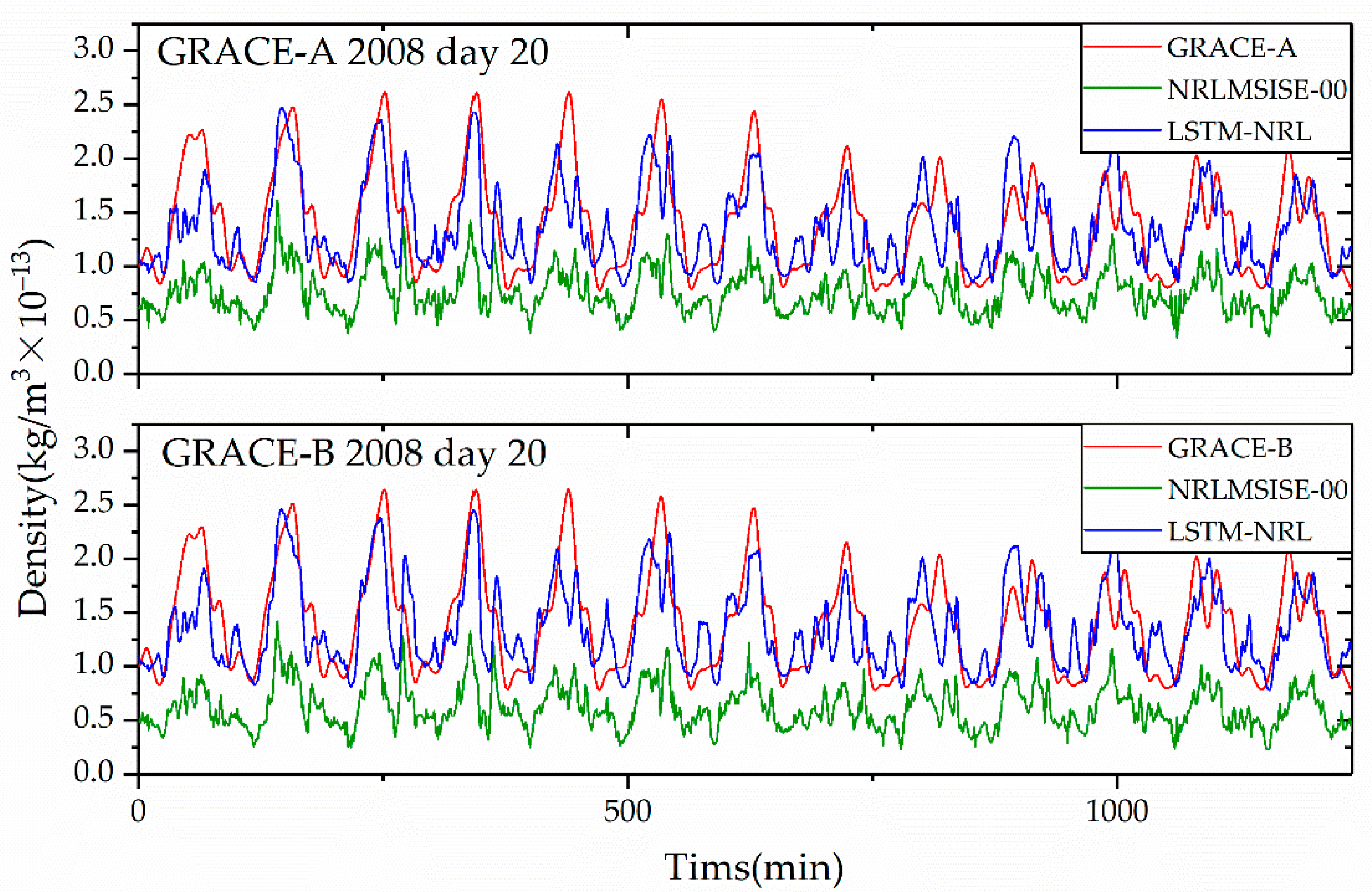
- Test 7: the purpose is to demonstrate the transferring performance of the LSTM-NRL model trained using the CHAMP data. Test 7 takes the density along the orbits of two GRACE satellites as test sets.
- Test 8: the purpose is to present the effect of the LSTM-NRL model on the orbital propagation accuracy.
2.5. Model Performance Evaluation
3. Results
3.1. Determination of the Time Delay and Sample Rate
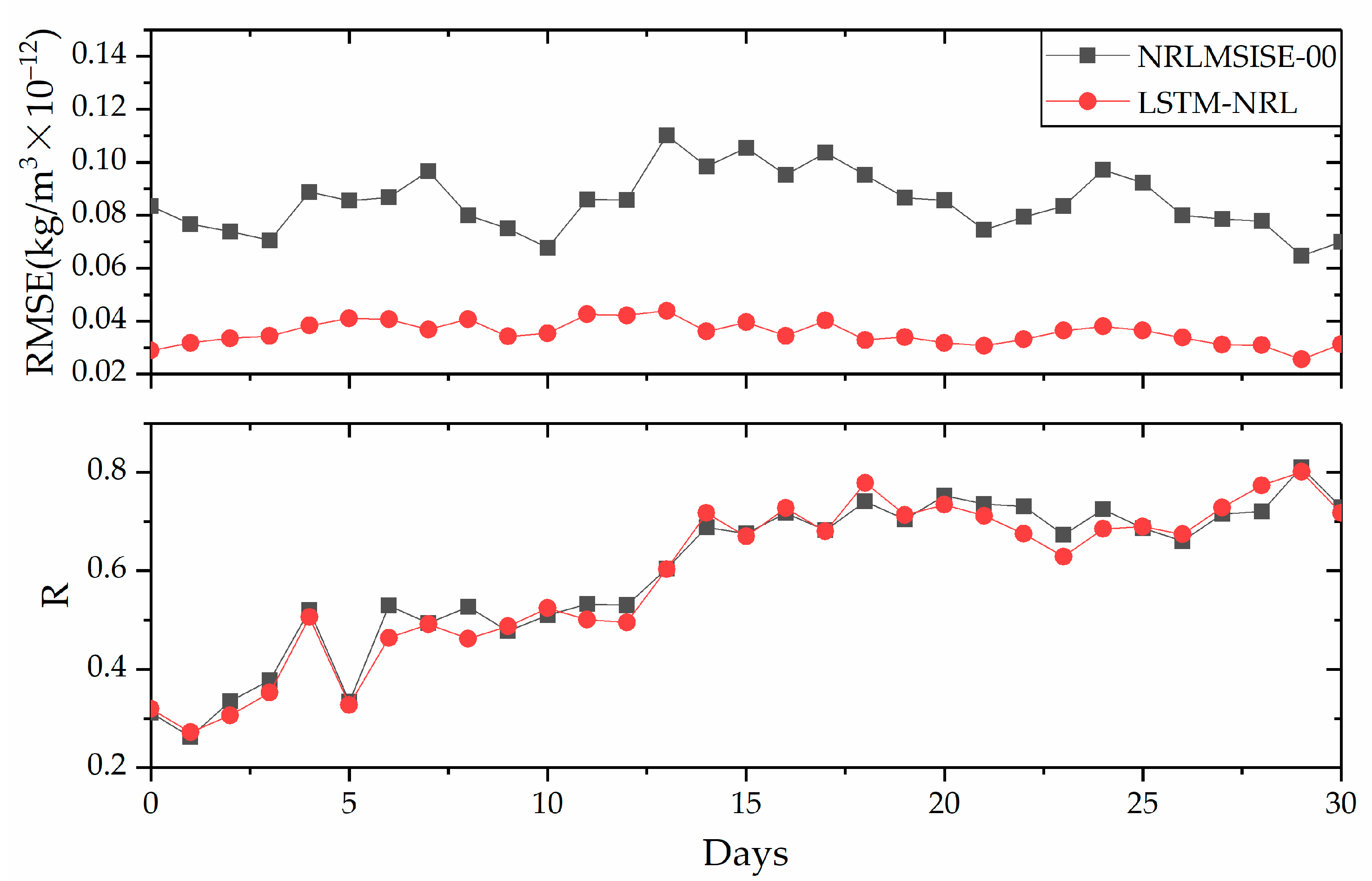
3.2. Extrapolation Performance of the LSTM-NRL over Long Time Span
3.3. Performance of the LSTM-NRL on Days of High and Low Solar and Geomagnetic Activity
3.4. Performance of the LSTM-NRL over the CHAMP Operational Life
3.5. Transferring Ability of the LSTM-NRL
3.6. Applying Calibrated Density to the Orbital Propagation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Montenbruck, O.; Gill, E.; Lutze, F. Satellite orbits: Models, methods, and applications. Appl. Mech. Rev. 2002, 55, B27–B28. [Google Scholar] [CrossRef]
- Prieto, D.M.; Graziano, B.P.; Roberts, P.C.E. Spacecraft drag modelling. Prog. Aerosp. Sci. 2014, 64, 56–65. [Google Scholar] [CrossRef] [Green Version]
- Qian, L.; Burns, A.G.; Emery, B.A.; Foster, B.; Lu, G.; Maute, A.; Richmond, A.D.; Roble, R.G.; Solomon, S.C.; Wang, W. The NCAR TIE-GCM: A community model of the coupled thermosphere/ionosphere system. Model. Ionos. Thermosphere Syst. 2014, 201, 73–83. [Google Scholar]
- Richmond, A.D.; Ridley, E.C.; Roble, R.G. A Thermosphere/ionosphere general-circulation model with coupled electrodynamics. Geophys. Res. Lett. 1992, 19, 601–604. [Google Scholar] [CrossRef]
- Ridley, A.; Deng, Y.; Toth, G. The global ionosphere—Thermosphere model. J. Atmos. Sol. Terr. Phys. 2006, 68, 839–864. [Google Scholar] [CrossRef]
- Emmert, J.T. Thermospheric mass density: A review. Adv. Space Res. 2015, 56, 773–824. [Google Scholar] [CrossRef]
- Chen, J.; Sang, J. Thermospheric mass density measurement from precise orbit ephemeris. Geod. Geodyn. 2016, 7, 210–215. [Google Scholar] [CrossRef] [Green Version]
- Deng, Y.; Ridley, A.J. Possible reasons for underestimating Joule heating in global models: E field variability, spatial resolution, and vertical velocity. J. Geophys. Res. Space Phys. 2007, 112. [Google Scholar] [CrossRef] [Green Version]
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSISE-00 empirical model of the atmosphere: Statistical comparisons and scientific issues. J. Geophys. Res. Space Phys. 2002, 107, 1468–1483. [Google Scholar] [CrossRef]
- Bowman, B.; Tobiska, W.K.; Marcos, F.; Huang, C.; Lin, C.; Burke, W. A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar]
- Bruinsma, S. The DTM-2013 thermosphere model. J. Space Weather Space Clim. 2015, 5, A1. [Google Scholar] [CrossRef] [Green Version]
- Marcos, F.A.; Kendra, M.J.; Griffin, J.M.; Bass, J.N.; Larson, D.R.; Liu, J.J. Precision low earth orbit determination using atmospheric density calibration. J. Astronaut. Sci. 1998, 46, 395–409. [Google Scholar] [CrossRef]
- Nazarenko, A.I.; Cefola, P.J.; Yurasov, V. Advances in the Astronautical Sciences. In Spaceflight Mechanics; Amer Astronautical Society: Springfield, VA, USA, 1998; Volume 99, pp. 1–2. [Google Scholar]
- Shi, C.; Li, W.; Li, M.; Zhao, Q.; Sang, J. Calibrating the scale of the NRLMSISE00 model during solar maximum using the two line elements dataset. Adv. Space Res. 2015, 56, 1–9. [Google Scholar] [CrossRef]
- Storz, M.F.; Bowman, B.R.; Branson, M.J.I.; Casali, S.J.; Tobiska, W.K. High accuracy satellite drag model (HASDM). Space Weather 2005, 36, 2497–2505. [Google Scholar]
- Bowman, B.; Storz, M. Time series analysis of HASDM thermospheric temperature and density corrections. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference and Exhibit, Monterey, CA, USA, 5–8 August 2002. [Google Scholar]
- Emmert, J.T.; Picone, J.M.; Lean, J.L.; Knowles, S.H. Global change in the thermosphere: Compelling evidence of a secular decrease in density. J. Geophys. Res. Space Phys. 2004, 109. [Google Scholar] [CrossRef]
- Picone, J.M.; Emmert, J.T.; Lean, J.L. Thermospheric densities derived from spacecraft orbits: Accurate processing of two-line element sets. J. Geophys. Res. Space Phys. 2005, 110, 110. [Google Scholar] [CrossRef]
- Cefola, P.J.; Proulx, R.J.; Nazarenko, A.I.; Yurasov, V.S. Advances in the Astronautical Sciences. In Astrodynamics; Univelt: Escondido, CA, USA, 2003; pp. 1–3. [Google Scholar]
- Doornbos, E.; Klinkrad, H.; Visser, P. Use of two-line element data for thermosphere neutral density model calibration. Adv. Space Res. 2008, 41, 1115–1122. [Google Scholar] [CrossRef]
- Sang, J.; Smith, C.; Zhang, K. Towards accurate atmospheric mass density determination Using precise positional information of space objects. Adv. Space Res. 2012, 49, 1088–1096. [Google Scholar] [CrossRef]
- Perez, D.; Bevilacqua, R. Neural Network based calibration of atmospheric density models. Acta Astronaut. 2015, 110, 58–76. [Google Scholar] [CrossRef]
- Perez, D.; Wohlberg, B.; Lovell, T.A.; Shoemaker, M.; Bevilacqua, R. Orbit-centered atmospheric density prediction using artificial neural networks. Acta Astronaut. 2014, 98, 9–23. [Google Scholar] [CrossRef]
- Gao, T.; Peng, H.; Bai, X. Calibration of atmospheric density model based on Gaussian Processes. Acta Astronaut. 2020, 168, 273–281. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Hanada, T. Storm-time atmospheric density modeling using neural networks and its application in orbit propagation. Adv. Space Res. 2014, 53, 558–567. [Google Scholar] [CrossRef]
- Mehta, P.M.; Walker, A.; Lawrence, E.; Linares, R.; Higdon, D.; Koller, J. Modeling satellite drag coefficients with response surfaces. Adv. Space Res. 2014, 54, 1590–1607. [Google Scholar] [CrossRef]
- Mehta, P.M.; Walker, A.C.; Sutton, E.K.; Godinez, H.C. New density estimates derived using accelerometers on board the CHAMP and GRACE satellites. Space Weather-the International. J. Res. Appl. 2017, 15, 558–576. [Google Scholar]
- Walker, A.; Mehta, P.; Koller, J. Drag Coefficient Model Using the Cercignani-Lampis-Lord Gas-Surface Interaction Model. J. Spacecr. Rockets 2014, 51, 1544–1563. [Google Scholar] [CrossRef]
- Sutton, E.K. Effects of Solar Disturbances on the Thermosphere Densities and Winds from CHAMP and GRACE Satellite Accelerometer Data. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2008. [Google Scholar]
- GFZ Data Services. Available online: https://dataservices.gfz-potsdam.de/portal/?q=champ* (accessed on 1 May 2021).
- Werbos, P.J. Backpropagation through Time—What it does and how to do it. Proc. IEEE 1990, 78, 1550–1560. [Google Scholar] [CrossRef] [Green Version]
- Williams, R.J.; Zipser, D. Gradient-based learning algorithms for recurrent. In Backpropagation: Theory, Architectures, and Applications; L. Erlbaum: Hillsdale, NJ, USA, 1995; p. 433. [Google Scholar]
- Hochreiter, S. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int. J. Uncertain. Fuzziness Knowl. Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Knipp, D.J.; Tobiska, W.K.; Emery, B.A. Direct and indirect thermospheric heating sources for solar cycles 21–23. Sol. Phys. 2004, 224, 495–505. [Google Scholar] [CrossRef]
- Bartels, J. The geomagnetic measures for the time-variations of solar corpuscular radiation, described for use in correlation studies in other geophysical fields. Ann. Intern. Geophys. 1957, 4, 227–236. [Google Scholar]
- EOP and Space Weather Data. Available online: https://celestrak.com/SpaceData/ (accessed on 1 May 2021).
- Kingma, D.P.; Ba, J.L. Adam: A method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]



| Texst | Time Span | Mean of F10.7 (sfu) | Mean of ap (nT) |
|---|---|---|---|
| Train | 1 January 2007–28 January 2007 | 80.34 | 8.43 |
| Test 1 | 31 January 2007 | 86.94 | 19.46 |
| Test 2 | 1 February 2007–28 February 2007 | 75.8 | 7.08 |
| Test 3 | 1 March 2007–29 February 2008 | 71.64 | 7.61 |
| Test 4-d30 | 30 January 2007 | 84.9 | 24 |
| Test 4-d231 | 19 August 2007 | 69.4 | 4 |
| Test 5-high | 28 April 2007 & 14 July 2007 & 11 December 2007 | 86.0 & 78.2 & 90.5 | 28.0 & 19.0 & 16.0 |
| Test 5-low | 13 April 2007 & 23 July 2007 & 18 November 2007 | 68.0 & 69.3 & 67.2 | 1.0 & 3.0 & 2.0 |
| Model | R | |||
|---|---|---|---|---|
| NRLMSISE-00 | - | - | 1.0487 | 0.8761 |
| LSTM-NRL | 10 | 60 | 0.2899 | 0.9000 |
| 20 | 60 | 0.2742 | 0.9093 | |
| 50 | 60 | 0.2822 | 0.9093 | |
| 100 | 60 | 0.2715 | 0.9105 | |
| 200 | 60 | 0.2616 | 0.9152 | |
| 300 | 60 | 0.2646 | 0.9157 | |
| 500 | 60 | 0.3053 | 0.9273 |
| Model | R | |||
|---|---|---|---|---|
| NRLMSISE-00 | - | - | 1.0487 | 0.8761 |
| LSTM-NRL | 200 | 30 | 0.3014 | 0.9057 |
| 200 | 60 | 0.2616 | 0.9152 | |
| 200 | 120 | 0.2667 | 0.9163 | |
| 200 | 180 | 0.3181 | 0.9137 | |
| 200 | 300 | 0.3632 | 0.8775 | |
| 200 | 600 | 0.3602 | 0.8720 |
| Model | Time Span | Test 2 | Test 3 | |
|---|---|---|---|---|
| LSTM-NRL | R | 1 month | 0.8859 | 0.9283 |
| RMSE () | 0.2115 | 0.3129 | ||
| NRLMSISE-00 | R | 1 year | 0.8569 | 0.9055 |
| RMSE () | 0.5747 | 0.9799 |
| Day | Model | RMSE | R | Improvement on RMSE |
|---|---|---|---|---|
| Test4-d30 () | NRLMSISE-00 | 0.9128 | 0.8643 | - |
| LSTM-NRL | 0.2987 | 0.9184 | 67.3% | |
| Test4-d231 ( | NRLMSISE-00 | 0.7653 | 0.9230 | - |
| LSTM-NRL | 0.2065 | 0.9440 | 73.0% |
| Day | Model | RMSE | R | |
|---|---|---|---|---|
| Test5-high | 2007d118 | LSTM-NRL | 0.5114 | 0.9403 |
| NRLMSISE-00 | 1.2177 | 0.9270 | ||
| 2007d195 | LSTM-NRL | 0.4908 | 0.8672 | |
| NRLMSISE-00 | 0.6937 | 0.8302 | ||
| 2007d345 | LSTM-NRL | 0.4029 | 0.7684 | |
| NRLMSISE-00 | 1.0659 | 0.8146 | ||
| Test5-low | 2007d103 | LSTM-NRL | 0.2122 | 0.9692 |
| NRLMSISE-00 | 0.9479 | 0.9657 | ||
| 2007d204 | LSTM-NRL | 0.2322 | 0.8975 | |
| NRLMSISE-00 | 0.5989 | 0.8303 | ||
| 2007d322 | LSTM-NRL | 0.1996 | 0.8032 | |
| NRLMSISE-00 | 1.0596 | 0.7489 |
| Year | Model | RMSE | R |
|---|---|---|---|
| 2003 () | NRLMSISE-00 | 0.9659 | 0.8668 |
| LSTM-NRL | 0.4393 | 0.9398 | |
| 2004 ( | NRLMSISE-00 | 0.6882 | 0.9075 |
| LSTM-NRL | 0.3886 | 0.9435 | |
| 2005 ( | NRLMSISE-00 | 0.7696 | 0.8902 |
| LSTM-NRL | 0.4575 | 0.9244 | |
| 2006 () | NRLMSISE-00 | 0.7705 | 0.9068 |
| LSTM-NRL | 0.3184 | 0.9346 | |
| 2007 ( | NRLMSISE-00 | 0.9277 | 0.9025 |
| LSTM-NRL | 0.2844 | 0.9331 | |
| 2008 () | NRLMSISE-00 | 1.3110 | 0.8988 |
| LSTM-NRL | 0.3611 | 0.9335 | |
| 2003~2008 () | NRLMSISE-00 | 0.9297 | 0.8721 |
| LSTM-NRL | 0.3791 | 0.9411 | |
| 2004~2008 ( | NRLMSISE-00 | 0.9221 | 0.8761 |
| LSTM-NRL | 0.3654 | 0.9395 |
| Year | Yearly RMSE Improvement | |
|---|---|---|
| LSTM-NRL | Perez (RTDNN-3inputs) 1 | |
| 2003 | 54.5% | - |
| 2004 | 43.1% | 14.7% |
| 2005 | 40.5% | 5.9% |
| 2006 | 58.7% | 28.6% |
| 2007 | 69.3% | 47.2% |
| 2008 | 72.5% | 45.0% |
| 2004–2008 | 60.4% | 32.6% |
| Satellite | Model | RMSE | R |
|---|---|---|---|
| CHAMP | NRLMSISE-00 | 1.0646 | 0.9269 |
| LSTM-NRL | 0.3783 | 0.9479 | |
| GRACE-A | NRLMSISE-00 | 0.0743 | 0.7256 |
| LSTM-NRL | 0.0357 | 0.7562 | |
| GRACE-B | NRLMSISE-00 | 0.0857 | 0.7231 |
| LSTM-NRL | 0.0358 | 0.7552 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yu, J.; Chen, J.; Sang, J. An Empirical Atmospheric Density Calibration Model Based on Long Short-Term Memory Neural Network. Atmosphere 2021, 12, 925. https://doi.org/10.3390/atmos12070925
Zhang Y, Yu J, Chen J, Sang J. An Empirical Atmospheric Density Calibration Model Based on Long Short-Term Memory Neural Network. Atmosphere. 2021; 12(7):925. https://doi.org/10.3390/atmos12070925
Chicago/Turabian StyleZhang, Yan, Jinjiang Yu, Junyu Chen, and Jizhang Sang. 2021. "An Empirical Atmospheric Density Calibration Model Based on Long Short-Term Memory Neural Network" Atmosphere 12, no. 7: 925. https://doi.org/10.3390/atmos12070925
APA StyleZhang, Y., Yu, J., Chen, J., & Sang, J. (2021). An Empirical Atmospheric Density Calibration Model Based on Long Short-Term Memory Neural Network. Atmosphere, 12(7), 925. https://doi.org/10.3390/atmos12070925





