Spatiotemporal Model Based on Deep Learning for ENSO Forecasts
Abstract
:1. Introduction
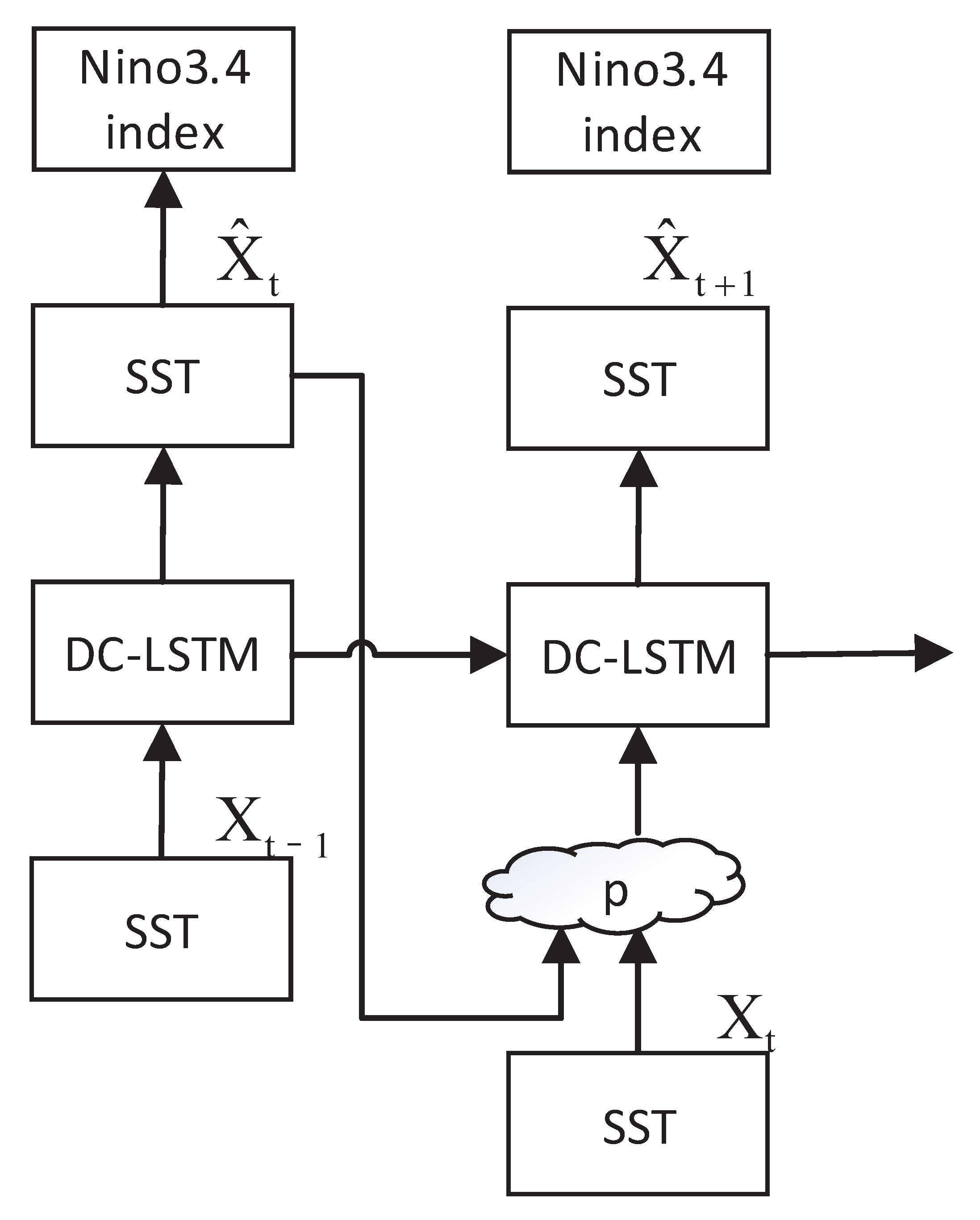
2. Materials and Methods
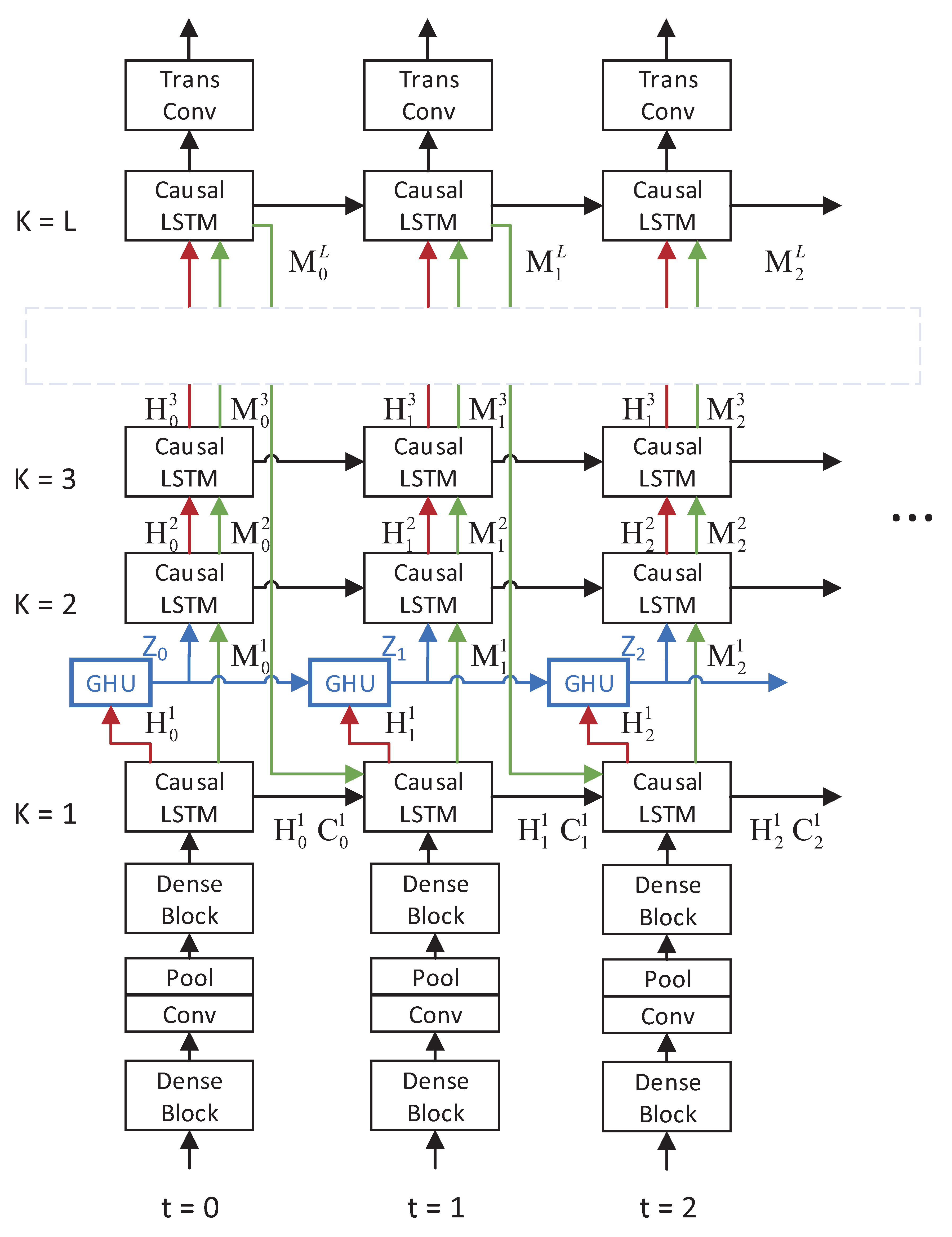
2.1. Causal LSTM
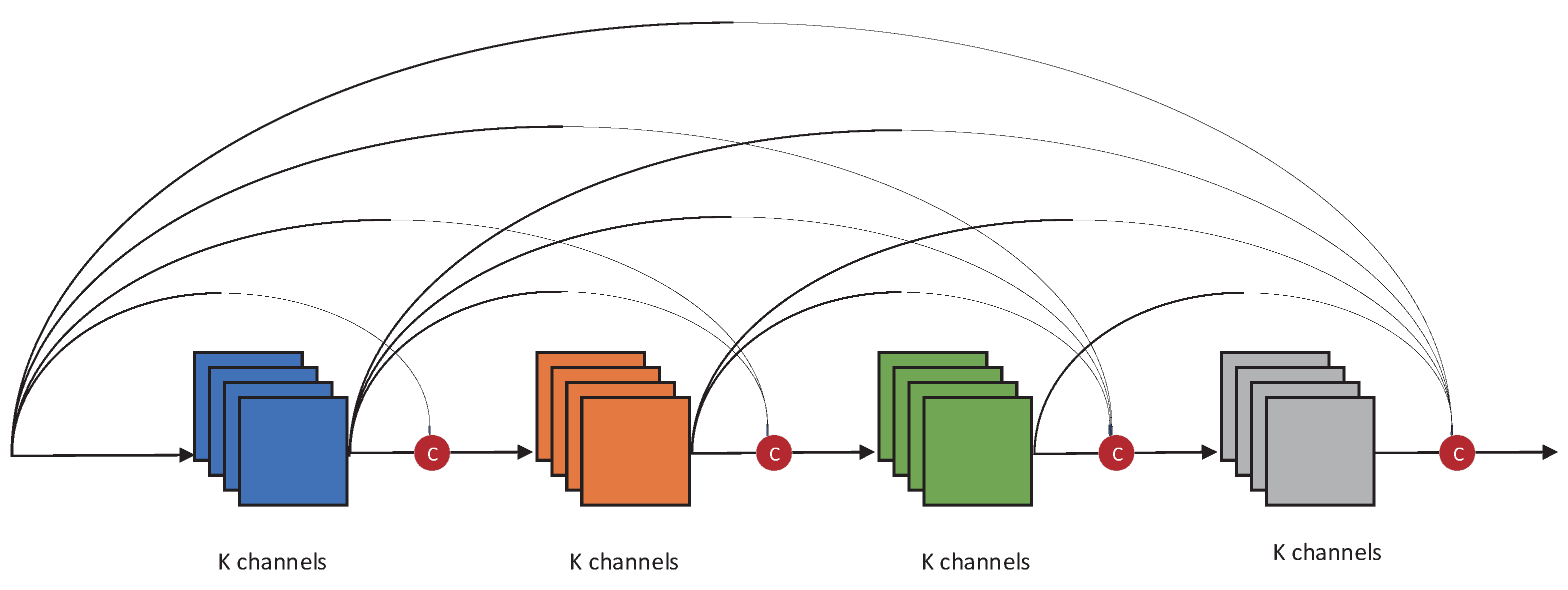
2.2. Dense Convolution Layer
3. Results
3.1. Data and Implementation
3.2. Training
- Use six different hyperparameters to preliminarily determine the number of stacked layers and hidden layer states of the network, find the network scale that is most suitable for the SSTA prediction problem, and avoid over-fitting;
- Determine the best predictor by comparing the effects of using SSTA alone and integrating T300 with U-wind and V-wind, respectively;
- Compare the ENSO correlation skill of the different prediction regions;
- Verify the improvement of forecasting skills by using historical simulation data;
- Compare the ENSO prediction skills for the trained DC-LSTM model with dynamic models and other deep learning models;
3.3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bjerknes, J. Atmospheric Teleconnections from the Equatorial PACIFIC1. Mon. Weather Rev. 1969, 97, 163. [Google Scholar] [CrossRef]
- Iizumi, T.; Luo, J.J.; Challinor, A.J.; Sakurai, G.; Yokozawa, M.; Sakuma, H.; Brown, M.E.; Yamagata, T. Impacts of El Niño Southern Oscillation on the global yields of major crops. Nat. Commun. 2014, 5, 3712. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhai, P.; Yu, R.; Guo, Y.; Li, Q.; Ren, X.; Wang, Y.; Xu, W.; Liu, Y.; Ding, Y. The strong El Niño of 2015/16 and its dominant impacts on global and China’s climate. J. Meteorol. Res. 2016, 30, 283–297. [Google Scholar] [CrossRef]
- Bamston, A.G.; Chelliah, M.; Goldenberg, S.B. Documentation of a highly ENSO-related sst region in the equatorial pacific: Research note. Atmos. Ocean 1997, 35, 367–383. [Google Scholar] [CrossRef]
- Alexander, M.A.; Matrosova, L.; Penland, C.; Scott, J.D.; Chang, P. Forecasting Pacific SSTs: Linear Inverse Model Predictions of the PDO. J. Clim. 2008, 21, 385–402. [Google Scholar] [CrossRef] [Green Version]
- Knaff, J.A.; Landsea, C.W. An El Niño-Southern Oscillation Climatology and Persistence (CLIPER) Forecasting Scheme. Weather Forecast. 1997, 12, 633–652. [Google Scholar] [CrossRef] [Green Version]
- Xue, Y.; Leetmaa, A. Forecasts of tropical Pacific SST and sea level using a Markov model. Geophys. Res. Lett. 2000, 27, 2701–2704. [Google Scholar] [CrossRef] [Green Version]
- Van Den Dool, H.M. Searching for analogues, how long must we wait? Tellus A 1994, 46, 314–324. [Google Scholar] [CrossRef]
- Barnston, A.; Dool, H.; Rodenhuis, D.; Ropelewski, C.; Kousky, V.; O’Lenic, E.; Livezey, R.; Zebiak, S.; Cane, M.; Barnett, T.; et al. Long-Lead Seasonal Forecasts—Where Do We Stand? Bull. Am. Meteorol. Soc. 1994, 75, 2097–2114. [Google Scholar] [CrossRef] [Green Version]
- Saha, S.; Moorthi, S.; Wu, X.; Wang, J.; Nadiga, S.; Tripp, P.; Behringer, D.; Hou, Y.T.; Chuang, H.Y.; Iredell, M.; et al. The NCEP Climate Forecast System Version 2. J. Clim. 2014, 27, 2185–2208. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.K.; L’Heureux, M.L.; Li, S.; DeWitt, D.G. Skill of Real-Time Seasonal ENSO Model Predictions during 2002–11: Is Our Capability Increasing? Bull. Am. Meteorol. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Luo, J.J.; Masson, S.; Behera, S.K.; Yamagata, T. Extended ENSO Predictions Using a Fully Coupled Ocean—Atmosphere Model. J. Clim. 2008, 21, 84–93. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, R.H.; Liu, T.; Duan, W.; Yang, D.; Zheng, F.; Ren, H.; Lian, T.; Gao, C.; Chen, D.; et al. Progress in ENSO prediction and predictability study. Natl. Sci. Rev. 2018, 5, 826–839. [Google Scholar] [CrossRef]
- Mcphaden, M.; Zebiak, S.; Glantz, M. ENSO as an integrating concept in Earth science. Science 2006, 314, 1740–1745. [Google Scholar] [CrossRef] [Green Version]
- Kinter, J.L., III; Luo, J.J.; Jin, E.K.; Wang, B.; Park, C.K.; Shukla, J.; Kirtman, B.P.; Kang, I.S.; Schemm, J.; Kug, J.S.; et al. Current status of ENSO prediction skill in coupled ocean-atmosphere models. Clim. Dyn. Obs. Theor. Comput. Res. Clim. Syst. 2008, 31, 647–664. [Google Scholar]
- Lima, C.H.R.; Lall, U.; Jebara, T.; Barnston, A.G. Machine Learning Methods for ENSO Analysis and Prediction. In Machine Learning and Data Mining Approaches to Climate Science, Proceedings of the 4th International Workshop on Climate Informatics, Boulder, CO, USA, 25–26 September 2015; Springer International Publishing: Berlin/Heidelberg, Germany, 2015; pp. 13–21. [Google Scholar]
- Nooteboom, P.; Feng, Q.; López, C.; Hernández-García, E.; Dijkstra, H. Using network theory and machine learning to predict El Niño. Earth Syst. Dyn. 2018, 9, 969–983. [Google Scholar] [CrossRef] [Green Version]
- Ham, Y.G.; Kim, J.H.; Luo, J.J. Deep learning for multi-year ENSO forecasts. Nature 2019, 573, 568–572. [Google Scholar] [CrossRef]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, QC, Canada, 8–13 December 2014; MIT Press: Cambridge, MA, USA, 2014; Volume 2, pp. 3320–3328. [Google Scholar]
- Zhang, H.; Chu, P.S.; He, L.; Unger, D. Improving the CPC’s ENSO Forecasts using Bayesian model averaging. Clim. Dyn. 2019, 53, 3373–3385. [Google Scholar] [CrossRef]
- Salman, A.G.; Kanigoro, B.; Heryadi, Y. Weather forecasting using deep learning techniques. In Proceedings of the 2015 International Conference on Advanced Computer Science and Information Systems (ICACSIS), Depok, Indonesia, 10–11 October 2015; pp. 281–285. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium 2010, Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar] [CrossRef]
- Feng, Q.Y.; Vasile, R.; Segond, M.; Gozolchiani, A.; Wang, Y.; Abel, M.; Havlin, S.; Bunde, A.; Dijkstra, H.A. ClimateLearn: A machine-learning approach for climate prediction using network measures. Geosci. Model Dev. Discuss. 2016, 2016, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Xie, A.; Yang, H.; Chen, J.; Sheng, L.; Zhang, Q. A Short-Term Wind Speed Forecasting Model Based on a Multi-Variable Long Short-Term Memory Network. Atmosphere 2021, 12, 651. [Google Scholar] [CrossRef]
- Aguilar-Martinez, S.; Hsieh, W.W. Forecasts of Tropical Pacific Sea Surface Temperatures by Neural Networks and Support Vector Regression. Int. J. Oceanogr. 2009, 2009, 167. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Wang, H.; Dong, J.; Zhong, G.; Sun, X. Prediction of Sea Surface Temperature Using Long Short-Term Memory. IEEE Geosci. Remote Sens. Lett. 2017, 14, 1745–1749. [Google Scholar] [CrossRef] [Green Version]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Finn, C.; Goodfellow, I.J.; Levine, S. Unsupervised Learning for Physical Interaction through Video Prediction. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 64–72. [Google Scholar]
- Brabandere, B.; Jia, X.; Tuytelaars, T.; Van Gool, L. Dynamic Filter Networks. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Barcelona, Spain, 5–10 December 2016; pp. 667–675. [Google Scholar]
- Wang, Y.; Jiang, L.; Yang, M.H.; Li, L.J.; Long, M.; Fei-Fei, L. Eidetic 3D LSTM: A Model for Video Prediction and Beyond. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, LA, USA, 6–9 May 2019. [Google Scholar]
- Srivastava, N.; Mansimov, E.; Salakhutdinov, R. Unsupervised learning of video representations using LSTMs. In Proceedings of the International Conference on Machine Learning, JMLR.org, Lille, France, 6–11 July 2015; Volume 37, pp. 843–852. [Google Scholar]
- Wang, Y.; Zhang, J.; Zhu, H.; Long, M.; Wang, J.; Yu, P.S. Memory in Memory: A Predictive Neural Network for Learning Higher-Order Non-Stationarity From Spatiotemporal Dynamics. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 9154–9162. [Google Scholar]
- Kalchbrenner, N.; Oord, A.; Simonyan, K.; Danihelka, I.; Vinyals, O.; Graves, A.; Kavukcuoglu, K. Video Pixel Networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; Doina, P., Yee Whye, T., Eds.; Volume 70, pp. 1771–1779. [Google Scholar]
- Wang, Y.; Long, M.; Wang, J.; Gao, Z.; Yu, P.S. PredRNN: Recurrent Neural Networks for Predictive Learning using Spatiotemporal LSTMs. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 879–888. [Google Scholar]
- Shi, X.; Gao, Z.; Lausen, L.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Deep learning for precipitation nowcasting: A benchmark and a new model. In Proceedings of the Conference and Workshop on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 5622–5632. [Google Scholar]
- Wang, Y.; Gao, Z.; Long, M.; Wang, H.; Yu, P.S. PredRNN++: Towards A Resolution of the Deep-in-Time Dilemma in Spatiotemporal Predictive Learning. In Proceedings of the International Conference on Machine Learning, PMLR, Stockholm, Sweden, 10–15 July 2018; Jennifer, D., Andreas, K., Eds.; Volume 80, pp. 5123–5132. [Google Scholar]
- Shi, X.; Chen, Z.; Wang, H.; Yeung, D.; Wong, W.; Woo, W. Convolutional LSTM Network: A machine learning approach for precipitation nowcasting. arXiv 2015, arXiv:1506.04214. [Google Scholar]
- Srivastava, R.K.; Greff, K.; Schmidhuber, J. Training very deep networks. arXiv 2015, arXiv:1507.06228. [Google Scholar]
- Huang, G.; Liu, Z.; Maaten, L.V.D.; Weinberger, K.Q. Densely Connected Convolutional Networks. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2261–2269. [Google Scholar] [CrossRef] [Green Version]
- Carton, J.A.; Giese, B.S. A Reanalysis of Ocean Climate Using Simple Ocean Data Assimilation (SODA). Mon. Weather Rev. 2008, 136, 2999–3017. [Google Scholar] [CrossRef]
- Bellenger, H.; Guilyardi, E.; Leloup, J.; Lengaigne, M.; Vialard, J. ENSO representation in climate models: From CMIP3 to CMIP5. Clim. Dyn. 2014, 42, 1999–2018. [Google Scholar] [CrossRef]
- Saha, S.; Nadiga, S.; Thiaw, C.; Wang, J.; Wang, W.; Zhang, Q.; Van den Dool, H.M.; Pan, H.L.; Moorthi, S.; Behringer, D.; et al. The NCEP Climate Forecast System. J. Clim. 2006, 19, 3483–3517. [Google Scholar] [CrossRef] [Green Version]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. arXiv 2015, arXiv:1412.6980. [Google Scholar]
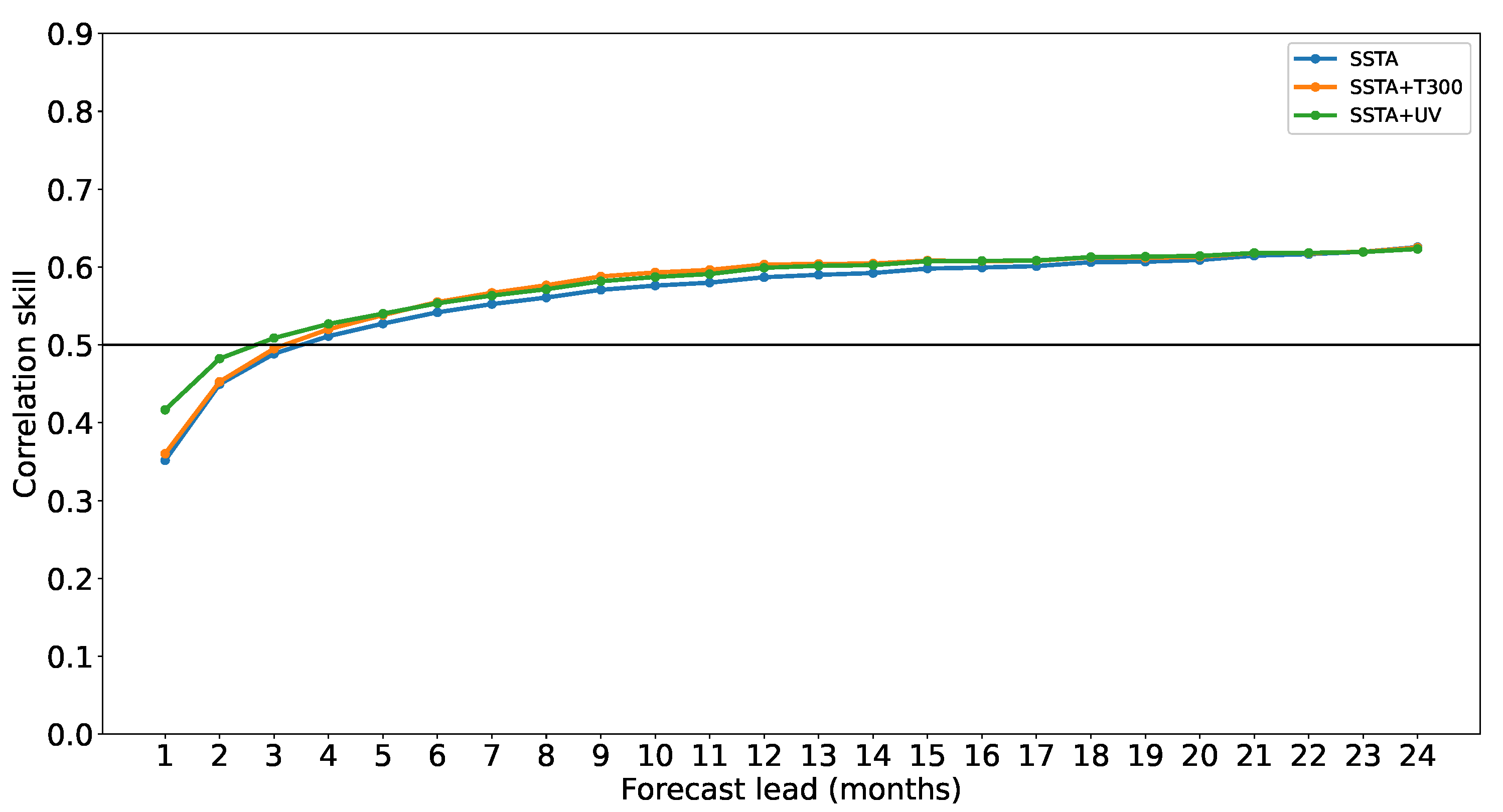
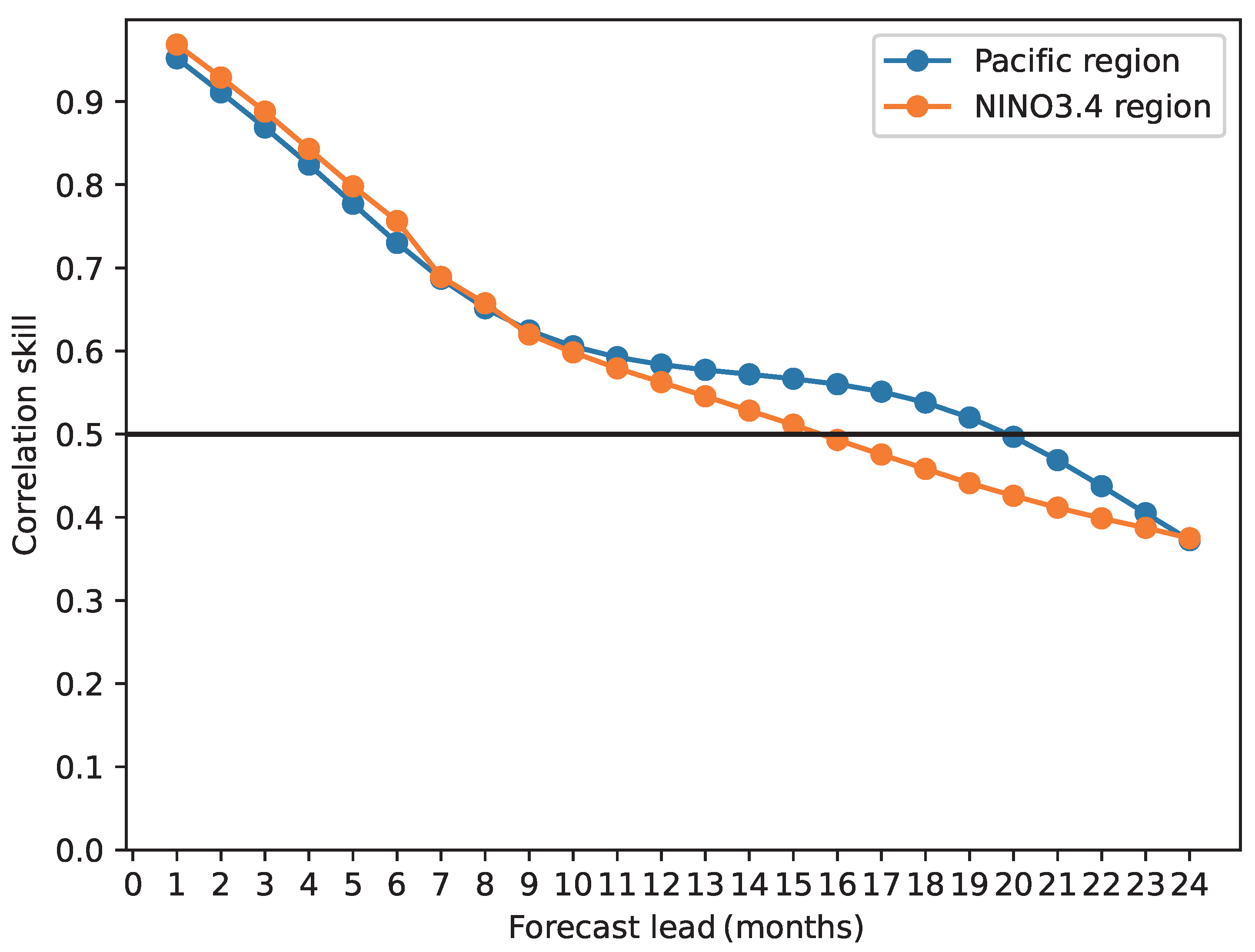
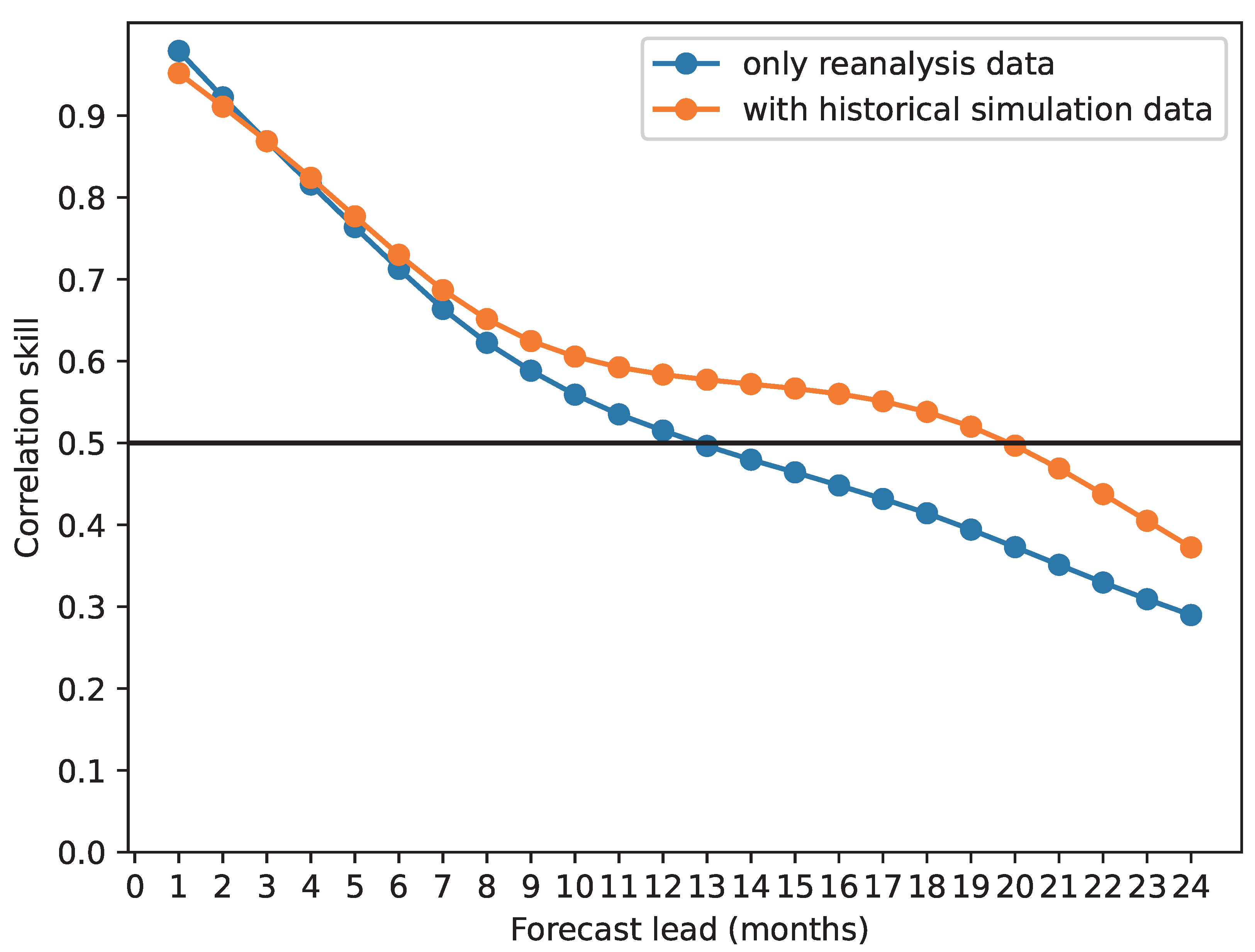

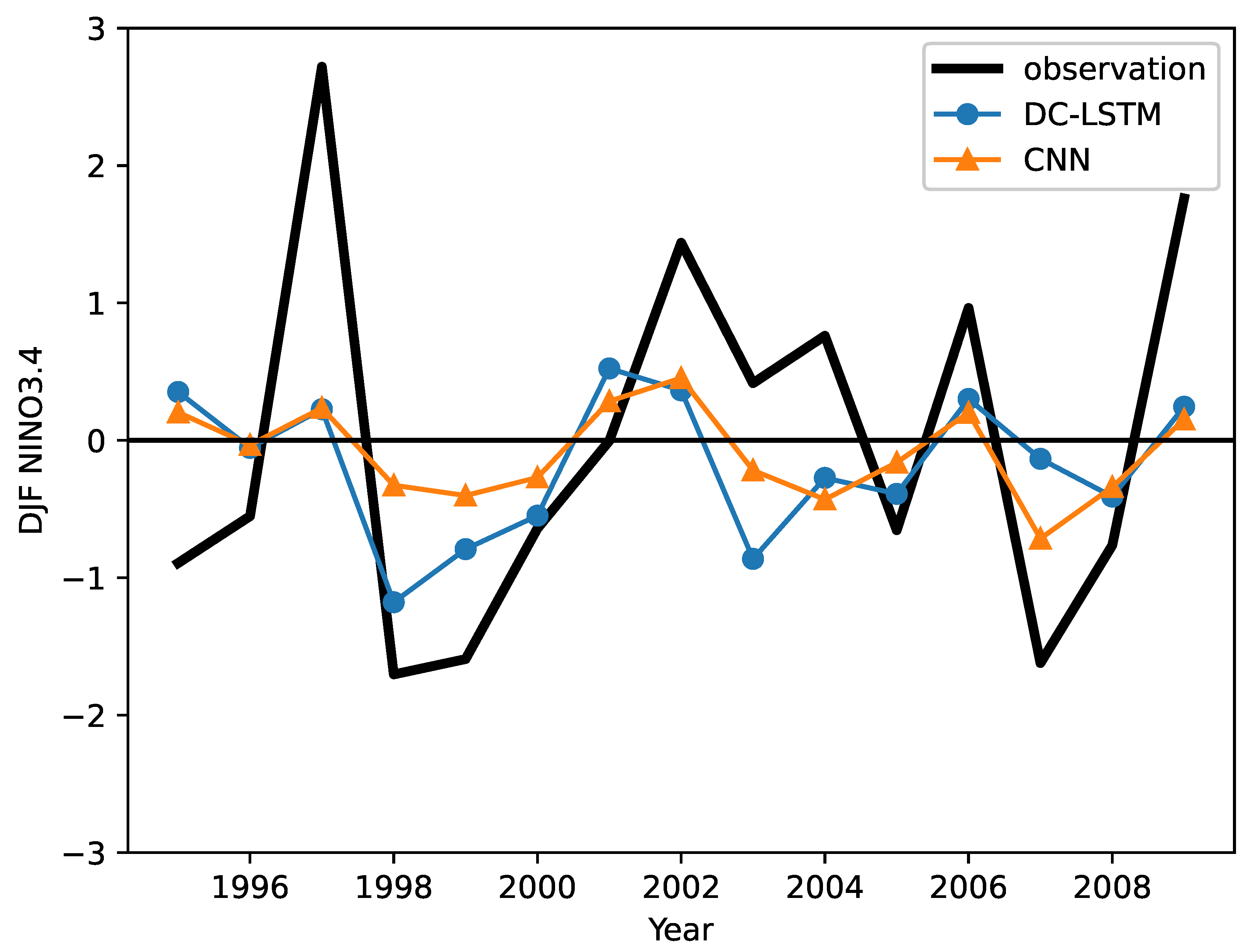
| Data | Peroid | |
|---|---|---|
| Training dataset | CMIP5 historical run | 1861–2004 |
| Reanalysis (SODA) | 1971–1973 | |
| Validation dataset | Reanalysis (GODAS) | 1994–2017 |
| CMIP ID | Modeling Group | Integration Period | Number of Ensemble Members |
|---|---|---|---|
| BCC-CSM1.1-m | Beijing Climate Center, China Meteorological Administration | JAN1850-DEC2012 | 1 |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis | JAN1850-DEC2005 | 5 |
| CCSM4 | National Center for Atmospheric Research | JAN1850-DEC2005 | 1 |
| CESM1-CAM5 | Community Earth System Model Contributors | JAN1850-DEC2005 | 1 |
| CMCC-CM | Centro Euro-Mediterraneo per l Cambiamenti Climatici | JAN1850-DEC2005 | 1 |
| CMCC-CMS | 1 | ||
| CNRM-CM5 | Centre National de Recherches Meteorologiques/Centre Europeen de Recherche et Formation Avancee en Calcul Scientifique | JAN1850-DEC2005 | 5 |
| CSIRO-Mk3-6-0 | Commonwealth Scientific and Industrial Research Organization in collaboration with Queensland Climate Change Centre of Excellence | JAN1850-DEC2005 | 5 |
| FIO-ESM | The First Institute of Oceanography, SOA, China | JAN1850-DEC2005 | 1 |
| GFDL-ESM2G | NOAA Geophysical Fluid Dynamics Laboratory | JAN1861 -DEC2005 | 1 |
| GISS-E2-H | NASA Goddard Institute for Space Studies | JAN1850-DEC2005 | 5 |
| HadGEM2-AO | National Institute of Meteorological Research/Korea Meteorological Administration | JAN1860-DEC2005 | 1 |
| HadCM3 | Met Office Hadley Centre (additional HadGEM2-ES realizations contributed by Instituto Nacional de Pesquisas Espaciais) | DEC1859-DEC2005 | 1 |
| HadGEM2-CC | DEC1859-NOV2005 | 1 | |
| HadGEM2-ES | DEC1859-NOV2005 | 4 | |
| IPSL-CM5A-MR | Institut Pierre-Simon Laplace | JAN1850-DEC2005 | 1 |
| MIROC5 | Atmosphere and Ocean Research Institute (The University of Tokyo), National Institute for Environmental Studies, and Japan Agency for Marine-Earth Science and Technology | JAN1850-DEC2012 | 1 |
| MPI-ESM-LR | Max-Planck-lnstrtut fur Meteorologie (Max Planck Institute for Meteorology) | JAN1850-DEC2005 | 3 |
| MRI-CGCM3 | Meteorological Research Institute | JAN1850-DEC 05 | 1 |
| NorESM1-M | Norwegian Climate Centre | JAN1850-DEC2005 | 1 |
| NorESM1-ME | 1 |
| Layer | RMSE | MAE | SSIM | |||
|---|---|---|---|---|---|---|
| Training | Validation | Training | Validation | Training | Validation | |
| 4 | 0.5708 | 0.5890 | 0.4022 | 0.4077 | 0.57 | 0.2863 |
| 5 | 0.5558 | 0.5863 | 0.3927 | 0.4083 | 0.62 | 0.2879 |
| 6 | 0.5419 | 0.5858 | 0.3833 | 0.4082 | 0.65 | 0.2881 |
| 7 | 0.5327 | 0.5951 | 0.3768 | 0.4158 | 0.66 | 0.2849 |
| 8 | 0.5233 | 0.6032 | 0.3757 | 0.4233 | 0.63 | 0.2840 |
| Hidden States | RMSE | MAE | SSIM | |||
|---|---|---|---|---|---|---|
| Training | Validation | Training | Validation | Training | Validation | |
| 64 | 0.5484 | 0.5950 | 0.3895 | 0.4131 | 0.62 | 0.2878 |
| 128 | 0.5419 | 0.5858 | 0.3833 | 0.4082 | 0.65 | 0.2881 |
| 192 | 0.5217 | 0.5956 | 0.3721 | 0.4142 | 0.66 | 0.2891 |
| 256 | 0.5211 | 0.6013 | 0.3701 | 0.4237 | 0.58 | 0.2887 |
| Model | COR | RMSE | MAE |
|---|---|---|---|
| CNN | 0.6237 | 0.5603 | 0.4142 |
| DC-LSTM | 0.6544 | 0.5558 | 0.3950 |
| Model | Number of Parameters | Time-Consuming |
|---|---|---|
| CNN | 319,953 | 0.1138 s |
| DC-LSTM | 36,130,304 | 0.5145 s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Geng, H.; Wang, T. Spatiotemporal Model Based on Deep Learning for ENSO Forecasts. Atmosphere 2021, 12, 810. https://doi.org/10.3390/atmos12070810
Geng H, Wang T. Spatiotemporal Model Based on Deep Learning for ENSO Forecasts. Atmosphere. 2021; 12(7):810. https://doi.org/10.3390/atmos12070810
Chicago/Turabian StyleGeng, Huantong, and Tianlei Wang. 2021. "Spatiotemporal Model Based on Deep Learning for ENSO Forecasts" Atmosphere 12, no. 7: 810. https://doi.org/10.3390/atmos12070810
APA StyleGeng, H., & Wang, T. (2021). Spatiotemporal Model Based on Deep Learning for ENSO Forecasts. Atmosphere, 12(7), 810. https://doi.org/10.3390/atmos12070810






