Performing Hydrological Monitoring at a National Scale by Exploiting Rain-Gauge and Radar Networks: The Italian Case
Abstract
1. Introduction
2. Tools and Methods
2.1. Study Area and Period
2.2. Data
2.3. Modified Conditional Merging
2.3.1. Description of the Method
2.3.2. Analysis of Rainfall Fields
2.4. Operational Hydrological Model at National Scale
3. Results
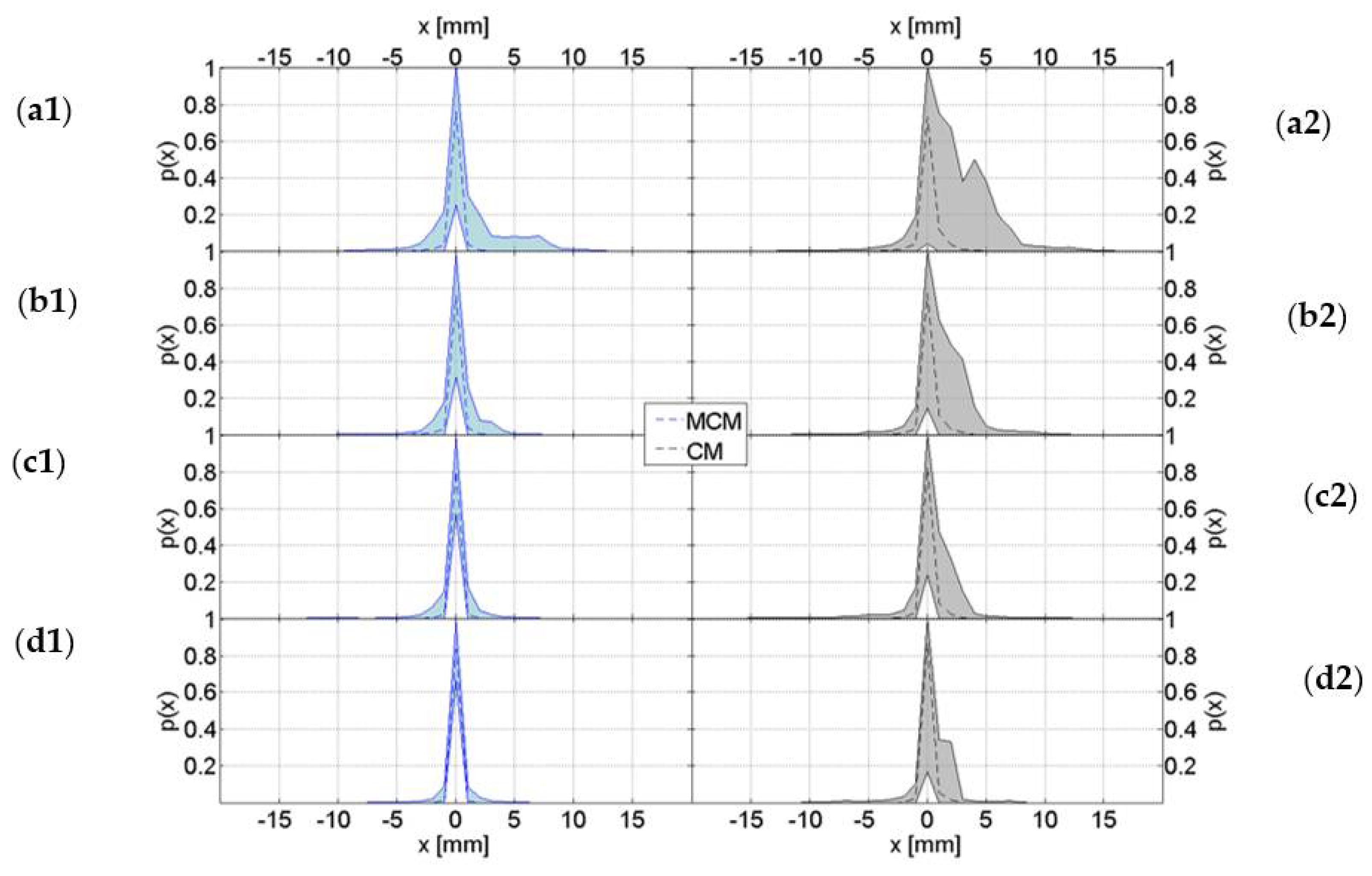
3.1. Analysis on Rainfall Fields
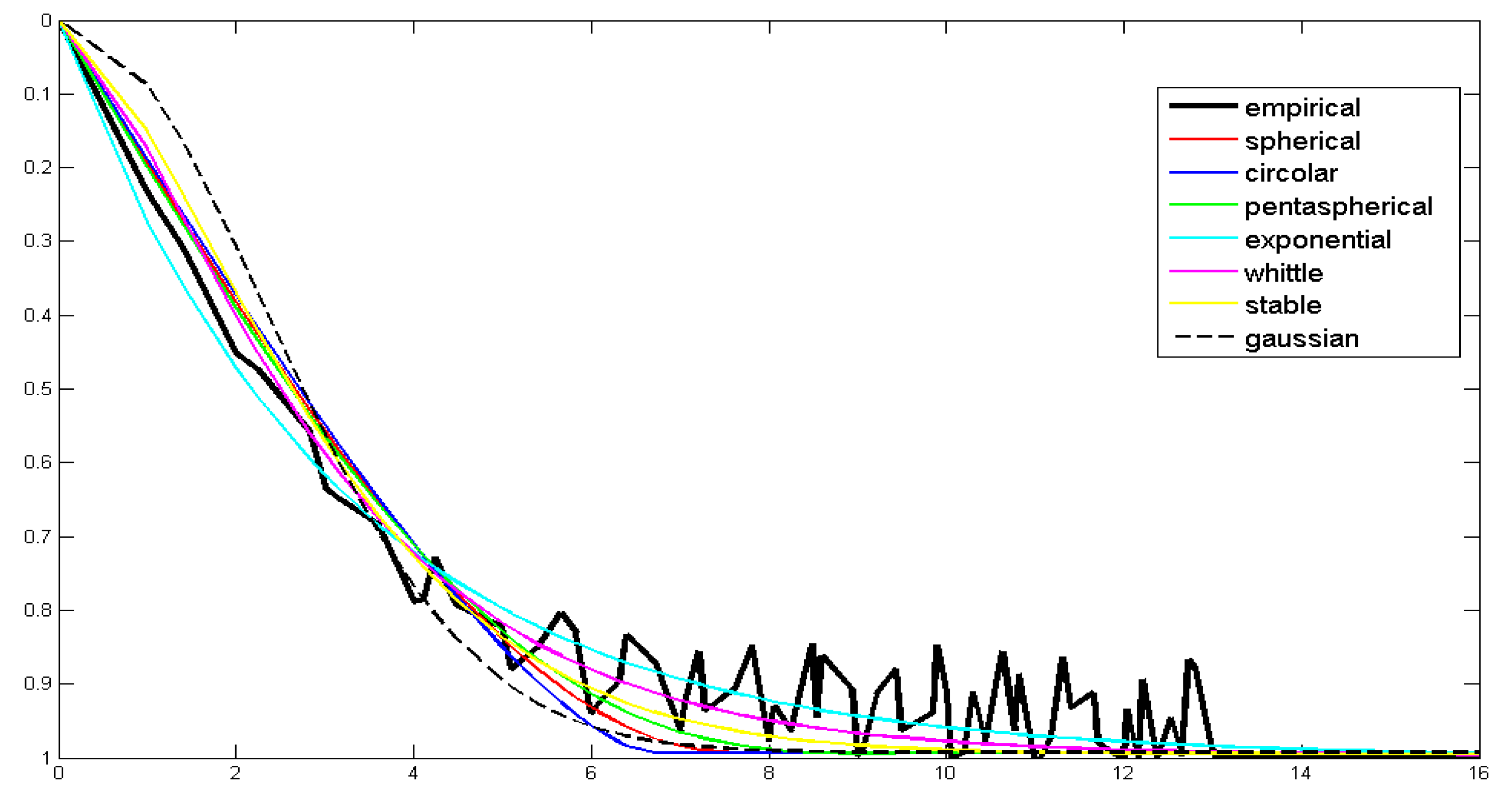
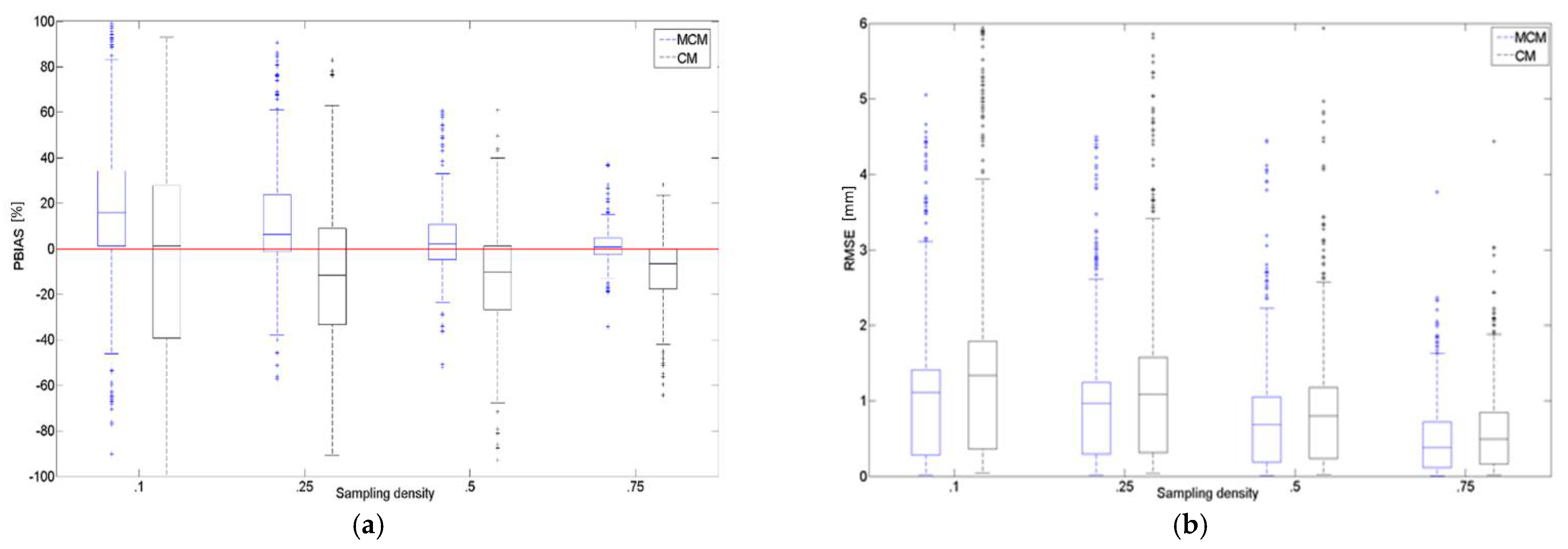
3.1.1. Cross-Validation of MCM
3.1.2. Catchment-Scale Comparison
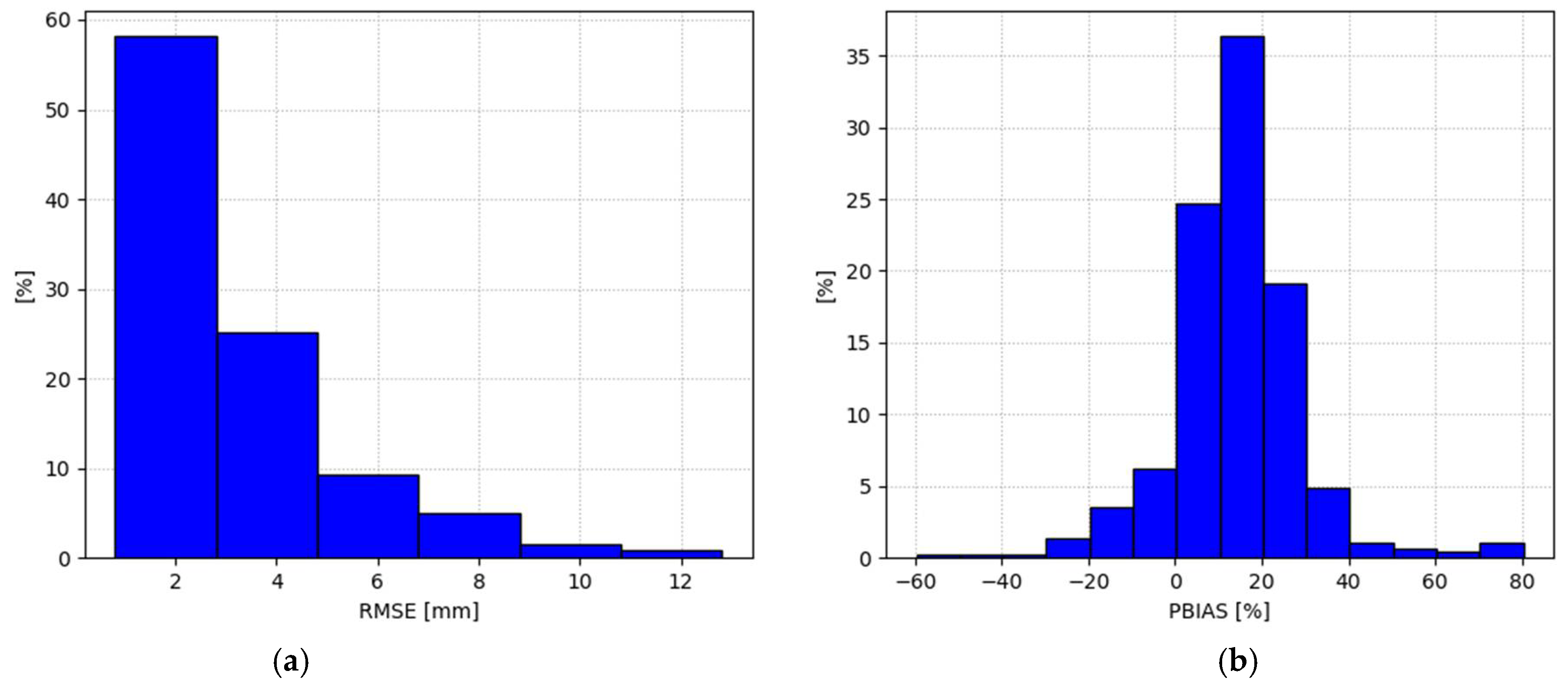
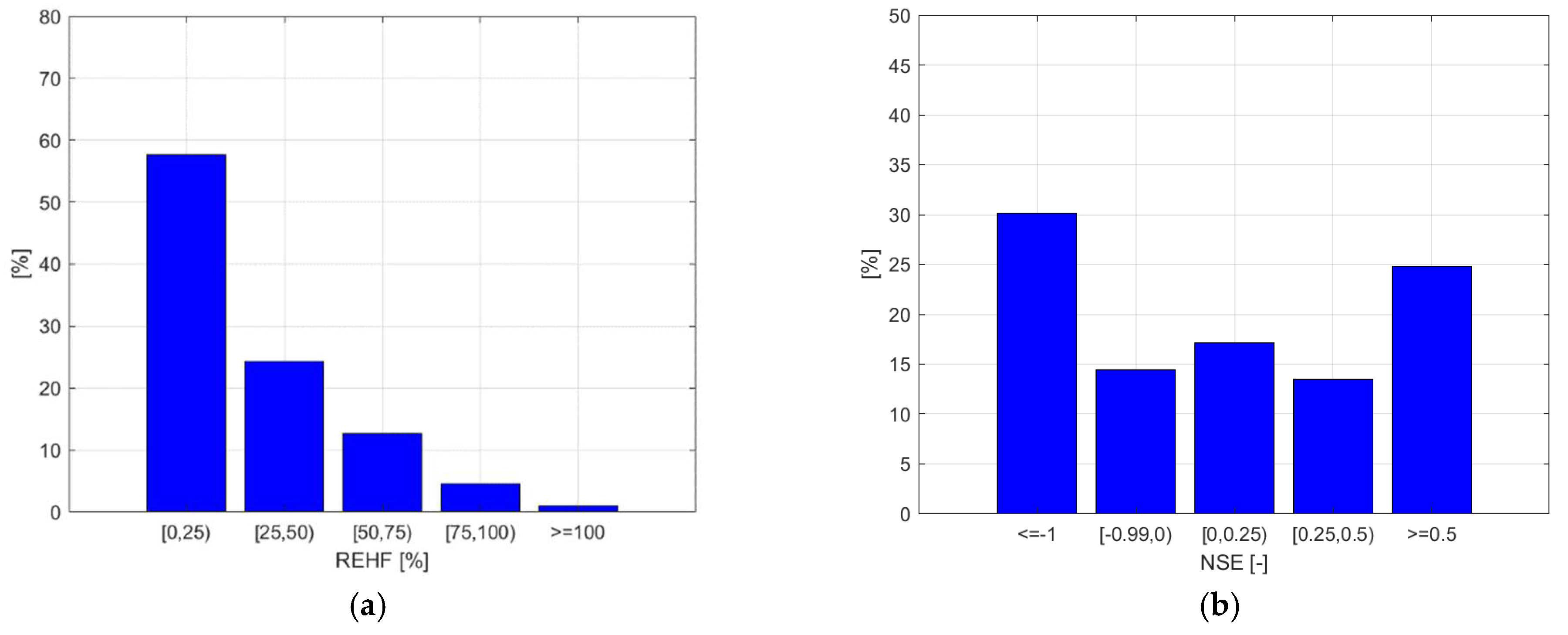
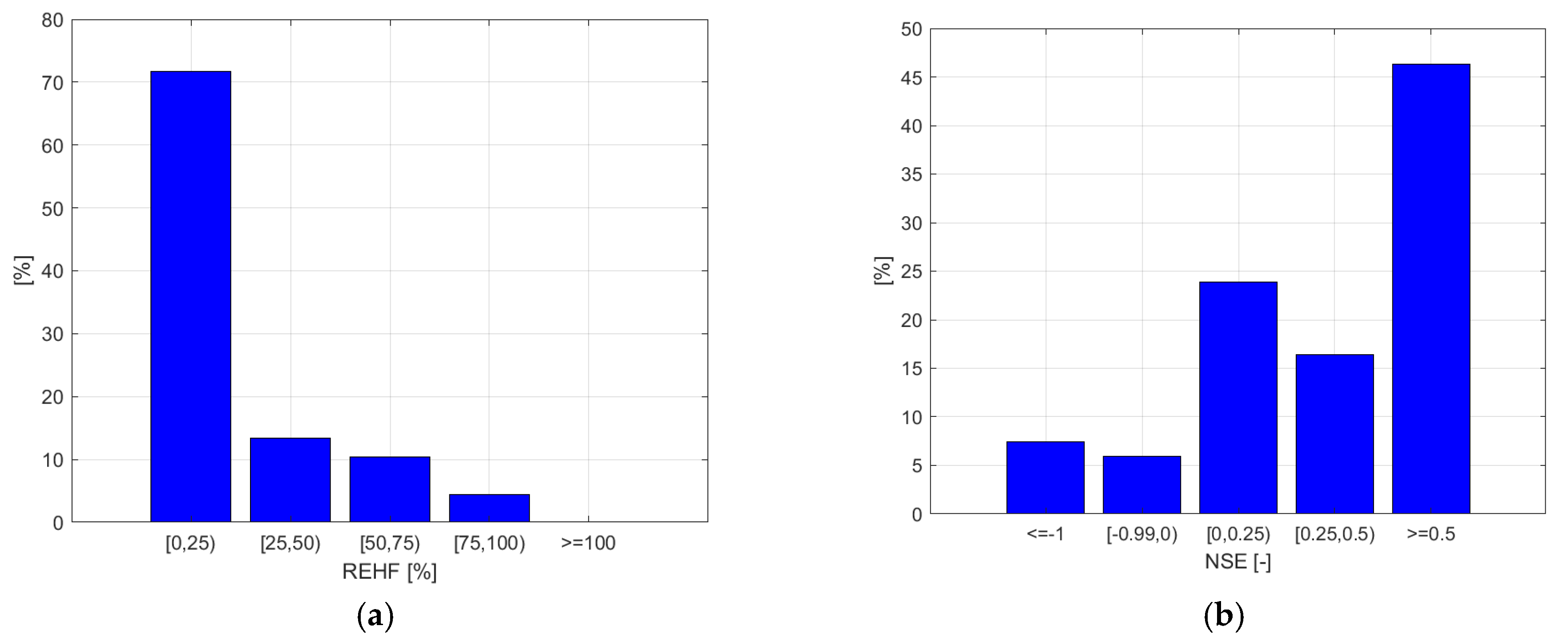
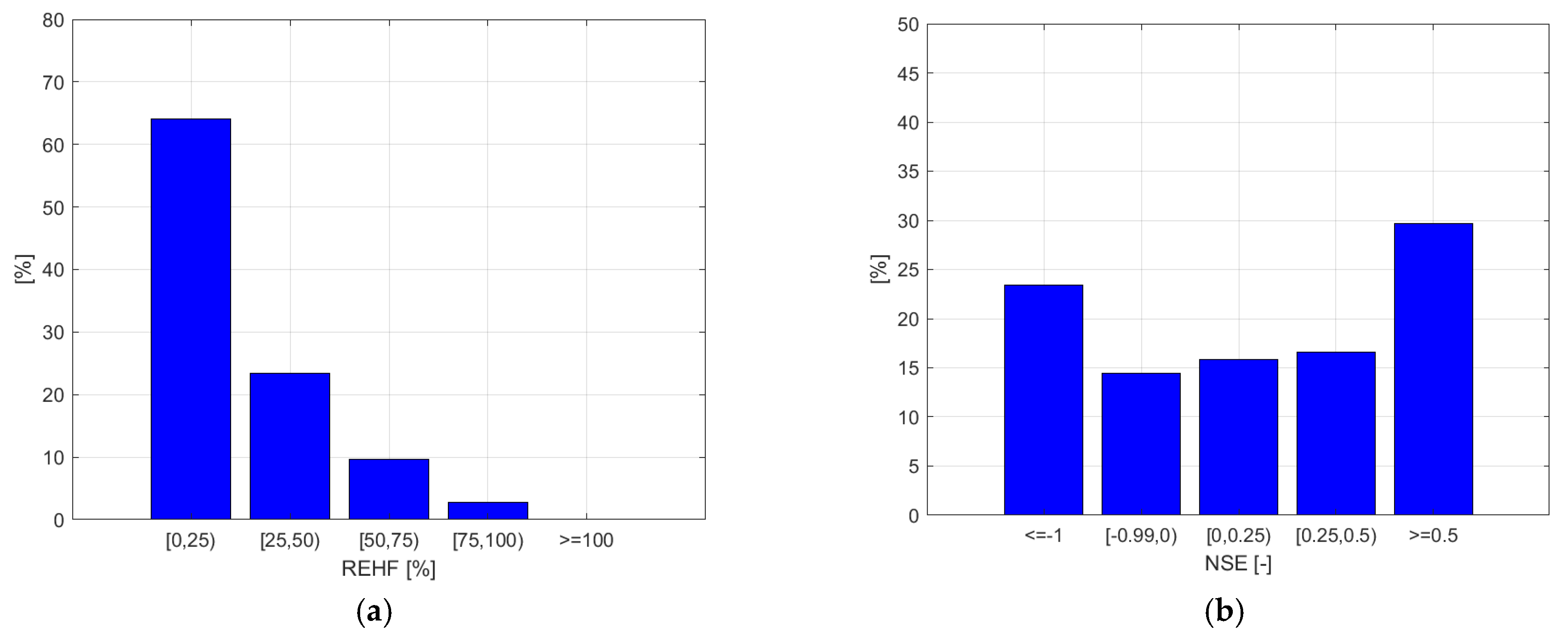
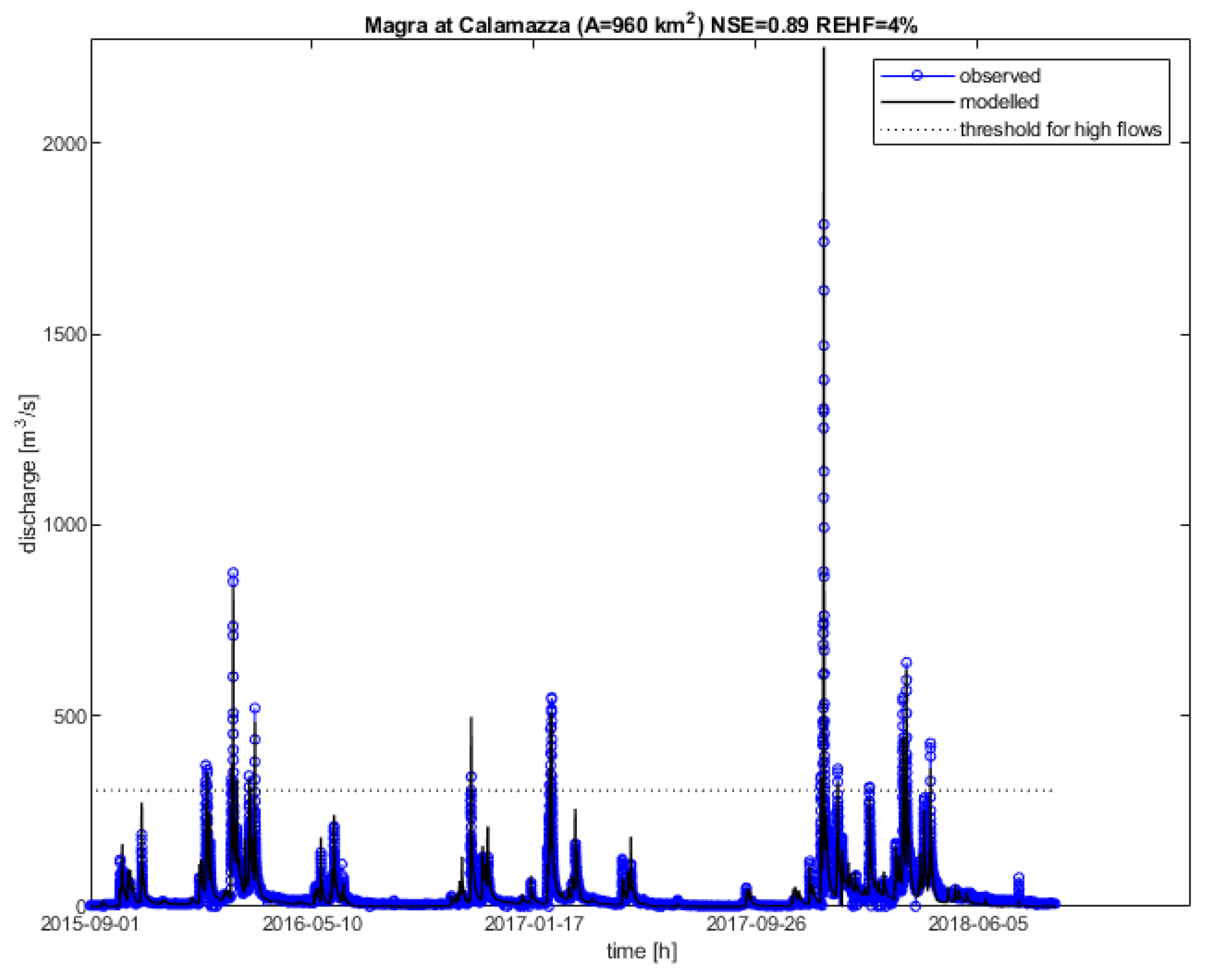
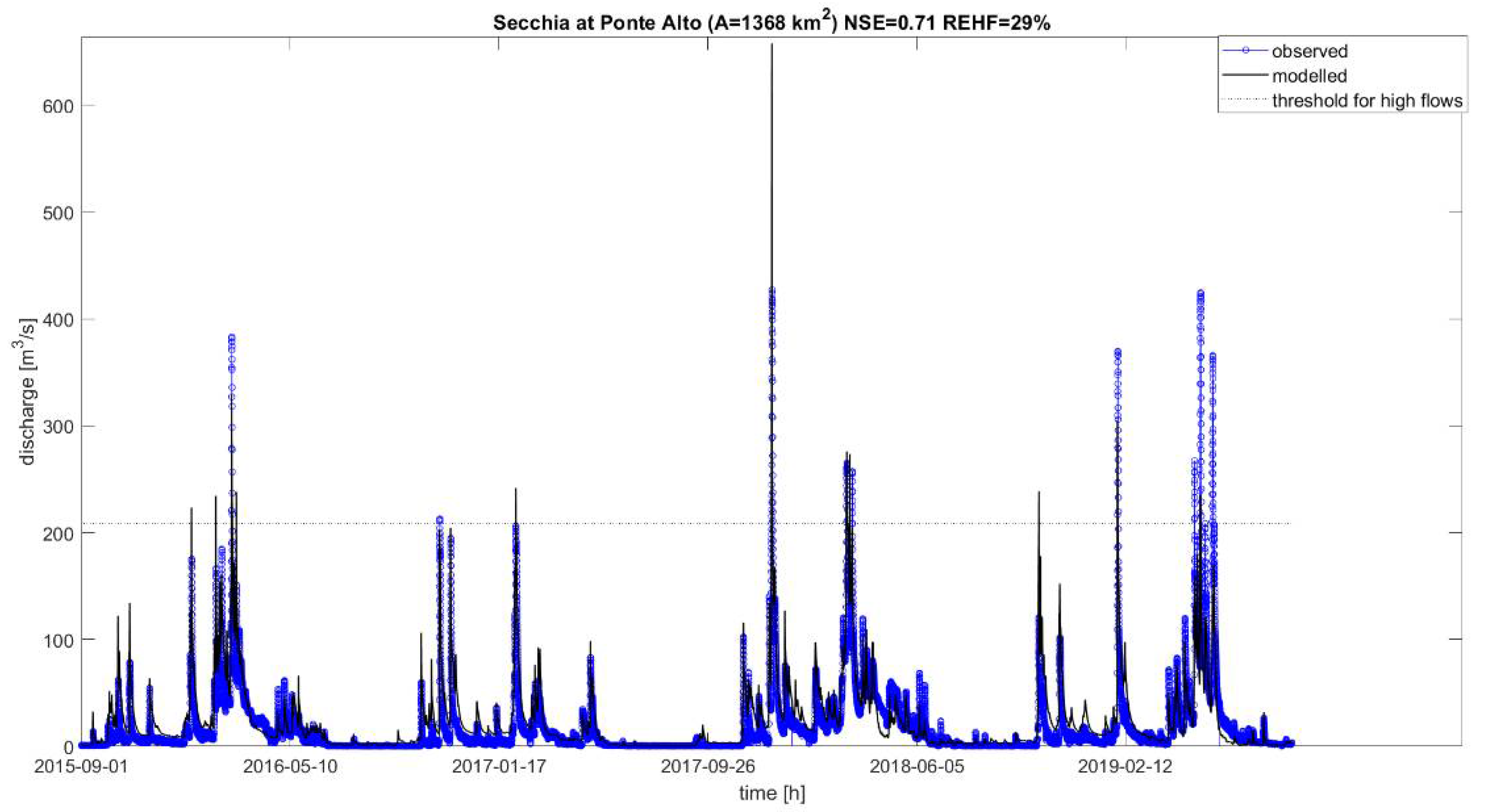
3.2. Performances of Hydrological Simulations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Rain-gauge rainfall accumulation on temporal domain (Figure A1).
- Radar observation accumulation over spatio-temporal domain (Figure A2);
- Interpolation of rain-gauge values (Figure A5);
- Interpolation of radar values sampled on rain-gauge locations and using the same local parameters as for rain-gauge interpolation (Figure A6);
- Difference between radar map and the interpolation of radar, to identify the small-scale structure of the event (Figure A7);
- Sum of the difference map (obtained in step 6) and the rain gauge interpolation, to force the output map passing through the rain gauge points with the structure from the radar observations (Figure A8).
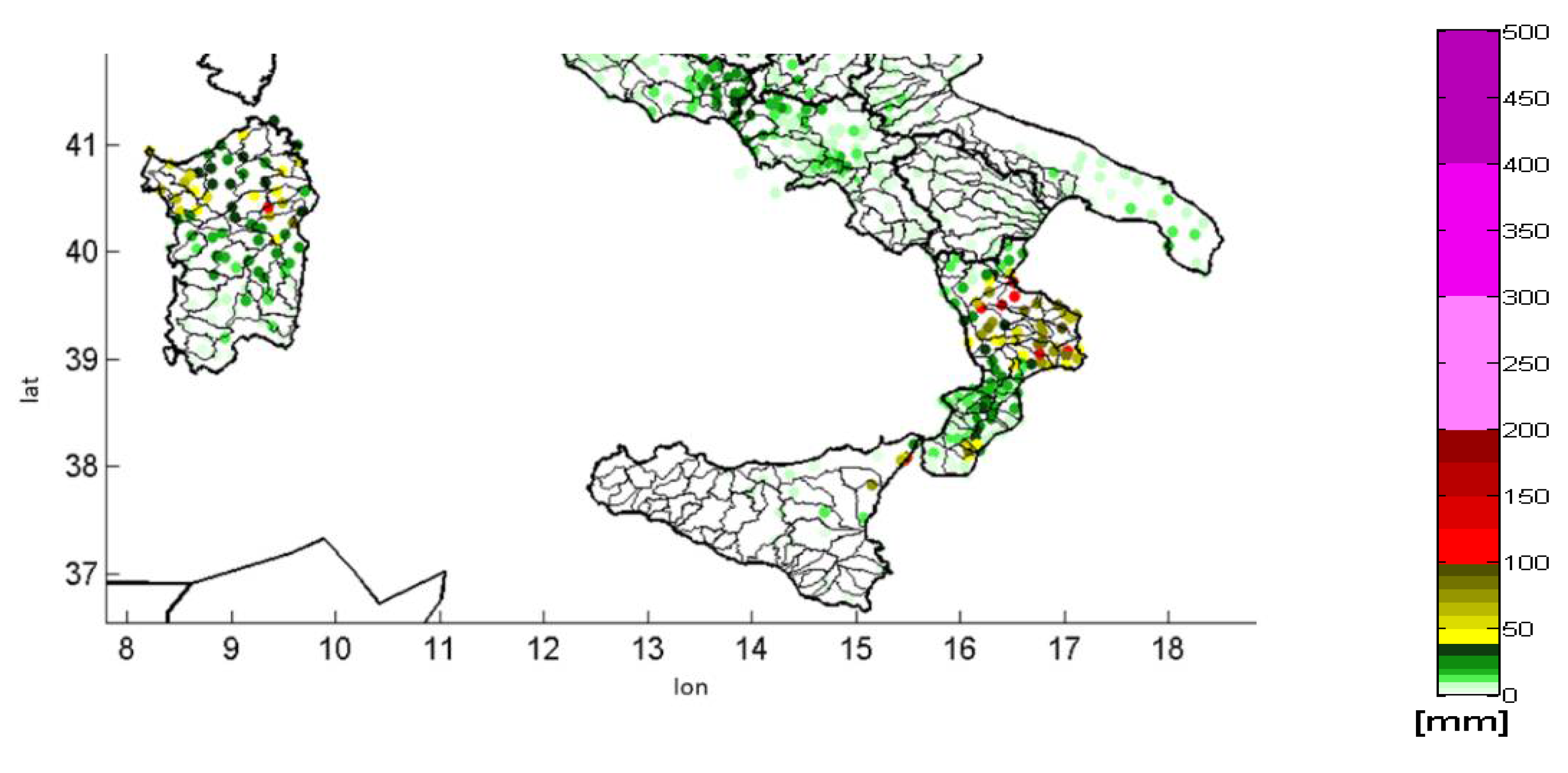
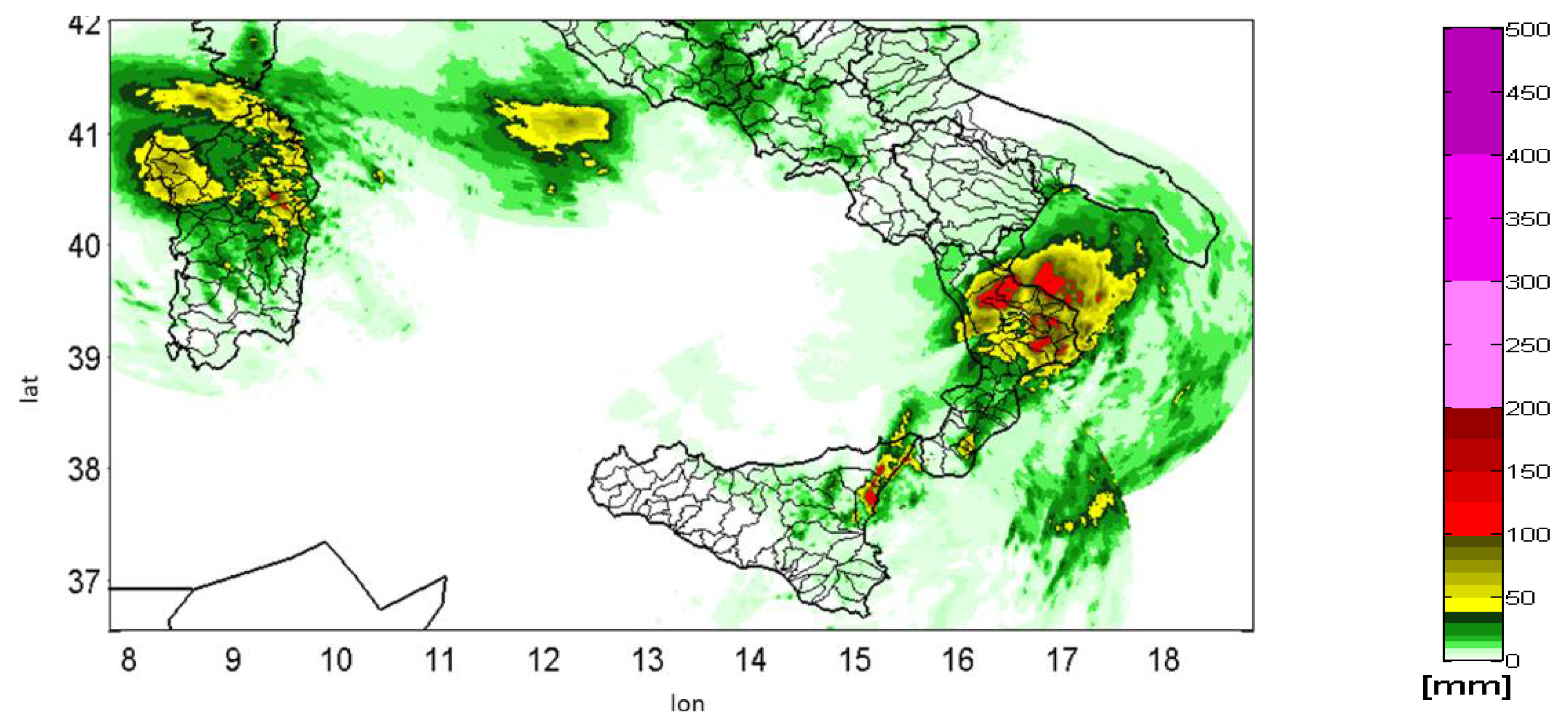
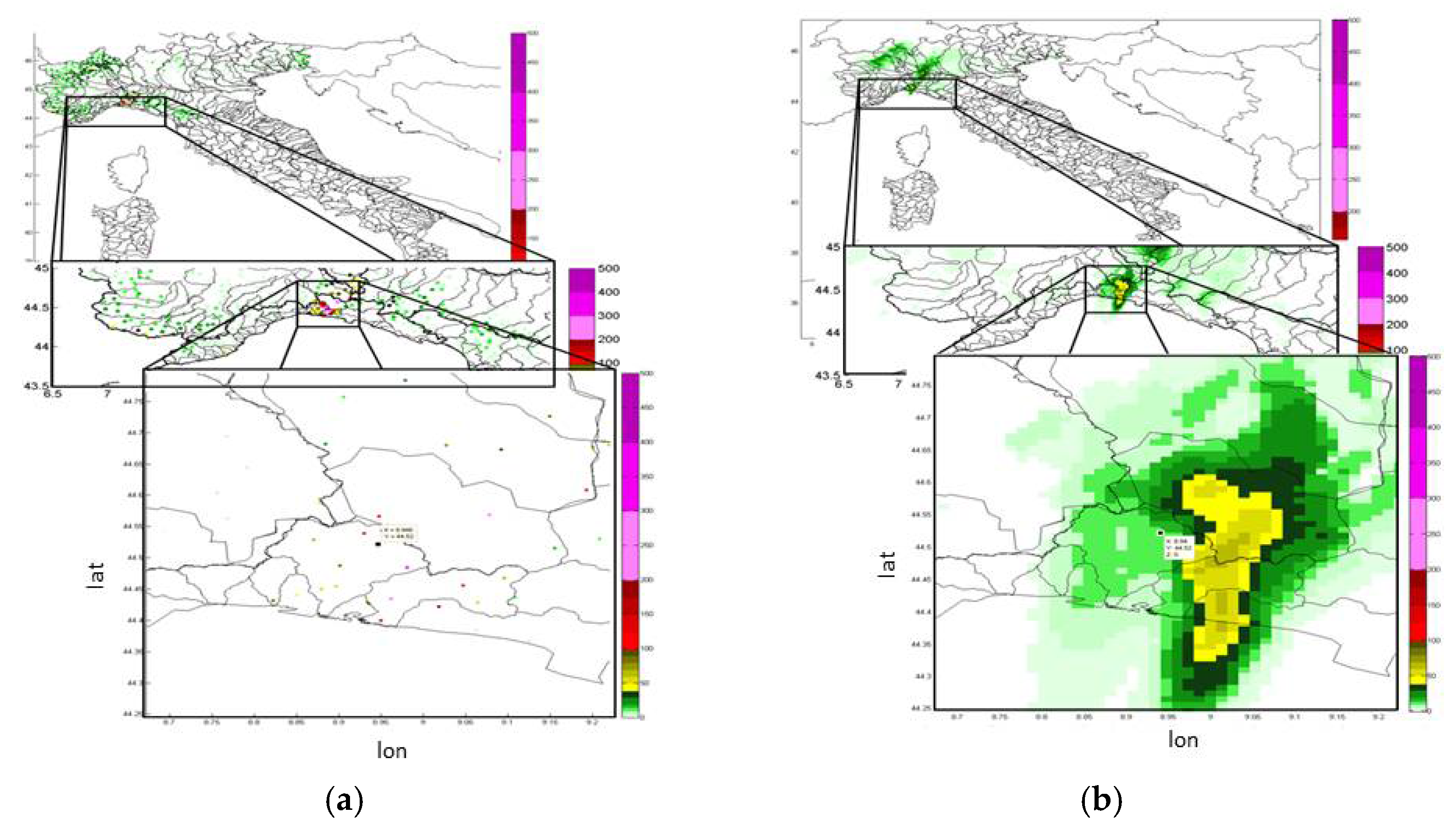

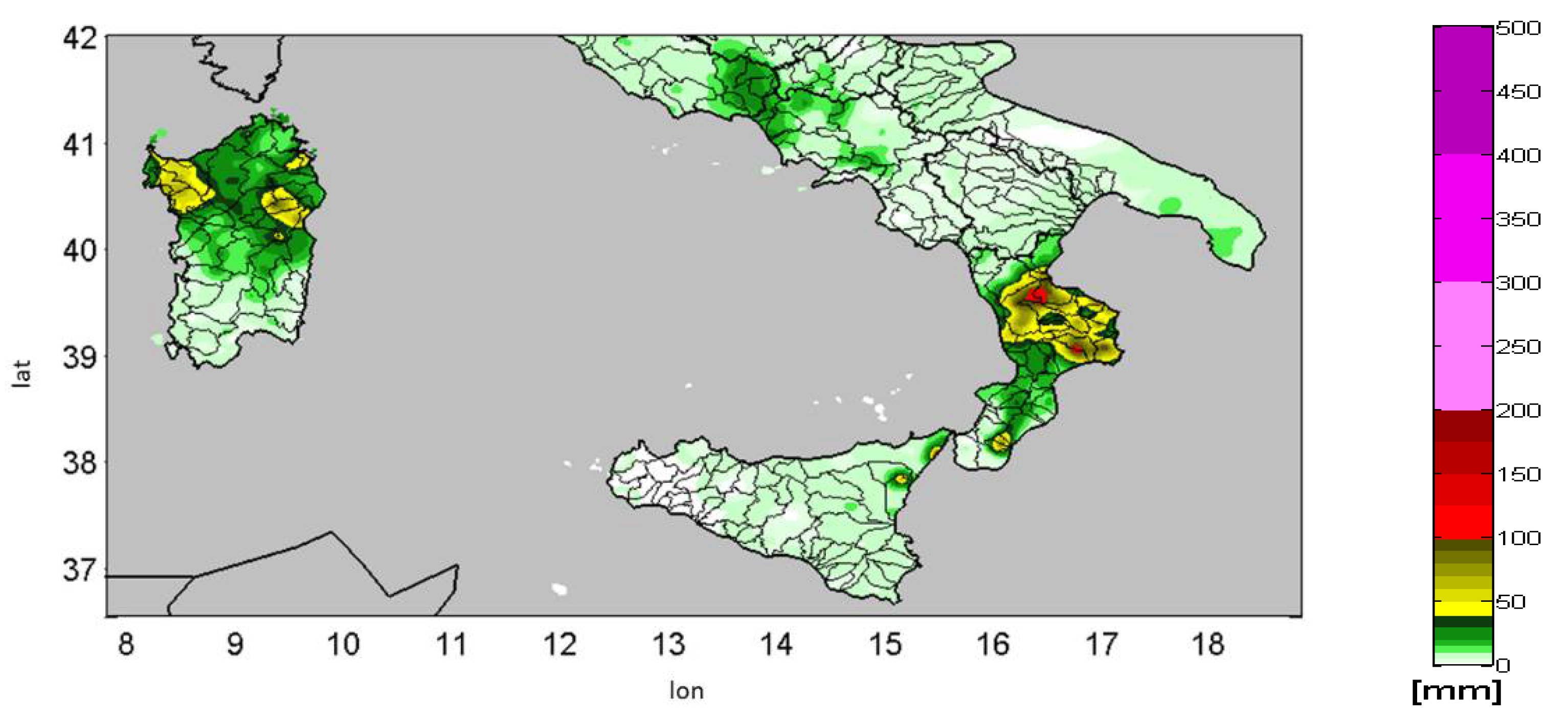
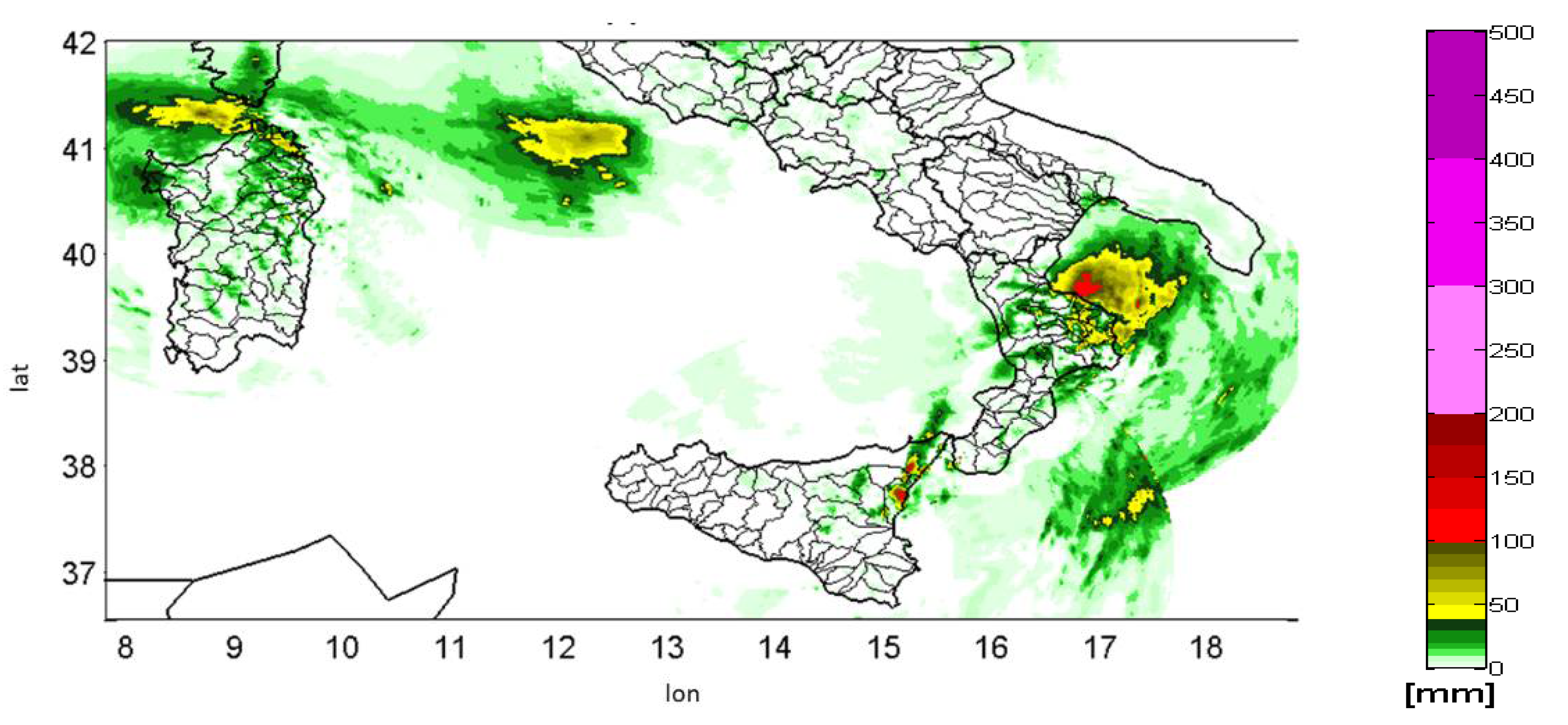
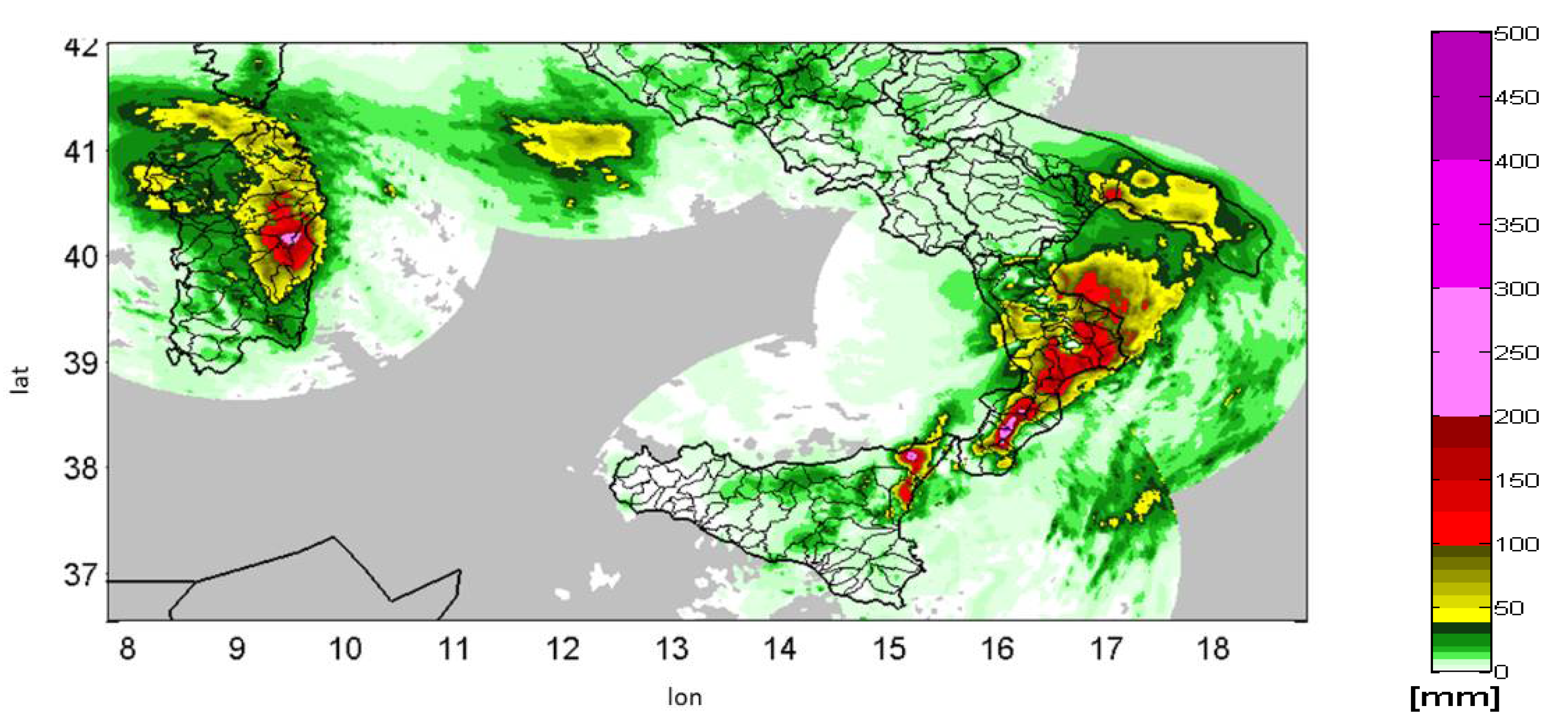
Appendix B
- Ground observations are preserved. This means that on the gauge location the output field maintains the measured values.
- Tendency to a selectable value. The field F(x, y) far from the gauge locations and their influence assumes a specific imposed value.
- Usage of a different structure of kernel. If information about the local field structure is available, it is possible to integrate it to improve the local estimation.
References
- Shakti, P.C.; Nakatani, T.; Misumi, R. The Role of the Spatial Distribution of Radar Rainfall on Hydrological Modeling for an Urbanized River Basin in Japan. Water 2019, 11, 1703. [Google Scholar] [CrossRef]
- Tilford, K.A.; Fox, N.I.; Collier, C.G. Application of weather radar data for urban hydrology. Meteorol. Appl. 2002, 9, 95–104. [Google Scholar] [CrossRef][Green Version]
- Berenguer, M.; Corral, C.; Sánchez-Diezma, R.; Sempere-Torres, D. Hydrological Validation of a Radar-Based Nowcasting Technique. J. Hydrometeorol. 2005, 6, 532–549. [Google Scholar] [CrossRef][Green Version]
- Silvestro, F.; Gabellani, S.; Rudari, R.; Delogu, F.; Laiolo, P.; Boni, G. Uncertainty reduction and parameter estimation of a distributed hydrological model with ground and remote-sensing data. Hydrol. Earth Syst. Sci. 2015, 19, 1727–1751. [Google Scholar] [CrossRef]
- Corral, C.; Berenguer, M.; Sempere-Torres, D.; Poletti, L.; Silvestro, F.; Rebora, N. Comparison of two early warning systems for regional flash flood hazard forecasting. J. Hydrol. 2019, 572, 603–619. [Google Scholar] [CrossRef]
- Orellana-Alvear, J.; Celleri, R.; Rollenbeck, R.; Muñoz, P.; Contreras, P.; Bendix, J. Assessment of Native Radar Reflectivity and Radar Rainfall Estimates for Discharge Forecasting in Mountain Catchments with a Random Forest Model. Remote Sens. 2020, 12, 1986. [Google Scholar] [CrossRef]
- Ochoa-Rodriguez, S.; Wang, L.-P.; Willems, P.; Onof, C. A Review of Radar-Rain Gauge Data Merging Methods and Their Potential for Urban Hydrological Applications. Water Resour. Res. 2019, 55, 6356–6391. [Google Scholar] [CrossRef]
- Zanchetta, A.D.L.; Coulibaly, P. Recent Advances in Real-Time Pluvial Flash Flood Forecasting. Water 2020, 12, 570. [Google Scholar] [CrossRef]
- Silvestro, F.; Gabellani, S.; Delogu, F.; Rudari, R.; Boni, G. Exploiting remote sensing land surface temperature in distributed hydrological modelling: The example of the Continuum model. Hydrol. Earth Syst. Sci. 2013, 17, 39–62. [Google Scholar] [CrossRef]
- Pagano, T.C.; Wood, A.W.; Ramos, M.-H.; Cloke, H.L.; Pappenberger, F.; Clark, M.P.; Cranston, M.; Kavetski, D.; Mathevet, T.; Sorooshian, S.; et al. Challenges of Operational River Forecasting. J. Hydrometeorol. 2014, 15, 1692–1707. [Google Scholar] [CrossRef]
- Alfieri, L.; Salamon, P.; Pappenberger, F.; Wetterhall, F.; Thielen, J. Operational early warning systems for water-related hazards in Europe. Environ. Sci. Policy 2012, 21, 35–49. [Google Scholar] [CrossRef]
- Emerton, R.E.; Stephens, E.M.; Pappenberger, F.; Pagano, T.C.; Weerts, A.H.; Wood, A.W.; Salamon, P.; Brown, J.D.; Hjerdt, N.; Donnelly, C.; et al. Continental and global scale flood forecasting systems. Wiley Interdiscip. Rev. Water 2016, 3, 391–418. [Google Scholar] [CrossRef]
- Pagliara, P.; Corina, A.; Burastero, A.; Campanella, P.; Ferraris, L.; Morando, M.; Rebora, N.; Versace, C. Dewetra, coping with emergencies. In Proceedings of the 8th International Conference on Information Systems for Crisis Response and Management: From Early-Warning Systems to Preparedness and Training, ISCRAM, Lisbon, Portugal, 8–11 May 2011. [Google Scholar]
- Italian Civil Protection Department. CIMA Research Foundation the Dewetra Platform: A Multi-perspective Architecture for Risk Management during Emergencies. In Business Information Systems; Springer Science and Business Media LLC: Berlin, Germany, 2014; Volume 196, pp. 165–177. [Google Scholar]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Parodi, A.; Lagasio, M.; Meroni, A.N.; Pignone, F.; Silvestro, F.; Ferraris, L. A hindcast study of the Piedmont 1994 flood: The CIMA Research Foundation hydro-meteorological forecasting chain. Bull. Atmos. Sci. Technol. 2020, 1, 297–318. [Google Scholar] [CrossRef]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future Köppen-Geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef]
- Seager, R.; Osborn, T.J.; Kushnir, Y.; Simpson, I.R.; Nakamura, J.; Liu, H. Climate Variability and Change of Mediterranean-Type Climates. J. Clim. 2019, 32, 2887–2915. [Google Scholar] [CrossRef]
- Blöschl, G.; Hall, J.; Parajka, J.; Perdigão, R.A.P.; Merz, B.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; Bonacci, O.; Borga, M.; et al. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef]
- Molini, L.; Parodi, A.; Siccardi, F. Dealing with uncertainty: An analysis of the severe weather events over Italy in 2006. Nat. Hazards Earth Syst. Sci. 2009, 9, 1775–1786. [Google Scholar] [CrossRef]
- Poletti, M.L.; Silvestro, F.; Davolio, S.; Pignone, F.; Rebora, N. Using nowcasting technique and data assimilation in a meteorological model to improve very short range hydrological forecasts. Hydrol. Earth Syst. Sci. 2019, 23, 3823–3841. [Google Scholar] [CrossRef]
- Avanzi, F.; Ercolani, G.; Gabellani, S.; Cremonese, E.; Pogliotti, P.; Filippa, G.; di Cella, U.M.; Ratto, S.; Stevenin, H.; Cauduro, M.; et al. Learning about precipitation lapse rates from snow course data improves water balance modeling. Hydrol. Earth Syst. Sci. 2021, 25, 2109–2131. [Google Scholar] [CrossRef]
- Alberoni, P.P.; Ferraris, L.; Marzano, F.S.; Nanni, S.; Pelosini, R.; Siccardi, F. The Italian radar network: Current status and future developments. In Proceedings of the ERAD02, Delft, The Netherlands, 18–22 November 2002; pp. 339–344. [Google Scholar]
- Vulpiani, G.; Pagliara, P.; Negri, M.; Rossi, L.; Gioia, A.; Giordano, P.; Alberoni, P.; Cremonini, R.; Ferraris, L.; Marzano, F.S. The Italian radar network within the national early-warning system for multi-risks management. In Proceedings of the ERAD08, Helsinki, Finland, 30 June–4 July 2008. [Google Scholar]
- Marshall, J.S.; Palmer, W.M.K. The distribution of raindrops with size. J. Atmos. Sci. 1984, 5, 165–166. [Google Scholar] [CrossRef]
- Bancheri, M.; Rigon, R.; Manfreda, S. The GEOframe-NewAge Modelling System Applied in a Data Scarce Environment. Water 2019, 12, 86. [Google Scholar] [CrossRef]
- Brunner, M.I.; Slater, L.; Tallaksen, L.M.; Clark, M. Challenges in modeling and predicting floods and droughts: A review. Wiley Interdiscip. Rev. Water 2021, e1520. [Google Scholar] [CrossRef]
- Alfieri, L.; Lorini, V.; Hirpa, F.A.; Harrigan, S.; Zsoter, E.; Prudhomme, C.; Salamon, P. A global streamflow reanalysis for 1980–2018. J. Hydrol. X 2020, 6, 100049. [Google Scholar] [CrossRef] [PubMed]
- Looper, J.P.; Vieux, B. An assessment of distributed flash flood forecasting accuracy using radar and rain gauge input for a physics-based distributed hydrologic model. J. Hydrol. 2012, 412–413, 114–132. [Google Scholar] [CrossRef]
- Germann, U.; Berenguer, M.; Sempere-Torres, D.; Zappa, M. REAL-Ensemble radar precipitation estimation for hydrology in a mountainous region. Q. J. R. Meteorol. Soc. 2009, 135, 445–456. [Google Scholar] [CrossRef]
- Gabella, M.; Joss, J.; Perona, G.; Galli, G. Accuracy of rainfall estimates by two radars in the same Alpine environment using gage adjustment. J. Geophys. Res. Space Phys. 2001, 106, 5139–5150. [Google Scholar] [CrossRef]
- Todini, E. A Bayesian technique for conditioning radar precipitation estimates to rain-gauge measurements. Hydrol. Earth Syst. Sci. 2001, 5, 187–199. [Google Scholar] [CrossRef]
- Ebtehaj, A.M.; Lerman, G.; Foufoula-Georgiou, E. Sparse regularization for precipitation downscaling. J. Geophys. Res. Space Phys. 2012, 117, D08107. [Google Scholar] [CrossRef]
- Xiao, R.; Chandrasekar, V. Development of a neural network based algorithm for rainfall estimation from radar observa-tions. IEEE Trans. Geosci. Remote Sens. 1997, 35, 160–171. [Google Scholar] [CrossRef]
- Goudenhoofdt, E.; Delobbe, L. Evaluation of radar-gauge merging methods for quantitative precipitation estimates. Hydrol. Earth Syst. Sci. 2009, 13, 195–203. [Google Scholar] [CrossRef]
- Jewell, S.A.; Gaussiat, N. An assessment of kriging-based rain-gauge–radar merging techniques. Q. J. R. Meteorol. Soc. 2015, 141, 2300–2313. [Google Scholar] [CrossRef]
- Wilson, J.W.; Brandes, E.A. Radar measurement of rainfall-A summary. Bull. Amer. Meteor. Soc. 1979, 60, 1048–1058. [Google Scholar] [CrossRef]
- Habib, E.; Krajewski, W.F.; Ciach, G.J. Estimation of Rainfall Interstation Correlation. J. Hydrometeorol. 2001, 2, 621–629. [Google Scholar] [CrossRef]
- Vulpiani, G.; Montopoli, M.; Passeri, L.D.; Gioia, A.G.; Giordano, P.; Marzano, F.S. On the use of dual-polarized C-band ra-dar for operational rainfall retrieval in mountainous areas. J. Appl. Meteorol. Climatol. 2012, 51, 405–425. [Google Scholar] [CrossRef]
- Petracca, M.; D’Adderio, L.P.; Porcù, F.; Vulpiani, G.; Sebastianelli, S.; Puca, S. Validation of GPM Dual-Frequency Precipitation Radar (DPR) Rainfall Products over Italy. J. Hydrometeorol. 2018, 19, 907–925. [Google Scholar] [CrossRef]
- Pignone, F.; Rebora, N.; Silvestro, F.; Castelli, F. GRISO (Generatore Random di Interpolazioni Spaziali da Osservazioni incerte) –Piogge. Rep 2010, 272, 353. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Davolio, S.; Silvestro, F.; Gastaldo, T. Impact of Rainfall Assimilation on High-Resolution Hydrometeorological Forecasts over Liguria, Italy. J. Hydrometeorol. 2017, 18, 2659–2680. [Google Scholar] [CrossRef]
- Silvestro, F.; Parodi, A.; Campo, L.; Ferraris, L. Analysis of the streamflow extremes and long-term water balance in the Liguria region of Italy using a cloud-permitting grid spacing reanalysis dataset. Hydrol. Earth Syst. Sci. 2018, 22, 5403–5426. [Google Scholar] [CrossRef]
- Madsen, H. Automatic calibration of a conceptual rainfall–runoff model using multiple objectives. J. Hydrol. 2000, 235, 276–288. [Google Scholar] [CrossRef]
- Alfieri, L.; Pappenberger, F.; Wetterhall, F.; Haiden, T.; Richardson, D.; Salamon, P. Evaluation of ensemble streamflow predictions in Europe. J. Hydrol. 2014, 517, 913–922. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
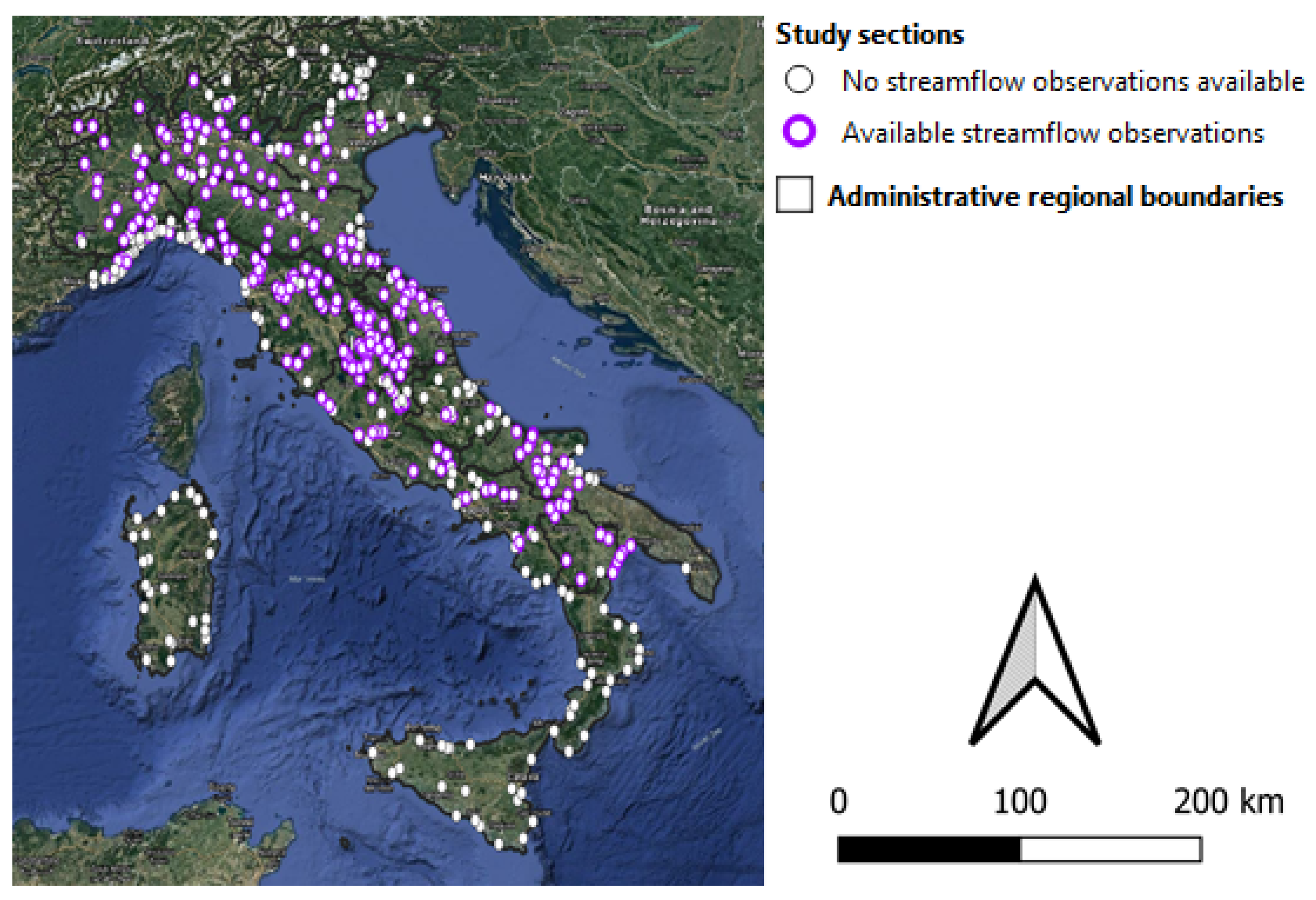
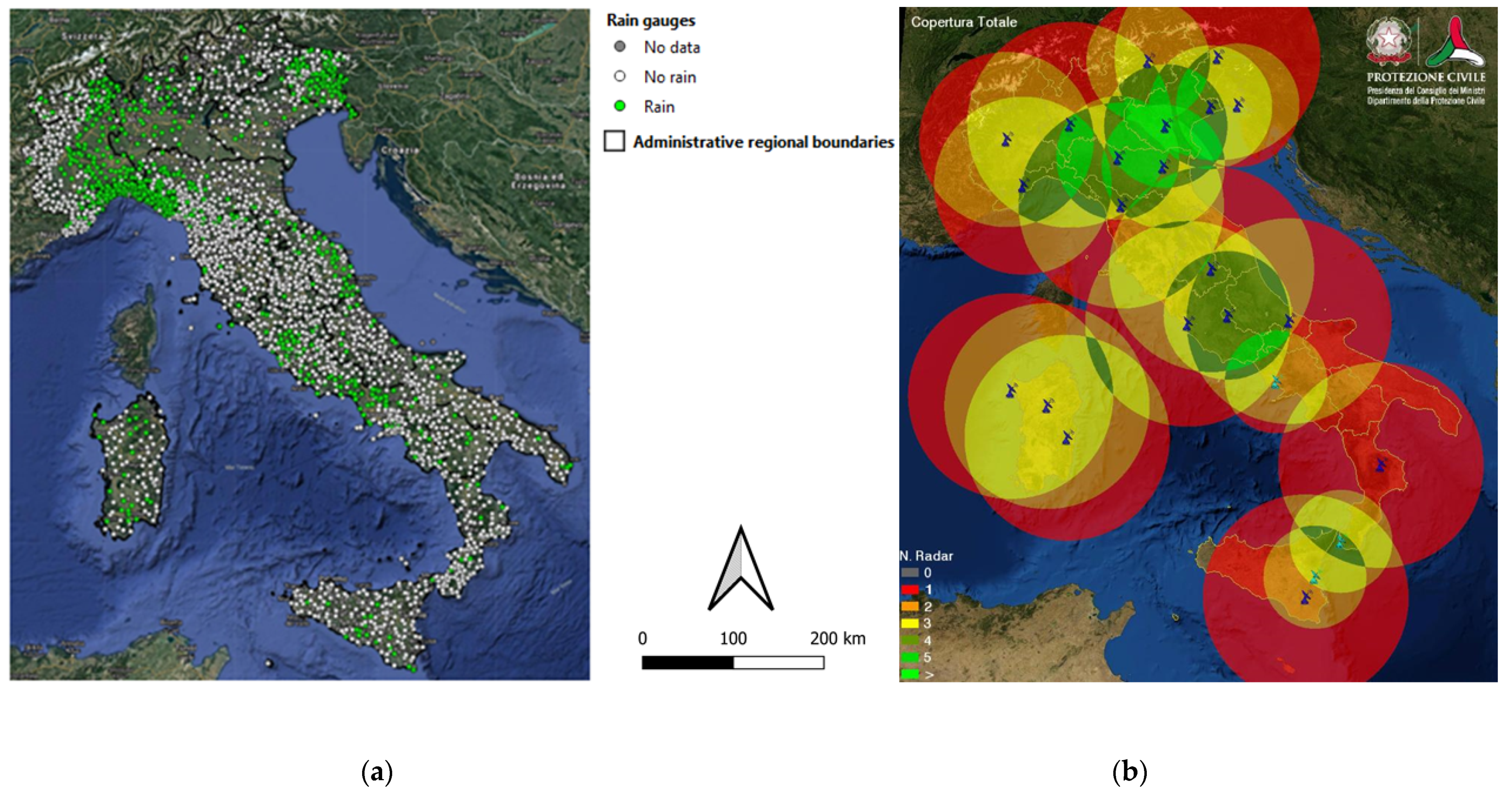

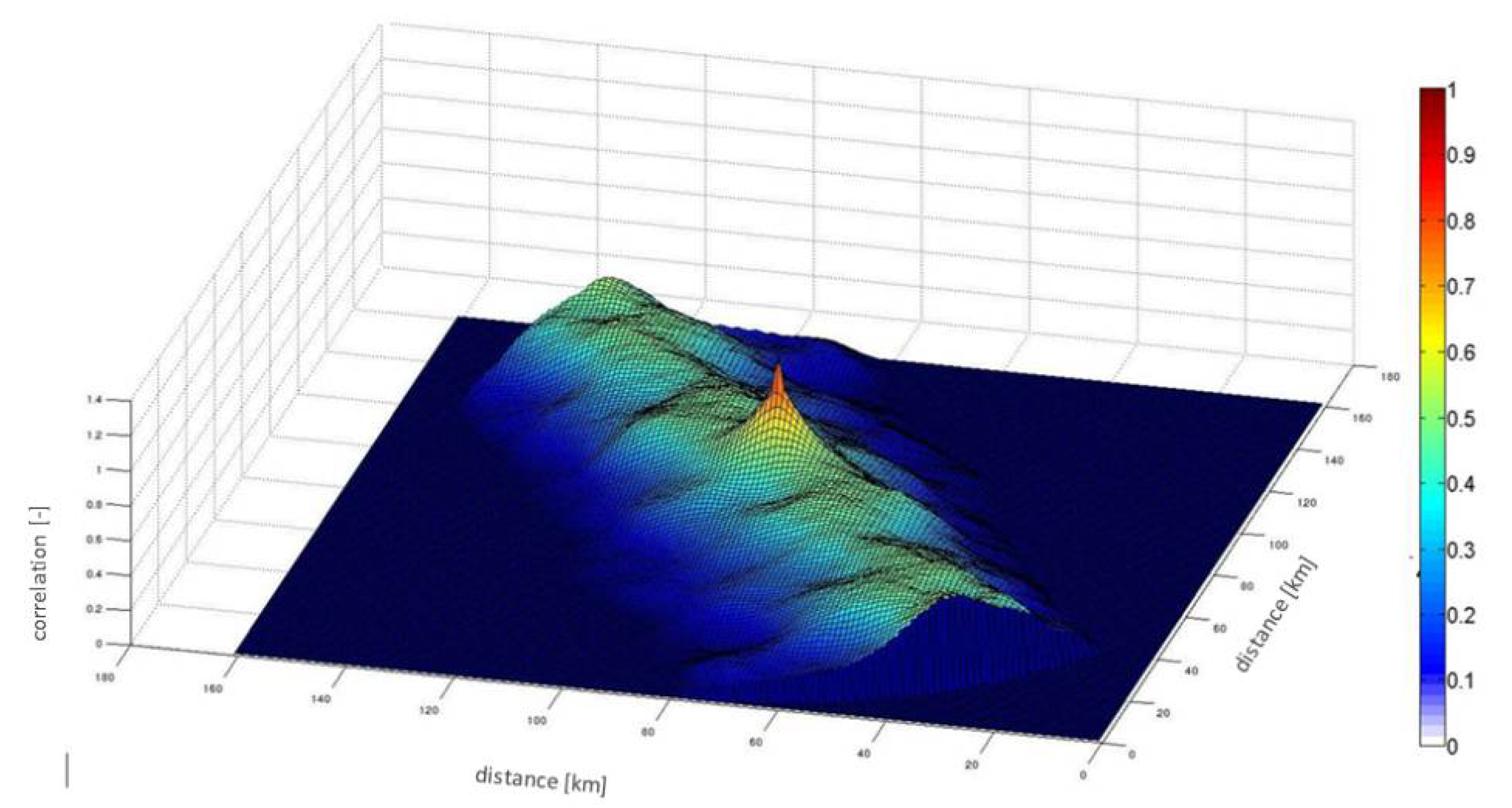

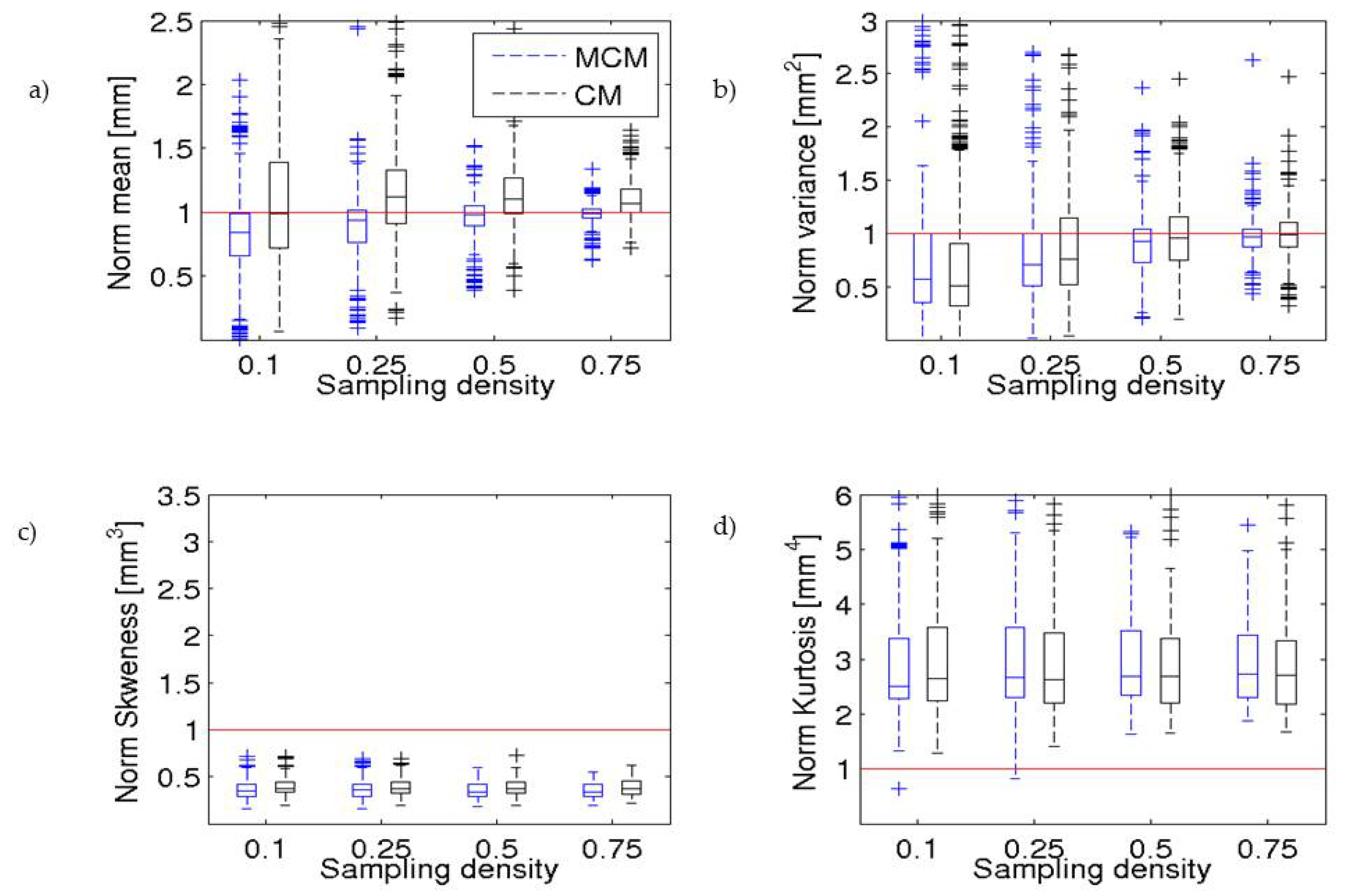
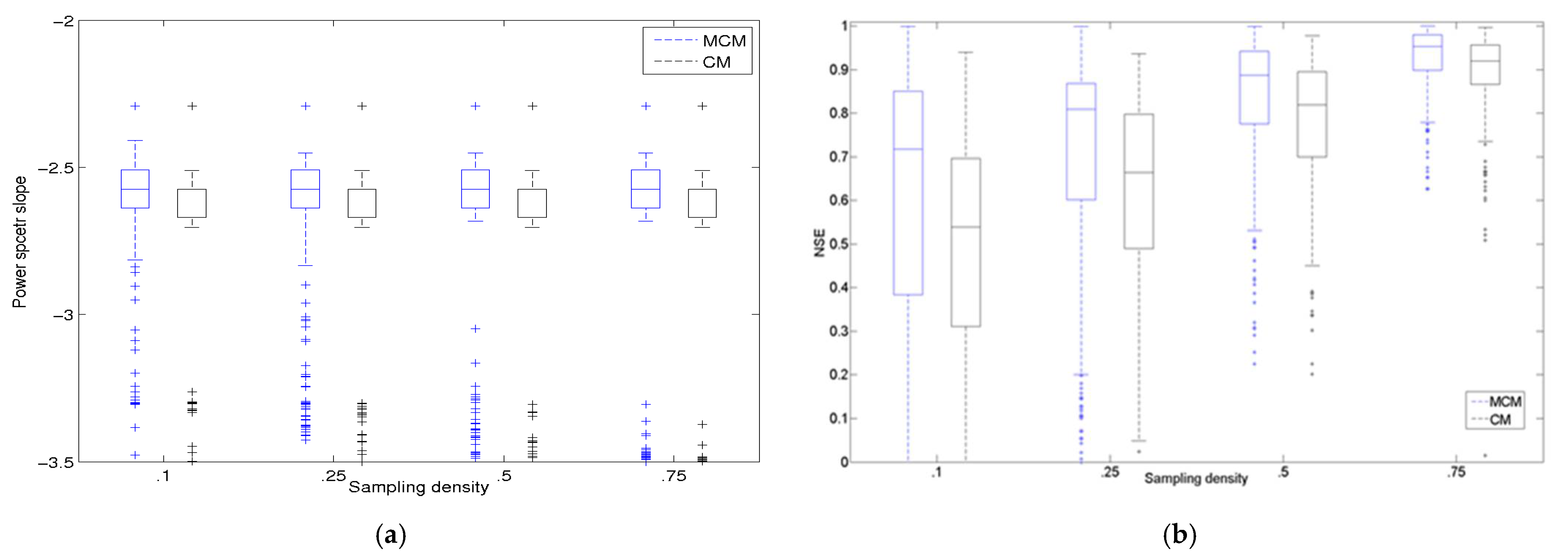


| Longitude | Latitude | Band | Polarization | Range (km) |
|---|---|---|---|---|
| 11.6239 | 44.6561 | C | double | 200 |
| 11.6739 | 45.3561 | C | single | 200 |
| 11.2072 | 46.4894 | C | single | 200 |
| 7.7239 | 45.0228 | C | double | 200 |
| 8.1906 | 44.2394 | C | double | 200 |
| 10.4906 | 44.7894 | C | double | 200 |
| 13.4739 | 45.7228 | C | double | 200 |
| 9.0072 | 40.4228 | C | double | 200 |
| 13.1800 | 42.0500 | C | single | 200 |
| 12.7906 | 45.6894 | C | single | 200 |
| 8.1700 | 40.5700 | C | double | 200 |
| 12.2300 | 41.9100 | C | single | 200 |
| 9.2800 | 45.3400 | C | single | 200 |
| 10.6072 | 43.9561 | C | double | 200 |
| 16.6239 | 39.3728 | C | double | 200 |
| 12.7906 | 42.8561 | C | double | 200 |
| 14.6239 | 41.9394 | C | double | 200 |
| 12.9739 | 46.5561 | C | double | 200 |
| 9.4938 | 39.8822 | C | double | 200 |
| 14.8239 | 37.1228 | C | double | 200 |
| 15.0498 | 37.4617 | X | double | 100 |
| 15.6500 | 38.0700 | X | double | 100 |
| 14.2750 | 40.8800 | X | double | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bruno, G.; Pignone, F.; Silvestro, F.; Gabellani, S.; Schiavi, F.; Rebora, N.; Giordano, P.; Falzacappa, M. Performing Hydrological Monitoring at a National Scale by Exploiting Rain-Gauge and Radar Networks: The Italian Case. Atmosphere 2021, 12, 771. https://doi.org/10.3390/atmos12060771
Bruno G, Pignone F, Silvestro F, Gabellani S, Schiavi F, Rebora N, Giordano P, Falzacappa M. Performing Hydrological Monitoring at a National Scale by Exploiting Rain-Gauge and Radar Networks: The Italian Case. Atmosphere. 2021; 12(6):771. https://doi.org/10.3390/atmos12060771
Chicago/Turabian StyleBruno, Giulia, Flavio Pignone, Francesco Silvestro, Simone Gabellani, Federico Schiavi, Nicola Rebora, Pietro Giordano, and Marco Falzacappa. 2021. "Performing Hydrological Monitoring at a National Scale by Exploiting Rain-Gauge and Radar Networks: The Italian Case" Atmosphere 12, no. 6: 771. https://doi.org/10.3390/atmos12060771
APA StyleBruno, G., Pignone, F., Silvestro, F., Gabellani, S., Schiavi, F., Rebora, N., Giordano, P., & Falzacappa, M. (2021). Performing Hydrological Monitoring at a National Scale by Exploiting Rain-Gauge and Radar Networks: The Italian Case. Atmosphere, 12(6), 771. https://doi.org/10.3390/atmos12060771





