AIM-E: E-Region Auroral Ionosphere Model

Abstract

The auroral oval is the high-latitude region of the ionosphere characterized by strong variability of its chemical composition due to precipitation of energetic particles from the magnetosphere. The complex nature of magnetospheric processes cause a wide range of dynamic variations in the auroral zone, which are difficult to forecast. Knowledge of electron concentrations in this highly turbulent region is of particular importance because it determines the propagation conditions for the radio waves. In this work we introduce the numerical model of the auroral E-region, which evaluates density variations of the 10 ionospheric species and 39 reactions initiated by both the solar extreme UV radiation and the magnetospheric electron precipitation. The chemical reaction rates differ in more than ten orders of magnitude, resulting in the high stiffness of the ordinary differential equations system considered, which was solved using the high-performance Gear method. The AIM-E model allowed us to calculate the concentration of the neutrals NO, N(⁴S), and N(²D), ions N⁺, N₂⁺, NO⁺, O₂⁺, O⁺(⁴S), O⁺(²D), and O⁺(²P), and electrons Ne, in the whole auroral zone in the 90‒150 km altitude range in real time. The model results show good agreement with observational data during both the quiet and disturbed geomagnetic conditions.

1. Introduction

The Earth’s ionosphere E-layer in the auroral zone is one of the primary indicators of solar influence on our planet. Satellite and ground-based ionospheric observations have limited temporal and spatial resolution, therefore the need for mathematical modeling arises. Models are widely used to analyze the ionosphere state when it is necessary to know the ionospheric parameters for any location and time.

Ionosphere numerical modeling provides a quantitative description of the ionospheric parameters and their spatial-temporal variations. These parameters are electron density, ion composition, ion and electron temperatures, ion velocity, and other parameters, depending on the modeling tasks. The ionospheric models can vary greatly in terms of computational accuracy, temporal and spatial resolution, computational costs (processor time, memory, etc.), purpose of use, and accessibility. There are a number of different ionospheric models described in the literature, but it should be noted that there is no universal approach that simultaneously satisfies all the requirements. The decision of which model to use depends on the goals and needs, computing resources, and the input data availability.

The E-region models, in most cases, are part of the global ionosphere or upper atmosphere models. The ionosphere global numerical models are a complex set of programs for solving the nonlinear differential equation systems. It should be noted that not all global models provide reliable results for the E-region at high latitudes. Depending on the given conditions, the global models can evaluate variations of the ionospheric parameters associated with solar activity cycles, seasonal and diurnal variations, and geomagnetic activity. Usually, the global models are computationally expensive and require supercomputers for global simulations. Therefore, such models are adequate for solving theoretical problems or for case studies, but not for the real time ionosphere monitoring.

Empirical ionosphere models are based on aggregated experimental data obtained by various methods. Usually, they are quite simple in calculations and can be used for real time diagnostics. However, the empirical models a priori do not include any dynamics and can demonstrate only a sequence of average states, and can satisfactorily describe only regular patterns of the ionosphere.

Another weakness of empirical models is the nonuniformity of the data coverage used to train the model. The most commonly used empirical model of the ionosphere is the global model International Reference Ionosphere (IRI), recommended by the Committee on Space Research (COSPAR) and the International Union of Radio Science (URSI) [1,2]. IRI-2016 is the latest modification of the model [3]. Like any empirical model, IRI is most accurate in regions with the densest observation coverage. Since most of the ionospheric data were obtained from the European and North American latitudes, these areas are best represented in the IRI. The Northern Hemisphere and continents are better described than the Southern Hemisphere and oceans, again due to obvious differences in data volume [4]. The IRI model can be used primarily for the middle latitudes. At the auroral and polar latitudes, the model based on observations from a small number of ground-based stations and satellites insufficient for an accurate modeling of this highly variable region. At the high latitudes, IRI can be applied only for rough evaluation of background ionospheric parameters, due to both low data coverage and high variability of the region considered [5]. A comparison of the IRI-2007 model with the vertical sounding data [6,7,8] shows that the model does not provide accurate calculation results for ionospheric parameters in disturbed geomagnetic conditions in the auroral zone and cannot be used for the auroral E-region.

There are a dozen models [9,10,11,12] that are used to study local processes in the auroral zone. For example, the Physicochemical Model of the Auroral Ionosphere [10] is a numerical model describing processes of the main excited and ionized atmospheric components interaction during auroral electron precipitation. The time-dependent, one-dimensional auroral model used in [11] is a combination of an electron transport code [13] and an auroral ionosphere kinetic model [14,15] evaluating the key E-region ions and minor neutral species over an altitude range 75–500 km. The thermosphere-ionosphere Fe/Fe⁺ (TIFe) model [16] was developed for the investigation of formation mechanisms of thermospheric Fe layers observed by lidar in Antarctica. Those models are intended mostly for the case studies, and they show good calculation results and accurately describe the local physical and chemical processes of the auroral ionosphere.

We present an E-Region Auroral Ionosphere Model (AIM-E) that calculates the ion composition and electron concentration in the high-latitude E-region, including the auroral zone using as input parameters the auroral electron fluxes: (1) measured directly along the satellite trajectory using directly measured electron precipitation flux; or (2) their distribution and spatio-temporal variation using the empirical precipitation model. The AIM-E ionosphere model’s advantage is flexibility of the input form of the photo-ionization source. The spectrum of solar extreme ultraviolet radiation can be specified in two ways: (1) using direct measurements of the photon flux spectrum from the such as TIMED satellite, for example; and (2) with the model EUVAC spectra, parameterized by the value of the daily index F10.7. The high-performance computation method allows the computer time to be reduced; therefore, the one-dimensional model can be used for fast calculations, and it shows the spatial distribution of electron concentration and other ionosphere parameters over the entire auroral zone.

2. Materials and Methods

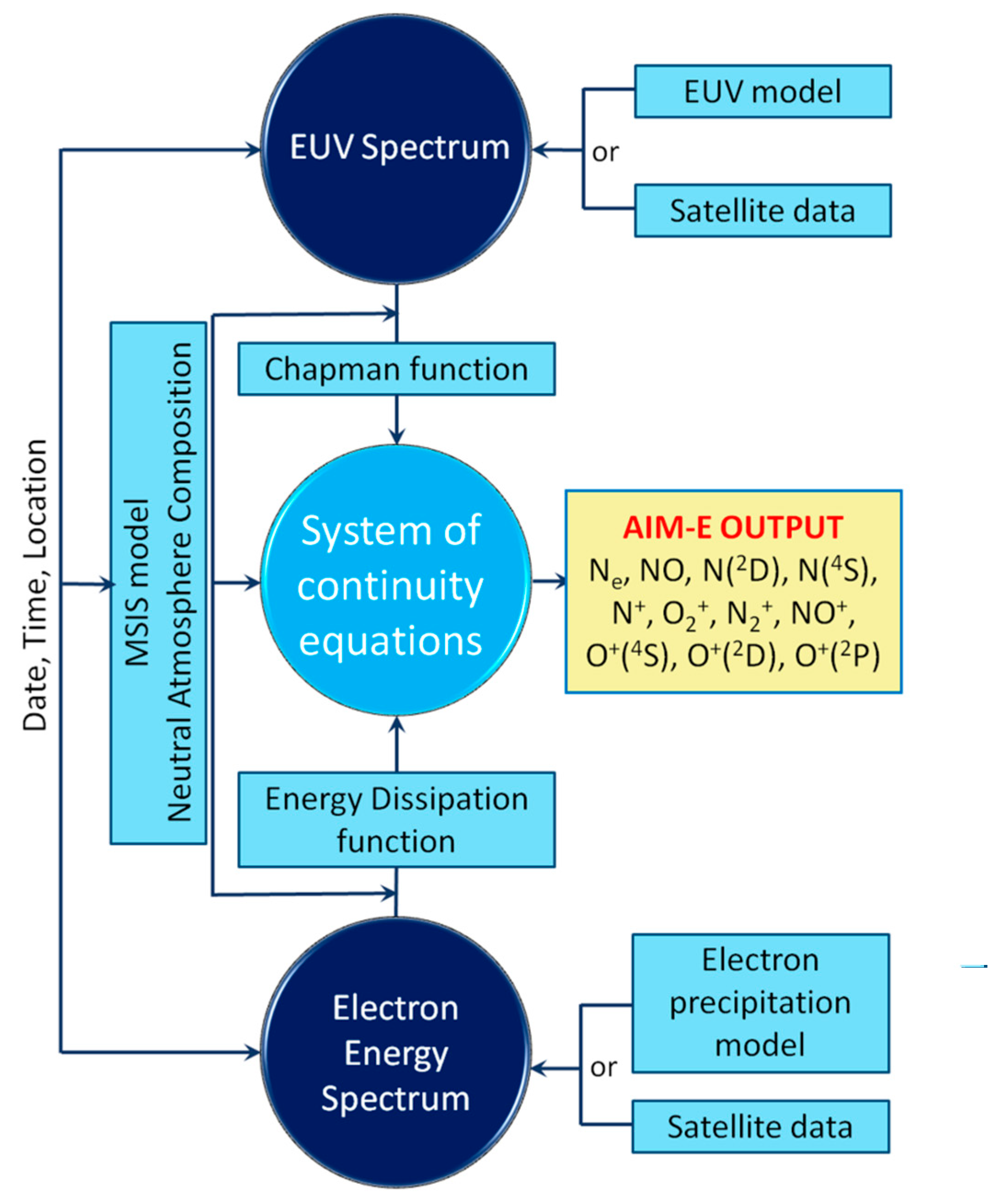
The main scope of the AIM-E model is real-time diagnostics of the high-latitude ionospheric E-region. AIM-E provides temporal and spatial density variations of the minor neutral species NO, N(⁴S), N(²D), ions N⁺, N₂⁺, NO⁺, O₂⁺, O⁺(⁴S), O⁺(²D), O⁺(²P) and electrons Ne. Figure 1 shows the general structure of the AIM-E model. Model input parameters are the solar EUV and auroral electron flux for the given date, time, and geographical coordinates, which can be set on the grid or in arbitrary locations. Neutral atmosphere composition and temperature are also input parameters of the model and they were taken from the NRLMSISE-00 model [17].

In quiet geomagnetic conditions during the daytime, the main ionization source, responsible for regular E layer formation, is EUV solar radiation in the wavelength range from 5 to 105 nm. For the night conditions, it is extremely important to take ionization by electrons of magnetospheric origin with energy 10–30 keV into account. During disturbed periods, sporadic ionization by the precipitating electrons plays a dominant role. In the AIM-E model, both the EUV solar radiation and the electron precipitation flux can be specified in two ways: (1) from the direct satellite measurements; and (2) from the empirical, the EUVAC model for solar radiation [18] and OVATION-Prime for electron precipitation [19]. Any other solar radiation EUV and energetic electron precipitation models can be used as AIM-E input source, depending on the modeling tasks.

Solar photons and magnetospheric electrons lose energy due to the absorption passing the atmosphere. This fact is taken into account using the extended Chapman function for the solar EUV radiation propagation [20] and the energy dissipation function for the precipitation electrons [21]. Photo-ionization (q_uv) and energetic electron (q_corp) ionization rates obtained for different ions come into a system of ten ordinary differential equations (ODE) (Appendix A). The initial solution of the ODE system is based on the equilibrium state of the E-layer, which reaches 39 chemical reactions between ionospheric species (Appendix B) in each location under specific solar and geomagnetic activity conditions. The numerical solution of the ODE system for neutrals and ions is implemented using the high-performance Gear method [22] (see Appendix D).

2.1. Photo-Ionization

The photo-ionization rate ${\mathrm{q}}_{\mathrm{j}}\left(\mathrm{z}\right)$ of the neutral gas j-th component is the number of photo-ionization acts per unit volume per unit of time at the altitude z, is determined by the expression [23]:

$${\mathrm{q}}_{\mathrm{j}}\left(\mathrm{z}\right)={\mathrm{n}}_{\mathrm{j}}{{\displaystyle \sum }}_{\mathsf{\lambda }}{\mathsf{\sigma }}_{\mathrm{j}\mathsf{\lambda }}^{\mathrm{i}}{\mathrm{I}}_{\mathsf{\lambda }}^{\infty }\exp (-{{\displaystyle \sum }}_{\mathrm{n}}{\mathsf{\sigma }}_{\mathrm{n}\mathsf{\lambda }}^{\mathrm{a}}{{\displaystyle \int }}_{\mathrm{z}}^{\infty }\mathrm{Ch}\left(\mathsf{\chi }\right){\mathrm{n}}_{\mathrm{n}}\mathrm{dz}),$$

(1)

where ${\mathrm{n}}_{\mathrm{j}}$—the concentration of the gas j, ${\mathsf{\sigma }}_{\mathrm{j}\mathsf{\lambda }}^{\mathrm{i}}$—the photoionization cross-section of the gas j by solar radiation at wavelength, λ, ${\mathsf{\sigma }}_{\mathrm{j}\mathsf{\lambda }}^{\mathrm{a}}$—the photo-absorption cross-section of the gas j by solar radiation at wavelength, λ, ${\mathrm{I}}_{\mathsf{\lambda }}^{\infty }$—the photon flux density at wavelength, λ at the top of the atmosphere, $\mathrm{Ch}\left(\mathsf{\chi }\right)$—the Chapman function.

The photon flux at the top of the atmospheric, ${\mathrm{I}}_{\mathsf{\lambda }}^{\infty }$ is the number of photons per unit area located perpendicular to the radiation direction per unit of time. The photo-absorption and photoionization rates for the neutral atmospheric components depend on the solar radiation wavelength. The photo-absorption and photo-ionization cross-sections for O, N₂, and O₂ were taken from [24]. Quantum yields of different states the atomic oxygen ions were taken from [25]. The numerical values of the cross-sections are given in Appendix C.

Calculation of the electron density using the auroral ionosphere model for the daytime can be done using two different methods of solar EUV radiation input: (1) a theoretically calculated EUV spectrum using EUVAC Solar Flux Model [16] parametrized on F10.7 index [26] (see example in Section 3.1); and (2) direct measurements of the solar EUV spectra obtained from spacecraft.

2.2. Electron Precipitation Ionization

During the disturbed periods, such as magnetospheric storms and substorms, ionospheric ionization in the auroral zone caused by particle precipitation can be several orders of magnitude higher than photoionization. Thus, it is crucial to take into account the energetic electron precipitation for adequate modeling of ion composition in the high latitude ionosphere.

The ion production rates for ionization of the atmospheric neutrals by auroral electrons are calculated using the approach described in [21].

According to Sergienko and Ivanov method [21] the ionization rate q_j(z) (cm⁻³ s⁻¹) of the certain ion j at the altitude z is defined by:

$${\mathrm{q}}_{\mathrm{j}}\left(\mathrm{z}\right)={\mathrm{P}}_{\mathrm{j}}\left(\mathrm{z}\right)\frac{\mathrm{W}\left(\mathrm{z}\right)}{{\mathsf{\epsilon }}_{\mathrm{j}}\left(\mathrm{z}\right)}$$

(2)

where: W(z) is the energy deposition function of the auroral electrons (eV cm⁻³ s⁻¹), P_j(z) is the deposited energy fraction expended in the excitation and ionization of the neutral j, and ε_j(z) is the “energy cost” for the ionization of the neutral j, that is, the average energy expended in the creation of an electron-ion pair of the neutral j (eV).

For mono-energetic electron flux with electron energy of E (eV) the energy deposition function can be expressed in term of the dimensionless dissipation function as:

$$\mathrm{w}\left(\mathrm{z},\mathrm{E}\right)=\mathsf{\rho }\left(\mathrm{z}\right) \frac{\mathsf{\Lambda }(\frac{\mathrm{s}\left(\mathrm{z}\right)}{\mathrm{R}\left(\mathrm{E}\right)})\mathrm{E}\left(1-\mathrm{Alb}\left(\mathrm{E}\right)\right)}{\mathrm{R}\left(\mathrm{E}\right)}$$

(3)

where: z is altitude (km), ρ(z) is the atmospheric mass density (g cm^–3), s(z) is the distance from the top of ionosphere z₀ to the altitude z in mass density units (g cm⁻²), R(E) is the average range of an electron in air (g cm^–2), Λ is the dimensionless dissipation function, E is the Energy (eV), and Alb(E) is an albedo flux, that is, the dimensionless function describing the part of the total energy contained in the initial electron flux that is back-scattered by the atmosphere.

For an arbitrary theoretical or experimental electron differential flux φ(E) at the top of the ionosphere the energy deposition function can be expressed by the integral:

$$\mathrm{W}\left(\mathrm{z}\right)={{\displaystyle \int }}_{{\mathrm{E}}_{\min }}^{{\mathrm{E}}_{\max }}\mathsf{\phi }\left(\mathrm{E}\right)\mathrm{w}\left(\mathrm{z},\mathrm{E}\right)\mathrm{dE}$$

(4)

φ(E) is the differential auroral electron flux at the top of the ionosphere (700 km) (eV⁻¹ cm⁻² s⁻¹).

All parameters in Equation (3) were taken from [21]. The production rates of the ion species involved in the model are calculated by substituting the Equation (4) into Equation (2) and using the “energy cost” presented in

Table 1. Energy cost for different ions.

Ion	${\mathbf{N}}_2^{+}$	${\mathbf{O}}_2^{+}$	${\mathbf{O}}^{+}\left(4\mathbf{S}\right)$	${\mathbf{O}}^{+}\left(2\mathit{P}\right)$	${\mathbf{O}}^{+}\left(2\mathbf{D}\right)$
Energy cost, eV	36.8	28.2	64.0	69.0	140.0

.

2.3. Aeronomy Block

The AIM-E module of ionospheric aeronomy is a solver of a system of ten first-order nonlinear ordinary differential equations (Appendix A). The equations represent the non-stationary one-dimensional continuity equations for ten species included in the model:

$$\frac{{\mathrm{dN}}_{\mathrm{i}}\left(\mathrm{z}, \mathrm{t}\right)}{\mathrm{dt}}={ \mathrm{Q}}_{\mathrm{i}}\left(\mathrm{z}, \mathrm{t}\right)-{\mathrm{L}}_{\mathrm{i}} \left(\mathrm{z}, \mathrm{t}\right),$$

(5)

where ${\mathrm{N}}_{\mathrm{i}}$ is the concentration of species i, ${\mathrm{Q}}_{\mathrm{i}}$, and ${\mathrm{L}}_{\mathrm{i}}$ are the production and loss rates of species i respectively at the altitude z. The diffusion term is omitted in the continuity equations, because the transport effects are negligible for the E-region ionosphere [27].

The production rates Q and the loss rates L include photo-ionization, ionization, and excitation by the auroral electron precipitation and chemical reactions.

The concentrations of the minor neutral components $\mathrm{NO}$, $\mathrm{N}\left(4\mathrm{S}\right)$, and $\mathrm{N}\left(2\mathrm{D}\right)$ and ions N⁺, ${\mathrm{N}}_2^{+}$, ${\mathrm{NO}}^{+}$, ${\mathrm{O}}_2^{+}$, ${\mathrm{O}}^{+}\left(4\mathrm{S}\right)$, ${\mathrm{O}}^{+}\left(2\mathrm{D}\right)$, and ${\mathrm{O}}^{+}\left(2\mathrm{P}\right)$ at the altitude range between 90 and 150 km are calculated. The initial conditions of the Cauchy problem of the $\mathrm{N}\left(4\mathrm{S}\right)$ and $\mathrm{N}\left(2\mathrm{D}\right)$ neutrals are set to zero.

The system is solved using an iterative procedure, which continues until the state of chemical equilibrium is reached for the given input conditions. The chemical reaction rates differ by more than 12 orders of magnitude. Such a wide range of the coefficient values results in high stiffness of the ODE system. Since the stiff ODE cannot be efficiently solved using explicit numerical schemes, a number of implicit methods were specially designed for such systems. Here we describe the application of the 4-th order iterative implicit scheme from the family of Gear methods [22], which is briefly summarized in Appendix D. Employment of the Gear method with step size adjustment dramatically decreased the computation costs when solving the stiff ODE system.

3. Results

In this section we present three examples of case studies that present the possible scope of applications of the AIM-E model: (1) monitoring of the regular E layer parameters; (2) calculation of the electron concentration vertical profiles along the satellite trajectory; and (3) evaluation of global electron distribution in the high latitude ionosphere using EUV and particle precipitation models as inputs.

3.1. Monitoring of the Regular E-Layer Parameters

During the day, the ionospheric regular E-layer plays an important role in the HF radio wave propagation (3–30 MHz). Knowing the current conditions and forecast of the regular E-layer is critical to ensuring long-distance logistics on land, at sea, and in the air.

A 3-day period of quiet geomagnetic conditions, 8–10 June 2017, was used to prove the ability of the AIM-E model to predict the main characteristics of regular E layer (mean Kp index for this period is equal 0.7 and mean AE = 67 nT). We compare the measured and calculated critical frequencies for a number of ground-based stations at auroral and subauroral latitudes—Gorkovskaya (GRK), Salekhard (SAH), Lovozero (LOZ), Pevek (PBK), Amderma (AMD), Tiksi (TIK), and Dikson (DIK). Geographic and corrected geomagnetic coordinates of the stations are given in the

Table 2. Geographic and corrected geomagnetic coordinates of high-latitude ionosphere vertical sounding stations.

Station Number	Station Code	Observation Point	Geographic Latitude	Geographic Longitude	Corrected Geomagnetic Latitude	Corrected Geomagnetic Longitude
1	GRK	Gorkovskaya	60.27° N	29.38° E	56.74° N	105.55° E
2	SAH	Salekhard	66.52° N	66.67° E	63.04° N	141.69° E
3	LOZ	Lovozero	68.00° N	35.02° E	64.67° N	113.47° E
4	PBK	Pevek	70.03° N	170.92° E	65.83° N	126.77° W
5	AMD	Amderma	69.60° N	60.20° E	66.04° N	136.48° E
6	TIK	Tiksi	71.35° N	128.54° E	66.65° N	160.40° W
7	DIK	Dickson	73.52° N	80.68° E	69.59° N	156.42° E

, the vertical sounding data provided by the Polar Geophysical Center of the Arctic and Antarctic Research Institute (https://geophys.aari.ru, accessed on 8 June 2021). A negligibility of the sporadic Es layer during this period allowed us to determine 406 values of critical frequency for the regular E layer (foE) from 504 available hourly ionograms.

For each time and observation point the AIM-E model with the EUVAC photon flux input was used to calculate the vertical profiles of the electron concentration in the altitude range from 90–130 km with 1 km step size. Using the EUVAC model parametrized on the F10.7 index as the AIM-E model input allowed us to calculate EUV solar radiation fluxes in the wavelength range from 5 nm to 105 nm, including 36 spectral lines.

The critical modeled frequency in MHz was determined from the value of the E-layer maximum electron concentration Ne [m⁻³] as:

$${\mathrm{f}}_{\mathrm{O}}\mathrm{E}=\sqrt{\frac{{\mathrm{N}}_{\mathrm{e}}}{1.24\times {10}^{10}}}$$

(6)

Figure 2 shows the diurnal variation of the foE measured (red lines) and modeled (blue dashed lines) foE during the considered 3-day period for the selected auroral and subauroral stations. The modeled foE values were in good agreement with measured values at all stations (correlation coefficient R = 0.982). This result shows that the AIM-E model can adequately describe the current state (and even a short-term forecast) of the ionosphere regular E layer, which is especially important in the absence of ionospheric data or during the strong D-region absorption events.

3.2. Calculation of the Vertical Electron Concentration Distribution along the Satellite Trajectory

In this section we present the calculation of electron concentration altitude profiles along the REIMEI satellite [28] pass across the auroral oval on 5 December 2007. During this intense electron precipitation event, the REIMEI satellite was in magnetic conjunction with EISCAT radar at 0:36:36 UT (0.610 h), enabling quantitative verification of the AIM-E model. The REIMEI spacecraft has a near-sun-synchronous orbit at 12:50–0:50 LT meridian and its altitude range is 610–670 km. Projection of the spacecraft trajectory along the IGRF-12 magnetic field [29] to the 110 km altitude is shown in Figure 3a. Figure 3b shows the REIMEI satellite differential electron energy flux measured in the energy range from 60 eV to 11 keV on 5 December 2007 during its passage of the auroral oval (00:35:45–00:37:17 UT (0.596–0.621 h)). The corresponding AIM-E solution for the electron concentration vertical profile (Figure 3c) has a clear response to a change of the precipitating electrons’ energy spectrum. A notable manifestation is an increase of the electron concentration by the ~2 order of magnitude and the sporadic Es-layer formation after 00:36:18 UT (0.605 h) due to the sharp increase of the ~3 keV electron flux.

We used the EISCAT Tromso UHF incoherent scattering radar observations (http://portal.eiscat.se/madrigal/, accessed on 6 June 2021) to perform a quantitative verification of the AIM-E results. The radar is located in Tromso, Norway (69°35′ N, 19°13′ E). The EISCAT experiment was carried out simultaneously with the REIMEI satellite passage and the moment of the conjugated measurements was at 0:36:36 UT (0.610 h). The EISCAT UHF radar operated the radar program Arc1 (altitude range: 96–422 km; spatial resolution: 0.9 km; temporal resolution: 0.44 s) with the antenna directed to the magnetic zenith. Figure 4 shows a sufficiently good agreement between the altitude profile of the electron concentration calculated with the AIM-E model (red line) and measured by incoherent scattering radar (blue line). The discrepancy between model and radar data can be explained by the fact that the observation of precipitating electrons by REIMEI spacecraft was not performed exactly over the incoherent scatter radar. The spatial distribution of the electron precipitation in the auroral region is very dynamic and has irregular structure, and the difference of even several tens of kilometers may lead to the observed uncertainty in the model results. The results obtained during the quiet geomagnetic conditions (Section 3.1), when solar EUV radiation dominates, indicate that the ODE system solution and the calculation methodology are correct.

3.3. Global Distribution of Ionospheric Composition

Using the empirical models of the solar EUV radiation and auroral electron precipitations, the AIM-E model allowed us to obtain spatial distribution of ionospheric parameters regardless of the availability of direct satellite measurements. An example of an electron concentration map, shown in Figure 5, demonstrates an ability of AIM-E to simulate the global distribution of ionospheric composition using modeled input parameters. For these calculations, the empirical EUVAC and OVATION-Prime models were used to provide the input photon and electron fluxes at the top of the ionosphere, respectively.

We adapted the OVATION-Prime model, which is based on the DMSP measurements and provides electron precipitation parameters in the high latitudes. Using the OVATION-Prime results as an input for the AIM-E model, we could calculate an instant ion and electron composition everywhere in the high-latitude ionosphere for the wide range of geophysical conditions. The OVATION-Prime model provides only three general precipitation parameters for each grid point—total energy flux, total electron flux, and average electron energy. The latter two quantities are used to reconstruct the energy spectrum of precipitating electrons assuming the Maxwellian distribution.

The calculations were carried out for the northern hemisphere, MLAT = 50–90° N, on a discrete grid MLT × MLAT = 0.25 × 0.25 h in the latitudinal interval in a solar-magnetic coordinate system (SM). The transition between the geographic and SM coordinate systems was performed using GEOPACK [30].

For each grid point, the altitude profile of the electron density was calculated from 90 to 150 km with the 1 km altitude step. Figure 5 shows maps of the maximum electron concentration of each vertical profile for two-time moments. The first moment (5:00 UT, 17 March 2013) corresponds to quiet geomagnetic conditions, and the second (17:00 UT, 17 March 2013) to the main phase of geomagnetic storm (SYM-H index decrease up to −130 nT and AE index reached ≈2700 nT).

During the quiet conditions at 5:00 UT, the electron concentration in the night side part of the auroral oval reaches ~10¹¹ m⁻³ due to electron precipitation from the magnetosphere, which is comparable to the ionization due to the EUV radiation on the day side. During the main phase of the storm at 17:00 UT, the situation changes drastically. The auroral oval expands to the low latitudes, and the maximum of electron concentration in the E-region increases by an order of magnitude, which demonstrates the dominant effect of corpuscular ionization in the auroral oval during geomagnetic disturbances. The movie for the diurnal dynamics of the maximum electron concentration during the geomagnetic storm on 17 March 2013 is attached in the supporting materials (Movie S1).

The AIM-E model makes it possible to obtain the spatial distribution of ionospheric parameters in the entire auroral zone under various geomagnetic conditions that may be useful when and where the direct ionospheric observations are absent.

Proper spatial distribution of the ionosphere E-region parameters is extremely important for solving practical and theoretical problems of the radio wave propagation. During the night periods, when the F2 layer degrades, the E-layer plays a major role in the radio communication on the short (up to 2500 km) single-hop radio tracks. This is especially relevant during the polar night. In such cases the global modelling of the E-layer can support the available observation data for more accurate auroral ionosphere monitoring.

4. Discussion

In this work we present a detailed description of an AIM-E numerical model that calculates the chemical composition of the high-latitude ionosphere in the altitude range from 90 to 150 km. The AIM-E model was developed specifically for the high-latitude ionospheric E-region and takes into account the variability of the magnetospheric electron precipitations that is very important for the active geomagnetic conditions. The model calculates the number densities of the 10 species, 3 neutrals $\mathrm{NO}$, $\mathrm{N}\left(4\mathrm{S}\right)$, and $\mathrm{N}\left(2\mathrm{D}\right)$, and 7 ions N⁺, ${\mathrm{N}}_2^{+}$, ${\mathrm{NO}}^{+}$, ${\mathrm{O}}_2^{+}$, ${\mathrm{O}}^{+}\left(4\mathrm{S}\right)$, ${\mathrm{O}}^{+}\left(2\mathrm{D}\right)$, and ${\mathrm{O}}^{+}\left(2\mathrm{P}\right)$. The neutral-ion kinetic of the model takes into account 39 chemical reactions and can be extended with additional reactions and species if necessary.

The model solves the system of stiff ordinary differential equations using the efficient 4th order implicit numerical scheme with variable integration step [22], which extremely reduces computational costs compared to commonly used explicit schemes. The high performance of the AIM-E model allows real-time calculation of the E-region ionosphere composition in the whole auroral zone under different geomagnetic conditions, taking into account high variability of the auroral electron precipitations.

In the photo-ionization module the solar EUV radiation spectrum can be set in two ways, by: (1) relatively rough empirical approximation using the daily F10.7 radio flux, continuously available since 1947 and suitable for ‘space climate’ investigations; and (2) direct measurements of the photon energy spectrum providing by, e.g., TIMED spacecraft every 97 min since 2002 which can be used for investigation of ‘space weather’ events, such as solar flares. The precipitating electron ionization module also has two input possibilities: (1) direct spacecraft measurements of the electron energy spectrum available from several low-altitude satellites, e.g., DMSP, NOAA POES, and REIMEI, providing an accurate local solution for vertical profile of chemical composition along the satellite trajectory; and (2) results of empirical model for electron precipitation (here we implement the OVATION-Prime model), which can be used for global scale simulation of the chemical composition in the high-latitude ionosphere.

The model results, calculated with different types of input parameters and for the different geomagnetic conditions, show a good agreement with ground-based ionospheric data (EISCAT UHF incoherent scattering radar and vertical sounding of the ionosphere). The model reproduced the ionospheric response to the geomagnetic substorm with a sufficient accuracy and can be used to describe the large-scale dynamics of the auroral oval during disturbed periods. The high computing performance allowed application of the AIM-E model in regular E-layer monitoring all over the auroral and subauroral zones, which is important for a real-time prediction of the radio wave propagation conditions. The AIM-E model can be applied to various practical tasks using input parameters such as solar EUV radiation and auroral electron flux from in situ measurements by satellites, or from the models, or as their combination depending on the modeling goals.

The AIM-E model was designed to become a useful tool for both operational and scientific applications in the Arctic and Antarctic ionosphere regions. The model can be used in a wide spectrum of scientific problems, including, but not limited to, various aspects of ionospheric chemistry, distribution of conductance, electric fields and currents, calculation of electron density, etc. In the operational mode, the model is suitable for real-time monitoring of the radio waves propagation conditions, which are crucial for the quality of communication in the most unstable auroral zone. The AIM-E model may also be utilized as a part of more complex space weather models as an efficient ionospheric module.