Abstract
The reparameterization of the geometry-free and geometry-based approaches to derive single-site ionospheric delays using Global Navigation Satellite System (GNSS) measurements is described. Kalman filtering is used to compute the geometry-free and geometry-based ionospheric delays in a forward computation procedure, aiming for a real-time application case. The numerical similarity and differences between the geometry-free and geometry-based ionospheric delays are assessed in terms of both formal and experimental errors (precision). The differences between geometry-free and geometry-based ionospheric delays are derived using two types of precise orbit and clock products. The effects of the precise orbit and clock residual errors are analyzed. The correlation coefficients between the L1 and L2 wide-lane ambiguities with the ionospheric delay are derived and analyzed. It is discovered that the geometry-based ionospheric delay is negatively correlated with geometry-based wide-lane ambiguities, while the geometry-free ionospheric delay and wide-lane ambiguities are much less correlated. A simulation analysis indicates that the impacts on geometry-based ionospheric delay estimates are partly coincided with the actual time-variant errors of the used orbit and clock in the line-of-sight direction.
1. Introduction
The ionosphere is defined as the ionized part of the Earth’s upper atmosphere, consisting of abundant ions and free electrons. The height of the ionosphere mainly ranges from about 50 km up to more than 1000 km, at which the propagation of electromagnetic waves can be significantly affected by free and energetic electrons [1]. The number of ions and free electrons declines above 1000 km [2]. The amount of ionization in the ionosphere varies largely with the amount of radiation received from the sun. The coupling processes among the ionosphere with the variable sun and other geospheres are highly complex and not yet well understood, and need further exploration. The ionosphere can reflect high-frequency (3–30 MHz) radio signals directed into the sky back toward the Earth. This feature is used for long range communication. Furthermore, the electromagnetic signals from satellites passing through the ionosphere will undergo bending and delay. Therefore, the impact of ionospheric activities on communication and remote sensing needs a continuous monitoring [3].
From a Global Navigation Satellite System (GNSS) application point of view, it is known that ionospheric delay is one of the major error sources for precise positioning and navigation [4]. The ionospheric information is crucial for both network real-time kinematic (RTK) and precise point positioning (PPP) techniques [5]. High-precision ionospheric delay products can remarkably accelerate convergence, improve the stability of the ambiguity solution, and promote positioning accuracy for PPP users [6,7,8]. Furthermore, ionospheric delay corrections play a vital role in the RTK positioning technique and static positioning over longer baselines [9], particularly for those single-frequency users [10].
Accurate ionosphere modellings relies on the ionospheric delays derived from individual reference sites. A common approach for obtaining slant ionospheric delays is the geometry-free approach. The geometry-free code and carrier phase observations are constructed to firstly eliminate or estimate the geometry related parameters as a whole, and to then estimate the ionospheric delay and the ambiguity term. The geometry-free approach makes use of code and phase observations on the basis of each single satellite. The single epoch solution of ionospheric delay relies on the accuracy of the code measurements, as there is no redundancy in dual-frequency cases for dual-frequency receivers. The averaged ambiguities over adjacent epochs are then taken as a level to restore the ionospheric delay term in each epoch. This has been called the carrier-to-code levelling (CCL) approach in previous studies [10,11,12,13,14,15,16]. The accuracy of the derived ionospheric delay in the approach is affected by the observation time period and by the noise of code observations and possible multipath errors [14]. The geometry-free approach has the advantage of simplicity without the need for a precise orbit and clock (OC). Therefore, it is widely used for global ionosphere modelling (GIM) [2,17,18].
Another approach to derive ionospheric delays is the geometry-based approach. This approach makes use of the standard PPP model to estimate the slant ionospheric delays and other parameters simultaneously using all visible satellites. The geometry-based approach needs the precise OC products to calculate the geometry distances between the satellites and the station coordinates. In particular, the satellite-receiver geometry (i.e., line-of-sight vectors between satellite and receiver) is present in the observation equations [14], which is why it is called the geometry-based approach (or model).
The slant ionospheric delays calculated by these two approaches have the same form (i.e., including the same elements), particularly for the dual-frequency case. In some earlier studies, the ionospheric delays derived from these two major approaches have been assessed and analyzed. By comparing the single differences of the ionospheric estimates between two collated receivers, Zhang et al. [15] concluded that the geometry-based approach can provide more accurate ionospheric delays than the geometry-free approach. Because of the possible multipath effect of single difference codes, the experimental errors of these two approaches are not as good as the expected formal errors. Nie et al. [19] demonstrated that the accuracy of the geometry-based and ambiguity-fixed ionospheric delays is more than one order of magnitude higher than that of the geometry-free ionospheric delays.
However, is the geometry-based ionospheric delay always more precise than its geometry-free counterpart? Is there any exception that could lead to a negative answer? In our previous research [20,21], it has been found that geometry-based wide-lane ambiguities are significantly affected when there are large errors in OC products. Similarly, will the geometry-based ionospheric delays suffer from similar impacts from OC errors? In this case, is the geometry-based ionospheric delay still more reliable than the geometry-free one? It is noticed that the role of OC residual errors has not been investigated in previous studies for the ionospheric delay. It seems that the orbit and clock products are always assumed to be precise enough. However, this is not the case for real-time applications, where, for example, GPS IIF satellites could have large errors of up to meters in real-time cases [22]. This has not attracted much attention in previous research. The impact of OC residual errors on ionospheric estimates should therefore be investigated. In addition, the geometry-free ionospheric delay estimates are often derived on the basis of an entire arc in order to have more precise ambiguity levelling [15,16,19,23,24,25] and, in this case, they cannot be computed in real-time. Therefore, the comparison and assessment of the ionospheric delays should be based on filtering solutions derived from current and past data, rather than smoothed solutions from the entire and continuous arc [26].
This contribution is an extension of our previous studies [20,21], aimed at the analysis of single-site ionospheric delays derived from both geometry-free and geometry-based approaches. First, ionospheric delays in a forward computation for both the geometry-free and geometry-based approach are derived for real-time usage. Second, the ionospheric delays with their corresponding formal errors from two approaches are compared and numerically analyzed. Third, the correlation between ionospheric delays and ambiguities are derived and assessed. In addition, two types of errors are simulated in the OC in the line-of-sight direction, and the impacts of these errors on the ionospheric delays are discussed. Finally, some conclusions are summarized.
2. Methodologies to Derive the Ionospheric Delays
There are basically two different terminologies for the approaches that are used to derive ionospheric delays (see [10,15,16,19,25]). The major difference is that one makes use of the geometry information between the satellite and receiver, while the other does not use the information. This section describes how the ionosphere observables are derived from geometry-free (GF) and geometry-based (GB) models. A recursive procedure is used to obtain the filtering solution, instead of to compute the smoothed solution. The study focuses on the GPS case without the loss of generality for other GNSS systems.
2.1. Ionospheric Delay Derived from the GF Model
The GF observation equation for measurements of code p and phase for a single satellite is directly expressed as follows [20,27]:
where is the expectations of the code and phase measurements, s (s = 1, 2, …, m) is the GPS satellite PRN number, i (i = 1, 2) is the frequency, and k is the current epoch. is the geometry part, which combines all non-dispersive terms, including the geometric range, satellite and receiver clock errors, and the tropospheric delay. , is the wavelength of frequency i. the ionospheric delay term in meters in the L1 signal. In the GF model, the geometric a priori information is not required. The receiver and satellite hardware delays are absorbed by other terms. For example, the carrier phase ambiguity terms, , include integer ambiguities plus parts of the code and phase delays, while the ionospheric delay term contains other parts of the satellite and receiver hardware delays as well, which is given as follows:
where and are the P1–P2 receiver and satellite differences of the code hardware delays (or biases), respectively. is the pure slant ionospheric delay. The multipaths of the code and phase are considered to be measurement noise and are not parametrized in the observation equations. However, they might have an impact on the solutions.
The epoch-wise solution including the ionospheric delay at epoch k can be derived from Equation (1), as follows:
The stochastic model for the observation is given as follows:
where is the elevation of the satellite at the epoch k, and and are prior formal errors (or precision) for the code and phase measurements, respectively. The variance–covariance of the derivatives is given as follows, according to the error propagation law:
Equations (3)–(5) are used to calculate the epoch-wise ionospheric delays and their variance–covariance for a single satellite. However, there is no redundancy for the epoch-wise estimation (i.e., four measurements for four parameters). The ionospheric delays rely on recursive filtering using multi-epoch solutions in order to increase precision.
The first epoch solution, k = 1, is used to initialize the filtering procedure. The state time propagation equation can be written as follows:
The measurement update equations are expressed as:
The stochastic model of the measurement equations is identical to Equation (4). Writing the equations of all satellites into one formation
where
2.2. Ionospheric Delay Derived from GB Model
To derive the ionospheric delays, the geometry related term, including the receiver coordinates and satellite OC corrections, needs to be precisely known. The observation equations for a single satellite are expressed as follows:
where and are observed minus computed values, which are computed from raw observations and station coordinates, as well as the precise satellite OC at epoch k; is the zenith tropospheric delay with mapping function ; and is the receiver clock error term. The GB ionospheric delay estimation makes use of all of the received satellites; therefore it has a redundancy (4n measurements minus 3n + 1 parameters, n > 4, n is the satellite number). The ionospheric delay term is denoted as follows:
and the ambiguity term is as follows:
The measurement update equation of all of the observed satellites in the matrix-vector form is expressed as follows:
where is the design matrix and is formed from Equation (15) for all of the visible satellites, and the parameters are defined as follows:
and the measurements of the code and phase of can be written in a vector form as follows:
where indicates the geometry-based observed minus the computed values. The stochastic model for the observation is the same as for the GF case.
The state time update equation is given as follows:
where is the transition matrix for the state from epoch k−1 to k. is computed from the assumed process noise of , multiplied with the time interval between epoch k − 1 and k.
2.3. Filtering Solution
The GF and GB solutions are obtained via the same recursive procedure. Assume that the filtering solution at epoch k − 1 is denoted as , and its covariance matrix is represented as , the parameters updated with the epoch solution at k are as follows:
where indicates gf or gb. The ionospheric parameter vector and its variance-covariance at the epoch solution k can be presented as:
where is the gain matrix:
The formal errors (or precision) used in the sequel are the standard deviations derived from the variance-covariances of Equation (25) for the corresponding parameters.
2.4. Correlation Coefficient Analysis
Assuming that the ionospheric delay and phase ambiguities at L1 and L2 are derived from the above GF and GB models, the part of the previously defined parameters (indicated as ‘p’) is expressed as follows:
The correlation coefficients between the ionospheric delay with phase ambiguities at L1 and L2 are calculated, respectively, as follows:
To derive the wide-lane (WL) ambiguity, we apply the transformation matrix ,
with the variance-covariance
The correlation coefficients between the ionospheric delays and WL ambiguities are calculated as follows:
The correlation coefficients are presented and analyzed in the experimental section.
3. Impact of OC Residual Errors on the GB Ionospheric Delay
For the GF ionospheric delay, geometry related terms, including OC, are eliminated without effects for individual satellites separately. Therefore, the OC errors have no impact on the GF ionospheric delay. It was found in our previous study that the OC residual errors make significant impact on L1 and L2 ambiguities, as well as on the WL ones in the GB model [20]. As the ionospheric delay and ambiguities are individual satellite dependent without contributions from other satellites, and are therefore highly correlated, the ionospheric delay will be also affected by OC residual errors. The analytical expression of ambiguities in [20] can be extended to the ionospheric delay term as follows:
where is the OC error being a constant bias in the line-of-sight (LOS) direction. The residual OC error is rarely a constant bias throughout an entire tracking period. It is very likely a time variant error that is caused by the changes of the LOS orbit error itself, as shown in [20]. In this case, it is not trivial to make a strict analytical expression, as the estimation procedure is rather complex both in the current epoch and in the correlation between epochs. An experimental analysis with a simulation will be demonstrated in later sections.
4. Methodologies to Derive the Ionospheric Delays
In order to analyze and compare the behavior of the ionospheric delay obtained with the GF and GB models and to evaluate the impacts of OC residual errors on GF and GB ionospheric delays, raw observations with a 1s sampling rate from 31 International GNSS Service (IGS) sites were downloaded from the IGS data base. Data from most of these sites were also employed in [20], in order to keep the research coherent. These sites are carefully selected and distributed around the globe (see Figure 1). From these, some sites located very close to each other were selected (e.g., GODN and GODZ, KOKV and KOKB, MRO1 and MNOR, CEBR and VILL, REDU and YEBE) in order as to assess the experimental errors of the derived ionospheric delays because they had almost the same LOS directions. The algorithms described in Section 2 were implemented. We processed the raw observations and derived the ionospheric delay; L1, L2, and WL ambiguities; and their variance–covariances for the GF and GB models, respectively. A quality control procedure was carried out to detect potential cycle-slips or loss of lock beforehand. When identified, the ambiguities and ionospheric delays were reset. The positions of the sites were fixed to their “ground truth” when the GB approach was applied. These “ground truth” positions were calculated from more than one day’s data in the static PPP mode. Two types of OC products were used for the GB model [28]. One of which was the final product provided by ESA, and the other one was the real-time product described in detail in [20,29]. The IGS final orbit accuracy was improved to 1–2 cm, and the RMS range of the satellite clock was stable within 1–2 cm after small biases were removed [30,31]. The date of these observations used in this study was 27 September 2017. The clock interval was 30 s and the orbital sampling rate was 15 min for the two types of OC products. We followed the same strategy of using the OC products as in the GB PPP model described in [20].
Figure 1.
Location of the selected International GNSS Service (IGS) sites.
The P1 and P2 observations were taken as priority in the processing when using the final OC product, while the C1 and P2 observations were used preferentially in the case of using the real-time OC product. In order to maintain consistency, a P1-C1 differential code bias (DCB) was used in the data processing, as some sites provided only C1 observations. The elevation-dependent data weighting was used in both GF and GB processing. The entire computing process was performed by a strictly forward computation. It should be mentioned that the unit of the slant ionospheric delay estimates was in meters (at L1 frequency) instead of total electron content units.
4.1. Analysis of GF and GB Ionospheric Delays
This study derives the GF and GB ionospheric delays for all of the selected sites. In order to look into their behavior, the GF and GB ionospheric delays and their formal errors for PRN 09 from site GODZ, using the ESA final product as an example, are displayed in Figure 2. On the top panel, it is seen that values of the GF epoch-wise ionospheric delays fluctuated widely within an 8-m range because these ionospheric delays were purely dominated by epoch-wise code observations with a high-frequency noise (as phase measurements are equivalently used to derive epoch-wise ambiguities). The filtering solutions of the GF ionospheric delay looked much smoother with a convergence period of about one hour. The entire variation was about 2 m. The GF filtered ionospheric delays were derived together with the averaged ambiguities from the observations of the current and all of the past epochs therefore, the term of the ionospheric delay was much smoother. The GB ionospheric delay converges within several minutes, much faster than its GF counterparts. The differences between the GF filtered ionospheric delay and GB ionospheric delay are dominated by the behavior of the GF filtered solutions at the convergence period, while they are stable and close to each other after about one hour. This is not a surprise as the ionospheric delay derived from two models with the same parameterization. In the bottom panel, it is obvious that the formal errors of GF epoch-wise ionospheric delay (above 2.0 m) are about two orders of magnitude larger than that of the GF filtered (about 3.0 cm after stabilized) and GB ionospheric delays (about 1.0 cm after stabilized), revealing that the GF epoch-wise ionospheric delays were surely not accurate. Compared with the GB ionospheric delay formal error, the GF filtered counterpart was about 2–3 times larger, suggesting that the GB ionospheric delay estimates were more precise than the GF ionospheric delay. This indicates that the GB and GF ionospheric delays are not equivalent, at least in terms of formal errors. In addition, a particular point is that all of these formal errors are shown as a “basin” shape, which is a trend with lower values towards the middle of the “basin” and higher values at the two ends. This is opposite to the satellite’s elevation. The basin indicates that the impact from the elevation-dependent weighting is clearly visible, even at the latter end of the observation pass after everything seems convergent.
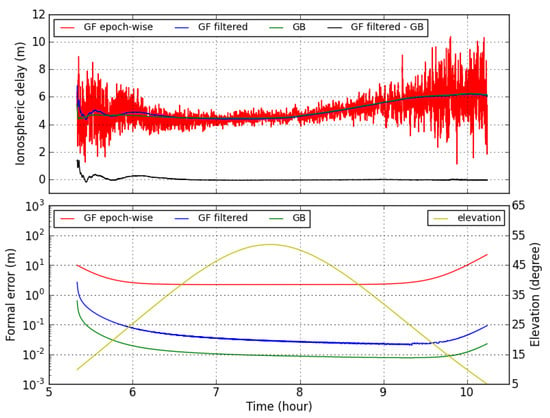
Figure 2.
Geometry-free (GF) epoch-wise (red), GF filtered (blue), and geometry-based (GB) (green) ionospheric delays (top) and their corresponding formal errors (bottom) for PRN 09 computed from the single receiver (GODZ) observations and the ESA final orbit and clock (OC) product. The differences between the GF filtered and GB ionospheric delay are shown in black in the top panel. The elevation of the PRN 09 is displayed in yellow in the bottom panel. GPS time is used for this figure and for all of the following figures as well.
Figure 3 displays the GB slant ionospheric delays of all visible GPS satellites computed for site GODZ with the ESA final products. It is clear that for each satellite, the ionospheric values changed less in the middle of the satellite pass, while they were increased during its first and last hours. It can be seen that there is a short convergence at the beginning for almost all satellites and an oscillation at the end for some satellites. The sharp drops are because cycle-slip or loss of tracking were detected for the satellite, which often happened in low elevations. In this case, the ambiguity term reset, resulting in rapid changes in ionospheric delays. The ionospheric delay seemed much larger during the period of h12-h23 than the period of h00-h12. It is noticed that the ionospheric delay values of PRN 22 and PRN 23 were negative (i.e., PRN 22 and PRN 23). This might be because these estimates contained satellite and receiver differential code bias, which could contribute to the negative values.
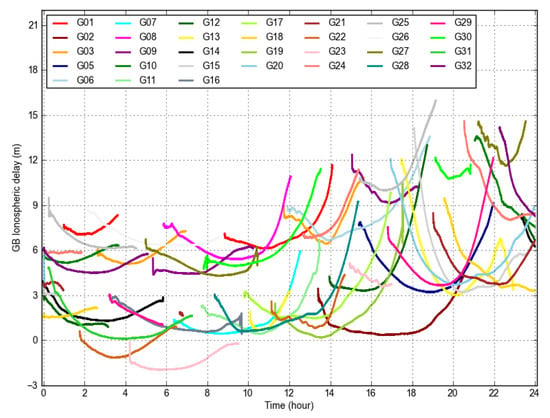
Figure 3.
GB ionospheric delay estimates for all of the observed satellites computed for the single receiver (GODZ) observations and the ESA final OC products.
For the purpose of intuitively representing the similarities and differences between the GF and GB ionospheric delay, we calculated the GF–GB ionospheric delay (GF filtered minus GB ionospheric delay, GF stands for geometry-free filtered in the sequel) of all of the visible GPS satellites using the final OC product for the sites GODZ and GODN (see Figure 4). The first hour of these differences are not displayed, because of the convergence period of particular GF ionospheric delay. The overall GFGB ionospheric delays at GODZ remained steady within the range of 0.4 m. As for each satellite, most values stayed stable in the range of 0.2 m, and they were slightly noisy in the beginning of the time series before subsequently becoming smooth and flat. The variation behavior for some satellites was similar for GODZ and GODN because the baseline was short (about 65.16 m). The pure slant ionospheric delays in Equation (2) were physically removed if the GB and GF ionospheric delays were ideally equivalent. The reality is that the ambiguity levelling errors, OC errors, and multipath errors could remain in these quantities; therefore, they were not identical. An offset was present for individual satellites. We observed some larger differences towards to the end of some of the arcs, often in low elevations because of the different measurement errors.
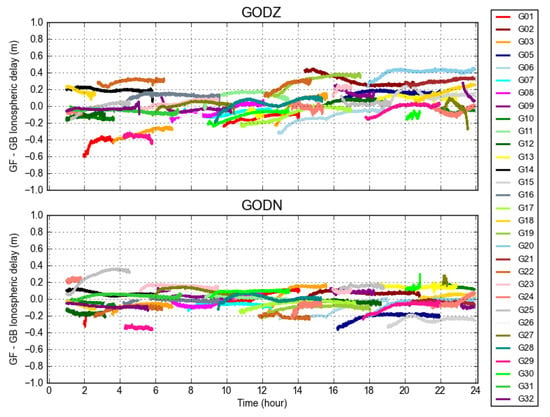
Figure 4.
Differences of GF filtered and GB ionospheric delays for all of the observed satellites computed for GODZ (top) and GODN (bottom) observations, and the ESA final OC products. The distance between GODZ and GODN is about 65.16 m.
4.2. Impact of OC on Ionospheric Delay Estimates
This section analyzed the impact of OC errors on ionospheric delay differences. Figure 5 displays the biases and standard deviations of the GF–GB ionospheric delays. It is seen that the GF–GB ionospheric delay of GODN had some similar characterizations to the GODZ counterpart, with an even smaller bias as a whole. The biases of these differences were mainly caused by the inaccurate ambiguity estimates in the forward computation, i.e., the so-called ambiguity levelling error mentioned in [14,15]. The spread of the GF–GB ionospheric delays for GODZ was relatively larger than that of GODN, indicating that the site of GODZ may have larger multipath errors. The standard deviations were below 0.08 m for GODZ and GODN.
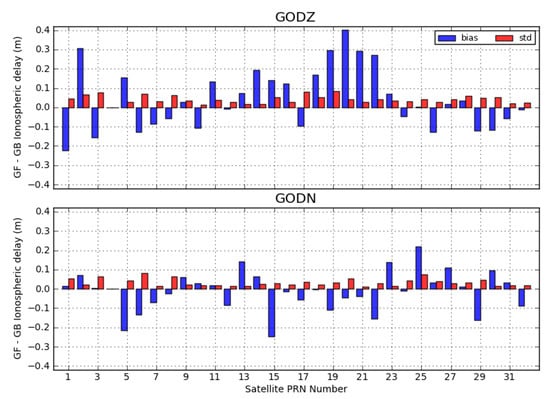
Figure 5.
Biases and standard deviations of the GF–GB ionospheric delays for all of the observed satellites computed for the GODZ (top) and GODN (bottom) observations and ESA final OC products.
Compared with Figure 4, Figure 6 employs real time OC to compute the GF–GB ionospheric delay for all of the visible GPS satellites at GODZ and GODN. It can be distinctly seen that the values of the ionospheric delay differences for most satellites (except PRN 09) were scattered between −0.7∼0.5 m, which is larger than that of the GF–GB ionospheric delay calculated by the ESA final product. This illustrates that the impact of two products on the ionospheric delays are different from this comparison. The quality of the real time product might not be as good as that of the final product in most cases (refer to [32]). In particular, the ionospheric delay differences of PRN 09 reached 1.4 m in the period of 6–10 h, which was much larger than their variations (about 0.1 m in Figure 7 for PRN 09). This certainly means that the GF ionospheric delays were not close to the GB ones for this case.
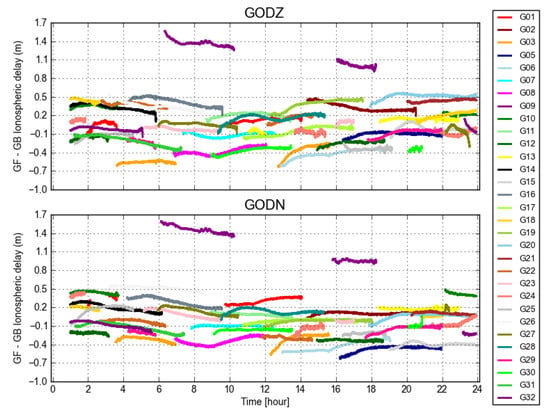
Figure 6.
Differences of GF filtered and GB ionospheric delays for all of the observed satellites computed from the receiver GODZ (top) and GODN (bottom) observations using real-time OC products.
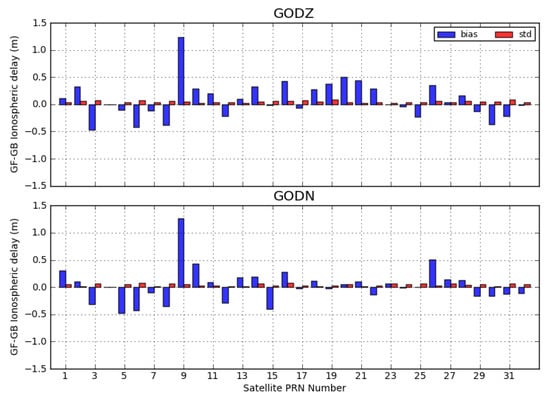
Figure 7.
Biases and standard deviations of GF–GB ionospheric delays for all of the observed satellites computed from the receiver GODZ (top) and GODN (bottom) observations with real-time OC products.
In order to further investigate whether this variation was caused by errors of OC products, we subtracted the GB ionospheric delays further between those derived from the final and real-time OC products. Figure 8 demonstrates the final minus real time GB ionospheric delays for all of the visible GPS satellites at sites GODZ and GODN. The statistics of Figure 8 are shown in Table A1. It can be seen that the values for all satellites were smoother and more stable than that shown in Figure 4 and Figure 6. This indicates that the impacts of site-related multipath errors were mainly removed for GODZ and GODN, retaining the OC differences of the LOS directions. This is also why both sites demonstrated almost the same pattern. The biases of the individual satellites mainly came from the contribution of the OC differences and the different code combinations used for the clock filtering. These biases were closer to GF–GB ionospheric delays shown in Figure 6, than that in Figure 4. This indicates that the OC differences mostly came from the real-time OC product. The GF–GB ionospheric delays of almost all of the satellites were within 0.4 m, except for PRN 09. We temporarily regarded 0.4 m biases as being in the normal range of two types of product. In this case, values up to 1.4 m of PRN 09 could be attributed to the differences between OC products. The real-time orbit of PRN 09 was likely incorrectly predicted because of the unclear attitude model of the GPS IIF satellites, which has not yet solved [22]. In the same way we also plotted the other co-located sites, such as KOKV/KOKB, REDU/YEBE, and MRO1/NNOR, which all demonstrated a similar behavior according to their corresponding locations (not shown here due to the space limit). It is known that the GF and GB ionospheric delays were not equivalent, and the GB ionospheric delay was more precise than the GF ones. However, if the OC was not precise enough, the GB ionospheric delay might absorb some OC errors, and consequently, the GF ionospheric delay might be more accurate than the GB ionospheric delay, e.g., PRN 09 in this case. More analyses will be given later.
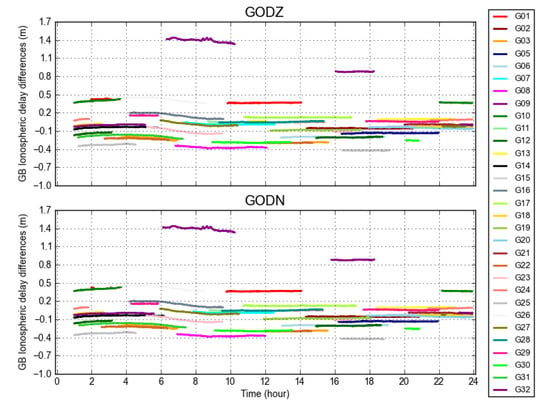
Figure 8.
Differences of GB ionospheric delays for all of the observed satellites computed from the receiver GODZ (top) and GODN (bottom) observations with final and real-time OC products.
4.3. Analysis of Ionospheric Delay Estimates from Co-Located Sites
In order to assess the consistency of the GF filtered and GB ionospheric delay, we implemented a co-location analysis for GODN and GODZ. Figure 9 displays the differences of GB between these two receivers and the GF counterpart, respectively, for all visible GPS satellites. The statistics of Figure 9 are shown in Table A2. In this case, the impacts of the orbit and clock errors were actually removed. Therefore, the GB ionospheric delay differences were the same, no matter the final or the real-time OC being used. It can be explicitly seen from Figure 9 that the variations of the GB ionospheric delay differences were maintained between −0.8 and −0.4 m at h01–h15, and −0.2 and −0.6 m at h15–h24. These values for each satellite during these two periods were relatively stable, without much oscillations. On the contrary, the variations of the GF ionospheric delay differences fluctuated from about 0.25 m to −1.20 m, which were significantly larger than that of the GB ionospheric delay differences. Meanwhile, the patterns of GF variations for each satellite were undulant, some values of which even reached 0.3 m. This indicates that the GB ionospheric delay had a better consistency compared with the GF ionospheric delay.
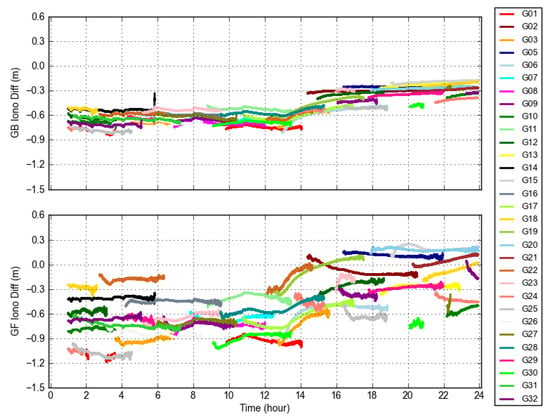
Figure 9.
GB ionospheric delay differences (top) and GF filtered ionospheric delay differences (bottom) between the receiver GODZ and GODN.
4.4. Correlation Analysis of Ionospheric Delay Estimates with Ambiguities
In our previous studies [20,21], it has been confirmed that OC errors affect the derived GB ambiguities. Figure 4, Figure 5 and Figure 6 indicate that OC also has an impact on the GB ionospheric delays. Therefore, it makes sense to investigate the correlation between the ionospheric delays and ambiguities of the individual satellites. Figure 10, taking GODZ as an example, presents the correlation coefficients between the ionospheric delay separately with L1, L2, and WL ambiguities derived from the GF and GB models, respectively.
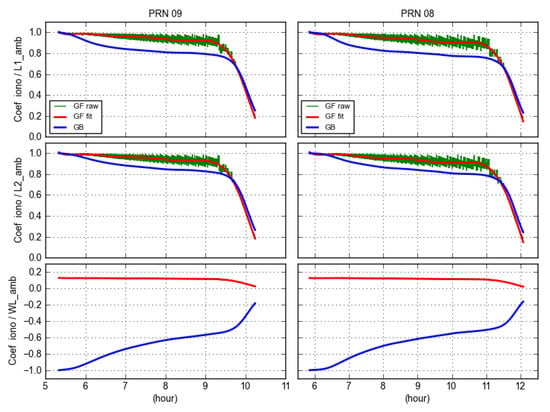
Figure 10.
Correlation coefficients between ionospheric delay and L1 ambiguity estimates (top), and L2 ambiguity estimates (middle), and WL ambiguity (bottom) for PRN 08 (right) and PRN 09 (left) at site GODZ. The derived GF raw coefficients are shown in green, the fitted line of the GF raw coefficients are shown in red, while the GB coefficients are indicated in blue. The least-square polynomial with a degree of 8 is used to fit the GF raw coefficients. The green lines of WL in the bottom panel are overwritten by the red curve.
As can be seen from Figure 10, the ionospheric delay was highly correlated with the L1 and L2 ambiguities for both GB and GF models throughout most of the observation period. The coefficient at the convergence period was about 0.999, and slowly decayed after the convergence using more observations, and sharply decreased at the end to about 0.180. The correlation for GB was smaller than that of the GF ones most of time, but was slightly larger during the last hour while the GF coefficients decreased faster than the GB ones. It is also noticed that the GB coefficients declined more than the GF ones after the convergence. This indicates that the GB ionospheric delays were more decorrelated with L1/L2 ambiguities than the GF ones, except for two ends of the satellite pass. It is obvious that the correlation behavior between the ionospheric delays with L1 and L2 ambiguities was rather similar. This high-correlation phenomena shows that the ionospheric delay and L1/L2 ambiguities depended on each other, and were difficult to separate in the process of estimation. If the L1/L2 ambiguities were not accurately estimated, it would cause errors in the ionospheric delay estimates, which is the ambiguity levelling issue.
Compared with the L1 and L2 ambiguities, the correlation coefficients between the ionospheric delay and WL ambiguity had a completely different behavior. It can be seen that the coefficients with GF WL ambiguities were remarkably smaller than those with L1 and L2 ambiguities. The GF WL coefficients started from about 0.130, remained stable until the last hour, and fell to 0.025 at the end. It is interesting to see that the correlation coefficient between the GB ionospheric delays and WL ambiguities were negative, starting from −0.999, gradually increasing to −0.500 during the last hour, and reacing −0.185 at the end. The variation pattern of the GB WL coefficients had some similarities with the GB L1 and L2 counterparts, but with opposite signs. This implies that the ionospheric delays could be affected by the OC errors in the opposite way to the WL ambiguity.
In order to further study the relationship between the GF ionospheric delay, GB ionospheric delay, GB WL ambiguity, and OC errors, we calculated the GB ionospheric delay differences and the GB WL ambiguity differences derived from two types of OC products (notice that the OC products are not used in the computation of the GF WL ambiguities and ionospheric delays, so there is no effect from the OC errors). The OC differences were also calculated in the LOS of the satellites. The WL ambiguities were multiplied with the wavelength, and so their units are in meter as well. Figure 11 demonstrates the various differences for PRN 09 and PRN 08 at site GODN, and PRN 09 at KOKV and MAJU, respectively. It can be seen that the GB differences were obviously affected by the OC, as they varied with the change of OC differences. It is noticeable that the GB ionospheric delayed difference likely had an opposite pattern compared with the GB WL ambiguity differences, while the latter had a similar behavior to the OC errors. Analogous behaviors appeared in the same receiver for different satellites and in the same satellite in different receivers, proving the repeatability of correlation. This indicates that the GB ionospheric delays were sometimes not accurate when the OC quality was not perfect, though most times, the GB ionospheric delays had smaller former errors, as indicated in Figure 2, and had smaller experimental errors, as shown in Figure 9.
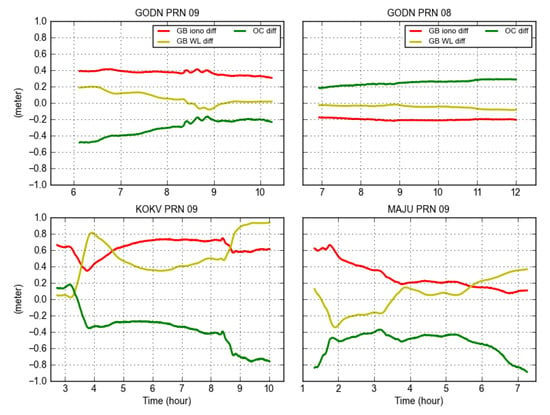
Figure 11.
GB ionospheric delay differences (red), GB WL ambiguity differences (yellow), and OC differences (green) computed using final and real-time OC products for PRN 09 (top left) and PRN 08 (top right) at site GODN, PRN 09 (bottom left) at site KOKV, and PRN 09 (bottom right) at site MAJU.
It has been confirmed in Figure 6 and Figure 7 that larger differences exist in the real time OC in LOS of PRN 09. The GF–GB ionospheric delay of PRN 09 is plotted in Figure 12 for all of the selected receivers derived from the final and real time products, respectively. The bias and standard deviation of the GF–GB ionospheric delay are shown in Table A3. It can be seen that the variations of GF–GB ionospheric delays computed by the final product are stable in the range of ±0.5 m, except for site YEBE. However, the real time counterparts had a maximum spread of 2.2 m, which was conspicuously larger than that of the final product. In particular, when PRN 09 with larger oscillations was tracked by many sites (1 h–12 h), the GF–GB ionospheric delays derived from the real-time products were much larger than those using the final OC product. In the period of 14h–24h, the GF–GB ionospheric delays had a similar pattern for both the final and real-time OC products.
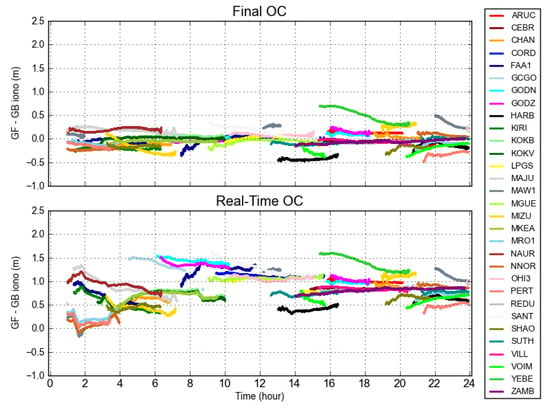
Figure 12.
GF–GB ionospheric delays for PRN 09 for all sites, GB ionospheric delays derived from the final OC (top) and real-time OC (bottom).
5. Simulation of OC Error Impacts
In order to further clearly and explicitly investigate the effects of OC errors on the GB WL ambiguities and ionospheric delays, two types of OC errors were simulated in the LOS direction for the whole tracking period of satellite PRN 09 at receiver GODN. The first one was a constant bias with 1 m, the other was a time-variant error of sines or cosines with 0.15 m amplitude and a 2 h period. Both kinds of errors were added into the PRN 09 of the final OC. The GB WL ambiguities and GB ionospheric delays were recomputed using OC products with simulated errors, then they were compared with the previous counterparts without simulated errors (see Figure 13). The differences between the simulated and original ambiguities and ionospheric delays were purely caused by simulated errors.
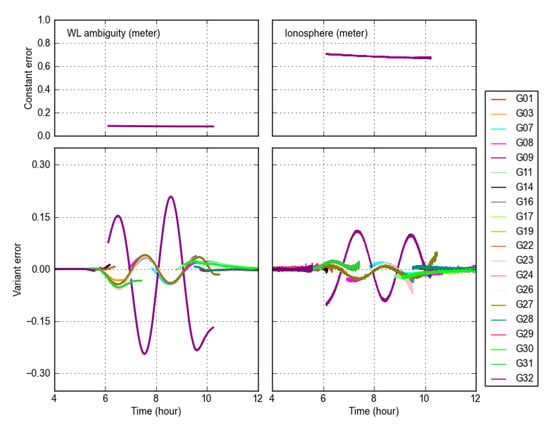
Figure 13.
Differences of GB WL ambiguities (left) and ionospheric delays (right) with and without the simulated errors (constant bias—top row; time-variant errors—bottom row) added to OC product of PRN 09 at GODN.
In terms of constant errors, we can see that the bias of WL ambiguities of PRN 09 was about 0.08 m (after multiplying by the wavelength), while there was no effect on the other satellites. The ionospheric delay differences slowly changed in time (top right panel in Figure 3), while the WL ambiguities stayed constant (top left panel in Figure 3). The bias of ionospheric delays was about 0.68 m, which was significantly larger than that of the WL ambiguities. This indicates that the WL ambiguities were less sensitive to the constant OC errors than the ionospheric delays. Likewise, the ionospheric delays and WL ambiguities of the other visible satellites were not affected by the constant OC errors.
In contrast, with time-variant errors, it was obvious that the OC errors had a noticeable influence not only on PRN 09, but also on other satellites. The effects on the WL ambiguities and ionospheric delays of PRN 09 also displayed sine or cosine behaviors, and amplitudes of 0.18 m and 0.13 m, respectively. Other satellites also showed similar fluctuations, but with smaller magnitudes. Different from the constant bias, the time-variant error effects on the ionospheric delays were obviously smaller than those on the ambiguities. Notice that the size of the time-variant errors added into PRN 09 OC were far smaller than the constant bias, whereas the effects on the ambiguities were significantly more variant than that on the ionospheric delays. This indicates that ambiguities and ionospheric delays were rather sensitive to the time-variant errors.
6. Conclusions
This contribution derives a slant ionospheric delay as well as L1, L2, and WL ambiguities using the GF approach and GB PPP model. Two types of orbit and clock products with different quality levels are used to compute the ionospheric delay and ambiguity terms. The differences between GF and GB ionospheric delays are mainly analyzed. The main results and conclusions are summarized as follows, with answers to the questions raised in the introduction.
The GF epoch-wise ionospheric delay is computed on the basis of single satellite measurements of a single epoch; therefore, there is no redundancy (four observations are used to estimate four parameters). The GF filtered ionospheric delay in each epoch is obtained from the ambiguities averaged over the previous and current epochs in a continuous satellite pass. The comparison of their former errors and the experimental errors indicates that the GF filtered ionospheric delay is smoother and more stable than that of GF epoch-wise one. The GB ionospheric delay makes use of all visible satellites from every epoch, so it has more redundancy (4n measurements minus 3n + 1 parameters, n > 4, n is satellite number). The GB ionospheric delay is more precise than the GF one, as the GB one has smaller formal and experimental errors of co-location analysis in a normal situation with the final orbit and clock product. However, in this contribution, it is found that when the real-time OC products are not accurate, a large orbit prediction error due to unknown attitude oscillation may bring significant errors in the estimated GB ionospheric delays. In this case, it is hard to claim that the GB ionospheric delay is more precise than the GF counterpart.
The correlations between the ionospheric delay and ambiguities, as well as orbit and clock, are analyzed. It is found that the correlation coefficients between the L1 and L2 ambiguities and the ionospheric delays of both GF and GB models are rather high, particularly at the beginning, and decrease gradually with more observations involved. The correlation coefficients of the L1 and L2 ambiguities with a GF ionospheric delay are higher than with the GB ones. However, the correction between WL ambiguity and ionospheric delay has different behaviors. It is discovered in this contribution for the first time that the GF ionospheric delay has much lower correlations with GF WL ambiguities than with the L1 and L2 ones, whereas the GB ionospheric delay is negatively correlated with GB WL ambiguities. In addition, the GF WL ambiguity is less correlated with the GF ionospheric delay than the GB WL ambiguity with the GB ionospheric delay. The WL GB ambiguities are negatively correlated with the OC errors, while the GB ionospheric delays are positively correlated with the OC errors.
Moreover, it is discovered that the differences in GB ionospheric delays using different OC products have a negative correlation with the OC errors. The GF–GB ionospheric delays from final and real-time OC are computed, and their similar variations can be seen from some co-location receivers, indicating that these GF–GB ionospheric delays are affected, resembling impacts from real-time OC errors in the LOS direction.
Furthermore, two types of OC errors are simulated, and their effects on WL ambiguities and ionospheric delay are analyzed. The effect from the constant OC bias on the WL ambiguity is still a constant, but the size is not much smaller than the OC bias itself. The ionospheric delay is obviously affected by the constant bias to a larger extend (about 0.7 times). As for time-variant errors, both ambiguities and ionospheric delays are remarkably affected. The size of the impact on WL ambiguities is larger than that on the ionospheric delays, in an opposite direction. In addition, the time-variant errors of the OC products in only one satellite could cause significant errors in ionospheric delays and WL ambiguities of all tracked satellites. The satellite with OC errors is affected the most. This reminds us that the GB model does not always produce a more precise ionospheric delay than the GF model. The quality of the orbit and clock, particularly in a real-time case, is a big consideration for the GB model in order to produce ionospheric delays. This answers the questions that we raised in the Introduction.
Author Contributions
G.C. provided the initial concept and methodology; Q.Z. helped to derive the equations in theory with G.C.; G.C. acquired the funding for the project. Q.Z. provided the software platform and results analysis. S.L. implemented the software part necessarily for this project and carried out the data processing as well as the experimental validation; S.L. visualized the results and wrote a draft of the paper. G.C., Q.Z., Z.H., and N.C. finalized the paper. All of the authors reviewed the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grant no. 41674015).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available on request.
Acknowledgments
The IGS is greatly acknowledged for providing GNSS raw data and precise orbit and clock products.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The statistics of Figure 8, Figure 9, and 12 are shown in Table A1, Table A2 and Table A3, respectively.

Table A1.
Statistics of Figure 8. Differences in GB ionospheric delays for all of the observed satellites computed from the receiver GODZ and GODN observations with final and real-time OC products.
Table A1.
Statistics of Figure 8. Differences in GB ionospheric delays for all of the observed satellites computed from the receiver GODZ and GODN observations with final and real-time OC products.
| PRN | GODZ | GODN | ||
|---|---|---|---|---|
| Bias | Standard Deviation | Bias | Standard Deviation | |
| 01 | 0.380 | 0.003 | 0.372 | 0.003 |
| 02 | −0.057 | 0.003 | −0.056 | 0.003 |
| 03 | −0.253 | 0.014 | −0.255 | 0.013 |
| 05 | −0.136 | 0.004 | −0.136 | 0.004 |
| 06 | −0.200 | 0.004 | −0.199 | 0.004 |
| 07 | 0.010 | 0.009 | 0.008 | 0.005 |
| 08 | −0.371 | 0.011 | −0.371 | 0.010 |
| 09 | 1.207 | 0.022 | 1.201 | 0.022 |
| 10 | 0.384 | 0.012 | 0.386 | 0.013 |
| 11 | 0.043 | 0.003 | 0.043 | 0.003 |
| 12 | −0.182 | 0.009 | −0.181 | 0.008 |
| 13 | 0.086 | 0.003 | 0.092 | 0.004 |
| 14 | −0.042 | 0.009 | −0.042 | 0.009 |
| 15 | −0.028 | 0.004 | −0.027 | 0.004 |
| 16 | 0.153 | 0.039 | 0.154 | 0.039 |
| 17 | 0.122 | 0.002 | 0.123 | 0.002 |
| 18 | −0.021 | 0.009 | −0.020 | 0.009 |
| 19 | −0.087 | 0.003 | −0.085 | 0.005 |
| 20 | −0.050 | 0.011 | −0.050 | 0.011 |
| 21 | 0.005 | 0.006 | 0.006 | 0.006 |
| 22 | −0.256 | 0.007 | −0.256 | 0.006 |
| 23 | −0.107 | 0.035 | −0.106 | 0.035 |
| 24 | 0.071 | 0.005 | 0.072 | 0.005 |
| 25 | −0.371 | 0.007 | −0.367 | 0.009 |
| 26 | 0.424 | 0.035 | 0.425 | 0.034 |
| 27 | 0.002 | 0.024 | 0.009 | 0.027 |
| 28 | 0.047 | 0.007 | 0.047 | 0.007 |
| 29 | 0.082 | 0.004 | 0.082 | 0.004 |
| 30 | −0.286 | 0.004 | −0.285 | 0.004 |
| 31 | −0.182 | 0.019 | −0.182 | 0.020 |
| 32 | −0.003 | 0.010 | −0.003 | 0.008 |

Table A2.
Statistics of Figure 9. GB ionospheric delay differences and GF filtered ionospheric delay differences between the receiver GODZ and GODN.
Table A2.
Statistics of Figure 9. GB ionospheric delay differences and GF filtered ionospheric delay differences between the receiver GODZ and GODN.
| PRN | GB Ionosphere Differences | GF Ionosphere Differences | ||
|---|---|---|---|---|
| Bias | Standard Deviation | Bias | Standard Deviation | |
| 01 | −0.777 | 0.006 | −0.950 | 0.035 |
| 02 | −0.307 | 0.007 | −0.077 | 0.063 |
| 03 | −0.683 | 0.015 | −0.830 | 0.088 |
| 05 | −0.254 | 0.003 | 0.111 | 0.020 |
| 06 | −0.564 | 0.074 | −0.552 | 0.088 |
| 07 | −0.650 | 0.016 | 0.669 | 0.042 |
| 08 | −0.700 | 0.018 | −0.733 | 0.037 |
| 09 | −0.659 | 0.012 | −0.607 | 0.033 |
| 10 | −0.686 | 0.010 | −0.696 | 0.027 |
| 11 | −0.525 | 0.016 | −0.408 | 0.041 |
| 12 | −0.632 | 0.017 | −0.372 | 0.046 |
| 13 | −0.234 | 0.014 | −0.268 | 0.025 |
| 14 | −0.539 | 0.013 | −0.412 | 0.014 |
| 15 | −0.195 | 0.013 | 0.191 | 0.029 |
| 16 | −0.589 | 0.013 | −0.452 | 0.014 |
| 17 | −0.590 | 0.062 | −0.632 | 0.114 |
| 18 | −0.527 | 0.015 | −0.151 | 0.046 |
| 19 | −0.479 | 0.087 | −0.081 | 0.151 |
| 20 | −0.271 | 0.012 | 0.178 | 0.013 |
| 21 | −0.292 | 0.014 | 0.041 | 0.048 |
| 22 | −0.584 | 0.010 | −0.175 | 0.075 |
| 23 | −0.535 | 0.013 | −0.556 | 0.048 |
| 24 | −0.763 | 0.008 | −0.549 | 0.033 |
| 25 | −0.790 | 0.019 | −0.899 | 0.039 |
| 26 | −0.686 | 0.022 | −0.847 | 0.039 |
| 27 | −0.620 | 0.021 | −0.697 | 0.030 |
| 28 | −0.565 | 0.033 | −0.537 | 0.069 |
| 29 | −0.643 | 0.013 | −0.387 | 0.025 |
| 30 | −0.692 | 0.014 | −0.870 | 0.053 |
| 31 | −0.645 | 0.018 | −0.738 | 0.038 |
| 32 | −0.716 | 0.015 | −0.585 | 0.027 |

Table A3.
Statistics of Figure 12. GF-GB ionospheric delays for PRN 09 for all sites, GB ionospheric delays are derived from final OC and real-time OC.
Table A3.
Statistics of Figure 12. GF-GB ionospheric delays for PRN 09 for all sites, GB ionospheric delays are derived from final OC and real-time OC.
| Stations | Final OC | Real-Time OC | ||
|---|---|---|---|---|
| Bias | Standard Deviation | Bias | Standard Deviation | |
| ARUC | 0.085 | 0.019 | 0.944 | 0.025 |
| CEBR | −0.049 | 0.011 | 0.843 | 0.011 |
| CHAN | −0.050 | 0.025 | 0.714 | 0.067 |
| CORD | 0.025 | 0.022 | 1.115 | 0.033 |
| FAA1 | −0.044 | 0.078 | 1.038 | 0.091 |
| GCGO | 0.137 | 0.056 | 1.377 | 0.091 |
| GODN | 0.062 | 0.023 | 1.263 | 0.038 |
| GODZ | 0.028 | 0.034 | 1.235 | 0.041 |
| HARB | −0.291 | 0.037 | 0.515 | 0.042 |
| KIRI | −0.209 | 0.020 | 0.539 | 0.160 |
| KOKB | 0.038 | 0.032 | 0.699 | 0.120 |
| KOKV | 0.012 | 0.028 | 0.671 | 0.108 |
| LPGS | −0.009 | 0.032 | 0.981 | 0.017 |
| MAJU | 0.184 | 0.046 | 0.881 | 0.202 |
| MAW1 | 0.247 | 0.064 | 0.878 | 0.103 |
| MGUE | −0.059 | 0.053 | 1.062 | 0.024 |
| MIZU | −0.041 | 0.114 | 0.653 | 0.068 |
| MKEA | −0.052 | 0.009 | 0.690 | 0.092 |
| MRO1 | −0.104 | 0.037 | 0.481 | 0.065 |
| NAUR | 0.190 | 0.036 | 0.939 | 0.118 |
| NNOR | −0.074 | 0.024 | 0.490 | 0.070 |
| OHI3 | 0.080 | 0.023 | 1.053 | 0.044 |
| PERT | −0.240 | 0.042 | 0.313 | 0.063 |
| REDU | −0.083 | 0.022 | 0.821 | 0.020 |
| SANT | 0.137 | 0.107 | 1.290 | 0.141 |
| SHAO | −0.178 | 0.040 | 0.535 | 0.050 |
| SUTH | −0.064 | 0.021 | 0.746 | 0.029 |
| VILL | −0.054 | 0.027 | 0.841 | 0.028 |
| VOIM | −0.219 | 0.080 | 0.609 | 0.077 |
| YEBE | 0.494 | 0.151 | 1.388 | 0.153 |
| ZAMB | −0.067 | 0.035 | 0.807 | 0.050 |
References
- Hobiger, T.; Jakowski, N. Atmospheric signal propagation. In Springer Handbook of Global Navigation Satellite Systems, 2nd ed.; Teunissen, P., Montenbruck, O., Eds.; Springer Nature: Cham, Switzerland, 2017; pp. 165–194. [Google Scholar]
- Hernández-Pajares, M.; Juan, J.M.; Sanz, J.; Aragón-Àngel, À.; García-Rigo, A.; Salazar, D.; Escudero, M. The ionosphere: Effects, GPS modeling and the benefits for space geodetic techniques. J. Geod. 2011, 85, 887–907. [Google Scholar] [CrossRef]
- Jakowski, N. Ionosphere Monitoring. In Springer Handbook of Global Navigation Satellite Systems, 2nd ed.; Teunissen, P., Montenbruck, O., Eds.; Springer Nature: Cham, Switzerland, 2017; pp. 1139–1162. [Google Scholar]
- Kleusberg, A.; Teunissen, P. GPS for Geodesy; Springer: Berlin/Heidelberg, Germany, 1998. [Google Scholar]
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. Space Phys. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Geng, J.; Meng, X.; Dodson, A.H.; Ge, M.; Teferle, F.N. Rapid re-convergences to ambiguity-fixed solutions in precise point positioning. J. Geod. 2010, 84, 705–714. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ge, M. Regional reference network augmented precise point positioning for instantaneous ambiguity resolution. J. Geod. 2011, 85, 151–158. [Google Scholar] [CrossRef]
- Geng, J.; Shi, C. Rapid initialization of real-time PPP by resolving undifferenced GPS and GLONASS ambiguities simultaneously. J. Geod. 2017, 91, 361–374. [Google Scholar] [CrossRef]
- Kashani, I.; Wielgosz, P.; Grejner-Brzezinska, D. The impact of the ionospheric correction latency on long baseline instantaneous kinematic GPS positioning. Surv. Rev. 2007, 39, 238–251. [Google Scholar] [CrossRef]
- Xiang, Y.; Gao, Y.; Shi, J.; Xu, C. Carrier phase-based ionospheric observables using PPP models. Geod. Geodyn. 2017, 8, 17–23. [Google Scholar] [CrossRef]
- Ciraolo, L.; Azpilicueta, F.; Brunini, C.; Meza, A.; Radicella, S.M. Calibration errors on experimental slant total electron content (TEC) determined with GPS. J. Geod. 2007, 81, 111–120. [Google Scholar] [CrossRef]
- Brunini, C.; Azpilicueta, F.J. Accuracy assessment of the GPS-based slant total electron content. J. Geod. 2009, 83, 773–785. [Google Scholar] [CrossRef]
- Stephens, P.; Komjathy, A.; Wilson, B.; Mannucci, A. New leveling and bias estimation algorithms for processing COSMIC/FORMOSAT-3 data for slant total electron content measurements. Radio Sci. 2011, 46. [Google Scholar] [CrossRef]
- Zhang, B.; Ou, J.; Yuan, Y.; Li, Z. Extraction of line-of-sight ionospheric observables from GPS data using precise point positioning. Sci. China Earth Sci. 2012, 55, 1919–1928. [Google Scholar] [CrossRef]
- Zhang, B. Three methods to retrieve slant total electron content measurements from ground-based GPS receivers and performance assessment. Radio Sci. 2016, 51, 972–988. [Google Scholar] [CrossRef]
- Chen, L.; Yi, W.; Song, W.; Shi, C.; Lou, Y.; Cao, C. Evaluation of three ionospheric delay computation methods for ground-based GNSS receivers. Gps Solut. 2018, 22, 125. [Google Scholar] [CrossRef]
- Schaer, S. Mapping and Predicting the Earth’s Ionosphere Using the Global Positioning System. Ph.D. Thesis, University of Berne, Berne, Switzerland, 1999. [Google Scholar]
- Mannucci, A.J.; Wilson, B.D.; Yuan, D.N.; Ho, C.H.; Lindqwister, U.J.; Runge, T.F. A global mapping technique for GPS-derived ionospheric total electron content measurements. Radio Sci. 1998, 33, 565–582. [Google Scholar] [CrossRef]
- Nie, W.; Xu, T.; Rovira-Garcia, A.; Zornoza, J.M.J.; Subirana, J.S.; González-Casado, G.; Chen, W.; Xu, G. The Impacts of the Ionospheric Observable and Mathematical Model on the Global Ionosphere Model. Remote Sens. 2018, 10, 169. [Google Scholar] [CrossRef]
- Chen, G.; Liu, S.; Zhao, Q. Analysis of Wide-Lane Ambiguities Derived from Geometry-Free and Geometry-Based Precise Point Positioning Models and Their Implication for Orbit and Clock Quality. Sensors 2018, 18, 1760. [Google Scholar] [CrossRef]
- Liu, S.; Chen, G.; Zhao, Q. Assessment of BeiDou-2 Orbit and Clock Quality Based on Analysis of Wide-Lane Ambiguities Derived from PPP Models. In Lecture Notes in Electrical Engineering, Proceedings of the China Satellite Navigation Conference (CSNC) 2019; J.B. Metzler: Stuttgart, Germany, 2019; pp. 174–183. [Google Scholar]
- Dilssner, F.; Springer, T.; Schnemann, E. Side-effects of a bad attitude: How GNSS spacecraft orientation errors affect solar radiation pressure modelling. In Proceedings of the EGU General Assembly 2015, Vienna, Austria, 12–17 April 2015. EGU General Assembly Conference Abstracts. [Google Scholar]
- Nie, W.; Xu, T.; Du, Y.; Gao, F.; Xu, G. Numerical Algebra Solution: A New Algorithm for the State Transition Matrix. Adv. Space Res. 2017, 60, 2620–2629. [Google Scholar] [CrossRef]
- Nie, W.; Xu, T.; Rovira-Garcia, A.; Zornoza, J.M.J.; Subirana, J.S.; González-Casado, G.; Chen, W.; Xu, G. Revisit the calibration errors on experimental slant total electron content (TEC) determined with GPS. Gps Solut. 2018, 22, 85. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, B.; Yuan, Y.; Li, M. Real-Time Precise Point Positioning (RTPPP) with raw observations and its application in real-time regional ionospheric VTEC modeling. J. Geod. 2018, 92, 1267–1283. [Google Scholar] [CrossRef]
- Verhagen, S.; Teunissen, P.J. Least-Squares Estimation and Kalman Filtering. In Springer Handbook of Global Navigation Satellite Systems; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2017; pp. 639–660. [Google Scholar]
- Teunissen, P. Basic Observation Equations. In Springer Handbook of Global Navigation Satellite Systems, 2nd ed.; Teunissen, P., Montenbruck, O., Eds.; Springer Nature: Cham, Switzerland, 2017; pp. 561–573. [Google Scholar]
- Kouba, J.; Héroux, P. Precise Point Positioning Using IGS Orbit and Clock Products. Gps Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, Q. Near-field surface displacement and permanent deformation induced by the Alaska Mw 7.5 earthquake determined by high-rate real-time ambiguity-fixed PPP solutions. Chin. Sci. Bull. 2014, 59, 4781–4789. [Google Scholar] [CrossRef]
- Héroux, P.; Kouba, J. GPS precise point positioning using IGS orbit products. Phys. Chem. Earthpart. A Solid Earth Geod. 2001, 26, 573–578. [Google Scholar] [CrossRef]
- Kouba, J. A Guide to using International GNSS Service (IGS) Products. 2009. Available online: https://kb.igs.org/hc/en-us/articles/201271873-A-Guide-to-Usingthe-IGS-Products.html (accessed on 5 May 2021).
- Kazmierski, K.; Sosnics, K.; Hadas, T. Quality assessment of multi-GNSS orbits and clocks for real-time precise point positioning. Gps Solut 2018, 22, 11. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).