Abstract
Line-of-sight wind profiles are derived from Doppler shifts in infrared solar occultation measurements from the Atmospheric Chemistry Experiment Fourier transform spectrometers (ACE-FTS), the primary instrument on SCISAT, a satellite-based mission for monitoring the Earth’s atmosphere. Comparisons suggest a possible eastward bias from 20 m/s to 30 m/s in ACE-FTS results above 80 km relative to some datasets but no persistent bias relative to other datasets. For instruments operating in a limb geometry, looking through a wide range of altitudes, smearing of the Doppler effect along the line of sight can impact the measured signal, particularly for saturated absorption lines. Implications of Doppler effect smearing are investigated for forward model calculations and volume mixing ratio retrievals. Effects are generally small enough to be safely ignored, except for molecules having a large overhang in their volume mixing ratio profile, such as carbon monoxide.
1. Introduction
The Atmospheric Chemistry Experiment (ACE), also known as SCISAT, is a Canadian-led satellite mission for remote sensing of Earth’s atmosphere [1,2]. The measurement technique employed for ACE is solar occultation. Using the sun as a light source, instruments collect a series of atmospheric transmittance measurements as the sun rises or sets from the orbiting satellite’s perspective, providing up to 30 measurement opportunities per day. The primary instrument is the Atmospheric Chemistry Experiment Fourier transform spectrometer (ACE-FTS), custom built by ABB in Quebec City, Canada, featuring high resolution (±25 cm maximum optical path difference, 0.02 cm−1 resolution), broad spectral coverage (750 cm−1 to 4400 cm−1), and a signal-to-noise ratio ranging from ~100:1 up to ~400:1 [3]. The instrument’s circular input aperture of 1.25 mrad subtends an altitude range of 3 km to 4 km (diameter) at the tangent point.
The purpose of the mission is to derive information on atmospheric constituents, providing altitude profiles for the volume mixing ratios (VMRs) of many molecules, along with aerosol extinction and atmospheric pressure and temperature [4]. However, the ACE-FTS is also capable of determining line-of-sight winds, inferred from Doppler shifts induced in atmospheric spectra by wind-driven motion of molecules in the atmosphere. This is an unplanned benefit of the mission, made possible by the frequency stability inherent in Michelson interferometers. A new ACE-FTS processing version (5.0) is underway that will include line-of-sight wind as a standard data product. ACE-FTS version 5.0 will also feature two additional molecules compared to version 4.1 [4], HOCl [5] and CH2F2 (HFC-32), and will extend the VMR retrievals for SO2 and ClO to higher altitude.
Knowledge of atmospheric winds is important for understanding dynamics and transport and for predicting how the atmospheric state will evolve. In the upper troposphere and lower stratosphere, horizontal wind information is provided by several sources: In situ measurements (e.g., from planes [6] and balloons [7,8]), ground-based lidar [8] and other types of ground-based remote sensing measurements [9], and lidar measurements from space [10]. In the upper mesosphere and lower thermosphere (UMLT), good coverage of horizontal winds is achieved through measuring Doppler shifts in airglow lines, a task currently performed by the TIMED Doppler Interferometer (TIDI) instrument on the Thermosphere Ionosphere Mesosphere Energetics and Dynamics (TIMED) satellite [11] and by the Michelson Interferometer for Global High-resolution Thermospheric Imaging (MIGHTI) instrument on the Ionospheric Connection Explorer (ICON) satellite [12], continuing the legacy of the Wind Imaging Interferometer (WINDII) [13], which flew on the Upper Atmosphere Research Satellite (UARS). On the UARS, there was also a triple etalon Fabry-Perot interferometer called the High-Resolution Doppler Imager (HRDI) that used O2 emissions to measure winds in this altitude region [14]. Mesospheric winds are also provided from ground-based measurements using the Na lidar and meteor radar [15,16], field-widened Michelson interferometers [17], and Fabry Perot interferometers [18]. Line-of-sight winds in the vicinity of the mesopause were derived using the Doppler shift in O2 emission lines from the Microwave Limb Sounder (MLS) instrument on the Aura satellite [19].
Technical challenges have historically made it difficult to perform wind measurements in the middle atmosphere (from roughly 30 km to 70 km) [20,21]. Rocket campaigns [22] provide good altitude coverage but are expensive and infrequent. Recent advancements in ground-based techniques have provided coverage in this altitude region from Rayleigh/Mie/Raman lidars [20] and microwave Doppler wind radiometers [23]. For middle atmospheric wind measurements from space, line-of-sight winds were determined from the Atmospheric Trace Molecule Spectroscopy Experiment (ATMOS) spectrometer flown on the space shuttle for Spacelab 3 in 1985 [24], and from the Superconducting Submillimeter-Wave Limb Emission Sounder (SMILES) mission [25], which was deployed on the International Space Station. Measurements from HRDI [14] extended into this altitude region, with measurements using O2 emissions reaching as low as 50 km and measurements using O2 absorption extending up to 40 km.
Using Doppler shifts in solar occultation measurements, the ACE-FTS will provide line-of-sight wind information from ~20 km to 140 km, featuring altitude coverage in both the UMLT and the relatively sparsely measured middle atmosphere. This paper describes how wind information is derived from ACE-FTS measurements, compares results to data from other sources, and describes how a variable Doppler shift along the line of sight impacts forward model calculations and retrievals for this limb-viewing instrument.
2. Winds from the ACE-FTS
Similar to the approach employed for the ATMOS mission [26], the line-of-sight component of atmospheric winds in the vicinity of the measurement tangent point (the location of closest approach to the Earth of a measured solar ray) can be derived from the apparent stretching of the spectrum’s wavenumber scale. At a particular wavenumber (σ), the wind velocity (v) near the tangent point can be calculated from the observed wavenumber shift (Δσ):
where c is the speed of light. For reference, a 50 m/s wind speed would induce a Doppler shift of roughly 4 × 10−4 cm−1 near 2350 cm−1, requiring great precision and stability in the instrument.
For atmospheric limb measurements, the instrument looks through a wide range of altitudes along the line of sight. This induces a smearing of the Doppler effect in the spectrum from differences in the apparent line position at each point along the path of a measured ray resulting from the variation in local line-of-sight wind speed. A rigorous determination of wind speed as a function of altitude would involve an inversion (similar to retrieving VMR profiles from ACE-FTS measurements), incorporating the altitude variation of the Doppler shift into the forward model and fitting for a wind profile that best reproduces the measured spectra, with a particular emphasis on matching the observed line positions. However, the measured signal is dominated by the contribution from the altitude region near the tangent point, a consequence of the exponential variation of pressure with altitude. Thus, in the absence of strong saturation (complete absorption near line center), line-of-sight wind speed near the tangent point can be estimated directly from the wavenumber shift between the measured spectrum and a calculated spectrum where Doppler effects are ignored.
Cross correlation was used to determine wavenumber shifts between measured and calculated spectra by finding the shift that maximized the correlation between the two spectra within a particular spectral window. Spectral windows were targeted to contain lines with a minimum peak absorption of 5% (to limit the impact of noise in the calculations) and a maximum peak absorption of 50% (to avoid saturation). At higher altitudes, broader spectral windows (10 cm−1 to 15 cm−1 wide where possible) containing several lines were employed to optimize the accuracy of the cross-correlation calculations. At lower altitudes, narrower spectral windows (generally 0.6 cm−1 to 2 cm−1 wide near 20 km) were employed to avoid saturated lines and excessive numbers of lines in a given window as the spectrum grew more crowded. At all altitudes, measured spectra were interpolated from their native 0.02 cm−1 grid to a 0.00125 cm−1 grid to improve the accuracy and stability of the cross-correlation calculation.
The atmosphere is divided into segments, as depicted in Figure 1. Above 46 km, the segments span 4 km in altitude (134 km to 138 km, 130 km to 134 km, etc.). Below 46 km, the segment size decreases with altitude (reproducing the typical decrease in ACE-FTS tangent height spacing resulting from atmospheric refraction), decreasing to just over 2 km near altitude 20 km. In each segment, a forward model calculation was used to generate a representative spectrum for that segment corresponding to a tangent height near the center using pressure, temperature, and VMR profiles from a particular occultation (sr10063, where sr stands for sunrise, and 10063 is the number of orbits since launch, comprising a unique identifier for the occultation), with spectroscopic parameters taken from The high resolution transmission molecular absorption (HITRAN) database 2016 [27], a line list maintained by the Harvard-Smithsonian Center for Astrophysics at Cambridge, USA. This representative spectrum was used in the determination of wavenumber shifts (via cross correlation) for any measurement with a tangent height falling in the given segment. Note that there could be significant differences between the representative spectrum and the measurement, particularly for the relative intensities of different lines. These differences could be minimized using the pressure and temperature profiles retrieved for the occultation in question to generate representative calculated spectra specific to that occultation. However, this would greatly increase the complexity of the analysis while providing a negligible gain in accuracy, since cross correlation is primarily sensitive to line positions, not the relative intensities of the lines.
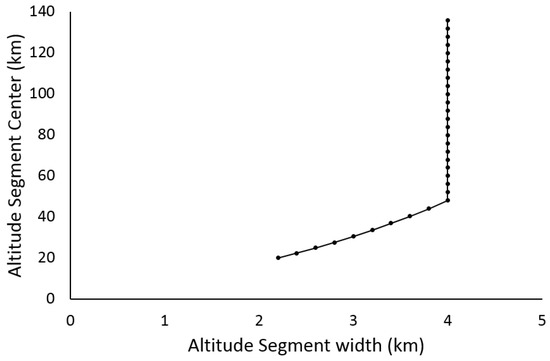
Figure 1.
Altitude segments employed in generating line-of-sight wind profiles from the ACE-FTS. Below 45 km, segment widths become smaller with decreasing altitude to track the typical compression of tangent height spacing in ACE-FTS measurements that results from atmospheric refraction.
Using cubic spline, wind profiles were interpolated from the measurement tangent height grid (which is irregular and varies from occultation to occultation) onto a fixed altitude grid with 1 km spacing. For results reported here, tangent heights were taken from version 4.1 retrievals [4]. Note that the altitude spacing between measurements varies with orbital geometry, ranging from less than 2 km to ~6 km. For occultations with large altitude spacing, there could be significant smoothing error from interpolating onto the standard 1 km grid with cubic spline. Wind profiles in ACE-FTS version 5.0 processing will also be provided on the measurement grid for users wanting to avoid this potential source of error.
The set of spectral windows used in each altitude segment is reported in Table A1 of Appendix A. Calculating the average relative shift (Δσ/σ) from multiple windows reduces noise effects and permits the use of a statistical filter (a 2-sigma filter on standard deviation) to remove spurious results. Note the strong overlap between some spectral windows at high altitude, a consequence of choosing broad windows to minimize errors in cross correlation while ensuring enough windows to perform statistical filtering of outliers.
Uncertainties for calculated line-of-sight winds are taken as the standard error of the mean for shifts determined from the various spectral windows. These uncertainties are a combination of random error from noise effects in the determination of the shifts and systematic errors from scatter in the results caused by inconsistencies in spectroscopic parameters. In preliminary results, these errors typically ranged from 3 m/s to ~10 m/s for altitudes below about 125 km. Above 125 km, larger uncertainties were observed, with the magnitude of the uncertainties strongly dependent on the strength of the available CO2 lines relative to the noise level in this altitude region.
Contributions to the spectral windows in Table A1 come primarily from various isotopologues of CO2, H2O, N2O, and CH4. The reliability of line positions from HITRAN 2016 is a major potential source of systematic error in the analysis. Selecting a set of spectral windows that yields consistent results for different molecules or different bands of a given molecule should hopefully minimize this error. CO lines were strictly avoided because of the large overhang in the molecule’s VMR profile. Some windows contain weak absorption from NO (which exhibits a similar VMR overhang) and do not significantly impact the cross-correlation analysis. Significant absorption from molecules such as O3 and HNO3 was avoided because of the high density of lines for these molecules and the strongly peaked nature of their VMR profiles.
In principle, it is possible to push the analysis to lower altitude, but the number of unsaturated lines becomes much more limited, non-Voigt effects (such as line mixing) become more pronounced, the accuracy of pressure shift information (generally much less reliable than line position information) starts to play a role, and refraction effects strongly impact instrument pointing, which could complicate the analysis. At this time, 19 km is the lower altitude limit for winds generated from ACE-FTS measurements, pending further study.
For line-of-sight winds derived from the ACE-FTS, we defined a positive wind as moving toward the instrument and away from the light source (the sun).
Note that this approach assumes a vertical wind profile, but there is geographic smearing from each measurement being at a slightly different location (with a slightly different look angle) as the satellite progresses in its orbit. This was ignored in the analysis, which contributed systematic errors to the results, the magnitude of which depends on the degree of geographic smearing for the given occultation.
Calibration
Winds generated from the ACE-FTS require calibration because factors other than atmospheric winds affect the wavenumber scale of the measured spectrum. The ACE-FTS instrument has an onboard metrology laser that is sensitive to temperature [3]. The temperature of this diode laser is actively controlled but still experiences minor variations over the course of an orbit. Based on onboard temperature readings from January 2020, the output of the diode laser (operating at 1550 nm) could shift up to 2.5 × 10−5 nm over the roughly 2-min span of an occultation event. This creates an altitude-dependent systematic error, with a discrepancy <5 m/s (expressing the resultant wavenumber shift in the measured spectrum in terms of an apparent relative velocity that would induce an equivalent Doppler shift) for winds measured at the end of an occultation relative to the beginning of the occultation. This discrepancy should be opposite in sign for sunrises (where solar flux on the satellite increases as it comes out of eclipse, causing a temperature increase) and sunsets (where solar flux on the satellite decreases as the sun moves behind the Earth from the orbiting satellite’s perspective).
In addition, the wavenumber scale of the measurement was corrected for relative motion of the satellite and the sun, a substantial shift from the >7 km/s orbital velocity of SCISAT. The velocity component along the line of sight was calculated from the Systems Tool Kit (STK, formerly Satellite Tool Kit) software package [28] using accurate orbital data for the satellite (ephemerides updated daily by the SCISAT Mission Operation Center). Note that this wavenumber scale correction (based on satellite-sun relative motion) represents an approximation for the satellite-atmosphere relative velocity, the actual quantity of interest for wavenumber calibration of atmospheric lines. Also, the wavenumber scale correction based on satellite-sun relative motion is missing the relative velocity component from the Earth rotating below the orbiting satellite. Explicitly accounting for this effect would require implementing a satellite-atmosphere calculation with STK, made challenging by impacts on instrument pointing from refraction and from clouds or aerosols, which (unlike satellite-sun velocity) are nearly impossible to estimate prior to a full analysis of the occultation.
In routine ACE-FTS processing prior to version 5.0, a final adjustment to the wavenumber scale was applied to approximately align high-altitude CO2 lines in the spectra with their expected ‘rest’ positions. The ACE-FTS features two detector regions [1], and this adjustment unfortunately introduced an inconsistency in the wavenumber scales for the two detector regions. This adjustment was therefore removed for the upcoming processing version 5.0, significantly improving the quality of the wind results derived from the spectra.
Raw ACE-FTS measurements contain both solar and atmospheric features, which raises the possibility of using the solar spectrum for absolute wavenumber calibration. Unfortunately, solar spectra in the raw measurements can vary significantly relative to the Doppler shifts expected from atmospheric winds, making them unsuitable as a calibration standard. If the footprint of the ACE-FTS field of view on the sun is not centered on the rotation axis, there will be a Doppler component from solar rotation, and Doppler shifts from convection in the solar atmosphere [29] will vary with the location viewed on the sun.
We can, however, use solar features in raw ACE-FTS measurements to evaluate altitude drifts in the wavenumber scale over the course of an occultation arising from either a drift in metrology laser temperature or errors in the wavenumber scale corrections applied based on STK-calculated satellite-sun relative velocities (which vary with altitude). Figure 2 shows the shift observed for solar features (again expressed in terms of the equivalent apparent shift in velocity) relative to the highest measurement in an occultation. Down to about 40 km, the positions of solar features in the raw spectra remain roughly constant, within ~5 m/s, suggesting a minimal drift from either the laser temperature or corrections applied for satellite-sun relative velocity. Below 40 km, solar features begin to shift in the spectra, increasing with decreasing altitude, topping the equivalent of 450 m/s near 20 km. This is an artifact from the ACE-FTS footprint moving on the sun as refraction effects distort the image of the solar disk seen from the satellite, and the pointing system automatically deflects to track the center of radiance. As the footprint moves on the sun, there are changes in the solar Doppler components (from solar rotation and solar atmospheric convection) averaged over the field of view.
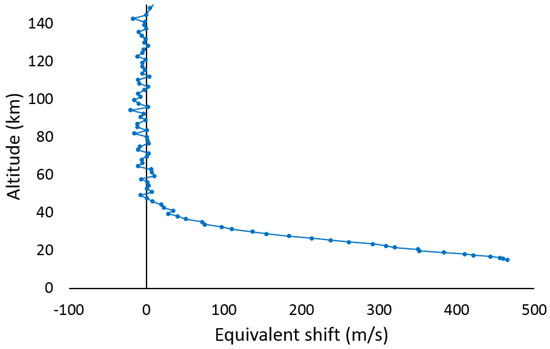
Figure 2.
Shifts in solar features relative to the highest measurement in sr10063, expressed in terms of the equivalent apparent change in velocity. The large apparent change at low altitude is an artifact from a change in the solar spectrum as the footprint of the ACE-FTS field of view moves on the sun.
A small component of the behavior of the shift below 40 km in Figure 2 comes from deficiencies in the correction applied for satellite-sun relative velocity. Changes in pointing from atmospheric effects (such as refraction and clouds/aerosols) were not considered in the STK calculations when these corrections were applied. Changes in pointing would slightly alter the velocity component along the line of sight compared to the calculation based purely on sun/satellite geometry. Calculations using STK suggest that errors from ignoring this change in geometry are negligible above ~25 km but increase with decreasing altitude below that, amounting to the order of 3 m/s in the 19 km to 20 km altitude range. The satellite-sun relative velocity is positive for sunrises (i.e., the instrument looks generally forward relative to the orbital motion) and negative for sunsets (the instrument looks counter to orbital motion). Thus, this systematic error will be opposite in sign for sunrises and sunsets.
With the solar spectrum deemed an inadequate calibration standard, we instead relied on an external source: Winds provided by the operational global weather assimilation and forecasting system from the Canadian Meteorological Center (see Buehner et al. [30] and the references therein for the evolution of the weather model over the course of the ACE mission). Pressure and temperature outputs from this system are routinely employed in the analysis of ACE-FTS occultations [4]. Wind data from the meteorological model typically extend up to 30 km, but the dearth of operational wind information in the middle atmosphere suggests that data points near the top of the altitude range might be less constrained by measured inputs. Therefore, wind data between 19 km and 24 km from the weather service were used for the calibration.
From the vector horizontal winds provided by the weather service, the component along the ACE-FTS line of sight can be calculated from
where U is the zonal component (east-west component, assumed positive moving eastward), V is the meridional component (north-south component, assumed positive moving northward), and θ is the angle between a vector pointing from the measurement tangent point toward geodetic north (the positive axis for meridional winds) and a vector pointing from the measurement tangent point toward the satellite (the positive axis for ACE-FTS winds). Note that θ − 90° is the angle between a vector pointing eastward from the tangent point (the positive axis for zonal winds) and the vector from the tangent point toward the satellite. The average value of the angle θ between altitudes 19 km and 24 km (the altitude region being used for the calibration) was calculated from STK.
An offset value was calculated from the average difference between measured ACE-FTS winds and the component of weather service winds along the ACE-FTS line of sight for altitudes between 19 km and 24 km. This offset was then subtracted from measured ACE-FTS winds at all altitudes.
Accuracy of wind information from the Canadian weather model has likely evolved over the course of the ACE mission, with improvements in the quality and breadth of wind data available for assimilation and improvements in the model itself. Errors in this information contribute a constant offset to the entire wind profile. The magnitude of errors in this calibration source may be evaluated in future studies during comparisons to independent wind measurements.
This calibration approach implicitly corrects for (among other things) the impact of ignoring the Earth’s rotation below the orbiting satellite. However, the Doppler shift associated with Earth’s rotation changes with altitude because the effective radius of rotation increases with increasing altitude. For example, during one full rotation, a point at an altitude of 100 km travels a greater distance than a point at 20 km in the same period of time (24 h), so the instantaneous tangent velocity is faster at 100 km.
With the simplifying assumptions of a spherical Earth and no change in tangent latitude with altitude for ACE-FTS measurements, the necessary correction for satellite-atmosphere relative velocity (Δvsat_atm) at altitude z can be calculated from geometry:
where θ − 90° is, as mentioned previously, the angle between a vector pointing eastward (the direction of Earth’s rotation) and the positive axis defined for ACE-FTS winds, zo is 21.5 km (the average of the 19–24 km range used for calibration), and 243600 is the time in seconds for the Earth to go through one full revolution (i.e., one day). The error from neglecting Earth’s rotation grows linearly with altitude and would therefore contribute to a bias at high altitude when calibrating the profile at 21.5 km. The extreme case would have the instrument looking directly eastward or westward for an occultation at the equator (latitude = 0°), where the error in the derived wind near 120 km would be just over 7 m/s. For the occultation sets employed in comparisons for this study, the average error from this effect would be at most 3–4 m/s at 120 km.
Note that the correction described above will not be routinely applied to ACE-FTS results. Applying such corrections will be left to the discretion of the data user.
3. Comparisons
Comparisons to coincident measurements provide a means to assess the quality of wind measurements from the ACE-FTS. In this section, comparisons are made to HRDI measurements from 2005, as well as TIDI and MIGHTI measurements from 2020. The geographic coverage from the ACE-FTS is limited, so it was necessary to choose a relatively relaxed set of coincidence criteria when searching for matches between ACE-FTS measurements and these three satellite missions: Within 2 h, 5° of latitude, and 10° of longitude. The inability to use tighter coincidence criteria may pose difficulties for comparisons of a potentially highly variable quantity such as wind, but reasonable results should be achievable if there are sufficient coincidences to average out differences arising from atmospheric variability.
Comparisons are also made to the Horizontal Wind Model 2014 (HWM14) [31], an empirical climatology model for horizontal winds from the troposphere through the thermosphere developed at the U.S. Naval Research Laboratory in Washington, D.C., as well as winds from the Modern-Era Retrospective Analysis for Research and Applications 2 (MERRA-2) [32], an atmospheric reanalysis incorporating inputs from a wide variety of observations.
Finally, comparisons are made to wind profiles from meteor radar observations over China [16], ground-based measurements that provide vector winds in the upper mesosphere and lower thermosphere by measuring Doppler shifts of electromagnetic radiation reflected from meteor ablation trails.
These comparisons are intended to provide some context for ACE-FTS results compared to existing datasets. More formal validation efforts and comparisons to additional data sources (e.g., ground-based Na-lidar measurements) will be carried out in future studies.
For ACE-FTS observations in the comparisons presented here, the instrument looks generally eastward for sunrise occultations and generally westward for sunset occasions. As noted previously, some systematic errors have effects that are opposite in sign for the two occultation types. Comparisons for sunrises and sunsets are considered separately to avoid inadvertent cancellation of systematic errors in the averages.
For all data sources, the component of the horizontal vector wind along the ACE-FTS line of sight was calculated using the formula in Equation (2), with the angle θ calculated from STK for a representative altitude for the comparison (e.g., 115 km for MIGHTI comparisons, 85 km for HWM14), although note that this angle typically differs by less than 1° from the value near 20 km employed during the calibration process.
3.1. HRDI
There is just over a year’s worth of overlap between the HRDI and ACE missions, from the start of ACE science activities in February 2004 to the end of HRDI operations in April 2005. Unfortunately, the satellites’ orbits were such that there were very few coincidences between the 2 missions with the given coincidence criteria: 5 coincidences for ACE-FTS sunrises and 23 coincidences for ACE-FTS sunsets. Figure 3 shows comparisons between ACE-FTS and HRDI results for several ACE-FTS sunsets having coincidences with multiple HRDI measurements where differences between the HRDI profiles are generally small (suggesting relatively low variability in the wind field). There are discrepancies, but these results show reasonably good agreement overall. Figure 4a shows the average profiles for the 5 sunrise coincidences, and Figure 4b shows the average results for the 23 sunset coincidences. The agreement for the sunset occultations is somewhat better than the agreement for the sunrises, likely a reflection of having more data to average out differences from atmospheric variability.
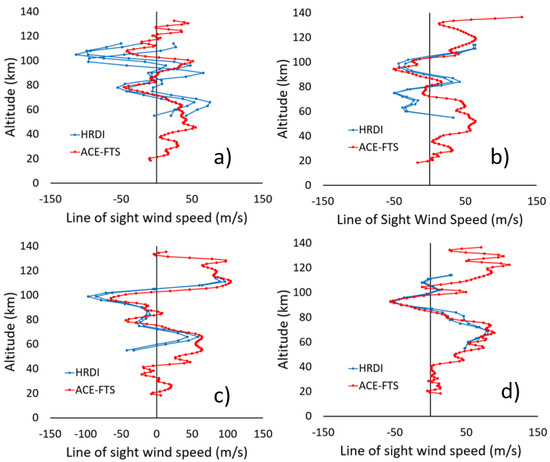
Figure 3.
Comparison between ACE-FTS winds (in red) and selected HRDI results (in blue) for cases where multiple HRDI measurements were coincident with a single ACE-FTS occultation. (a) ss3475 (where ss stands for sunset), measured 4 April 2004; (b) ss3486, measured 5 April 2004; (c) ss5302, measured 5 August 2004; and (d) ss5341, measured 9 August 2004.
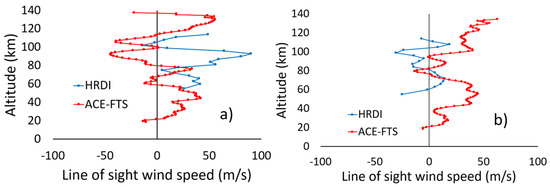
Figure 4.
(a) The average HRDI (in blue) and ACE-FTS (in red) winds along the ACE-FTS line of sight for 5 coincidences with ACE-FTS sunrises. (b) The same as (a) but for the 23 HRDI coincidences with ACE-FTS sunsets.
The average profiles in Figure 4b generally exhibit a high bias in the ACE-FTS results. Note, however, that this is not persistent in the comparison dataset. In Figure 3a, ACE-FTS results show a high bias near 100 km but match well near 75 km. In Figure 3b, ACE-FTS results match well near 100 km but show a high bias near 70 km.
3.2. MIGHTI
All available coincidences between ACE-FTS occultations and horizontal vector wind data for the green wavelength imager from MIGHTI were found from 1 January to 30 June 2020. This set consists of just under 500 coincidences from 57 occultations for ACE-FTS sunsets and a similar number of coincidences from 71 occultations for sunrises. A small number of outliers (comparisons where winds from the two instruments were very different, typically associated with a limited altitude range for the MIGHTI results) were removed from the sunset comparisons. No data were filtered from the ACE-FTS sunrise comparisons. The results are presented in Figure 5, truncating ACE-FTS results below 80 km and MIGHTI data above 140 km to better show the overlapping altitude range. The shapes of the profiles agree extremely well, particularly for ACE-FTS sunrises, but there is a clear systematic offset of 30 m/s, opposite in sign for sunrises and sunsets.
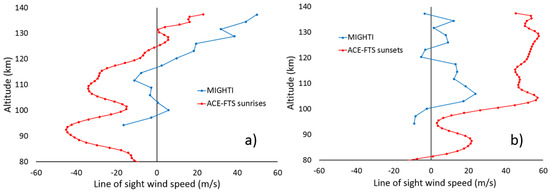
Figure 5.
Average wind profiles for MIGHTI (in blue) and ACE-FTS (in red) coincident results from January to June 2020. (a) Results for ACE-FTS sunrises; (b) Results for ACE-FTS sunsets.
3.3. TIDI
TIDI data are available over the entire duration of the ACE mission, more than 17 years to date. For this preliminary comparison, coincidences were limited to the same timespan as was used for the comparisons with MIGHTI: From January to June 2020. Comparisons with earlier years of TIDI data will be performed at a later date when the official ACE-FTS version 5.0 results become available. The comparison set with TIDI consists of 242 coincidences (among 199 occultations) for ACE-FTS sunsets and 81 coincidences (among 79 occultations) for sunrises. No data were filtered in the comparison. The results are shown in Figure 6, once again truncating ACE-FTS data below 80 km to better see the overlapping altitude region.
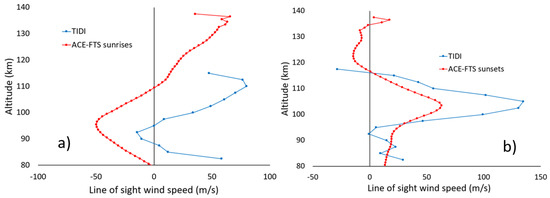
Figure 6.
Average wind profiles for TIDI (in blue) and ACE-FTS (in red) coincident results from January to June 2020. (a) Results for ACE-FTS sunrises; (b) Results for ACE-FTS sunsets.
In Figure 6a, coincident TIDI and ACE-FTS sunrise results appear to show a systematic bias similar to that seen in the comparisons with MIGHTI. For the ACE-FTS sunset comparisons in Figure 6b, both curves exhibit a peak at the same altitude, but the TIDI results are roughly a factor of 2 larger. The reason for this discrepancy is unknown and perhaps warrants further investigation. It is worth noting that ACE-FTS measurements always occur near the terminator between night and day, where the sharp gradient in airglow distribution represents a major challenge when using airglow to infer winds [33].
3.4. HWM14
The HWM14 empirical model can calculate horizontal vector winds at the location of any occultation given inputs for time, location (latitude, longitude, and altitude), and the 3-h index for geomagnetic activity (ap). Because HWM14 is a climatology, leveraging the information inherent in this empirical model involves comparing the averages of large numbers of occultations rather than comparing individual occultations. The HWM14 model was used to calculate ACE-FTS line-of-sight winds corresponding to all occultations from January to July 2020, excluding occultations during the time periods of the polar vortex (winter and early spring for the given hemisphere), because a model could not be expected to reproduce significant atmospheric perturbations associated with this phenomenon. Occultations were separated by type (sunrise and sunset), as well as by geographic region: Northern (latitude > 45° N), tropical and subtropical (latitude between 30° S and 30° N), and southern (latitude < 45° S).
Comparisons to HWM14 results are presented in Figure 7. There is generally good agreement in the layering of the wind profiles (i.e., the altitude structure). For sunrises, other than the northern results in Figure 7c, there is good agreement below ~75 km and a low bias in ACE-FTS results for higher altitudes. The magnitude of the bias at high altitude is similar in magnitude to the low bias observed in sunrise MIGHTI comparisons in Figure 5a. Sunset results indicate a high bias in ACE-FTS results at all altitudes, similar in magnitude to the offset from the MIGHTI sunset comparisons in Figure 5b.
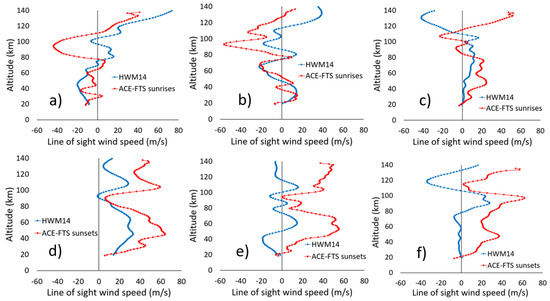
Figure 7.
Comparisons between average line-of-sight wind profiles from the ACE-FTS (in red) and the average results from the Horizontal Wind Model 2014 (in blue) calculated at the ACE-FTS occultation times and locations from January to July 2020. (a) Southern (latitude < 45° S) ACE-FTS sunrises, the average of 544 profiles. (b) Tropical and subtropical (30° S to 30° N) sunrises, 208 profiles. (c) Northern (latitude > 45° N) sunrises, 371 profiles. (d) Southern sunsets, the average of 879 profiles. (e) Tropical and subtropical sunsets, 213 profiles. (f) Northern sunsets, 304 profiles.
3.5. MERRA-2
Model outputs from MERRA-2, provided on grids of time, latitude, longitude, and altitude are available for all ACE-FTS occultations. For comparison, we extracted the MERRA-2 altitude profiles for zonal and meridional winds closest in latitude, longitude, and time to the ACE-FTS result. With the resolution of the MERRA-2 grid and the degree of variability of the MERRA-2 winds for the selected ACE-FTS results, interpolation to the ACE-FTS measurement time and the location was deemed unnecessary. Figure 8 provides comparisons between MERRA-2 winds along the ACE-FTS line of sight (calculated from MERRA-2 horizontal vector winds using Equation (2) and individual ACE-FTS occultations on a particular day (26 April 2020)). These occultations cover a small range of tropical latitudes (9 °S to 13 °S) and a full range of longitudes as the Earth rotates below the orbiting satellite over the course of the day.
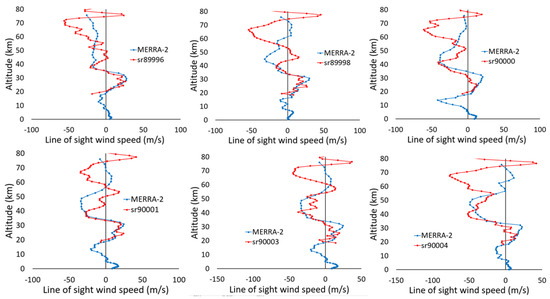
Figure 8.
Comparisons of MERRA-2 results to a set of tropical ACE-FTS sunrise occultations on 26 April 2020.
In Figure 8, the agreement is always good near 20 km, which means the wind data from the Canadian Meteorological Center employed in the calibration is consistent with MERRA-2. Agreement is typically very good up to 40 km or so, but some differences occur at higher altitudes. For example, the ACE-FTS results indicate the presence of a persistent wind feature near altitude 65 km (the ACE-FTS looks generally eastward for this set of occultations, so a negative wind speed means the wind moves eastward, away from the instrument), which was not captured in the MERRA-2 results. This illustrates a potential role for ACE-FTS winds, providing information in the middle atmosphere that MERRA-2 appears to be missing.
3.6. Meteor Radar
A network of VHF all-sky meteor radar stations from the Institute of Geology and Geophysics from the Chinese Academy of Science has provided a long-term dataset for winds in the altitude range from 70 km to 110 km [16]. Vector winds at four locations in China (Mohe: 52.5° N, 122.3° E; Beijing: 40.3° N, 116.2° E; Wuhan: 30.5° N, 114.6° E; and Sanya: 18.3° N, 109.6° E) are reported at hourly intervals.
Preliminary observations were carried out for coincidences between ACE-FTS measurements and the two more northern stations (Mohe and Beijing), which feature more coincidences with ACE-FTS than the two more southern stations. Figure 9 shows comparisons between ACE-FTS results and Mohe results projected onto the ACE-FTS line of sight for the two times bracketing the ACE-FTS measurement (the hourly results just before and just after the ACE measurement). These results were selected to show instances where the agreement between the two datasets were very good.
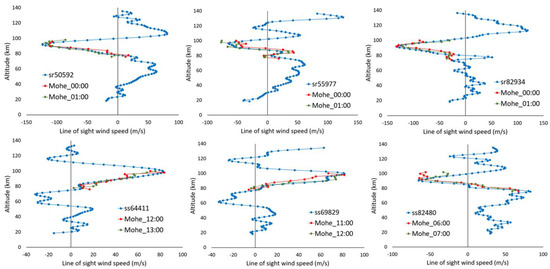
Figure 9.
Selected comparisons between coincident ACE-FTS line-of-sight winds (in blue) and vector winds projected onto the ACE-FTS line of sight for hourly results from the Mohe meteor radar station (52.5° N, 122.3° E) prior to (in red) and after (in green) the ACE-FTS measurement. Three sunrise comparisons are shown in the top row: sr50592 (measured 4 January 2013 at 00:20), sr55977 (measured 4 January 2014 at 00:05), and sr82934 (measured 4 January 2019 at 00:30). The bottom row shows comparisons with ACE-FTS sunsets: ss64411 (measured 29 July 2015 at 12:02), ss69829 (measured 9 January 2016 at 07:45), and ss82480 (measured 4 December 2018 at 06:45).
The agreement between ACE-FTS and Mohe results is typically quite good, if not always to the same level as the results shown in Figure 9. On occasion, there is very good agreement in one altitude region and larger discrepancies in a different region, similar to comparisons in Figure 3a,b with HRDI results. On rarer occasions, there was a roughly 30 m/s bias between the two results, more in line with the bias observed with MIGHTI results. More investigation is required to evaluate if observed discrepancies relate to problems with the measurements or simple geophysical variability because the measurements are not truly coincident, and whether conditions associated with comparisons showing ~30 m/s offsets between ACE-FTS and Mohe results might provide insight into the observed biases with airglow results.
Similarly, Figure 10 shows selected comparisons with results from the Beijing meteor radar station, instances where the agreement was deemed to be very good. Results from the Beijing station exhibited a few more instances of offsets of 30 m/s than observed with Mohe comparisons.
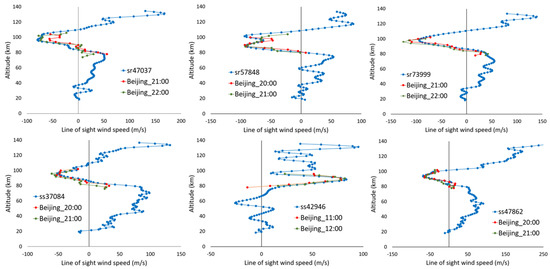
Figure 10.
Selected comparisons between coincident ACE-FTS line of sight winds (in blue) and vector winds projected onto the ACE-FTS line of sight for hourly results from the Beijing meteor radar station (40.3° N, 116.2° E) prior to (in red) and after (in green) the ACE-FTS measurement. Three sunrise comparisons are shown in the top row: sr47037 (measured 7 May 2012 at 21:25), sr57848 (measured 10 May 2014 at 20:55), and sr73999 (measured 8 May 2017 at 00:30). The bottom row shows comparisons with ACE-FTS sunsets: ss37084 (measured 2 July 2010 at 20:50), ss42946 (measured 4 August 2011 at 11:25), and ss47862 (measured 2 July 2012 at 20:35).
In the preliminary observations for these two datasets, there was no indication of a persistent bias with ACE-FTS results, unlike the comparisons with airglow wind measurements from MIGHTI and TIDI and some of the HWM14 comparisons in Figure 7.
4. Impact on Retrievals
Forward model calculations involve tracing the path of measured light ray through the atmosphere, integrating the amount of absorption experienced along the way. They are central to the retrieval process, i.e., the determination of altitude profiles for atmospheric quantities such as pressure, temperature, and constituent VMRs. Parameters in forward model calculations for the quantities of interest are adjusted (e.g., using least-squares fitting) until the calculated spectrum matches the measured spectrum as well as possible.
The retrieval process for the ACE-FTS has been described in previous publications [4,34,35] but will be briefly outlined here. Below 18 km, pressure and temperature are taken from analysis-run outputs of the Canadian Meteorological Center weather model, and tangent heights are determined from the N2 collision induced absorption continuum [36]. Between 18 km and 42 km, pressure and temperature are determined from fitting N2 quadrupole lines and CO2 lines with the CO2 VMR profile fixed to expectations [37], while tangent height separations are constrained to obey hydrostatic equilibrium [34,35]. Above 42 km, where refraction and clouds do not impact instrument pointing, tangent height separations are fixed to values calculated from STK. A value is determined for pressure near 42 km, and the pressure profile above 42 km is generated by integrating the equation for hydrostatic equilibrium using the fitted temperatures and STK-calculated tangent height separations in this altitude region [34], with the average molecular mass as a function of altitude taken from NRLMSIS-00 software calculations [38]. CO2 lines are employed in the analysis above 42 km, with the CO2 VMR profile fixed to expectations up to ~60 km and fitted using a five-parameter empirical function at higher altitudes [34]. Pressure, temperature, and CO2 VMR profiles are generated up to ~125 km. Above this altitude, the shape of the pressure and temperature profiles are taken from NRLMSIS-00 calculations, while the shape of the CO2 VMR profile in this region is determined from an analysis of CO2 lines between 110 km and 140 km with pressure and temperature profiles fixed to NRLMSIS-00 outputs [4].
With pressure and temperature profiles and measurement tangent heights fixed to the results of the pressure/temperature analysis, VMR profiles for the various molecules and isotopologues of interest are retrieved. All retrievals employ global fitting [39] (i.e., fitting for everything simultaneously) with a Levenberg–Marquardt nonlinear least squares approach [40]. ACE-FTS analysis does not employ optimal estimation [41]. To determine profiles, quantities are retrieved at measurement tangent heights and interpolated onto a standard 1 km altitude grid for forward model calculations. If measurements are too close together, a retrieval grid coarser than the measurement spacing is employed to suppress unphysical oscillations in the retrieved profiles without the need to explicitly apply smoothing.
In recent years, much emphasis has been placed on improving the accuracy of forward model calculations, particularly in terms of moving toward more complex line shapes [42,43]. Gradients in Doppler shifts along the line of sight are routinely ignored in forward model calculations, and it is worth considering what repercussions this might have on calculation accuracy, along with the resulting impact on retrievals.
4.1. Forward Model
Instruments employing a limb-viewing geometry, featuring long path lengths and a wide range of altitudes along the line of sight, are susceptible to smearing of the Doppler effect. As a light ray travels through the atmosphere, the apparent (Doppler-shifted) position of a particular line varies as the local wind speed varies, leading to an artificial broadening (i.e., smearing) of the absorption feature. If the width of the measured line is much smaller than the instrumental line width, as is the case for the ACE-FTS for altitudes above 20 km, there will be no visible change in the shape of the measured line in the absence of saturation effects. The measured line it will maintain the appearance of the instrumental line shape with a simple shift in position. The magnitude of the shift depends on the altitude variation of pressure and the associated molecule’s VMR profile. As discussed previously, the exponential variation of pressure with altitude strongly weighs the shift toward the Doppler shift from winds near the tangent point.
The situation changes with the onset of saturation. When the region near the line center is completely saturated (all the light near line center is absorbed), the calculated signal becomes significantly less sensitive to changes in VMR. A Doppler shift moves the line to a different wavenumber, where the signal is not completely saturated, yielding an increase in absorption. Additional effects can occur when saturation broadening approaches or surpasses the instrumental line width, making the shape (not just the strength) of the measured spectral feature sensitive to the wind profile. Note that wind speed must vary with altitude to impart a smearing of the line. A strong wind that was constant with altitude would induce a wavenumber shift in a line but no change in line intensity or shape. Large, sharp gradients in wind speed with altitude would create the largest smearing effects in line shape.
Including Doppler effect smearing in forward model calculations is straightforward. For the ACE-FTS, forward model calculations were divided into 1 km layers. Within each layer, a Doppler shift was applied to the position of each line included in the calculation, following the expression in Equation (1) based on the wind speed determined for the layer and the line’s rest position.
The impact of including Doppler effect smearing in the calculated spectrum is illustrated in Figure 11 for a tangent height near 59.5 km in sr10063. Although not evident in Figure 11, the center of the CO line was saturated in the ‘monochromatic spectrum’ (the spectrum before convolving with the instrumental line shape). The magnitude of the change induced in the calculated spectrum from including Doppler effect smearing was strongly dependent on the gradient in the wind profile. The retrieved wind profile for this occultation, shown in Figure 12, features a significant gradient in the altitude range from 65 km to 75 km, spreading the absorption across a range of wavenumbers, which reduced the impact of saturation and yielded an increase in absorption signal. The difference in Figure 11 is very small but well above the noise level in this wavenumber region (roughly 400:1), which means it could alter the VMR retrieval for this molecule.
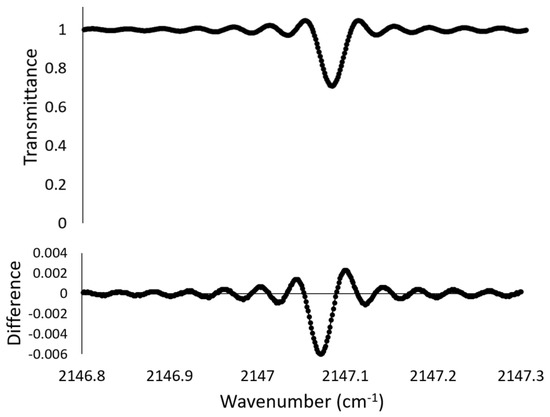
Figure 11.
Top: The calculated CO spectrum for a tangent height near 59.5 km in occultation sr10063. Bottom: The difference in the calculated spectrum when Doppler effect smearing was included versus when it was ignored. Absorption was greater in the case where Doppler effect smearing was included.
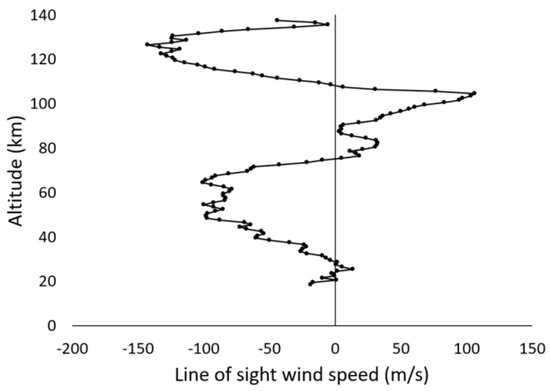
Figure 12.
The line-of-sight wind speed profile for occultation sr10063, with a significant gradient in the altitude range from 65 km to 75 km that induced a change in the calculated spectrum from Doppler effect smearing.
4.2. VMR Retrievals
For the most part, simply avoiding saturation effects in a microwindow set is sufficient to avoid problems from ignoring Doppler effect smearing. The microwindow set employed in the pressure-temperature retrieval strictly avoids even small amounts of saturation and therefore has negligible sensitivity to the wind profile. Strong saturation was avoided for VMR retrievals wherever possible, but the microwindow sets for some targets in version 4.1 processing contain a degree of saturation. Generally, differences in VMR retrievals with and without the inclusion of Doppler effect are very small, less than 1%, and can be safely ignored, but there are situations where VMR retrieval differences are significant and unavoidable (where there are significant gradients in wind speed in particular altitude regions).
Figure 13 shows the VMR profile for CO in the occultation sr10063. This molecule has a very large overhang in the VMR profile. For a tangent height near 65 km, CO lines used in the retrieval experienced a degree of saturation (as discussed previously). A significant portion of the calculated signal came from altitudes above the tangent point, but with slightly different wavenumber locations for line center at different altitudes thanks to the gradient in wind speed. Consequently, the retrieved CO VMR near the base of the overhang changed dramatically when Doppler effect smearing was included in the forward model, by more than 20% near 65 km, and with significant differences extending down below 40 km. From the inset plot in Figure 13, it is evident that CO was not close to zero near 65 km, so it is not a matter of a small change in a small number yielding an inflated percentage. This altitude region is particularly sensitive to gradients in the wind profile because it is at the bottom of the large overhang in the CO VMR profile.
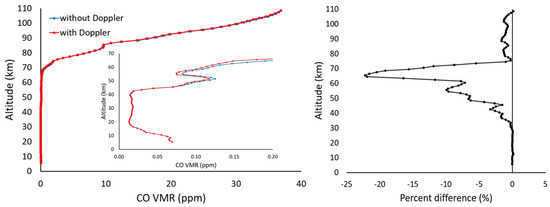
Figure 13.
Left: Retrieved CO VMR profiles for occultation sr10063 with and without Doppler effect smearing included in the forward model. The inset magnifies the results below 70 km. Right: The percentage difference between the 2 profiles.
Significant differences were also seen in the retrieval of NO VMR, another molecule with a large overhang in its VMR profile. Although NO lines typically do not saturate, Doppler effect smearing induced apparent wavenumber offsets relative to other (much stronger) lines in the microwindows, leading to a slight misalignment of the measured and calculated spectra, which impacts the retrieval.
Note that applying a constant shift (as a function of altitude) to the wind profile would not change the calculated signal (there would be no spread in the location of line center) and would therefore have no impact on the retrievals. Occultations with minimal gradients in the wind profile experience little change in the calculated spectrum and therefore little change in the retrieval results.
With no measure of ‘truth’ in the CO VMR profile, there is no way to assess whether the results shown in Figure 13 represent an improvement in the absolute accuracy. However, the changes are consistent with expectations for the effect. Spreading the absorption in wavenumber reduces the impact of saturation, yielding a stronger calculated signal, which, in turn, would lead to a smaller retrieved VMR.
5. Conclusions
Line-of-sight winds were derived from wavenumber shifts in ACE-FTS measurements for the altitude range 20 km to 140 km. With ACE-FTS sampling, it is not possible to derive vector winds, but the coverage of the underserviced middle altitude region and the long timeframe of the measurements (more than 17 years to date) could make this dataset a valuable resource for improving the fidelity of winds in model calculations. Line-of-sight wind profiles will be a standard data product in the upcoming ACE-FTS processing version 5.0.
Uncertainties in ACE-FTS winds, estimated from internal scatter among a set of spectral windows employed in the determination of Doppler shifts, typically range from 3 m/s to 10 m/s for altitudes below 125 km. These uncertainties account for both random errors (from noise effects) and systematic scatter from spectroscopic inconsistencies for lines in different spectral windows. There could be additional systematic errors (not estimated here) from using different sets of spectral windows at different altitudes. Uncertainties might be reduced by refining the set of spectral windows to improve internal consistency. Improved accuracy might also be achieved by performing retrievals for wind profiles rather than estimating the wind at the tangent point directly from the observed shift in the measurement.
Comparisons to airglow wind measurements and HWM14 calculations showed a possible systematic bias with ACE-FTS results, from roughly 20 m/s to 30 m/s in magnitude and opposite in sign for sunrises and sunsets. Potential sources of bias in ACE-FTS results (pointing deflection from clouds and refraction near the calibration altitude region and neglecting altitude variations in contributions from the Earth’s rotation) could not account for the observed differences. Another potential error source not considered in the analysis, spectroscopic inconsistencies between spectral windows at different altitudes, would not explain the observed biases. The offset resulting from this source would have the same sign for both sunrises and sunsets. It is possible that there are different sources of systematic error for ACE-FTS results that have not been considered, and it is also possible that systematic errors in the comparison data (or mapping the data to the ACE-FTS line of sight) could contribute the bias. No persistent bias was observed in preliminary comparisons to meteor radar results.
Gradients in wind speed with altitude lead to a smearing of the Doppler effect for limb-viewing instruments in situations where absorbing lines experience a degree of saturation. Shifting the location of line center can reduce the impact of saturation and yield increased absorption where the line is shifted to a wavenumber region that is not completely saturated. This can result in significant differences in the retrievals for molecules with large overhangs in their VMR profile (CO and NO). Other molecules have shown significantly less sensitivity in preliminary studies (with changes in retrieved VMR typically less than 1%) to Doppler effect smearing. The effect can therefore readily be ignored for molecules other than CO and NO unless the gradient in wind speed grows sufficiently large.
Doppler effect smearing compounds with increasing wavenumber because the Doppler shift is proportional to wavenumber. A theoretical future solar occultation mission operating in a higher wavenumber range than the ACE-FTS (but with a similar resolution) might find significant effects for molecules other than CO and NO. Doppler shifts are relatively large in the visible and ultraviolet, but the lower resolution typical for limb-viewing instruments operating in these spectral ranges likely suppresses impacts on the retrieval results.
Author Contributions
Conceptualization, C.D.B.; Formal analysis, C.D.B.; Resources, J.S. and J.C.; Software, C.D.B.; Supervision, P.F.B.; Visualization, C.D.B.; Writing—original draft, C.D.B.; Writing—review & editing, J.S., J.C. and P.F.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Canadian Space Agency, grant number 9F045-180032/001/MTB.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The ACE-FTS data can be obtained via the distribution website (http://databace.scisat.ca/, accessed on 23 May 2021) (registration required). The HRDI and TIDI data can be freely accessed via anonymous login to an ftp site (ftp://tidi.engin.umich.edu/, accessed on 23 May 2021). The MIGHTI data can be freely accessed via anonymous login to an ftp site (ftp://icon-science.ssl.berkeley.edu/pub/, accessed on 23 May 2021). The HWM14 software can be downloaded from the website https://map.nrl.navy.mil/map/pub/nrl/HWM/HWM14/, accessed on 23 May 2021. The MERRA-2 data are available at MDISC, managed by the NASA Goddard Earth Sciences Data and Information Services Center (https://disc.gsfc.nasa.gov/datasets?project=MERRA-2, accessed on 23 May 2021) (registration required). The meteor radar data used in this study can be obtained from the World Data System website (http://wdc.geophys.ac.cn/dbList.asp?dType=MetPublish, accessed on 23 May 2021) (registration required).
Acknowledgments
Funding is provided by the Canadian Space Agency. Thanks to Yves Rochon and Debora Griffin at Environment Canada for supplying wind from the weather model outputs. Thanks to Hugo Bourque at the ACE-FTS instrument provider ABB for investigations involving drift in the output of the metrology laser.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Spectral windows employed in the determination of Doppler shifts from ACE-FTS measurements in the determination of line-of-sight winds.
Table A1.
Spectral windows employed in the determination of Doppler shifts from ACE-FTS measurements in the determination of line-of-sight winds.
| Altitude Range (km) | Spectral Windows (cm−1) |
|---|---|
| 114–138 | 2320–2333, 2325–2338, 2330–2343, 2355–2367, 2360–2372, 2365–2377 |
| 110–114 | 2308–2318, 2313–2323, 2317–2327, 2342–2355, 2368–2378, 2373–2383 |
| 106–110 | 2300–2312, 2306–2316, 2310–2322, 2345–2354, 2372–2384 |
| 102–106 | 2266–2279, 2287–2297, 2300–2312, 2305–2315, 2310–2320, 2373–2384, 3592–3607, 3617–3631, 3696–3711, 3719–3733 |
| 98–102 | 2262–2276, 2273–2287, 2281–2294, 2287–2300, 2294–2306, 2300–2314, 2374–2384, 3592–3602, 3602–3612, 3614–3624, 3624–3634, 3690–3701, 3701–3712, 3716–3726, 3726–3736 |
| 94–98 | 2259–2273, 2266–2279, 2273–2287, 2281–2293, 2287–2300, 2294–2306, 2300–2312, 2375–2386, 3586–3597, 3597–3609, 3609–3620, 3620–3632, 3632–3644, 3684–3696, 3696–3708, 3708–3721, 3721–3735 |
| 90–94 | 2250–2260, 2259–2273, 2267–2279, 2273–2287, 2279–2292, 2287–2300, 2294–2304, 2300–2310, 2376–2386, 3580–3592, 3592–3604, 3604–3616, 3616–3628, 3628–3638, 3684–3697, 3731–3740 |
| 86–90 | 2244–2256, 2251–2261, 2256–2266, 2279–2290, 2298–2308, 2379–2388, 3578–3590, 3610–3616, 3631–3642, 3676–3689, 3712–3716, 3736–3744 |
| 82–86 | 2239–2250, 2245–2255, 2250–2260, 2255–2266, 2300–2308.5, 2381–2389, 3573–3584, 3634–3644, 3672–3684, 3739–3749 |
| 78–82 | 1645–1655, 2239–2253, 2383–2390, 3570–3580, 3638–3650, 3670–3682, 3741–3748.5 |
| 74–78 | 1455–1466, 1496–1508, 1538–1548, 1552–1562, 1567–1577, 1616–1628, 1630–1640, 1645–1655, 1662–1672, 1681–1691, 1695–1707, 1712–1722, 1729–1741, 1761–1773, 2239–2252, 2384–2391, 3567–3578, 3640.5–3650.5, 3742–2753, 3796–3808, 3843–3855 |
| 70–74 | 1436–1449, 1464–1477, 1487–1499, 1516–1526, 1559–1571, 1627–1638, 1667–1677, 1682–1692, 1704–1716, 1761–1773, 2234–2247, 2384–2390, 3560–3574, 3642–3654, 3874–3887, 3884–3894 |
| 66–70 | 1428–1438, 1470–1480, 1480–1491, 1508–1519, 1525–1535, 1543–1555, 1561.5–1569.5, 1600–1610, 1637–1645, 1654–1662, 1671–1681, 1681–1691, 1707–1716, 1722–1732, 1742–1752, 1775–1786, 2234–2245, 2384.5–2390.5, 3038–3049, 3550–3560, 3560–3570, 3643–3649, 3657–3668, 3874–3884 |
| 62–66 | 1403–1413, 1423–1433, 1443–1453, 1475–1485, 1526–1532, 1543–1553, 1561.4 1569.4, 1587–1597, 1600–1611, 1663–1669, 1676–1682, 1686–1694, 1707–1717, 1723–1733, 1741–1750, 1779.5–1791.5, 2045–2055, 2386–2392, 3047–3059, 3550.5–3561.5, 3780–3790 |
| 58–62 | 1421–1429, 1443–1453, 1475–1487, 1500–1505, 1548–1553, 1577–1587, 1588–1598, 1599–1609, 1640–1645, 1656–1662, 1676–1682, 1706.7 1714.7, 1720–1728, 1774–1780, 1793.5 1798.5, 1940–1950, 1963–1973, 1988–2000, 2042–2054, 2229.5–2236.5, 2388–2393, 3030–3040, 3125–3135, 3440–3450, 3474.4 3488.5, 3760–3765, 3770.2–3778.2, 3827–3831, 3844–3851, 3891.5–3898.5 |
| 54–58 | 1364–1373, 1377–1387, 1408–1418, 1431–1436, 1438–1447, 1449–1455, 1465.7–1471.7, 1482–1487, 1500–1505, 1523–1525, 1577–1585, 1588–1598, 1598–1608, 1638–1645, 1656–1662, 1676.4–1680.4, 1735.5–1738.5, 1752–1756, 1758–1761, 1776–1780, 1781–1784, 1794–1799, 1803–1808, 1940–1950, 1954–1968, 1982–1990, 2039–2049, 2220–2230, 2389–2393, 3130–3141, 3176–3186, 3385–3398, 3420–3432, 3440–3450, 3771–3779, 3891.5–3898.5 |
| 50–54 | 1311–1323, 1323–1333, 1345–1357, 1377–1387, 1407.5–1416.5, 1425–1429, 1431–1436, 1439–1447, 1481.5–1486.5, 1535–1538, 1577–1585, 1588–1598, 1604.5–1608.5, 1618–1622, 1639–1645, 1656–1662, 1672–1674.5, 1676–1679, 1701.5–1704, 1710.5–1713, 1719–1723, 1735–1739, 1752–1756, 1758–1761.5, 1776.5–1779.5, 1781–1784, 1945–1956, 1957–1967, 1982–1990, 1992–2000, 2038–2047, 2218–2228, 2390.2–2394.2, 3125–3135, 3174–3180, 3354–3366, 3384–3398, 3419–3432, 3438–3444, 3466–3476, 3760–3765 |
| 46–50 | 1325–1331, 1344–1350, 1350–1359, 1376–1383, 1396–1399, 1408–1416, 1425.5–1429.5, 1439–1447, 1453–1455, 1483–1487, 1571–1575, 1586–1593, 1595–1600, 1628.5–1633.5, 1655–1660, 1672–1674, 1676–1678.5, 1680.5–1682.5, 1691–1695, 1702–1704, 1711–1713.5, 1720–1723, 1752,1755, 1781–1784.5, 1793.5–1795.5, 1803–1807, 1952–1963, 1982–1990, 1992–2000, 2038–2045, 2390.7–2394.7, 2818–2829, 3124–3132, 3307–3315, 3361–3369, 3421–3432, 3460–3468, 3786–3793, 3845–3849.3 |
| 42.2–46 | 1251–1258, 1264–1267, 1274–1277, 1277–1282, 1307–1310.5, 1312–1316, 1328–1331, 1379–1384, 1388–1393, 1407.5–1415.5, 1425–1429, 1466.5–1469.5, 1474–1476, 1491–1496, 1499.5–1501.5, 1544–1545, 1546–1549, 1561–1564, 1565.5–1568.5, 1580–1586, 1628.5–1633.5, 1655–1660, 1672–1674, 1676–1679, 1762–1766, 1769–1770.6, 1781.5–1784.5, 1796.5–1799, 1952–1963, 1992–2000, 2391.4–2394.4, 2434–2445, 2818–2829, 3182–3188, 3332–3340, 3355–3364, 3401–3414, 3426–3434, 3788–3796, 3845–3849.3 |
| 38.6–42.2 | 1466.5–1471, 1474–1475.5, 1491–1495, 1546–1549, 1551–1554, 1561–1564, 1565.5–1568, 1571–1575, 1578–1587, 1597–1601, 1936–1942, 1961.8–1965.6, 2391.4–2396.4, 2400–2412, 2412–2425, 2433–2441, 2441–2450, 2619.5–2630, 2808–2819, 2820–2827, 2830–2834, 2852–2860, 2876–2882, 2898–2903, 2908–2913, 3142–3146, 3345–3355, 3401–3414, 3432–3439, 3448–3457, 3790–3796, 3832–3834 |
| 35.2–38.6 | 1439–1446, 1453–1454, 1466.5–1469, 1481.5–1484.5, 1491.1–1495.1, 1528.8–1531, 1561–1564, 1565.8–1568, 1753.5–1755.5, 1955.3–1960.7, 2391.9–2396.2, 2412–2425, 2433–2446, 2544–2554, 2554–2564, 2600.5–2609.5, 2619.5–2630, 2808–2816, 2823–2827, 2829–2837, 2839–2845, 2848–2856, 2887–2894.5, 2897.3–2899.5, 2908–2913, 3344–3355, 3400–3410, 3408–3419, 3432–3441, 3452–3461, 3468–3474, 3475.1–3480.1, 3908–3915, 4068–4075 |
| 32–35.2 | 1449–1451, 1452.5–1454, 1467–1471, 1481.5–1485.5, 1492–1495, 1502–1504.5, 1518.5–1520, 1528.7–1530, 1565.9–1568, 1578–1581, 1891–1893.5, 1928–1930.5, 1937–1941.5, 1950–1953, 1956–1959, 2391.9–2396.2, 2412–2425, 2433–2446, 2467.5–2478.5, 2480–2491, 2491–2498, 2505–2517, 2528–2538, 2538–2547, 2558–2568, 2603–2611, 2613–2617.5, 2619–2628, 2644–2648, 2654–2659, 2689–2695, 2833–2839, 2850–2853, 2859–2861, 2871.2–2873.5, 3314–3322.5, 3342–3349, 3368.5–3376, 3408–3414, 3767–3768.5, 3773–3776, 3787–3789, 3908–3915, 3964–3968 |
| 29–32 | 1442–1446, 1450–1451, 1460–1464, 1468–1471, 1483–1486, 1503–1504.5, 1518–1519.7, 1552.5–1553.4, 1566.3–1568.3, 1658–1660, 1663.7–1668, 1891.3–1893.5, 1914.4–1914–4, 1920.4–1921.2, 1930.2–1931.8, 2392–2397, 2433–2446, 2454–2464, 2464–2470, 2482–2493, 2504–2511, 2516–2527, 2527–2535, 2561.5–2564.5, 2587–2593, 2604–2612, 2613–2617, 2619–2625, 2626.3–2630, 2638.5–2641, 2647–2656, 2668–2674, 2850–2853, 3314–3322.5, 3343–3345.5, 3370–3380, 3767–3768.5, 3809–3813.5, 3888.5–3890.5 |
| 26.2–29 | 1442–1445.5, 1468–1471, 1658–1660, 1665.3–1667, 1920.5–1921.3, 1940.2–1941.4, 1947–1951, 2430–2440, 2458–2466, 2488–2493, 2517–2525, 2526.5–2528.5, 2590–2598, 2605.5–2613, 2618.5–2622, 2623.5–2628.5, 2649–2654, 2657–2663, 2667–2672, 2673–2677, 3328–3331, 3376–3383, 3434–3441, 3809–3810, 3812.7–3814.3, 3845–3846.1, 3921–3923 |
| 23.6–26.2 | 1492.1–1492.8, 1513–1514.5, 1530–1531, 2429.7–2431.2, 2460.9–2463.4, 2490–2493.5, 2513–2514, 2516.8–2522, 2562.7–2564, 2594.3–2597.7, 2610–2613, 2615.5–2618, 2620–2621.8, 2631.8–2632.7, 2643–2645, 2658–2661, 3304–3307, 3328–3334, 3386.3–3390.3, 3760.8–3762, 3813.8–3814.8, 3908–3910 |
| 21.2–23.6 | 1513–1514.4, 1530–1531, 1947–1948, 2429–2430.4, 2434.4–2435, 2460.5–2462.9, 2491.9–2493.5, 2508–2511.4, 2516.5–2519.5, 2610.4–2612.9, 2615.4–2618, 2641–2642.5, 2658.4–2661.4, 2826.2–2827.8, 2889.8–2892.8, 3317.5–3318.7, 3328–3329, 3337.3–3338.8, 3386.3–3390.3, 3760.8–3762, 3790–3791.8, 3810.6–3812, 3912.8–3913.9, 3921–3922 |
| 19–21.2 | 1478.5–1480.5, 1484–1484.7, 2426.6–2428.6, 2429.3–2430.5, 2434.4–2435, 2437.1–2437.7, 2445.06–2445.66, 2460.5–2462, 2491–2491.5, 2491.8–2493.6, 2516.5–2517, 2518–2519.5, 2520.3–2521, 2521.4–2522, 2523.7–2524.3, 2594.9–2595.5, 2605.4–2605.9, 2611–2613, 2615.5–2617.5, 2636–2636.8, 2652.8–2654, 2658.4–2659, 3330–3334, 3389.2–3392.2, 3921–3922 |
References
- Bernath, P.F.; McElroy, C.T.; Abrams, M.C.; Boone, C.D.; Butler, M.; Camy-Peyret, C.; Carleer, M.; Clerbaux, C.; Coheur, P.; Colin, R.; et al. Atmospheric Chemistry Experiment (ACE): Mission overview. Geophys. Res. Lett. 2005, 32, L15S01. [Google Scholar] [CrossRef]
- Bernath, P.F. The Atmospheric Chemistry Experiment (ACE). J. Quant. Spectrosc. Radiat. Transf. 2017, 186, 3–16. [Google Scholar] [CrossRef]
- Bujis, H.L.; Soucy, M.-A.; Lachance, R.L. ACE-FTS Hardware and Level 1 Processing. In The Atmospheric Chemistry Experiment ACE at 10: A solar occultation anthology; Bernath, P.F., Ed.; A. Deepak Publishing: Hampton, Virginia, USA, 2013; pp. 53–80. [Google Scholar]
- Boone, C.D.; Bernath, P.F.; Cok, D.; Jones, S.C.; Steffen, J. Version 4 Retrievals for the Atmospheric Chemistry Experiment Fourier Transform Spectrometer (ACE-FTS) and Imagers. J. Quant. Spectrosc. Radiat. Transf. 2020, 247, 106939. [Google Scholar] [CrossRef]
- Bernath, P.F.; Dodandodage, R.; Boone, C.D.; Crouse, J. HOCl retrievals from the Atmospheric Chemistry Experiment. J. Quant. Spectrosc. Radiat. Transf. 2021, 107559. [Google Scholar] [CrossRef]
- Khelif, D.; Burns, S.P.; Friehe, C.A. Improved Wind Measurements on Research Aircraft. J. Atmos. Ocean. Technol. 1999, 16, 860–875. [Google Scholar] [CrossRef]
- Duruisseau, F.; Huret, N.; Andral, A.; Camy-Peyret, C. Assessment of the ERA-interim Winds Using High-Altitude Stratospheric Balloons. J. Atmos. Sci. 2017, 74, 2065–2080. [Google Scholar] [CrossRef]
- Kumer, V.-M.; Reuder, J.; Furevik, B.R. A Comparison of LiDAR and Radiosonde Wind Measurements. Energy Procedia 2014, 53, 214–220. [Google Scholar] [CrossRef]
- Martner, B.E.; Wuertz, D.B.; Stankov, B.B.; Strauch, R.G.; Westwater, E.R.; Gage, K.S.; Ecklund, W.L.; Martin, C.L.; Dabberdt, W.F. An Evaluation of Wind Profiler, RASS, and Microwave Radiometer Performance. Bull. Am. Meteorol. Soc. 1993, 74, 599–614. [Google Scholar] [CrossRef]
- Lux, O.; Lemmerz, C.; Weiler, F.; Marksteiner, U.; Witschas, B.; Rahm, S.; Geiss, A.; Reitebuch, O. Intercomparison of Wind Observations from the European Space Agency’s Aeolus Satellite Mission and the ALADIN Airborne Demonstrator. Atmos. Meas. Tech. 2020, 13, 2075–2097. [Google Scholar] [CrossRef]
- Killeen, T.L.; Wu, Q.; Solomon, S.C.; Ortland, D.A.; Skinner, W.R.; Niciejewski, R.J.; Gell, D.A. TIMED Doppler Interferometer: Overview and Recent Results. J. Geophys. Res. Space Phys. 2006, 111, A10S01. [Google Scholar] [CrossRef]
- Englert, C.R.; Harlander, J.M.; Brown, C.M.; Marr, K.D.; Miller, I.J.; Stump, J.E.; Hancock, J.; Peterson, J.Q.; Kumler, J.; Morrow, W.H.; et al. Michelson Interferometer for Global High-resolution Thermospheric Imaging (MIGHTI): Instrument Design and Calibration. Space Sci. Rev. 2017, 212, 1–32. [Google Scholar] [CrossRef]
- Shepherd, G.G.; Thuillier, G.; Gault, W.A.; Solheim, B.H.; Hersom, C.; Alunni, J.M.; Brun, J.-F.; Brune, S.; Charlot, P.; Cogger, L.L.; et al. Windii, the Wind Imaging Interferometer on the Upper Atmosphere Research Satellite. J. Geophys. Res. Atmos. 1993, 98, 10725–10750. [Google Scholar] [CrossRef]
- Hays, P.B.; Wu, D.L.; The HRDI Science Team. Observations of the Diurnal Tide from Space. J. Atmos. Sci. 1994, 51, 3077–3093. [Google Scholar] [CrossRef]
- Liu, A.Z.; Hocking, W.K.; Franke, S.J.; Thayaparan, T. Comparison of Na Lidar and Meteor Radar Wind Measurements at Starfire Optical Range, NM, USA. J. Atmos. Sol. Terr. Phys. 2001, 64, 31–40. [Google Scholar] [CrossRef]
- Tang, Q.; Zhou, Y.; Du, Z.; Zhou, C.; Qiao, J.; Liu, Y.; Chen, G. A Comparison of Meteor Radar Observation over China Region with Horizontal Wind Model (HWM14). Atmosphere 2021, 12, 98. [Google Scholar] [CrossRef]
- Kristofferson, S.K.; Ward, W.E.; Brown, S.; Drummond, J.R. Calibration and Validation of the Advanced E-region Wind Interferometer. Atmos. Meas. Tech. 2020, 13, 1761–1776. [Google Scholar] [CrossRef]
- Brum, C.G.M.; Tepley, C.A.; Fentzke, J.T.; Robles, E.; dos Santos, P.T.; Gonzalez, S.A. Long Term Changes in the Thermospheric Neutral Winds over Arecibo: Climatology Based on over Three Decades of Fabry-Perot Observations. J. Geophys. Res. 2012, 117, A00H14. [Google Scholar] [CrossRef]
- Wu, D.L.; Schwartz, M.J.; Waters, J.W.; Limpasuvan, V.; Wu, Q.; Killeen, T.L. Mesospheric Doppler Wind Measurements from Aura Microwave Limb Sounder (MLS). Adv. Space Res. 2008, 42, 1246–1252. [Google Scholar] [CrossRef]
- Baumgarten, G. Doppler Rayleigh/Mie/Raman Lidar for Wind and Temperature Measurements in the Middle Atmosphere up to 80km. Atmos. Meas. Tech. 2010, 3, 1509–1518. [Google Scholar] [CrossRef]
- Rüfenacht, R.; Baumgarten, G.; Hildebrand, J.; Schranz, F.; Matthias, V.; Stober, G.; Lübken, F.-J.; Kämpfer, N. Intercomparison of Middle-Atmospheric Winds in Observations and Models. Atmos. Meas. Tech. 2018, 11, 1971–1987. [Google Scholar] [CrossRef]
- Rufenacht, R.; Murk, A.; Kampfer, N.; Eriksson, P.; Buehler, S.A. Middle-Atmospheric Zonal and Meridional Wind Profiles from Polar, Tropical and Midlatitudes with the Ground-Based Microwave Doppler Wind Radiometer WIRA. Atmos. Meas. Tech. 2014, 7, 4491–4505. [Google Scholar] [CrossRef]
- Kumar, G.K.; Kumar, K.K.; Baumgarten, G.; Ramkumar, G. Validation of MERRA Reanalysis Upper Level Winds Over Low Latitudes with Independent Rocket Sounding Data. J. Atmos. Sol. Terr. Phys. 2015, 123, 48–54. [Google Scholar] [CrossRef]
- Van Cleef, G.W.; Shaw, J.H. Zonal Winds Between 25 and 120 km Obtained from Solar Occultation Spectra. Geophys. Res. Lett. 1987, 14, 1266–1268. [Google Scholar] [CrossRef]
- Baron, P.; Murtagh, D.P.; Urban, J.; Sagawa, H.; Ochiai, S.; Kasai, Y.; Kikuchi, K.; Khosrawi, F.; Kornich, H.; Mizobuchi, S.; et al. Observation of Horizontal Winds in the Middle-Atmosphere between 30° S and 55° N During the Northern Winter 2009–2010. Atmos. Chem. Phys. 2013, 13, 6049–6064. [Google Scholar] [CrossRef]
- Shaw, J.H. Atmospheric Winds from Occultation Spectra. Appl. Opt. 1985, 24, 2433–2436. [Google Scholar] [CrossRef]
- Gordon, I.E.; Rothman, L.S.; Hill, C.; Kochanov, R.V.; Tan, Y.; Bernath, P.F.; Birk, M.; Boudon, V.; Campargue, A.; Chance, K.V.; et al. The HITRAN 2016 Molecular Spectroscopic Database. J. Quant. Spectrosc. Radiat. Transf. 2017, 203, 3–69. [Google Scholar] [CrossRef]
- Systems Tool Kit Version 10; Software Used for Satellite Orbit Propagation; Analytical Graphics Inc.: Exton, PA, USA; Available online: https://www.agi.com/products/stk (accessed on 23 May 2021).
- Lohner-Bottcher, L.; Schmidt, W.; Schlichenmaier, R.; Steinmetz, T.; Holzwarth, R. Convective Blueshifts in the Solar Atmosphere III. High-Accuracy Observations of Spectral Lines in the Visible. Astron. Astrophys. 2019, 624, A57. [Google Scholar] [CrossRef]
- Buehner, M.; McTaggart-Cowan, R.; Beaulne, A.; Charette, C.; Garand, L.; Heilliette, S.; Lapalme, E.; Laroche, S.; MacPherson, S.R.; Morneau, J.; et al. Implementation of Deterministic Weather Forecasting Systems based on Ensemble-Variational Data Assimilation at Environment Canada. Part I: The Global System. Mon. Weather Rev. 2015, 143, 2532–2559. [Google Scholar] [CrossRef]
- Drob, D.P.; Emmert, J.T.; Meriwether, J.W.; Makela, J.; Doornbos, E.; Conde, M.; Hernandez, G.; Noto, J.; Zawdie, K.A.; McDonald, S.E.; et al. An Update to the Horizontal Wind Model (HWM): The Quiet Time Atmosphere. Earth Space Sci. 2015, 2, 301–319. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Harding, B.J.; Makela, J.J.; Englert, C.R.; Marr, K.D.; Harlander, J.M.; England, S.L.; Immel, T.J. The MIGHTI Wind Retrieval Algorithm: Description and Verification. Space Sci. Rev. 2017, 212, 585–600. [Google Scholar] [CrossRef]
- Boone, C.D.; Nassar, R.; Walker, K.A.; Rochon, Y.; McLeod, S.D.; Rinsland, C.P.; Bernath, P.F. Retrievals for the Atmospheric Chemistry Experiment Fourier-Transform Spectrometer. Appl. Opt. 2005, 44, 7218–7231. [Google Scholar] [CrossRef] [PubMed]
- Boone, C.D.; Walker, K.A.; Bernath, P.F. Version 3 Retrievals for the Atmospheric Chemistry Experiment Fourier Transform Spectrometer (ACE-FTS). In The Atmospheric Chemistry Experiment ACE at 10: A Solar Occultation Anthology; Bernath, P.F., Ed.; A. Deepak Publishing: Hampton, VA, USA, 2013; pp. 103–127. [Google Scholar]
- Boone, C.D.; Bernath, P.F. Tangent Height Determination from the N2 Continuum for the Atmospheric Chemistry Experiment Fourier Transform Spectrometer. J. Quant. Spectrosc. Radiat. Transf. 2019, 238, 106481. [Google Scholar] [CrossRef]
- Toon, G.C.; Wunch, D. A Stand-Alone a priori Profile Generation Tool for GGG2014 Release. CaltechDATA. 2017. Available online: https://data.caltech.edu/records/250 (accessed on 23 May 2021).
- Picone, J.M.; Hedin, A.E.; Drob, D.P.; Aikin, A.C. NRLMSIS-00 Empirical Model of the Atmosphere: Statistical Comparisons and Scientific Issues. J. Geophys. Res. 2002, 107, 1468–1483. [Google Scholar] [CrossRef]
- Carlotti, M. Global-Fit Approach to the Analysis of Limb-Scanning Atmospheric Measurements. Appl. Opt. 1988, 27, 3250–3254. [Google Scholar] [CrossRef] [PubMed]
- Press, W.H.; Flannery, B.P.; Teukolsky, S.A.; Vetterling, W.T. Numerical Recipes in FORTRAN 77, 2nd ed.; Cambridge University Press: Cambridge, UK, 1992; pp. 675–683. [Google Scholar]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding, Theory and Practice; World Scientific: Singapore, 2000. [Google Scholar]
- Boone, C.D.; Walker, K.A.; Bernath, P.F. Speed-Dependent Voigt Profile for Water Vapor in Infrared Remote Sensing Applications. J. Quant. Spectrosc. Radiat. Transf. 2007, 105, 525–532. [Google Scholar] [CrossRef]
- Tran, H.; Ngo, N.H.; Hartmann, J.-M. Efficient Computation of Some Speed-Dependent Isolated Line Profiles. J. Quant. Spectrosc. Radiat. Transf. 2013, 129, 199–203. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).