Flooding Risk Assessment and Analysis Based on GIS and the TFN-AHP Method: A Case Study of Chongqing, China
Abstract
1. Introduction
2. Materials and Methods
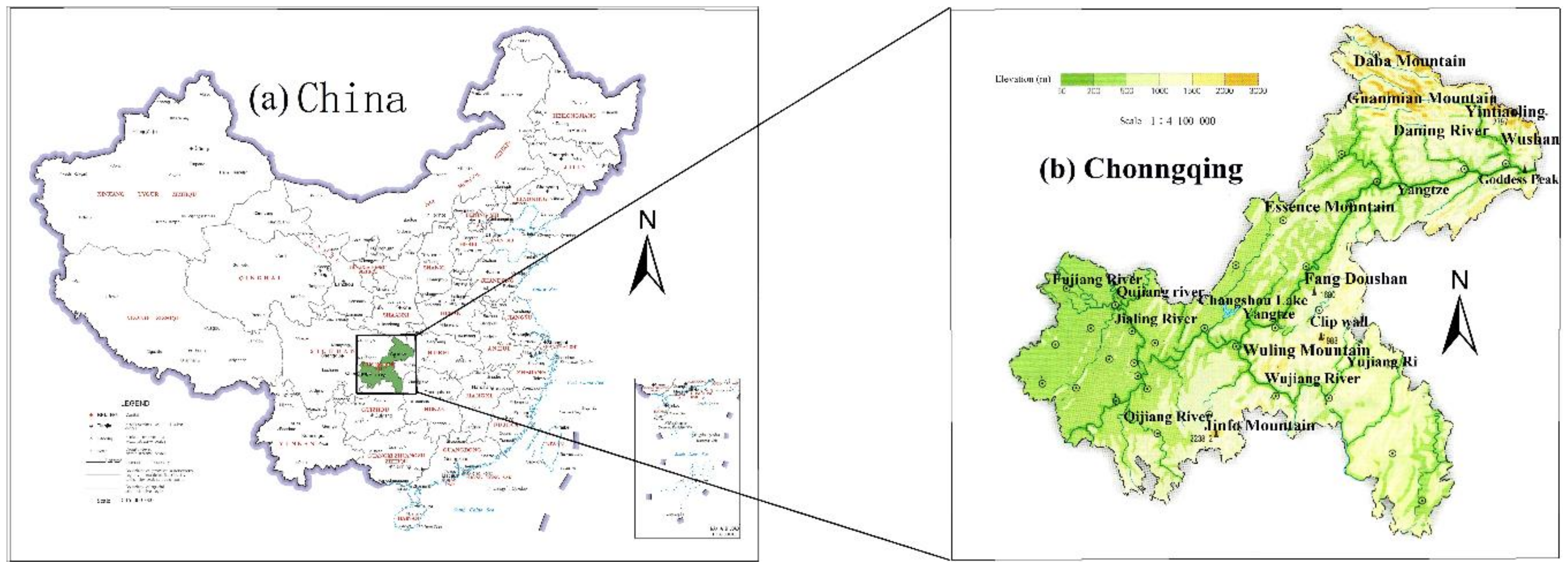
2.1. Study Area and Data
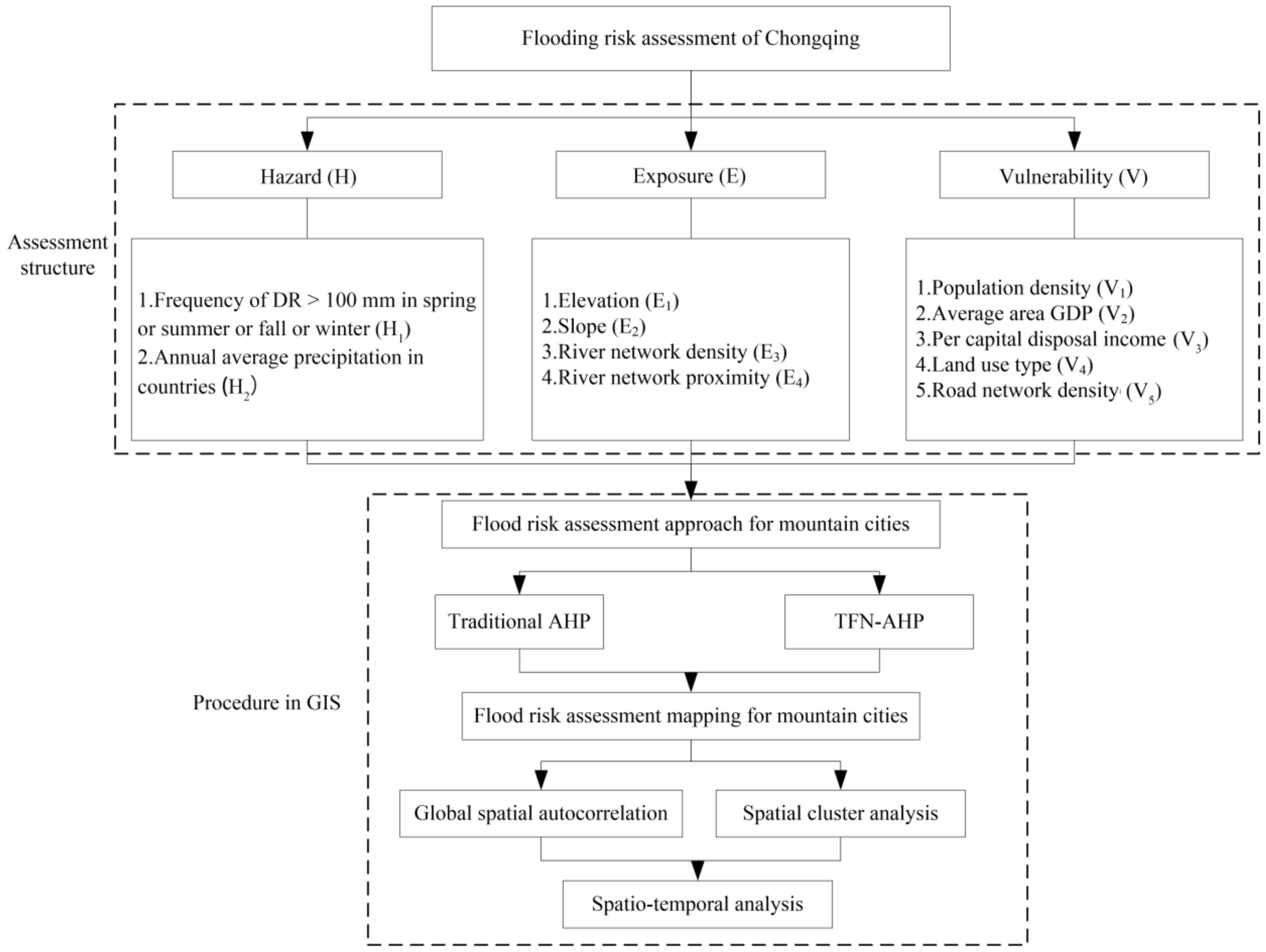
2.2. Research Framework
2.3. Flood Risk Assessment Method
2.3.1. Analytical Hierarchy Process (AHP)
2.3.2. Triangular Fuzzy Number-Based Analytical Hierarchy Process (TFN-AHP)
2.3.3. Incorporation of AHP and TFN-AHP into GIS
2.4. Assessment Indexes
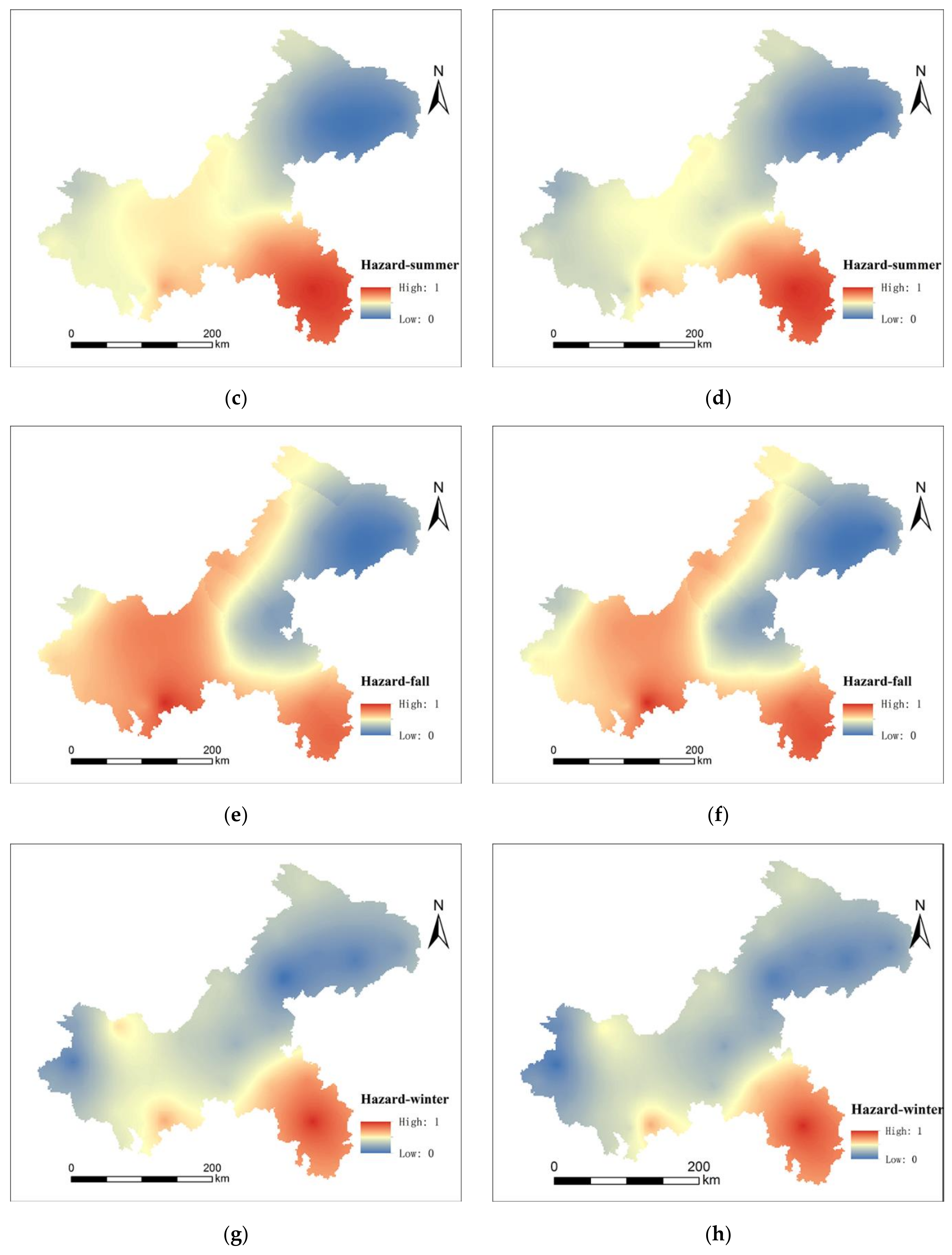
2.4.1. Hazard Index
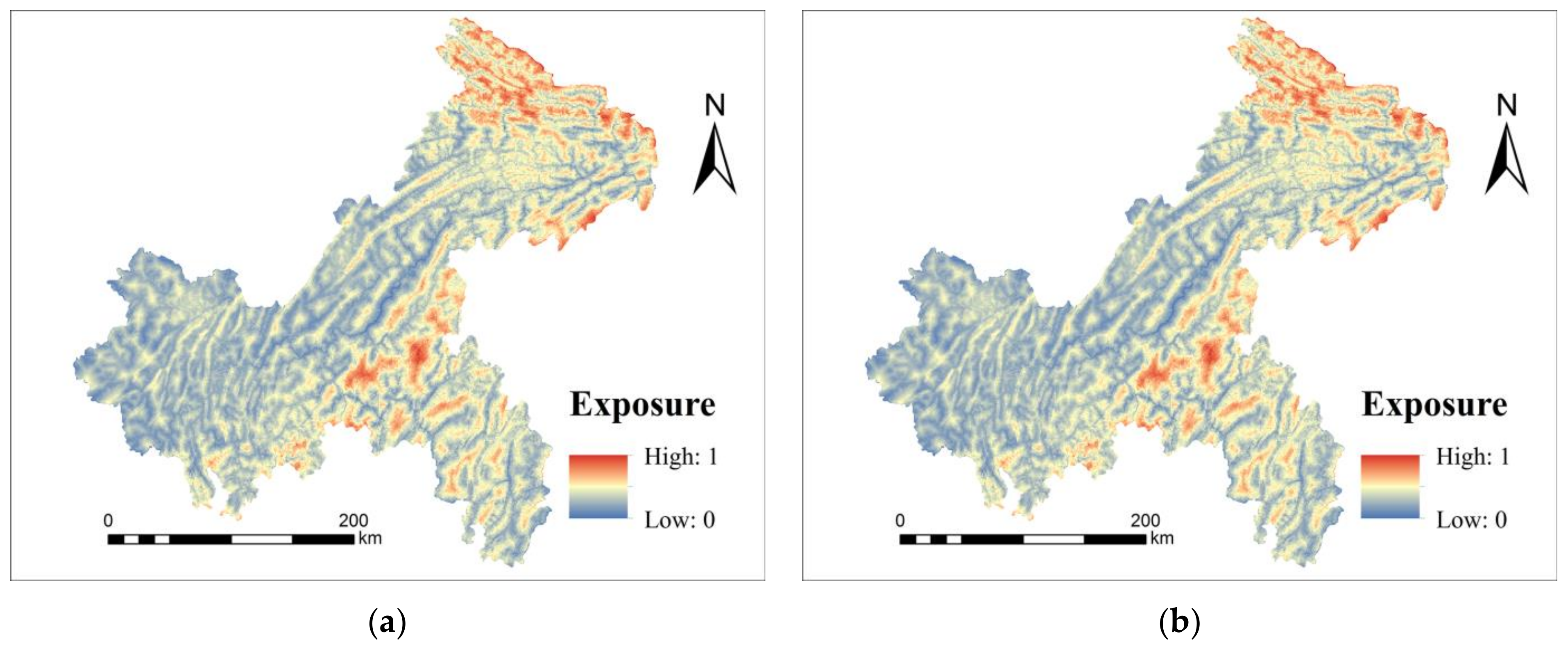
2.4.2. Exposure Index
2.4.3. Vulnerability Index
2.5. Weight Calibration
2.5.1. AHP Weight
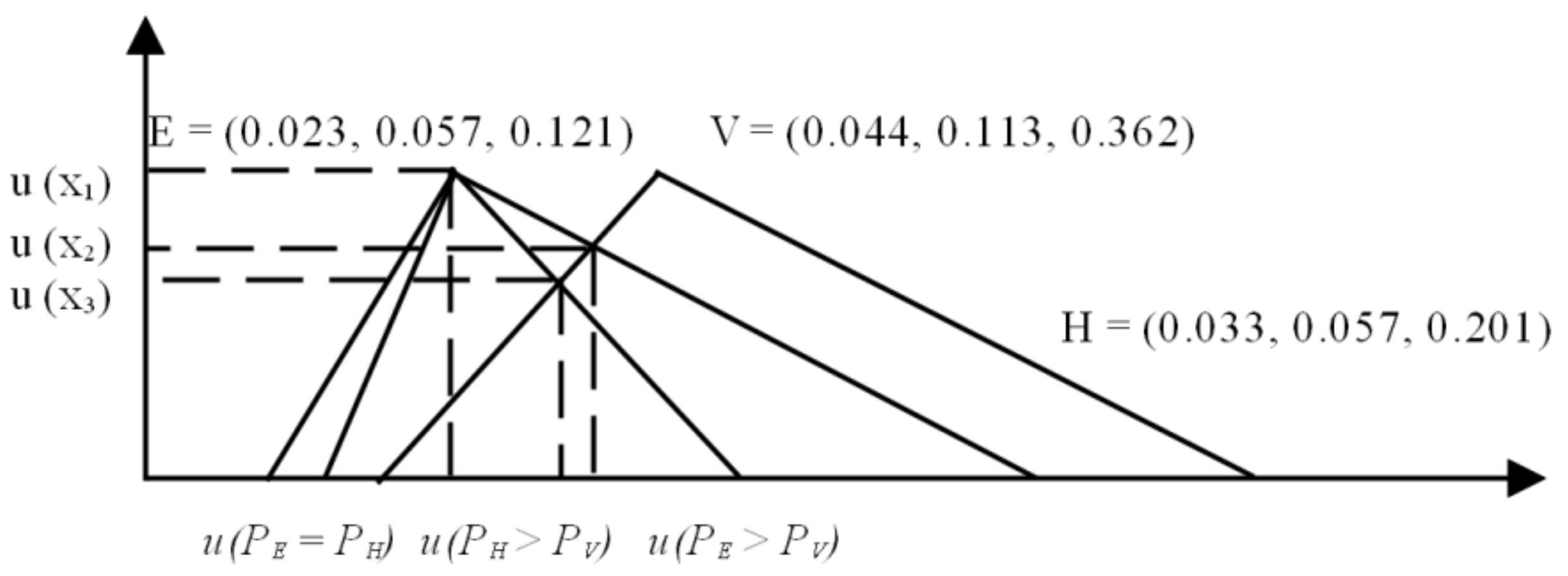
2.5.2. FN-AHP Weight
2.6. Spatio-Temporal Analysis Method
3. Results
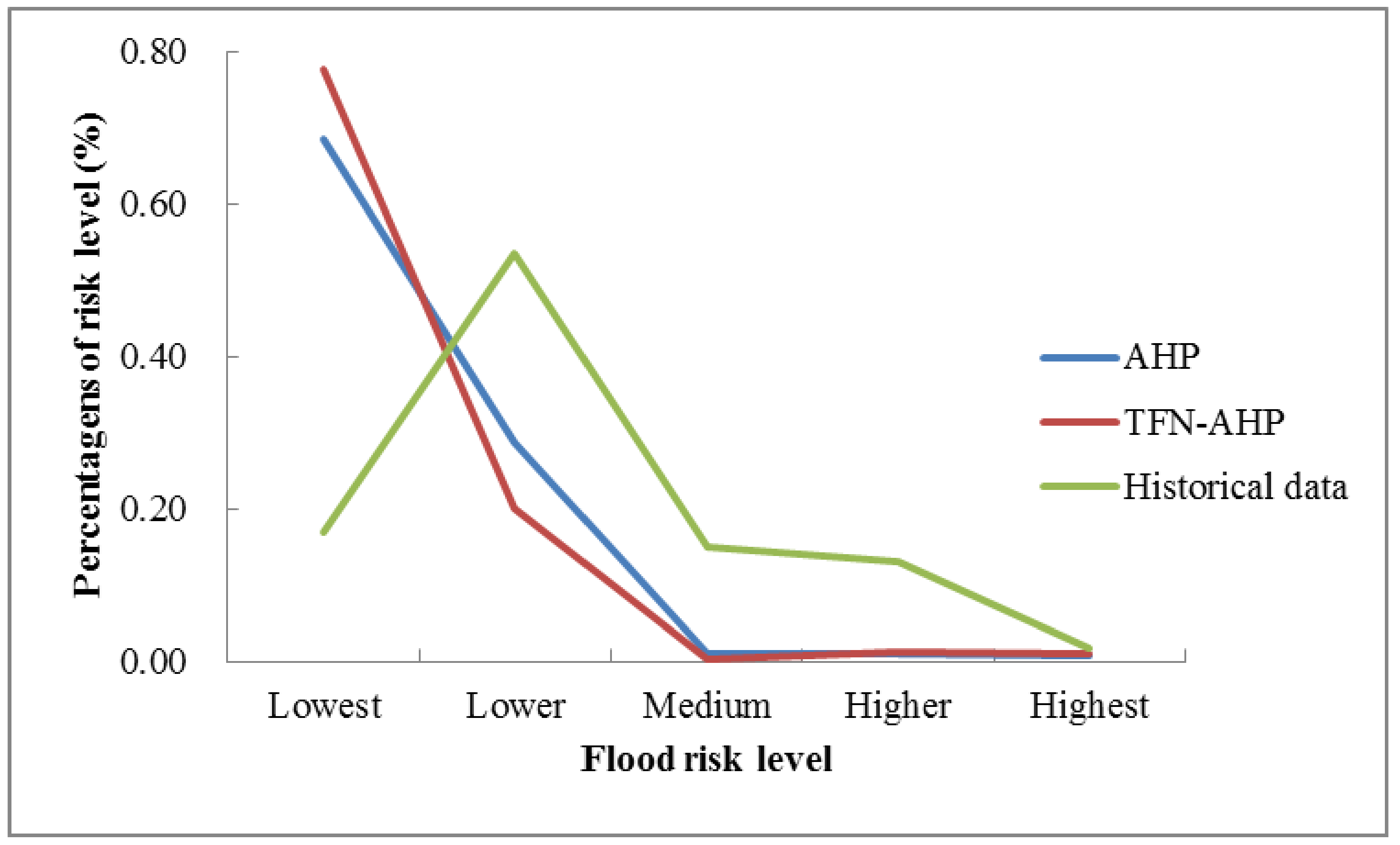
3.1. Comparative Analysis of Flood Risk of AHP and TFN-AHP Methods
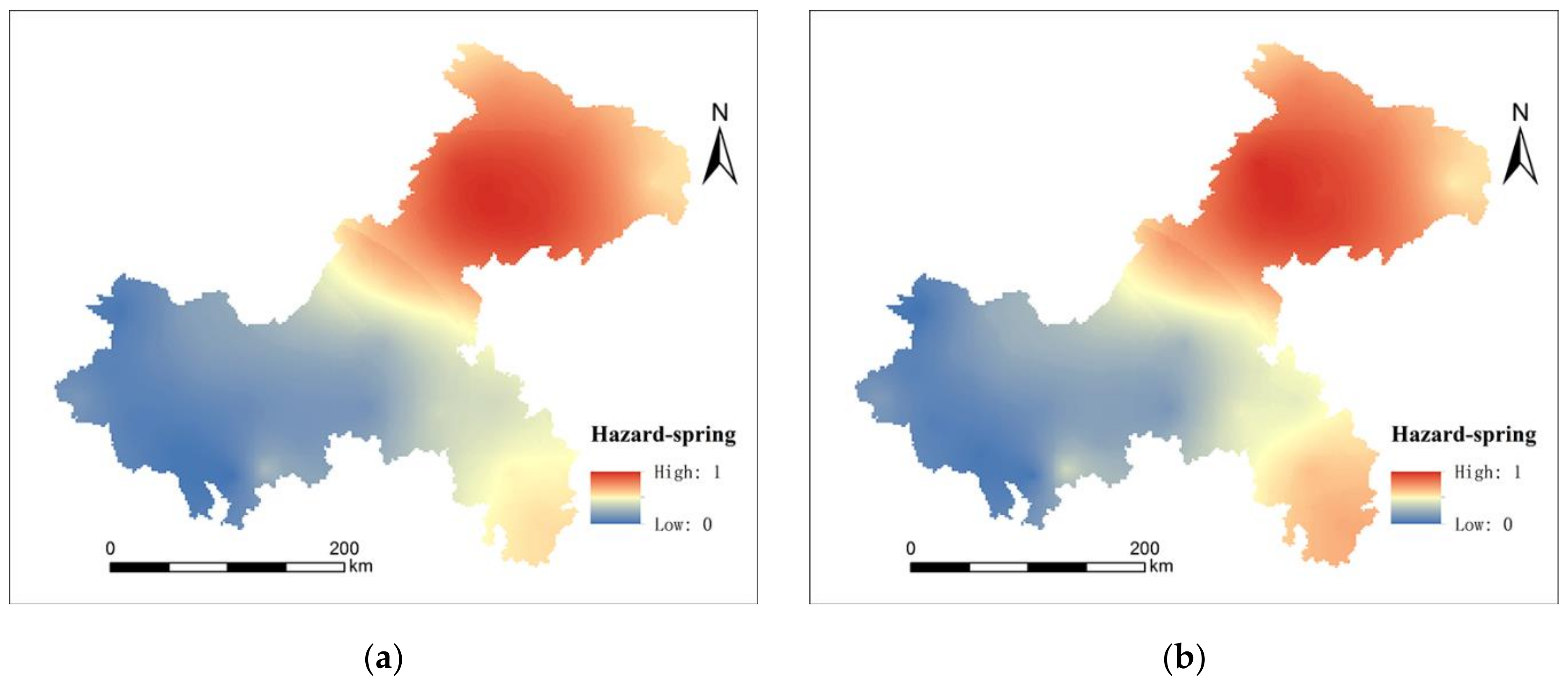
3.1.1. Hazard Results
3.1.2. Exposure Results
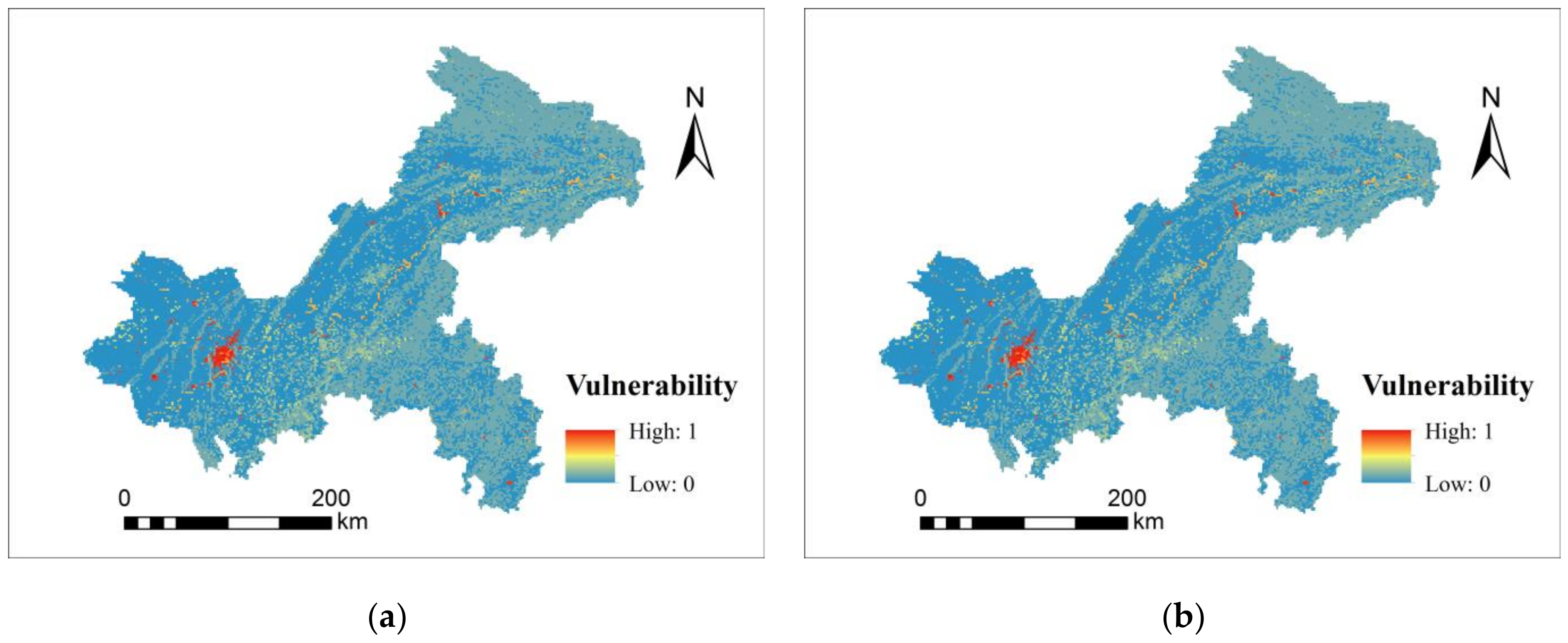
3.1.3. Vulnerability Results
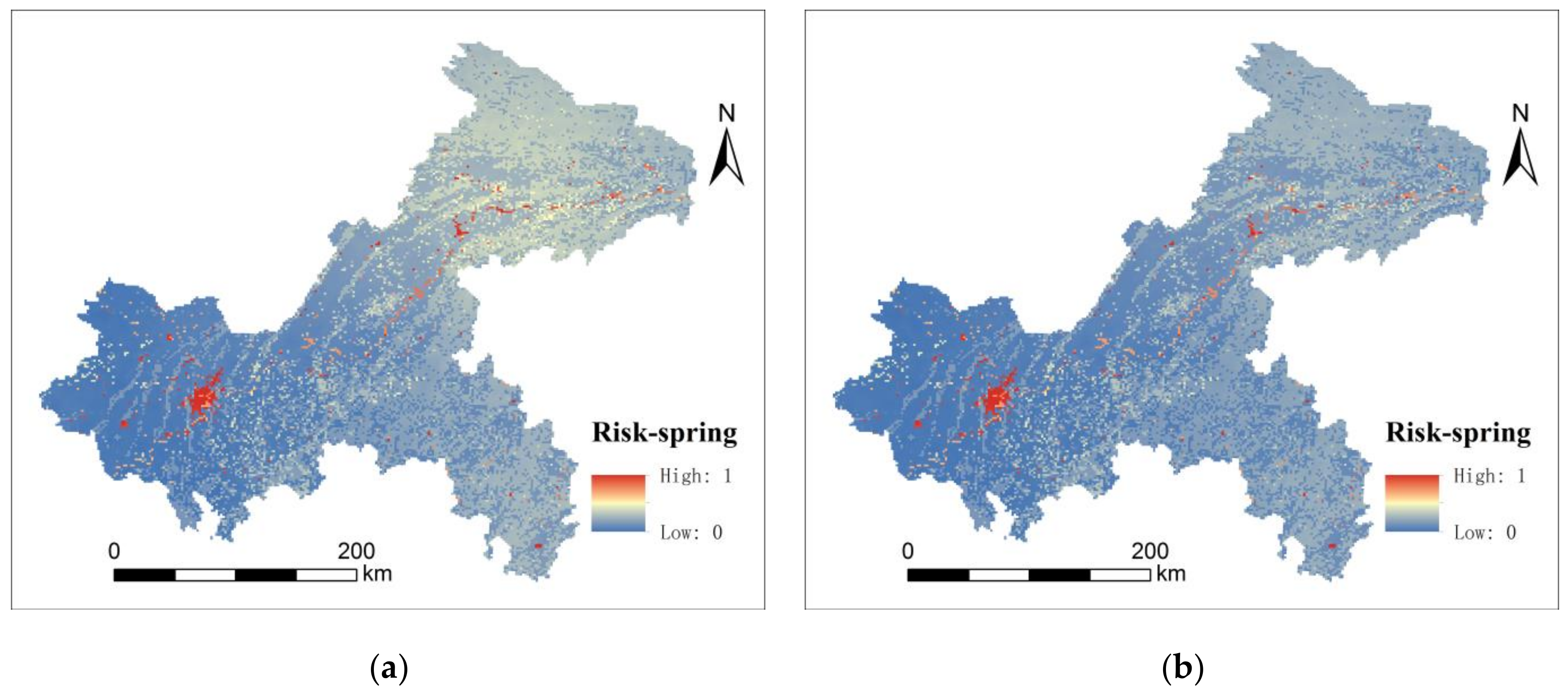
3.1.4. Flood Risk Results
3.2. Temporal-Spatial Analysis of Flooding Risk
3.2.1. Seasonal Difference of Flooding Risk
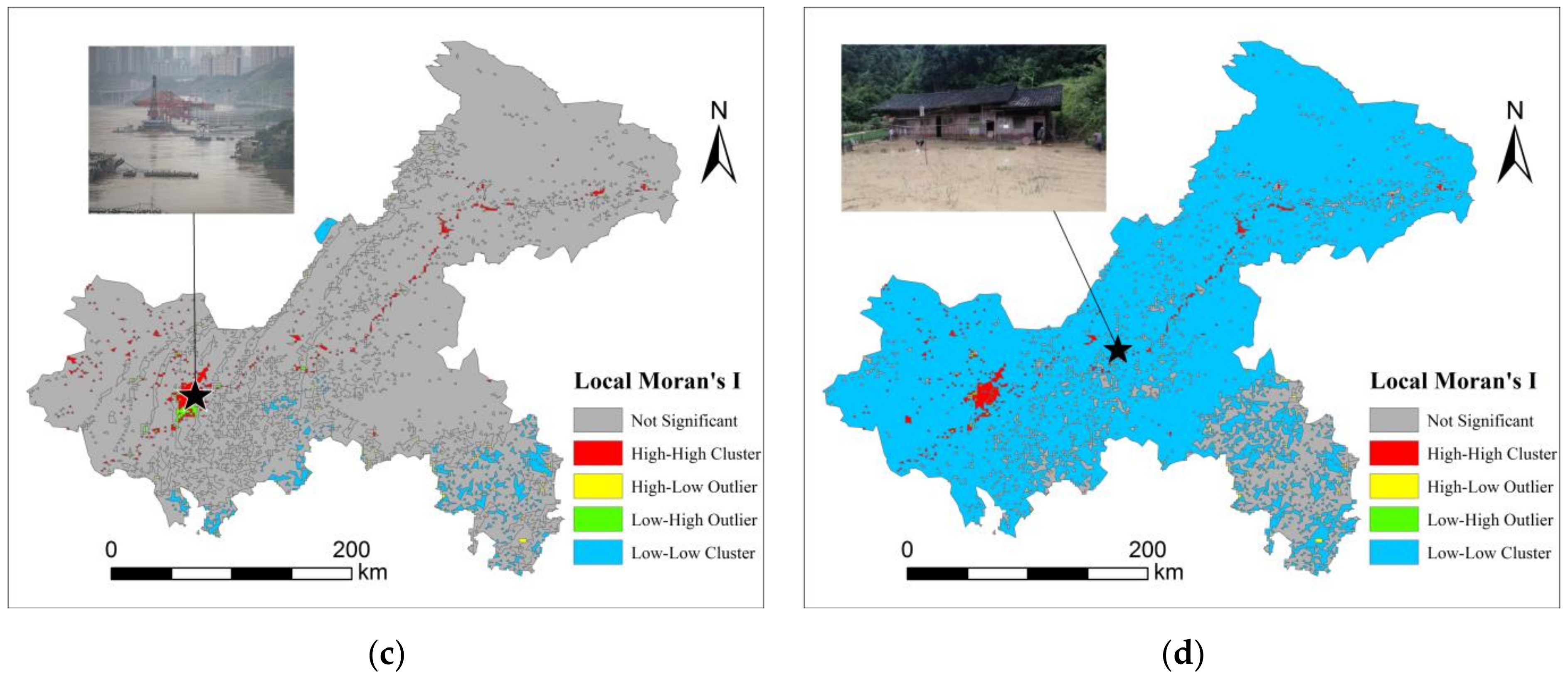
3.2.2. Spatial Analysis of Flooding Risk
3.2.3. Temporal-Spatial Analysis of Flooding Risk
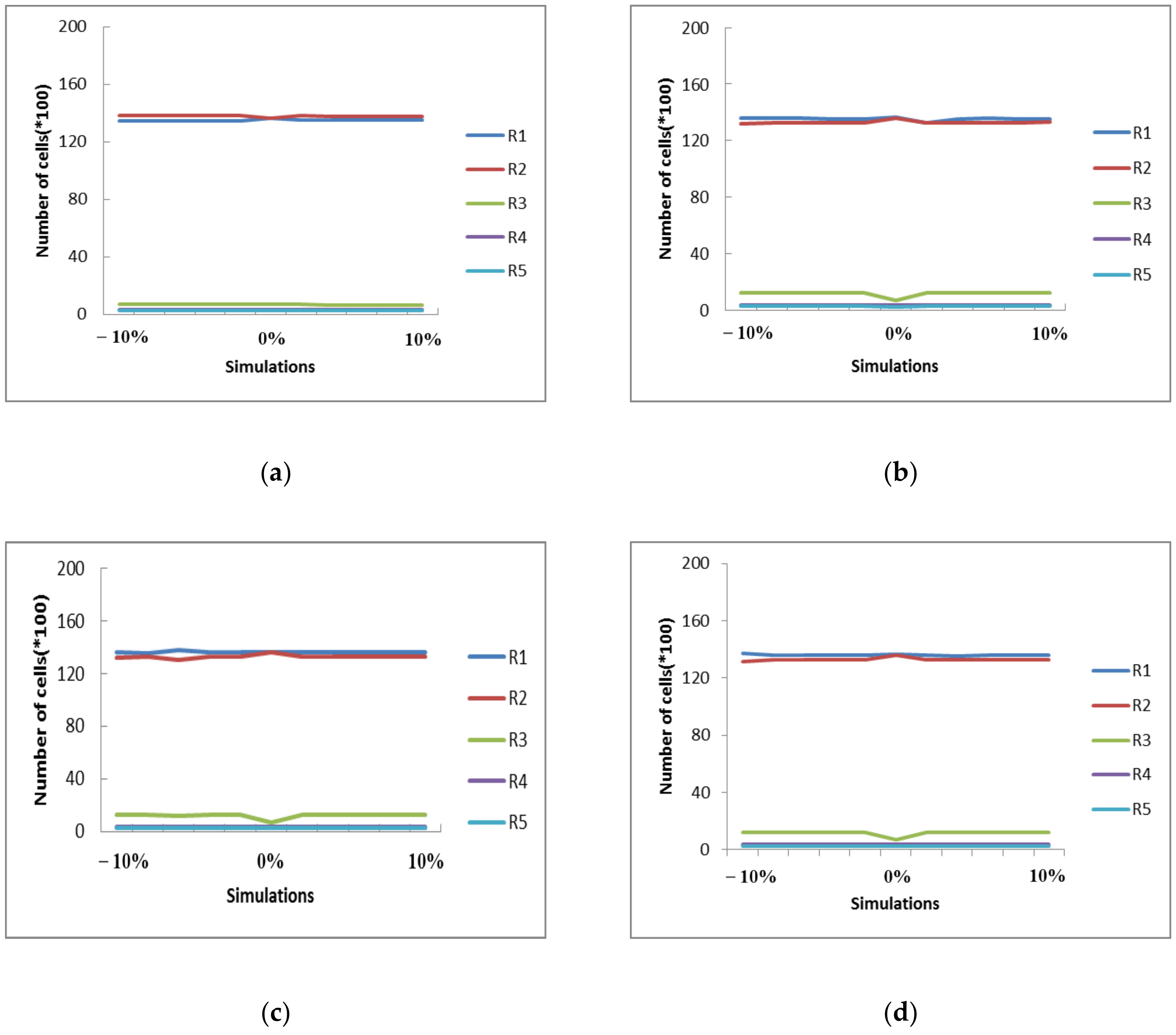
3.3. Sensitivity Analysis of Assessment Factors’ Weights
4. Discussion
4.1. Efficiency and Limitation
4.2. Reflections and Suggestions
5. Conclusions
- The comparison between AHP and TFN-AHP demonstrated that TFN-AHP is more effective with relatively higher accuracy, particularly in the hazard and exposure layers. The flood-risk maps were consistent with flooding risk regions obtained from historical data, especially for the high-risk regions.
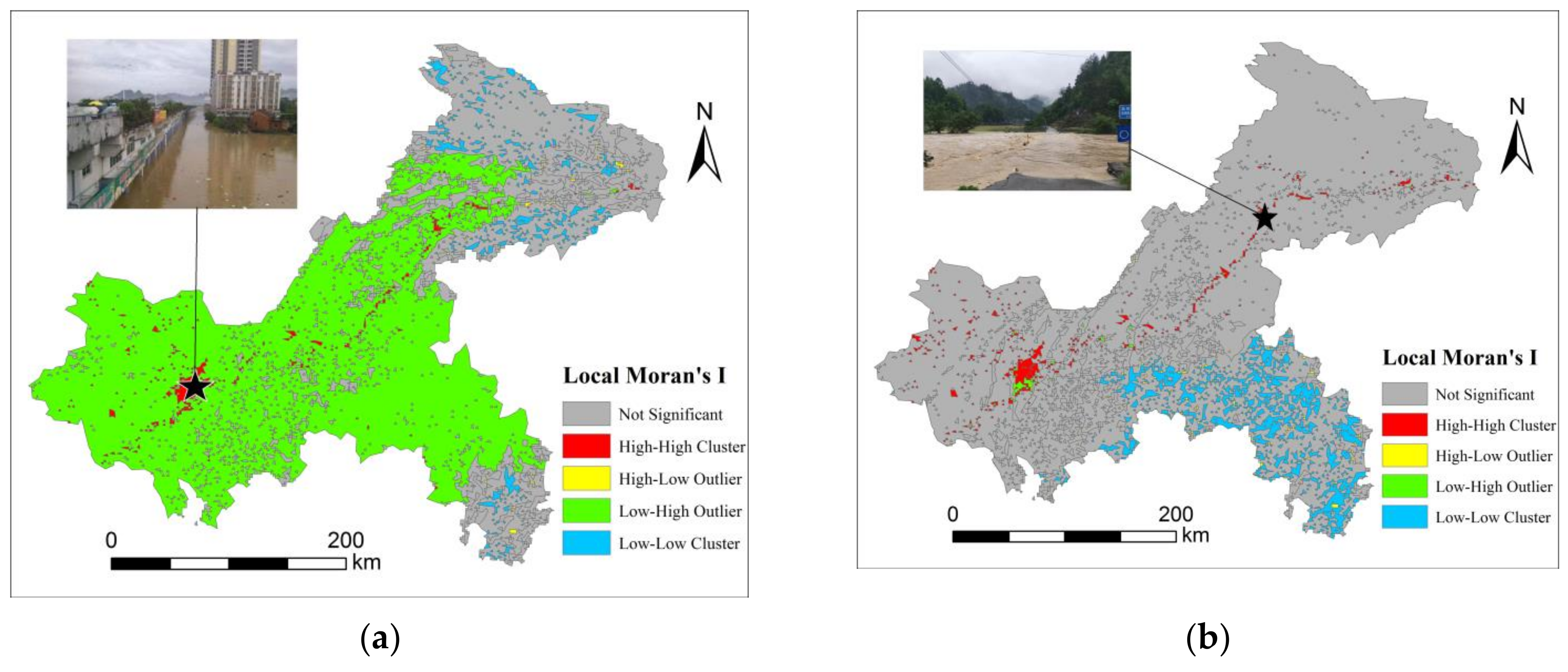
- The results of Global Moran’s I index showed that there exists a spatial autocorrelation of flood risk in Chongqing. Further, the indication of Anselin Local Moran’s I was the spatial distribution of hot spots, mainly located in main urban areas and areas along the Yangtze River all year round in Chongqing.
- The results of the sensitivity analysis revealed three groups with various sensitivity to weight changes. Indicators like V4 are the most sensitive, followed by factors such as E2, E3 and E4, and indexes like H1.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, R.; Gong, Z.; Gao, G.; Shah, A.A. Comparative analysis of Multi-Criteria Decision-Making methods for flood disaster risk in the Yangtze River Delta. Int. J. Disaster Risk Reduct. 2020, 51, 101768. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Yang, J. Perspectives for flood risk assessment and management for mega-city metro system. Tunn. Undergr. Space Technol. 2019, 84, 31–44. [Google Scholar] [CrossRef]
- Petit-Boix, A.; Sevigne-Itoiz, E.; Rojas-Gutierrez, L.A.; Barbassa, A.P.; Josa, A.; Rieradevall, J.; Gabarrell, X. Floods and consequential life cycle assessment: Integrating flood damage into the environmental assessment of stormwater Best Management Practices. J. Clean. Prod. 2017, 162, 601–608. [Google Scholar] [CrossRef]
- Cai, T.; Li, X.Y.; Ding, X.; Wang, J.; Zhan, J. Flood risk assessment based on hydrodynamic model and fuzzy comprehensive evaluation with GIS technique. Int. J. Disaster Risk Reduct. 2019, 35, 101077. [Google Scholar] [CrossRef]
- Sarmah, T.; Das, S.; Narendr, A.; Aithal, B.H. Assessing human vulnerability to urban flood hazard using the analytic hierarchy process and geographic information system. Int. J. Disaster Risk Reduct. 2020, 50, 101659. [Google Scholar] [CrossRef]
- Fang, J.; Hu, J.; Shi, X.; Zhao, L. Assessing disaster impacts and response using social media data in China: A case study of 2016 Wuhan rainstorm. Int. J. Disaster Risk Reduct. 2019, 34, 275–282. [Google Scholar] [CrossRef]
- Sajjad, M.; Chan, J.C.L.; Kanwal, S. Integrating spatial statistics tools for coastal risk management: A case-study of typhoon risk in mainland China. Ocean Coast. Manag. 2020, 184, 105018. [Google Scholar] [CrossRef]
- Thaler, T.; Hartmann, T. Justice and flood risk management: Reflecting on different approaches to distribute and allocate flood risk management in Europe. Nat. Hazards 2016, 83, 129–147. [Google Scholar] [CrossRef]
- Romanescu, G.; Hapciuc, O.E.; Minea, I.; Iosub, M. Flood vulnerability assessment in the mountain-plateau transition zone: A case study of Marginea village (Romania). J. Flood Risk Manag. 2018, 11, S502–S513. [Google Scholar] [CrossRef]
- Sakamoto, T.; Van Nguyen, N.; Kotera, A.; Ohno, H.; Ishitsuka, N.; Yokozawa, M. Detecting temporal changes in the extent of annual flooding within the Cambodia and the Vietnamese Mekong Delta from MODIS time-series imagery. Remote Sens. Environ. 2007, 109, 295–313. [Google Scholar] [CrossRef]
- Williams, P.; Kliskey, A.; McCarthy, M.; Lammers, R.; Alessa, L.; Abatzoglou, J. Using the Arctic water resources vulnerability index in assessing and responding to environmental change in Alaskan communities. Clim. Risk Manag. 2019, 23, 19–31. [Google Scholar] [CrossRef]
- Fan, Q.; Tian, Z.; Wang, W. Study on Risk Assessment and Early Warning of Flood-Affected Areas when a Dam Break Occurs in a Mountain River. Water 2018, 10, 1369. [Google Scholar] [CrossRef]
- Lin, K.; Chen, H.; Xu, C.-Y.; Yan, P.; Lan, T.; Liu, Z.; Dong, C. Assessment of flash flood risk based on improved analytic hierarchy process method and integrated maximum likelihood clustering algorithm. J. Hydrol. 2020, 584, 124696. [Google Scholar] [CrossRef]
- Zhang, J.Y.; Chen, Y.B. Risk Assessment of Flood Disaster Induced by Typhoon Rainstorms in Guangdong Province, China. Sustainability 2019, 11, 2738. [Google Scholar] [CrossRef]
- Terzi, S.; Torresan, S.; Schneiderbauer, S.; Critto, A.; Zebisch, M.; Marcomini, A. Multi-risk assessment in mountain regions: A review of modelling approaches for climate change adaptation. J. Environ. Manag. 2019, 232, 759–771. [Google Scholar] [CrossRef] [PubMed]
- Qianzhu, Z.; Huoming, Z.; Yang, L.; Ruiyi, Z.; Qiang, G.; Jianmei, Y.; Kun, S. Research on Chongqing Mountain Flood Disaster Risk Assessment System Based on AHP-GIS. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2019; Volume 330. [Google Scholar] [CrossRef]
- Black, A.R.; Burns, J.C. Re-assessing the flood risk in Scotland. Sci. Total. Environ. 2002, 294, 169–184. [Google Scholar] [CrossRef]
- Newman, J.P.; Maier, H.R.; Riddell, G.A.; Zecchin, A.C.; Daniell, J.E.; Schaefer, A.M.; van Delden, H.; Khazai, B.; O’Flaherty, M.J.; Newland, C.P. Review of literature on decision support systems for natural hazard risk reduction: Current status and future research directions. Environ. Model. Softw. 2017, 96, 378–409. [Google Scholar] [CrossRef]
- Gigovic, L.; Pamucar, D.; Bajic, Z.; Drobnjak, S. Application of GIS-Interval Rough AHP Methodology for Flood Hazard Mapping in Urban Areas. Water 2017, 9, 360. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.-N.; Zhou, W.-H. Flood risk assessment of metro systems in a subsiding environment using the interval FAHP-FCA approach. Sustain. Cities Soc. 2019, 50, 101682. [Google Scholar] [CrossRef]
- Wang, X.W.; Xie, H.J. A Review on Applications of Remote Sensing and Geographic Information Systems (GIS) in Water Resources and Flood Risk Management. Water 2018, 10, 608. [Google Scholar] [CrossRef]
- Yin, Z.e.; Yin, J.; Xu, S.; Wen, J. Community-based scenario modelling and disaster risk assessment of urban rainstorm waterlogging. J. Geogr. Sci. 2011, 21, 274–284. [Google Scholar] [CrossRef]
- Lin, T.; Liu, X.F.; Song, J.C.; Zhang, G.Q.; Jia, Y.Q.; Tu, Z.Z.; Zheng, Z.H.; Liu, C.L. Urban waterlogging risk assessment based on internet open data: A case study in China. Habitat Int. 2018, 71, 88–96. [Google Scholar] [CrossRef]
- Lyu, H.-M.; Zhou, W.-H.; Shen, S.-L.; Zhou, A.-N. Inundation risk assessment of metro system using AHP and TFN-AHP in Shenzhen. Sustain. Cities Soc. 2020, 56, 102103. [Google Scholar] [CrossRef]
- Yang, X.L.; Ding, J.H.; Hou, H. Application of a triangular fuzzy AHP approach for flood risk evaluation and response measures analysis. Nat. Hazards 2013, 68, 657–674. [Google Scholar] [CrossRef]
- Enaruvbe, G.; Yesuf, G. Spatial analysis of flood disaster in Delta State, Nigeria. Ife Res. Publ. Geogr. 2016, 11, 52–58. [Google Scholar]
- Zhao, M.; Sun, Z.; Zeng, Y. Exploring urban risk reduction strategy based on spatial statistics and scenario planning. J. Clean. Prod. 2020, 264, 121688. [Google Scholar] [CrossRef]
- Santos, M.; Bateira, C.; Soares, L.; Hermenegildo, C. Hydro-geomorphologic GIS database in Northern Portugal, between 1865 and 2010: Temporal and spatial analysis. Int. J. Disaster Risk Reduct. 2014, 10, 143–152. [Google Scholar] [CrossRef]
- Guo, N.J.; Ren, Y.J.; Tang, X.L. The temporal and spatial evolution of natural disasters in China. Geojournal 2019, 84, 1515–1530. [Google Scholar] [CrossRef]
- Huang, C.; Chen, Y.; Wu, J. Mapping spatio-temporal flood inundation dynamics at large river basin scale using time-series flow data and MODIS imagery. Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 350–362. [Google Scholar] [CrossRef]
- Bathrellos, G.D.; Skilodimou, H.D.; Soukis, K.; Koskeridou, E. Temporal and spatial analysis of flood occurrences in the drainage basin of pinios river (thessaly, central greece). Land 2018, 7, 106. [Google Scholar] [CrossRef]
- Ovando, A.; Martinez, J.-M.; Tomasella, J.; Rodriguez, D.A.; von Randow, C. Multi-temporal flood mapping and satellite altimetry used to evaluate the flood dynamics of the Bolivian Amazon wetlands. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 27–40. [Google Scholar] [CrossRef]
- Zhao, J.; Jin, J.; Xu, J.; Guo, Q.; Hang, Q.; Chen, Y. Risk assessment of flood disaster and forewarning model at different spatial-temporal scales. Theor. Appl. Clim. 2018, 132, 791–808. [Google Scholar] [CrossRef]
- Fang, D.X.; Dong, X.N.; Deng, C.; Wu, Z.; Hai, C.; Gao, S.; Huang, A.N. The temporal and spatial distribution characteristics of precipitation in Chongqing from 2008 to 2016. Atmos. Sci. 2020, 44, 327–340. (In Chinese) [Google Scholar]
- Zhong, C.; Ren, X.M.; Zhou, X.Q.; Luo, L.X.; Wang, J.L.; Li, Y.N. The temporal and spatial distribution of precipitation in Chongqing. J. Sichuan Norm. Univ. Nat. Sci. Ed. 2003, 171–176. (In Chinese) [Google Scholar] [CrossRef]
- News, C. Protecting the Three Gorges Reservoir Is Still the Core Task of Chongqing Water Conservancy during the “14th Five-Year Plan” Period. 2020. Available online: https://baijiahao.baidu.com/s?id=1683873717686562323&wfr=spider&for=pc (accessed on 17 April 2021).
- Lyu, H.-M.; Shen, S.-L.; Zhou, A.; Zhou, W.-H. Data in flood risk assessment of metro systems in a subsiding environment using the interval FAHP-FCA approach. Data Brief 2019, 26, 104468. [Google Scholar] [CrossRef] [PubMed]
- Rahmati, O.; Zeinivand, H.; Besharat, M. Flood hazard zoning in Yasooj region, Iran, using GIS and multi-criteria decision analysis. Geomatics Nat. Hazards Risk 2016, 7, 1000–1017. [Google Scholar] [CrossRef]
- Zhang, N.; Alipour, A. Multi-scale robustness model for highway networks under flood events. Transport. Res. Part D Transport. Environ. 2020, 83, 102281. [Google Scholar] [CrossRef]
- Sugumaran, R.; Larson, S.R.; DeGroote, J.P. Spatio-temporal cluster analysis of county-based human West Nile virus incidence in the continental United States. Int. J. Health Geogr. 2009, 8, 1–19. [Google Scholar] [CrossRef]
- Ghosh, K.G. Analysis of Rainfall Trends and its Spatial Patterns During the Last Century over the Gangetic West Bengal, Eastern India. J. Geovisualization Spat. Anal. 2018, 2, 15. [Google Scholar] [CrossRef]
- Berta, A.A.; Eyasu, E.; Teshome, S.; Legese, F.G. Land use/land cover change effect on soil erosion and sediment delivery in the Winike watershed, Omo Gibe Basin, Ethiopia. Sci. Total Environ. 2020, 728, 138776. [Google Scholar] [CrossRef]
- Yuping, C.; Hui, Y.; Yijuan, Y.; Chunling, Z.; Ping, G.; Liyue, Z.; Liya, F.; Daiqi, Y. Relationships of ozone formation sensitivity with precursors emissions, meteorology and land use types, in Guangdong-Hong Kong-Macao Greater Bay Area, China. J. Environ. Sci. 2020, 94, 1–13. [Google Scholar] [CrossRef]
- Xiao, Y.; Yi, S.; Tang, Z. Integrated flood hazard assessment based on spatial ordered weighted averaging method considering spatial heterogeneity of risk preference. Sci. Total Environ. 2017, 599, 1034–1046. [Google Scholar] [CrossRef]
- Yariyan, P.; Avand, M.; Abbaspour, R.A.; Torabi Haghighi, A.; Costache, R.; Ghorbanzadeh, O.; Janizadeh, S.; Blaschke, T. Flood susceptibility mapping using an improved analytic network process with statistical models. Nat. Hazards Risk 2020, 11, 2282–2314. [Google Scholar] [CrossRef]
- Surwase, T.; Manjusree, P.; Nagamani, P.V.; Jaisankar, G. Novel technique for developing flood hazard map by using AHP: A study on part of Mahanadi River in Odisha. SN Appl. Sci. 2019, 1, 1196. [Google Scholar] [CrossRef]
- Ali, S.A.; Parvin, F.; Pham, Q.B. GIS-based comparative assessment of flood susceptibility mapping using hybrid multi-criteria decision-making approach, naïve Bayes tree, bivariate statistics and logistic regression: A case of Topľa basin, Slovakia. Ecol. Indic. 2020, 117, 106620. [Google Scholar] [CrossRef]
- McMahan, B.; Gerlak, A.K. Climate risk assessment and cascading impacts: Risks and opportunities for an electrical utility in the U.S. Southwest. Clim. Risk Manag. 2020, 29, 100240. [Google Scholar] [CrossRef]
- Lawrence, J.; Blackett, P.; Cradock-Henry, N.A. Cascading climate change impacts and implications. Clim. Risk Manag. 2020, 29, 100234. [Google Scholar] [CrossRef]

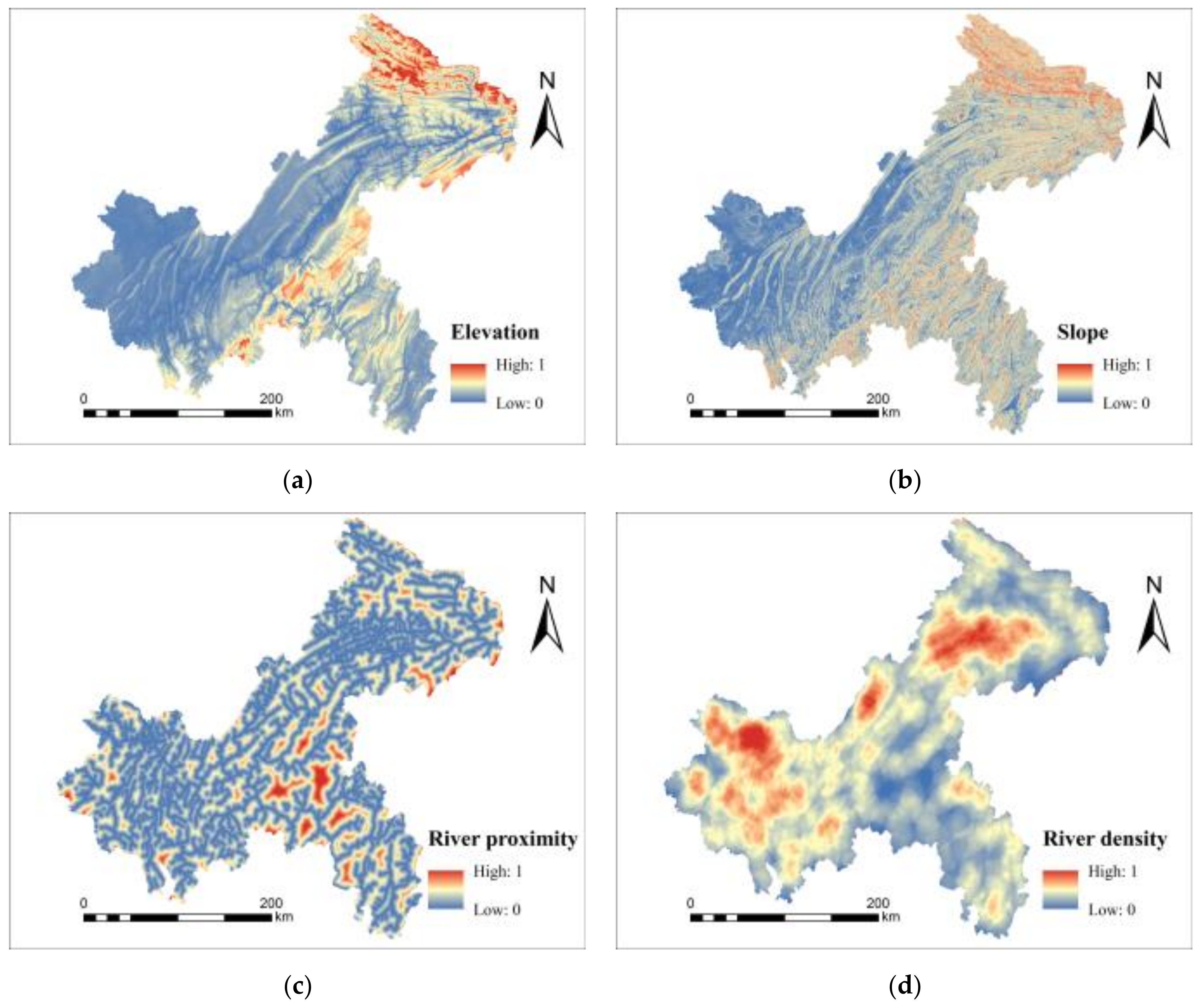
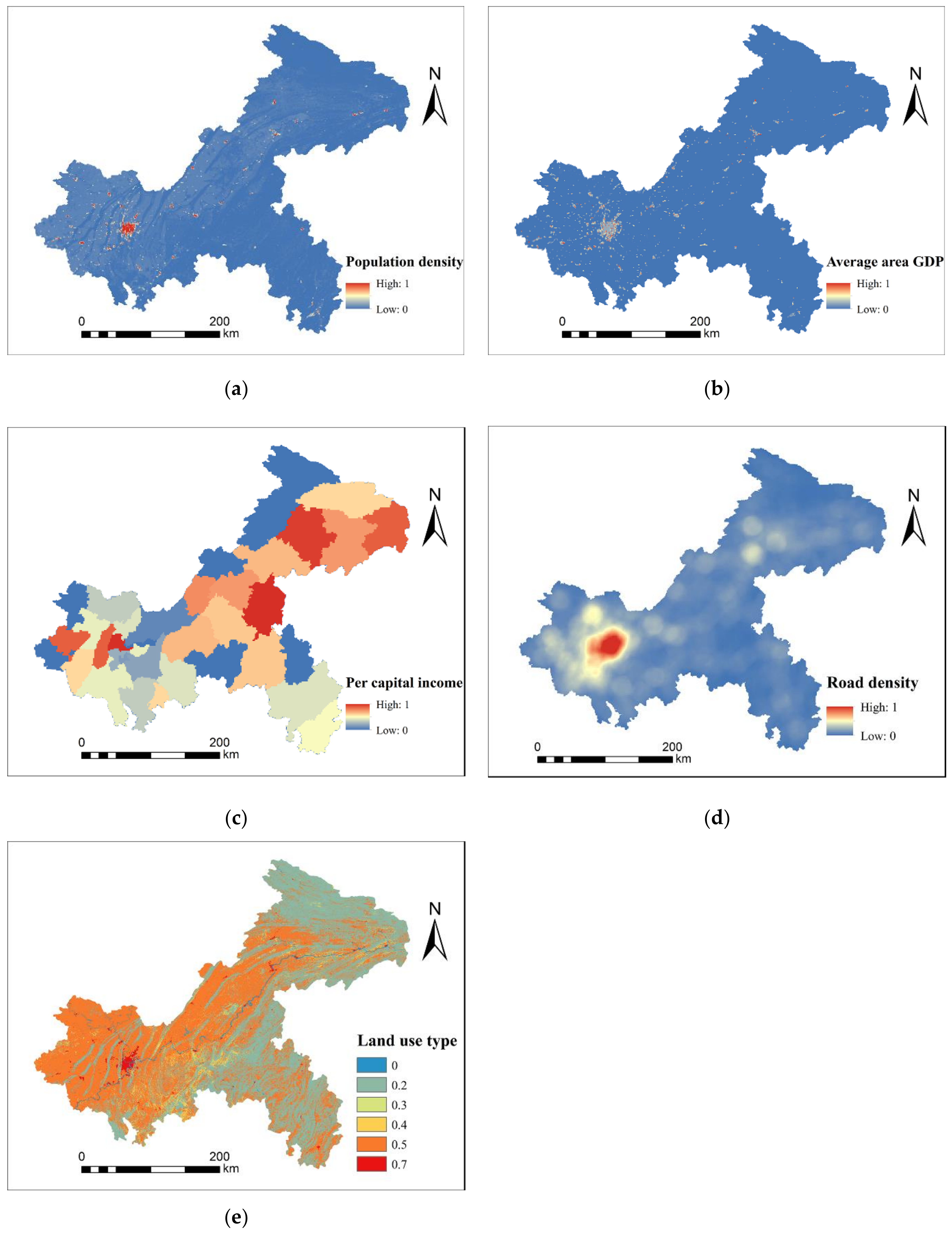

| Data Name | Data Type | Source |
|---|---|---|
| Climate data | Average annual precipitation in counties | China Meteorological Data Network (http://data.cma.cn/, accessed on 11 May 2021) |
| Rainstorm frequency, annual precipitation | ||
| Terrain data | The Digital Elevation Model (DEM) | Geospatial Data Cloud (http://www.gscloud.cn/, accessed on 11 May 2021) |
| Socio-economic data | Population density, average area GDP | the Global Change Scientific Research Data Publishing System (http://www.geodoi.ac.cn/WebCn/Default.aspx, accessed on 11 May 2021) |
| Per capita disposable income | Chongqing Statistical Yearbook (http://data.tjj.cq.gov.cn/, accessed on 11 May 2021) | |
| Land cover types | the National Geographic Information Directory Service System (http://www.webmap.cn/main.do?method=index accessed on 17 April 2021) | |
| Road and river network | OpenStreetMap (https://www.openstreetmap.org/ accessed on 17 April 2021) |
| Linguistic Terms | Fuzzy Number | Triangular Fuzzy Scale | Reciprocal Triangular Fuzzy Number |
|---|---|---|---|
| Equally important | 1 | (1, 1, 1) | (1, 1, 1) |
| Almost equally important | 1′ | (1, 1, 3) | (1/3, 1, 1) |
| Intermediate value | 2′ | (1, 2, 4) | (1/4, 1/2, 1) |
| Moderately more important | 3′ | (1, 3, 5) | (1/5, 1/3, 1) |
| Intermediate value | 4′ | (2, 4, 6) | (1/6, 1/4, 1/2) |
| Strongly more important | 5′ | (3, 5, 7) | (1/7, 1/5, 1/3) |
| Intermediate value | 6′ | (4, 6, 8) | (1/8, 1/6, 1/4) |
| Very strongly more important | 7′ | (5, 7, 9) | (1/9, 1/7, 1/5) |
| Intermediate value | 8′ | (6, 8, 10) | (1/10, 1/8, 1/6) |
| Extremely more important | 9′ | (7, 9, 11) | (1/11, 1/9, 1/7) |
| IndexLayer | AHP (W0) | Pi | TFN-AHP (W0) | AHP (Wb) | Pi | TFN-AHP (Wb) | |
| H | 0.540 | (0.132, 0.25, 0.732) | 0.454 | H1 | 0.667 | (0.250, 0.750, 1.875) | 0.574 |
| H2 | 0.333 | (0.150, 0.250, 0.625) | 0.426 | ||||
| E | 0.163 | (0.093, 0.25, 0.439) | 0.233 | E1 | 0.278 | (0.113, 0.327, 1.042) | 0.318 |
| E2 | 0.160 | (0.122, 0.420, 1.042) | 0.157 | ||||
| E3 | 0.095 | (0.069, 0.132, 0.481) | 0.194 | ||||
| E4 | 0.467 | (0.048, 0.121, 0.280) | 0.332 | ||||
| V | 0.297 | (0.176, 0.5, 1.318) | 0.313 | V1 | 0.354 | (0.073, 0.249, 0.764) | 0.3 |
| V2 | 0.269 | (0.092, 0.283, 0.764) | 0.291 | ||||
| V3 | 0.188 | (0.094, 0.240, 0.623) | 0.27 | ||||
| V4 | 0.112 | (0.082, 0.179, 0.462) | 0.076 | ||||
| V5 | 0.078 | (0.025, 0.048, 0.124) | 0.063 |
| Index Layer | H | E | V | Pi |
|---|---|---|---|---|
| H | (1, 1, 1) | (1, 1, 3) | (0.25, 0.5, 1) | (0.033, 0.057, 0.201) |
| E | (0.33, 1, 1) | (1, 1, 1) | (0.25, 0.5, 1) | (0.023, 0.057, 0.121) |
| V | (1, 2, 4) | (1, 2, 4) | (1, 1, 1) | (0.044, 0.113, 0.362) |
| Sub-Index Layer | H1 | H2 | Pi |
|---|---|---|---|
| H1 | (1, 1, 1) | (1, 3, 5) | (0.250, 0.750, 1.875) |
| H2 | (0.2, 0.33, 1) | (1, 1, 1) | (0.150, 0.250, 0.625) |
| Sub-Index Layer | E1 | E2 | E3 | E4 | Pi |
|---|---|---|---|---|---|
| E1 | (1, 1, 1) | (1, 1, 3) | (1, 2, 4) | (1, 3, 5) | (0.113, 0.327, 1.042) |
| E2 | (0.33, 1, 1) | (1, 1, 1) | (1, 3, 5) | (2, 4, 6) | (0.122, 0.420, 1.042) |
| E3 | (0.25, 0.5, 1) | (0.2, 0.33, 1) | (1, 1, 1) | (1, 1, 3) | (0.069, 0.132, 0.481) |
| E4 | (0.2, 0.33, 1) | (0.17, 0.25, 0.5) | (0.33, 1, 1) | (1, 1, 1) | (0.048, 0.121, 0.280) |
| Sub-Index Layer | V1 | V2 | V3 | V4 | V5 | Pi |
|---|---|---|---|---|---|---|
| V1 | (1, 1, 1) | (1, 2, 4) | (1, 3, 5) | (1, 3, 5) | (1, 2, 4) | (0.073, 0.249, 0.764) |
| V2 | (0.25, 0.5, 1) | (1, 1, 1) | (2, 4, 6) | (1, 3, 5) | (2, 4, 6) | (0.092, 0.283, 0.764) |
| V3 | (0.2, 0.33, 1) | (0.17, 0.25, 0.5) | (1, 1, 1) | (2, 4, 6) | (3, 5, 7) | (0.094, 0.240, 0.623) |
| V4 | (0.2, 0.33, 1) | (0.2, 0.33, 1) | (0.17, 0.25, 0.5) | (1, 1, 1) | (4, 6, 8) | (0.082, 0.179, 0.462) |
| V5 | (0.25, 0.5, 1) | (0.17, 0.25, 0.5) | (0.14, 0.2, 0.33) | (0.125, 0.17, 0.25) | (1, 1, 1) | (0.025, 0.048, 0.124) |
| Variable | Spring | Summer | Fall | Winter |
|---|---|---|---|---|
| Z | 38.28 | 54.34 | 34.69 | 49.62 |
| P | 0 | 0 | 0 | 0 |
| Level | Flood Risk Value | |
|---|---|---|
| Very low risk | <0.1 | |
| Low risk | 0.1–0.3 | |
| Moderate risk | 0.3–0.7 | |
| High risk | 0.7–0.9 | |
| Very high risk | >0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, S.; Fan, J.; Yang, W. Flooding Risk Assessment and Analysis Based on GIS and the TFN-AHP Method: A Case Study of Chongqing, China. Atmosphere 2021, 12, 623. https://doi.org/10.3390/atmos12050623
Cai S, Fan J, Yang W. Flooding Risk Assessment and Analysis Based on GIS and the TFN-AHP Method: A Case Study of Chongqing, China. Atmosphere. 2021; 12(5):623. https://doi.org/10.3390/atmos12050623
Chicago/Turabian StyleCai, Shunyao, Jiamin Fan, and Wei Yang. 2021. "Flooding Risk Assessment and Analysis Based on GIS and the TFN-AHP Method: A Case Study of Chongqing, China" Atmosphere 12, no. 5: 623. https://doi.org/10.3390/atmos12050623
APA StyleCai, S., Fan, J., & Yang, W. (2021). Flooding Risk Assessment and Analysis Based on GIS and the TFN-AHP Method: A Case Study of Chongqing, China. Atmosphere, 12(5), 623. https://doi.org/10.3390/atmos12050623





