Polarimetric Radar Characteristics of Tornadogenesis Failure in Supercell Thunderstorms
Abstract
1. Introduction
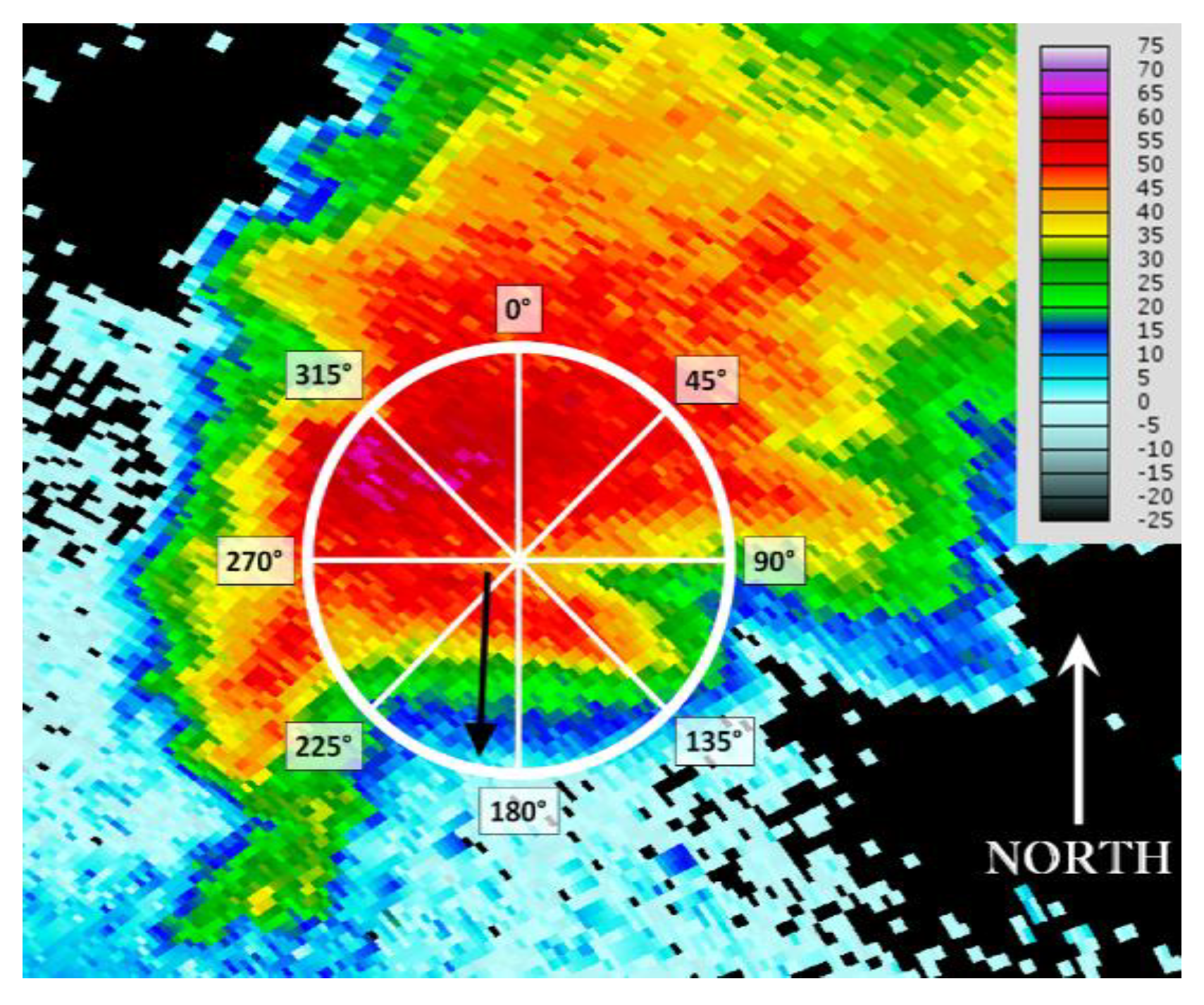
2. Data and Methods
3. Results
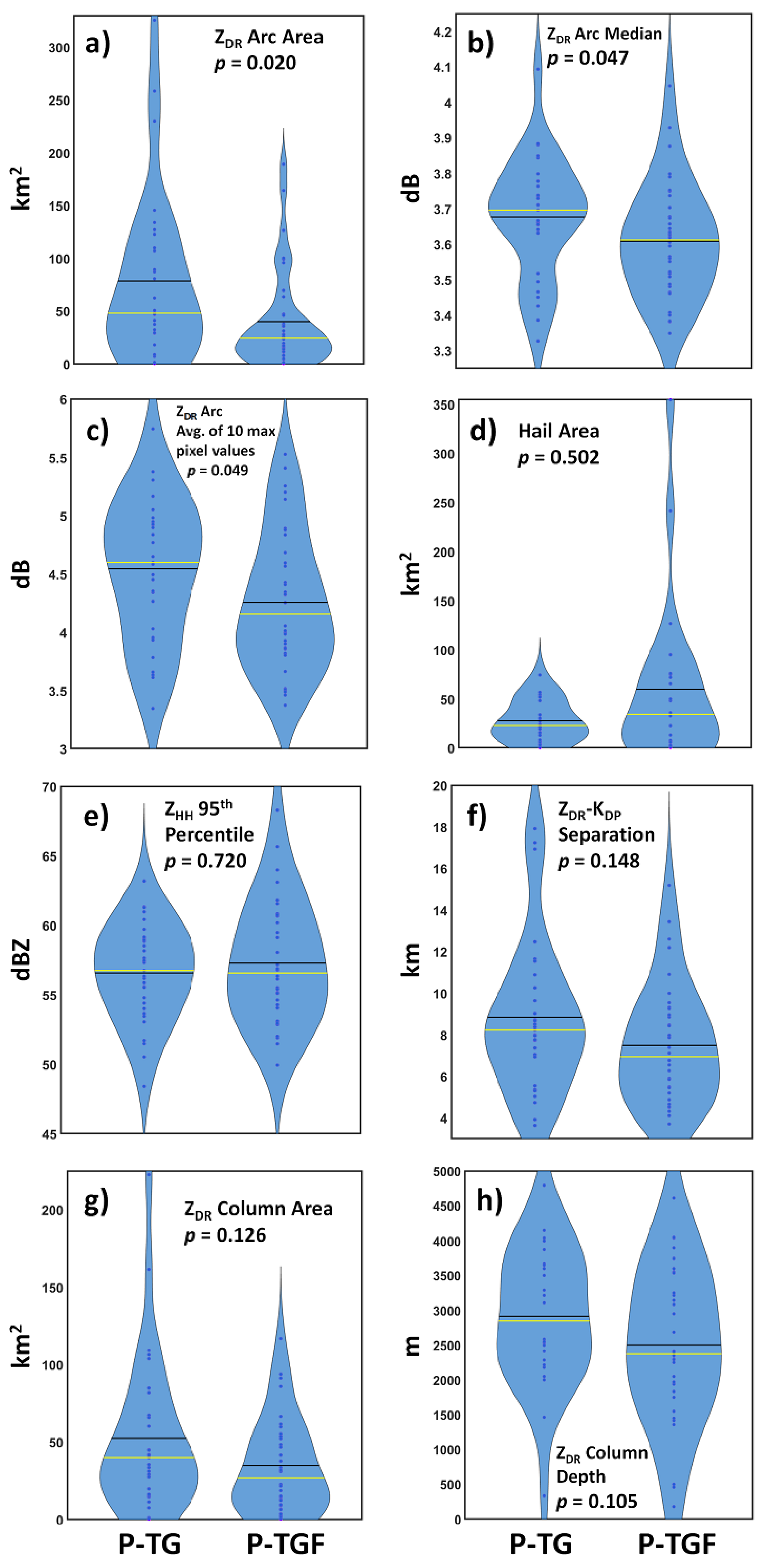
3.1. Comparisons between Radar Metric Distributions
3.2. Comparisons between Radar Metric Change Leading Up to Tornadogenesis/TGF
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumjian, M.R.; Ryzhkov, A.V. Polarimetric signatures in supercell thunderstorms. J. Appl. Meteor. Climatol. 2008, 47, 1940–1961. [Google Scholar] [CrossRef]
- Romine, G.S.; Burgess, D.W.; Wilhelmson, R.B. A dual-polarization-radar-based assessment of the 8 May 2003 Oklahoma City area tornadic supercell. Mon. Weather Rev. 2008, 136, 2849–2870. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S.; Straka, J.M.; Rasmussen, E.N. Polarimetric radar observations at low levels during tornado life cycles in a small sample of classic Southern Plains supercells. J. Appl. Meteor. Climatol. 2008, 47, 1232–1247. [Google Scholar] [CrossRef][Green Version]
- Tanamachi, R.L.; Heinselman, P.L. Rapid-scan, polarimetric observations of central Oklahoma severe storms on 31 May 2013. Weather Forecast. 2016, 31, 19–42. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S. Polarimetric variability of classic supercell storms as a function of environment. J. Appl. Meteor. Climatol. 2016, 55, 1907–1925. [Google Scholar] [CrossRef]
- Snyder, J.C.; Ryzhkov, A.V.; Kumjian, M.R.; Khain, A.P.; Picca, J. A ZDR column detection algorithm to examine convective storm updrafts. Weather Forecast. 2015, 30, 1819–1844. [Google Scholar] [CrossRef]
- French, M.M.; Burgess, D.W.; Mansell, E.R.; Wicker, L.J. Bulk hook echo raindrop sizes retrieved using mobile, polarimetric Doppler radar observations. J. Appl. Meteor. Climatol. 2015, 54, 423–450. [Google Scholar] [CrossRef]
- Houser, J.L.; Bluestein, H.B.; Snyder, J.C. Finescale radar examination of the tornadic debris signature and weak-echo reflectivity band associated with a large, violent tornado. Mon. Weather Rev. 2016, 144, 4101–4130. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S. Polarimetric radar metrics related to tornado life cycles and intensity in supercell storms. Mon. Weather Rev. 2017, 145, 3671–3686. [Google Scholar] [CrossRef]
- McKeown, K.E.; French, M.M.; Tuftedal, K.S.; Kingfield, D.M.; Bluestein, H.B.; Reif, D.W.; Wienhoff, Z.B. Rapid-scan and polarimetric radar observations of the dissipation of a violent tornado on 9 May 2016 near Sulphur, Oklahoma. Mon. Weather Rev. 2020, 148, 3951–3971. [Google Scholar] [CrossRef]
- Van Den Broeke, M.S. A preliminary polarimetric radar comparison of pretornadic and nontornadic supercell storms. Mon. Weather Rev. 2020, 148, 1567–1584. [Google Scholar] [CrossRef]
- Trapp, R.J. Observations of nontornadic low-level mesocyclones and attendant tornadogenesis failure during VORTEX. Mon. Weather Rev. 1999, 127, 1693–1705. [Google Scholar] [CrossRef]
- Brooks, H.E.; Doswell III, C.A.; Wilhelmson, R.B. The role of midtropospheric wind in the evolution and maintenance of low-level mesocyclones. Mon. Weather Rev. 1994, 122, 126–136. [Google Scholar] [CrossRef][Green Version]
- Finley, C.A.; Lee, B.D.; Grzych, M.; Karstens, C.D.; Samaras, T.M. Mobile mesonet observations of the rear-flank downdraft evolution associated with a violent tornado near Bowdle, SD on 22 May 2010. Preprints. In Proceedings of the 25th Conference on Severe Local Storms, Denver, CO, USA, 2010; Available online: https://ams.confex.com/ams/25SLS/techprogram/paper_176132.htm (accessed on 28 April 2021).
- Trapp, R.J.; Davies-Jones, R. Tornadogenesis with and without a dynamic pipe effect. J. Atmos. Sci. 1997, 54, 113. [Google Scholar] [CrossRef]
- Markowski, P.M.; Straka, J.M.; Rasmussen, E.N. Direct surface thermodynamic observations within the rear-flank downdrafts of nontornadic and tornadic supercells. Mon. Weather Rev. 2002, 130, 1692–1721. [Google Scholar] [CrossRef]
- Naylor, J.; Gilmore, M.S. Vorticity evolution leading to tornadogenesis and tornadogenesis failure in simulated supercells. J. Atmos. Sci. 2014, 71, 1201–1217. [Google Scholar] [CrossRef][Green Version]
- Coffer, B.E.; Parker, M.D.; Dahl, J.M.L.; Wicker, L.J.; Clark, A.J. Volatility of tornadogenesis: An ensemble of simulated nontornadic and tornadic supercells in VORTEX2 environments. Mon. Weather Rev. 2017, 145, 4605–4625. [Google Scholar] [CrossRef]
- Coffer, B.E.; Parker, M.D. Is there a “tipping point” between simulated nontornadic and tornadic supercells in VORTEX2 environments? Mon. Weather Rev. 2018, 146, 2667–2693. [Google Scholar] [CrossRef]
- National Centers for Environmental Information. Storm Events Database. Available online: ahttps://www.ncdc.noaa.gov/stormevents/ (accessed on 18 March 2021).
- Trapp, R.J.; Wheatley, D.M.; Atkins, N.T.; Przybylinski, R.W.; Wolf, R. Buyer beware: Some words of caution on the use of severe wind reports in postevent assessment and research. Weather Forecast. 2006, 21, 408–415. [Google Scholar] [CrossRef]
- Thompson, R.L.; Edwards, R.; Hart, J.A.; Elmore, K.L.; Markowski, P. Close proximity soundings within supercell environments obtained from the Rapid Update Cycle. Weather Forecast. 2003, 18, 1243–1261. [Google Scholar] [CrossRef]
- Cooper, D.T.; Vorst, A.B. Assessing the utility of normalized rotation in detecting tornado development along the Allegheny front. In Proceedings of the Northeast Regional Operational Workshop XVII, Albany, NY, USA, 3 November 2016. [Google Scholar]
- Gibson, M. 2017: FAQ: NROT and GR-MDA products. In GRlevelx User Forums; Gibson Ridge Software, LLC: Suwanee, GA, USA; Available online: http://www.grlevelx.com/owners/ (accessed on 10 March 2021).
- Torres, S.; Curtis, C. Initial implementation of super-resolution data on the NEXRAD networ. In Proceedings of the 23rd International Conference on Interactive Information Processing Systems for Meteorology, Oceanography, and Hydrolog, American Meteor Society, San Antonio, TX, USA, 2007; Available online: https://ams.confex.com/ams/87ANNUAL/techprogram/paper_116240.htm (accessed on 28 April 2021).
- Wilson, M.B.; Van Den Broeke, M.S. An automated Python algorithm to quantify ZDR arcs and KDP-ZDR separation signatures in supercells. J. Atmos. Ocean. Technol. 2021, 38, 371–386. [Google Scholar] [CrossRef]
- Picca, J.; Ryzhkov, A. A dual-wavelength polarimetric analysis of the 16 May 2010 Oklahoma City extreme hailstorm. Mon. Weather Rev. 2012, 140, 1385–1403. [Google Scholar] [CrossRef]
- Palmer, R.D.; Bodine, D.; Kumjian, M.; Cheong, B.; Zhang, G.; Cao, Q.; Bluestein, H.; Ryzhkov, A.; Yu, T.; Wang, Y. Observations of the 10 May 2010 tornado outbreak using OU-PRIME: Potential for new science with high-resolution polarimetric radar. Bull. Am. Meteorol. Soc. 2011, 92, 871–891. [Google Scholar] [CrossRef]
- Crowe, C.; Schultz, C.; Kumjian, M.; Carey, L.; Petersen, W. Use of dual-polarization signatures in diagnosing tornadic potential. Electron. J. Oper. Meteorol. 2012, 13, 57–78. [Google Scholar]
- Dawson, D.T.; Mansell, E.R.; Jung, Y.; Wicker, L.J.; Kumjian, M.R.; Xue, M. Low-level ZDR signatures in supercell forward flanks: The role of size sorting and melting of hail. J. Atmos. Sci. 2014, 71, 276–299. [Google Scholar] [CrossRef]
- Zrnić, D.S.; Bringi, V.N.; Balakrishnan, N.; Aydin, K.; Chandrasekar, V.; Hubbert, J. Polarimetric measurements in a severe hailstorm. Mon. Weather Rev. 1993, 121, 2223–2238. [Google Scholar] [CrossRef]
- Illingworth, A.J.; Goddard, J.W.F.; Cherry, S.M. Polarization radar studies of precipitation development in convective storms. Quart. J. R. Meteorol. Soc. 1987, 113, 469–489. [Google Scholar] [CrossRef]
- Brandes, E.A.; Vivekanandan, J.; Tuttle, D.J.; Kessinger, C.J. A study of thunderstorm microphysics with multiparameter radar and aircraft observations. Mon. Weather Rev. 1995, 123, 3129–3143. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V.; Melnikov, V.M.; Schuur, T.J. Rapid-scan super-resolution observations of a cyclic supercell with a dual-polarization WSR-88D. Mon. Weather Rev. 2010, 138, 3762–3786. [Google Scholar] [CrossRef]
- Bunkers, M.J.; Klimowski, B.A.; Zeitler, J.W.; Thompson, R.L.; Weisman, M.L. Predicting supercell motion using a new hodograph technique. Weather Foreacst. 2000, 15, 61–79. [Google Scholar] [CrossRef]
- Bunkers, M.J. Observations of right-moving supercell motion forecast errors. Weather Forecast. 2018, 33, 145–159. [Google Scholar] [CrossRef]
- Loeffler, S.D.; Kumjian, M.R.; Jurewicz, M.; French, M.M. Differentiating between tornadic and nontornadic supercells using polarimetric radar signatures of hydrometeor size sorting. Geophys. Res. Lett. 2020, 47, e2020GL088242. [Google Scholar] [CrossRef]
- Corder, G.W.; Foreman, D.I. Nonparametric Statistics: A Step-by-Step Approach, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014; p. 288. [Google Scholar]
- Lemon, L.R.; Doswell III, C.A. Severe thunderstorm evolution and mesocyclone structure as related to tornadogenesis. Mon. Weather Rev. 1979, 107, 1184–1197. [Google Scholar] [CrossRef]
- Fischer, J.; Dahl, J.M.L. The relative importance of updraft and cold pool characteristics in supercell tornadogenesis using highly idealized simulations. J. Atmos. Sci. 2020, 77, 4089–4107. [Google Scholar] [CrossRef]
- Kumjian, M.R.; Ryzhkov, A.V. Storm-relative helicity revealed from polarimetric radar measurements. J. Atmos. Sci. 2009, 66, 667–685. [Google Scholar] [CrossRef]
- Adlerman, E.J.; Droegemeier, K.K. The sensitivity of numerically simulated cyclic mesocyclogenesis to variations in model physical and computational parameters. Mon. Weather Rev. 2002, 130, 2671–2691. [Google Scholar] [CrossRef]
- Loeffler, S.D.; Kumjian, M.R. Quantifying the separation of enhanced ZDR and KDP regions in nonsupercell tornadic storms. Weather Forecast. 2018, 33, 1143–1157. [Google Scholar] [CrossRef]
- Brandes, E.A. Mesocyclone evolution and tornadogenesis: Some observations. Mon. Weather Rev. 1978, 106, 995–1011. [Google Scholar] [CrossRef][Green Version]
- Adlerman, E.J.; Droegemeier, K.K.; Davies-Jones, R.P. A numerical simulation of cyclic mesocyclogenesis. J. Atmos. Sci. 1999, 56, 2045–2069. [Google Scholar] [CrossRef]
| Date | Radar | Analysis Period | FFA | FL | ZDR Calibration Factor |
|---|---|---|---|---|---|
| 26–27 April 2012 | KOHX | 2330–0000 | 190 | 3852 | 0.203 |
| 30 April 2012 | KDDC | 2222–2252 | 160 | 3907 | 0.575 |
| 10 May 2012 | KEWX | 1816–1846 | 140 | 4020 | −0.518 |
| 8–9 June 2012 | KMQT | 2343–0013 | 190 | 3999 | −0.012 |
| 18 March 2013 | KFFC | 2140–2210 | 180 | 3278 | −0.100 |
| 31 March 2013 | KINX | 0205–0235 | 190 | 2885 | 0.026 |
| 31 March 2013 | KSRX | 0350–0420 | 200 | 3000 | −0.361 |
| 17 April 2013 | KFDR | 2320–2350 | 180 | 4639 | −0.523 |
| 15 May 2013 | KFWS | 2311–2341 | 190 | 4614 | −0.128 |
| 18–19 May 2013 | KDDC | 2348–0018 | 180 | 3635 | 0.007 |
| 19 May 2013 | KTLX | 2052–2122 | 160 | 4369 | −0.526 |
| 19 May 2013 | KTLX | 2230–2300 | 160 | 4369 | −0.526 |
| 20 May 2013 | KINX | 2021–2051 | 170 | 4167 | 0.353 |
| 20 May 2013 | KEAX | 2127–2157 | 140 | 3563 | −0.261 |
| 30 May 2013 | KINX | 2319–2349 | 190 | 4708 | 0.206 |
| 30 May 2013 | KTLX | 2228–2258 | 200 | 4708 | −0.365 |
| 18 June 2013 | KRAX | 2200–2230 | 180 | 4460 | −0.591 |
| 19 June 2013 | KLBB | 2202–2232 | 190 | 4812 | −0.062 |
| 28 August 2013 | KDTX | 0324–0354 | 215 | 4845 | −0.273 |
| 30–31 August 2013 | KBIS | 2340–0010 | 190 | 4561 | −0.259 |
| 11 May 2014 | KUEX | 1956–2026 | 140 | 3368 | −0.010 |
| 27 April 2015 | KFWS | 0139–0209 | 180 | 3502 | −0.166 |
| 8 May 2015 | KFDR | 2052–2122 | 150 | 4223 | −0.550 |
| 19 May 2015 | KTLX | 1910–1940 | 180 | 4000 | −0.073 |
| 27 May 2015 | KDDC | 1933–2003 | 180 | 3764 | 0.026 |
| 4 June 2015 | KFTG | 2208–2238 | 180 | 4560 | 0.016 |
| 18 September 2015 | KEAX | 2239–2309 | 180 | 4497 | 0.004 |
| 2 February 2016 | KDGX | 2018–2048 | 130 | 3242 | 0.206 |
| 24 February 2016 | KRAX | 2030–2100 | 115 | 2992 | 0.205 |
| 29 April 2016 | KFDR | 1959–2029 | 160 | 3923 | 0.194 |
| 21 October 2017 | KFDR | 2153–2223 | 140 | 4047 | −0.383 |
| Date | Radar | Analysis Period | FFA | FL | ZDR Calibration Factor |
|---|---|---|---|---|---|
| 1 June 2012 | KAMA | 2303–2333 | 150 | 4735 | 0.114 |
| 2 April 2013 | KGRK | 1940–2010 | 150 | 3800 | −0.388 |
| 7–8 April 2013 | KSGF | 2250–2320 | 190 | 3374 | −0.157 |
| 25 May 2013 | KUDX | 2110–2140 | 180 | 4131 | −0.121 |
| 24–25 July 2013 | KUEX | 2336–0006 | 200 | 4275 | −0.269 |
| 6–7 August 2013 | KMPX | 2238–2308 | 180 | 3885 | −0.039 |
| 13 August 2013 | KDIX | 1222–1252 | 180 | 4079 | −0.315 |
| 14–15 August 2013 | KAMA | 2321–2351 | 190 | 4660 | 0.237 |
| 14 October 2013 | KDDC | 1936–2006 | 170 | 3816 | 0.161 |
| 26–27 October 2013 | KFWS | 2338–0008 | 170 | 3567 | −0.440 |
| 3 April 2014 | KICT | 0137–0207 | 140 | 3828 | 0.183 |
| 24 April 2014 | KDYX | 0007–0037 | 170 | 4215 | −0.101 |
| 10 May 2017 | KFDX | 0457–0527 | 170 | 4303 | −0.329 |
| 18 May 2017 | KVNX | 2118–2148 | 130 | 3948 | −0.162 |
| 12 June 2017 | KCYS | 2054–2124 | 140 | 4554 | 0.107 |
| 28 June 2017 | KDMX | 2210–2240 | 200 | 4363 | −0.285 |
| 29 May 2018 | KDDC | 2038–2108 | 170 | 4463 | −0.143 |
| 2 October 2018 | KPBZ | 2056–2126 | 210 | 3919 | 0.109 |
| 24 March 2019 | KLSX | 2234–2304 | 160 | 2733 | −0.035 |
| 30 April 2019 | KSRX | 2310–2340 | 180 | 3950 | −0.188 |
| 7 May 2019 | KAMA | 2048–2118 | 170 | 4093 | 0.032 |
| 20 May 2019 | KLBB | 1902–1932 | 160 | 4549 | 0.022 |
| 23 May 2019 | KSGF | 0215–0245 | 170 | 4491 | 0.150 |
| 25 May 2019 | KLBB | 1853–1923 | 130 | 4530 | 0.033 |
| 27 May 2019 | KIWX | 2141–2211 | 180 | 3903 | 0.315 |
| 30 May 2019 | KLWX | 1832–1902 | 150 | 4027 | 0.894 |
| 24 March 2020 | KGWX | 2328–2358 | 180 | 4048 | 0.128 |
| 22 April 2020 | KPOE | 2204–2234 | 190 | 3887 | 0.153 |
| 20 May 2020 | KPUX | 0031–0101 | 130 | 4767 | −0.160 |
| 23 May 2020 | KDVN | 1708–1738 | 160 | 3619 | 0.087 |
| 23 May 2020 | KFDR | 0029–0059 | 120 | 4253 | −0.399 |
| 23 May 2020 | KSRX | 0213–0243 | 180 | 4266 | 0.046 |
| 23–24 May 2020 | KAMA | 2321–2351 | 200 | 4452 | 0.155 |
| 7–8 June 2020 | KBIS | 2337–0007 | 120 | 4230 | −0.049 |
| 20 June 2020 | KLNX | 2238–2308 | 200 | 3990 | −0.390 |
| 27 June 2020 | KLSX | 2125–2155 | 170 | 4529 | 0.313 |
| Variable | Units | Sample References |
|---|---|---|
| Storm speed of forward motion | m s−1 | [35,36] |
| Storm direction of motion | degrees | [35,36] |
| Area of ZDR arc | km2 | [1,9,11,26] |
| Mean pixel value in ZDR arc | dB | [11,26] |
| Median pixel value in ZDR arc | dB | [26] |
| Standard deviation of pixel values in ZDR arc | dB | [26] |
| Avg. of 10 highest pixel values in ZDR arc | dB | [26,29] |
| Base-scan polarimetrically-inferred hail area | km2 | [1,11] |
| KDP foot area | km2 | [26,37] |
| Storm area with ZHH > 35 dBZ | km2 | [9] |
| Avg. of pixels exceeding 95th percentile of ZHH | dBZ | [11,26] |
| Separation distance, KDP foot/ZDR arc centroids | km | [26,37] |
| KDP foot/ZDR arc separation angle | degrees | [26,37] |
| Area of 1 dB ZDR column 1 km above 0 °C level | km2 | [9] |
| Maximum ZDR column depth | km | [6,11] |
| Average ZDR column depth | km | [11] |
| Variable | Units | Pre-TG Avg. | Pre-TGF Avg. | p-Value |
|---|---|---|---|---|
| Storm speed of forward motion | m s−1 | 11.1 | 12.8 | 0.060 |
| Storm direction of motion | degrees | 253.6 | 266.8 | 0.432 |
| Area of ZDR arc | km2 | 78.6 | 40.0 | 0.020 |
| Mean pixel value in ZDR arc | dB | 3.69 | 3.64 | 0.090 |
| Median pixel value in ZDR arc | dB | 3.68 | 3.61 | 0.047 |
| Standard deviation of pixel values in ZDR arc | dB | 0.37 | 0.31 | 0.062 |
| Avg. of 10 highest pixel values in ZDR arc | dB | 4.54 | 4.26 | 0.049 |
| Base-scan polarimetrically-inferred hail area | km2 | 27.8 | 59.9 | 0.502 |
| KDP foot area | km2 | 149.4 | 148.7 | 0.768 |
| Storm area with ZHH >35 dBZ | km2 | 1188.0 | 1782.9 | 0.584 |
| Avg. of pixels exceeding 95th percentile of ZHH | dBZ | 56.6 | 57.3 | 0.720 |
| Separation distance, KDP foot/ZDR arc centroids | km | 8.84 | 7.48 | 0.148 |
| KDP foot/ZDR arc separation angle | degrees | 78.4 | 79.4 | 0.932 |
| Area of 1 dB ZDR column 1 km above 0 °C level | km2 | 52.3 | 34.9 | 0.126 |
| Maximum ZDR column depth | km | 2.91 | 2.50 | 0.105 |
| Average ZDR column depth | km | 1.42 | 1.30 | 0.285 |
| Variable | Units | Pre-TG Avg. | Pre-TGF Avg. | p-Value |
|---|---|---|---|---|
| Storm speed of forward motion | m s−1 | −0.40 | 0.29 | 0.215 |
| Storm direction of motion | degrees | 0.73 | 5.70 | 0.382 |
| Area of ZDR arc | km2 | 21.6 | 8.9 | 0.634 |
| Mean pixel value in ZDR arc | dB | −0.01 | −0.02 | 0.634 |
| Median pixel value in ZDR arc | dB | 0.01 | −0.02 | 0.317 |
| Standard deviation of pixel values in ZDR arc | dB | −0.00 | −0.05 | 0.491 |
| Avg. of 10 highest pixel values in ZDR arc | dB | 0.04 | −0.14 | 0.302 |
| Base-scan polarimetrically-inferred hail area | km2 | 2.7 | −13.1 | 0.207 |
| KDP foot area | km2 | 20.4 | −10.1 | 0.213 |
| Storm area with ZHH > 35 dBZ | km2 | −30.9 | 207.8 | 0.205 |
| Avg. of pixels exceeding 95th percentile of ZHH | dBZ | −0.12 | −0.61 | 0.120 |
| Separation distance, KDP foot/ZDR arc centroids | km | 0.36 | 0.52 | 0.736 |
| KDP foot/ZDR arc separation angle | degrees | −5.30 | 2.20 | 0.277 |
| Area of 1 dB ZDR column 1 km above 0 °C level | km2 | 11.2 | 0.2 | 0.549 |
| Maximum ZDR column depth | km | −0.04 | 0.09 | 0.707 |
| Average ZDR column depth | km | −0.04 | 0.06 | 0.367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Den Broeke, M. Polarimetric Radar Characteristics of Tornadogenesis Failure in Supercell Thunderstorms. Atmosphere 2021, 12, 581. https://doi.org/10.3390/atmos12050581
Van Den Broeke M. Polarimetric Radar Characteristics of Tornadogenesis Failure in Supercell Thunderstorms. Atmosphere. 2021; 12(5):581. https://doi.org/10.3390/atmos12050581
Chicago/Turabian StyleVan Den Broeke, Matthew. 2021. "Polarimetric Radar Characteristics of Tornadogenesis Failure in Supercell Thunderstorms" Atmosphere 12, no. 5: 581. https://doi.org/10.3390/atmos12050581
APA StyleVan Den Broeke, M. (2021). Polarimetric Radar Characteristics of Tornadogenesis Failure in Supercell Thunderstorms. Atmosphere, 12(5), 581. https://doi.org/10.3390/atmos12050581






