Surface and Tropospheric Response of North Atlantic Summer Climate from Paleoclimate Simulations of the Past Millennium
Abstract
1. Introduction
2. Materials and Methods
2.1. Model Simulations
2.1.1. MPI-ESM-P
2.1.2. CESM-LME
2.2. Methods
3. Results
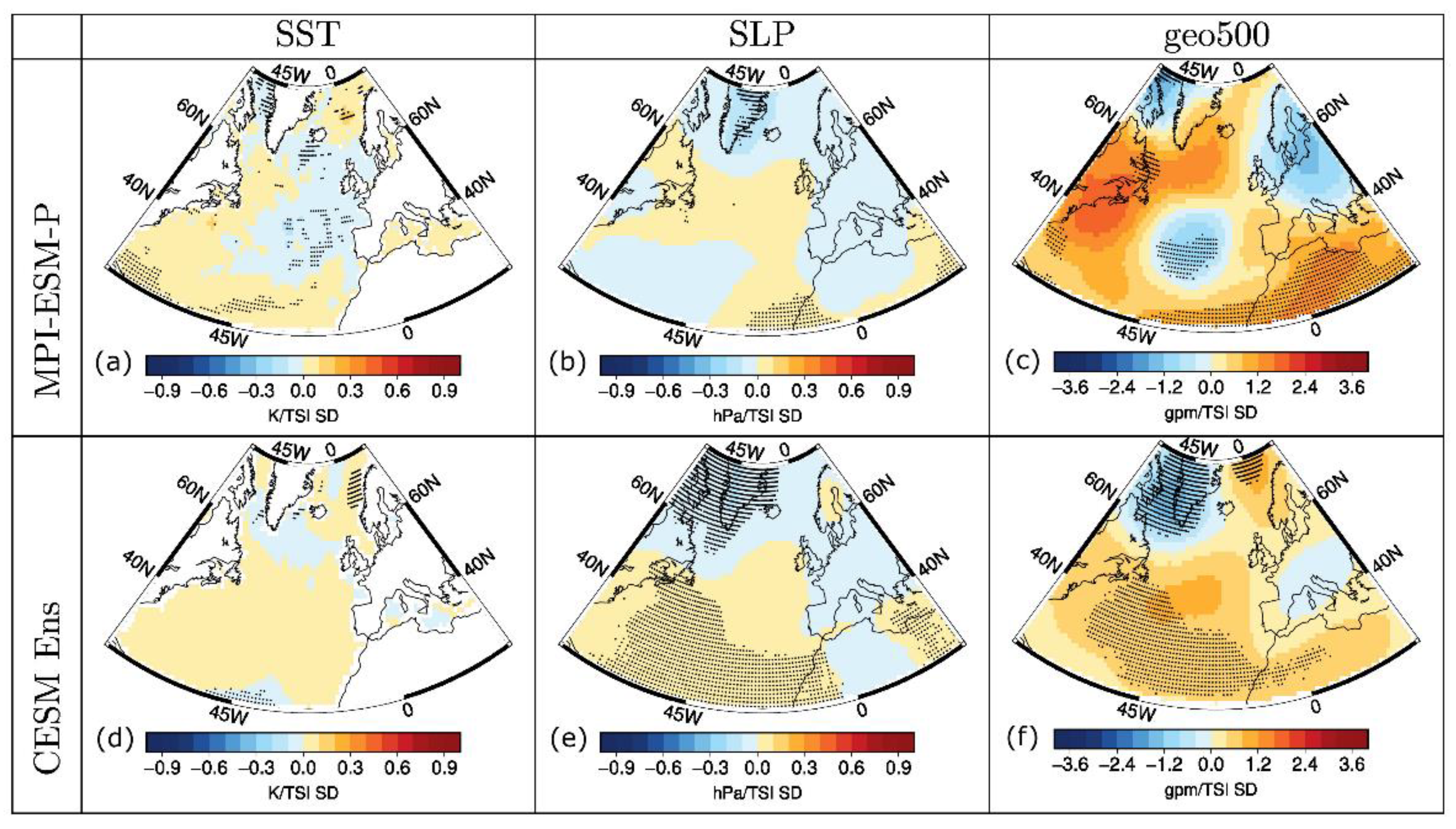
3.1. Linear Methods
3.2. Lagged Climatic Response
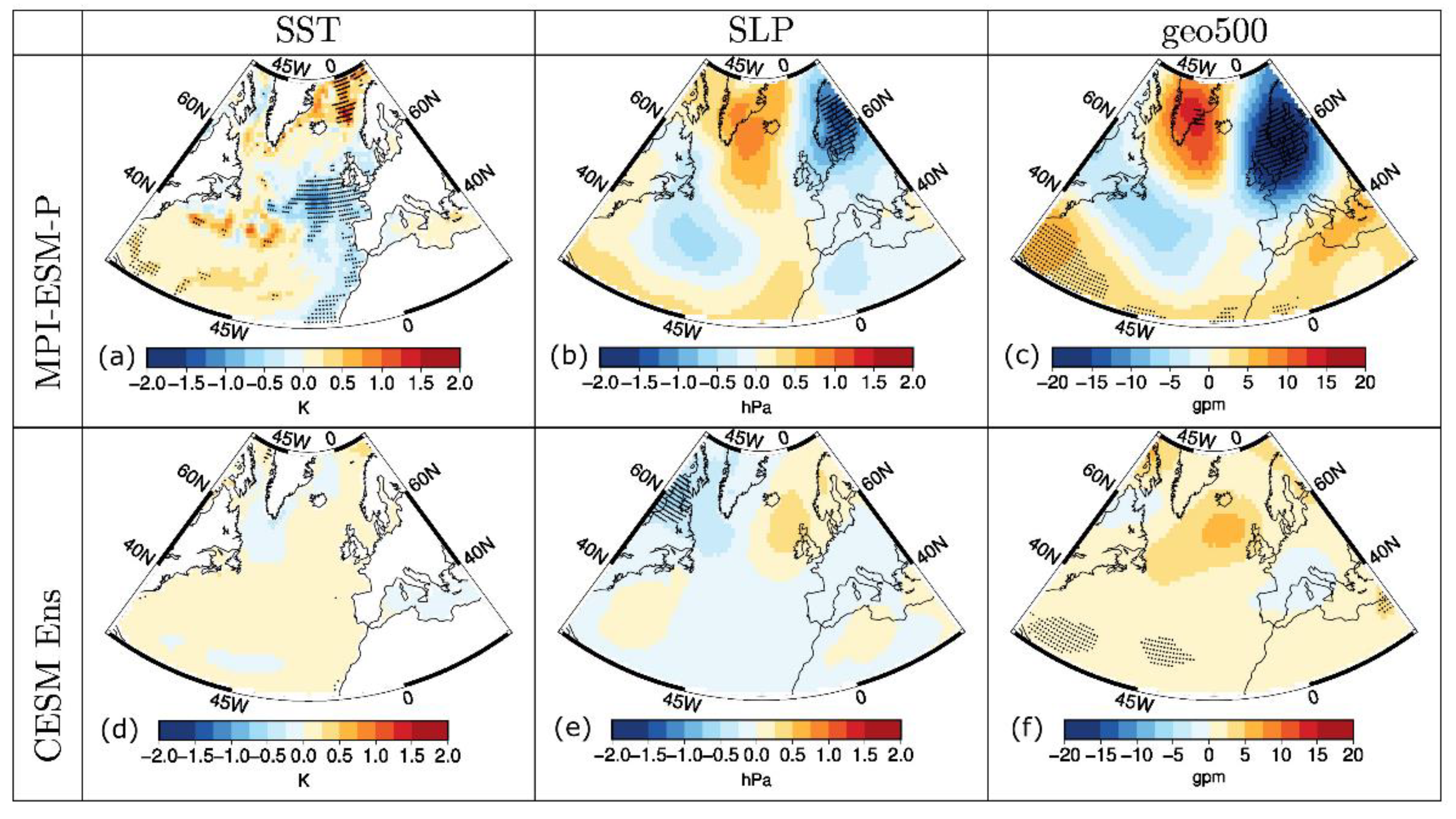
3.3. Composite Analysis
3.4. Common TSI Signals in the CESM Ensemble
4. Discussion
4.1. Sea Surface Temperature TSI Response
4.2. Tropospheric TSI Response and Dynamical Considerations
5. Conclusions
- The statistical methods used indicate similar results for the CESM tropospheric forced response, agreeing on a weak response with decreased SLP over Greenland (−0.1 hPa per TSI SD) and increased geo500 over the subtropics (+0.8 gpm per TSI SD). This response is weak at all lags studied, with the values of the correlation coefficient being r = 0.1 for SLP and r = 0.3 for geo500.
- The solar signal was not robustly identified during the preindustrial period in the summer SSTs of the CESM ensemble mean over the NA basin. This result was indicated by linear methods and composite analysis, and further justified from the analysis of the PiControl simulations.
- The investigation of the CESM individual ensemble members signified that, for the low TSI scaling, model internal variability is larger than the changes induced by TSI forcing in single model simulations regarding surface and tropospheric variables. This result is further supported by the SNR values being lower than 0.4 for the climatic variables studied.
- The control simulations of the two ESMs used in our study indicate that spurious correlation patterns between climatic variables and TSI may arise with linear regression, Pearson correlation, and composite analysis when using single model simulations.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mitchell, J.F.B.K.D.; Hegrel, G.C.; Zwiers, F.W.; Allen, M.R.; Marengo, J. Chapter 3 Detection of climate change and attribution of causes. In Climate Change 2001: The Scientific Basis; Houghton, J.T., Ding, Y., Griggs, D.J., Noguer, M., van der Linden, P.J., Dai, X., Maskell, K., Johnson, C.A., Eds.; Cambridge University Press: Cambridge, UK, 2001; pp. 696–738. [Google Scholar]
- Crowley, T.J. Causes of climate change over the past 1000 years. Science 2000, 289, 270–277. [Google Scholar] [CrossRef]
- Free, M.; Robock, A. Global warming in the context of the Little Ice Age. J. Geophys. Res. Atmos. 1999, 104, 19057–19070. [Google Scholar] [CrossRef]
- Hegerl, G.C.; Crowley, T.J.; Hyde, W.T.; Frame, D.J. Climate sensitivity constrained by temperature reconstructions over the past seven centuries. Nature 2006, 440, 1029–1032. [Google Scholar] [CrossRef] [PubMed]
- Shindell, D.T.; Schmidt, G.A.; Miller, R.L.; Mann, M.E. Volcanic and solar forcing of climate change during the preindustrial era. J. Clim. 2003, 16, 4094–4107. [Google Scholar] [CrossRef]
- Haigh, J.D. The role of stratospheric ozone in modulating the solar radiative forcing of climate. Nature 1994, 370, 544. [Google Scholar] [CrossRef]
- Lean, J. The Sun’s variable radiation and its relevance for Earth. Annu. Rev. Astron. Astrophys. 1997, 35, 33–67. [Google Scholar] [CrossRef]
- Lilensten, J.; De Wit, T.D.; Matthes, K. Earth’s Climate Response to a Changing Sun: A Review of the Current Understanding by the European Research Group TOSCA; EDP Sciences: Paris, France, 2016. [Google Scholar]
- Seppälä, A.; Clilverd, M.A. Energetic particle forcing of the Northern Hemisphere winter stratosphere: Comparison to solar irradiance forcing. Front. Phys. 2014, 2, 25. [Google Scholar] [CrossRef]
- Shindell, D.; Rind, D.; Balachandran, N.; Lean, J.; Lonergan, P. Solar cycle variability, ozone, and climate. Science 1999, 284, 305–308. [Google Scholar] [CrossRef]
- Matthes, K.; Funke, B.; Andersson, M.E.; Barnard, L.; Beer, J.; Charbonneau, P.; Clilverd, M.A.; de Wit, T.D.; Haberreiter, M.; Hendry, A.; et al. Solar forcing for CMIP6 (v3. 2). Geosci. Model Dev. 2017, 10, 2247–2302. [Google Scholar] [CrossRef]
- Eddy, J.A. The maunder minimum. Science 1976, 192, 1189–1202. [Google Scholar] [CrossRef]
- Chiodo, G.; García-Herrera, R.; Calvo, N.; Vaquero, J.M.; Añel, J.A.; Barriopedro, D.; Matthes, K. The impact of a future solar minimum on climate change projections in the Northern Hemisphere. Environ. Res. Lett. 2016, 11, 034015. [Google Scholar] [CrossRef]
- Ermolli, I.; Matthes, K.; de Wit, T.D.; Krivova, N.A.; Tourpali, K.; Weber, M.; Unruh7, Y.C.; Gray, L.; Langematz, U.; Pilewskie, P.; et al. Recent variability of the solar spectral irradiance and its impact on climate modelling. Atmos. Chem. Phys. 2013, 13, 3945–3977. [Google Scholar] [CrossRef]
- Haigh, J.D. The Sun and the Earth’s climate. Living Rev. Sol. Phys. 2007, 4, 1–64. [Google Scholar] [CrossRef]
- Ineson, S.; Maycock, A.C.; Gray, L.J.; Scaife, A.A.; Dunstone, N.J.; Harder, J.W.; Knight, J.R.; Lockwood, M.; Manners, J.C.; Wood, R.A. Regional climate impacts of a possible future grand solar minimum. Nat. Commun. 2015, 6, 7535. [Google Scholar] [CrossRef] [PubMed]
- Fligge, M.; Solanki, S. The solar spectral irradiance since 1700. Geophys. Res. Lett. 2000, 27, 2157–2160. [Google Scholar] [CrossRef]
- Vieira, L.E.A.; Solanki, S.K.; Krivova, N.A.; Usoskin, I. Evolution of the solar irradiance during the Holocene. Astron. Astrophys. 2011, 531, A6. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Lean, J.; Sheeley Jr, N. Modeling the Sun’s magnetic field and irradiance since 1713. Astrophys. J. 2005, 625, 522. [Google Scholar] [CrossRef]
- Kopp, G.; Lean, J.L. A new, lower value of total solar irradiance: Evidence and climate significance. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Prša, A.; Harmanec, P.; Torres, G.; Mamajek, E.; Asplund, M.; Capitaine, N.; Christensen-Dalsgaard, J.; Depagne, É.; Haberreiter, M.; Hekker, S.; et al. Nominal values for selected solar and planetary quantities: IAU 2015 Resolution B3. Astron. J. 2016, 152, 41. [Google Scholar] [CrossRef]
- Enfield, D.B.; Mestas-Nuñez, A.M.; Trimble, P.J. The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental US. Geophys. Res. Lett. 2001, 28, 2077–2080. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Folland, C.K. A change in the summer atmospheric circulation over the North Atlantic. Clivar Exch. 2002, 25, 52–54. [Google Scholar]
- Sutton, R.T.; Dong, B. Atlantic Ocean influence on a shift in European climate in the 1990s. Nat. Geosci. 2012, 5, 788. [Google Scholar] [CrossRef]
- Fritts, H. Tree Rings and Climate; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Schöne, B.R.; Houk, S.D.; Freyre Castro, A.D.; Fiebig, J.; Oschmann, W.; Kröncke, I.; Dreyer, W.; Gosselck, F. Daily growth rates in shells of Arctica islandica: Assessing sub-seasonal environmental controls on a long-lived bivalve mollusk. Palaios 2005, 20, 78–92. [Google Scholar] [CrossRef]
- Pyrina, M. North Atlantic Ocean Decadal Variability Over the Past Millennium from Climate Model Simulations and Proxy Based Reconstructions. Ph.D. Thesis, University of Hamburg, Hamburg, Germany, 2017. [Google Scholar]
- Hegerl, G.C.; Crowley, T.J.; Baum, S.K.; Kim, K.Y.; Hyde, W.T. Detection of volcanic, solar and greenhouse gas signals in paleo-reconstructions of Northern Hemispheric temperature. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Swingedouw, D.; Terray, L.; Cassou, C.; Voldoire, A.; Salas-Mélia, D.; Servonnat, J. Natural forcing of climate during the last millennium: Fingerprint of solar variability. Clim. Dyn. 2011, 36, 1349–1364. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, J.; Zhang, S. Variations of the global annual mean surface temperature during the past 2000 years: Results from the CESM1. Theor. Appl. Climatol. 2019, 137, 2877–2887. [Google Scholar] [CrossRef]
- Lean, J.L.; Rind, D.H. How natural and anthropogenic influences alter global and regional surface temperatures: 1889 to 2006. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Reynolds, D.J.; Scourse, J.D.; Halloran, P.R.; Nederbragt, A.J.; Wanamaker, A.D.; Butler, P.G.; Richardson, C.A.; Heinemeier, J.; Eiriksson, J.; Knudsen, K.L.; et al. Annually resolved North Atlantic marine climate over the last millennium. Nat. Commun. 2016, 7, 13502. [Google Scholar] [CrossRef]
- Sejrup, H.; Lehman, S.J.; Haflidason, H.; Noone, D.; Muscheler, R.; Berstad, I.M.; Andrews, J.T. Response of Norwegian Sea temperature to solar forcing since 1000 AD. J. Geophys. Res. Ocean. 2010, 115. [Google Scholar] [CrossRef]
- Chen, H.; Ma, H.; Li, X.; Sun, S. Solar influences on spatial patterns of Eurasian winter temperature and atmospheric general circulation anomalies. J. Geophys. Res. Atmos. 2015, 120, 8642–8657. [Google Scholar] [CrossRef]
- Salby, M.L.; Callaghan, P.F. Evidence of the solar cycle in the tropical troposphere. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Sfîcă, L.; Iordache, I.; Voiculescu, M. Solar signal on regional scale: A study of possible solar impact upon Romania’s climate. J. Atmos. Sol. Terr. Phys. 2018, 177, 257–265. [Google Scholar] [CrossRef]
- van Loon, H.; Meehl, G.A.; Arblaster, J.M. A decadal solar effect in the tropics in July–August. J. Atmos. Sol. Terr. Phys. 2004, 66, 1767–1778. [Google Scholar] [CrossRef]
- Jiang, H.; Eiríksson, J.; Schulz, M.; Knudsen, K.-L.; Seidenkrantz, M.-S. Evidence for solar forcing of sea-surface temperature on the North Icelandic Shelf during the late Holocene. Geology 2005, 33, 73–76. [Google Scholar] [CrossRef]
- Moffa-Sánchez, P.; Born, A.; Hall, I.R.; Thornalley, D.J.; Barker, S. Solar forcing of North Atlantic surface temperature and salinity over the past millennium. Nat. Geosci. 2014, 7, 275. [Google Scholar] [CrossRef]
- Lockwood, M. Solar influence on global and regional climates. Surv. Geophys. 2012, 33, 503–534. [Google Scholar] [CrossRef]
- Le, T.; Sjolte, J.; Muscheler, R. The influence of external forcing on subdecadal variability of regional surface temperature in CMIP5 simulations of the last millennium. J. Geophys. Res. Atmos. 2016, 121, 1671–1682. [Google Scholar] [CrossRef]
- Misios, S.; Mitchell, D.M.; Gray, L.J.; Tourpali, K.; Matthes, K.; Hood, L.; Schmidt, H.; Chiodo, G.; Thiéblemont, R.; Rozanov, E.; et al. Solar signals in CMIP-5 simulations: Effects of atmosphere–ocean coupling. Q. J. R. Meteorol. Soc. 2016, 142, 928–941. [Google Scholar] [CrossRef]
- Mitchell, D.; Misios, S.; Gray, L.J.; Tourpali, K.; Matthes, K.; Hood, L.; Schmidt, H.; Chiodo, G.; Thieblemont, R.; Rozanov, E.; et al. Solar signals in CMIP-5 simulations: The stratospheric pathway. Q. J. R. Meteorol. Soc. 2015, 141, 2390–2403. [Google Scholar] [CrossRef]
- Thiéblemont, R.; Matthes, K.; Omrani, N.-E.; Kodera, K.; Hansen, F. Solar forcing synchronizes decadal North Atlantic climate variability. Nat. Commun. 2015, 6, 8268. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Lohmann, K.; Zanchettin, D. Enhanced 20th century heat transfer to the Arctic simulated in context of climate variations over last millennium. Clim. Past 2014, 10, 2201–2213. [Google Scholar] [CrossRef]
- Schmidt, G.A.; Jungclaus, J.H.; Ammann, C.M.; Bard, E.; Braconnot, P.C.; Crowley, T.J.; Delaygue, G.; Joos, F.; Krivova, N.A.; Muscheler, R.; et al. Climate forcing reconstructions for use in PMIP simulations of the last millennium (v1. 0). Geosci. Model Dev. 2011. [Google Scholar] [CrossRef]
- Stevens, B.; Giorgetta, M.; Esch, M.; Mauritsen, T.; Crueger, T.; Rast, S.; Salzmann, M.; Schmidt, H.; Bader, J.; Block, K. Atmospheric component of the MPI-M Earth System Model: ECHAM6. J. Adv. Model. Earth Syst. 2013, 5, 146–172. [Google Scholar] [CrossRef]
- Jungclaus, J.; Fischer, N.; Haak, H.; Lohmann, K.; Marotzke, J.; Matei, D.; Mikolajewicz, U.; Notz, D.; Storch, J. Characteristics of the ocean simulations in the Max Planck Institute Ocean Model (MPIOM) the ocean component of the MPI-Earth system model. J. Adv. Model. Earth Syst. 2013, 5, 422–446. [Google Scholar] [CrossRef]
- Giorgetta, M.A.; Jungclaus, J.; Reick, C.H.; Legutke, S.; Bader, J.; Böttinger, M.; Brovkin, V.; Crueger, T.; Esch, M.; Fieg, K. Climate and carbon cycle changes from 1850 to 2100 in MPI-ESM simulations for the Coupled Model Intercomparison Project phase 5. J. Adv. Model. Earth Syst. 2013, 5, 572–597. [Google Scholar] [CrossRef]
- Kinne, S.; O’Donnel, D.; Stier, P.; Kloster, S.; Zhang, K.; Schmidt, H.; Rast, S.; Giorgetta, M.; Eck, T.F.; Stevens, B. MAC-v1: A new global aerosol climatology for climate studies. J. Adv. Model. Earth Syst. 2013, 5, 704–740. [Google Scholar] [CrossRef]
- Lohmann, K.; Mignot, J.; Langehaug, H.R.; Jungclaus, J.H.; Matei, D.; Otterå, O.H.; Gao, Y.; Mjell, T.L.; Ninnemann, U.S.; Kleiven, H.F. Using simulations of the last millennium to understand climate variability seen in palaeo-observations: Similar variation of Iceland–Scotland overflow strength and Atlantic Multidecadal Oscillation. Clim. Past Discuss. 2015, 11, 203–216. [Google Scholar] [CrossRef]
- Otto-Bliesner, B.L.; Brady, E.C.; Fasullo, J.; Jahn, A.; Landrum, L.; Stevenson, S.; Rosenbloom, N.; Mai, A.; Strand, G. Climate variability and change since 850 CE: An ensemble approach with the community earth system model. Bull. Am. Meteorol. Soc. 2016, 97, 735–754. [Google Scholar] [CrossRef]
- Hurrell, J.W.; Holland, M.M.; Gent, P.R.; Ghan, S.; Kay, J.E.; Kushner, P.J.; Lamarque, J.-F.; Large, W.G.; Lawrence, D.; Lindsay, K. The community earth system model: A framework for collaborative research. Bull. Am. Meteorol. Soc. 2013, 94, 1339–1360. [Google Scholar] [CrossRef]
- Mills, M.J.; Schmidt, A.; Easter, R.; Solomon, S.; Kinnison, D.E.; Ghan, S.J.; Neely III, R.R.; Marsh, D.R.; Conley, A.; Bardeen, C.G. Global volcanic aerosol properties derived from emissions, 1990–2016, 2014, using CESM1 (WACCM). J. Geophys. Res. Atmos. 2016, 121, 2332–2348. [Google Scholar] [CrossRef]
- Iacono, M.J.; Delamere, J.S.; Mlawer, E.J.; Shephard, M.W.; Clough, S.A.; Collins, W.D. Radiative forcing by long-lived greenhouse gases: Calculations with the AER radiative transfer models. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Neale, R.B.; Chen, C.-C.; Gettelman, A.; Lauritzen, P.H.; Park, S.; Williamson, D.L.; Conley, A.J.; Garcia, R.; Kinnison, D.; Lamarque, J.-F. Description of the NCAR Community Atmosphere Model (CAM 5.0); NCAR Technical Note NCAR/TN-486+ STR; NCAR: Boulder, CO, USA, 2010; pp. 1–12. [Google Scholar]
- Chervin, R.M. Interannual variability and seasonal climate predictability. J. Atmos. Sci. 1986, 43, 233–251. [Google Scholar] [CrossRef][Green Version]
- Dütsch, H. Vertical ozone distribution on a global scale. Pure Appl. Geophys. 1978, 116, 511–529. [Google Scholar] [CrossRef]
- Schulzweida, U.; Müller, R.; Kornblüh, L.; Ansorge, C.; Quast, R. CDO–Climate Data Operators–v1. 5.9; Center for Marine and Atmos. Sciences (ZMAW), Max-Planck Institute for Meteorology, University of Hamburg: Hamburg, Germany, 2012; Available online: https://code.zmaw.de/projects/cdo (accessed on 20 January 2019).
- Gray, L.J.; Scaife, A.A.; Mitchell, D.M.; Osprey, S.; Ineson, S.; Hardiman, S.; Butchart, N.; Knight, J.; Sutton, R.; Kodera, K. A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns. J. Geophys. Res. Atmos. 2013, 118, 13405–413420. [Google Scholar] [CrossRef]
- Ebisuzaki, W. A method to estimate the statistical significance of a correlation when the data are serially correlated. J. Clim. 1997, 10, 2147–2153. [Google Scholar] [CrossRef]
- Schreiber, T.; Schmitz, A. Improved surrogate data for nonlinearity tests. Phys. Rev. Lett. 1996, 77, 635. [Google Scholar] [CrossRef] [PubMed]
- Maher, N.; Matei, D.; Milinski, S.; Marotzke, J. ENSO change in climate projections: Forced response or internal variability? Geophys. Res. Lett. 2018, 45, 11,390–11,398. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M.; Matthes, K.; Sassi, F.; van Loon, H. Amplifying the Pacific climate system response to a small 11-year solar cycle forcing. Science 2009, 325, 1114–1118. [Google Scholar] [CrossRef]
- Gray, L.J.; Beer, J.; Geller, M.; Haigh, J.D.; Lockwood, M.; Matthes, K.; Cubasch, U.; Fleitmann, D.; Harrison, G.; Hood, L. Solar influences on climate. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Kodera, K.; Kuroda, Y. Dynamical response to the solar cycle. J. Geophys. Res. Atmos. 2002, 107. [Google Scholar] [CrossRef]
- Dima, M.; Voiculescu, M. Global patterns of solar influence on high cloud cover. Clim. Dyn. 2016, 47, 667–678. [Google Scholar] [CrossRef]
- Meehl, G.A.; Arblaster, J.M.; Branstator, G.; Van Loon, H. A coupled air–sea response mechanism to solar forcing in the Pacific region. J. Clim. 2008, 21, 2883–2897. [Google Scholar] [CrossRef]
- White, W.B.; Lean, J.; Cayan, D.R.; Dettinger, M.D. Response of global upper ocean temperature to changing solar irradiance. J. Geophys. Res. Oceans 1997, 102, 3255–3266. [Google Scholar] [CrossRef]
- Jin, C.; Wang, B.; Liu, J.; Ning, L.; Yan, M. Decadal variability of northern Asian winter monsoon shaped by the 11-year solar cycle. Clim. Dyn. 2019, 53, 6559–6568. [Google Scholar] [CrossRef]
- Ammann, C.M.; Joos, F.; Schimel, D.S.; Otto-Bliesner, B.L.; Tomas, R.A. Solar influence on climate during the past millennium: Results from transient simulations with the NCAR Climate System Model. Proc. Natl. Acad. Sci. USA 2007, 104, 3713–3718. [Google Scholar] [CrossRef]
- Gray, L.; Woollings, T.; Andrews, M.; Knight, J. Eleven-year solar cycle signal in the NAO and Atlantic/European blocking. Q. J. R. Meteorol. Soc. 2016, 142, 1890–1903. [Google Scholar] [CrossRef]
- Scaife, A.A.; Ineson, S.; Knight, J.R.; Gray, L.; Kodera, K.; Smith, D.M. A mechanism for lagged North Atlantic climate response to solar variability. Geophys. Res. Lett. 2013, 40, 434–439. [Google Scholar] [CrossRef]
- Yukimoto, S.; Kodera, K.; Thiéblemont, R. Delayed North Atlantic Response to Solar Forcing of the Stratospheric Polar Vortex. SOLA 2017, 13, 53–58. [Google Scholar] [CrossRef]
- Turner, T.E.; Swindles, G.T.; Charman, D.J.; Langdon, P.G.; Morris, P.J.; Booth, R.K.; Parry, L.E.; Nichols, J.E. Solar cycles or random processes? Evaluating solar variability in Holocene climate records. Sci. Rep. 2016, 6, 23961. [Google Scholar] [CrossRef] [PubMed]
- Blaauw, M.; Van Geel, B.; Van Der Plicht, J. Solar forcing of climatic change during the mid-Holocene: Indications from raised bogs in The Netherlands. Holocene 2004, 14, 35–44. [Google Scholar] [CrossRef]
- Nichols, J.E.; Huang, Y. Hydroclimate of the northeastern United States is highly sensitive to solar forcing. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Swindles, G.T.; Patterson, R.T.; Roe, H.M.; Galloway, J.M. Evaluating periodicities in peat-based climate proxy records. Quat. Sci. Rev. 2012, 41, 94–103. [Google Scholar] [CrossRef]
- Harrison, S.P.; Bartlein, P.J.; Prentice, I.C. What have we learnt from palaeoclimate simulations? J. Quat. Sci. 2016, 31, 363–385. [Google Scholar] [CrossRef]
- Harrison, S.P.; Bartlein, P.; Izumi, K.; Li, G.; Annan, J.; Hargreaves, J.; Braconnot, P.; Kageyama, M. Evaluation of CMIP5 palaeo-simulations to improve climate projections. Nat. Clim. Chang. 2015, 5, 735–743. [Google Scholar] [CrossRef]
- Ludwig, P.; Gómez-Navarro, J.J.; Pinto, J.G.; Raible, C.C.; Wagner, S.; Zorita, E. Perspectives of regional paleoclimate modeling. Ann. N. Y. Acad. Sci. 2019, 1436, 54. [Google Scholar] [CrossRef] [PubMed]
- Lovejoy, S.; Varotsos, C. Scaling regimes and linear/nonlinear responses of last millennium climate to volcanic and solar forcings. Earth Syst. Dyn. 2016, 7, 133–150. [Google Scholar] [CrossRef]
- Adolphi, F.; Muscheler, R.; Svensson, A.; Aldahan, A.; Possnert, G.; Beer, J.; Sjolte, J.; Björck, S.; Matthes, K.; Thiéblemont, R. Persistent link between solar activity and Greenland climate during the Last Glacial Maximum. Nat. Geosci. 2014, 7, 662–666. [Google Scholar] [CrossRef]
- Saarni, S.; Muschitiello, F.; Weege, S.; Brauer, A.; Saarinen, T. A late Holocene record of solar-forced atmospheric blocking variability over Northern Europe inferred from varved lake sediments of Lake Kuninkaisenlampi. Quat. Sci. Rev. 2016, 154, 100–110. [Google Scholar] [CrossRef]
- Davini, P.; Cagnazzo, C.; Neale, R.; Tribbia, J. Coupling between Greenland blocking and the North Atlantic Oscillation pattern. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Woollings, T.; Lockwood, M.; Masato, G.; Bell, C.; Gray, L. Enhanced signature of solar variability in Eurasian winter climate. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Barriopedro, D.; García-Herrera, R.; Huth, R. Solar modulation of Northern Hemisphere winter blocking. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Ineson, S.; Scaife, A.A.; Knight, J.R.; Manners, J.C.; Dunstone, N.J.; Gray, L.J.; Haigh, J.D. Solar forcing of winter climate variability in the Northern Hemisphere. Nat. Geosci. 2011, 4, 753–757. [Google Scholar] [CrossRef]
- Xoplaki, E.; Trigo, R.; García-Herrera, R.; Barriopedro, D.; D’Andrea, F.; Fischer, E.; Gimeno, L.; Gouveia, C.; Hernández, E.; Kuglitsch, F. The Climate of the Mediterranean Region; Elsevier: Amsterdam, The Netherlands, 2012; Chapter 6; pp. 347–417. [Google Scholar]
- Strestik, J. Solar Variability as an Input to the Earth’s Environment. In Proceedings of the International Solar Cycle Studies (ISCS) Symposium 2003, Tatranská Lomnica, Slovakia, 23–28 June 2003; pp. 393–396. [Google Scholar]
- Zambri, B.; Robock, A. Winter warming and summer monsoon reduction after volcanic eruptions in Coupled Model Intercomparison Project 5 (CMIP5) simulations. Geophys. Res. Lett. 2016, 43, 10920–10928. [Google Scholar] [CrossRef]
- Cai, M.; Tung, K.-K. Robustness of dynamical feedbacks from radiative forcing: 2% solar versus 2× CO2 experiments in an idealized GCM. J. Atmos. Sci. 2012, 69, 2256–2271. [Google Scholar] [CrossRef]
- Misios, S.; Schmidt, H. The role of the oceans in shaping the tropospheric response to the 11 year solar cycle. Geophys. Res. Lett. 2013, 40, 6373–6377. [Google Scholar] [CrossRef]
- Ortega, P.; Lehner, F.; Swingedouw, D.; Masson-Delmotte, V.; Raible, C.C.; Casado, M.; Yiou, P. A model-tested North Atlantic Oscillation reconstruction for the past millennium. Nature 2015, 523, 71–74. [Google Scholar] [CrossRef]
- Jerez, S.; Montavez, J.P.; Jimenez-Guerrero, P.; Gomez-Navarro, J.J.; Lorente-Plazas, R.; Zorita, E. A multi-physics ensemble of present-day climate regional simulations over the Iberian Peninsula. Clim. Dyn. 2013, 40, 3023–3046. [Google Scholar] [CrossRef]


| Model | MPI-ESM-P | CESM1-CAM5 |
|---|---|---|
| Institute (country) | MPI-M (Germany) | NSF-DOE-NCAR (USA) |
| High Top (H)—Low Top (L) classification | H | L |
| Ozone Implementation | Prescribed (but scales with the strength of the TSI variation) | Semi-Offline |
| Number of simulations/ simulation name, and forcings used for the solar-only forcing experiments | 1/MPI-R1 Solar forcing [18], Orbital forcing parameters and well mixed-greenhouse gases [46] | 4/E1, E2, E3, E4 Solar forcing [18], Orbital forcing parameters and well mixed-greenhouse gases [46] |
| Years with TSI > 2.2 SD | Years with TSI < –1.4 SD |
|---|---|
| 857, 858, 859, 868, 869, 870, 923, 924, 925, 934, 935, 936, 945, 946, 947, 957, 1100, 1133, 1143, 1144, 1145, 1606, 1770, 1771, 1772 | 1442, 1443, 1444, 1445, 1449, 1450, 1451, 1680, 1681, 1682, 1683, 1684, 1685, 1686, 1687, 1691, 1692, 1693, 1694, 1695 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pyrina, M.; Moreno-Chamarro, E.; Wagner, S.; Zorita, E. Surface and Tropospheric Response of North Atlantic Summer Climate from Paleoclimate Simulations of the Past Millennium. Atmosphere 2021, 12, 568. https://doi.org/10.3390/atmos12050568
Pyrina M, Moreno-Chamarro E, Wagner S, Zorita E. Surface and Tropospheric Response of North Atlantic Summer Climate from Paleoclimate Simulations of the Past Millennium. Atmosphere. 2021; 12(5):568. https://doi.org/10.3390/atmos12050568
Chicago/Turabian StylePyrina, Maria, Eduardo Moreno-Chamarro, Sebastian Wagner, and Eduardo Zorita. 2021. "Surface and Tropospheric Response of North Atlantic Summer Climate from Paleoclimate Simulations of the Past Millennium" Atmosphere 12, no. 5: 568. https://doi.org/10.3390/atmos12050568
APA StylePyrina, M., Moreno-Chamarro, E., Wagner, S., & Zorita, E. (2021). Surface and Tropospheric Response of North Atlantic Summer Climate from Paleoclimate Simulations of the Past Millennium. Atmosphere, 12(5), 568. https://doi.org/10.3390/atmos12050568






