Abstract
Free energy of water aerosol plasma was calculated using the Debye–Hückel method. It was established that free energies of droplets, ions and simultaneously of all charged particles had local minima (metastable states) at certain concentrations and charges of particles. The calculation results were confirmed by experimental data taken from the literature on a droplet cluster in water vapor and droplet structures in water fog. The possible connection of metastable states with the phenomenon of drop coalescence and rain formation in real clouds, as well as with the generation of stable spatially arranged drop structures, has been indicated.
1. Introduction
It is known that water droplets of up to 10 µm in diameter grow in clouds due to diffusion and water vapor condensation. Droplets of more than 50 µm increase in size mainly due to gravitational coalescence. The mechanism of fast growth of droplets in the size interval between 10 and 50 µm is unclear. Modern theories suggest from hours to tens of hours for this process, when in reality, it takes from 15 to 20 min [1,2,3]. In the literature, this problem is called “condensation-coalescence bottleneck in rain formation”.
On the way to solving this problem, the possibilities of accelerating coalescence due to electrostatic interactions of droplets with each other and with an external electric field have been investigated [4,5,6,7,8]. Another area of research has been the study of the turbulence-induced increase in the number of collisions of drops, leading to the acceleration of coalescence [1,9,10,11,12,13,14]. However, in recent years, experimental data have appeared in the literature suggesting that water droplets in aerosols tend to form stable, spatially ordered structures [15,16,17,18]. Ordered structures can hinder the development of turbulence and turbulence-induced acceleration of coalescence. In ordered structures, the inter-droplet distance is many times greater than the droplet size. Examples of these structures are droplet clusters in water vapor [15,16] and droplet chains (and other structures of 10 droplets or more) in water fog [17,18].
The reasons for the formation of ordered droplet structures are currently not fully understood. In [19], the possibility of the formation of ordered structures from electrically charged water droplets was considered. The electric charge of droplets always exists due to the processes of trapping gas ions by droplets and electrification during their evaporation/condensation. In [19], it was analytically shown that in an ideal plasma consisting of charged water droplets and light ions, which compensated for the droplet charge, the formation of an ordered state of droplets was possible. The possibility of electrocoalescence of droplets inside droplet structures was also hypothesized. However, the detailed mechanism of coalescence remained unclear. In this work, on the basis of an equilibrium nonideal model of a droplet-ionic plasma, the free energies of charged droplets and ions were numerically calculated and analyzed for the presence of extrema. It was shown that the free energies of charged particles had local minima; that is, the plasma could be in a metastable state. The boundaries of plasma existence in this state were determined. It was shown that the calculation results correlated with the experimental data on a droplet cluster in vapor and droplet structures in fog. The regions of plasma parameters were shown, in which the droplets tended to either coalesce or form stable spatially ordered structures.
2. Problem Statement and Solving Procedure
Water droplets in aerosols are charged during the selective adsorption of air ions on the droplet surfaces [8] as well as in the frequent processes of evaporation and condensation of water molecules, protons and hydroxide ions on the droplet surface [20]. Depending on the prevailing process, the water droplets can be charged negatively or positively. Vapor protons and hydroxide ions can associate in complexes with several water molecules and represent light charge carriers. These carriers can recombine with each other, forming electrically neutral water molecules. On the whole, the droplet-ionic plasma of aerosols is an open, nonequilibrium system. In it, the energy distribution of charge carriers may significantly differ from the Boltzmann distribution typical for equilibrium systems. Nevertheless, it is the equilibrium idea that lies at the basis of studying various plasmas.
In this study, we supposed that the droplet-ionic plasma was in a state of equilibrium and consisted of charged particles of three sorts: water droplets and light-negative and positive ions. The distribution of particles by energies was described by Boltzmann statistics, in general, with individual equilibrium temperatures for each sort. We supposed that particle collisions were not frequent so that the particle gas in the volume under study could be seen as ideal if particles were electrically neutral. For this ideality, it was required that the particle’s free path be less than the lateral size of this volume. Plasma nonideality was caused by electrostatic interaction of particles. Radius, concentration and temperature of water droplets with a charge in the units of elementary charge Z >> 1 (for definitiveness, the charge was negative; one could just as well choose a positive charge) were marked as R−z, N−z, T−z; for light positive ions, respectively—R+i, N+i, T+i;, and for negative ions—R−i, N−i, T−i. It will be shown below that the proposed equilibrium model leads to results coherent with the experiment. The experiment, and only it, can serve as a justification for the used model.
The electrical neutrality equation in the plasma model selected looks as follows:
and in calculation for one droplet:
where 1 is the droplet charge, 2 is the negative ions’ charge, 3 is the positive ions ‘charge and χ = N−i/N+i is the share of the negative ions’ charge from the positive charge.
We calculated the free energy of the plasma following the Debye–Hückel calculation scheme [21], which was also described in detail by Landau and Lifshitz [22]. The free energy of a plasma includes the free energy of an ideal gas and the electrostatic correction to it. To determine the electrostatic correction, we used the Poisson–Boltzmann equation for the self-consistent potential of a charged particle: for example, a water droplet, in an electrically neutral spherical volume of plasma. We assumed that the radius of the spherical volume was many times greater than the Debye radius, and the spherical volume contained many particles of all kinds. Having determined the charged droplet potential in plasma, we subtracted therefrom the purely Coulomb potential of the droplet itself. Thus, we found the potential generated by plasma on the droplet surface. Using this potential, we calculated the electrostatic correction to the free energy. After that, we calculated the complete free energy of a droplet and studied it for availability of a minimum. Similarly, we studied, for extreme values, the free energies of the positive and negative ions as well as the complete free energy of all the plasma charge carriers.
2.1. Free Energy of a Charged Droplet
Figure 1 shows an electrically quasi-neutral, spherical volume with radius d for calculation of potential of the central charged droplet. The complete charge of the plasma inside the d-sphere is considered to be equal to zero. The number of droplets inside the sphere, including the central droplet, are marked as Q (Q >> 1), the number of positive ions is ZQ(1 − χ)−1 and the number of negative ions is χZQ(1 − χ)−1. The minimum value of radius d with the fixed value of Q is d0 = R−z(Q/a)1/3. This is reached when the droplets are packed tightly. a is the factor of space filling within a ball of the same radius. For example, for a face-centered cubic arrangement, a = 0.74. We considered all charge carriers, except the central particle, to be equally distributed (spread) inside the d-sphere, as well as their electrical charge. To calculate the potential of a charged drop, we used the equations of a continuous medium.
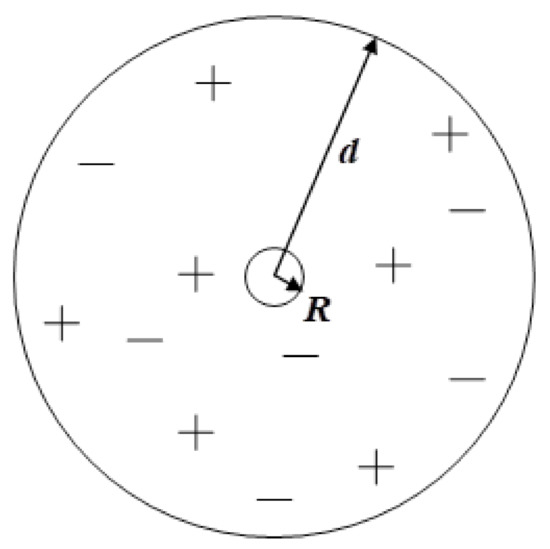
Figure 1.
Spherical, electrically neutral volume with radius d for calculation of potential of the central charged particle with radius R.
It should be noted that the time of the settled life of the droplet in the center of d-volume is determined by the period of droplet-acoustic oscillations (to be more exact, not in d-volume, but in the sphere of the Debye radius). This time exceeds the period of ion-acoustic oscillations. Hence, in the Poisson–Boltzmann equation, correlation of all ions and charged droplets has to be taken into account. In this study, the particles’ correlation means the process of redistribution of charged particles’ concentration in space under influence of the central particle φ−z. The correlation will be accounted for if the functions of ions and charged droplet distribution are represented in the form of the Boltzmann distribution, respectively , , . Here , , , is the free volume, k is the Boltzmann constant and e is the elementary charge.
The Poisson–Boltzmann equation for the potential of a charged droplet and boundary conditions for its derivative looks as follows:
where Δ is a Laplacian in spherical coordinates and ε0 is an electrical constant.
The first boundary condition (2a) describes the intensity of the electric field on the surface of a charged droplet. The second boundary condition (2b) describes field intensity at the surface of the d-volume equal to zero due to electrical neutrality of the volume. Note that boundary conditions (2) determine the value of potential to the accuracy of the constant summand. Further, in the formulae for calculation of the free energy, this constant summand of potential will have to be subtracted; i.e., instead of φ−z(r), we will use φ−z(r) − φ−z(d).
The problem was solved numerically. For this, the Poisson–Boltzmann equation was brought to an equivalent system of two ordinary differential equations of the first order. The system was solved by the fourth-order Runge–Kutta method with the fixed integration step, implemented in the ‘rkfixed’ function from the Mathcad 11 software [23]. The solution required the initial conditions for the potential and its derivative at one of the boundaries but not the values of the derivative at two various boundaries, as in our case (2). For this reason, the shooting method was used. At the boundary r = R−z the potential derivative was set in accordance with boundary condition (2a), and the value of the potential at this boundary was selected so that at the other boundary r = d the electric field assumed a value determined by boundary condition (2b). Note that the equation system contains areas of quick and slow changing solutions. Hence, it was convenient to shift to variable steps of integration over r. For this purpose, in equation (1), the variable r = exp(y) was replaced and then the equation was solved using the Runge-Kutta method with fixed steps of integration over variable y. The function ‘rkfixed’ would return the differential equations system solution value matrix set at the interval [ln(R−z),ln(d)]. The number of the result matrix lines was selected as 104.
From the potential found at point r = R−z we subtracted the purely Coulomb potential of the charged droplet and thus determined the potential created by plasma on the surface of the droplet φP−z:
The electrical (correlational) energy of the droplet was equal to . The free energy of the particle F−z was calculated using formula
where the first summand describes the free energy of mechanical movement of the droplet in ideal gas, and the second summand describes the electrical correlational adjustment to the free energy in accordance with the known thermodynamic formula [22].
2.2. Free Energy of Positive and Negative Ions
In order to determine the free energy of a positive ion, the spherical volume was used as in Figure 1, with an ion located in the center thereof. The time of settled life of an ion in the center of a sphere is comparable with the period of ion-acoustic oscillations. Hence, the ion’s correlation has to be considered, and the correlation of charged droplets should not be considered because there is not enough time for droplets’ correlation due to their massive size. Therefore, the carriers’ concentration will be recorded as follows [22]:
, , where , , , .
The Poisson–Boltzmann equation and boundary conditions for ion potential φ+i look similar to (1), (2).
In order to determine the free energy of a negative ion, the spherical volume, Figure 1, was also suitable, with a negative ion located in the center thereof.
Carriers concentrations are represented as follows , , , where , , , .
The free energy of all plasma particles as calculated for a single charged droplet was calculated as follows, pursuant to the electrical neutrality equation:
3. Results and Discussion
Water aerosols with charged water droplets and ions that compensate for droplet charge under natural conditions are isothermal plasmas with temperatures often close to standard ones. At such temperatures, the Boltzmann distribution function, for example, for positive ions in the field of a central positive ion, works quite satisfactorily, and for negative ions in the field of a central positive ion at small distances from it, it ceases to hold, since the exponent factor in the distribution function appears to be much greater than one . The last inequality is the condition for the strong nonideality of the plasma with respect to ions. In such cases, in order to obtain acceptable solutions, “kitchen” methods are used: for example, cutting off the interaction potential at small inter-particle distances [24]. In order to obtain a probable solution at standard temperature we used another method. We assumed the negative ions’ temperature, formally, to be very high, and the temperature of positive ions and droplets was considered to be close to standard. At the same time, the exponent factor in the negative ions distribution function decreased, and the Boltzmann formula was quite efficient. We obtained solutions by gradually decreasing the negative ion’s temperature until the solution started diverging. Obtaining a diverging solution meant that the Boltzmann distribution ceased to be met. We analytically continued the solution results at high temperatures in the low temperature area and thus found the solution of interest at the standard temperature of negative ions. This was the essence of the formal mathematical method. Note that the application of this method to another object—to a dusty plasma—no longer becomes formal, but has a physical meaning because the electron temperature can significantly exceed the temperature of dust particles and ions. Figure 2 shows functions of free energy of a charged droplet and positive and negative ions and the free energy of all charge carriers to the distance between droplet surfaces . The free energy of a negative ion (at the formal temperature T−i = 5000 K) does not have local minima and monotonously increases as the distance between droplets surfaces δ decreases. The free energy of a positive ion passes through the maximum point and further decreases with the distance δ decrease until zero. The free energy of a charged droplet, as well as the free energy of simultaneously all charge carriers, passes the maximum point first and then the local minimum point as the distance δ decreases. The area of distances with a positive slope of the graph of free energy of the positive ion, the droplet and simultaneously all particles is the attraction area, correspondingly, of single particles and plasma on the whole. Therefore, in droplet-ionic plasma, metastable states can occur corresponding to the energetically favorable fixed positions of droplets. Such favorable states are reached by means of correlation of charge carriers in plasma. Metastable states of droplets and positive ions, as well as plasma on the whole, can be reached at optimum plasma parameters provided by external technical devices.
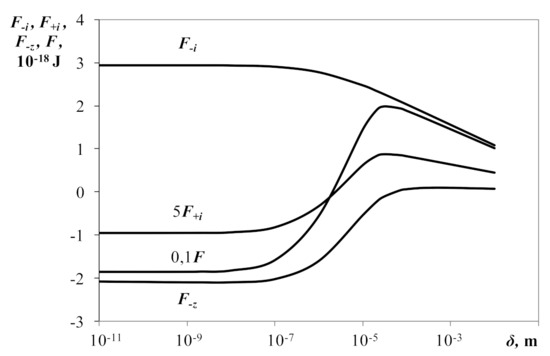
Figure 2.
Free energies of charged droplet F−z, positive ion F+i, negative ion F−i and free energy of all charge carriers F subject to the distance between surfaces of the nearest droplets δ. T−i = 5000 K, T−z = T+i = 300 K, Z = 100, R−z = 10−6 m, R-i = R+i = 10−10 m, χ = 0.01.
Figure 3 shows charts of distances δmax and δmin between surfaces of charged droplets at points of maximum and minimum free energies of a droplet (curves 1′, 1), ion (2′, 2) and simultaneously all charge carriers (3′, 3), subject to temperature T−i. The figure shows that the width of the droplet’s attraction area on the scale δ (between curves 1′ and 1) did not depend on temperature T−i. In addition, the attraction area of positive ions (between curves 2′ and 2) and of all charge carriers (between curves 3′ and 3) existed only at temperatures T−i below 104 K (when the charge value selected is Z = 500). Note that when the negative ion’s temperature is T−i < 4000 K, curves 2′ and 3′ sharply turned upward, tending to infinite values. This meant that at such temperatures, the Boltzmann distribution ceased to operate. Sharp aspirations of the curves upward are not shown in Figure 3. Instead, curves 2′ and 3′ were analytically extended to low temperatures based on behavior at high temperatures. It is obvious from the figure that the position of these curves weakly depended on the temperature in temperature range T−i < 5000 K.
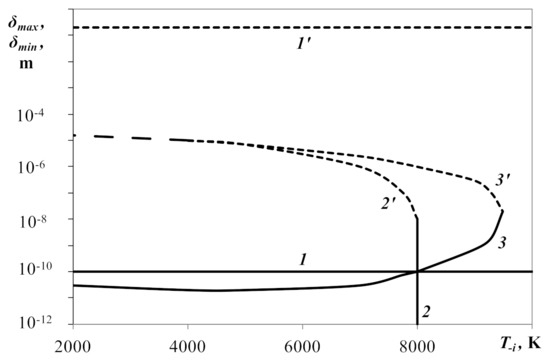
Figure 3.
Distances between surfaces of charged droplets δmax and δmin, respectively, at points of maximum and minimum free energies of the droplet (curves 1′, 1), positive ion (2′, 2) and all charge carriers (3′, 3), subject to temperature T−i. Z = 500, T−z = T+i = 300 K, R−z = 10−6 m, R−i = R+i = 10−10 m, χ = 0.01.
Checking the dependence of δmax and δmin on the value of χ showed that the boundaries of the regions of attraction for droplets, positive ions and plasma on the whole remained constant, at least when χ varied in the interval χ = [10−3, 10−1].
Figure 4 shows charts of distances δmax and δmin for free energies of a droplet (curves 1′, 1), a positive ion (2′, 2) and simultaneously all charge carriers (3′, 3), subject to the value of charge Z of the droplet when its radius is 10−6 m. Curves (4′, 4), (5′, 5), (6′, 6) are the same curves for droplet radius R−z = 10−8 m. According to the figure, the droplet’s attraction area exists when the charge is Z > 1. The width of the attraction area increases on scale δ with an increase of Z. The attraction areas of the positive ions, and simultaneously all charge carriers, exist with any value of charge Z, starting from one and greater. They also expand with an increase of Z.
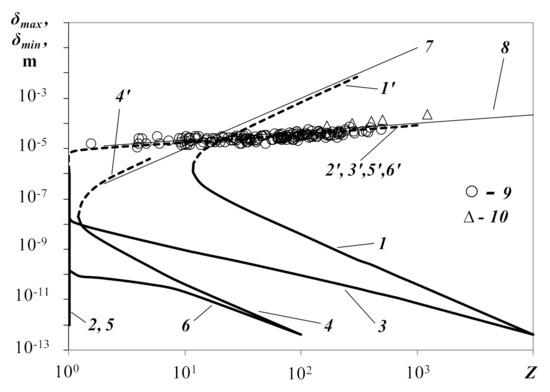
Figure 4.
Distances between droplet surfaces δmax and δmin, respectively, at points of maximum and minimum free energies of a droplet (curves 1′, 1), positive ion (2′, 2) and all charge carriers (3′, 3), subject to droplet charge Z with its radius R−z = 10−6 m. Curves (4′, 4), (5′, 5) and (6′, 6) are similar curves for droplet radius R−z = 10−8 m. T−i = 5000 K, T−z = T+i = 300 K, χ = 0.01. 7, 8 are approximation curves, 9 are data on droplet structures in water fog and 10 are experimental data on droplet clusters in water vapor.
Curves 1′ and 2′ of Figure 4 satisfactorily approximate with analytical functions 7 and 8, obtained from the conditions of equality of potential and kinetic energy, respectively, of a charged droplet and ion. For a droplet, the condition is (Lz is the Debye radius, defined by the parameters of all charge carriers (Lz >> R−z)) for an ion (Li is the Debye radius, determined by the parameters of ions (Li >> R+i)). From the first condition, we obtain the analytical function , which is shown in Figure 4, curve 7. Coincidence with curve 1′, as we mentioned, is satisfactory. On this curve, the inter-droplet distance is equal to approximately one Debye radius Lz, δ ≈ Lz. The second condition leads to the analytical function , which passes significantly lower than curve 2′. For coincidence with curve 2′, we need to assume that a positive ion in plasma increases concentration of negative ions near its surface 106-107 times with its field (for this, electrical potential of about 5 V is enough, which is obtained at the distance from the ion’s surface equal to the ion’s radius). Next, we obtain function (curve 8), which satisfactorily approximates curve 2′. Curves 7 and 8 separate the area of plasma ideality from the area of nonideality. Below curve 7, the plasma is nonideal for charged droplets, and below curve 8, it is nonideal for ions.
The special behavior of curves 1′ and 4′ in Figure 4 has to be noted. When we attempted to obtain solutions at Z > 30 and Z > 5 for curves 1′ and 4′, respectively, these curves sharply turned upward, tending to infinite values. This behavior of the curves was also explained by the fact that the Boltzmann distribution, in this case for positive ions in the field of charged droplets, ceased to operate. The noted tendency of the curves toward infinity was considered unreliable and was not displayed graphically.
We will note once more that the curves in Figure 4 were calculated with a temperature of negative ions of T−i = 5000 K. We suppose that these curves are also true for a temperature of negative ions which is close to standard. This statement is based on the fact that the position of curves 2′ and 3′ in Figure 3 weakly depends on the temperature at T−i < 5000 K.
The calculations we performed showed the possibility of the existence of metastable states in the equilibrium model of droplet-ionic plasma. The metastable state is achieved at a local minimum of the free plasma energy. Let us compare the obtained theoretical results with the experimental data on water aerosols at temperatures close to standard: The experimental data, for comparison, were taken from reference sources on droplet clusters [25] occurring in vapor over the surface of heated water and droplet structures which were spontaneously generated in free water fog [26,27]. Data on droplet radius, charge, and inter-droplet distance within regular droplet structures were extracted from the sources.
The experimental data are depicted by markers 9 (5 values) and 10 (167 values) in Figure 4. The figure shows that all experimental points fall on curve 3′, or in the immediate vicinity of it. Recall that curve 3′ is the upper boundary of the region of confinement of all plasma particles simultaneously. In other words, it corresponds to a local maximum of free energy. The position of curve 3′ does not depend on the radius of the droplets (when comparing curves 3′ and 6′, they coincide).
Satisfactory coincidence of the theoretical curve 3′ with the experimental values can serve as confirmation of the acceptability of the chosen equilibrium plasma model for describing the states of real plasma of water aerosols. The results obtained can serve as an incentive to analyze the possible mechanisms of the emergence of spatially ordered droplet structures in water aerosols. According to the model we have considered, the existence of such structures can be a consequence of the tendency of the plasma to a metastable state.
Why did the experimental points fall on curve 3′ and not on curve 3, which corresponded to the minimum values of free energy (the lower boundary of the plasma confinement region)? Possibly, this was due to the problem of removal of heat released during the compression of the plasma during the transition from curve 3′ to curve 3. The increase in temperature during compression can push the plasma out of the confinement region, and the plasma will expand again. The problem of an increase in temperature, perhaps, does not arise when single droplets approach each other, and they are able to reach the state lying on curve 3.
With the help of the theoretical charts of Figure 4, a physical explanation for droplet coalescence in water aerosols and clouds can be proposed. In reality, we assumed that coalescence was possible for distances between droplet surfaces less than 10−10 m when inter-atom forces came in action. For droplets of small radius R−z = 10−8 m, the lower boundary of the plasma confinement area (curve 6) was located on the δ scale below the value of 10−10 m at any Z ≥ 1. That is why small droplets could coalesce. For droplets of greater radius R−z = 10−6 m, coalescence was impossible when the particle charge value was Z < 102 due to great inter-droplet distance according to the position of the lower boundary of the confinement area (curve 3). For even larger droplets, for example, R−z = 10−4 m, coalescence was impossible at higher charge values Z < 105–106. Thus, large droplets without a very large charge did not coalesce and could form spatially arranged structures because of electrostatic attraction between droplets in plasma. Small droplets are prone to coalescence.
4. Conclusions
The results obtained in this study show the possibility of the existence of metastable states of charged particles, ions and simultaneously all charge carriers in the equilibrium model of plasma of water aerosols. These states are reached through the correlation of charge carriers located between charged droplets.
The possibility of striving for a metastable state of a real droplet-ionic plasma is confirmed by the experimental data taken from reference literature on droplet clusters in water vapor and droplet structures in fog. The possible relationship of metastable states to the phenomenon of droplet coalescence was noted.
The conclusions made in this study can be useful for further advanced understanding of processes flowing in clouds and fog, and in particular, in solution of the “condensation-coalescence bottleneck in rain formation” problem. The study results can also be useful in studying the mechanisms of the formation of dust and colloidal crystals.
Author Contributions
Investigation, A.V.S., V.A.D. and A.A.Y. All authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
The work has been performed under the state task of the Tyumen Science Centre of the Siberian Branch of the Russian Academy of Sciences IX.135.2.4.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interests.
References
- Khain, A.; Pinsky, M.; Elperin, T.; Kleeorin, N.; Rogachevskii, I.; Kostinski, A. Critical comments to results of investigations of drop collisions in turbulent clouds. A review. Atmos. Res. 2007, 86, 1–20. [Google Scholar] [CrossRef]
- Devenish, B.J.; Bartello, P.; Brenguier, J.L.; Collins, L.R. Droplet growth in warm turbulent clouds. Q. J. R. Meteorol. Soc. 2012, 138, 1401–1429. [Google Scholar] [CrossRef]
- Grabowski, W.W.; Wang, L.P. Growth of cloud droplets in a turbulent environment. Annu. Rev. Fluid Mech. 2013, 45, 293–324. [Google Scholar] [CrossRef]
- Fuchs, N.A. On the stationary charge distribution on aerosol particles in a bipolar ionic atmosphere. Geofis. Pura Appl. 1963, 51, 185–193. [Google Scholar] [CrossRef]
- Gunn, R. The statistical electrification of aerosols by ionic diffusion. J. Colloid Sci. 1955, 10, 107–119. [Google Scholar] [CrossRef]
- Gatti, M.; Kortshagen, U. Analytical model of particle charging in plasmas over a wide range of collisionality. Phys. Rev. E 2008, 78, 046402. [Google Scholar] [CrossRef]
- Gopalakrishnan, R.; Hogan, C.J. Coulomb-influenced collisions in aerosols and dusty plasmas. Phys. Rev. E 2012, 85, 026410. [Google Scholar] [CrossRef]
- Ivlev, L.S.; Dovgalyuk, Y.A. Physics of Atmospheric Aerosol Systems; SPb. NIIH of St. Petersburg State University: Saint-Petersburg, Russia, 1999. [Google Scholar]
- Wang, L.P.; Orlando, A.; Rosa, B.; Grabowski, W.W. Turbulent collision efficiency of heavy particles relevant to cloud droplets. New J. Phys. 2008, 10, 075013. [Google Scholar] [CrossRef]
- Elperin, T.; Kleeorin, N.; Liberman, M.A.; L’vov, V.S.; Rogachevskii, I. Clustering of aerosols in atmospheric turbulent flow. Environ. Fluid Mech. 2007, 7, 173–193. [Google Scholar] [CrossRef][Green Version]
- Pinsky, M.B.; Khain, A.P. Collisions of small drops in a turbulent flow. Part II: Effects of flow accelerations. J. Atmos. Sci. 2004, 61, 1926–1939. [Google Scholar] [CrossRef]
- Ghosh, S.; Davila, J.; Hunt, J.C.R.; Srdic, A.; Fernando, H.J.S.; Jonas, P. How turbulence enhances coalescence of settling particles with applications to rain in clouds. Proc. R. Soc. Lond. A 2005, 461, 3059–3088. [Google Scholar] [CrossRef]
- Elperin, T.; Kleeorin, N.; Liberman, M.; Rogachevskii, I. Tangling clustering instability for small particles in temperature stratified turbulence. Phys. Fluids 2013, 25, 085104. [Google Scholar] [CrossRef]
- Eidelman, A.; Elperin, T.; Kleeorin, N.; Melnik, B.; Rogachevskii, I. Tangling clustering of inertial particles in stably stratified turbulence. Phys. Rev. E 2010, 81, 056313. [Google Scholar] [CrossRef]
- Fedorets, A.A. Droplet claster. JETP Lett. 2004, 79, 372–377. [Google Scholar] [CrossRef]
- Shavlov, A.V.; Dzhumandzhi, V.A. Geometrical parameters of a water dropwise cluster. J. Exp. Theor. Phys. 2012, 114, 253–258. [Google Scholar] [CrossRef]
- Shavlov, A.V.; Sokolov, I.V.; Romanyuk, S.N.; Dzhumandzhi, V.A. Dropwise chains as the elements of water fog spatial structure. Phys. Lett. A 2013, 377, 1740–1746. [Google Scholar] [CrossRef]
- Shavlov, A.V.; Sokolov, I.V.; Khazan, V.L.; Romanyuk, S.N. Viscosity of water fog. Phys. Scr. 2014, 89, 125402. [Google Scholar] [CrossRef]
- Shavlov, A.V.; Dzhumandzhi, V.A. Metastable states and coalescence of charged water drops inside clouds and fog. J. Aerosol Sci. 2016, 91, 54–61. [Google Scholar] [CrossRef]
- Shavlov, A.V.; Dzhumandzhi, V.A.; Yakovenko, A.A. Charge of water droplets during evaporation and condensation. J. Aerosol Sci. 2018, 123, 17–26. [Google Scholar] [CrossRef]
- Debye, P.; Huckel, E.; Physik, Z. Physik, Z. Zur Theorie der Elektrolyte; Springer: Berlin/Heidelberg, Germany, 1923; Volume 24, p. 185. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics, Vol. 5: Statistical Physics, 3rd ed.; Part 1; Pergamon: Oxford, UK, 1980. [Google Scholar]
- Mathcad 11: User’s Guide; Mathsoft Engineering & Education, Inc.: Cambridge, MA, USA, 2002.
- Kalitkin, N.N. Inadequacy of the Debye asymptotics. Math. Model. 2005, 17, 40–52. [Google Scholar]
- Shavlov, A.V.; Dzhumandzhi, V.A.; Romanyuk, S.N. Sound oscillation of dropwise cluster. Phys. Lett. A 2012, 376, 2049–2052. [Google Scholar] [CrossRef]
- Shavlov, A.V.; Sokolov, I.V.; Dzhumandzhi, V.A. Viscosity and electric properties of water aerosols. Dokl. Phys. 2016, 61, 429–434. [Google Scholar] [CrossRef]
- Shavlov, A.V.; Sokolov, I.V.; Hazan, V.L.; Dzhumandzhi, V.A. Spatial structure of water fog. Dokl. Earth Sci. 2015, 461, 422–426. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).