In this section, GRA was used evaluate and analyze the air quality of Taiyuan city before and during the outbreak of COVID-19. Then, a prediction model of AQI in Taiyuan was established by using ISOA-SVR and compared with other predicted models.
5.1. Analysis of Air Pollution Assessment Results
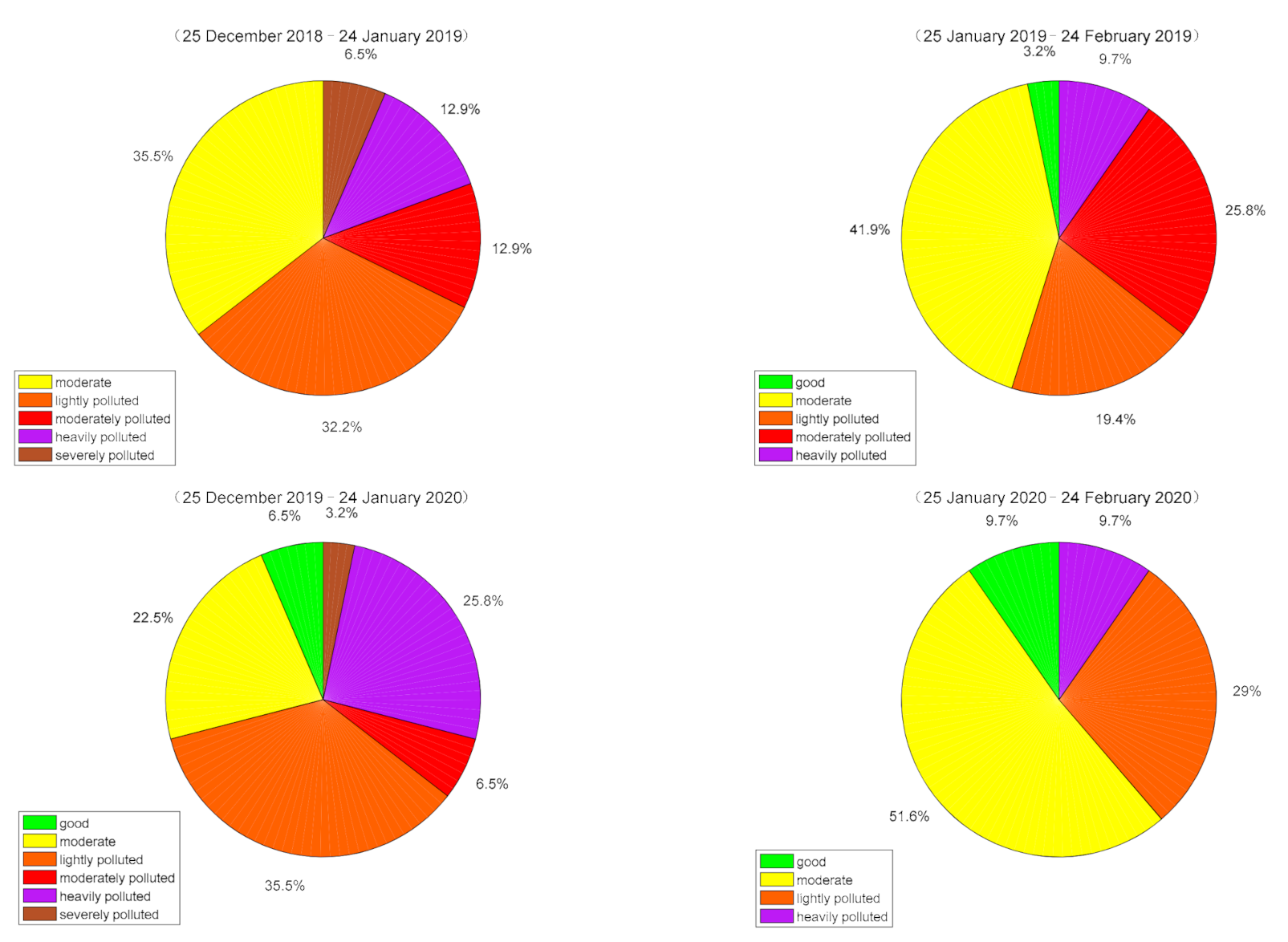
Before applying the GRA method to analyze the influence of air pollution factors on AQI, a simple numerical statistical analysis of AQI and each air pollution factor in four time periods was carried out. The four time periods mentioned here include the COVID-19 locking period (25 January 2020 to 24 February 2020), before the outbreak of COVID-19 (25 December 2019 to 24 January 2020), the same period in 2019 (25 January 2019 to 24 February 2019) and one other time period (25 December 2018 to 24 January 2019), each of which has 31 days. In addition, according to the technical regulation of ambient air quality index (AQI) (HJ 1130-2020) issued by the China Ministry of Environment of Protection, AQI can be divided into six levels (0~50 ‘good’, 51~100 ‘moderate’, 101~150 ‘lightly polluted’, 151~200 ‘moderately polluted’, 201~300 ‘heavily polluted’ and >300 ‘severely polluted’) [
29]. This paper takes these as the standards to analyze the air pollution in the above four periods. The statistical results of AQI are shown in
Figure 3 and
Table 1. In the 31 days of the COVID-19 locking period (25 January 2020 to 24 February 2020), there were three days of good, 16 days of moderate, nine days of lightly polluted and three days of heavily polluted air quality, and there was no moderately polluted or severely polluted weather. In the 31 days before the outbreak of COVID-19 (25 December 2019 to 24 January 2020), respectively, and another day with severely polluted air quality the days with good and moderate grades were two and seven, respectively, the days with lightly polluted, moderately polluted and heavily polluted were 11, two and eight. In the same period of 2019 (25 January 2019 to 24 February 2019), the days of good and moderate were one and 13 respectively, the days of lightly polluted, moderately polluted and heavily polluted were six, eight and three respectively, and there was no severely polluted weather. In the fourth period (25 December 2018 to 24 January 2019), the days of good and moderate weather were zero and 11 respectively, the days of lightly polluted were 10 days, the days of moderately polluted were four days, the days of heavily polluted were four days and the days of severely polluted were two days. From these statistics, it can be seen that the air quality of the COVID-19 locking period (25 January 2020 to 24 February 2020) was significantly better than the other three periods. In fact, during the period of COVID-19 lock-in, the total number of days with good and moderate air quality was 19 days, accounting for 61.3% (19/31), and there was no severely polluted weather. However, in the other three time periods, the total number of good and moderate days of air quality were 9, 14 and 11, respectively, which did not reach 50%. In the locking period of COVID-19 (25 January 2020 to 24 February 2020), only three days reached or exceeded the moderately polluted level, accounting for 9.7% (3/31), and the other three time periods were 11 days, 11 days and 10 days, respectively, which exceeded 30%. In addition, before the outbreak of COVID-19 (25 December 2019 to 24 January 2020), and in the fourth period (25 December 2018 to 24 January 2019), there were one day and two days of severely polluted weather, respectively. All these indicate that during the period of epidemic prevention and control, the factories stopped production and motor vehicles were restricted and stopped, which played a positive role in improving air quality.
Figure 4 and
Table 2 show the average values of AQI and pollutant concentrations over the above four time periods. It can be seen that compared with the other three periods, except for the increase of the average concentration of O
3, the average value of AQI and the average concentration of other pollutants decreased significantly during the COVID-19 locking period (25 January 2020 to 24 February 2020). The average value reflects the overall level of data. Combining these results with the statistical results in
Table 1 shows that the air quality in the locking period of COVID-19 was significantly better than in the other three periods. In fact, good weather accounted for 61.3% (19/31) in the COVID-19 locking period (25 January 2020 to 24 February 2020). Compared with 29% (9/31) before the outbreak of COVID-19, 45.1% (14/31) in the same period of 2019 and 35.5% (11/31) in the fourth period, there were 32.3% (10/31), 16.2% (5/31) and 25.8% (8/31) more, respectively. The number of days reaching and exceeding the moderately polluted level accounted for 9.7% (3/31), which was 25.8% (8/31), 25.8% (8/31) and 22.6% (7/31) less than that before the outbreak of COVID-19 (35.5% (11/31)) for the same period in 2019 (35.5% (11/31)) and the fourth period (32.2% (10/31)) respectively. There was no severely polluted weather during the period of COVID-19 lock-in. In addition, the average value of AQI during the locking period of COVID-19 was 102, which is smaller than the other three time periods (141, 122, 141). These results show that the prevention and control measures of COVID-19 had great restrictions on the movement of people, transportation, engineering construction, industrial production and commercial trade activities. Industrial emissions and automobile exhaust were greatly reduced, and air quality was significantly improved.
From the literature [
29], we know that AQI is calculated by the concentration values of PM
2.5, PM
10, SO
2, CO, NO
2, O
3 and other pollutants. From previous numerical statistical analysis, we know that compared with the other three time periods the AQI and the pollution concentration changed greatly during the COVID-19 locking period. So, did the impact of these air pollutants on AQI change greatly? Next, we used the GRA method to analyze the gray relational degree of each pollution factor and AQI in the above four time periods, and made a comparative analysis of the situation in different time periods. The analysis and comparison results are shown in
Figure 5 and
Table 3,
Table 4,
Table 5 and
Table 6.
It can be seen from
Table 3 and
Table 4 that during the COVID-19 locking period (25 January 2020 to 24 February 2020), compared with before the outbreak of COVID-19 (25 December 2019 to 24 January 2020), the impact of PM
10 was slightly enhanced, the impact of PM
2.5, SO
2 and CO was basically the same as that in the earlier period, the impact of NO
2 was slightly weakened and the impact of O
3 was significantly enhanced. Compared with the same period in 2019 (25 January 2019 to 24 February 2019), the impacts of PM
10 and O
3 were significantly enhanced, the impacts of PM
2.5 and CO were basically the same as before and the impacts of SO
2 and NO
2 were slightly weakened.
The results in
Table 5 show that in the same period of 2019 (25 January 2019 to 24 February 2019) compared with its earlier period (25 December 2018 to 24 January 2019), the impact of PM
2.5, SO
2 and NO
2 was significantly weakened, the impact of PM
10 was basically the same as that of the earlier period, the impact of CO was slightly weakened and the impact of O
3 was slightly enhanced. It can be seen from
Table 6 that before the outbreak of COVID-19 (25 December 2019 to 24 January 2020), compared with the same period in 2018 (25 December 2018 to 24 January 2019), the impact of PM
2.5, SO
2 and NO
2 was significantly weakened, the impact of PM
10 was significantly enhanced and the impact of CO and O
3 was significantly enhanced.
Based on the analysis of the results in
Table 3,
Table 4,
Table 5 and
Table 6 and
Figure 5, it can be seen that although there were some differences in the impact changes of pollutants on air quality (AQI) in different comparison periods, the changes were similar in the corresponding comparison periods. PM
10 and PM
2.5 had great influence on AQI. These results indicate that although the impact of various air pollutants on AQI had some changes due to the outbreak of COVID-19, most of the changes were not significant. Therefore, it is feasible to use the data before the outbreak of COVID-19 to predict the data during the outbreak of COVID-19, but there are also some challenges.
5.2. AQI Prediction Results and Analysis
In this part, we used five prediction models, such as ISOA-SVR, SOA-SVR, PSO-SVR, SCA-SVR and WOA-SVR, to predict the monthly average AQI values from September 2019 to June 2020, and the daily AQI values for 15–24 February 2020. In addition, in order to ensure the reliability of the experiment, each group of experiments of each model was run separately for 30 times, and the prediction results compared and analyzed.
The sampling time of Experiment 1 was from December 2013 to June 2020, with a total of 79 groups of monthly average air quality data. The first 69 groups were used as the training set and the remaining 10 groups as the test set. The sampling time of Experiment 2 was from 1 January 2020 to 24 February 2020. There were 55 groups of daily air quality data, including the first 45 groups as the training set and the remaining 10 groups as the test set. In the experiment, the AQI value of the sixth group was predicted by inputting the AQI value of the first five groups and the pollutant value of the fifth group, and then sliding forward was carried out to eliminate the random fluctuation in the historical statistical series, and to eliminate the influence of season and random factors to make more accurate predictions. The fitness convergence curve of training data and the test results of test data (including MSE, RMSE, MAPE and run time) were obtained by running each prediction model.
5.2.1. Results and Analysis of Experiment 1
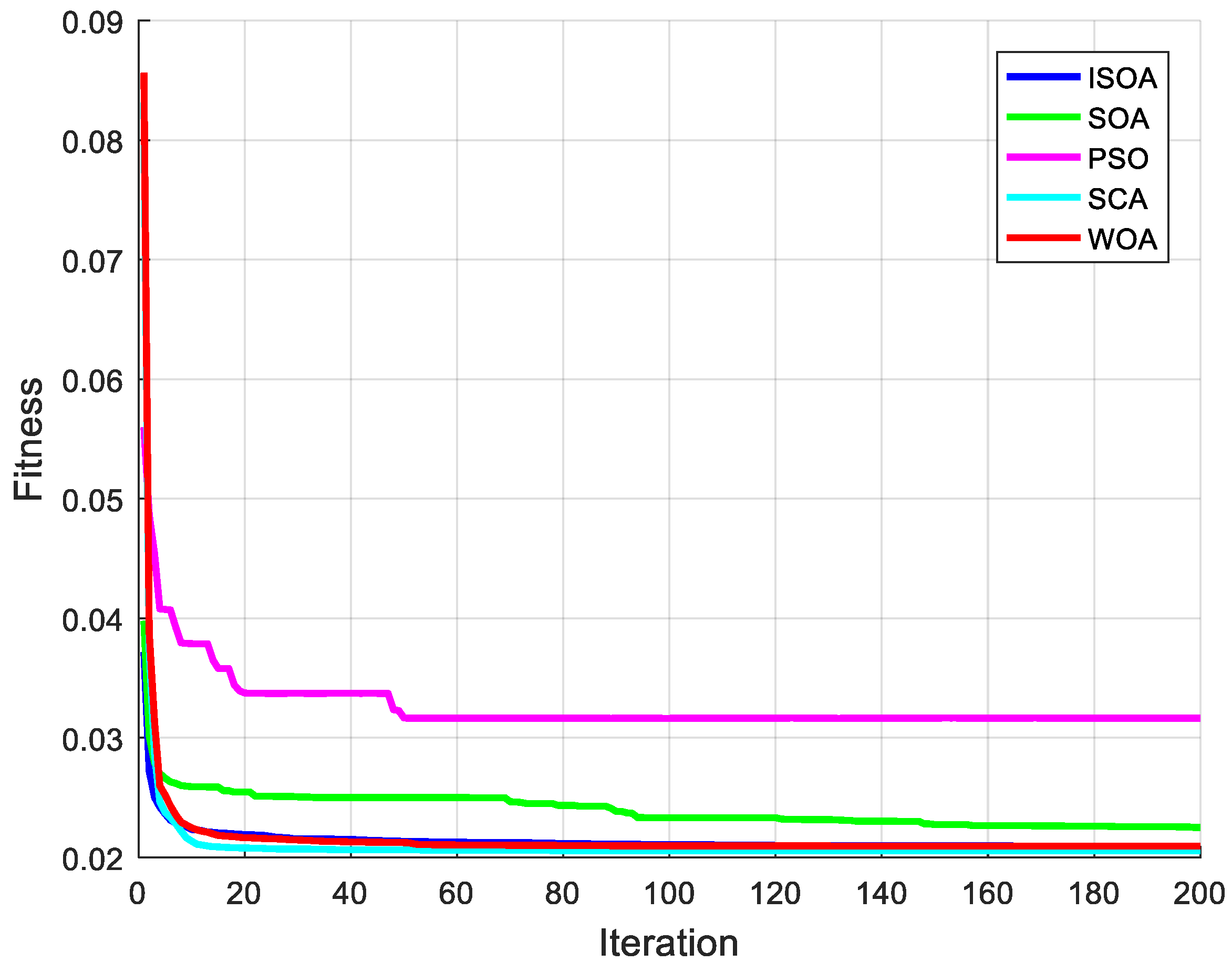
As can be seen from
Figure 6, the convergence effect of fitness functions of ISOA, SCA and WOA were similar, but SOA was slightly worse, and the worst was PSO. The training results in
Table 7 show that ISOA-SVR was the best, MSE, RMSE and MAPE were 1.299370396, 0.010565973 and 9.064760441, SCA-SVR was 1.386464339, 0.012714389 and 9.62641542, and WOA-SVR were 1.367865788, 0.012364791 and 9.463121198, respectively. From the evaluation index values of the prediction results in
Table 8, we found that the three index values of the prediction results of ISOA-SVR were the best, which were 3.379206115, 0.03090546 and 14.03810752, respectively. WOA-SVR was slightly worse than the ISOA-SVR algorithm, SOA-SVR and SCA-SVR were similar, both slightly lower than WOA-SVR, and PSO-SVR was the worst. In fact, we found from the prediction results in
Table 9 that the prediction result of ISOA-SVR achieved the optimal value or suboptimal value in 6/10, which was the best among the five algorithms.
5.2.2. Results and Analysis of Experiment 2
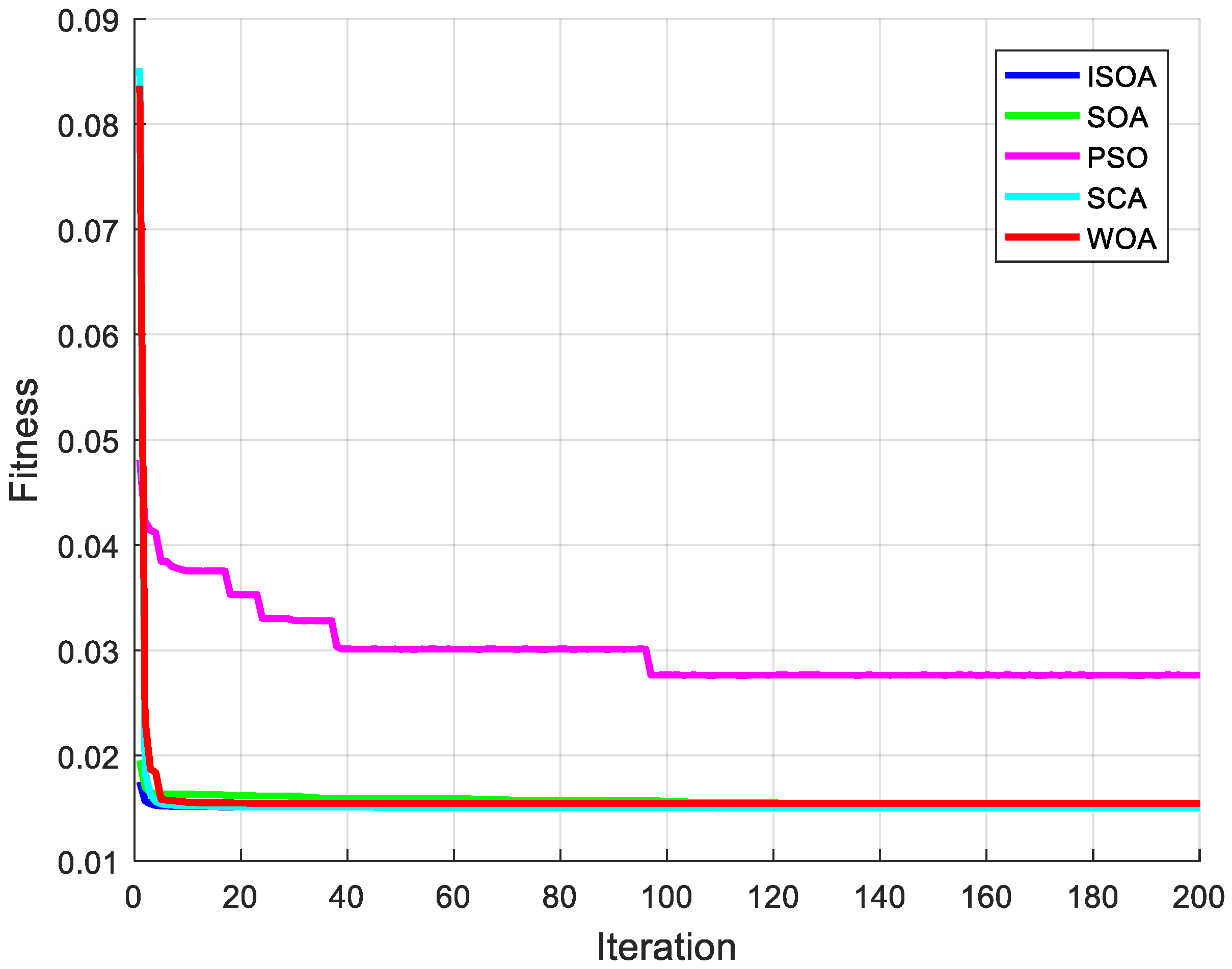
We can see from
Figure 7 that the convergence effect of fitness function of ISOA, SOA, SCA and WOA were similar, but the convergence effect of PSO was a little worse. From the MSE, RMSE and MAPE of the training results in
Table 10, we found that the training results of ISOA-SVR (13.37973604, 0.163687428 and 28.1740733) were slightly worse than the best SOA-SVR (12.90917741, 0.162034198 and 28.71513087), but better than other algorithms. From the three evaluation index values of the prediction results in
Table 11, we can see that the prediction results of ISOA-SVR were the best (6.147418336, 0.185148465 and 37.28176518), SOA-SVR was slightly worse than the ISOA-SVR algorithm, SCA-SVR was better than WOA-SVR and was slightly lower than SOA-SVR; the worst was PSO-SVR. In fact, from the prediction results in
Table 12, we found that the prediction result of ISOA-SVR achieved the optimal value or suboptimal value in 7/10, which was the best among the five algorithms.
Combined with the results of Experiment 1 and Experiment 2, we can conclude that the proposed ISOA-SVR prediction model had better generalization ability and robustness than other prediction models tested in this study. This good result is attributed to the three characteristics of the ISOA algorithm: one is the exponential balance of local and global optimization; the second is the adaptive ability of particles themselves and groups and the third is the diversity of particles. These make the algorithm avoid falling into local minimums in the process of optimization. In addition, the weight parameters introduced in the ISOA algorithm can balance the global exploration and local development ability of particles and accelerate the convergence speed of the algorithm.