Downscaling and Evaluation of Seasonal Climate Data for the European Power Sector
Abstract
1. Introduction
2. Experiments (Data and Methods)
2.1. Data
2.1.1. Seasonal Forecasts
2.1.2. Reanalysis Data
2.2. Methods
2.2.1. EPISODES
2.2.2. Model Configuration
2.2.3. Adaptation to Climate Forecasts
2.2.4. Adaptation to a Different Region
2.2.5. Evaluation: Hindcast Skill and Bias
3. Results and Discussion
3.1. Hindcast Skill
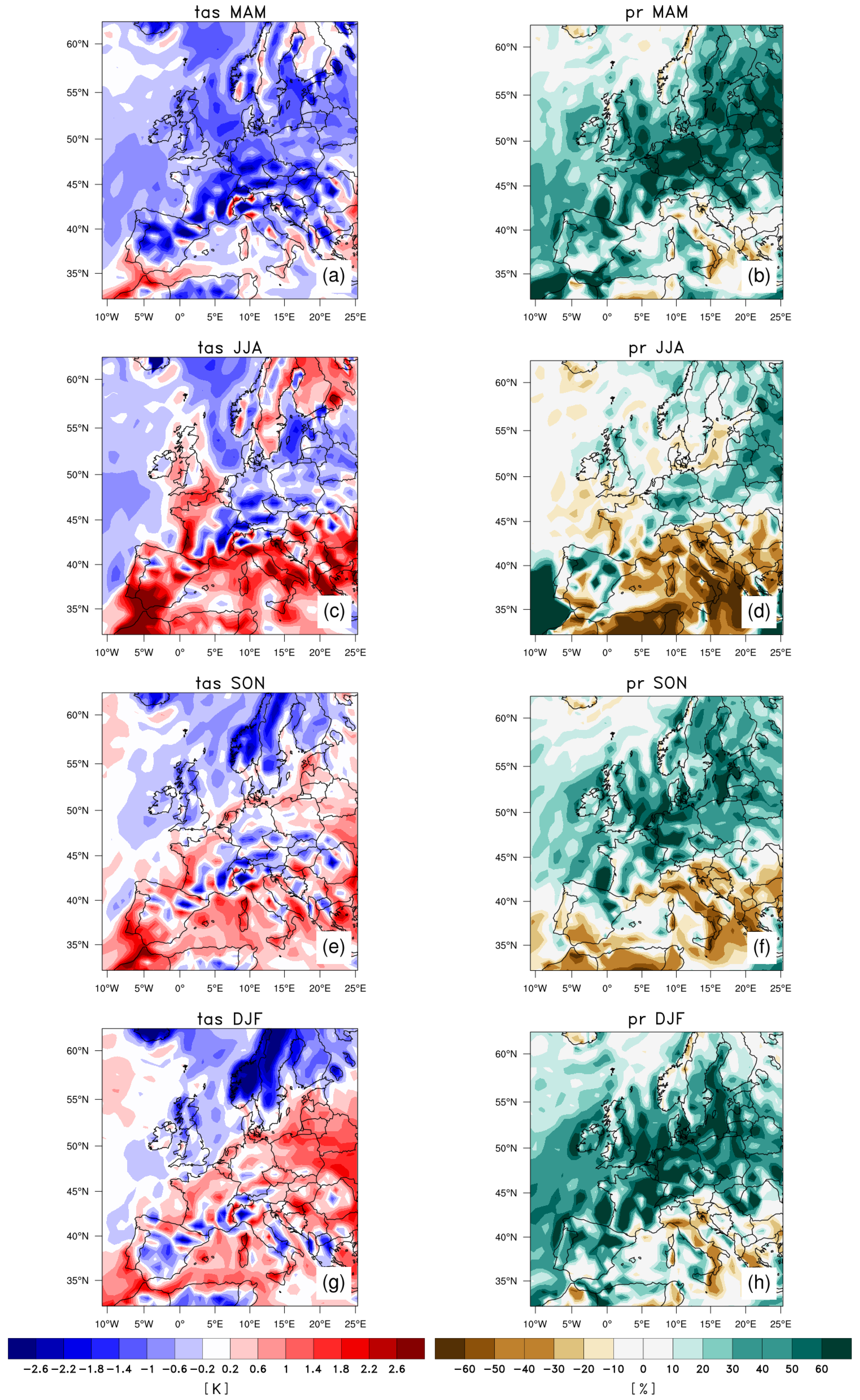
3.1.1. Global Model Output
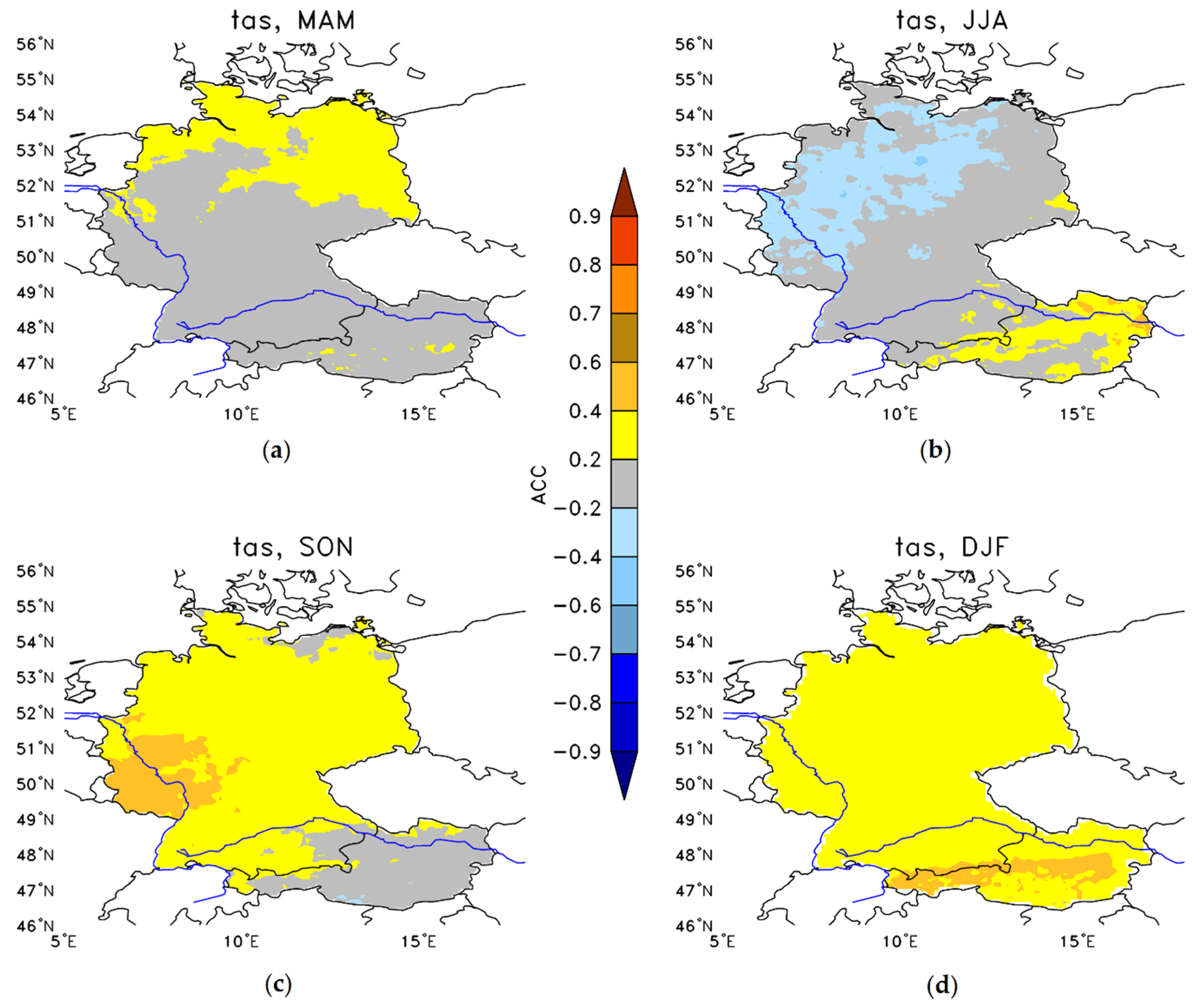
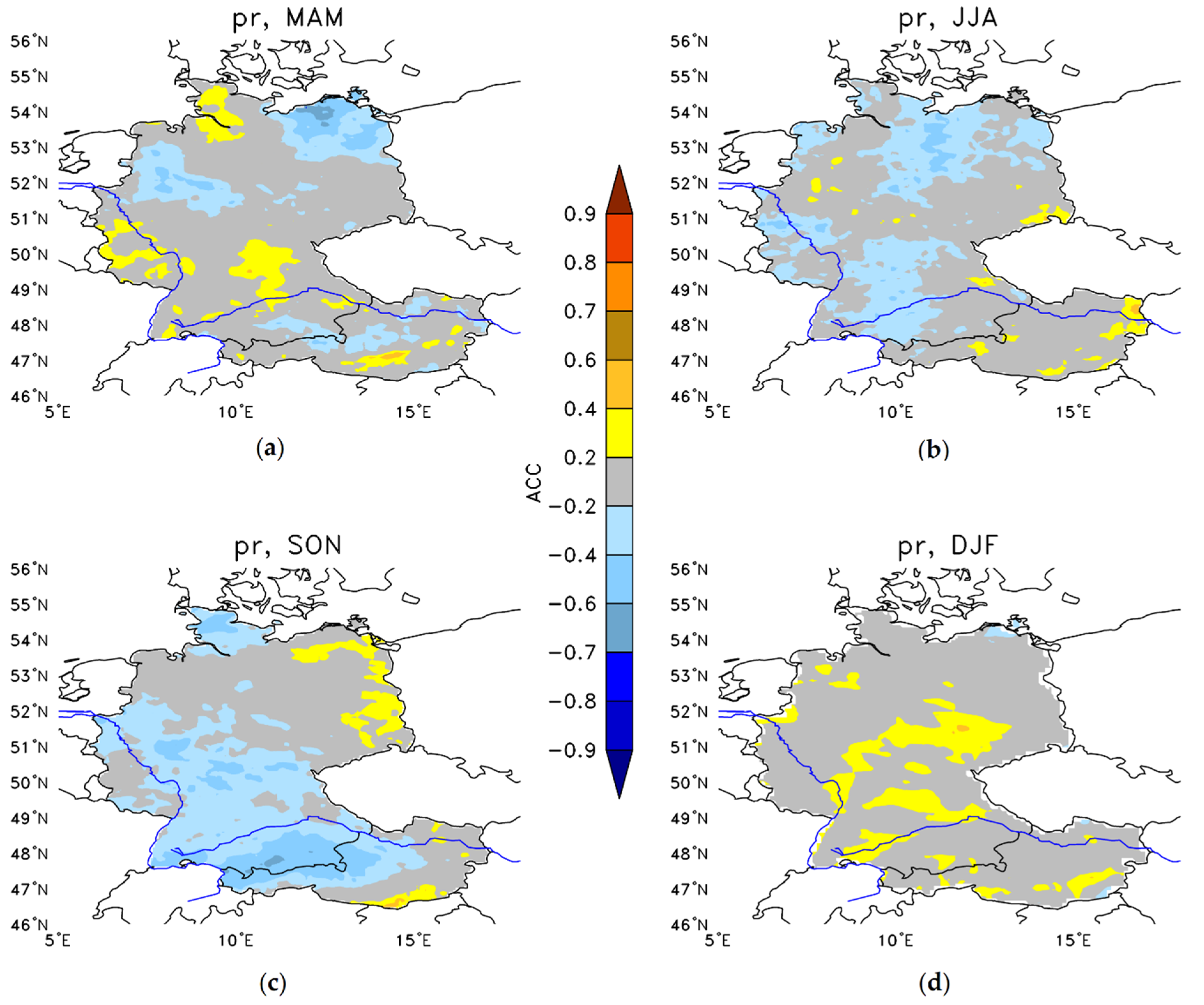
3.1.2. Statistical Downscaling Results
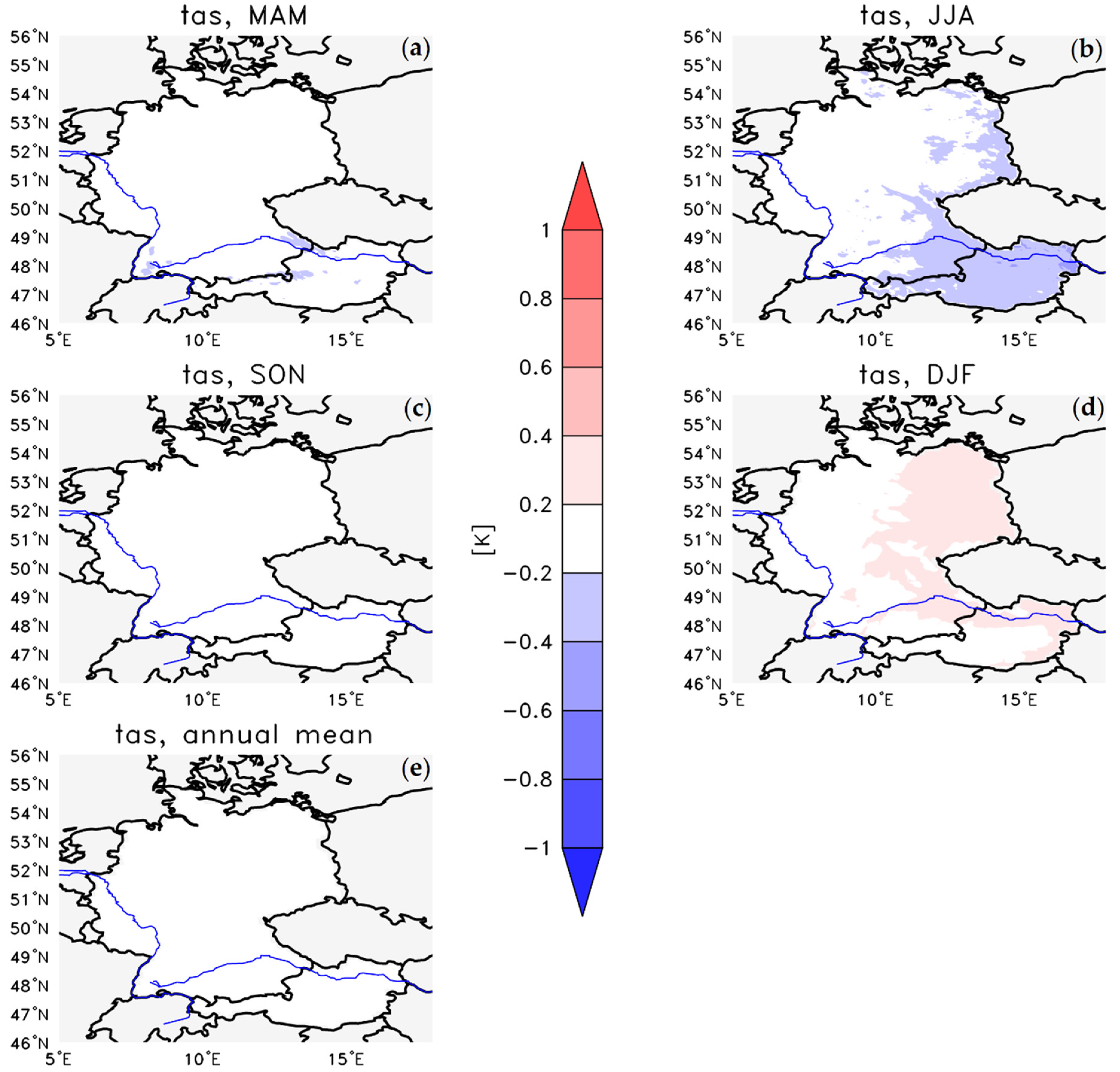
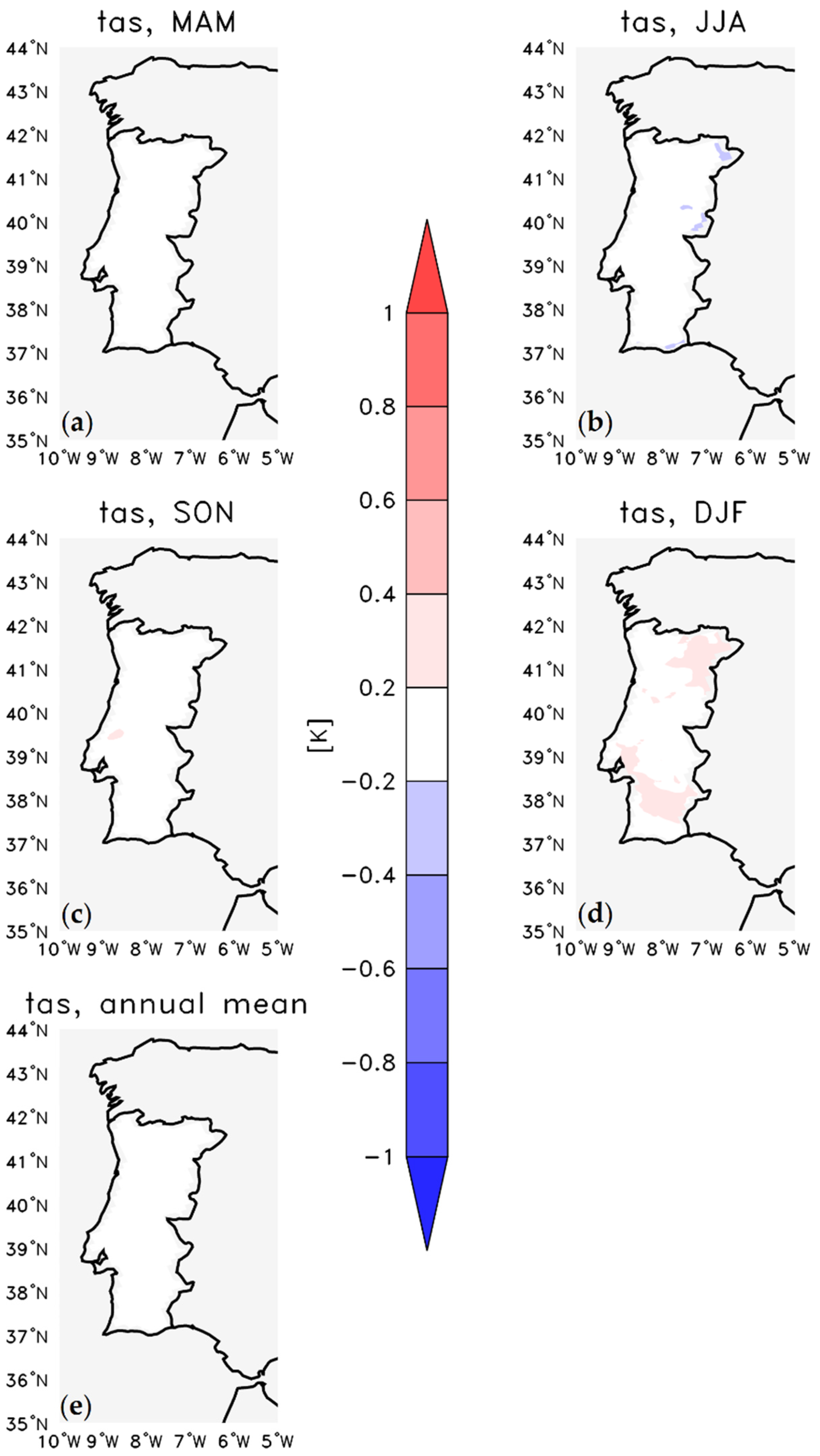
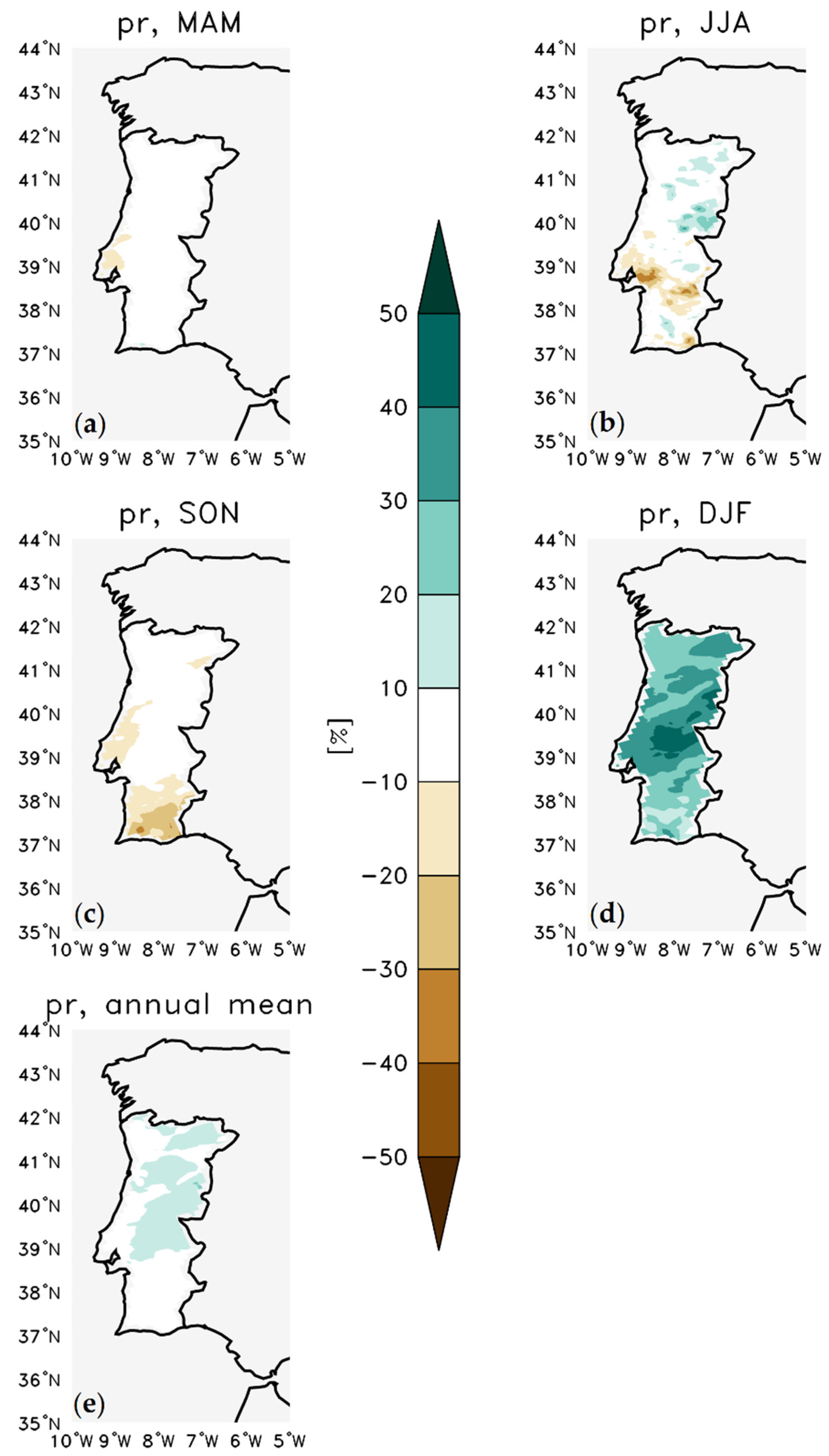
3.2. Bias
3.2.1. Temperature
3.2.2. Precipitation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gøtke, N.; Julkowska, D.; Serrano, J.; Ispas, I.; Amanatidou, E. Analysis of ERA-NET Cofund Actions under Horizon 2020; Final Report of the Expert Group; European Commission Publications: Luxembourg, 2016. [Google Scholar]
- Simoes, S.G.; Amorim, F.; Frohlich, K.; Ostermoeller, J.; Saint-Drenan, Y.-M.; Assoumou, E.; Siggini, G.; Sessa, V.; Ranchin, T.; Gschwind, B.; et al. Clim2power—Translating climate data into power plants operational guidance. In Proceedings of the ICEE 2019—4th International Conference on Energy and Environment: Bringing together Engineering and Economics, Guimarães, Portugal, 16–17 May 2019; pp. 629–634. [Google Scholar]
- Amorim, F.; Simoes, S.G.; Siggini, G.; Assoumou, E. Introducing climate variability in energy systems modelling. Energy 2020, 206, 118089. [Google Scholar] [CrossRef]
- Simoes, S.; Nijs, W.; Ruiz, P.; Sgobbi, A.; Thiel, C. Comparing policy routes for low-carbon power technology deployment in EU—An energy system analysis. Energy Policy 2017, 101, 353–365. [Google Scholar] [CrossRef]
- Kling, H.; Stanzel, P.; Fuchs, M.; Nachtnebel, H.-P. Performance of the COSERO precipitation–runoff model under non-stationary conditions in basins with different climates. Hydrol. Sci. J. 2015, 60, 1374–1393. [Google Scholar] [CrossRef]
- Beça, P.; Simoes, S.G.; Mujtaba, B.; Diogo, P.; Amorim, F.; Carvalho, S.; Paes, P. CLIM2POWER Project: Seasonal forecasting for hydropower capacity in the Douro river basin—Portuguese case study. In Proceedings of the ECCA—European Climate Change Adaptation Conference, Lisbon, Portugal, 28–31 May 2019. [Google Scholar]
- Bollmeyer, C.; Keller, J.D.; Ohlwein, C.; Wahl, S.; Crewell, S.; Friederichs, P.; Hense, A.; Keune, J.; Kneifel, S.; Pscheidt, I.; et al. Towards a high-resolution regional reanalysis for the European CORDEX domain. Q. J. R. Meteorol. Soc. 2015, 141, 1–15. [Google Scholar] [CrossRef]
- MacLachlan, C.; Arribas, A.; Peterson, K.A.; Maidens, A.; Fereday, D.; Scaife, A.A.; Gordon, M.; Vellinga, M.; Williams, A.; Comer, R.E.; et al. Global Seasonal forecast system version 5 (GloSea5): A high-resolution seasonal forecast system. Q. J. R. Meteorol. Soc. 2015, 141, 1072–1084. [Google Scholar] [CrossRef]
- Batté, L.; Déqué, M. Randomly correcting model errors in the ARPEGE-Climate v6.1 component of CNRM-CM: Applications for seasonal forecasts. Geosci. Model Dev. 2016, 9, 2055–2076. [Google Scholar] [CrossRef]
- Johnson, S.J.; Stockdale, T.N.; Ferranti, L.; Balmaseda, M.A.; Molteni, F.; Magnusson, L.; Tietsche, S.; Decremer, D.; Weisheimer, A.; Balsamo, G.; et al. SEAS5: The new ECMWF seasonal forecast system. Geosci. Model Dev. 2019, 12, 1087–1117. [Google Scholar] [CrossRef]
- Scaife, A.A.; Arribas, A.; Blockley, E.; Brookshaw, A.; Clark, R.T.; Dunstone, N.; Eade, R.; Fereday, D.; Folland, C.K.; Gordon, M.; et al. Skillful long-range prediction of European and North American winters. Geophys. Res. Lett. 2014, 41, 2514–2519. [Google Scholar] [CrossRef]
- Dobrynin, M.; Domeisen, D.I.V.; Müller, W.A.; Bell, L.; Brune, S.; Bunzel, F.; Düsterhus, A.; Fröhlich, K.; Pohlmann, H.; Baehr, J. Improved Teleconnection-Based Dynamical Seasonal Predictions of Boreal Winter. Geophys. Res. Lett. 2018, 45, 3605–3614. [Google Scholar] [CrossRef]
- Fröhlich, K.; Dobrynin, M.; Isensee, K.; Gessner, C.; Paxian, A.; Pohlmann, H.; Haak, H.; Brune, S.; Früh, B.; Baehr, J. The German Climate Forecast System: GCFS. J. Adv. Model. Earth Syst. 2021, 13, e2020MS002101. [Google Scholar] [CrossRef]
- Feldmann, H.; Pinto, J.G.; Laube, N.; Uhlig, M.; Moemken, J.; Pasternack, A.; Früh, B.; Pohlmann, H.; Kottmeier, C. Skill and added value of the MiKlip regional decadal prediction system for temperature over Europe. Tellus A Dyn. Meteorol. Oceanogr. 2019, 71, 1618678. [Google Scholar] [CrossRef]
- Reyers, M.; Pinto, J.G.; Moemken, J. Statistical–dynamical downscaling for wind energy potentials: Evaluation and applications to decadal hindcasts and climate change projections. Int. J. Climatol. 2015, 35, 229–244. [Google Scholar] [CrossRef]
- Manzanas, R.; Lucero, A.; Weisheimer, A.; Gutiérrez, J.M. Can bias correction and statistical downscaling methods improve the skill of seasonal precipitation forecasts? Clim. Dyn. 2017, 50, 1161–1176. [Google Scholar] [CrossRef]
- Manzanas, R.; Gutiérrez, J.M.; Fernández, J.; van Meijgaard, E.; Calmanti, S.; Magariño, M.E.; Cofiño, A.S.; Herrera, S. Dynamical and statistical downscaling of seasonal temperature forecasts in Europe: Added value for user applications. Clim. Serv. 2018, 9, 44–56. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Kreienkamp, F.; Paxian, A.; Früh, B.; Lorenz, P.; Matulla, C. Evaluation of the empirical–statistical downscaling method EPISODES. Clim. Dyn. 2018, 52, 991–1026. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Kreienkamp, F.; Lorenz, P.; Geiger, T. Statistically Downscaled CMIP6 Projections Show Stronger Warming for Germany. Atmosphere 2020, 11, 1245. [Google Scholar] [CrossRef]
- Müller, W.A.; Jungclaus, J.H.; Mauritsen, T.; Baehr, J.; Bittner, M.; Budich, R.; Bunzel, F.; Esch, M.; Ghosh, R.; Haak, H.; et al. A Higher-resolution Version of the Max Planck Institute Earth System Model (MPI-ESM1.2-HR). J. Adv. Model. Earth Syst. 2018, 10, 1383–1413. [Google Scholar] [CrossRef]
- Baehr, J.; Piontek, R. Ensemble initialization of the oceanic component of a coupled model through bred vectors at seasonal-to-interannual timescales. Geosci. Model Dev. 2014, 7, 453–461. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Zuo, H.; Balmaseda, M.A.; Mogensen, K. The new eddy-permitting ORAP5 ocean reanalysis: Description, evaluation and uncertainties in climate signals. Clim. Dyn. 2017, 49, 791–811. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J.; et al. The NCEP/NCAR 40-Year Reanalysis Project. Bull. Am. Meteorol. Soc. 1996, 77, 437–472. [Google Scholar] [CrossRef]
- Kotlarski, S.; Szabó, P.; Herrera, S.; Räty, O.; Keuler, K.; Soares, P.M.; Cardoso, R.M.; Bosshard, T.; Pagé, C.; Boberg, F.; et al. Observational uncertainty and regional climate model evaluation: A pan-European perspective. Int. J. Climatol. 2019, 39, 3730–3749. [Google Scholar] [CrossRef]
- Niermann, D.; Borsche, M.; Kaiser-Weiss, A.K.; Kaspar, F. Evaluating renewable-energy-relevant parameters of COSMO-REA6 by comparison with satellite data, station observations and other reanalyses. Meteorol. Z. 2019, 28, 347–360. [Google Scholar] [CrossRef]
- Kaspar, F.; Niermann, D.; Borsche, M.; Fiedler, S.; Keller, J.; Potthast, R.; Rösch, T.; Spangehl, T.; Tinz, B. Regional atmospheric reanalysis activities at Deutscher Wetterdienst: Review of evaluation results and application examples with a focus on renewable energy. Adv. Sci. Res. 2020, 17, 115–128. [Google Scholar] [CrossRef]
- Jacob, D.; Petersen, J.; Eggert, B.; Alias, A.; Christensen, O.B.; Bouwer, L.M.; Braun, A.; Colette, A.; Déqué, M.; Georgievski, G.; et al. EURO-CORDEX: New high-resolution climate change projections for European impact research. Reg. Environ. Chang. 2014, 14, 563–578. [Google Scholar] [CrossRef]
- Rauthe, M.; Steiner, H.; Riediger, U.; Mazurkiewicz, A.; Gratzki, A. A Central European precipitation climatology ? Part I: Generation and validation of a high-resolution gridded daily data set (HYRAS). Meteorol. Z. 2013, 22, 235–256. [Google Scholar] [CrossRef]
- Schulzweida, U. Climate Data Operators (CDO) User Guide; Zenodo: Meyrin, Switzerland, 2018. [Google Scholar]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Illing, S.; Kadow, C.; Kunst, O.; Cubasch, U. MurCSS: A Tool for Standardized Evaluation of Decadal Hindcast Systems. J. Open Res. Softw. 2014, 2, e24. [Google Scholar] [CrossRef]
- Kaiser-Weiss, A.K.; Borsche, M.; Niermann, D.; Kaspar, F.; Lussana, C.; Isotta, F.A.; van den Besselaar, E.; van der Schrier, G.; Undén, P. Added value of regional reanalyses for climatological applications. Environ. Res. Commun. 2019, 1. [Google Scholar] [CrossRef]
- Lockhoff, M.; Zolina, O.; Simmer, C.; Schulz, J. Representation of Precipitation Characteristics and Extremes in Regional Reanalyses and Satellite- and Gauge-Based Estimates over Western and Central Europe. J. Hydrometeorol. 2019, 20, 1123–1145. [Google Scholar] [CrossRef]
- Scherrer, S.C. Temperature monitoring in mountain regions using reanalyses: Lessons from the Alps. Environ. Res. Lett. 2020, 15, 044005. [Google Scholar] [CrossRef]
- Mishra, N.; Prodhomme, C.; Guemas, V. Multi-model skill assessment of seasonal temperature and precipitation forecasts over Europe. Clim. Dyn. 2018, 52, 4207–4225. [Google Scholar] [CrossRef]





| Selector Fields and Predictors | Pressure Levels |
|---|---|
| Mean daily geopotential height | 1000 hPa, 850 hPa, 700 hPa, 500 hPa, 250 hPa |
| Mean daily air temperature | 1000 hPa, 850 hPa, 700 hPa, 500 hPa, 250 hPa |
| Mean daily relative humidity | 1000 hPa, 850 hPa, 700 hPa, 500 hPa |
| Mean daily specific humidity | 1000 hPa, 850 hPa, 700 hPa, 500 hPa |
| Vorticity | 1000 hPa, 850 hPa, 700 hPa, 500 hPa |
| Geopotential horizontal differences East–West | 1000 hPa, 850 hPa, 700 hPa, 500 hPa |
| Geopotential horizontal differences North–South | 1000 hPa, 850 hPa, 700 hPa, 500 hPa |
| Relative topography | 1000–850 hPa, 1000–700 hPa, 850–700 hPa |
| Advection of temperature | 1000 hPa, 850 hPa, 700 hPa, 500 hPa |
| Advection of specific humidity | 1000 hPa, 850 hPa, 700 hPa, 500 hPa |
| Pseudopotential temperature | 850 hPa, 700 hPa, 500 hPa |
| Season | MAM | JJA | SON | DJF |
|---|---|---|---|---|
| Selector field 1 | Relative topography 1000–850 hPa | Mean daily air temperature 850 hPa | Vorticity 1000 hPa | Vorticity 1000 hPa |
| Selector field 2 | Advection specific humidity 850 hPa | Geopotential horiz. diff. N-S 850 hPa | Relative topography 1000–850 hPa | Geopotential horiz. diff. N-S 700 hPa |
| Predictor | Mean daily air temperature 1000 hPa | Mean daily air temperature 1000 hPa | Mean daily air temperature 1000 hPa | Mean daily air temperature 1000 hPa |
| Season | MAM | JJA | SON | DJF |
|---|---|---|---|---|
| Selector field 1 | Mean daily relative humidity 700 hPa | Mean daily relative humidity 700 hPa | Mean daily geopotential 500 hPa | Mean daily relative humidity 850 hPa |
| Selector field 2 | Relative topography 850–700 hPa | Geopotential horiz. diff. N-S 850 hPa | Geopotential horiz. diff. N-S 850 hPa | Geopotential horiz. diff. N-S 850 hPa |
| Predictor | Geopotential horiz. diff. N-S 850 hPa | Mean daily relative humidity 850 hPa | Relative topography 850–700 hPa | Advection specific humidity 850 hPa |
| Season | MAM | JJA | SON | DJF |
|---|---|---|---|---|
| Selector field 1 | Mean daily relative humidity 700 hPa | Vorticity 850 hPa | Mean daily relative humidity 700 hPa | Mean daily relative humidity 850 hPa |
| Selector field 2 | Mean daily specific humidity 850 hPa | Geopotential horiz. diff. N-S 700 hPa | Advection specific humidity 500 hPa | Advection specific humidity 700 hPa |
| Predictor | Geopotential horiz. diff. N-S 700 hPa | Mean daily relative humidity 850 hPa | Mean daily relative humidity 1000 hPa | Mean daily relative humidity 850 hPa |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ostermöller, J.; Lorenz, P.; Fröhlich, K.; Kreienkamp, F.; Früh, B. Downscaling and Evaluation of Seasonal Climate Data for the European Power Sector. Atmosphere 2021, 12, 304. https://doi.org/10.3390/atmos12030304
Ostermöller J, Lorenz P, Fröhlich K, Kreienkamp F, Früh B. Downscaling and Evaluation of Seasonal Climate Data for the European Power Sector. Atmosphere. 2021; 12(3):304. https://doi.org/10.3390/atmos12030304
Chicago/Turabian StyleOstermöller, Jennifer, Philip Lorenz, Kristina Fröhlich, Frank Kreienkamp, and Barbara Früh. 2021. "Downscaling and Evaluation of Seasonal Climate Data for the European Power Sector" Atmosphere 12, no. 3: 304. https://doi.org/10.3390/atmos12030304
APA StyleOstermöller, J., Lorenz, P., Fröhlich, K., Kreienkamp, F., & Früh, B. (2021). Downscaling and Evaluation of Seasonal Climate Data for the European Power Sector. Atmosphere, 12(3), 304. https://doi.org/10.3390/atmos12030304






