Correction of Eddy Covariance Based Crop ET Considering the Heat Flux Source Area
Abstract
1. Introduction
1.1. Flux Footprint Modeling
1.2. Motivation and Objectives
2. Materials and Methods
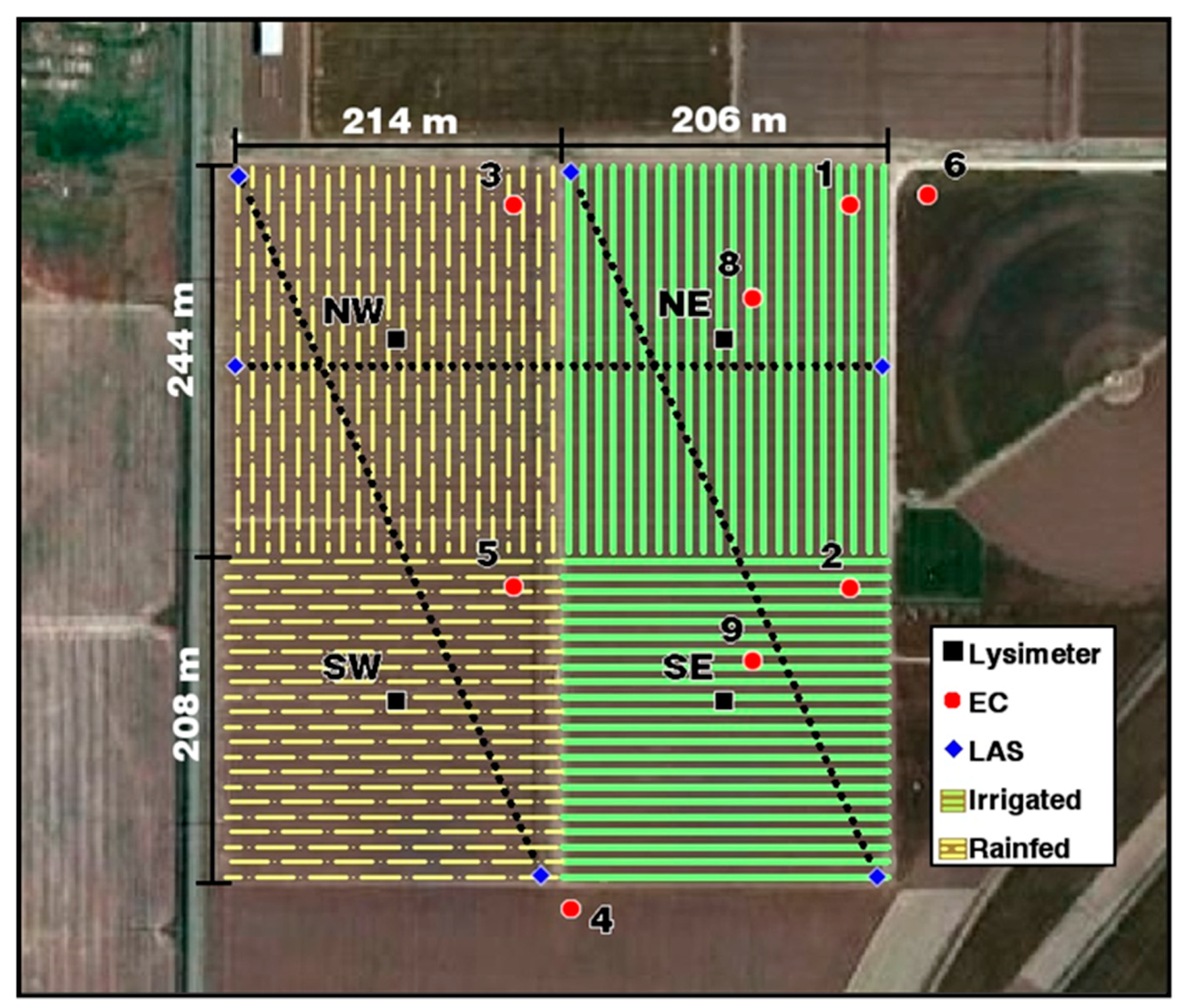
2.1. Site Description
2.1.1. Large Monolith Weighing Lysimeters
2.1.2. Eddy Covariance Energy Balance System
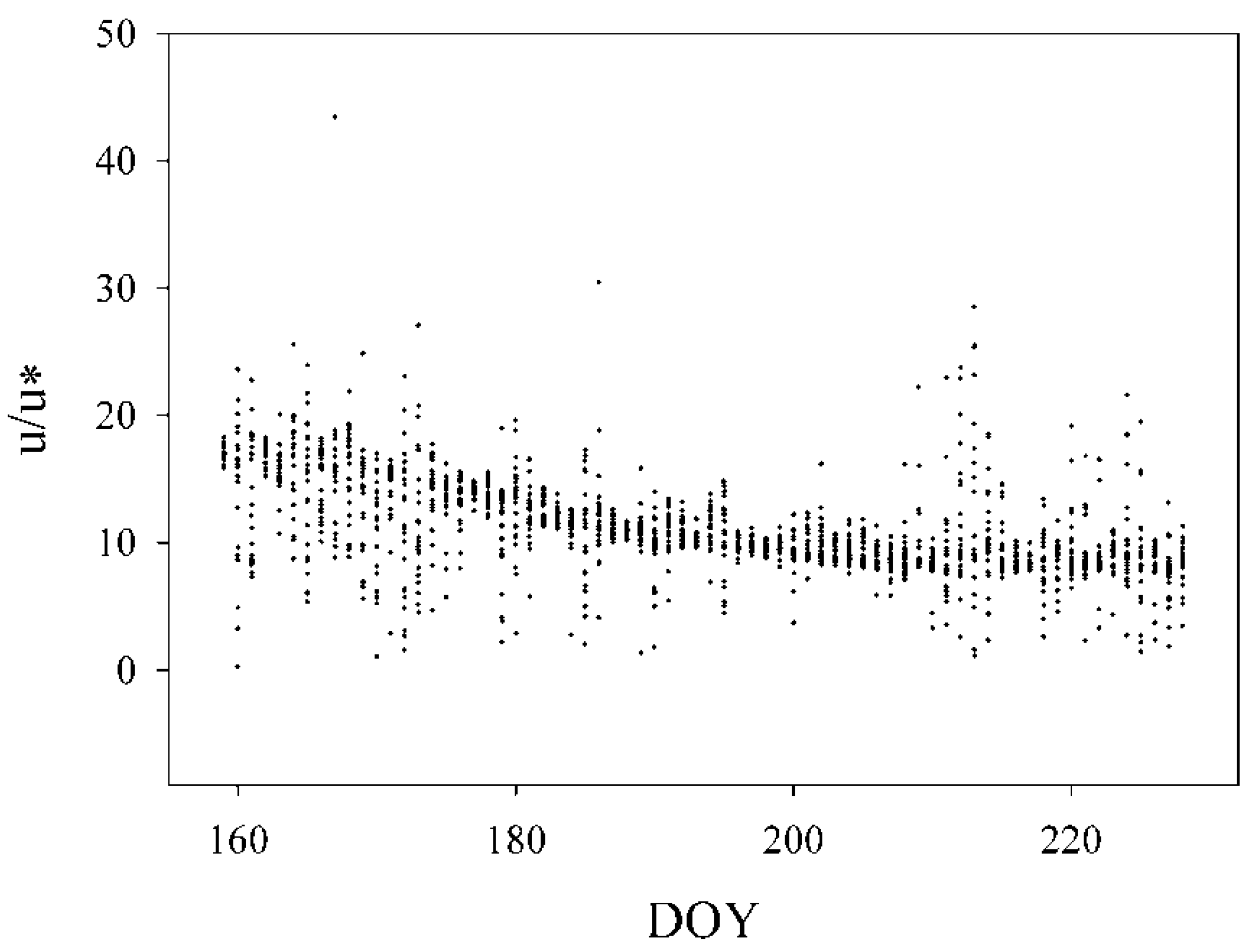
2.2. Eddy Covariance Data Processing
2.3. Footprint Modeling Methodology
2.3.1. Schuepp Model
2.3.2. Hsieh Model
2.3.3. Crosswind Function
2.3.4. Kormann and Meixner Model
2.4. Footprint Validation Procedure
2.5. ET Correction Using Footprint Fractions
2.6. Statistical Analysis
3. Results and Discussion
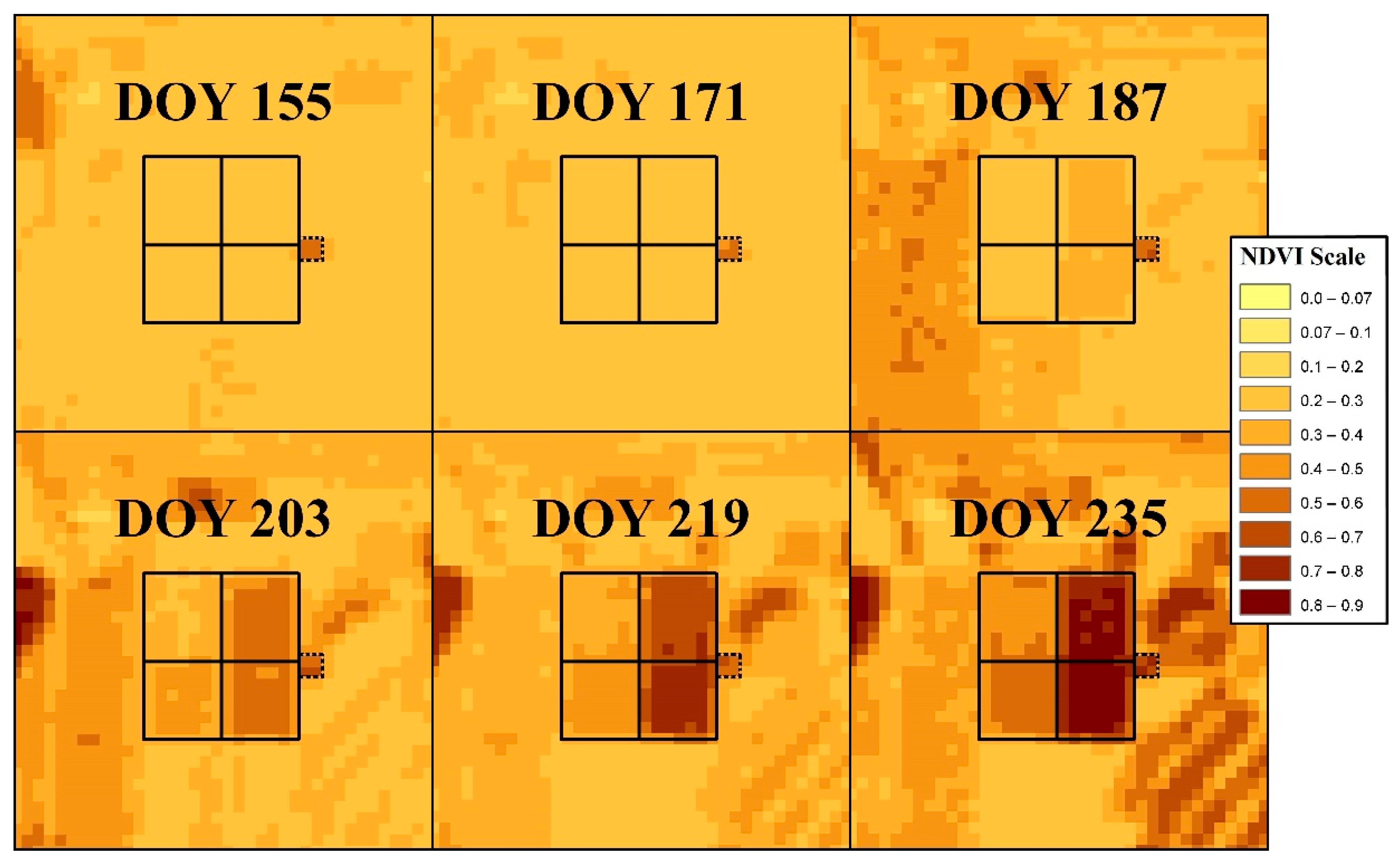
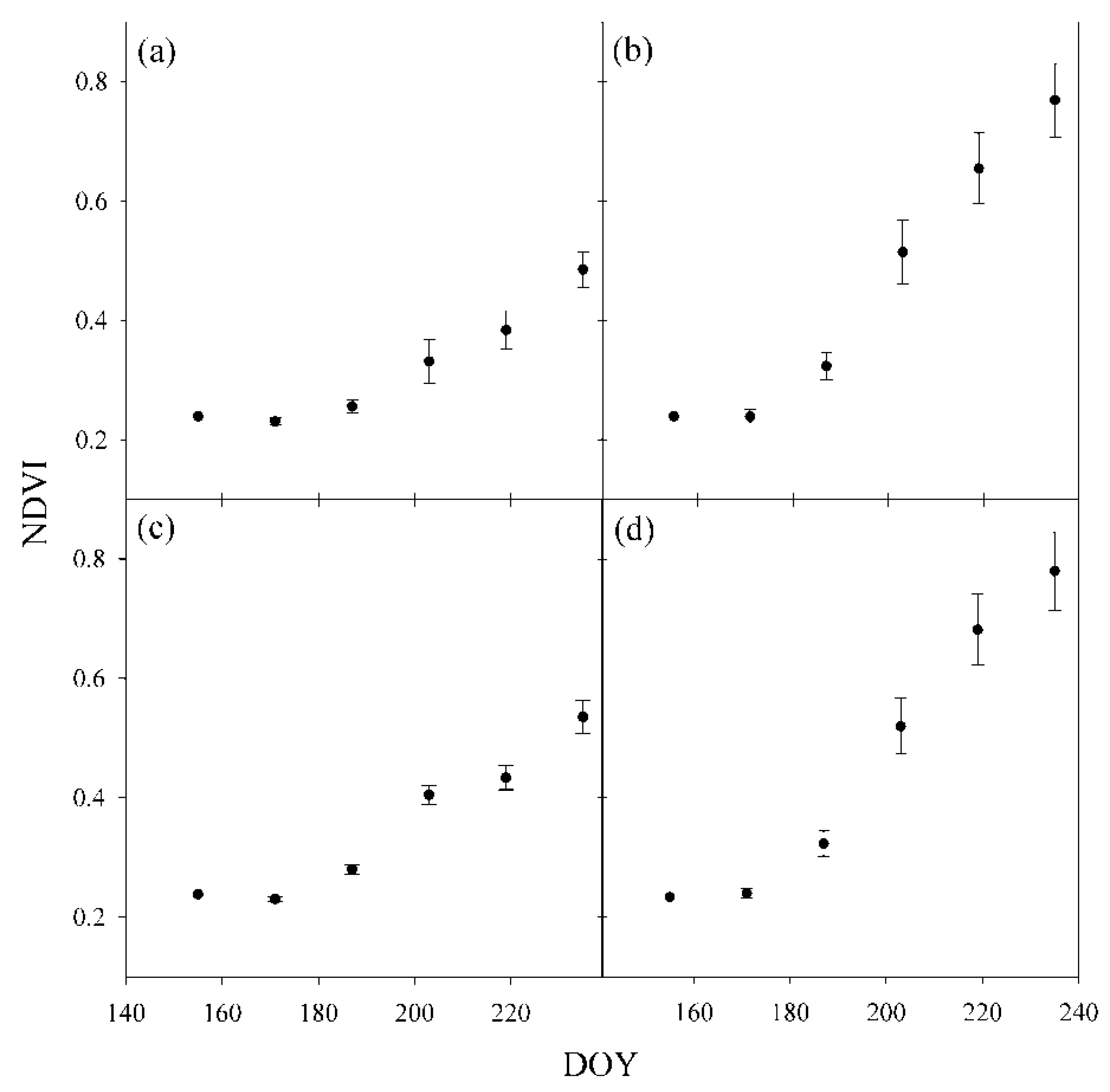
3.1. Surface Roughness
3.2. Footprint Validation
3.3. Correction using Footprint Fractions Evaluation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Coefficient | Field | |||
| NE | SE | NW | SW | |
| a | 0.7581 | 0.8459 | 0.5498 | 0.6310 |
| b | 12.1172 | 12.5446 | 8.1581 | 9.4304 |
| x0 | 195.7687 | 196.3583 | 198.1321 | 197.6266 |
| Coefficient | Field | |||
| NE | SE | NW | SW | |
| a | 3.1487 | 4.0667 | 1.0217 | 2.3990 |
| b | 4.4535 | 5.4043 | 9.2699 | 13.5256 |
| x0 | 211.0799 | 212.4062 | 201.8607 | 220.1325 |
Appendix B. MATLAB Code for the S90 and H2000 Footprint Models
| clear |
| clc |
| %Import data from Excel spreadsheet |
| temp=xlsread('SandH_input.xlsx'); |
| S=temp(:,1); |
| H=temp(:,2); |
| D=temp(:,3); |
| E=temp(:,4); |
| theta=temp(:,5); |
| xprime=xlsread('xprime.xlsx'); |
| yprime=xlsread('yprime.xlsx'); |
| NE=xlsread('NE.xlsx'); |
| SE=xlsread('SE.xlsx'); |
| SW=xlsread('SW.xlsx'); |
| NW=xlsread('NW.xlsx'); |
| output=NaN(size(theta,1),10); |
| for i=1:size(theta,1) |
| %Rotate coordinates into mean wind direction |
| if (theta(i)>(-360)) andand (theta(i)<360) |
| X=-yprime*sin(theta(i)*pi/180)+xprime*cos(theta(i)*pi/180); |
| Y=yprime*cos(theta(i)*pi/180)+xprime*sin(theta(i)*pi/180); |
| %Calculate the footprint functions |
| for m=1:size(xprime,1) |
| for n=1:size(xprime,2) |
| if X(m,n)>0 |
| F_S(m,n)=(S(i)/(X(m,n)^2))*exp(-S(i)/X(m,n))*exp(- |
| (Y(m,n)^2)/(2*(D(i)*X(m,n)^E(i))^2))/ |
| (sqrt(2*pi)*D(i)*X(m,n)^E(i)); |
| F_H(m,n)=(H(i)/(X(m,n)^2))*exp(-H(i)/X(m,n))*exp(- |
| (Y(m,n)^2)/(2*(D(i)*X(m,n)^E(i))^2))/ |
| (sqrt(2*pi)*D(i)*X(m,n)^E(i)); |
| else |
| F_S(m,n)=0; |
| F_H(m,n)=0; |
| end |
| end |
| end |
| %Calculate the cumulative footprint weight for each field |
| output(i,1)=sum(sum(F_S)); |
| FNE_S=F_S.*NE; |
| output(i,2)=sum(sum(FNE_S)); |
| FSE_S=F_S.*SE; |
| output(i,3)=sum(sum(FSE_S)); |
| FSW_S=F_S.*SW; |
| output(i,4)=sum(sum(FSW_S)); |
| FNW_S=F_S.*NW; |
| output(i,5)=sum(sum(FNW_S)); |
| output(i,6)=sum(sum(F_H)); |
| FNE_H=F_H.*NE; |
| output(i,7)=sum(sum(FNE_H)); |
| FSE_H=F_H.*SE; |
| output(i,8)=sum(sum(FSE_H)); |
| FSW_H=F_H.*SW; |
| output(i,9)=sum(sum(FSW_H)); |
| FNW_H=F_H.*NW; |
| output(i,10)=sum(sum(FNW_H)); |
| end |
| end |
Appendix C. MATLAB Code for the KM01 Footprint Model
| clear |
| clc |
| %Import data from Excel spreadsheet |
| temp=xlsread('KM_input_1NE.xlsx'); |
| A=temp(:,1); |
| B=temp(:,2); |
| C=temp(:,3); |
| D=temp(:,4); |
| E=temp(:,5); |
| theta=temp(:,6); |
| xprime=xlsread('xprime1.xlsx'); |
| yprime=xlsread('yprime1.xlsx'); |
| NE=xlsread('NE.xlsx'); |
| SE=xlsread('SE.xlsx'); |
| SW=xlsread('SW.xlsx'); |
| NW=xlsread('NW.xlsx'); |
| output=NaN(size(theta,1),5); |
| for i=1:size(theta,1) |
| %Rotate coordinates into mean wind direction |
| if (theta(i)>(-360)) andand (theta(i)<360) |
| X=-yprime*sin(theta(i)*pi/180)+xprime*cos(theta(i)*pi/180); |
| Y=yprime*cos(theta(i)*pi/180)+xprime*sin(theta(i)*pi/180); |
| %Calculate the footprint weights |
| for m=1:size(xprime,1) |
| for n=1:size(xprime,2) |
| if X(m,n)>0 |
| F(m,n)=(1/(sqrt(2*pi)*D(i)*X(m,n)^E(i)))*exp( |
| -(Y(m,n)^2/(2*(D(i)*X(m,n)^E(i))^2))) |
| *C(i)*X(m,n)^-A(i)*exp(-B(i)/X(m,n)); |
| else |
| F(m,n)=0; |
| end |
| end |
| end |
| output(i,1)=sum(sum(F)); |
| %Calculate cumulative footprint weight for each field |
| FNE=F.*NE; |
| output(i,2)=sum(sum(FNE)); |
| FSE=F.*SE; |
| output(i,3)=sum(sum(FSE)); |
| FSW=F.*SW; |
| output(i,4)=sum(sum(FSW)); |
| FNW=F.*NW; |
| output(i,5)=sum(sum(FNW)); |
| end |
| end |
References
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manag. 2011, 98. [Google Scholar] [CrossRef]
- Howell, T.A.; Schneider, A.D.; Dusek, D.A.; Marek, T.H.; Steiner, J.L. Calibration and scale performance of Bushland weighing lysimeters. Trans. Am. Soc. Agric. Eng. 1995, 38. [Google Scholar] [CrossRef]
- Schmid, H.P.; Oke, T.R. A model to estimate the source area contributing to turbulent exchange in the surface layer over patchy terrain. Q. J. R. Meteorol. Soc. 1990, 116. [Google Scholar] [CrossRef]
- Schuepp, P.H.; Leclerc, M.Y.; MacPherson, J.I.; Desjardins, R.L. Footprint prediction of scalar fluxes from analytical solutions of the diffusion equation. Bound. Layer Meteorol. 1990, 50. [Google Scholar] [CrossRef]
- Masseroni, D.; Corbari, C.; Mancini, M. Effect of the Representative Source Area for Eddy Covariance Measuraments on Energy Balance Closure for Maize Fields in the Po Valley, Italy. Int. J. Agric. For. 2012, 1, 1–8. [Google Scholar] [CrossRef]
- Schmid, H.P. Footprint modeling for vegetation atmosphere exchange studies: A review and perspective. Agric. For. Meteorol. 2002, 113. [Google Scholar] [CrossRef]
- Vesala, T.; Kljun, N.; Rannik, Ü.; Rinne, J.; Sogachev, A.; Markkanen, T.; Sabelfeld, K.; Foken, T.; Leclerc, M.Y. Flux and concentration footprint modelling: State of the art. Environ. Pollut. 2008, 152. [Google Scholar] [CrossRef] [PubMed]
- Hsieh, C.I.; Katul, G.; Chi, T.W. An approximate analytical model for footprint estimation of scalar fluxes in thermally stratified atmospheric flows. Adv. Water Resour. 2000, 23. [Google Scholar] [CrossRef]
- Kormann, R.; Meixner, F.X. An analytical footprint model for non-neutral stratification. Bound. Layer Meteorol. 2001, 99. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Olioso, A.; Antonioletti, R.; Brisson, N. Evaluation of the Penman-Monteith model for estimating soybean evapotranspiration. Irrig. Sci. 2004, 23. [Google Scholar] [CrossRef]
- Saito, M.; Miyata, A.; Nagai, H.; Yamada, T. Seasonal variation of carbon dioxide exchange in rice paddy field in Japan. Agric. For. Meteorol. 2005, 135. [Google Scholar] [CrossRef]
- Rogiers, N.; Eugster, W.; Furger, M.; Siegwolf, R. Effect of land management on ecosystem carbon fluxes at a subalpine grassland site in the Swiss Alps. Theor. Appl. Climatol. 2005, 80. [Google Scholar] [CrossRef]
- Hammerle, A.; Haslwanter, A.; Schmitt, M.; Bahn, M.; Tappeiner, U.; Cernusca, A.; Wohlfahrt, G. Eddy covariance measurements of carbon dioxide, latent and sensible energy fluxes above a meadow on a mountain slope. Bound. Layer Meteorol. 2007, 122. [Google Scholar] [CrossRef]
- Li, F.; Kustas, W.P.; Anderson, M.C.; Prueger, J.H.; Scott, R.L. Effect of remote sensing spatial resolution on interpreting tower-based flux observations. Remote Sens. Environ. 2008, 112. [Google Scholar] [CrossRef]
- Timmermans, W.J.; Bertoldi, G.; Albertson, J.D.; Olioso, A.; Su, Z.; Gieske, A.S.M. Accounting for atmospheric boundary layer variability on flux estimation from RS observations. Int. J. Remote Sens. 2008, 29. [Google Scholar] [CrossRef]
- Chen, B.; Black, T.A.; Coops, N.C.; Hilker, T.; Trofymow, J.A.; Morgenstern, K. Assessing tower flux footprint climatology and scaling between remotely sensed and eddy covariance measurements. Bound. Layer Meteorol. 2009, 130. [Google Scholar] [CrossRef]
- Clement, R. EdiRe Data Software; University of Edinburgh: Edinburgh, UK, 1999. [Google Scholar]
- Mauder, M.; Foken, T. TK3; University of Bayreuth: Bayreuth, Germany, 2011. [Google Scholar]
- Leclerc, M.Y.; Thurtell, G.W. Footprint prediction of scalar fluxes using a Markovian analysis. Bound. Layer Meteorol. 1990, 52. [Google Scholar] [CrossRef]
- Kljun, N.; Kormann, R.; Rotach, M.W.; Meixer, F.X. Comparison of the Langrangian footprint model LPDM-B with an analytical footprint model. Bound. Layer Meteorol. 2003, 106. [Google Scholar] [CrossRef]
- Foken, T.; Leclerc, M.Y. Methods and limitations in validation of footprint models. Agric. For. Meteorol. 2004, 127, 223–234. [Google Scholar] [CrossRef]
- Cooper, D.I.; Eichinger, W.E.; Archuleta, J.; Hipps, L.; Kao, J.; Leclerc, M.Y.; Neale, C.M.; Prueger, J. Spatial source-area analysis of three-dimensional moisture fields from lidar, eddy covariance, and a footprint model. Agric. For. Meteorol. 2003, 114. [Google Scholar] [CrossRef]
- Beyrich, F.; Herzog, H.J.; Neisser, J. The LITFASS project of DWD and the LITFASS-98 experiment: The project strategy and the experimental setup. Theor. Appl. Climatol. 2002, 73. [Google Scholar] [CrossRef]
- Rannik, U.; Aubinet, M.; Kurbanmuradov, O.; Sabelfeld, K.K.; Markkanen, T.; Vesala, T. Footprint analysis for measurements over a heterogeneous forest. Bound. Layer Meteorol. 2000, 97. [Google Scholar] [CrossRef]
- Schmid, H.P. Experimental design for flux measurements: Matching scales of observations and fluxes. Agric. For. Meteorol. 1997, 87. [Google Scholar] [CrossRef]
- Marcolla, B.; Cescatti, A. Experimental analysis of flux footprint for varying stability conditions in an alpine meadow. Agric. For. Meteorol. 2005, 135. [Google Scholar] [CrossRef]
- Evett, S.R.; Kustas, W.P.; Gowda, P.H.; Anderson, M.C.; Prueger, J.H.; Howell, T.A. Overview of the Bushland Evapotranspiration and Agricultural Remote sensing EXperiment 2008 (BEAREX08): A field experiment evaluating methods for quantifying ET at multiple scales. Bushland Evapotranspiration Agric. Remote Sens. Exp. 2012, 50, 4–19. [Google Scholar] [CrossRef]
- Howell, T.A.; Evett, S.R.; Tolk, J.A.; Schneider, A.D. Evapotranspiration of Full-, Deficit-Irrigated, and Dryland Cotton on the Northern Texas High Plains. J. Irrig. Drain. Eng. 2004, 130. [Google Scholar] [CrossRef]
- New, L. AgriPartner Irrigation Result Demonstrations 2007; Texas AgriLife Extension Service: Amarillo, TX, USA, 2008. [Google Scholar]
- Marek, T.H.; Schneider, A.D.; Howell, T.A.; Ebeling, L.L. Design and construction of large weighing monolithic lysimeters. Trans. Am. Soc. Agric. Eng. 1988, 31. [Google Scholar] [CrossRef]
- Evett, S.R.; Schwartz, R.C.; Howell, T.A.; Louis Baumhardt, R.; Copeland, K.S. Can weighing lysimeter ET represent surrounding field ET well enough to test flux station measurements of daily and sub-daily ET? Adv. Water Resour. 2012, 50, 79–90. [Google Scholar] [CrossRef]
- Evett, S.R.; Tolk, J.A.; Howell, T.A. Time Domain Reflectometry Laboratory Calibration in Travel Time, Bulk Electrical Conductivity, and Effective Frequency. Vadose Zone J. 2005, 4. [Google Scholar] [CrossRef]
- Evett, S.; Schwartz, R. Internal Report to BEAREX08 Users of CS616 Soil Water Sensor Data: Correction Algorithm, 2009.
- Lee, X.; Massman, W.; Law, B. (Eds.) Handbook of Micrometeorology; Atmospheric and Oceanographic Sciences Library; Springer: Dordrecht, The Netherlands, 2005; Volume 29, ISBN 978-1-4020-2264-7. [Google Scholar]
- Burba, G.; DJ, A. A Brief Practical Guide to Eddy Covariance Flux Measurements: Principles and Workflow Examples for Scientific and Industrial Applications; LI-COR Biosciences: Lincoln, NE, USA, 2010; ISBN 978-0-61543013-3. [Google Scholar]
- Vickers, D.; Mahrt, L. Quality control and flux sampling problems for tower and aircraft data. J. Atmos. Ocean. Technol. 1997, 14. [Google Scholar] [CrossRef]
- McMillen, R.T. An eddy correlation technique with extended applicability to non-simple terrain. Bound. Layer Meteorol. 1988, 43. [Google Scholar] [CrossRef]
- Kaimal, J.; Finnigan, J. Atmospheric Boundary Layer Flows: Their Structure and Measurement; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. Q. J. R. Meteorol. Soc. 1980, 106. [Google Scholar] [CrossRef]
- Moore, C.J. Frequency response corrections for eddy correlation systems. Bound. Layer Meteorol. 1986, 37. [Google Scholar] [CrossRef]
- Schotanus, P.; Nieuwstadt, F.T.M.; De Bruin, H.A.R. Temperature measurement with a sonic anemometer and its application to heat and moisture fluxes. Bound. Layer Meteorol. 1983, 26. [Google Scholar] [CrossRef]
- Campbell, G.S.; Norman, J.M. An Introduction to Environmental Biophysics; Springer: New York, NY, USA, 1998; ISBN 978-0-387-94937-6. [Google Scholar]
- Raupach, M.R. Drag and drag partition on rough surfaces. Bound. Layer Meteorol. 1992, 60. [Google Scholar] [CrossRef]
- Raupach, M.R. Simplified expressions for vegetation roughness length and zero-plane displacement as functions of canopy height and area index. Bound. Layer Meteorol. 1994, 71. [Google Scholar] [CrossRef]
- Raupach, M. Corrigenda. Bound. Layer Meteorol. 1995, 76. [Google Scholar] [CrossRef][Green Version]
- Stull, R.B. An introduction to boundary layer meteorology. Introd. Bound. Layer Meteorol. 1988. [Google Scholar] [CrossRef]
- Foken, T.; Wichura, B. Tools for quality assessment of surface-based flux measurements. Agric. For. Meteorol. 1996, 78. [Google Scholar] [CrossRef]
- Thomas, C.; Foken, T. Re-evaluation of Integral Turbulence Characteristics and Their Parameterisations. In Proceedings of the 15th Conference on Turbulence and Boundary Layers, Wageningen, The Netherlands, 14–19 July 2002. [Google Scholar]
- Gash, J.H.C. A note on estimating the effect of a limited fetch on micrometeorological evaporation measurements. Bound. Layer Meteorol. 1986, 35. [Google Scholar] [CrossRef]
- Calder, K. Some Recent British Work on the Problme of Diffusion in the Lower Atmosphere. In Proceedings of the U.S. Tecnology Conference on Air Pollution, McGraw-Hill, New York, NY, USA, 3 October 2002; 1952; pp. 787–792. [Google Scholar]
- Dyer, A.J. A review of flux-profile relationships. Bound. Layer Meteorol. 1974, 7. [Google Scholar] [CrossRef]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180. [Google Scholar] [CrossRef]
- Pasquill, F. Atmospheric Diffusion, 2nd ed.; J. Wiley & Sons: New York, NY, USA, 1974. [Google Scholar]
- Schmid, H.P. Source areas for scalars and scalar fluxes. Bound. Layer Meteorol. 1994, 67. [Google Scholar] [CrossRef]
- Neftel, A.; Spirig, C.; Ammann, C. Application and test of a simple tool for operational footprint evaluations. Environ. Pollut. 2008, 152. [Google Scholar] [CrossRef] [PubMed]
- Willmott, C.J. Some comments on the evaluation of model performance. Bull. Am. Meteorol. Soc. 1982, 63. [Google Scholar] [CrossRef]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. 1985, 90. [Google Scholar] [CrossRef]
- Kriegler, F.J.; Malila, W.A.; Nalepka, R.F.; Richardson, W. Preprocessing Transformations and Their Effects on Multispectral Recognition. In Proceedings of the 6th International Symposium on Remote Sensing of Environment, Willow Run Laboratories, Ann Arbor, MI, USA, 13–16 October 1969; Volume II, p. 97. [Google Scholar]
- U.S. Geological Survey EarthExplorer. Available online: https://earthexplorer.usgs.gov/ (accessed on 3 October 2011).
- Alfieri, J.G.; Kustas, W.P.; Prueger, J.H.; Hipps, L.E.; Chávez, J.L.; French, A.N.; Evett, S.R. Intercomparison of Nine Micrometeorological Stations During the BEAREX08 Field Campaign. J. Atmos. Ocean. Technol. 2011. [Google Scholar] [CrossRef][Green Version]

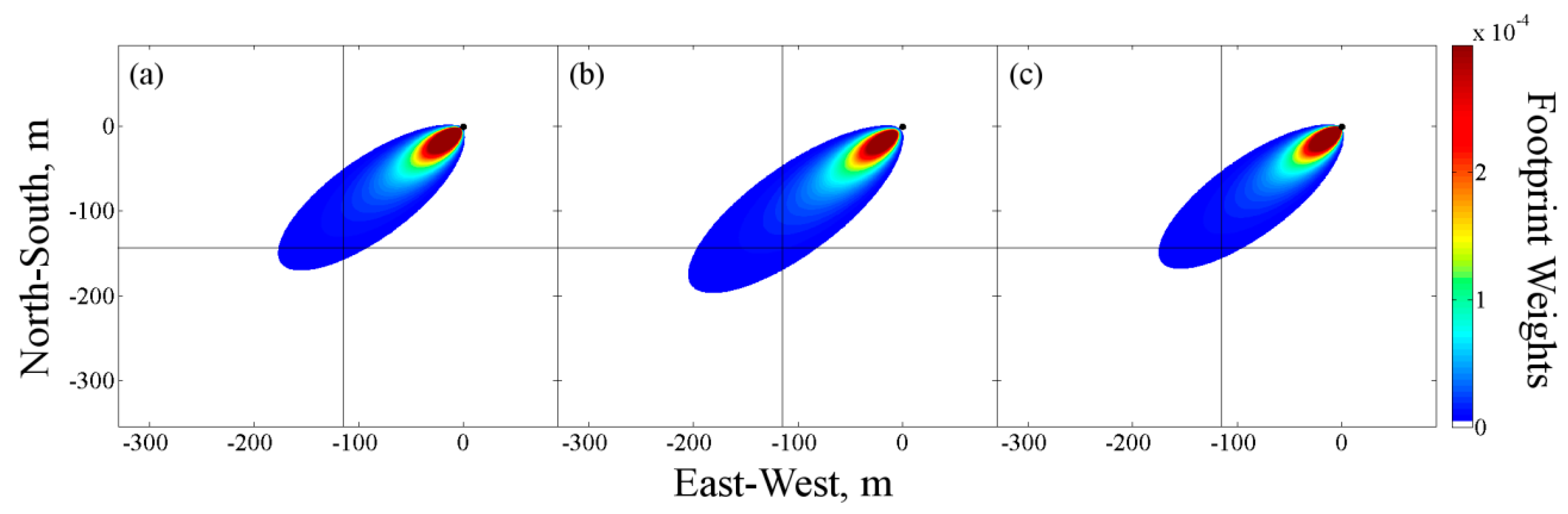
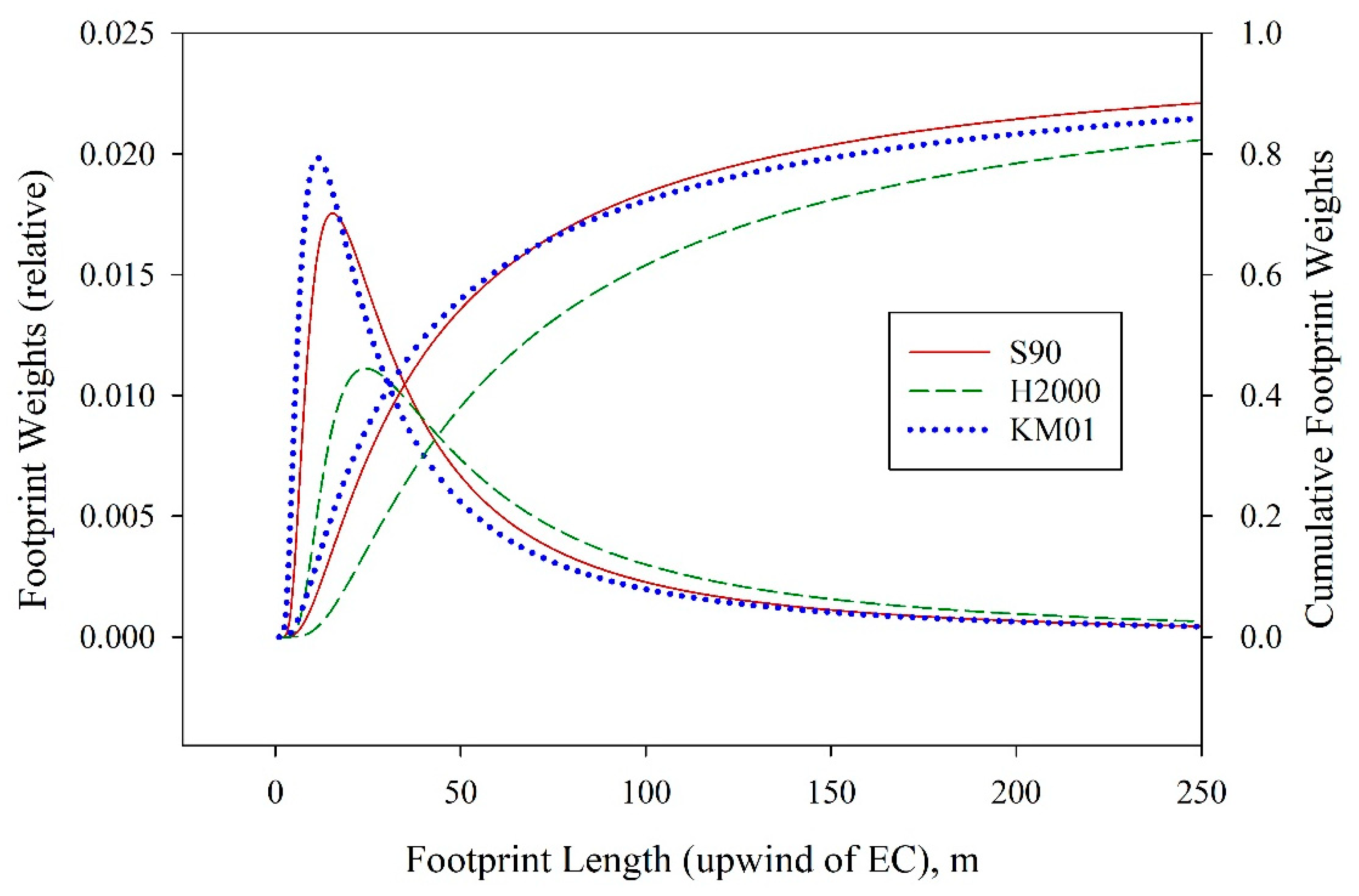
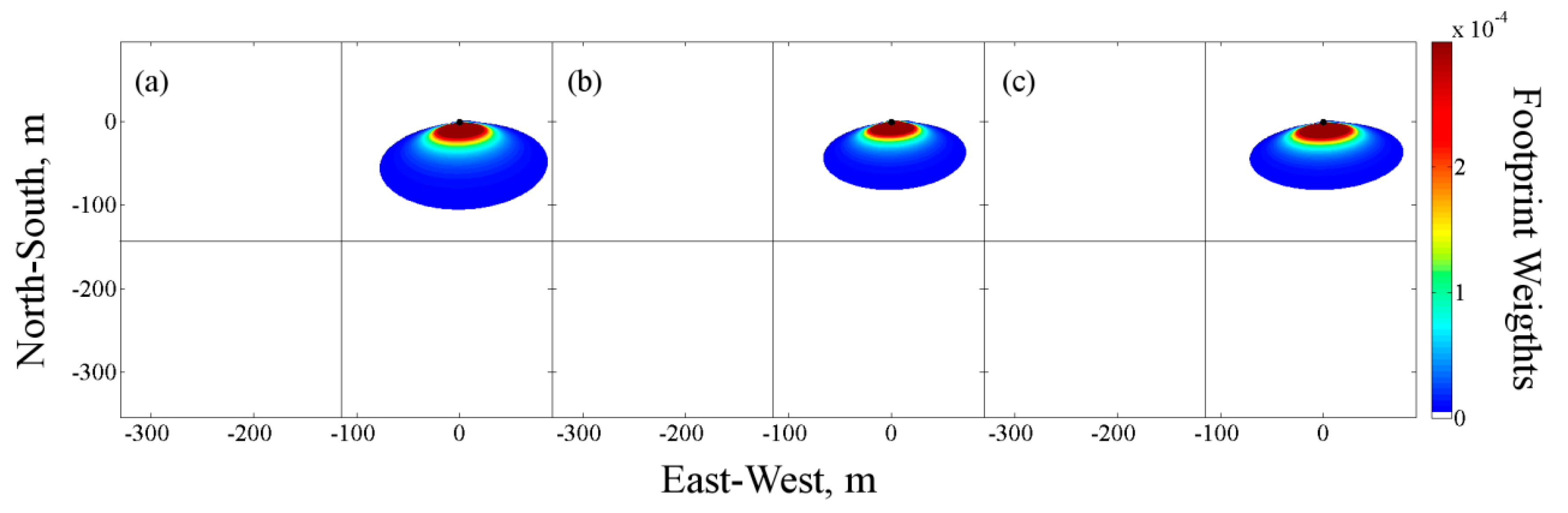
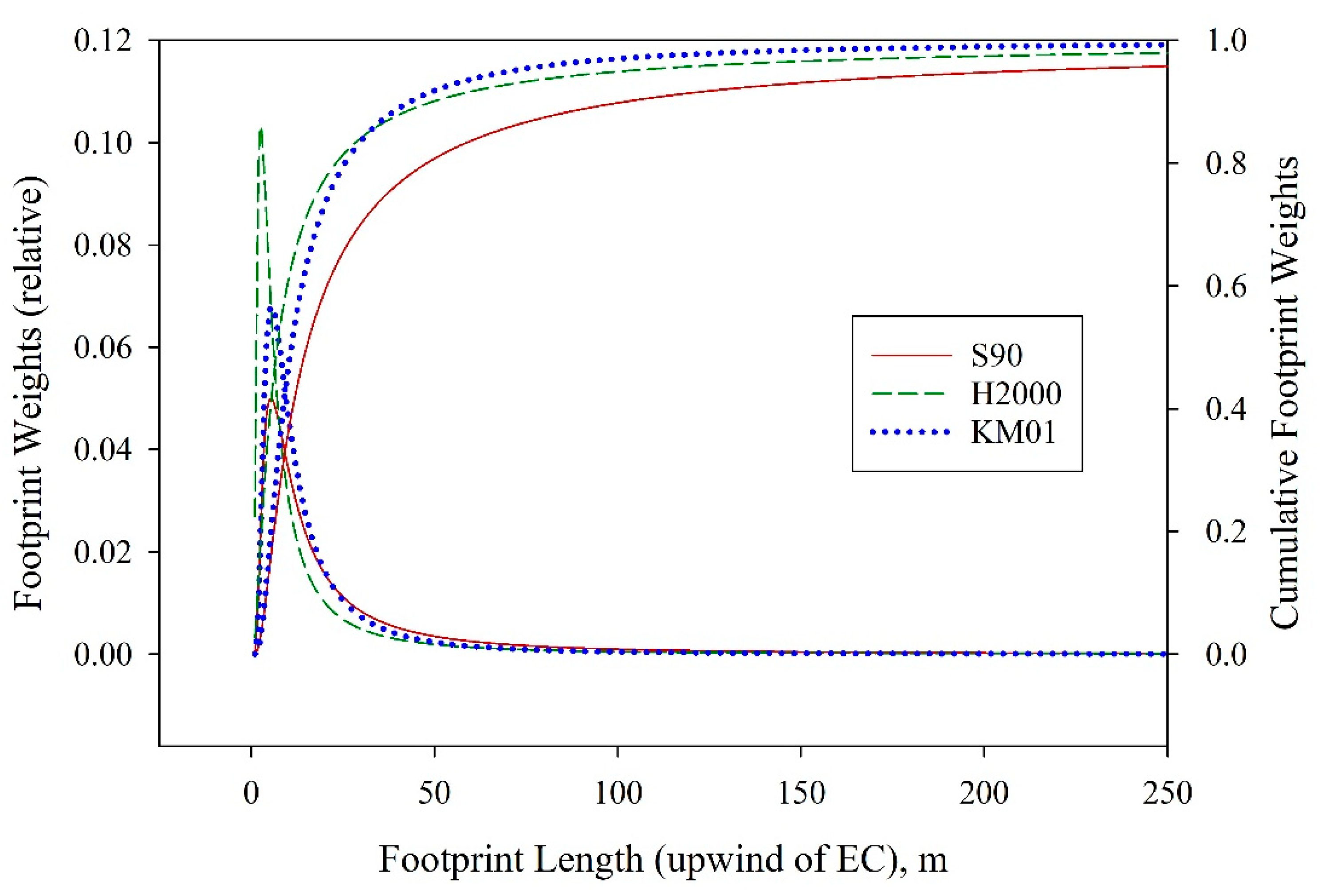
| Instrument | EC8 | EC1, EC2, EC3, EC5 | Lysimeters |
|---|---|---|---|
| 3D Sonic Anemometer | CSAT3 1 | CSAT3 1 | — |
| Open Path Gas Analyzer | LI-7500 2 | LI-7500 2 | — |
| Fine Wire Thermocouple | FW05 1 | FW05 1 | — |
| Air Temp/Relative Humidity | HMP45C 3 | HMP45C 3 | HMP45C 3 |
| Barometer | CS106 1 | — | — |
| Net Radiometer | — | CNR1 5 | REBS Q*7.1 4, KandZ CM14 5, KandZ CGR3 5 |
| Soil Heat Flux Plates | (2) REBS HFT-3 4 | (3) REBS HFT-1.1 4 | (4) REBS HFT-1.1 4 |
| Soil Temperature | (4) TCAV 1 | (6) TMTSS-020G-6 6 | (8) TMTSS-020G-6 6 |
| Soil Water Content | (2) CS616 1 | (3) CS616 1 | — |
| Precipitation Gauge | — | — | Qualimetrics 6011B 7 |
| Datalogger | CR3000 1 | CR5000 1 | CR7X 1 |
| CSAT Azimuth | 225° | 180° | — |
| Measurement Height | 2.5 m | 2.25 m | — |
| Sampling frequency | 20 Hz 7 | 20 Hz 7 | 0.17 Hz |
| Procedure | EdiRe Commands | |
|---|---|---|
| 1 | Extract raw time series data | Extract |
| 2 | Calculate wind direction | Wind direction |
| 3 | Remove spikes | Despike |
| 4 | Calculate and remove lag between instruments | Cross correlate, Remove lag |
| 5 | Rotate coordinates | Rotation coefficients, Rotation |
| 6 | Calculate means, standard deviations, skewness, and kurtosis | 1 chn statistics |
| 7 | Calculate covariances and fluxes | Latent heat of evaporation, Sensible heat flux coefficient, 2 chn statistics |
| 8 | Calculate friction velocity and stability | User defined, Stability - Monin Obukhov |
| 9 | Calculate and apply frequency response corrections | Frequency response |
| 10 | Calculate and apply Schotanus H correction | Sonic T - heat flux correction |
| 11 | Calculate and apply WPL correction | Webb correction |
| 12 | Iterate steps 8–11 two times | |
| 13 | Convert LE to ET (mm h−1) | User defined |
| 14 | Calculate roughness length | Roughness length (z0) |
| 15 | Calculate stationarity | Stationarity |
| Footprint Model | N | MBE | MBE | RMSE | RMSE | Slope | Intercept | R2 |
|---|---|---|---|---|---|---|---|---|
| (mm h−1) | (%) | (mm h−1) | (%) | (mm h−1) | ||||
| S90 | 38 | −0.10 | −24.45 | 0.12 | 16.66 | 0.68 | 0.027 | 0.85 |
| H2000 | 31 | −0.10 | −21.60 | 0.12 | 15.71 | 0.64 | 0.052 | 0.83 |
| KM01 | 40 | −0.09 | −22.09 | 0.11 | 15.54 | 0.69 | 0.032 | 0.83 |
| Footprint Model by Period | N | MBE | MBE | RMSE | RMSE | Slope | Intercept | R2 |
|---|---|---|---|---|---|---|---|---|
| (mm h−1) | (%) | (mm h−1) | (%) | (mm h−1) | ||||
| DOY 158-194 | ||||||||
| S90 | 4 | −0.04 | −8.04 | 0.05 | 7.70 | 0.71 | 0.069 | 0.98 |
| H2000 | 18 | −0.04 | −6.08 | 0.08 | 10.91 | 0.60 | 0.106 | 0.93 |
| KM01 | 15 | −0.05 | −6.27 | 0.10 | 11.96 | 0.58 | 0.117 | 0.96 |
| DOY 195-228 | ||||||||
| S90 | 32 | −0.03 | −3.30 | 0.10 | 10.80 | 0.89 | 0.048 | 0.84 |
| H2000 | 37 | −0.03 | −3.46 | 0.10 | 10.67 | 0.88 | 0.053 | 0.83 |
| KM01 | 46 | −0.04 | −4.76 | 0.10 | 11.39 | 0.89 | 0.038 | 0.82 |
| DOY 158-228 | ||||||||
| S90 | 36 | −0.03 | −3.83 | 0.09 | 10.50 | 0.91 | 0.030 | 0.87 |
| H2000 | 55 | −0.03 | −4.32 | 0.09 | 10.75 | 0.89 | 0.032 | 0.88 |
| KM01 | 61 | −0.04 | −5.13 | 0.10 | 11.54 | 0.87 | 0.039 | 0.85 |
| EC System per Period | Cumulative Footprint | ||||
|---|---|---|---|---|---|
| NE | SE | NW | SW | Combined | |
| DOY 158-194 | |||||
| EC8 | 69 | 11 | 1 | 3 | 85 |
| EC3 | 4 | 1 | 74 | 5 | 83 |
| EC5 | 0 | 3 | 0 | 76 | 79 |
| DOY 195-228 | |||||
| EC8 | 80 | 6 | 1 | 1 | 88 |
| EC3 | 2 | 1 | 84 | 3 | 90 |
| EC5 | 0 | 1 | 0 | 85 | 87 |
| DOY 158-228 | |||||
| EC8 | 77 | 7 | 1 | 2 | 87 |
| EC3 | 3 | 1 | 80 | 4 | 87 |
| EC5 | 0 | 2 | 0 | 82 | 84 |
| Footprint Model | N | MBE | MBE | RMSE | RMSE | Slope | Intercept | R2 |
|---|---|---|---|---|---|---|---|---|
| (mm h−1) | (%) | (mm h−1) | (%) | (mm h−1) | ||||
| Stable | ||||||||
| S90 | 19 | −0.03 | −3.16 | 0.12 | 12.75 | 0.85 | 0.090 | 0.73 |
| H2000 | 21 | −0.05 | −4.36 | 0.13 | 14.10 | 0.77 | 0.139 | 0.62 |
| KM01 | 26 | −0.05 | −6.32 | 0.13 | 14.14 | 0.85 | 0.063 | 0.71 |
| Unstable | ||||||||
| S90 | 17 | −0.03 | −4.58 | 0.05 | 7.20 | 0.83 | 0.057 | 0.88 |
| H2000 | 34 | −0.03 | −4.30 | 0.05 | 8.01 | 0.82 | 0.048 | 0.88 |
| KM01 | 35 | −0.03 | −4.32 | 0.07 | 9.13 | 0.76 | 0.077 | 0.81 |
| Footprint Model | N | MBE | MBE | RMSE | RMSE | Slope | Intercept | R2 |
|---|---|---|---|---|---|---|---|---|
| (mm h−1) | (%) | (mm h−1) | (%) | (mm h−1) | ||||
| DOY158-194 | ||||||||
| No Ftp Adjustment | ||||||||
| S90 | 4 | −0.04 | −10.78 | 0.04 | 7.57 | 1.13 | −0.093 | 0.98 |
| H2000 | 18 | −0.02 | −7.85 | 0.06 | 10.23 | 1.30 | −0.137 | 0.92 |
| KM01 | 15 | −0.01 | −7.23 | 0.08 | 11.65 | 1.42 | −0.189 | 0.93 |
| Ftp Adjustment | ||||||||
| S90 | 4 | 0.02 | 2.00 | 0.04 | 6.04 | 1.30 | −0.108 | 0.98 |
| H2000 | 18 | 0.03 | 3.47 | 0.09 | 12.15 | 1.50 | −0.165 | 0.92 |
| KM01 | 15 | 0.03 | 4.01 | 0.10 | 13.91 | 1.61 | −0.217 | 0.94 |
| DOY195-228 | ||||||||
| No Ftp Adjustment | ||||||||
| S90 | 21 | −0.07 | −9.01 | 0.13 | 12.84 | 0.80 | 0.080 | 0.84 |
| H2000 | 25 | −0.07 | −9.70 | 0.13 | 12.73 | 0.81 | 0.063 | 0.85 |
| KM01 | 28 | −0.07 | −10.32 | 0.12 | 12.59 | 0.82 | 0.049 | 0.85 |
| Ftp Adjustment | ||||||||
| S90 | 21 | 0.00 | 0.59 | 0.11 | 11.23 | 0.92 | 0.063 | 0.84 |
| H2000 | 25 | 0.00 | 0.06 | 0.11 | 10.83 | 0.93 | 0.051 | 0.85 |
| KM01 | 28 | −0.01 | −1.18 | 0.10 | 10.20 | 0.94 | 0.032 | 0.86 |
| DOY158-228 | ||||||||
| No Ftp Adjustment | ||||||||
| S90 | 25 | −0.07 | −9.29 | 0.12 | 12.15 | 0.82 | 0.056 | 0.87 |
| H2000 | 43 | −0.05 | −8.93 | 0.11 | 11.75 | 0.87 | 0.027 | 0.88 |
| KM01 | 43 | −0.05 | −9.24 | 0.11 | 12.27 | 0.87 | 0.025 | 0.86 |
| Ftp Adjustment | ||||||||
| S90 | 25 | 0.01 | 0.81 | 0.11 | 10.58 | 0.94 | 0.049 | 0.87 |
| H2000 | 43 | 0.01 | 1.49 | 0.10 | 11.40 | 0.98 | 0.025 | 0.88 |
| KM01 | 43 | 0.01 | 0.63 | 0.10 | 11.63 | 0.99 | 0.020 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Joy, S.L.; Chávez, J.L. Correction of Eddy Covariance Based Crop ET Considering the Heat Flux Source Area. Atmosphere 2021, 12, 281. https://doi.org/10.3390/atmos12020281
Joy SL, Chávez JL. Correction of Eddy Covariance Based Crop ET Considering the Heat Flux Source Area. Atmosphere. 2021; 12(2):281. https://doi.org/10.3390/atmos12020281
Chicago/Turabian StyleJoy, Stuart L., and José L. Chávez. 2021. "Correction of Eddy Covariance Based Crop ET Considering the Heat Flux Source Area" Atmosphere 12, no. 2: 281. https://doi.org/10.3390/atmos12020281
APA StyleJoy, S. L., & Chávez, J. L. (2021). Correction of Eddy Covariance Based Crop ET Considering the Heat Flux Source Area. Atmosphere, 12(2), 281. https://doi.org/10.3390/atmos12020281







