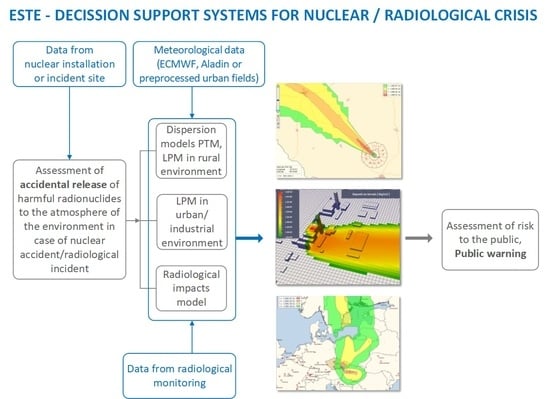
2.1. Lagrangian Particle Model: Specific Set-Up Assumptions in ESTE
The LPM uses a large number of independent particles to describe the diffusion of radionuclides in the atmosphere, and it performs a simulation of the movement and dispersion of particles inside the wind field. Each particle carries a specific amount of radionuclides from the radioactive cloud. In general, the wind field consists of a mean wind field and a turbulent field. The basic equations for the particle positions are:
where x
i as the i-th component of (x
1,x
2,x
3) specifies the position of the particle (at the times t and t + Δt), ∆t is the time step, U
i as the
i-th component of (U
1,U
2,U
3) is the velocity vector of the mean wind field at the given position (x,y,z), and (u
1,u
2,u
3) is the turbulent component of velocity vector. The mean wind field is included in the provided numerical weather-prediction data (NWP data) directly. The LPM model of the ESTE system requires NWP data for its run. The model is able to apply various sources of NWP data; for example, data from the European Centre for Medium-Range Weather Forecasts (ECMWF), or data from the National Weather Service of the National Oceanic and Atmospheric Administration, USA (NWS/NOAA). The turbulent component of velocity vector is expressed using Langevin equation [
9].
where a is the drift term and b is the diffusion term. Both of them are a function of particle position and turbulent velocity. dW
j is incremental components of a Wiener process, here a Gaussian random variable. The LPM implemented in ESTE is based on a theoretical description of the FLEXPART model [
10], and therefore both drift and diffusion terms obtain the form as in the FLEXPART model [
10].
The implementation in ESTE was validated successfully several times in various projects, e.g., a comparison in [
11] was performed directly with the FLEXPART model implemented in TAMOS (the Austrian emergency response modeling system).
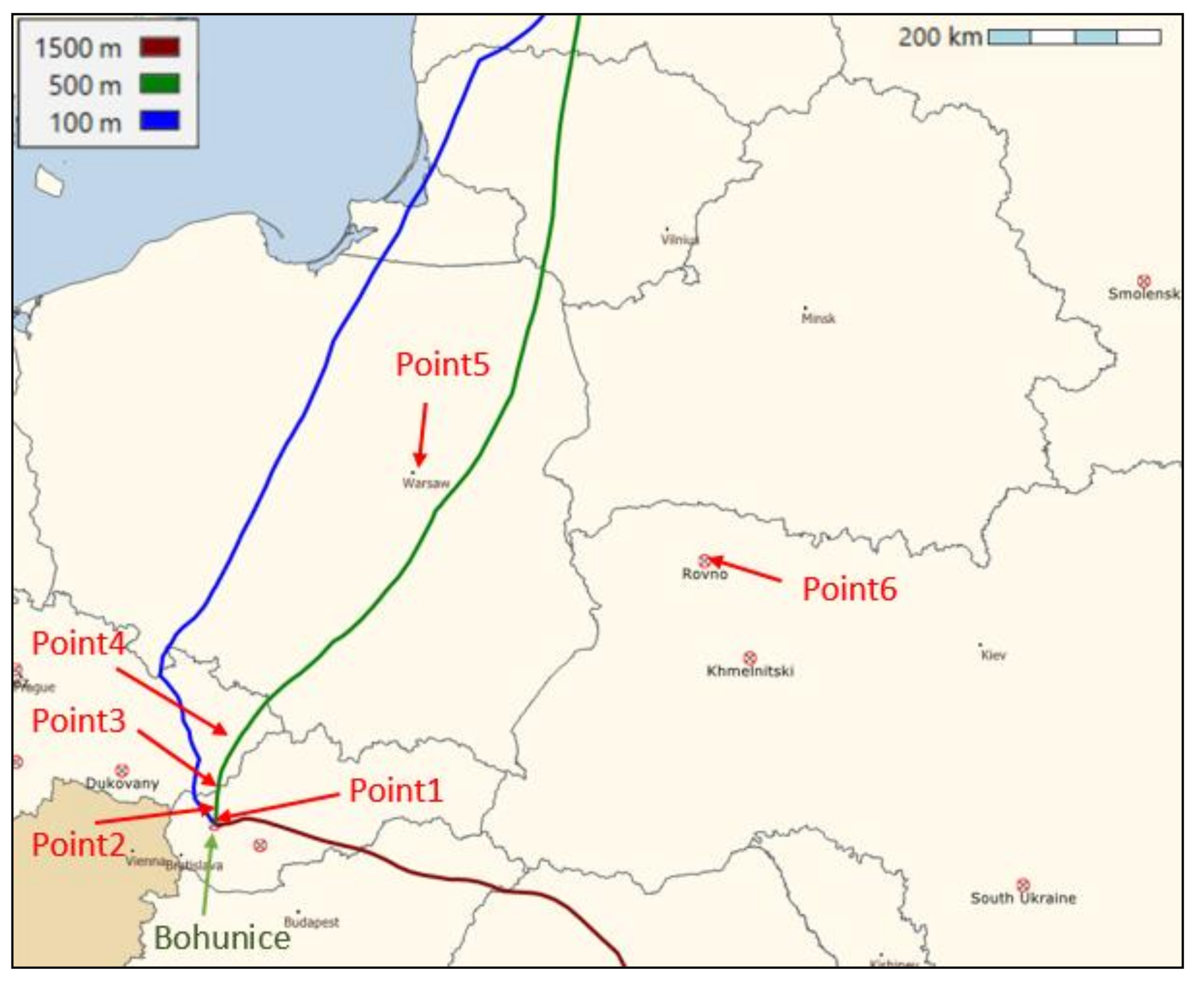
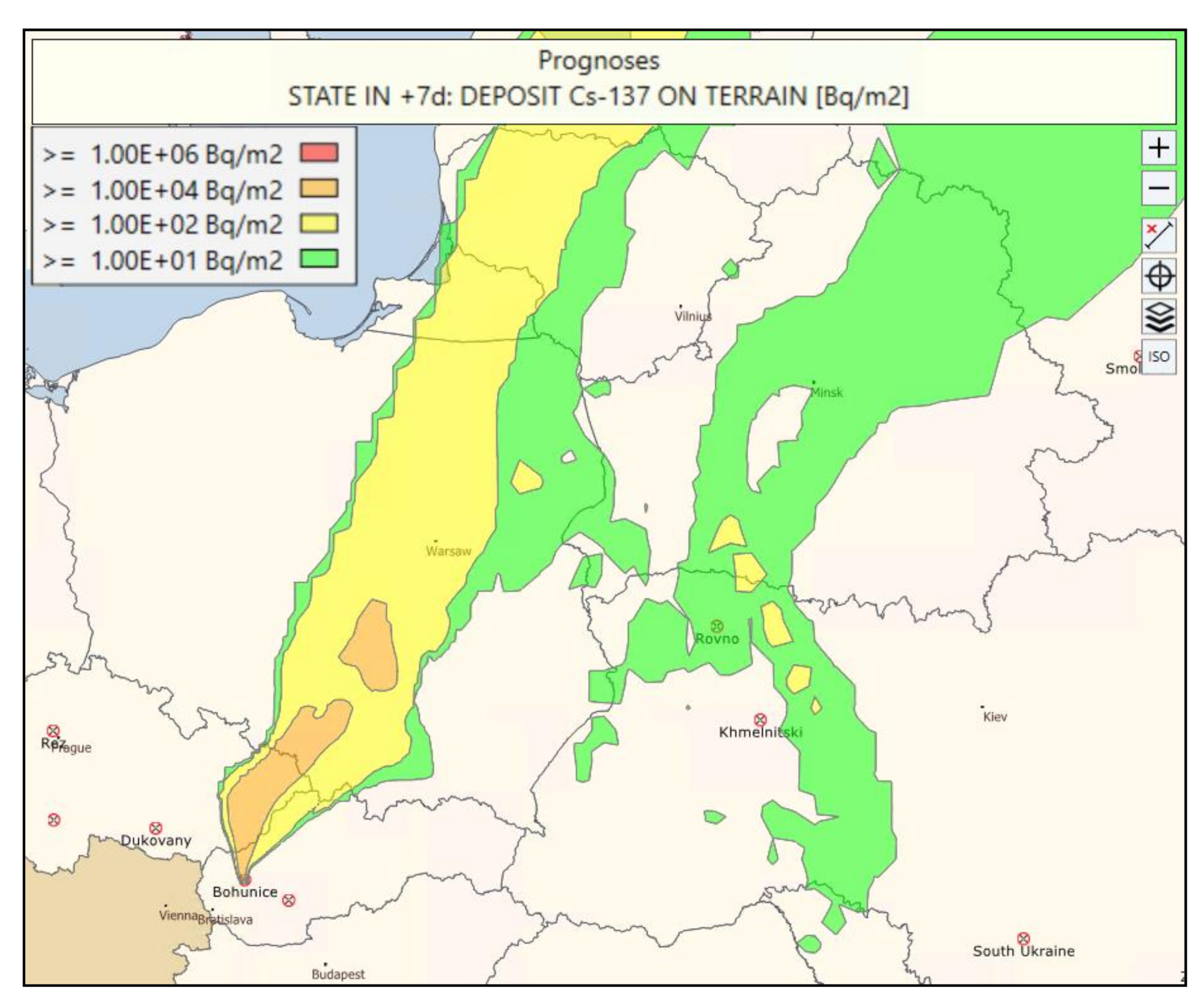
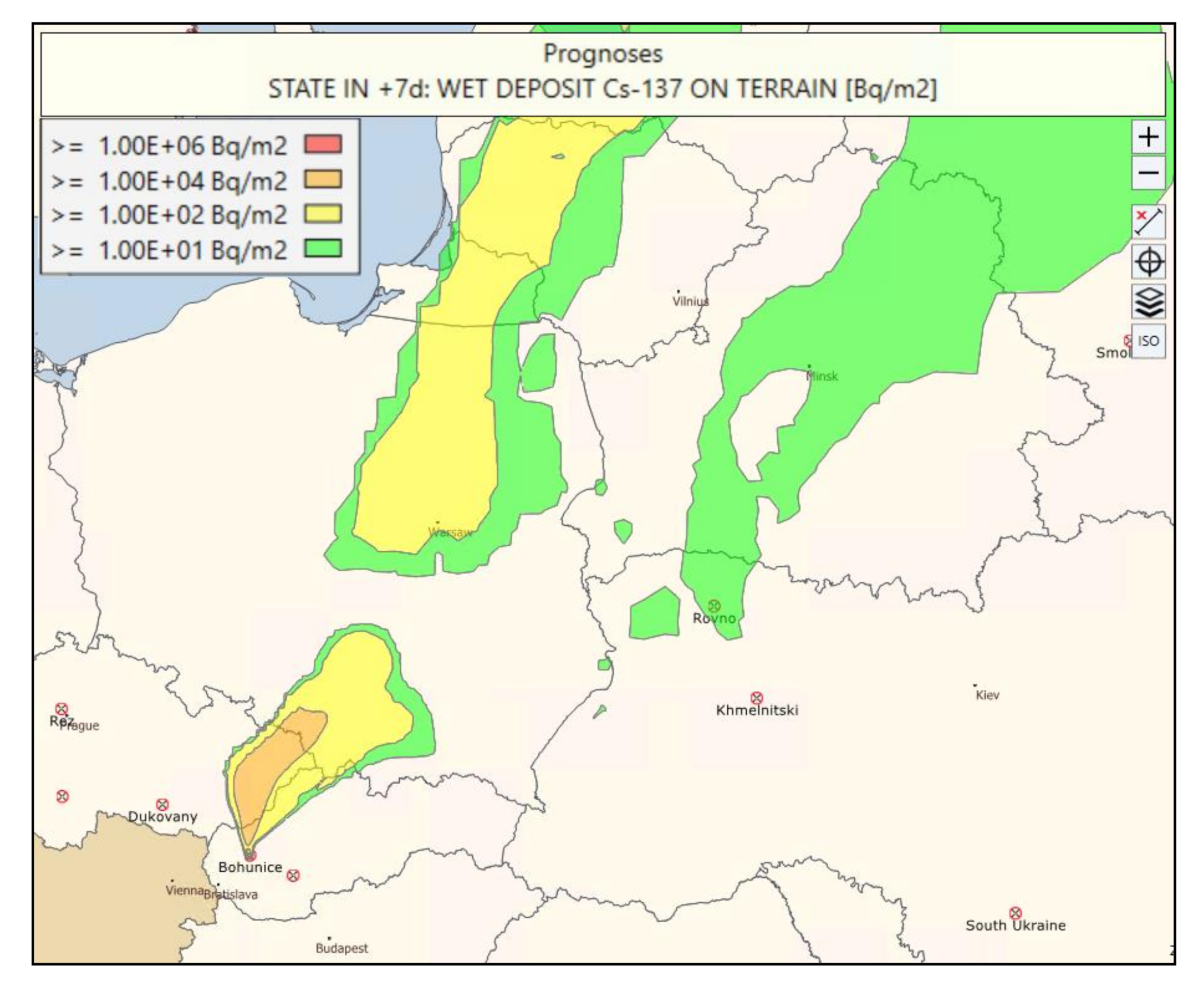
Moreover, the implemented LPM model in the ESTE system enabled the simulation of impacts of the Fukushima accident, even at transcontinental distances. Here, we focus only on the simple comparison of the transport time (a further comparison was not performed due to its complexity). In the
Supplementary Materials, in which a visualization in the form of video of the performed simulation is included (
video S3), the impacts on Europe, especially on central Europe, were the center of interest. The simulation shows modeled atmospheric dispersion in the northern hemisphere of the released I-131 (equal to 1.5 × 10
17 Bq as estimated by ESTE, based on a reverse estimation from the dose rate measured in the area of the nuclear power plant (NPP), and on assumption of partial core damage or partial melting in SFP [
12]). The release was modeled from March 12 to 14, 2011. The results of dispersion and radiological impacts are visualized in subsequent days, from March 15 to March 30, 2011. The control forecast of the operational archive of the ECMFW data was applied. A basic estimate resulting from the simulation is that the airborne contamination would reach the central Europe approximately on March 24, 2011. For a comparison, the first reported measurement of I-131 in the Czech Republic was on March 23 [
13], which represents an acceptable result.
Specific aspects of the LPM of ESTE that have influence on dispersion and radiation impacts calculation are:
Dry deposition—characterized by deposition velocity ν
d (in m.s
−1), which is specified for various types of airborne material (e.g., gases, aerosols, iodine forms) and ground features (e.g., urban, forest, water). Deposited material in time step Δt is then calculated as:
where m is the amount of activity born by particles in the lowest reference layer with the height
h.
Wet deposition—following the model in [
14], this is governed in the LPM of ESTE (and in the implemented PTM as well) by the washout coefficient Λ, which depends on the precipitation rate I (in mm/h):
cwo is the coefficient of wet deposition, and is set to
cwo = 1.3 × 10
−4 s
−1 for elemental iodine,
cwo = 1.3 ×10
−6 s
−1 for organic iodine, and
cwo = 2.6 × 10
−5 s
−1 for all radionuclides in aerosol form. The deposited material in time step Δt is assumed to follow the formula:
where the approach applied in ESTE assumes the washout along the whole height of the atmospheric boundary layer (ABL), and the height of the clouds is not taken into account.
Release points—the position of the leakage point affects the impacts in the vicinity of nuclear facility in which the accident took place, but the leakage point in a real nuclear disaster can be uncertain and unknown. Generally, the leakage of harmful radionuclides can occur in any part of the containment structure in case of containment leakage, in the outlet of the plant ventilation stack, or in the outlet of the containment ventilation system. Moreover, the inner conditions inside the nuclear facility, like overpressure, fire, and explosions, can considerably affect the leakage conditions. The initial spatial distribution of the release points in the LPM of the ESTE system can be set up as a point source at a given height, a line-shape source, a source in the shape of a cylinder, or a hemisphere. In ESTE systems running in nuclear crisis centers, an assumption of a vertical-line-shaped source is applied, with the line center at the height of the realized release pathways. The center might be located at the height of the containment building, or at the height of the roof of the machinery room, at the height of the outlet of the reactor building ventilation stack, or at the outlet of the containment annulus ventilation. The performed study of the influence of initial spatial distribution of the release points at the beginning of the dispersion calculation is presented and discussed in
Section 3.2.
Height of the bottom reference layer of air—this is the air layer that is used to evaluate the air concentration over the ground surface, applied in dry-deposition calculations, as well as in impact calculations (especially for effective dose by inhalation). As the previous aspect of the simulation setup, the modeled bottom-air-layer height above ground also affects the calculated impacts in the vicinity of the nuclear facility in which the accident took place. In the LPM of the ESTE system, the height of the bottom layer of air is set to 100 m. The results of our study of the influence of the height of the bottom reference layer of air are presented and discussed in
Section 3.3.
Total number of modeled particles—the accuracy of dispersion calculation and radiological impacts calculation is determined by the total number of modeled particles. A relatively high number of particles is expected for the calculation in order to achieve an acceptable level of accuracy. The higher the number of particles, the longer the time to carry out the calculations. The time is strictly controlled in decision-support systems like ESTE that are in real operation in nuclear crisis centers. An acceptable time to carry out the calculations in local scale and mesoscale is about 15 min. In the case of ESTE, the parameters affecting the duration of impact calculation, to which the number of particles belongs, are set to fulfill this time limit. Naturally, if the calculations are performed at a large or global scale where the modeled phenomenon is on the level of several days or weeks (for example, modeling of the atmospheric transport and impacts of the Fukushima accident to central Europe), then the time limit for duration of the calculation is less strict, allowing a longer calculation and a higher number of modeled particles. Our study of the influence of the total number of modeled particles is presented and discussed in
Section 3.1.
Number of radionuclides in the source term—the nuclear reactor core inventory consists of more than 1000 various isotopes created as a result of nuclear fission. At the same time, many of them are short-lived isotopes or isotopes with a negligible radiological impact. In case of a nuclear disaster, about 50 isotopes have the potential to be released into the environment in a significant amount, and also to cause a significant threat to humans and the environment. This group is covered by the set of radionuclides (
Table 1) assumed at the input, in all modeled processes of the LPM in ESTE, as well as in radiological models of ESTE.
calculation of radiological parameters includes evaluation of the following quantities:
Committed effective dose by inhalation: the instant dose rate DR
inhal and the integral dose D
inhal are calculated as:
where C
0 is the actual air concentration, C
int is the time-integrated concentration in the bottom reference layer for radionuclide n, BR is the breathing rate, depending on the age category, and CF
inhal is the conversion factor for the committed effective dose for inhalation, depending on the age and nuclide.
External dose by deposition: the instant dose rate is calculated as:
where D
0 (n) is the deposition of radionuclide n on the terrain, CF
depo is the conversion factor for the external dose via deposition, as a function of radionuclide.
External dose by cloudshine: the instant dose rate is calculated as:
where C
0(n) is the air concentration in the bottom reference layer, and CF
cloud is the conversion factor for cloudshine, and dependent on the radionuclide. The factors represent an approach of semi-infinite cloud of constant concentration, i.e., the point of interest, either a radiation monitor or a human, is immersed in the activity of the air hemisphere with constant concentration.
2.2. Puff Trajectory Model
The Puff trajectory model (PTM) implemented in ESTE is a puff transport model combined with a Gaussian dispersion model in the horizontal direction and with a model based on a diffusion equation in the vertical direction. The release consists of puffs, and each puff carries a particular amount of the released radionuclides, which is the released activity per a specific time period, e.g., in units [Bq/1 h] or [Bq/10 min].
Basic model components and assumptions of the implemented PTM are:
Advection: The trajectories of the puffs are obtained as integrated paths for the wind field of numerical weather prediction data:
where U, V represent horizontal components of the wind field, and x and y are the characterized position of the puff in the given times t and t + ∆t. Both components U and V are dependent on height, and the height is taken as the height of center of mass of the puff.
Vertical dispersion: The puffs are distributed in many vertical layers, and the carried activity is mixing among these layers. In the ESTE system, the model works with the assumption of a division of the atmosphere into 10 equally thick layers. Diffusion coefficients are characterized using formulas [
14]. In that applied approach, they are functions of the Pasquill category of stability and functions of the height above the terrain. The assumed height of the atmosphere, here meaning air between the ground and the atmospheric boundary layer (ABL), is related to the Pasquill category of stability (see [
14]). In cases of very unstable conditions (i.e., category A) and very stable conditions (i.e., category F), which represent two extreme situations, the height of ABL is 1600 m and 200 m above the ground, respectively.
Horizontal dispersion: This is represented by a Gaussian model, where the puff sigma functions depend on wind speed, category stability, and travel distance. The included sigma functions [
15] are dealing with rural and urban environments, as well as calm conditions (applying Briggs and Gifford formulas). The applied Briggs formulas are listed in
Table 2.
Further assumptions and details of the implemented PTM are described in [
1].
The assumed layer approach for vertical diffusion defines only mean, evenly distributed concentrations within the given layer. The bottom air layer is the reference layer for the calculation of air concentration, applied in the calculation of deposition and radiological parameters.
The height of the release, together with timing and nuclide composition of the release, are the attributes of the source term. The release height specifies one of the calculation layers in which the release point is situated and in which we assume an even distribution of released radioactive material. Releases as a function of time are realized as series of puffs, where each puff carries the specific amount of the leaked activity corresponding to a specific time interval of the release. Time intervals that express the course of the leak in time are 15 min to 1 h. Any number of puffs can be modeled simultaneously from different locations at the same or different heights, or from the same location but at different heights.
The calculated radiological parameters are defined in a similar manner as for LPM, with a few exceptions. The committed effective dose by inhalation and external dose by deposition were evaluated using the same approach as described above.
External dose by cloudshine in large distance from the release point is evaluated using the approach of a semi-infinite cloud of constant concentration. However, for distances up to 2–5 km from the release point, the presumption about immersion into the hemisphere with air volume activity is not valid. Therefore, for these distances, a specific model approach that enables it to account for the contribution of airborne activity of nuclides in the puff dispersed in various heights to gamma dose rate at a point 1 m above the ground was created and applied in ESTE.
2.3. Dispersion in Urban or Industrial Area
For the calculation of the dispersion of radionuclides and radiological impacts in urban or industrial area, specifically in areas with a size of 1–4 km
2 and a non-flat surface, a specific implementation of the Lagrangian Particle Model was applied in ESTE. The procedure is analogous to mesoscale calculations (see
Section 2.1). Two potential examples of situations and events considered as cases for application of radiological impacts calculation in an urban area are: accidental releases within the area of a nuclear power plant, or application of a radiological dispersal device (dirty bomb) in an inhabited urban area (e.g., city centers).
A specific feature of the impact calculation for an urban area is the inclusion of the effect of present buildings. Particularly in the case of a detailed and more-accurate calculation, the applied meteorological data have to reflect the position, shape, and size of buildings in the impacted area. The applied wind field follows the distribution of streets and buildings, as well as the dispersion coefficient as a field parameter, which reflects the distribution of turbulence in the given urban area. Since each urban locality is practically unique, the corresponding urban meteorological fields have to be evaluated uniquely if greater accuracy is required.
The calculation of urban meteorological fields requires calculation of a variant of Navier–Stokes equations or other effective versions in which point meteorological data from direct meteorological measurements or from predicted meteorological data represent a boundary and initial condition for solving the equations. For example, the point meteorological data could be a meteorological measurement in one point at various heights that, due to its position and quality, could be considered as representative of the boundary condition of the inlet boundaries. In practice, the urban wind-field calculation is a time-consuming process, and therefore a questionable aspect within an emergency response (as it is so for mesoscale distances, where the numerical weather-prediction data are applied as the source of wind-field data, prepared beforehand). Therefore, an application of the urban meteorological field that reflects the actual condition on the impacted site should be based on the precalculated set of urban meteorological fields. In an emergency, the applied urban meteorological field is chosen as the most adequate to the actually measured condition. Obviously, the ensemble of the precalculated fields determines the accuracy of such an approach: the larger the ensemble used, the more accurate the obtained result is. A guide for preparation of such a precalculated ensemble might be the probabilistic distribution of meteorological situations for the given site.
In the model of ESTE [
16], the urban meteorological field was calculated as a solution to the Reynolds-averaged Navier–Stokes equations for buoyant, incompressible fluid with the Boussinesq approximation and omitting the time-derivative term (thus resulting in steady-state flow solution):
where u and u’ are the mean and fluctuating parts of the velocity (resp. their ith-component), ν is the kinematic viscosity, ρ is the density, p is the pressure, g
i is the acceleration due to gravity, and R
ij is the Reynolds stress tensor, representing the turbulent fluctuations.
In the implemented approach, the equations are solved using the semi-implicit method for pressure-linked equations (SIMPLE) algorithm [
17]. The applied computational method is completed by the definition of turbulence closure; in case of ESTE, by the application of the k–ε closure model [
18]. The whole urban model represents a standard basic approach for evaluation of an urban wind field with turbulences.
Finally, the boundary conditions are required to define vertical profiles of wind and several turbulence parameters, where these profiles are expressed as functions of the friction velocity, the Obukhov length, and the mean sensible heat flux [
19]. All three parameters were evaluated using observed meteorological quantities (wind speed, temperature).
The described 3D urban approach in the area of a nuclear power plant was applied in the ESTE system implementation at the Mochovce NPP in Slovakia. The area is non-trivial from the point of view of the present build-up area: there are buildings for the four units (two in operation and two in the final phases of construction), eight cooling towers, and many auxiliary buildings.
In real application, the computational meteorological fields are precalculated in the form of a large ensemble, instead of involving the calculation of the wind field during an emergency response (or during crisis center training). Each element of the ensemble is characterized by three parameters (directly observable or derivable from observation):
Category stability, for which three cases are taken into account: unstable weather conditions (in that case, the vertical profiles on the boundaries for the calculated fields were specified by Monin–Obukhov length, L = 100 m), neutral weather conditions (L = infinity) and stable weather conditions (L = −100 m).
Wind direction: taking into account 36 different wind directions (with a uniform step of 10°). The wind direction specifies direction of the wind entered into the meteorological field calculation as a boundary condition.
Wind speed: taking into account 40–50 values of wind speed (depending on the stability category), ranging from low wind speed of about 0.2 m/s to 9 m/s (stable weather), to 25 m/s (neutral and unstable weather). The wind speed means the wind rate at the height of 10 m in the specification of the boundary condition for calculation of the meteorological fields.
In the 3D model of Mochovce NPP, the computational area is discretized on cells with a size of 20 m × 20 m. The whole domain has a size of 2800 m × 1400 m. A visualization of the 3D model is shown in
Figure 1.
The Lagrangian dispersion model for urban environment is based on theoretical description of [
9,
20]. The basic transport equations of the urban LPM are again Equation (1). Here, the mean wind of Equation (1) represents the averaged wind over a specific time interval (10 min) in the computational domain, and the mean wind is calculated as a solution of the Navier–Stokes equations.
The vector u
i in (1) represents the random walk term of the wind. The diffusion term in Equation (2) obtains a simple form:
where C is a universal constant, ε is the mean turbulent kinetic energy dissipation rate and is one outcome of Equation (11), dt is the time step, and δ
ij is Kroneker delta. The drift term from Equation (2) is calculated as the Thompson’s simplest solution for diffusion in three dimensions. It is a function of the Reynolds stress tensor τ, another outcome of Equation (11), but it is more technical, therefore for more details we refer to [
9,
20]. This approach is implemented in several other urban dispersion models as well, e.g., the QUICPLUME model [
21].
The outcome of the dispersion simulation was a concentration of airborne radionuclides and deposited material. Dry deposition A
dd on a surface is calculated using a similar approach as described above in (2), except for the inclusion of the surface orientation parameter c
so:
For example, c
so for aerosols is equal to 1 if the surface normal is vertical, and it is equal to 0.1 if the surface normal is oriented horizontally [
22,
23]. C
0 is the air concentration in the particular cell whose surfaces are considered as they undergo contamination by deposition. The evaluation of wet deposition takes into account all cells above the particular horizontal surface, but the vertical surfaces are assigned as zero wet deposition.
The radiological parameters are calculated for ground cells, i.e., cells having at least one ground or building surface. Such cells are potential locations for being occupied by persons. In the case of committed effective dose by inhalation, the instant dose rate DRinhal and the integral dose Dinhal for a particular cell are calculated using Equations (5) and (6), but with C0 as the actual air concentration in the given cell and Cint as the time-integrated concentration in that cell.
The dose rate in the case of an external dose by cloudshine is calculated as a sum of the contribution of all cells j to the dose for the particular cell i as follows:
where C
0(j) is the air concentration in the contributing cell, SF is shielding factor (equal to 1 if there is no building along a straight line between the cell centers of i and j, and equal to 0 if there is a building), CF
cloud is the conversion factor for cloudshine, as a function of the nuclide and of the distance between cell centers i and j.
Similarly, the dose rate of the external dose by deposition is calculated as a sum of contribution of all ground and building surfaces j to the dose for the particular cell as follows:
where D
0(j) is the deposit on the contributing cell. SF is shielding factor (equal to 1 if there is no building along a straight line between the cell centers of i and j, and equal to 0 if there is a building), CF
depo is the conversion factor for the external dose via deposition, as a function of the nuclide and of the distance between cell centers i and j. The factors CF
cloud and CF
depo are prepared as a precalculated library (prepared by calculation using MCNP code version 5 [
24]), for various distances between the cells and various cell sizes.
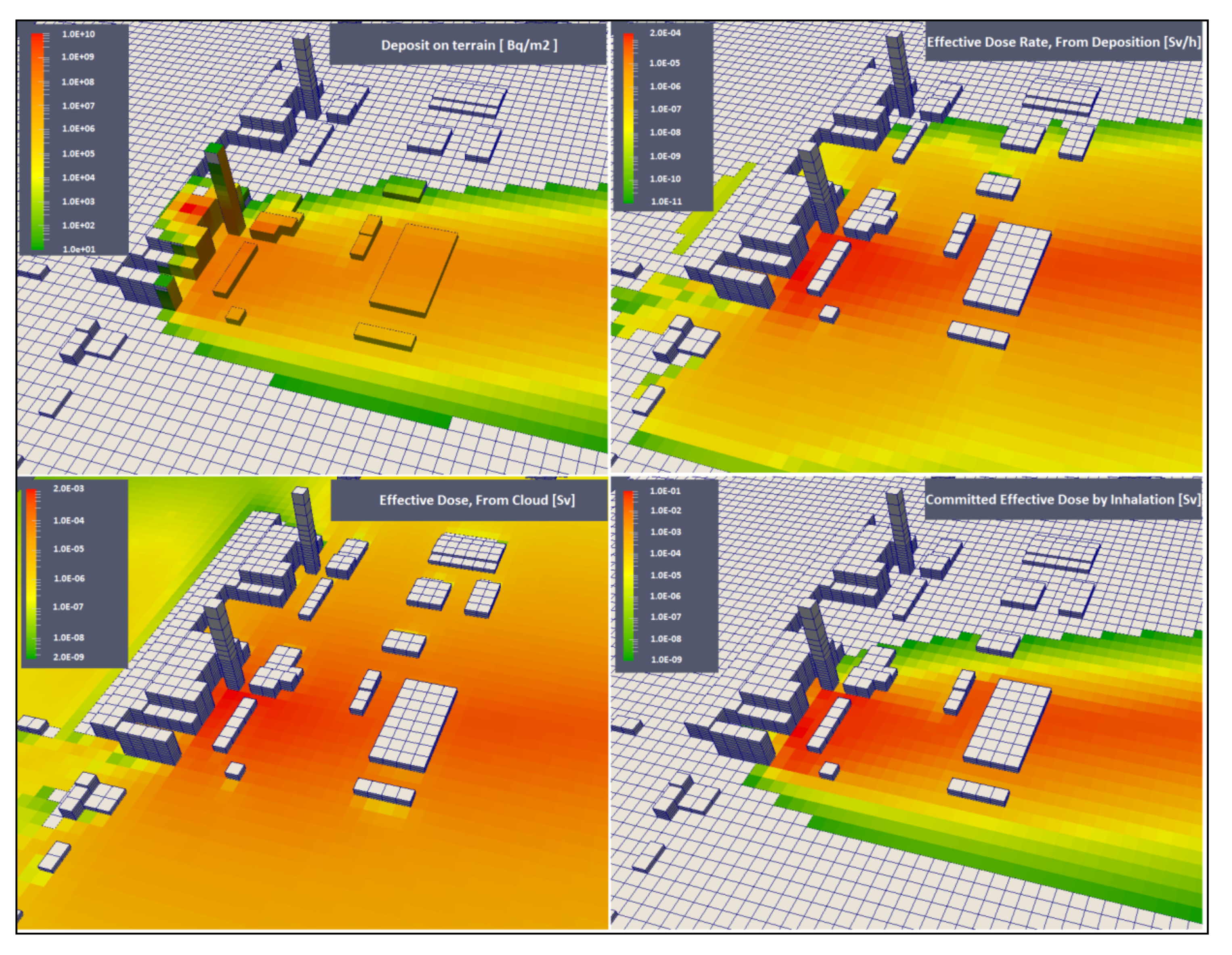
An example of results for a release in an urban environment is shown in
Figure 2. The simulation was done for a release of 1.0 × 10
15 Bq of Cs-137 from the roof of the reactor building. Shown is the deposit on all surfaces (buildings and ground), the effective dose rate corresponding to this deposit, the effective dose rate from the cloud during the duration of the release, and the committed effective dose by inhalation. Doses and dose rate were calculated for ground cells.