Abstract
A statistical analysis of the relation between exceptional solar events and daily numbers of deaths in the Czech Republic is presented. In particular, we concentrate on diseases of the nervous system (group VI from ICD-10—International Statistical Classification of Diseases and Related Health Problems 10th Revision) and diseases of the circulatory system (group IX from ICD-10). We demonstrate that the neurological diseases exhibit greater instability during the period of rising and falling solar activity. We study the daily numbers of deaths, separately for both sexes and two age groups (under 39 and 40+), during the Solar Cycles No. 23 and No. 24. We focus on exceptionally strong solar events in this period, such as the “Bastille Day event” on 14 July 2000, “Halloween solar storm” on 28 October 2003, and events on 7 January 1997, 2 April 2000, and on 7 September 2005. Special attention is paid to “St. Patrick’s Day storm” on 17 March 2015, the strongest geomagnetic storm of the Solar Cycle No. 24 that occurred following a coronal mass ejection (CME). We investigate the changes in the daily numbers of deaths during 1 month before and 1 month after these exceptional solar events. We take specific storm dynamics of their geophysical parameters into consideration. It has been verified that, for diseases of the nervous system, women are generally more sensitive than men. On the contrary, this differences between men and women have not been found for diseases of the circulatory system. Our findings suggest that the impact of the hazardous space weather conditions on human health depends on the specific dynamic and strength of the solar storm.
1. Introduction
The aim of this paper is to statistically examine whether there are changes in daily numbers of deaths during the period one month before and after a severe solar storm.
Electromagnetic field has an effect on specific acute conditions of patients with brain, nerve, or heart diseases. Two major mechanisms of the influence of solar activity on human health are the effects of magnetic field and the influence of radiation. The magnetic field affects non-specifically the nervous system and hormonal activity. On days of magnetic storms, changes in blood clotting, sedimentation rates, and pulse are detected [1,2,3,4,5]. The direct physical influence of high-energy solar radiation, especially during solar flares, has a global impact on living organisms, as well as on human health [6]. It is assumed that neuropsychological diseases exhibit greater instability during the periods of rising and falling solar activity [7]. In some works, the Schumann resonance is also mentioned as a possible influence mechanism of the solar and geomagnetic activity on human health [8,9].
Correlations with solar activity, and interestingly also with cosmic rays, were identified [10,11,12,13,14]. These effects were also noted [15,16,17] as the onset and course of diseases of the nervous system and genetic disorders. A similar study was conducted by Reference [18] and reached similar results. According to these studies, geomagnetic activity plays only a minor role in the cardiovascular mortality. This finding was also confirmed in a study by Reference [19]. Exceptional solar events affect the human circulatory system indirectly through the concentration of electric charges and also changes in the magnetic field in the environment in which the monitored population lives [20]. Moreover, the impact of geomagnetic disturbances may depend on solar magnetic field polarity [21], the course and phase of the solar cycle, and on the strength of the exceptional solar events during the given period of observation [22,23,24,25,26,27]. The recent studies investigate also the simultaneous effects of space weather and meteorological situations on cardiovascular diseases [28,29].
Generally, the mortality in the Czech Republic (population of about 10 million) during the investigated period of years from 1994 to 2015 has significantly decreased. Registration of deaths by cause of death is very stable in the Czech Republic in the long-term. The most frequent group of causes of death are in diseases of the circulatory system; in 2013 their share in the total standardized death rate (standardized by WHO European standard) was 44.8% (43.1% in men and 46.8% in women). In 2012, according to the Eurostat data Healthy Life Years (HLY), the values 62.3 years of 75.1 years of life expectancy at birth for men and 64.1 years of 81.2 years of life expectancy at birth for women were reached [30]. With the increase in life expectancy, an increasing incidence of neurodegenerative diseases in the elderly occurs.
The time series of daily aggregated numbers of deaths by cause, men and women separately at the age groups under 39 and 40+ were used in this study. The data were provided by Czech Statistical Office. The whole observed period belongs to time of validity of ICD-10 (International Statistical Classification of Diseases and Related Health Problems 10th Revision). For detailed analysis, causes of death of the chapter VI, diseases of the nervous system, and IX, diseases of the circulatory system of ICD-10, were chosen. Time series of daily numbers of deaths per group of diagnoses of ICD-10 VI, diseases of the nervous system (G00–G99), and IX, circulatory system diseases (I00–I99), per group of diagnoses together were used for the analysis, due to the length of the observed period. We choose the analysis of daily numbers of deaths for the whole group of diagnoses due to low daily numbers of deaths for detailed diagnoses separated by sex and two age groups [31].
According to the description of detailed diagnoses and already performed studies [6,10,13], there is no presumption that an acute severe reaction of the human organism to changes in geophysical parameters could have a delay of more than 30 days. The period of 30 days was chosen to monitor specific changes in the number of deaths after a solar storm because there is no assumption that the acute deterioration after the solar/geomagnetic storm could be causally reflected in mortality over a longer period than 30 days in the conditions of medical care in the Czech Republic. Moreover, according to the description of detailed diagnoses and previously performed studies [31,32,33,34], it is not likely that an acute severe reaction of the human organism to the changes in geophysical parameters could have a longer delay than 30 days. The same long period before and after the solar storm was analyzed. To compare the characteristics, a period with lower solar activity was chosen, namely just 30 days before the solar storm. We focused to the situations when solar-flare or shock waves associated with coronal mass ejections produce strong solar energetic particles (SEP) events. These periods were then confronted with periods of solar storms and their temporal impact.
We investigated the changes in the daily numbers of deaths during period of years 1994–2015. The whole observed period belongs to the time of validity of the International Classification of Diseases, 10th revision (ICD-10), and the unified version of the electronic coding system IRIS (Language independent coding system) was operated throughout this period in the Czech Republic [35]. We focused on exceptionally strong solar events in this period:
- -
- geomagnetic storm on 7 January 1997,
- -
- storm on 2 April 2000, associated with the solar flare of class X20,
- -
- storm on 14 July 2000, Bastille Day Event, associated with solar flare of class X5,
- -
- storm on 28 October 2003, Halloween Solar Storms, associated with solar flare of class X17,
- -
- storm on 7 September 2005, associated with solar flare of class X1, and
- -
- storm on 17 March 2015, St. Patrick’s Day Event, associated with solar flare of class G4.
These storms were selected according to the NWRA/CoRA catalog, NorthWest Research Associates in Boulder, CA, USA, and the Deutsches GeoForschungsZentrum so that they occurred evenly throughout the study period. The radiation solar activity indices F10.7 (Intensity of the Sun radio flux) [36], the geomagnetic solar activity indices Kp planetary index, and Dst (Disturbance Storm Time), and Proton density and Proton Flux > 30 MeV (FP30) represent the solar activity in models.
The analyzed solar storms are marked in the graph of the course of solar and geophysical parameters in Figure 1. The figure shows the changes (from top to bottom) of the values of the three-hour Kp index, the hourly values of the Dst index, the daily values of the solar radio flux F10.7, and the hourly PF30 values of the solar proton flux with energy greater than 30 MeV in the observed period. The Kp index was chosen in the model to represent the geomagnetic activity in geographical latitudes where the territory of the Czech Republic lies [36]. Dst was used to determine the onset time of a geomagnetic storm.
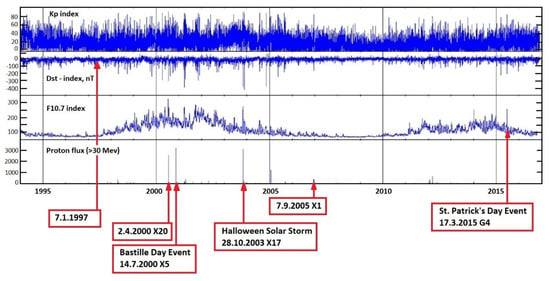
Figure 1.
Solar activity variability during the investigated period from years 1994 to 2015 belonging to the Solar Cycles No. 23 and No. 24.
For the terrestrial impact scenario, it is important if the observed geographic location is affected on day or night side of the Earth. We focused especially on whether specific geographic location of the Czech Republic was affected during daylight or night time.
2. Data and Methods
2.1. Data Sets
The daily numbers of deaths from causes of death from groups IX. circulatory system diseases (I00–I99) resp. VI, diseases of the nervous system (G00–G99) in groups by sex and age, which met the criteria of observation frequency for time series analysis using graphical models of conditional independence, and the series of geophysical and solar parameters expressing the level of solar activity were included in the graphical model (solar radio flux F10.7, geomagnetic index Kp, and solar proton flux > 30MeV PF30) between the observed periods of 30 days before and after of the above-mentioned solar storms. Figure 2 and Figure 3 illustrate the daily numbers of deaths per analyzed cause of death group in these periods. The panels (a)–(f) of Figure 2 and Figure 3 show the histograms of daily numbers of deaths for each individual solar storm in groups of diagnosis. In the graphs of numbers of deaths, the day of the solar storm, i.e., the middle of the observed period, is always marked with a black bar. Three-day moving averages of the total daily number of deaths are marked with dots.
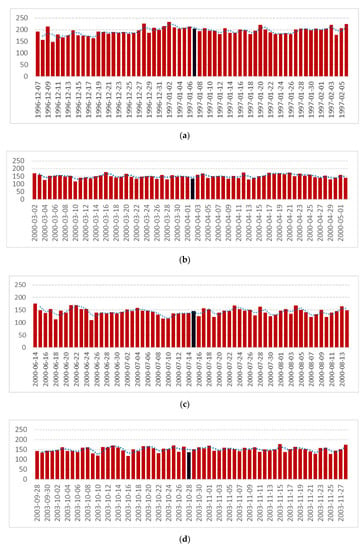
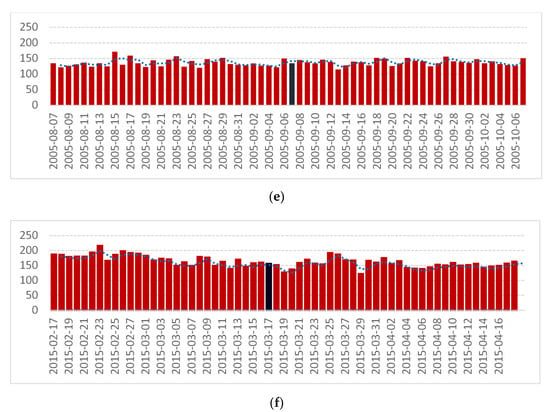
Figure 2.
Daily numbers of deaths from diseases of the circulatory system (I00–I99) during exceptionally strong solar events in period of years 1994–2015. (a) Geomagnetic storm on 7 January 1997, (b) X20 class storm on 2 April 2000, (c) class X5 storm on 14 July 2000, Bastille Day Event, (d) class X17 storm on 28 October 2003, Halloween Solar Storms, (e) class X1 storm on 7 September 2005, and (f) class G4 storm on 17 March 2015, St. Patrick’s Day event.
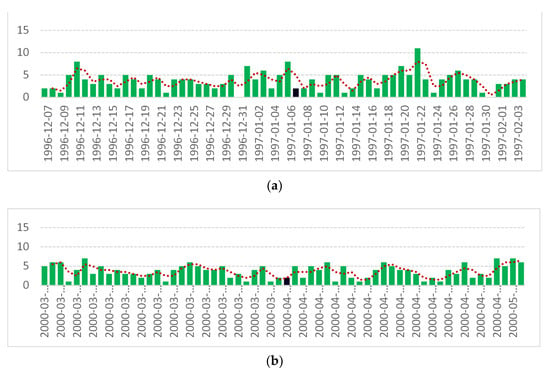
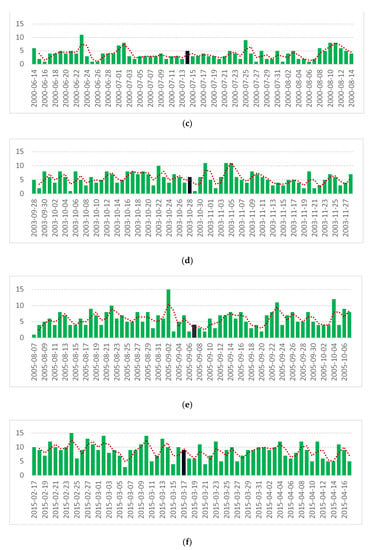
Figure 3.
Daily numbers of deaths from diseases of the nervous system (G00–G99) during exceptionally strong solar events in period of years 1994–2015. (a) Geomagnetic storm on 7 January 1997, (b) X20 class storm on 2 April 2000, (c) class X5 storm on 14 July 2000, Bastille Day Event, (d) class X17 storm on October 28, 2003, Halloween Solar Storms, (e) class X1 storm on 7 September 2005, and (f) class G4 storm on 17 March 2015, St. Patrick’s Day event.
2.2. Method
We used the method of graphical models of conditional dependencies (CIG) [37], a stochastic way to find out dependencies between solar and geomagnetic parameters. Due to the character of the solved problem, this method appears useful for studying the conditional dependence between physical parameters in evolving solar cycle and daily numbers of deaths.
The graphical models are important modern instrument of multivariate statistics. They are used for description and transparent representation of structure of the dependence relationships in a given set of random vectors. Today, they start to be used in the Atmospheric and Oceanic Sciences [38]. Probabilistic graphical models for climate data analysis has been developed by References [39,40,41], to determine which variables interact, and how strongly, and to decide if the data can be condensed without loss of information. The theoretical basis to this technique is the concept of conditional independence, and the prime theoretical and practical tool is the conditional independence graph [37,42].
Here, we consider a structure dependence relationship of the random vector component part. We take all full graphs of conditional independence relationships for selecting tests of fit graphs. In this method, the best likelihood estimation of variance matrix in conditions given by graphical model is found [43,44,45]. The graphical model with graph G is system of probability distribution of random vector X which matches conditional independence of graph G. Graph G = (V, E) of a graphical model with k vertices for k-dimensional random vector is the group of likelihood probability distribution of a vector X which satisfies the conditional independence given by graph G [45]. Graph vertex V represents the variable of a random vector, and edge E between two vertices represents dependence of these variables. If there is no edge between two vertices, the pair of variables is independent. Entire graph has edges between all pairs of vertices.
For selecting the particular graphical model by goodness-of Ht test, we used the program Backward2 [37] (pp.182–185) realized in Mathematica 8.0 software. Calculations were performed for the above mentioned solar storms, always separately for the period before and after the solar storm. Due to computational complexity, the geomagnetic index Dst was not finally used in the resulting graphical models of conditional independence. The random vector employed in our models reads:
where I is the daily number of deaths in the group of diagnoses by age and sex, Kp is geomagnetic index, F10.7 solar radio flux, and PF30 is solar radio flux > 30 MeV. The number of realizations of this random vector is 31 (lengths of observed periods before and after solar storm in days). All graphs in the calculations have 4 vertices, so the maximum number of possible graphs in each calculation is 63. These time series were tested for independence and normality of logarithmic data series. The test of the normality of logarithmical series (and not of the series themselves) is the mathematical assumption for computing the maximum likelihood estimator of the constrained covariance matrix. The test of independency of the logarithmic data (log (K/Kt−1) = log Kt − log Kt−1) is applied, based on a differentiated sign test, where Kt is the value of the realization of random vector in time t, and Kt−1 is the value of realization of random vector in previous time (t−1) [37]. The data are transformed by differences of logarithms to fulfill the assumption of normality and independence of observed realizations within this step. In the absence of the assumption of local normality, calculation is terminated and the model cannot be created.
X = (I; Kp; F10.7; PF30),
The logarithmic likelihood function was used in the form:
where N is a random sample size, θ unknown parameter, S likelihood estimator, W is maximum likelihood estimator of model with entire graph G, and l is logarithmic likelihood function (setting the unknown parameters θi by maximization of the likelihood function through unknown parameters set [46]). The likelihood function requirements follow from the graphical model selection, using the goodness-of Ht test to select the graphical model with data. The test statistics has the deviance with χ2 asymptotic probability distribution. The deviance of the excluded edge of the graphical model was computed by IPF (Iterative Proportional Fitting) algorithm [37]. The difference of the deviancies of the model G2 (model with excluded edge) and model G1 (tested model) was, therefore, given by:
2 log l(W) = θ − N (W−1S)T − N log det W,
dev* = − [ dev f2 − dev f1 ] = (dev(G2) − dev(G1)) < 3.84.
In our selection of minimized model, all edges with computed deviance less than 3.84 (the critical value 3.84 is the standard 5% point of χ2 (1) distribution with 1 degree of freedom), as in equation (3), were excluded from the entire graph. The stopping threshold for this calculation, thus, was the value 0.05 [47].
3. Results
The number of deaths of men and women in the age group over 40 completed years including, for all the mentioned solar storms, passed the tests for independence and normality of logarithmic data series. These are age groups 0–39 years for men and women with diseases of the circulatory system and nervous system.
The results of the calculation of graphical models of conditional independence for both groups of diagnoses at the time of the analyzed solar storms are presented in the Table 1 and Table 2. For each investigated solar storm, the table contains the parameters of the minimized graphical models before (before SEP) and after the solar storm (post-SEP), for the analyzed groups by sex and age. For each model, the table also shows the total deviance of the minimized model.

Table 1.
Summary of conditional independence graphs (CIG) model computation, diseases of the circulatory system (I00–I99).

Table 2.
Summary of conditional independence graphs (CIG) model computation. Diseases of the nervous system (G00–G99).
The graph vertices represent the components of a random vector (F10.7, Kp, PF30), the edges between two vertices represent the dependences of these variables. For the residual components of the random vector of the model, it is indicated whether the given edge remained in the resulting minimized model by X mark (the edge is in the model) or by a dash (the edge was excluded from the model). Furthermore, in the tables, we present the number of edges in the final model, the total sum of the degree of freedom f in the model calculation, and p-value of the test model is shown. The stopping threshold for calculation was 0.05. Thus, if the p-value of the test of the minimized model is greater than 0.05, the model is statistically significant. If the time series did not pass the test for independence and normality of logarithmic data series (due to the uncertainty of the variance matrix it was not possible to calculate the model), this information is given in the relevant row in the tables. The results for women up to and including 39 completed years are indicated by the title of the Females 0–39 panel, and the results for women aged 40 and over completed years inclusive are indicated by the title of the Females 40+ panel. The results for men up to and including 39 completed years are indicated by the title of the panel Males 0–39, and the results for men aged 40 and more completed years inclusive are indicated by the title of the panel Males 40+. For age groups in which the number of deaths is lower due to the nature of the disease, the results of the model calculation are not statistically significant.
In the period of 30 days before and after the storm on 28 October 2003 (Halloween Solar Storms), conditional dependence was found in all monitored groups by age and sex (except women 0–39 years when time series failed the test for normality and independence of logarithmic data) with the solar proton flux FP30. In contrast, in a severe solar storm on 17 March 2015 (St. Patrick’s Day event), which hit Earth in the early morning hours of local time in the Czech Republic, the conditional dependence of the number of deaths on the solar proton flux PF30 was reflected in only two studied groups. Due to the fluctuations of the monitored indices of solar and geophysical activity even in the period before the storm, it is possible to observe a conditional dependence on the Kp index in this storm.
In the group of nervous system diseases in the period 30 days after the solar storm, an increase in the conditional dependence was found for the daily number of deaths in men and women over 40 years compared to the pre-storm period for the solar radio flux F10.7 and solar proton flux FP30.
The results of the our analysis, performed by the method of graphical models of conditional independence for the group of nervous system diseases, showed the conditional dependence of the daily number of deaths during the solar storm on 28 October 2003 (Halloween Solar Storms), for all monitored age groups on solar radio flux F10.7 and solar proton flux PF30. At the time of the solar storm on 14 July 2000 (Bastille Day Event), all age groups except men over the age of 40 were found to be dependent on the solar proton flux PF30 before the storm. No connection between the daily number of deaths and all indices of solar and geomagnetic activity was found in the group of diseases of the nervous system, during any period of the observed solar storms.
In none of the resulting graphical models, unconditionally independent component or sub vectors of geophysical indices appear. The connection of the daily number of deaths with all indices of the solar and geomagnetic activity was found in the group of diseases of the circulatory system during the solar storm on 2 April 2000 and the storm on 28 October 2003 (Halloween Solar Storms) for women over the age of 40, during the solar storm on 14 July 2000 (Bastille Day Event), in men over the age of 40. This is probably related to the time of day in the Czech Republic, when the storm hit the Earth. At the time of these solar storms, the influence of the components of the solar and geomagnetic activity was complex.
4. Discussion
It is, thus, possible to identify specific changes in the connection of time series of daily number of deaths of men and women over 40 years of circulatory system diseases and nervous system diseases in the time series of solar radio flux F10.7, geomagnetic index Kp, and solar proton flux PF30 between observed periods before and after monitored solar storms. Such connection is consistent with the results published in References [19,21], where the influence of the geomagnetic field was also identified and a connection with the geomagnetic parameters (Kp).
The results of the present analysis are influenced by the geoefficiency of the analyzed solar storm and the time course of the monitored indices of solar and geophysical activity. These results during the periods of four major solar storms (storm of 2 April 2000, storm of 14 July 2000 Bastille Day Event, storm of 28 October 2003 Halloween Solar Storms, and storm of 17 March 2015 St. Patrick’s Day event) show a clearer difference in the connection of time series in the comparison of the analyzed periods before and after a solar storm than three solar storms with a less pronounced course (storm of 7 January 1997 and storm of 7 September 2005). This conclusion is consistent with other studies that show that the impact of solar activity on human health also depends on the intensity of the solar events occurring during a given observational period [22,23].
The assumption that there is no significant effect of solar proton flux PF30 and solar radio flux F10.7 during severe solar storms was confirmed, when the solar storm occurred during the night of local time in the Czech Republic. The analysis took into account the specific conditions of the population in the Czech Republic in the observed period. They correspond to local effect of the observed solar storms, the differential characteristics of the population living in the Czech Republic, the level of health care in the monitored period, and other determinants of the health status of the population. Thus, it is possible that the same geophysical manifestation may have a different effect in a different population.
5. Conclusions
The impact of exceptional solar events is evident in the case of neurological diseases, and less evident for circulatory diseases, when SEP during daylight time cause larger effect in changes of daily numbers of deaths.
For all solar storms described in this paper, it can be observed that daily numbers of deaths in the diagnostic groups VI, diseases of nervous system (G00–G99), and IX, diseases of circulatory system (I00–I99), according to age and sex, differ in statistical characteristics in the time period 30 days before solar storm and 30 days after solar storm. For age groups with a low daily numbers of deaths due to the character of the diseases, the results are not significant.
For time periods after strong solar storms, a connection between daily numbers of deaths for diseases of circulatory system and geomagnetic index Kp, Solar proton flux PF30, and solar radio flux F10.7 was identified. For men in age group over 40 years a higher conditional dependence with solar radio flux F10.7 and geomagnetic index Dst was observed after the event. For women over 40 years of age, a higher conditional dependence with geomagnetic index Kp was also identified.
In none of the resulting graphical models do unconditionally independent components or sub-vectors of geophysical index vectors appear. The connection of the daily number of deaths with all indices of the solar and geomagnetic activity was found in the group of diseases of the circulatory system during the solar storm on 2 April 2000, and the storm on 28 October 2003 (Halloween Solar Storms), for women in the age group over 40; and solar storm 14 July 2000 (Bastille Day Event), in men over the age of 40. This is probably related to the day time in the Czech Republic, when the storm hit the Earth.
Funding
This research was funded by the Czech Science Foundation, grant number SAV-18-04.
Data Availability Statement
Number of deaths by cause: Czech Statistical Office (CZSO), [online]. [cit. 2019-11-02]. <https://www.czso.cz/csu/czso/obypz_cr>. Kp index: World Data Center for Geomagnetism, Kyoto University, Japan. The data used for time series assembling was provided in case of Kp by World Data Center for Geomagnetism, Kyoto University, Japan, [online]. [cit. 2020-04-01]. <http:/wdc.kugi.kyoto-u.ac.jp/kp/index.html>. In case of F10.7 by NWRA/CoRA, NorthWest Research Associates, Boulder, USA, [online]. [cit. 2020-04-01]. <http:/www.nwra.com/spawx/spawx.html>.Dst, F10.7: Space Physics Interactive Data Resource, National Geophysical Data Center, Boulder, USA. Proton density, Proton Flux: OMNIWeb Plus, NASA/Goddard Space Flight Center, USA, https://omniweb.gsfc.nasa.gov.Solar cycle evolving: NWRA/CoRA, NorthWest Research Associates, Boulder, USA; Deutsches GeoForschungs Zentrum, Germany.
Acknowledgments
The support under the grant SAV-18-04 by the Czech Science Foundation is acknowledged. World Data Center for Geomagnetism, Deutsches GeoForschungsZentrum (GFZ), NWRA/CoRA, NorthWest Research Associates, and UK Solar System Data Centre (UKSSDC) Rutherford Appleton Laboratory is acknowledged for providing geomagnetic measurement.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Otsuka, K.; Cornélissen, G.; Weydahl, A.; Holmeslet, B.; Hansen, T.; Shinagawa, M.; Kubo, Y.; Nishimura, Y.; Omori, K.; Yano, S.; et al. Geomagnetic disturbance associated with decrease in heart rate variability in a subarctic area. Biomed. Pharmacother. 2000, 55, 51–56, ISSN 0753-3322. [Google Scholar] [CrossRef]
- Azcárate, T.; Mendoza, B.; Levi, J. Influence of geomagnetic activity and atmospheric pressure on human arterial pressure during the solar cycle 24. Adv. Space Res. 2016, 58, 2116–2125, ISSN 0273-1177. [Google Scholar] [CrossRef]
- Gurfinkel, Y.; Vasin, A.L.; Pishchalnikov, R.Y.; Sarimov, R.M.; Sasonko, M.L.; Matveeva, T.A. Geomagnetic storm under laboratory conditions: Randomized experiment. Int. J. Biometeorol. 2017, 62, 501–512. [Google Scholar] [CrossRef]
- Gurfinkel, Y.I.; At’kov, O.Y.; Vasin, A.L.; Breus, T.K.; Sasonko., M.L.; Pishchalnikov, R.Y. Effect of zero magnetic field on cardiovascular system and microcirculation. Life Sci. Space Res. 2016, 8, 1–7, ISSN 2214-5524. [Google Scholar] [CrossRef] [PubMed]
- Cornelissen, G.; Halberg, F.; Breus, T.; Syutkina, E.V.; Baevsky, R.; Weydahl, A.; Watanabe, Y.; Otsuka, K.; Siegelova, J.; Fiser, B.; et al. Non-photic solar associations of heart rate variability and myocardial infarction. J. Atmospheric Sol. Terr. Phys. 2002, 64, 707–720. [Google Scholar] [CrossRef]
- Katsavrias, C.; Preka-Papadema, P.; Moussas, X.; Apostolou, T.; Theodoropoulou, A.; Papadima, T. Helio-geomagnetic influence in cardiological cases. Adv. Space Res. 2013, 51, 96–106, ISSN 0273-1177. [Google Scholar] [CrossRef]
- Johnsen, S.; Lohmann, K.J. The physics and neurobiology of magnetoreception. Nat. Rev. Neurosci. 2005, 6, 703–712. [Google Scholar] [CrossRef]
- Mitsutake, G.; Otsuka, K.; Hayakawa, M.; Sekiguchi, M.; Cornelissen, G.; Halberg, F. Does Schumann resonance affect our blood pressure? Biomed. Pharmacother. 2005, 59 (Suppl. 1), S10–S14. [Google Scholar] [CrossRef]
- Cherry, N. Schumann Resonances, a plausible biophysical mechanism for the human health effects of Solar/Geomagnetic Activity. Nat. Hazards 2002, 26, 279–331. [Google Scholar] [CrossRef]
- Stoupel, E.; Kalediene, R.; Petrauskiene, J.; Starkuviene, S.; Abramson, E.; Israelevich, P.; Sulkes, J. Clinical Cosmobiology: Distribution of Deaths during 180 Months and Cosmophysical Activity. The Lithuanian Study, 1990–2004. The Role of Cosmic Ray; Study Report; Division of Cardiology Rabin Medical Center Tel Aviv University: Tel Aviv, Israel, 2004. [Google Scholar]
- Watanabe, Y.; Cornellissen, G.; Halberg, F.; Otsuka, K.; Ohkawa, S.I. Associations by signatures and coherences between the human circulation and helio- and geomagnetic activity. Biomed. Pharmacother. 2001, 55 (Suppl. 1), 76–83. [Google Scholar] [CrossRef]
- Stoupel, E.; Kalediene, R.; Petrauskiene, J.; Starkuviene, S.; Abramson, E.; Israelevich, P.; Sulkes, J. Twenty years study of solar, geomagnetic, cosmic ray activity links with monthly deaths number (n-850304). J. Biomed. Sci. Eng. 2011, 4, 426–434. [Google Scholar] [CrossRef]
- Stoupel, E. The effect of geomagnetic activity on cardiovascular parameters. Biomed. Pharmacother. 2002, 56, 247. [Google Scholar] [CrossRef]
- Stoupel, E.; Birk, E.; Kogan, A.; Klinger, G.; Abramson, E.; Israelevich, P.; Sulkes, J.; Linder, N. Congenital heart disease: Correlation with fluctuations in cosmophysical activity, 1995-2005. Int. J. Cardiol. 2009, 135, 207–210. [Google Scholar] [CrossRef] [PubMed]
- Halberg, F.; Cornelissen, G.; Otsuka, K.; Watanabe, Y.; Katinas, G.; Burioka, N.; Delyukov, A.; Gorgo, Y.; Zhao, Z.; Weydahl, A.; et al. 21-year biological and physical cycles, magnetic storms and myocardial infarctions. Neuro Endocrinol. Lett. 2000, 21, 233. [Google Scholar]
- Halberg, F.; Cornélissen, G.; Otsuka, K.; Fiser, B.; Mitsutake, G.; Wendt, H.; Johnson, P.; Gigolashvili, M.; Breus, T.; Sonkowsky, R.; et al. Near 10-Year and Longer Periods Modulate Circadians: Intersecting Anti-aging and Chronoastrobiological Research. J. Gerontol. A Biol. Sci. Med. Sci. 2001, 56, M304–M324. [Google Scholar] [CrossRef]
- Halberg, F.; Cornélissen, G.; Otsuka, K.; Fiser, B.; Mitsutake, G.; Wendt, H.; Johnson, P.; Gigolashvili, M.; Breus, T.; Sonkowsky, R.; et al. Incidence of sudden cardiac death, myocardial infarction and far- and near-transyears. Biomed. Pharmacother. 2005, 59, S239–S261, ISSN 0753-3322. [Google Scholar] [CrossRef]
- Dorman, L.I.; Iucci, N.; Ptitsyna, N.G.; Villoresi, G. Cosmic rays as indicator of space weather influence on frequency of infract myocardial, brain strokes, car and train accidents. In Proceedings of the 27th International Cosmic Ray Conference, Hamburg, Germany, 7–15 August, 2001; p. 3511. [Google Scholar]
- Ebrille, E.; Konecny, T.; Konecny, D.; Spacek, R.; Jones, P.; Ambroz, P.; DeSimone, C.V.; Powell, B.D.; Hayes, D.L.; Friedman, P.A.; et al. Correlation of Geomagnetic Activity With Implantable Cardioverter Defibrillator Shocks and Antitachycardia Pacing. In Mayo Clinic Proceedings; Elsevier: Amsterdam, The Netherlands, February 2015; Volume 90, pp. 202–208. [Google Scholar]
- Podolská, K. The Impact of Ionospheric and Geomagnetic Changes on Mortality from Diseases of the Circulatory System. J. Stroke Cerebrovasc. Dis. 2018, 27, 404–417. [Google Scholar] [CrossRef]
- Mavromichalaki, H.; Preka-Papadema, P.; Theodoropoulou, A.; Paouris, E.; Apostolou, T. A study of the possible relation of the cardiac arrhythmias occurrence to the polarity reversal of the solar magnetic field. Adv. Space Res. 2017, 59, 366–378. [Google Scholar] [CrossRef]
- Vencloviene, J.; Babarskiene, R.; Milvidaite, I.; Kubilius, R.; Stasionyte, J. The effect of solar–geomagnetic activity during hospital admission on coronary events within 1 year in patients with acute coronary syndromes. Adv. Space Res. 2013, 52, 2192–2198. [Google Scholar] [CrossRef]
- Vencloviene, J.; Antanaitiene, J.; Babarskiene, R. The association between space weather conditions and emergency hospital admissions for myocardial infarction during different stages of Solar activity. J. Atmospheric Sol. Terr. Phys. 2016, 149, 52–58. [Google Scholar] [CrossRef]
- Jaruševičius, G.; Rugelis, T.; McCraty, R.; Landauskas, M.; Berškienė, K.; Vainoras, A. Correlation between Changes in Local Earth’s Magnetic Field and Cases of Acute Myocardial Infarction. Int. J. Environ. Res. Public Health. 2018, 15, 399. [Google Scholar] [CrossRef] [PubMed]
- Geronikolou, S.; Leontitsis, A.; Petropoulos, V.; Davos, C.; Cokkinos, D.; Chrousos, G. Cyclic stroke mortality variations follow sunspot patterns. F1000Research 2020, 9, 1088. [Google Scholar] [CrossRef] [PubMed]
- Vencloviene, J.; Radisauskas, R.; Vaiciulis, V.; Kiznys, D.; Bernotiene, G.; Kranciukaite-Butylkiniene, D.; Tamosiunas, A. Associations between Quasi-biennial Oscillation phase, solar wind, geomagnetic activity, and the incidence of acute myocardial infarction. Int. J. Biometeorol. 2020, 64, 1207–1220. [Google Scholar] [CrossRef] [PubMed]
- Kiznys, D.; Vencloviene, J.; Milvidaite, I. The associations of geomagnetic storms, fast solar wind, and stream interaction regions with cardiovascular characteristic in patients with acute coronary syndrome. Life Sci. Space Res. 2020, 25, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Vencloviene, J.; Babarskiene, R.; Slapikas, R.; Sakalyte, G. The association between phenomena on the sun, geomagnetic activity, meteorological variables, and cardiovascular characteristic of patients with myocardial infarction. Int. J. Biometeorol. 2013, 57, 797–804. [Google Scholar] [CrossRef]
- Pishchalnikov, R.Y.; Gurfinkel, Y.I.; Sarimov, R.M.; Vasin, A.L.; Sasonko, M.L.; Matveeva, T.A.; Binhi, V.N.; Baranov, M.V. Cardiovascular response as a marker of environmental stress caused by variations in geomagnetic field and local weather. Biomed. Signal Process. Control. 2019, 51, 401–410. [Google Scholar] [CrossRef]
- ÚZIS ČR: Czech Health Statistics Yearbook 2015; ÚZIS ČR: Prague, Czech Republic, 2016.
- Cífková, R.; Škodová, Z.; Bruthans, J.; Holub, J.; Adámková, V.; Jozífová, M.; Galovcová, M.; Wohlfahrt, P.; Krajčoviechová, A.; Petržílková, Z.; et al. Longitudinal trends in cardiovascular mortality and blood pressure levels, prevalence, awareness, treatment, and control of hypertension in the Czech population from 1985 to 2007/2008. J. Hypertens. 2010, 28, 2196–2203. [Google Scholar] [CrossRef]
- Cífková, R.; Bruthans, J.; Wohlfahrt, P.; Krajčoviechová, A.; Šulc, P.; Jozífová, M.; Eremiášová, L.; Pudil, J.; Linhart, A.; Widimský, J.; et al. 30-year trends in major cardiovascular risk factors in the Czech population, Czech MONICA and Czech post-MONICA, 1985-2016/17. PLoS ONE 2020, 15, e0232845. [Google Scholar] [CrossRef]
- Cífková, R.; Bruthans, J.; Wohlfahrt, P.; Krajčoviechová, A.; Šulc, P.; Eremiášová, L.; Pudil, J.; Linhart, A.; Widimský, J.; Filipovský, J.; et al. The prevalence of major cardiovascular risk factors in the Czech population in 2015–2018. The Czech post-MONICA study. COR ET VASA 2020, 62, 6–15. [Google Scholar] [CrossRef]
- Bruthans, J.; Cífková, R.; Lánská, V.; O’Flaherty, M.; Critchley, J.A.; Holub, J.; Janský, P.; Zvárová, J.; Capewell, S. Explaining the decline in coronary heart disease mortality in the Czech Republic between 1985 and 2007. Eur. J. Prev. Cardiol. 2014, 21, 829–839. [Google Scholar] [CrossRef]
- Poppová, M. IRIS: Language-Independent Software for Coding Causes of Death—Implementation in Czech Republic. IRIS: Jazykově nezávislý software pro kódování příčin smrti—implementace v ČR. Demografie 2011, 53, 392–396. [Google Scholar]
- Tapping, K.F. The 10.7 cm solar radio flux (F10.7). Space Weather 2013, 11, 394–406. [Google Scholar] [CrossRef]
- Whittaker, J. Graphical Models in Applied Multivariate Statistics; Wiley: New York, NY, USA, 1990; pp. 182–185. [Google Scholar]
- Tsonis, A.; Roebber, P. The architecture of the climate network. Physica A 2004, 333, 497–504. [Google Scholar] [CrossRef]
- Ebert-Uphoff, I.; Deng, Y. Causal discovery for climate networks. Res. Rep. 2010. Available online: http://smartech.gatech.edu/handle/1853/36564 (accessed on 11 July 2019).
- Ebert-Uphoff, I.; Deng, Y. Causal discovery for climate research using graphical models. J. Clim. 2012. [Google Scholar] [CrossRef]
- Bannerjee, A. Probabilistic graphical models for climate data analysis, paper presented at Supercomputing Workshop on Climate Knowledge Discovery (CKD-SC11). IEEE Comput. Soc. Seattle Wash 2011. [Google Scholar] [CrossRef]
- Lauritzen, S.L. Graphical Models; Oxford Science Publications: New York, NY, USA, 1996; ISBN 0-19-852219-3. [Google Scholar]
- Buhl, S. On the existence of maximum likelihood estimators for graphical Gaussian models. Scand. J. Statist. 1993, 20, 263–270. [Google Scholar]
- Cramer, E. Conditional iterative proportional fitting for Gaussian distributions. J. Multivar. Anal. 1998, 65, 261–276. [Google Scholar] [CrossRef]
- Jordan, M.I. Graphical models. Stat. Sci. 2004, 19, 140–155. [Google Scholar] [CrossRef]
- Koller, D.; Friedman, N. Probabilistic Graphical Models–Principles and Techniques, 1st ed.; MIT Press: Cambridge, MA, USA, 2009; 1280, ISBN 978-0-262-01319-2. [Google Scholar]
- Edwards, D. Introductions to Graphical Modeling, 2nd ed.; Includes MIM software; Springer: New York, NY, USA, 2000; ISBN 978-1-4612-0493-0. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).