Abstract
The modelling of thermal exposure in outdoor urban environments is a highly topical challenge in modern climate research. This paper presents the results derived from a new micrometeorological model that employs an integrated biometeorology module to model Universal Thermal Climate Index (UTCI). This is PALM-4U, which includes an integrated human body-shape parameterization, deployed herein for a pilot domain in Prague, Czech Republic. The results highlight the key role of radiation in the spatiotemporal variability of thermal exposure in moderate-climate urban areas during summer days in terms of the way in which this directly affects thermal comfort through radiant temperature and indirectly through the complexity of turbulence in street canyons. The model simulations suggest that the highest thermal exposure may be expected within street canyons near the irradiated north sides of east–west streets and near streets oriented north–south. Heat exposure in streets increases in proximity to buildings with reflective paints. The lowest heat exposure during the day may be anticipated in tree-shaded courtyards. The cooling effect of trees may range from 4 °C to 9 °C in UTCI, and the cooling effect of grass in comparison with artificial paved surfaces in open public places may be from 2 °C to 5 °C UTCI. In general terms, this study illustrates that the PALM modelling system provides a new perspective on the spatiotemporal differentiation of thermal exposure at the pedestrian level; it may therefore contribute to more climate-sensitive urban planning.
1. Introduction
Human thermal environments have attracted the interest of many researchers in recent decades [], and their conclusions have found applications in a wide range of fields, including public health, medicine, physiology, sport, biometeorology, and engineering []. The issue of human thermal comfort in the outdoor urban environment, however, has received relatively little attention until recently []. Nevertheless, climate change and burgeoning populations in urban areas have led to conditions under which thermal stress and strain are severely and ever-more-frequently impacting the everyday lives of billions of urban citizens around the globe []. The past two decades have therefore seen a rapid acceleration in interest in human thermal comfort in cities, leading to work that has attracted substantial attention on the part of urban climatologists, bio-meteorologists, and urban planners []. At the moment, urban planning has come to the point at which it is demanding reliable thermal exposure prediction tools in the interests of health risk assessment and adaptation to climatic change [,,]. The benefits of the application of such research to the well-being and health of urban dwellers have been clearly documented by many studies [,]. However, a spatiotemporally complex, scientifically clearly described, reliable, and widely recognized thermal exposure simulation model for urban areas has not yet been made available. Indeed, modelling of thermal exposure in outdoor urban environments remains a topical and very challenging task for urban climate research [,]. This paper responds to the challenge by presenting the first results of the PALM modelling system [], a new and sophisticated micrometeorological model that employs a biometeorology module in the computation of Universal Thermal Climate Index (UTCI) [,]. It may well contribute to progress in the field. The simulations presented herein were performed for a domain in Prague-Dejvice, Czech Republic. At outset, they were validated against a study by [].
The particular aims of this investigation were (a) to analyze the spatiotemporal patterns of thermal exposure in a moderate-climate urban area during summer days in the context of key environmental parameters of the human thermal environment—mean radiant temperature (MRT), air temperature (T), humidity (H), and wind speed (v); (b) to provide detailed analyses of the temporal variability of thermal exposure based on the UTCI index in a range of selected public urban places; and finally (c) to discuss further improvements to and application of the model in an analysis of thermal comfort in a complex urban environment and its practical usefulness in urban planning.
2. Theoretical Background
2.1. Thermal Exposure in Urban Areas
Heat exchange between the human body and the environment is driven by radiation, convection, evaporation, and conduction []. The quantity of heat exchanged depends upon four key environment-related parameters associated with thermal exposure: air temperature (T), humidity (H), wind speed (v; more precisely, air velocity), and radiation (r, frequently summarized as the integrating variable of mean radiant temperature (MRT)). Two human-related parameters are also critical: activity and clothing []. The interactions between these six factors are intrinsic to human thermal exposure [], which may be expressed by several thermal/biometeorological indices. Among others, the UTCI [,] and PET (physiologically equivalent temperature) [], in particular, are the most frequently used indices in studies addressing thermal comfort in urban areas []. A systematic review of the existing indices can be found in [].
Within a city, the thermal, moisture, aerodynamic, and radiation conditions are markedly different from those in the countryside []. Enhanced heat accumulation in a city results from the prevalence of horizontally and vertically oriented impervious surfaces giving rise to intensive absorption of short-wave and long-wave radiation and its manifold reflections []. Furthermore, the enclosed spaces between buildings lead to the absorption of emitted long-wave radiation (in other words, to the reduction in heat loss through radiation). A further source of extra heat is related to human activities in urban environments: anthropogenic heat emissions (e.g., from transportation, industry, and air-conditioning), together with the lack of evapotranspiration in the absence of soil and vegetation. All these factors result in a complex spatiotemporal pattern of T, H, v, and MRT in urban areas [,,,,,,] and increased human thermal exposure in outdoor urban environments [,].
In the past, studies of thermal comfort in urban areas have employed in situ measurements of the environmental parameters T, H, v, and r (usually in an approximate calculation of MRT) to calculate one of the thermal indices []. However, as indicated above, results based on in situ measurements lack sensitivity to the enormous spatial variations in human thermal exposure in urban areas []. It is therefore difficult to obtain data for the spatial representation of thermal exposure in a whole urban area [,]. This problem may be addressed by means of modelling techniques.
2.2. Modelling Thermal Exposure in the Urban Environment
During the last two decades, substantial progress in modelling urban microclimate processes has been associated with computational fluid dynamics (CFD) models, e.g., MITRAS [], ENVI-met [], MUKLIMO_3 [,], UrbClim [], and most recently the PALM modelling system (e.g., [,,]). However, the modelling of urban canopy-layer processes at a fine-scale resolution remains a challenging task, where uncertainty is an inevitable part of the modelling process [,].
Difficulties and uncertainties are particularly associated with the heterogeneity of surface characteristics (e.g., roughness, albedo, emissivity, heat capacity, plant canopy, and others) as well as a variety of human activities (e.g., anthropogenic heat and air pollution). Together, these result in high variability among elements of the urban atmosphere (e.g., T, H, MRT, and wind components). The length scales of surface heterogeneities in urban areas lie in the 1–100 m range. Therefore, models with input grids far below the kilometer scale are required to resolve the characteristic atmospheric features triggered by a specific urban environment. In view of this fact, atmospheric modelling of urban areas usually considers a limited number of relevant processes; otherwise, it is performed at coarser resolutions that cannot properly describe the conditions within street canyons. One of the greatest challenges lies in which approach to take for turbulence simulation. This may be formulated as some repeatedly asked question: is it sufficient to use a parameterized model of turbulence (e.g., Reynolds-averaged Navier–Stokes (RANS)) or is it more efficient to utilize a large-eddy simulation model (LES) with explicitly resolved turbulence []? Modern, increasing computational capabilities would appear to render the application of more detailed LES-based models more attractive [].
LES models solve the three-dimensional prognostic equations for momentum, temperature, humidity, and other scalar quantities (such as chemical species). PALM-4U is the first open-source meteorological model based on LES principles, and it includes most urban canopy-related processes. This study utilizes several modules embedded in PALM, in particular, a land surface (LSM), plant canopy (PCM), and radiation model that employs external radiation forcing from the Weather Research and Forecasting (WRF) model in our setting. Other PALM-4U components were also applied: the Cartesian topography, building surface model (BSM, formerly urban surface model—USM; see []), the radiative transfer model (RTM) [], the human biometeorology module (BIO) [], and online chemistry modules. The setup also utilized online and offline domain-nesting PALM-4U features. A new approach to MRT calculation in RTM (see Section 4.2.1) facilitates a BIO module with more precise calculation of derived biometeorological indices such UTCI (as well as PET), which have been found to be the most suitable for application in obstacle-resolving meteorology models []. This provides a new perspective on the spatiotemporal differentiation of the physical level of thermal comfort at the pedestrian level by means of validated model results [].
3. Study Area and Meteorological Conditions
3.1. Domain Description
The study area is located in the northwest part of the center of Prague, the capital city of the Czech Republic (Figure 1). The model was configured in two nested domains. The parent domain measures 4000 × 4000 m, height 3000 m, at a resolution of 10 m with vertical stretching from 250 m to 20 m. The purpose of such a domain is to allow proper simulation of convection effects and description of the orography of the area. The nested child domain, used for the next analysis, measures 1440 × 1440 m, height 250 m, at a resolution of 2 m. Its purpose is to model the area of interest at a resolution that permits representation of the processes within street canyons (see [,]). The parent domain includes highly complex terrain in its northwest and southwest parts. The child domain may be described as a densely built-up area with specific urban conditions created by a traffic circle (Vítězné náměstí) in combination with two boulevards: Evropská/Čs. Armády running south-to-east and Jugoslávských Partyzánů/Svatovítská running north-to-south (Figure 1). Moreover, this section of the town has been identified as a “hot-spot” and vulnerable area to high temperatures during heat waves in previous studies (e.g., []). The eastern and, partially, the southern parts of the child domain consist of the historical residential areas typical of Prague-Dejvice, with a combination of old and new buildings and a variety of other urban components (such as gardens, parks, and parking lots). Most of the southwestern and northeastern parts of the domain are sparsely built-up. Specific to the area are green intra-blocks with gardens and trees, usually with pervious surfaces. In contrast, the historical centers of Prague usually feature impervious intra-blocks (Figure 1). Most building heights along the streets range between approx. 20 m and 30 m, with the highest building in the domain at 60 m. Both main boulevards are around 40 m wide. The boulevards do not feature much green vegetation, except for Jugoslávských Partyzánů, where tall broadleaf trees (±20 m) grow. The majority of other trees are located in the intra-blocks and parks. The whole domain is north-facing; the mean elevation of the child domain is 225 m a.s.l. (elevation spread ±15 m).
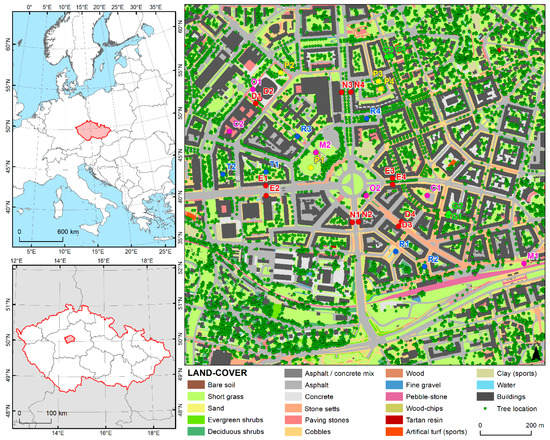
Figure 1.
Location of the Prague-Dejvice domain in Europe (top left) and the Czech Republic (bottom left): the right map(right) represents the land-cover categories in Prague-Dejvice with respect to the PALM input data standard (PIDS), with tree positions, and the locations of selected points. The red points are located in the east–west (E1–4) and north–south (N1–4)-oriented streets with or without a few trees; the green points (G1–4) are located in densely planted streets; the blue points indicate densely planted gardens in courtyards (T1–2) and “piazzettas” (R1–4); the pink points are placed on impervious surfaces, often public markets (M1–2), closed courtyards (C1–2), or beer gardens (O1–2); and the yellow points are located on open grass surfaces (P1–2) or on children’s playgrounds (P3 is on sand, and P4 is on artificial grass). The vector geodata for the left maps were provided by the ESRI (Environmental Systems Research Institute, Europe NUTS 0 Boundaries).
3.2. Meteorological Conditions
The summer episode from 19 to 21 July 2018 was used for this analysis []. Synoptically, the weather was influenced by a high-pressure ridge centered over northern Germany on 19 July 2018, moving to the Baltic Sea/northern Poland on 21 July 2018. The daily maximum temperature exceeded 30 °C only on 21 July (30.1 °C); the previous days’ maxima were 27.6 °C and 28.1 °C, respectively (the daily regime of measured air temperature is in Figure A10 in Appendix D). The beginning of the period was partially cloudy, largely mid-altitude altostratus forming in the morning and early afternoon of 19 July. The period between the afternoon of 19 July and the late afternoon of 21 July was mostly clear, with some high-altitude cirrus. The late afternoon and evening of 21 July was cloudy, mostly with low-level cumulus. The highest values of relative humidity occurred at night (93%), dropping to 27% during the day. The wind above roof level was northwesterly, light, mostly below 3.2 m·s−1, and often as low as 1.6 m·s−1. The peak measured wind speeds of 3.1–4.5 m·s−1 were observed in the afternoon of 19 July 2018. The time of sunset was 19:02 UTC on 19 July 2015, and the time of sunrise and solar noon on 20 July were 03:15 and 11:08 UTC, respectively (for more details, see []).
4. Data and Methods
4.1. GIS Data
BSM and LSM require the input of a number of material input parameters to resolve the energy balance equations. These detail the surface in terms of albedo, emissivity, roughness length, thermal conductivity, and capacity of the skin layer and the volume in terms of thermal capacity and volumetric thermal conductivity. Similarly, RTM requires detailed descriptions of the albedo and emissivity of surfaces. When operating at the high resolution involved in the test case herein (2 m), ground surfaces and the nature of walls and roofing materials become very heterogeneous. Any bulk parameter setting would therefore be inadequate. Detailed settings of these parameters, wherever possible, were the only option. To obtain these data, a supplementary, on-site data collection campaign was conducted to create a database of the fine geospatial data. This included information concerning the wall, ground, and roof materials; colors; roughness; and window fraction, which were used to estimate surface and material properties. Each surface was described in terms of material category, albedo, and emissivity. Categories were assigned parameters estimated on the basis of surface and storage material composition and thickness. The parameters of LSM surface layers were assigned according to the properties of the corresponding PALM LSM category. BSM materials utilized a special set of categories and their parameters; the first two layers were inferred from the properties of the material near the surface, which may differ from the rest of the volume. Each tree was described by its position and vertically stratified leaf-area density (LAD). The trunk and crown were measured separately; estimated perimeters and heights were available for each, while crowns were categorized by shape. LAD decreases towards the center of the crown as a result of the higher branches-to-leaves ratio that occurs there. Building heights were available from the Prague 3D model, maintained by the Prague Institute of Planning and Development. All descriptions of surfaces, materials, trees, and their properties were collected in GIS formats and then preprocessed into the PALM-4U input files (according to the PALM input data standard) corresponding to the particular domain setup. For details of input data collection and processing, see [].
4.2. PALM-4U Model Setup
The dynamic core of the PALM-4U model was configured with the Wicker and Skamarock 5th-order advection scheme [] and the multigrid pressure solver [,]. The radiative fluxes were adapted from the WRF simulation, and their interactions with the urban canopy layer, including the resolved plant canopy, were modelled by the embedded RTM model []. The surface energy balance for the individual surfaces (vegetation, pavement, buildings, and water) was calculated by the LSM and BSM components; see []. The dynamic and energy processes arising out of resolved trees and shrubs were modelled by PCM.
The initial and boundary conditions for the parent domain of the PALM-4U simulations were obtained from the WRF model. WRF (version 4.0.3) was run on three nested domains with horizontal resolutions of 9 km, 3 km, and 1 km and at 49 vertical levels. The inner domain contained 84 × 84 grid points. The configuration was standard, but parameterizations were chosen in light of decreasing possible discrepancies that might arise from the boundary conditions. NOAH LSM (National Centers for Environmental Prediction/Oregon State University/Air Force/Hydrologic Research Lab model) and RRTMG (is Rapid Radiative Transfer Model) radiation were used in all simulations. The Yonsei University scheme was chosen for parameterization of the planetary boundary layer (PBL). Apart from all of the above, no other urban parameterization was used in the WRF model (all urban processes were simulated in PALM). MODIS (Moderate-resolution imaging spectroradiometer) land-use categories were used without modification. WRF output data were collected from overlapping runs with 12 h durations, initialized from the Global Forecast System (GFS) operational analyses and predictions. The first six hours of each run served as a spin-up, and the following hours (7–12) were used for the generation of boundary conditions for offline nesting. As the WRF-supplied air flow lacks a turbulent part, any additional turbulence was added at the border of the parent domain by PALM’s embedded Synthetic Turbulence Generator (STG) module in every PALM model time-step.
4.2.1. Mean Radiant Temperature Calculation
MRT is of particular importance in determining thermal exposure. With the new angular discretization scheme in place, RTM version 3.0 also added a method for calculating the mean radiant temperature (MRT) []. MRT at an arbitrary point in space is defined as the temperature of an imaginary object for which that object would be in radiative equilibrium with its surroundings, meaning that the absorbed irradiance would be equal to the emitted radiance.
Considering both long-wave (LW) and short-wave (SW) radiant fluxes for a hypothetical object with emissivity and SW albedo , MRT can be derived from the equilibrium equation together with the Stefan–Boltzmann law:
where is the mean SW irradiance of the hypothetical object and is its mean LW irradiance.
This novel calculation method facilitates the simulation of either a spherical black-globe thermometer or an arbitrary generic object of specified albedo, emissivity, and shape. The clothed human body constitutes a special case of such a shape in simulation; it is tall and narrow, and it therefore affected by radiation from the sides proportionally more than by radiation from above. The MRT values calculated in RTM in the form of average SW and LW irradiances for the hypothetical human body were then used to compute other elements of human thermal comfort in a newly added biometeorology module (BIO; see [,]).
The angular discretization scheme in RTM calculates MRT by means of weighted averaging of SW and LW irradiance from all discretized directions. The weights applied to particular directions were used for parametrization of the shape of the simulated object. RTM currently offers three different built-in body shape parametrizations, selectable by the variable mrt_geom. For mrt_geom = 0, the weights are identical in all directions, simulating a spherical object (a black globe thermometer if and ). The second scheme (mrt_geom = 1) was recommended by the authors of the BIO module, based on their earlier implementation of MRT in the BIO module []. In this scheme, the weight formula for zenith angle theta () is given as follows:
with the default values of parameters a = 0.88 and b = 0.12 prescribed by the BIO module authors. However, this formula lacks a scientific description and evaluation. Moreover, its geometrical representation is not adequate for simulation of a human being. It is asymmetrical vertically (the highest weight is slightly above the horizon), and directions below ≈10 degrees from nadir have zero weight. These issues necessitated the implementation of another shape parameterization scheme.
This scheme (mrt_geom = 2) simulates a spheroid S specified by the vertically oriented symmetry half-axis a and half-axis b. Because the symmetry axis is vertical, the weight for a specific direction depends on only the zenith angle and is proportional to the area of the orthographic projection of S from that direction. The orthographic projection shape is the ellipse with half-axes and b, where b is independent of and the area of is directly proportional to . To calculate , a vertical cross section is taken through the centre of S. In this cross section, S is replaced by ellipse E with half-axes a and b and is the line segment formed by orthographic projection of E from zenith angle .
The equation of a generic tangent line to ellipse at point , is given as
.
Points , lie on ellipse ; hence, . The tangent of the angle between a horizontal line and tangent is equal to its slope:
Coordinates , of the tangent point, given angle , would be as follows:
This gives two solutions for two tangents, and , from which the positive for and negative for are selected. Then, is given as
The origin-crossing line parallel to tangent is given as
.
The distance between two generic parallel lines is described parametrically as equals , so the distance between and its origin-crossing parallel equals
and the distance between and is double that:
The parameters a and b can be specified using configuration parameter mrt_geom_params; the default values are a = 0.88 and b = 0.12. The results in this study were obtained by means of the ellipsoid scheme (mrt_geom = 2) with default values of a and b.
4.2.2. Universal Thermal Climate Index calculation
Calculation of UTCI is based on the Fiala-UTCI multi-node dynamic of human heat transfer and regulation model [] and includes a clothing model reflecting behavioral adaptation of clothing insulation by the general urban population in response to actual outdoor temperatures []. UTCI is then defined as the isothermal air temperature of the reference condition that would elicit the same dynamic response of the physiological model for any combination of T, H, v, and r []. UTCI have been already previously successfully employed in a bioclimate simulation in Prague during a heat wave period at the regional scale []. In this study, UTCI with ellipsoidal MRT parameterization set in RTM (see Section 4.2.1, MRT) was calculated using the BIO module [] implemented in PALM-4U. The analyzed outputs represent 10-min averages of the calculated UTCI. These values were calculated at every time step of the model, which varies in a range from 0.1 to 1.0 s depending on prevailing meteorological conditions.
4.3. Model Validation
Although the primary aim of this study lies elsewhere, it is directly relevant to summarize the results of a preliminary validation check made against an existing PALM modelling study of the same area []. This was performed by an observation team in situ, checking the model against the actual conditions measured “on the ground”.
First, the WRF results with atmospheric soundings for Praha-Libuš (WMO ID 11520), the meteorological station closest to our domain of interest, were validated. The profiles modelled generally correspond well with station measurements, with some notable exceptions in the surface layer. This is very important to the study herein because the boundary conditions for the PALM simulations were taken from the lower levels. The model tends to show less of a diurnal range, underestimating stability by night and instability during the day. The differences were typically between 1 and 2 K, with only 12 UTC on 21 July exhibiting a difference of ≈4 K (see Figure 8 []). The global radiation from the WRF simulations for the summer campaign show very good agreement with the observations. Only in the noon period on 21 July were the maxima in WRF around 25 W·m−2 higher, quite possibly due to an underestimation of the cloud cover in the WRF simulation (see Figure 8 []).
Wall and surface temperatures were measured by FLIR SC660 for the 66 ground (horizontal) and 73 wall (vertical) evaluation points representing various surface types []. It is not possible to describe such a number of results in detail, so only the most important points will be presented. Generally, at vertical surfaces, the modelled surface temperature agrees fairly well with the observed one in the case of traditional buildings constructed in brick or building blocks; the differences here were typically between 0 K and 3 K. Modern buildings with complex wall structures, e.g., mosaics of metal, glass, and/or plastic, typically exhibit lower agreement. Specific cases involved buildings with glassy or glass-like material surfaces or buildings with high percentages of window fractions. A glassy surface usually reflects the sky or the opposite building(s). Consequently, the derived surface temperature primarily represents the surface temperature of the reflected object (wall, pavement, tree crown, or sky) and not the observed object itself. This type of building is not possible to validate by this mode of measurement.
The differences between observations and models for horizontal surfaces were usually lower, typically between 0 K and 2 K. The validation results demonstrated that modelling of real grassy surfaces in urban environments constitutes a definite challenge. The energy balance of grassy areas may depend strongly on soil-water content, assumed plant canopy, or their direct connection with deeper soil horizon layers, largely unknown to this study. Also revealed was the close dependency of the modelled surface temperature for surfaces in street canyons upon dual rows of trees and on proper representation of leaf-area density (LAD), which was especially challenging where crowns form an umbrella-like covering. The model underestimated street surface temperature by up to 5 K at one study point, although such surfaces were modelled well in other tree-shaded locations. Large tree crowns tend to become arranged in clusters with free space between them. At the same time, the modelled cells are homogenous and the clusters are randomly distributed. More detail concerning surface temperature validation may be found in Section 4.3 in [].
A comparison of the modelled and observed wall heat fluxes at ground-floor level (see Figure 30 []) showed similarities in the daily cycles of a similar amplitude. The model slightly overestimated the observed values (by approximately 5–10 W·m−2), while the corresponding modelled surface temperature agreed fairly well with the observations. The modelled wall heat flux at first-floor level (see Figure 31 []) showed a pronounced daily cycle, while the observed wall heat flux showed only a weak daily cycle of significantly lower amplitude. The modelled surface temperature, however, showed a lower amplitude (higher night-time and lower day-time temperatures) compared with the observations. This behavior suggests an underestimation of the walls’ insulation properties for the modelled wall configuration.
Air temperature was validated at three different locations (see Figure 32 []). Day-time temperatures fit well, with differences lower than 1 K in general. Only one station, located in Sinkuleho kolej, was temporarily affected by tree canopy in its immediate surroundings, and its differences reached 3 K in maxima. Nighttime temperatures were affected by marked cooling on 19–22 July, which was not captured well by LES, probably due to a misrepresentation of stable conditions []. Differences during the coldest part of the night may reach 2.5 K. The final validated variable was wind speed. Wind speeds of under 1 m·s−1 were observed in urban canyons during the measuring campaign (see Figure 33 []). The model results generally agree well with the observations.
5. Results
5.1. Spatiotemporal Pattern of Thermal Exposure in Urban Area
For a better understanding of the spatiotemporal pattern of thermal exposure, it is worth considering the map of land-cover categories for Prague-Dejvice classified to PIDS classes and with marked tree positions (see Figure 1).
At the beginning of the simulation, in the late-night hours before sunrise (00:00–03:00 UTC; +02:00 CEST), the typical spatial UTCI/thermal exposure pattern of the “late-night phase” in an urban environment may be observed (Figure 2, left). No thermal stress is predicted in the area of interest (see Figure A9 in Appendix D). Nevertheless, the highest values of UTCI at this stage are usually close to the walls of buildings, arising out of the sensible heat flux and LW radiation emitted from them. Thermal radiation from the walls is at its most intense in narrow alleys and in smaller courtyards with dense tree canopies. Dense trees exert a strong influence on the radiative cooling of surfaces. Conversely, low UTCI values are usually associated with open spaces with few or no trees during the late-night phase (mainly open grass areas, squares, and parking lots). Such low UTCI values are mainly attributable to a lower MRT associated with more rapid radiative cooling due to a large sky-view factor (mainly in cases of clear skies). Moreover, air flow and lower air temperatures play a minor role in reducing MRT, as opposed to UTCI.
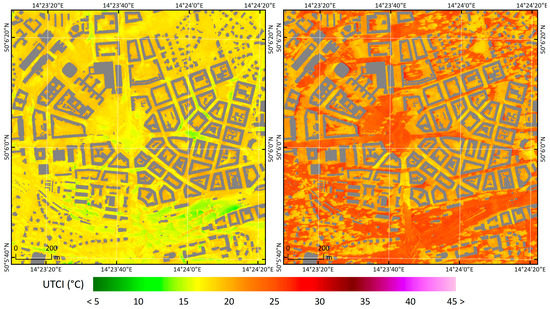
Figure 2.
Spatial variability of the universal thermal comfort index (UTCI) in Prague-Dejvice on 20 July 2018 at 02:00 (left) and 05:30 (right) UTC: the mean radiant temperature (MRT) values for the same times appear in Figure A8 in Appendix C. The land-cover categories in Prague-Dejvice, classified by the PALM input data standard (PIDS) classes with tree positions, may be found in Figure 1.
During sunrise, the spatial pattern of thermal exposure changes swiftly. Gradually, moderate heat stress is expected to be experienced in more than 50% of the area (see Figure A9 in Appendix D). At this time, known as the “transient morning phase”, the spatial pattern is determined primarily by direct sunlight (i.e., the component of MRT linked to short-wave radiation). In open spaces, this change creates a west-to-east gradient with the highest UTCI values in the immediate vicinity of east-facing walls, with a sharp transition between irradiated and shaded areas (Figure 2 right). UTCI values generally rise rapidly in wider street canyons running east–west, while they remain low in streets with an approximately north–south orientation due to persistent shading. Lower UTCI values in the shadows of the trees also become apparent. UTCI values in courtyards rise slowly due to persistent shading, and these sites exhibit the lowest UTCI values at this time of the day.
The onset of the third phase in the city, known as the “morning phase” of the spatial thermal exposure pattern, may be observed between 06–07 UTC (+02:00 CEST). At this stage, heat stress is already expected to be experienced in most of the area and the percentage of area under strong heat stress gradually increases. UTCI equalizes progressively in north-to-south and west-to-east streets (Figure 3, left). In north-to-east streets, long-wave radiation, the result of higher surface temperature, increasingly contributes to MRT values, while MRT rises rapidly due to direct short-wave radiation. The highest UTCI values are bound to the surroundings of the south-to-east and the sunlit south faces of buildings. Low UTCI values in the shade of vegetation and buildings are already clearly evident. Closed courtyards with a lower proportion of higher vegetation begin to heat up rapidly, leading to a steep rise in UTCI values.
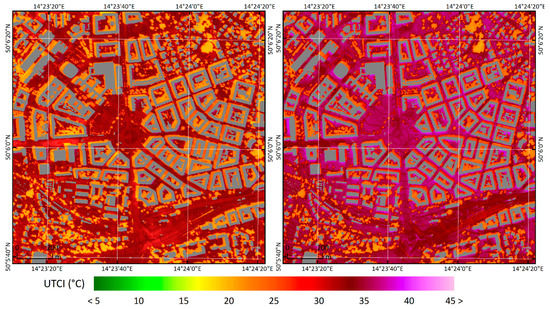
Figure 3.
Spatial variability of universal thermal comfort index (UTCI) in Prague-Dejvice on 20 July 2018 at 08:30 (left) and 12:30 (right) UTC: the MRT values for the same times appear in Figure A8 in Appendix C. The land-cover categories in Prague-Dejvice, classified by the PIDS classes with tree positions, may be found in Figure 1.
The highest daily averages of UTCI values are reached during the “afternoon” phase of the spatial thermal exposure pattern, which begins between 10 and 11 UTC (+02:00 CEST). It is noticeable that the UTCI peaks occur approximately 2–3 h earlier than peaks in air temperature. At this stage, up to 70% of the area experiences strong heat stress (see Figure A9 in Appendix D). Such high UTCI values reflect the daily maximum of MRT values as a consequence of high surface temperature and its associated emission of long-wave radiation, combined with high values of short-wave radiation remaining from direct sunlight. The maximum UTCI values shift from south-facing to southwest-facing walls on buildings within directly irradiated areas, where in some cases, very strong heat stress is predicted (Figure 3, right). However, a strongly developing turbulent flow results in increased spatiotemporal variability of the UTCI pattern. The values within individual courtyards vary widely depending on the quantity and location of their vegetation. Areas of relatively lower UTCI values in the shade of vegetation are clearly evident during the afternoon phase. The lowest UTCI values may be observed on land with larger, compact groups of abundant trees with high, thick crowns (gardens and parks).
The “evening transition” phase of the spatial thermal exposure pattern in the city typically begins between 14 and 15 UTC (+02:00 CEST). Progressive shading is the dominant factor in spatial UTCI variability. Consequently, the share of area under strong heat stress conditions gradually decreases (see Figure A9 in Appendix D). In most areas, the UTCI pattern exhibits an east–west gradient, with a sharp break at the shadow border (Figure 4 left). The highest UTCI values are bound to neighborhoods in which the walls of the buildings face west. The courtyards shade progressively and occur in localities with relatively lower values of UTCI.
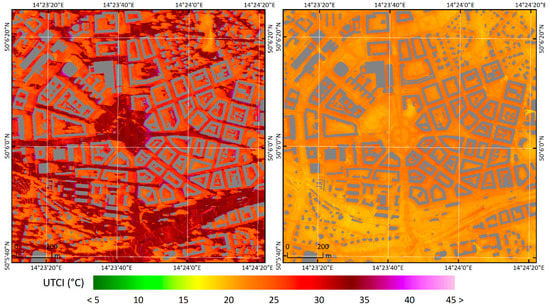
Figure 4.
Spatial variability of universal thermal comfort index (UTCI) in Prague-Dejvice on 20 July 2018 at 16:30 (left) and 20:30 (right) UTC: the MRT values for the same times appear in Figure A8 in Appendix C. The land-cover categories in Prague-Dejvice, classified by the PIDS classes with tree positions, may be found in Figure 1.
The “early night phase” of the spatial thermal exposure pattern begins to develop between 18 and 19 UTC (+02:00 CEST) immediately after sunset (Figure 4, right). The highest UTCI values are strongly linked to narrow streets and especially to courtyards with a high proportion of impervious surfaces, typically asphalt or concrete; however, no thermal stress is expected to be experienced in most of the area (see Figure A9 in Appendix D). This is mainly due to high MRT values arising out of a combination of sensible heat flux from the buildings, long-wave radiation, and limited ventilation. On the other hand, MRT values in open localities with lawn/grass decrease rapidly; UTCI values in these localities steadily approach those expected for parks and gardens at any given time. The spatial UTCI distribution pattern of the early night phase works towards the pattern characteristic of the late-night phase (see above).
5.2. Daily Course of UTCI in an Urban Area
The presentation of results that appears below focuses on the daily course of UTCI in representative locations of the characteristic types of urban environment: (i) streets (N1–4, G1–4); (ii) courtyards (C1–2, T1–2); and (iii) open public places in the form of outside seating terraces (O1–2), market-places (M1 and M2), paved playgrounds (P1–2), grassy playgrounds (P3–4); and “pizzettas” (R1–4).
5.2.1. Streets (Canyons)
Thermal comfort on streets is largely dictated in the daily course of UTCI by street orientation (east-to-west/west-to-east and north-to-south/south-to-north streets) and by the location of the point analyzed (south/north and east/west).
A north-to-south street is characterized by a single daily maximum of UTCI values. In the morning to noon phase, UTCI maxima for the west sides of streets (near east-facing walls; points N1 and N3) arise before noon and the maxima for the east sides of streets (near west-facing walls; points N2 and N4) shift to the afternoon. Finally, both sides of the streets show similar UTCI values at noon (Figure 5). However, the results herein suggest that UTCI maxima on the east sides of streets (near west-facing walls) reach values of up to 5 °C higher than those on the west sides of streets (near east-facing walls); thus, the intensity of solar heating is the same as that of the already-heated surface (warmed by short-wave reflection and long-wave emission during morning hours).
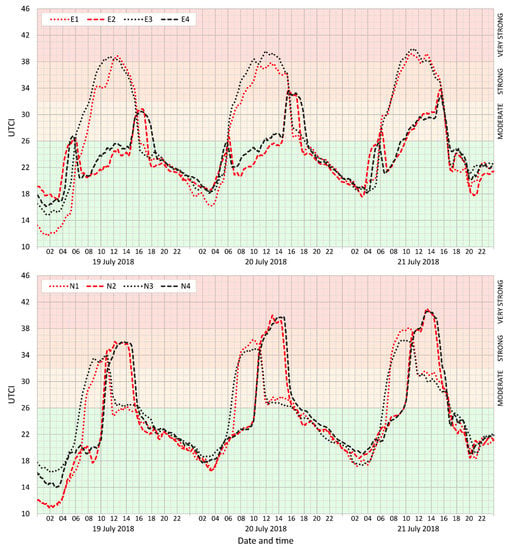
Figure 5.
Moving averages (n = 5) of the UTCI index in selected street-canyon locations (the E points are located in streets running east-to-west, the even numbers are from southern locations, and the odd numbers are from northern locations; N indicates a north–south canyon, the even numbers are eastern locations, and the odd numbers are western locations): the MRT values for the same times appear in Figure A2 in Appendix B.
For a street running east-to-west, the difference between the north (irradiated) and south (largely shaded) sides of the street are characteristic. On the south sides of streets (near north-facing walls; points E2 and E4), two daily UTCI maxima occur, bounded by short spells of direct insolation—lower in the early morning and higher in the late afternoon (Figure 5). On the northern side of the irradiated parts of east-to-west streets (near south-facing walls), the UTCI values are substantially higher and there is a single maximum of UTCI following the period of maximum insolation (points E1 and E3; see Figure 5).
In general, the highest UTCI values in urban canyons occur during the afternoon on the insolated north side of east-to-west streets and on the east side of streets running northeasterly. These parts exhibited over 38 °C UTCI for several hours, a figure that generates very high heat stress. However, model simulations indicate that, when direct irradiation ceases, UTCI values on both sides of these streets show relatively small and constant differences in MRT and UTCI during the night. At the same time, predicted fluctuations in the daily course of UTCI values during the daytime are generally higher for east-to-west streets than for north-to-south streets. This phenomenon is predominantly attributable to turbulent air flow in an urban canyon: higher air velocity on the irradiated side leads to the ascent of hot air, then cooler and warm air above the roofs mix, and colder air descends on the shaded side (see Figure 6). At the same time, Figure 6 is proof that insulation of a south-oriented wall can modify the vortexes in street (see the following discussion in Section 6.1).
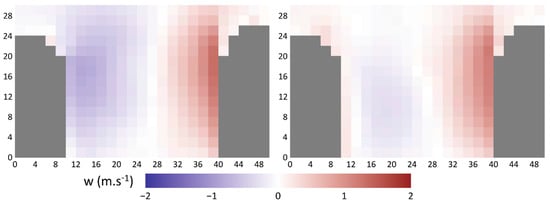
Figure 6.
Ten minute averages of the vertical wind component proving the modification of thermodynamics in an urban canyon (w, positive = upwards) between points E3 and E4 in an east-to-west canyon at 10:00 (left) and 13:30 (right) UTC on 20 July 2018: the view runs east to west (the buildings are grey, while the one on the right has a south-facing wall). Axis units are expressed in meters.
Moving beyond the effects of the side of the street, it is important to note that the results herein further indicate that the localities of points E1 and E3 returned relatively higher values of UTCI than the localities of points E2 and E4. In other words, the thermal and radiative properties of the northern, irradiated part of the street and adjacent buildings have a strong influence on thermal comfort not only in the irradiated part but also in the shaded part of the street. This effect is more pronounced for east-to-west streets than for north-to-south streets. Nevertheless, considering the results for points G1–4 (see UTCI index on Figure A1 in Appendix A and MRT on Figure A7 in Appendix B), a substantial street-level cooling effect may be attributed to the trees, which substantially reduces daily UTCI maxima and increases nighttime UTCI minima only slightly.
5.2.2. Courtyards
Four representative points were selected: two in courtyards with dense trees (T1 and T2) and the other two in largely paved courtyards with little vegetation (C1 and C2). The results for the daytime show that the UTCI values in the courtyards with trees were 5–10 °C lower than those in the paved courtyards. The trees mitigate spells of moderate heat stress substantially, thus avoiding the occurrence of strong heat stress (Figure 7). Maximum UTCI values occurred in the afternoons. However, this tendency may alter with respect to the irradiance of the courtyard. Small and closed courtyards are usually shaded by neighborhood buildings, and insolation is usually lower as a result. Interestingly, during the first part of the night, the UTCI values remained slightly higher in paved courtyards, a response to higher surface temperatures arising out of heat accumulation in the grounds and walls of buildings. Higher levels of long-wave radiation emitted by the tree crowns in comparison with the radiation from the sky contribute to higher MRT and consequently to higher UTCI values in the course of night in a similar fashion to the situation in street canyons (see Section 5.2.1). During the second part of the night, the UTCI differences between paved courtyards and green courtyards with trees vanish, while phases of higher UTCI values in courtyards with trees may appear. Nevertheless, in all cases, UTCI values during the night remain substantially below the level of thermal stress (Figure 7).
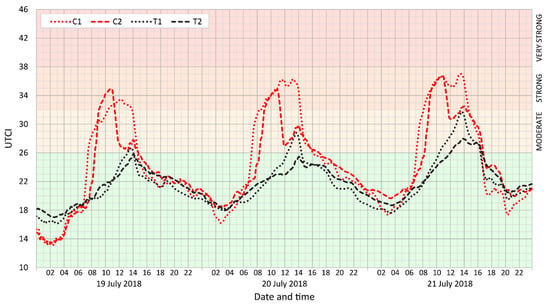
Figure 7.
Moving averages (n = 5) of UTCI in selected locations: C points are located in closed courtyards, and T points are located in courtyards with densely-planted trees. The MRT values for the same times appear in Figure A3 in Appendix B.
5.2.3. Public Places
Finally, representative points in selected public open spaces, as represented by market-places (M1–2), outside seating terraces (O1–2), paved playgrounds (P1–2), grassy playgrounds (P3–4), and “piazzettas” (small squares in built-up areas; R1–2) were analyzed.
The daily maxima of the UTCI values in open public places are bounded by relatively long periods of strong or even very strong heat stress (Figure 8). Only in piazzettas partly shaded by trees did the daily UTCI maxima occur before noon and were heat-stress conditions substantially reduced. During the night, no heat-stress conditions were anticipated in any of the public spaces investigated. The results further suggest quite small differences in UTCI (≈2–5 °C) between paved and grassy open spaces (playgrounds). These were more pronounced at the beginning of the simulation period since soil-moisture content decreased progressively in response to continuous hot, dry weather during the simulated period.
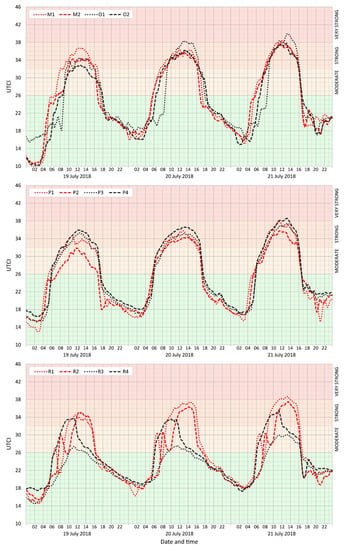
Figure 8.
Moving averages (n = 5) of UTCI in selected locations: open areas, often with public markets (M1–2) and beer gardens (O1–2), open grass surfaces (P1–2) and children’s playgrounds (P3 is on sand, and P4 is on artificial grass), and “piazzettas” (densely planted squares in built-up areas) (R1–4). The MRT values for the same times appear in Figure A4, Figure A5 and Figure A6 in Appendix B.
6. Discussion and Conclusions
6.1. Thermal Exposure in a Moderate-Climate Urban Environment
This study demonstrates the spatiotemporal variability of human thermal exposure and its key environmental parameters by means of the newly developed PALM-4U model and its biometeorology module. It utilizes the well-established UTCI index in a pilot study covering a moderate-climate urban area in Prague-Dejvice during a hot spell.
Six phases of spatial pattern of UTCI in urban environments during hot sunny days—night, sunrise transitional, morning, afternoon, sunset transitional, and early night—are described. Those phases are especially driven by variability in radiative heat, here represented by MRT as a key factor in thermal exposure [,,]. The importance of innovative approaches to MRT, as employed in this study, is thus highlighted. The new shape parameterization scheme described in Section 4.2.1 constitutes a clear, scientific description and is more appropriate to representation of the human body than previous approaches. It is capable of providing new perspectives on MRT accuracy in micro-scale simulations as well as of providing a valuable source of data for validation in future studies.
The results also emphasize that the spatiotemporal variability of the wind has important effects on thermal exposure in urban areas [,]. The effects on thermal exposure of the complexity of turbulence in street canyons [,] as well as in cross-ventilated building areas [,,] have been particularly difficult to quantify in the absence of information concerning wind velocity components in street canyons. In urban canyons without trees, only the primary vortex with its leeward side near the overheated surfaces and the windward side near shaded surfaces has been modelled with any regularity, following the description that appears in []. However, during typical sunny weather conditions, when the wind speed above a roof falls below 4 m·s−1, a nonuniform heat flux warms the air near the walls. This may lead to changes in the strength and shape of the primary vortex (see Figure 17 in []). The intensity of the vortex changes in response to street orientation, surface materials, and physical properties, including window fraction.
On the other hand, this study suggests that, in moderate-climate urban areas, the heterogeneity of humidity generally has only a minor effect on the spatiotemporal variability of thermal exposure and thermal comfort (for details, see e.g., [,,]). Similarly, the role of the much-addressed spatiotemporal variability of temperature fields in urban areas [,,] is implied to have a comparatively lower effect on thermal exposure in urban areas than MRT; however, further research and analyses are needed.
Focusing more specifically on particular urban structures, the highest thermal exposure is to be expected near the irradiated north sides of east-to-west streets [,,,]. However, the results herein suggest that the same level of heat exposure, or even higher, may also be observed around north-to-south streets during particular periods of the day. On the other hand, thermal exposure in courtyards with largely paved surfaces during the daytime is lower than that in open public spaces and compared to exposure in the irradiated parts of streets in the same period. These results need to be further verified and analyzed with respect to the complexity of the specific microclimate of courtyards []. It is important to note that heat exposure in streets increases where there is a high percentage of window fraction in the buildings and/or where highly reflective paints predominate on both sides of the street (irradiated and shaded) []. It is appropriate to hypothesize that this effect may be attributed to the strong reflection of short-wave radiation. This would then be followed by the absorption of reflected radiation by pavements, which are usually of lower albedo and higher roughness (this needs to be verified by a specially targeted validation campaign).
That trees have a substantial role to play in the reduction of thermal exposure in street canyons and open public places is evident both from the results herein and previous studies. Model simulations estimate the cooling effect of trees within a range from 4 °C to 9 °C UTCI during the day, and they anticipate only minor UTCI increases during the night. These numbers tally closely with empirical studies conducted in various cities in the central European region [,,]. As a general rule, it could be said that trees decrease thermal stress during the day but may increase it during the night [,,]. Turning to the combination of street orientation and reduction of heat exposure attributable to trees, the model herein lies in agreement with the observations made by [], anticipating a more marked cooling effect from trees on north-to-south streets than on east-to-west streets. However, the size, shape, height, crown spread, LAD, and the location of trees with respect to the investigated point also play important roles [,,,].
The presence of grass rather than artificial paved surfaces in open public places leads to less pronounced cooling effects in a range between 2 °C and 5 °C UTCI. These numbers probably remain, however, somewhat overestimated when a comparison is made with empirical studies performed in this region [,,]. The cooling effect of the grass in the urban environments depends heavily on soil moisture and other conditions (e.g., the structure of the soil layers and the LAD). A decrease in the soil moisture, in particular, leads to an increase in surface temperature. This effect has been modelled [] and observed []. Furthermore, on summer days, grass on high-quality soil and subsoil layers typically exhibits higher soil moisture than surfaces with only a shallow, separate soil layer (e.g., non-irrigated green tram-lines) [].
6.2. Model and Simulation Limits, Validation, and Further Development
This study applied the PALM modelling system, SVN revision 4508 []. The model was validated [] and provides similar or slightly higher values than the observations made in comparable central European environments (e.g., [,]). Nevertheless, both the model itself and its configuration still have some limitations. An exhaustive description of the model limitations appears in []; only those that may affect biometeorology are mentioned here.
First, the results herein demonstrate that urban macro-structure (geometry and orientation) in combination with the radiative and thermal characteristics of surfaces, both horizontal and vertical, have a substantial effect on human thermal exposure in built-up areas [,]. However, acquiring data concerning the radiative and thermal characteristics of surfaces in a real urban environment at the required levels of complexity and accuracy within reasonable financial limits constitutes a difficult challenge. We put substantial effort into the collection of detailed data, including the performance of an extensive field campaign, but a certain level of generalization and model uncertainty is still present in the input data. At the same time, the sensitivity tests carried out on the results of the input data allow a level of detail appropriate to modern modelling techniques []. It should also be noted that these modelling simulations were primarily validated with respect to air temperature, surface temperature, wind velocity, and concentration of air pollution (NOX and PM10) [].
Further, the model was configured without PALM’s building energy model (BEM), and the inner temperature of buildings was considered constant for the purposes of the simulation. In summer, a constant indoor temperature may certainly be perceived as a simplification, particularly for buildings without air conditioning in which the indoor temperature partially follows the diurnal cycle of the outdoor temperature. It needs to be taken into account that, for the simulated domain, almost no information concerning the quantity and placement of A/C systems was available. On the other hand, the majority of the buildings in the study area are old apartment houses, presumably without central A/C systems. There were no visible individual A/C units on the walls. Thus, it may be deduced that few A/C systems were to be expected in the domain.
The current method of discretization of terrain and buildings in PALM also introduces a limitation. PALM utilizes the Cartesian model grid, actually meaning that the entire volume of each grid cell contains either atmosphere (free air or air with a plant canopy included) or an obstacle (terrain or building). As a consequence, every model surface that is made up of a boundary between obstacle and air has its normal parallel to one of the grid axes. If the modelled domain contains uneven terrain or walls, the discretization may create artificial steps that affect UTCI, the most transparent bioclimatic index. Nevertheless, a comparison with the model results employing PET and other bioclimatic indices apart from UTCI could prove useful.
Regardless of the fact that further direct comparisons would be beneficial, the results of this study demonstrate the substantial potential of the model in the study of spatiotemporal patterns of thermal exposure in urban areas as well as in analyses of the influence of blue, green, and grey features on thermal exposure. The PALM-4U model, with its biometeorology module, covers thermal exposure (i.e., physical level of thermal comfort) in urban areas at an unprecedented level of complexity and resolution. Its application may facilitate substantial progress in research into thermal comfort and resulting heat stress in urban areas. Vital urban planning applications follow from this. However, the quality of the model output depends heavily on the quality of input data. Further long-term interdisciplinary cooperation in developing models for urban climate research is required as well as collaboration in the preparation and organization of the detailed spatial input data essential to most potential applications of the models.
Author Contributions
Coordinate the study, conduct the literature review and prepare the underlying concept of the paper, J.G., M.L.; participate in the model development and test, perform the simulation, and interpret the results, J.R. and P.K.; simulation processing, visualization, and interpretation of the results, J.G. and M.L. design the paper and discuss results, E.S.K. All coauthors participated in the text preparation and its revisions. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support was provided by the Operational Program Prague—Growth Pole of the Czech Republic project “Urbanization of weather forecast, air-quality prediction, and climate scenarios for Prague” (CZ.07.1.02/0.0/0.0/16_040/0000383), which is co-financed by the EU. Coauthor J.G. was supported by the Czech Academy of Sciences under the program for research and mobility support of starting researchers (MSM100302001).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Input data for a model are available on our archivation server (see http://hdl.handle.net/11104/0315416). PALM SVN code version is cited in litarature and archived in DOI repository.
Acknowledgments
The terrain-mapping campaign of building properties was co-financed by the Strategy AV21 project “Energy interactions of buildings and the outdoor urban environment”, financed by the Czech Academy of Sciences. We would like to thank Jiří Cajthaml and the students of the Faculty of Civil Engineering of the Czech Technical University, Prague, for their help with the terrain-mapping campaign. The PALM simulations, and pre- and postprocessing were performed on the HPC infrastructure of the Institute of Computer Science of the Czech Academy of Sciences (ICS), supported by the long-term strategic development financing of the ICS (RVO:67985807). Parts of the simulations were performed on the supercomputer of the IT4I Czech supercomputing center, supported by The Ministry of Education, Youth, and Sports from the Large Infrastructures for Research, Experimental Development, and Innovations project “IT4Innovations National Supercomputing Center—LM2015070“. The WRF and CAMx simulations were performed on the HPC infrastructure of the Department of Atmospheric Physics of the Faculty of Mathematics and Physics of Charles University, Prague, supported by the Operational Program Prague—Growth Pole of the Czech Republic project “Urbanization of weather forecast, air-quality prediction, and climate scenarios for Prague” (CZ.07.1.02/0.0/0.0/16_040/0000383), which is co-financed by the EU. Tony Long (Carsphairn, Scotland) helped work up the English.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| BIO | biometeorology module in PALM |
| BEM | building energy model |
| H | relative humidity (%) |
| LAD | leaf area density |
| LES | large-eddy simulation |
| LSM | land surface module |
| LW | long-wave (e.g., radiation) |
| MRT | mean radiant temperature |
| PALM | parallelized large-eddy simulation model |
| PET | physiologically equivalent temperature |
| RTM | radiative transfer model |
| SW | short-wave (e.g., radiation) |
| T | air temperature (2 m; °C) |
| UTCI | Universal Thermal Climate Index |
| v | wind speed (m·s−1) |
| WRF | Weather Research and Forecasting model |
Appendix A

Figure A1.
Moving averages (n = 5) of UTCI in points located in densely planted streets (G1–4).
Appendix B
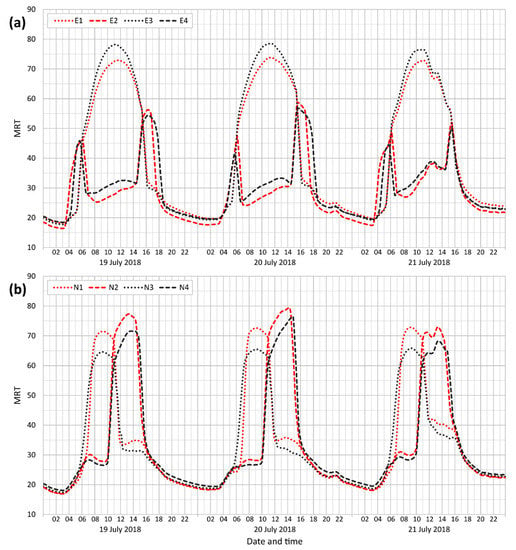
Figure A2.
Moving averages (n = 5) of the MRT index in selected street-canyon locations (E points (a) are located in east-to-west streets, the even numbers represent southern locations, and the odd numbers are northern locations; N (b) represents the north–south canyons, the even numbers represent eastern locations, and the odd numbers are western locations).
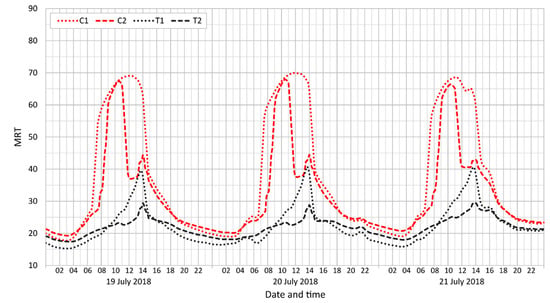
Figure A3.
Moving averages (n = 5) of the MRT in selected locations: C points are located in closed courtyards, and T points are located in courtyards with densely planted trees.

Figure A4.
Moving averages (n = 5) of the MRT in open areas, often with public markets (M1–2) and beer gardens (O1–2).
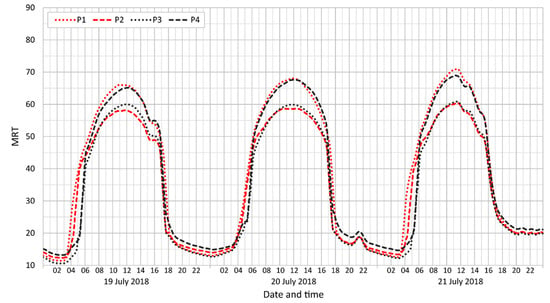
Figure A5.
Moving averages (n = 5) of the MRT in open areas with open grass surfaces (P1–2) and children’s playgrounds (P3 is on sand, and P4 is on artificial grass).

Figure A6.
Moving averages (n = 5) of the MRT in open areas with densely planted squares in built-up areas, known as “piazzettas” (R1–4).

Figure A7.
Moving averages (n = 5) of the MRT at points located in densely planted streets (G1–4).
Appendix C

Figure A8.
Spatial variability of the mean radiant temperature (MRT) in Prague-Dejvice on 20 July 2018 at 02:00 (a), 05:30 (b), 08:30 (c), 12:30 (d), 16:30 (e), and 20:30 (f) UTCI.
Appendix D
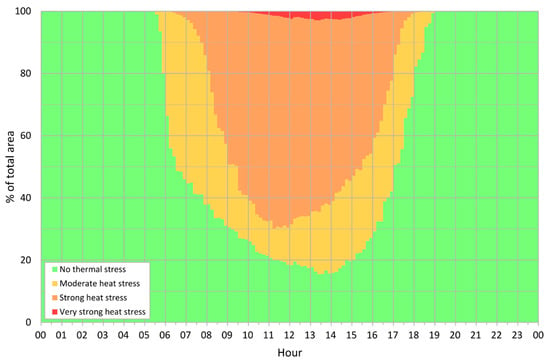
Figure A9.
Temporal distribution of the thermal stress category in Prague-Dejvice on 20 July: the colors represent the percent of total area affected by different levels of stress.

Figure A10.
Daily courses of air temperature measured at meteorological stations in Prague and surroundings on 19–21 July 2018: the dashed line indicates the urban station, and the numbers in brackets are WMO station IDs.
References
- Parsons, K. Human Thermal Environments: The Effects of Hot, Moderate, and Cold Environments on Human Health, Comfort, and Performance, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014; 635p. [Google Scholar] [CrossRef]
- Potchter, O.; Cohen, P.; Lin, T.P.; Matzarakis, A. Outdoor human thermal perception in various climates: A comprehensive review of approaches, methods and quantification. Sci. Total Environ. 2018, 631, 390–406. [Google Scholar] [CrossRef] [PubMed]
- Revi, A.; Satterthwaite, D.E.; Aragón-Durand, F.; Corfee-Morlot, J.; Kiunsi, R.B.R.; Pelling, M.; Roberts, D.C.; Solecki, W. Urban areas. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects; Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 535–612. [Google Scholar] [CrossRef]
- Hondula, D.M.; Balling, R.C., Jr.; Andrade, R.; Krayenhoff, S.; Middel, A.; Urban, A.; Georgescu, M.; Sailor, D.J. Biometeorology for cities. Int. J. Biometeorol. 2017, 61, 59–69. [Google Scholar] [CrossRef] [PubMed]
- Chen, L.; Ng, E. Outdoor thermal comfort and outdoor activities: A review of research in the past decade. Cities 2012, 29, 118–125. [Google Scholar] [CrossRef]
- Urban, A.; Kyselý, J. Comparison of UTCI with other thermal indices in the assessment of heat and cold effects on cardiovascular mortality in the Czech Republic. Int. J. Environ. Res. Public Health 2014, 11, 952–967. [Google Scholar] [CrossRef] [PubMed]
- Vanos, J.K.; Baldwin, J.W.; Jay, O.; Ebi, K.L. Simplicity lacks robustness when projecting heat-health outcomes in a changing climate. Nat. Commun. 2020, 11, 1–5. [Google Scholar] [CrossRef]
- Vanos, J.K.; Warland, J.S.; Gillespie, T.J.; Kenny, N.A. Review of the physiology of human thermal comfort while exercising in urban landscapes and implications for bioclimatic design. Int. J. Biometeorol. 2010, 54, 319–334. [Google Scholar] [CrossRef]
- Demuzere, M.; Orru, K.; Heidrich, O.; Olazabal, E.; Geneletti, D.; Orru, H.; Bhave, A.G.; Mittal, N.; Feliu, E.; Faehnle, M. Mitigating and adapting to climate change: Multi-functional and multi-scale assessment of green urban infrastructure. J. Environ. Manag. 2014, 146, 107–115. [Google Scholar] [CrossRef]
- Geletič, J.; Lehnert, M.; Savić, S.; Milošević, D. Modelled spatiotemporal variability of outdoor thermal comfort in local climate zones of the city of Brno, Czech Republic. Sci. Total Environ. 2018, 624, 385–395. [Google Scholar] [CrossRef]
- Stewart, I.D. Why should urban heat island researchers study history? Urban Clim. 2019, 30, 100484. [Google Scholar] [CrossRef]
- Maronga, B.; Banzhaf, S.; Burmeister, C.; Esch, T.; Forkel, R.; Fröhlich, D.; Fuka, V.; Gehrke, K.F.; Geletič, J.; Giersch, S.; et al. Overview of the PALM model system 6.0. Geosci. Model Dev. 2020, 13, 1335–1372. [Google Scholar] [CrossRef]
- Jendritzky, G.; Havenith, G.; Weihs, P.; Batchvarova, E. Towards a Universal Thermal Climate Index UTCI for Assessing the Thermal Environment of the Human Being; Final Report COST Action; COST (European Cooperation in Science and Technology): Brussels, Belgium, 2009; pp. 1–26. [Google Scholar]
- Jendritzky, G.; de Dear, R.; Havenith, G. UTCI—Why another thermal index? Int. J. Biometeorol. 2012, 56, 421–428. [Google Scholar] [CrossRef]
- Resler, J.; Eben, K.; Geletič, J.; Krč, P.; Rosecký, M.; Sühring, M.; Belda, M.; Fuka, V.; Halenka, T.; Huszár, P.; et al. Validation of the PALM model system 6.0 in real urban environment; case study of Prague-Dejvice, Czech Republic. Geosci. Model Dev. Discuss. 2020. [Google Scholar] [CrossRef]
- Fischereit, J.; Schlünzen, K.H. Evaluation of thermal indices for their applicability in obstacle-resolving meteorology models. Int. J. Biometeorol. 2018, 62, 1887–1900. [Google Scholar] [CrossRef] [PubMed]
- Fanger, P.O. Thermal Comfort; McGraw-Hill Book Company: New York, NY, USA, 1970. [Google Scholar] [CrossRef]
- Höppe, P. The physiological equivalent temperature—A universal index for the biometeorological assessment of the thermal environment. Int. J. Biometeorol. 1999, 43, 71–75. [Google Scholar] [CrossRef] [PubMed]
- Stewart, I.D. A systematic review and scientific critique of methodology in modern urban heat island literature. Int. J Climatol. 2011, 31, 200–217. [Google Scholar] [CrossRef]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ. 2003, 86, 370–384. [Google Scholar] [CrossRef]
- Chandler, T.J. Selected Bibliography on Urban Climate; WMO Technical Note No. 276; WMO: Geneva, Switzerland, 1970; p. 392. [Google Scholar]
- Oke, T.R. Review of Urban Climatology, 1968–1973; WMO Technical Note No. 134; WMO: Geneva, Switzerland, 1974; p. 152. [Google Scholar]
- Oke, T.R. Review of Urban Climatology, 1973–1976; WMO Technical Note No. 169; WMO: Geneva, Switzerland, 1979; p. 539. [Google Scholar]
- Yoshino, M. Development of urban climatology and problems today. Energy Build. 1990, 15, 1–10. [Google Scholar] [CrossRef]
- Arnfield, A.J. Two decades of urban climate research: A review of turbulence, exchanges of energy and water, and the urban heat island. Int. J. Climatol. 2003, 23, 1–26. [Google Scholar] [CrossRef]
- Mills, G. Urban climatology: History, status and prospects. Urban Clim. 2014, 10, 479–489. [Google Scholar] [CrossRef]
- Oke, T.R.; Mills, G.; Christen, A.; Voogt, J.A. Urban Climates; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar] [CrossRef]
- Kántor, N.; Kovács, A.; Lin, T.P. Looking for simple correction functions between the mean radiant temperature from the “standard black globe” and the “six-directional” techniques in Taiwan. Theor. Appl. Climatol. 2015, 121, 99–111. [Google Scholar] [CrossRef]
- Schnell, I.; Potchter, O.; Yaakova, Y.; Epstein, Y. Human exposure to environmental health concern by types of urban environment: The case of Tel Aviv. Environ. Pollut. 2016, 208, 58–65. [Google Scholar] [CrossRef] [PubMed]
- Schlünzen, K.H.; Hinneburg, D.; Knoth, O.; Lambrecht, M.; Leitl, B.; López, S.; Lüpkes, C.; Panskus, H.; Renner, E.; Schatzmann, M.; et al. Flow and transport in the obstacle layer: First results of the micro-scale model MITRAS. J. Atmos. Chem. 2003, 44, 113–130. [Google Scholar] [CrossRef]
- Bruse, M. Envi-Met 3.0: Updated Model Overview; University of Bochum: Bochum, Germany, 2004; Available online: http://www.envi-met.net/documents/papers/overview30.pdf (accessed on 20 November 2020).
- Sievers, U. Das Kleinskalige Strömungsmodell MUKLIMO_3 Teil 1: Theoretische Grundlagen, PC-Basisversion und Validierung; Berichte des Deutschen Wetterdienstes, Band 240; Deutschen Wetterdienstes: Offenbach, Germany, 2008. [Google Scholar]
- Sievers, U. Das Kleinskalige Strömungsmodell MUKLIMO_3 Teil 2: Thermodynamische Erweiterungen; Berichte des Deutschen Wetterdienstes, Band 248; Deutschen Wetterdienstes: Offenbach, Germany, 2016. [Google Scholar]
- De Ridder, K.; Lauwaet, D.; Maiheu, B. UrbClim—A fast urban boundary layer climate model. Urban Clim. 2015, 12, 21–48. [Google Scholar] [CrossRef]
- Resler, J.; Krč, P.; Belda, M.; Juruš, P.; Benešová, N.; Lopata, J.; Vlček, O.; Damašková, D.; Eben, K.; Derbek, P.; et al. PALM-USM v1.0: A new urban surface model integrated into the PALM large-eddy simulation model. Geosci. Model Dev. 2017, 10, 3635–3659. [Google Scholar] [CrossRef]
- Krč, P.; Resler, J.; Fuka, V.; Sühring, M.; Salim, M. Radiative Transfer Model 3.0 integrated into the PALM model system 6.0. Geosci. Model Dev. Discuss. 2020. [Google Scholar] [CrossRef]
- Fröhlich, J.; von Terzi, D. Hybrid LES/RANS methods for the simulation of turbulent flows. Prog. Aerosp. Sci. 2008, 44, 349–377. [Google Scholar] [CrossRef]
- Fröhlich, D.; Matzarakis, A. Calculating human thermal comfort and thermal stress in the PALM model system 6.0. Geosci. Model Dev. 2020, 13, 3055–3065. [Google Scholar] [CrossRef]
- Geletič, J.; Lehnert, M.; Jurek, M. Spatiotemporal variability of air temperature during a heat wave in real and modified landcover conditions: Prague and Brno (Czech Republic). Urban Clim. 2020, 31, 100588. [Google Scholar] [CrossRef]
- Wicker, L.J.; Skamarock, W.C. Time-Splitting Methods for Elastic Models Using Forward Time Schemes. Mon. Weather Rev. 2002, 130, 2088–2097. [Google Scholar] [CrossRef]
- Hackbusch, W. Introductory Model Problem. In Multigrid Method and Application; Graham, R.L., Jolla, L., Eds.; Springer: Berlin/Heidelberg, Germany, 1985; pp. 17–39. [Google Scholar] [CrossRef]
- Maronga, B.; Gryschka, M.; Heinze, R.; Hoffmann, F.; Kanani-Sühring, F.; Keck, M.; Ketelsen, K.; Letzel, M.O.; Sühring, M.; Raasch, S. The Parallelized Large-Eddy Simulation Model (PALM) version 4.0 for atmospheric and oceanic flows: Model formulation, recent developments, and future perspectives. Geosci. Model Dev. 2015, 8, 2515–2551. [Google Scholar] [CrossRef]
- Fiala, D.; Havenith, G.; Bröde, P.; Kampmann, B.; Jendritzky, G. UTCI-Fiala multi-node model of human heat transfer and temperature regulation. Int. J. Biometeorol. 2012, 56, 429–441. [Google Scholar] [CrossRef] [PubMed]
- Havenith, G.; Fiala, D.; Błazejczyk, K.; Richards, M.; Bröde, P.; Holmér, I.; Rintamaki, H.; Benshabat, Y.; Jendritzky, G. The UTCI-clothing model. Int. J. Biometeorol. 2012, 56, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Novák, M. Use of the UTCI in the Czech Republic. Geogr. Pol. 2013, 86, 21–28. [Google Scholar] [CrossRef]
- Mayer, H.; Holst, J.; Dostal, P.; Imbery, F.; Schindler, D. Human thermal comfort in summer within an urban street canyon in Central Europe. Meteorol. Z. 2008, 17, 241–250. [Google Scholar] [CrossRef]
- Kántor, N.; Unger, J. The most problematic variable in the course of human-biometeorological comfort assessment—The mean radiant temperature. Open Geosci. 2011, 3, 90–100. [Google Scholar] [CrossRef]
- Eliasson, I.; Knez, I.; Westerberg, U.; Thorsson, S.; Lindberg, F. Climate and behaviour in a Nordic city. Landsc. Urban Plan. 2007, 82, 72–84. [Google Scholar] [CrossRef]
- Lehnert, M.; Tokar, V.; Jurek, M.; Geletič, J. Summer thermal comfort in Czech cities: Measured effects of blue and green features in city centres. Int. J. Biometeorol. 2020. [Google Scholar] [CrossRef]
- Eliasson, I.; Offerle, B.; Grimmond, C.S.B.; Lindqvist, S. Wind fields and turbulence statistics in an urban street canyon. Atmos. Environ. 2006, 40, 1–16. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerod. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Arinami, Y.; Akabayashi, S.; Tominaga, Y.; Sakaguchi, J. Performance evaluation of single-sided natural ventilation for generic building using large-eddy simulations: Effect of guide vanes and adjacent obstacles. Build. Environ. 2019, 164, 68–80. [Google Scholar] [CrossRef]
- Shirzadi, M.; Tominaga, Y.; Mirzaei, P.A. Experimental and Steady-RANS CFD Modelling of Cross-ventilation in Moderately-dense Urban Areas. Sustain. Cities Soc. 2020, 52, 101849. [Google Scholar] [CrossRef]
- Oke, T.R. Street design and urban canopy layer climate. Energy Build. 1988, 11, 103–113. [Google Scholar] [CrossRef]
- Kántor, N.; Égerházi, L.; Unger, J. Subjective estimation of thermal environment in recreational urban spaces—Part 1: Investigations in Szeged, Hungary. Int. J. Biometeorol. 2012, 56, 1075–1088. [Google Scholar] [CrossRef] [PubMed]
- Richards, K. Urban and rural dewfall, surface moisture, and associated canopy-level air temperature and humidity measurements for Vancouver, Canada. Bound. Layer Meteorol. 2005, 114, 143–163. [Google Scholar] [CrossRef]
- Fortuniak, K.; Kłysik, K.; Wibig, J. Urban–rural contrasts of meteorological parameters in Łódź. Theor. Appl. Climatol. 2006, 84, 91–101. [Google Scholar] [CrossRef]
- Lehnert, M.; Geletič, J.; Dobrovolný, P.; Jurek, M. Temperature differences among local climate zones established by mobile measurements: Two central European cities. Clim. Res. 2018, 75, 53–64. [Google Scholar] [CrossRef]
- Bokwa, A.; Geletič, J.; Lehnert, M.; Žuvela-Aloise, M.; Hollósi, B.; Gál, T.; Skarbit, N.; Dobrovolný, P.; Hajto, M.J.; Kielar, R.; et al. Heat load assessment in Central European cities using an urban climate model and observational monitoring data. Energy Build. 2019, 201, 53–69. [Google Scholar] [CrossRef]
- Dian, C.; Pongrácz, R.; Dezső, Z.; Bartholy, J. Annual and monthly analysis of surface urban heat island intensity with respect to the local climate zones in Budapest. Urban Clim. 2020, 31, 100573. [Google Scholar] [CrossRef]
- Mayer, H.; Höppe, P. Thermal comfort of man in different urban environments. Theor. Appl. Climatol. 1987, 38, 43–49. [Google Scholar] [CrossRef]
- Mayer, H.; Kuppe, S.; Holst, J.; Imbery, F.; Matzarakis, A. Human Thermal Comfort below the Canopy of Street Trees on a Typical Central European Summer Day; Berichte des Meteorologischen Instituts der Albert-Ludwigs-Universität Freiburg; University of Freiburg: Breisgau, Germany, 2009; pp. 211–219. [Google Scholar]
- Belda, M.; Eben, K.; Fuka, V.; Geletič, J.; Kanani-Sühring, F.; Krč, P.; Maronga, B.; Resler, J.; Benešová, N.; Sühring, M.; et al. Sensitivity analysis of the PALM model system 6.0 in the urban environment. Geosci. Model Dev. Discuss. 2020. [Google Scholar] [CrossRef]
- Oke, T.R. Initial Guidance to Obtain Representative Meteorological Observations at Urban Sites; World Meteorological Organization: Geneva, Switzerland, 2006; p. 47. [Google Scholar]
- Kántor, N.; Kovács, A.; Takács, Á. Small-scale human-biometeorological impacts of shading by a large tree. Open Geosci. 2016, 8, 231–245. [Google Scholar] [CrossRef]
- Coutts, A.M.; White, E.C.; Tapper, N.J.; Beringer, J.; Livesley, S.J. Temperature and human thermal comfort effects of street trees across three contrasting street canyon environments. Theor. Appl. Climatol. 2016, 124, 55–68. [Google Scholar] [CrossRef]
- Middel, A.; Krayenhoff, E.S. Micrometeorological determinants of pedestrian thermal exposure during record-breaking heat in Tempe, Arizona: Introducing the MaRTy observational platform. Sci. Total Environ. 2019, 687, 137–151. [Google Scholar] [CrossRef] [PubMed]
- Gulyás, Á.; Unger, J.; Matzarakis, A. Assessment of the microclimatic and human comfort conditions in a complex urban environment: Modelling and measurements. Build. Environ. 2006, 41, 1713–1722. [Google Scholar] [CrossRef]
- Lindberg, F.; Grimmond, C.S.B. The influence of vegetation and building morphology on shadow patterns and mean radiant temperatures in urban areas: Model development and evaluation. Theor. Appl. Climatol. 2011, 105, 311–323. [Google Scholar] [CrossRef]
- Takács, Á.; Kiss, M.; Hof, A.; Tanács, E.; Gulyás, Á.; Kántor, N. Microclimate modification by urban shade trees–an integrated approach to aid ecosystem service based decision-making. Procedia Environ. Sci. 2016, 32, 97–109. [Google Scholar] [CrossRef]
- Morakinyo, T.E.; Kong, L.; Lau, K.K.L.; Yuan, C.; Ng, E. A study on the impact of shadow-cast and tree species on in-canyon and neighborhood’s thermal comfort. Build. Environ. 2017, 115, 1–17. [Google Scholar] [CrossRef]
- Lee, H.; Mayer, H.; Kuttler, W. Impact of the spacing between tree crowns on the mitigation of daytime heat stress for pedestrians inside E-W urban street canyons under Central European conditions. Urban For. Urban Green. 2020, 48, 126558. [Google Scholar] [CrossRef]
- Bongardt, B. Stadtklimatologische Bedeutung kleiner Parkanlagen: Dargestellt am Beispiel des Dortmunder Westparks (Essener Ökologische Schriften); Westarp Wissenschaften: Hohenwarsleben, Germany, 2006; Volume 24, 268p, ISBN 978-3894321109. [Google Scholar]
- Müller, N.; Kuttler, W.; Barlag, A.B. Counteracting urban climate change: Adaptation measures and their effect on thermal comfort. Theor. Appl. Climatol. 2014, 115, 243–257. [Google Scholar] [CrossRef]
- Lehnert, M. The soil temperature regime in the urban and suburban landscapes of Olomouc, Czech Republic. Morav. Geogr. Rep. 2013, 21, 27–36. [Google Scholar] [CrossRef]
- Resler, J.; Eben, K.; Geletič, J.; Krč, P.; Rosecký, M.; Sühring, M.; Belda, M.; Fuka, V.; Halenka, T.; Huszár, P.; et al. PALM 6.0 revision 4508; Leibniz University: Hannover, Germany, 2020. [Google Scholar] [CrossRef]
- Kántor, N.; Chen, L.; Gál, C.V. Human-biometeorological significance of shading in urban public spaces—Summertime measurements in Pécs, Hungary. Landsc. Urban Plan. 2018, 170, 241–255. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).