Characteristic Analysis of Dual-Polarization Weather Radar Echoes of Convective Precipitation and Snowfall in the Mount Everest Region

Abstract

This paper introduces the X-band weather radar dual-polarization parameters of isolated convective cell precipitation and meso/microscale snowfall on Mount Everest and presents the first precipitation observations based on dual-polarization weather radar in this area. Compared with the Chengdu Plain, Mount Everest experienced convective precipitation on smaller horizontal and vertical scales with a narrower Z_dr probability density spectrum (uniformly distributed around approximately 0). The Z_h profile on Mount Everest displayed two peaks, unlike that over the plains, and the precipitation at the strong convective core was denser. Furthermore, during winter snowfall on the northern slope of Mount Everest, when the boundary layer exhibited sufficient water vapor and dynamic uplift, due to the low boundary layer temperature (<0 °C), water vapor produced stratiform clouds in the middle and lower layers (approximately 1.5 km above ground level (AGL)). Water vapor condensation at 1.5–2.5 km AGL led to latent heat release, which increased the temperature of regional stratiform clouds with increasing height. Consequently, the temperature at the stratiform cloud top height (2.5 km AGL) unexpectedly exceeded 0 °C. Additionally, the −20 °C isotherm was at approximately 4 km AGL, indicating that the middle- and upper-layer atmospheric temperatures remained low. Therefore, thermal instability occurred between the stratiform cloud top height and the middle/upper atmosphere, forming convective motion. These findings confirm the occurrence of elevated winter snowfall convection above Mount Everest and may have certain reference value for retrieving raindrop size distributions, quantitatively estimating precipitation, and parameterizing cloud microphysical processes in numerical prediction models for the Qinghai-Tibetan Plateau.

1. Introduction

With a total area of approximately 2.5 million km² and an average elevation exceeding 4000 m, the Qinghai-Tibetan Plateau is the highest plateau in the world. The climate of the Qinghai-Tibetan Plateau is characterized by many hours of sunshine, strong radiation, low temperatures, frequent and strong winds, and a relatively small sum of the temperature on the days with an average temperature ≥10 °C. In summer, the weather can be warm or cool and rainy with hail, while in winter, cold weather persists with large amounts of snow. Under the joint action of the climatic characteristics of plateau and mountainous regions and the warm and humid air flow in the southern Indian Ocean, the weather in this region not only directly drives the climate and weather changes in eastern and southwestern China but also greatly impacts the occurrence of climate change in the Northern Hemisphere [1].

A radar is an electronic device that uses electromagnetic waves to detect targets. Radars have numerous advantages: they can detect long-distance targets during both daytime and night time, they can operate under any weather condition, and they have a certain penetration ability. Therefore, radars have become indispensable not only in the military but also in the fields of social and economic development (in applications such as flood early warning, soil vegetation cover imaging, weather forecasting, and environmental monitoring). As a result, according to the different detection methods of radar antennas, many different types of radar have been developed, such as conventional Doppler radar, synthetic aperture radar, dual-polarization Doppler radar, and phased-array radar.

Ground-based, vehicular and space borne Doppler weather radar techniques are widely used in the field of atmospheric remote sensing. In particular, in recent years, dual-polarization Doppler weather radar has undergone rapid development [2]. Unlike traditional single-polarization weather radars, dual-polarization radars can emit and receive both horizontally and vertically polarized waves. Therefore, this technology can obtain dual-polarization physical parameters, which contain more abundant information about changes in precipitation processes than the parameters provided by single-polarization radar. In addition to traditional physical quantities, such as the reflectivity, velocity, and spectral width, dual-polarization physical parameters include the differential reflectivity (Z_dr), copolar correlation coefficient (ρ_hv), differential phase (Φ_dp), and range derivative-specific differential phase (K_dp) [3].

These dual-polarization physical quantities can reflect the shape, that is, the degree of nonsphericity, of hydrometeor particles [4]. Therefore, the distributions of the type and quantity of condensate particles in three-dimensional space can be more accurately estimated than with traditional physical parameters, and the fine structural characteristics of precipitation clouds can be better reflected. Consequently, dual-polarization radar is highly important for better understanding cloud microphysical processes, performing the early warning and nowcasting of disastrous weather, obtaining quantitative precipitation estimates (QPEs), and assimilating radar data [5].

Dual-polarization radar observations have been employed by a number of scholars for research on the evolutionary characteristics of the three-dimensional structure of precipitation weather. Andric et al. [6] used the range height indicator (RHI) data of dual-polarization Doppler radar to analyze the vertical structure and vertical changes in the polarization parameters for winter storms. Mariko et al. [7] observed raindrops, snow, and graupel in Arctic deep mixed-phase clouds based on X-band radar RHI data and proposed a classification method for precipitation particles in different phases. Ryzhkov et al. [8] used quasi-vertical profiles (QVPs) to process and display polarization weather radar data; according to their study, this method could reveal the temporal evolution of the microphysical processes generated by precipitation. Bukovcic et al. [9] performed a detailed analysis on the structure and maintenance mechanism of winter snowfall clouds based on dual-polarization weather radar, which provided a satisfactory reference for research on the evolutionary characteristics of vertical structures in the snowfall process. In addition, Li et al. [10] used Tropical Rainfall Measuring Mission (TRMM) satellite data for the statistical analysis of strong convective weather on the Qinghai-Tibetan Plateau and showed that the Qinghai-Tibetan Plateau is more likely than plains areas to trigger small-scale convective weather. These studies all provide references for analyzing the cloud microphysical processes of convective precipitation (snow) weather on the northern slope of Mount Everest.

The outfield radar observations adopted herein belong to the first small-scale weather system observation test carried out in the Mount Everest region. The observation device is an X-band dual-polarization weather radar designed and developed by Chengdu 784 Factory, China. The observational data were selected mainly to investigate summer precipitation from July to August 2020 and winter snowfall from December 2020 to January 2021 on the northern slope of Mount Everest. Compared with S-band and C-band weather radar, X-band dual-polarization radar is more sensitive to hydrometeor particles in plateau areas. For instance, it can sensitively identify droplets, small ice crystals, supercooled water, small ice-water mixtures, and small raindrops [11]. Moreover, the antenna volume of X-band radar is small, and therefore, it is easy to transport and thus highly convenient for mobile observations. Furthermore, the radial range resolution of X-band radar is higher than that of S/C-band radar. In addition, radiosonde data from the Tibet Dingri meteorological station, ground automatic station data, Fengyun-4 (FY4) satellite data, and meteorological reanalysis data were combined to analyze the roles of dynamic fields, humidity, and thermal conditions in the development and evolution of precipitation (snow) on the plateau. The results of this study may help characterize the vertical structure of the X-band dual-polarization weather radar echoes of precipitation (snow) in Qomolangma, thereby providing an important basis for understanding the microphysical mechanism of cloud precipitation over the Qinghai-Tibetan Plateau [1].

2. X-Band Dual-Polarization Radar and Data Quality Control

An X-band all solid-state dual-polarization weather radar was installed at the Comprehensive Observation and Research Station of Atmosphere and Environment on Mount Everest, Chinese Academy of Sciences, on 1 June 2019, and the equipment began to operate formally on 2 June 2019. The radar station is located on the northern slope of Mount Everest, 86.00° east longitude and 28.35° north latitude, at an elevation of 4296 m [12].

The radar adopts long- and short-pulse horizontally and vertically polarized electromagnetic waves and operates in double transmitting and double receiving modes. The radar scanning mode is mainly volume scan (VOL), accompanied by partial RHI. Due to the obstruction of the surrounding terrain, the minimum initial elevation of the volume scan is 5°.

Table 1. Basic parameters of the X-band dual-polarization weather radar.

Parameter Name	Parameter Value	Unit	Definition
$\lambda$	3.2	$\mathrm{cm}$	radar wavelength
$P$	50	$\mathrm{w}$	peak power
${\theta }_h$	1.27	°	horizontal beam width
${\theta }_v$	1.3	°	vertical beam width
$\mathrm{PRF}$	1000	$\mathrm{Hz}$	pulse repetition frequency
$\tau$	80	$\mathsf{\mu }\mathrm{s}$	pulse width:1 short, 2 long
$R_{\max }$	150	km	maximum sounding radius
$H_{\max }$	24	km	maximum soundingheight
$V_r$	−8~8	m/s	unambiguous velocity range
$\rho$	120	m	radial distance resolution

summarizes the basic observation parameters of the radar. The straight-line distance from the top of Mount Everest to the radar is approximately 40 km, with the peak being nearly 3° west of south of the radar station.

According to the principle of electromagnetic wave scattering [2], X-band dual-polarization radar is more sensitive to weak precipitation particles than S/C-band dual-polarization radar. However, its shorter wavelength is likely to cause larger attenuation of Z_h and Z_dr [13,14]. The differential phase (Φ_dp) is the accumulated phase difference between the polarizations during wave propagation when detecting nonspherical precipitation particles, and this value contains the forward scattering phase difference φ_dp and backward scattering phase difference $\delta$. As the wavelength of X-band dual-polarization radar is short, the $\delta$ value increases with increases in the equivalent diameter of raindrops and detection distance, causing a phase superposition effect of $\delta$; this effect interferes with echo signals, leading to jitter in the Φ_dp value [15]. Therefore, it is necessary to perform quality control for the raw observational data of the X-band dual-polarization physical parameters.

The attenuation rates of both Z_h and Z_dr are linearly correlated with K_dp [14]. Based on the Z_h-K_dp relationship reported by Bi et al. [15], an attenuation correction for Z_h can be implemented.

However, the correction for the attenuation of Z_dr is more complex than that for the attenuation of Z_h. The primary reason is that the incident angles of vertically polarized beams vary with an increase in elevation [16], leading to an exponential reduction in Z_dr with increasing antenna elevation. In addition, the larger the Z_dr value is, the greater the rate of reduction. The correction method for Z_dr is provided in Equation (1):

$$Z_{dr}(0)=\frac{{\cos }^4\alpha \ast Z_{dr}(\alpha )}{{\left(1-\sqrt{Z_{dr}(\alpha )}{\sin }^2\alpha \right)}^2}$$

(1)

where Z_dr(α) represents the Z_dr value at a certain elevation and Z_dr(0) represents the corresponding value uniformly corrected to an elevation of 0°. After the elevation is corrected, the attenuation is corrected as follows:

$$Z^{\ast }{}_{dr}(r)=Z_{dr}(r)+2{\displaystyle {\int }_{r_1}^{r_2}0.04916K_{\mathrm{dp}}(r)dr}$$

(2)

where r₁ and r₂ represent radial distances from the radar station, $Z^{\ast }{}_{dr}(r)$ represents the real differential reflectivity after the attenuation correction, and 0.04916 is the linear coefficient between the differential reflectance attenuation rate and differential propagation phase shift rate of the X-band dual-polarization weather radar on the Qinghai-Tibetan Plateau [15]. Figure 1 and Figure 2 show the effects of the attenuation correction on Z_h and Z_dr, respectively, based on the abovementioned methods.

As shown in Figure 1 and Figure 2, after applying the attenuation corrections to the Z_h and Z_dr values of the X-band dual-polarization weather radar on the northern slope of Mount Everest, the actual values are larger than the original values. Furthermore, with increases in the original values and observation distance, the increase in the actual values becomes more obvious. To solve the problem of jitter in Φ_dp, we perform median filtering of the window along the radial distance to quality control the values of Φ_dp:

$$\begin{array}{l}S=\sqrt{\frac{{\displaystyle \sum _{\mathrm{i}=1}^5{\left({\Phi }_{dpi}-\overline{{\Phi }_{dp}}\right)}^2}}{5}}\\ \left|{\Phi }_{dpi}-{\Phi }_{dpmid}\right|>S,{\Phi }_{dpi}={\Phi }_{dpmid},\mathrm{i}\in [1,5]\end{array}$$

(3)

where S represents the mean square deviation of Φ_dp in five consecutive distance bins along the radial direction and Φ_dpmid represents the median of the five points. The phase difference jitter caused by the δ value is assessed based on whether the absolute value of the difference between Φ_dp and Φ_dpmid is larger than S. Figure 3 shows the results of a comparison between the Φ_dp values before and after implementing quality control during a strong convective precipitation event on the northern slope of Mount Everest.

As shown in Figure 3, after performing quality control on the original Φ_dp data from the X-band dual-polarization weather radar on the northern slope of Mount Everest, the phase difference jitter interference caused by the δ value is noticeably smoothed and suppressed.

3. Radar Sounding Experiment Results and Analysis in the Mount Everest Region

3.1. Convective Precipitation Weather

Continuous live observational data from the X-band dual-polarization weather radar on the northern slope of Mount Everest from 08:00 to 09:00 (UTC) on 17 July 2020, were selected for analysis. Figure 4 shows the T-logp generated by the sounding data for the Tibetan Dingri station at 00:00 (UTC) on 17 July 2020. As shown in Figure 4, the wind direction is easterly at 500–300 hPa, and turns to be westerly at approximately 500 hPa, where obvious wind shear appears. Above 300 hPa, the wind direction turns easterly, with noticeable vertical wind shear. The T-Td values of the middle and bottom layers below 450 hPa with abundant water vapor are very small. The altitude of the lifting condensation level (LCL) is only approximately 1 km relative to the elevation of the station. The Showalter index (Si) is <−3 °C, the K index is equal to 26, and the atmospheric thermal structure is unstable, which results in convective precipitation. Figure 5 shows the observational data from the FY4 satellite at 08:19 (UTC) on 17 July 2020. Figure 5a shows a visible light channel image, and the albedo at the station (red circle) is 0.47, which indicates that the vertical depth of the cloud body was large at this time. Figure 5b shows a longwave infrared channel image; the cloud top brightness temperature at the station (red circle) is 0.47 °C, which indicates that the cloud top was at a high altitude at this time. Finally, Figure 5c shows an image from the high-level water vapor channel, and the brightness temperature of water vapor at the station (red circle) is −26.93 °C, which indicates that the atmospheric water vapor content was very high.

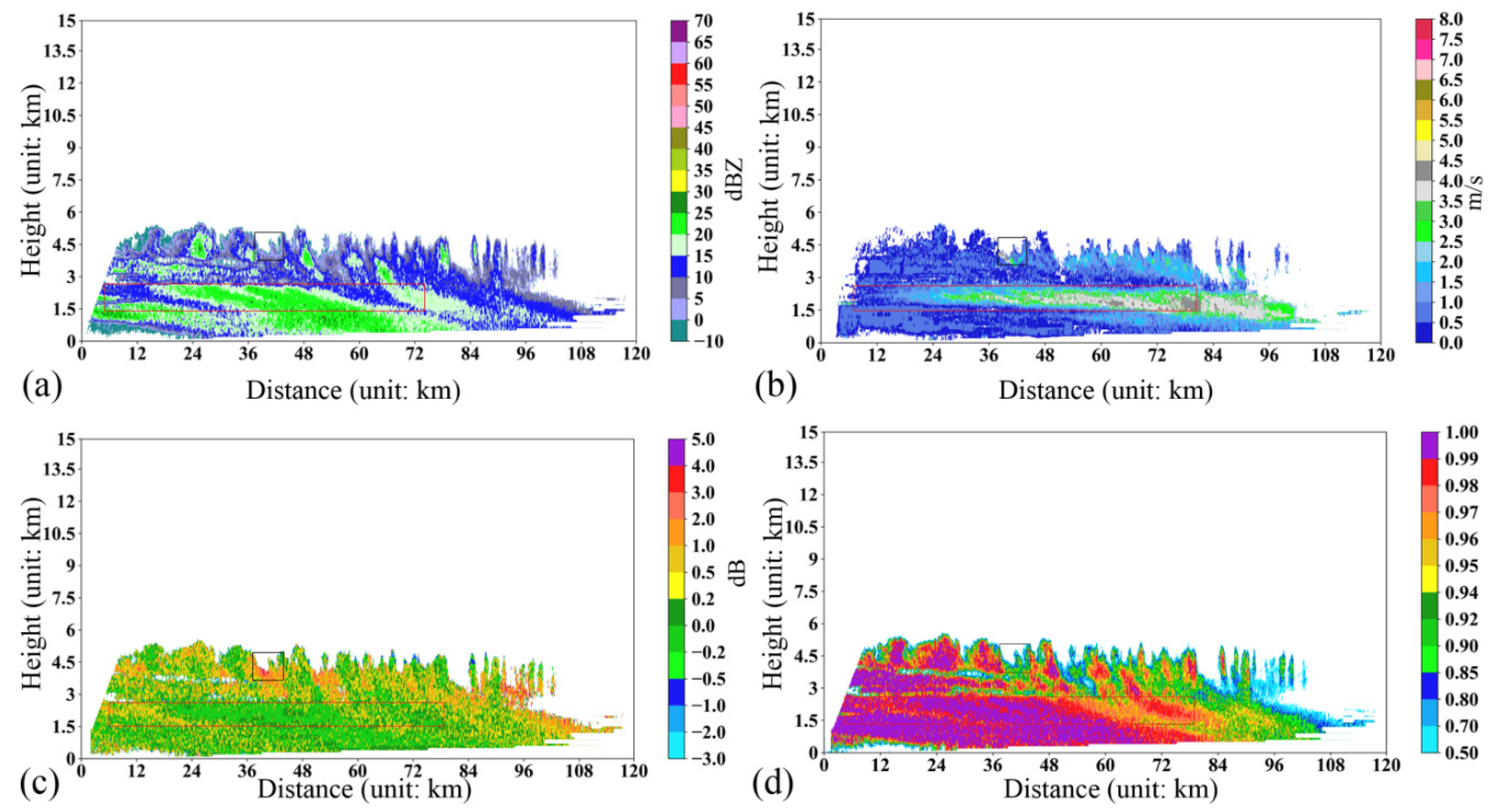
Figure 6a–d shows the dual-polarization physical quantities of convective single cells on the northern slope of Mount Everest observed simultaneously at 8:23 (UTC) on 17 July 2020, using plan position indicator (PPI) detection mode at an elevation of 9°. As shown in Figure 6a, the horizontal scale of convective precipitation observed at this elevation is approximately 35 km from east to west and approximately 8.4 km from north to south. The height above ground level (AGL) is approximately 4 km. There is a strong convective core with reflectivity >40 dBZ (indicated by the black circle in Figure 6a), which corresponds to the anticyclone divergence field at the same position in the black circle in Figure 6b. In addition, there is an area with large Z_dr values at the same position in the black circle in Figure 6c, and the ρ_hv value at the corresponding position in Figure 6d is close to 1, which indicates that a strong convective core appears at this position and that the shape of raindrops is oblate. Obvious wind field convergence appears in the red frame in Figure 6b, which corresponds to the developing convective echo at the same position in the red frame in Figure 6a. In addition, the Z_dr value at the same position in the red frame in Figure 6c is close to 0 dB, and the ρ_hv value at the corresponding position in Figure 6d is low, which indicates that there is a new precipitation echo triggered by convective upward movement at this position and that the precipitation cloud is mixed with small raindrops and ice crystals that are approximately spherical in shape.

Figure 7 shows the vertical profiles obtained by using X-band dual-polarization weather radar in RHI detection mode when the convective precipitation weather developed to a mature stage. Figure 7a shows the reflectivity distribution at 08:23 (UTC) on 17 July 2020, and Figure 7b shows the reflectivity distribution at 08:33 (UTC) on 17 July 2020. Figure 8a–d shows the distributions of the velocity, Z_dr, K_dp, and ρ_hv based on Figure 7a, and Figure 8e–h shows the distributions of the velocity, Z_dr, K_dp, and ρ_hv based on Figure 7b. As shown in Figure 7a, there is a mature, long, and narrow convective precipitation echo at a radial distance of 16–25 km from the radar station; the vertical extent is between 9 and 2 km AGL. Due to the low-level beam blockage, no precipitation echo signals are observed. Most of the Z_h values of the whole layer are above 30 dBZ, with the strong echo center (>40 dBZ) appearing at 4–5 km AGL. At 4.5 km AGL, obvious convective updrafts and downdrafts are observed (Figure 8a–d), which is consistent with the center position of the strong echo in Figure 7a. Most of the Z_dr values are between −1 and 1 dB, and the K_dp values are distributed mainly between −1° and 2°. The ρ_hv values are very large and are basically greater than 0.98. The ground rain gauge shows that the cumulative precipitation in this period is 21.3 mm. Therefore, during the period in which the convective precipitation on the northern slope of Mount Everest develops to a mature stage, the total precipitation is lower than that in the plains area. Furthermore, in this region, the particle phase indicates approximately spherical raindrops, and the number of flat ellipses along the horizontal axis is equivalent to that of the long ellipses along the vertical axis. Figure 7b shows the evolved echo of the single mature convective cell after ten minutes; at radial distances of 18–26 km from the radar station, the top height of the narrow convective precipitation echo is more than 10 km AGL, which is noticeably higher than that at the mature stage 10 min prior, and it has moved horizontally approximately 2 km to the northwest. Within 2 km AGL, no precipitation echo signals are observed due to the low-level beam blockage. The Z_h values of the whole layer are noticeably weakened, most of which are between 20 and 30 dBZ, with that at the center of the strongest echo <35 dBZ. The height of the vertical wind shear drops to 4 km AGL, and the updrafts are weak and concentrated at the bottom of the precipitation cloud (Figure 8e–h). The interior of the whole precipitation cloud layer is basically composed of downdrafts. Most of the Z_dr values are between −3 and 2 dB, and the K_dp values are distributed mainly between −2° and 3°. The ρ_hv values below 5 km AGL are significantly lower than those in Figure 8d, with an average below 0.95. The ground rain gauge shows that the rain intensity during this period is 6.1 mm/h. Therefore, with the passage of time, the convective precipitation on the northern slope of Mount Everest gradually weakens after reaching the mature stage, and the rain intensity of the whole layer is remarkably weaker than that in the mature stage. The middle and bottom layers contain raindrops and a semi-melted rain–hail mixture with a low correlation coefficient. Furthermore, large, oblate raindrops also exist. All these factors contribute to a high Z_dr value. The coexistence of raindrops and graupels is confirmed by observations from a ground laser raindrop spectrometer. The middle and high layers contain relatively consistent small spherical ice crystals with a high correlation coefficient. This observation is verified by the data observed in the middle and high atmospheric layers by sensors equipped on unmanned aerial vehicles (UAVs).

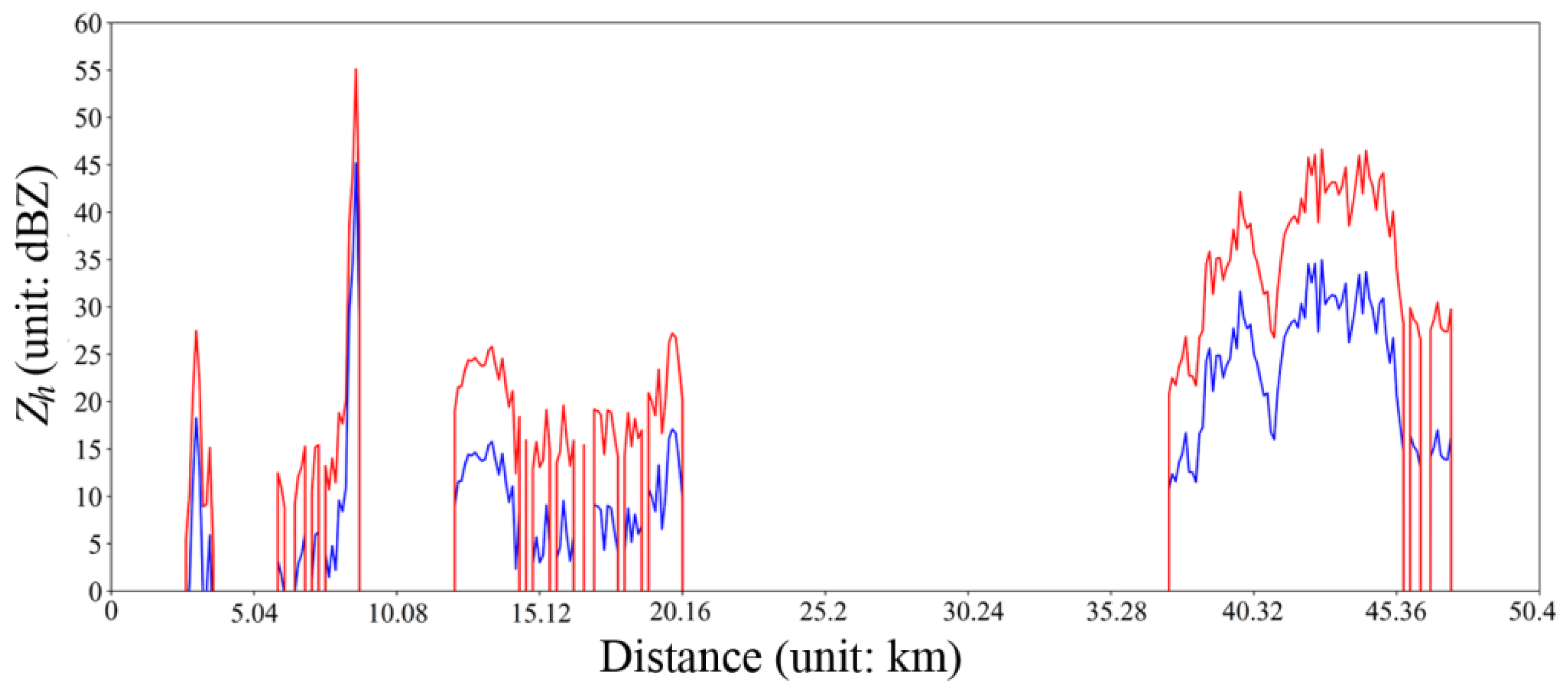
Figure 9 presents a vertical profile of Z_h comparing cases of medium- and small-scale severe convective weather over plain and plateau areas. In this figure, the y axis indicates the altitude (height above sea level). The red stars in the figure represent the profile of this severe convective precipitation weather event in the Qomolangma area, while the blue stars represent the profile of a strong convective precipitation event in the Chengdu Plain. As shown in this figure, the vertical extent of strong convective precipitation over the plain area is approximately 12 km, whereas that over Mount Everest is noticeably shallower (approximately 8.5 km). In terms of the range of Z_h values, the values over the plain area range from −5 to 43 dBZ, while those over the northern slope of Mount Everest are within only 15–45 dBZ. On the other hand, upon analyzing the variation trend of Z_h of the strong convective precipitation with height in Qomolangma, the red stars in the figure reveal two Z_h peaks with increasing height, and the first peak is approximately 4.7 km AGL. The Z_h values near the ground surface are only 15–25 dBZ. From the blue stars in the figure, the value of strong convective precipitation over the Chengdu Plain exceeds 40 dBZ from the boundary layer, which slowly reaches the peak at 2 km AGL and then decreases exponentially with increasing altitude.

The reasons for the above phenomena are analyzed. The following equation can be derived after simplifying the atmospheric vertical motion equation and the ideal gas equation of state [17]:

$$\{\begin{array}{l}\frac{dw}{dt}=-\frac{1}{\rho }\frac{\partial P}{\partial h}-\left(g+g^{\prime }\right)+f_u+f_v\\ PV=nRT\end{array}$$

(4)

where w is the vertical velocity, p is the atmospheric pressure, h is the height, g is the gravitational constant of acceleration, g’ is the disturbance due to gravity, f_v is the vertical component of the tide-generating force, f_u is the vertical Coriolis force, V is the gas block volume, n is the number moles of air within the volume V, R is the gas constant, and T is the air temperature. Compared with f_v, buoyancy and the perturbations due to p, gravity, and various forces have much greater impacts on the vertical motions within the atmosphere. Then, the following expression can be obtained:

$$\frac{dw}{dt}\propto -\frac{\partial T}{\partial h}$$

(5)

Equation (5) indicates that in a convective weather system, the acceleration of the vertical motion of the air block is directly proportional to its rate of temperature decrease. In the same time period, the greater the rate of temperature decrease is, the greater the vertical movement speed of the gas block.

Based on 10 years of scientific research on the southwest vortex (SWV) and the atmosphere over the Tibetan Plateau, although the altitudes of the Chengdu Plain and Mount Everest differ greatly, the altitude of the tropopause is basically consistent between them at approximately 12 km, and the temperature in both regions is Tst. Under the action of solar radiation, the surface temperatures on the plains and Mount Everest both reach Ts. Then, the relative heights from the tropopause to the surfaces of the plateau and the plain are ΔH1 and ΔH2, respectively, and ΔH1 << ΔH2; and the vertical atmospheric velocities over the plateau and plain are w1 and w2, respectively. Therefore, the following expression can be obtained:

$$\{\begin{array}{l}\frac{Ts-Tst}{\Delta H1}\cong 1.41\frac{Ts-Tst}{\Delta H2}\\ \frac{dw1}{dt}\cong 1.41\frac{dw2}{dt}\end{array}$$

(6)

Equation (6) indicates that the acceleration of vertical atmospheric motion over the plateau is generally greater than that over the plain; that is, air flows rise faster and thus are more likely to trigger strong isolated convective cells. In addition, in the field of fluid dynamics, it is widely accepted that the vertical extent and size of a convective cell are positively proportional to its horizontal extent and size. Based on Figure 9 and Figure 10, as well as Equation (6), this theory is well evidenced by the outcome of this work; i.e., the vertical depth of the convective cell in the Mount Everest region is noticeably shallower than that over the Chengdu Plain, and its horizontal extent is noticeably narrower than that above the plain.

Figure 10 shows the probability density distribution of the Z_dr values in medium- and small-scale convective precipitation. The red curve in the figure is the probability density of the Z_dr values for PPI precipitation on the northern slope of Mount Everest within distances of 18–25 km from the radar station at an elevation of 9°, and the blue curve is the probability density of Z_dr for strong convective precipitation on the Chengdu Plain within distances of 70–80 km from the radar station at an elevation of 2.5°. In addition, both data samples were collected from a height of 3 km AGL. Comparing these curves shows that the spectral distribution of Z_dr in the severe convective precipitation above the Chengdu Plain is wide, the most frequent occurrence of raindrops is approximately 5–6 dB, and the occurrence frequency of positive Z_dr values is much greater than that of negative values. In contrast, the spectral distribution of Z_dr in the convective precipitation on the northern slope of Mount Everest is narrow, the most frequent occurrence of raindrops is observed at approximately 0–0.5 dB, and the occurrence frequencies of positive and negative Z_dr values are basically equivalent. These findings further suggest that during the microphysical process of convective precipitation, all liquid raindrops are the results of the collision of mid- and high-layer crystals with supercooled water and their subsequent melting. Due to the unique high-altitude topographic features of the Mount Everest region, the vertical growth depth of convective precipitation is restricted and is noticeably shallower than that in the Chengdu Plain area. Ice crystal particles do not melt completely when falling into the boundary layer, and the raindrops that reach the ground tend to maintain a round shape. Therefore, the Z_dr values in the Mount Everest region are normally distributed approximately 0 with a narrow spectral width.

3.2. Snow Weather

The T-logp diagram calculated from the radiosonde data from the Dingri station at 08:00 (UTC+8) on 22 April 2021, is shown in Figure 11. Within a vertical height of less than 1 km from the station, the wind direction suddenly changes from a westerly wind to an easterly wind. Strong vertical wind shear can be observed near the boundary layer, and the whole layer exhibits clockwise rotation of the wind in the vertical direction, which is conducive to the development of convection. The level of free convection (LFC) is close to the boundary layer and lower than the LCL; in addition, the convective available potential energy (CAPE) reaches 2300 J/kg, and the storm intensity index (SII) equals 211.4, which indicates that the atmospheric thermal structure of the whole layer is extremely unstable. On the other hand, the cloud bottom height, namely, the convective condensation level (CCL), is less than 2 km AGL, which indicates that water vapor condenses quickly due to the low temperature and high humidity at the boundary layer, forming stratus clouds in the middle and low layers of the atmosphere. Within these stratus clouds, the condensation of water vapor releases latent heat, which increases the temperature and humidity at the top of the stratus clouds to form a thermally unstable structure in the middle- and high-level atmosphere. In addition, above 400 hPa, the wind speed exceeds 70 m/s. The Bernoulli effect of this strong wind speed further serves to lift the middle and high-level air flows, which is likely to lead to elevated convective snowfall.

Figure 12 shows the observational data from the FY4 satellite at 09:30 (UTC+8) on 22 April 2021. Figure 12a shows the longwave infrared image. The cloud top brightness temperature at the station (red circle) is 0.47 °C, which indicates that the cloud top is at a high altitude at this time. Figure 12b shows the image from the high-level water vapor channel. The brightness temperature of the water vapor at the station (red circle) is −26.93 °C, which indicates that the atmospheric water vapor content is very high.

Figure 13a–d shows the Z_h, Z_dr, K_dp, and ρ_hv data observed by the X-band dual-polarization weather radar on the northern slope of Mount Everest at 09:45 (UTC+8) on 22 April 2021, at an elevation of 5° in PPI mode. As shown in Figure 13a, the horizontal extent of the whole echo area is approximately 200 × 200 km. The maximum vertical height above the ground is approximately 9 km, and the height of the echo within the red circle is approximately 7.5 km AGL. Within this area, all Z_h values are <25 dBZ, the Z_dr values are large (close to 3 dB), the K_dp values have a wide span ranging from −0.2° to 1.7°, and the average ρ_hv is low (<0.95). Many nonspherical ice crystal particles and supercooled water droplets are observed in this area by UAV sensors (Figure 14). The UAV was provided by Soarability, Shenzhen, China, and was technically supported by the University of Auckland, New Zealand. The UAV carried a small and lightweight atmospheric aerosol and hydrometeor monitoring instrument named Sniffer4D. The output products are summarized in

Table 2. Basic products of Sniffer4D on the UAV.

Product	Unit	Definition
Observation time	/	UTC+8 time
Relative height	km	Vertical height above ground level
Longitude	°	/
Latitude	°	/
Temperature	°C	Centigrade
Relative humidity	%	Ratio of actual water vapor pressure to saturated water vapor pressure
Atmospheric pressure	hPa	/
Hydrometeor phase	/	Nine categories in total: ice crystal, small raindrops, large raindrops, supercooled water, wet snow, dry snow, graupels, small soft hails, and hails
PM2.5 concentration	${\mathsf{\mu }\mathrm{g}/\mathrm{m}}^3$	Mass of PM2.5 aerosols per unit volume

. These findings are basically consistent with the radar polarization eigenvalues of ice crystal particles during snowfall in North America reported by Doviak et al. [3].

Figure 15 shows the velocity and spectral width data simultaneously acquired at an elevation of 5° in radar PPI detection mode. As shown in Figure 15a, at radial distances of approximately 50–55 km from the radar station, an obvious wind shear zone is observed (within the black circle), and its vertical height is approximately 4–5 km AGL. From the convergence at a low level (near 4 km) to the divergence at a high level (near 5 km), this vertical wind shear promotes the upward movement of convection. In addition, ambiguous velocities are detected in both the lower and middle-upper layers, which indicates that the wind speed in the whole layer is high. These findings are consistent with the radiosonde data. The suction effect of strong wind speeds is conducive to the rapid development of convective movement and maintains strong snowfall. As shown in Figure 15b, there is an annular area with large spectral widths (approximately 5 m/s) at 4–5 km AGL corresponding to the area of the abovementioned ice crystal particles and vertical wind shear. These results indicate that there is a strong velocity disturbance for a large number of condensate particles within this height range that promotes the strong attachment of ice crystals and supercooled water [18] and the formation of ice crystal clouds.

Figure 16a–d shows vertical profiles of the dual-polarization physical quantities Z_h, sw, Z_dr, and ρ_hv obtained simultaneously in RHI mode along an azimuth of 250°. The horizontal extent of the whole echo area is approximately 100 km, and the vertical height extends from the boundary layer to approximately 6 km AGL. Figure 17 shows vertical profiles of Z_h, sw, Z_dr, and ρ_hv within vertical heights of 0–6 km AGL at a radial distance of 39 km from the radar station as well as their corresponding relationship with the isotherm. The black box in Figure 16 shows that the vertical height of this position is approximately 4–4.5 km AGL. Furthermore, the −20 °C isotherm is located above 4 km, where Z_h is <10 dBZ, the Z_dr valuesare distributed between 1 and 4 dB, and sw reaches 4 m/s. On the other hand, ρ_hv is smaller than 0.92, and ρ_hv is defined as follows [19]:

$${\rho }_{hv}=\frac{{{\displaystyle \sum }}_{i=1}^m\left({\overline{Z}}_H-Z_{Hi}\right)\left({\overline{Z}}_V-Z_{Vi}\right)}{{\left(\left[{{\displaystyle \sum }}_{i=1}^m{({\overline{Z}}_H-Z_{H,i})}^2\right]\left[{{\displaystyle \sum }}_{i=1}^m{({\overline{Z}}_V-Z_{V,i})}^2\right]\right)}^{0.5}}$$

(7)

Based on Equation (7), ρ_hv is determined by the correlation between the reflectivity factor of horizontally polarized electromagnetic waves in the form of pulse signals in m groups and that of the vertically polarized electromagnetic waves. Therefore, ρ_hv can effectively reflect the mixing degree of hydrometeor particles within a unit volume: a higher ρ_hv value indicates a higher phase diversity of hydrometeor particles and a higher mixing degree; conversely, a smaller ρ_hv value indicates greater phase consistency among the hydrometeor particles and a lower mixing degree.

In combination with the UAV observations in this area, high-density nonspherical ice crystal particles and supercooled water are present in the investigated area that manifests as a high-reflectivity zone [20]. At this high altitude, due to the low temperature and strong wind turbulence, supercooled water and ice crystal particles (snowflakes) collide repeatedly and freeze instantaneously on the surface, resulting in a strong attachment growth effect. In this way, small ice crystals gradually grow into large ice crystals and begin to fall. When approaching the ground, due to the increase in temperature, their outer layer melts into high-density wet snow. Based on the data from the ground laser raindrop spectrometer at the corresponding position, the 24h cumulative snowfall at this time is approximately 2.6 mm, reaching the level of moderate snowfall, and the particle phase state is melted snow on the surface. On the other hand, according to the red box in Figure 16, within the height range of 1.5–2.5 km AGL, there is a precipitation echo area with small Z_h values (approximately 15–25 dBZ), a wide range of Z_dr values (approximately from −1 to 0.8 dB), a maximum sw value close to 5 m/s, and a very high ρ_hv value > 0.98. As shown in Figure 17, the temperature of the boundary layer below 1.5 km AGL is less than 0 °C, but the temperature at approximately 2.5 km is >0 °C, which indicates that the warming phenomenon occurs between 1.5 and 2.5 km; i.e., the temperature changes from negative to positive. This finding further suggests that warm stratus clouds may be present in the area bounded by this red box. During this snowfall event, the bottom of the stratiform clouds is approximately 1.5 km AGL, and the temperature of the boundary layer within 1.5 km AGL is lower than 0 °C.

In addition, as shown in Figure 11, at an altitude of 5.5 km (approximately 1 km AGL), the wind direction suddenly changes from a westerly wind in the lower layer to an easterly wind in the upper layer with obvious vertical wind shear; the atmosphere here is characterized by low temperature, high humidity, and strong dynamic uplift. As shown in Figure 17, the temperature of the boundary layer below 1.5 km AGL is very low (<0 °C), and the strong dynamic uplift caused by vertical wind shear transports sufficient water vapor to the boundary layer; consequently, water vapor condenses above 1.5 km AGL to form stratiform clouds. During the condensation of water vapor at approximately 1.5–2.5 km AGL, latent heat is released. For this reason, the temperature of the stratiform clouds in this area increases with increasing relative height. At a height of 2.5 km AGL, the temperature at the top of the stratiform clouds reaches >0 °C. On the other hand, Figure 17 indicates that the −20 °C isotherm is located at approximately 4km AGL, which shows that the middle- and upper-layer atmospheric temperatures remain quite low. Therefore, the thermal instability between the top of the stratiform clouds (>2.5 km) and the middle and upper atmospheric layers (<4 km) generates convective movement, which reveals that the winter snowfall in Qomolangma has the characteristics of elevated convection.

4. Discussion

This study is the first to use X-band dual-polarization weather radar to observe the weather characteristics of convective precipitation and snowfall in Qomolangma. According to the results, the mechanisms that trigger convective precipitation on the northern slope of Mount Everest are basically the same as those in the plains, which meet the three necessary conditions of dynamic uplift, thermal instability, and sufficient water vapor. In addition, the typical dual-polarization physical quantity characteristics of sleet with hail are also observed near the ground, and this phenomenon is further verified by a ground rain gauge; this finding once again confirms the typical climatic characteristics of warm or cool and rainy summers with many hail days on Mount Everest [1]. On the other hand, according to our analysis, most of the convective cells in this area are scattered with multiple isolated convective cell radar echoes; this property differs greatly from the conditions in the plains, which may be related to the plateau mountain climate and complex mountain topography.

Based on observations of convective precipitation, compared with that over the plain, the evolution of a single convective cell over the mountainous area of Mount Everest is rapid, usually lasting only 10–20 min, and the total amount of cumulative precipitation is lower than that in the plains reported in the literature [7,8]. Furthermore, as shown in Figure 6 and Figure 9, the scale of the isolated convective cell on the northern slope of Mount Everest is smaller than that in the plain area both horizontally and vertically. In addition, as shown in Figure 10, the probability density spectrum of Z_dr of the convective precipitation over the Chengdu Plain is wide with a broad range (from −2 to 10 dB), and the Z_dr value of the most frequent occurrence of raindrops is approximately 5–6 dB. In contrast, the spectrum distribution of Z_dr of the convective precipitation over the northern slope of Mount Everest is narrow, and the Z_dr value of the most frequent occurrence of raindrops is approximately 0–0.5 dB. Based on these findings, the raindrops of the convective precipitation on the northern slope of Mount Everest are nearly spherical, whereas those in the plain area are basically oblate along the horizontal axis. Therefore, the raindrop shape on the northern slope of Mount Everest is quite different from that in the plain area.

This study has some limitations. First, to date, only one X-band dual-polarization radar has been installed. Consequently, the observation range and the quality of the observed data impose certain restrictions on the acquisition of complete data forthe investigated region. In the future, S/L-band phased-array weather radar will be introduced for joint networking observations, as phased-array antenna scanning can greatly improve the temporal and spatial resolutions. On the one hand, collaborative networking observations can compensate for radar blind areas, and on the other hand, this technique can easily invert the velocity values to obtain the U and V wind fields, which will help to better understand the development and evolution of precipitation weather systems and cloud microphysical structures in Qomolangma. Second, these radar field observations reveal that the K_dp values of the X-band dual-polarization radar experienced a calibration deviation, which varied both temporally and spatially. According to the literature [21], this phenomenon might be explained by the association of the atmospheric ambient temperature in the plateau area with temporal and spatial variations. Furthermore, a low signal-to-noise ratio (SNR) can cause low values of the dual-polarization physical quantities, which affects the accuracy of inverting the precipitation particle raindrop spectrum and of QPEs [22,23]. All these problems remain to be solved in the future. Third, in this study, the initial elevation for all RHI scan modes is 5°, which resulted in missing information for the boundary layers at moderate and long distances from the radar station. Therefore, in future field radar observations, artificial fixed-point directional tracking and scanning observations will be adopted. At azimuths not shielded by ground objects or terrain, RHI scanning can start at an elevation of 0° to obtain the evolutionary characteristics of the precipitation structure in these boundary layers [24].

5. Conclusions

In these field observations, X-band dual-polarization radar was used for the first time to observe and analyze convective precipitation and snowfall on the northern slope of Mount Everest atop the Qinghai-Tibetan Plateau. X-band dual-polarization radar has the advantages of high temporal and spatial resolutions, high sensitivity to small precipitation particles, and a strong ability to detect cloud droplets (low water content) and cloud ice crystal particles.

Based on the observed data, most of the convective precipitation on the northern slope of Mount Everest is scattered, with multiple isolated convective single-cell echoes; the horizontal scale is normally <20 km, and the vertical depth is <9 km. The altitude of the intense echo center of the convective cells above the ground is high and not in the boundary layer, and convective cells appear and disappear rapidly. In addition, in terms of the probability density spectrum distribution of Z_dr in the convective precipitation, the convective precipitation raindrops on the northern slope of Mount Everest are nearly spherical. Overall, the Tibetan Plateau tends to be more likely than the plain area to trigger precipitation from multiple isolated convective cells.

Furthermore, according to the observations of snow weather on the northern slope of Mount Everest in winter, high-density nonspherical ice crystal particles and supercooled water appear near the −20 °C isotherm, which manifest as a high-reflectivity zone. Warm stratus clouds are observed near the boundary layer. The ground temperature at the bottom of the warm stratus clouds is low with a large amount of water vapor being transported, which results in the condensation of water vapor in the middle and lower layers to form stratus clouds. In the condensation of water vapor, latent heat is released and increases the temperature at the top of the stratus clouds, which produces thermal instability with low temperatures in the middle and upper layers [25]. The initiation of vertical convection once again promotes an increase in water vapor, revealing the characteristics of elevated convection in winter snowfall over the northern slope of Mount Everest.