Abstract
As a major threat to aviation flight safety, it is particularly important to make accurate judgments and forecasts of the ice accumulation environment. Radar is widely used in civil aviation and meteorology, and has the advantages of high timeliness and resolution. In this paper, a variety of machine learning methods are used to establish the relationship between radar data and icing index (Ic) to determine the ice accumulation environment. The research shows the following. (1) A linear model was established, based on the scattering rate factor (Zh), radial velocity (v), spectral width (w), velocity standard deviation (σ) detected by 94 GHz millimeter wave radar, and backward attenuation coefficient (β) detected by 905 nm lidar, so linear regression was carried out. After principal component analysis (PCA), the correction determination coefficient of the linear equation was increased from 0.7127 to 0.7240. (2) Ice accumulation was unlikely for samples that were significantly off-center. By clustering the data into three or four categories, the proportion of icing lattice points could be increased from 18.81% to 33.03%. If the clustering number was further increased, the ice accumulation ratio will not be further increased, and the increased classification is reflected in the classification of pairs of noises and the possibility of omission is also increased. (3) Considering the classification and nonlinear factors of ice accumulation risk, the neural network method was used to judge the ice accumulation environment. Two kinds of neural network structures were established for quantitative calculation: Structure 1 first distinguished whether there was ice accumulation, and further calculated the icing index for the points where there was ice accumulation; Structure 2 directly calculated the temperature and relative humidity, and calculated the icing index according to definition. The accuracy of the above two structures could reach nearly 60%, but the quantitative judgment of the ice accumulation index was not ideal. The reasons for this dissatisfaction may be the small number of variables and samples, the interval between time and space, the difference in instrument detection principle, and the representativeness of the ice accumulation index. Further research can be improved from the above four points. This study can provide a theoretical basis for the diagnosis and analysis of the aircraft ice accumulation environment.
1. Introduction
Common causes of aircraft icing include: (1) encountering clouds with super-cooled water droplets during flight; (2) being contaminated prior to takeoff; and (3) encountering high concentrations of ice crystals during flight [1]. Ice accumulation in different parts of the aircraft can easily damage the aerodynamic characteristics or power system of the aircraft, or cause the pilot to misjudge the flight status of the aircraft, thus causing accidents. In 1994, American Eagle Flight 4184 crashed due to ice pack, but the investigation report noted that there was no significant weather report of ice pack at the time of the accident [2]. In 2009, when Air France Flight 447 was flying over the Atlantic Ocean, the autopilot disconnected due to ice jam in the Pitot tube, and then the pilot misjudged the flight status and made an improper operation, resulting in the plane crash [3]. An investigation of 803 aviation accidents in the United States between 1975 and 1988 found that these accidents were partly or wholly related to ice accumulation on aircraft [4]. Although there are many anti-icing and deicing devices installed on modern aircraft [5,6,7], air accidents caused by ice pack still occur from time to time. Therefore, it is of great significance to establish a time-efficient and high-resolution algorithm for judging an ice pack environment.
There are many classical icing diagnosis and prediction algorithms abroad [8,9,10,11]. The commonly used instruments for remote sensing data inversion of aircraft ice pack include dual-wavelength radar, weather radar, meteorological satellite, microwave radiometer, etc. [12,13,14]. GOES (Geostationary Operational Environmental Satellite) is used to identify cloud features and super-cooled water to classify ice accumulation [15,16]. Javier et al. [17] demonstrated that the WRF (weather research and forecasting) model is capable of correctly detecting icing associated with mountain waves. Merino et al. [18] used in-cloud microphysics measurements taken during 10 flights of a C-212 research aircraft under winter conditions. Bolgiani et al. [19] studied the risk of ice accumulation near Adolfo Suárez Madrid-Barajas International Airport based on a WRF model and satellite data. Pereira [20], based on ECMWFs (European Center for Medium-Range Weather Forecasts), presented a verification of different icing algorithms for two periods. Part 25: Airworthiness Standards for Transport Aircraft of the FAA (Federal Aviation Administration) provides conditions for atmospheric icing in Appendix C and conditions for freezing of super-cooled large droplets in Appendix O [21].
Some scholars have studied the shape and severity of body ice accumulation using a neural network algorithm [22,23,24]. Dong [25] proposed an ice accumulation fault detection system based on deep learning. Li et al. [26] established the relationship between flight conditions and aircraft ice accumulation. Kolbakir et al. [27] found that plasma brakes could prevent the wing from icing. Zhang et al. [28] proposed a probabilistic method under considering subjective and objective parameters uncertainties based on the Monte Carlo method for estimating the airplane icing severity. Zhou et al. [29] presented the reach ability analysis based on the level set method. Cao et al. [30] established an engineering prediction method of aerodynamic derivatives based on an individual component CFD (computational fluid dynamics) calculation and narrow strip theory. Liu et al. [31] presented a comprehensive aircraft icing simulation tool implemented in a Navier–Stokes parallel multi-block solver. Wang et al. [32] established a safety analysis model to quantify the safety degree of aircraft icing under the fuzzy inputs and fuzzy state.
In conclusion, the data from various scholars’ studies on the aircraft ice accumulation environment mainly focused on the conventional observation data, and there are few studies based on radar data. In the past research, the authors have conducted a preliminary qualitative study on the aircraft ice accumulation environment in China [33]. Therefore, in this paper, based on the detection data of millimeter wave radar and Lidar, linear regression, principal component analysis, cluster analysis, and neural network methods are used to study the direct inversion of ice index to realize the quantitative judgment of the ice environment by radar data. This method can improve the resolution and timeliness of the environmental judgment of ice accumulation.
2. Materials and Methods
2.1. Data
The Science and Technology Facilities Council (STFC) at Chilbolton Observatory in the UK is home to many meteorological and atmospheric science research observation systems. The Chilbolton Facility for Atmospheric and Radio Research (CFARR) has multiple radar and Lidar as well as observation equipment such as radiometers at different bands, weather sensors, rain gauges, and cloud cameras. The sources of radar data used in this paper include cloud radar and Lidar, among which the 94 GHz cloud radar (Galileo radar) is located at 51.145° N, 1.437° W, and the Lidar (905 nm Vaisala CT75K Lidar Ceilometer) is located at 51.145° N, 1.427° W [34]. The millimeter-wave radar data used in this paper includes radar scattering rate factor (Zh), radial velocity (v), spectral width (w), and velocity standard deviation (σ), and the Lidar data used was backward attenuation coefficient (β). The website is http://data.ceda.ac.uk/badc/chilbolton/data (accessed on 1 September 2020).
The sounding data are from the Department of Atmospheric Science, University of Wyoming (UW, http://www.weather.uwyo.edu/upperair/sounding.html, accessed on 1 September 2020). The radiosonde data of Herstmonceux Station (position: 50.90° N, 0.32° E, station number: 03882) from several stations near Chilbolton were selected as the radiosonde data corresponding to the radar data in this paper, and the geographical location is shown in Figure 1. According to the altitude, temperature, and relative humidity information of the station, the ice accumulation index was calculated as the reference of the radar data. Since the grid points of the radiosonde data and radar data do not match perfectly, the linear interpolation method was used to interpolate the radiosonde data to the corresponding height according to the height of each grid point in the radar data, and then the icing index was calculated to generate training set and test set to realize the training and test of the model. Obviously, there will be errors in linear interpolation, and the interpolation result may not be equal to the real temperature and humidity at the corresponding height. This error may be greater when interpolation is interpolated outward.
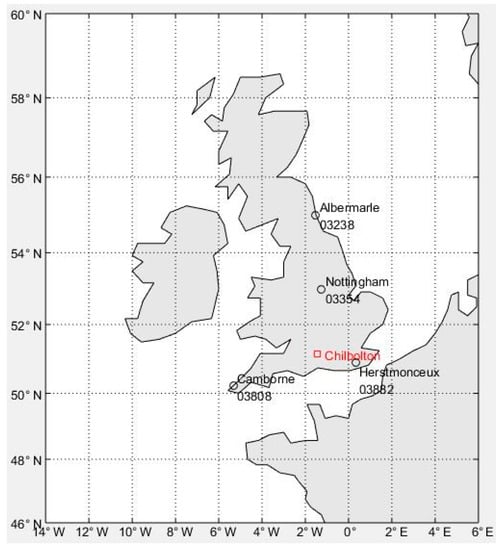
Figure 1.
Location of Chilbotton Station and sounding stations. The figure shows the location and number of multiple sites around Chilbotton, with Herstmonceux being the closest.
2.2. Icing Index
The ICAO (International Civil Aviation Organization) recommends using the icing index ‘IC’:
where RH is the relative humidity (%), T is the temperature (°C), RH is less than 50%, or T is outside the range of −14 °C to 0 °C, so no ice accumulation occurs. The output range of IC is 0–100. The larger the value, the stronger the ice accretion [35].
2.3. Methods
Equation (2) is used for standardized calculation:
is the sample mean, and S is the sample standard deviation. After processing, the mean value of each variable is 0, and the standard deviation is 1. This processing can eliminate the influence of dimension and order of magnitude on the data analysis and algorithm model. Variables with * in this paper refer to those after standardized processing.
PCA is a commonly used dimensionality reduction algorithm for high-dimensional data. Its idea is to construct a new hyperplane, that is, a linear combination of existing coordinates to express all samples. The eigenvalues and eigenvectors of the covariance matrix were solved, the eigenvalues were sorted from largest to smallest, and the eigenvectors corresponding to the first q eigenvalues were taken as the solutions of the PCA [36].
The clustering algorithm used in this paper was the K-means algorithm. In this algorithm, K clustering centers are selected to cluster all samples into K classes, and the sum of the distances between each sample and its clustering center is calculated to describe the closeness of the samples around the mean vector in the cluster. When sum is the minimum, this clustering method is considered to be reasonable. Since it is difficult to find the optimal solution directly, the iterative method is adopted. Given K centers of the primary election, the iterative method is used to gradually generate the optimal solution [37].
Neural networks can be used for regression and classification to build possible relationships between inputs and outputs. The most fundamental component of a neural network is the neuron model. The neuron receives input signals from N neurons in the previous layer, and the signals are transmitted through weighted connections. The total input value received by the neuron is compared with the threshold value and processed through the “activation function” set by the network to obtain the output signal. Many such neurons are connected according to a certain hierarchical structure to obtain the neural network [38].
2.4. Feasibility Analysis
Since the discussion in this paper was mainly based on cloud radar data, the relationship between cloud radar data and radiosonde data was first analyzed to illustrate the feasibility of using cloud radar data to judge ice accumulation. Statistics were conducted on whether the radar measured data and whether the grid point was interpolated to obtain ice accumulation. The results are shown in Table 1.

Table 1.
Correspondence between cloud radar data and icing.
According to the statistics in Table 2, among the total 7320 samples, only 431 samples had an ice accumulation risk, which is not reflected in the radar data. Meanwhile, considering the geographical deviation of Chilbolton and Herstmonceux and the interference of interpolation on the sounding data, the data volume of such samples may be even smaller in the real situation. This indicates that it is meaningful to establish the relationship between radar data and icing index to judge ice accumulation.

Table 2.
Correlation coefficient matrix.
3. Contributions of Radar Data to Icing Index
The 0 h data collected by Galileo’s cloud radar and Lidar in November 2003 consisted of 192 altitudes per day for 26 days. Among them, cloud radar and Lidar obtained data, and a total of 48 data points with icing were obtained according to interpolation. These 48 samples are the training set discussed in this section.
First, variables were standardized according to Equation (2). After standardization, the correlation coefficients between dependent variables and independent variables and between independent variables are given in Table 2.
The linear equation between the icing index and five standardized variables was established:
According to the data in Table 2, the icing index was more closely correlated with the reflectivity factor and spectral width, but it could also be seen that these data had strong autocorrelation and a large amount of information overlap. The principal component analysis method was used to process the data below, and the obtained variance contribution of variables and the correlation coefficient between the converted variables and ice accumulation index are given in Table 3, while the maximum absolute value of the autocorrelation coefficient between the new independent variables was also <10−15, suggesting that each variable does not contain overlapping information.

Table 3.
Variable contribution and transformation matrix.
It can be found in Table 3 that X1, which had the largest variance contribution, had very little correlation with the ice accumulation index, which may indicate that X1 mainly represents a large amount of noise contained in radar data. In general, all new variables with a cumulative contribution rate of 85% are selected after principal component analysis. Therefore, the expressions of X1, X2, X3 and X4 are given below:
Considering the variance contribution and correlation coefficient, the following three linear regression equations were established:
Table 4 shows the test statistics of the four regression equations:

Table 4.
Test statistics.
Through the calculation of F statistics, the hypothesis test of α = 0.001 under the corresponding degree of freedom was passed, that is, there was a 99.9% confidence that the linear relationship of the above four formulas was significant. In terms of statistics, Equation (3) had the largest coefficient of determination, Equation (9) had the largest corrected coefficient of determination and the smallest p value and error variance, and Equation (10) had the largest F value. This statistic can illustrate the following points:
- (1)
- It is significant to use principal component analysis to process data in this study;
- (2)
- Although the variable X1 contains a lot of information, introducing X1 into the linear regression will reduce the correction determination coefficient and linear significance of the equation, and increase the error variance, so it is reasonable not to introduce X1, which also confirms that X1 mainly represents the noise in the radar data; and
- (3)
- Although the correlation coefficient of X2 and X3 is small, and the opposite value of their correlation is similar, it will cause the loss of a lot of the main information in the sample if they are removed.
4. Qualitative Classifications of Radar Data
As can be seen from Table 1, for the samples with radar data, only 18.81% of them had icing risk, while 81.19% had no icing risk, indicating that those with and without ice accumulation should be separated as far as possible to reduce the false alarm rate. Millimeter wave has a better ability of penetrating clouds, but Lidar detection is easily affected by clouds and aerosols and may cause errors [39,40,41]. In the discussion in Section 3, it was found that the velocity standard deviation had little correlation and contribution to the icing index. Meanwhile, in order to increase the number of training samples, millimeter-wave radar data were used in the discussion of the following paper. In this part, the method of cluster analysis adopted was based on the three variables of Zh, v, and w. A total of 1510 daily 0 h data were collected by the Galileo cloud radar in November 2003. First, these 1510 groups of variables were standardized. As shown in Figure 2, cluster analysis was conducted on the standardized variables, which were grouped into two to seven categories, respectively.
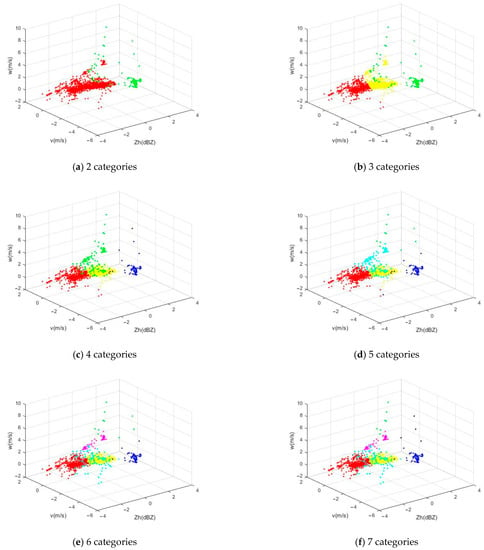
Figure 2.
Radar data clustering analysis. From (a–f), the number of clusters increases from two to seven, respectively. In (a), red is category A and green is category B. After the number of categories is increased, the color and category number remain unchanged, and the newly added color is a new category (category C to category G).
After many experiments, it was proven that the algorithm was convergent, regardless of how the initial clustering center was selected. The final clustering center was the same. For the convenience of illustration, we arranged the clustering centers in the order as shown in Table 5, and named them from category A to category G.

Table 5.
Cluster analysis results.
The classification results were compared with the icing index corresponding to the sample to discuss the proportion of the samples with icing risk in each category. The statistical results are shown in Table 6.

Table 6.
Risk proportion of each type of sample icing.
It can be seen from Table 6 that ice accumulation information was mainly contained in Class A and Class C, but it was difficult to extract obvious features, and impossible to show ice accumulation for samples that deviated significantly from the center value. According to Table 7, when the number of classifications increased from two to three, the proportion of ice accumulation risk of newly generated Class C reached 28.82%; when the number of classifications increased to four, the proportion of ice accumulation risk of Class C was further increased to 33.03%, but there was already one missing sample in Class B. With the further increase in the number of classifications, overfitting began to appear. Further classifications only improved the classification of noise and increased the possibility of omission. To sum up, it is more appropriate to take the classification number of clustering samples as three or four categories.

Table 7.
Statistics of judgment results of icing accretion.
5. Quantitative Judgment of Icing Index
According to the previous discussion, linear regression has good significance, but cannot judge whether there is ice accumulation. The clustering algorithm can improve the ice accumulation proportion, but the effect is not obvious. The difficulty of this problem lies in the following two points: first, it is necessary to distinguish whether there is an ice accumulation risk at this point, and it is necessary to further calculate the icing index only for points with ice accumulation risk; second, ice accumulation is a complex nonlinear problem, and the linear equation given by linear regression is difficult to fully reflect the nonlinear relationship between the physical quantities. A neural network approach has the advantage of solving these two difficulties. Therefore, two kinds of neural network structures were designed, as shown in Figure 3.
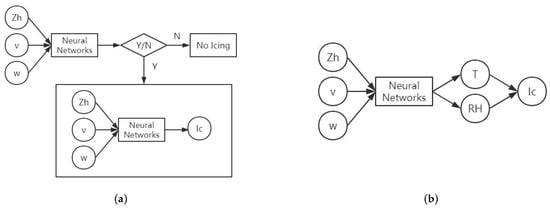
Figure 3.
Calculation of icing index based on neural network. Structure 1 takes the Zh, v, and w as input to judge whether there is icing. For points with icing, another network is used to calculate the icing index, and for points without icing, it is directly output no-icing. Structure 2 takes the Zh, v, and w as input, takes temperature and relative humidity as output, and calculates the icing index according to Equation (1). (a) Neural Network Structure 1; (b) Neural Network Structure 2.
Here, the training set was 0 h data in November 2003, and the test set was 0 h data in November 2008. The results were calculated respectively according to the linear model and two kinds of neural network structures. All neural networks adopted the BP (back propagation) neural network, which is divided into three layers. Except for the input layer and output layer shown in Figure 3, the hidden layer had 30 neurons. If the network calculation times reaches 10,000 times, no iteration will be performed, and other parameters are default values. The statistics and analysis of the results include the following two parts. First, the statistical algorithm can judge whether there is ice accumulation or not, aiming at the grid point of data detected by millimeter wave radar. We defined the following four kinds of results as: A is the “observation that may be ice, may actually think ice”; B is the “observation that can’t be ice, may actually think ice”; C is the “observation that may be icing, actually thought impossible to ice”; and D is the “observation that impossible to ice, actually thought impossible to ice”. The second is the quantitative error of the Icing Index.
The following statistics are defined [42]:
Correct rate
Error rate
Hit rate
Empty rate
Non-response rate
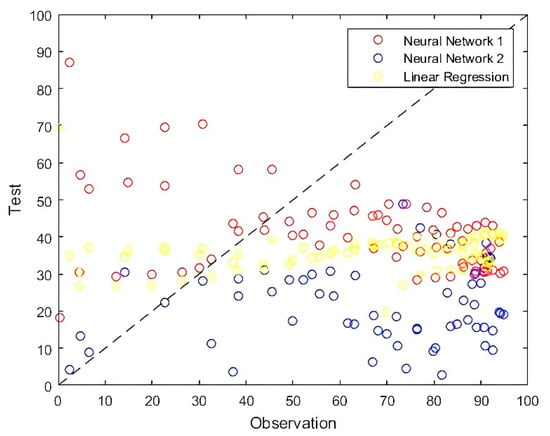
Figure 4.
Test errors.
As can be seen from Table 7 and Figure 4, the two networks had similar results. From the judgment of ice accumulation, both could achieve almost or more than 50% of the judgment accuracy, the error was mainly an empty report, and the possibility of missing reports was controlled to a very low level. Linear regression and two kinds of neural networks had poor effects on the quantitative determination of index, and it is difficult to provide an accurate icing index. We provide a reasonable explanation of this problem in the next section.
6. Discussions
6.1. The Correspondence between Radar Data and Sounding Data
According to Table 1, 5.888% of the data lacked correspondence, and this phenomenon was more obvious in Figure 5.
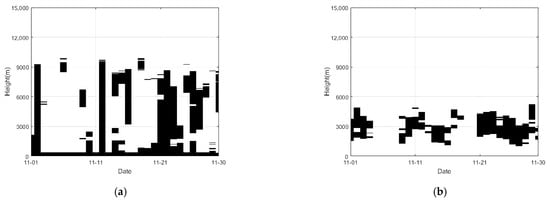
Figure 5.
Comparison of millimeter-wave radar data and radiosonde Data in November 2003. (a) Galileo Radar; (b) Sounding.
As shown in Figure 5, due to the mismatch between radar data and sounding data, some data lacked correspondence. There are two reasons for this mismatch. First, there is a certain distance between Chilbolton and Herstmonceux, so there is a certain difference in the atmospheric environment between the two places, resulting in the mismatch. Second, the millimeter-wave radar, Lidar, and radiosonde used in this paper had some differences in the detection principles. The radar was set up on the ground or on the top of the building to carry out measurement and inversion by means of remote sensing. Restricted by the band they use, the objects of detection are different. Millimeter-wave radars mostly detect cloud particles [39], while Lidars are susceptible to aerosols near the ground [40,41]. Most radiosondes are set up on balloons or rockets for direct detection [43,44].
6.2. Cause Analysis of Test Results
The changes in various weather processes and the overall climate environment may bring significant influences in a short time, which is reflected in the rapid changes in the microphysical characteristics of liquid water content, particle size, rainfall rate, and so on. In this study, due to the limitation of the data volume of CFARR, data in the same month of two years were selected for training and testing, but the temperature and humidity environment of these two months were different to some extent.
As can be seen from Figure 6, compared with the average temperature and average relative humidity in November 2003 and November 2008, the temperature and relative humidity in 2008 were significantly lower than those in 2003 at a height below 5 km. The temperature was about 2–3 °C lower, and the relative humidity was about 5–10% lower. Combined with Figure 5, the icing index also changed significantly within a month. The icing threat in November 2003 was relatively more stable, and was strongest in late November 2003. In the early part of November 2008, when the air humidity was higher, the icing index was higher, so the corresponding liquid water content may increase, while the humidity was significantly lower in the late part of November 2008, and the icing index was smaller. The millimeter-wave radar also did not detect the corresponding clouds or liquid water. In addition, studies have shown that, in some cases, relative humidity cannot completely represent the threat possibility of icing, and it is currently difficult to accurately conduct numerical weather prediction on the ice [45,46], and the relative humidity is defined as vapor pressure and the ratio of saturated vapor pressure, so cannot be used to directly determine the air liquid water content, particle size, and other factors. Therefore, the inaccurate judgment may be caused by this factor.
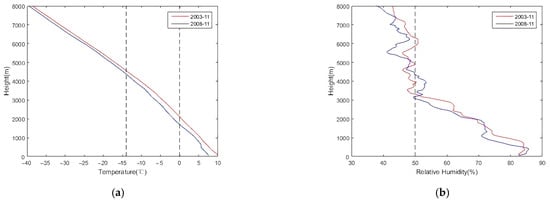
Figure 6.
Profiles of average temperature and relative humidity in November 2003 and November 2008. (a) Monthly average temperature profile; (b) Monthly average RH profile. Considering the definition of Icing Index, vertical dash lines are added to illustrate the range of possible icing.
7. Conclusions
Based on CFARR millimeter-wave radar and Lidar data and the basis of the ICAO icing index using a variety of machine learning and statistical methods, from the perspective of both qualitative and quantitative, gradually thorough methods of using radar data are given to judge expression of aircraft icing conditions and methods. The training set and testing set confirmed that PCA, cluster analysis, and neural network methods had certain significance, respectively, and some of the problems and possible improvements for discussion and analysis. This current study is a first step for the development of a diagnosis tool of an aircraft icing environment.
- (1)
- Combined with the data of Lidar and millimeter-wave radar, the principal component analysis method was used to improve the correction determination coefficient to 0.7240, and the noise in the data was effectively eliminated.
- (2)
- Clustering analysis can increase the proportion of ice accumulation samples from 18.81% to 33.03%. If the classification number continues to increase, there will be overfitting, so it is difficult to further improve this proportion. However, the samples that significantly deviate from the central value can be considered as impossible for ice accumulation and excluded.
- (3)
- Two kinds of neural networks are constructed, which have similar performance on the judgment results of the test set, and can reach more than a 50% accuracy rate. The error is mainly shown as a false report, and the omission rate is very low, but it is difficult to calculate the ice accumulation index quantitatively.
- (4)
- Possible reasons for inaccurate quantitative judgment include inconsistency between the location of the radar station and the sounding station, a great difference between the samples of the training set and the test set, and the ice accumulation index cannot fully represent the ice accumulation environment, etc.
This study can be further improved from the following points: (1) select more matching data from the same site for training; (2) introduce more new variables that may improve the significance and accuracy of the judgment; (3) select indexes that are more objective and accurate for the expression of icing threat to carry out the above experiment; and (4) modify the algorithm to consider the physical properties of the model.
Author Contributions
B.X. conceived and designed the experiments, performed the experiments, analyzed the data, and wrote the paper; J.W., J.C. (Jiahan Cai), Y.W. and J.C. (Jiang Chen) helped in the discussion and revision; J.W. reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (41905026); the 63rd Batch of China Postdoctoral Science Foundation in General (2018M631554); the Open Fund by Key Laboratory of Aerosol-Cloud-Precipitation of CMA-NUIST (KDW1703); and the Key Laboratory of Middle Atmosphere and Global Environment Observation (LAGEO-2019-05).
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to acknowledge the CFARR and the UW for providing the observation data and precise products. Thanks to Jiang Qinglin and Xu Junhui for their help in the revision process.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cao, Y.; Tan, W.; Wu, Z. Aircraft icing: An ongoing threat to aviation safety. Aerosp. Sci. Technol. 2018, 75, 353–385. [Google Scholar] [CrossRef]
- NTSB. In-Flight Icing Encounter and Loss of Control Simmons Airlines, D.B.A. American Eagle Flight 4184 Avions De Transport Regional (ATR) Model 72–212, N401AM, Roselawn, Indiana 31 October 1994; National Transportation Safety Board: Washington, DC, USA, 1996; pp. 44–61.
- BEA. Final Report On the Accident on 1 June 2009 to the Airbus A330–203 Registered F-GZCP Operated by Air France Flight AF 447 Rio de Janeiro—Paris; French Civil Aviation Safety Investigation Authority: Paris, France, 2012; pp. 76–77.
- Cole, J.; Sand, W. Statistical study of aircraft icing accidents. In Proceedings of the 29th Aerospace Science Meeting, Reno, NV, USA, 7–10 January 1991; American Institute of Aeronautics: Washington, DC, USA, 1991. [Google Scholar] [CrossRef]
- Zilio, C.; Patricelli, L. Aircraft anti-ice system: Evaluation of system performance with a new time dependent mathematical model. Appl. Therm. Eng. 2014, 63, 40–51. [Google Scholar] [CrossRef]
- Grzesik, N.; Kowalik, K. Fuzzy Controller for Aircraft Anti-Icing System—Initial Design and Analysis. Solid State Phenom; Trans Tech Publications Ltd.: Stafa-Zurich, Switzerland, 2016; Volume 251, pp. 218–223. [Google Scholar] [CrossRef]
- Su, Q.; Chang, S.; Zhao, Y.; Zheng, H. A Review of Loop Heat Pipes for Aircraft Anti-Icing Applications. Appl. Therm. Eng. 2017, 130, 528–540. [Google Scholar] [CrossRef]
- Thompson, G.; Bruintjes, R.T.; Brown, B.G. Intercomparison of in-flight icing algorithms: Part I: WISP94 realtime icing prediction and evaluation program. Weather Forecast 1997, 12, 878–889. [Google Scholar] [CrossRef]
- Kelsch, M.; Wharton, L. Comparing PIREPs with NAWAU Turbulence and Icing Forecast: Issues and Results. Weather Forecast 1996, 11, 385–390. [Google Scholar] [CrossRef]
- Rotondo, D.; Cristofaro, A.; Johansen, T.A. Diagnosis of Icing and Actuator Faults in UAVs Using LPV Unknown Input Observers. J. Intell. Robot. Syst. 2017, 91, 651–665. [Google Scholar] [CrossRef]
- Carriere, M.; Alquier, S.; Bot, L. Statistical Verification of Forecast Icing Risk Indices. Meteor. Appl. 1997, 4, 115–130. [Google Scholar] [CrossRef]
- Gosset, M.; Sauvageot, H. A Dual-Wavelength Radar Method for Ice-Water Characterization in Mixed-Phase Clouds. J. Atmos. Ocean. Technol. 1992, 9, 538–547. [Google Scholar] [CrossRef][Green Version]
- Vivekanandan, J.; Zhang, G.; Politovich, M.K. An Assessment of Droplet Size and Liquid Water Content Derived from Dual-Wavelength Radar Measurements to the Application of Aircraft Icing Detection. J. Atmos. Ocean. Technol. 2001, 18, 1787–1798. [Google Scholar] [CrossRef]
- Gaussiat, N.; Sauvageot, H.; Illingworth, A.J. Cloud Liquid Water and Ice Content Retrieval by Multiwavelength Radar. J. Atmos. Ocean. Technol. 2003, 20, 1264–1275. [Google Scholar] [CrossRef][Green Version]
- Rauber, R.; Tokay, A. An Explanation for the Existence of Supercooled Water at the Top of Cold Clouds. J. Atmos. Sci. 1991, 48, 1005–1023. [Google Scholar] [CrossRef]
- Ellrod, G.P.; Bailey, A. Assessment of Aircraft Icing Potential and Maximum Icing Altitude from Geostationary Meteorological Satellite Data. Weather Forecast 2007, 22, 160–174. [Google Scholar] [CrossRef]
- Javier, D.F.; Lara, Q.H.; Pedro, B. Mountain Waves Analysis in the Vicinity of the Madrid-Barajas Airport Using the WRF Model. Adv. Meteorol. 2020. [Google Scholar] [CrossRef]
- Merino, A.; Ortega, E.G.; González, S.F. Aircraft Icing: In-Cloud Measurements and Sensitivity to Physical Parameterizations. Geophys. Res. Lett. 2019, 46, 11559–11567. [Google Scholar] [CrossRef]
- Bolgiani, P.; González, S.F.; Martin, M.L. Analysis and numerical simulation of an aircraft icing episode near Adolfo Suárez Madrid-Barajas International Airport. Atmos. Res. 2017, 200, 60–69. [Google Scholar] [CrossRef]
- Pereira, M.B. Comparison of in-flight aircraft icing algorithms based on ECMWF forecasts. Meteorol. Appl. 2016, 22, 705–715. [Google Scholar] [CrossRef]
- Federal Aviation Administration. Part 25—Airworthiness Standards: Transport Category Airplanes. Available online: https://www.ecfr.gov/cgi-bin/ECFR?page=browse (accessed on 1 September 2020).
- Matthew, D.J.; Kamran, R. Using artificial neural networks and self-organizing maps for detection of airframe icing. J. Aircr. 2001, 38, 224–230. [Google Scholar] [CrossRef]
- Ogretim, E.; Huebsch, W.; Shinn, A. Aircraft ice accretion prediction based on neural networks. J. Aircr. 2006, 43, 233–240. [Google Scholar] [CrossRef]
- Dong, Y. An application of Deep Neural Networks to the in-flight parameter identification for detection and characterization of aircraft icing. Aerosp. Sci. Technol. 2018, 77, 34–49. [Google Scholar] [CrossRef]
- Dong, Y. Implementing Deep Learning for Comprehensive Aircraft Icing and Actuator/Sensor Fault Detection/Identification. Eng. Appl. Artif. Intell. 2019, 83, 28–44. [Google Scholar] [CrossRef]
- Li, S.; Qin, J.; He, M. Fast Evaluation of Aircraft Icing Severity Using Machine Learning Based on XGBoost. Aerospace 2020, 7, 36. [Google Scholar] [CrossRef]
- Kolbakir, C.; Hu, H.; Liu, Y. An experimental study on different plasma actuator layouts for aircraft icing mitigation. Aerosp. Sci. Technol. 2020, 107, 106325. [Google Scholar] [CrossRef]
- Zhang, F.; Huang, Z.; Yao, H. Icing severity forecast algorithm under both subjective and objective parameters uncertainties. Atmos. Environ. 2016, 128, 263–267. [Google Scholar] [CrossRef]
- Zhou, C.; Li, Y.; Zheng, W. Safety Analysis for Icing Aircraft during Landing Phase Based on Reachability Analysis. Math. Probl. Eng. 2018, 14. [Google Scholar] [CrossRef]
- Cao, Y.; Tan, W.; Su, Y. The Effects of Icing on Aircraft Longitudinal Aerodynamic Characteristics. Mathematics 2020, 8, 1171. [Google Scholar] [CrossRef]
- Liu, T.; Cai, J.; Qu, K. In-flight icing simulation for two-dimensional configurations. Int. J. Mod. Phys. B 2020, 34, 2040068. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Z.; Shi, Y. Aircraft icing safety analysis method in presence of fuzzy inputs and fuzzy state. Aerosp. Sci. Technol. 2018, 82, 172–184. [Google Scholar] [CrossRef]
- Wang, J.; Xie, B.; Cai, J. The Distribution of Aircraft Icing Accretion in China—Preliminary Study. Atmosphere 2020, 11, 876. [Google Scholar] [CrossRef]
- CEDA Achieve. Dataset Collection: Chilbolton Facility for Atmospheric and Radio Research (CFARR): Surface, Radar and Lidar Measurements (1998-Present). Available online: https://catalogue.ceda.ac.uk/uuid/7cbc3fc19bfa037a48ba4cba4b93544d (accessed on 1 September 2020).
- Liu, F.L.; Sun, L.T.; Li, S.J. Study on Methods of Aircraft Icing Diagnosis and Forecast. Meteorol. Environ. Sci. 2011, 34, 26–30. [Google Scholar] [CrossRef]
- Scholkopf, B.; Smola, A.; Muller, K. Nonlinear Component Analysis as a Kernel Eigenvalue Problem. Neural. Comput. 1998, 10, 1299–1319. [Google Scholar] [CrossRef]
- Aloise, D.; Deshpande, A.; Hansen, P. NP-hardness of Euclidean Sum-of-squares Clustering. Mach. Learn. 2009, 75, 245–248. [Google Scholar] [CrossRef]
- Kohonen, T. An Introduction to Neural Computing. Neural Networks. 1988, 1, 3–16. [Google Scholar] [CrossRef]
- White, A.B.; Fairall, C.W.; Frisch, A.S. Recent Radar Measurements of Turbulence and Microphysical Parameters in Marine Boundary Layer Clouds. Atmos. Res. 1996, 40, 177–221. [Google Scholar] [CrossRef]
- Ghazal, F.; Robert, S.; Joseph, D.M. Classification of lidar measurements using supervised and unsupervised machine learning methods. Atmos. Meas. Tech. 2021, 14, 391–402. [Google Scholar] [CrossRef]
- Romain, C.; Matthew, B. Aerosol light extinction and backscattering: A review with a lidar perspective. J. Quant. Spectrosc. Radiat. Transf. 2020, 262, 107492. [Google Scholar] [CrossRef]
- Brown, B.G.; Thompson, G.; Bruintjes, R.T. Intercomparison of in-flight icing algorithms: Part II: Statistical verification results. Weather Forecast 1997, 12, 890–914. [Google Scholar] [CrossRef]
- Thorne, P.W.; Lanzante, J.; Peterson, T. Tropospheric temperature Trends: History of an Ongoing Controversy. Wires. Clim. Chang. 2011, 2, 66–88. [Google Scholar] [CrossRef]
- Chernykh, I.V.; Aldukhov, O.A. Temperature and Humidity Trends in the Lower Atmospheric 2-km Layer over the Russian Arctic According to Radiosonde Data. Russ. Meteorol. Hydrol. 2020, 45, 615–622. [Google Scholar] [CrossRef]
- Gultepe, I.; Agelin-Chaab, M.; Komar, J. A Meteorological Supersite for Aviation and Cold Weather Applications. Pure Appl. Geophys. 2018, 176, 1977–2015. [Google Scholar] [CrossRef]
- Gultepe, I.; Sharman, R.; Williams, P.D. A Review of High Impact Weather for Aviation Meteorology. Pure Appl. Geophys. 2019, 176, 1869–1921. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).