A Haze Prediction Model in Chengdu Based on LSTM

Abstract

Air pollution with fluidity can influence a large area for a long time and can be harmful to the ecological environment and human health. Haze, one form of air pollution, has been a critical problem since the industrial revolution. Though the actual cause of haze could be various and complicated, in this paper, we have found out that many gases’ distributions and wind power or temperature are related to PM2.5/10’s concentration. Thus, based on the correlation between PM2.5/PM10 and other gaseous pollutants and the timing continuity of PM2.5/PM10, we propose a multilayer long short-term memory haze prediction model. This model utilizes the concentration of O₃, CO, NO₂, SO₂, and PM2.5/PM10 in the last 24 h as inputs to predict PM2.5/PM10 concentrations in the future. Besides pre-processing the data, the primary approach to boost the prediction performance is adding layers above a single-layer long short-term memory model. Moreover, it is proved that by doing so, we could let the network make predictions more accurately and efficiently. Furthermore, by comparison, in general, we have obtained a more accurate prediction.

1. Introduction

The air pollution incidents caused by haze have often occurred in metropolises such as Los Angeles and London. Respiratory diseases caused by haze have killed ten thousand people and caused widespread public panic [1,2]. In China, social industrialization and urbanization have brought economic development, while the awareness and measures for environmental protection have lagged [2,3,4,5].

Sichuan Basin is an area of severe haze pollution in the western part of China. In the 74 major cities monitored, the average annual concentration of PM2.5 ranged from 26 to 160 μg/m³, the average concentration was 72 μg/m³, the proportion of qualified cities was 4.1%, and the average annual concentration of PM10 ranged from 47 to 305 μg/m³, the average concentration was 118 μg/m³, and the proportion of qualified cities was 14.9%. In the following years, haze pollution has been alleviated, but the overall pollution situation is still not optimistic.

The prevention and prediction of haze have become the focus of the public and researchers. The haze research mainly focuses on two aspects: the cause of haze and the prediction of haze. Hinton et al. [6] studied photochemical haze in Los Angeles. They concluded that primary pollutants emitted by motor vehicles and chemical plants and secondary chemical pollutants caused by photochemistry are the primary pollutants. Gupta [7,8] compared the PM10 concentration between the residential and industrial areas in Kolkata, India, and found that soot and motor vehicle emissions had the most significant impact on haze pollution in the area. Minguillón et al. [9] used a positive definite matrix to analyze the main components and formation factors of PM2.5 in Switzerland. Ho et al. [10] collected and tested the chemical composition of PM2.5 in the suburbs of Hong Kong, evaluated the relatively enriched factors in the crustal elements, and used multivariate correlation techniques to determine the source of PM2.5 and its impact.

In terms of haze prediction, researchers have used many different methods to predict haze pollution in different regions. Haze prediction methods include multivariate statistical methods [11,12,13,14], chemical transformation models [15,16,17], and prediction methods based on remote sensing satellite imagery [3,18,19,20,21].

RNN (recurrent neural network) and LSTM (long short-term memory) [22,23,24,25,26,27] have been gradually applied to haze prediction. Qin et al. [28] proposed the new concentration prediction scheme of urban PM 2.5 based on CNN (convolutional neural network) and LSTM. Tsai et al. [29] used RNN and LSTM networks to predict air pollution in Taiwan. Li et al. [16] developed a hybrid called the CNN-LSTM model, which is used to predict the concentration of PM2.5 in Beijing in the next 24 h. Bai et al. [30] proposed an E-LSTM neural network, which constructs multiple LSTM models in different modes for integrated learning with an hourly PM 2.5 concentration forecast. Our time series model did show a better result [26,31,32,33].

In this paper, we applied neural network methods to predict the concentration of haze pollutants, including PM2.5 and PM10. First, we argued that the concentration of PM2.5/PM10 is related to other gaseous pollutants, such as O₃, CO, NO₂, SO₂, and the concentration of PM2.5/PM10 has time series continuity, which means that the curve of concentration is smooth. Furthermore, the concentration at different times is correlated within a certain time window. Based on the two assumptions, we collected real-time PM2.5, PM10, O₃, CO, NO₂, and SO₂ concentrations published by six ground monitoring stations in Chengdu from 1 June 2014 to 30 June 2017, and meteorological data, such as wind power and temperature. Then, we analyzed the correlation between the collected data and PM2.5, constructed different datasets for predicting PM2.5 and PM10, respectively, and constructed a haze prediction model based on LSTM. The LSTM-based haze prediction model uses the O₃, CO, NO₂, SO₂ concentrations, and PM2.5/PM10 concentrations in the last 24 h as inputs to predict future PM2.5/PM10 concentrations. We also focused on adjusting the haze prediction model’s hidden layers to explore the model’s best performance.

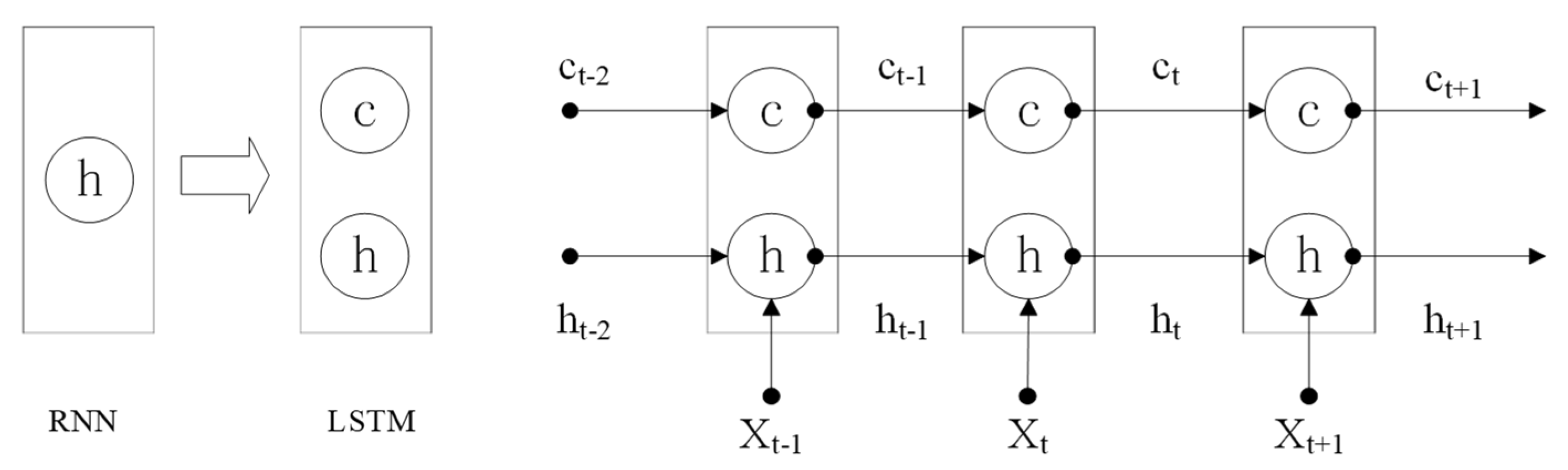
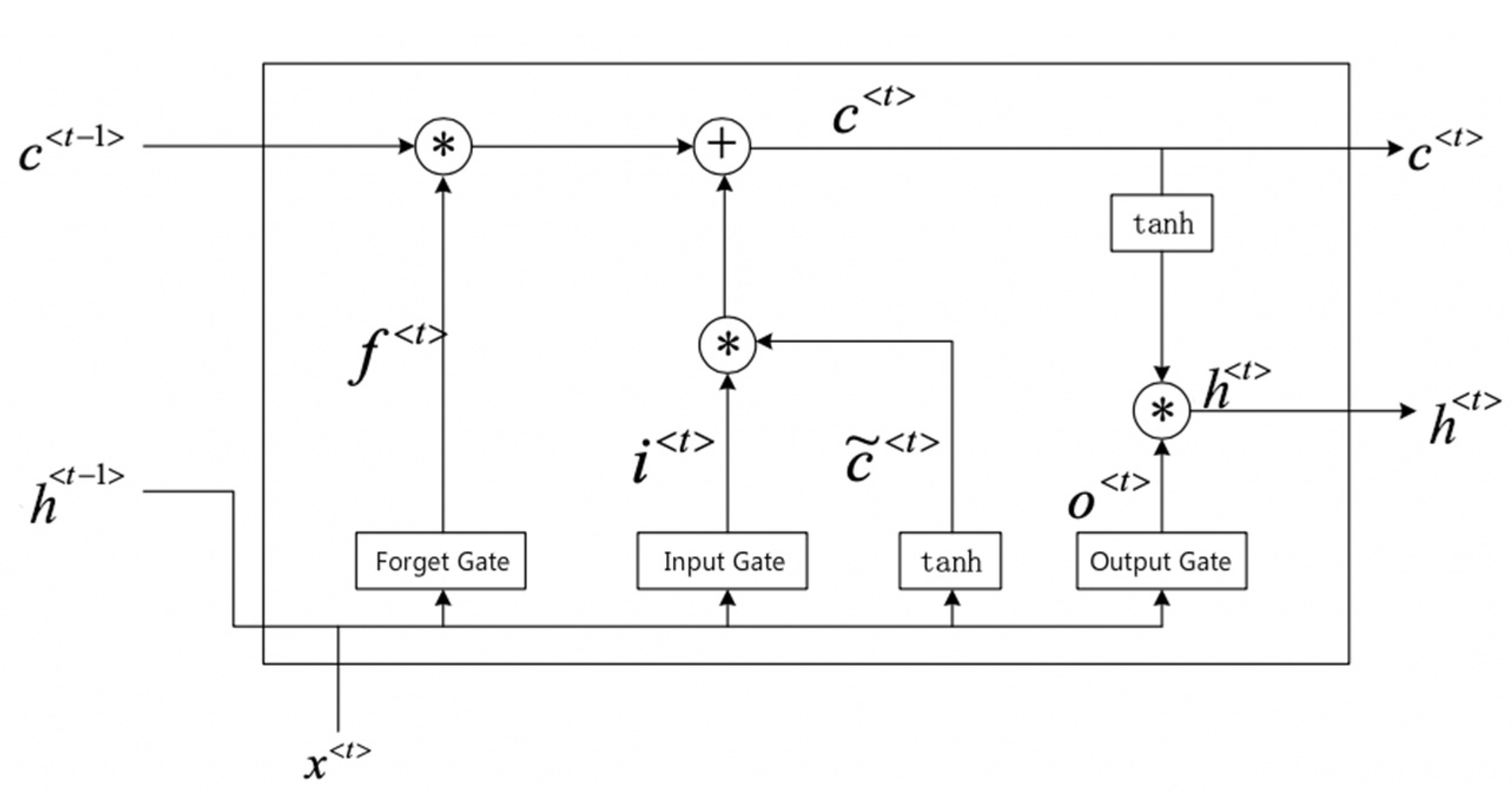
2. Approach

The long short-term memory [34] neural network (LSTM) is a new deep machine learning network built on RNN. In order to avoid the vanishing gradient issue and the gradient explosion problem, a long-term delay process is added to the network. Thus, the state unit can keep the error stream, which successfully solves the defects that exist in the RNN and has been widely used in many fields.

RNN has only one hidden layer state, so short-term input is compassionate when dealing with time series, while long-term input is relatively slow. Therefore, LSTM adds a cell state based on the RNN network for long-term state preservation. An unrolled LSTM is shown in Figure 1. It represents the input of the LSTM network at t-time, the output, and the LSTM network’s cell state of the LSTM network at T-1 time. These three data are the input, output, and cell state of the LSTM network at t-time, and X, h, and c are vectors.

The LSTM implements the preservation, update, and input of long-term state c through the internal forget gate, input, and output gate, as shown in Figure 2. The forget gate and output gate control the cell state of the LSTM. They respectively determine the preserved information of the cell state and the preserved information of the input at the moment of t. The output gate controls the parts of the cell state that we want to include in the output.

Gates are the full connection layers, and the expression of the gate is as shown in Formula (1), where the input and output are all represented by vectors. The output is the real number vector with a range of [0, 1]. Thus, in Formula (1), W denotes the gate’s weight matrix, and b represents the error vector. σ is the sigmoid function, whose output ranges from 0 to 1 and determines whether the input can pass through the gate.

$$g\left(x\right)=\sigma \left(Wx+b\right)$$

(1)

The forget gate is shown in Formula (2). It allows the LSTM to forget the memories based on the current input selectively. The input of the forget gates is the input of the current time and the output of the hidden layer node at the previous time. Weight matrix W and error b are used to adjust the input. The sigmoid function is used to filter out outdated information that is useless for the current output.

$$f_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)$$

(2)

The calculation of the input gate is shown in (3). The input gate controls input information. W_i represents the weight matrix of the output gate, and b_i represents the bias of the input gate.

$$i_t=\sigma \left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)$$

(3)

The input state unit $c_t^{\prime }$ at the current time t is calculated through the output of the network at the time t − 1 and the input at the time t, as shown in (4).

$$c_t^{\prime }=\mathit{tanh}(W_c\left[h_{t-1},x_t\right]+b_c)$$

(4)

Therefore, the cell state at the current time c_t can be obtained by the Formula (5), where the symbol $°$ denotes the elementwise multiplication.

$$c_t=f_t\circ c_{t-1}+i_t\circ c_t^{\prime }$$

(5)

The output gate can be expressed as (6). Output gate controls the influence of long-term information on the current output. The output of the long-term memory neural network is determined according to the output gate and cell state, as shown in (7).

$$o_t=\sigma \left(W_o\left[h_{t-1},x_t\right]+b_o\right)$$

(6)

$$h_t=o_t\circ \mathit{tanh}(c_t)$$

(7)

3. Dataset

In order to predict PM2.5 and PM10 concentrations, we collected two types of data: gas concentration data and meteorological data [7]. First, we collected the real-time concentration data of PM2.5, PM10, O₃, CO, NO₂, and SO₂ released by six ground monitoring stations in the Chengdu urban area from 1 June 2014 to 30 June 2017. The data update frequency is once an hour. PM2.5, PM10, O₃, and SO₂ units: μg/m³ and CO, NO₂ units: mg/m³. We used the average concentration simultaneously in six ground monitoring stations as gas concentration data in Chengdu. Moreover, we have collected the temperature, humidity, and wind data released by the China Weather Network (WEATHER) as meteorological data (http://www.cnemc.cn/ (accessed on 16 October 2019)).

The six monitoring stations selected in the study cover the whole urban area of Chengdu and can completely monitor the changes of air quality in Chengdu. The geographical location of the ground monitoring stations in Chengdu is shown in Figure 3.

3.1. Correlation Analysis

Since autumn and winter are higher frequency seasons of haze than spring and summer, it can be assumed that haze has different causes in different seasons. When studying the correlation between haze and meteorological conditions, we selected pollutant concentrations such as PM2.5, PM10, O₃, CO, NO₂, and SO₂ and the meteorological data such as temperature, humidity, and wind power in two different time ranges (from 0:00 on 4 July 2016 to 23:00 on 10 July 2016, and from 0:00 on 24 December 2016 to 23:00 on 30 December 2016). The correlation analysis tool in MATLAB was used to complete the correlation analysis between meteorological factors and PM2.5. The results are shown in

Table 1. Correlation coefficient value of PM2.5 and meteorological factors.

Correlation Coefficient	Highest Temperature	Lowest Temperature	Humidity	Wind Power	O3	CO	NO2	PM10	SO2
winter	0.29	−0.01	−0.25	−0.35	−0.13	0.49	0.54	0.79	0.48
summer	0.38	−0.05	−0.22	−0.38	−0.56	0.67	0.38	0.95	0.39

.

The correlation coefficient table shows that in winter, the pollutant most related to PM2.5 is PM10, followed by NO₂, CO, SO₂. O₃, wind power, and temperature have a low correlation. However, in summer, the correlation between meteorological factors and PM2.5 is different. The correlation ranking is PM10 ≧ CO ≧ O₃ ≧ SO₂ ≧ NO₂. If the | correlation coefficient | < 0.4, it has a low correlation; if 0.4 ≤ | correlation coefficient | < 0.7, it has a significant linear correlation; if 0.7 ≤ | correlation coefficient | 1, it is highly correlated. In general, PM2.5 in Chengdu has a low correlation with temperature, humidity, and wind power, a significant correlation with CO, SO₂, NO₂, and O₃, and a high correlation with PM10.

Because PM2.5 and PM10 are both essential factors affecting haze, this paper uses PM2.5 and PM10 concentration to represent haze pollution, which is also the research object of our LSTM-based haze prediction model. According to the correlation analysis results, PM2.5 has a low correlation with temperature, humidity, and wind power in the short term. It is considered that the weather parameters are stable in the short term. Therefore, we selected CO, SO₂, NO₂, O₃, historical PM10, and historical PM2.5 as inputs to train the haze prediction model and achieve the goal of predicting the concentration of PM2.5/PM10.

3.2. Data Completion

The collected PM2.5, PM10, O₃, CO, NO₂, and SO₂ concentration data totaled 26,120. This paper calculates the mean of the previous and next state’s concentration data. It completes the time series of missing data, as shown in Formula (8). The final data set contains PM2.5, PM10, O₃, CO NO₂, and SO₂ concentration adequate data in 27,380 moments.

$$X_t=\frac{1}{2}\left(X_{t-1}+X_{t+1}\right)$$

(8)

In (8), $X_t$ represents the missing concentration data at the current time, $X_{t-1 }$ represents the concentration data at the previous moment, and $X_{t }$ represents the concentration data at the next time point. Furthermore, it is for sure that this could add additional noise to the dataset since we are just filling missing points with roughly generated data. We do not need to complete most of the dataset because the final dataset is only 3% greater than the vanilla one, which is tolerable for machine learning tasks.

3.3. Standardized Processing

In the neural network, large-value data tends to increase the proportion of influence on the model and makes the model lose the characteristic properties of the data with low value. Therefore, to avoid errors caused by different numerical ranges, we convert all historical concentration data to −1~1 (9).

$$X^{\prime }=\frac{X-\overline{X}}{X_{max}-X_{min}}$$

(9)

$X^{\prime }$ denotes the concentration data after the standardized processing, $X$ represents the original concentration data, $\overline{X}$ denotes the mean of the concentration data, $X_{max}$ denotes the maximum value, and $X_{min}$ represents the minimum value.

In this paper, we base on the assumption that the PM2.5 or PM10 concentration at the next moment is related to its short-term historical data and the O₃, CO, NO₂, and SO₂ concentration values at the same moment. Therefore, we reconstructed the dataset and used the PM2.5 concentration in the past 24 h. The current PM10, O₃, CO, NO₂, and SO₂ concentration values were training data, and the corresponding ground truth was the current PM2.5 concentration. Similarly, we also constructed a dataset for predicting the concentration of PM10. Again, the PM10 concentration in the past 24 h and the PM2.5, O₃, CO, NO₂, and SO₂ concentration values at the current time were used as training data. The ground truth was the current time PM10 concentration. Finally, we divided the reorganized dataset into the training set, verification set, and test set according to 80%, 10%, and 10%.

4. Experiment and Result

4.1. Evaluation

This research is a simulation experiment of realizing the prediction model based on Python-TensorFlow framework.

In order to reflect the prediction accuracy of the haze prediction model at different levels, we used numerical evaluation and hierarchical evaluation. We used the root-mean-square error (RMSE) [35] as a numerical evaluation method to reflect the overall accuracy of the model’s haze prediction values, as shown in (10).

$$RMSE=\sqrt{\frac{1}{m}{\displaystyle \sum }_i^m{\left(T_i-P_i\right)}^2}$$

(10)

In (10), i refers to the number of a test sample, m refers to the total number of predicted simples, T_i represents the actual concentration of the test sample, the ground-truth, with the unit: μg/m³, and P_i represents the predicted concentration value with the unit: μg/m³.

We divided the PM2.5 and PM10 concentrations into six grades based on the Air Quality Index (AQI) to assess the model’s error in macroscopic pollution levels, as shown in

Table 2. PM2.5 and PM10 levels.

Level	1	2	3	4	5	6
Level range (μg/m3)	0–35	36–75	76–115	116–150	151–250	>250

. If the prediction result and the result are at the same level, the prediction result is judged to be excellent; if the prediction result and the result are adjacent, the prediction result is determined to be acceptable; if the prediction result is different from the result by two levels or more, the predicted result is unacceptable.

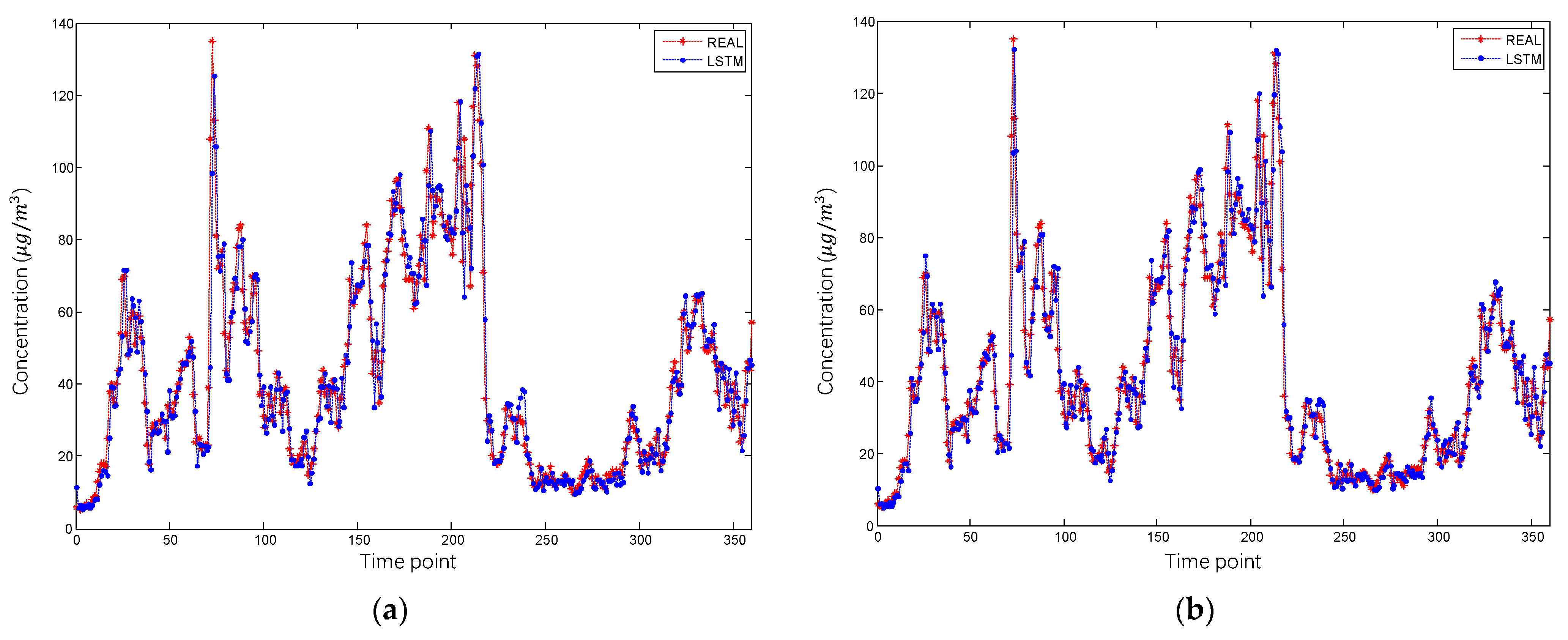
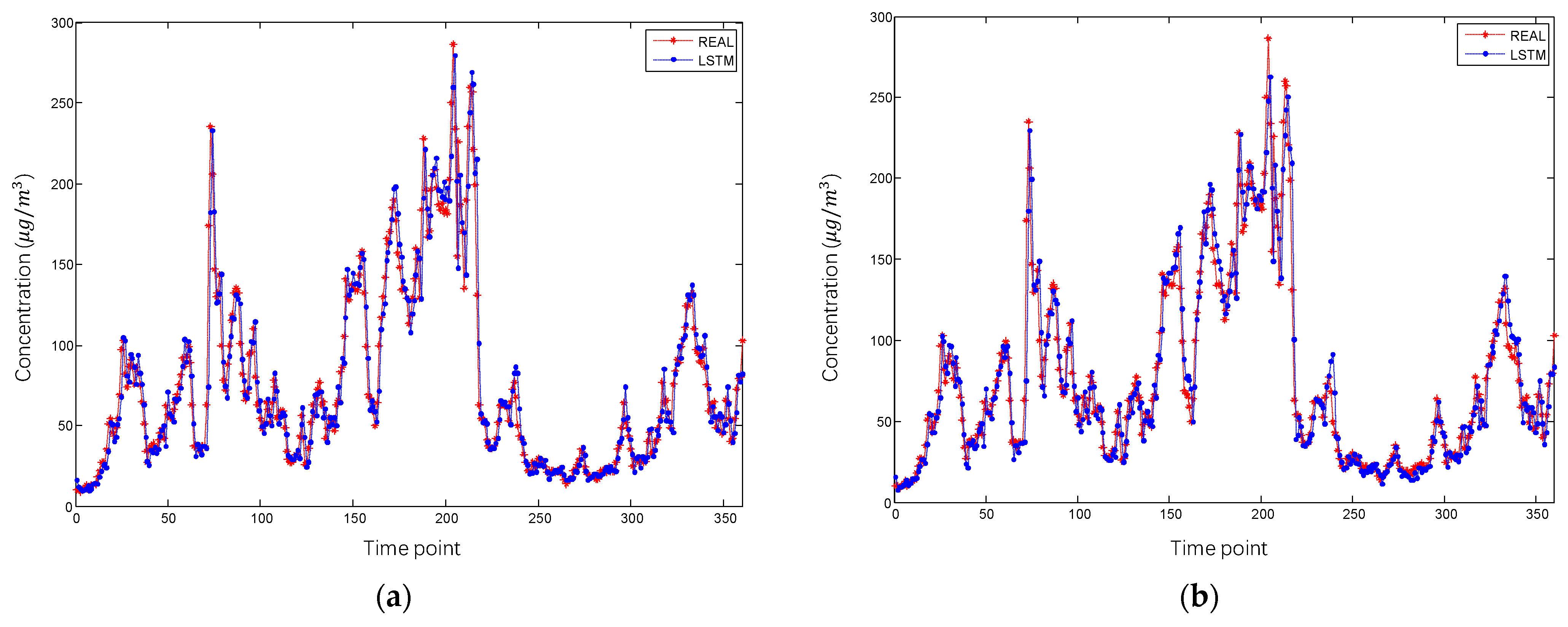
4.2. Result

In this paper, by changing the dataset, we used the LSTM-based haze prediction model to predict the concentration of PM2.5 and PM10, respectively. The number of input layer nodes was 29, and the number of output layer nodes was 1. While predicting the PM2.5 concentration, the inputs were the PM10, O₃, CO, NO₂, and SO₂ at the n hour and the PM2.5 concentration in the last 24 h. The output was the PM2.5 concentration at n hour. While predicting the PM10 concentration, the inputs were the PM2.5, O₃, CO, NO₂, and SO₂ at the n time, and the PM10 concentration in the last 24 h. The output was the PM10 concentration at the n hour.

The initialization parameters were as follows: the weight gradient learning rate was set to 0.01, the visible layer node bias was initialized to 0.05, the hidden layer node bias was initialized to 0.1, the target error was set to 0.005, and the iteration number was 5000.

We have also conducted several experiments to study the effect of different hidden layers on prediction accuracy. In order to more directly reflect the prediction result of PM2.5/PM10 and calculate the accuracy of the experiment, we selected the prediction data and actual data of 360 consecutive moments to demonstrate. We performed five experiments on each model with different hidden layer numbers and selected the best result. The prediction results of PM2.5 concentration in different hidden layers based on the LSTM-based haze prediction model are shown in

Table 3. PM2.5 prediction results with different hidden layers.

Hidden Layers	Neuron Distribution	PM2.5 RMSE μg/m3	Excellent	Acceptable	Unacceptable
1	10	10.95	80.83%	18.89%	0.28%
2	10 9	9.72	81.67%	18.33%	0.00%
3	10 9 8	8.81	84.44%	15.56%	0.00%
4	10 9 8 7	8.41	83.89%	16.11%	0.00%
5	10 9 8 7 6	8.18	85.28%	14.72%	0.00%
6	10 9 8 7 6 5	8.31	84.72%	15.28%	0.00%
7	10 9 8 7 6 5 4	8.11	86.39%	13.61%	0.00%
8	10 9 8 7 6 5 4 3	8.23	85.56%	14.44%	0.00%

.

The PM2.5 prediction results show that even if the LSTM has only one hidden layer, the RMSE of the prediction result is only 10.95, which is a lower error level. Thus, the prediction level of PM2.5 is generally consistent with the actual situation, which indicates the high correlation between the input data and the concentration of PM2.5.

In fixing the number of hidden layer nodes, the prediction accuracy is related to the number of hidden layers. Therefore, the increase in the number of hidden layers generally improves the prediction accuracy of PM2.5, both at RMSE and level evaluation. However, the accuracy of the prediction result brought by the increase of the hidden layer also has a bottleneck. For example, when the hidden layer is 7, the mean square error is 8.11, the excellent is 86.39%, the acceptable is 13.61%, and the unacceptable is 0%. Figure 4 shows the PM2.5 prediction results of hidden layer 5 and hidden layer 7, respectively.

We used the same method to predict the concentration of PM10. The predicted PM10 concentrations in different hidden layers based on the LSTM-based haze prediction model are shown in

Table 4. PM10 prediction results with different hidden layers.

Hidden Layers	Neuron Distribution	PM10 RMSE μg/m3	Excellent	Acceptable	Unacceptable
1	10	18.95	73.89%	25.28%	0.83%
2	10 9	17.02	78.61%	21.11%	0.28%
3	10 9 8	16.66	79.72%	20.00%	0.28%
4	10 9 8 7	16.05	80.56%	19.17%	0.28%
5	10 9 8 7 6	15.40	81.11%	18.89%	0.00%
6	10 9 8 7 6 5	15.48	81.11%	18.89%	0.00%
7	10 9 8 7 6 5 4	15.41	81.67%	18.33%	0.00%
8	10 9 8 7 6 5 4 3	15.40	81.39%	18.61%	0.00%

.

Increasing the number of the hidden layer can improve the prediction accuracy of PM10 to a certain extent, reducing the RMSE of the prediction result and improving the acceptability of the level prediction. For example, the haze prediction model with 7 hidden layers has the best result, where the root-mean-square error is 15.41, the excellent is 81.67%, the acceptable is 18.33%, and the unacceptable is 0%. Figure 5 shows the PM10 prediction results of hidden layer 5 and hidden layer 7, respectively. However, the root-mean-square error value is also very close when the hidden layers are 5, 6, and 8. This shows that the improvement of hidden layers above five can hardly increase the accuracy of the predicted concentration of PM10, which is the limitation imposed by the LSTM model.

Compared with Table 3, the RMSE of PM10 is always more significant than the RMSE of PM2.5. The haze prediction model also produces a more significant deviation in the PM10 level prediction. The excellent and acceptable levels are both reduced by about 5% compared to the PM2.5 level prediction. Analyzing the result accuracy of PM2.5 and PM10, we argue that the model fits well with the correlation between O₃, CO, NO₂, SO₂, and haze pollutants and achieves accurate predictions both on haze concentration and level.

5. Discussion

This paper shows that LSTM with multiple layers stacked could dramatically increase the prediction’s accuracy. Moreover, it is correlated to the general rule of deep learning models: a deep structure could better cope with complicated multi-dimension datasets than models with limited depth.

Furthermore, using correlation analysis could let us decide which part of the whole dataset should be included, which prevents us from just pouring all data into the network to waste time and damage the accuracy.

Compared with the CNN+LSTM model in [28], the multilayer LSTM model proposed in this paper can achieve more accurate results. The reason may be that the six monitoring stations selected in this article are all from Chengdu, with even distance intervals. The climate data except for the main pollutants are similar. Therefore, the mutual influence between the data is small, leading to more accurate results. Compared with [29], its paper mentions that in the past 3, 8, 24, and 72 h forecast results, 72 h is the best forecast accuracy. We used the data of the past 24 h to predict PM2.5, and the result is better than its 72 h forecast accuracy. Compared with [16], the original text uses the previous week’s data (7 days) as the input of the data model. This paper uses the data 24 h ago as the input, which reduces the amount of calculation. Compared with [30], our multilayer LSTM shows more accurate and less biased results. We found that our model made more accurate predictions for such prediction tasks.

To keep increasing the model’s accuracy and improve its ability to generalize, we are considering the following methods.

• We could feed the network with more data from areas adjacent to the target area whose haze concentration is what we want to predict. Haze is always a meteorological phenomenon, which indicates that the appearance of haze should be related to what is happening around the target area. For instance, if there is a signal of a powerful wind around the target area yet such signal is not included in our data, we could make a massive error because a powerful wind is likely to take pollutants away. Therefore, including data from adjacent areas could better fit the reality.
• A combination of different genres of deep learning models could be potentially helpful to increase accuracy. For example, we could consider that using a convolutional neural network to analyze a satellite photo could be helpful to give our sequential model a complete overall view of what is going to happen.
• Deep learning models always show their abilities when there are so many dimensions of the input. Thus, it is reasonable to add more parameters to the model to generate a prediction. In conclusion, adding extra dimensions should be considered as a way to improve accuracy.
• Since the GRU cell is generally a suitable replacement for the LSTM cell, since its complexity is lower yet the outcome remains much the same or even better, it is reasonable and worthy to use GRU to make predictions instead of LSTM. However, accuracy-wise speaking, LSTM is sufficient.
• Network Architecture Search (NAS), for instance, a Bayesian theory-based searching method [36], could help optimize our settings about the hyperparameters so that accuracy could be improved even further.

Since our experiment shows that gas concentration data work when using them as materials to make haze concentration predictions, we are considering the potential of utilizing neural networks to make predictions because neural networks could learn some patterns of meteorological phenomena. However, even if we know much about the mechanics behind many meteorological phenomena, we can hardly predict what will take place a few more days later because there are too many noises and uncertain interferences. We can achieve better accuracy through neural networks because our simulation methods are limited when generating long-term predictions.

Since the volume of meteorological data could be tremendous, it makes sense to use deep learning structures to learn the hidden patterns. Therefore, in future work, besides achieving better performance when using current data to predict the target quantity, there is also a need to develop models for predicting the future since simulation does have its limitations.

6. Conclusions

This paper proposes a multilayer LSTM haze prediction model to predict the PM2.5/PM10 concentration in Chengdu, utilizing O₃, CO, NO₂, SO₂, and PM2.5/PM10 in the last 24 h as inputs. Analyzing the result accuracy of PM2.5 and PM10, we argued that the model fits well with the correlation between O₃, CO, NO₂, SO₂, and haze pollutants and achieves accurate predictions both on haze concentration and level. At the same time, the prediction results show that, within a certain range, the greater the number of hidden layers, the higher the prediction accuracy. When a specific value is reached, the accuracy is roughly equivalent. Under the same network, the prediction accuracy of PM2.5 is significantly higher than that of PM10. Besides pre-processing the data, the primary approach to boost the prediction performance is adding layers above a single-layer LSTM model. Moreover, it is proved that by doing so, we could let the network make predictions more accurately and efficiently.