Abstract
Surface energy budgets are important to the ecohydrology of complex terrain, where land surfaces cycle in and out of shadows creating distinct microclimates. Shading in such environments can help regulate downstream flow over the course of a growing season, but our knowledge on how shadows impact the energy budget and consequently ecohydrology in montane ecosystems is very limited. We investigated the influence of horizon shade on the surface energy fluxes of a subalpine headwater wetland in the Canadian Rocky Mountains during the growing season. During the study, surface insolation decreased by 60% (32% due to evolving horizon shade and 28% from seasonality). The influence of shade on the energy budget varied between two distinct periods: (1) Stable Shade, when horizon shade was constant and reduced sunlight by 2 h per day; and (2) Dynamic Shade, when shade increased and reduced sunlight by 0.18 h more each day, equivalent to a 13% reduction in incoming shortwave radiation and 16% in net radiation. Latent heat flux, the dominant energy flux at our site, varied temporally because of changes in incoming radiation, atmospheric demand, soil moisture and shade. Horizon shade controlled soil moisture at our site by prolonging snowmelt and reducing evapotranspiration in the late growing season, resulting in increased water storage capacity compared to other mountain wetlands. With the mounting risk of climate-change-driven severe spring flooding and late season droughts downstream of mountain headwaters, shaded subalpine wetlands provide important ecohydrological and mitigation services that are worthy of further study and mapping. This will help us better understand and protect mountain and prairie water resources.
1. Introduction
Mountain regions have been termed the “water towers of the world” due to their importance in regulating the global water balance and providing a water source disproportionate to their surface area [1,2]. These regions cover 20% of the Earth’s terrestrial surface [3], but contribute 40 to 60% of annual surface runoff [4]. The Canadian Rocky Mountains represent one of North America’s largest water towers, since they store and distribute water resources to over 13 million people residing in the Canadian Provinces of British Columbia, Alberta and Saskatchewan, in addition to the U.S. States of Washington and Oregon [5]. Runoff from the Rockies supplies the Athabasca, Saskatchewan, Columbia and Fraser Rivers—all important water resources for Canadian agriculture, the generation of hydroelectricity, municipal water and industry operations downstream [5]. Most of these downstream locations have minimal precipitation during the summer months [6], relying on runoff from the Rockies during that time.
Runoff from mountain ecosystems is under threat from climate warming. A recent special Intergovernmental Panel on Climate Change report on high mountain areas [7] highlighted that snowpack has been reduced in recent years due to warmer air temperatures experienced at higher elevations. These warmer temperatures also result in earlier spring snowmelt, which can lead to earlier peak flows. There is also evidence that vegetation density and composition at higher elevations has increased in recent decades due to warming [7,8]. This can lead to increased leaf area and greater evapotranspiration (ET) over time, which in turn would change flow rates during the key summer and late growing seasons. For example, Goulden and Bales [9] found that at elevations above about 2000 m in the Sierra Nevada Mountains, vegetation was limited by cold temperatures instead of soil moisture, like those at lower elevations. As a result, they found that warming projected at high elevation sites by year 2100, could increase ET by 28% and decrease river flow by 26% [9].
In montane areas, however, the elevation, slope and aspect of topographical features create surface horizon shadows, contributing to lower daily radiative input in shaded areas compared to surrounding non-shaded areas [10,11,12,13]. Horizon shadows occur when a land surface is shaded from surrounding topography (i.e., a summit, headwall, or ridge), because it is below the local horizon and blocked from direct-beam irradiance [14,15]. Here, land can cycle in and out of shade in daily and/or seasonal cycles, which promote large differences in incoming solar radiation over small distances and reduce the amount of incoming energy for snowmelt and plant photosynthesis [15]. The resulting microclimates can delay the timing of snowmelt in spring [16], and produce cooler air and surface temperatures during the growing season [17,18,19,20], helping to reduce ET. In this way, shade can help mitigate the negative impacts of increasing air temperatures at high elevations, especially during the growing season when the vegetation is active. However, shade can also reduce heat stress and increase the amount of diffuse radiation reaching vegetation, which can enhance their overall photosynthesis and impact ET [21]. This, in turn, can result in reduced flow rates from affected headwater ecosystems. Our understanding of how shadows impact the energy budget and consequently ET in montane ecosystems is very limited [22,23,24], yet important to help improve our understanding and modelling of the spatial variability of montane cryospheric processes [7,25,26,27].
One of the key montane ecosystems that helps store and regulate water flow at the headwaters are wetlands [28]. Flow regulation by montane wetlands helps provide a steady water supply to reservoirs for consumption and irrigation downstream, especially when water resources are scarce in the late growing season [29]. The goal of this study was to quantify the influence of seasonal horizon shade on the surface energy budget and consequently the ET, of a subalpine headwater wetland during the growing season. The specific objectives of this study were to: (1) quantify spatial and temporal patterns of horizon shade at a headwater wetland (~2000 m a.s.l.) over the course of a growing season; (2) measure and partition the growing season surface energy budget of the wetland; and (3) quantify and analyze the influence of horizon shade on the wetland’s microclimate, components of the surface energy budget, and consequently, ET.
2. Study Site
The study was conducted at Bonsai wetland, a subalpine headwater wetland (2083 m a.s.l.) on Fortress Mountain (50.82° N, 115.21° W) located 80 km west of Calgary, Alberta (Figure 1a). The study site is at a privately owned alpine ski resort in the Kananaskis Valley, which marks the front range of the Canadian Rocky Mountains. A tall (~500 m), steep headwall marks the southern boundary of the wetland, while an ephemeral tarn located 200 m to the north of the headwall marks the northern boundary. Canadian and Fortress Ridges (~150 m in elevation) are the drainage divides 500 m to the east and 1.7 km to the west of the wetland (Figure 1c). Classified as a marsh meadow according to the Windell et al. [30] classification scheme for Rocky Mountain montane and subalpine wetlands [31], the wetland is defined by silt and clay soils and shade tolerant vegetation like Equisetum, Salix and Castilleja raupii. Located directly beneath the headwall, it covers approximately 1 ha area (Figure 1c). The wetland is mostly flat, with an average slope of 6 degrees (a 3 m change in elevation over 50 m in horizontal distance) from the stream confluence to the talus slopes. The headwall to the south and ridge to the east of the wetland provide a topographic barrier to solar radiation, resulting in seasonal shading of the site. This shading creates a microclimate that promotes a thick snowpack, long snow-covered season, an extended spring melt and a constrained growing period compared to other more exposed areas on Fortress Mountain (Figure 2).
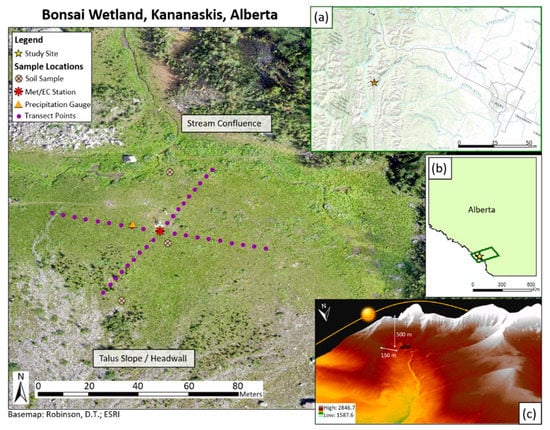
Figure 1.
Map of Bonsai—our subalpine wetland research site, the location of equipment/sampling, its location in the province of Alberta and the Eastern Rockies (a,b) and LIDAR imagery of the basin with daily sun path and topographic boundary elevations. Note that the image is looking south in (c) and the black outline is the wetland study area.

Figure 2.
Images of the seasonal evolution of our research site during (a) Snow Melt, (b) Green-Up, (c) Peak Growing Season and (d) Late Growing Season. Images were taken during the 2018 field campaign on (a) 18 June, (b) 6 July, (c) 26 July and (d) 28 September.
Surface water from two streams meet at a confluence in the north-central section of the wetland and drain into the tarn, which feeds Galatea Creek and later, the Kananaskis River (a tributary to the Bow River). The two stream branches follow the east and west boundaries of the wetland, and are fed by springs emerging from talus deposits [32]. The eastern stream floods during spring-melt and water pools above the ground surface for several weeks in the north-east corner. Following spring melt, the stream in the west flows continuously during the growing season, but the stream in the east often dries by midseason.
Climate conditions at the Marmot Basin Research Station (Mt Allan: 1391 m.a.s.l.), 14 km north of Fortress Mountain, indicate that the Kananaskis Range is dominated by continental air masses, with long and cold winters and an average temperature of −15 °C from January to March [33]. The average annual precipitation is approximately 900 mm in the valleys and mid-elevations, but increases to 1140 mm above the treeline [34]. Historically, 65 to 70% of average precipitation occurs as snowfall [33]. Due to low temperatures and high snowfall, snow cover persists in the basin from November to June [15] with a melt period that lasts from April until July [33]. The closest Environment and Climate Change Canada (ECCC) weather station (ID 3053600), with more than 30 years of climate records, is located 28 km north of the study site at an elevation of 1391 m a.s.l. (51.03° N, 115.03° W). The most recent 30-year (1981–2010) record from this weather station indicates that average temperature for the summer months of June, July, August and September are 11.4 °C (±1.1), 14.5 °C (±1.5), 13.8 °C (±1.5) and 9.4 °C (±1.9) per day, respectively. The average annual minimum air temperature is −6.2 °C in December and the maximum is 14.5 °C in July (Figure 3a). Average annual precipitation is 639.3 mm, with 119.4 mm, 64.9 mm and 70.8 mm falling over the summer months of June, July and August (Figure 3b).
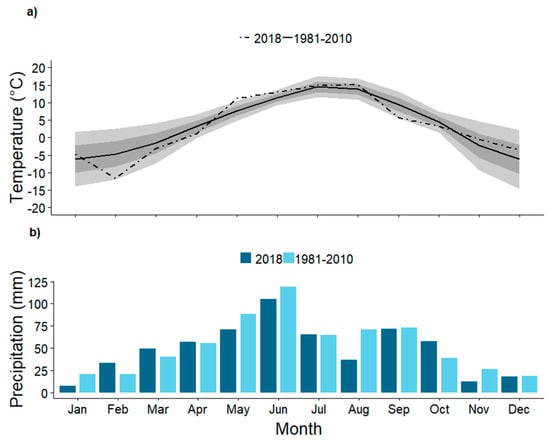
Figure 3.
Comparison of 2018 air temperature, Tair (dashed line, (a) and precipitation (dark blue, (b) to that of the 30-year (1981–2010) climate normal measured at a nearby Environment and Climate Change Canada weather station. In (a) darker grey and lighter grey shaded areas represent one and two Standard deviations around the 30-year mean Tair (solid line), respectively.
3. Materials and Methods
3.1. Meteorological Data
A meteorological tower was installed in the centre of the wetland and instrumented with equipment to measure meteorological variables. Meteorological equipment was in place from 7 June to 10 September, to monitor the 2018 growing season—this included late snowmelt season (7 to 23 June), so that we could capture the start of the growing season on 24 June. Wind speed was measured at a height of 3.8 m (R.M. Young 05103 anemometer, Traverse City, MI, USA), while net radiation, Q*, (NR Lite2; Kipp and Zonen, Delft, the Netherlands) and photosynthetically active radiation (PAR) (LI-190R; LI-COR, Lincoln, NE, USA) were measured at 3.05 m. No pyranometer was present at the site due to logistical and budget constraints. Air temperature (Ta) and relative humidity (RH) were measured at 3.4 m (HMP-155; Vaisala, Helsinki, Finland). Ground heat storage (Qg) was calculated as the average of two heat flux plate measurements (Thermal Sensor HFP01; HukseFlux, Delft, the Netherlands). There was only a 1% gap in Qg data. This gap was filled by assuming Qg = 10% * Q*. Two ECH2O EC—5 sensors (Meter Group, Hopkins, WA, USA) measured the average soil moisture at 10 cm depths. Soil temperature (Ts) was measured at 3 depths below the ground surface (2, 5 and 10 cm) with Soil Thermistors (Li-7900–180; LI-COR, Lincoln, NE, USA). Data were recorded on a 9210XLite Logger (Sutron; Stirling, VA, USA), sampled every 10 s and averaged every 30 min. Rainfall was measured at a nearby meteorological station, approximately 350 m north of the wetland site, at the same elevation, using a tipping bucket rain gauge data logger (Onset Computer Corp., Bourne, MA, USA). Additionally, images of the site were taken in three-hour intervals from 06:00 to 21:00 on a Moultrie Wingscapes time lapse camera from 25 May to 7 September 2018.
3.2. Eddy Covariance Measurements
The latent (Qe) and sensible (Qh) energy fluxes were measured with eddy covariance (EC) instrumentation during the same period as the meteorological data. EC measurements at the wetland site were collected with a three-dimensional sonic anemometer (CSAT3; Campbell Scientific Inc., Logan, UT, USA) and an open-path infrared CO2/H2O gas analyzer (IRGA) (LI-7500; LI-COR Inc., Lincoln, NE, USA) mounted at a height of 3 m above the surface, on the meteorological tower described above. The EC system sampled fluxes at a frequency of 10 Hz, with 30-min averages calculated and recorded on a data logger (CR1000; Campbell Scientific Inc., Logan, UT, USA). The IRGA was calibrated at the beginning and end of the study period, to account for any drift in sensor sensitivity, which remained less than 5% over the duration of the study period.
Of the possible 4571 half-hours of EC data during our study period (7 June at 14:00 to 10 September at 19:30), only 3736 half-hours were collected and went on for further data processing. The 18% initial data loss was due to power outages. The collected raw EC data were processed internally by the datalogger at the site, using the software provided by Campbell Scientific (Campbell Scientific Inc., Logan, UT, USA), which completes all standard raw data corrections and processing, including air density correction for open path sensors [35], corrections for coordinate rotation (double coordinate rotation was used), time lag and sensor separation, following common Fluxnet protocols [36,37,38,39,40,41]. The resulting half-hour fluxes were then processed in a custom R-Software script, which filtered the data to ensure each half-hour had at least 80% of 18,000 high frequency records. Further outliers were removed by comparison to a moving average for 10 half-hour means, plus/minus 3 standard deviations of neighboring values and by checking for physically improbable values. The Kljun et al. [42] footprint analysis was used to constrain the measured fluxes to be within 80% of the desired site boundaries, using their FFP R-functions. Footprint distances were input as 50 m north, 64 m north-east (22.6° to 67.5°), 70 m east (67.6° to 112.5°), 71 m south-east (112.6° to 157.5°), 30 m south (157.6° to 202.5°), 30 m south-west (202.6° to 247.5°), 130 m west (247.6° to 292.5°) and 9 m north-west (292.6° to 337.5°). Footprint analysis removed about 30% of the data. Thereafter, the data were filtered for low turbulence (using a friction velocity (u*) threshold of 0.15 m/s), which resulted in an additional 15% of data removal. After filtering for quality control, footprint and low-turbulence, only 26.7% of the original data remained (998 half-hours, distributed throughout the study period). Qe was gapfilled as follows: Qe was converted to ET using latent heat of vaporization and converting W/m2 to mm/half-hour units; potential evapotranspiration (PET) was calculated for each half-hour using the Priestley-Taylor equation [43]; a ratio of ET to PET for each available half-hour was calculated following Petrone et al. [44]; this ratio was gapfilled for all missing half-hours using the MDS method outlined in Reichstein et al. [45] with Q*, VPD and u* used as the gap-filling conditions, when this was not possible the seasonal mean was used. The gapfilled ratio and calculated PET for all half-hours were used to gapfill-ET, which was then converted to Qe to provide gapfilled Qe. Qh was then gapfilled by solving the energy balance equation (Q* = Qe + Qh + Qg) by using the measured, gapfilled Q*, Qe and Qg. The Bowen ratio (ß) was calculated as the ratio of sensible heat (Qh) to latent heat (Qe). In this manuscript, the gap filled data were used to delineate and justify growing season partitioning and timeseries plots. Non-gapfilled data was used in statistical analysis.
3.3. Horizon Shade Model
Bonsai experienced variable horizon shade over the course of its growing season. In order to estimate the hours of shade over the study period, we made use of modelling as described below.
Coordinates of the meteorological tower at our study site were input into www.suncalc.org (accessed on 1 September) [46]—a website that provides solar data for selected dates and times across the globe. This tool provided the azimuth, altitude and shadow length every 15 min for clear-sky days from 7 June to 10 September. Clear sky days were selected based on personal daily field observations, while at the site and for days when incoming shortwave radiation followed the expected smooth rise in the morning, peak at midday and decrease into the evening [47]. Flat-lined days were eliminated for this portion of the analysis to avoid any overcast sky conditions. All records were downloaded and compiled into a single table, negative altitude values (time when the sun was below the horizon) were removed to avoid error in the horizon shade calculation. These data, along with a 2 m digital elevation model (DEM), were used as input into a horizon shade model (HSM) in ArcMap (v10.6). First, horizon shade rasters were created via the hill shade tool for each 15-min interval of azimuth and altitude. Each horizon shade raster was then clipped to the study area, and reclassified to set shadows to 0 and all other values to 1. Using the raster calculator, all horizon shade rasters were integrated into one horizon shade raster where each pixel represented the total shade value for that day. Each value for the summed horizon shade raster was converted to total hours shaded for each clear sky day, using
where shade value was the value of the summed horizon shade raster.
3.4. Solar Radiation Model
To calculate daily incoming shortwave radiation (K↓) across the study site, the area solar radiation tool was used in ArcMap (v10.6). This tool derived incoming K↓ based on a geometric solar radiation model (SRM) [48], and accounted for the surrounding topography using the same DEM used for the horizon shade rasters. Only daylight hours were input to the SRM, to ensure that the results would be comparable to the horizon shade model. The output was then run through the “int” tool in ArcMap (v10.6) to convert the value of each raster to an integer by means of truncation. Next, “extract by mask” (ArcMap v10.6) was used to isolate the wetland values from the rest of the basin. Final K↓ values for the wetland were then overlain on the horizon shade raster to compare hours shaded and K↓.
To quantify the amount of intercepted radiation by the headwall, the SRM was run for a ridge located 2.4 km north of the wetland with no topographic barrier to block K↓. K↓ at the wetland was then subtracted from K↓ at the ridge and the difference was assumed to approximate the amount of radiation directly intercepted by the headwall. To calculate K↓, measured PAR values over the entire study period were converted to W/m2 by multiplying by 0.219 as indicated in the Plant Growth Chamber Handbook [49] that was adapted from [50], then multiplied by 2 to represent the full spectrum of K↓.
3.5. Shade and Seasonal Phases
To help isolate the seasonal impact of shade in our analysis, our data were divided into the periods of Stable Shade with constant average daily shade (7 June to 30 July) and Dynamic Shade with increasing average daily shade (31 July to 10 September), as determined from the HSM. In addition to the two shade periods, we present and discuss our results in terms of four “seasonal phases”, defined as Snow Melt (7 to 23 June); Green-Up (24 June to 20 July); Peak Growing Season (21 July to 23 August); and Late Growing Season (24 August to 10 September). The seasonal phases were determined from personal observations and measurements of snowpack thickness and vegetation phenology at the site. We used field-log notes on snowpack, soil moisture and vegetation growth, combined with analysis of photos taken by a time lapse camera at the site. The two shade periods were used to assess how shade impacted and coincided with seasonality of the site. Stable Shade conditions occurred during Snowmelt, Green-Up and the first 10 days of Peak Growing Season. Dynamic Shade conditions dominated most of the Peak Growing Season and throughout all of the Late Growing Season at our site.
3.6. Statistical Analysis
To ensure that shade hours were appropriate to use in a statistical analysis, the amount of shade hours were first compared to the intercepted radiation by the headwall. It was found that intercepted K↓ increased alongside hours of shade as the season progressed, indicating that increased shade reduced K↓. A linear regression model was used to understand the influence of shade (independent variable) on components of the energy budget (dependent variables). Since the ouput from the HSM was the independent variable, parametric testing was acceptable to use in this particular analysis of the study.
Latent heat flux, Qe, is equivalent to evapotranspiration, which in turn is a major component of the water cycle at our site. To understand which environmental variables explained most of the temporal variability in observed latent heat flux, we considered a correlation matrix between all measured meteorological variables and Qe. Our dataset contained a number of continuous environmental variables of interest for every half-hour, including: Tair, relative humidity (RH), photosynthetically active radiation (PAR), calculated vapour pressure deficit (VPD) from Tair and RH, total precipitation for each half hour (PPT), cumulative precipitation, soil temperature at 2 cm depth, soil temperature averaged over 2, 5 and 10 cm depths, soil moisture averaged from two locations at 10 cm depths and the sum of incoming solar radiation calculated from daily sums of observed PAR in W/m2, Qg and Q*. In this part of the analysis, we used only non-gapfilled data. Furthermore, we restricted this particular analsyis to the dataset from the Peak Growing season, to avoid the confounding effects of developing and senescing foliage during the Green Up and Late Growing seasons. Peak Growing Season was also the only season that experienced both Stable and Dynamic shade conditions. Since meteorological values and EC data were collected on separate instruments and loggers, there were half-hours where EC values were present, but the corresponding meteorological variables were not. As a result, the final dataset used for analysis of latent heat flux variability had 326 half-hour values (n = 326), of which 230 belonged to Dynamic Shade and 97 to Stable Shade conditions. A categorical variable (fShade) was used to group the data into Stable and Dynamic Shade during the analysis. fShade had a value of 1 if the half-hour belonged to the Stable Shade period and a value of 0 if it belonged to the Dynamic Shade period. In finding the best fitted model to explain Qe variability, we considered linear and non-linear model fits with random effects (such as day of year or half-hour) to account for any temporal variability due to the timeseries-nature of our data. The best fitted model was identified using Akaike’s Information Criterion (AIC) and Bayesian Information Criteria (BIC) selection criterions and residual plots following the methods of Zuur et al. [51]. The model with the lowest AIC value or the largest change (Δ) in AIC was deemed as the best fitted model to our dataset, and its comprising variables were deemed to be most important in explaining variability in the dependent variable. To determine the relative contribution of each explanatory variable in the best-fitted model, we compared the “full” model with those that had each of the individual explanatory variables removed, one at a time. Again, the difference in AIC and 1:1-plots of observed Qe versus that predicted by each model were compared.
All statistical analyses were performed and summarized in R-software and R-Studio with a number of packages as outlined below. Before any analysis was conducted on clear sky days, the data were assessed for normality with a Shapiro-Wilks normality test [52]. These analysis were performed and summarized with R packages dplyr [52], reshape2 [53], tidyr [54] and forcats [55], then illustrated with ggplot2 [56] in RStudio [57]. The Shapiro-Wilks test concluded that all daily data were normaly distributed (p > 0.05), with the exception of the output from the HSM. The sample size from the SRM was too large to compute with a Shapiro-Wilks test (n > 5000), so it was analyzed with a Quantile-Quantile (Q-Q) plot. The Q-Q plot indicated that daily K↓ was non-normal so non-parametric testing was used to analyze the HSM and SRMs. Analysis of temporal variability in Qe was conducted using “stats” [57] and “lattice” [58] for preliminary and correlation analysis and then “nlme” [59] and “mgvc” [60] for model development and selection.
4. Results
4.1. Spatial and Temporal Patterns of Horizon Shade
Horizon shade fluctuated temporally and spatially across the wetland. At the beginning of the study, shade was more pronounced in the south-west (SW) corner and decreased in intensity along a diagonal gradient towards the north-east (NE) corner (Figure 4a). Over the same time, a ridge sheltered the east side of the basin, resulting in increased shade east of the wetland and the tarn (Figure 4a). July presented a similar spatial pattern in shade as June, but with higher shade intensity (Figure 4b). By the end of July, the horizon shadow established an average of 3–4 h of shade per day through much of the wetland (Figure 4b). Shade continued to increase into August, strongly influenced by the headwall at the wetland. By the middle of August, shade no longer increased in a diagonal pattern across the wetland (SW→ NE), but rather straight from the headwall to the stream (S→ N) (Figure 4c). This change in the spatial pattern covered a larger portion of the wetland, resulting in a rapid increase in the hours of shade per day from the beginning to the end of the month.
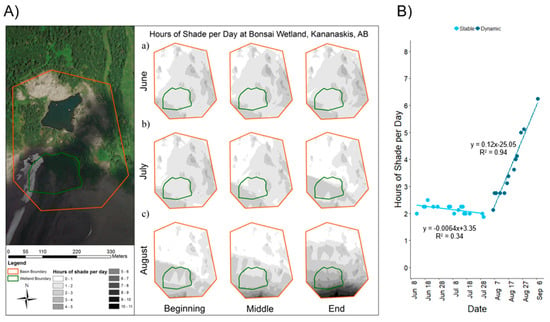
Figure 4.
(A) Horizon shade model results for the beginning, middle and end of each month for (a) June, (b) July and (c) August during the 2018 study period. Inset image illustrates the position and orientation of the study site (enclosed by the wetland boundary) relative to the surrounding topography, with the wetland boundary highlighted with a green line. (B) Stable Shade (7 June to 30 July), illustrated by light blue circles, has a consistent average daily shade value of 2 (y = −0.01x + 3.35, R2 = 0.34) while Dynamic Shade (31 July to 10 September), dark blue circles, increases rapidly over time (y = 0.12x − 25.05, R2 = 0.94).
Overall, the wetland received an average of 2.8 (±1.1) hours of shade per day over the study period (largely in the morning and afternoon hours). During the Stable Shade period, however, which included Snowmelt, Green-up and some of the Peak Growing Season, daily shade was about 2.1 h per day. Afterwards, the site transitioned into the Dynamic Shade period, during which average hours of shade per day increased from 2.1 to 5.0. During Dynamic Shade, which included a large part of the Peak Growing and all of Late Growing Season, shade increased by 0.12 h per day (y = 0.12x − 25.05) (Figure 4B), decreasing sunlight by 0.18 h per day (y = −0.18x + 52.06). The differences in shading experienced by our site during the study period closely affected the energy budget and its components, and contributed to the different “seasonal phases” in the energy budgets we observed.
4.2. Growing Season Surface Energy Budget of a Shaded Subalpine Wetland
Maximum daily net radiation (Q*), sensible heat flux (Qh), latent heat flux (Qe) and ground heat flux (Qg), occurred on 20 June, 14 July, 17 July and 19 June, respectively (Table 1; Figure 5). The temporal difference in energy aligned with changes in maximum downwelling solar radiation (K↓) and shading. During the study period, maximum daily (24-h average) Q* (196 W/m2) occurred one day before the summer solstice when the sun was near its highest position in the sky (Figure 5). Even though the wetland was snow-covered and had a higher albedo in June, the summer solstice provided greater net energy due to longer days with less shading than later in the summer. When the site became entirely snow free in the middle of July, daily Q* was 100 W/m2, which was almost half the amount measured during the seasonal maximum on 20 June (Figure 5). Therefore, vegetation buried under snow throughout June (snow depth of 68 cm on 7 June and 25 cm on 19 June), could not utilize the daily seasonal maximum available energy (i.e., the difference between net and ground heat flux, Q*-Qg) for transpiration. Qg reached its maximum on 19 June, when large contributions of energy were used to thaw exposed ground during the period of peak snowmelt (Figure 5). Qe and Qh each reached their maximums in the middle of July, a typical time for peak vegetative productivity in mountain meadow and tundra ecosystems [61,62,63]. It was also beneficial for plants to have relatively “unobstructed” sunlight during Green-Up and the beginning of the Peak Growing Season.

Table 1.
Average daytime, defined as time when Q* > 10 W/m2, range of incoming solar radiation (K↓) and components of the energy balance during the clear sky days within each phase of the study period (W/m2).
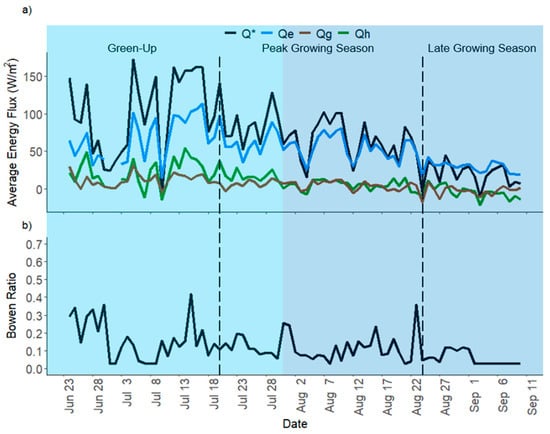
Figure 5.
Gap filled timeseries data for daily average: (a) net radiation (Q*), sensible heat flux (Qh), latent heat flux (Qe) and ground heat flux (Qg) in W/m2 observed or derived from measurements at the site; and (b) Bowen ratio (β). The light blue vertical highlighted area represents the Stable Shade period of our study and darker blue vertical highlighted area the Dynamic Shade period.
Qe represented the largest component of Q* over the entire study period. From 16 July onwards, Qe comprised a larger percentage of Q* because of decreases in Qh and Qg. K↓ followed a similar trend, as Q* through much of the Peak Growing Season, but was higher in Snow Melt than Green-Up, when shade was stable at around 2 h per day. During daytime hours only (i.e., PAR > 10 W/m2) on clear sky days, Q* was highest during the Green-Up period (236 W/m2) and lowest during Late Growing Season (78 W/m2) (Table 1). When the entire site became snow free during Peak Growing Season, vegetation had an average of 31 W/m2 less energy per day to use for evapotranspiration than during Green-Up (Qe, Table 1). During Snow Melt, Qh and Qg utilized a greater proportion of Q*, as snow temperature increased and the soil began to thaw. The Bowen ratio remained relatively constant over the study period, but spiked from 20 June to 30 June with a daily average of 0.34 (Figure 5b). Outside of the seasonal maximum, ß remained constant throughout Green-Up, Peak Growing Season and Late Growing Season, averaging approximately 0.1 per day.
4.3. Influence of Horizon Shade on Wetland’s K↓, Microclimate and Energy Budget
4.3.1. Effect of Horizon Shade on Incoming Solar Radiation
We found that measured and modelled K↓ for clear sky days had good agreement (y = 0.96x + 368.93, R2 = 0.96, n = 16). Modelled K↓ slightly overestimated observed by 11 W/m2 per hour until the middle of July, and by 85 W/m2 per hour from mid-July to early September (Figure 6a). Differences between observed and modeled K↓ can be attributed to the assumption of clear sky conditions, as some clouds and/or fog were likely present on the clear days. Additionally, differences likely arose from the conversions used to calculate downwelling K↓ (i.e., from measured PAR). However, the models showed important trends in intercepted K↓.
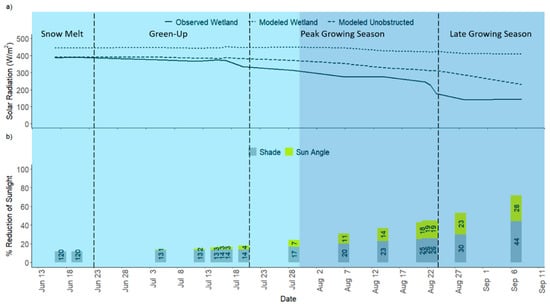
Figure 6.
(a) Observed incoming solar radiation at the wetland (solid line), modelled incoming solar radiation at the wetland (dashed line) and modelled solar radiation atop Fortress Ridge (dotted line); and (b) the relative contribution of horizon shade and seasonality (changes in sun angle over time) to the reduction of incoming shortwave radiation at the study site. The light blue vertical highlighted area represents the Stable Shade period of our study and darker blue vertical highlighted area the Dynamic Shade period.
The shaded wetland site received 59, 97 and 140 W/m2 less radiation per hour than the unobstructed (ridge) location during the Green-Up, Peak Growing Season and Late Growing Season, respectively (Figure 6a). These hourly reductions translated to 1400 W/m2 more K↓ being intercepted by the headwall per day at the end of the study (10 September) compared to the beginning (17 June). On average, there was 951 W/m2 of intercepted K↓ per day during Stable Shade, compared to 1526 W/m2 of intercepted K↓ per day during Dynamic Shade. During the Dynamic Shade period, significant linear correlations were found between hours of shade and K↓ (R2 = 0.50, p < 0.05, y = −32.3x + 312.5) (Figure 8b). For every hour increase in shade, K↓ decreased by 32 W/m2. Shade also had a strong influence on modeled K↓, reducing it by 10% (35 W/m2) per hour during the period of Dynamic Shade (Figure 8b), which encompassed most of the Peak and Late Growing Seasons.
Sunlight hours were reduced at the wetland by two concurrent methods: changes to the sun’s position in the sky over time and horizon shade. To determine the relative contribution of each effect on overall changes in K↓, we first identified clear sky days during the study (i.e., no clouds) to run a SRM at the wetland and ridgetop. The estimated values for the ridgetop represented K↓ only affected by changing sun-angle (over time) with no impact of horizon shade. Estimated K↓ values for the wetland included both effects: sun-angle and horizon shade. Since the study began close to the Northern Hemisphere’s summer solstice (20 June, doy 170), early season results from the ridgetop represented a good approximation for the theoretical maximum amount of sunlight the wetland could receive. This maximum was used as a reference to help understand the percent reduction of sunlight overtime due to changes in sun angle and position in the sky (yellow in Figure 6b). The difference between ridgetop and wetland values (calculated as % difference with respect to the ridge top value) illustrate the influence of horizon shade on K↓ at the wetland (grey in Figure 6b). Since both ridge and wetland estimates of K↓ were affected by the sun’s position in the sky, the difference between those values and any seasonal influence from the sun’s position cancelled out. We found that horizon shade had a strong influence at the site by the end of our study period, decreasing sunlight by greater margins than seasonal changes associated with sun angle (Figure 6b). The overall reductions in K↓ at the site were 72% by the end of the study, when compared to the start of the study, with 28% of that due to sun angle (seasonality) and 44% due to horizon shade (Figure 6b). At the start of the study, horizon shade only contributed 12% to daily reductions in sunlight at the site. These changes in shade reflected congruent changes in the site’s climate conditions and energy budget during the study period, as described in more detail below.
4.3.2. Effect of Horizon Shade on Site’s Climatic Conditions
Monthly air temperatures during the 2018 study period at the Environment and Climate Change Canada (ECCC) (ID 3053600) station fell within 2 standard deviations of the 30-year (1981–2010) climate normal for the station, indicating that this was a normal and representative growing season based on air temperature (Figure 3a). The only exception was the month of May, which was warmer than the 30-year average. During the study period, air temperatures remained within the higher end of the expected range, other than in September when it was cooler than the 30-year average (Figure 3a).
At our study site, measured average daily air temperature during the study period (7 June to 10 September) was 9 °C (±4.1), with a daily maximum of 18.6 °C on 10 August and a daily minimum of 0.8 °C on 11 June (Figure 7a). Tair increased during Green Up, remained relatively constant during Peak Growing season and followed a downward trend in Late Growing Season because of increased shade at our site (Figure 5b). The ground surface remained frozen until 20 June, when the soil (Ts 2 cm depth) quickly thawed over three days, increasing in temperature from −0.3 °C to 7.4 °C (Figure 7a). This thaw period in the soil profile coincided with the onset of patchy snow free conditions near the tower. Since the rate of snowmelt in shaded areas only increased once K↓ intensified and days lengthened [16], the amount of sunlight hours our site received was critical. This study identified that snowmelt occurred around the summer solstice in Northern Hemisphere (20 June), when the sun was at its maximum intensity for the area. During this time the wetland experienced a consistent 2 h of shade per day, indicating that the combined effects of solar maximum and minimal shade promoted snowmelt at the wetland.
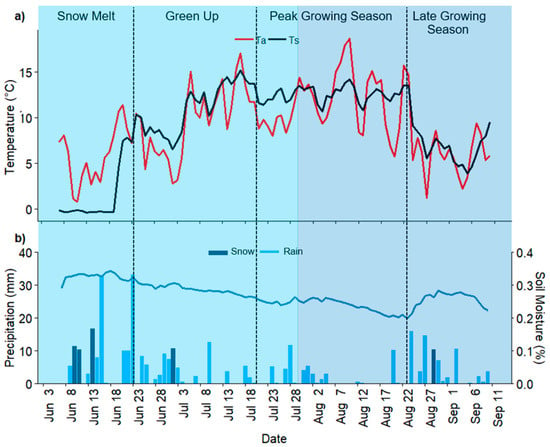
Figure 7.
Climate trends observed over 2018 field season at our wetland site. (a) air temperature (Ta) and surface soil temperature (Ts) at 2 cm; (b) precipitation defined by snow and rain and soil moisture (measured at 10 cm depth in the middle of the wetland at the meteorological tower). The light blue vertical highlighted area represents the Steady shade period of our study and darker blue vertical highlighted area the Dynamic shade period.
Total precipitation for the wetland during the 2018 study period was 339 mm (276 mm rain; 63 mm snow), less than the historical average annual rainfall of Marmot Basin (360 mm), located 14 km north of the research site in the Kananaskis Range (Figure 7b). Overall rainfall from June to September 2018 was 49 mm less than the ECCC 30-year climate normal for that time. When comparing individual months, only July and September received the normal amount of rainfall, while the other months had less than the 30-year normal, thus making 2018 a drier summer.
4.3.3. Effect of Horizon Shade on Site’s Surface Energy Budget and Implications for ET
During the Dynamic Shade period, significant linear correlations were found between hours of shade and Q* (R2 = 0.55, p < 0.05, y = −27.8x + 233.6), hours of shade and Qh (R2 = 0.29, p < 0.05, y = −5.9x + 48.4) and hours of shade and Qe (R2 = 0.63, p < 0.001 y = −17.9x + 149.4) (Figure 8b). For every hour increase in shade, during the Dynamic Shade period, Q*, Qh and Qe decreased by 28, 18 and 6 W/m2, respectively, at an average of 16% compared to the Stable Shade period.
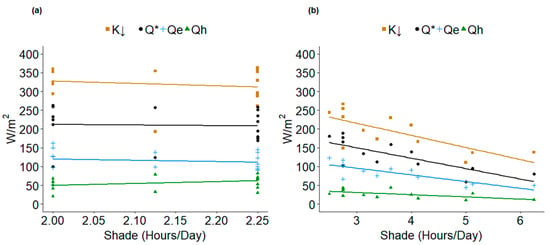
Figure 8.
Relationship between hours of shade and solar radiation (K↓) y = −32.3x + 312.5, net radiation (Q*) y = −27.8x + 233.6, latent heat flux (Qe) y = −5.9x + 48.4 and sensible heat flux (Qh) y = −17.9x + 149.4 on clear sky days during the periods of (a) Stable Shade and (b) Dynamic Shade at Bonsai wetland, Fortress Mountain, Alberta, 2018. Regression equations represent the relationship during the period of Dynamic Shade.
As the growing season progressed from Peak to Late season, shade decreased the amount of incoming radiation, which resulted in decreased Qe and increased soil moisture (Figure 9). This decrease was more pronounced compared to the seasonal increase from Green-Up to Peak Growing Season. The overall result was also a pronounced decrease in ET during the Late Growing Season (Figure 9).
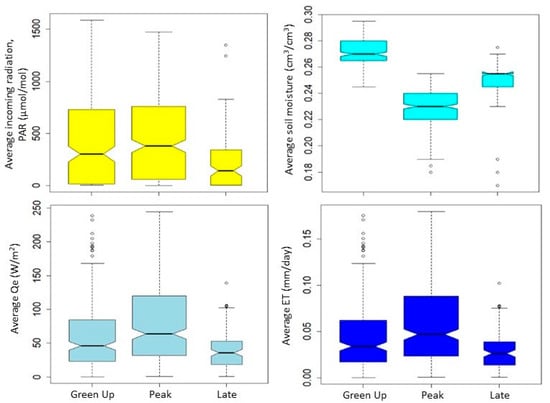
Figure 9.
Boxplots showing the seasonal progression of measured, non-gapfilled: daily averaged incoming PAR, daily averaged latent heat flux (Qe), daily averaged soil moisture at top 10 cm and daily averaged evapotranspiration at Bonsai during the growing season.
We further focused our analysis on Peak Growing season, as it was the only season when both Dynamic and Stable shade were present and vegetation fully developed and active at the site. In the month of August, a 3-h increase in shade resulted in a 48% reduction in energy (Q*, Qe and Qh) during Peak Growing Season, highlighting the rapid decline in energy and a short window for growth. Horizon shade had a clear influence on the energy budget when analyzing diurnal trends on clear sky days during the Peak Growing Season. Days with Stable Shade had an average of 15.8 (±0.2) daylight hours with a maximum Q* of 513 W/m2 at 12:30, while Dynamic Shade days had an average of 14.9 (±0.4) daylight hours and a maximum Q* of 380 W/m2 at 12:30 (Figure 10). During the midday hours of Stable Shade, there were brief decreases in Q* from 13:30 to 15:00 and 17:00 to 18:00; while during Dynamic Shade the periods of midday shading were prolonged and resulted in larger decreases in Q*, lasting from 13:00 to 16:00 (Figure 10). This inherently impacted the energy budget of the wetland, as it was shaded during the hours of the maximum radiative input. During each period, negative radiation after sunrise was caused by horizon shade, where a time lag for positive radiation resulted from when the sun first appeared above the ridge and headwall.
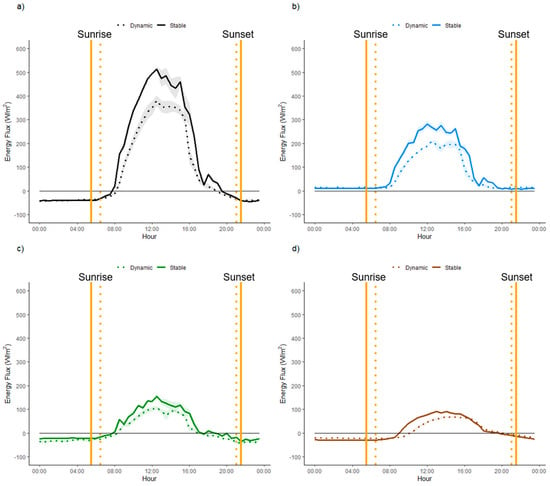
Figure 10.
Diurnal Peak Growing Season energy budget contributions defined by (a) net radiation (Q*), (b) latent heat flux (Qe), (c) sensible heat flux (Qh) and (d) ground heat flux (Qg) for Stable Shade (21 July to 30 July) and Dynamic Shade (31 July to 23 August). 95% confidence intervals are shaded around each diurnal flux, while the average sunrise and sunset for Stable Shade (solid) and Dynamic Shade (dashed) are also listed.
Next, we investigated which measured environmental variables best explained the temporal variability in Qe during the Peak Growing Season. Our attention mainly focused on Qe, as it was equivalent to evapotranspiration through latent heat of vaporization and was the largest component of Q*, making it the energy flux most correlated to hours of shade. The results from preliminary correlations analysis between the different continuous variables we analyzed (Table S1 in Supplementary Materials) showed that most of the variability in Qe was closely related to incoming radiation (PAR), VPD, soil temperature at 2 cm depth and average soil moisture. Some of the variables were highly correlated (Tair and VPD), since VPD is calculated from Tair and RH (Table S1 in Supplementary Materials). We decided to retain VPD as it captured both variables and was more physiologically interesting and meaningful when analyzing Qe. Our model analysis showed that the best-fitted model (i.e., the one with the lowest AIC, highest Δ AIC, see Table S2 in Supplementary Materials) had incoming PAR, VPD, soil moisture (SM) and Shade as the key explanatory variables for the temporal variability in Qe at the wetland. While individually, Qe showed the highest correlation to PAR (see Tables S1 and S2 in Supplementary Materials), the remaining variables also contributed in the order of VPD, SM and Shade. Shade was a categorical variable, while the others were continuous. Overall, this model accounted for 86.5% of the variability in observed values (i.e., R2 = 0.8651 for the predicted vs. observed 1:1 fit). The relationship was also found to be non-linear, requiring the use of a general additive modelling approach for the best-fitted model.
5. Discussion
5.1. Temporal and Spatial Patterns of Shade
The spatial patterns in shade were similar to results found in other studies of solar radiation distribution and variability in mountain terrain with north-south orientation [15,64]. The S and W areas of the wetland had a seasonal average of 3.0 and 2.8 h of shade per day, compared to 2.1 and 2.5 h of shade per day in the N and E. These spatial patterns explained the thick snowpack along the western and southern margins of the wetland and why snow remained there longer into Peak Growing Season, as late as August in 2018. An August snowpack was also reported via satellite imagery at this site in 2012, further supporting the spatial correlation between shade and snow cover (Figure 4).
Similar to [65], our study found that surrounding trees and topography of various heights reduced K↓ during midday hours. However, aspect and/or site orientation (azimuth and inclination angle) also significantly altered the amount of radiation received at the surface [66]. Since our site was located north of a headwall and west of a ridge, it received preferential shading from surrounding topography, delaying local sunrise and advancing local sunset. Therefore, landscapes in mountain ranges with north-south orientation are more influenced by shading than sun declination (i.e., seasonality) during the growing season.
The difference between modeled and actual K↓ in our study was because the HSM only accounted for perfect clear sky conditions, while actual observations were the best available clear days, but may still have had some interference from clouds and fog. The study by [64] found that shade reduced modeled K↓ by an average of 45 W/m2 (18% per day) across the whole watershed, and that higher elevations (1489 m a.s.l.) received 11% less K↓ than lower elevations (707 m a.s.l.). Our study performed a more detailed analysis than [64], as we calculated an average over the entire season, while Oliphant et al. [64] focused on one day during the peak growing season. Oliphant et al. [64] provided a more general analysis for K↓ at a large basin-wide scale, while our study performed a more detailed characterization of shade within a smaller confined subalpine wetland.
5.2. Growing Season Subalpine Wetland Surface Energy Trends
The timing of seasonal maxima in energy fluxes observed at our study site (mid-June) were consistent with those reported for similar sites in literature on mountain energy balance (i.e., June to early July in [61,67,68,69]. This was a product of the sun’s higher altitude and azimuth during this time of year, resulting in increased sunlight hours and less horizon shade in complex terrain. The relative contributions of peak Qe and Qh was driven by differences in moisture conditions and windspeeds, resulting in different Bowen ratios [70,71]. Konzelmann et al. [68] observed altitudinal differences in Qe contributions in the Swiss Alps, where Qe comprised 65% of the energy input at a meadow plateau (2220 m a.s.l.) and 85% at a valley meadow (1680 m a.s.l.). From 1 to 27 August, the corresponding ß in their study was 0.51 and 0.1 at the plateau and valley, respectively [68]. This was similar to our results at Bonsai, where Qe comprised 82% of the energy budget, with an average ß of 0.1 during the same time period. Mountain ecosystems with high Qe and low ß are a result of a low sky view factor, due to the presence of shade, high surface moisture availability and meadow vegetation [68,70,71]. At our site, available energy (Q*-Qg) was highest during Green-Up (Figure 6a). Sensible heat was also highest during Green-Up (Table 1), which contributed enough energy for a slow melt process. However, even though the overall maximum available energy occurred in Green-Up, the percent contribution of Qe to the energy budget remained constant from Snow Melt to the end of the Green-Up (62–66%), likely due to the melting snow and minimal ET contributions from soil and vegetation. The subsequent increase of Qe during the Peak Growing Season (86%) was from vegetation at the site leafing-out (e.g., Abies lasiocarpa; Larix laricina, Salix) and beginning to transpire, visualized by the greening of vegetation in Figure 2c. However, this did not last long as shade increased during the Peak Growing Season, and Qe decreased into the Late Growing season at a faster pace than the increase from Green-Up to Peak Growing Season (Figure 6 and Figure 10). Overall, our results show that shaded mountain areas may be important in maintaining water levels downstream, due to slower snowmelt in spring and early summer and decreased ET in the late growing season.
5.3. Impact of Horizon Shade on Incoming Solar Radiation, Microclimate and the Energy Budget
This study was the first of its kind to quantify the impact of shade on the components of surface energy budget in a shaded, subalpine wetland. We showed that horizon shade had a strong impact on our site’s latent heat flux, which dominated the growing season surface energy budget. Stable Shade in spring reduced the amount of K↓ reaching the site and resulted in longer snowpack duration, while Dynamic Shade in later Peak and Late Growing Seasons reduced overall site Qe and ET. Shaded wetland ecosystems in montane environments can act as stores of water that get slowly released from the alpine to downstream systems over the growing season. However, further studies including snow and vegetation analysis and inventories will be required to identify and quantify the strength of this storage, especially across various sites.
At our wetland, 87% of temporal variability in Qe was explained by a non-linear relationship with incoming radiation (PAR), vapour pressure deficit (VPD), soil moisture and Shade—as a categorical variable. Most of the variability in Qe was explained by the temporal variability of PAR. We found that each hourly increase of shade at our study site reduced K↓ and Q* by 13% and 16%, respectively. Oliphant et al. [64] found complementary results where daily average Q* decreased by 20% in areas with increased surface complexity. Therefore, when shade decreased K↓ throughout the period of Peak Growing Season, diffuse radiation may have maintained ET and stabilized Qe, which supported plant productivity. Radiation-use efficiency (RUE), or the amount of biomass accumulated per unit of intercepted K↓, across a variety of ecosystems has been found to be higher under diffuse radiation than direct radiation, because of the plant’s physiological response to microclimate conditions during cloud cover [21,72]. Therefore, diffuse radiation resulted in greater light penetration into the canopy and more efficient distribution of light between leaves [21,72]. This greater (and more equal) access to light stimulated photochemical reactions within the plant, and resulted in greater stomatal opening [72]. Therefore, ET at the wetland may not decrease significantly alongside shade because of more optimal conditions for photosynthesis provided by diffuse shortwave radiation. However, further studies are required to fully quantify the relationship between shade and ET and the role of diffuse radiation at our site.
6. Conclusions
This study is the first to attempt to quantify the impact of shade on the components of surface energy budget in a shaded, subalpine wetland. We conclude that horizon shade can have a profound negative effect on the local energy budget, helping shaded wetland ecosystems store snowpack water for longer periods of time in spring and reduce water losses by evapotranspiration later in the growing season. With the mounting risk of severe late season drought and spring flooding in western North America under future climate change, shaded mountain wetlands in the Rockies can become increasingly important for downstream flow regulation. We therefore recommend completing additional studies to expand the inventory of mountain wetlands and enhance the knowledge of surface energy budget dynamics within shaded montane ecosystems across various mountain networks. Once such studies become available, we will be able to more accurately quantify the role of shade on the localized surface energy budget of complex terrain and its contribution to late season runoff downstream. Such knowledge will also help us advance the development of hydrological models for complex mountainous terrain.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/atmos12111473/s1, Figure S1: Rose diagrams showing the frequency distribution and cardinal direction of wind speed and latent heat flux by physiological season, Figure S2: Rose diagrams showing the frequency distribution and cardinal direction of wind speed and latent heat flux by shade period, Figure S3: Comparison of Surface Energy Balance Closure for the different seasons and shade periods, Table S1: Correlation matrix between key continuous variables during the Peak Growing Season, Table S2: Evaluation of individual explanatory variable contributions to model fit, Table S3: Linear fits to Surface Energy Balance Closure Scatter Plots in Figure S3.
Author Contributions
Conceptualization, R.M.P. and D.M.H.; methodology, R.M.P., D.M.H. and B.V.H.; software, A.G., B.V.H. and M.K.; validation, D.M.H., A.G., B.V.H. and M.K.; formal analysis, D.M.H.; investigation, R.M.P. and D.M.H.; resources, M.K.; data curation, A.G. and M.K.; writing—original draft preparation, D.M.H.; writing—review and editing, R.M.P., D.M.H., M.K. and B.V.H.; visualization, D.M.H. and M.K.; supervision, R.M.P.; project administration, R.M.P.; and funding acquisition, R.M.P. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Alberta Innovates-Energy and Environment Solutions under Grants 2347 and 2335 20007947; Canada First Research Excellence Fund under Global Water Futures Program; and Canadian Natural Science and Engineering Research Council Discovery Grant Program under Grant RGPN-04182-2017; Canadian Natural Science and Engineering Research Council CREATE Program under Grant 463960-2015.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
In the spirit of reconciliation, we acknowledge that this research was conducted on the traditional territories of the Blackfoot Confederacy (Siksika, Kainai, Piikani), the Tsuut’ina, the Îyâxe Nakoda Nations, the Métis Nation (Region 3) and all people who make their homes in the Treaty 7 region of Southern Alberta (Calgary Foundation, 2019). We would like to thank our funding partners, Global Water Futures, Alberta Innovates and the Canadian Natural Science and Engineering Research Council (NSERC) Discovery and CREATE grants programs for the financial support on research conducted within this project. We would also like to thank the shareholders of Fortress Mountain Resort and their Management team for site access, logistical support and wildlife awareness. Special thanks goes to Chris Chevalier (President), Chris Mueller (Director of Operations), Thomas Heath (Managing Director) and Mel Folden (Maintenance). Thank you to Jessica Williamson, Sheryl Chau and Lindsey Langs for their assistance in data collection during summer 2018. Finally, thank you to Matt Bolding, Calvin Lei and Jordyn Reynolds from the Rooney Lab (University of Waterloo) for conducting the vegetation survey and sharing raw data, John Pomeroy (University of Saskatchewan) for precipitation data and to Derek Robinson and Benjamin Meinen (University of Waterloo) for performing drone flights and providing the ESRI base map.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lininger, H.; Weingartner, R.; Grosejean, M. Mountains of the World: Water Towers for the 21st Century. In Proceedings of the United Nations Commission on Sustainable Development, New York, NY, USA, 20 April–1 May 1998; Paul Haupt Publishers: Bern, Switzerland, 1998; p. 32. [Google Scholar]
- Messerli, B.; Viviroli, D.; Weingartner, R. Mountains of the World: Vulnerable Water Towers for the 21st Century. AMBIO Spec. Rep. 2004, 13, 29–34. [Google Scholar] [CrossRef]
- Ives, J.D.; Messerli, B. Declared by United Nations as ‘‘International Year of the Mountains”. Arct. Antarct. Alp. Res. 1999, 3, 211–213. [Google Scholar] [CrossRef]
- Grusson, Y.; Sun, X.; Gascoin, S.; Sauvage, S.; Raghavan, S.; Anctil, F.; Sáchez-Pérez, J.-M. Assessing the capability of the SWAT model to simulate snow, snow melt and streamflow dynamics over an alpine watershed. J. Hydrol. 2015, 531, 574–588. [Google Scholar] [CrossRef]
- Fang, X.; Pomeroy, J.W.; Ellis, C.R.; MacDonald, M.K.; DeBeer, C.M.; Brown, T. Multi-variable evaluation of hydrological model predictions for a headwater basin in the Canadian Rocky Mountains. Hydrol. Earth Syst. Sci. 2013, 17, 1635–1639. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impactsof a warming climate on water availability in snow-dominated region. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef]
- Hock, R.; Rasul, G.; Adler, C.; Cáceres, B.; Gruber, S.; Hirabayashi, Y.; Jackson, M.; Kääb, A.; Kang, S.; Kutuzov, S.; et al. High Mountain Areas. In IPCC Special Report on the Ocean and Cryosphere in a Changing Climate; IPCC: Geneva, Switzerland, 2019. [Google Scholar]
- Tague, C.; Dugger, A.L. Ecohydrology and climate change in the mountains of the western USA—A review of research and opportunities. Geogr. Compass 2010, 4, 1648–1663. [Google Scholar] [CrossRef]
- Goulden, M.L.; Bales, R.C. Mountain runoff vulnerability to increased evapotranspiration with vegetation expansion. Proc. Natl. Acad. Sci. USA 2014, 111, 14071–14075. [Google Scholar] [CrossRef] [PubMed]
- Oke, T. Boundary Layer Climates, 2nd ed.; Methuen & Co Limited: New York, NY, USA, 1987. [Google Scholar]
- Spokas, K.; Forcella, F. Estimating hourly incoming solar radiation from limited meteorological data. Weed Sci. 2006, 54, 182–189. [Google Scholar] [CrossRef]
- Ebrahimi, S.; Marshall, S.J. Surface energy balance sensitivity to meteorological variability on Haig Glacier, Canadian Rocky Mountains. Cryosphere 2016, 10, 2799–2819. [Google Scholar] [CrossRef]
- Ma, Y.; Pinker, R.T.; Wonsick, M.M.; Li, C. Shortwave Radiative Fluxes on Slopes. J. Appl. Meteorol. Climatol. 2016, 55, 1513–1532. [Google Scholar] [CrossRef]
- Essery, R.; Marks, D. Scaling and parametrization of clear-sky solar radiation over complex topography. J. Geophys. Res. 2007, 112, 1–12. [Google Scholar] [CrossRef]
- Marsh, C.B.; Pomeroy, J.W.; Spiteri, R.J. Implications of mountain shading on calculating energy for snowmelt using unstructured triangular meshes. Hydrol. Process. 2012, 26, 1767–1778. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Pomeroy, J.W.; Revuelto, J.; Vicente-Serrano, S.M. Response of snow processes to climate change: Spatial variability in a small basin in the Spanish Pyrenees: Response of snow processes to climate change. Hydrol. Process. 2013, 27, 2637–2650. [Google Scholar] [CrossRef]
- Ackerly, D.D. The geography of climate change: Implications for conservation biogeography. Divers. Distrib. 2010, 16, 476–487. [Google Scholar] [CrossRef]
- Scherrer, D.; Korner, C. Topographically controlled thermal-habitat differentiation buffers alpine plant diversity against climate warming. J. Biogeogr. 2011, 38, 406–416. [Google Scholar] [CrossRef]
- Graae, B.J.; De Frenne, P.; Kolb, A.; Brunet, J.; Chabrerie, O.; Verheyen, K.; Pepin, N.; Heinken, T.; Zobel, M.; Shevtsova, A.; et al. On the use of weather data in ecological studies along altitudinal and latitudinal gradients. Oikos 2012, 121, 3–19. [Google Scholar] [CrossRef]
- Lenoir, J. Local temperatures inferred from plant communities suggest strong spatial buffering of climate warming across Northern Europe. Glob. Chang. Biol. 2013, 19, 1470–1481. [Google Scholar] [CrossRef]
- Gu, L.; Baldocchi, D.; Vernma, S.B.; Black, T.A.; Vesala, T.; Falge, E.M.; Dowty, P.R. Advantages of diffuse radiation for terrestrial ecosystem productivity. J. Geophys. Res. 2002, 107, ACL 2-1–ACL 2-23. [Google Scholar] [CrossRef]
- Bickford, C.P.; Hunt, J.E.; Heenan, P.B. Microclimate characteristics of alpine bluff ecosystems of New Zealand’s South Island, and implications for plant growth. N. Z. J. Ecol. 2011, 35, 273. [Google Scholar]
- Larcher, W. Physiological Plant Ecology, 4th ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Onipchenko, V.; Blinnikov, M.S.; Aksenova, A.A. Experimentl Evaluation of Shading Effects in Seasonal Dynamics of Four Alpine Communities in Northwestern Caucasus, Russia. Arct. Antarct. Alp. Res. 2001, 33, 330–339. [Google Scholar] [CrossRef]
- Beniston, M. Climatic change in mountain regions: A review of possible impacts. Clim. Chang. 2003, 59, 5–31. [Google Scholar] [CrossRef]
- Beniston, M.; Farinotti, D.; Stoffel, M.; Andreassen, L.M.; Coppola, E.; Eckert, N.; Fantini, A.; Giacona, F.; Hauck, C.; Huss, M.; et al. The European mountain cryosphere: A review of its current state, trends, and future challenges. Cryosphere 2018, 12, 759–794. [Google Scholar] [CrossRef]
- Pepin, N.; Bradley, R.S.; Diaz, H.F.; Baraër, M.; Caceres, E.B.; Forsythe, N.; Fowler, H.; Greenwood, G.; Hashmi, M.Z.; Liu, X.D.; et al. Elevation-dependent warming in mountain regions of the world. Nat. Clim. Chang. 2015, 5, 424. [Google Scholar]
- Colvin, S.A.; Sullivan, S.M.P.; Shirey, P.D.; Colvin, R.W.; Winemiller, K.O.; Hughes, R.M.; Fausch, K.D.; Infante, D.M.; Olden, J.D.; Bestgen, K.R.; et al. Headwater streams and wetlands are critical for sustaining fish, fisheries, and ecosystem services. Fisheries 2019, 44, 73–91. [Google Scholar] [CrossRef]
- Aber, J.; Pavri, F.; Aber, S. High-Latitude and High-Altitude Wetlandc Case Studies; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; pp. 336–357. [Google Scholar]
- Windell, J.T.; Willard, B.E.; Cooper, D.J.; Foster, S.Q.; Knud-Hansen, C.F.; Rink, L.P.; Kiladis, G.N. Wetlands, An Ecological Characterization of Rocky Mountain Montane and Subalpine. U. S. Fish Wildl. Serv. Biol. Rep. 1986, 86, 298. [Google Scholar]
- Alberta Environment and Sustainable Resource Development (ESRD). Alberta Wetland Classification System; Water Policy Branch, Policy and Planning Division: Edmonton, AB, Canada, 2015. [Google Scholar]
- Christensen, C.W. A Geophysical Study of Alpine Groundwater Processes and Their Geologic Controls in the Southeastern Canadian Rocky Mountains. Masters’s Thesis, University of Calgary, Calgary, AB, Canada, 2017. [Google Scholar]
- DeBeer, C.M.; Pomeroy, J.W. Modelling snow melt and snowcover depletion in a small alpine cirque, Canadian Rocky Mountains. Hydrol. Process. 2009, 23, 2584–2599. [Google Scholar] [CrossRef]
- Storr, D. Precipitation variations in a small forested watershed. In Proceedings of the Snow Conference Proceedings 35th Annual Meetings, Boise, ID, USA, 18–20 April 1967; pp. 11–17. [Google Scholar]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of flux measurements for density effects due to heat and water vapour transfer. R. Meteorol. Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Aubinet, M.; Vesala, T.; Papale, D. Eddy Covariance: A Practical Guide to Measurement and Data Analysis; Springer & Business Media: Dordrechet, The Netherlands, 2012. [Google Scholar]
- Kaimal, J.C.; Finnigan, J.J. Atmospheric Boundary Layer Flows: Their Structure and Management; Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Burba, G.; Schmidt, A.; Scott, R.L.; Nakai, T.; Kathilankal, J.; Fratini, G.; Hanson, C.; Law, B.; McDermitt, D.K.; Eckles, R.; et al. Calculating CO2 and H2O eddy covariance fluxes from an enclosed gas analyzer using an instantaneous mixing ratio. Glob. Chang. Biol. 2012, 18, 385–399. [Google Scholar] [CrossRef]
- Brown, S.M.; Petrone, R.M.; Chasmer, L.; Mendoza, C.; Lazerjan, M.S.; Landhausser, S.M.; Silins, U.; Leach, J.; Devito, K.J. The influence of rooting zone soil moisture on evapotranspiration from above and within a western boreal plain aspen forest. Hydrol. Process. 2013, 28, 4449–4462. [Google Scholar] [CrossRef]
- Foken, T.; Leclerc, M.Y. Methods and limitations in validation of footprint models. Agric. For. Meteorol. 2004, 127, 223–234. [Google Scholar] [CrossRef]
- Petrone, R.; Chasmer, L.; Hopkinson, C.; Silins, U.; Landhausser, S.; Kljun, N.; Devito, K. Effects of harvesting and drought on CO2 and H2O fluxes in an aspen-dominated western boreal plain forest:early chronosequence recovery. Can. J. For. Res. 2015, 45, 87–100. [Google Scholar] [CrossRef]
- Kljun, N.; Calanca, P.; Rotach, M.W.; Schmid, H.P. A simple two-dimensional parameterisation for Flux Footprint Prediction (FFP). Geosci. Model Dev. 2015, 8, 3695–3713. [Google Scholar] [CrossRef]
- Priestley, C.H.; Taylor, R.J. On the Assessment of Surface Heat Flux and Evaporation Using Large-Scale Parameters. Mon. Weather. Rev. 1972, 100, 81–92. [Google Scholar] [CrossRef]
- Petrone, R.M.; Waddington, J.M.; Price, J.S. Ecosystem scale evapotranspiration and net CO2 exchange from a restored peatland. Hydrol. Process. 2001, 15, 2839–2845. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the separation of net ecosystem exchange into assimilation and ecosystem respiration: Review and improved algorithm. Glob. Chang. Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Hoffmann, T. Retrieved from SunCalc. 2018. Available online: https://www.suncalc.org/ (accessed on 15 April 2019).
- Mahmood, R.; Schargorodski, M.; Rappin, E.; Griffin, M.; Collins, P.; Knupp, K.; Quilligan, A.; Wade, R.; Cary, K. The Total Solar Eclipse of 2017: Meteorological Observations from a Statewide Mesonet and Atmospheric Profiling System. Bull. Am. Meteorol. Soc. 2020, 1, E720–E737. [Google Scholar] [CrossRef]
- Fu, P.; Rich, M.P.A. geometric solar radiation model with applications in agriculture and forestry. Comput. Electron. Agric. 2002, 37, 25–35. [Google Scholar] [CrossRef]
- McFarlane, J.C.; Sager, J.C. No. 340: Chapter 1—Radiation. In Plant Growth Chamber Handbook; Langhans, R.W., Tibbitts, T.W., Eds.; North Central Region Research Publication: Ames, IA, USA, 1998. [Google Scholar]
- Thimijan, R.W.; Heins, R.D. Photometric, radiometric and quantum light units of measure: A review of procedures for interconversion. Hortic. Sci. 1983, 18, 818–822. [Google Scholar]
- Zuur, A.F.; Ieno, E.N.; Walker, N.J.; Saveliev, A.A.; Smith, G.M. Introduction. In Mixed effects Models and Extensions in Ecology with R. Statistics for Biology and Health; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Wickham, H.; Francois, R.; Henry, L.; Muller, K. dplyr: A Grammar of Data Manipulation. 2018. Available online: https://CRAN.R-project.org/package=dplyr (accessed on 9 October 2019).
- Wickham, H. Reshaping Data with the reshape Package. J. Stat. Softw. 2007, 21, 1–20. Available online: http://www.jstatsoft.org/v21/i12/ (accessed on 9 October 2019). [CrossRef]
- Wickham, H.; Henry, L. tidyr: Easily Tidy Data with ‘spread()’. 2019. Available online: https://CRAN.R-project.org/package=tidyr (accessed on 9 October 2019).
- Wickham, H. forcats: Tools for Working with Categorical Variables (Factors). 2019. Available online: https://CRAN.R-project.org/package=forcats (accessed on 9 October 2019).
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis 2016; Springer: New York, NY, USA, 2016. [Google Scholar]
- RStudio Team. RStudio: Integrated Development Environment for R; RStudio, Inc.: Bonston, MA, USA, 2016; Available online: http://www.rstudio.com/ (accessed on 9 October 2019).
- Sarkar, D.; Le Meur, N.; Gentleman, R. Using flowViz to visualize flow cytometry data. Bioinformatics 2008, 24, 878–879. [Google Scholar] [CrossRef]
- Pinheiro, J.; Bates, D.; DebRoy, S.; Sarkar, D.; R Core Team. nlme: Linear and Nonlinear Mixed Effects Models. R Package Version 3.1-153. 2021. Available online: https://CRAN.R-project.org/package=nlme (accessed on 7 September 2021).
- Wood, S.N. Generalized Additive Models: An Introduction with R, 2nd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar] [CrossRef]
- Knowles, J.F.; Blanken, P.D.; Williams, M.W.; Chowanski, K.M. Energy and surface moisture seasonally limit evaporation and sublimation from snow-free alpine tundra. Agric. For. Meteorol. 2012, 157, 106–115. [Google Scholar] [CrossRef]
- Cao, S.; Cao, G.; Feng, Q.; Han, G.; Lin, Y.; Yuan, J.; Cheng, S. Alpine wetland ecosystem carbon sink and its controls at the Qinghai Lake. Environ. Each Sci. 2017, 76, 1–15. [Google Scholar] [CrossRef]
- Millar, D.J.; Cooper, D.J.; Dwire, K.A.; Hubbard, R.M.; von Fischer, J. Mountain Peatlands Range from CO2 Sinks at High Elevations to Sources at Low Elevations: Implications for a Change Climate. Ecosystems 2017, 20, 416–432. [Google Scholar] [CrossRef]
- Oliphant, A.J.; Spronken-Smith, R.A.; Sturman, A.P.; Owens, I.F. Spatial Variability of Surface Radiation Fluxes in Mountainous Terrain. J. Appl. Meteorol. 2003, 42, 113–128. [Google Scholar] [CrossRef]
- Howard, R.; Stull, R. Forecasting Sun versus Shade in Complex Terrain for the 2010 Winter Olympic and Paralympic Games. Bull. Am. Meteorol. Soc. 2011, 92, 1303–1309. [Google Scholar] [CrossRef][Green Version]
- Matzinger, N.; Andretta, M.; Gorsel, E.V.; Vogt, R.; Ohmura, A.; Rotach, M.W. Surface radiation budget in an Alpine valley. Q. J. R. Meteorol. Soc. 2003, 129, 877–895. [Google Scholar] [CrossRef]
- LeDrew, E.F. The energy balance of a mid-latitude alpine site during the growing season. Arct. Alp. Res. 1975, 7, 301–314. [Google Scholar] [CrossRef]
- Konzelmann, T.; Calanca, P.; Muller, G.; Menzel, L.; Lang, H. Energy Balance and Evapotranspiration in a High Mountain Area during Summer. J. Appl. Meteorol. 1997, 36, 966–973. [Google Scholar] [CrossRef]
- Flerchinger, G.N.; Marks, D.; Reba, M.L.; Yu, Q.; Seyfried, M.S. Surface fluxes and water balance of spatially varying vegetation within a small mountainous headwater catchment. Hydrol. Earth Syst. Sci. 2010, 14, 965–978. [Google Scholar] [CrossRef]
- Bowers, J.D.; Bailey, W.G. Summer Energy Balance Regimes for Alpine Tundra, Plateau Mountain, Alberta, Canada. Arct. Alp. Res. 1989, 21, 135–143. [Google Scholar] [CrossRef]
- Blanken, P.D. The effect of winter drought on evaporation from a high-elevation wetland. J. Geophys. Res. Biogeosci. 2014, 119, 1354–1369. [Google Scholar] [CrossRef]
- Urban, O.; Janouš, D.; Acosta, M.; Czerný, R.; Markova, I.; Navratil, M.; Pavelka, M.; Pokorný, R.; Šprtová, M.; Zhang, R.; et al. Ecophysiological controls over the net ecosystem exchange of mountain spruce stand. Comparison of the response in direct vs. diffuse solar radiation. Glob. Chang. Biol. 2007, 13, 157–168. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).