Generating Flood Hazard Maps Based on an Innovative Spatial Interpolation Methodology for Precipitation
Abstract
:1. Introduction
2. Materials and Methods
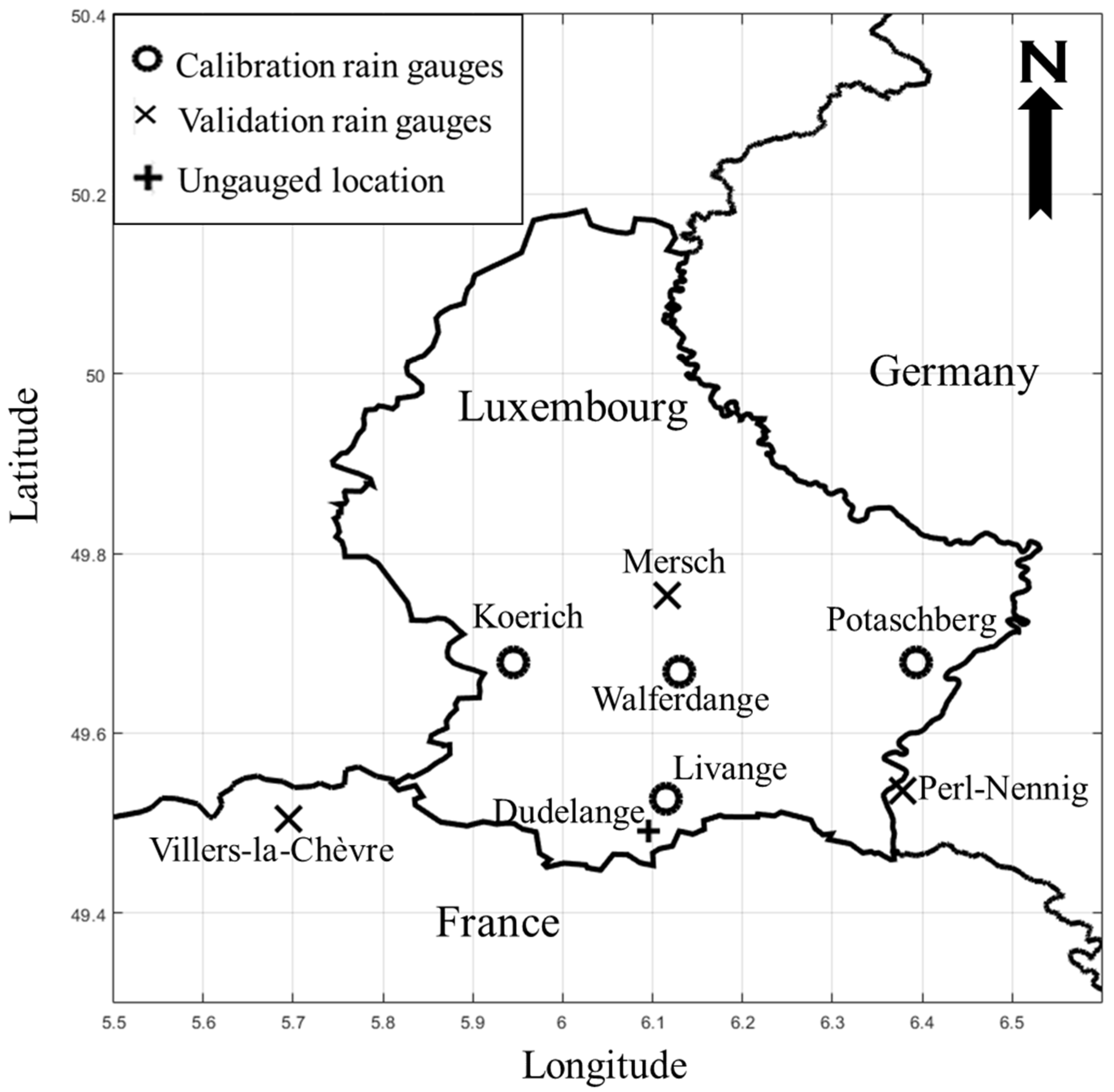
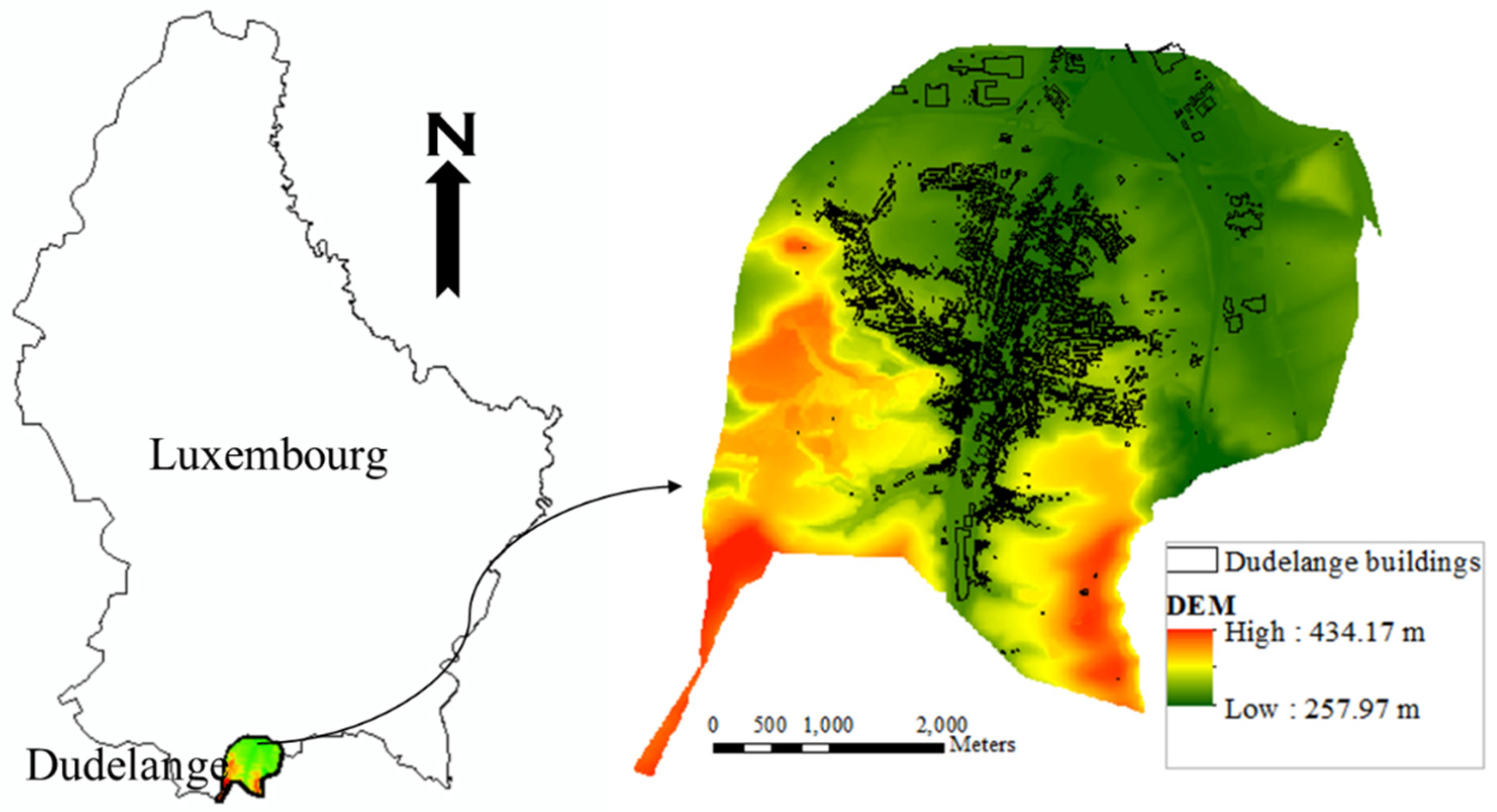
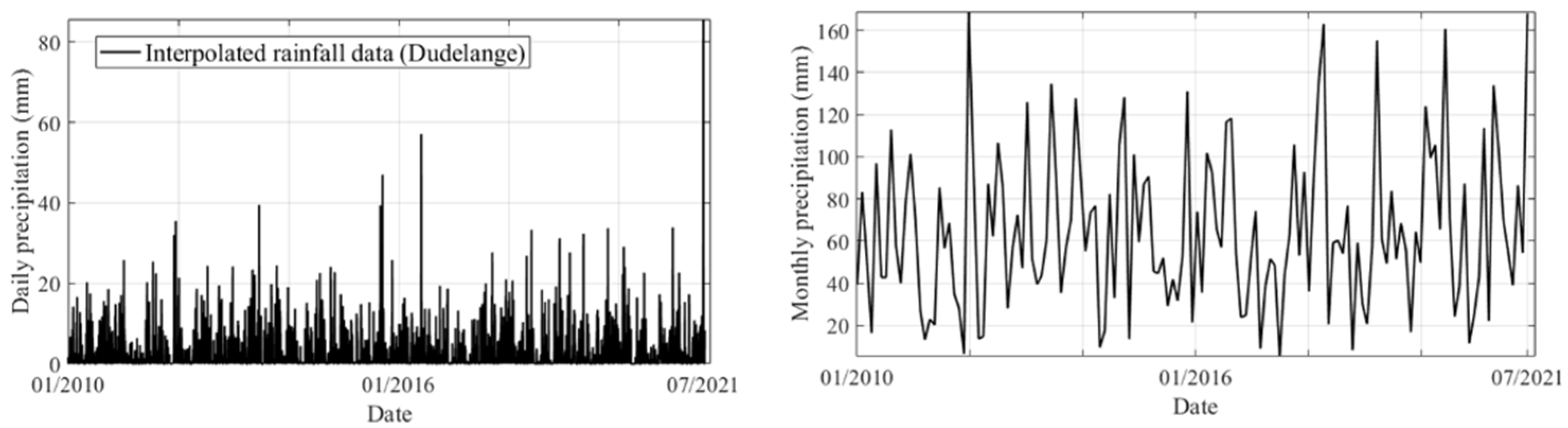
2.1. Study Area and Data
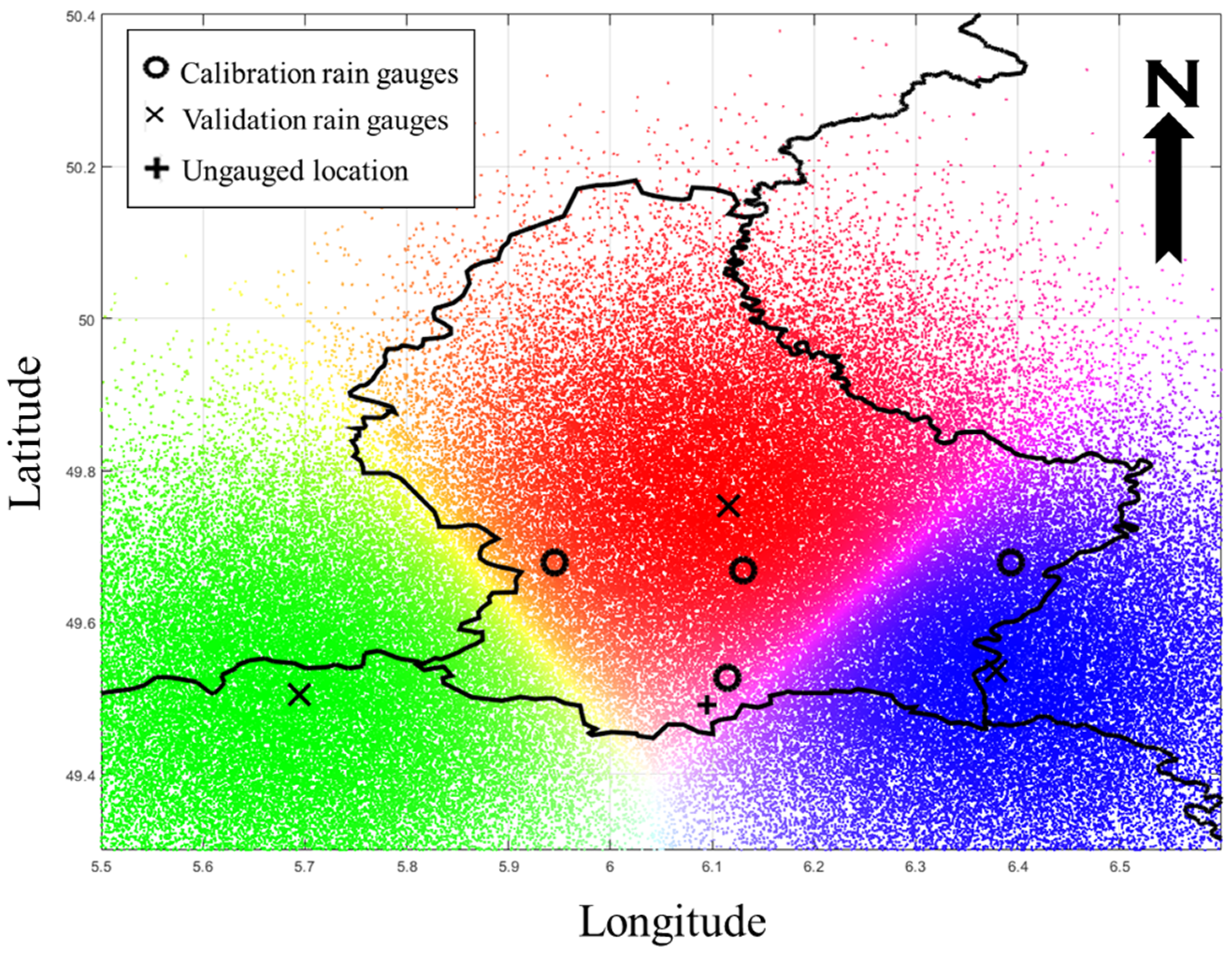
2.2. Estimation of Rainfall Data Using the i-FCM Clustering Method
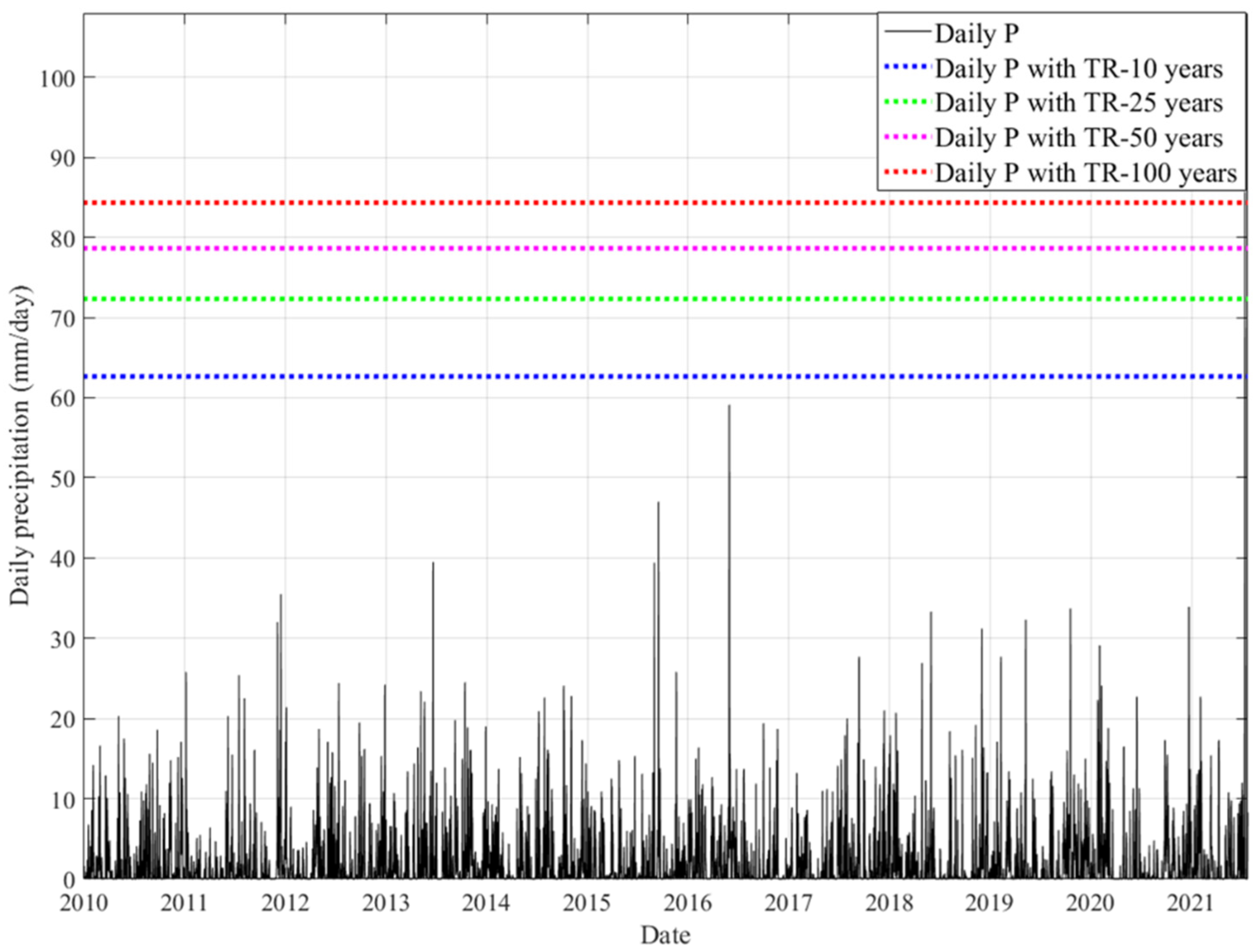
2.3. Return Period (Tr) Estimation for Maximum Daily Rainfall
2.4. Flood Hazard Maps Using LISFLOOD FP Model
3. Results and Discussion
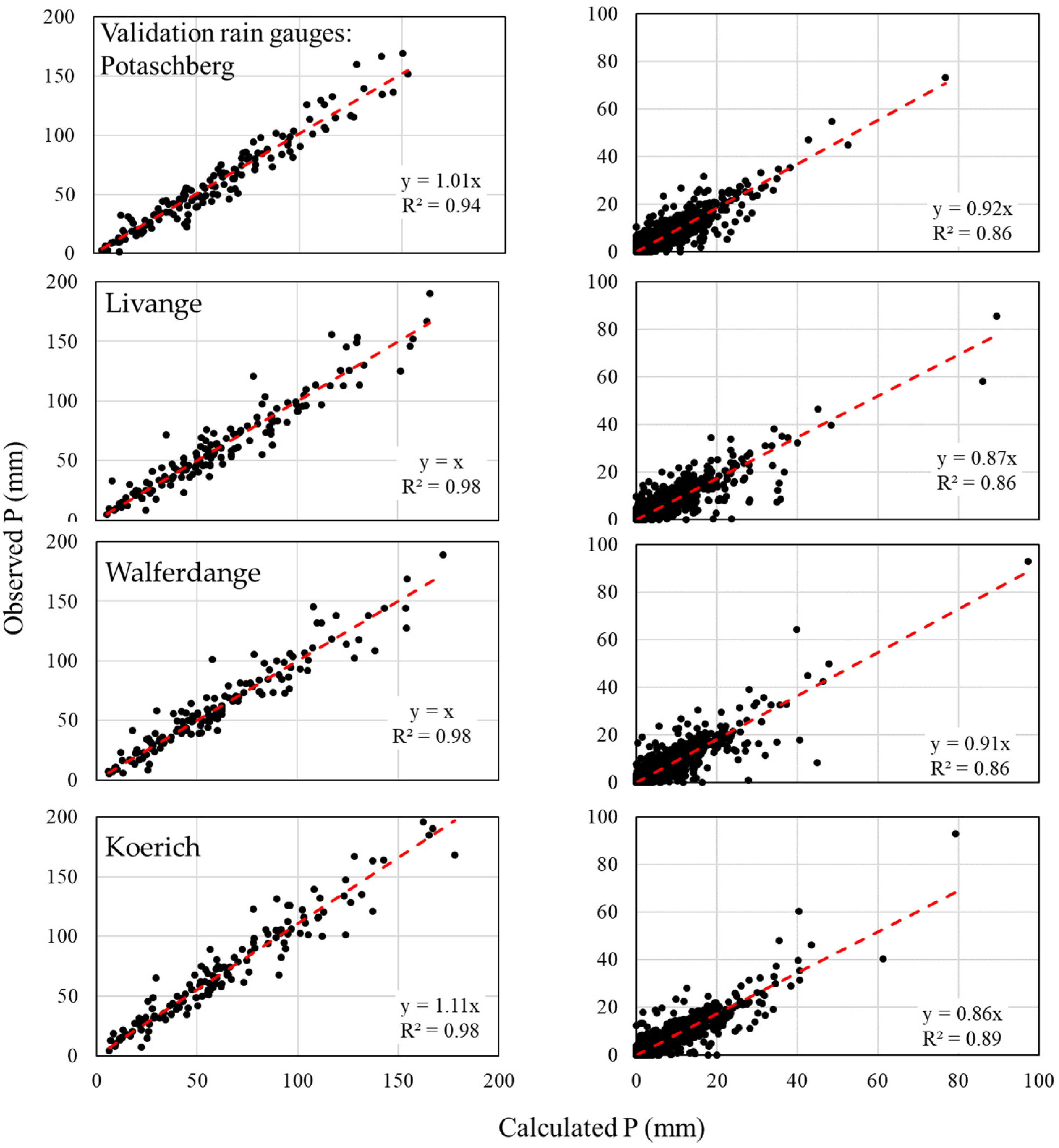
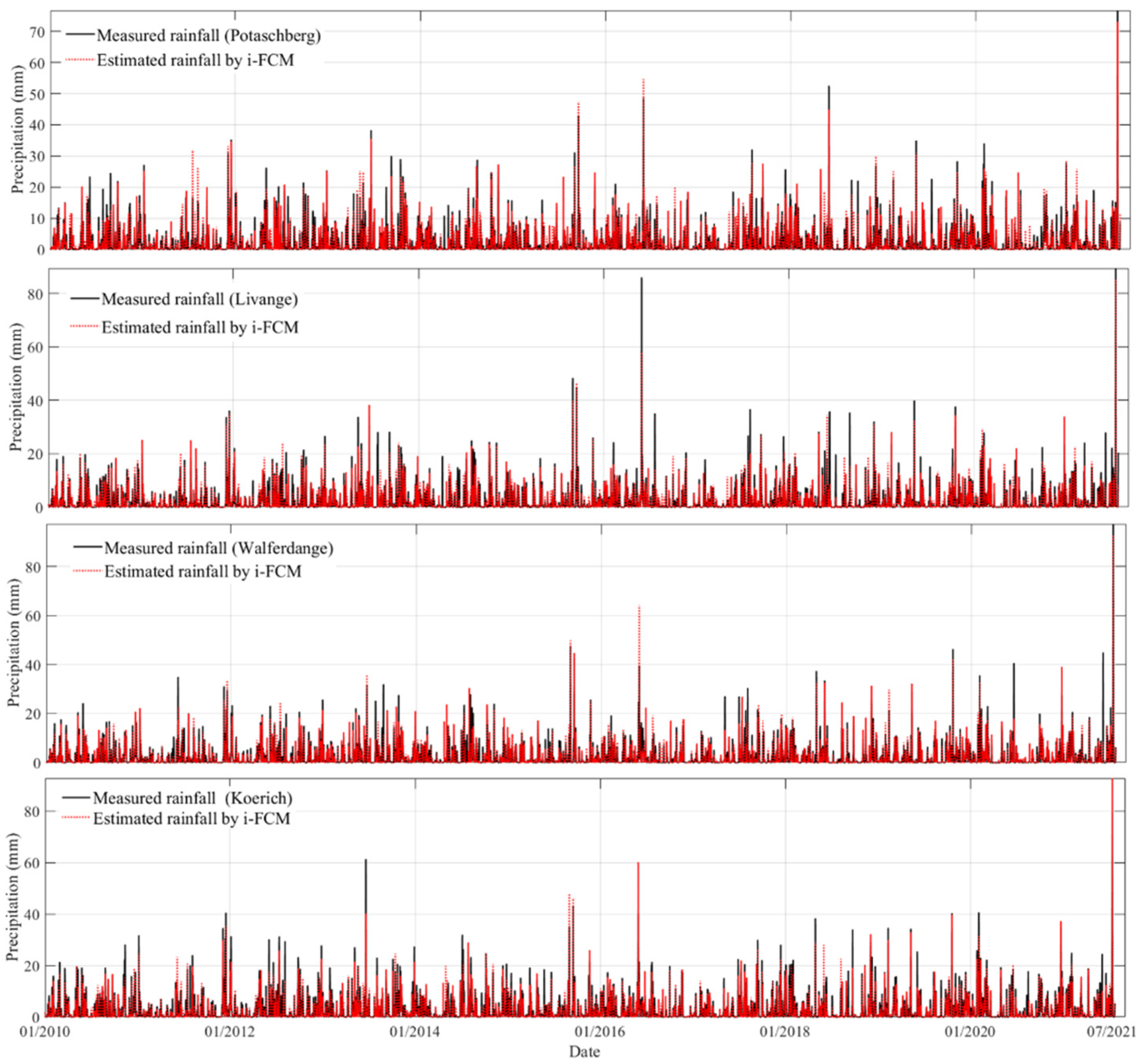
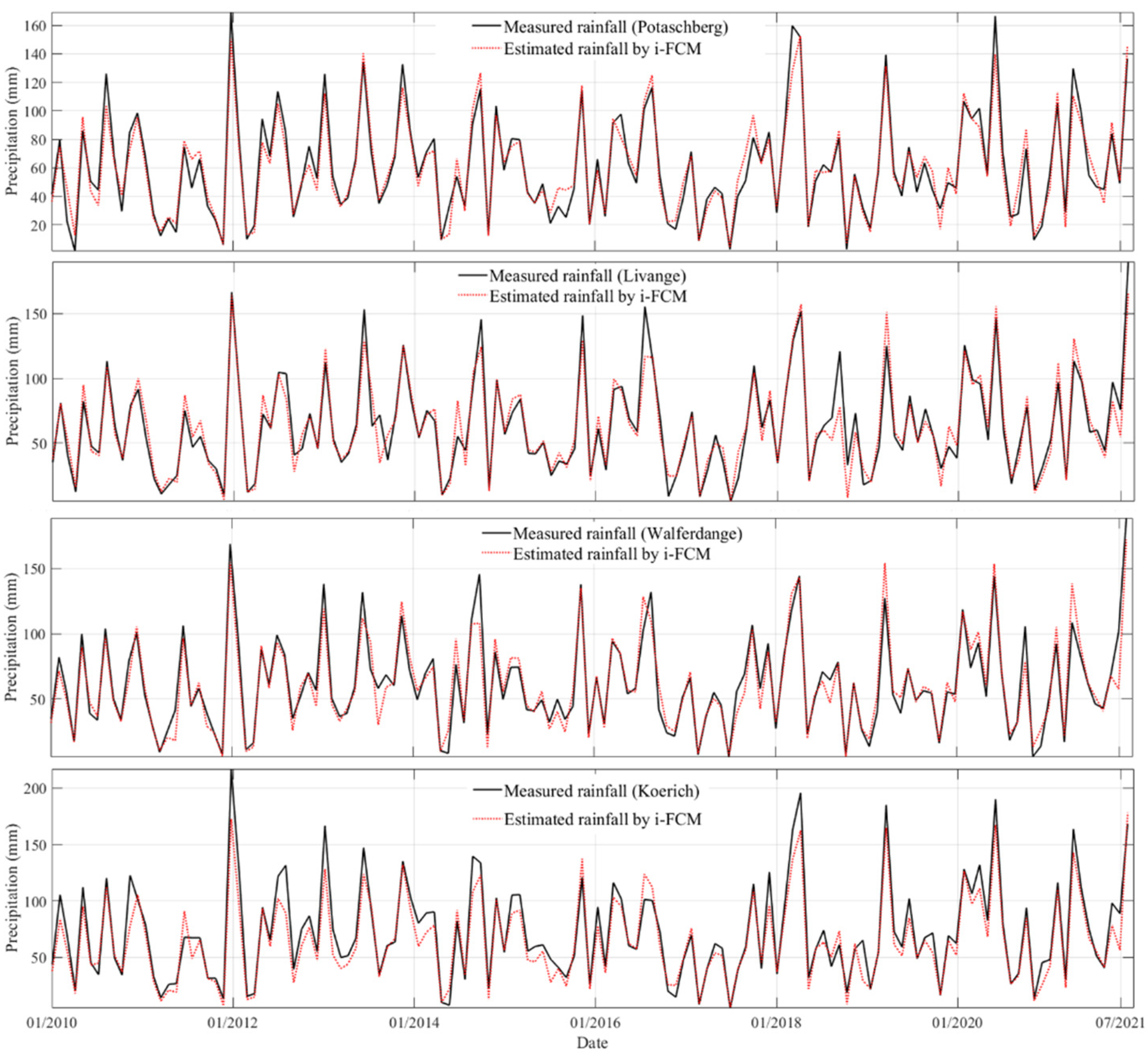
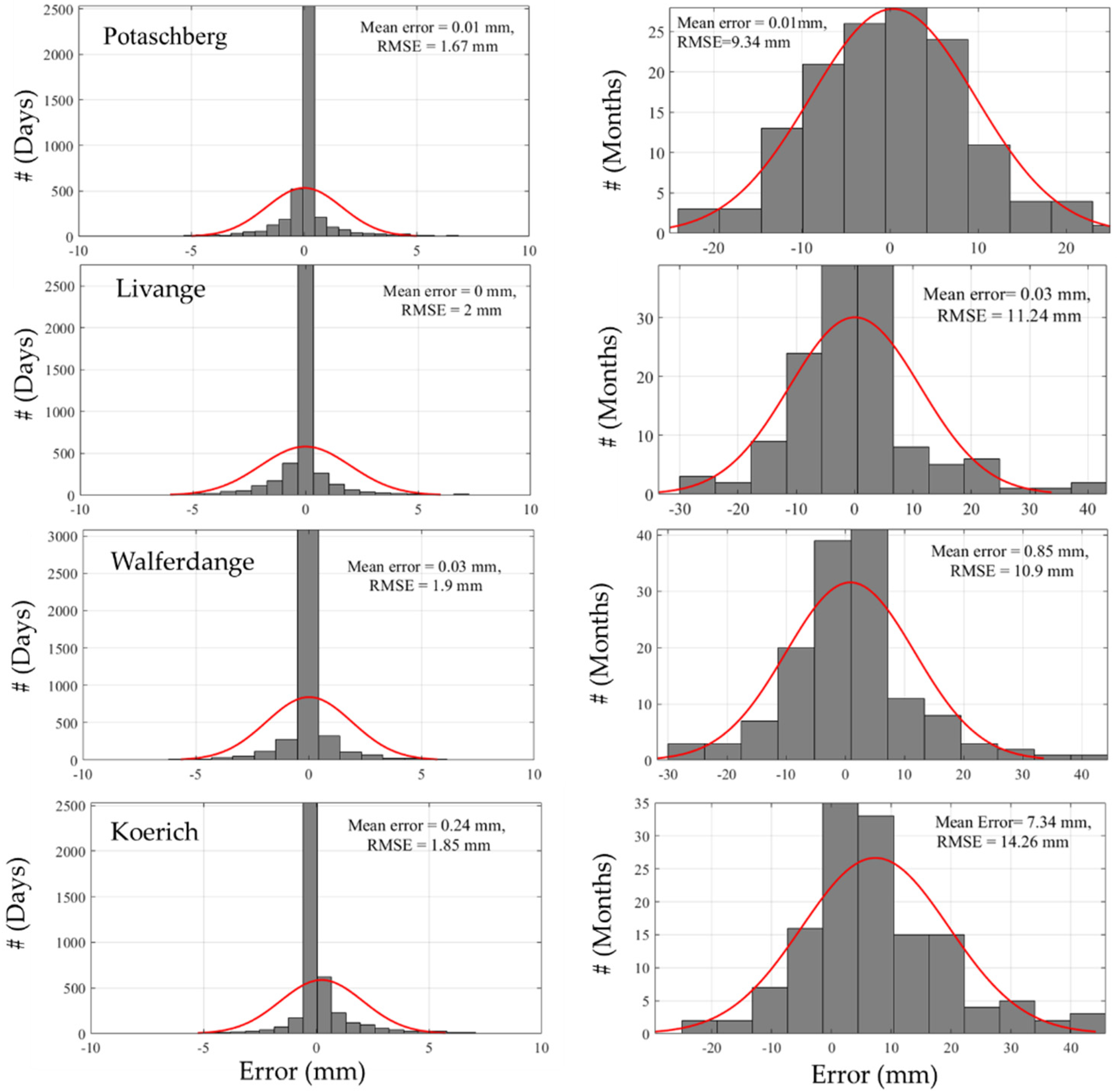
3.1. i-FCM Spatial Interpolation for Precipitation
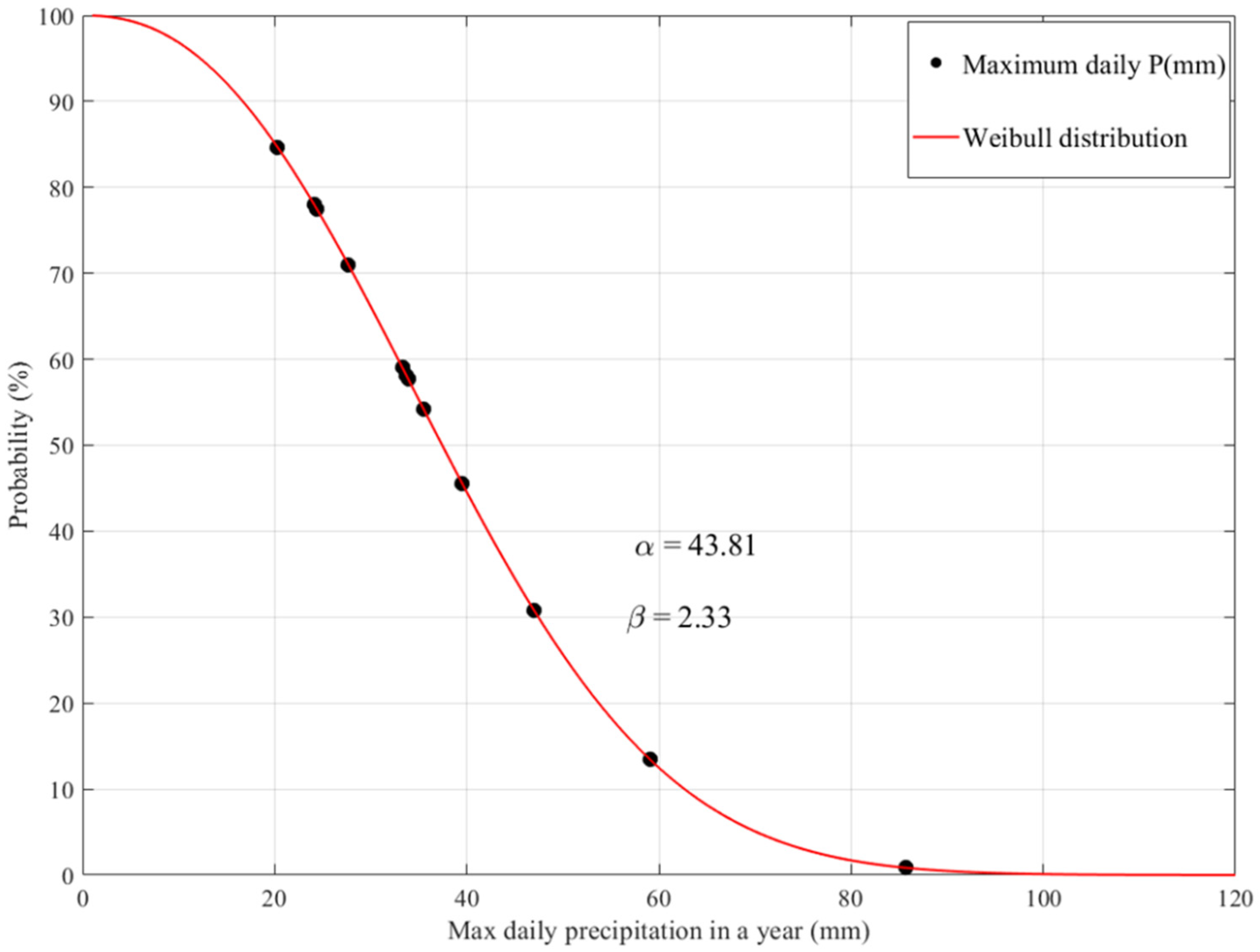
3.2. Estimation of Maximum Daily Rainfall Return Periods Using Two-Parameter Weibull Distribution
3.3. Generating Flood Hazards Maps Using LISFLOOD FP Model
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- IPCC. Summary for policymakers. In Climate Change 2007: The Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Zare, M.; Koch, M. An Analysis of MLR and NLP for Use in River Flood Routing and Comparison with the Muskingum Method. In Proceedings of the 11th International Conference on Hydroscience & Engineering (ICHE), Hamburg, Germany, 29 September–2 October 2014; pp. 505–513. [Google Scholar]
- Courty, L.G.; Rico-Ramirez, M.Á.; Pedrozo-Acuña, A. The Significance of the Spatial Variability of Rainfall on the Numerical Simulation of Urban Floods. Water 2008, 10, 207. [Google Scholar] [CrossRef] [Green Version]
- Crochet, P.; Jóhannesson, T.; Jónsson, T.; Sigurðsson, O.; Björnsson, H.; Pálsson, F.; Barstad, I. Estimating the Spatial Distribution of Precipitation in Iceland Using a Linear Model of Orographic Precipitation. J. Hydrometeorol. 2007, 8, 1285–1306. [Google Scholar] [CrossRef]
- Hu, Q.; Li, Z.; Wang, L.; Huang, Y.; Wang, Y.; Li, L. Rainfall Spatial Estimations: A Review from Spatial Interpolation to Multi-Source Data Merging. Water 2019, 11, 579. [Google Scholar] [CrossRef] [Green Version]
- Drogue, G.; Ben Khediri, W. Catchment model regionalization approach based on spatial proximity: Does a neighbor catchment-based rainfall input strengthen the method? J. Hydrol. Reg. Stud. 2016, 8, 26–42. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A.; Aliev, R.A. Fuzzy Logic Theory and Applications, Part I and Part II; World Scientific Publishing Co.: Singapore, 2018. [Google Scholar]
- Çakıt, E.; Karwowski, W. Fuzzy Inference Modeling with the Help of Fuzzy Clustering for Predicting the Occurrence of Adverse Events in an Active Theater of War. Appl. Artif. Intell. 2015, 29, 945–961. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Jafari, M.M.; Ojaghlou, H.; Zare, M.; Schumann, G.J. Application of a Novel Hybrid Wavelet-ANFIS/Fuzzy C-Means Clustering Model to Predict Groundwater Fluctuations. Atmosphere 2021, 12, 9. [Google Scholar] [CrossRef]
- Ayvaz, M.T.; Karahan, H.; Aral, M.M. Aquifer parameter and zone structure estimation using kernel-based fuzzy c-means clustering and genetic algorithm. J. Hydrol. 2007, 343, 240–253. [Google Scholar] [CrossRef]
- Zare, M.; Koch, M. Groundwater level fluctuations simulation and prediction by ANFIS- and hybrid Wavelet-ANFIS/Fuzzy C-Means (FCM) clustering models: Application to the Miandarband plain. J. Hydro-Environ. Res. 2018, 18, 63–76. [Google Scholar] [CrossRef]
- Pal, N.R.; Bezdek, J.C. On cluster validity for the fuzzy c-means model. IEEE Trans. Fuzzy Syst. 1995, 3, 370–379. [Google Scholar] [CrossRef]
- Hirsch, R.M. Probability plotting position formulas for flood records with historical information. J. Hydrol. 1987, 96, 185–199. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; McGraw-Hill: New York, NY, USA, 1988. [Google Scholar]
- Cunnane, C. Unbiased plotting positions—A review. J. Hydrol. 1978, 37, 205–222. [Google Scholar] [CrossRef]
- Zare, M.; Koch, M. Hybrid signal processing/machine learning and PSO optimization model for conjunctive management of surface–groundwater resources. Neural Comput. Appl. 2021, 33, 13. [Google Scholar] [CrossRef]
- Pook, L.P. Approximation of Two Parameter Weibull Distribution by Rayleigh Distributions for Fatigue Testing; National Engineering Laboratory Report 694; East Kilbride: Glasgow, UK, 1984. [Google Scholar]
- Neal, J.; Schumann, G.; Bates, P. A subgrid channel model for simulating river hydraulics and floodplain inundation over large and data sparse areas. Water Resour. Res. 2012, 48, W11506. [Google Scholar] [CrossRef]
- Hawker, L.; Neal, J.; Tellman, B.; Liang, J.; Schumann, G.; Doyle, C.; Sullivan, J.A.; Savage, J.; Tshimanga, R. Comparing earth observation and inundation models to map flood hazards. Environ. Res. Lett. 2020, 15, 12. [Google Scholar] [CrossRef]
- Bates, P.; Trigg, M.; Neal, J.; Dabrowa, A. LISFLOOD-FP User Manual, Code Release 5.9.6; University of Bristol: Bristol, UK, 2013. [Google Scholar]
- Ramsbottom, D.; Floyd, P.; Penning-Rowsell, E. Flood Risks to People Phase 1, R&D Technical Report FD2317; DEFRA: London, UK, 2003.
- Beck, J.V.; Arnold, K.J. Parameter Estimation in Engineering and Science; John Wiley & Sons: Hoboken, NJ, USA, 1977; p. 522. [Google Scholar]


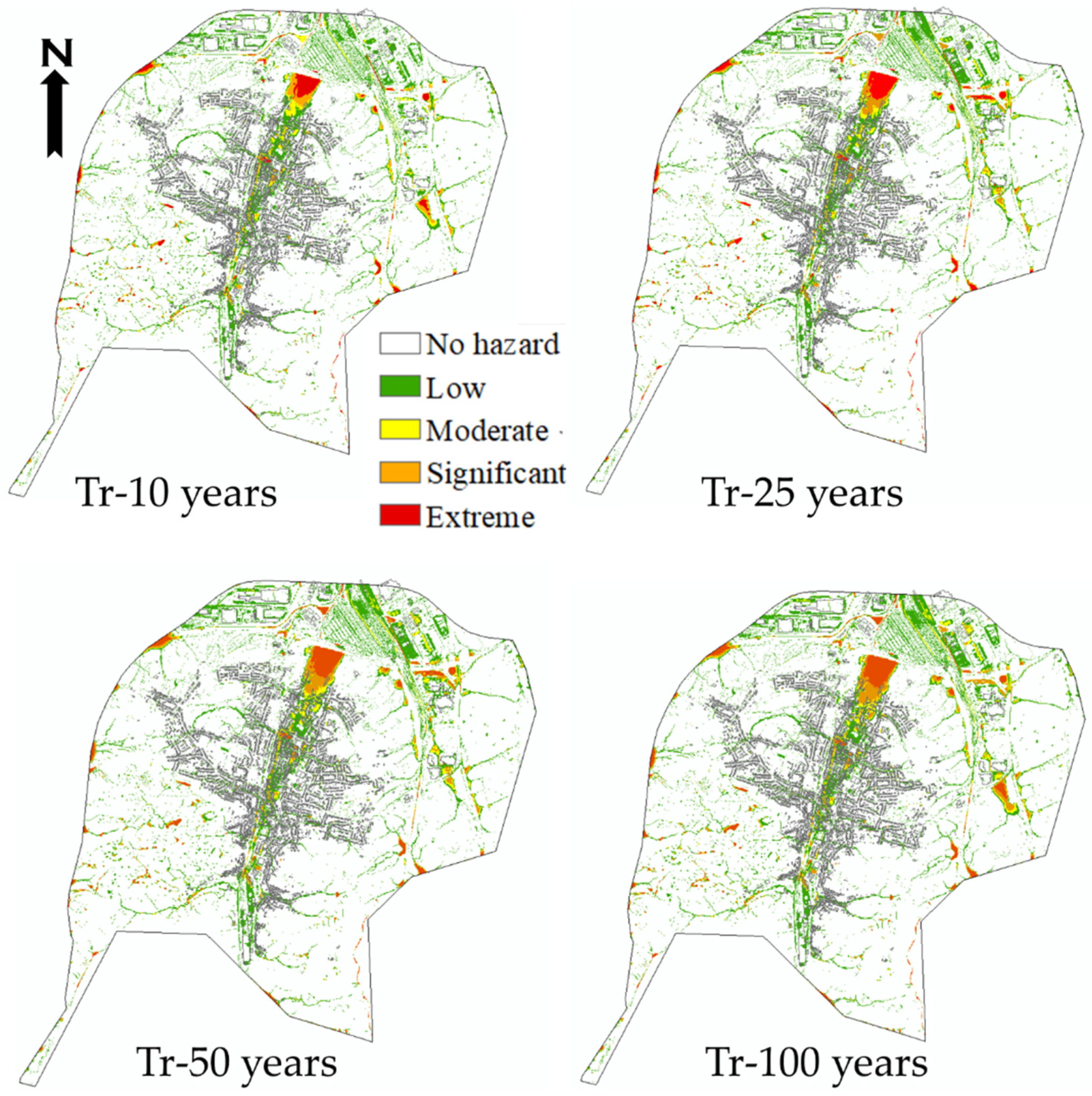
| Flood Hazard Rating | Degree of Flood Hazard | Description |
|---|---|---|
| 0 | No hazard | - |
| <0.75 | Low | Caution; Very low danger |
| 0.75–1.25 | Moderate | Danger for some |
| 1.25–2.5 | Significant | Danger for most |
| >2.5 | Extreme | Danger for all |
| Hazard Rating | Tr-10 | Tr-25 | Tr-50 | Tr-100 |
|---|---|---|---|---|
| 0.75–1.25 | 30.20 | 32.91 | 35.54 | 33.16 |
| 1.25–2.5 | 23.99 | 29.80 | 29.27 | 34.17 |
| >2.5 | 19.44 | 24.42 | 27.90 | 30.36 |
| Sum (ha) | 73.63 | 87.13 | 92.71 | 97.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zare, M.; Schumann, G.J.-P.; Teferle, F.N.; Mansorian, R. Generating Flood Hazard Maps Based on an Innovative Spatial Interpolation Methodology for Precipitation. Atmosphere 2021, 12, 1336. https://doi.org/10.3390/atmos12101336
Zare M, Schumann GJ-P, Teferle FN, Mansorian R. Generating Flood Hazard Maps Based on an Innovative Spatial Interpolation Methodology for Precipitation. Atmosphere. 2021; 12(10):1336. https://doi.org/10.3390/atmos12101336
Chicago/Turabian StyleZare, Mohammad, Guy J.-P. Schumann, Felix Norman Teferle, and Ruja Mansorian. 2021. "Generating Flood Hazard Maps Based on an Innovative Spatial Interpolation Methodology for Precipitation" Atmosphere 12, no. 10: 1336. https://doi.org/10.3390/atmos12101336
APA StyleZare, M., Schumann, G. J.-P., Teferle, F. N., & Mansorian, R. (2021). Generating Flood Hazard Maps Based on an Innovative Spatial Interpolation Methodology for Precipitation. Atmosphere, 12(10), 1336. https://doi.org/10.3390/atmos12101336







