Effects of Linewidth Broadening Method on Recoil of Sodium Laser Guide Star
Abstract
:1. Introduction
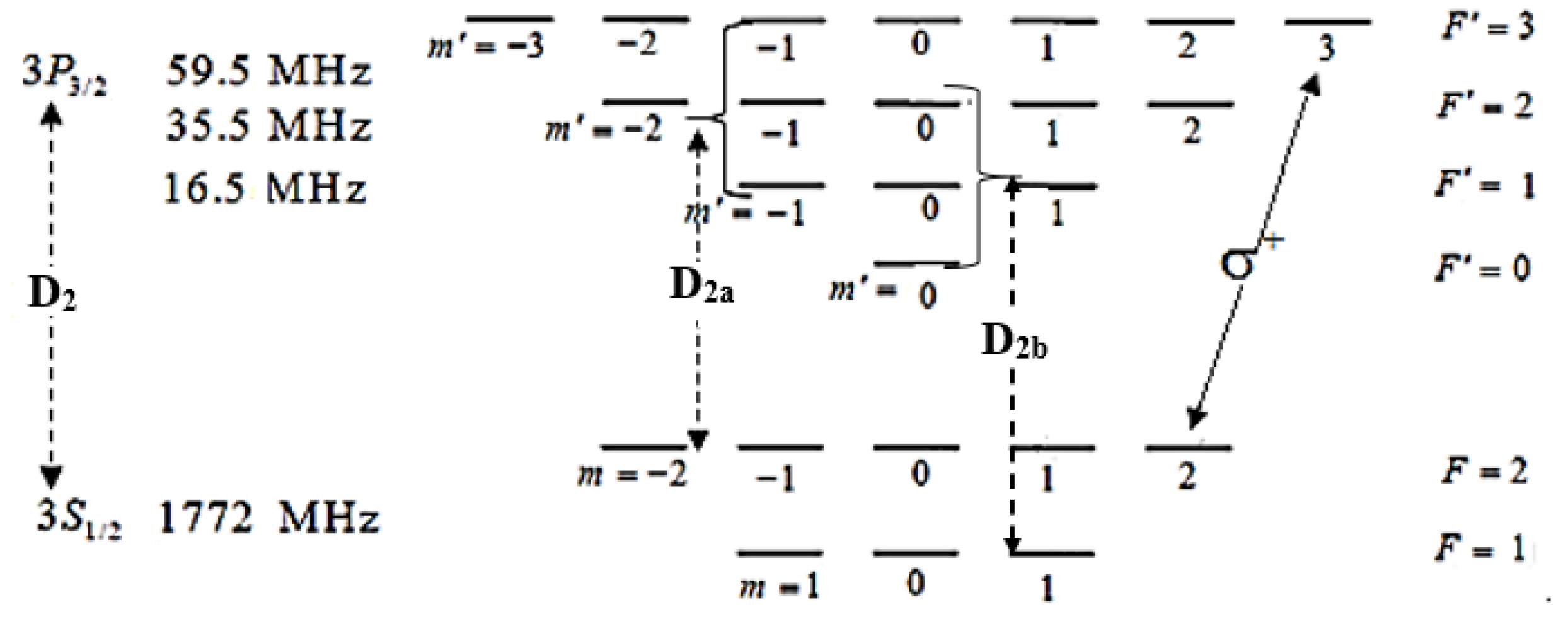
2. Theoretical Models
3. Methods and Parameters
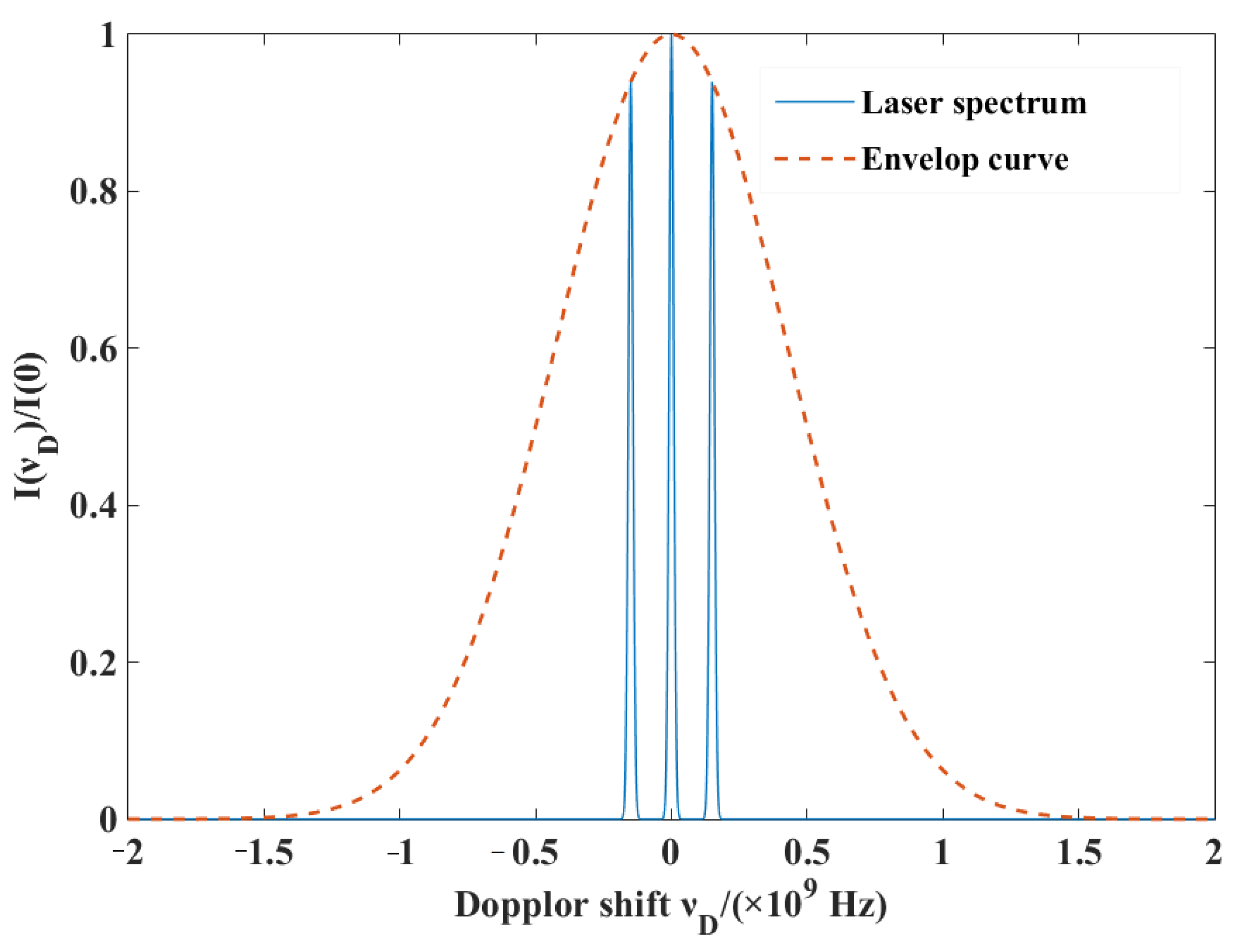
3.1. Numerical Simulation Methods
3.2. Simulation Parameters
4. Results and Analysis
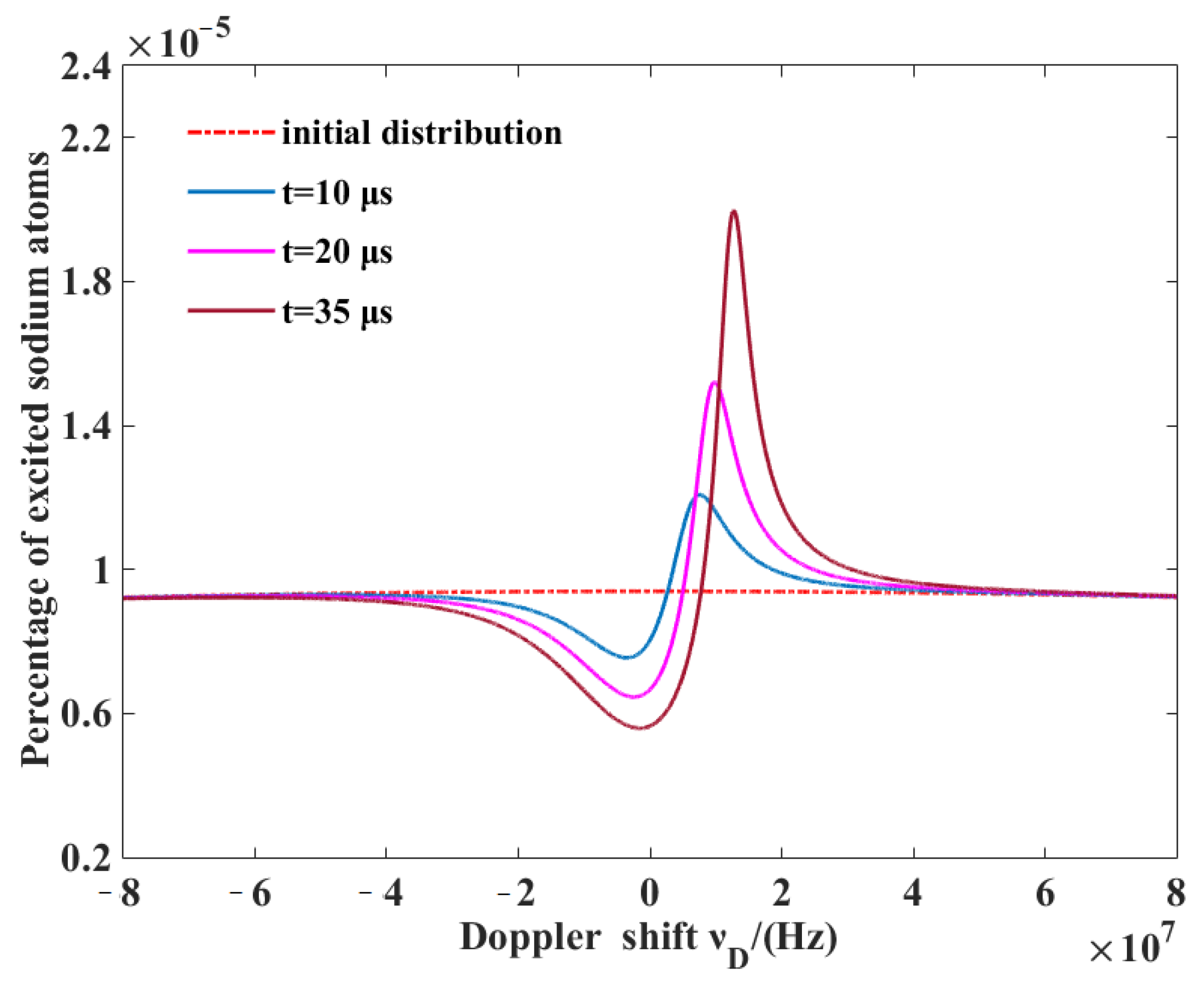
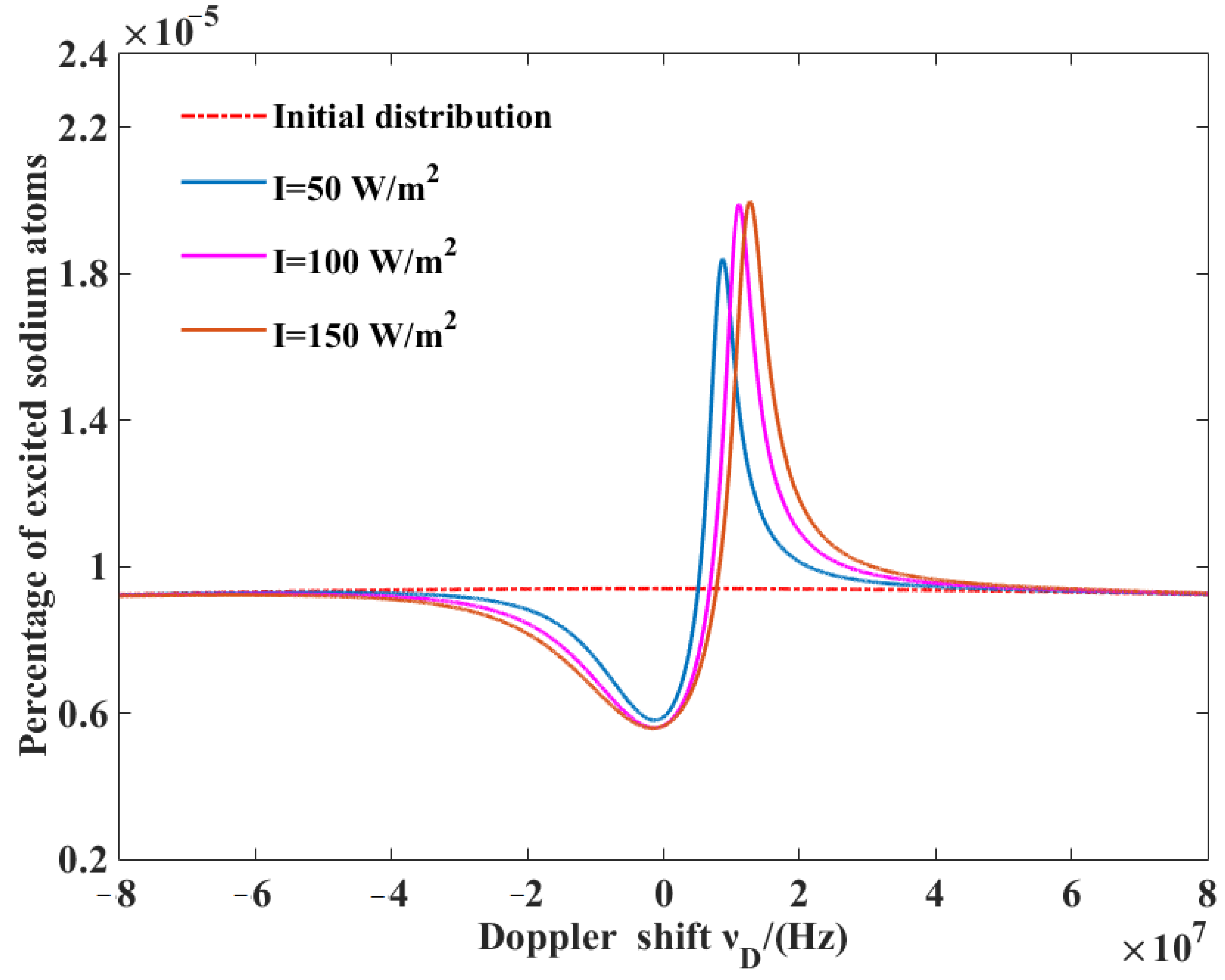
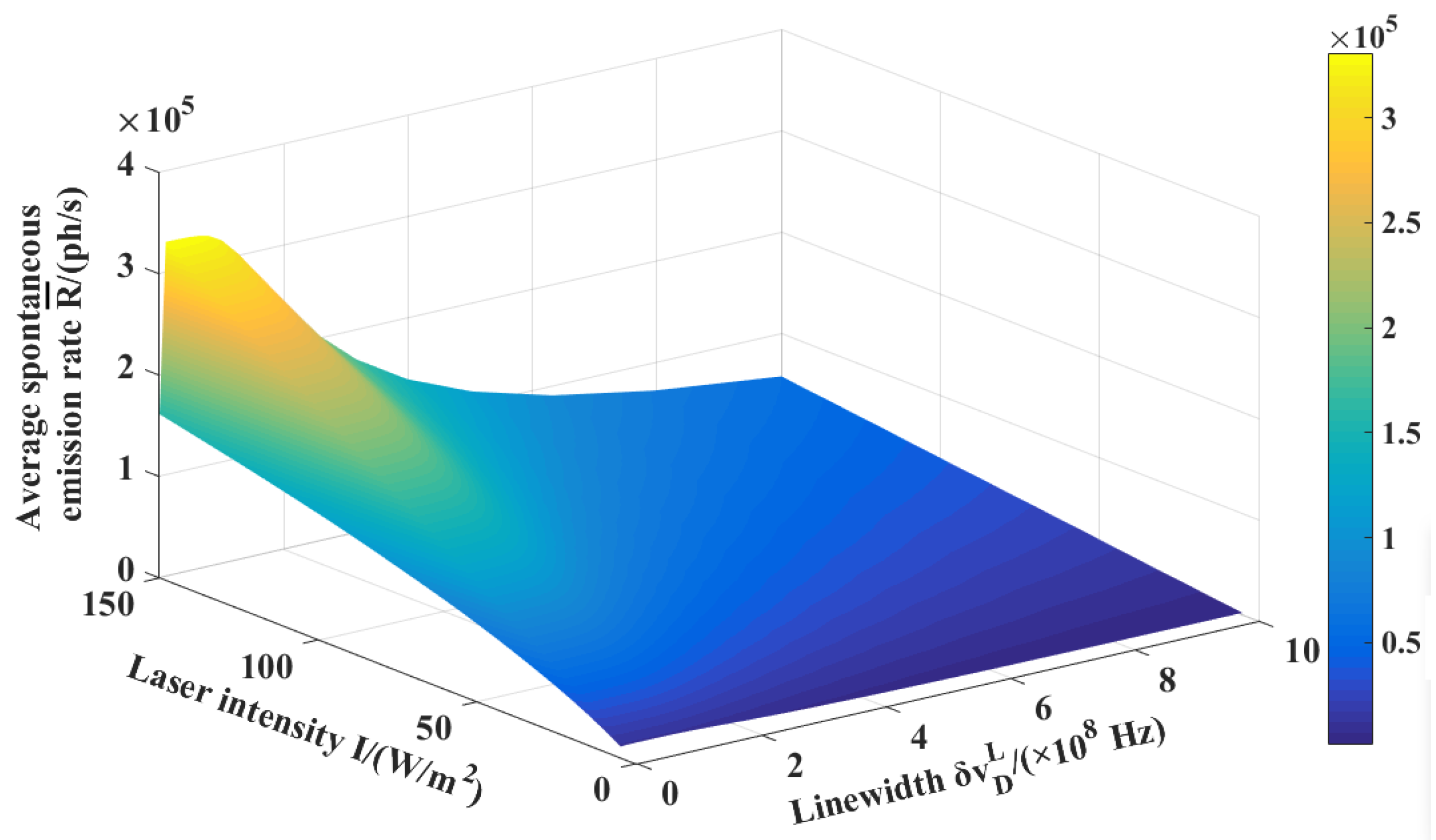
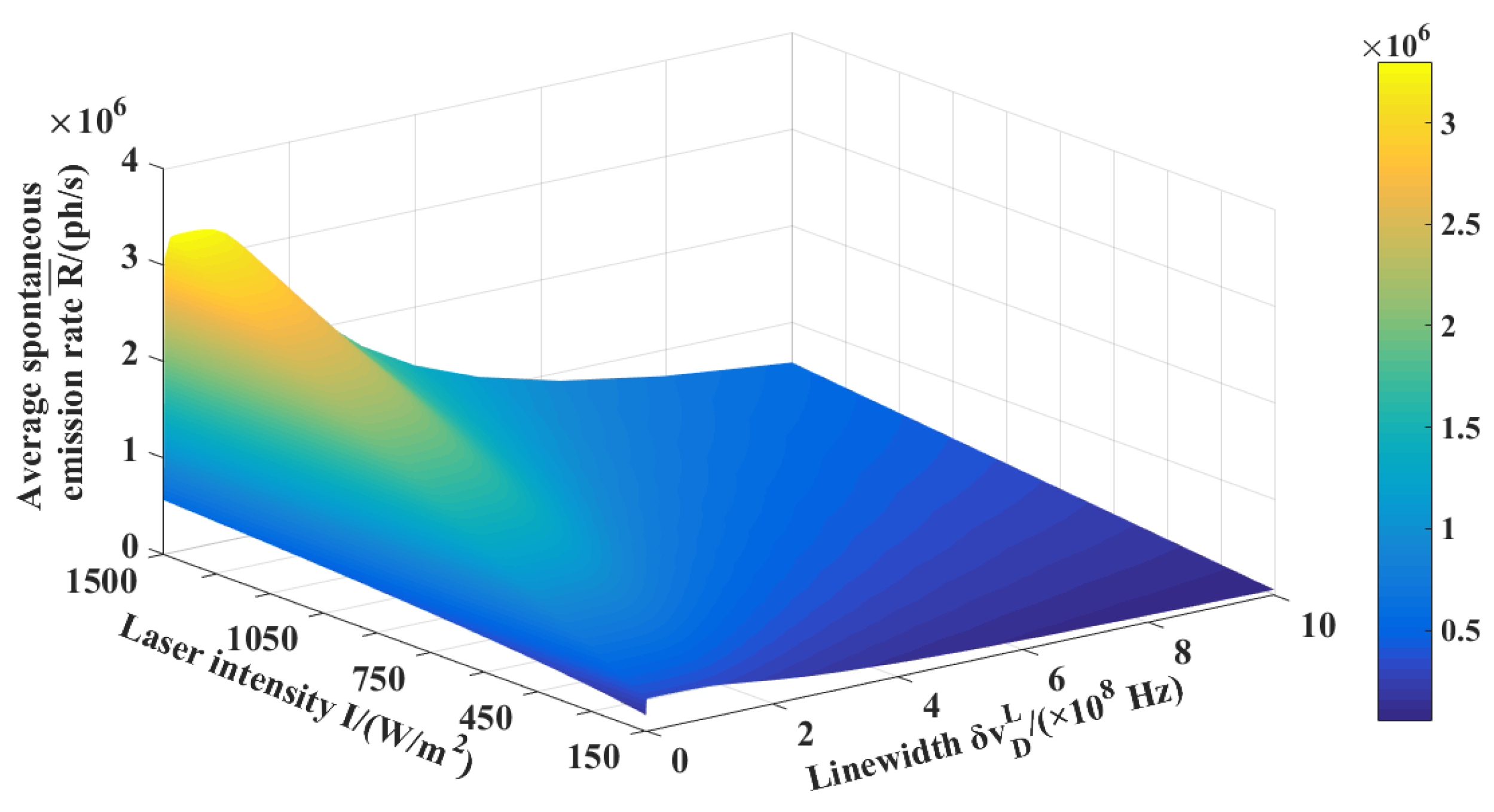
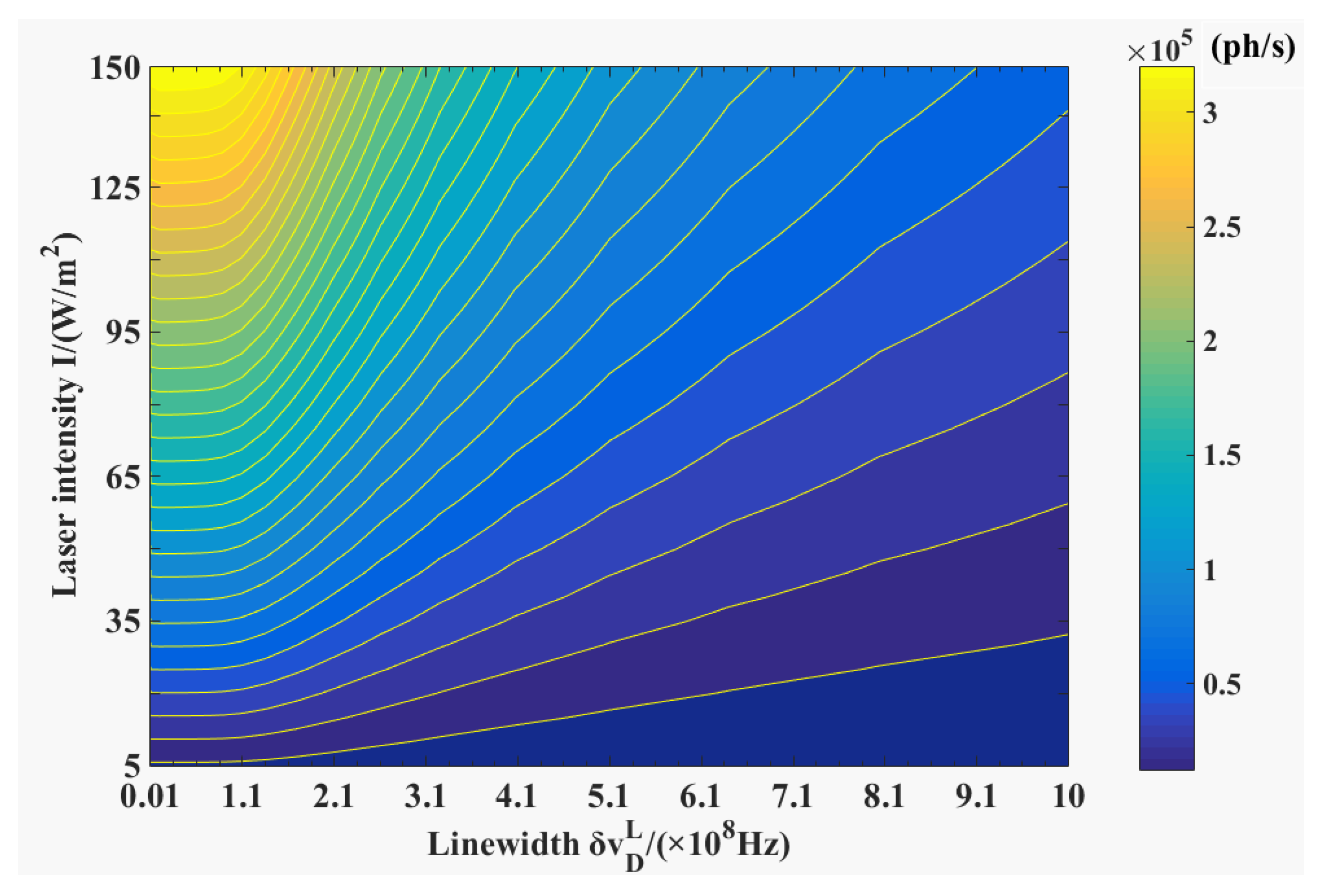
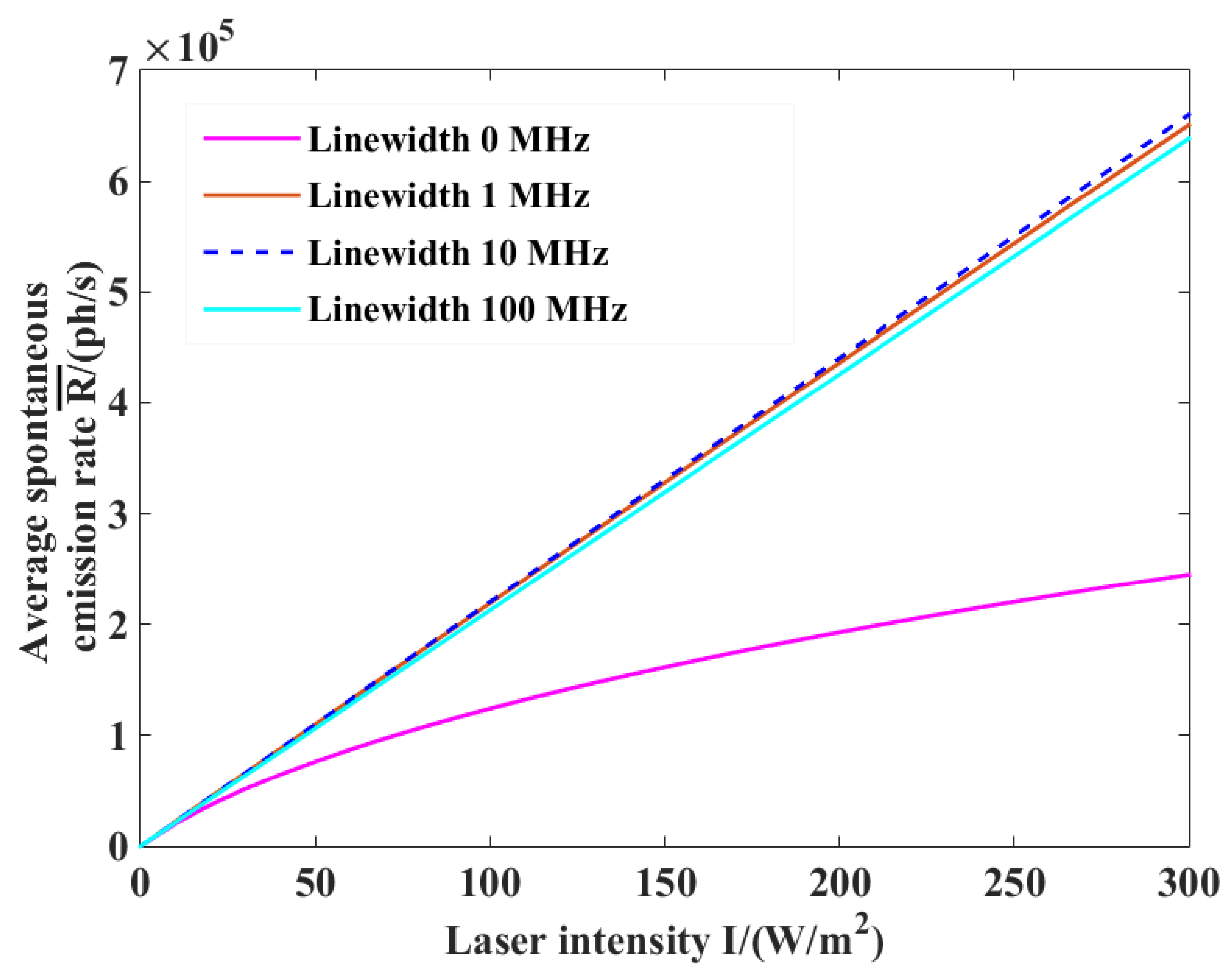
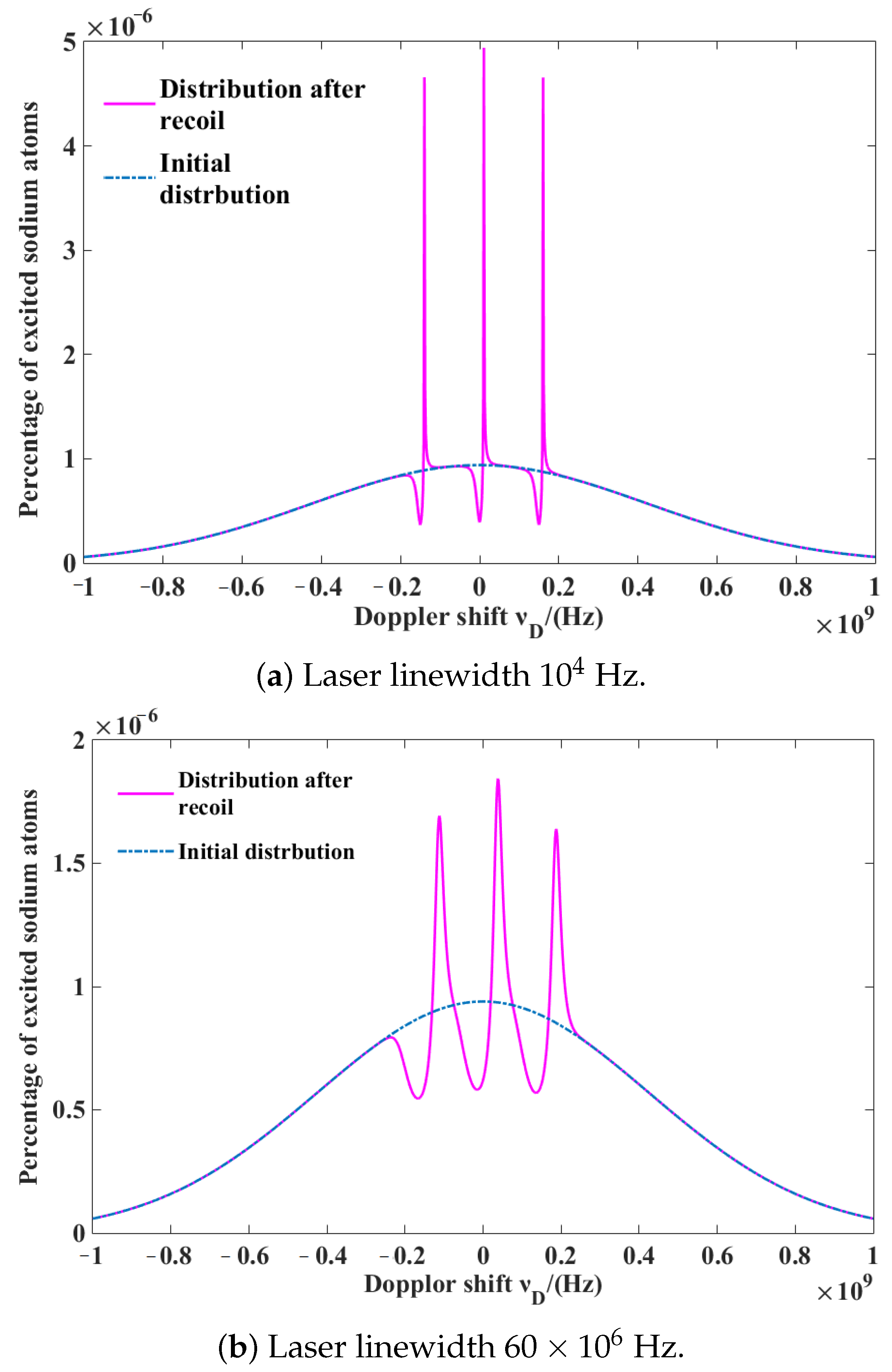
4.1. Recoil and Linewidth Broadening
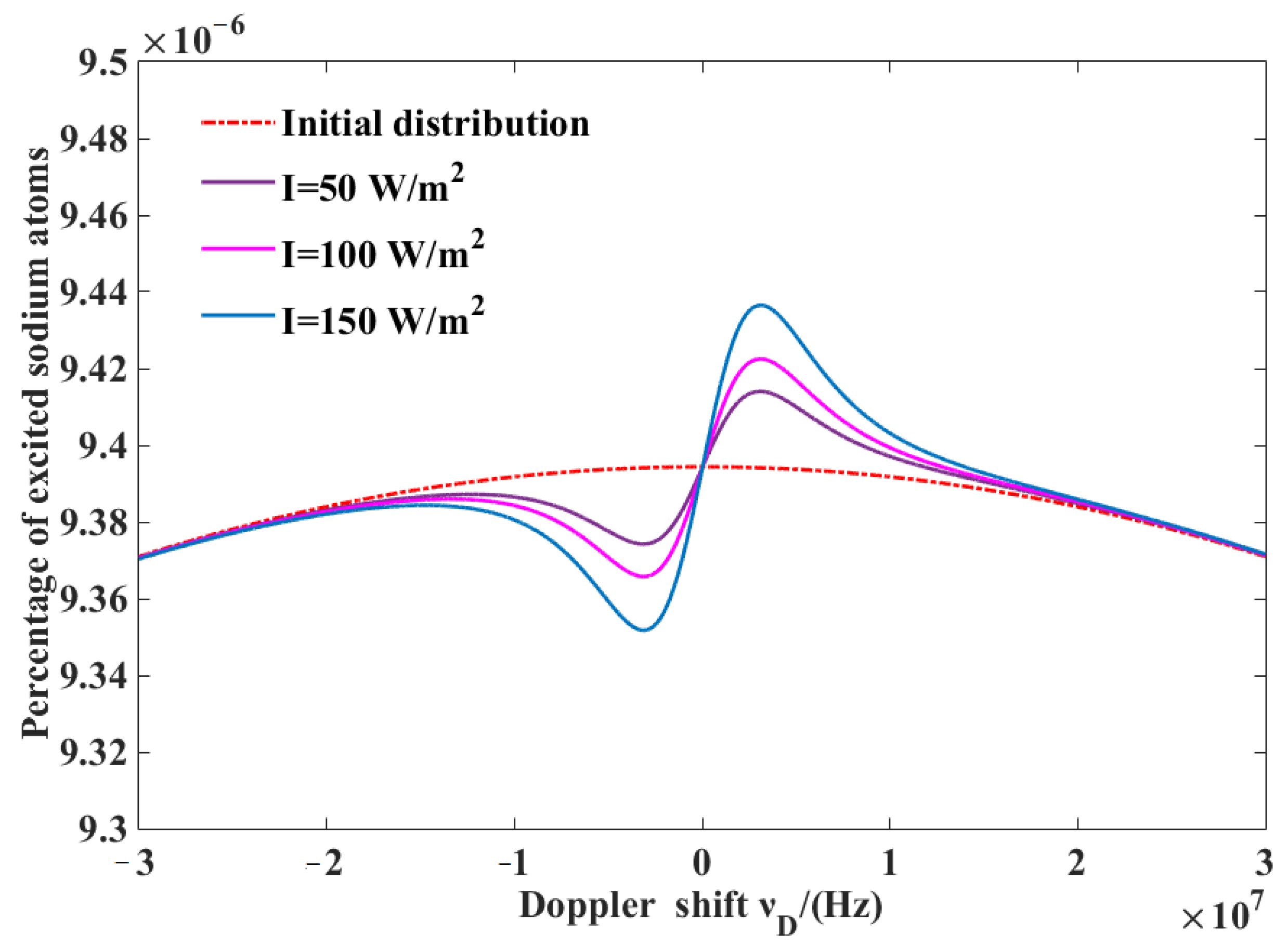
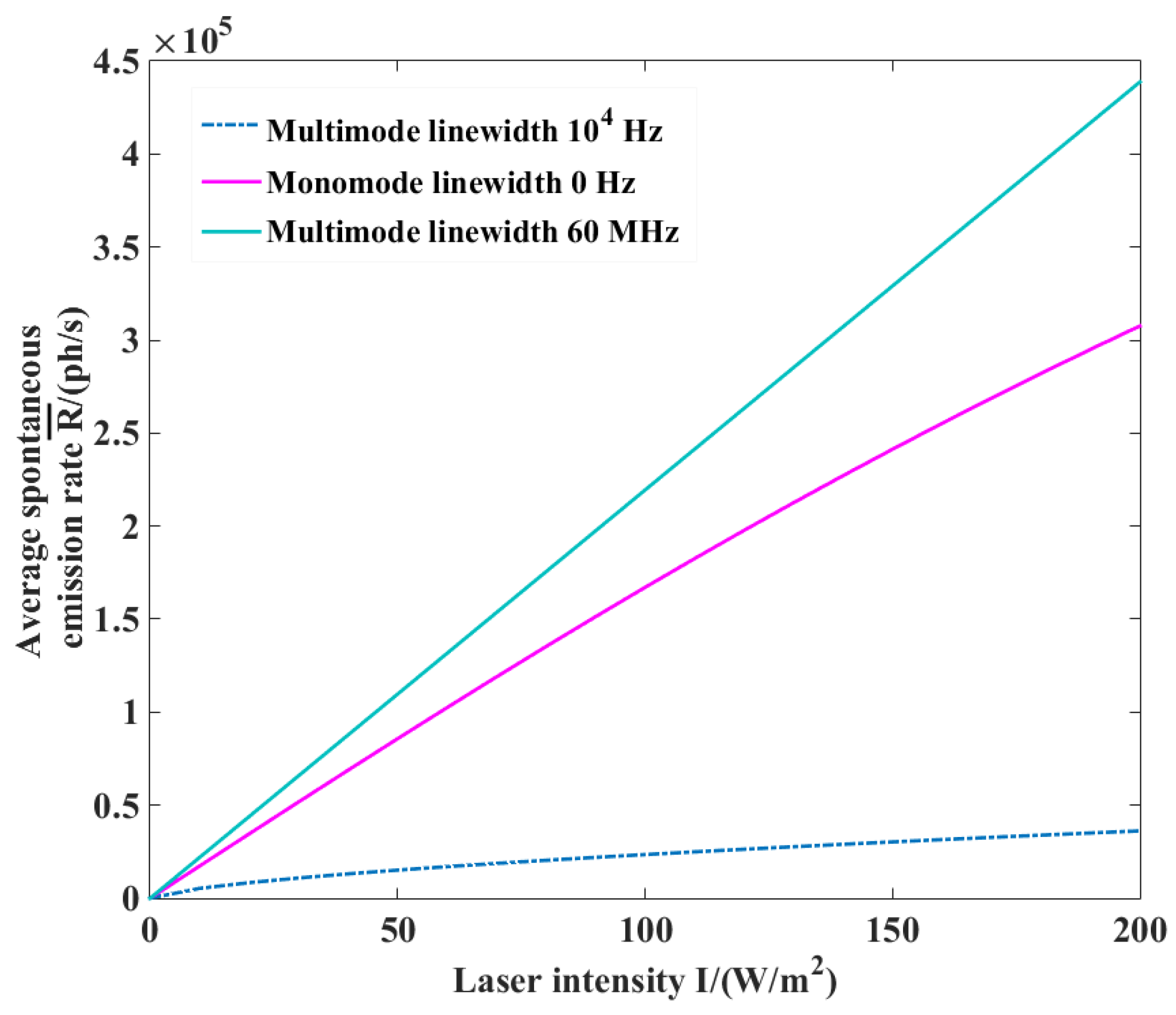
4.2. Choice of Optimal Laser Linewidth
5. Discussions
5.1. Effects of Linewidth Broadening on the Return Photons and Spot Sizes
5.2. Considerations of Linewidth Broadening Method
5.3. Effects of Linewidth Broadening on Recoil of the Multi-Mode Laser
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jonas, H.; Jörg, G. The global mesospheric sodium layer observed by Odin/OSIR-IS in 2004–2009. J. Atmos. Solar-Terr. Phys. 2011, 73, 2221–2227. [Google Scholar]
- Holzlölner, R.; Rochester, S.M.; Bonaccini, C.D.; Budker, D.; Higbie, J.M.; Hackenberg, W. Optimization of cw sodium laser guide star efficiency. Astron. Astrophys. 2010, 510, A20. [Google Scholar] [CrossRef] [Green Version]
- Bian, Q.; Bo, Y.; Zuo, J.; Li, M.; Dong, R.; Deng, K.; Xu, Z. Investigation of return photons from sodium laser beacon excited by a 40-watt facility-class pulsed laser for adaptive optical telescope applications. Sci. Rep. 2018, 8, 9222. [Google Scholar] [CrossRef] [PubMed]
- Hillman, P.D.; Drummond, J.D.; Denman, C.A.; Fugate, R.Q. Simple Model, including Recoil, for the Brightness of Sodium Guide Stars created from CW Single Frequency Fasors and Comparison to Measurements. In Proceedings of the Astronomical Telescopes and Instrumentation: Synergies Between Ground and Space, Marseille, France, 23 June 2008. [Google Scholar]
- Telle, J.; Drummond, J.; Hillman, P.; Denman, C. Simulations of mesospheric sodium guidestar radiance. In Proceedings of the Lasers and Applications in Science and Engineering, San Jose, CA, USA, 19 January 2008. [Google Scholar]
- Pedreros Bustos, F.; Holzlöhner, R.; Rochester, S.; Bonaccini Calia, D.; Hellemeier, J.; Budk, D. Frequency chirped continuous-wave sodium laser guide stars: Modeling and optimization. J. Opt. Soc. Am. B 2020, 37, 1208–1218. [Google Scholar] [CrossRef]
- Chamoun, J.; Digonnet, M. Aircraft-navigation-grade laser-driven FOG with Gaussian-noise phase modulation. Opt. Lett. 2017, 42, 1600–1603. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Qian, X.; Li, Y.; Rao, R. Calculation and analysis of the number of return photons from Sodium Laser Beacon excited by the long pulse laser with circular polarization. Chin. Phys. B 2014, 12, 240–248. [Google Scholar] [CrossRef]
- Milonni, P.W.; Fugate, R.Q.; Telle, J.M. Analysis of measured photon returns from sodium beacons. Opt. Soc. Am. A 1998, 15, 218–233. [Google Scholar] [CrossRef]
- Jeys, T.H. Development of a mesospheric sodium laser beacon for atmospheric adaptive optics. In Proceedings of the LEOS ’90. IEEE Lasers and Electro-Optics Society Annual Meeting, Boston, MA, USA, 6–8 November 1990. [Google Scholar]
- Mcclelland, J.J.; Kelley, M.H. Detailed look at aspects of optical pumping in sodium. Phys. Rev. A 1985, 31, 3704–3710. [Google Scholar] [CrossRef]
- Milonni, P.W.; Thode, L.E. Theory of mesospheric sodium fluorescence excited by pulse trains. Appl. Opt. 1992, 31, 785–800. [Google Scholar] [CrossRef]
- Pique, J.P.; Moldovan, I.C.; Fesquet, V. Concept for polychromatic laser guide stars: One-photon excitation of the 4P3/2 level of a sodium atom. J. Opt. Soc. Am. A 2006, 23, 2817–2828. [Google Scholar] [CrossRef] [Green Version]
- Morris, J.R. Efficient excitation of a mesospheric sodium laser guide star by intermediate -duration pulses. J. Opt. Soc. Am. A 1994, 11, 832–845. [Google Scholar] [CrossRef]
- Milonni, P.W.; Fearn, H. Theory of continuous-wave excitation of the sodium beacon. J. Opt. Soc. Am. A 1999, 16, 2555–2566. [Google Scholar] [CrossRef]
- Rodolphe, C.; Olivier, L.; Glen, H.; Bradley, C.; Kate, J. Experimental assessment of the matched filter for laser guide star wavefront sensing. Appl. Opt. 2009, 48, 1198–1211. [Google Scholar]
- Liu, X.; Qian, X.; Zhu, W.; Rao, R.; Wei, X.; Lu, C. Characteristics of return photons from the polychromatic laser guide star excited by a long pulse laser with 330 nm wavelength. In Proceedings of the Conference on Laser Technology and Optoelectronics, Chengdu, China, 17–20 October 2019. [Google Scholar]
- Moussaoui, N.; Holzlöhner, R.; Hackenberg, W.; Bonaccini, C.D. Dependence of sodium laser guide star photon return on the geomagnetic field. Astron. Astrophys. 2009, 501, 793–799. [Google Scholar] [CrossRef]
- Drummond, J.; Novotny, S.; Denman, C.; Hillman, P.; Telle, J. The Sodium LGS Brightness Model over the SOR. In Proceedings of the Advanced Maui Optical and Space Surveillance Technologies Conference, Wailea, HI, USA, 12–15 September 2007. [Google Scholar]
- Qian, X.; Zhu, W.; Rao, R.Z. Long-distance propagation of pseudo-partially coherent Gaussian Schell-model beams in atmospheric turbulence. Chin. Phys. B 2012, 21, 094202. [Google Scholar] [CrossRef]
- Chen, H.; Ji, X.; Li, X.; Wang, T.; Zhao, Q.; Zhang, H. Energy focusability of annular beams propagating through atmospheric turbulence along a slanted path. Opt. Laser Technol. 2015, 71, 22–28. [Google Scholar] [CrossRef]
- Jin, K.; Wei, K.; Feng, L.; Bo, Y.; Zuo, J.; Li, M.; Fu, C.; Dai, X.; Bian, Q.; Yao, J.; et al. Photon Return On-Sky Test of Pulsed Sodium Laser Guide Star with D-2b Repumping. Publ. Astron. Soc. Pac. 2015, 127, 749–756. [Google Scholar] [CrossRef]
- Harding, C.M.; Johnston, R.A.; Lane, R.G. Fast Simulation of a Kolmogorov Phase Screen. Appl. Opt. 1999, 38, 2161–2170. [Google Scholar] [CrossRef]
- Greenwood, D.P. Bandwidth specification for adaptive optics systems. J. Opt. Soc. Am. 1977, 67, 390–393. [Google Scholar] [CrossRef]
- Ji, X.; Pu, Z.; Ji, G.; Jia, X. Regions of spreading of partially coherent beams propagating through non-kolmogorov turbulence. Opt. Commun. 2014, 322, 109–113. [Google Scholar] [CrossRef]
- Chen, M.; Gao, T.; Hu, S.; Zeng, Q.; Liu, L.; Li, G. Simulating Non-Kolmogorov turbulence phase screens based on equivalent structure constant and its influence on simulations of beam propagation. Results Phys. 2017, 7, 3596–3602. [Google Scholar] [CrossRef]
- Yan, H.X.; Li, S.S.; Zhang, D.L.; Chen, S. Numerical simulation of an adptive optcs system with laser propagation in the atmosphere. Appl. Opt. 2000, 38, 3023–3031. [Google Scholar] [CrossRef] [PubMed]
- Rubio, J.A.; Belmonte, A.; Comerón, A. Numerical simulation of long-path spherical wave propagation in three-dimensional random media. Opt. Eng. 1999, 38, 1462–1469. [Google Scholar] [CrossRef] [Green Version]
- Parenti, R.R.; Sasiela, R.J. Laser-guide-star systems for astronomical applications. J. Opt. Soc. Am. A 1994, 11, 288–309. [Google Scholar] [CrossRef]
- Pennington, D.M. Laser Guided Adaptive Optics for High-Resolution Astronomy. In Proceedings of the Conference on Lasers and Electro-Optics, Long Beach, CA, USA, 19–22 May 2002. [Google Scholar]
- Pique, J.P.; Farinotti, S. Efficient modeless laser for a mesospheric sodium laser guide star. J. Opt. Soc. Am. B 2003, 20, 2093–2101. [Google Scholar] [CrossRef] [Green Version]
- Denman, C.A.; Drummond, J.D.; Hillman, P.D.; Steven, J.N.; Telle, J.M. Characteristics of sodium guidestars created by the 50-watt FASOR and first closed-loop AO results at the Starfire Optical Range. In Proceedings of the Advances in Adaptive Optics II, Orlando, FL, USA, 24–31 May 2006. [Google Scholar]
- D’Orgeville, C.; Rigaut, F.J.; Ellerbroek, B.L. LGS AO photon return simulations and laser requirements for the Gemini LGS AO program. In Proceeding of the SPIE Astronomical Telescopes and Instrumentation, Adaptive Optical Systems Technology, Munich, Germany, 27 March 2000. [Google Scholar]




| Variable Names | Symbols | Values |
|---|---|---|
| Laser parameters | ||
| Center wavelength of laser | nm | |
| Linewidth of continuous wave laser | 0– GHz | |
| Laser polarization | ||
| Laser beam quality factor | ||
| Diameter of laser launch | D | 40 cm |
| Zenith of laser launch | ||
| Angle between directions of laser beam and geomagnetic field vector | ||
| Sodium parameters | ||
| Linewidth of sodium atomic distributions at sodium layer | GHz | |
| Life time of excited sodium atoms | 16 ns | |
| Backscattering coefficient of excited sodium atoms | ||
| Column density of sodium layer | cm | |
| Cycle time of sodium atomic collisions | 35 s | |
| Altitude of sodium layer centroid | L | 92 km |
| Atmospheric, magnetic field parameters | ||
| Atmospheric transmissivity | ||
| Mesospheric magnetic field | B | Gs |
| Laser Power (W) | 10 | 20 | 30 |
|---|---|---|---|
| Laser linewidth | |||
| 10 0 | 10 0 | 10 0 | |
| Return photons | |||
| 5.36 3.56 | 10.72 6.50 | 16.08 9.10 | |
| Effective radius | |||
| 0.426 0.426 | 0.418 0.418 | 0.422 0.422 | |
| Laser Power (W) | 40 | 50 | 60 |
| Laser linewidth | |||
| 10 0 | 10 0 | 10 0 | |
| Return photons | |||
| 21.43 11.26 | 26.795 13.05 | 32.15 15.29 | |
| Effective radius | |||
| 0.413 0.413 | 0.406 0.406 | 0.413 0.413 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Qian, X.; He, R.; Liu, D.; Cui, C.; Fan, C.; Yuan, H. Effects of Linewidth Broadening Method on Recoil of Sodium Laser Guide Star. Atmosphere 2021, 12, 1315. https://doi.org/10.3390/atmos12101315
Liu X, Qian X, He R, Liu D, Cui C, Fan C, Yuan H. Effects of Linewidth Broadening Method on Recoil of Sodium Laser Guide Star. Atmosphere. 2021; 12(10):1315. https://doi.org/10.3390/atmos12101315
Chicago/Turabian StyleLiu, Xiangyuan, Xianmei Qian, Rui He, Dandan Liu, Chaolong Cui, Chuanyu Fan, and Hao Yuan. 2021. "Effects of Linewidth Broadening Method on Recoil of Sodium Laser Guide Star" Atmosphere 12, no. 10: 1315. https://doi.org/10.3390/atmos12101315
APA StyleLiu, X., Qian, X., He, R., Liu, D., Cui, C., Fan, C., & Yuan, H. (2021). Effects of Linewidth Broadening Method on Recoil of Sodium Laser Guide Star. Atmosphere, 12(10), 1315. https://doi.org/10.3390/atmos12101315






