Assessment and Calibration of a Low-Cost PM2.5 Sensor Using Machine Learning (HybridLSTM Neural Network): Feasibility Study to Build an Air Quality Monitoring System
Abstract
:1. Introduction
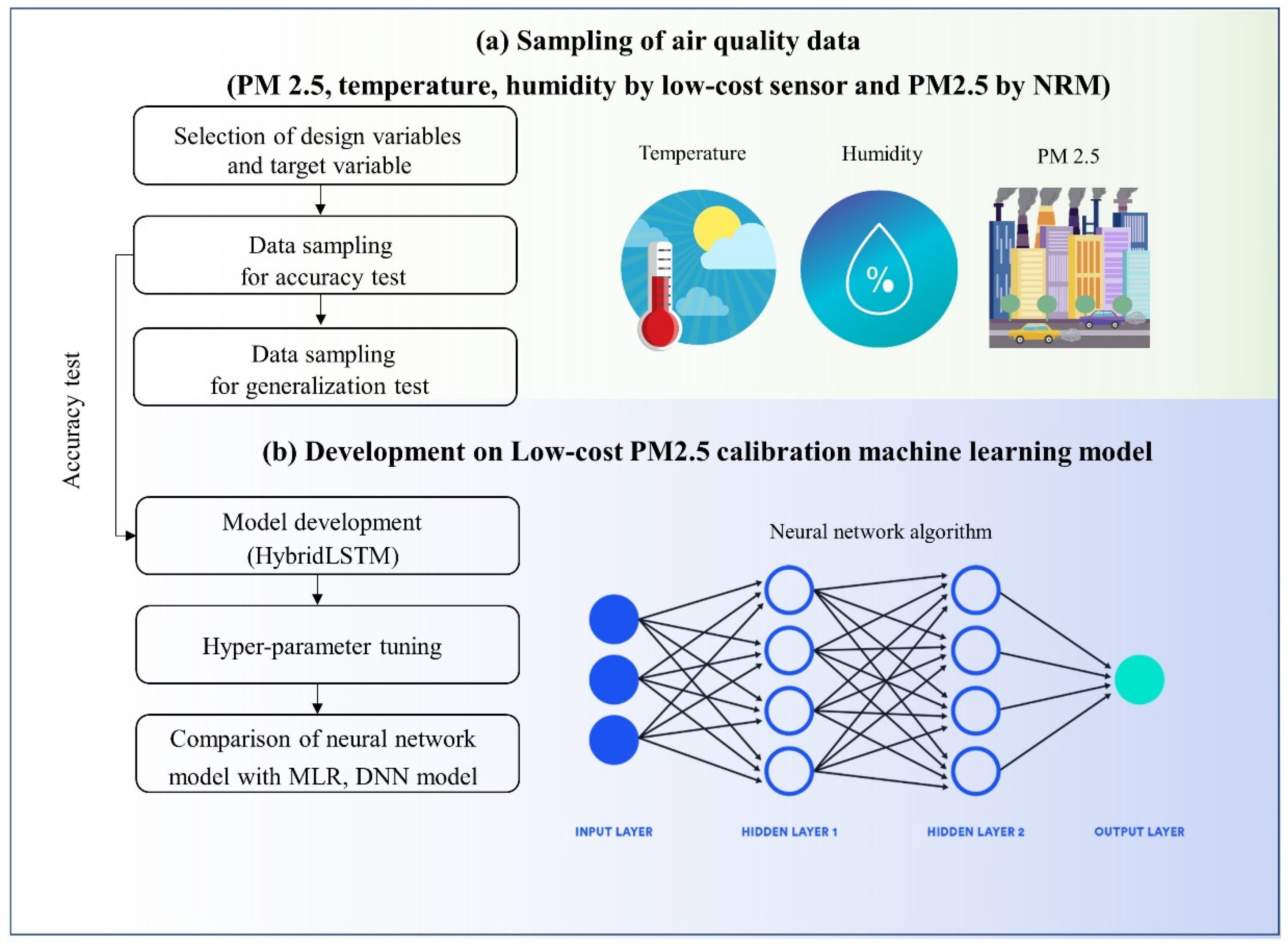
2. Methods
2.1. Data Sampling to Develop Calibration Machine Learning (ML) Model
2.1.1. Air Quality Measurement Instruments
2.1.2. Dataset for Calibration Machine Learning (ML) Modeling
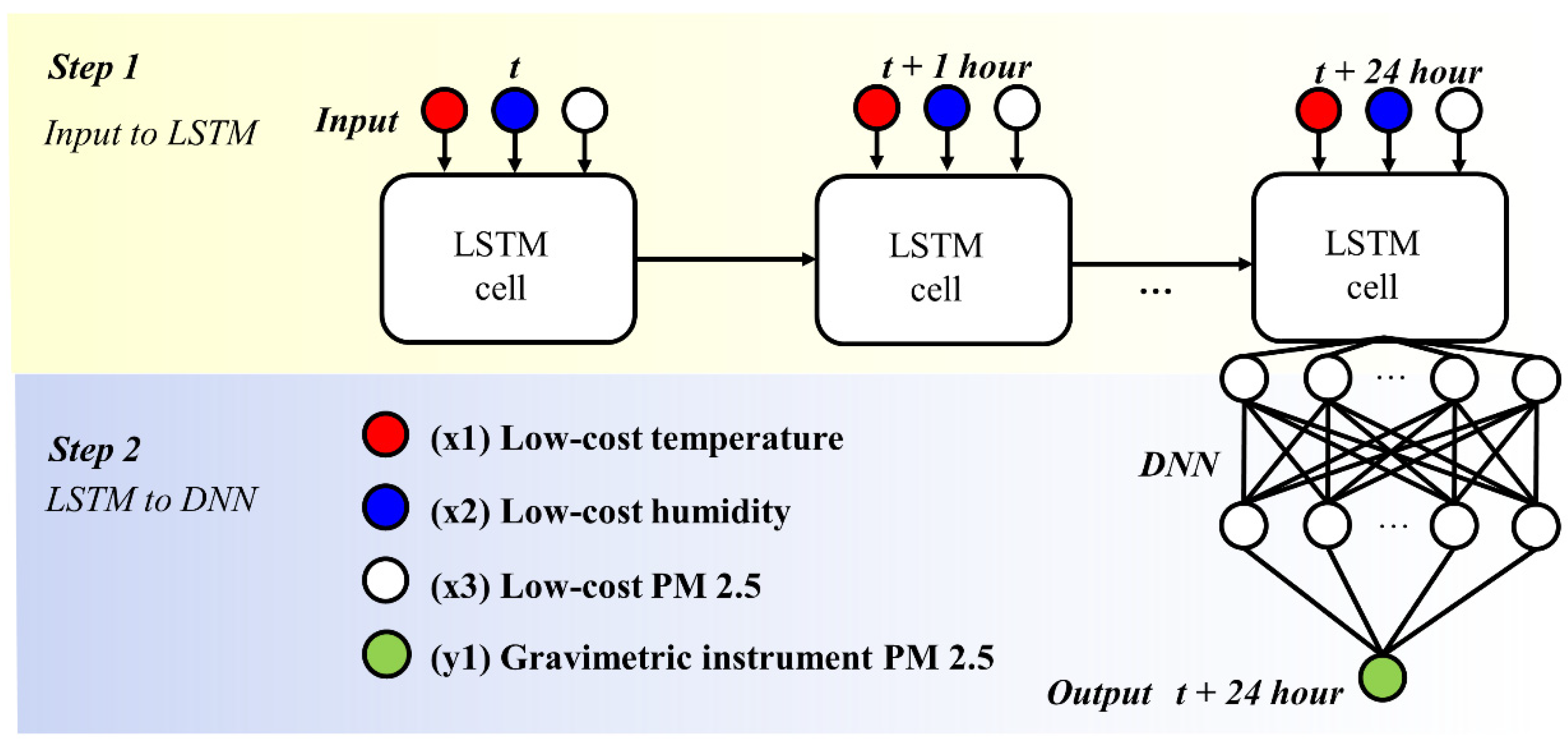
2.2. Machine Learning Algorithm
2.3. Benchmark Method
3. Results
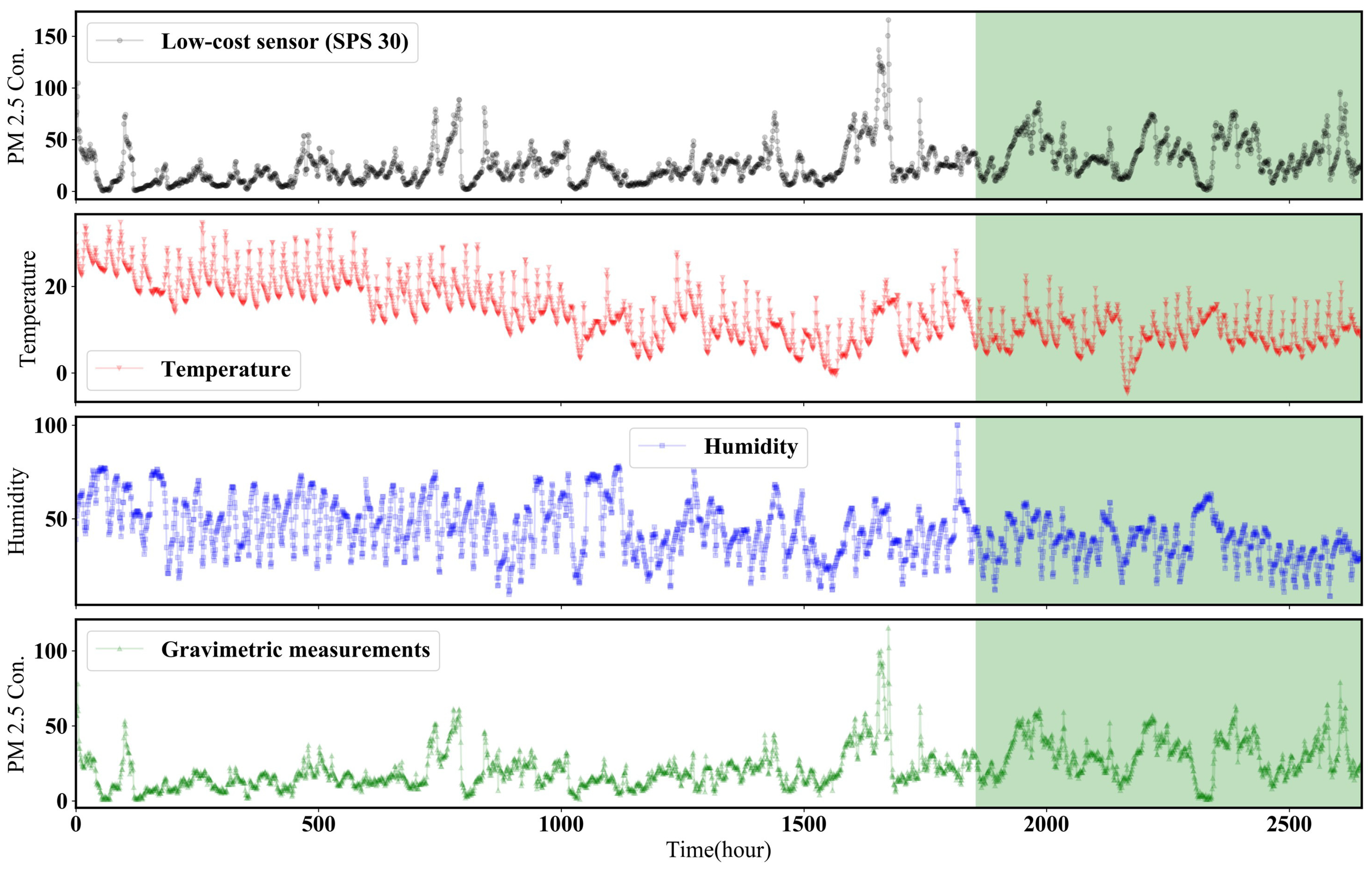
3.1. Data Sampling to Develop Machine Learning Model
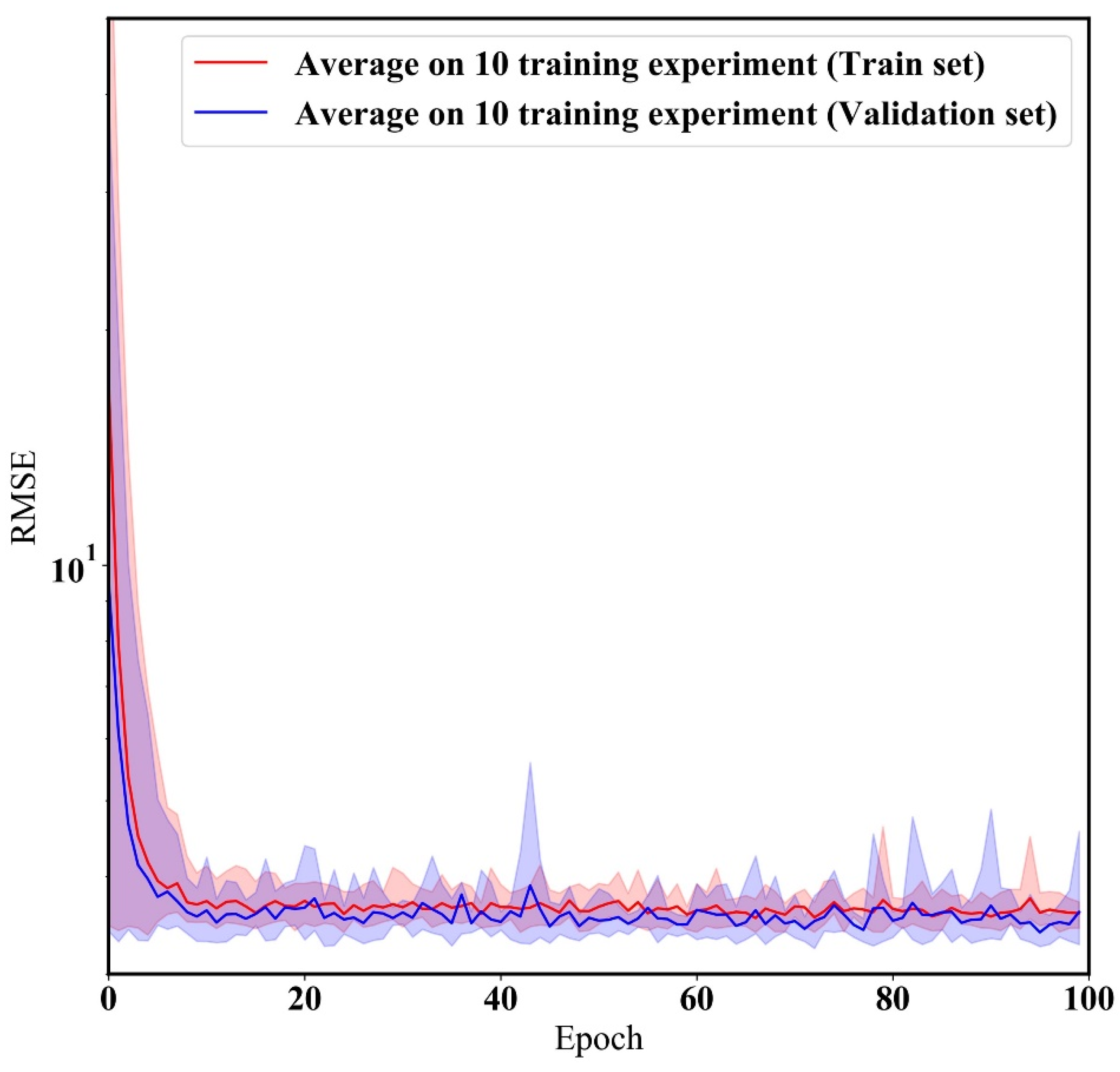
3.2. Hyper-Parameter Optimization of HybridLSTM
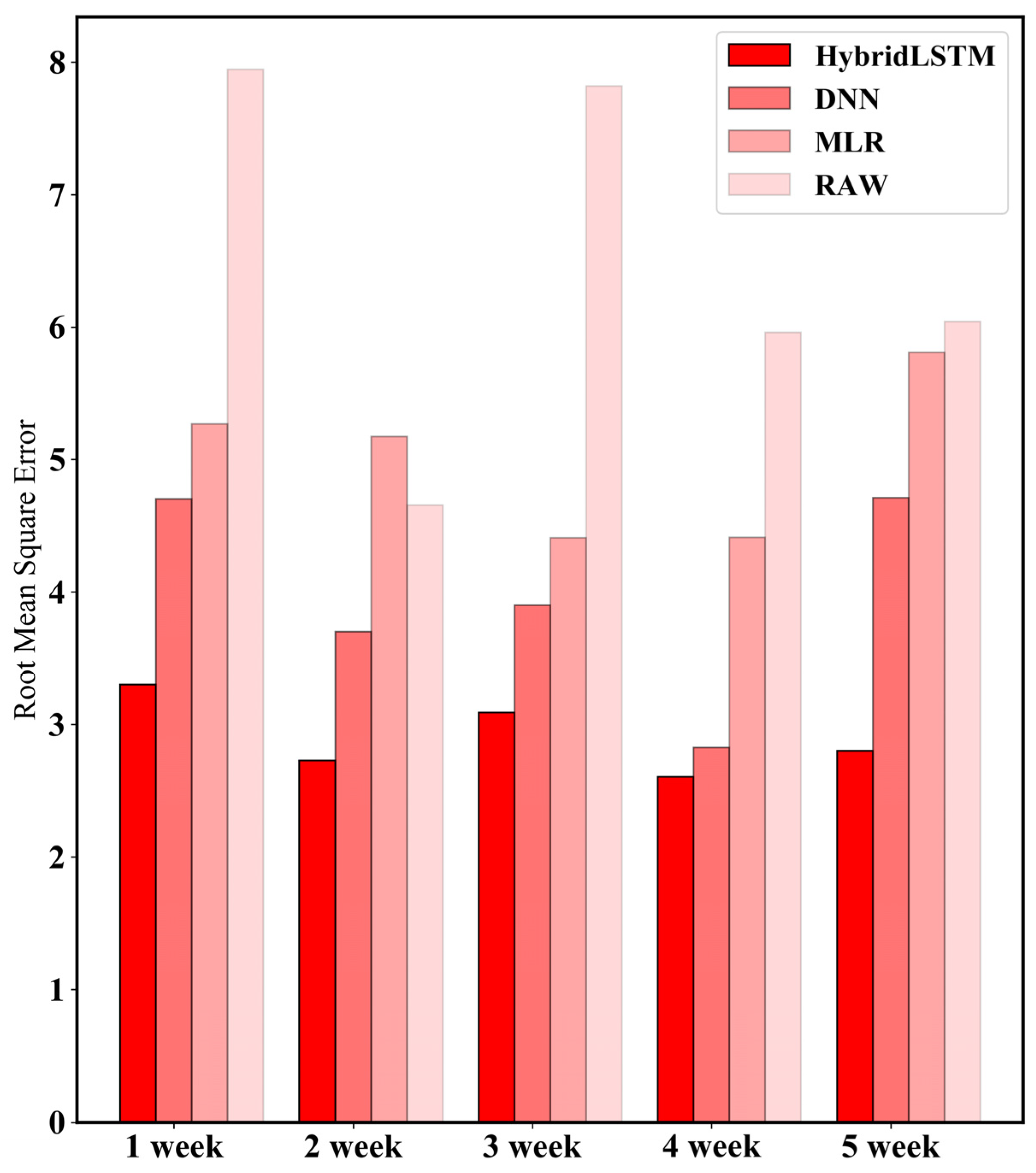
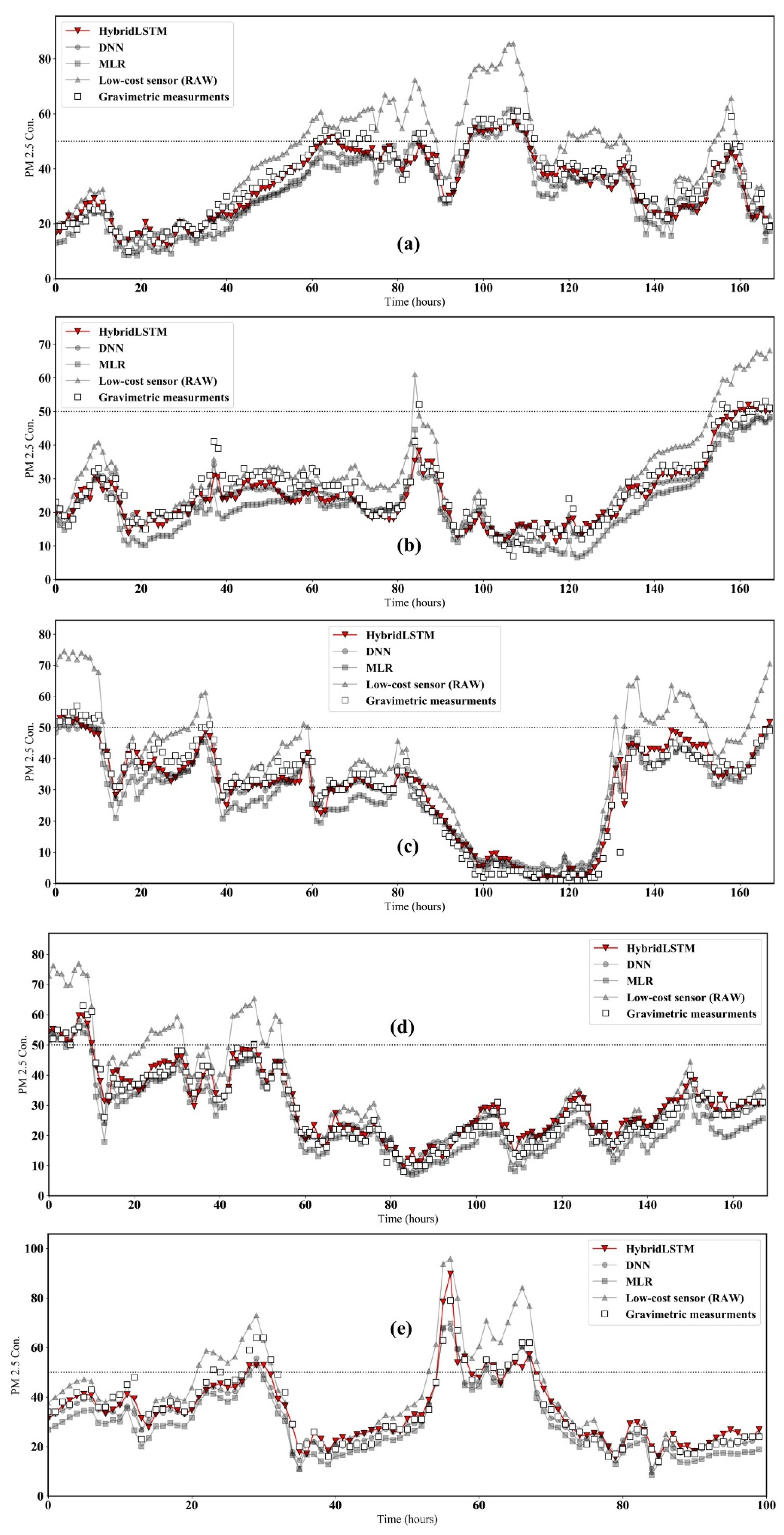
3.3. Comparison of Accuracy among Proposed Model, Benchmark and Low-Cost Sensor
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Conti, M.E.; Ciasullo, R.; Tudino, M.B.; Matta, E.J. The industrial emissions trend and the problem of the implementation of the Industrial Emissions Directive (IED). Air Qual. Atmos. Health 2015, 8, 151–161. [Google Scholar] [CrossRef]
- Morawska, L.; Thai, P.K.; Liu, X.; Asumadu-Sakyi, A.; Ayoko, G.; Bartonova, A.; Bedini, A.; Chai, F.; Christensen, B.; Dunbabin, M.; et al. Applications of low-cost sensing technologies for air quality monitoring and exposure assessment: How far have they gone? Environ. Int. 2018, 116, 286–299. [Google Scholar] [CrossRef] [PubMed]
- Steinle, S.; Reis, S.; Sabel, C.E.; Semple, S.; Twigg, M.M.; Braban, C.F.; Leeson, S.R.; Heal, M.R.; Harrison, D.; Lin, C.; et al. Personal exposure monitoring of PM2.5 in indoor and outdoor microenvironments. Sci. Total Environ. 2015, 508, 383–394. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, J.; Mattewal, S.K.; Patel, S.; Biswas, P. Evaluation of nine low-cost-sensor-based particulate matter monitors. Aerosol Air Qual. Res. 2020, 20, 254–270. [Google Scholar] [CrossRef] [Green Version]
- Tahsiin, F.; Anggraeni, L.; Chandra, I.; Salam, R.A.; Bethaningtyas, H. Analysis of Indoor Air Quality Based on Low-Cost Sensors. Int. J. Adv. Sci. Eng. Inf. Technol. 2020, 10, 2627–2633. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhu, X.; Chen, C.; Ge, Y.; Wang, W.; Zhao, Z.; Cai, J.; Kan, H. On-field test and data calibration of a low-cost sensor for fine particles exposure assessment. Ecotoxicol. Environ. Saf. 2021, 211, 111958. [Google Scholar] [CrossRef] [PubMed]
- Kim, S.; Park, S.; Lee, J. Evaluation of performance of inexpensive laser based PM2.5 sensor monitors for typical indoor and outdoor hotspots of South Korea. Appl. Sci. 2019, 9, 1947. [Google Scholar] [CrossRef] [Green Version]
- Shi, J.; Chen, F.; Cai, Y.; Fan, S.; Cai, J.; Chen, R.; Kan, H.; Lu, Y.; Zhao, Z. Validation of a light-scattering PM2.5 sensor monitor based on the long-term gravimetric measurements in field tests. PLoS ONE 2017, 12, e0185700. [Google Scholar] [CrossRef] [PubMed]
- Badura, M.; Batog, P.; Drzeniecka-Osiadacz, A.; Modzel, P. Evaluation of low-cost sensors for ambient PM2.5 monitoring. J. Sens. 2018, 2018, 5096540. [Google Scholar] [CrossRef] [Green Version]
- Vogt, M.; Schneider, P.; Castell, N.; Hamer, P. Assessment of low-cost particulate matter sensor systems against optical and gravimetric methods in a field co-location in norway. Atmosphere 2021, 12, 961. [Google Scholar] [CrossRef]
- Zusman, M.; Schumacher, C.S.; Gassett, A.J.; Spalt, E.W.; Austin, E.; Larson, T.V.; Carvlin, G.; Seto, E.; Kaufman, J.D.; Sheppard, L. Calibration of low-cost particulate matter sensors: Model development for a multi-city epidemiological study. Environ. Int. 2020, 134, 105329. [Google Scholar] [CrossRef] [PubMed]
- Si, M.; Xiong, Y.; Du, S.; Du, K. Evaluation and Calibration of a Low-cost Particle Sensor in Ambient Conditions Using Machine Learning Technologies. Atmos. Meas. Tech. 2019, 13, 1693–1707. [Google Scholar] [CrossRef] [Green Version]
- Załuska, M.; Gładyszewska-Fiedoruk, K. Regression model of PM2.5 Concentration in a single-family house. Sustainability 2020, 12, 5952. [Google Scholar] [CrossRef]
- Gilliam, J.H.; Hall, E.S. Reference and Equivalent Methods Used to Measure National Ambient Air Quality Standards (NAAQS) Criteria Air Pollutants; Environmental Protection Agency: Washington, DC, USA, 2016; Volume 1, pp. 2016–2017. [Google Scholar] [CrossRef]
- Kim, Y.; Kim, Y.; Yang, C.; Park, K.; Gu, G.X.; Ryu, S. Deep learning framework for material design space exploration using active transfer learning and data augmentation. Npj Comput. Mater. 2021, 7, 1–7. [Google Scholar] [CrossRef]
- Wei, J.; Yang, F.; Ren, X.C.; Zou, S. A short-term prediction model of PM2.5 concentration based on deep learning and mode decomposition methods. Appl. Sci. 2021, 11, 6915. [Google Scholar] [CrossRef]
- Yang, G.; Lee, H.M.; Lee, G. A hybrid deep learning model to forecast particulate matter concentration levels in Seoul, South Korea. Atmosphere 2020, 11, 348. [Google Scholar] [CrossRef] [Green Version]
- Park, D.; Cha, J.; Kim, M.; Go, J.S. Multi-objective optimization and comparison of surrogate models for separation performances of cyclone separator based on CFD, RSM, GMDH-neural network, back propagation-ANN and genetic algorithm. Eng. Appl. Comput. Fluid Mech. 2020, 14, 180–201. [Google Scholar] [CrossRef]
- Park, D.; Go, J.S. Design of cyclone separator critical diameter model based on machine learning and cfd. Processes 2020, 8, 1521. [Google Scholar] [CrossRef]



| Variables | Minimum | Maximum | Average | Standard Deviation |
|---|---|---|---|---|
| Temperature | −4.713 | 34.76 | 13.96 | 6.96 |
| Humidity | 8.55 | 99.99 | 43.51 | 19.45 |
| Low-cost PM2.5 | 0.39 | 165.56 | 27.11 | 19.45 |
| Gravimetric PM2.5 | 1 | 115 | 22.15 | 14.21 |
| Optimized Parameters | Values |
|---|---|
| Callback | 24 |
| Number of layers | 5 |
| DNN Node | 8/12/24/12/4 |
| Learning rate | 0.0065 |
| Batch size | 15 |
| Epoch | 100 |
| Optimization algorithm | Adam |
| Decrease Rate of RMSE | 1 Week | 2 Week | 3 Week | 4 Week | 5 Week |
|---|---|---|---|---|---|
| 29.77% | 26.28% | 20.74% | 7.77% | 40.55% | |
| 37.33% | 47.27% | 29.88% | 43.33% | 50.86% | |
| 58.45% | 41.4% | 60.46% | 58.05% | 52.76% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, D.; Yoo, G.-W.; Park, S.-H.; Lee, J.-H. Assessment and Calibration of a Low-Cost PM2.5 Sensor Using Machine Learning (HybridLSTM Neural Network): Feasibility Study to Build an Air Quality Monitoring System. Atmosphere 2021, 12, 1306. https://doi.org/10.3390/atmos12101306
Park D, Yoo G-W, Park S-H, Lee J-H. Assessment and Calibration of a Low-Cost PM2.5 Sensor Using Machine Learning (HybridLSTM Neural Network): Feasibility Study to Build an Air Quality Monitoring System. Atmosphere. 2021; 12(10):1306. https://doi.org/10.3390/atmos12101306
Chicago/Turabian StylePark, Donggeun, Geon-Woo Yoo, Seong-Ho Park, and Jong-Hyeon Lee. 2021. "Assessment and Calibration of a Low-Cost PM2.5 Sensor Using Machine Learning (HybridLSTM Neural Network): Feasibility Study to Build an Air Quality Monitoring System" Atmosphere 12, no. 10: 1306. https://doi.org/10.3390/atmos12101306
APA StylePark, D., Yoo, G.-W., Park, S.-H., & Lee, J.-H. (2021). Assessment and Calibration of a Low-Cost PM2.5 Sensor Using Machine Learning (HybridLSTM Neural Network): Feasibility Study to Build an Air Quality Monitoring System. Atmosphere, 12(10), 1306. https://doi.org/10.3390/atmos12101306







