Data-Driven Wildfire Risk Prediction in Northern California
Abstract
1. Introduction
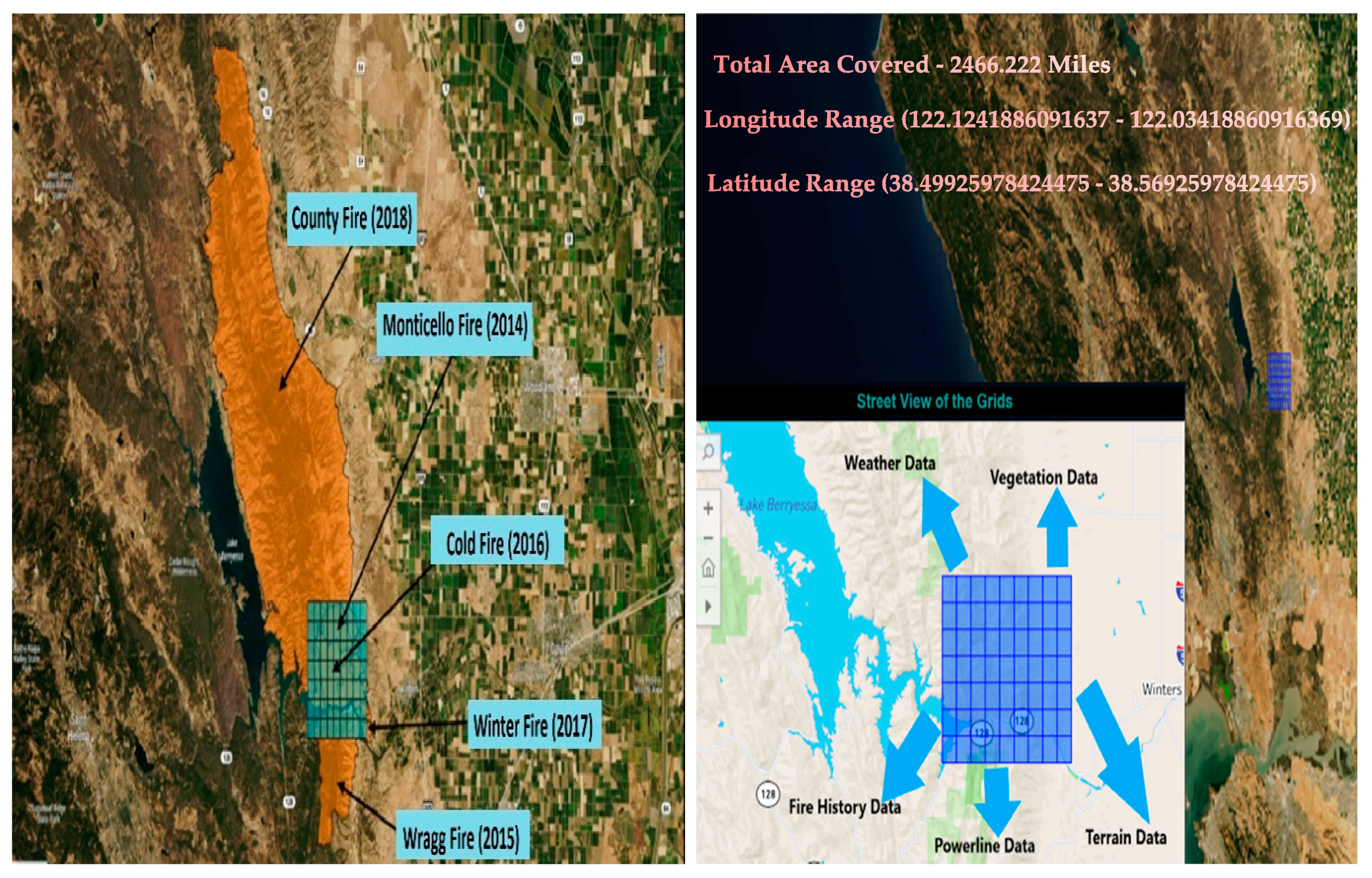
2. Study Area and Datasets
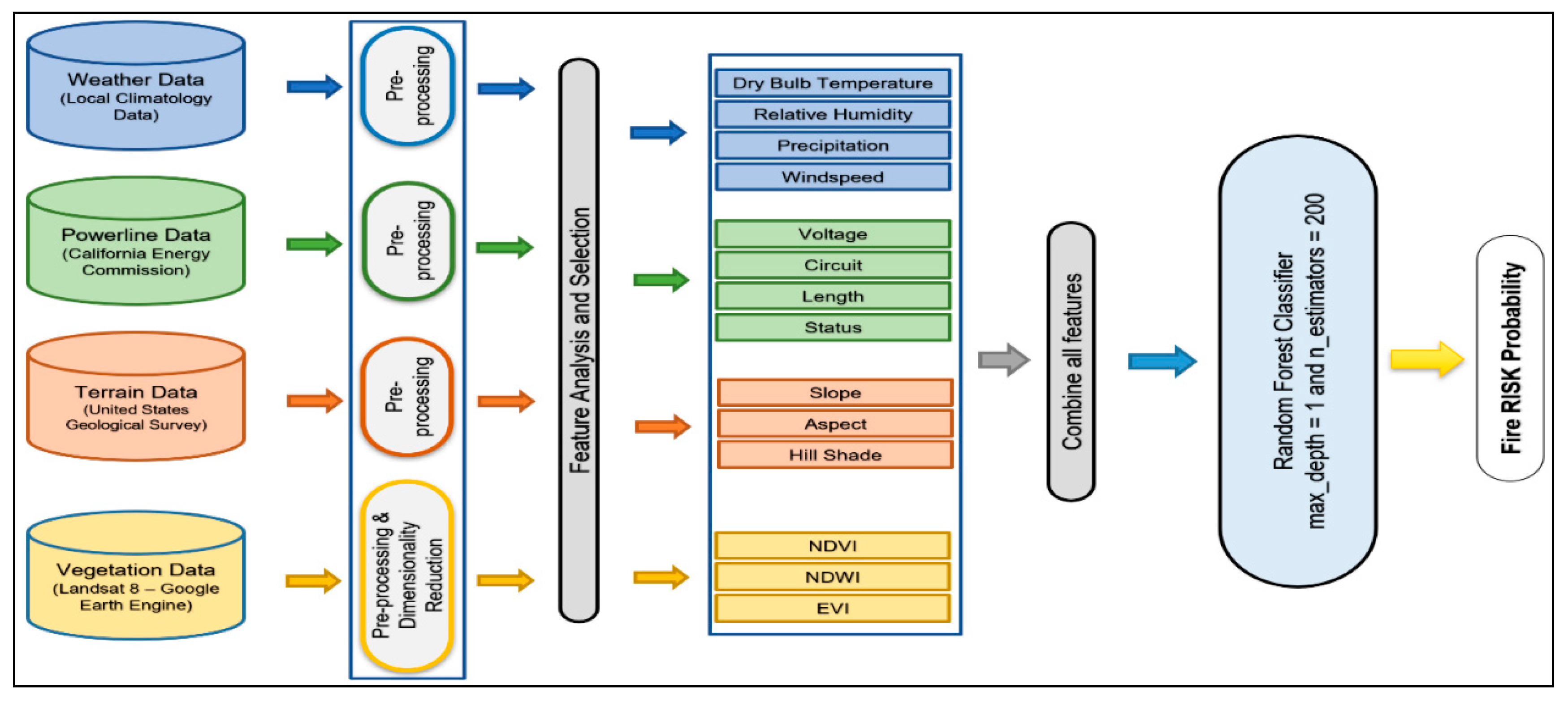
2.1. Data Sources
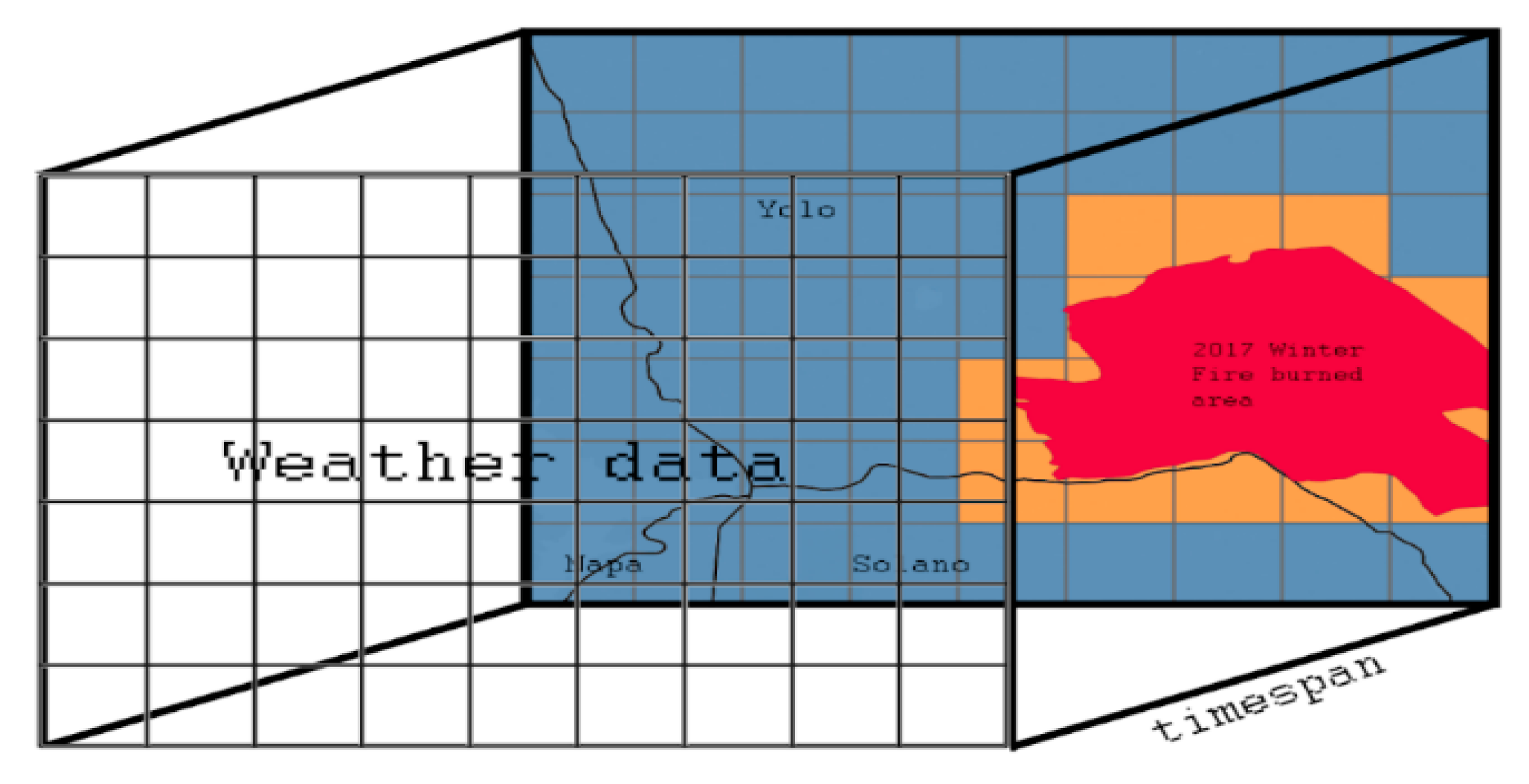
2.2. Data Pre-Processing
- A.
- Fire history data processing
- B.
- Weather data processing
- For a single station, if the previous and next hour record is present for the missing value, we took the mean of the previous and next hour record and filled the missing value
- For a single station, if there is consecutive data missing for up to 10 days, we took the previous years’ data of the same date
- C.
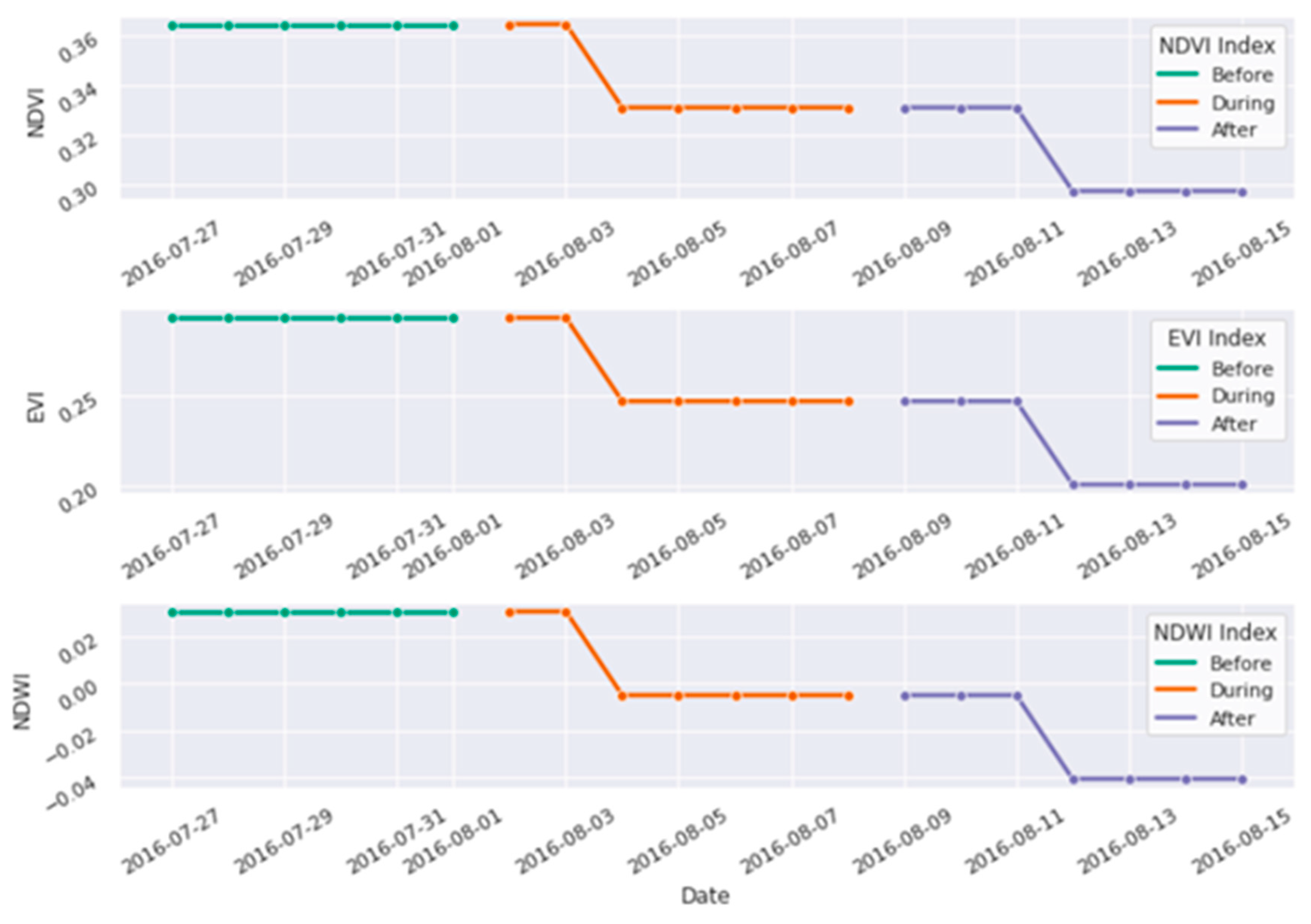
- Vegetation data processing
- D.
- Powerline data processing
- E.
- Terrain data processing
- (1)
- Degree: The inclination of the slope is calculated in degrees. The values range from 0 to 90.
- (2)
- Scaled: The inclination of the slope is calculated the same as degrees, but the z-factor is adjusted for scale.
- (3)
- Percent Rise: The inclination of the slope is output as percentage values. The values range from 0 to essentially infinity. A flat surface is 0 percent, and a 45-degree surface is 100 percent, and as the surface becomes more vertical, the percent rise becomes increasingly larger.
3. Wildfire Risk Prediction Models
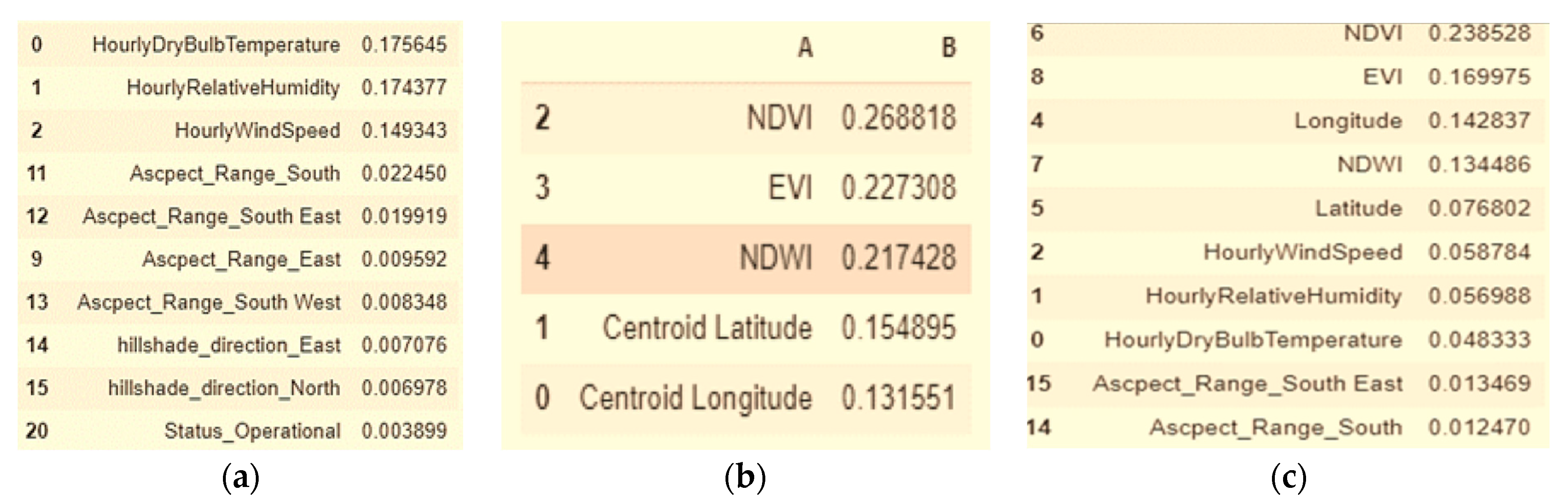
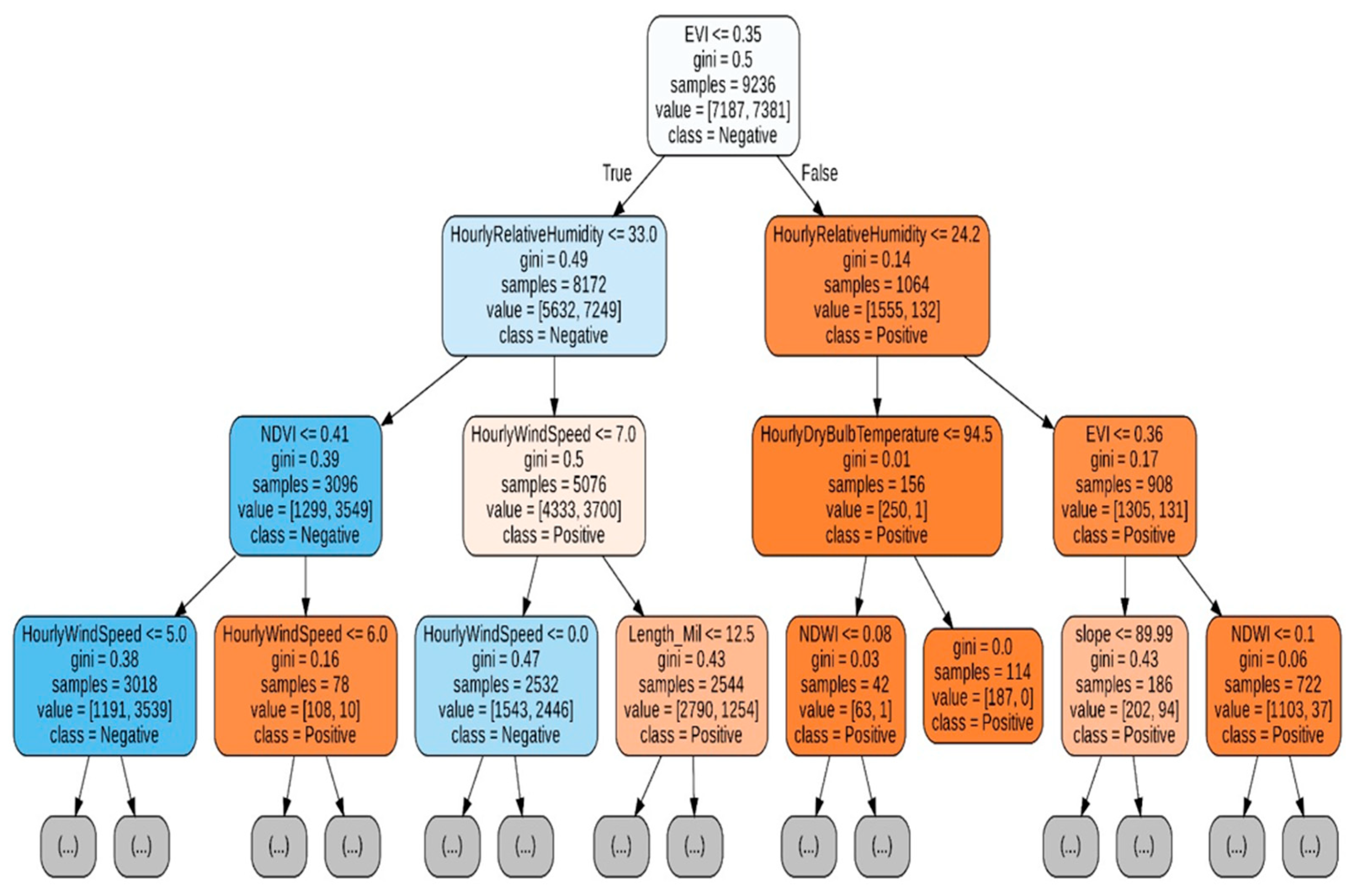
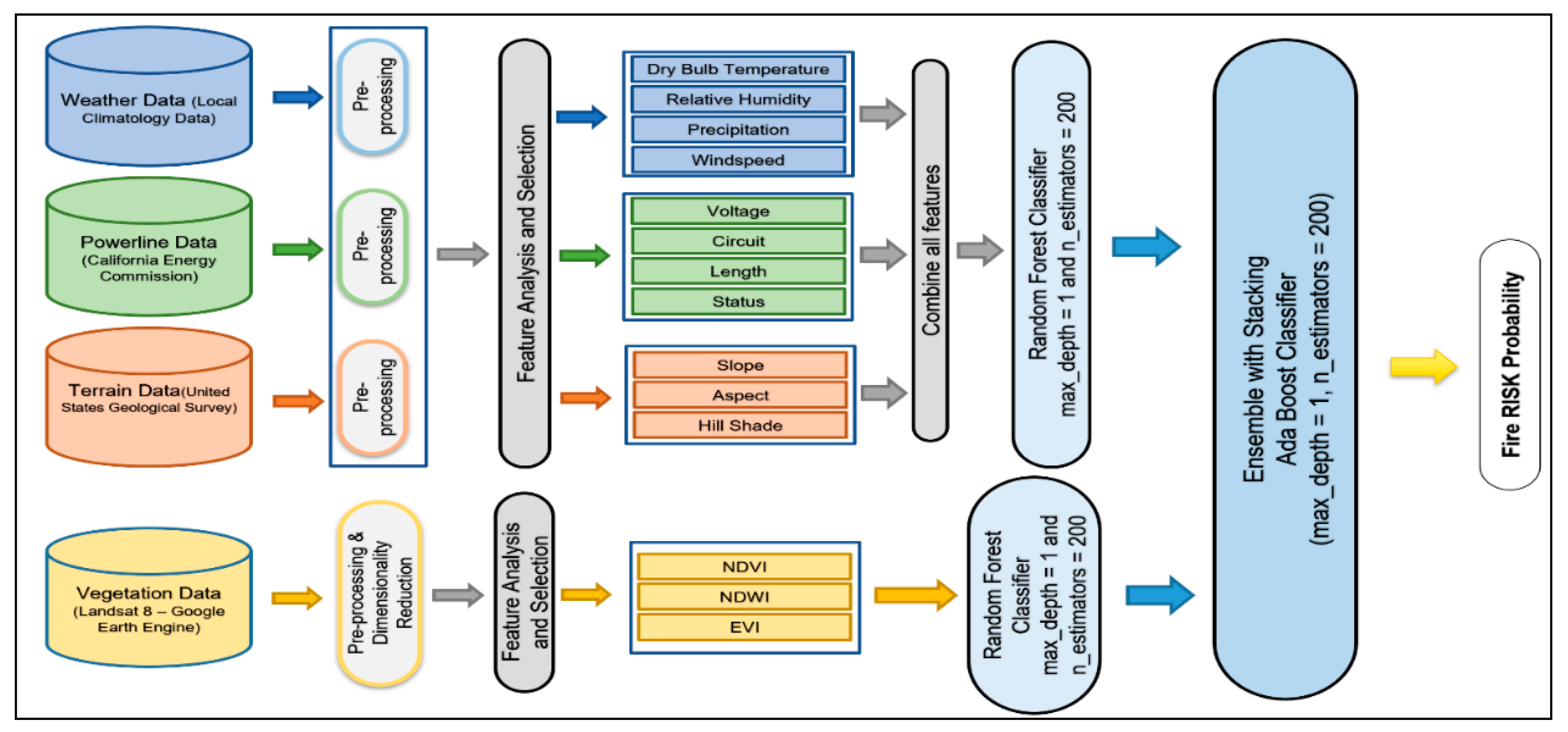
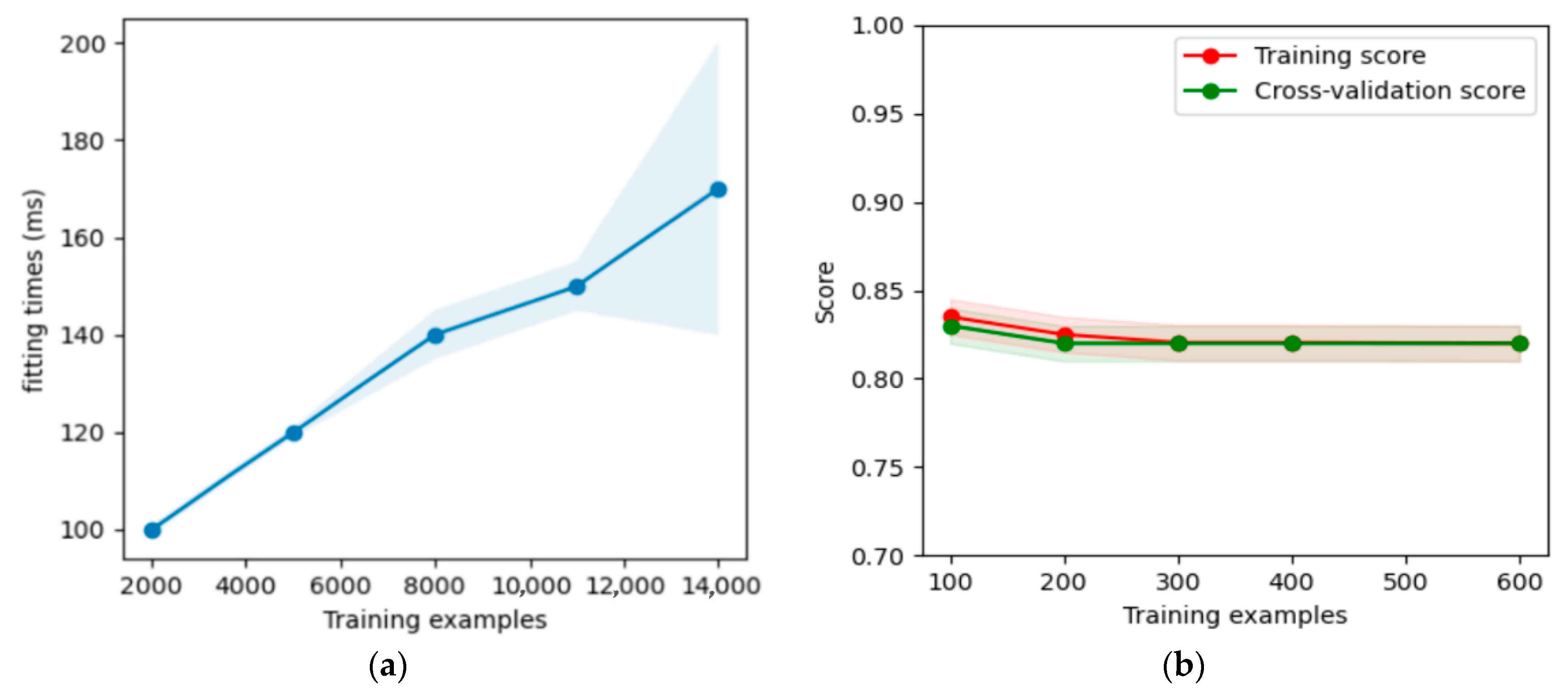
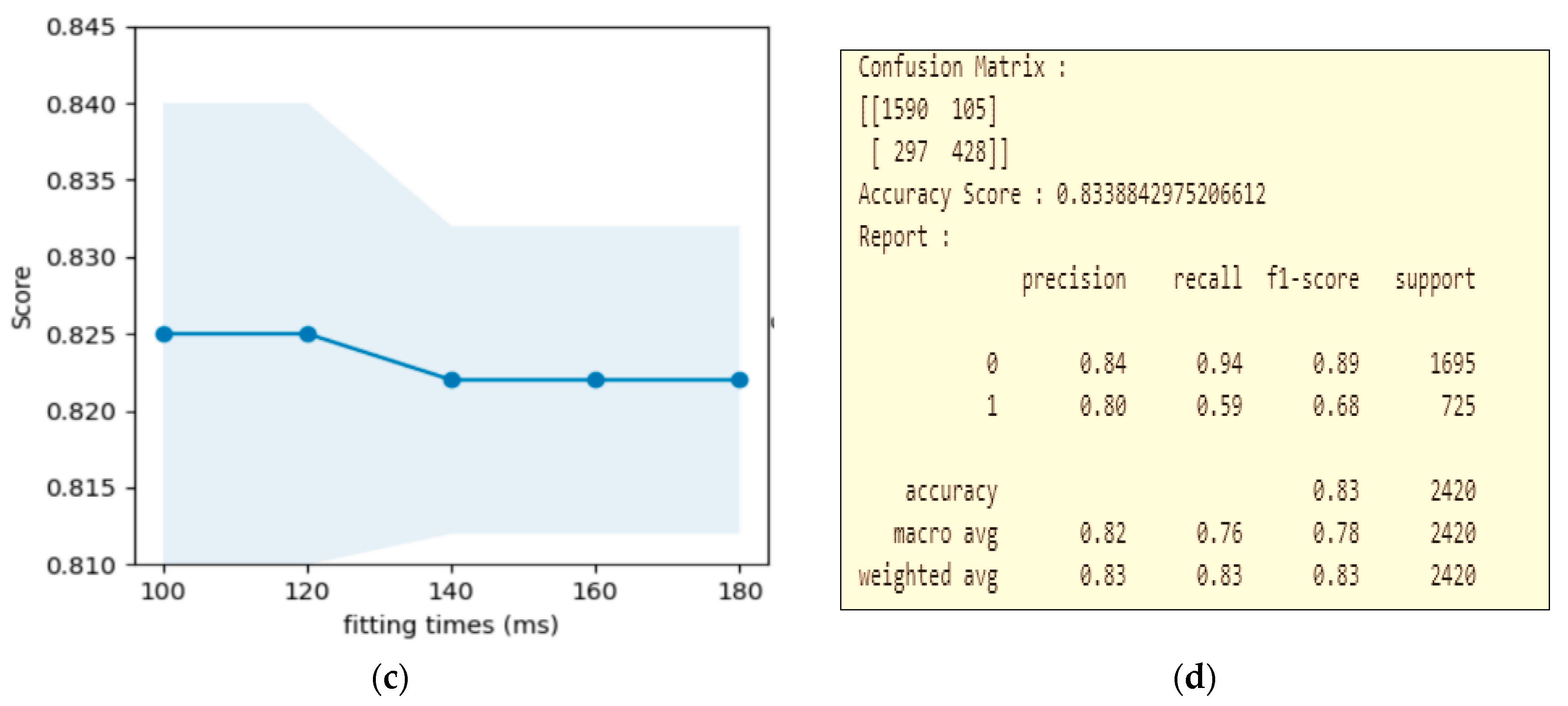
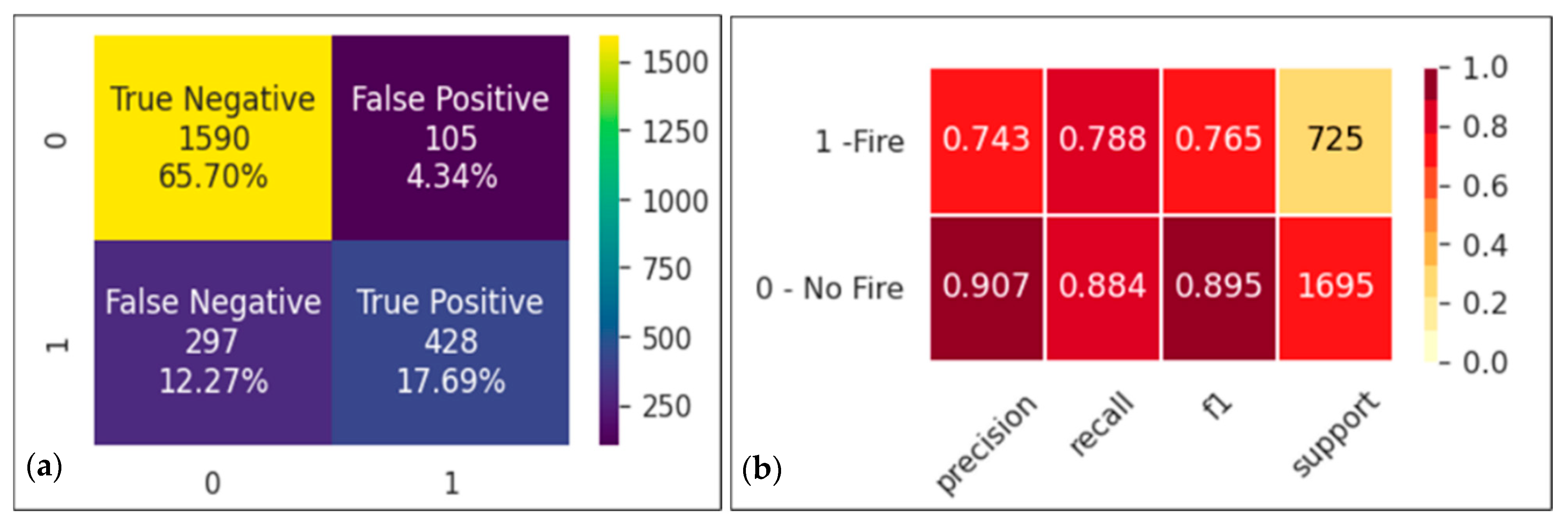
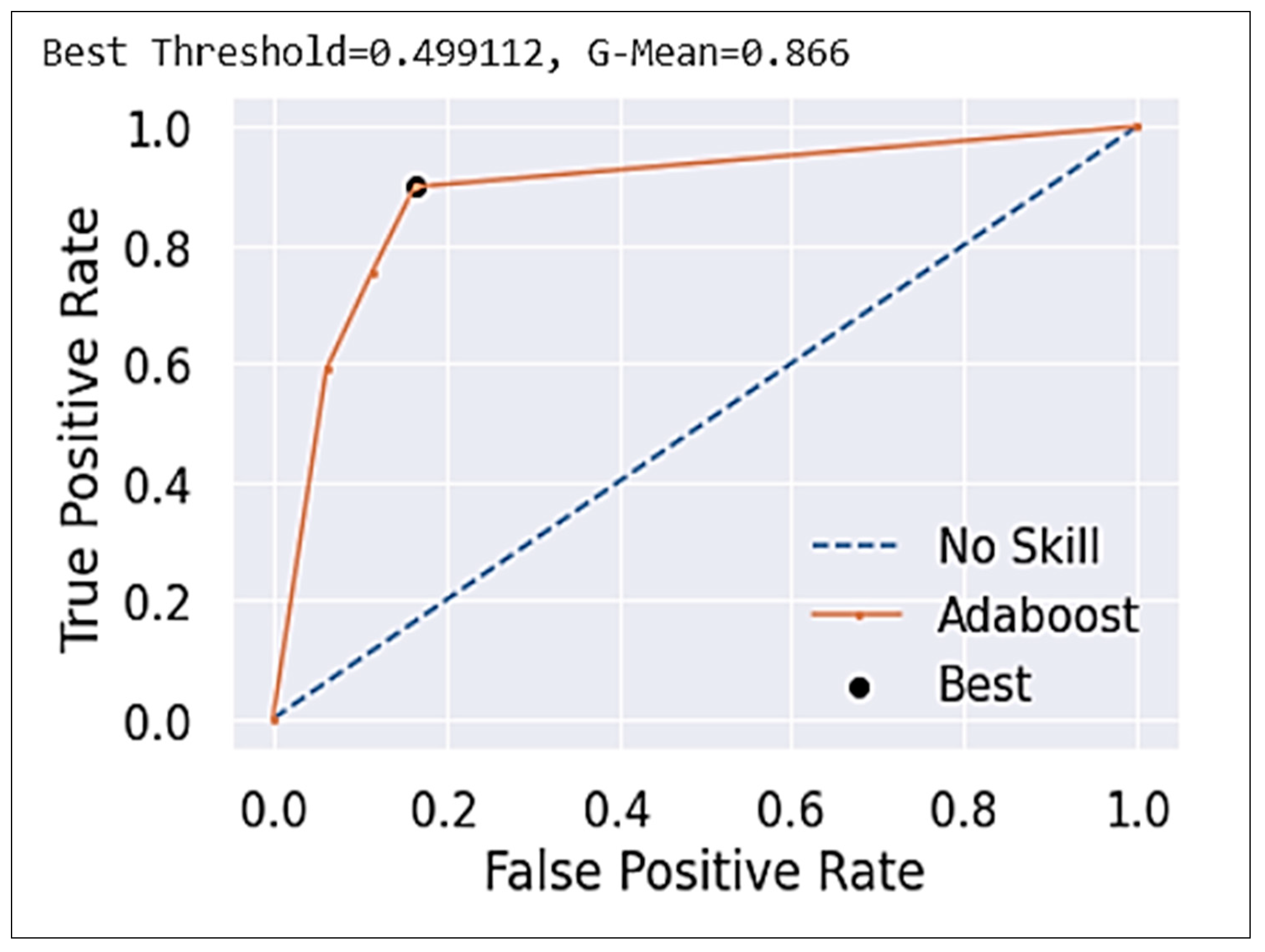
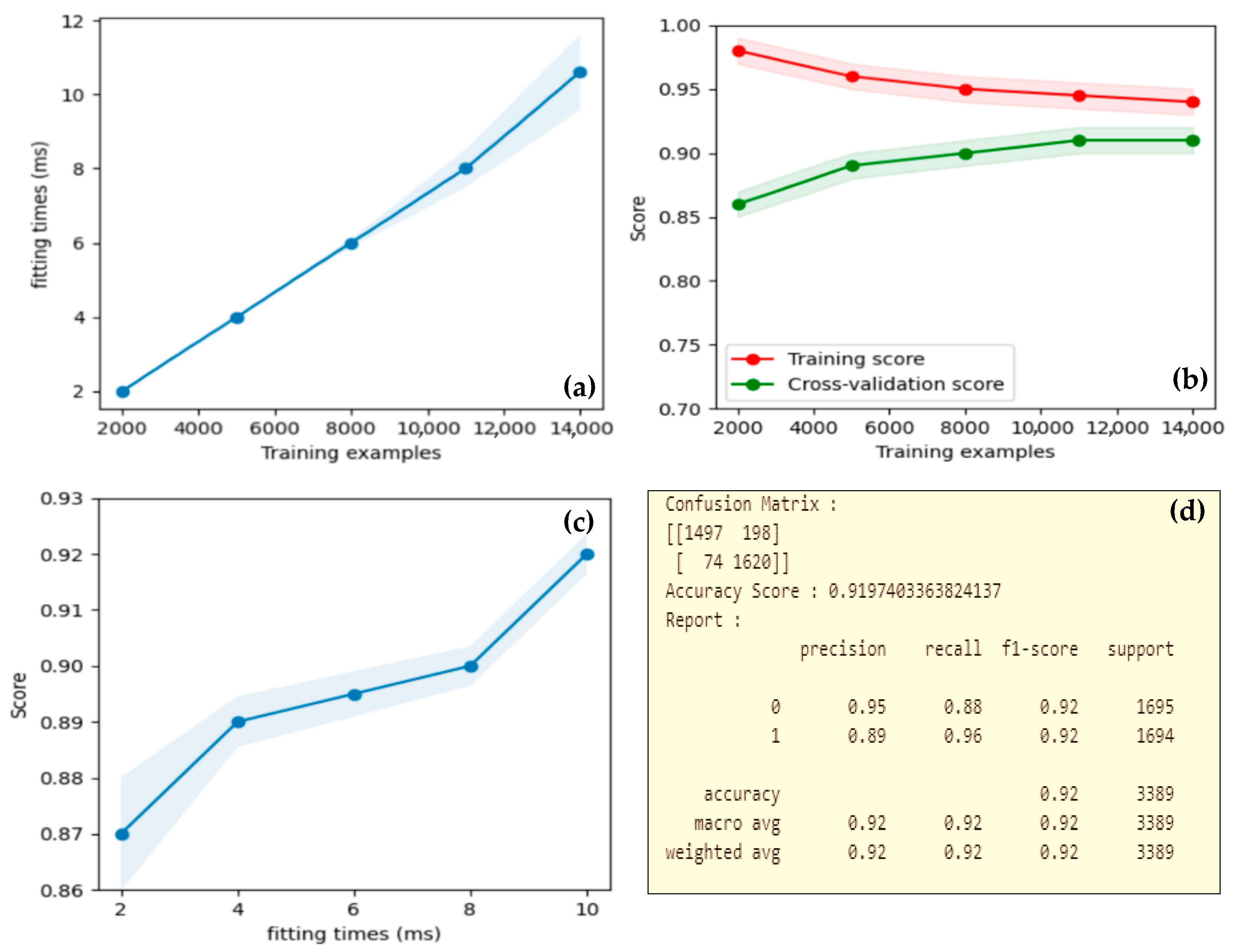
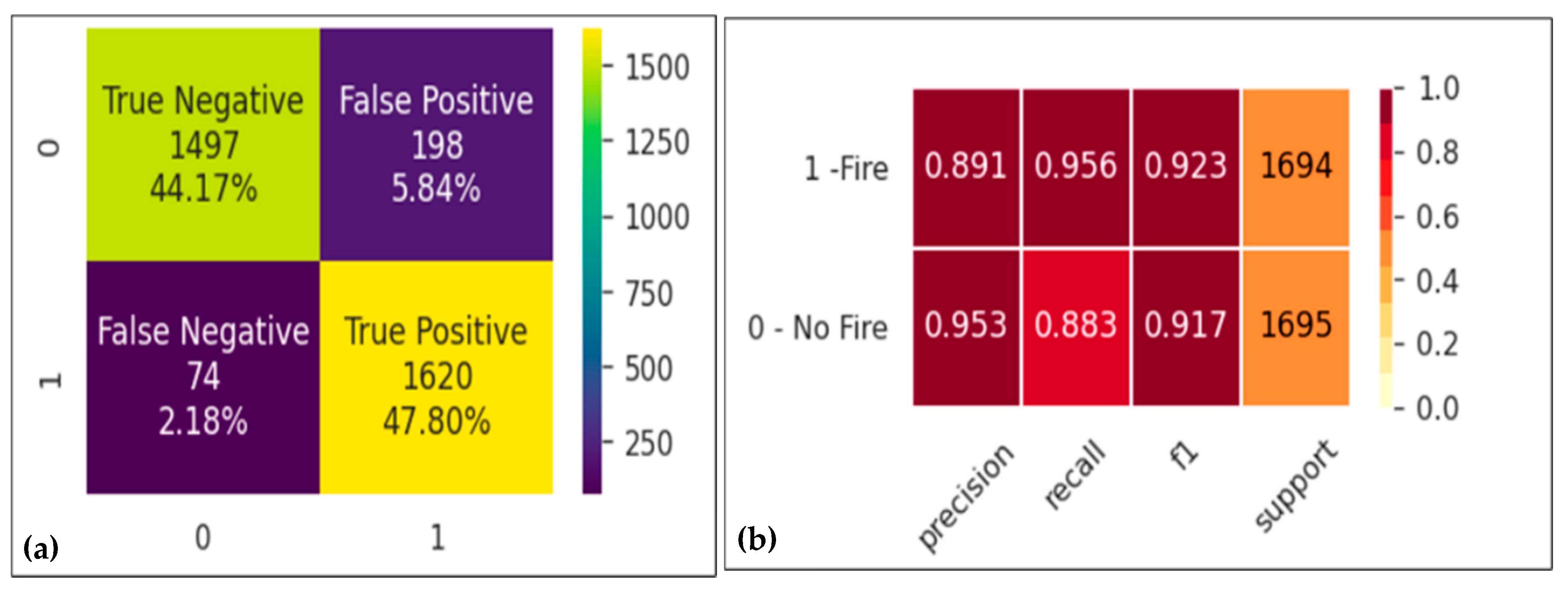
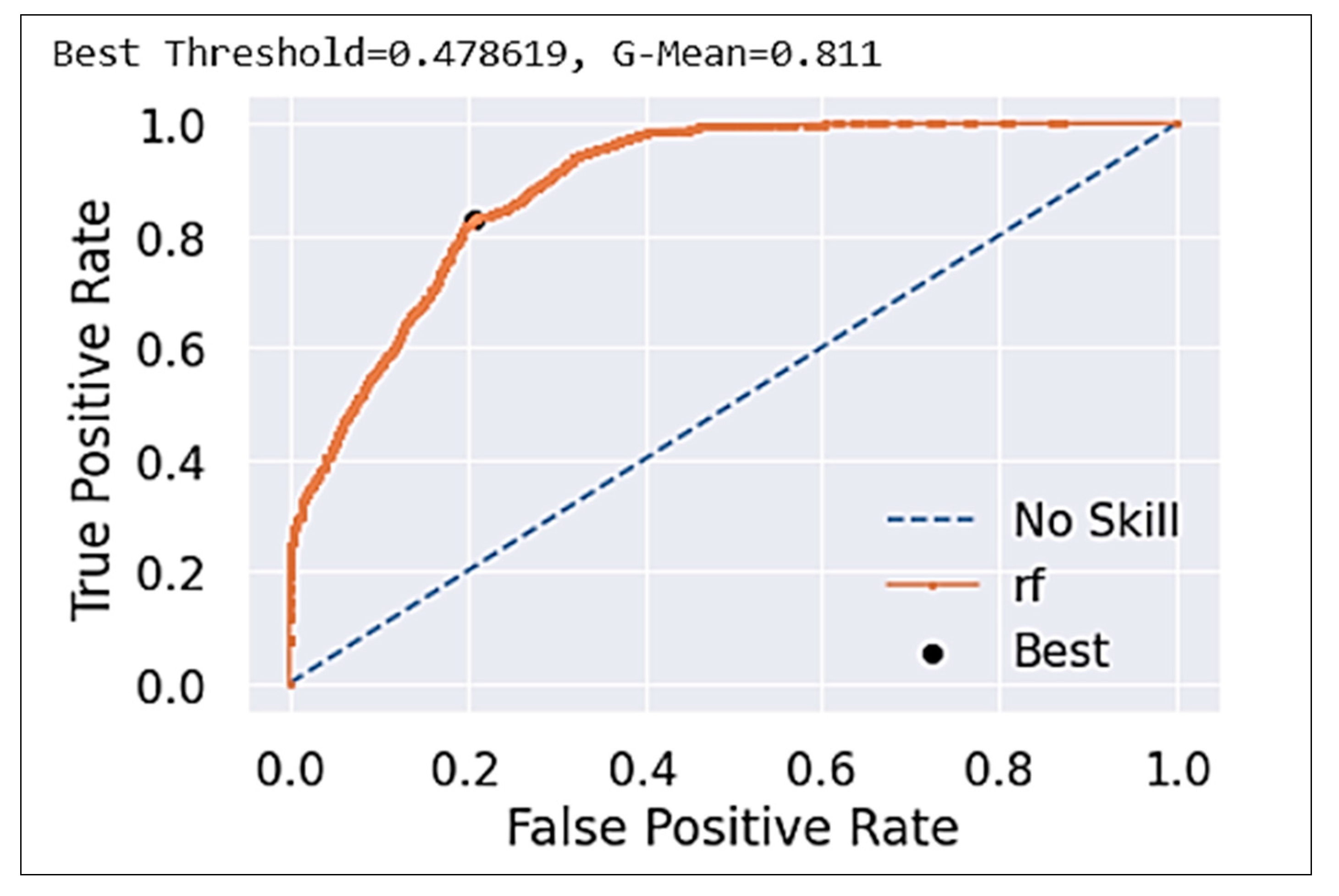
3.1. An Ensemble Model
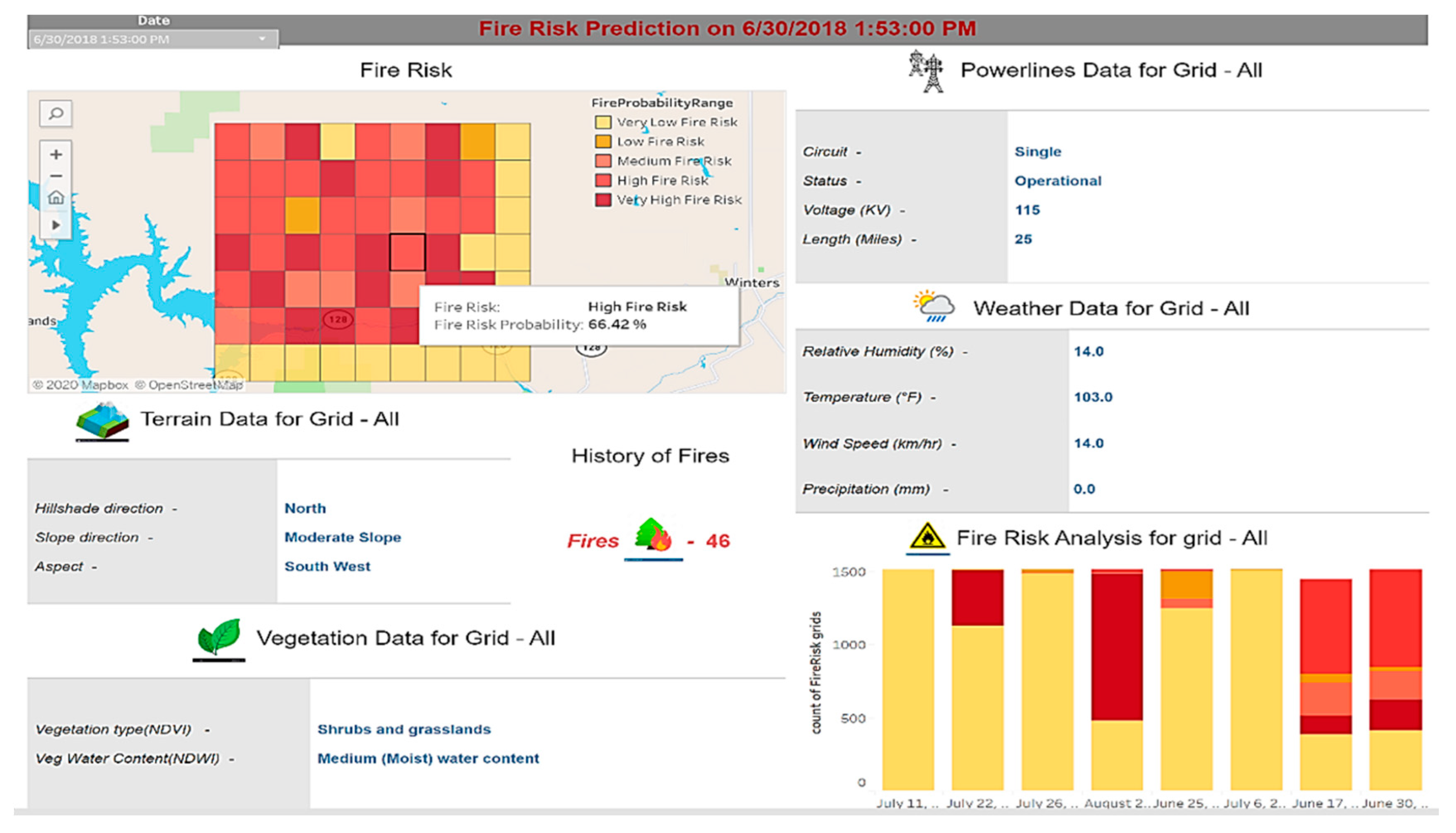
3.2. Combined Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Saleh, Y.; Hamid, R.P.; Sayed, N.M.; Soheila, P.; Saeedeh, E.; John, P.T. A Machine learning framework for multi-hazards modeling and mapping in a mountainous area. Sci. Rep. 2020, 10, 12144. [Google Scholar]
- World Economic Forum. Available online: https://www.weforum.org/agenda/2019/05/the-vicious-climate-wildfire-cycle (accessed on 9 May 2019).
- Calmatters. Available online: https://calmatters.org/explainers/californias-worsening-wildfires-explained/ (accessed on 20 August 2020).
- Scasta, J.; Weir, J.; Stambaugh, M. Droughts and Wildfires in Western U.S. Rangelands 2016, 38, 197–203. [Google Scholar] [CrossRef]
- California Department of Forestry and Fire Protection. Available online: https://www.fire.ca.gov/stats-events/ (accessed on 13 January 2021).
- Tiziano, G.; Bachisio, A.; Grazia, P.; Pierpaolo, D. An Improved Cellular Automata for Wildfire Spread. Procedia Comput. Sci. 2015, 51, 2287–2296. [Google Scholar]
- Bianchinia, G.; Caymes-Scutariab, P.; Méndez-Garabettiab, M. Evolutionary-Statistical System: A parallel method for improving forest fire spread prediction. J. Comput. Sci. 2015, 6, 58–66. [Google Scholar] [CrossRef]
- Miguel, M.G.; Germán, B.; Paola, C.S.; María, L.T. Increase in the quality of the prediction of a computational wildfire behavior method through the improvement of the internal metaheuristic. Fire Safe. J. 2016, 82, 49–62. [Google Scholar]
- Andrés, C.; Ana, C.; Tomàs, M. Applying Probability Theory for the Quality Assessment of a Wildfire Spread Prediction Framework Based on Genetic Algorithms. Sci. World J. 2013, 2013, 728414. [Google Scholar]
- Andrés, C.; Ana, C.; Tomàs, M. Response time assessment in forest fire spread simulation: An integrated methodology for efficient exploitation of available prediction time. Environ. Model. Softw. 2014, 54, 153–164. [Google Scholar]
- Andrés, C.; Ana, C.; Tomàs, M. Relieving Uncertainty in Forest Fire Spread Prediction by Exploiting Multicore Architectures. Procedia Comput. Sci. 2015, 51, 1752–1761. [Google Scholar]
- Philippe, J.G.; Guru, J.B.; BabuMagda, B. A Novel Visualization Environment to Support Modelers in Analyzing Data Generated by Cellular Automata, the Lecture Notes in Computer Science book series. In Proceedings of the International Conference on Digital Human Modeling and Applications in Health, Safety, Ergonomics and Risk Management, Toronto, ON, Canada, 23 June 2016; pp. 529–540. [Google Scholar]
- George, E.S.; Imad, H.E.; George, M.; Uchechukwu, C.W. Artificial Intelligence for Forest Fire Prediction. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechanotrics, Montreal, ON, Canada, 6–9 July 2010. [Google Scholar]
- Onur, S.; Suha, B.; Cenk, D. Mapping regional forest fire probability using artificial neural network model in a Mediterranean forest ecosystem. Geomat. Nat. Haz. Risk 2016, 7, 1645–1658. [Google Scholar]
- Stojanova, D.; Kobler, A.; Ogrinc, P.; Ženko, B.; Džeroski, S. Estimating the risk of fire outbreaks in the natural environment. Data Min. Knowl. Discov. 2011, 24, 411–442. [Google Scholar] [CrossRef]
- Guruh, F.S.; Khabib, M. Predicting Size of Forest Fire Using Hybrid Model. In Proceedings of the Conference ICT-EurAsia 2014: Information and Communication Technology, Bali, Indonesia, 14–17 April 2014; pp. 316–327. [Google Scholar]
- Marcos, R.; Juan, R. An insight into machine-learning algorithms to model human-caused wildfire occurrence. Environ. Model Softw. 2014, 57, 192–201. [Google Scholar]
- Famiglietti, C.; Holtzman, N.; Campolo, J. Satellite-Based Prediction of Fire Risk in Northern California. Stanford University; Final Report, 2018. [Google Scholar]
- Salehi, M.; Rusu, L.I.; Lynar, T.; Phan, A. Dynamic and Robust Wildfire Risk Prediction System: An Unsupervised Approach. In Proceedings of the KDD ’16: The 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Dutta, R.; Das, A.; Aryal, J. Big data integration shows Australian bush-fire frequency is increasing significantly. R. Soc. Open Sci. 2016, 3, 150241. [Google Scholar] [CrossRef] [PubMed]
- Fire Perimeters GIS Data, California Department of Forestry and Fire Protection. Available online: https://frap.fire.ca.gov/frap-projects/fire-perimeters/ (accessed on 13 January 2021).
- NAIP Imagery, United States Department of Agriculture from Service Agency. Available online: https://www.fsa.usda.gov/programs-and-services/aerial-photography/imagery-programs/naip-imagery/ (accessed on 13 January 2021).
- Staff, S.X. Proba-V images Portuguese forest fire. Phys. Org. 2017.
- El-Nesr, M. Filling Gaps of a Time-Series Using Python. Medium. Available online: https://medium.com/@drnesr/filling-gaps-of-a-time-series-using-python-d4bfddd8c460 (accessed on 31 December 2018).
- Landsat Science, NASA. Available online: https://landsat.gsfc.nasa.gov/landsat-8/ (accessed on 20 February 2020).
- NDVI, NDBI & NDWI Calculation Using Landsat 7, 8. Asian Institute. Available online: https://www.linkedin.com/pulse/ndvi-ndbi-ndwi-calculation-using-landsat-7-8-tek-bahadur-kshetri/ (accessed on 30 September 2018).
- Landsat Surface Reflectance-Derived Spectral Indices. USGS. Available online: https://www.usgs.gov/media/images/landsat-surface-reflectance-and-enhanced-vegetation-index (accessed on 13 January 2021).
- Brownlee, J. SMOTE Oversampling for Imbalanced Classification with Python. Machine Learning Mastery. 17 January 2020. [Google Scholar]
| Paper ID | Region | Purpose and Area of Study | ML Model | Accuracy (in Percentage) | Data Params | |||
|---|---|---|---|---|---|---|---|---|
| Fire History | Weather | Land | Other | |||||
| Famiglietti, C., et al. (2018) | Lebanon | Fire Risk prediction | SVM | 96.00% | Daily Number of Fire | Temperature, Humidity, Solar radiation, Precipitation | N.A. | N.A. |
| Dutta, R., et al. (2016) | Slovenia | Fire outbreak predictive model | IBk | 80.50% | Fire History | Temperature, Humidity, Wind Speed, Solar radiation, Precipitation, Transpiration & Evaporation, Weather Forecast | Land usages, Altitude, Soil Moisture | Traffic Corridor, Settlement Map |
| NB | 81.00% | |||||||
| J48 | 78.60% | |||||||
| JRip | 81.50% | |||||||
| LogR | 83.00% | |||||||
| SVM | 83.00% | |||||||
| AdaBoost | 83.30% | |||||||
| BagJ48 | 84.90% | |||||||
| RF | 82.50% | |||||||
| Bnet | 81.70% | |||||||
| NB | 55.32% | |||||||
| DT | 86.07% | |||||||
| RF | 66.69% | |||||||
| KNN | 86.08% | |||||||
| SVM | 91.31% | |||||||
| BRT | 73.00% | |||||||
| SVM | 70.90% | |||||||
| LR | 68.60% | |||||||
| El-Nesr, M. (2018) | Blue Mountains, Australia | Fire risk prediction | CBFR | 85–90% | Daily Number of Fire | N.A. | Elevation | N.A. |
| NASA (2020) | Australia | Wildfire hotspot prediction | KNN | 91.76% | Fire History | Humidity, Wind Speed, Solar radiation, Transpiration and Evaporation, Heat Flux, Vapor Pressure | Soil Moisture | N.A. |
| Bagging Tree | 94.53% | |||||||
| Ensemble | 91.00% | |||||||
| Our Model | Monticello and Winters, California | Wildfire risk prediction | RF | 91.76% | Fire History, Daily Number of fires | Temperature, Humidity, Precipitation, Wind Speed, Wind, Rain, Weather forecast | Slope, Hill-shade, Aspect | Vegetation Indices, Remote sensing, Powerline |
| Ensemble | 91.00% | |||||||
| Data | Data Type | Sources | Time Range |
|---|---|---|---|
| Fire History | Shape file | Fire and Resource Assessment Program (FRAP), CAL Fire, United States Forest MSDA Project, Service region, Bureau of Land Management, and National park service | 2015–2018 |
| Weather | Censor data (CSV file) | Climate Data Online (CDO) and Local Climatology Data (LCD) | 2015–2018 |
| Vegetation | Remote-sensing satellite data | Landsat 8 satellite using Google Earth Engine (GEE) | 2014–2019 |
| Powerline | Shape file | California Energy Commission | N.A. |
| Terrain | DEM file | United States Geological Survey (USGS) | N.A. |
| Data Used | Positive Target Data | Negative Target Data |
|---|---|---|
| Type I | Data during fire | 7 Days before fire |
| Type II | Data on fire start date | Data before the fire |
| Type III | Data before fire | Data after fire |
| Type IV | Data on fire start date, excluding no-fire grids | Data before the fire, excluding no-fire grids |
| Model | Accuracy | Hyper-Parameters Used |
|---|---|---|
| Random Forest | 92 | n_estimators = 200 |
| Adaboost | 91.5 | n_estimators = 50, learning_rate = 1 |
| Gradient Boosting trees | 90.5 | loss=deviance, n_estimators = 100 |
| Weighted Decision Trees | 89.1 | criterion = gini, splitter = best |
| MLP | 86.1 | activation = Softmax, solver = adam |
| LSTM | 91.6 | Dropout = 0.2, activation = Softmax |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Malik, A.; Rao, M.R.; Puppala, N.; Koouri, P.; Thota, V.A.K.; Liu, Q.; Chiao, S.; Gao, J. Data-Driven Wildfire Risk Prediction in Northern California. Atmosphere 2021, 12, 109. https://doi.org/10.3390/atmos12010109
Malik A, Rao MR, Puppala N, Koouri P, Thota VAK, Liu Q, Chiao S, Gao J. Data-Driven Wildfire Risk Prediction in Northern California. Atmosphere. 2021; 12(1):109. https://doi.org/10.3390/atmos12010109
Chicago/Turabian StyleMalik, Ashima, Megha Rajam Rao, Nandini Puppala, Prathusha Koouri, Venkata Anil Kumar Thota, Qiao Liu, Sen Chiao, and Jerry Gao. 2021. "Data-Driven Wildfire Risk Prediction in Northern California" Atmosphere 12, no. 1: 109. https://doi.org/10.3390/atmos12010109
APA StyleMalik, A., Rao, M. R., Puppala, N., Koouri, P., Thota, V. A. K., Liu, Q., Chiao, S., & Gao, J. (2021). Data-Driven Wildfire Risk Prediction in Northern California. Atmosphere, 12(1), 109. https://doi.org/10.3390/atmos12010109







