Dynamics of Mechanical Oscillator Mechanism for Stratospheric Gravity Waves Generated by Convection
Abstract
1. Introduction
2. Dynamics
2.1. Governing Equations and Boundary Conditions
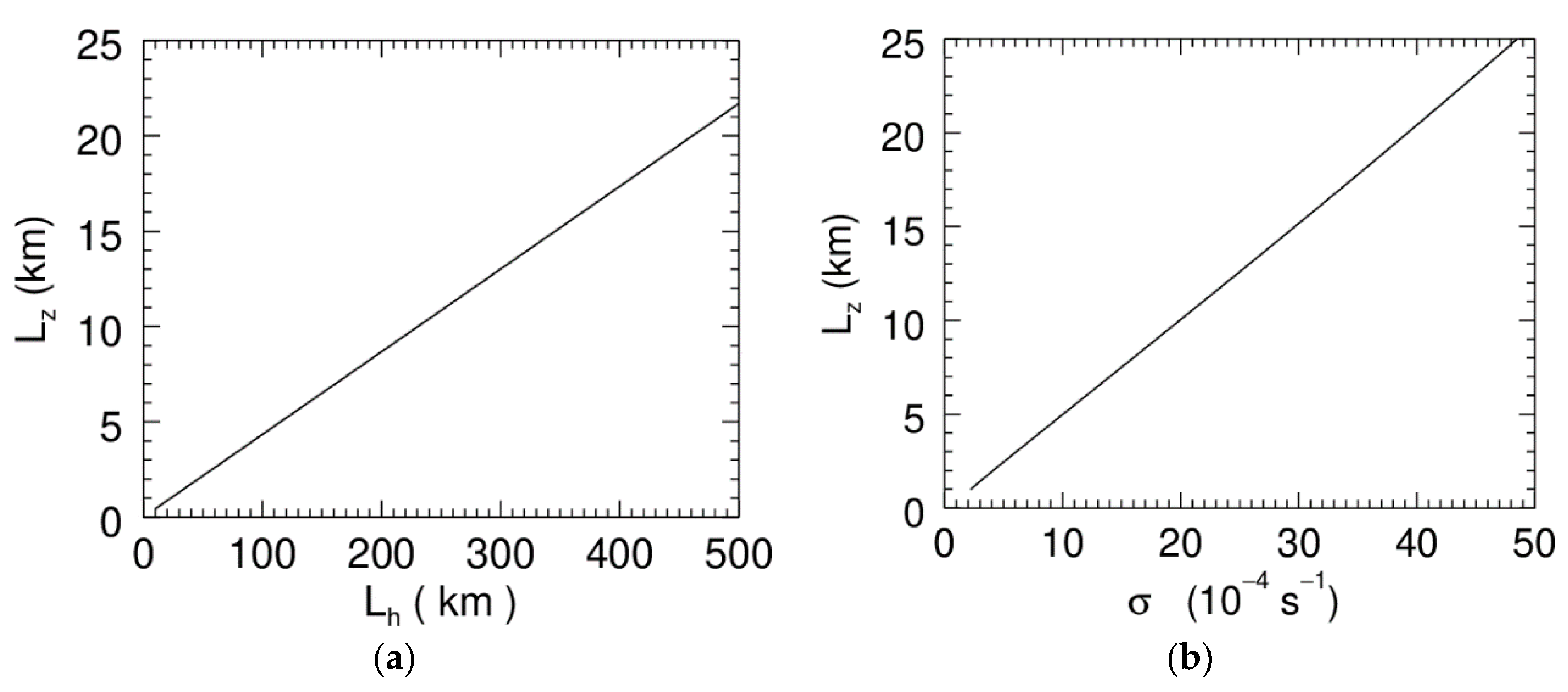
2.2. Wave Resonance
2.3. Analytical Results
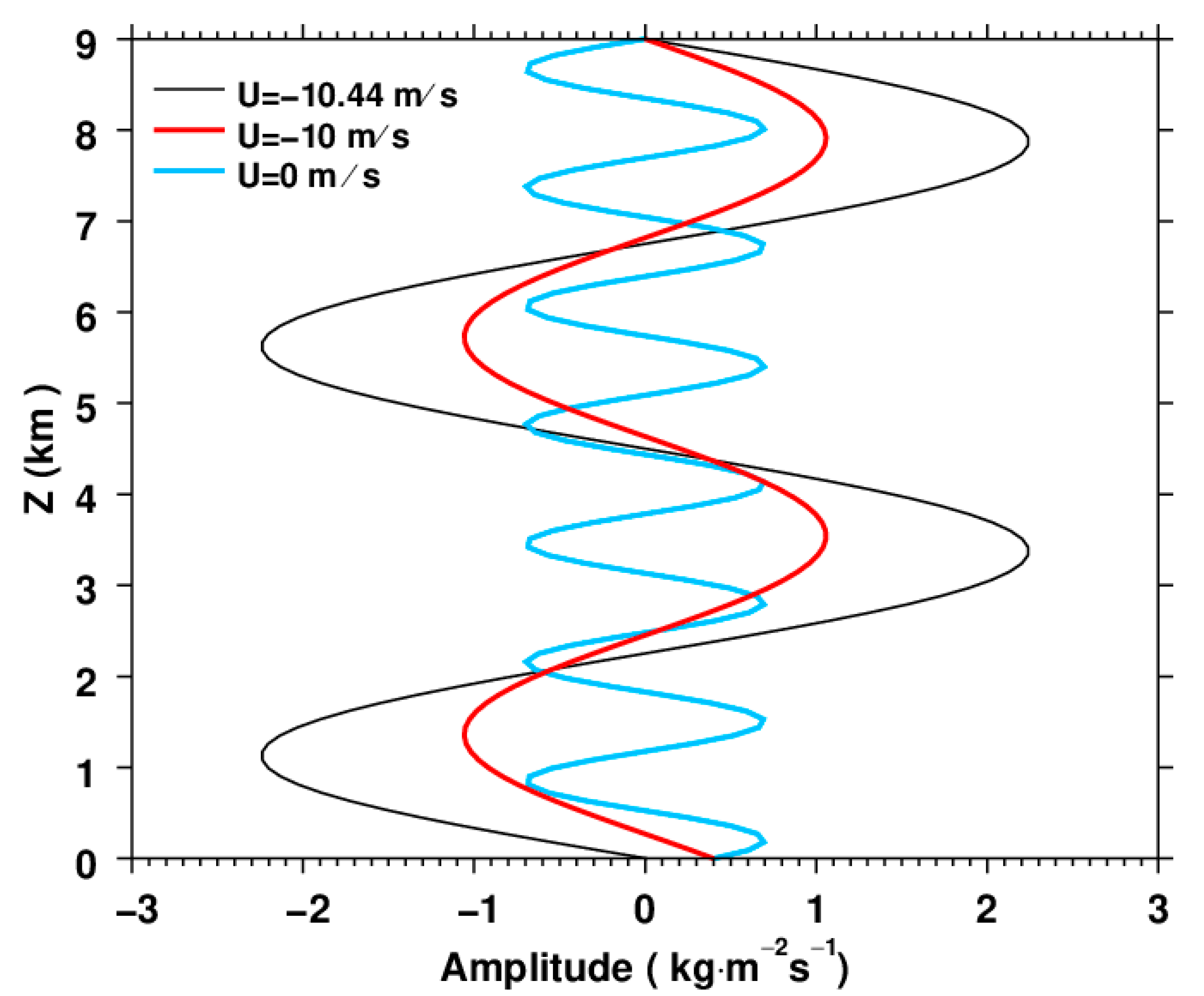
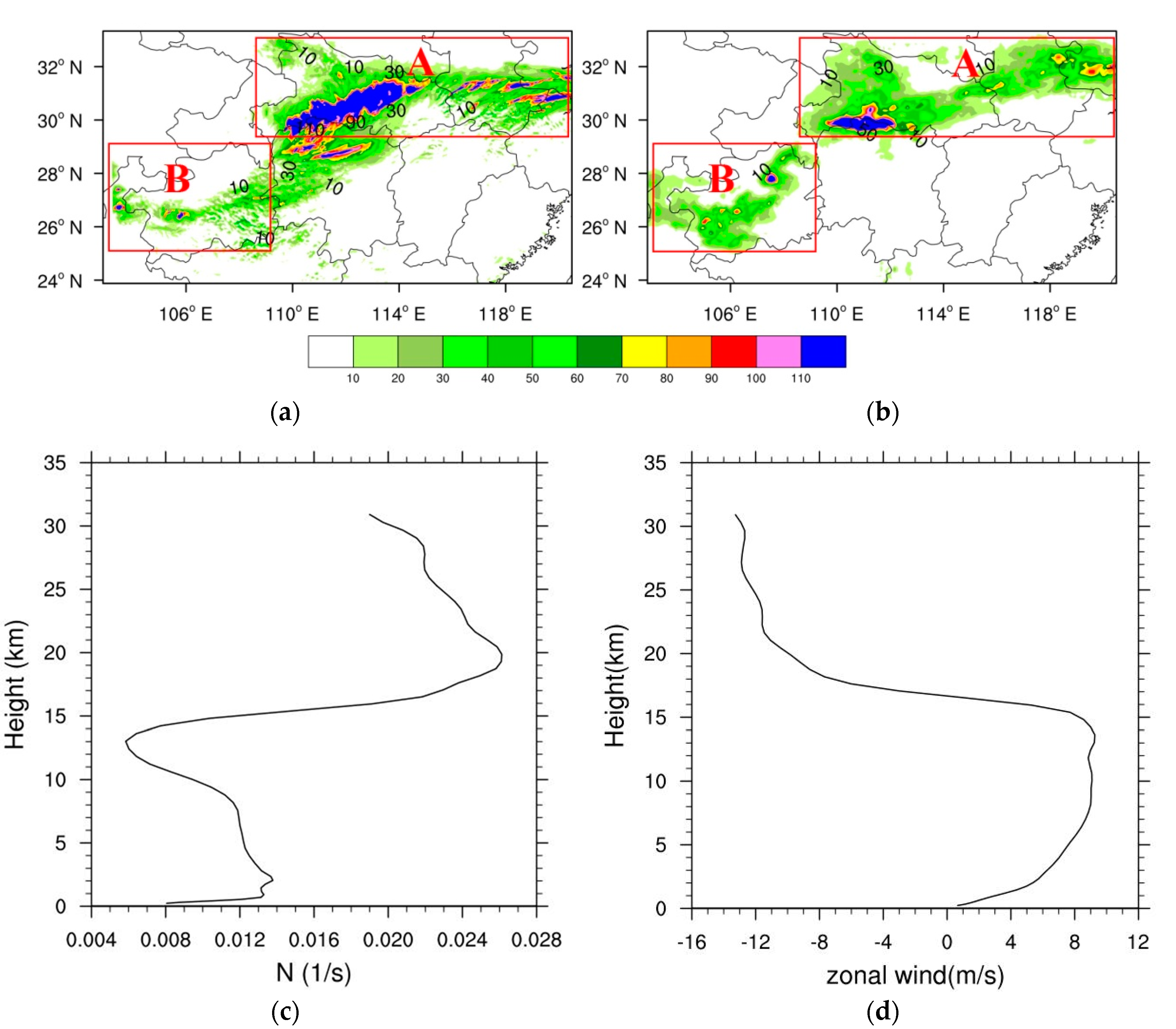
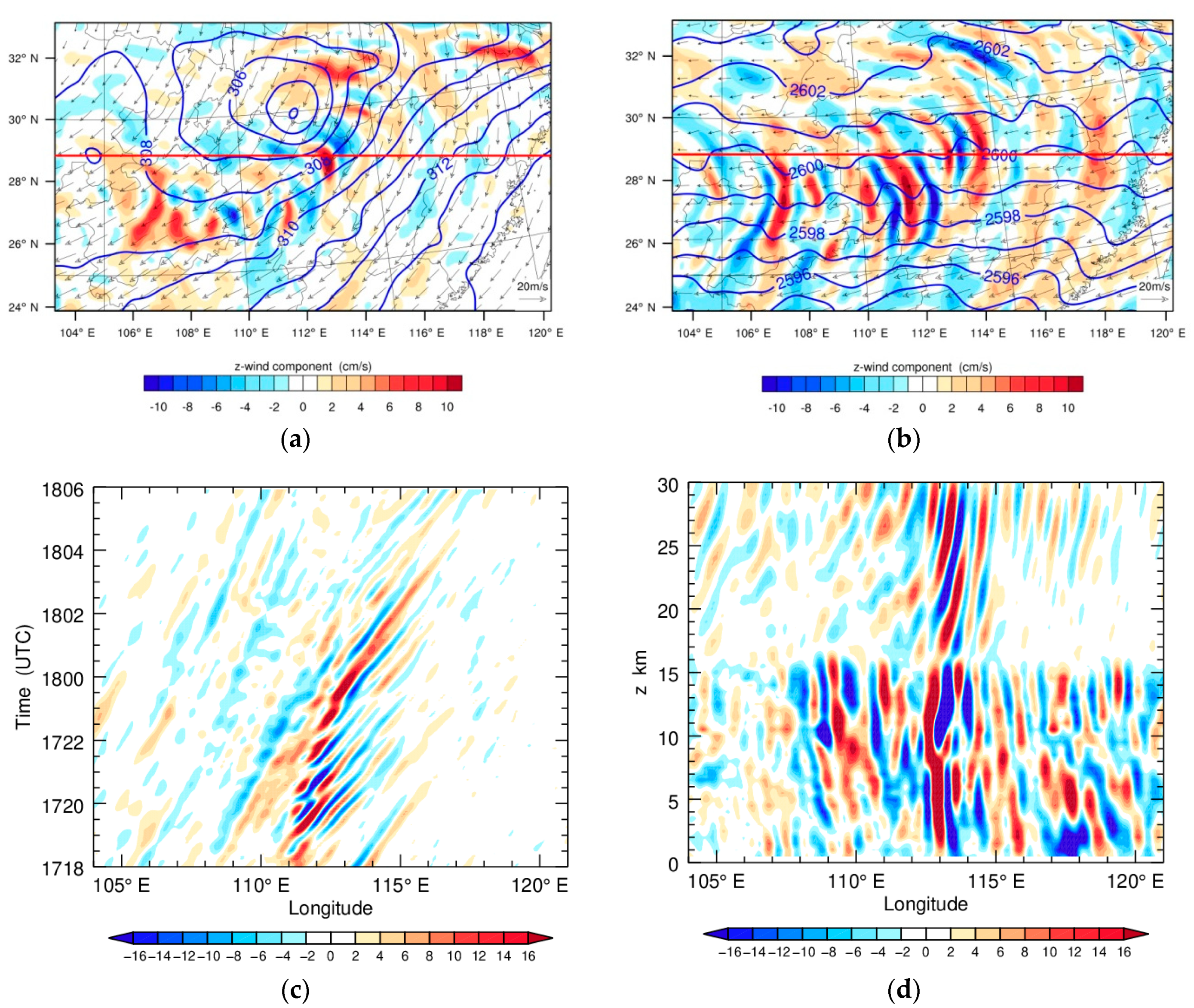
3. Numerical Simulations
3.1. Model
3.2. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Holton, J.R.; Haynes, P.H.; McIntyre, M.E.; Douglass, A.R.; Road, R.B.; Pfister, L. Stratosphere–troposphere exchange. Rev. Geophys. 1995, 33, 403–439. [Google Scholar] [CrossRef]
- Fritts, D.C.; Alexander, M.J. Gravity wave dynamics and effects in the middle atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Cohen, N.Y.; Boos, W.R. Modulation of subtropical stratospheric gravity waves by equatorial rainfall. Geophys. Res. Lett. 2016, 43, 466–471. [Google Scholar] [CrossRef]
- Alexander, M.J.; Grimsdell, A.W.; Stephan, C.C.; Hoffmann, L. MJO-related intraseasonal variation in the stratosphere: Gravity waves and zonal winds. J. Geophys. Res. Atmos. 2018, 123, 775–788. [Google Scholar] [CrossRef]
- Chen, L.; Bian, J.C.; Liu, Y.; Qiao, S. Statistical analysis of inertial gravity wave parameters in the lower stratosphere over Northern China. Clim. Dyn. 2019, 52, 563–575. [Google Scholar] [CrossRef]
- Xu, X.; Wang, Y.; Xue, M.; Zhu, K. Impacts of horizontal propagation of orographic gravity waves on the wave drag in the stratosphere and lower mesosphere. J. Geophys. Res. Atmos. 2017, 122, 11301–11312. [Google Scholar] [CrossRef]
- Clark, T.L.; Hauf, T.; Kuettner, J.P. Convectively forced internal gravity waves: Results from two-dimensional numerical experiments. Q. J. R. Meteorol. Soc. 1986, 112, 899–925. [Google Scholar] [CrossRef]
- Snyder, C.; Skamarock, W.C.; Rotunno, R. Frontal dynamics near and following frontal collapse. J. Atmos. Sci. 1993, 50, 3194–3212. [Google Scholar] [CrossRef]
- Zhang, F. Generation of mesoscale gravity waves in the upper-tropospheric jet–front systems. J. Atmos. Sci. 2004, 61, 440–457. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, F. Mesoscale gravity waves in moist baroclinic jet–front systems. J. Atmos. Sci. 2014, 71, 929–952. [Google Scholar] [CrossRef]
- Pfister, L.; Scott, S.; Loewenstein, M. Mesoscale disturbances in the tropical stratosphere excited by convection: Observations and effects on the stratospheric momentum budget. J. Atmos. Sci. 1993, 50, 1058–1075. [Google Scholar] [CrossRef][Green Version]
- Alexander, M.J.; Vincent, R.A. Gravity waves in the tropical lower stratosphere: A model study of seasonal and interannual variability. J. Geophys. Res. Atmos. 2000, 105, 17983–17993. [Google Scholar] [CrossRef]
- Vadas, S.L. Compressible F-plane solutions to body forces, heatings, and coolings, and application to the primary and secondary gravity waves generated by a deep convective plume. J. Geophys. Res. Space Phys. 2013, 118, 2377–2397. [Google Scholar] [CrossRef]
- Chen, D.; Chen, Z.Y.; Lü, D.R. Spatiotemporal spectrum and momentum flux of the stratospheric gravity waves generated by a typhoon. Sci. China Earth Sci. 2013, 56, 54–62. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, L.; Peng, J.; Guan, J. Mesoscale Gravity Waves in the Mei-Yu Front System. J. Atmos. Sci. 2018, 75, 587–609. [Google Scholar] [CrossRef]
- Lin, Y.L.; Smith, R.B. Transient dynamics of airflow near a local heat source. J. Atmos. Sci. 1986, 43, 40–49. [Google Scholar] [CrossRef][Green Version]
- Bretherton, C.S. Group velocity and the linear response of stratified fluids to internal heat or mass sources. J. Atmos. Sci. 1988, 45, 81–93. [Google Scholar] [CrossRef]
- Piani, C.; Durran, D.R.; Alexander, M.J.; Holton, J.R. A numerical study of three-dimensional gravity waves triggered by deep tropical convection and their role in the dynamics of the QBO. J. Atmos. Sci. 2000, 57, 3689–3702. [Google Scholar] [CrossRef]
- Sayed, A.A.M.; Campbell, L.J. A two-layer model for steady-amplitude gravity waves and convection generated by a thermal forcing. J. Atmos. Sci. 2018, 75, 2199–2216. [Google Scholar] [CrossRef]
- Beres, J.H.; Alexander, M.J.; Holton, J.R. Effects of tropospheric wind shear on the spectrum of convectively generated gravity waves. J. Atmos. Sci. 2002, 59, 1805–1824. [Google Scholar] [CrossRef]
- Lai, C.; Yue, J.; Xu, J. Suomi NPP VIIRS/DNB imagery of nightglow gravity waves from various sources over China. Adv. Space Res. 2017, 59, 1951–1961. [Google Scholar] [CrossRef]
- Pierce, A.D.; Coroniti, S.C. A mechanism for the generation of acoustic–gravity waves during thunderstorm formation. Nature 1966, 210, 1209–1210. [Google Scholar] [CrossRef]
- Fovell, R.; Durran, D.; Holton, J.R. Numerical simulations of convectively generated stratospheric gravity waves. J. Atmos. Sci. 1992, 49, 1427–1442. [Google Scholar] [CrossRef]
- Alexander, M.J.; Pfister, L. Gravity wave momentum flux in the lower stratosphere over convection. Geophys. Res. Lett. 1995, 22, 2029–2032. [Google Scholar] [CrossRef]
- Lane, T.P.; Reeder, M.J.; Clark, T.L. Numerical modeling of gravity wave generation by deep tropical convection. J. Atmos. Sci. 2001, 58, 1249–1274. [Google Scholar] [CrossRef]
- Lane, T.P.; Reeder, M.J. Convectively generated gravity waves and their effect on the cloud environment. J. Atmos. Sci. 2001, 58, 2427–2440. [Google Scholar] [CrossRef]
- Chun, H.-Y.; Song, I.-S.; Horinouchi, T. Momentum flux spectrum of convectively forced gravity waves: Can diabatic forcing be a proxy for convective forcing? J. Atmos. Sci. 2005, 62, 4113–4120. [Google Scholar] [CrossRef]
- Choi, E.-H.; Chun, H.-Y. Generation mechanisms of convectively induced internal gravity waves in a three-dimensional framework. Asia-Pac. J. Atmos. Sci. 2014, 50, 163–177. [Google Scholar] [CrossRef]
- Lecoanet, D.; Quataert, E. Internal gravity wave excitation by turbulent convection. R. Astron. Soc. 2013, 430, 2363–2376. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, L. Semi-circle theorem of unstable spectrum distribution of heterotropic perturbation and the upper bound estimation of its growth rate. Adv. Atmos. Sci. 2002, 19, 35–44. [Google Scholar]
- Peng, J.; Zhang, L.; Luo, Y.; Zhang, Y. Mesoscale energy spectra of the Mei-Yu front system. Part I: Kinetic energy spectra. J. Atmos. Sci. 2014, 71, 37–55. [Google Scholar] [CrossRef]
- Du, Y.; Zhang, F. Banded convective activity associated with mesoscale gravity waves over southern China. J. Geophys. Res. Atmos. 2019, 124, 1912–1930. [Google Scholar] [CrossRef]
- Kim, S.-Y.; Chun, H.-Y.; Wu, D.L. A study on stratospheric gravity waves generated by Typhoon Ewiniar: Numerical simulations and observations. Geophys. Res. Lett. 2009, 114, D22104. [Google Scholar] [CrossRef]
| Background Flow (m s−1) | Horizontal Wave Speed (m s−1) | Vertical Wavelength (km) | ||
|---|---|---|---|---|
| Case 1 | 4.63 | 1.3 | 0.017 | |
| Case 2 | 4.63 | 4.37 | 0.03 | |
| Case 3 | 4.63 | 4.5 | 2.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Zhang, L.; Zhang, M.; Wang, Y. Dynamics of Mechanical Oscillator Mechanism for Stratospheric Gravity Waves Generated by Convection. Atmosphere 2020, 11, 942. https://doi.org/10.3390/atmos11090942
Yu S, Zhang L, Zhang M, Wang Y. Dynamics of Mechanical Oscillator Mechanism for Stratospheric Gravity Waves Generated by Convection. Atmosphere. 2020; 11(9):942. https://doi.org/10.3390/atmos11090942
Chicago/Turabian StyleYu, Shiwang, Lifeng Zhang, Ming Zhang, and Yuan Wang. 2020. "Dynamics of Mechanical Oscillator Mechanism for Stratospheric Gravity Waves Generated by Convection" Atmosphere 11, no. 9: 942. https://doi.org/10.3390/atmos11090942
APA StyleYu, S., Zhang, L., Zhang, M., & Wang, Y. (2020). Dynamics of Mechanical Oscillator Mechanism for Stratospheric Gravity Waves Generated by Convection. Atmosphere, 11(9), 942. https://doi.org/10.3390/atmos11090942





