Evaluation of the Four-Dimensional Ensemble-Variational Hybrid Data Assimilation with Self-Consistent Regional Background Error Covariance for Improved Hurricane Intensity Forecasts
Abstract
1. Introduction
- the self-consistent high-resolution regional HWRF ensembles are used instead of the coarser-resolution GFS ensembles to derive the flow-dependent error covariance for the GSI hybrid data assimilation system to properly resolve the error covariance of the TC inner core following the study in [9];
2. Methodology
2.1. HWRF Model
2.2. Data Assimilation (DA) Schemes
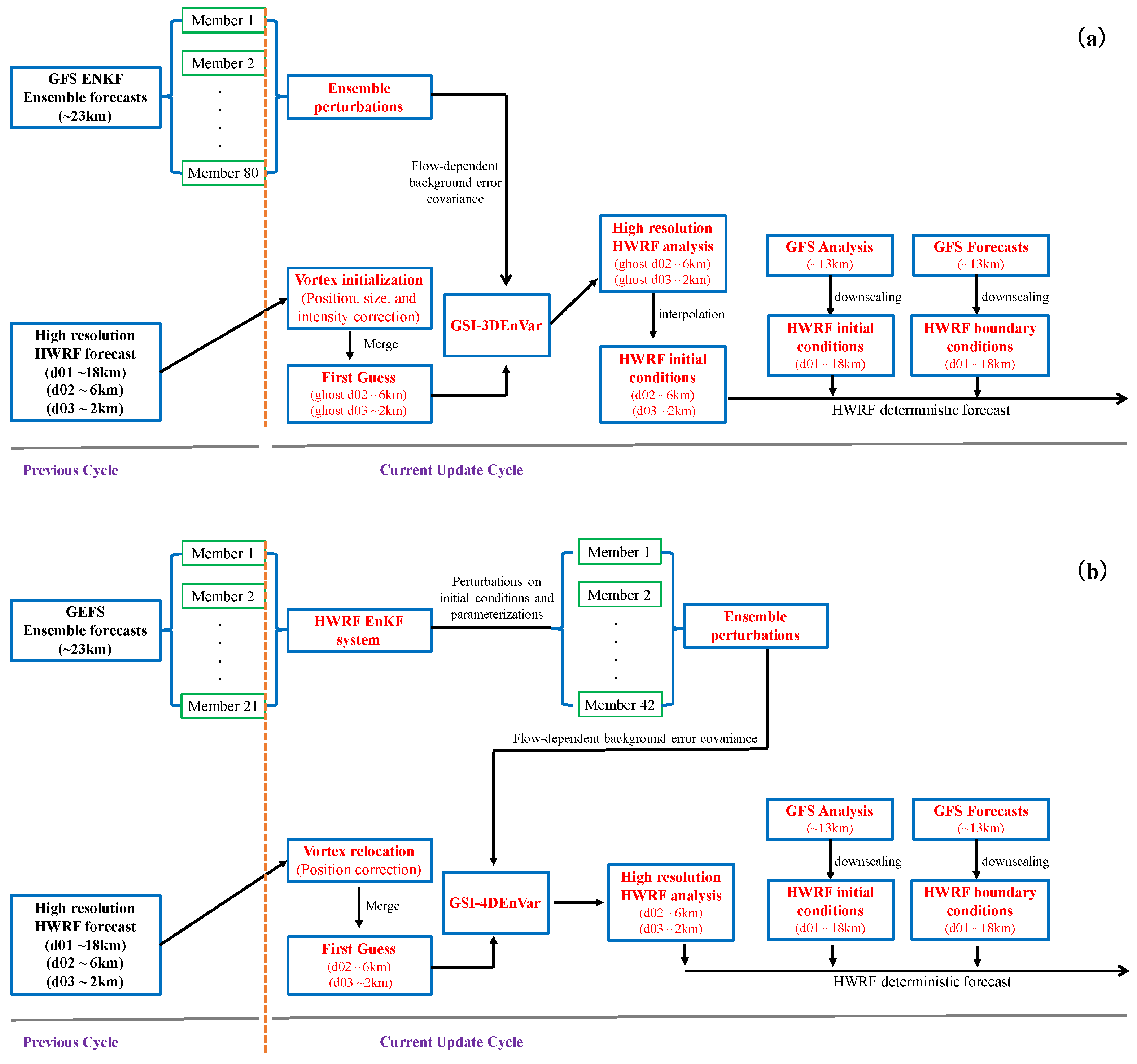
2.3. HWRF Initialization Frameworks
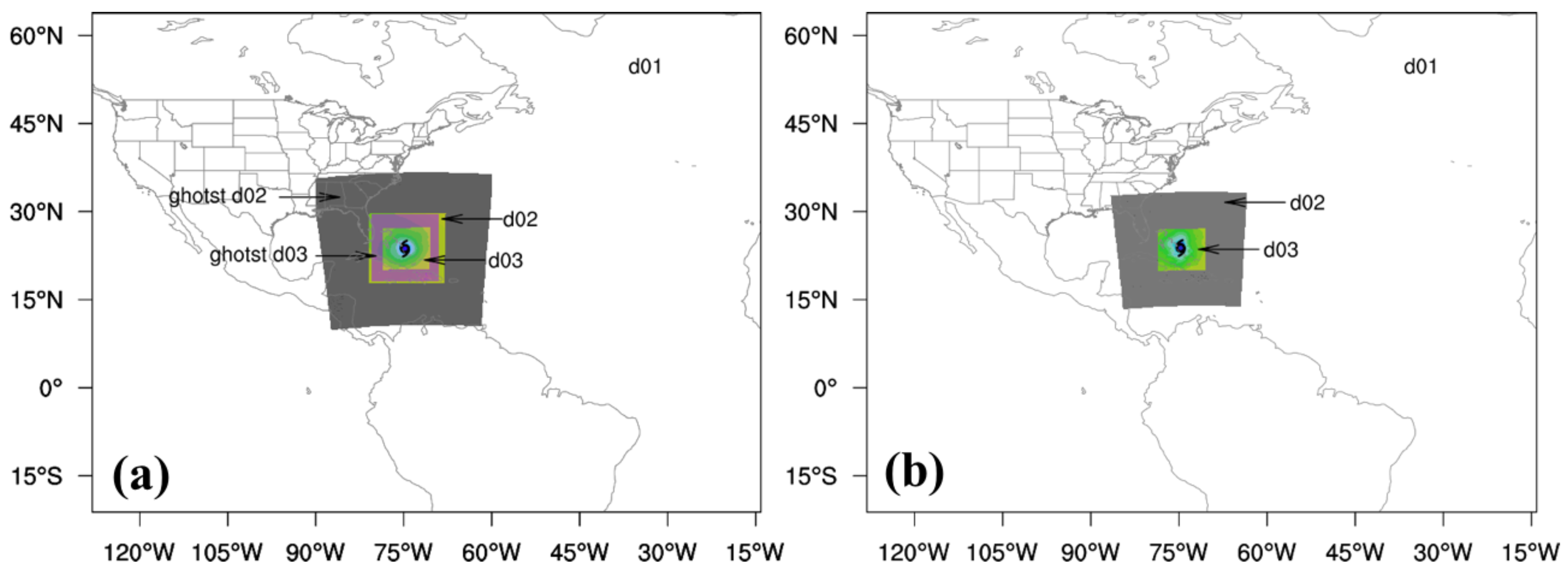
- VI is applied to the previous cycle’s HWRF forecasts in the d01 (∼18 km), d02 (∼6 km), and d03 (∼2 km) domains (see Figure 2a) to provide the first guess for DA. The VI enables the relocation, resizing, and intensity correction of the vortex using the NHC tropical cyclone vital statistics (TCVitals) database in order to correct the storm position and intensity approach to the real-time estimation.
- After VI, the improved initial conditions in d01, d02, and d03 are merged into two large domains, ghost d02 (∼6 km) and ghost d03 (∼2 km) (see Figure 2a). The ghost d02 and ghost d03 domains are an extension of forecast domains d02 and d03, respectively. The size of ghost d02 (ghost d03) is about two times larger than that of d02 (d03). The goal of this approach is to include more observations in the GSI-3DEnVar DA system for HWRF and to obtain a more realistic analysis near the domain boundaries of d02 and d03.
- Observations available for the operational HWRF are then assimilated into ghost d02 and ghost d03 by the GSI-3DEnVar system to further improve the initial conditions for the HWRF forecast. The 6-h NCEP operational GFS 80-member ensemble forecast at a resolution of T574 (∼23 km) from the previous analysis cycle is used to provide the flow-dependent background error covariance for GSI-3DEnVar within a 6-h DA window. We note that GSI-3DEnVar does not consider the temporal evolution of error covariances.
- After DA, the model fields in ghost d02 and ghost d03 are then interpolated back into the d02 and d03 domains to form the initial conditions of these two domains. The initial conditions in d01 are downscaled from GFS real-time analysis in the current HWRF analysis cycle. In addition, a “blending” scheme is activated after the VI and DA processes. This scheme blends the vortex from the VI process with the vortex after DA, and uses the blended vortex in the final analysis for the HWRF forecast. The effect of this scheme will eliminate the DA increments within 150 km of the center below 400 hPa. The details for this procedure can be referred to [10]. Moreover, the GFS forecasts are used to provide the boundary conditions for the HWRF model. With all of above information, the deterministic HWRF forecast during a specific period (e.g., 126 h) is made.
- A parallel run of the HWRF regional ensemble system [26] initialized by the forecasts from the Global Ensemble Forecast System (GEFS) is performed first to generate a 42-member self-consistent HWRF ensemble at 6-km resolution. Here, the self-consistent means that the ensemble forecasts use the same resolution and model configurations as the HWRF model. The detailed treatments and parameters used for HWRF ensemble forecasts follow those in Zhang et al. [26]. These 42-member self-consistent HWRF ensembles (6 km) are then used to provide the flow-dependent background error covariances for the GSI-4DEnVar DA system in 4DEnVar initialization framework. In this way, the DA system considers the temporal evolution of error covariances via the use of four-dimensional ensemble perturbations that are provided by high-resolution, self-consistent HWRF ensemble forecasts.
- Vortex relocation is performed on the previous cycle’s HWRF forecasts in the d02 (∼6 km) and d03 (∼2 km) domains (see Figure 2b) before DA. Vortex relocation corrects the storm position based on the NHC tropical cyclone vital statistics (TCVitals) database without changes in storm size and intensity. In addition, the size of d02 in Figure 2b for 4DEnVar initialization framework is about two times larger than that in Figure 2a for the 3DEnVar initialization framework, which is used to include more observations in the GSI-4DEnVar system and to obtain a more realistic analysis in the storm environment. The sizes of d01 and d03 in Figure 2b are the same as those in Figure 2a.
- After vortex relocation, the observations available for operational HWRF are then assimilated directly into d02 and d03 by the GSI-4DEnVar system to further improve the initial conditions in these domains. In GSI-4DEnVar, the DA window is divided into 6 observational bins; the 3-h, 4-h, 5-h, 6-h, 7-h, 8-h, and 9-h self-consistent HWRF 42-member ensemble forecasts from the first step are used to provide the flow-dependent background error covariance, realizing the time evolution of background error covariance within a 6-h DA window. We note that the 1-h observational bins are used in this study for GSI-4DEnVar as the previous study has demonstrated that the performance of GSI-4DEnVar can be enhanced with a denser observational bin [19].
- As in the 3DEnVar initialization framework, the initial conditions in d01 (Figure 2b) for 4DEnVar initialization framework are also downscaled from the GFS real-time analysis in the current HWRF analysis cycle. This is combined with the analyses from the above step for d02 and d03 to provide the initial conditions for the HWRF forecast. The GFS forecasts are still used to provide the boundary conditions. Finally, a deterministic HWRF forecast for a specific time period (e.g., 126 h) can be made.
3. Performances on the Simulation of the Rapid Weakening of Hurricane Joaquin
3.1. Balances in HWRF Initial Conditions
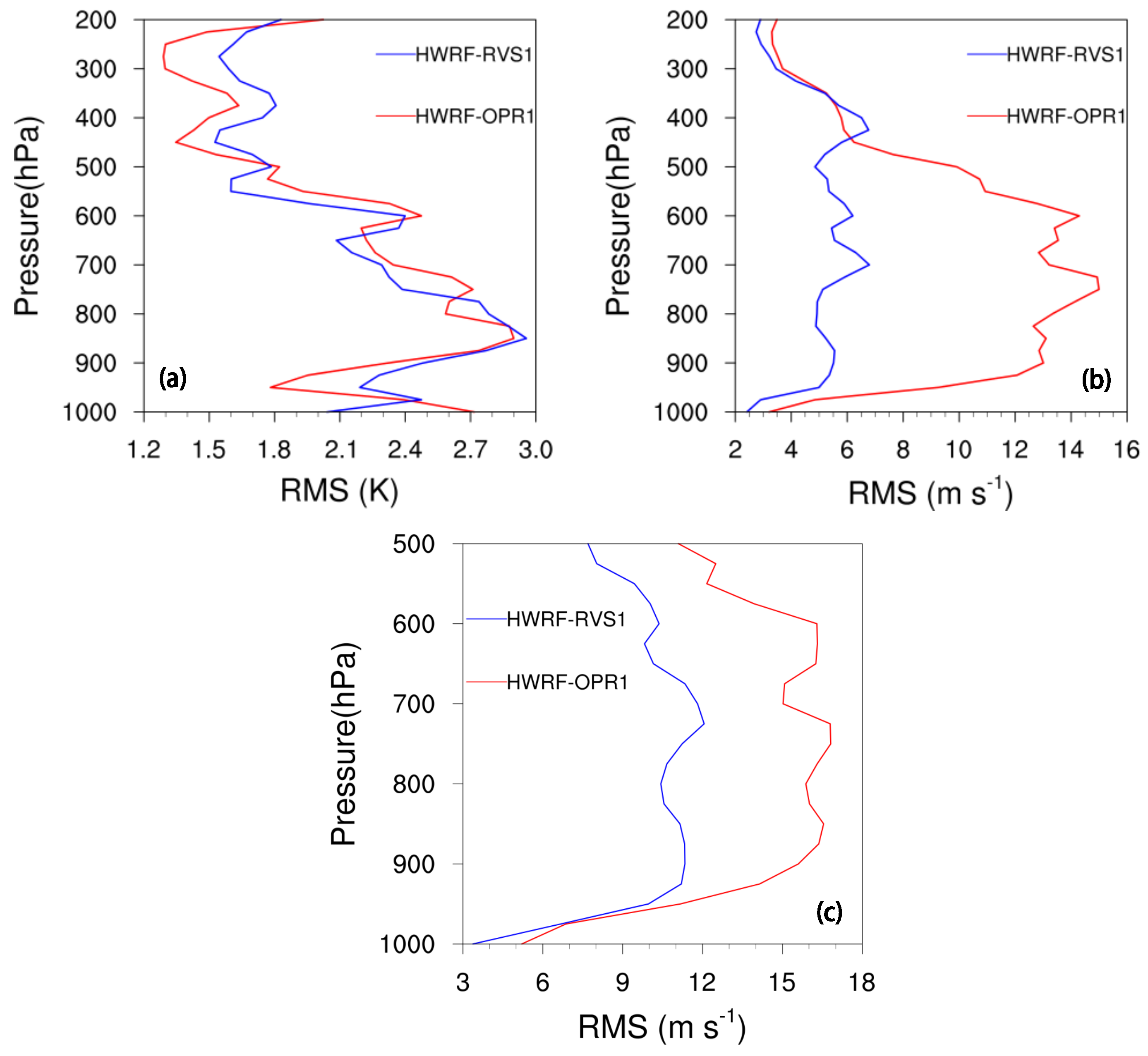
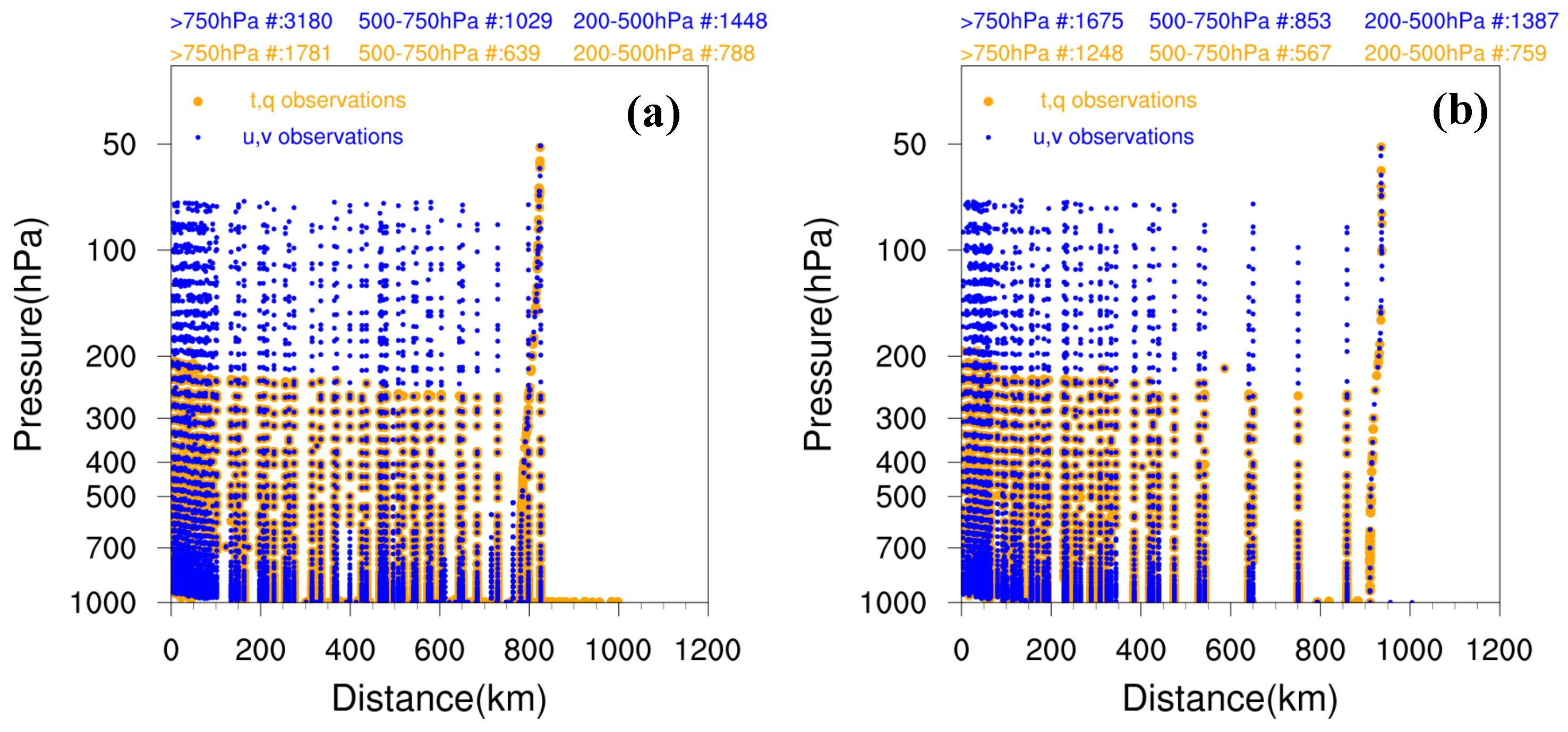
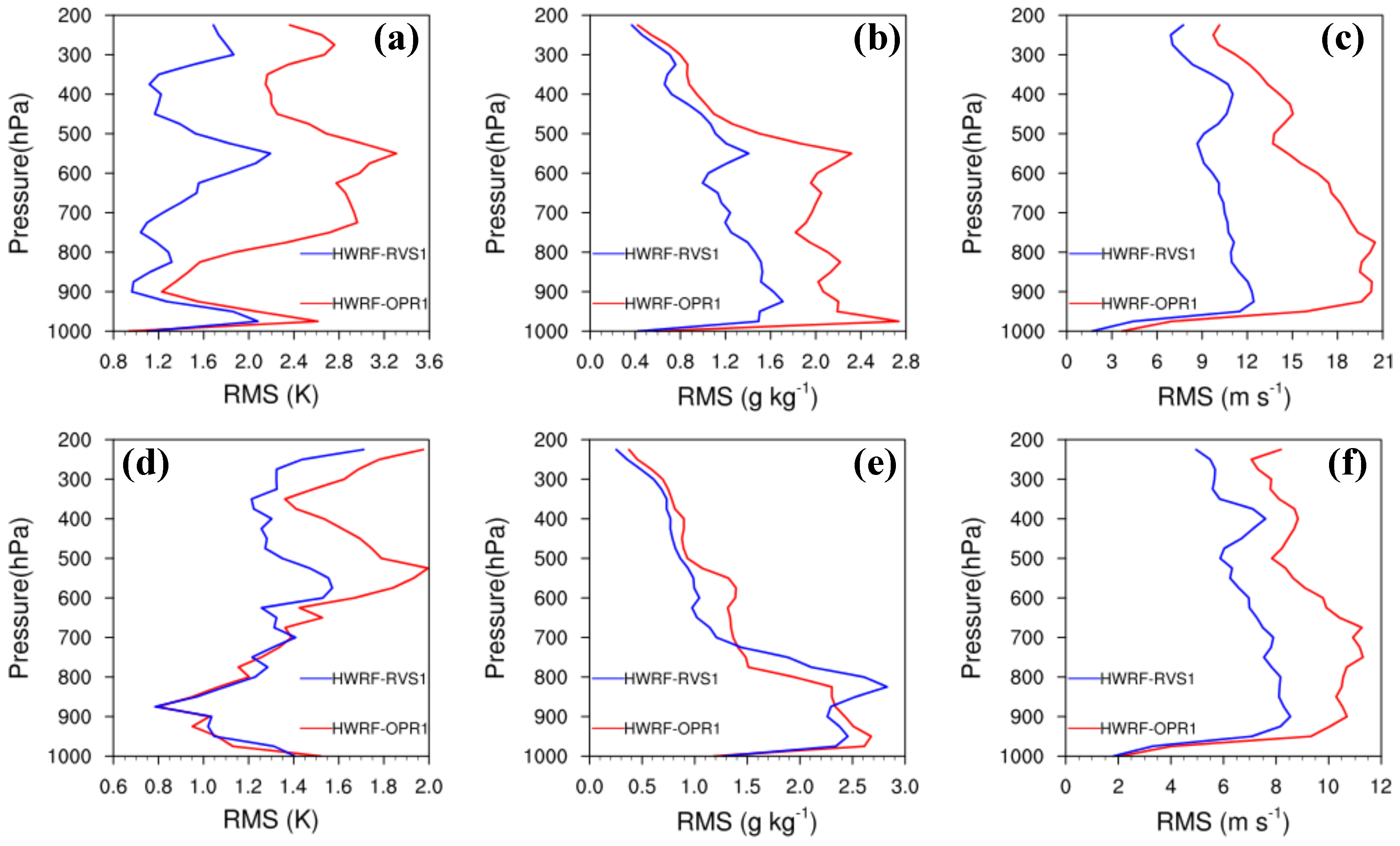
3.1.1. Fit to Observations
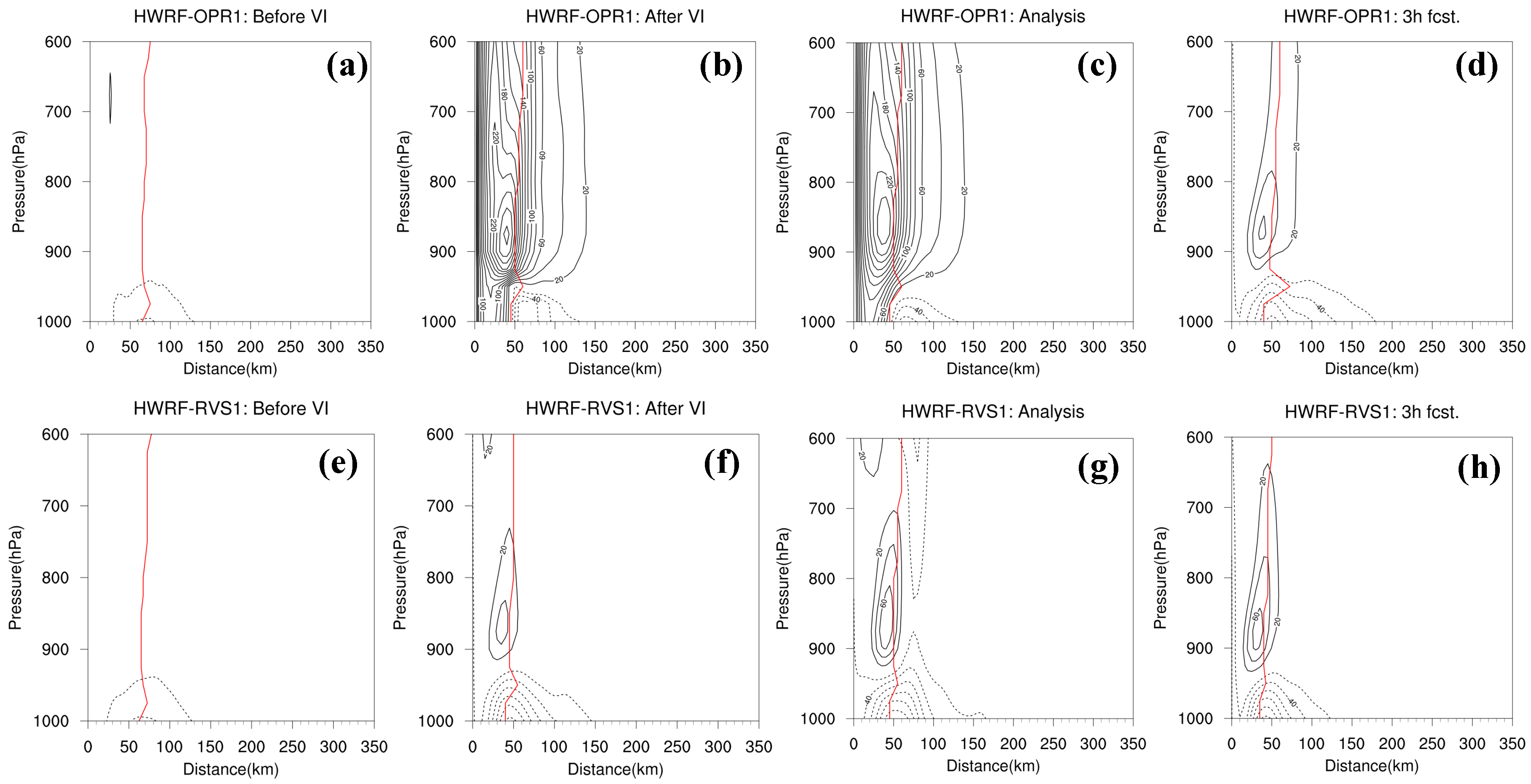
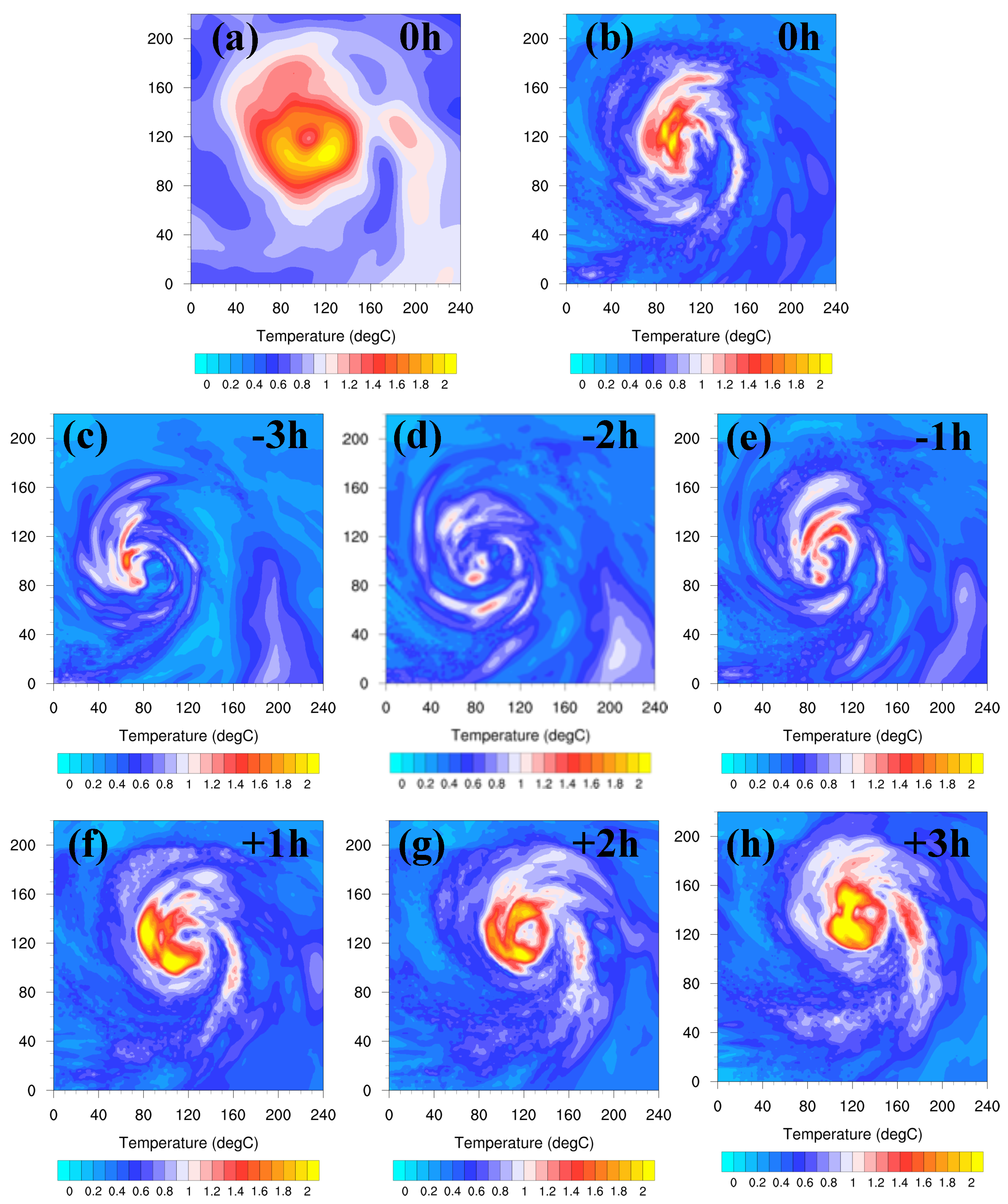
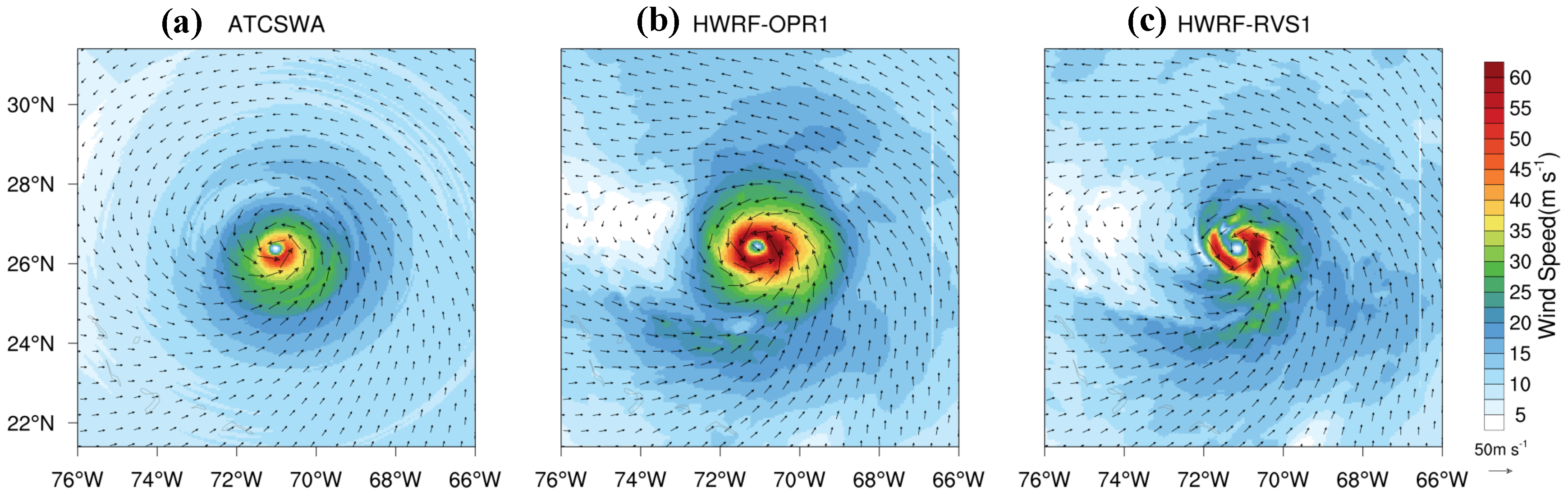
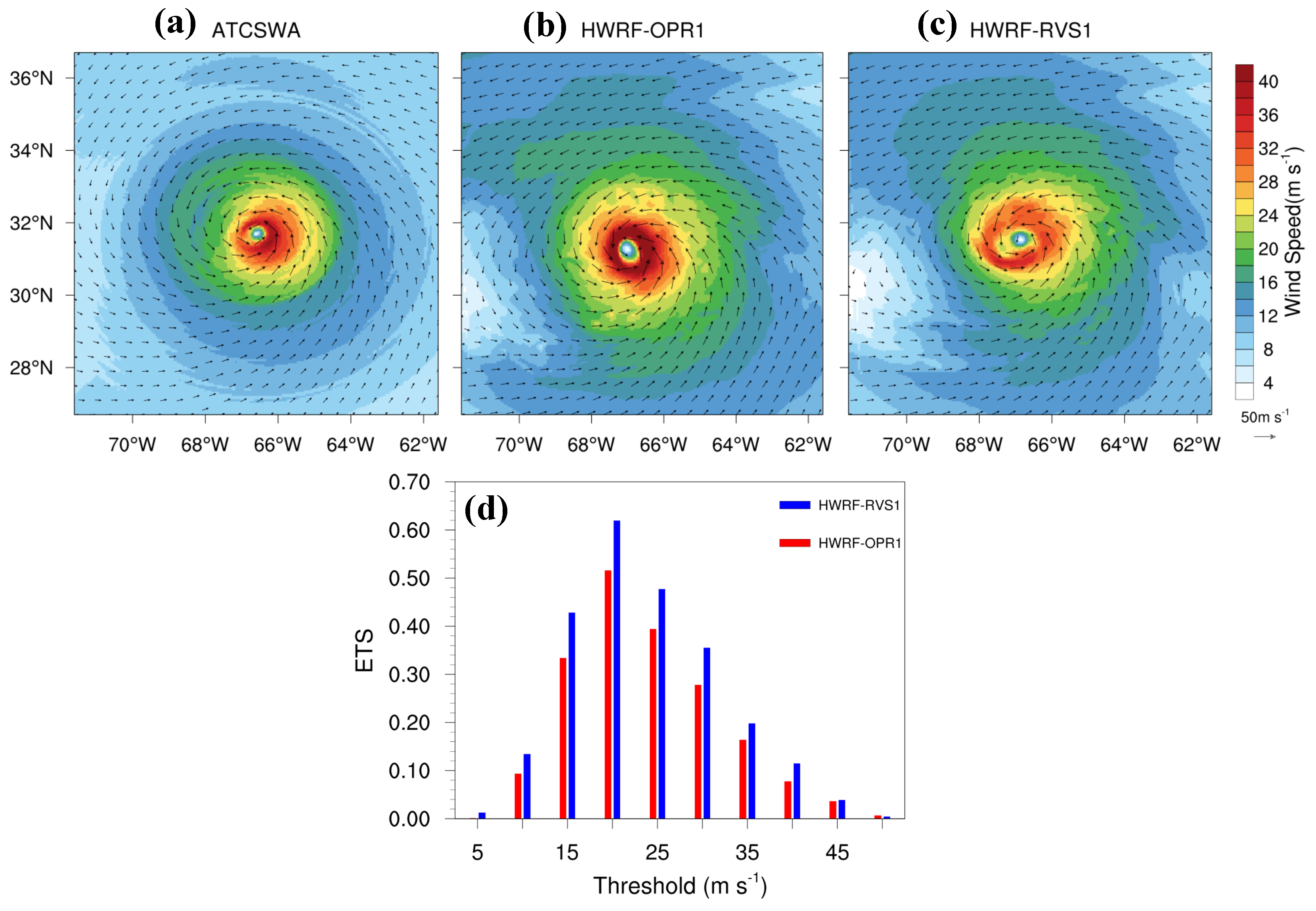
3.1.2. Analysis of Storm Structure
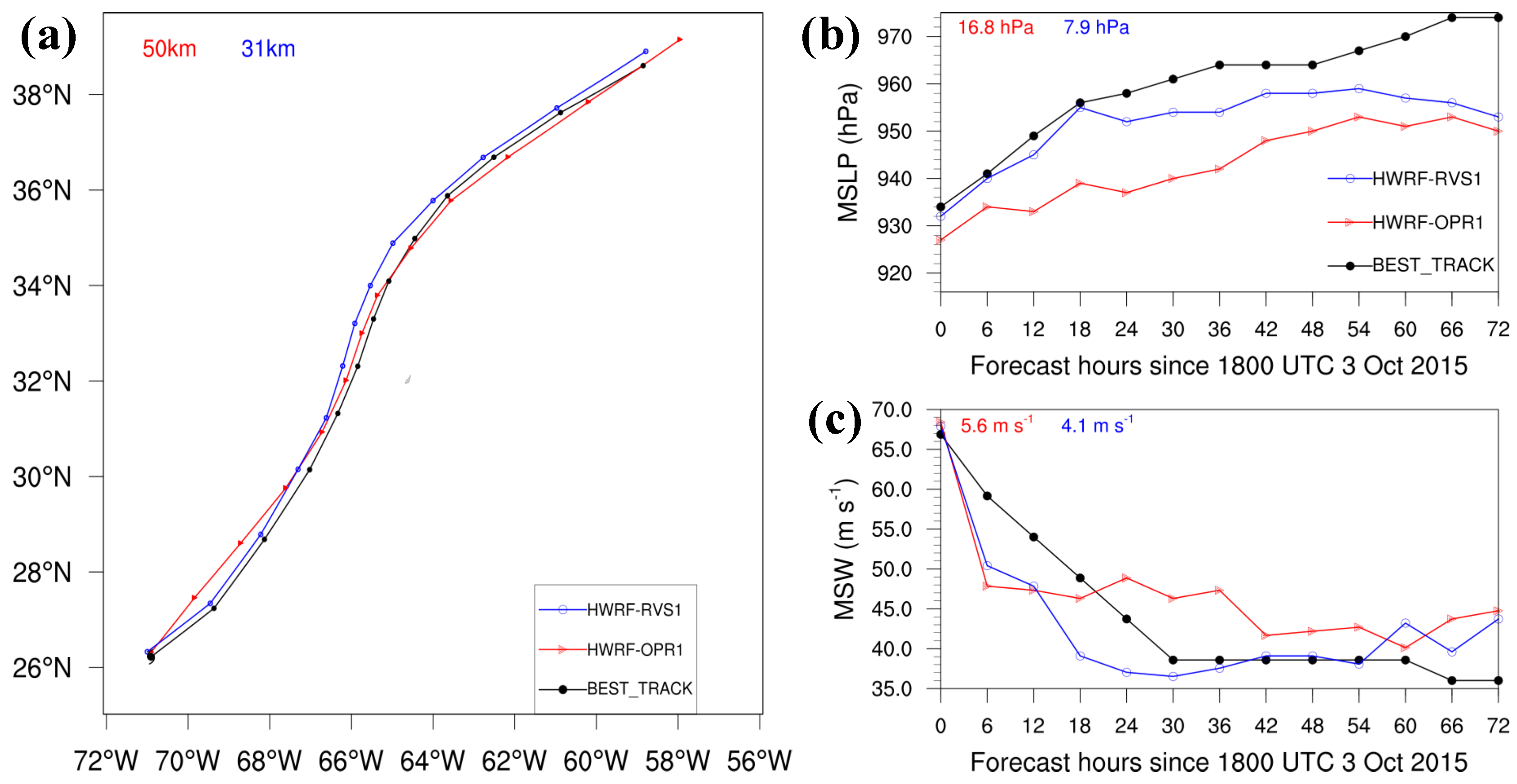
3.1.3. HWRF Forecast
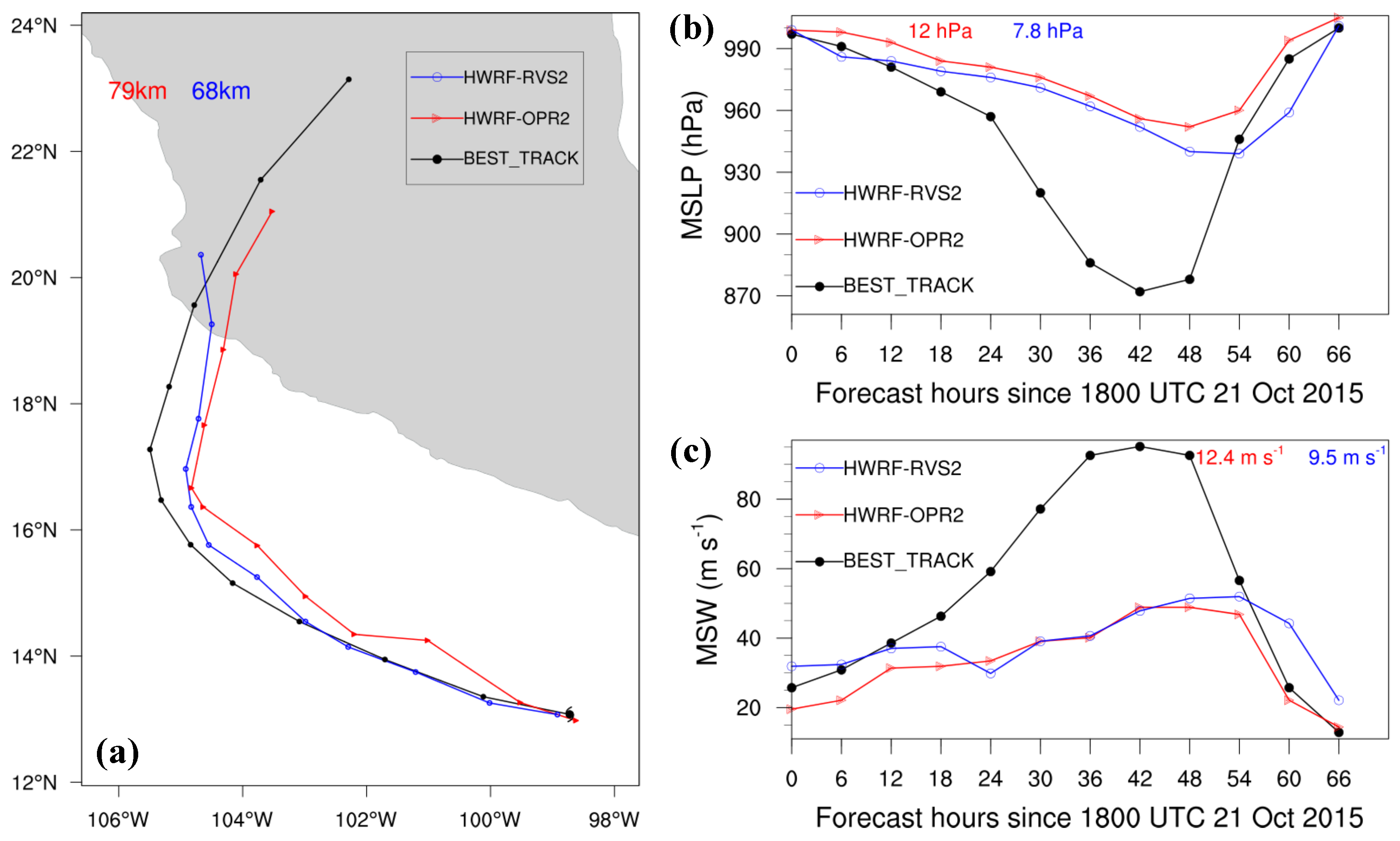
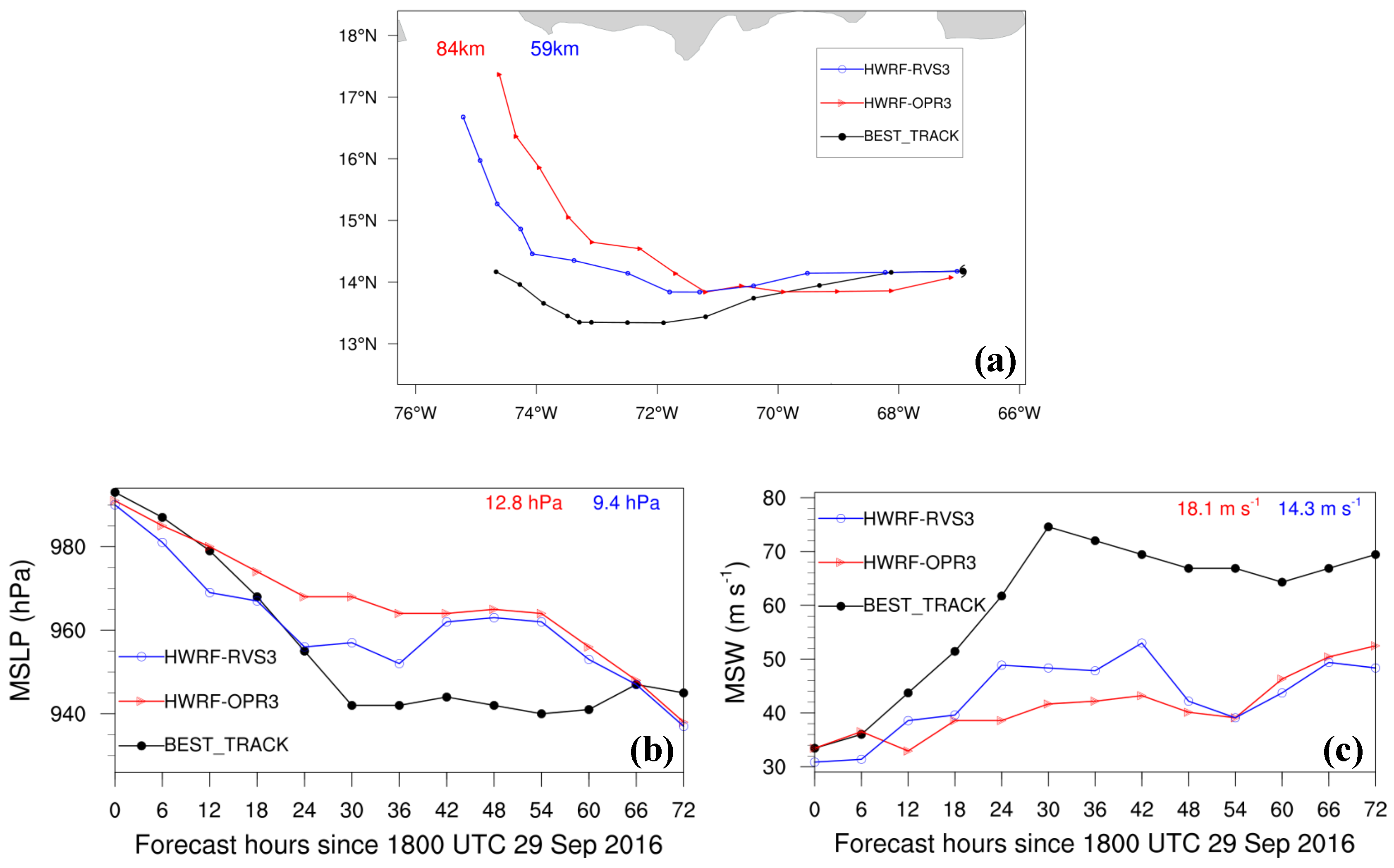
4. Forecasts of the Rapid Intensification of Hurricanes Patricia and Matthew
5. Concluding Remarks
- 4DEnVar initialization framework has shown the potential of leading to a better HWRF forecast of Hurricanes Joaquin, Patricia, and Matthew during their changes in intensity. Compared with the simulations with the 3DEnVar initialization framework, the 4DEnVar initialization framework leads to a reduction in track, MSLP, and MSW forecast errors, at least in the first 24-h forecast in all the HWRF simulations. However, the extent of the improvement is sensitive to the specific case. Specifically, the 4DEnVar initialization framework produces substantial improvements in the forecast of the rapid weakening of Hurricane Joaquin, while it produces weak improvements in the forecasts of the rapid intensification of Hurricanes Patricia and Matthew.
- Further diagnoses for Hurricane Joaquin indicate that 4DEnVar initialization framework, which does not use size and intensity correction in the vortex initialization, can significantly alleviate the gradient imbalances in the HWRF initial conditions produced by the operational initialization framework. In addition, 4DEnVar initialization framework can enhance the performance of DA, as it produces smaller HWRF analysis errors than the operational initialization framework does. This is because DA in 4DEnVar initialization framework not only involves the variation of the background error covariances within the DA window, but also uses high-resolution self-consistent HWRF ensembles that can provide detailed storm-scale features, which enhances the incorporation of observational information into the model initial conditions.
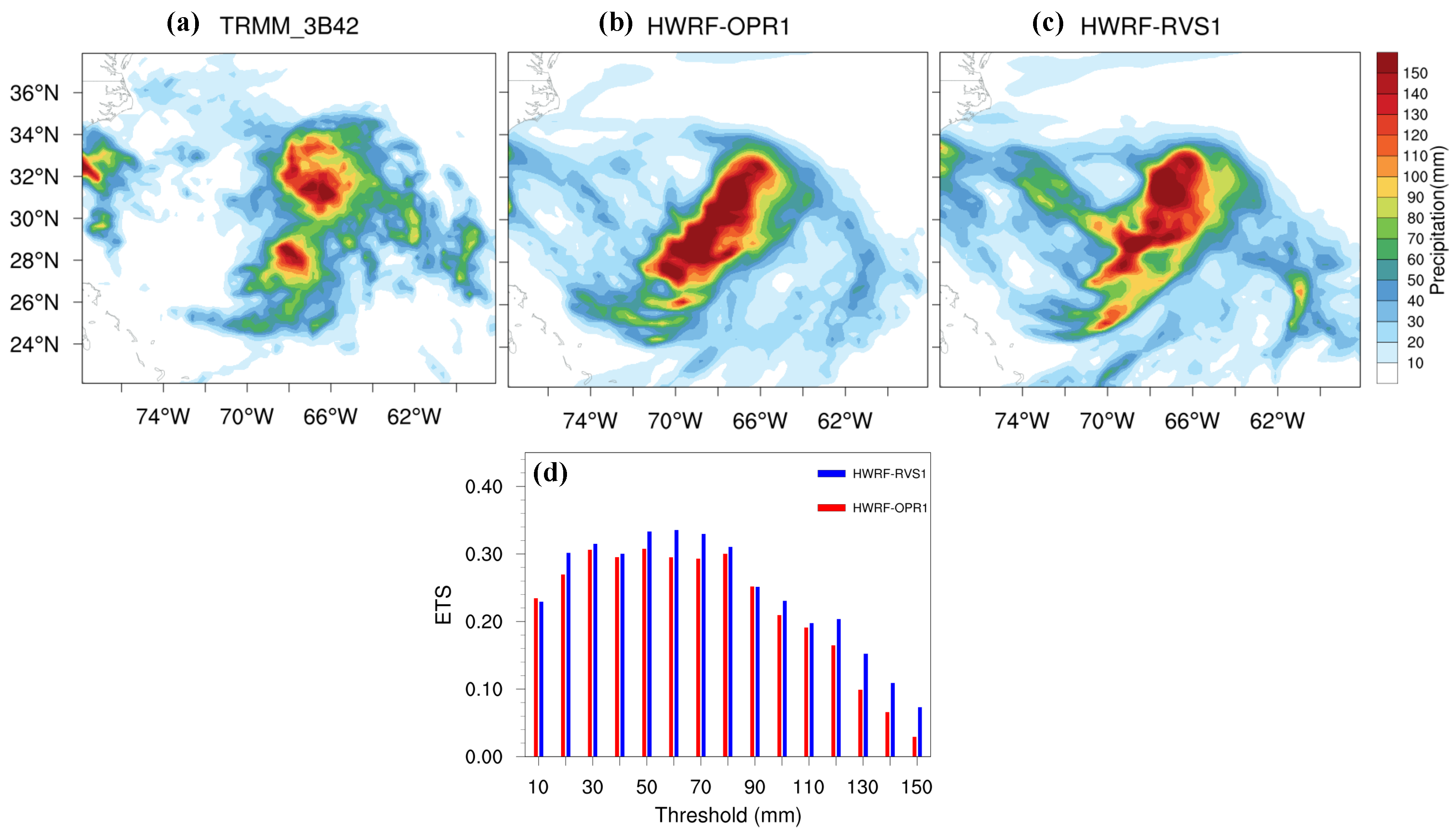
- The evaluation of the HWRF-forecasted 10-m wind and accumulated precipitation for Hurricane Joaquin shows that 4DEnVar initialization framework produces higher ETS scores for wind and precipitation during the intensity changes of Hurricane Joaquin than the operational initialization framework does. This indicates that 4DEnVar initialization framework also has the potential to improve quantitative wind and precipitation forecasts in HWRF.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NCEP | National Centers for Environmental Prediction |
| GEFS | Global Ensemble Forecast System |
| GSI | Gridpoint Statistical Interpolation |
| GSI-3DEnVar | GSI-based three-dimensional ensemble-variational hybrid data assimilation system |
| GSI-4DEnVar | GSI-based four-dimensional ensemble-variational hybrid data assimilation system |
| HWRF | Hurricane Weather Research and Forecasting model |
| GFS | NCEP Global Forecast System |
References
- Elsberry, R.L. Achievement of USWRP Hurricane Landfall Research Goal. Bull. Am. Meteorol. Soc. 2005, 86, 643–646. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, F.; Pu, Z. Numerical simulation of the rapid intensification of Hurricane Katrina (2005): Sensitivity to boundary layer parameterization schemes. Adv. Atmos. Sci. 2017, 34, 482–496. [Google Scholar] [CrossRef]
- Elsberry, R.L.; Lambert, T.D.B.; Boothe, M.A. Accuracy of Atlantic and Eastern North Pacific Tropical Cyclone Intensity Forecast Guidance. Weather Forecast. 2007, 22, 747–762. [Google Scholar] [CrossRef]
- Zhang, F.; Weng, Y.; Gamache, J.F.; Marks, F.D. Performance of convection-permitting hurricane initialization and prediction during 2008? 2010 with ensemble data assimilation of inner-core airborne Doppler radar observations. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Rogers, R.; Aberson, S.; Aksoy, A.; Annane, B.; Black, M.; Cione, J.; Dorst, N.; Dunion, J.; Gamache, J.; Goldenberg, S.; et al. NOAA’S Hurricane Intensity Forecasting Experiment: A Progress Report. Bull. Am. Meteorol. Soc. 2013, 94, 859–882. [Google Scholar] [CrossRef]
- DeMaria, M.; Mainelli, M.; Shay, L.K.; Knaff, J.A.; Kaplan, J. Further Improvements to the Statistical Hurricane Intensity Prediction Scheme (SHIPS). Weather Forecast. 2005, 20, 531–543. [Google Scholar] [CrossRef]
- DeMaria, M.; DeMaria, R.T.; Knaff, J.A.; Molenar, D.A. Tropical Cyclone Lightning and Rapid Intensity Change. Mon. Weather Rev. 2012, 140, 1828–1842. [Google Scholar] [CrossRef]
- National Hurricane Center Forecast Verification. 2017. Available online: https://www.nhc.noaa.gov/verification/verify5.shtml (accessed on 12 April 2019).
- Pu, Z.; Zhang, S.; Tong, M.; Tallapragada, V. Influence of the Self-Consistent Regional Ensemble Background Error Covariance on Hurricane Inner-Core Data Assimilation with the GSI-Based Hybrid System for HWRF. J. Atmos. Sci. 2016, 73, 4911–4925. [Google Scholar] [CrossRef]
- Hurricane Weather Research and Forecasting (HWRF) Model: 2015 Scientific Documentation. 2015. Available online: https://opensky.ucar.edu/islandora/object/technotes%3A535/datastream/PDF/download/citation.pdf (accessed on 22 March 2020).
- Liu, Q.; Surgi, N.; Lord, S.; Wu, W.; Parrish, S.; Gopalakrishnan, S.; Waldrop, J.; Gamache, J. Hurricane Initialization in HWRF Model. Preprints. In Proceedings of the 27th Conference on Hurricanes and Tropical Meteorology, Monterey, CA, USA, 24–28 April 2006. [Google Scholar]
- Wu, W.S.; Purser, R.J.; Parrish, D.F. Three-Dimensional Variational Analysis with Spatially Inhomogeneous Covariances. Mon. Weather Rev. 2002, 130, 2905–2916. [Google Scholar] [CrossRef]
- Wang, X.; Parrish, D.; Kleist, D.; Whitaker, J. GSI 3DVar-Based Ensemble? Variational Hybrid Data Assimilation for NCEP Global Forecast System: Single-Resolution Experiments. Mon. Weather Rev. 2013, 141, 4098–4117. [Google Scholar] [CrossRef]
- Lu, X.; Wang, X.; Li, Y.; Tong, M.; Ma, X. GSI-based ensemble-variational hybrid data assimilation for HWRF for hurricane initialization and prediction: Impact of various error covariances for airborne radar observation assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 223–239. [Google Scholar] [CrossRef]
- Tallapragada, V.; Kieu, C.; Kwon, Y.; Trahan, S.; Liu, Q.; Zhang, Z.; Kwon, I.H. Evaluation of Storm Structure from the Operational HWRF during 2012 Implementation. Mon. Weather Rev. 2014, 142, 4308–4325. [Google Scholar] [CrossRef]
- Wang, X.; Lei, T. GSI-Based Four-Dimensional Ensemble?Variational (4DEnsVar) Data Assimilation: Formulation and Single-Resolution Experiments with Real Data for NCEP Global Forecast System. Mon. Weather Rev. 2014, 142, 3303–3325. [Google Scholar] [CrossRef]
- Zhang, S.; Pu, Z.; Velden, C. Impact of Enhanced Atmospheric Motion Vectors on HWRF Hurricane Analyses and Forecasts with Different Data Assimilation Configurations. Mon. Weather Rev. 2018, 146, 1549–1569. [Google Scholar] [CrossRef]
- Kleist, D.T.; Ide, K. An OSSE-Based Evaluation of Hybrid Variational?Ensemble Data Assimilation for the NCEP GFS. Part II: 4DEnVar and Hybrid Variants. Mon. Weather Rev. 2015, 143, 452–470. [Google Scholar] [CrossRef]
- Zhang, S.; Pu, Z. Numerical Simulation of Rapid Weakening of Hurricane Joaquin with Assimilation of High-Definition Sounding System Dropsondes during the Tropical Cyclone Intensity Experiment: Comparison of Three- and Four-Dimensional Ensemble? Variational Data Assimilation. Weather Forecast. 2019, 34, 521–538. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.G.; Marks, F.; Zhang, X.; Bao, J.W.; Yeh, K.S.; Atlas, R. The Experimental HWRF System: A Study on the Influence of Horizontal Resolution on the Structure and Intensity Changes in Tropical Cyclones Using an Idealized Framework. Mon. Weather Rev. 2011, 139, 1762–1784. [Google Scholar] [CrossRef]
- Janjic, Z.; Gall, Z.; Pyle, M.E. Scientific Documentation for the NMM Solver; (No. NCAR/TN-477+STR); National Center for Atmospheric Research University Corporation for Atmospheric Research: Boulder, CO, USA, 2010; 54p. [Google Scholar] [CrossRef]
- Data Types Used by the GSI Analysis System. 2018. Available online: https://www.emc.ncep.noaa.gov/mmb/data_processing/prepbufr.doc/ (accessed on 12 April 2019).
- Wang, X. Incorporating Ensemble Covariance in the Gridpoint Statistical Interpolation Variational Minimization: A Mathematical Framework. Mon. Weather Rev. 2010, 138, 2990–2995. [Google Scholar] [CrossRef]
- Buehner, M.; Morneau, J.; Charette, C. Four-dimensional ensemble-variational data assimilation for global deterministic weather prediction. Nonlinear Process. Geophys. 2013, 20, 669–682. [Google Scholar] [CrossRef]
- Lorenc, A.C.; Bowler, N.E.; Clayton, A.M.; Pring, S.R.; Fairbairn, D. Comparison of Hybrid-4DEnVar and Hybrid-4DVar Data Assimilation Methods for Global NWP. Mon. Weather Rev. 2015, 143, 212–229. [Google Scholar] [CrossRef]
- Zhang, Z.; Tallapragada, V.; Kieu, C.; Trahan, S.; Wang, W. HWRF Based Ensemble Prediction System Using Perturbations from GEFS and Stochastic Convective Trigger Function. Trop. Cyclone Res. Rev. 2014, 3, 145–161. [Google Scholar] [CrossRef]
- Berg, R. National Hurricane Center Tropical Cyclone Report, Hurricane Joaquin (AL112015). NOAA/National Hurricane Center, 2016; 36p. Available online: https://www.nhc.noaa.gov/data/tcr/AL112015_Joaquin.pdf (accessed on 12 April 2019).
- Knaff, J.A.; Longmore, S.P.; DeMaria, R.T.; Molenar, D.A. Tropical Cyclone Lightning and Rapid Intensity Change. J. Appl. Meteor. Climatol. 2015, 54, 463–478. [Google Scholar] [CrossRef]
- Knaff, J.A.; Zehr, R.M. Reexamination of tropical cyclone wind—Pressure relationships. Weather Forecast. 2007, 22, 71–88. [Google Scholar] [CrossRef]
- ONR Tropical Cyclone Intensity 2015 NASA WB-57 HDSS Dropsonde Data. 2016. Available online: https://data.eol.ucar.edu/dataset/488.004 (accessed on 12 April 2019).
- Kimberlain, T.; Blake, E.; Cangialosi, J. National Hurricane Center Tropical Cyclone Report, Hurricane Patricia (EP202015). NOAA/National Hurricane Center, 2016; 32p. Available online: https://www.nhc.noaa.gov/data/tcr/EP202015_Patricia.pdf (accessed on 12 April 2019).
- Stewart, S. National Hurricane Center Tropical Cyclone Report, Hurricane Matthew (AL142016). NOAA/National Hurricane Center, 2017; 96p. Available online: https://www.nhc.noaa.gov/data/tcr/AL142016_Matthew.pdf (accessed on 12 April 2019).
- Hurricane Weather Research and Forecasting (HWRF) Model: 2018 Scientific Documentation. 2018. Available online: https://dtcenter.org/sites/default/files/community-code/hwrf/docs/scientific_documents/HWRFv4.0a_ScientificDoc.pdf (accessed on 22 March 2020).
- Cui, Z.; Pu, Z.; Tallapragada, V.; Atlas, R.; Ruf, C.S. A Preliminary Impact Study of CYGNSS Ocean Surface Wind Speeds on Numerical Simulations of Hurricanes. Geophys. Res. Lett. 2019, 46, 2984–2992. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Wang, X. Improving Hurricane Analyses and Predictions with TCI, IFEX Field Campaign Observations, and CIMSS AMVs Using the Advanced Hybrid Data Assimilation System for HWRF. Part II: Observation Impacts on the Analysis and Prediction of Patricia (2015). Mon. Weather Rev. 2020, 148, 1407–1430. [Google Scholar] [CrossRef]
| Configuration | HWRF 3DEnVar Initialization Framework | HWRF 4DEnVar Initialization Framework |
|---|---|---|
| DA scheme | GSI-3D-EnVar | GSI-4D-EnVar |
| Flow-dependent error covariance | GFS 80-member ensembles (∼23 km) | HWRF 42-member ensembles (∼6 km) |
| Vortex initialization | Vortex relocation & Intensity correction | Vortex relocation |
| DA domains | ghost d02 (30 × 30) | d02 (25 × 25) |
| ghost d03 (12 × 12) | d03 (7.5 × 9) | |
| Forecast domains | d01 (80 × 80) | d01 (80 × 80) |
| d02 (13 × 13) | d02 (25 × 25) | |
| d03 (7.5 × 9) | d03 (7.5 × 9) |
| Exps. | HWRF Initialization | Hurricane Case | DA Period a | Simulation Period |
|---|---|---|---|---|
| HWRF-OPR1 | 3DEnVar (Figure 1a) | Joaquin (2015) | 1800 UTC 02–1800 UTC 03 October | 1800 UTC 03–1800 UTC 06 October |
| HWRF-RVS1 | 4DEnVar (Figure 1b) | Joaquin (2015) | 1800 UTC 02–1800 UTC 03 October | 1800 UTC 03–1800 UTC 06 October |
| HWRF-OPR2 | 3DEnVar (Figure 1a) | Patricia (2015) | 1800 UTC 20–1800 UTC 21 October | 1800 UTC 21–1800 UTC 24 October |
| HWRF-RVS2 | 4DEnVar (Figure 1b) | Patricia (2015) | 1800 UTC 20–1800 UTC 21 October | 1800 UTC 21–1800 UTC 24 October |
| HWRF-OPR3 | 3DEnVar (Figure 1a) | Matthew (2016) | 1800 UTC 28–1800 UTC 29 September | 1800 UTC 29 September–1800 UTC 02 October |
| HWRF-RVS3 | 4DEnVar (Figure 1b) | Matthew (2016) | 1800 UTC 28–1800 UTC 29 September | 1800 UTC 29 September–1800 UTC 02 October |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Pu, Z. Evaluation of the Four-Dimensional Ensemble-Variational Hybrid Data Assimilation with Self-Consistent Regional Background Error Covariance for Improved Hurricane Intensity Forecasts. Atmosphere 2020, 11, 1007. https://doi.org/10.3390/atmos11091007
Zhang S, Pu Z. Evaluation of the Four-Dimensional Ensemble-Variational Hybrid Data Assimilation with Self-Consistent Regional Background Error Covariance for Improved Hurricane Intensity Forecasts. Atmosphere. 2020; 11(9):1007. https://doi.org/10.3390/atmos11091007
Chicago/Turabian StyleZhang, Shixuan, and Zhaoxia Pu. 2020. "Evaluation of the Four-Dimensional Ensemble-Variational Hybrid Data Assimilation with Self-Consistent Regional Background Error Covariance for Improved Hurricane Intensity Forecasts" Atmosphere 11, no. 9: 1007. https://doi.org/10.3390/atmos11091007
APA StyleZhang, S., & Pu, Z. (2020). Evaluation of the Four-Dimensional Ensemble-Variational Hybrid Data Assimilation with Self-Consistent Regional Background Error Covariance for Improved Hurricane Intensity Forecasts. Atmosphere, 11(9), 1007. https://doi.org/10.3390/atmos11091007






