The Summer Surface Energy Budget of the Ice-Free Area of Northern James Ross Island and Its Impact on the Ground Thermal Regime
Abstract
1. Introduction
- To quantify the summer surface energy budget over the ice-free area on the Ulu Peninsula;
- To identify the connection between components of the surface energy budget and verify if the energy fluxes differ between the western and eastern side of the AP; and
- To determine the effect of snow cover and cloudiness on the surface energy budget and ground thermal regime.
2. Material and Methods
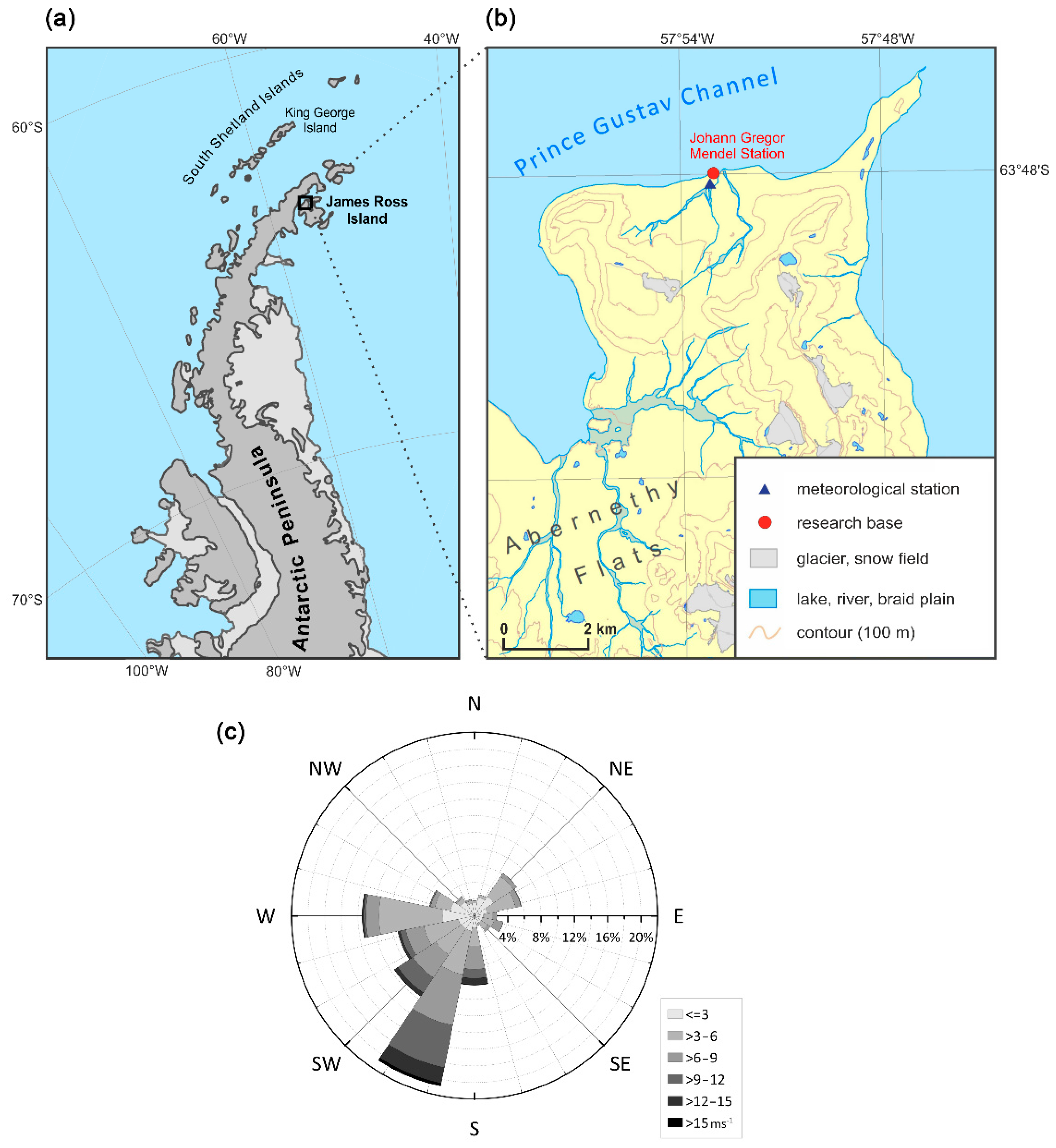
2.1. Study Site and Instrumentation
2.2. Data Processing and Analysis
2.3. Measurement Accuracy
3. Results
3.1. Meteorological Conditions and Energy Budget Components
3.2. Ground Temperature Response to the Largest Surface Energy Fluxes
3.3. Longer-Term Influence of Surface Energy Budget Components on Ground Temperature Variation
3.4. Impact of Snow Cover and Cloudiness
4. Discussion
4.1. Surface Energy Budget Components in Polar Regions
4.2. Surface Energy Budget Impact on Ground Thermal Regime
4.3. Snow Cover and Cloudiness Effects
5. Conclusions
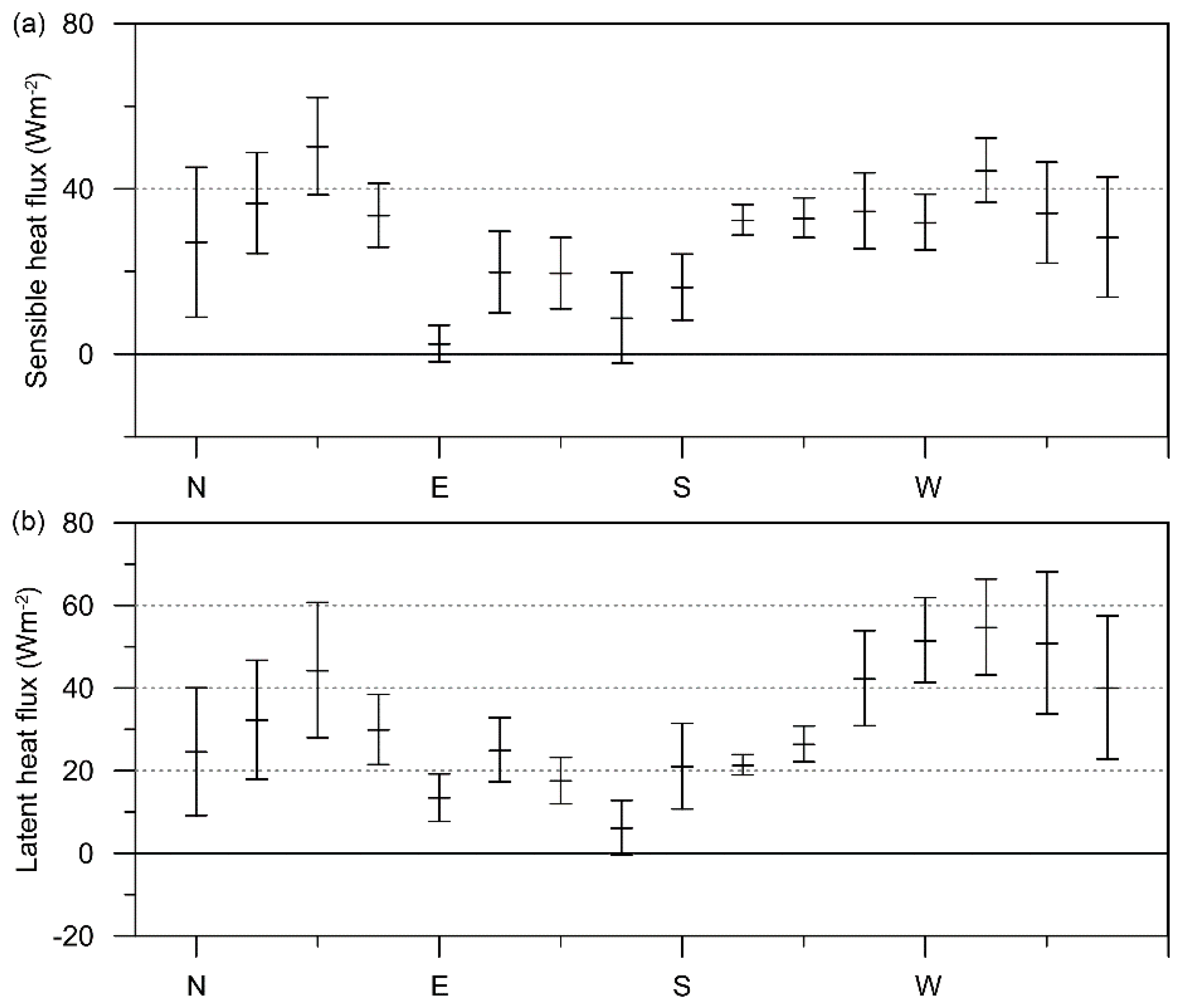
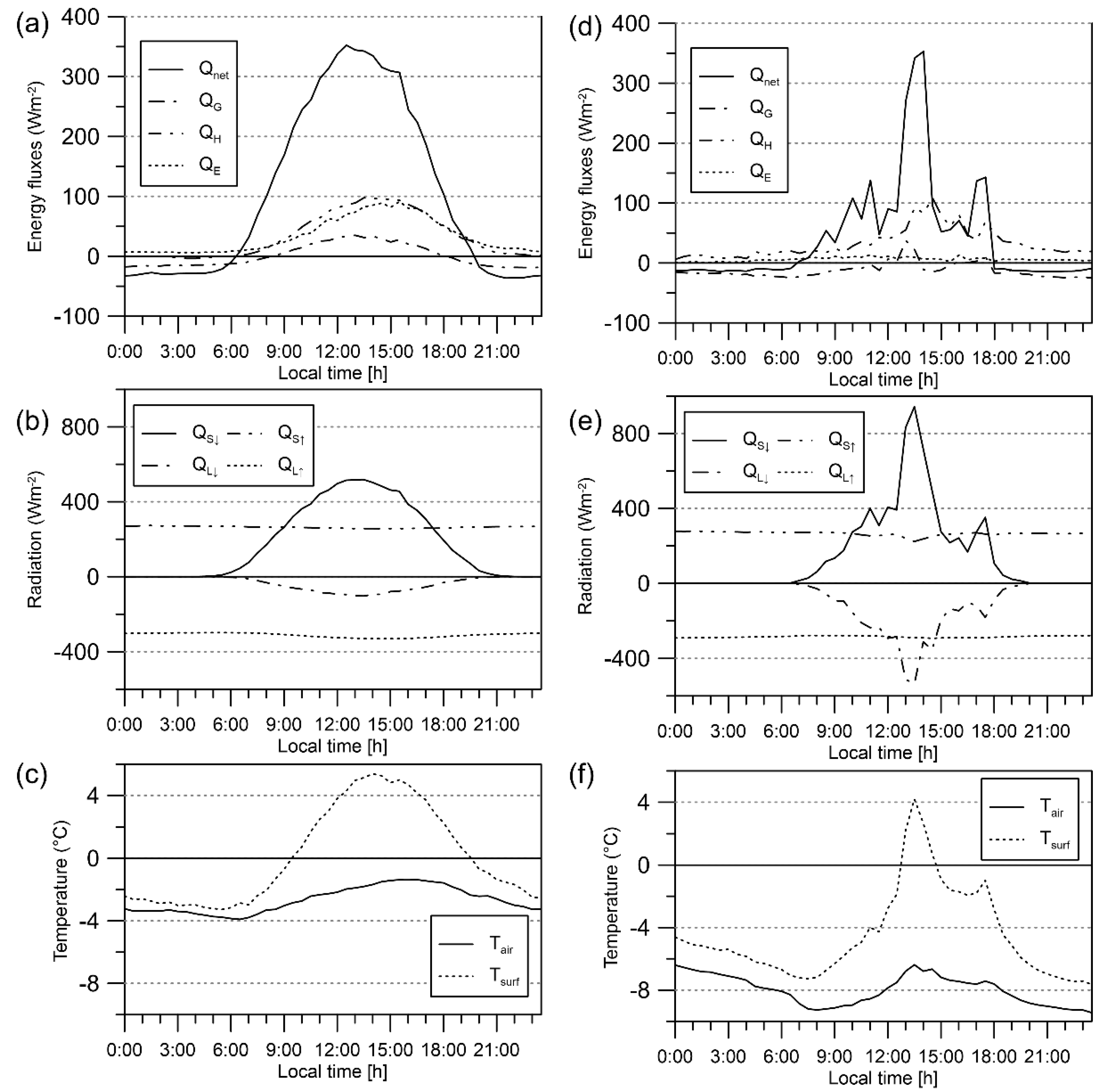
- Mean Qnet reached 102.5 W m−2, while the highest mean daily Qnet was 253 W m−2. Mean QG was only 0.5 W m−2 and yet 46% of the time the ground was a heat source for the atmosphere. Mean QE was only by 0.4 Wm−2 higher than mean QH. Mean QE was up to 19.6 W m−2 higher than mean QH when the wind blew from west–south-westerly to north–west-northerly sector (236.5° to 348.5°), showing the influence of increased moisture availability from the sea.
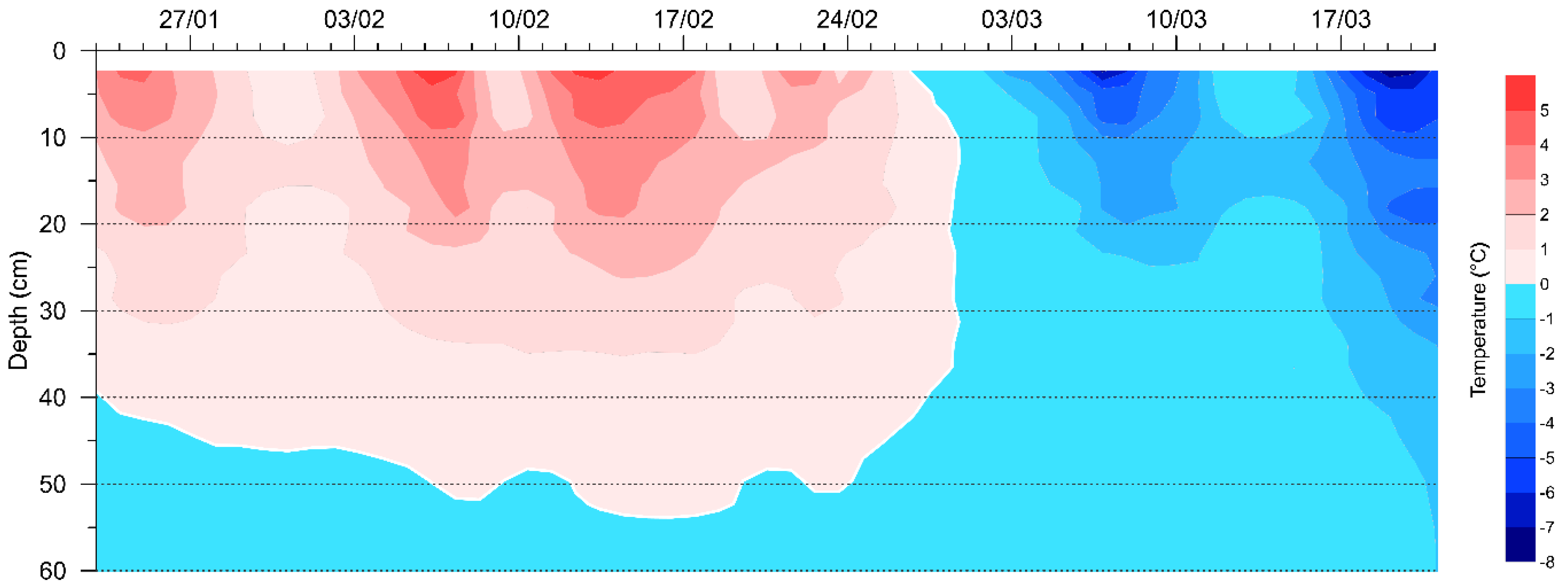
- The ground thermal regime was affected by surface energy budget components to the depth of 50 cm. The strongest relationship was found between QG and the ground surface temperature, with a delay growing along with increasing depth. The active layer refroze at the end of February after a sequence of three days with continuously negative QG.
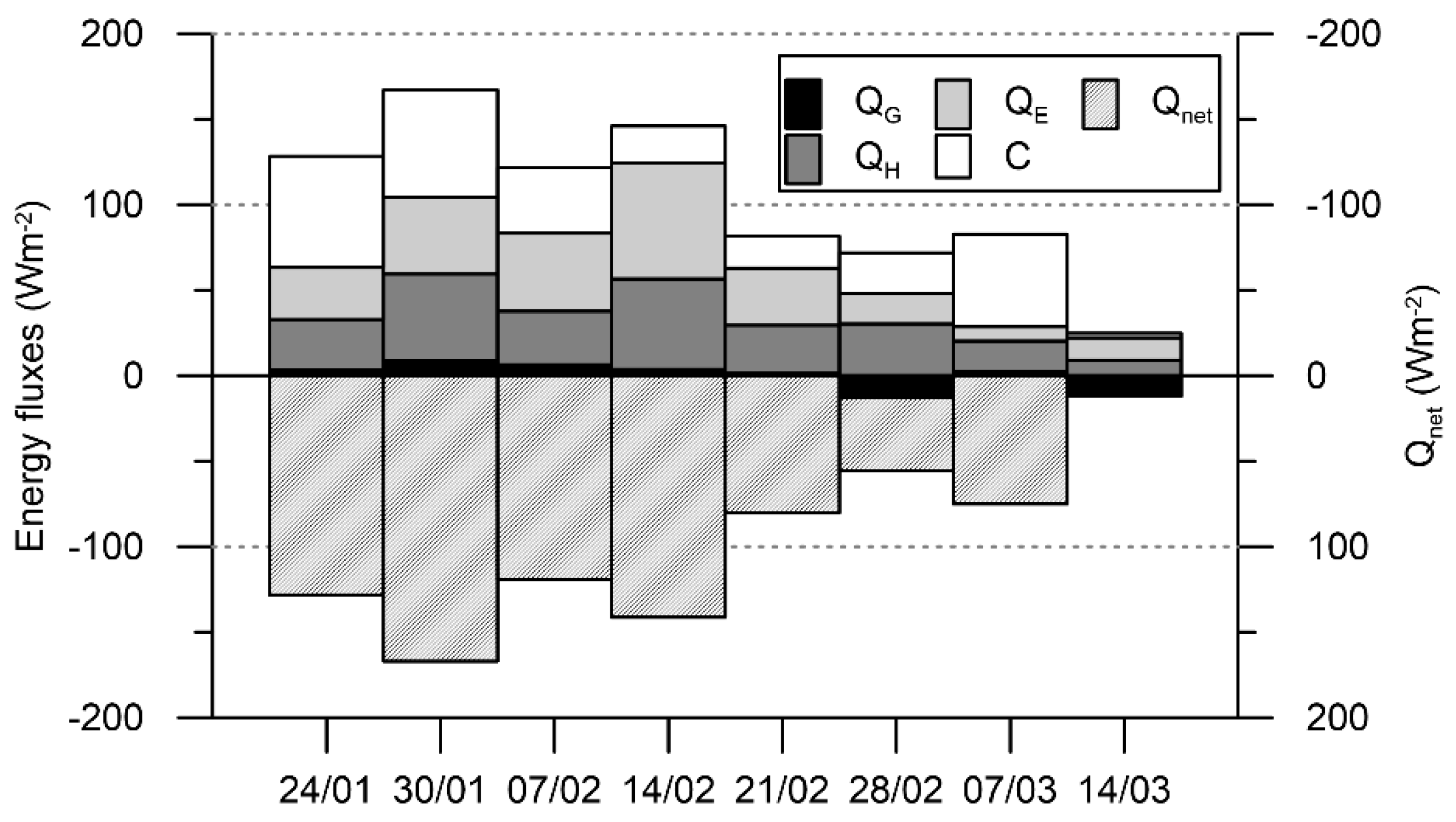
- The case studies have shown that an increase of cloud cover led to a decrease of both mean daily Qnet and QG which caused cooling in ground thermal profile. On a clear-sky day, the situation was vice versa.
- Insulation by snow cover was not observed, as QG was 13.2 W m−2 below average and the ground was cooling in the whole profile during a sample day with snow cover.
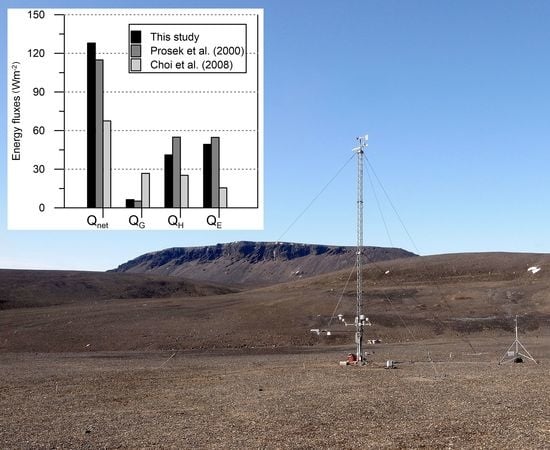
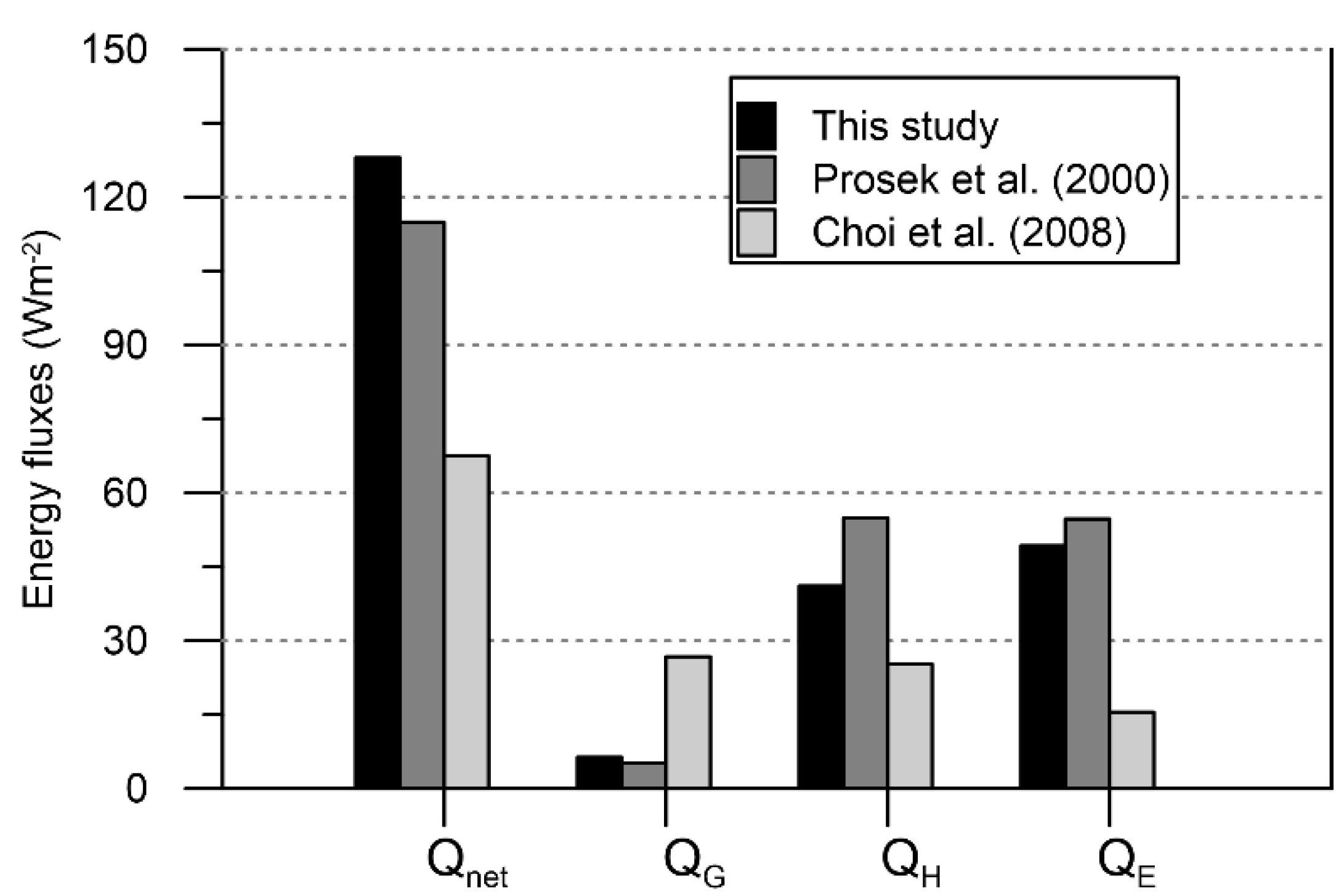
- By comparison with other studies, we concluded that Qnet was higher on the eastern side of the AP due to less cloudiness affected by regional atmospheric patterns. Mean QG reached similar values on the eastern and western side of the AP and comprised about 5% of Qnet, approximately four-times less than was observed in the Arctic summer months. Mean QE was, on both sides of the AP, approximately the same as QH, even though the ratio of QH to Qnet varied by 15% among the studies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| QS↓ (Wm−2) | QS↑ (Wm−2) | QL↓ (Wm−2) | QL↑ (Wm−2) | Qnet (Wm−2) | Albedo |
| 182.7 ± 9.3 | 33.4 ± 2.2 | 264.4 ± 1.2 | 311.1 ± 1.1 | 102.5 ± 7.2 | 0.25 ± 0.06 |
| QG (Wm−2) | QH (Wm−2) | QE (Wm−2) | Tair (°C) | Tsurf (°C) | GT50 (°C) |
| 0.5 ± 1.1 | 32.8 ± 2.0 | 33.2 ± 2.3 | −2.5 ± 0.2 | 0.1 ± 0.2 | −0.2 ± 0.0 |
References
- King, J.C.; Turner, J. Antarctic Meteorology and Climatology; Cambridge University Press: Cambridge, UK, 1997; pp. 1–425. [Google Scholar]
- Burton-Johnson, A.; Black, M.; Fretwell, P.T.; Kaluza-Gilbert, J. An automated methodology for differentiating rock from snow, clouds and sea in Antarctica from Landsat 8 imagery: A new rock outcrop map and area estimation for the entire Antarctic continent. Cryosphere 2016, 10, 1665–1677. [Google Scholar] [CrossRef]
- Fox, A.J.; Cooper, A.P.R. Climate-change indicators from archival aerial photography of the Antarctic Peninsula. Ann. Glaciol. 1998, 27, 636–642. [Google Scholar] [CrossRef]
- ATCM. Antarctic Trial of WWF’s Rapid Assessment of Circum-Arctic Ecosystem Resilience (RACER) Conservation Planning Tool: Results of RACER Workshop Focused on James Ross Island. Information paper by Great Britain and Czechia. In Proceedings of the 38th Antarctic Treaty Consultative Meeting, Sofia, Bulgaria, 14 December 2015. [Google Scholar]
- Lee, J.R.; Raymond, B.; Bracegirdle TJChadès, I.; Fuller, R.A.; Shaw, J.D.; Terauds, A. Climate change drives expansion of Antarctic ice-free habitat. Nature 2017, 547, 49–54. [Google Scholar] [CrossRef] [PubMed]
- Turner, J.; Lu, H.; White, I.; King, J.C.; Phillips, T.; Hosking, J.S.; Bracegirdle, T.J.; Marshall, G.J.; Mulvaney, R.; Deb, P. Absence of 21st century warming on Antarctic Peninsula consistent with natural variability. Nature 2016, 535, 411–415. [Google Scholar] [CrossRef]
- Oliva, M.; Navarro, F.; Hrbacek, F.; Hernández, A.; Nývlt, D.; Pereira, P.; Ruiz-Fernández, J.; Trigo, R. Recent regional climate cooling on the Antarctic Peninsula and associated impacts on the cryosphere. Sci. Total Environ. 2017, 580, 210–223. [Google Scholar] [CrossRef]
- Gonzalez, S.; Fortuny, D. How robust are the temperature trends on the Antarctic Peninsula? Antarct. Sci. 2018, 30, 322–328. [Google Scholar] [CrossRef]
- Bintanja, R. The local surface energy balance of the Ecology Glacier, King George Island, Antarctica: Measurements and modelling. Antarct. Sci. 1995, 7, 315–325. [Google Scholar] [CrossRef]
- Braun, M.; Saurer, H.; Vogt, S.; Simões, J.C.; Goßmann, H. The Influence of Large-Scale Atmospheric Circulation on the Surface Energy Balance of the King George Island Ice Cap. Int. J. Climatol. 2001, 21, 21–36. [Google Scholar] [CrossRef]
- King, J.C.; Argentini, S.A.; Anderson, P.S. Contrasts between the summertime surface energy balance and boundary layer structure at Dome C and Halley stations, Antarctica. J. Geophys. Res. 2006, 11, D02105. [Google Scholar] [CrossRef]
- Vihma, T.; Johansson, M.M.; Launiainen, J. Radiative and turbulent surface heat fluxes over sea ice in the western Weddell Sea in early summer. J. Geophys. Res. 2009, 114, C04019. [Google Scholar] [CrossRef]
- Choi, T.; Lee, B.Y.; Kim, S.-J.; Yoon, Y.J.; Lee, H.-C. Net radiation and turbulent energy exchanges over a non-glaciated coastal area on King George Island during four summer seasons. Antarct. Sci. 2008, 20, 99–111. [Google Scholar] [CrossRef]
- Jonsell, U.Y.; Navarro, F.J.; Bañón, M.; Lapazaran, J.J.; Otero, J. Sensitivity of a distributed temperature-radiation index melt model based on AWS observations and surface energy balance fluxes, Hurd Peninsula glaciers, Livingston Island, Antarctica. Cryosphere 2012, 6, 539–552. [Google Scholar] [CrossRef]
- Alves, M.; Soares, J. Diurnal Variation of Soil Heat Flux at an Antarctic Local Area during Warmer Months. Appl. Environ. Soil. Sci. 2016, 2016, 9. [Google Scholar] [CrossRef]
- Perrson, P.O.G.; Stone, R.S.; Grachev, A.; Matrosova, L. Processes Affecting the Annual Surface Energy Budget at High-Latitude Terrestrial Sites. In Proceedings of the EGU Conference, Vienna, Austria, 22–27 April 2012. [Google Scholar]
- Prosek, P.; Janouch, M.; Láska, K. Components of the energy balance of the ground surface and their effect of the thermics of the substrata of the vegetation oasis at Henryk Arctowski Station, King George Island, South Shetland Islands. Polar Rec. 2000, 36, 3–18. [Google Scholar] [CrossRef]
- Foken, T. The Energy Balance Problem: An Overview. Ecol. Appl. 2008, 18, 1351–1367. [Google Scholar] [CrossRef]
- Lunardini, V.J. Heat Transfer in Cold Climates; Van Nostrand-Reinhold: New York, NY, USA, 1981; pp. 1–731. [Google Scholar]
- Roth, K.; Boike, J. Quantifying the thermal dynamics of a permafrost site near Ny-Ålesund, Svalbard. Water Resour. Res. 2001, 37, 2901–2914. [Google Scholar] [CrossRef]
- Williams, P.J.; Smith, M.W. The Frozen Earth: Fundamentals of Geocryology; Cambridge University Press: Cambridge, UK, 1989; pp. 1–306. [Google Scholar]
- Ling, F.; Zhang, T. A numerical model for surface energy balance and thermal regime of the active layer and permafrost containing unfrozen water. Cold Reg. Sci. Technol. 2004, 38, 1–15. [Google Scholar] [CrossRef]
- Hrbáček, F.; Kňažková, M.; Nývlt, D.; Láska, K.; Mueller, C.W.; Ondruch, J. Active layer monitoring at CALM-S site near J. G. Mendel Station, James Ross Island, eastern Antarctic Peninsula. Sci. Total Environ. 2017, 601–602, 987–997. [Google Scholar] [CrossRef] [PubMed]
- Eugster, W.; Rouse, W.R.; Pielke, R.A.; Mcfadden, J.P.; Baldocchi, D.D.; Kittel, T.G.; Chapin, I.I.I.F.S.; Liston, G.E.; Vidale, P.L.; Vaganov, E.; et al. Land-atmosphere energy exchange in Arctic tundra and boreal forest: Available data and feedbacks to climate. Glob. Chang. Biol. 2000, 6, 84–114. [Google Scholar] [CrossRef]
- Van Wessem, J.M.; Reijmer, C.H.; Van de Berg, W.J.; van Den Broeke, M.R.; Cook, A.J.; van Ulft, L.H.; van Meijgaard, E. Temperature and wind climate of the Antarctic Peninsula as simulated by a high-resolution regional atmospheric climate mode. J. Clim. 2015, 28, 7306–7326. [Google Scholar] [CrossRef]
- Kavan, J.; Ondruch, J.; Nývlt, D.; Hrbáček, F.; Carrivick, J.L.; Láska, K. Seasonal hydrological and suspended sediment transport dynamics in proglacial streams, James Ross Island, Antarctica. Geogr. Ann. A 2017, 99, 38–55. [Google Scholar] [CrossRef]
- Bohuslavová, O.; Macek, P.; Redčenko, O.; Láska, K.; Nedbalová, L.; Elster, J. Dispersal of lichens along a successional gradient after deglaciation of volcanic mesas on northern James Ross Island, Antarctic Peninsula. Polar Biol. 2018, 41, 2221–2232. [Google Scholar] [CrossRef]
- Hrbáček, F.; Oliva, M.; Láska, K.; Ruiz-Fernández, J.; De Pablo, M.A.; Vieira, G.; Ramos, M.; Nývlt, D. Active layer thermal regime in two climatically contrasted sites of the Antarctic Peninsula region [Régimen termal de la capa activa en dos áreas climáticamente. contrastadas de la Península Antártica]. Cuad. Investig. Geogr. 2016, 42, 457–474. [Google Scholar]
- Langer, M.; Westermann, S.; Muster, S.; Piel, K.; Boike, J. The surface energy balance of a polygonal tundra site in northern Siberia—Part 1: Spring to fall. Cryosphere 2011, 5, 151–171. [Google Scholar] [CrossRef]
- Wilks, D. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; pp. 1–704. [Google Scholar]
- Fuchs, M. Heat flux. In Methods of Soil Analysis. Part I. Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; SSSA Book Series no. 5; SSSA: Madison, WI, USA, 1986; pp. 957–968. [Google Scholar]
- Sauer, T.J.; Horton, R. Micrometeorology in Agricultural Systems. Agronomy Monograph no. 47; American Society of Agronomy, Crop Science Society of America; Soil Science Society of America: Madison, WI, USA, 2005; pp. 1–154. [Google Scholar]
- Foken, T. Micrometeorology; Springer: Berlin/Heidelberg, Germany, 2008; pp. 1–1306. [Google Scholar]
- Liu, H.; Foken, T. A modified Bowen ratio method to determine sensible and latent heat fluxes. Meteorol. Z. 2001, 10, 71–80. [Google Scholar] [CrossRef]
- Gromke, C.; Manes, C.; Walter, B.; Lehning, M.; Guala, M. Aerodynamic Roughness Length of Fresh Snow. Bound-Layer Meteorol. 2011, 141, 21–34. [Google Scholar] [CrossRef]
- Liu, C.; Li, Y.; Yang, Q.; Wang, L.; Wang, X.; Li, S.; Gao, Z. On the surface fluxes characteristics and roughness lengths at Zhongshan station, Antarctica. Int. J. Digit. Earth 2019, 12, 878–892. [Google Scholar] [CrossRef]
- Harrison, R.G. Meteorological Measurements and Instrumentation; Wiley Blackwell: Chichester, UK, 2015; pp. 1–257. [Google Scholar]
- Westermann, S.; Lüers, J.; Langer, M.; Piel, K.; Boike, J. The annual surface energy budget of a high-arctic permafrost site on Svalbard, Norway. Cryosphere 2009, 3, 245–263. [Google Scholar] [CrossRef]
- Ambrozova, K.; Laska, K.; Hrbacek, F.; Kavan, J.; Ondruch, J. Air temperature and lapse rate variation in the ice-free and glaciated areas of northern James Ross Island, Antarctic Peninsula, during 2013–2016. Int. J. Climatol. 2019, 39, 643–657. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Burba, G.; Anderson, D. A Brief Practical Guide to Eddy Covariance Flux Measurements: Principles and Workflow Examples for Scientific and Industrial Applications; LI-COR Biosciences: Lincoln, NE, USA, 2010; 212p. [Google Scholar]
- Fourier, J. The Analytical Theory of Heat; Dover Publications: New York, NY, USA, 1955; pp. 1–66. [Google Scholar]
- Kejna, M.; Przybylak, R.; Araźny, A. The Influence of Cloudiness and Synoptic Situations on the Solar Radiation Balance in the Area of Kaffiøyra (NW Spitsbergen) in the Summer Seasons 2010 and 2011. Bull. Geogr. Phys. Geogr. Ser. 2012, 5, 77–95. [Google Scholar] [CrossRef]
- Ohmura, A. Comparative Energy Balance Study for Arctic Tundra, Sea Surface, Glaciers and Boreal Forests. Geojournal 1984, 8, 221–228. [Google Scholar] [CrossRef]
- Rott, H.; Obleitner, F. The Energy Balance of Dry Tundra in West Greenland. Arct. Alp. Res. 1992, 24, 352–362. [Google Scholar] [CrossRef]
- Harding, R.J.; Lloyd, C.R. Fluxes of water and energy from high latitude tundra sites in Svalbard. Nord. Hydrol. 1998, 29, 267–284. [Google Scholar] [CrossRef]
- Scherrer, D.; Parlow, E.; Ritter, N.; Siegrist, F. Klimaoökologie und Fernerkundung. In Methoden und Datenübersicht der Forschungsgruppen der Geowissenschaftlichen Spitzbergen-Expeditionen 1990 und 1991 zum Liefdefjorden (Datenband) Materialien zur Physiogeographie; Leser, H., Ed.; Geographisches Institut: Basel, Switzerland, 1993; Volume 15, pp. 51–58; appendix 121–151. [Google Scholar]
- Sjøblom, A. Turbulent fluxes of momentum and heat over land in the High-Arctic summer: The influence of observation techniques. Polar Res. 2014, 33, 1–17. [Google Scholar] [CrossRef]
- Migała, K.; Wojtuń, B.; Szymański, W.; Muskała, P. Soil moisture and temperature variation under different types of tundra vegetation during the growing season: A case study from the Fuglebekken catchment, SW Spitsbergen. Catena 2014, 116, 10–18. [Google Scholar] [CrossRef]
- Hrbáček, F.; Láska, K.; Engel, Z. Effect of Snow Cover on the Active-Layer Thermal Regime–A Case Study from James Ross Island, Antarctic Peninsula. Permafr. Periglac. Process. 2016, 27, 307–315. [Google Scholar] [CrossRef]
- Ambach, W. The Influence of Cloudiness on the Net Radiation Balance of a Snow Surface with High Albedo. J. Glaciol. 1974, 13, 73–84. [Google Scholar] [CrossRef][Green Version]
- Kejna, M.; Maturilli, M.; Araźny, A.; Sobota, I. Radiation balance diversity on NW Spitsbergen in 2010–2014. Pol. Polar Res. 2017, 39, 61–82. [Google Scholar] [CrossRef]


| Parameter | Instrument | Company | Height/Depth (m) | Accuracy | Measuring Interval | Recording Interval |
|---|---|---|---|---|---|---|
| Net radiation | CNR4 Net Radiometer | Kipp Zonen, the Netherlands | 1 | Longwave radiation: ±10%, Shortwave radiation: ±4% | 10 s | 5 min |
| Wind components | USA-1 Sonic Anemometer | Metek, Germany | 2 | 0.1 ms−1 or 2% | 10 s−1 | 5 min |
| Ground heat flux | HFP01 heat flux plates | Huksefluks, the Netherlands | −0.05 | ±20% | 30 min | 30 min |
| Air temperature | EMS33H Sensor | EMS Brno, Czech Republic | 2 | ±0.15 °C | 10 s | 5 min |
| Relative humidity | EMS33H Sensor | EMS Brno, Czech Republic | 2 | ±1% | 10 s | 5 min |
| Atmospheric pressure | TMAG | CRESSTO, Czech Republic | 1 | ±2 Pa | 10 s | 5 min |
| Snow depth | Ultrasonic snow depth sensor | Judd Comm., USA | 1 | ± 1 cm | 2 h | 2 h |
| Ground surface temperature | PT100/8 resistance thermometer | EMS Brno, Czech Republic | −0.02, −0.05, −0.10, −0.20, −0.50, −0.75 | ±0.15 °C | 30 min | 30 min |
| Flux | Error (%) | Reason | Reference |
|---|---|---|---|
| QL↓ (Qnet) | 10 | Measurement accuracy for longwave radiation | CNR4 Net Radiometer manual |
| Qnet | 3.4 | Spatial heterogeneity of albedo around the measuring site | [38] |
| QH | 25 | Local circulation systems formation due to complex orography | [39,41] |
| QH | 10 | Use of buoyancy flux instead of true sensible heat flux | [34] |
| QE | 33 | Choice of z0 (see comment in the text) | Sensitivity testing |
| QG | 20 | Measurement accuracy of the instrument | HFP01 heat flux plate manual |
| QH, QE, QG | - | Different footprint area | [40] |
| Variable 1 | Variable 2 | 0 Day | 1 Day | 2 Days | 3 Days |
|---|---|---|---|---|---|
| Qnet vs. | Tsurf | 0.71 | 0.66 | 0.64 | 0.59 |
| GT30 | 0.52 | 0.70 | 0.71 | 0.68 | |
| GT50 | 0.48 | 0.64 | 0.67 | 0.64 | |
| GT75 | −0.15 | −0.08 | −0.01 | 0.01 | |
| QG vs. | Tsurf | 0.84 | 0.72 | 0.58 | 0.54 |
| GT30 | 0.38 | 0.59 | 0.66 | 0.65 | |
| GT50 | 0.34 | 0.44 | 0.58 | 0.60 | |
| GT75 | −0.01 | −0.02 | −0.02 | 0.05 | |
| Tair vs. | Tsurf | 0.95 | 0.79 | 0.63 | 0.61 |
| GT30 | 0.66 | 0.77 | 0.77 | 0.71 | |
| GT50 | 0.60 | 0.65 | 0.72 | 0.70 | |
| GT75 | −0.01 | −0.01 | 0.02 | 0.11 |
| QS↓ | QS↑ | QL↓ | QL↑ | Qnet | Albedo | QG | QH | QE | QG + QH+ QE | Tair | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| QS↓ | 1.00 | −0.04 | −0.19 | 0.72 | 0.91 | −0.50 | 0.78 | 0.44 | 0.64 | 0.76 | 0.62 |
| QS↑ | −0.04 | 1.00 | −0.28 | −0.41 | −0.33 | 0.76 | −0.20 | −0.19 | −0.16 | −0.30 | −0.34 |
| QL↓ | −0.19 | −0.28 | 1.00 | 0.30 | 0.02 | −0.15 | 0.02 | 0.20 | 0.20 | 0.24 | 0.34 |
| QL↑ | 0.72 | −0.41 | 0.30 | 1.00 | 0.79 | −0.65 | 0.85 | 0.34 | 0.81 | 0.83 | 0.96 |
| Qnet | 0.91 | −0.33 | 0.02 | 0.79 | 1.00 | −0.71 | 0.76 | 0.60 | 0.72 | 0.87 | 0.67 |
| albedo | −0.50 | 0.76 | −0.15 | −0.65 | −0.71 | 1.00 | −0.54 | −0.29 | −0.41 | −0.56 | −0.53 |
| QG | 0.78 | −0.20 | 0.02 | 0.85 | 0.76 | −0.54 | 1.00 | 0.22 | 0.67 | 0.72 | 0.84 |
| QH | 0.44 | −0.19 | 0.20 | 0.34 | 0.60 | −0.29 | 0.22 | 1.00 | 0.50 | 0.71 | 0.18 |
| QE | 0.64 | −0.16 | 0.20 | 0.81 | 0.72 | −0.41 | 0.67 | 0.50 | 1.00 | 0.91 | 0.78 |
| QG + QH + QE | 0.76 | −0.30 | 0.24 | 0.83 | 0.87 | −0.56 | 0.72 | 0.71 | 0.91 | 1.00 | 0.75 |
| Tair | 0.62 | −0.34 | 0.34 | 0.96 | 0.67 | −0.53 | 0.84 | 0.18 | 0.78 | 0.75 | 1.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ambrožová, K.; Hrbáček, F.; Láska, K. The Summer Surface Energy Budget of the Ice-Free Area of Northern James Ross Island and Its Impact on the Ground Thermal Regime. Atmosphere 2020, 11, 877. https://doi.org/10.3390/atmos11080877
Ambrožová K, Hrbáček F, Láska K. The Summer Surface Energy Budget of the Ice-Free Area of Northern James Ross Island and Its Impact on the Ground Thermal Regime. Atmosphere. 2020; 11(8):877. https://doi.org/10.3390/atmos11080877
Chicago/Turabian StyleAmbrožová, Klára, Filip Hrbáček, and Kamil Láska. 2020. "The Summer Surface Energy Budget of the Ice-Free Area of Northern James Ross Island and Its Impact on the Ground Thermal Regime" Atmosphere 11, no. 8: 877. https://doi.org/10.3390/atmos11080877
APA StyleAmbrožová, K., Hrbáček, F., & Láska, K. (2020). The Summer Surface Energy Budget of the Ice-Free Area of Northern James Ross Island and Its Impact on the Ground Thermal Regime. Atmosphere, 11(8), 877. https://doi.org/10.3390/atmos11080877