A Method for Retrieving Stratospheric Aerosol Extinction and Particle Size from Ground-Based Rayleigh-Mie-Raman Lidar Observations
Abstract
1. Introduction
2. The ALOMAR Rayleigh-Mie-Raman (RMR) Lidar
3. Retrieval Approach
3.1. Retrieval Assumptions
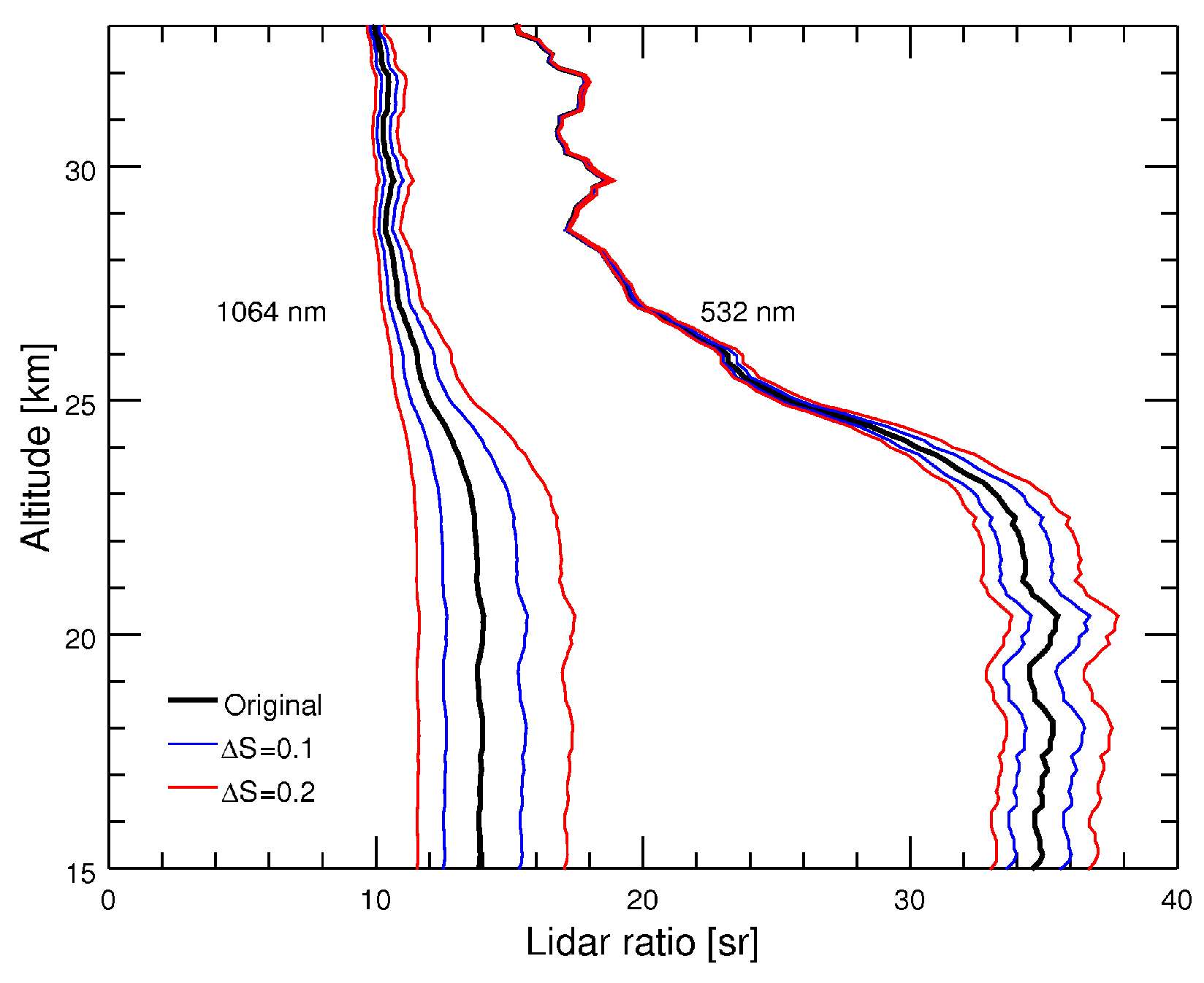
3.2. Retrieval of Aerosol Particle Size Information
3.3. Radius Ambiguity
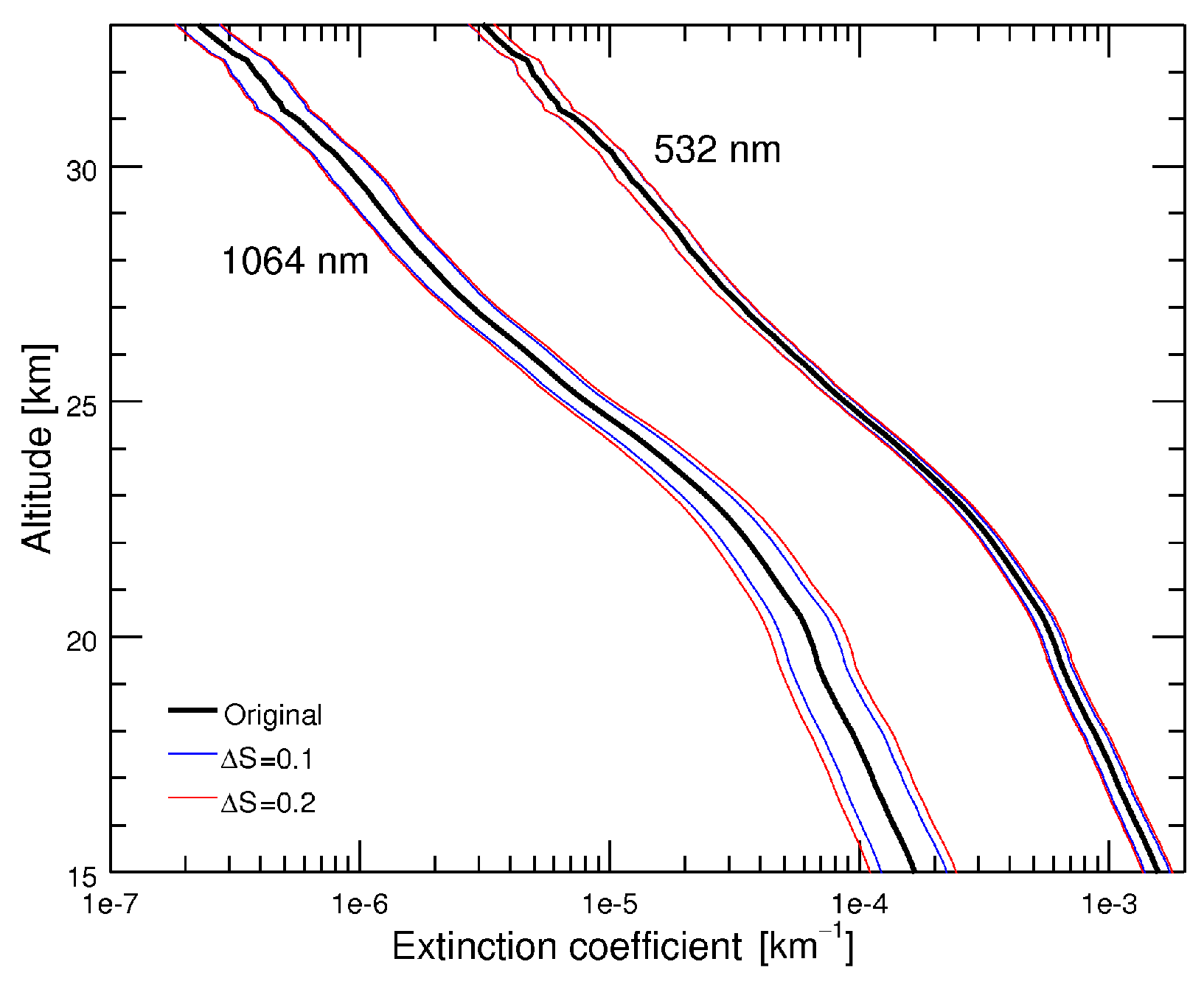
3.4. Derivation of Extinction Profiles
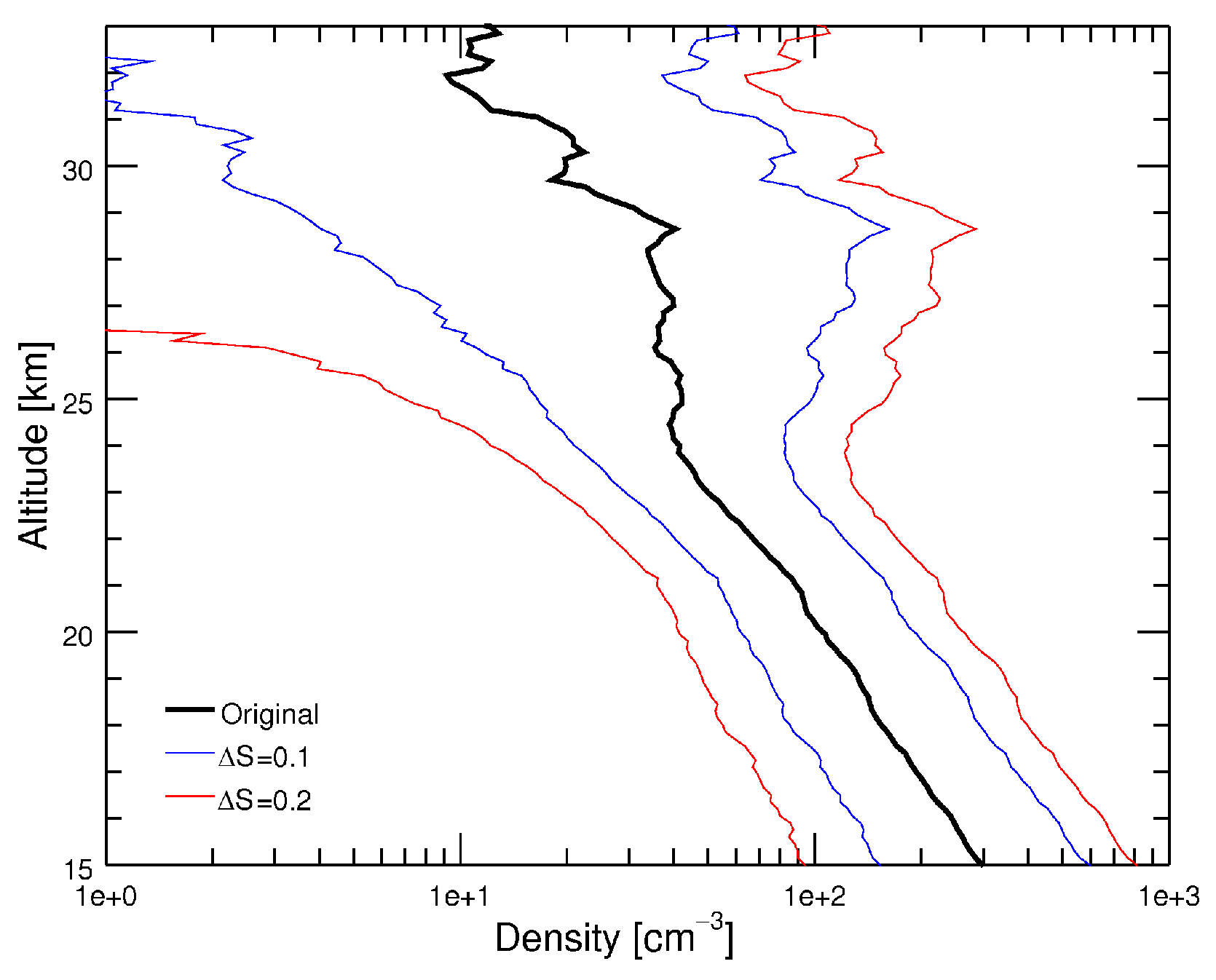
3.5. Particle Number Density Estimation
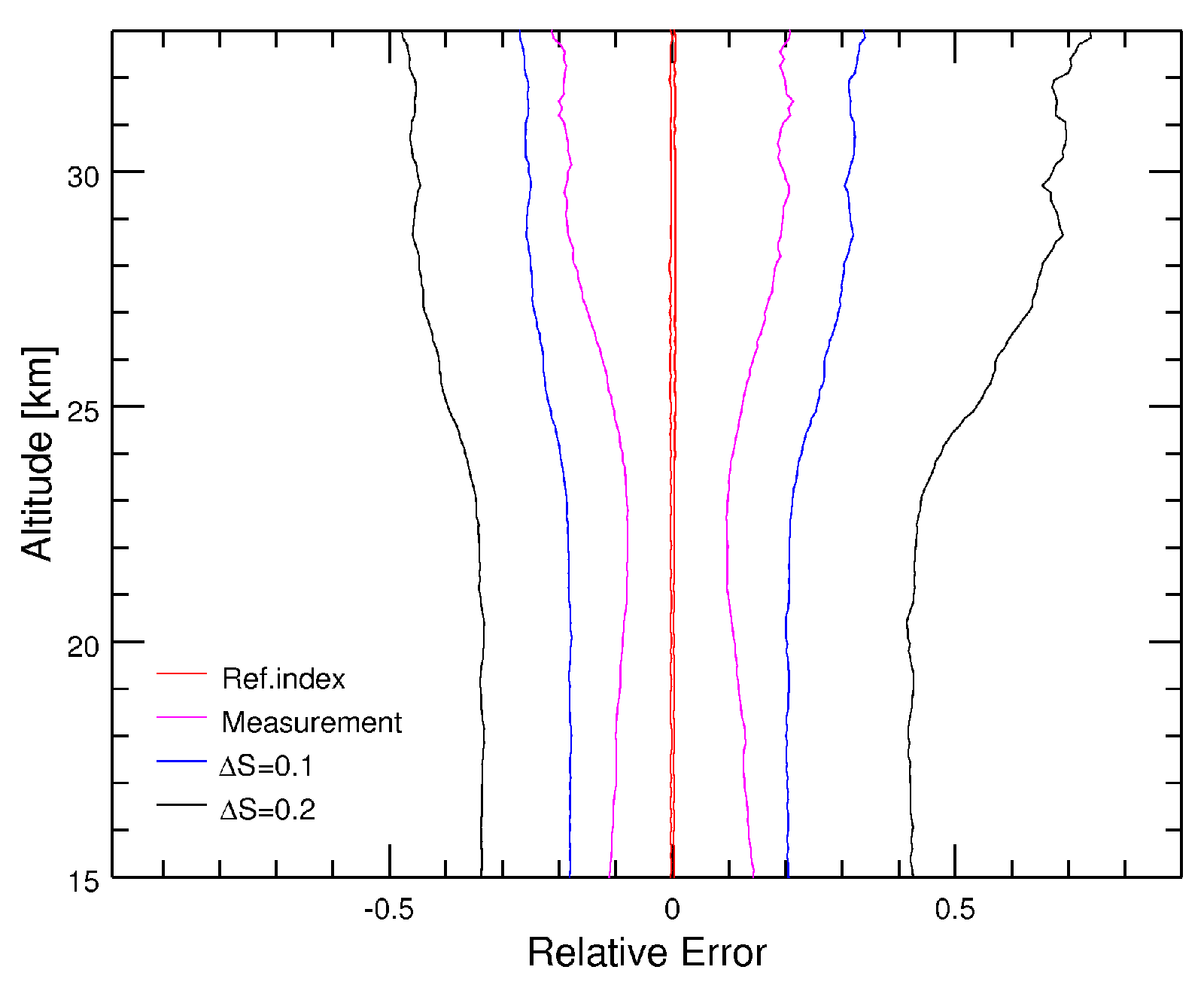
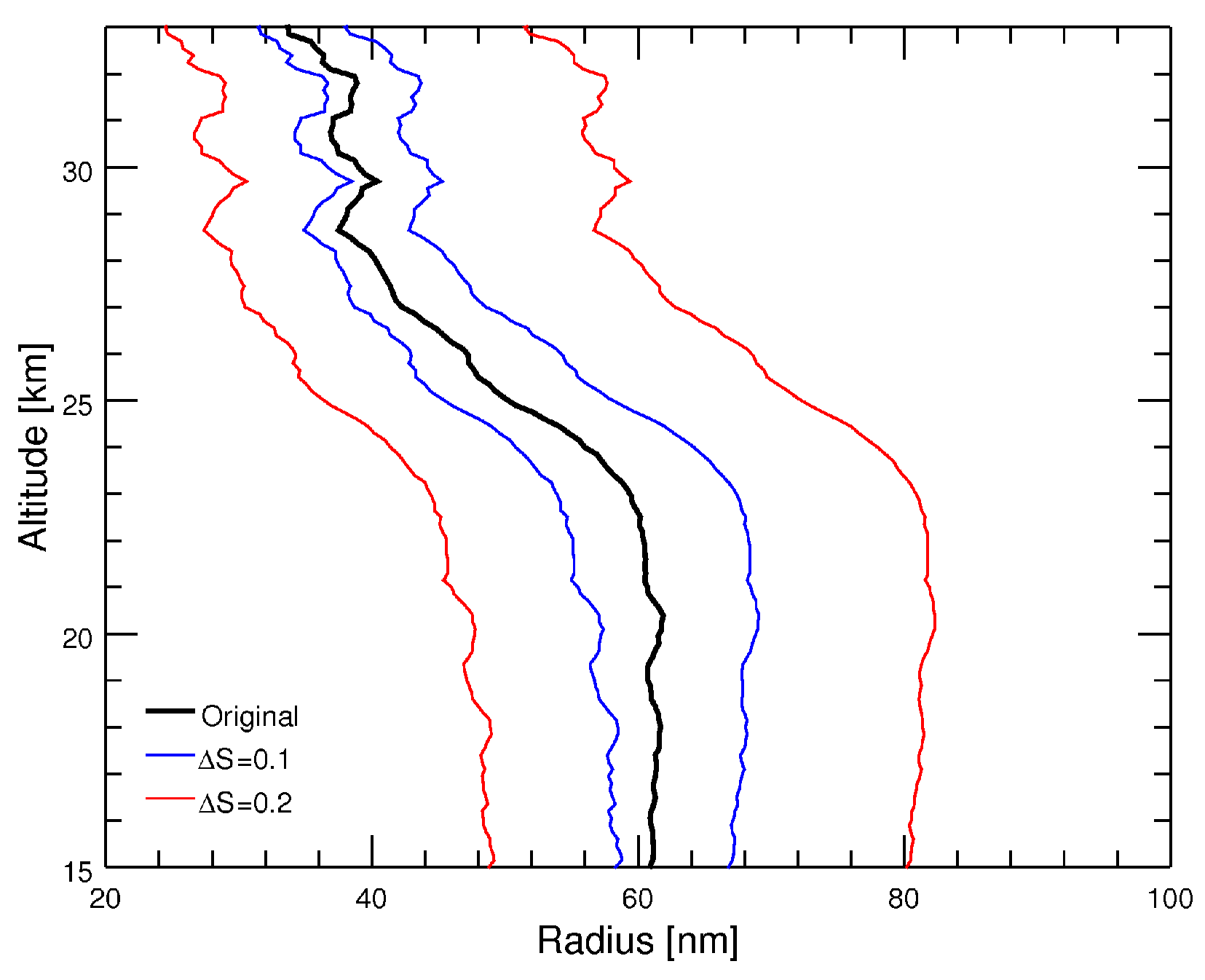
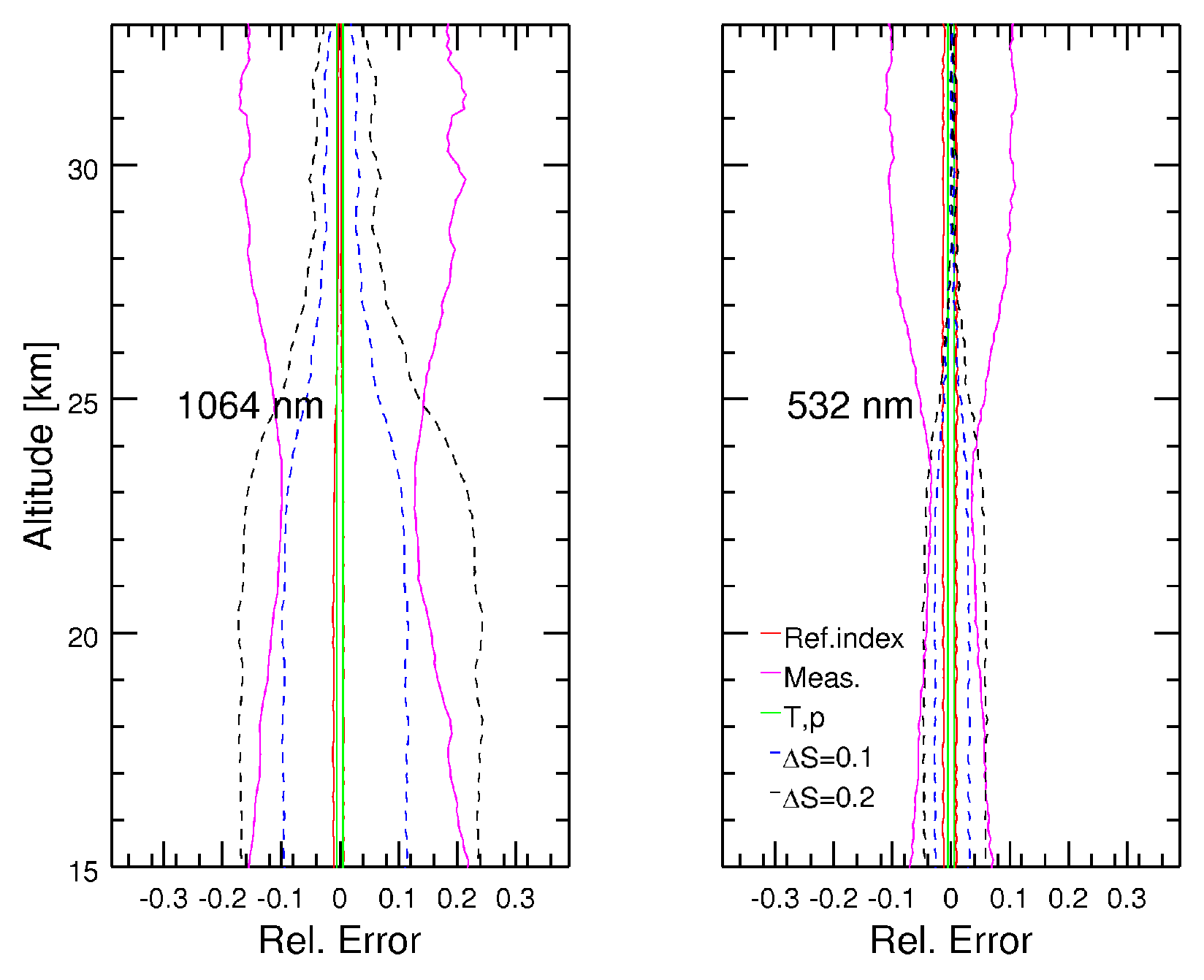
4. Error Estimation
5. Comparison with Independent Observations
5.1. Comparison of Particle Size Retrievals
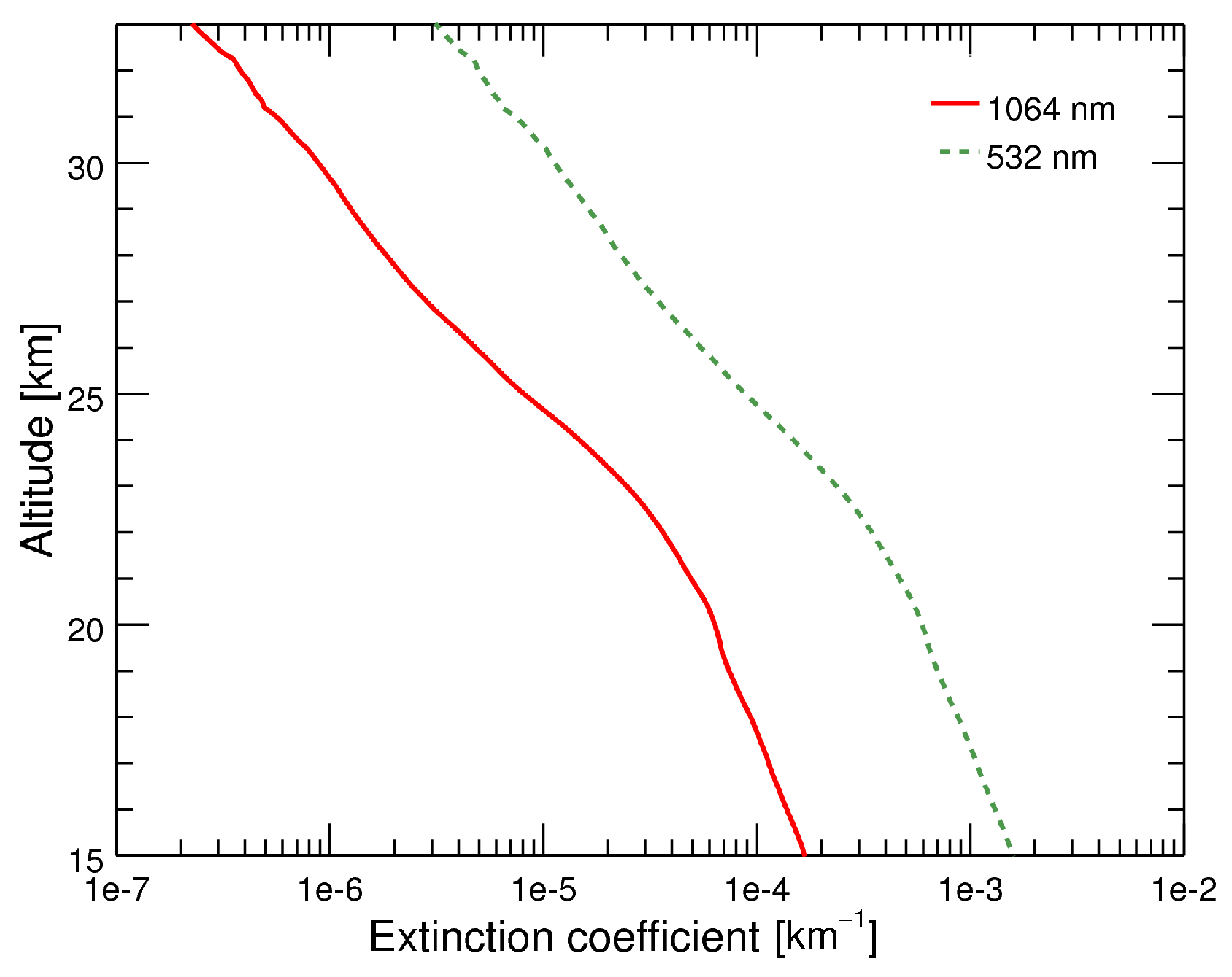
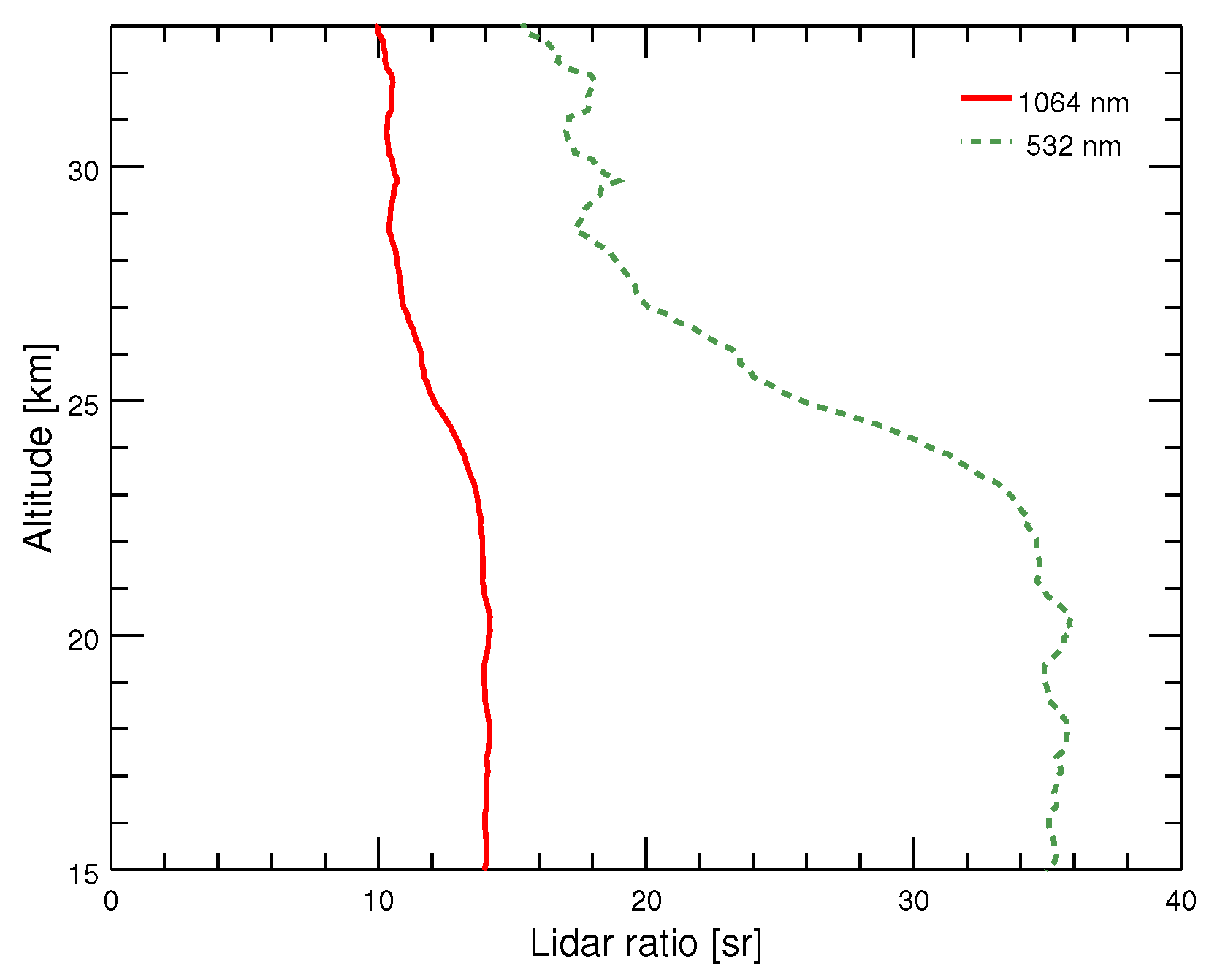
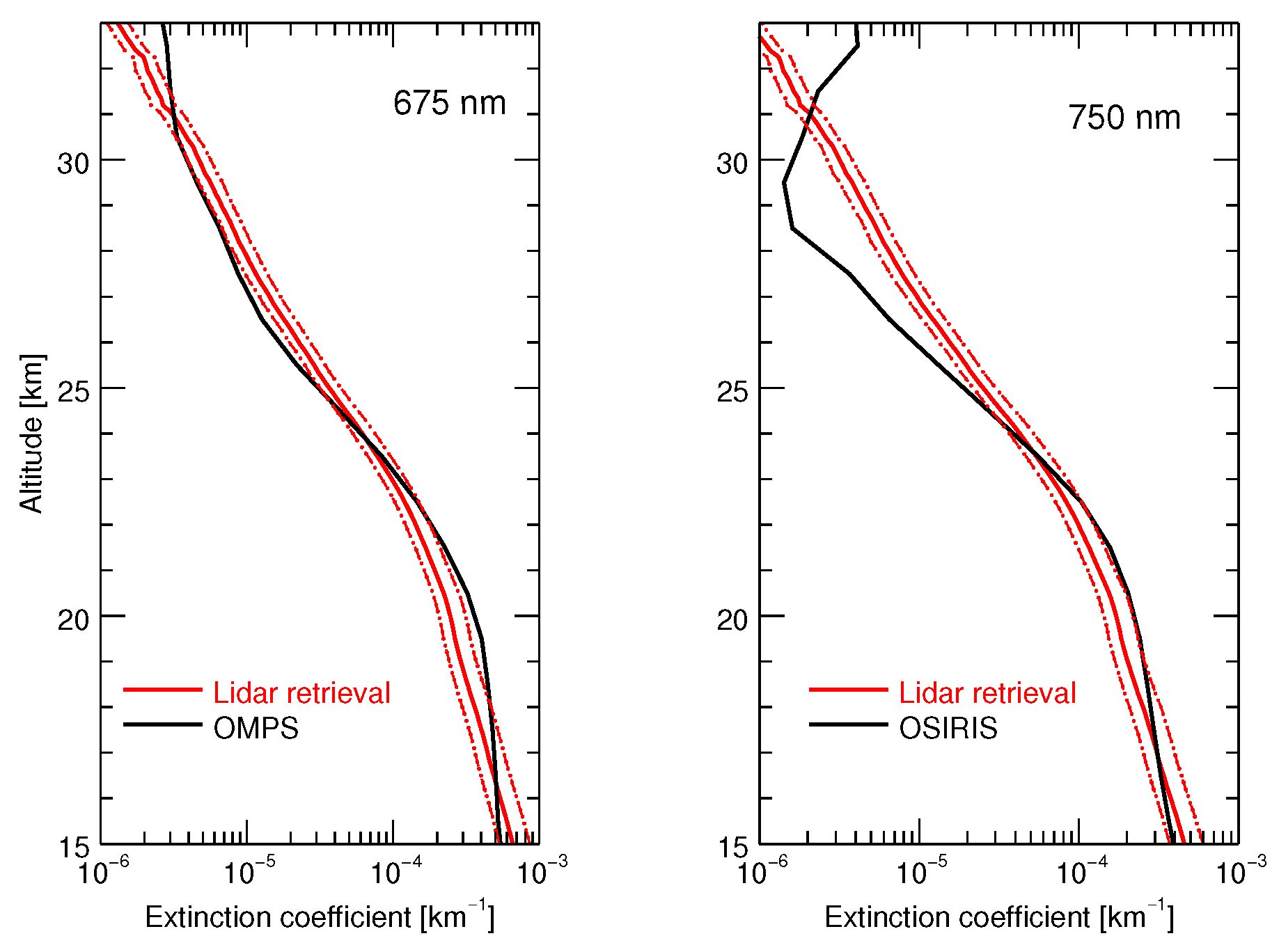
5.2. Comparison of Extinction Profiles
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kremser, S.; Thomason, L.W.; von Hobe, M.; Hermann, M.; Deshler, T.; Timmreck, C.; Toohey, M.; Stenke, A.; Schwarz, J.P.; Weigel, R.; et al. Stratospheric aerosol—Observations, processes and impact on climate. Rev. Geophys. 2016, 54, 278–335. [Google Scholar] [CrossRef]
- von Savigny, C.; Timmreck, C.; Buehler, S.A.; Burrows, J.P.; Giorgetta, M.A.; Hegerl, G.; Hoose, C.; Quaas, J.; Malinina, E.; Rozanov, A.; et al. The Research Unit VolImpact: Revisiting the volcanic impact on atmosphere and climate—Preparations for the next big volcanic eruption. Met. Z. 2020, 29, 3–18. [Google Scholar] [CrossRef]
- Crutzen, P.J. The possible importance of CSO for the sulfate layer of the stratosphere. Geophys. Res. Lett. 1976, 3, 73–76. [Google Scholar] [CrossRef]
- Timmreck, C. Modeling the climatic effects of large volcanic eruptions. WIREs Clim. Chang. 2012, 3, 545–564. [Google Scholar] [CrossRef]
- Curtius, J.; Weigel, R.; Vössing, H.-J.; Wernli, H.; Werner, A.; Volk, C.-M.; Konopka, P.; Krebsbach, M.; Schiller, C.; Roiger, A.; et al. Observations of meteoric material and implications for aerosol nucleation in the winter Arctic lower stratosphere derived from in situ particle measurements. Atmos. Chem. Phys. 2005, 5, 3053–3069. [Google Scholar] [CrossRef]
- Robock, A. Volcanic Eruptions and Climate. Rev. Geophys. 2000, 38, 191–219. [Google Scholar] [CrossRef]
- Dutton, E.G.; Christy, J.R. Solar radiative forcing at selected locations and evidence for global lower tropospheric cooling following the eruptions of El Chichon and Pinatubo. Geophys. Res. Lett. 1992, 19, 2313–2316. [Google Scholar] [CrossRef]
- Brasseur, G.; Granier, C. Mount Pinatubo aerosols, chlorofluorocarbons, and ozone depletion. Science 1992, 25, 1239–1242. [Google Scholar] [CrossRef]
- Tie, X.; Brasseur, G. The response of stratospheric ozone to volcanic eruptions: Sensitivity to atmospheric chlorine loading. Geophys. Res. Lett. 1995, 22, 3035–3038. [Google Scholar] [CrossRef]
- Langematz, U.; Tully, M.; Calvo, N.; Dameris, M.; de Laat, A.T.J.; Klekociuk, A.; Müller, R.; Young, P. Polar Stratospheric Ozone: Past, Present, and Future, Chapter 4 in Scientific Assessment of Ozone Depletion: 2018, Global Ozone Research and Monitoring Project—Report No. 58; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- von Zahn, U.; von Cossart, G.; Fiedler, J.; Fricke, K.H.; Nelke, G.; Baumgarten, G.; Rees, D.; Hauchecorne, A.; Adolfsen, K. The ALOMAR Rayleigh/Mie/Raman lidar: Objectives, configuration and performance. Ann. Geophys. 2000, 18, 815–833. [Google Scholar] [CrossRef]
- Blum, U.; Khosrawi, F.; Baumgarten, G.; Stebel, K.; Müller, R.; Fricke, K.H. Simultaneous lidar observations of a polar stratospheric cloud on the east and west sides of the scandinavian mountains and microphysical box model calculations. Ann. Geophys. 2006, 24, 3267–3277. [Google Scholar] [CrossRef][Green Version]
- Jumelet, J.; Bekki, S.; David, C.; Keckhut, P. Statistical estimation of stratospheric particle size distribution by combining optical modelling and lidar scattering measurements. Atmos. Chem. Phys. 2008, 8, 5435–5448. [Google Scholar] [CrossRef]
- von Savigny, C.; Hoffmann, C. Issues related to the retrieval of stratospheric-aerosol particle size information based on optical measurements. Atmos. Meas. Tech. 2020, 13, 1909–1920. [Google Scholar] [CrossRef]
- Langenbach, A.; Baumgarten, G.; Fiedler, J.; Lübken, F.-J.; von Savigny, C.; Zalach, J. Year-round stratospheric aerosol backscatter ratios calculated from lidar measurements above Northern Norway. Atmos. Meas. Tech. 2019, 12, 4065–4076. [Google Scholar] [CrossRef]
- von Cossart, G.; Fiedler, J.; von Zahn, U. Size distributions of NLC particles as determined from 3-color observations of NLC by ground-based lidar. Geophys. Res. Lett. 1999, 26, 1513–1516. [Google Scholar] [CrossRef]
- Baumgarten, G.; Fiedler, J.; von Cossart, G. The size of noctilucent cloud particles above ALOMAR (69N,16E): Optical modeling and method description. Adv. Space Res. 2007, 40, 772–784. [Google Scholar] [CrossRef]
- Yue, G.K.; Deepak, A. Retrieval of stratospheric aerosol size distribution from atmospheric extinction of solar radiation at two wavelengths. Appl. Opt. 1983, 22, 1639–1645. [Google Scholar] [CrossRef]
- Palmer, K.F.; Williams, D. Optical Constants of Sulfuric Acid; Application to the Clouds of Venus. Appl. Opt. 1975, 14, 208–219. [Google Scholar] [CrossRef]
- Deshler, T. A review of global stratospheric aerosol: Measurement, importance, life cycle, and local stratospheric aerosol. Atmos. Res. 2008, 90, 223–232. [Google Scholar] [CrossRef]
- Bingen, C.; Fussen, D.; Vanhellemont, F. A global climatology of stratospheric aerosol size distribution parameters derived from SAGE II data over the period 1984–2000: 1. Methodology and climatological observations. J. Geophys. Res. 2004, 109, D06201. [Google Scholar] [CrossRef]
- Bohren, C.F.; Huffman, D.R. Absorption and Scattering of Light by Small Particles; Wiley Science Paperback Series; Wiley Professional Paperback Edition: Hoboken, NJ, USA, 1998. [Google Scholar]
- Bucholtz, A. Rayleigh-scattering calculations for the terrestial atmosphere. Appl. Opt. 1995, 34, 2765–2773. [Google Scholar] [CrossRef] [PubMed]
- Mie Scattering Routines, University of Oxford, Departement of Physics. Available online: http://eodg.atm.ox.ac.uk/MIE/index.html (accessed on 31 December 2018).
- Bourassa, A.E.; Degenstein, D.A.; Llewellyn, E.J. Retrieval of stratospheric aerosol size information from OSIRIS limb scattered sunlight spectra. Atmos. Chem. Phys. 2008, 8, 6375–6380. [Google Scholar] [CrossRef]
- McLinden, C.A.; McConnell, J.C.; McElroy, C.T.; Griffioen, E. Observations of stratospheric aerosol using CPFM polarized limb radiances. J. Atmos. Sci. 1999, 56, 233–240. [Google Scholar] [CrossRef]
- Ugolnikov, O.S.; Maslov, I.A. Investigations of the Background Stratospheric Aerosol Using Multicolor Wide-Angle Measurements of the Twilight Glow Background. Cosm. Res. 2018, 56, 85–93. [Google Scholar] [CrossRef]
- Deshler, T.; Hervig, M.E.; Hofmann, D.J.; Rosen, J.M.; Liley, J.B. Thirty years of in situ stratospheric aerosol size distribution measurements from Laramie, Wyoming (41∘ N), using balloon-borne instruments. J. Geophys. Res. 2003, 108, 4167. [Google Scholar] [CrossRef]
- Wrana, F. Charakterisierung der Größenverteilung Stratosphärischer Aerosole Mittels Multispektraler Satellitengestützter Extinktionsmessungen. Master’s Thesis, Institute of Physics, University of Greifswald, Greifswald, Germany, 2019. [Google Scholar]
- European Centre for Medium-Range Weather Forecasts (ECMWF). The ERA-Interim Reanalysis Dataset, Copernicus Climate Change Service (C3S). Available online: https://apps.ecmwf.int/datasets/data/interim-full-moda/levtype=pl/ (accessed on 15 January 2019).
- Khaykin, S.M.; Godin-Beekmann, S.; Keckhut, P.; Hauchecorne, A.; Jumelet, J.; Vernier, J.P.; Bourassa, A.; Degenstein, D.A.; Rieger, L.A.; Bingen, C.; et al. Variability and evolution of the midlatitude stratospheric aerosol budget from 22 years of ground-based lidar and satellite observations. Atmos. Chem. Phys. 2017, 17, 1829–1845. [Google Scholar] [CrossRef]
- Trickl, T.; Giehl, H.; Jäger, H.; Vogelmann, H. 35 yr of stratospheric aerosol measurements at Garmisch-Partenkirchen: From Fuego to Eyjafjallajökull. Atmos. Chem. Phys. 2013, 13, 5205–5225. [Google Scholar] [CrossRef]
- Mattis, I.; Ansmann, A.; Müller, D.; Wandinger, U.; Althausen, D. Multiyear aerosol observations with dualwavelength Raman lidar in the framework of EARLINET. J. Geophys. Res. 2004, 109, D132035. [Google Scholar] [CrossRef]
- Sakai, T.; Uchino, O.; Nagai, T.; Liley, B.; Morino, I.; Fujimoto, T. Longterm variation of stratospheric aerosols observed with lidars over Tsukuba, Japan, from 1982 and Lauder, New Zealand, from 1992 to 2015. J. Geophys. Res. Atmos. 2016, 121, 283–293. [Google Scholar] [CrossRef]
- Bingen, C.; Fussen, D.; Vanhellemont, F. A global climatology of stratospheric aerosol size distribution parameters derived from SAGE II data over the period 1984–2000: 2. Reference data. J. Geophys. Res. 2004, 109, D06202. [Google Scholar] [CrossRef]
- Bingen, C.; Vanhellemont, F.; Fussen, D. A new regularized inversion method for the retrieval of stratospheric aerosol size distributions applied to 16 years of SAGE II data (1984–2000): Method, results and validation. Ann. Geophys. 2003, 21, 797–804. [Google Scholar] [CrossRef][Green Version]
- Llewellyn, E.J.; Lloyd, N.D.; Degenstein, D.A.; Gattinger, R.L.; Petelina, S.V.; Bourassa, A.E.; Wiensz, J.T.; Ivanov, E.V.; McDade, I.C.; Solheim, B.H.; et al. The OSIRIS instrument on the Odin satellite. Can. J. Phys. 2004, 82, 411–422. [Google Scholar] [CrossRef]
- Murtagh, D.; Frisk, U.; Merino, F.; Ridal, M.; Jonsson, A.; Stegman, J.; Witt, G.; Eriksson, P.; Jiménez, C.; Megie, G.; et al. An overview of the Odin Atmospheric Mission. Can. J. Phys. 2002, 80, 309–319. [Google Scholar] [CrossRef]
- Bourassa, A.E.; Rieger, L.A.; Lloyd, N.D.; Degenstein, D.A. Odin-OSIRIS stratospheric aerosol data product and SAGE III intercomparison. Atmos. Chem. Phys. 2012, 12, 605–614. [Google Scholar] [CrossRef]
- Jaross, G.; Bhartia, P.K.; Chen, G.; Kowitt, M.; Haken, M.; Chen, Z.; Xu, P.; Warner, J.; Kelly, T. OMPS Limb Profiler instrument performance assessment. J. Geophys. Res. Atmos. 2014, 119, 4399–4412. [Google Scholar] [CrossRef]
- DeLand, M.; Bhartia, P.; Xu, P.; Zhu, T. OMPS Limb Profiler Aerosol Extinction Product AER675: Version 0.5 Product Description. Available online: https://ozoneaq.gsfc.nasa.gov/media/docs/OMPS_LP_AER675_V0.5_Product_Description.pdf (accessed on 15 January 2019).
- Angström, A. On the atmospheric transmission of Sun radiation and on dust in the air. Geogr. Ann. 1929, 11, 156–166. [Google Scholar]
- Rieger, L.; Bourassa, A.; Degenstein, D. Merging the OSIRIS and SAGE II stratospheric aerosol records. J. Geophys. Res. Atmos. 2015, 120. [Google Scholar] [CrossRef]
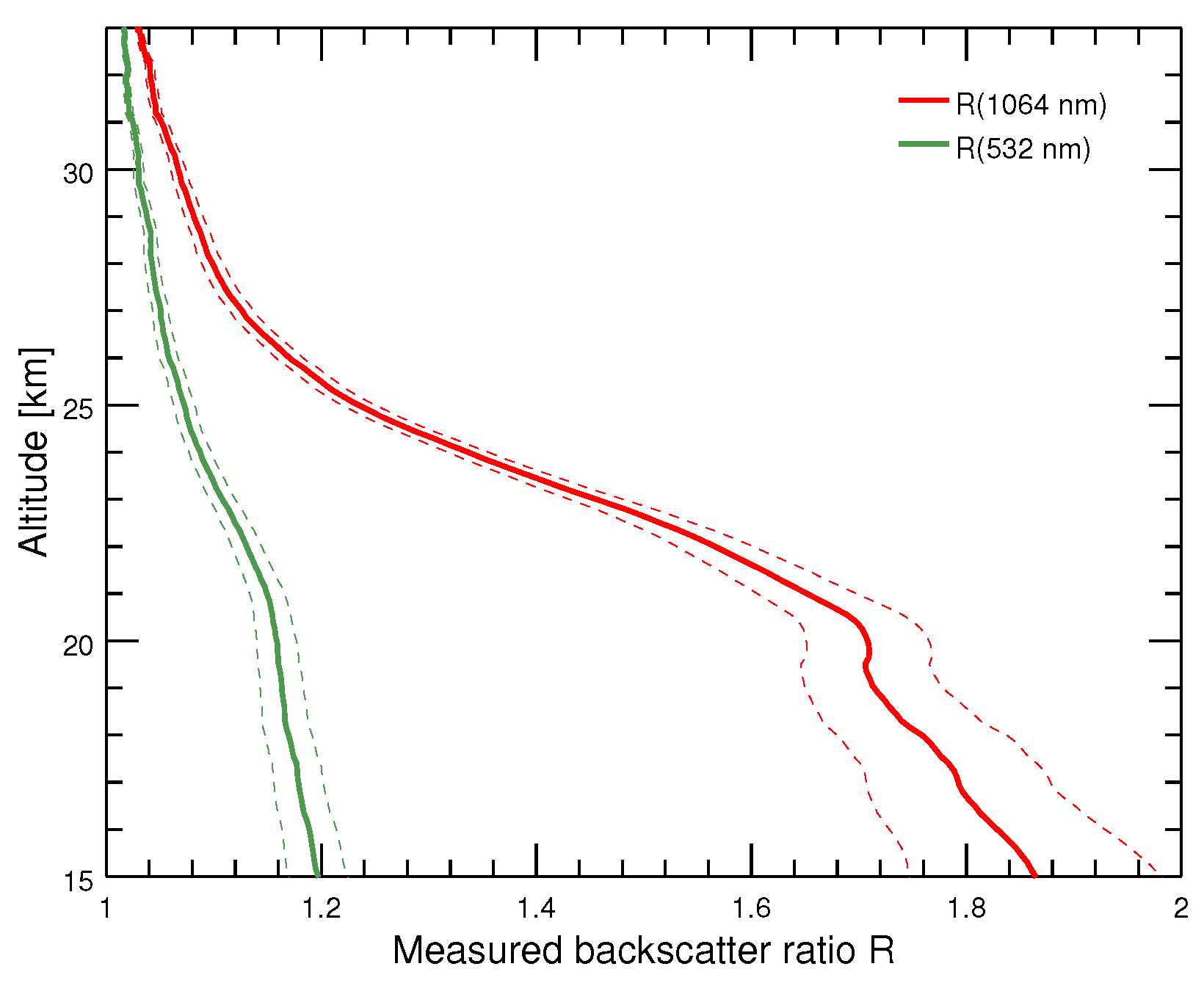
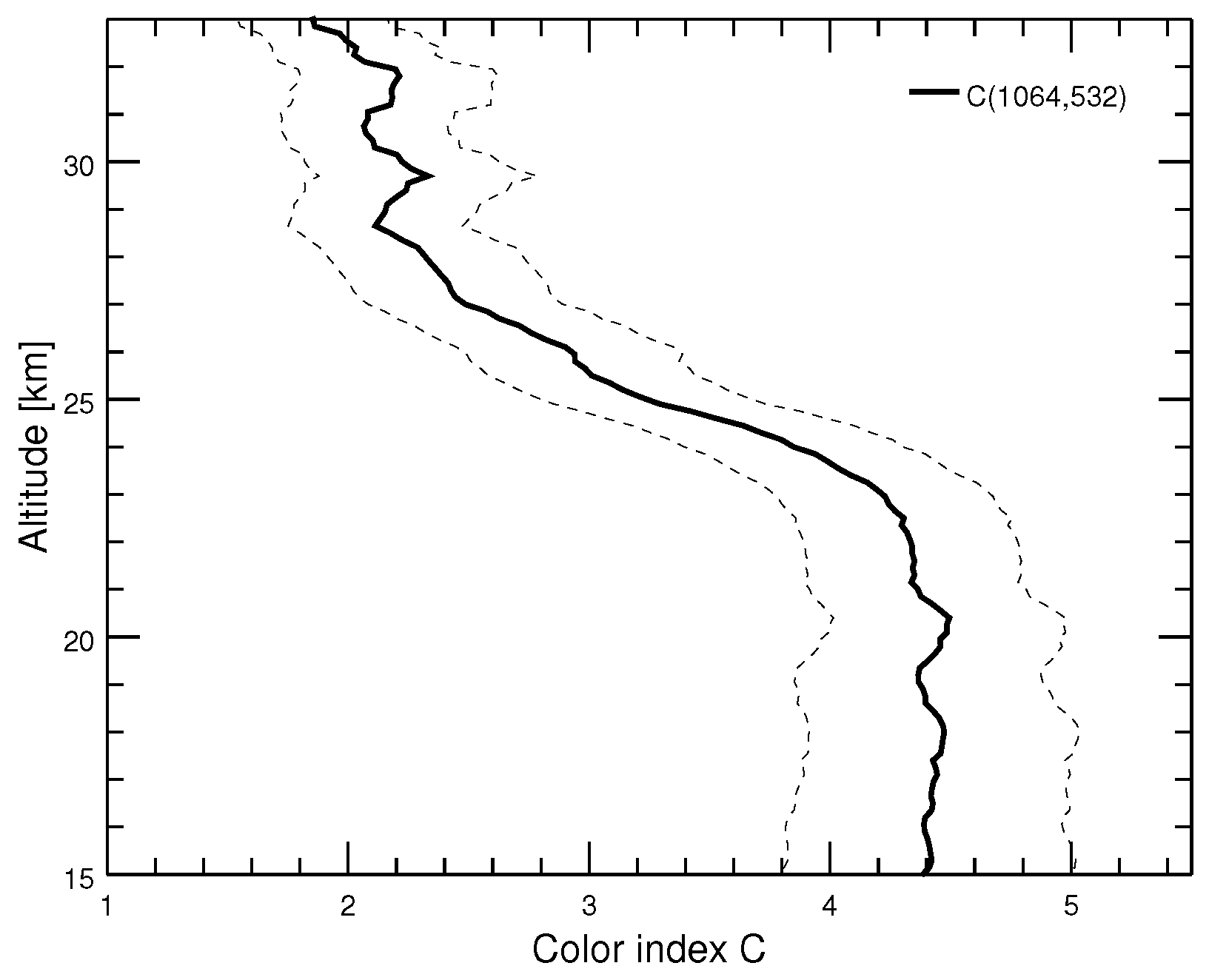
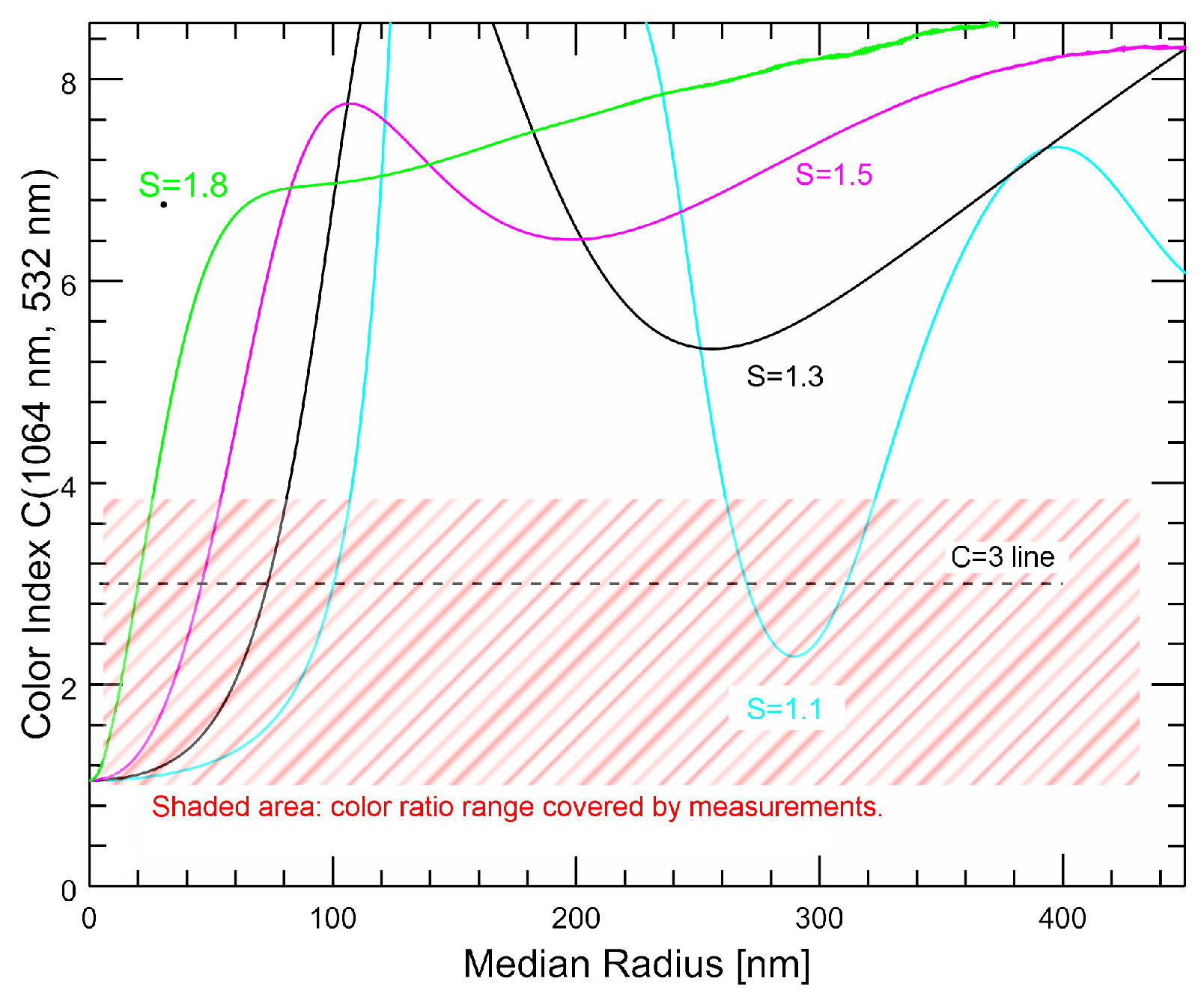
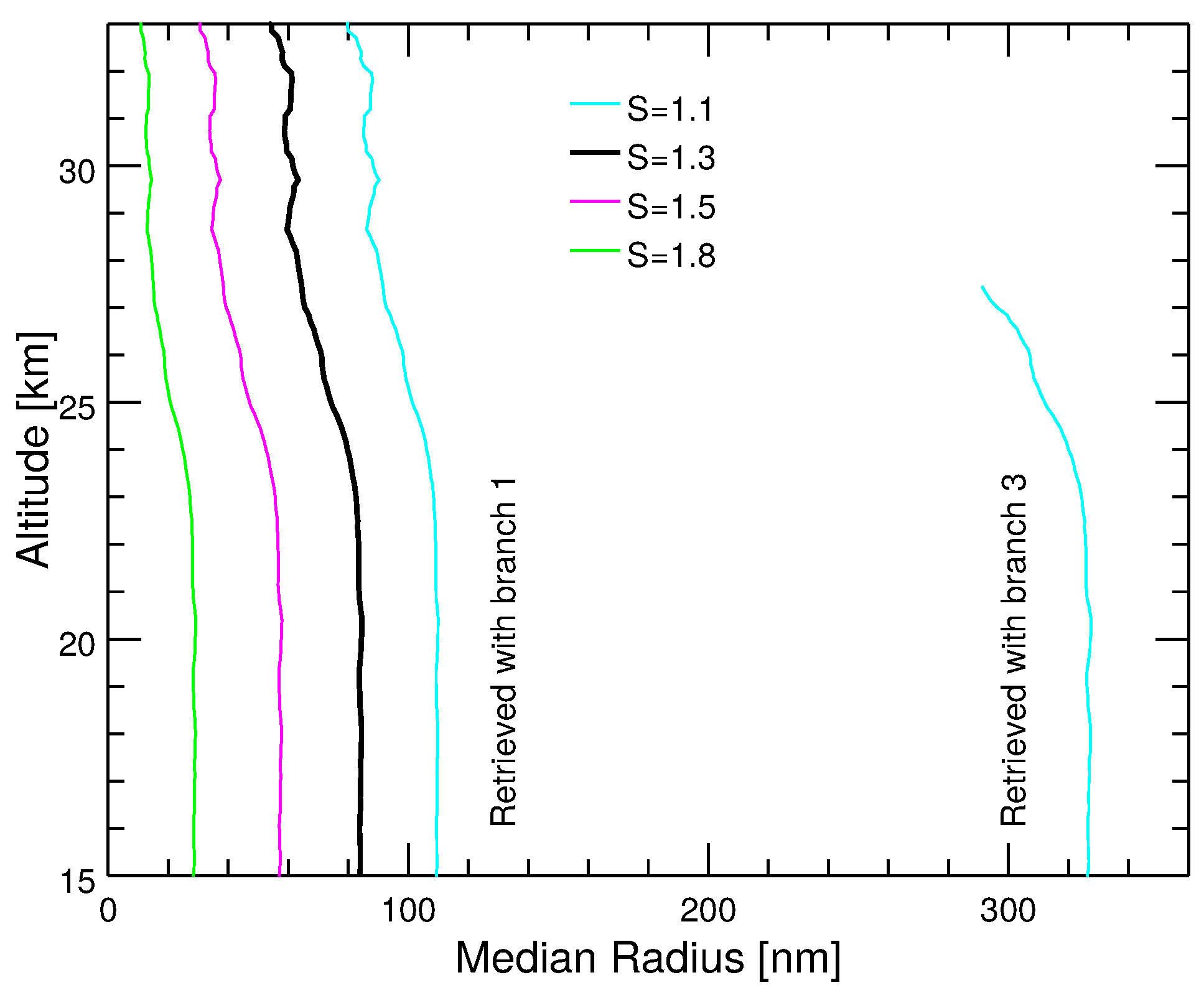

| Symbol | Quantity | Unit |
|---|---|---|
| Backscatter ratio | dimensionless | |
| Mie scattering coefficient | ||
| Rayleigh scattering coefficient | ||
| Scattering angle ( for lidar observations) | degrees | |
| Mie scattering phase function | ||
| Rayleigh scattering phase function | ||
| Mie volume scattering coefficient | ||
| Rayleigh volume scattering coefficient | ||
| Aerosol particle number density | ||
| Air molecule number density | ||
| Mie scattering cross section | ||
| Rayleigh scattering cross section | ||
| Median aerosol radius | nm | |
| Wavelength | nm | |
| z | Altitude | km |
| S | Particle size distribution width | dimensionless |
| Color index from backscatter ratios | dimensionless |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zalach, J.; von Savigny, C.; Langenbach, A.; Baumgarten, G.; Lübken, F.-J.; Bourassa, A. A Method for Retrieving Stratospheric Aerosol Extinction and Particle Size from Ground-Based Rayleigh-Mie-Raman Lidar Observations. Atmosphere 2020, 11, 773. https://doi.org/10.3390/atmos11080773
Zalach J, von Savigny C, Langenbach A, Baumgarten G, Lübken F-J, Bourassa A. A Method for Retrieving Stratospheric Aerosol Extinction and Particle Size from Ground-Based Rayleigh-Mie-Raman Lidar Observations. Atmosphere. 2020; 11(8):773. https://doi.org/10.3390/atmos11080773
Chicago/Turabian StyleZalach, Jacob, Christian von Savigny, Arvid Langenbach, Gerd Baumgarten, Franz-Josef Lübken, and Adam Bourassa. 2020. "A Method for Retrieving Stratospheric Aerosol Extinction and Particle Size from Ground-Based Rayleigh-Mie-Raman Lidar Observations" Atmosphere 11, no. 8: 773. https://doi.org/10.3390/atmos11080773
APA StyleZalach, J., von Savigny, C., Langenbach, A., Baumgarten, G., Lübken, F.-J., & Bourassa, A. (2020). A Method for Retrieving Stratospheric Aerosol Extinction and Particle Size from Ground-Based Rayleigh-Mie-Raman Lidar Observations. Atmosphere, 11(8), 773. https://doi.org/10.3390/atmos11080773




