Physics-Based Simulations of Flow and Fire Development Downstream of a Canopy
Abstract
1. Introduction
2. Problem Description and Methodology
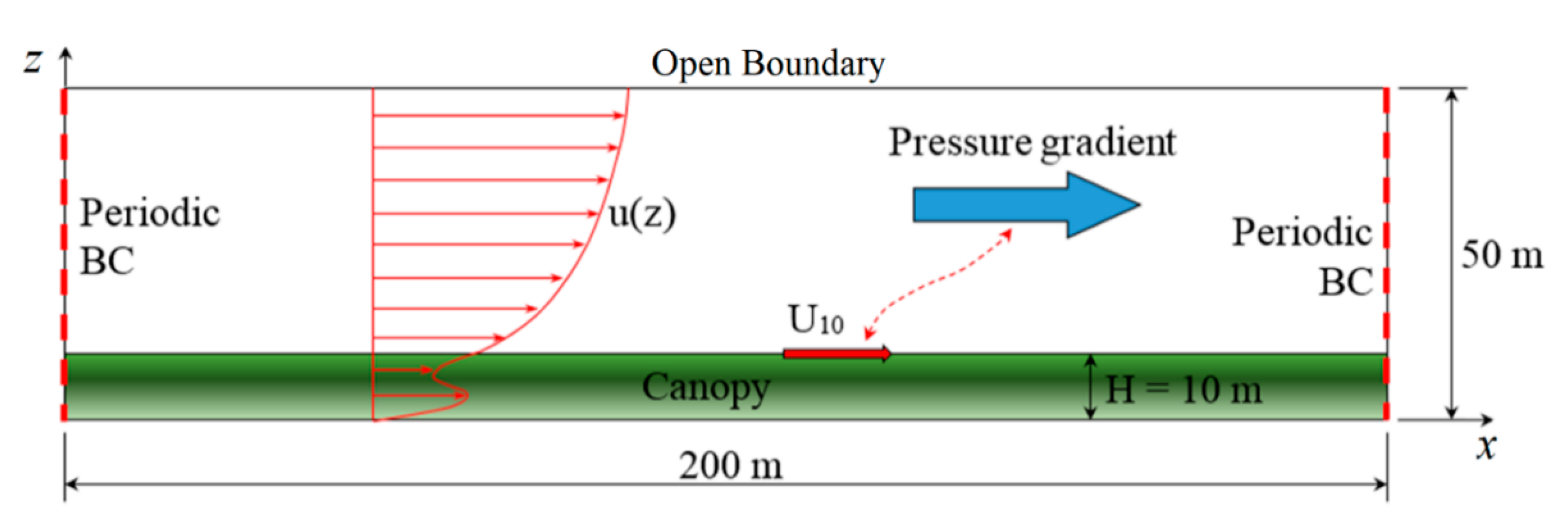
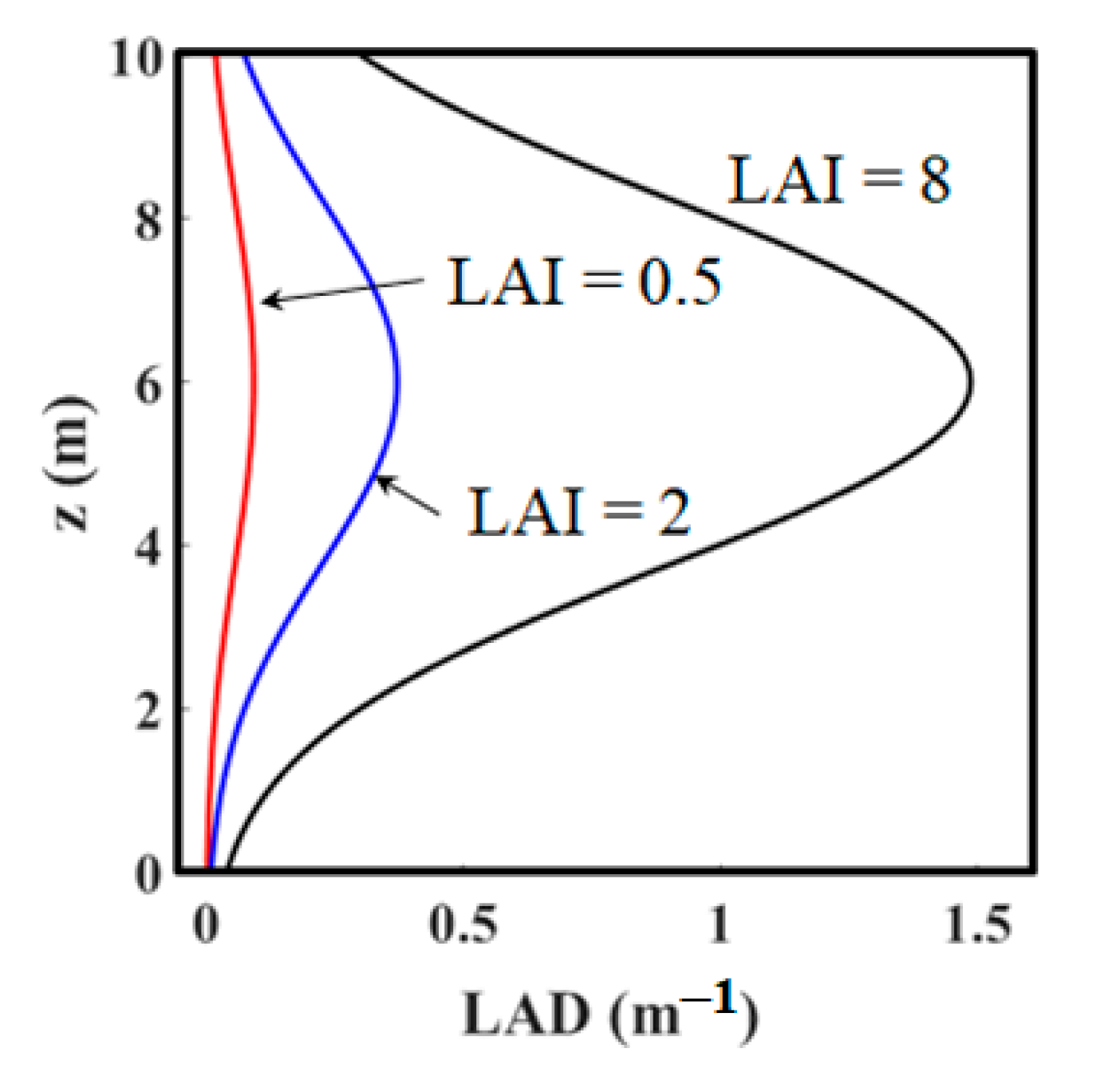
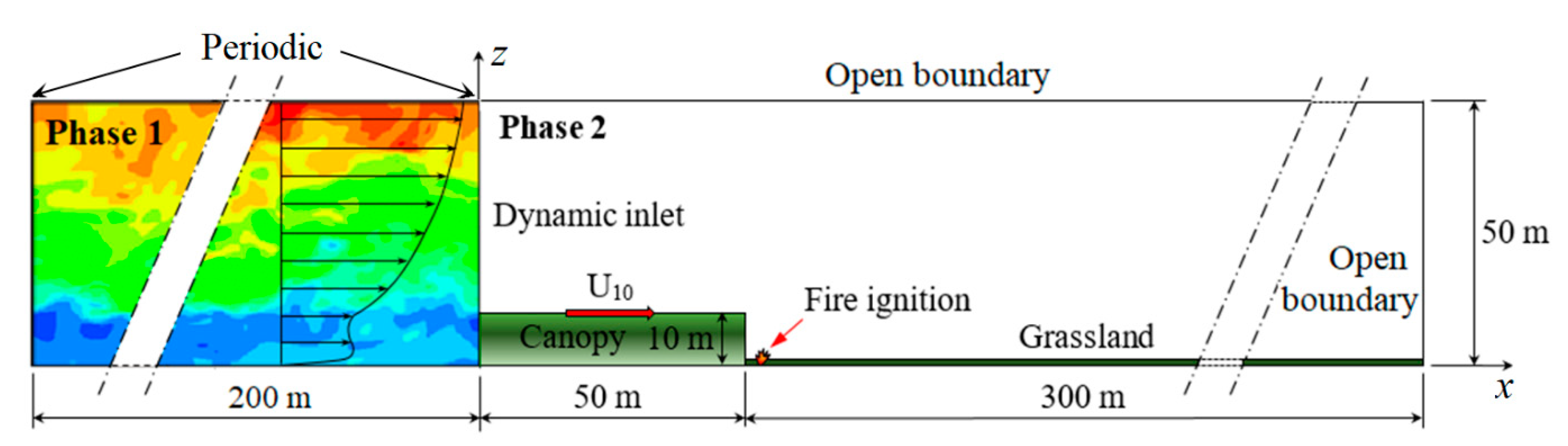
2.1. Problem Description and Approach
2.2. Mathematical Model
2.3. Numerical Method
3. Results and Discussion
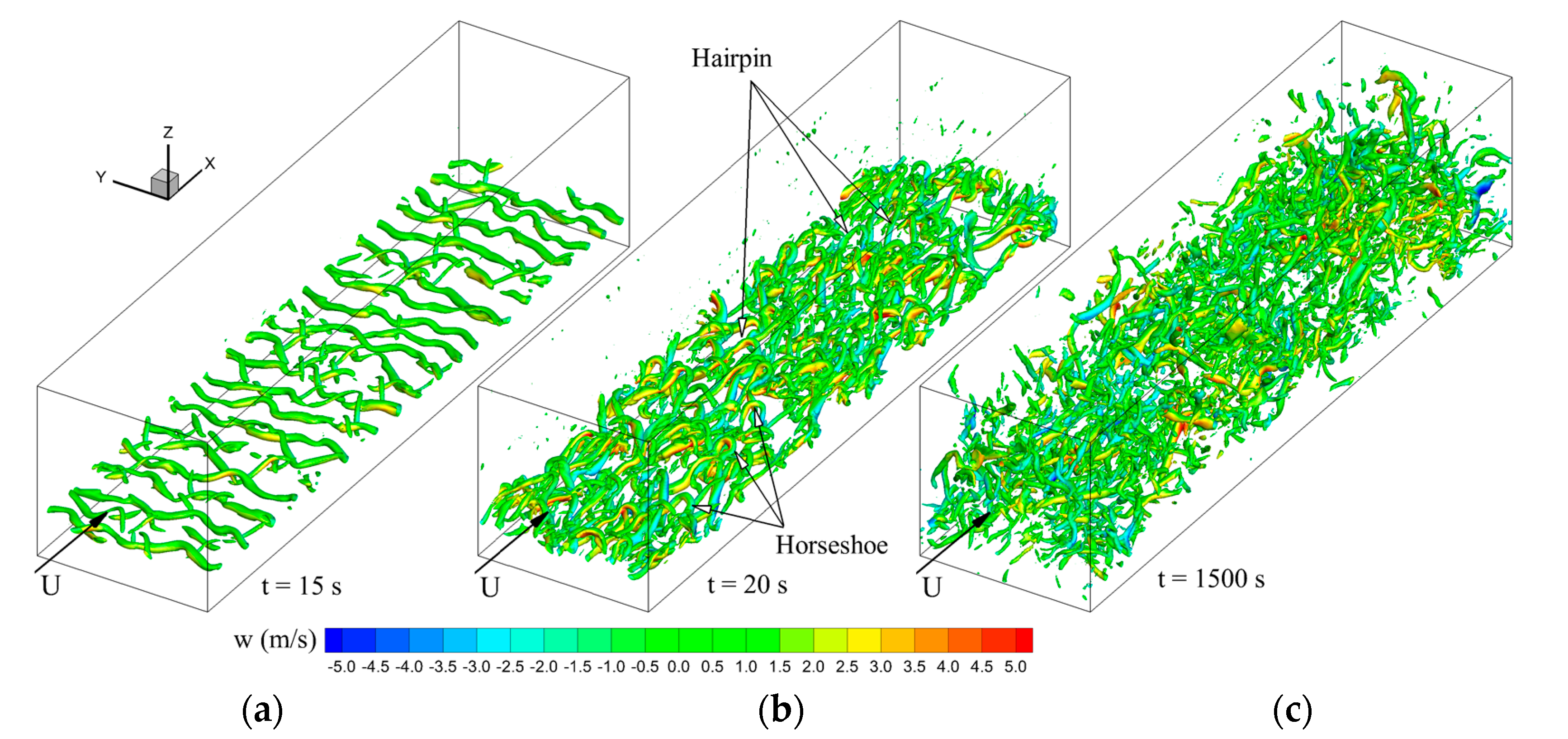
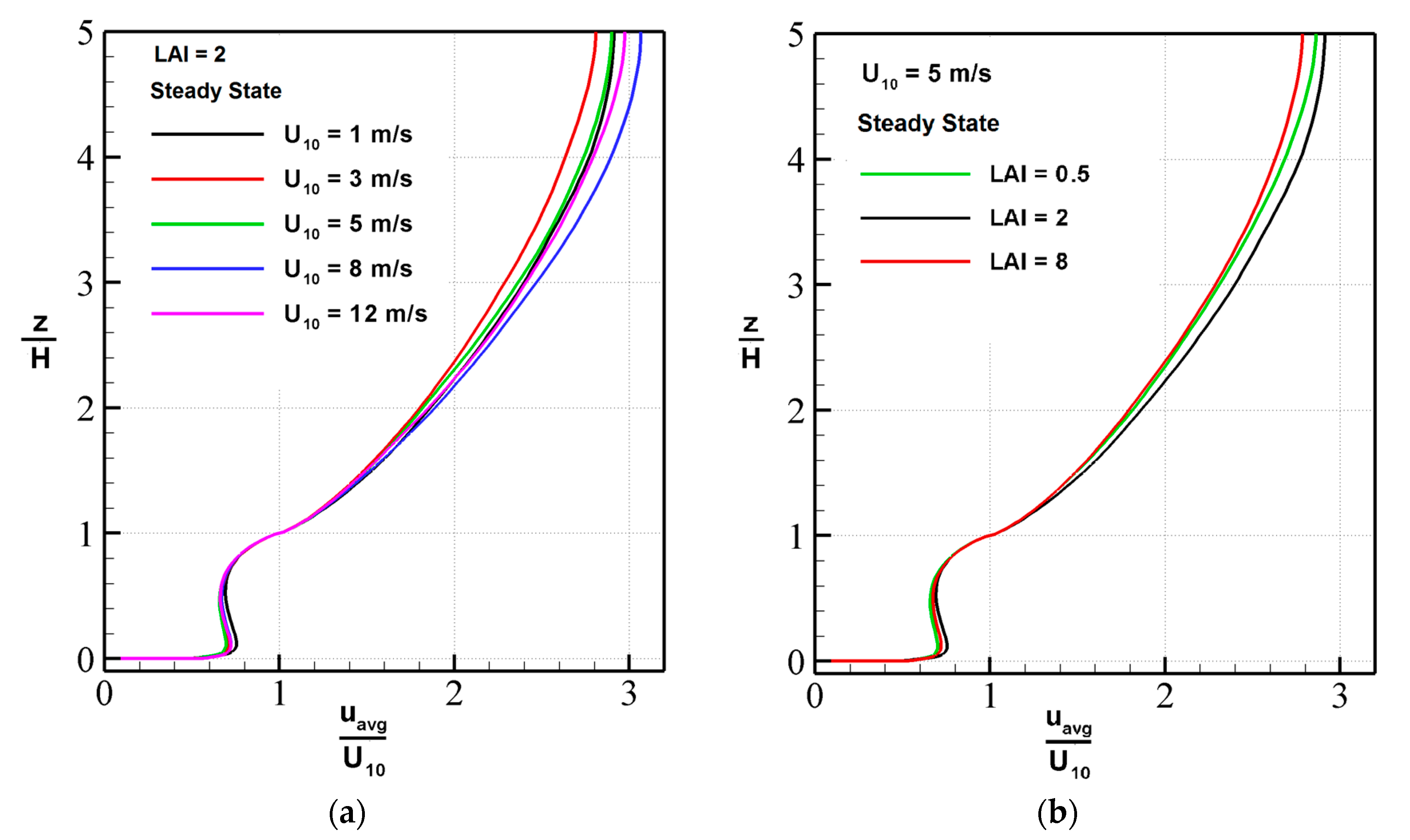
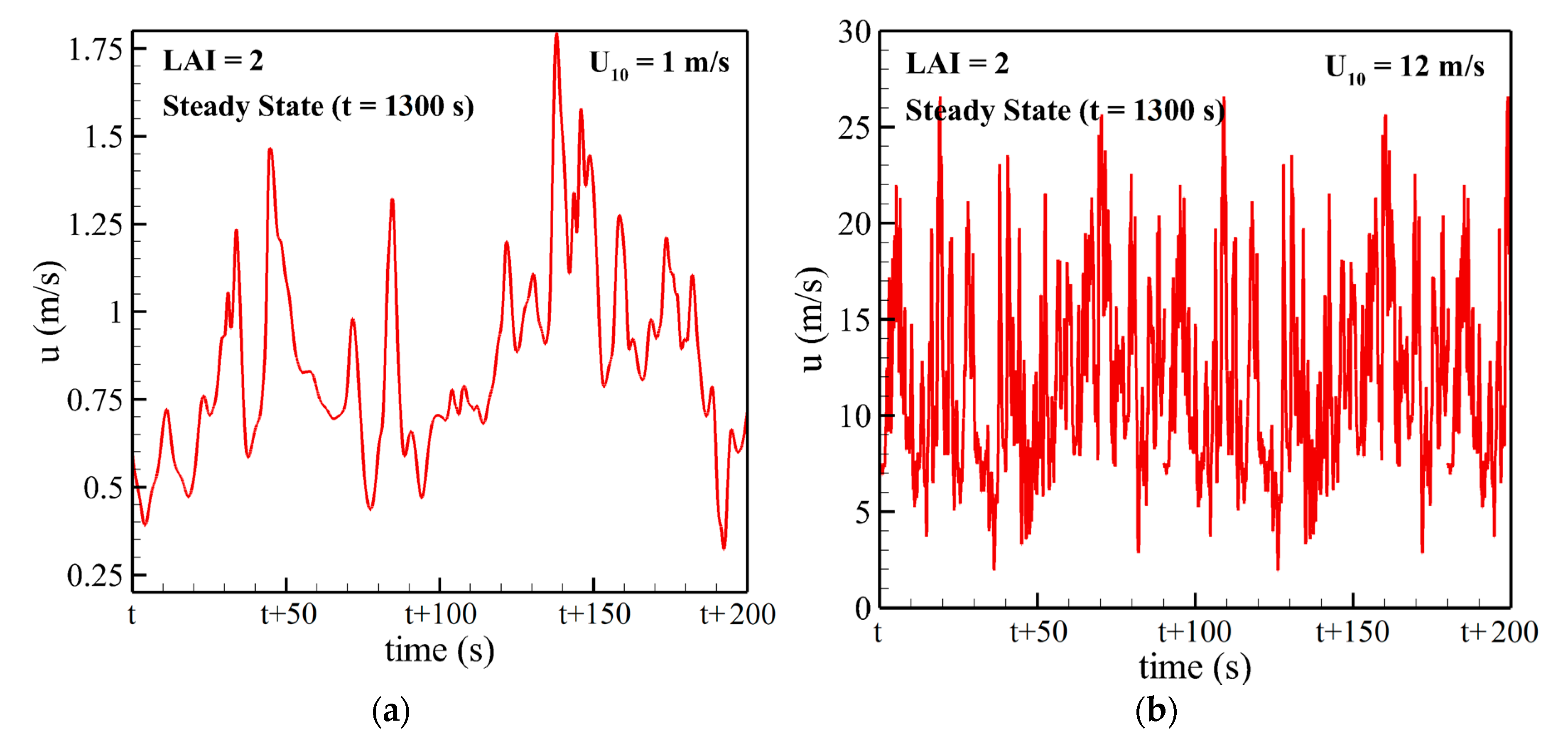
3.1. Phase 1: ABL Flow Over a Tree Canopy
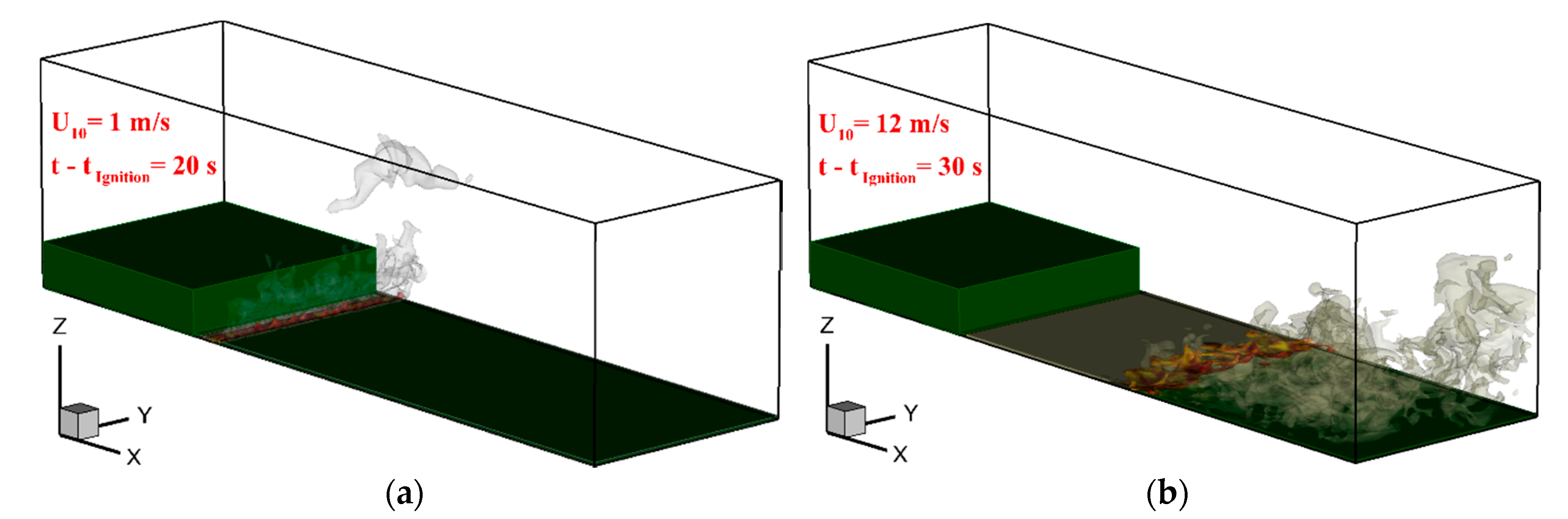
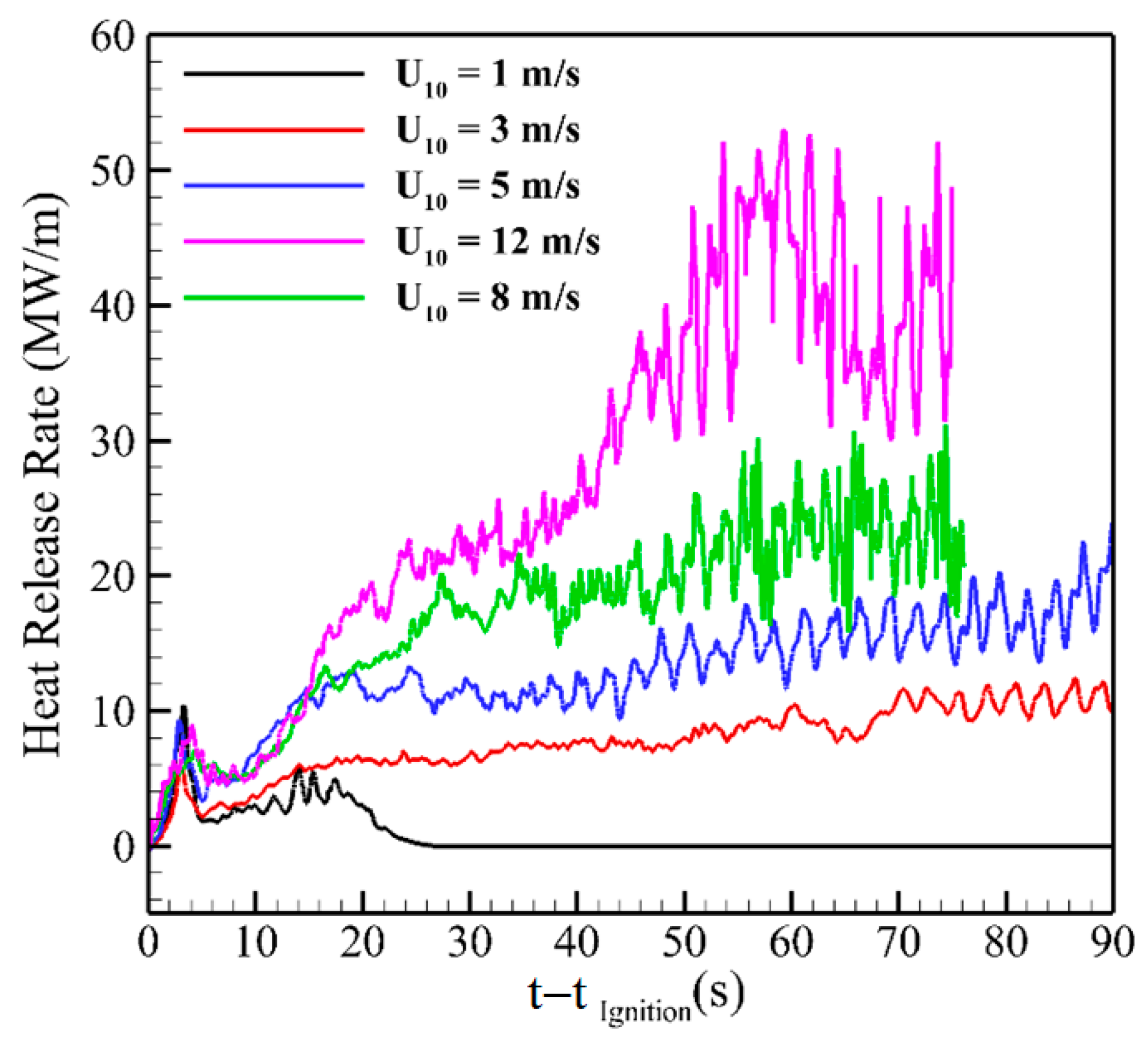
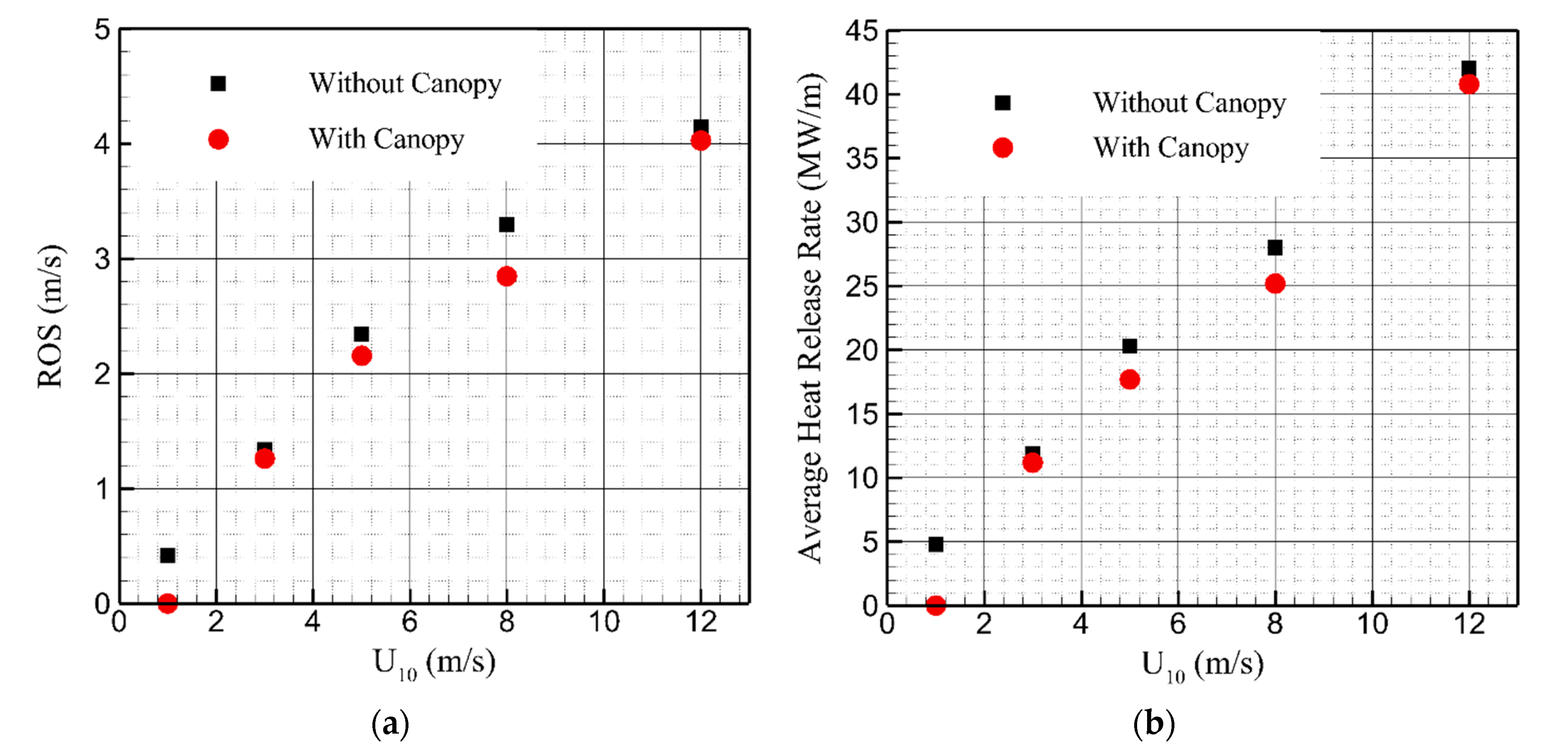
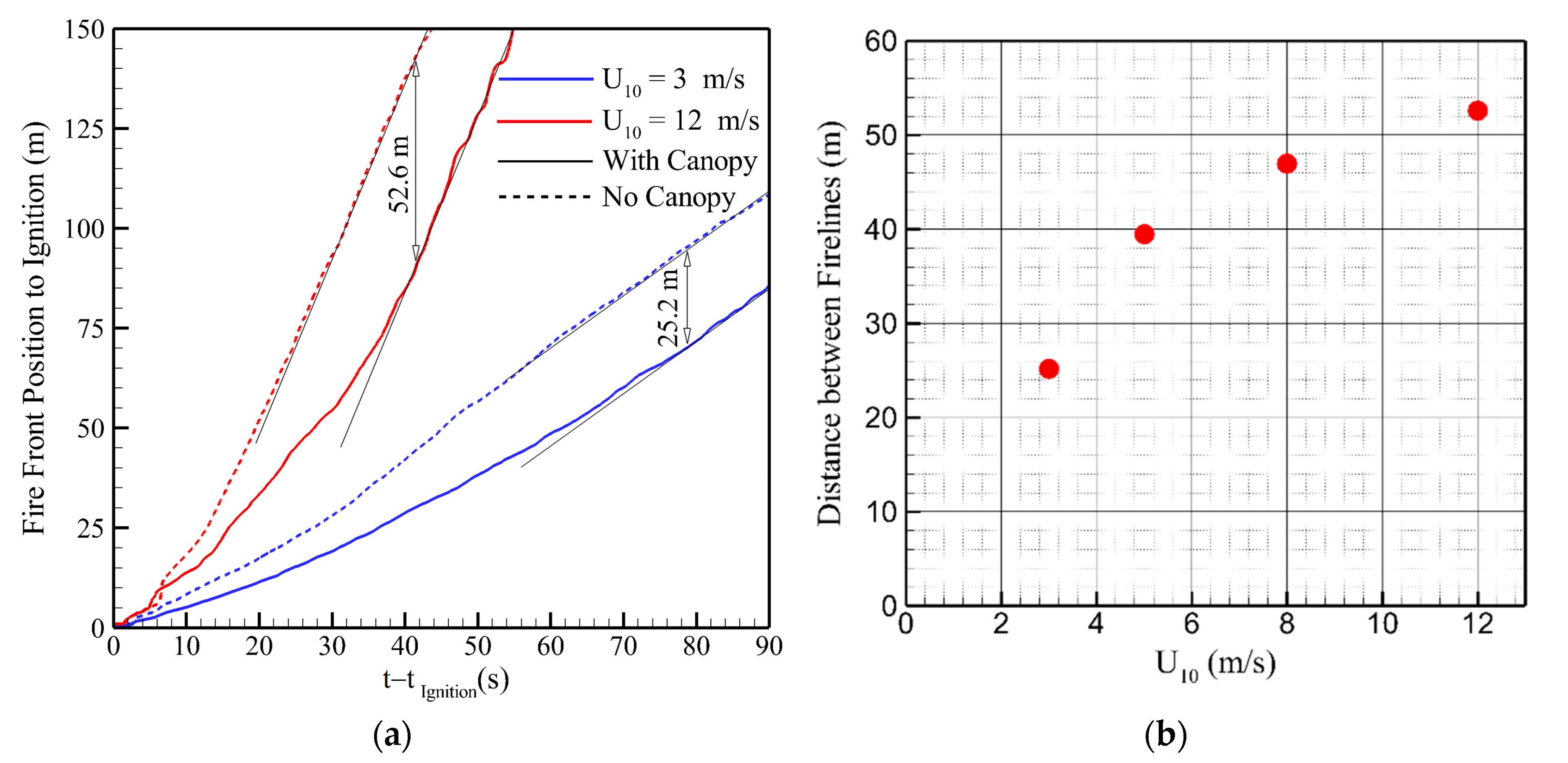
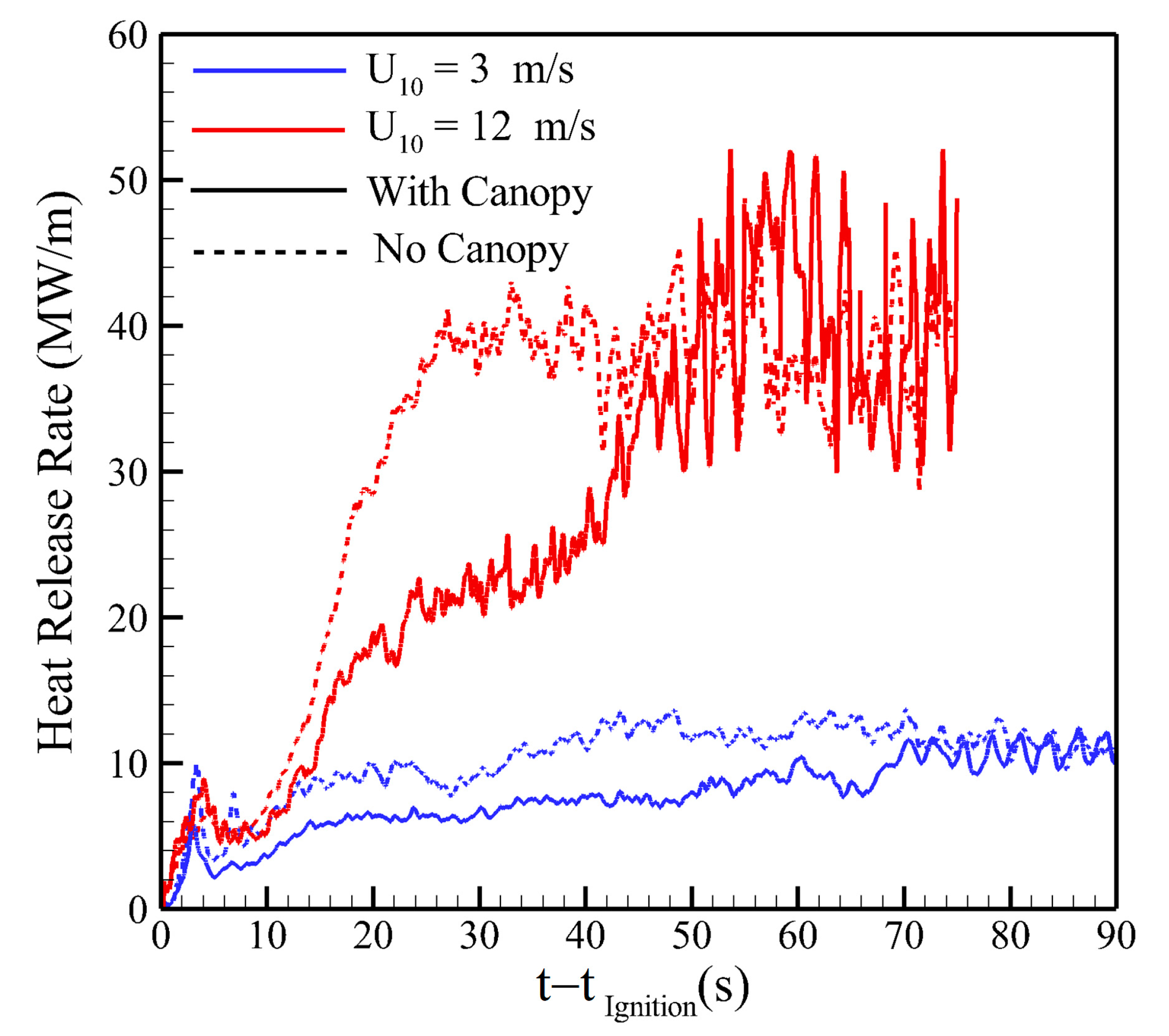
3.2. Phase 2: Grassland Fire Spread Downstream of a Tree Canopy
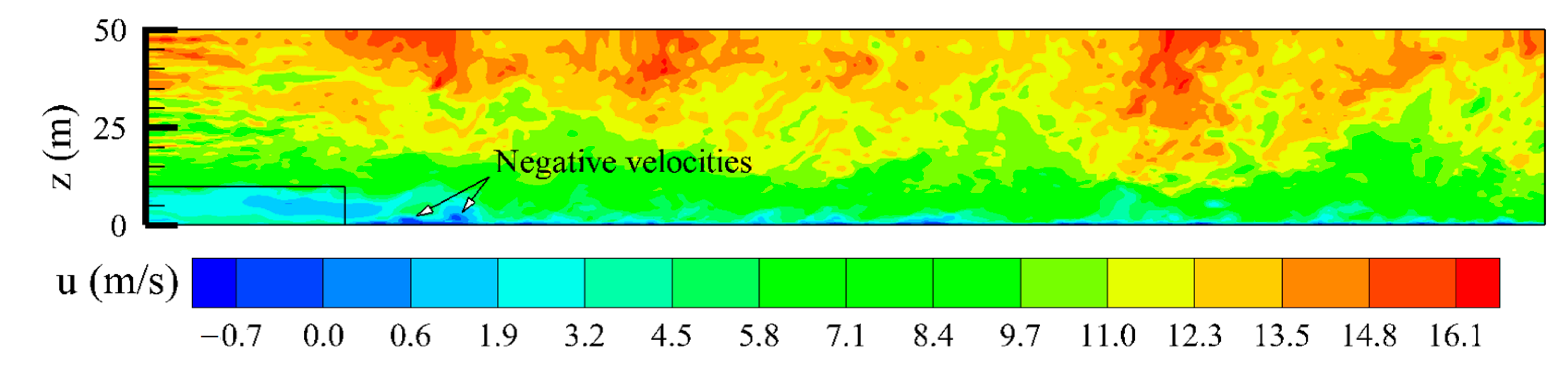
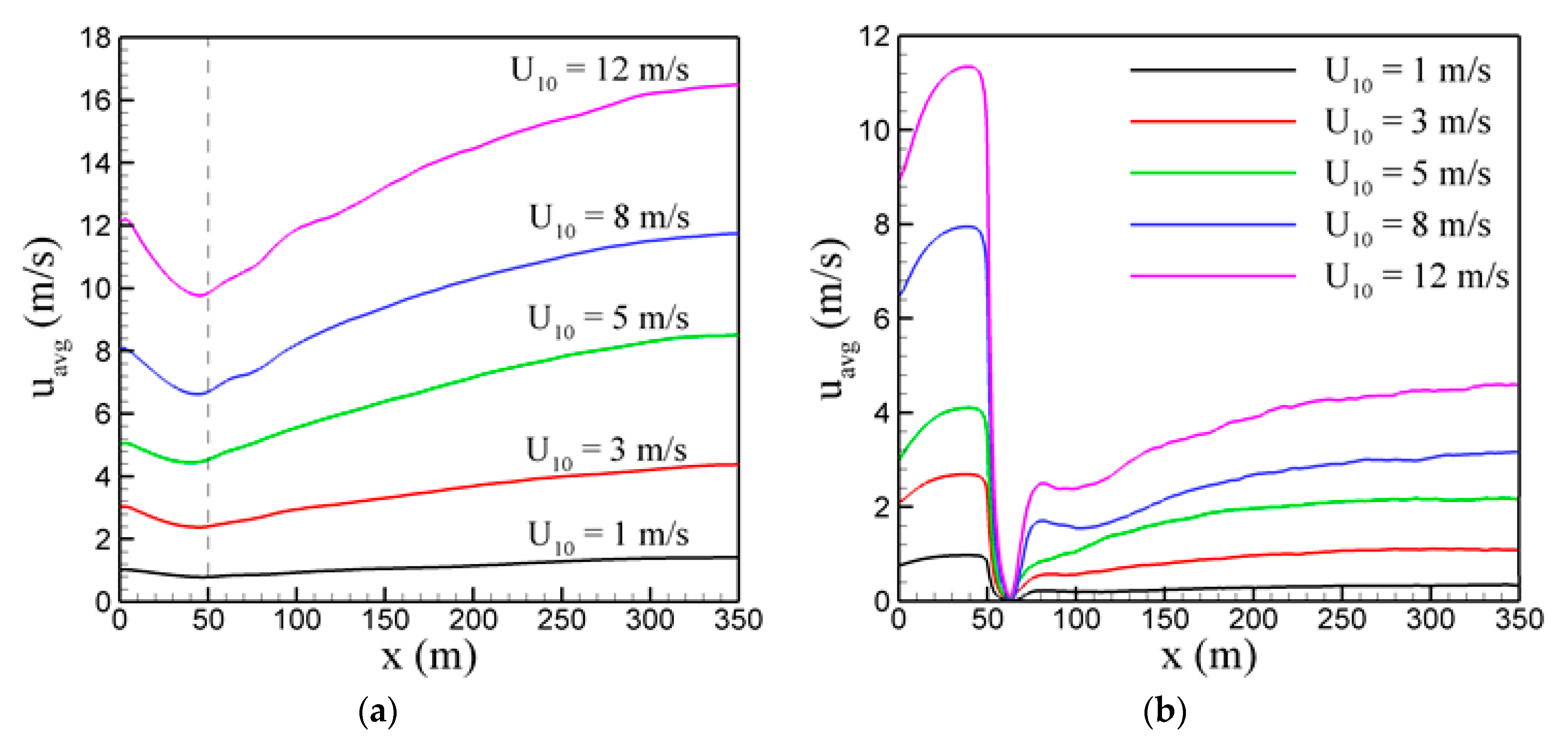
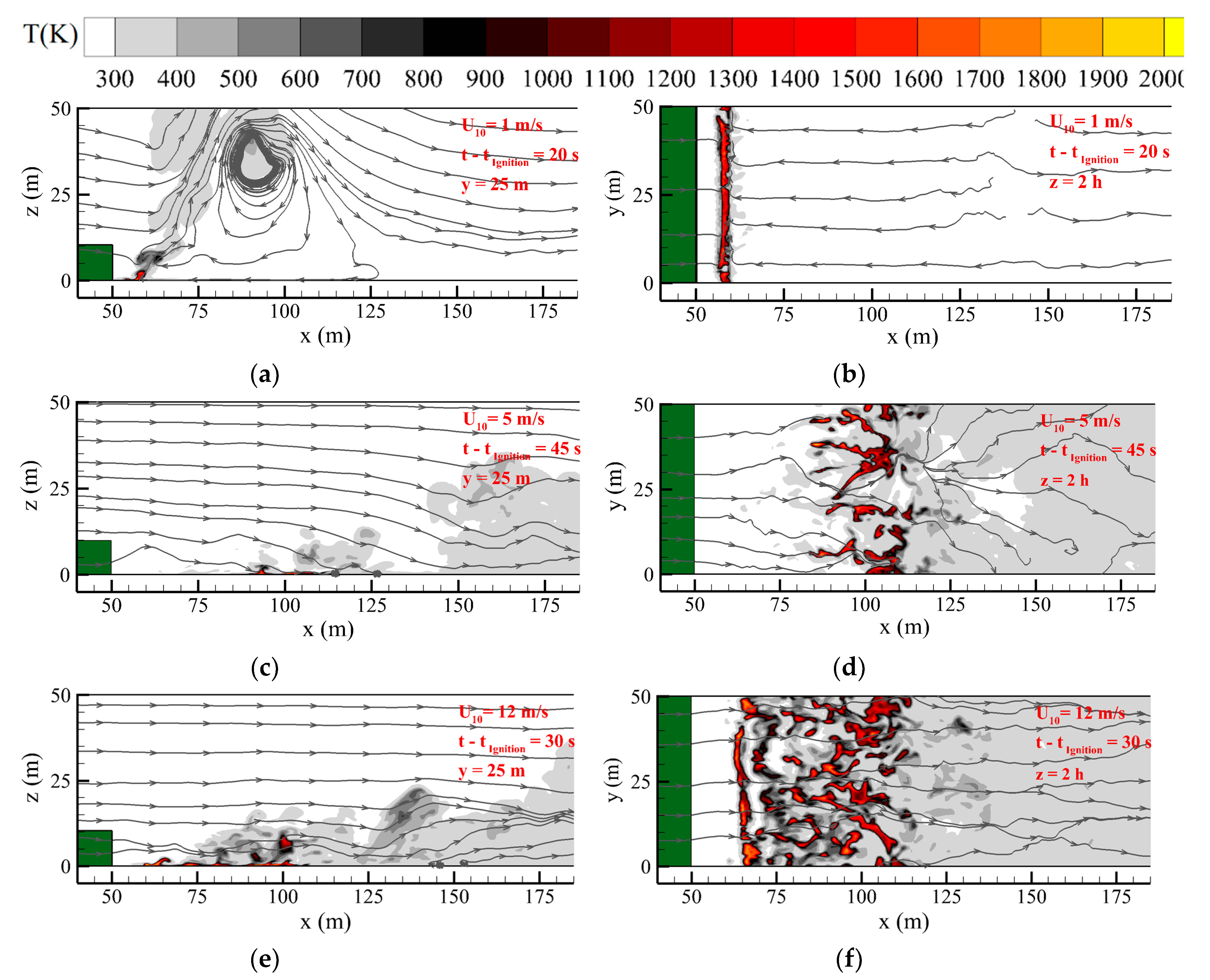
3.2.1. Flow Redevelopment
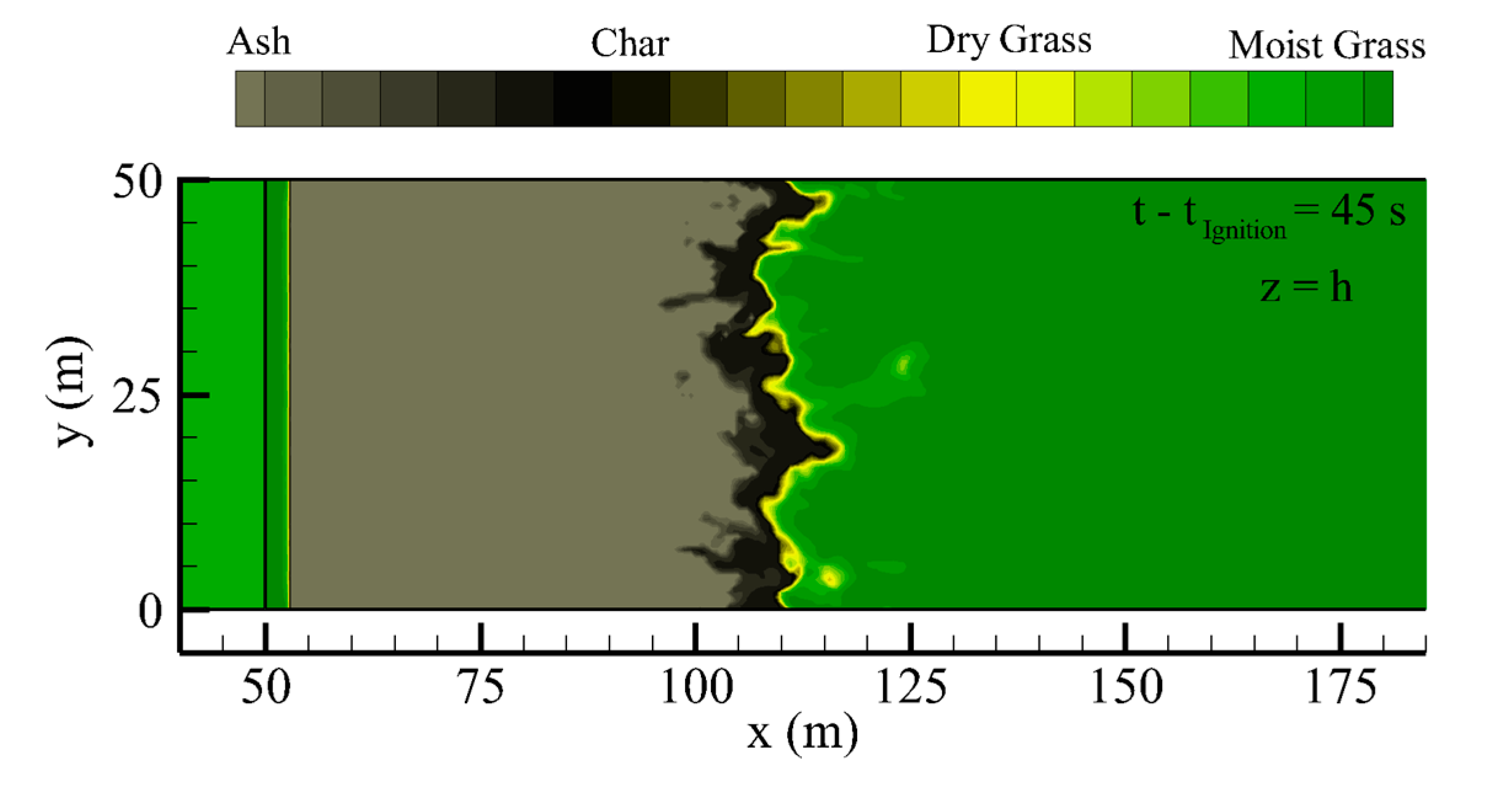
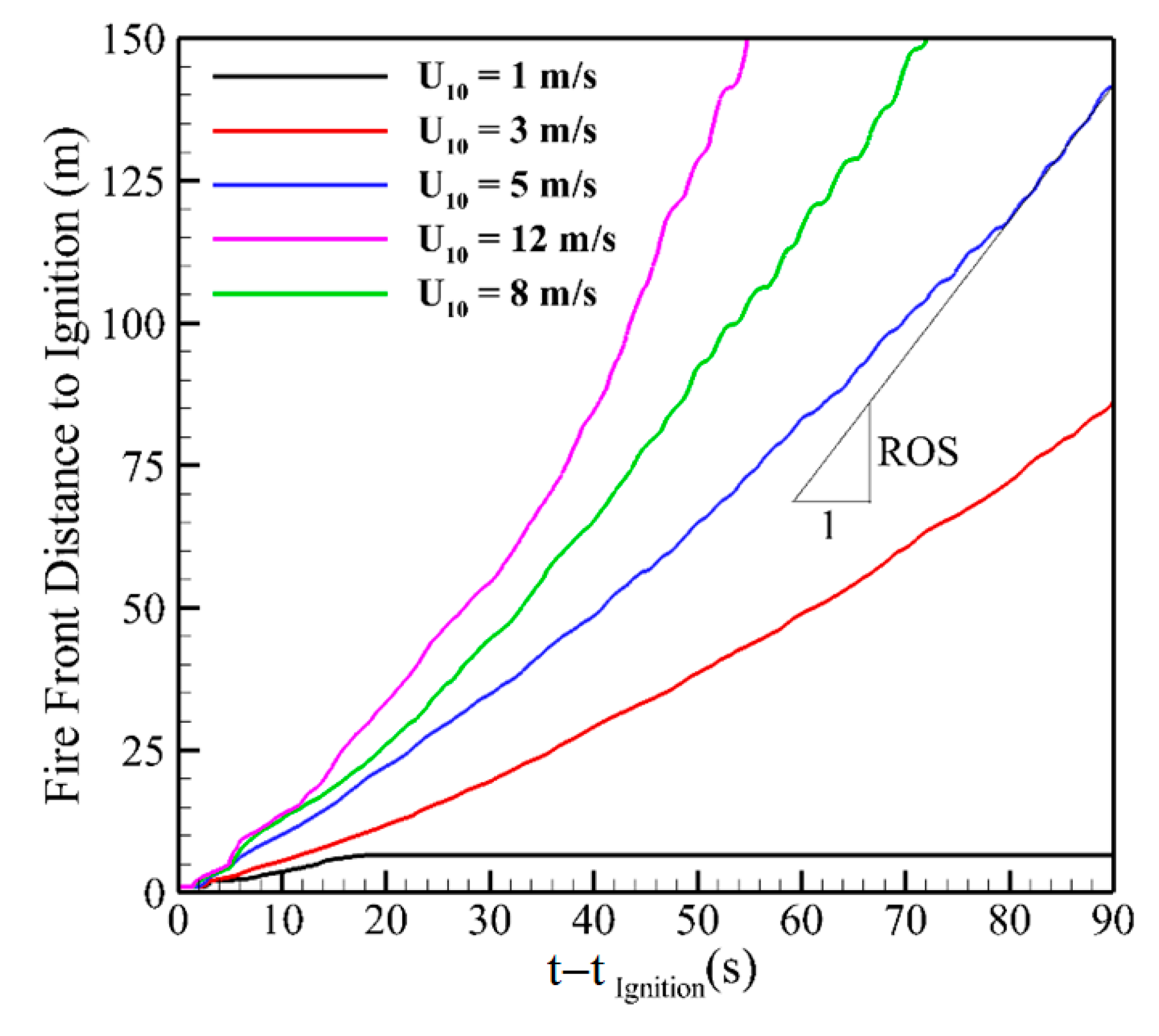
3.2.2. Fire Spread
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ABL | Atmospheric Boundary Layer |
| CD | Drag coefficient |
| h | Grassland height, m |
| H | Canopy height, m |
| HRR | Heat Release Rate, W |
| LAD | Leaf Area Density, m−1 |
| LAI | Leaf Area Index |
| LES | Large Eddy Simulation |
| M | Grass moisture content, % |
| NC | Byram convection number |
| Q | 2nd invariant of the velocity tensor gradient, s−2 |
| RoS | Rate of Spread, m·s−1 |
| t | time, s |
| u, v, w | Flow velocity components, m·s−1 |
| U10 | 10-m wind speed, m·s−1 |
| WRF | Wind Reduction Factor |
| x, y, z | Space coordinates, m |
| αS | Fuel volume fraction |
| ΔH | Reaction heat, J.kg−1 |
| ρS | Fuel density, kg·m−3 |
| σS | Fuel surface-to-volume ratio, m−1 |
| ω | Reaction rate, kg·s−1 |
References
- The Guardian. Explainer: How Effective Is Bushfire Hazard Reduction on Australia’s Fires? Available online: https://www.theguardian.com/australia-news/2020/jan/05/explainer-how-effective-is-bushfire-hazard-reduction-on-australias-fires (accessed on 5 June 2020).
- Moon, K.; Duff, T.J.; Tolhurst, K.G. Sub-canopy forest winds: Understanding wind profiles for fire behaviour simulation. Fire Saf. J. 2019, 105, 320–329. [Google Scholar] [CrossRef]
- McArthur, A.G. Fire Behaviour in Eucalypt Forests; Leaflet No. 107; Forestry and Timber Bureau: Canberra, Australia, 1967. [Google Scholar]
- Andrews, P.L. Modeling Wind Adjustment Factor and Midflame Wind Speed for Rothermel’s Surface Fire Spread Model; Contract N° RMRS-GTR-266; Rocky Mountain Research Station, Department of Agriculture/Forest Service: Fort Collins, CO, USA, 2012.
- Cassiani, M.; Katul, G.G.; Albertson, J.D. The effects of canopy leaf area index on airflow across forest edges: Large-eddy simulation and analytical results. Bound. Layer Meteorol. 2008, 126, 433–460. [Google Scholar] [CrossRef]
- Bohrer, G.; Katul, G.G.; Walko, R.L.; Avissar, R. Exploring the effects of microscale structural heterogeneity of forest canopies using large-eddy simulations. Bound. Layer Meteorol. 2009, 132, 351–382. [Google Scholar] [CrossRef]
- Dupont, S.; Bonnefond, J.-M.; Irvine, M.R.; Lamaud, E.; Brunet, Y. Long-distance edge effects in a pine forest with a deep and sparse trunk space: In situ and numerical experiments. Agric. For. Meteorol. 2011, 151, 328–344. [Google Scholar] [CrossRef]
- Dupont, S.; Irvine, M.; Bonnefond, J.-M.; Lamaud, E.; Brunet, Y. Turbulent structures in a pine forest with a deep and sparse trunk space: Stand and edge regions. Bound. Layer Meteorol. 2012, 143, 309–336. [Google Scholar] [CrossRef]
- Belcher, S.E.; Harman, I.N.; Finnigan, J.J. The wind in the willows: Flows in forest canopies in complex terrain. Annu. Rev. Fluid Mech. 2012, 44, 479–504. [Google Scholar] [CrossRef]
- Schlegel, F.; Stiller, J.; Bienert, A.; Maas, H.G.; Queck, R.; Bernhofer, C. Large-eddy simulation study of the effects on flow of a heterogeneous forest at sub-tree resolution. Bound. Layer Meteorol. 2015, 154, 27–56. [Google Scholar] [CrossRef]
- Sutherland, D.; Philip, J.; Ooi, A.; Moinuddin, K. Simulations of surface fire propagating under a canopy: Flame angle and intermittency. In Proceedings of the 8th ICFFR, Advances in Forest Fire Research 2018, Coimbra, Portugal, 9–16 November 2018; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2018; pp. 1303–1307. [Google Scholar] [CrossRef]
- Morvan, D.; Dupuy, J.L. Modeling the propagation of a wildfire through a Mediterranean shrub using a multiphase formulation. Combust. Flame 2004, 138, 199–210. [Google Scholar] [CrossRef]
- Frangieh, N.; Morvan, D.; Meradji, S.; Accary, G.; Bessonov, O. Numerical simulation of grassland fires behavior using an implicit physical multiphase model. Fire Saf. J. 2018, 102, 37–47. [Google Scholar] [CrossRef]
- Gavrilov, K.; Morvan, D.; Accary, G.; Lyubimov, D.; Meradji, S. Numerical simulation of coherent turbulent structures and of passive scalar dispersion in a canopy sub-layer. Comput. Fluids 2013, 78, 54–62. [Google Scholar] [CrossRef]
- Gavrilov, K.; Accary, G.; Morvan, D.; Dmitry, L.; Meradji, S.; Bessonov, O. Numerical simulation of coherent structures over plant canopy. Flow Turb. Comb. 2011, 86, 89–111. [Google Scholar] [CrossRef]
- Nepf, H.; Ghisalberti, M.; White, B.; Murphy, E. Retention time and dispersion associated with submerged aquatic canopies. Water Resour. Res. 2007, 43, 4. [Google Scholar] [CrossRef]
- Hu, X.; Lee, X.; Stevens, D.E.; Smith, R.B. A numerical study of nocturnal wavelike motion in forests. Bound. Meteorol. 2002, 102, 199–223. [Google Scholar] [CrossRef]
- Frangieh, N.; Accary, G.; Morvan, D.; Meradji, S.; Bessonov, O. Wildfires front dynamics: 3D structures and intensity at small and large scales. Combust. Flame 2020, 211, 54–67. [Google Scholar] [CrossRef]
- Frangieh, N.; Morvan, D.; Accary, G.; Meradji, S. Front’s dynamics of quasi-infinite grassland fires. In Proceedings of the 8th ICFFR, Advances in Forest Fire Research 2018, Coimbra, Portugal, 9–16 November 2018; Viegas, D.X., Ed.; Imprensa da Universidade de Coimbra: Coimbra, Portugal, 2018; pp. 1024–1034. [Google Scholar] [CrossRef]
- Morvan, D.; Meradji, S.; Accary, G. Physical modelling of fire spread in Grasslands. Fire Saf. J. 2009, 44, 50–61. [Google Scholar] [CrossRef]
- Morvan, D.; Accary, G.; Meradji, S.; Frangieh, N.; Bessonov, O. A 3D physical model to study the behavior of vegetation fires at laboratory scale. Fire Saf. J. 2018, 101, 39–52. [Google Scholar] [CrossRef]
- Grishin, A.M. Mathematical Modeling of Forest Fires and New Methods for Fighting Them; Albini, F., Ed.; Publishing House of the Tomsk University: Tomsk, Russia, 1997. [Google Scholar]
- Morvan, D.; Dupuy, J.L. Modeling of fire spread through a forest fuel bed using a multiphase formulation. Combust. Flame 2001, 127, 1981–1994. [Google Scholar] [CrossRef]
- Morvan, D.; Meradji, S.; Accary, G. Wildfire behavior study in a Mediterranean pine stand using a physically based model. Combust. Sci. Technol. 2008, 180, 230–248. [Google Scholar] [CrossRef]
- Favre, A.; Kovasznay, L.S.G.; Dumas, R.; Gaviglio, J.; Coantic, M. La Turbulence en Mécanique des Fluides; Gauthier-Villars: Paris, France, 1976. [Google Scholar]
- Cox, G. Combustion Fundamentals of Fire; Academic Press: Cambridge, MA, USA, 1995. [Google Scholar]
- Gavrilov, K. Numerical Modeling of Atmospheric Flow over Forest Canopy. Ph.D. Thesis, Aix-Marseille University, Marseille, France, 2001. [Google Scholar]
- Kee, R.J.; Rupley, F.M.; Miller, J.A. The Chemkin Thermodynamic Data Base; Technical Report SAND87-8215B; Sandia National Laboratories: Albuquerque, NM, USA, 1990. [Google Scholar]
- Magnussen, B.F.; Mjertager, B.H. On mathematical modeling of turbulent combustion. Combust. Sci. Technol. 1998, 140, 93–122. [Google Scholar]
- Syed, K.J.; Stewart, C.D.; Moss, J.B. Modelling soot formation and thermal radiation in buoyant turbulent diffusion flames. Symp. (Int.) Combust. 1991, 23, 1533–1541. [Google Scholar] [CrossRef]
- Moss, J.B. Turbulent diffusion flames. In Forest Fire Control and Use; Cox, G., Ed.; Academic Press: London, UK, 1990. [Google Scholar]
- Nagle, J.; Strickland-Constable, R.F. Oxidation of carbon between 1000–2000 °C. In Proceedings of the 5th Conference on Carbon, State College, PA, USA, 19–23 June 1961; Pergamon Press: Oxford, UK, 1962; pp. 154–164. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley and Sons: Hoboken, NJ, USA, 1996. [Google Scholar]
- Siegel, R.; Howell, J.R. Thermal Radiation Heat Transfer, 3rd ed.; Hemisphere Publishing Corporation: Washington, DC, USA, 1992. [Google Scholar]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; Hemisphere Publishing: New York, NY, USA, 1980. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics, the Finite Volume Method; Prentice Hall: Upper Saddle River, NJ, USA, 2007. [Google Scholar]
- Li, Y.; Rudman, M. Assessment of higher-order upwind schemes incorporating FCT for convection-dominated problems. Numer. Heat Transf. Part B Fundam. 1995, 27, 1–21. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M.; Leonard, A. Computational Methods for Fluid Dynamics; Springer: New York, NY, USA, 2002. [Google Scholar] [CrossRef]
- Modest, M.F. Radiative Heat Transfer; Academic Press: Cambridge, MA, USA, 2003. [Google Scholar]
- Kaplan, C.R.; Baek, S.W.; Oran, E.S.; Ellzey, J.L. Dynamics of a strongly radiating unsteady ethylene jet diffusion flame. Combust. Flame 1994, 96, 1–21. [Google Scholar] [CrossRef]
- Accary, G.; Bessonov, O.; Fougere, D.; Meradji, S.; Morvan, D. Optimized parallel approach for 3D modelling of forest fires behaviour. In LNCS; Malyshkin, V., Ed.; Parallel Computing Technologies; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4671, pp. 96–102. [Google Scholar] [CrossRef]
- Accary, G.; Bessonov, O.; Fougere, D.; Gavrilov, K.; Meradji, S.; Morvan, D. Efficient parallelization of the preconditioned conjugate gradient method. In LNCS; Malyshkin, V., Ed.; Parallel Computing Technologies; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5968, pp. 60–72. [Google Scholar] [CrossRef]
- Bessonov, O.; Meradji, S. Efficient Parallel Solvers for the FireStar3D Wildfire Numerical Simulation Model. In LNCS; Malyshkin, V., Ed.; Parallel Computing Technologies; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11657, pp. 140–150. [Google Scholar] [CrossRef]
- Khalifah, A.; Accary, G.; Meradji, S.; Scarella, G.; Morvan, D.; Kahine, K. Three-dimensional numerical simulation of the interaction between natural convection and radiation in a differentially heated cavity in the low Mach number approximation using the discrete ordinates method. In Proceedings of the 4th Int. Conf. on Thermal Engineering: Theory and Application, Abu Dhabi, UAE, 12–14 January 2009. [Google Scholar]
- Accary, G.; Meradji, S.; Fougere, D.; Morvan, D. Towards a numerical benchmark for 3D mixed-convection low Mach number flows in a rectangular channel heated from below. J. Fluid Dyn. Mater. Sci. 2008, 141, 1–7. [Google Scholar]
- Finnigan, J. Turbulence in plant canopies. Annu. Rev. Fluid Mech. 2000, 32, 519–571. [Google Scholar] [CrossRef]
- Hunt, J.C.; Wray, A.A.; Moin, P. Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the Summer Program 1988; Center for Turbulence Research: Stanford, CA, USA, 1988; pp. 193–208. [Google Scholar]
- Amiro, B.D. Drag coefficients and turbulence spectra within three boreal forest canopies. Bound. Layer Meteorol. 1990, 52, 227–246. [Google Scholar] [CrossRef]
- Dupont, S.; Brunet, Y. Edge flow and canopy structure: A large-eddy simulation study. Bound. Layer Meteorol. 2008, 126, 51–71. [Google Scholar] [CrossRef]
- Raupach, M.R.; Bradley, E.F.; Ghadiri, H. A Wind Tunnel Investigation into the Aerodynamics Effect of Clearings on the Nesting of Abbott’s Boody on Christmas Island; Internal Report; CSIRO, Centre for Environmental Mechanics: Canberra, Australia, 1987. [Google Scholar]
- Massman, W.J.; Forthofer, J.M.; Finney, M.A. An improved canopy wind model for predicting wind adjustment factors and wildland fire behavior. Canad. J. For. Res. 2017, 47, 594–603. [Google Scholar] [CrossRef]
- Byram, G.M. Combustion of forest fuels. In Forest Fire: Control and Use; Davis, K.P., Ed.; McGraw Hill: New York, NY, USA, 1959; pp. 61–89. [Google Scholar]
- Morvan, D.; Frangieh, N. Wildland fires behaviour: Wind effect versus Byram’s convective number and consequences upon the regime of propagation. Int. J. Wildland Fire 2018, 27, 636–641. [Google Scholar] [CrossRef]
- Dold, J.W.; Zinoviev, A. Fire eruption through intensity and spread rate interaction mediated by flow attachment. Combust. Theor. Model. 2009, 13, 763–793. [Google Scholar] [CrossRef]
- Moinuddin, K.A.M.; Sutherland, D.; Mell, W. Simulation study of grass fire using a physics-based model: Striving towards numerical rigour and the effect of grass height on the rate of spread. Int. J. Wildland Fire 2018, 27, 800–814. [Google Scholar] [CrossRef]
- Cheney, N.P.; Gould, J.S.; Catchpole, W.R. Prediction of fire spread in grasslands. Int. J. Wildland Fire 1998, 8, 1–13. [Google Scholar] [CrossRef]
- Linn, R.R.; Cunningham, P. Numerical simulations of grass fires using a coupled atmosphere-fire model: Basic fire behavior and dependence on wind speed. J. Geophys. Res. Atmos. 2005, 110, 110. [Google Scholar] [CrossRef]
- Rothermel, R.C. A Mathematical Model for Predicting Fire Spread in Wildland Fuels; Research Paper INT-115; USDA Forest Service: Washington, DC, USA, 1972.
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Accary, G.; Sutherland, D.; Frangieh, N.; Moinuddin, K.; Shamseddine, I.; Meradji, S.; Morvan, D. Physics-Based Simulations of Flow and Fire Development Downstream of a Canopy. Atmosphere 2020, 11, 683. https://doi.org/10.3390/atmos11070683
Accary G, Sutherland D, Frangieh N, Moinuddin K, Shamseddine I, Meradji S, Morvan D. Physics-Based Simulations of Flow and Fire Development Downstream of a Canopy. Atmosphere. 2020; 11(7):683. https://doi.org/10.3390/atmos11070683
Chicago/Turabian StyleAccary, Gilbert, Duncan Sutherland, Nicolas Frangieh, Khalid Moinuddin, Ibrahim Shamseddine, Sofiane Meradji, and Dominique Morvan. 2020. "Physics-Based Simulations of Flow and Fire Development Downstream of a Canopy" Atmosphere 11, no. 7: 683. https://doi.org/10.3390/atmos11070683
APA StyleAccary, G., Sutherland, D., Frangieh, N., Moinuddin, K., Shamseddine, I., Meradji, S., & Morvan, D. (2020). Physics-Based Simulations of Flow and Fire Development Downstream of a Canopy. Atmosphere, 11(7), 683. https://doi.org/10.3390/atmos11070683







