Estimating the Effect of Radiative Feedback Uncertainties on Climate Response to Changes in the Concentration of Stratospheric Aerosols

Abstract

Using the two-box energy balance model (EBM), we explore the climate system response to radiative forcing generated by variations in the concentrations of stratospheric aerosols and estimate the effect of uncertainties in radiative feedbacks on changes in global mean surface temperature anomaly used as an indicator of the response of the climate system to external radiative perturbations. Radiative forcing generated by stratospheric sulfate aerosols from the second-largest volcanic eruption in the 20th century, the Mount Pinatubo eruption in June 1991, was chosen for this research. The global mean surface temperature response to a specified change in radiative forcing is estimated as a convolution of the derived impulse response function corresponding to EBM with a function that describes the temporal change in radiative forcing. The influence of radiative feedback uncertainties on changes in the global mean surface temperature is estimated using several “versions” of the EBM. The parameters for different “versions” were identified by applying a specific procedure for calibrating the two-box EBM parameters using the results of climate change simulations conducted with coupled atmosphere–ocean general circulation models from the Coupled Model Intercomparison Project phase 5 (CMIP5). Changes in the global mean surface temperature caused by stratospheric aerosol forcing are found to be highly sensitive not only to radiative feedbacks but also to climate system inertia defined by the effective heat capacity of the atmosphere–land–ocean mixed layer system, as well as to deep-ocean heat uptake. The results obtained have direct implications for a better understanding of how uncertainties in climate feedbacks, climate system inertia and deep-ocean heat uptake affect climate change modelling.

1. Introduction

Natural and anthropogenic atmospheric aerosols substantially influence the Earth’s climate by both directly and indirectly affecting the planetary energy balance, redistribution of radiative fluxes and the formation of thermal and dynamic structures of the ocean and atmosphere (see [1,2] and references cited herein). The climatic effect of atmospheric aerosols depends on their optical properties (scattering and absorption coefficients, single scattering albedo, Ångström exponent, particle size distribution and particle number) as well as the aerosols’ residence time (lifetime) in the atmosphere (e.g., [3,4,5,6]). The residence time is in turn determined by the particle sizes and the altitude of the aerosol layer (plume). Tiny stratospheric aerosols (e.g., volcanic sulfate aerosols) have one of the most significant effects on the climate since their lifetime can be up to several years, which is much longer than the residence time of the tropospheric aerosols (e.g., [7,8]). The stratospheric sulfate aerosol layer is an almost purely scattering medium for shortwave solar radiation. Therefore, some of the incoming solar radiation is reflected back into space, contributing to the near-surface cooling. However, stratospheric sulfate aerosol plume is a weakly absorbing medium for the infrared terrestrial radiation. Sulfate aerosols artificially injected into the stratosphere, due to their optical properties, are considered as a potential measure to mitigate anthropogenic global warming (e.g., [9,10,11,12] and references cited herein).

Currently, climate models of varying degrees of complexity play their role as our main tools for expanding our scientific understanding of the influence of stratospheric aerosols on the Earth’s climate change and its variability in the past, present and future. In climate studies, two main measures—equilibrium climate sensitivity (ECS) and transient climate response (TCR)—are commonly used to estimate the climate system response to a given external radiative forcing caused by various agents, including stratospheric aerosols. Meanwhile, it has long been known that different climate models demonstrate varying extents of climate system response since the range of climate sensitivity in climate models is quite wide (e.g., [13,14,15]). This uncertainty in climate sensitivity results in a large extent from intermodel differences in the strength of radiative feedback processes that are inherent in the physical climate system [16,17,18,19,20,21,22,23].

From the standpoint of control theory, feedback loops represent regulatory mechanisms that amplify (positive feedback) or diminish (negative feedback) the effects of external radiative forcing, thereby determining the climate sensitivity [24]. Observations and climate model simulations show that feedback loops jointly amplify the climate system response (in terms of surface temperature) to external radiative forcing [21,25]. In the context of the climate system, feedbacks can be analyzed within the global top-of-atmosphere (TOA) linear forcing-feedback framework [26,27]:

$$N=F-R=F-\lambda \mathsf{\Delta }T,$$

(1)

where $N$ is the global-mean net downward radiative flux at the TOA representing the rate of increase in heat stored in the climate system, $F$ is the radiative forcing (positive downwards) imposed on the climate system due to changes in concentrations of radiatively active atmospheric components, $R$ is the radiative response of the climate system (positive upwards) to change in the global mean surface temperature $\Delta T$ and $\lambda (\mathrm{W} {\mathrm{m}}^{-2} {\mathrm{K}}^{-1}$) is the climate response parameter which characterizes the net climate feedback strength (in the scientific literature, the parameter $\lambda$ is also referred to as the climate feedback parameter). The sign convention used in Equation (1) corresponds to the so-called “positive-stable” climate feedback (for details, please refer to Gregory et al. [27]).

The global mean surface temperature change $\Delta T$ is considered relative to an unperturbed steady state of the climate system for which $N=F=0$ and therefore, $R=0$. In a perturbed steady state $F=\lambda \Delta T$ and therefore, $\lambda =F/\Delta T$. The inverse of the feedback parameter $\alpha =1/\lambda (\mathrm{K} {\mathrm{W}}^{-1}{\mathrm{m}}^2$), is called the climate sensitivity parameter. Thus, the change in global-mean surface temperature $\Delta T$ due to radiative forcing $F$, once the climate system reaches the equilibrium state, is defined as $\Delta T=F/\lambda =\alpha F$. If, for example, the radiative forcing $F=F_{2\times }$, where $F_{2\times }$ is the radiative forcing induced by a doubling of the atmospheric carbon dioxide (CO₂) concentration, then the ECS is given by $\mathsf{\Delta }{T}_{s, 2\times }^{eq}=\alpha F_{2\times }$. There is a wide variety of both positive and negative feedback mechanisms in the Earth’s climate system. Some of them are important in terms of their influence on the climate system response to external radiative forcing [25]. However, the strength of the feedback estimates in Coupled Model Intercomparison Project phase 5 (CMIP5) models [28] varies noticeably [29], which causes significant intermodel differences in the global-mean temperature response to a given radiative forcing.

In this paper, we apply the two-layer energy balance model (EBM) [30,31] to explore the climate system response to radiative forcing generated by variations in stratospheric aerosol concentrations, and ultimately to better understand how the uncertainties in climate feedbacks affect changes in global mean surface temperature anomaly used as an indicator of the response of the climate system to external radiative perturbations. Radiative forcing generated by stratospheric sulfate aerosols from the second-largest volcanic eruption of the 20th century, the Mount Pinatubo eruption in June 1991, was chosen for this research. Hansen et al. [32] suggested using the Pinatubo case as a test of climate sensitivity to a given forcing since the availability of data for Pinatubo allows one to accurately determine the magnitude of stratospheric aerosol forcing. The climate system response to a specified change in radiative forcing is estimated as a convolution of the derived impulse response function corresponding to EBM with a function that describes the temporal change in radiative forcing. The influence of radiative feedback uncertainties on changes in the global mean surface temperature is estimated using several EBM “versions”, the parameters of which were identified by applying a specific procedure for calibrating the two-box EBM parameters using the results of climate change simulations with coupled atmosphere–ocean general circulation models from the CMIP5 [29].

2. Materials and Methods

2.1. The Model

We used the two-box EBM [30,31] which, in stochastic formulation, has previously been applied to estimate the effects of parametric uncertainty on climate variability [19,20]. In this EBM, the climate system was divided into two subsystems: the upper box that corresponds to the atmosphere, the land surface and the ocean mixed layer, and the lower box that represents the deep ocean. The state of each box was characterized by the globally averaged temperature anomalies $\Delta T$ and $\Delta T_D$ with respect to their reference (equilibrium) values $T_0$ and $T_{D,0}$. Equations that describe the evolution over time of the model state variables $\Delta T$ and $\Delta T_D$ under the influence of radiative forcing F are of the form:

$$C\frac{d\Delta T}{dt}=-\lambda \Delta T-\gamma \left(\Delta T-\Delta T_D\right)+F$$

(2)

$$C_D\frac{d\Delta T_D}{dt}=\gamma \left(\Delta T-\Delta T_D\right),$$

(3)

where $C$ and $C_D$ are the effective heat capacities of the upper and lower boxes of the model; $\gamma$ is a heat exchange parameter describing the interactions between the boxes. Temperature anomaly of the upper box $\Delta T$ is identified with the global-mean surface air temperature perturbation.

In the absence of radiative feedbacks (i.e., with only the ”Planck” response), we can define the so-called “reference-system climate sensitivity parameter” ${\alpha }_0$ [16,24]:

$${\alpha }_0={\left(4\epsilon \sigma T_0^3\right)}^{-1}\approx 0.30 \mathrm{K} {\mathrm{W}}^{-1}{\mathrm{m}}^2,$$

(4)

where $\epsilon$ is the Earth’s emissivity [33]; $\sigma =5.67·{10}^{-8} \left(\mathrm{kg} {\mathrm{s}}^{-3} {\mathrm{K}}^{-4}\right)$ is the Stephan–Boltzmann constant; $T_0=288 \mathrm{K}$ is the reference global mean surface temperature. The reference climate sensitivity parameter ${\alpha }_0$ gives a long-term (equilibrium) surface temperature increase $\Delta T_0\approx 1.1$ °C in response to radiative forcing due to the doubling of the CO₂ concentration.

Along with the feedback parameter $\lambda$, we can also consider the dimensionless feedback coefficient (factor) f [16], which is a fraction of the climate system output “signal” sent back to its input defined by the following expression: $f=1-{\alpha }_0/\alpha$. Then, the response of the climate system $\Delta T$ to the radiative forcing $F$ is given by $\Delta T=\mathsf{\Delta }{T}_0/\left(1-f\right)=G\mathsf{\Delta }{T}_0,$ where $G=1/\left(1-f\right)$ is the climate system gain. It is obvious that the negative feedback ($-\infty <f<0$) reduces the gain ($G<1)$ and, therefore, taking negative feedback into account weakens the climate system response to radiative forcing. In contrast, positive feedback ($0<f<1$) enhances the gain ($G>1$) and, thus, amplifies the climate system response. It is clear that climate feedbacks fall into this range [24]. If $f\ge 1$, then the perturbed climate system is unable to reach the new equilibrium state, therefore, this case is hardly applicable to the climate system [24]. Note that in a (linear) EBM, different feedbacks are considered as additive: $f=f_1+f_2+\dots +f_n$ [34]. Equation $\Delta T=G\mathsf{\Delta }{T}_0$ shows that the relationship between the absolute uncertainty in the system response $\delta \left(\Delta T\right)$ and the absolute uncertainty in the feedback factor $\delta f$ is nonlinear: $\delta \left(\Delta T\right)=\mathsf{\Delta }{T}_0{G}^2\delta f$. In climate studies, the uncertainty in system response to radiative forcing can be evaluated employing multiple models (an ensemble-based approach to climate simulations and projections). In this case, the feedback uncertainty can be given by the variance ${\sigma }_{\Delta T}^2={\sigma }_f^2\mathsf{\Delta }{T}_0/{\left(1-\overline{f}\right)}^2=\mathsf{\Delta }{T}_0{\overline{G}}^2{\sigma }_f^2,$ where $\overline{f}$ is the model-mean feedback factor, ${\sigma }_f$ its standard deviation, and ${\sigma }_{\Delta T}$ is the standard deviation of the climate system response $\Delta T$.

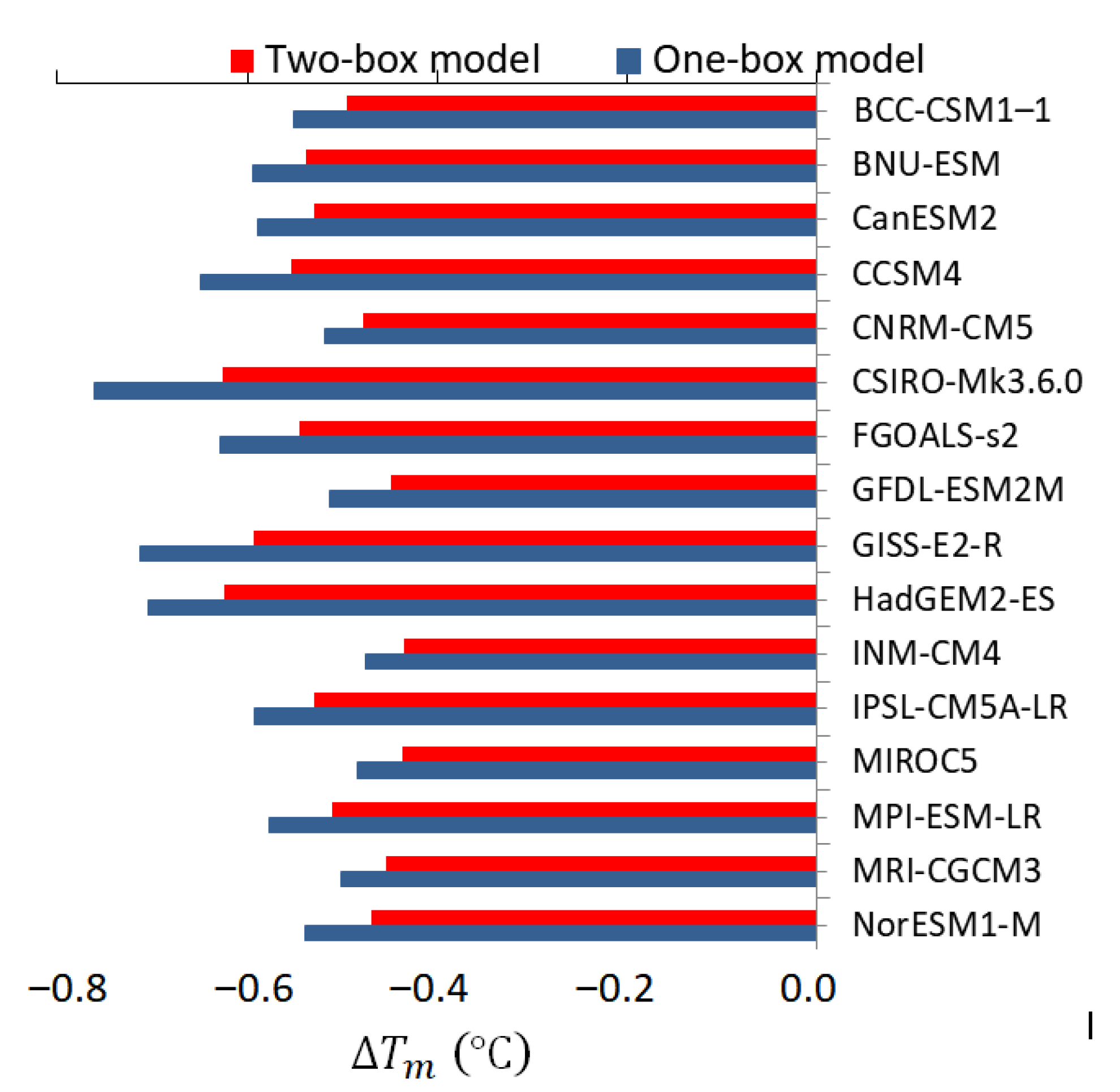
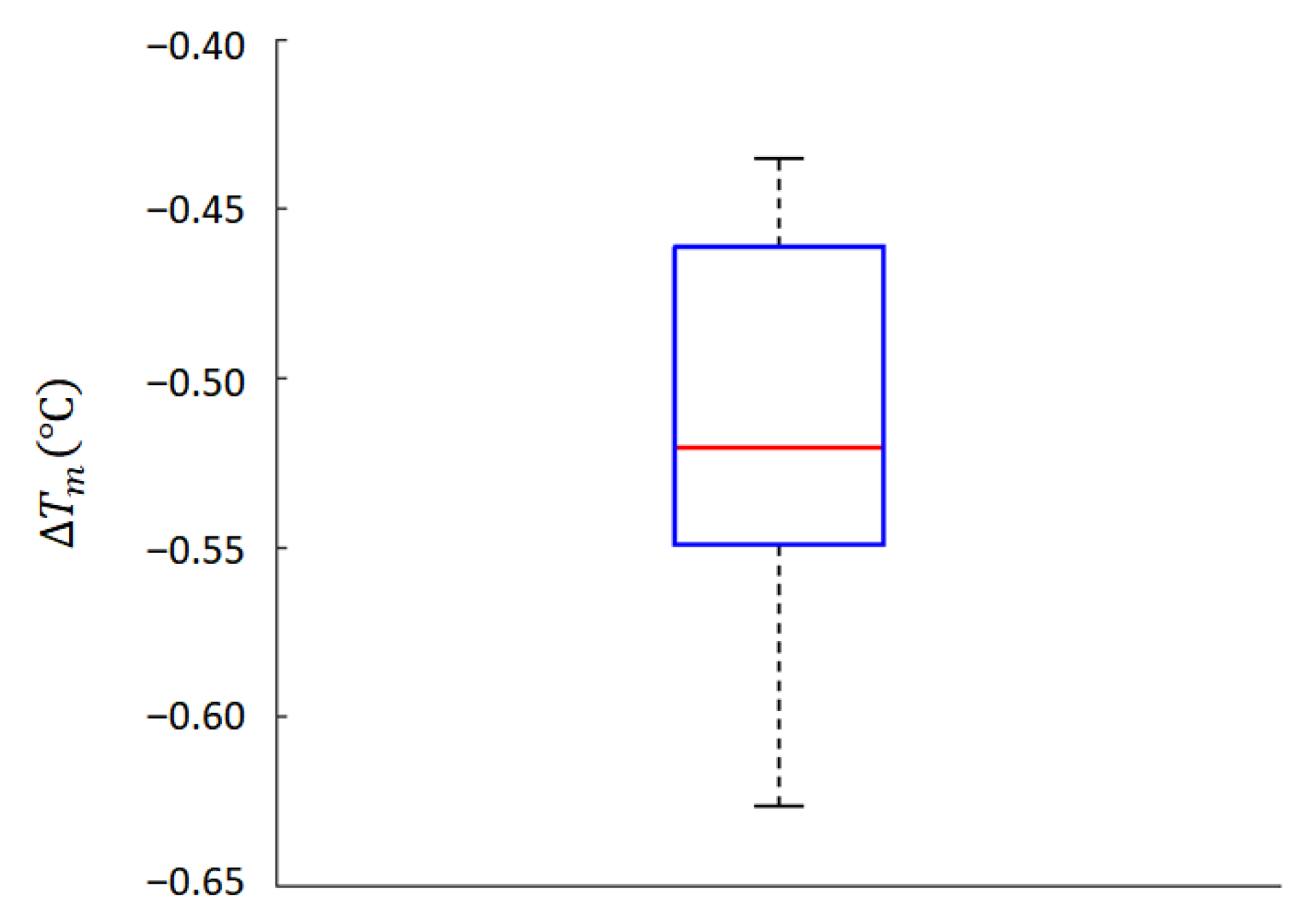
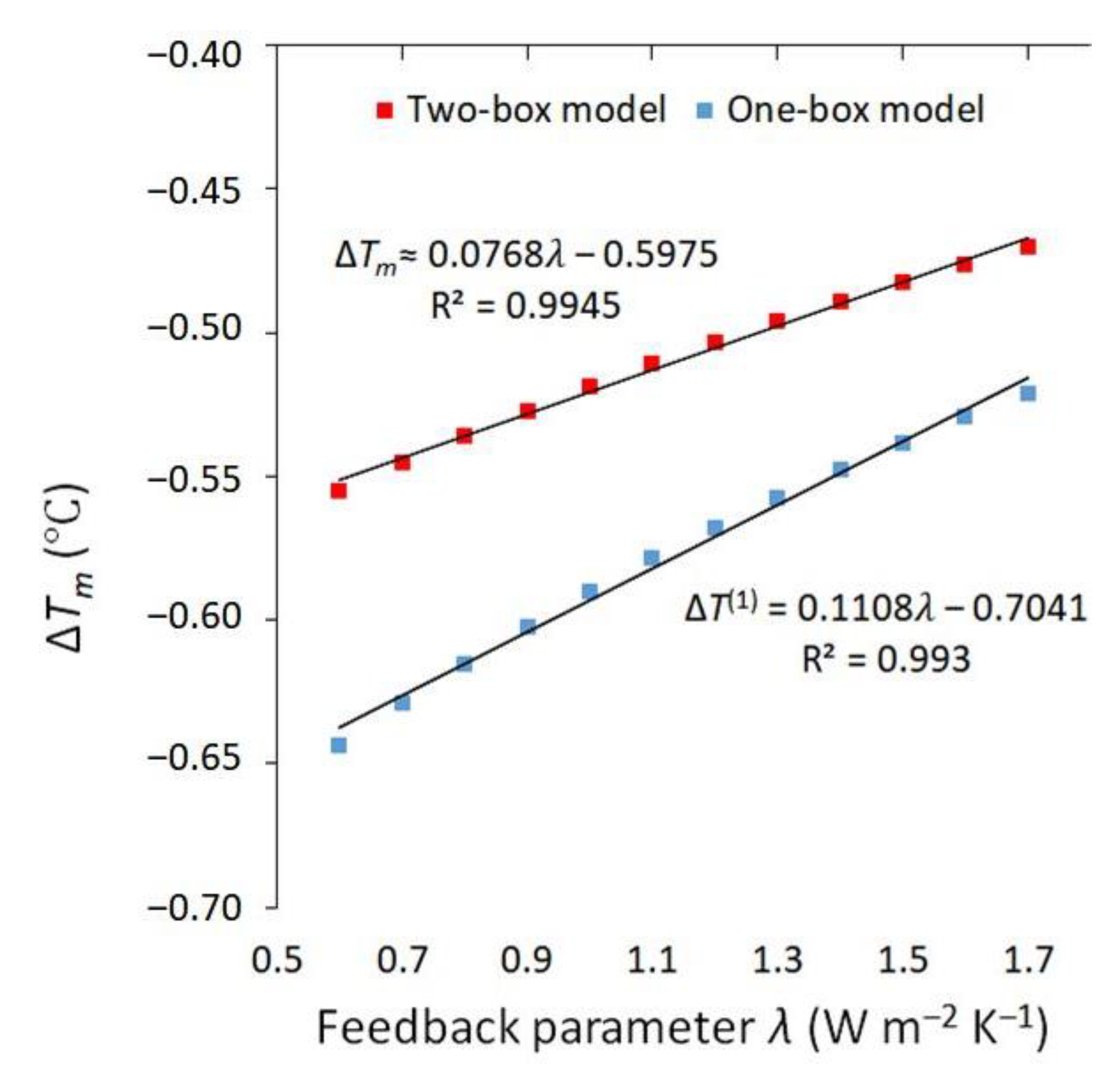
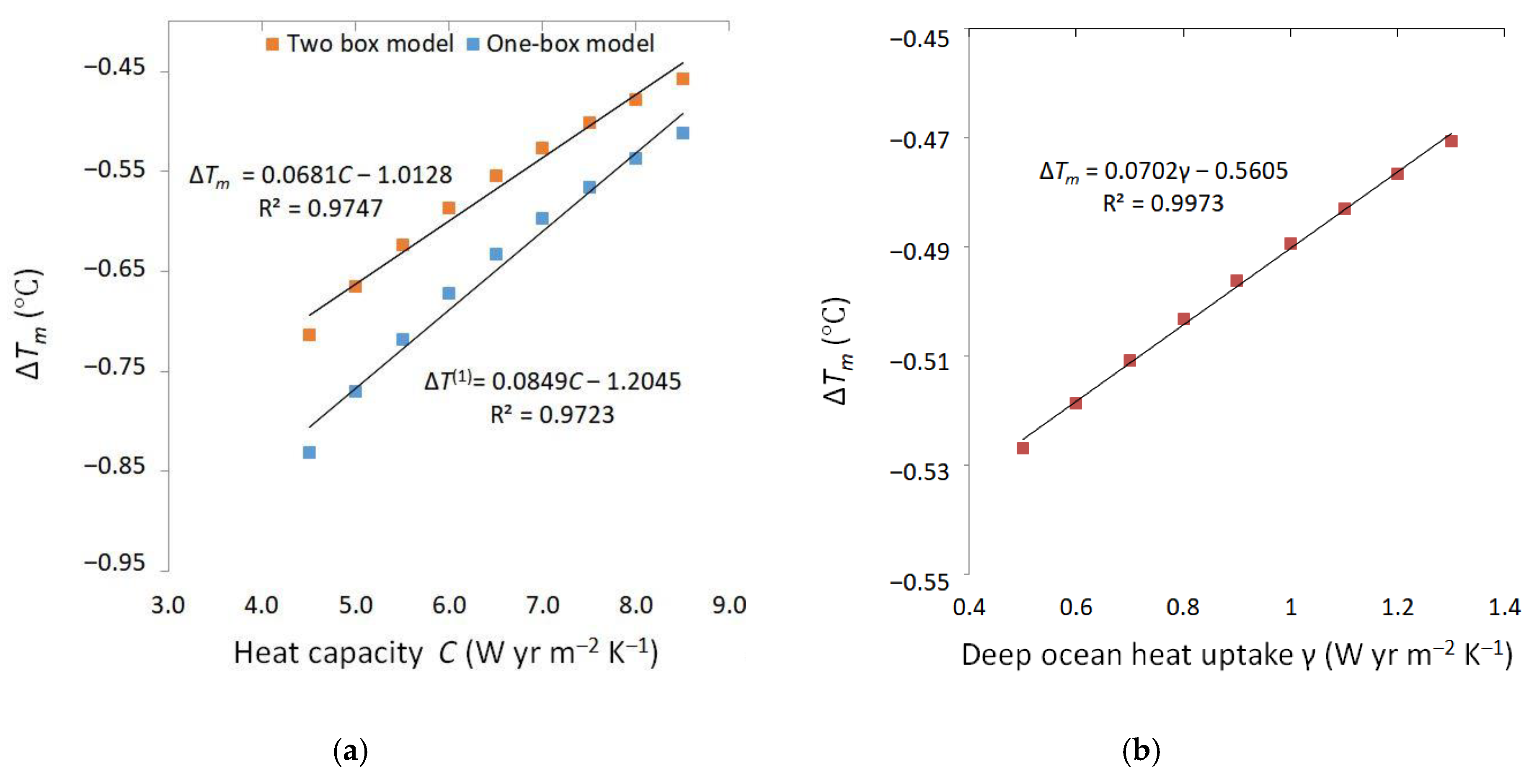
The two-box EBM includes four free parameters, $C$, $C_D$, λ and γ, and a radiative forcing amplitude parameter $F$, which affect the time evolution of the state variables $\Delta T$ and $\Delta T_D$. Model parameter values used in this study were taken from [29] (see

Table 1. The thermal inertia parameters $C$ and $C_D$, deep-ocean heat uptake $\gamma$, climate feedback parameter $\lambda$, and climate feedback factor $f$ estimates of the Coupled Model Intercomparison Project phase 5 (CMIP5) models used in this study, and their multimodel mean and standard deviation given for the 16-model ensemble (all parameter values, with the exception of the climate feedback factor, are taken from [29]).

	Model	Parameter
		$\mathit{C}\left({\mathbf{W}\mathbf{yr}\mathbf{m}}^{\mathbf{-}\mathbf{2}}{\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$	${\mathit{C}}_{\mathit{D}}\left({\mathbf{W}\mathbf{yr}\mathbf{m}}^{\mathbf{-}\mathbf{2}}{\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$	$\mathit{\gamma }\left({\mathbf{W}\mathbf{m}}^{\mathbf{-}\mathbf{2}}{\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$	$\mathit{\lambda }\left({\mathbf{W}\mathbf{m}}^{\mathbf{-}\mathbf{2}}{\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$	f
1	BCC-CSM1-1	7.6	53	0.67	1.21	0.64
2	BNU-ESM	7.4	90	0.53	0.93	0.72
3	CanESM2	7.3	71	0.59	1.03	0.69
4	CCSM4	6.1	69	0.93	1.24	0.63
5	CNRM-CM5	8.4	99	0.50	1.11	0.67
6	CSIRO-Mk3.6.0	6.0	69	0.88	0.61	0.82
7	FGOALS-s2	7.0	127	0.76	0.88	0.74
8	GFDL-ESM2M	8.1	105	0.90	1.34	0.60
9	GISS-E2-R	4.7	126	1.16	1.70	0.49
10	HadGEM2-ES	6.5	82	0.55	0.65	0.81
11	INM-CM4	8.6	317	0.65	1.51	0.55
12	IPSL-CM5A-LR	7.7	95	0.59	0.79	0.76
13	MIROC5	8.3	145	0.76	1.58	0.53
14	MPI-ESM-LR	7.3	71	0.72	1.14	0.66
15	MRI-CGCM3	8.5	64	0.66	1.26	0.62
16	NorESM1-M	8.0	105	0.88	1.11	0.67
	Mean	7.3	106	0.73	1.13	0.66
	STD	1.1	62	0.18	0.31	0.09

). These values were identified via the specific procedure of calibrating the two-box EBM parameters from the results of climate change simulations performed using coupled atmosphere–ocean general circulation models from the CMIP5. As the base values of the model parameters, we will consider the rounded values of the multi-model means of the CMIP5 fitted values: $=7.3$ ${\mathrm{W}\mathrm{yr}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$, $C_D=$106 ${\mathrm{W}\mathrm{yr}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$, $\gamma =0.73$ ${\mathrm{W}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$ and $\lambda =1.13$ ${\mathrm{W}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$, which corresponds to $f=0.66$. Certainly, all CMIP5 models are similar since they are based on the same basic physical laws and principles and describe the evolution of the same (climate) system. Meanwhile, some characteristics of CMIP5 models (e.g., the description of physical processes and cycles, the numerical algorithms and spatial resolution) differ from each other [15]. This can be one of the greatest sources of differences in CMIP5 model parameter estimates. As in [29], the feedback parameters used in this study represent the instantaneous global radiative response at the TOA to global mean surface temperature changes, irrespective of how those variations occur. In contrast to complex climate models, in which the total feedback parameter is regarded as the “sum” of various individual feedback parameters, in EBMs the total feedback parameter is only considered. The values of the total feedback parameters listed in Table 1 were derived based on the assumption that the net radiative flux change at the TOA is induced by a quadrupling of the atmospheric CO₂ concentration. However, as shown in [35], the global anthropogenic aerosol radiative feedback parameter is “indistinguishable” from the GHG feedback parameter. Thus, the use of the values of the total feedback parameter obtained in [29] is a fairly reasonable assumption.

For convenience of further discussion, we note that model Equations (2) and (3) can be easily converted to a linear second-order differential equation describing a damped harmonic oscillator driven by a force that depends on time:

$$\frac{d\Delta T_D^2}{d^{2}t}+2\beta \frac{d\Delta T_D}{dt}+{\omega }_0^2\Delta T_D=\frac{\gamma }{C{C}_D}F\left(t\right),$$

(5)

where ${\omega }_0=\sqrt{\lambda \gamma /C{C}_D}$ is the angular resonance frequency, and $\beta =\left[\left(\lambda +\gamma \right)C_D+\gamma C\right]/\left(2C{C}_D\right)$ is the damping coefficient.

The analysis of the above second-order differential equation, which is equivalent to the system of first order linear differential Equations (2) and (3), shows that the climate system response to radiative forcing is characterized by the “fast” ${\tau }_f$ and the “slow” ${\tau }_s$ relaxation times given, respectively, by

$${\tau }_f=\frac{\beta }{{\omega }_0^2}\left(1-\sqrt{1-{\omega }_0^2/{\beta }^2}\right), {\tau }_s=\frac{\beta }{{\omega }_0^2}\left(1+\sqrt{1-{\omega }_0^2/{\beta }^2}\right).$$

(6)

For the base parameter values, we obtain ${\tau }_f\approx 3.9 \mathrm{yr}$ and ${\tau }_s\approx 242 \mathrm{yr}$.

2.2. The Global Radiative Forcing Due to Stratospheric SulfateA

In general, estimating the response of the climate system to radiative forcing produced by variations in the atmospheric concentrations of radiatively active gases and natural and anthropogenic aerosols requires quite a complex radiation transfer model. However, in the two-box EBM, an external radiative forcing is defined as a change in the planetary radiative balance at the TOA (or in other words, as the net radiative flux change at the TOA). In this study, to obtain an estimate of radiative forcing $F_A$ produced by stratospheric sulfate aerosols, we apply a simplified single-factor parameterization scheme [6], in which the aerosol optical depth (or thickness) ${\tau }_A$ at the wavelength 550 nm is used as a determining parameter to account for the optical properties of aerosol particles that scatter solar shortwave radiation for the case of a uniform layer of aerosols:

$$F_A\left(t\right)=-\zeta {\tau }_A\left(t\right),$$

(7)

where $\zeta =25$ ${\mathrm{W}\mathrm{m}}^{-2}$ is the empirical parameter [6], and ${\tau }_A$ is the global mean optical depth of stratospheric aerosols.

In this study, the temporal change in ${\tau }_A$ was specified in accordance with the GISS (Goddard Institute for Space Studies) aerosol data products [36] for the period 1989–2012 (the span of time from 2 years before to 21 years after the Pinatubo volcanic eruption in June 1991). The total amount of sulfur dioxide ${\mathrm{SO}}_2$ injected into the stratosphere as a result of the Pinatubo eruption is considerably uncertain and ranged from 10 to 20 Tg ([37,38] and references cited herein). Sulfur dioxide formed sulfate aerosols, which rapidly spread around the Earth reaching global coverage about 1 year after the eruption. We highlight that Hansen et al. [32] specifically suggested using the Pinatubo case as a test of climate sensitivity to a given forcing since the availability of data for Pinatubo allows accurate determination of the magnitude of stratospheric aerosol forcing.

2.3. Technique for the Solution of EBM Equations

Since the two-box EBM is linear, the response of the global mean surface temperature anomaly $\Delta T$ to radiative perturbation caused by stratospheric aerosols can be estimated as a convolution of the impulse response function (IRF) for continuous-time dynamical system (2)–(3) with a function that describes the change in radiative forcing $F_A\left(t\right)$ [39]. Let $g\left(t\right)$ be the IRF for the system described by Equations (2) and (3). Then $\Delta T$ is given by [40]

$$\Delta T\left(t\right)=\left[g\ast F_A\right]\left(t\right)={{\displaystyle \int }}_0^{t}g\left(\tau \right)F_A\left(t-\tau \right)d\tau .$$

(8)

where $\left[g\ast F_A\right]\left(t\right)$ denotes convolution of $g$ and $F_A$ over a finite time range $\left[0, t\right]$.

In the general case, the impulse characteristic $g\left(t\right)$ of a linear dynamical system is the response of a system to the input specified as a Dirac delta function $\delta \left(t\right)$ with zero initial conditions. To find the IRF of a linear continuous-time dynamical system we can take the inverse Laplace transform of the system’s transfer function $H\left(s\right)$: $g\left(t\right)={ℒ}^{-1}\left\{H\left(s\right)\right\}$, where $ℒ$ is the symbol of the Laplace operator, and $s$ is a complex variable known as the complex frequency. In turn, the transfer function of the two-box EBM can be obtained by taking the Laplace transform of differential equations (2) and (3) with zero initial conditions. Omitting intermediate calculation, we give the final expression for the transfer function of system (2) and (3) [40]:

$$H\left(s\right)=\frac{\gamma +s{C}_D}{s^{2}C{C}_D+s\left[\gamma C+\left(\gamma +\lambda \right)C_D\right]+\gamma \lambda }.$$

(9)

Taking the inverse Laplace transform of the transfer function (9), we have [40]

$$g\left(t\right)=\frac{{\tau }_f{\tau }_f}{C\left({\tau }_f-{\tau }_f\right)}\left[\left(\frac{1}{{\tau }_f}-\frac{\gamma }{C_D}\right)e^{-t/{\tau }_f}-\left(\frac{1}{{\tau }_s}-\frac{\gamma }{C_D}\right)e^{-t/{\tau }_s}\right].$$

(10)

The IRF (10) completely characterizes the dynamic properties of EBMs (2)–(3) affected by any, but sufficiently small, time dependent external radiative perturbation.

3. Results and Discussion

To validate the proposed IRF-based technique for calculating the global mean surface temperature anomaly $\Delta T$ in response to external radiative perturbation, we performed calculations using two idealized forcing scenarios for which analytical solutions are available. These are (a) step forcing, which instantly jumps from 0 to the value of $F_{4\times }\approx 6.9 {\mathrm{W}\mathrm{m}}^{-2}$ [2] at $t=0$, and then remains constant (abrupt quadrupling of atmospheric CO₂ scenario) and (b) linear forcing that corresponds to 1% yearly CO₂ concentration growth (1 pct CO₂ scenario), for which $F\left(t\right)=F_{1pct{\mathrm{CO}}_2}\left(t\right)=\eta t$, where $\eta =5.2857 \mathrm{W} {\mathrm{m}}^{-2} {\mathrm{yr}}^{-1}$ [12,40]. These two idealized scenarios are standard radiative forcing scenarios used to obtain the estimates of ECS and TCR from global climate models [28].

For a step forcing, the analytical solution for the global mean surface temperature anomaly $\Delta T$ as a function of time is given by

$$\Delta T\left(t\right)=\frac{F_{4\times }}{\lambda }\left[1-{\alpha }_1{e}^{-t/{\tau }_f}-{\alpha }_2{e}^{-t/{\tau }_s}\right].$$

(11)

Here ${\alpha }_1=\left(1-v_{22}\right)/\left(v_{12}-v_{22}\right)$ and ${\alpha }_2=\left(1-v_{12}\right)/\left(v_{22}-v_{12}\right)$, where $v_{12}$ and $v_{22}$ are the components of eigenvectors (for further details, see Appendix A).

For a linear forcing, the anomaly $\Delta T$ is calculated using the following formula:

$$\Delta T\left(t\right)={\beta }_1{e}^{-t/{\tau }_f}-{\beta }_2{e}^{-t/{\tau }_s}-\frac{\eta \left(C+C_D\right)}{{\lambda }^2}+\frac{\eta }{\lambda }t,$$

(12)

where the coefficients ${\beta }_1$ and ${\beta }_2$ depend on the model parameters. The formulas for calculating ${\beta }_1$ and ${\beta }_2$ are omitted due to lack of space [40].

As shown in [40], the approximate solutions are in agreement with the exact analytical solutions. For both forcing scenarios, the relative error is lower than 1%, while the largest absolute error is about $0.04$ °C.

Figure 1a illustrates the time evolution of the global mean total optical depth ${\tau }_A$ at the wavelength 550 nm for the case of the Mount Pinatubo eruption. In order to isolate the global mean surface temperature signal induced by volcanic aerosols, we removed the radiative effects of background stratospheric aerosols by assuming that their total optical depth ${\tau }_b$ is ~0.005 [41]. This allows us to neglect the influence of radiative perturbation caused by background stratospheric aerosols on the global mean surface temperature change. The value of ${\tau }_b$ is given by the mean of stratospheric aerosol optical depth at the wavelength 550 nm for the 18 months preceding the Mount Pinatubo eruption. Thus, the optical depth of the stratospheric aerosols used in calculations is defined by ${\tau }_A={\tau }_{\mathrm{GISS}}-{\tau }_b$, where ${\tau }_{\mathrm{GISS}}$ is the aerosol optical depth taken from the GISS aerosol data products [36].

As shown in Figure 1a, the global mean total optical depth would rise rapidly to a maximum value of ~0.15 by the beginning of 1992, and then exponentially decrease to insignificant values by 1995. A similar behaviour is inherent in radiative forcing generated by volcanic stratospheric aerosols, since the relationship between the total optical depth and the top-of-the-atmosphere radiative forcing (7) is linear. The corresponding changes in the global mean surface temperature anomalies, derived using various EBMs with parameters listed in Table 1, are presented in Figure 1b. As reflected in this figure, all models show an abrupt cooling after the Mount Pinatubo eruption. However, the changes in global mean surface temperature anomaly due to radiative perturbation generated by volcanic aerosols vary noticeably between the different EBMs (see Figure 2). The lowest global mean surface temperature $\Delta T_m$, taken as an indicator of the climate system changes in response to a volcanic aerosol forcing, occurs about 1.5–2 years after the eruption of Pinatubo.

To evaluate the model ensemble, we used standard statistical measures such as mean, standard deviation (StD) and the range of changes in $\Delta T_m$. Multi-model ensemble mean volcanic cooling $‹\Delta T_m›$ is about $-0.52$ °C with a full range of $-0.43–-0.63$ °C, and the ensemble StD is ~0.06 °C. The strongest response $\Delta T_m\approx -0.63$ °C was obtained using the CSIRO (Commonwealth Scientific and Industrial Research Organisation) model with the feedback parameter $\lambda =0.61{\mathrm{W}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$, while the smallest response $\Delta T_m\approx -0.43$ °C was calculated using the INM (Institute of Numerical Mathematics) model with $\lambda =1.51{\mathrm{W}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$. As shown in previously published studies (e.g., [32,38,41]), the Pinatubo volcanic aerosol plume caused short-term global surface cooling of up to 0.4–0.6 °C. Thus, the results obtained by the two-box EBM are reasonably accurate despite the multi-model ensemble spread of $~0.2$ °C for $\Delta T_m$. For reference, Figure 2 presents the results obtained by the one-box EBM commonly used in theoretical climate studies. The main equation of this model can be derived from Equations (2) and (3) with the condition $\gamma \to 0$. Calculations show that omitting the deep-ocean heat uptake ($\gamma =0$) leads to an increase in the climate system response to volcanic radiative forcing by about 15%.

Figure 3, which to a certain extent compliments Figure 2, provides the box-whisker plot that summarizes the descriptive statistical measures (median, minimum and maximum values of $\Delta T_m$, lower and upper quartiles) obtained from the multi-model ensemble. The whiskers show the range of $\Delta T_m$ obtained from the 16 realizations, while the box displays the interquartile range (the range between the first and third quartiles or, in other words, the middle 50% of the distribution), and the red line indicates the median.

Since all model parameters affect the response of global mean surface temperature to external radiative forcing, in order to estimate the effect of only the feedback parameter $\lambda$ on $\Delta T_m$, we performed a series of numerical experiments in which multi-model mean (or base) values of $C$, $C_D$ and $\gamma$ were assigned, while the parameter $\lambda$ changed in the range of $0.6-1.7$1 ${\mathrm{W}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$ (see Table 1). This so-called “One-factor-at-a-time” method [19] is a commonly used approach in sensitivity analysis of dynamical systems including climate models [20]. As can be seen in Figure 4, the variable $\Delta T_m$ is almost linearly dependent on the feedback parameter $\lambda$. The relationship between $\Delta T_m$ and $\lambda$ can be represented by the following linear equation: $\Delta T_m=0.0768\lambda -0.5975$. A value of $R^2\approx 0.99$ indicates a strong correlation between $\Delta T_m$ and $\lambda$. The results obtained from the one-box EBM are shown in Figure 4, for reference.

It is, however, well known (e.g., [21]) that the level of uncertainty in climate feedbacks is still high. Since the uncertainty in feedbacks is the essential source of uncertainty in the response of the Earth’s climate system to the anthropogenic greenhouse gas emissions, radiative feedback mechanisms are predominantly explored in the context of longer-term climatic changes measured on inter-annual, decadal and century scales. However, even at present, the intermodel spread in climate sensitivity, which is one of the main indices that measures the relationships between the increase in greenhouse gases (GHG) in the atmosphere and the magnitude of climate change, remains large, mainly due to the uncertainties in the representations of radiative feedbacks in state-of-the-art climate models. In this paper, we intended to estimate the effect of radiative feedback uncertainties on the short-term response of the climate system to a sharp radiative perturbation due to volcanic aerosols injected into the stratosphere by the 1991 Mount Pinatubo eruption.

To estimate the influence of feedback uncertainties on the climate system response to volcanic aerosol radiative forcing, we used the sensitivity coefficient $S_{\lambda }$ defined as the partial derivative of $\Delta T_m$ with respect to λ, i.e., $S_{\lambda }=\partial \left(\Delta T_m\right)/\partial \lambda$ [19,20,42]. Then, the impact of feedback uncertainty on the model output can be quantified as follows: $\delta \left(\Delta T_m\right)\approx S_{\lambda }\delta \lambda$, where the variation $\delta \lambda$ characterizes the uncertainty in the parameter $\lambda$, and $\delta \left(\Delta T_m\right)$ is the change (uncertainty) in the global mean surface temperature anomaly caused by $\delta \lambda$. For linear regression of the form $y=ax+b$, the sensitivity coefficient is simply the slope $a$ of the regression line. From the equation that relates $\Delta T_m$ and $\lambda$ (see above), one can find that $S_{\lambda }=0.0768$ ${\mathrm{m}}^2{\mathrm{K}}^2{\mathrm{W}}^{-1}$.

Assuming the absolute uncertainty in the feedback parameter $\lambda$ is $\delta \lambda =\pm 0.7 {\mathrm{W}\mathrm{m}}^{-2}{\mathrm{K}}^{-1}$ (1-sigma uncertainty) [18,21], then the absolute uncertainty in $\Delta T_m$ caused by $\delta \lambda$ is $\delta \left(\Delta T_m\right)\approx \pm 0.05$ °C, and the fractional (or percentage) uncertainty is about $\pm 10.4$%. Recall that the fractional uncertainty is given by the ratio of the absolute uncertainty $\delta \left(\Delta T_m\right)$ to the multi-model average value ${\overline{\Delta T}}_m$. For comparison, we also present results based on the one-box EBM: the absolute uncertainty in $\Delta T_m$ is $\delta \left(\Delta T^{\left(1\right)}\right)\approx \pm 0.08$ °C and the fractional uncertainty is about $\pm 15.0$% for the same uncertainty in the feedback parameter.

Using a similar approach, we can estimate the impact of uncertainties in each of the model parameters on the climate system response $\Delta T_m$ to volcanic stratospheric aerosol forcing, and thereby rank model parameters based on their relative contribution to the uncertainty in $\Delta T_m$, as well as assess the relative role and importance of feedback parameter uncertainty in the overall model uncertainty. Figure 5 shows the dependences of $\Delta T_m$ on the effective heat capacity C of the upper box model (a) and on the deep-ocean heat uptake parameter γ (b). The corresponding sensitivity coefficients that characterize the influence of the uncertainties in parameters C and γ on the uncertainty in $\Delta T_m$ are, respectively, $S_C\approx 0.0681 {\mathrm{m}}^2{\mathrm{K}}^2{\mathrm{W}}^{-1}{\mathrm{yr}}^{-1}$ and $S_{\gamma }\approx 0.0702$ ${\mathrm{m}}^2{\mathrm{K}}^2{\mathrm{W}}^{-1}$. The sensitivity coefficient characterizing the response of a model to variations in the parameter $C_D$ is estimated at around $2\times {10}^{-6}$ ${\mathrm{m}}^2{\mathrm{K}}^2{\mathrm{W}}^{-1}{\mathrm{yr}}^{-1}$. If the uncertainties $\delta C$, $\delta \gamma$ and $\delta C_D$ are given, then we can estimate their effect on the uncertainty in $\Delta T_m$ using these sensitivity coefficients.

Let us assume that all parameter values are known with some degree of uncertainty. Thus, each model parameter $p$ can be expressed in the standard form as $p_0\pm \delta p$, where $p_0$ is the base value of the parameter $p$, and $\delta p$ is the characteristic of the uncertainty range. For the sake of illustration, we consider the case when the uncertainty in each of the parameters is ±10% in relation to its base value, i.e., $p=p_0\pm 0.1p_0$.

Table 2. Absolute $\delta \left(\Delta T_m\right)$ (°C) and relative $\left[\delta \left(\Delta T_m\right)/{\overline{\Delta T}}_m\right]$ (%) uncertainties in model output caused by ±10% uncertainty in model parameters.

Parameter	$\mathit{\lambda } \left(\mathbf{W} {\mathbf{m}}^{\mathbf{-}\mathbf{2}} {\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$	$\mathit{C} \left(\mathbf{W} \mathbf{y}\mathbf{r} {\mathbf{m}}^{\mathbf{-}\mathbf{2}} {\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$	${\mathit{C}}_{\mathit{D}}\left(\mathbf{W} \mathbf{y}\mathbf{r} {\mathbf{m}}^{\mathbf{-}\mathbf{2}} {\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$	$\mathit{\gamma } \left(\mathbf{W} {\mathbf{m}}^{\mathbf{-}\mathbf{2}} {\mathbf{K}}^{\mathbf{-}\mathbf{1}}\right)$
Parameter uncertainty	±0.113	±0.73	±10.60	±0.073
$\delta \left(\Delta T_m\right)$ (°C)	±8.68 × 10−3	±4.97 × 10−2	±2.11 × 10−5	±5.12 × 10−3
$\left[\delta \left(\Delta T_m\right)/{\overline{\Delta T}}_m\right]\times 100\%$	±1.68	±9.62	±0.0041	±0.99

illustrates how the uncertain model parameters affect the uncertainty in model output $\Delta T_m$. In other words, this table shows the effect of parameter uncertainties on variation in the global mean surface temperature anomaly $\delta \left(\Delta T_m\right)$. Analysis of this table suggests that the variations in $\Delta T_m$ caused by uncertainties in the parameters λ and γ are quantities of the same order of magnitude. The influence of uncertainty in the parameter C on variations in $\Delta T_m$ is about one order of magnitude greater than affects caused by $\delta \lambda$ and $\delta \gamma$, whereas the influence of $\delta C_D$ on $\delta \left(\Delta T_m\right)$ is one order of magnitude less than affects due to $\delta \lambda$ and $\delta \gamma$.

The relative uncertainty in the model output $\Delta T_m$ due to the uncertainty in the parameter C is ~6 times as large as the relative uncertainty in $\Delta T_m$ due to the uncertainty in the feedback parameter $\lambda$, while the latter, in turn, is ~1.7 times as large as the relative uncertainty due to the uncertainty in the parameters γ. The uncertainty in deep-ocean heat capacity $C_D$ has a negligible influence on $\delta \left(\Delta T_m\right)$. These results provide some basis to suggest that the parameter C is the most influential model parameter and thus affects $\Delta T_m$ to the greatest extent. Parameters $\lambda$ and γ rank second and third, respectively, followed by the parameter $C_D$. This conclusion is accurate only if the range of uncertainty in all model parameters is given by the same fraction of the corresponding base parameter value (in our particular case we use a 10% uncertainty range). In fact, the range of uncertainty can vary from parameter to parameter. Thus, ranking the model parameters according to their degree of influence on the model output is not such a trivial problem as it might seem, and therefore requires special consideration. However, that important aspect is beyond the scope of our study. This paper seeks to only explore the influence of the uncertainty in radiative feedbacks on the variations in the magnitude of the global mean surface temperature anomaly due to radiative forcing generated by stratospheric aerosols.

4. Conclusions

In this paper, using the two-box EBM with several sets of parameter values that correspond to CMIP5 models, we have examined the effect of uncertainties in radiative feedbacks on the short-term response of the climate system to sharp radiative perturbation due to volcanic aerosols injected into the stratosphere by the 1991 Mount Pinatubo eruption. The impulse response method was applied to determine the globally averaged surface temperature anomalies that result from radiative forcing generated by volcanic stratospheric aerosols. We have considered two idealized forcing scenarios, one is linear and the other is step forcing, to show the computational accuracy of the impulse response technique. The global mean surface temperature anomalies in response to volcanic radiative forcing were estimated by considering 16 sets of EBM parameter values. The obtained quantitative estimates allow for the conclusion that the uncertainty inherent in feedbacks significantly affects the response of the climate system to volcanic aerosol forcing, thereby generating surface temperature uncertainties on short time scales. In addition, the effect of uncertainties in EBM parameters on the uncertainty in global mean surface temperature anomalies was estimated using a sensitivity analysis approach. However, care should be used in interpreting the results obtained, since the modelling framework is simple and idealized to a certain extent. Nevertheless, we expect that our approach and results obtained will be useful in providing a way to explore the effects of radiative feedbacks on the climate system response to external forcing whether of natural or man-made origin.