Atmospheric Pollutant Dispersion over Complex Terrain: Challenges and Needs for Improving Air Quality Measurements and Modeling
Abstract
1. Introduction
2. Atmospheric Processes and Pollutant Dispersion over Complex Terrain
2.1. Temperature Stratification
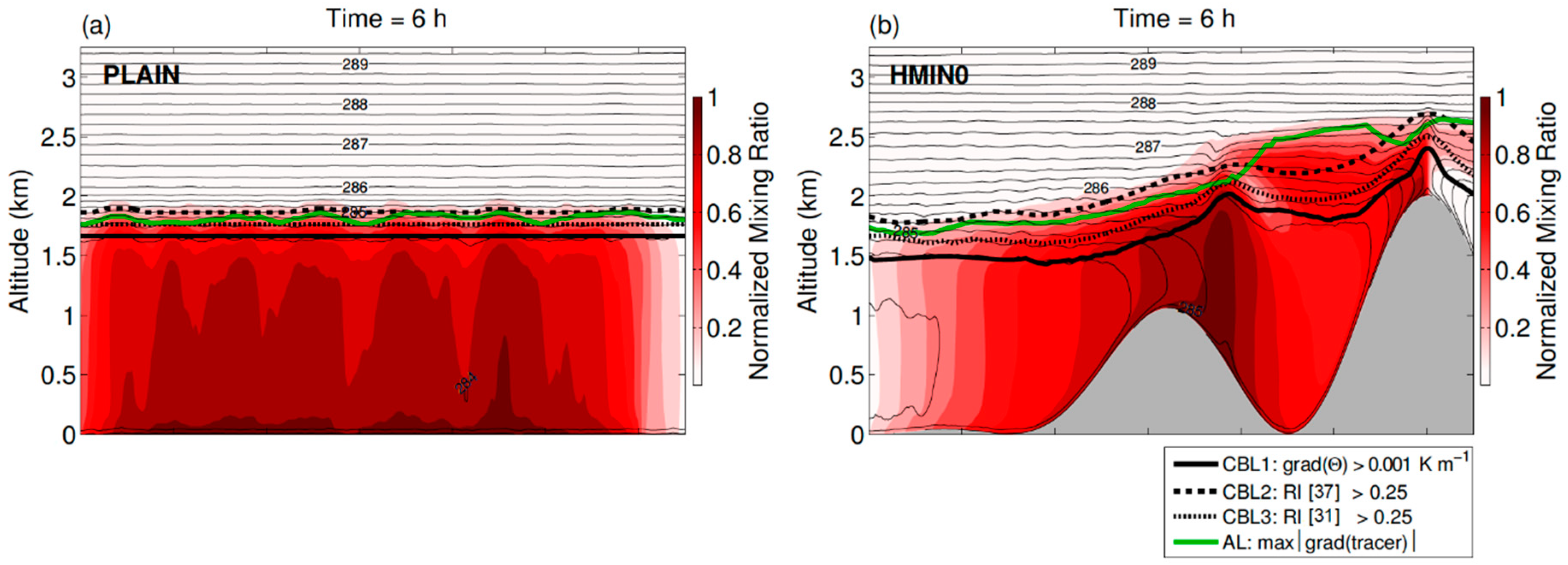
2.2. Mountain Boundary Layer Height
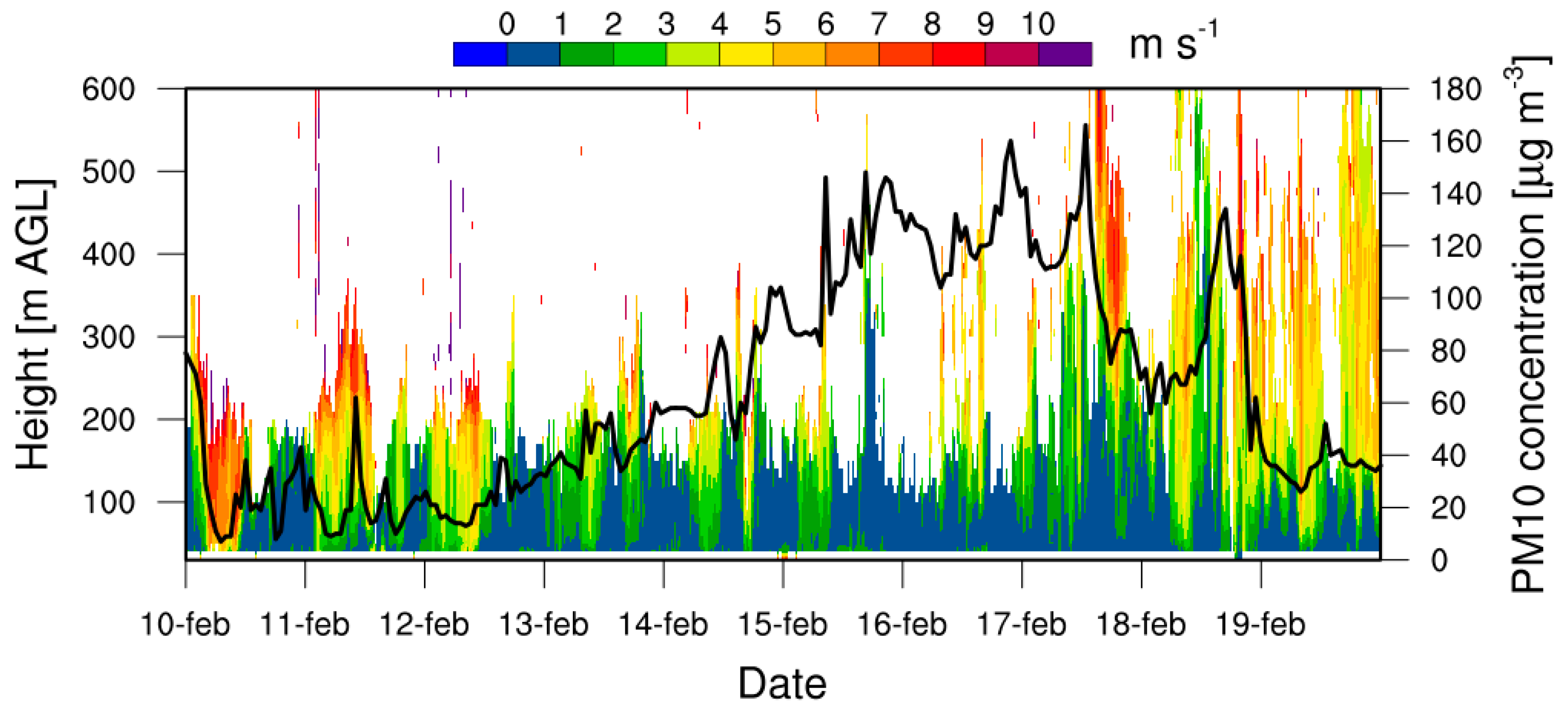
2.3. Strong Synoptic Forcing
2.4. Weak Synoptic Forcing and Thermally Driven Flows
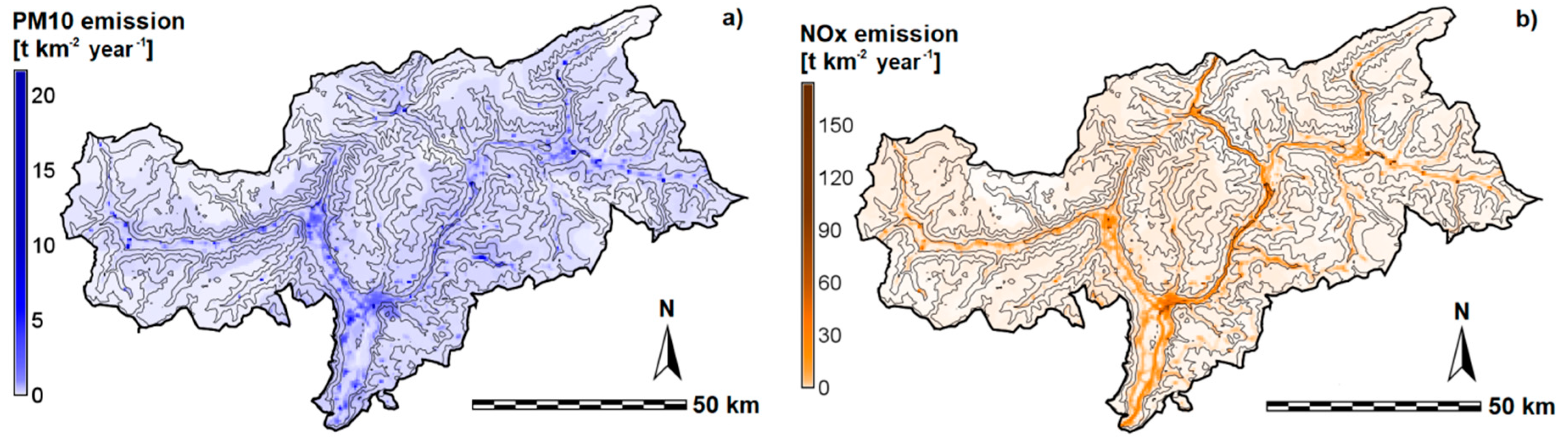
2.5. Urban Areas
3. Observational Techniques Supporting Air Quality Management and Pollutant Dispersion Modeling
3.1. Meteorological Measurements
3.1.1. Point Measurements
3.1.2. Scintillometry
3.1.3. Lidars
3.1.4. Airborne Observations
3.2. Air Quality Measurements
3.2.1. Past Projects
3.2.2. Innovative Measurements
3.2.3. Remote Sensing
4. Meteorological Modeling for Pollutants Dispersion Applications over Complex Terrain
4.1. Meteorological Modeling Resolution
4.2. Turbulence Parameterizations
4.3. Land Surface Parameterizations
4.4. Urban Areas
5. Pollutant Dispersion Modeling over Complex Terrain
5.1. Input Data for Dispersion Models
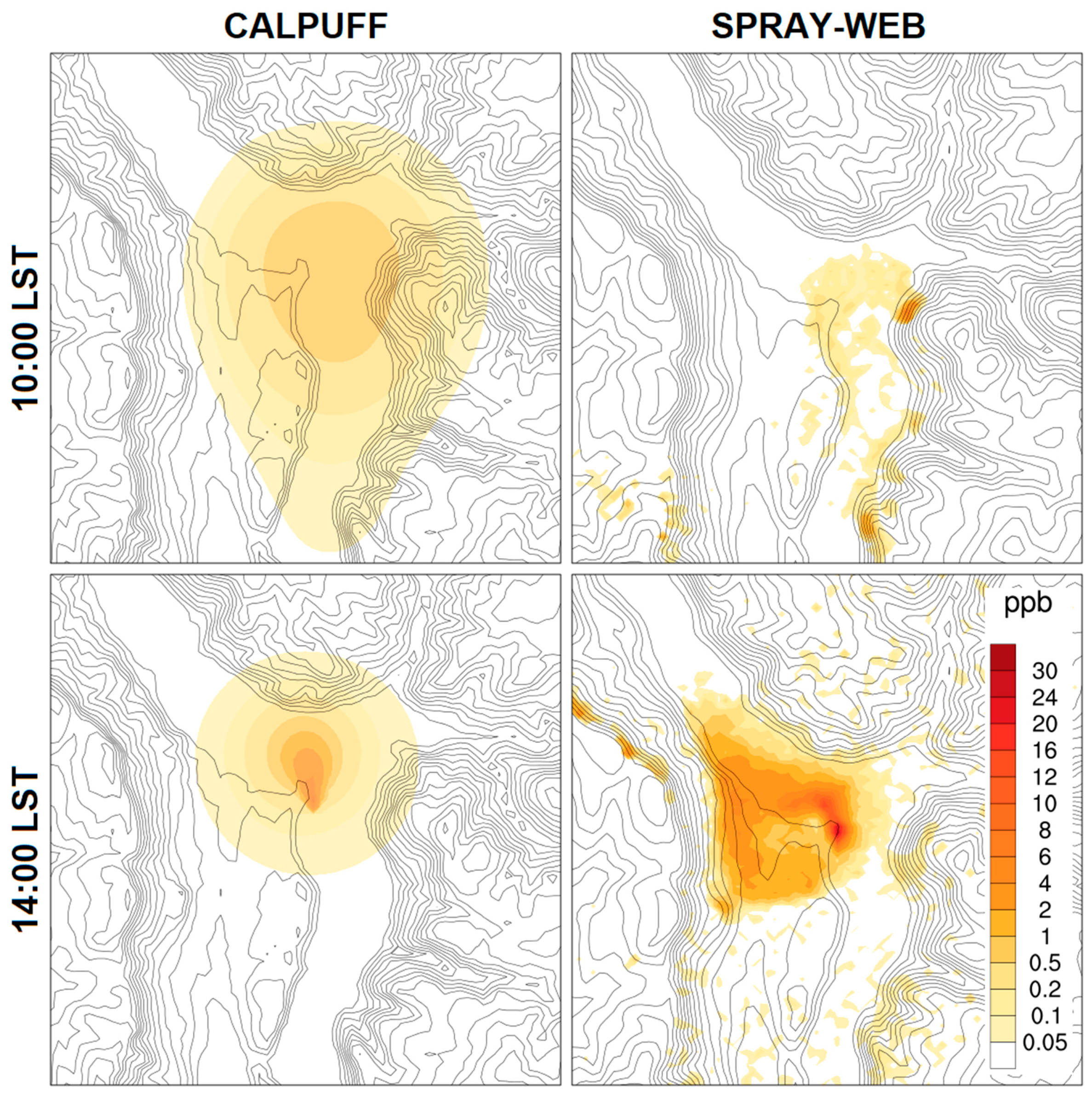
5.2. Eulerian vs. Lagrangian Models
5.3. Small-Scale Features Matter
5.4. Low Wind Speeds and Meandering
5.5. Plume Rise
5.6. Odor Dispersion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Price, M.F.; Byers, A.C.; Friend, D.A.; Kohler, T.; Price, L.W. Mountain Geography Physical and Human Dimensions, 1st ed.; University of California Press: Berkeley, CA, USA, 2013; p. 400. [Google Scholar]
- FAO. Mapping the Vulnerability of Mountain Peoples to Food Insecurity; Food and Agriculture Organization of the United Nations: Rome, Italy, 2015; p. 66. [Google Scholar]
- BAKBASEL. Benchmarking du Tourisme—Le Secteur Suisse du Tourisme en Comparaison Internationale, Report for the SECO Swiss State Secretariat for Economic Affairs; BAK Basel Economics AG: Basel, Switzerland, 2011; p. 112. [Google Scholar]
- Alpine Convention. The Alps. People and Pressures in the Mountains, the Facts at a Glance; Permanent Secretariat of the Alpine Convention: Innsbruck, Austria, 2010; p. 31. ISBN 978-8-89051-582-8. [Google Scholar]
- Cemin, A.; Antonacci, G. Inventario Delle Emissioni in Atmosfera; Environmental Protection Agency Autonomous Province of Bolzano: Bolzano, Italy, 2016; p. 38. [Google Scholar]
- Felzer, B.S.; Cronin, T.; Reilly, J.M.; Melillo, J.M.; Wang, X. Impacts of ozone on trees and crops. Comptes Rendus Geosci. 2007, 339, 784–798. [Google Scholar] [CrossRef]
- Seibert, P.; Kromp-Kolb, H.; Kasper, A.; Kalina, M.; Puxbaum, H.; Jost, D.T.; Schwikowski, M.; Baltensperger, U. Transport of polluted boundary layer air from the Po Valley to high-Alpine sites. Atmos. Environ. 1998, 32, 4075–4085. [Google Scholar] [CrossRef]
- Wotawa, G.; Kröger, H.; Stohl, A. Transport of ozone towards the Alps—Results from trajectory analyses and photochemical model studies. Atmos. Environ. 2000, 34, 1367–1377. [Google Scholar] [CrossRef]
- Diémoz, H.; Barnaba, F.; Magri, T.; Pession, G.; Dionisi, D.; Pittavino, S.; Tombolato, I.K.F.; Campanelli, M.; Ceca, L.S.D.; Hervo, M.; et al. Transport of Po Valley aerosol pollution to the northwestern Alps—Part 1: Phenomenology. Atmos. Chem. Phys. 2019, 19, 3065–3095. [Google Scholar] [CrossRef]
- Heimann, D.; de Franceschi, M.; Emeis, S.; Lercher, P.; Seibert, P. Air Pollution, Traffic Noise and Related Health Effects in the Alpine Space—A Guide for Authorities and Consulters; Department of Civil and Environmental Engineering, University of Trento: Trento, Italy, 2007; p. 335. [Google Scholar]
- de Franceschi, M.; Zardi, D. Study of wintertime high pollution episodes during the Brenner-South ALPNAP measurement campaign. Meteor. Atmos. Phys. 2009, 103, 237–250. [Google Scholar] [CrossRef]
- Trini Castelli, S.; Belfiore, G.; Anfossi, D.; Elampe, E.; Clemente, M. Modelling the meteorology and traffic pollutant dispersion in highly complex terrain: The ALPNAP alpine space project. Int. J. Environ. Pollut. 2011, 44, 235–243. [Google Scholar] [CrossRef]
- Falocchi, M.; Tirler, W.; Giovannini, L.; Tomasi, E.; Antonacci, G.; Zardi, D. A dataset of tracer concentrations and meteorological observations from the Bolzano Tracer EXperiment (BTEX) to characterize pollutant dispersion processes in an Alpine valley. Earth Syst. Sci. Data 2020, 12, 277–291. [Google Scholar] [CrossRef]
- Tomasi, E.; Ferrero, E.; Giovannini, L.; Falocchi, M.; Antonacci, G.; Jimenez, P.; Kosovic, B.; Alessandrini, S.; Zardi, D.; delle Monache, L. Turbulence parameterizations for dispersion in sub-kilometer horizontally non-homogeneous flows. Atmos. Res. 2019, 228, 122–136. [Google Scholar] [CrossRef]
- Lareau, N.P.; Crosman, E.; Whiteman, C.D.; Horel, J.D.; Hoch, S.; Brown, W.; Horst, T.W. The persistent cold-air pool study. Bull. Amer. Meteor. Soc. 2013, 94, 51–63. [Google Scholar] [CrossRef]
- Fiedler, F.; Borrell, P. TRACT: Transport of air pollutants over complex terrain. In Transport and Chemical Transformation of Pollutants in the Troposphere; Borrell, P., Borrell, P.M., Eds.; Springer: Berlin, Germany, 2000; Volume 1, pp. 239–283. [Google Scholar]
- Desiato, F.; Finardi, S.; Brusasca, G.; Morselli, M.G. TRANSALP 1989 experimental campaign-I. Simulation of 3D flow with diagnostic wind field models. Atmos. Environ. 1998, 32, 1141–1156. [Google Scholar] [CrossRef]
- Anfossi, D.; Desiato, F.; Tinarelli, G.; Brusasca, G.; Ferrero, E.; Sacchetti, D. TRANSALP 1989 experimental campaign—II. Simulation of a tracer experiment with Lagrangian particle models. Atmos. Environ. 1998, 32, 1157–1166. [Google Scholar] [CrossRef]
- Wotawa, G.; Kromp-Kolb, H. The research project VOTALP—General objectives and main results. Atmos. Environ. 2000, 34, 1319–1322. [Google Scholar] [CrossRef]
- Doran, J.C.; Fast, J.D.; Horel, J. The VTMX 2000 campaign. Bull. Amer. Meteor. Soc. 2002, 83, 537–554. [Google Scholar] [CrossRef]
- Cava, D.; Schipa, S.; Giostra, U. Investigation of low-frequency perturbations induced by a steep obstacle. Bound. Layer Meteorol. 2005, 115, 27–45. [Google Scholar] [CrossRef]
- Falocchi, M.; Giovannini, L.; de Franceschi, M.; Zardi, D. A method to determine the characteristic time scales of quasi-isotropic surface-layer turbulence over complex terrain: A case study in the Adige Valley (Italian Alps). Q. J. R. Meteorol. Soc. 2019, 145, 495–512. [Google Scholar] [CrossRef]
- Mortarini, L.; Ferrero, E.; Falabino, S.; Trini Castelli, S.; Richiardone, R.; Anfossi, D. Low-frequency processes and turbulence structure in a perturbed boundary-layer. Q. J. R. Meteorol. Soc. 2013, 139, 1059–1072. [Google Scholar] [CrossRef]
- Neff, W.D.; King, C.W. The accumulation and pooling of drainage flows in a large basin. J. Appl. Meteorol. 1989, 28, 518–529. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Bian, X.; Zhong, S. Wintertime evolution of the temperature inversion in the Colorado plateau basin. J. Appl. Meteorol. 1999, 38, 1103–1117. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Zhong, S.; Shaw, W.J.; Hubbe, J.M.; Bian, X.; Mittelstadt, J. Cold pools in the Columbia basin. Weather Forecast. 2001, 16, 432–447. [Google Scholar] [CrossRef]
- Clements, C.B.; Whiteman, C.D.; Horel, J.D. Cold-air-pool structure and evolution in a mountain basin: Peter Sinks, Utah. J. Appl. Meteorol. 2003, 42, 752–768. [Google Scholar] [CrossRef]
- Conangla, L.; Cuxart, J.; Jiménez, M.A.; Martínez-Villagrasa, D.; Miró, J.R.; Tabarelli, D.; Zardi, D. Cold-air pool evolution in a wide Pyrenean valley. Int. J. Climatol. 2018, 38, 2852–2865. [Google Scholar] [CrossRef]
- Quimbayo-Duarte, J.A.; Staquet, C.; Chemel, C.; Arduini, G. Dispersion of tracers in the stable atmosphere of a valley opening on a plain. Bound. Layer Meteorol. 2019, 172, 291–315. [Google Scholar] [CrossRef]
- Lehner, M.; Rotach, M.W. Current challenges in understanding and predicting transport and exchange in the atmosphere over mountainous terrain. Atmosphere 2018, 9, 276. [Google Scholar] [CrossRef]
- Seibert, P.; Beyrich, F.; Gryning, S.-E.; Joffre, S.; Rasmussen, A.; Tercier, P. Review and intercomparison of operational methods for the determination of the mixing height. Atmos. Environ. 2000, 34, 1001–1027. [Google Scholar] [CrossRef]
- de Wekker, S.F.J.; Kossmann, M. Convective boundary layer heights over mountainous terrain—A review of concepts. Front. Earth Sci. 2015, 3, 77. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Allwine, K.J.; Fritschen, L.J.; Orgill, M.M.; Simpson, J.R. Deep valley radiation and surface energy budget microclimates. Part I: Radiation. J. Appl. Meteorol. 1989, 28, 414–426. [Google Scholar] [CrossRef]
- Rotach, M.W.; Andretta, M.; Calanca, P.; Weigel, A.P.; Weiss, A. Boundary layer characteristics and turbulent exchange mechanisms in highly complex terrain. Acta Geophys. 2008, 56, 194–219. [Google Scholar] [CrossRef]
- Lang, M.N.; Gohm, A.; Wagner, J.S. The impact of embedded valleys on daytime pollution transport over a mountain range. Atmos. Chem. Phys. 2015, 15, 11981–11998. [Google Scholar] [CrossRef]
- Arduini, G.; Chemel, C.; Staquet, C. Local and non-local controls of a persistent cold-air pool in the Arve River valley. Q. J. R. Meteorol. Soc. 2020. [Google Scholar] [CrossRef]
- Vogelezang, D.H.P.; Holtslag, A.A.M. Evaluation and model impacts of alternative boundary-layer height formulations. Bound. Layer Meteorol. 1996, 81, 245–269. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Doran, J.C. The relationship between overlying synoptic-scale flows and winds within a valley. J. Appl. Meteorol. 1993, 32, 1669–1682. [Google Scholar] [CrossRef]
- Mayr, G.J.; Armi, L. The influence of downstream diurnal heating on the descent of flow across the Sierras. J. Appl. Meteorol. Climatol. 2010, 49, 1906–1912. [Google Scholar] [CrossRef]
- Zardi, D.; Whiteman, D. Diurnal mountain wind systems. In Mountain Weather Research and Forecasting: Recent Progress and Current Challenges; Chow, F., de Wekker, S., Snyder, B., Eds.; Springer Atmospheric Sciences: Dordrecht, The Netherlands, 2013; pp. 35–119. [Google Scholar]
- Serafin, S.; Adler, B.; Cuxart, J.; De Wekker, S.F.J.; Gohm, A.; Grisogono, B.; Kalthoff, N.; Kirshbaum, D.; Rotach, M.; Schmidli, J.; et al. Exchange processes in the atmospheric boundary layer over mountainous terrain. Atmosphere 2018, 9, 102. [Google Scholar] [CrossRef]
- Barbante, C.; Boutron, C.; Moreau, A.-L.; Ferrari, C.; van de Velde, K.; Cozzi, G.; Turettab, C.; Cesconab, P. Seasonal variations in nickel and vanadium in Mont Blanc snow and ice dated from the 1960s and 1990s. J. Environ. Monit. 2002, 4, 960–966. [Google Scholar] [CrossRef] [PubMed]
- Leukauf, D.; Gohm, A.; Rotach, M.W.; Wagner, J.S. The impact of the temperature inversion breakup on the exchange of heat and mass in an idealized valley: Sensitivity to the radiative forcing. J. Appl. Meteorol. Climatol. 2015, 54, 2199–2216. [Google Scholar] [CrossRef]
- Whiteman, C.D. Mountain Meteorology: Fundamentals and Applications; Oxford University Press: New York, NY, USA, 2000; p. 368. [Google Scholar]
- Vergeiner, I.; Dreiseitl, E. Valley winds and slope winds—Observations and elementary thoughts. Meteorol. Atmos. Phys. 1987, 36, 264–286. [Google Scholar] [CrossRef]
- Largeron, Y.; Staquet, C. The atmospheric boundary layer during wintertime persistent inversions in the Grenoble valleys. Front Earth Sci. 2016, 4, 70. [Google Scholar] [CrossRef]
- Sabatier, T.; Paci, A.; Canut, G.; Largeron, Y.; Dabas, A.; Donier, J.-M.; Douffet, T. Wintertime local wind dynamics from scanning Doppler Lidar and air quality in the Arve river valley. Atmosphere 2018, 9, 118. [Google Scholar] [CrossRef]
- Chemel, C.; Arduini, G.; Staquet, C.; Largeron, Y.; Legain, D.; Tzanos, D.; Paci, A. Valley heat deficit as a bulk measure of wintertime particulate air pollution in the Arve River Valley. Atmos. Environ. 2016, 128, 208–215. [Google Scholar] [CrossRef]
- Mortarini, L.; Stefanello, M.; Degrazia, G.; Roberti, D.; Trini Castelli, S.; Anfossi, D. Characterization of wind meandering in low-wind speed conditions. Bound. Layer Meteorol. 2016, 161, 165–182. [Google Scholar] [CrossRef]
- Allwine, K.J.; Whiteman, C.D. Ventilation of pollutants trapped in valleys: A simple parameterization for regional-scale dispersion models. Atmos. Environ. 1988, 22, 1839–1845. [Google Scholar] [CrossRef]
- Quimbayo-Duarte, J.A.; Staquet, C.; Chemel, C.; Arduini, G. Impact of along-valley orographic variations on the dispersion of passive tracers in a stable atmosphere. Atmosphere 2019, 10, 225. [Google Scholar] [CrossRef]
- Gohm, A.; Harnisch, F.; Vergeiner, J.; Obleitner, F.; Schnitzhofer, R.; Hansel, A.; Fix, A.; Neininger, B.; Emeis, S.; Schäfer, K. Air pollution transport in an Alpine valley: Results from airborne and ground-based observations. Bound. Layer Meteorol. 2009, 131, 441–463. [Google Scholar] [CrossRef]
- Silcox, G.D.; Kelly, K.E.; Crosman, E.T.; Whiteman, C.D.; Allen, B.L. Wintertime PM2.5 concentrations during persistent, multi-day cold-air pools in a mountain valley. Atmos. Environ. 2012, 46, 17–24. [Google Scholar] [CrossRef]
- Largeron, Y.; Staquet, C. Persistent inversion dynamics and wintertime PM10 air pollution in Alpine valleys. Atmos. Environ. 2016, 135, 92–108. [Google Scholar] [CrossRef]
- Whiteman, C.D.; McKee, T.B. Breakup of temperature inversions in deep mountain valleys: Part II. Thermodynamic model. J. Appl. Meteorol. 1982, 21, 290–302. [Google Scholar] [CrossRef]
- Renfrew, I.A. The dynamics of idealized katabatic flow over a moderate slope and ice shelf. Q. J. R. Meteorol. Soc. 2004, 130, 1023–1045. [Google Scholar] [CrossRef]
- Largeron, Y.; Staquet, C.; Chemel, C. Characterization of oscillatory motions in the stable atmosphere of a deep valley. Bound. Layer Meteorol. 2013, 148, 439–454. [Google Scholar] [CrossRef]
- Weissmann, M.; Braun, F.; Gantner, L.; Mayr, G.; Rham, S.; Reitebuch, O. The Alpine mountain-plain circulation: Airborne Doppler lidar measurements and numerical simulations. Mon. Weather Rev. 2005, 133, 3095–3109. [Google Scholar] [CrossRef]
- Kossmann, M.; Corsmeier, U.; de Wekker, S.F.J.; Fiedler, F.; Vögtlin, S.; Kalthoff, N.; Güsten, H.; Neininger, B. Observations of handover processes between the atmospheric boundary layer and the free troposphere over mountainous terrain. Contrib. Atmos. Phys. 1999, 72, 329–350. [Google Scholar]
- Henne, S.; Furger, M.; Nyeki, S.; Steinbacher, M.; Neininger, B.; de Wekker, S.F.J.; Dommen, J.; Spichtinger, N.; Stohl, A.; Prévôt, A.S.H. Quantification of topographic venting of boundary layer air to the free troposphere. Atmos. Chem. Phys. 2004, 4, 497–509. [Google Scholar] [CrossRef]
- Henne, S.; Dommen, J.; Neininger, B.; Reimann, S.; Staehelin, J.; Prévôt, A.S.H. Influence of mountain venting in the Alps on the ozone chemistry of the lower free troposphere and the European pollution export. J. Geophys. Res. Atmos. 2005, 110, D22307. [Google Scholar] [CrossRef]
- Ahmadov, R.; McKeen, S.; Trainer, M.; Banta, R.; Brewer, A.; Brown, S.; Edwards, P.M.; de Gouw, J.A.; Frost, G.J.; Gilman, J.; et al. Understanding high wintertime ozone pollution events in an oil- and natural gas-producing region of the western US. Atmos. Chem. Phys. 2015, 15, 411–429. [Google Scholar] [CrossRef]
- Neemann, E.M.; Crosman, E.T.; Horel, J.D.; Avey, L. Simulations of a cold-air pool associated with elevated wintertime ozone in the Uintah Basin, Utah. Atmos. Chem. Phys. 2015, 15, 135–151. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M. Analysis of the urban thermal fingerprint of the city of Trento in the Alps. J. Appl. Meteorol. Climatol. 2011, 50, 1145–1162. [Google Scholar] [CrossRef]
- Hidalgo, J.; Pigeon, G.; Masson, V. Urban-breeze circulation during the CAPITOUL experiment: Experimental data analysis approach. Meteorol. Atmos. Phys. 2008, 102, 223–241. [Google Scholar] [CrossRef]
- Giovannini, L.; Laiti, L.; Serafin, S.; Zardi, D. The thermally driven diurnal wind system of the Adige Valley in the Italian Alps. Q. J. R. Meteorol. Soc. 2017, 143, 2389–2402. [Google Scholar] [CrossRef]
- Kossmann, M.; Sturman, A. The surface wind field during winter smog nights in Christchurch and coastal Canterbury, New Zealand. Int. J. Climatol. 2004, 24, 93–108. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates, 2nd ed.; Routledge: London, UK, 1987; p. 435. [Google Scholar]
- Kuttler, W.; Dutemeyer, D.; Barlag, A.-B. Influence of regional and local winds on urban ventilation in Cologne, Germany. Meteor. Z. 1998, 7, 77–87. [Google Scholar] [CrossRef]
- Piringer, M.; Baumann, K. Modifications of a valley wind system by an urban area—Experimental results. Meteorol. Atmos. Phys. 1989, 71, 117–125. [Google Scholar] [CrossRef]
- Salamanca, F.; Martilli, A.; Yague, C. A numerical study of the urban heat island over Madrid during the DESIREX (2008) field campaign with WRF and an evaluation of simple mitigation strategies. Int. J. Climatol. 2012, 32, 2372–2386. [Google Scholar] [CrossRef]
- Giovannini, L.; Zardi, D.; de Franceschi, M.; Chen, F. Numerical simulations of boundary-layer processes and urban-induced alterations in an Alpine valley. Int. J. Climatol. 2014, 34, 1111–1131. [Google Scholar] [CrossRef]
- Rendón, A.M.; Salazar, J.F.; Palacio, C.A. Effects of urbanization on the temperature inversion breakup in a mountain valley with implications for air quality. J. Appl. Meteorol. Climatol. 2014, 53, 840–858. [Google Scholar]
- Rendón, A.M.; Salazar, J.F.; Wirth, V. Daytime air pollution transport mechanisms in stable atmospheres of narrow versus wide urban valleys. Environ. Fluid Mech. 2020. [Google Scholar] [CrossRef]
- Durán, L.; Rodríguez-Muñoz, I.; Sánchez, E. The Peñalara mountain meteorological network (1999–2014): Description, preliminary results and lessons learned. Atmosphere 2017, 8, 203. [Google Scholar] [CrossRef]
- Clements, W.E.; Archuleta, J.A.; Gudiksen, P.H. Experimental design for the 1984 ASCOT field study. J. Appl. Meteorol. 1989, 28, 405–413. [Google Scholar] [CrossRef]
- Lothon, M.; Lohou, F.; Pino, D.; Couvreux, F.; Pardyjak, E.R.; Reuder, J.; de Arellano, J.V.-G.; Durand, P.; Hartogensis, O.; Legain, D.; et al. The BLLAST field experiment: Boundary-layer late afternoon and sunset turbulence. Atmos. Chem. Phys. 2014, 14, 10931–10960. [Google Scholar] [CrossRef]
- Wulfmeyer, V.; Behrendt, A.; Bauer, H.-S.; Kottmeier, C.; Corsmeier, U.; Blyth, A.; Craig, G.; Schumann, U.; Hagen, M.; Crewell, S.; et al. The convective and orographically-induced precipitation study: A research and development project of the world weather research program for improving quantitative precipitation forecasting in low-mountain regions. Bull. Amer. Meteor. Soc. 2008, 89, 1477–1486. [Google Scholar]
- Rotach, M.W.; Calanca, P.; Graziani, G.; Gurtz, J.; Steyn, D.G.; Vogt, R.; Andretta, M.; Christen, A.; Cieslik, S.; Connolly, R.; et al. Turbulence structure and exchange processes in an Alpine Valley: The Riviera project. Bull. Amer. Meteor. Soc. 2004, 85, 1367–1385. [Google Scholar] [CrossRef]
- Fernando, H.J.S.; Pardyjak, E.; Di Sabatino, S.; Chow, F.K.; de Wekker, S.F.J.; Hoch, S.W.; Hacker, J.; Pace, J.C.; Pratt, T.; Pu, Z.; et al. The MATERHORN: Unraveling the intricacies of mountain weather. Bull. Amer. Meteor. Soc. 2015, 96, 1945–1967. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Muschinski, A.; Zhong, S.; Fritts, D.; Hoch, S.W.; Hahnenberger, M.; Yao, W.; Hohreiter, V.; Behn, M.; Cheon, Y.; et al. Metcrax 2006: Meteorological experiments in arizona’s meteor crater. Bull. Amer. Meteor. Soc. 2008, 98, 1665–1680. [Google Scholar] [CrossRef]
- Lehner, M.; Whiteman, C.D.; Hoch, S.W.; Crosman, E.T.; Jeglum, M.E.; Cherukuru, N.W.; Calhoun, R.; Adler, B.; Kalthoff, N.; Rotunno, R.; et al. The metcrax II experiment. Bull. Amer. Meteor. Soc. 2016, 97, 217–235. [Google Scholar] [CrossRef]
- Grubišić, V.; Doyle, J.; Kuettner, J.; Mobbs, S.; Smith, R.B.; Whiteman, C.D.; Dirks, R.; Czyzyk, S.; Cohn, S.A.; Vosper, S.; et al. The terrain-induced rotor experiment. Bull. Amer. Meteor. Soc. 2008, 89, 1513–1533. [Google Scholar] [CrossRef]
- Rotach, M.W.; Zardi, D. On the boundary-layer structure over highly complex terrain: Key findings from MAP. Q. J. R. Meteorol. Soc. 2007, 133, 937–948. [Google Scholar] [CrossRef]
- Baldocchi, D.; Falge, E.; Gu, L.; Olson, R.; Hollinger, D.; Running, S.; Anthoni, P.; Bernhofer, C.; Davis, K.; Evans, R.; et al. FLUXNET: A new tool to study the temporal and spatial variability of ecosystem-scale carbon dioxide, water vapor, and energy flux densities. Bull. Amer. Meteor. Soc. 2001, 82, 2415–2434. [Google Scholar] [CrossRef]
- Zielis, S.; Etzold, S.; Zweifel, R.; Eugster, W.; Haeni, M.; Buchmann, N. NEP of a Swiss subalpine forest is significantly driven not only by current but also by previous year’s weather. Biogeosciences 2014, 11, 1627–1635. [Google Scholar] [CrossRef]
- Montagnani, L.; Manca, G.; Canepa, E.; Georgieva, E.; Acosta, M.; Feigenwinter, C.; Janous, D.; Kerschbaumer, G.; Lindroth, A.; Minach, L.; et al. A new mass conservation approach to the study of CO2 advection in an alpine forest. J. Geophys. Res. Atmos. 2009, 114, D07306. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B. Drag coefficient and turbulence intensity in conifer canopies. Agric. For. Meteorol. 2004, 121, 197–206. [Google Scholar] [CrossRef]
- Pullens, J.W.M.; Sottocornola, M.; Kiely, G.; Toscano, P.; Gianelle, D. Carbon fluxes of an alpine peatland in Northern Italy. Agric. For. Meteorol. 2016, 220, 69–82. [Google Scholar] [CrossRef]
- Hörtnagl, L.; Wohlfahrt, G. Methane and nitrous oxide exchange over a managed hay meadow. Biogeosciences 2014, 11, 7219–7236. [Google Scholar] [CrossRef]
- Rotach, M.W.; Stiperski, I.; Fuhrer, O.; Goger, B.; Gohm, A.; Obleitner, F.; Rau, G.; Sfyri, E.; Vergeiner, J. Investigating exchange processes over complex topography: The Innsbruck-Box (i-Box). Bull. Amer. Meteor. Soc. 2017, 98, 787–805. [Google Scholar] [CrossRef]
- Stiperski, I.; Rotach, M.W. On the measurement of turbulent fluxes over complex mountainous topography. Bound. Layer Meteorol. 2016, 159, 97–121. [Google Scholar] [CrossRef]
- De Franceschi, M.; Zardi, D.; Tagliazucca, M.; Tampieri, F. Analysis of second order moments in the surface layer turbulence in an Alpine valley. Q. J. R. Meteorol. Soc. 2009, 135, 1750–1765. [Google Scholar] [CrossRef]
- Richiardone, R.; Giampiccolo, R.; Ferrarese, S.; Manfrin, M. Detection of flow distortion and systematic errors in sonic anemometry using the planar fit method. Bound. Layer Meteorol. 2008, 128, 277–302. [Google Scholar] [CrossRef]
- Oldroyd, H.J.; Pardyjak, E.R.; Huwald, H.; Parlange, M.B. Adapting tilt corrections and the governing flow equations for steep, fully three-dimensional, mountainous terrain. Bound. Layer Meteorol. 2016, 159, 539–565. [Google Scholar] [CrossRef]
- Oldroyd, H.J.; Pardyjak, E.R.; Huwald, H.; Parlange, M.B. Buoyant turbulent kinetic energy production in steep-slope katabatic flow. Bound. Layer Meteorol. 2016, 161, 405–416. [Google Scholar] [CrossRef]
- Weiss, A. Determination of Stratification and Turbulence of the Atmospheric Surface Layer for Different Types of Terrain by Optical Scintillometry. Ph.D. Thesis, Swiss Federal Institute of Technology, Zurich, Switzerland, 2002. [Google Scholar]
- Weiss, A.; Hennes, M.; Rotach, M.W. Derivation of refractive index- and temperature gradients from optical scintillometry for the correction of atmospheric induced problems in highly precise geodetic measurements. Surv. Geophys. 2001, 22, 589–596. [Google Scholar] [CrossRef]
- Pianezze, J. Modélisation de la Structure Verticale de la Turbulence Optique en Milieu Naturel. Ph.D. Thesis, Université Joseph Fourier, Grenoble, France, 2013. [Google Scholar]
- Ward, H.C. Scintillometry in urban and complex environments: A review. Meas. Sci. Technol. 2017, 28, 064005. [Google Scholar] [CrossRef]
- Hartogensis, O.K.; Watts, C.J.; Rodriguez, J.-C.; de Bruin, H.A.R. Derivation of an effective height for scintillometers: La Poza experiment in northwest Mexico. J. Hydrometeorol. 2003, 4, 915–928. [Google Scholar] [CrossRef]
- Di Girolamo, P.; Cacciani, M.; Summa, D.; Scoccione, A.; De Rosa, B.; Behrendt, A.; Wulfmeyer, V. Characterisation of boundary layer turbulent processes by the Raman lidar BASIL in the frame of HD(CP)(2) observational prototype experiment. Atmos. Chem. Phys. 2017, 17, 745–767. [Google Scholar] [CrossRef]
- Whiteman, C.D.; Lehner, M.; Hoch, S.W.; Adler, B.; Kalthoff, N.; Haiden, T. Katabatically driven cold air intrusions into a basin atmosphere. J. Appl. Meteorol. Climatol. 2018, 57, 435–455. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J.; Gottschall, J.; Courtney, M.S. Can wind lidars measure turbulence? J. Atmos. Ocean. Technol. 2011, 28, 853–868. [Google Scholar] [CrossRef]
- Bonin, T.A.; Choukulkar, A.; Brewer, W.A.; Sandberg, S.P.; Weickmann, A.M.; Pichugina, Y.L.; Banta, R.M.; Oncley, S.P.; Wolfe, D.E. Evaluation of turbulence measurement techniques from a single Doppler lidar. Atmos. Meas. Tech. 2017, 10, 3021–3039. [Google Scholar] [CrossRef]
- Chan, P.W. Atmospheric turbulence in complex terrain: Verifying numerical model results with observations by remote-sensing instruments. Meteorol. Atmos. Phys. 2009, 103, 145–157. [Google Scholar] [CrossRef]
- Adler, B.; Kalthoff, N. The impact of upstream flow on the atmospheric boundary layer in a valley on a mountainous island. Bound. Layer Metetorol. 2016, 158, 429–452. [Google Scholar] [CrossRef]
- Wildmann, N.; Bodini, N.; Lundquist, J.K.; Bariteau, L.; Wagner, J. Estimation of turbulence dissipation rate from Doppler wind lidars and in situ instrumentation for the Perdigão 2017 campaign. Atmos. Meas. Tech. 2019, 12, 6401–6423. [Google Scholar] [CrossRef]
- Haid, M.; Gohm, A.; Umek, L.; Ward, H.C.; Lehner, L.; Muschinski, T.; Rotach, M.W. Bestimmung der räumlichen verteilung turbulenter größen in komplexem gelände mit mehreren doppler wind lidaren (determination of the spatial distribution of turbulent characteristics in complex topography using several Doppler lidars). In Proceedings of the DACH, Garmisch-Partenkirchen, Germany, 18–22 March 2019. [Google Scholar]
- Adler, B.; Kalthoff, N. Multi-scale transport processes observed in the boundary layer over a mountainous island. Bound. Layer Metetorol. 2014, 153, 515–537. [Google Scholar] [CrossRef]
- De Franceschi, M.; Rampanelli, G.; Sguerso, D.; Zardi, D.; Zatelli, P. Development of a measurement platform on a light airplane and analysis of airborne measurements in the atmospheric boundary layer. Ann. Geophys. 2003, 46, 269–283. [Google Scholar]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G. Residual kriging analysis of airborne measurements: Application to the mapping of atmospheric boundary-layer thermal structures in a mountain valley. Atmos. Sci. Lett. 2013, 14, 79–85. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; de Franceschi, M.; Rampanelli, G. Atmospheric boundary layer structures associated with the Ora del Garda wind in the Alps as revealed from airborne and surface measurements. Atmos. Res. 2013, 132–133, 473–489. [Google Scholar] [CrossRef]
- Laiti, L.; Zardi, D.; Giovannini, L.; de Franceschi, M.; Rampanelli, G. Analysis of the diurnal development of a lake-valley circulation in the Alps based on airborne and surface measurements. Atmos. Chem. Phys. 2014, 14, 9771–9786. [Google Scholar] [CrossRef]
- Vecenaj, Z.; Belusic, D.; Grubisic, V.; Grisogono, B. Along-coast features of Bora-related turbulence. Bound. Layer Meteorol. 2012, 143, 527–545. [Google Scholar] [CrossRef]
- Strauss, L.; Serafin, S.; Haimov, S.; Grubišić, V. Turbulence in breaking mountain waves and atmospheric rotors estimated from airborne in situ and Doppler radar measurements. Q. J. R. Meteorol. Soc. 2015, 141, 3207–3225. [Google Scholar] [CrossRef] [PubMed]
- Weigel, A.P.; Chow, F.K.; Rotach, M.W. On the nature of turbulent kinetic energy in a steep and narrow Alpine valley. Bound. Layer Meteorol. 2007, 123, 177–199. [Google Scholar] [CrossRef]
- Mauder, M.; Desjardins, R.L.; MacPherson, I. Scale analysis of airborne flux measurements over heterogeneous terrain in a boreal ecosystem. J. Geophys. Res. Atmos. 2007, 112, D13112. [Google Scholar] [CrossRef]
- Baur, F. Determination of Turbulent Fluxes of Airborne Data in Complex Terrain Using Wavelet Analysis. Master’s Thesis, University of Innsbruck, Innsbruck, Austria, 2015. [Google Scholar]
- Elston, J.; Argrow, B.; Stachura, M.; Weibel, D.; Lawrence, D.; Pope, D. Overview of small fixed-wing unmanned aircraft for meteorological sampling. J. Atmos. Ocean. Technol. 2015, 32, 97–115. [Google Scholar] [CrossRef]
- Calmer, R.; Roberts, G.C.; Preissler, J.; Sanchez, K.J.; Derrien, S.; O’Dowd, C. Vertical wind velocity measurements using a five-hole probe with remotely piloted aircraft to study aerosol–cloud interactions. Atmos. Meas. Tech. 2018, 11, 2583–2599. [Google Scholar] [CrossRef]
- Subramanian, B.; Chokani, N.; Abhari, R.S. Drone-based experimental investigation of three-dimensional flow structure of a multi-megawatt wind turbine in complex terrain. J. Sol. Energy Eng. 2015, 137, 051007. [Google Scholar] [CrossRef]
- European Topic Centre on Air Pollution and Climate Change Mitigation. Available online: https://acm.eionet.europa.eu/databases/airbase (accessed on 2 January 2019).
- Im, U.; Bianconi, R.; Solazzo, E.; Kioutsioukis, I.; Badia, A.; Balzarini, A.; Baro, R.; Bellasio, R.; Brunner, D.; Chemel, C.; et al. Evaluation of operational on-line-coupled regional air quality models over Europe and North America in the context of AQMEII phase 2. Part I: Ozone. Atmos. Environ. 2015, 115, 404–420. [Google Scholar] [CrossRef]
- Schultz, M.G.; Akimoto, H.; Bottenheim, J.; Buchmann, B.; Galbally, I.E.; Gilge, S.; Helmig, D.; Koide, H.; Lewis, A.C.; Novelli, P.C.; et al. The global atmosphere watch reactive gases measurement network. Elementa Sci. Anthrop. 2015, 3. [Google Scholar] [CrossRef]
- World Meteorological Organization. WMO Global Atmosphere Watch (GAW) Implementation Plan: 2016–2023; World Meteorological Organization: Geneva, Switzerland, 2017; p. 75. [Google Scholar]
- Cristofanelli, P.; Brattich, E.; Decesari, S.; Landi, T.C.; Maione, M.; Putero, D.; Tositti, L.; Bonasoni, P. High-Mountain Atmospheric Research—The Italian Mt. Cimone WMO/GAW Global Station (2165 m a.s.l.); Springer International Publishing: Cham, Switzerland, 2018; p. 135. [Google Scholar]
- Brattich, E.; Liu, H.; Tositti, L.; Considine, D.B.; Crawford, J.H. Processes controlling the seasonal variations in 210Pb and 7Be at the Mt. Cimone WMO-GAW global station, Italy: A model analysis. Atmos. Chem. Phys. 2017, 17, 1061–1080. [Google Scholar] [CrossRef]
- Holzinger, R.; Kasper-Giebl, A.; Staudinger, M.; Schauer, G.; Rockmann, T. Analysis of the chemical composition of organic aerosol at the Mt. Sonnblick observatory using a novel high mass resolution thermal-desorption proton-transfer-reaction mass-spectrometer (hr-TD-PTR-MS). Atmos. Chem. Phys. 2010, 10, 10111–10128. [Google Scholar] [CrossRef]
- Karl, T.; Fall, R.; Crutzen, P.J.; Jordan, A.; Lindinger, W. High concentrations of reactive biogenic VOCs at a high altitude site in late autumn. Geophys. Res. Lett. 2001, 28, 507–510. [Google Scholar] [CrossRef]
- Bianchi, F.; Trostl, J.; Junninen, H.; Frege, C.; Henne, S.; Hoyle, C.R.; Molteni, U.; Herrmann, E.; Adamov, A.; Bukowiecki, N.; et al. New particle formation in the free troposphere: A question of chemistry and timing. Science 2016, 352, 1109–1112. [Google Scholar] [CrossRef] [PubMed]
- Rohrer, F.; Berresheim, H. Strong correlation between levels of tropospheric hydroxyl radicals and solar ultraviolet radiation. Nature 2006, 442, 184–187. [Google Scholar] [CrossRef] [PubMed]
- Deolal, S.P.; Henne, S.; Ries, L.; Gilge, S.; Weers, U.; Steinbacher, M.; Staehelin, J.; Peter, T. Analysis of elevated springtime levels of Peroxyacetyl nitrate (PAN) at the high Alpine research sites Jungfraujoch and Zugspitze. Atmos. Chem. Phys. 2014, 14, 12553–12571. [Google Scholar] [CrossRef]
- Wagner, A.; Blechschmidt, A.M.; Bouarar, I.; Brunke, E.G.; Clerbaux, C.; Cupeiro, M.; Cristofanelli, P.; Eskes, H.; Flemming, J.; Flentje, H.; et al. Evaluation of the MACC operational forecast system—Potential and challenges of global near-real-time modelling with respect to reactive gases in the troposphere. Atmos. Chem. Phys. 2015, 15, 14005–14030. [Google Scholar] [CrossRef]
- Molina, L.T.; Madronich, S.; Gaffney, J.S.; Apel, E.; de Foy, B.; Fast, J.; Ferrare, R.; Herndon, S.; Jimenez, J.L.; Lamb, B.; et al. An overview of the MILAGRO 2006 Campaign: Mexico City emissions and their transport and transformation. Atmos. Chem. Phys. 2010, 10, 8697–8760. [Google Scholar] [CrossRef]
- Wilczak, J.M.; Glendening, J.W. Observations and mixed-layer modeling of a terrain-induced mesoscale gyre: The Denver cyclone. Mon. Weather Rev. 1988, 116, 2688–2711. [Google Scholar] [CrossRef][Green Version]
- Vu, K.T.; Dingle, J.H.; Bahreini, R.; Reddy, P.J.; Apel, E.C.; Campos, T.L.; DiGangi, J.P.; Diskin, G.S.; Fried, A.; Herndon, S.C.; et al. Impacts of the Denver Cyclone on regional air quality and aerosol formation in the Colorado Front Range during FRAPPÉ 2014. Atmos. Chem. Phys. 2016, 16, 12039–12058. [Google Scholar] [CrossRef]
- Baier, B.C.; Brune, W.H.; Miller, D.O.; Blake, D.; Long, R.; Wisthaler, A.; Cantrell, C.; Fried, A.; Heikes, B.; Brown, S.; et al. Higher measured than modeled ozone production at increased NOx levels in the Colorado Front Range. Atmos. Chem. Phys. 2017, 17, 11273–11292. [Google Scholar] [CrossRef]
- Ortega, J.; Turnipseed, A.; Guenther, A.B.; Karl, T.G.; Day, D.A.; Gochis, D.; Huffman, J.A.; Prenni, A.J.; Levin, E.J.T.; Kreidenweis, S.M.; et al. Overview of the manitou experimental forest observatory: Site description and selected science results from 2008 to 2013. Atmos. Chem. Phys. 2014, 14, 6345–6367. [Google Scholar] [CrossRef]
- Hunter, J.F.; Day, D.A.; Palm, B.B.; Yatavelli, R.L.N.; Chan, A.W.H.; Kaser, L.; Cappellin, L.; Hayes, P.L.; Cross, E.S.; Carrasquillo, A.J.; et al. Comprehensive characterization of atmospheric organic carbon at a forested site. Nat. Geosci. 2017, 10, 748–753. [Google Scholar] [CrossRef]
- Baltensperger, U.; Streit, N.; Weingartner, E.; Nyeki, S.; Prevot, A.S.H.; van Dingenen, R.; Virkkula, A.; Putaud, J.P.; Even, A.; ten Brink, H.; et al. Urban and rural aerosol characterization of summer smog events during the PIPAPO field campaign in Milan, Italy. J. Geophys. Res. Atmos. 2002, 107, 8193. [Google Scholar] [CrossRef]
- Ezcurra, A.; Benech, B.; Echelecou, A.; Santamaría, J.M.; Herrero, I.; Zulueta, E. Influence of local air flow regimes on the ozone content of two Pyrenean valleys. Atmos. Environ. 2013, 74, 367–377. [Google Scholar] [CrossRef]
- Gheusi, F.; Ravetta, F.; Delbarre, H.; Tsamalis, C.; Chevalier-Rosso, A.; Leroy, C.; Augustin, P.; Delmas, R.; Ancellet, G.; Athier, G.; et al. Pic 2005, a field campaign to investigate low-tropospheric ozone variability in the Pyrenees. Atmos. Res. 2011, 101, 640–665. [Google Scholar] [CrossRef]
- Karl, T.; Guenther, A.; Lindinger, C.; Jordan, A.; Fall, R.; Lindinger, W. Eddy covariance measurements of oxygenated volatile organic compound fluxes from crop harvesting using a redesigned proton-transfer-reaction mass spectrometer. J. Geophys. Res. Atmos. 2001, 106, 24157–24167. [Google Scholar] [CrossRef]
- Wolff, V.; Trebs, I.; Foken, T.; Meixner, F.X. Exchange of reactive nitrogen compounds: Concentrations and fluxes of total ammonium and total nitrate above a spruce canopy. Biogeosciences 2010, 7, 1729–1744. [Google Scholar] [CrossRef]
- Asaf, D.; Rotenberg, E.; Tatarinov, F.; Dicken, U.; Montzka, S.A.; Yakir, D. Ecosystem photosynthesis inferred from measurements of carbonyl sulphide flux. Nat. Geosci. 2013, 6, 186–190. [Google Scholar] [CrossRef]
- Nemitz, E.; Jimenez, J.L.; Huffman, J.A.; Ulbrich, I.M.; Canagaratna, M.R.; Worsnop, D.R.; Guenther, A.B. An eddy-covariance system for the measurement of surface/atmosphere exchange fluxes of submicron aerosol chemical species—First application above an urban area. Aerosol Sci. Technol. 2008, 42, 636–657. [Google Scholar] [CrossRef]
- Deventer, M.J.; von der Heyden, L.; Lamprecht, C.; Graus, M.; Karl, T.; Held, A. Aerosol particles during the Innsbruck Air Quality Study (INNAQS): Fluxes of nucleation to accumulation mode particles in relation to selective urban tracers. Atmos. Environ. 2018, 190, 376–388. [Google Scholar] [CrossRef]
- Karl, T.; Apel, E.; Hodzic, A.; Riemer, D.D.; Blake, D.R.; Wiedinmyer, C. Emissions of volatile organic compounds inferred from airborne flux measurements over a megacity. Atmos. Chem. Phys. 2009, 9, 271–285. [Google Scholar] [CrossRef]
- Karl, T.; Misztal, P.K.; Jonsson, H.H.; Shertz, S.; Goldstein, A.H.; Guenther, A.B. Airborne flux measurements of BVOCs above Californian oak forests: Experimental investigation of surface and entrainment fluxes, OH densities, and Damkohler numbers. J. Atmos. Sci. 2013, 70, 3277–3287. [Google Scholar] [CrossRef]
- Davison, B.; Taipale, R.; Langford, B.; Misztal, P.; Fares, S.; Matteucci, G.; Loreto, F.; Cape, J.N.; Rinne, J.; Hewitt, C.N. Concentrations and fluxes of biogenic volatile organic compounds above a Mediterranean macchia ecosystem in western Italy. Biogeosciences 2009, 6, 1655–1670. [Google Scholar] [CrossRef]
- Spirig, C.; Neftel, A.; Ammann, C.; Dommen, J.; Grabmer, W.; Thielmann, A.; Schaub, A.; Beauchamp, J.; Wisthaler, A.; Hansel, A. Eddy covariance flux measurements of biogenic VOCs during ECHO 2003 using proton transfer reaction mass spectrometry. Atmos. Chem. Phys. 2005, 5, 465–481. [Google Scholar] [CrossRef]
- Rantala, P.; Jarvi, L.; Taipale, R.; Laurila, T.K.; Patokoski, J.; Kajos, M.K.; Kurppa, M.; Haapanala, S.; Siivola, E.; Petaja, T.; et al. Anthropogenic and biogenic influence on VOC fluxes at an urban background site in Helsinki, Finland. Atmos. Chem. Phys. 2009, 9, 1971–1987. [Google Scholar] [CrossRef]
- Langford, B.; Davison, B.; Nemitz, E.; Hewitt, C.N. Mixing ratios and eddy covariance flux measurements of volatile organic compounds from an urban canopy (Manchester, UK). Atmos. Chem. Phys. 2016, 16, 7981–8007. [Google Scholar]
- Wolfe, G.M.; Hanisco, T.F.; Arkinson, H.L.; Bui, T.P.; Crounse, J.D.; Dean-Day, J.; Goldstein, A.; Guenther, A.; Hall, S.R.; Huey, G.; et al. Quantifying sources and sinks of reactive gases in the lower atmosphere using airborne flux observations. Geophys. Res. Lett. 2015, 42, 8231–8240. [Google Scholar] [CrossRef]
- Velasco, E.; Pressley, S.; Grivicke, R.; Allwine, E.; Coons, T.; Foster, W.; Jobson, B.T.; Westberg, H.; Ramos, R.; Hernandez, F.; et al. Eddy covariance flux measurements of pollutant gases in urban Mexico City. Atmos. Chem. Phys. 2009, 9, 7325–7342. [Google Scholar] [CrossRef]
- Vaughan, A.R.; Lee, J.D.; Misztal, P.K.; Metzger, S.; Shaw, M.D.; Lewis, A.C.; Purvis, R.M.; Carslaw, D.C.; Goldstein, A.H.; Hewitt, C.N.; et al. Spatially resolved flux measurements of NOx from London suggest significantly higher emissions than predicted by inventories. Faraday Discuss. 2016, 189, 455–472. [Google Scholar] [CrossRef]
- Ammann, C.; Wolff, V.; Marx, O.; Bruemmer, C.; Neftel, A. Measuring the biosphere-atmosphere exchange of total reactive nitrogen by eddy covariance. Biogeosciences 2012, 9, 4247–4261. [Google Scholar] [CrossRef]
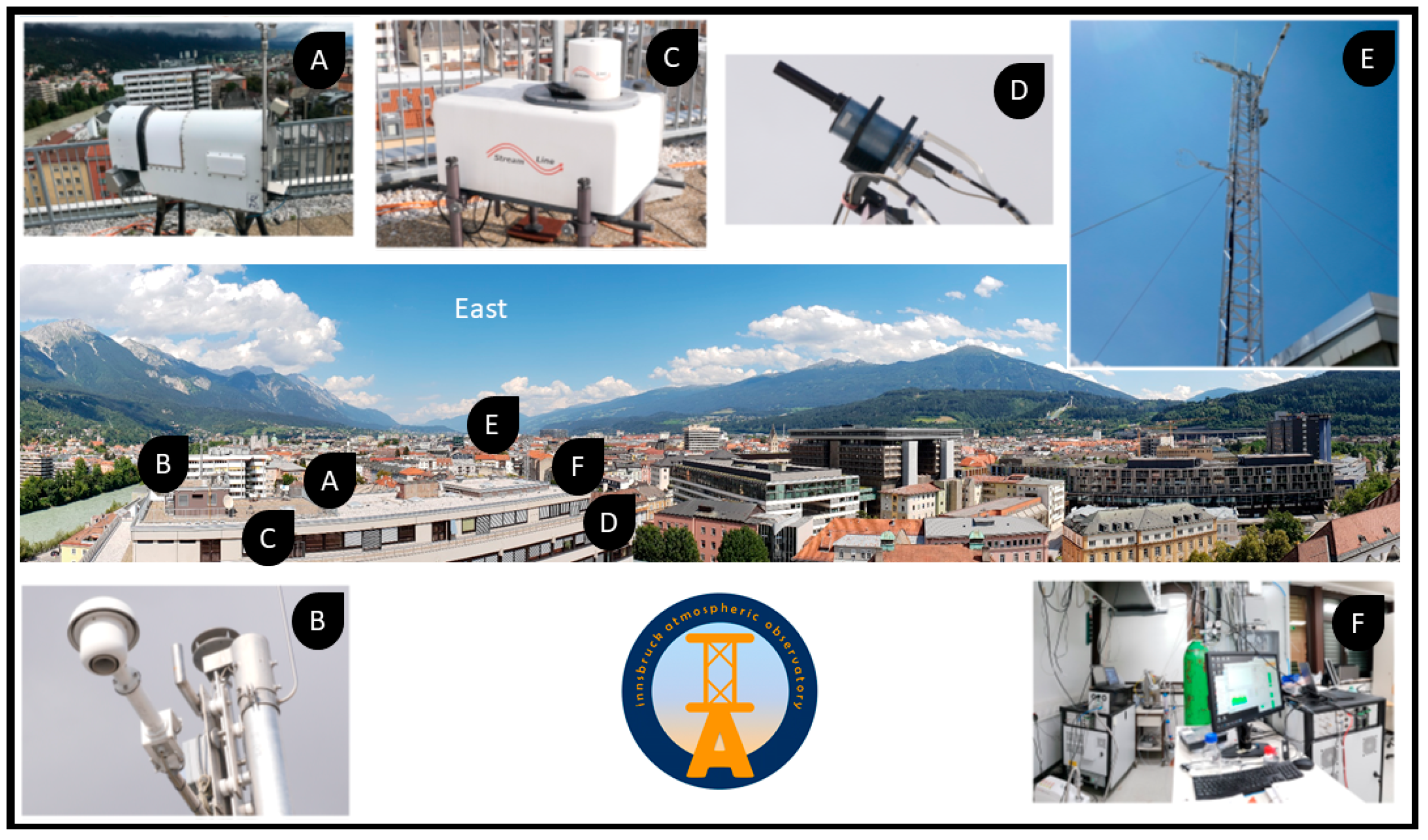
- Karl, T.; Gohm, A.; Rotach, M.W.; Ward, H.C.; Graus, M.; Cede, A.; Wohlfahrt, G.; Hammerle, A.; Haid, M.; Tiefengraber, M.; et al. Studying urban climate and air quality in the Alps: The Innsbruck atmospheric observatory. Bull. Amer. Meteor. Soc. 2020, 101, E488–E507. [Google Scholar] [CrossRef]
- Monroy, J.G.; Lilienthal, A.J.; Blanco, J.L.; Gonzalez-Jimenez, J.; Trincavelli, M. Probabilistic gas quantification with MOX sensors in open sampling systems—A gaussian process approach. Sens. Actuator B Chem. 2013, 188, 298–312. [Google Scholar] [CrossRef]
- Sun, Y.-F.; Liu, S.-B.; Meng, F.-L.; Liu, J.-Y.; Zhen, J.; Kong, L.-T.; Liu, J.-H. Metal oxide nanostructures and their gas sensing properties: A review. Sensors 2012, 12, 2610–2631. [Google Scholar] [CrossRef] [PubMed]
- WMO. Low-Cost Sensors for the Measurement of Atmospheric Composition: Overview of Topic and Future Applications; World Meteorological Organization: Geneva, Switzerland, 2018; p. 46. [Google Scholar]
- Cavaliere, A.; Carotenuto, F.; Di Gennaro, F.; Gioli, B.; Gualtieri, G.; Martelli, F.; Matese, A.; Toscano, P.; Vagnoli, C.; Zaldei, A. Development of low-cost air quality atations for next generation monitoring networks: Calibration and validation of PM2.5 and PM10 sensors. Sensors 2018, 18, 2843. [Google Scholar] [CrossRef] [PubMed]
- Althausen, D.; Engelmann, R.; Baars, H.; Heese, B.; Ansmann, A.; Müller, D.; Komppula, M. Portable Raman Lidar PollyXT for automated profiling of aerosol backscatter, extinction, and depolarization. J. Atmos. Ocean. Technol. 2009, 26, 2366–2378. [Google Scholar] [CrossRef]
- Harnish, F.; Gohm, A.; Fix, A.; Schnitzhofer, R.; Hansel, A.; Neininger, B. Spatial distribution of aerosols in the Inn Valley atmosphere during wintertime. Meteorol. Atmos. Phys. 2009, 103, 223–235. [Google Scholar] [CrossRef]
- Meister, A.; Fix, A.; Flentje, H.; Wirth, M.; Ehret, G. TropOLEX: A new tuneable airborne lidar system for the measurement of tropospheric ozone. In Proceedings of the 6th International Symposium on Tropospheric Profiling, Leipzig, Germany, 14–20 September 2003. [Google Scholar]
- Chazette, P.; Couvert, P.; Randriamiarisoa, H.; Sanak, J.; Bonsang, B.; Moral, P.; Berthier, S.; Salanave, S.; Toussaint, F. Three-dimensional survey of pollution during winter in French Alps valleys. Atmos. Environ. 2005, 39, 35–47. [Google Scholar] [CrossRef]
- Kreher, K.; van Roozendael, M.; Hendrick, F.; Apituley, A.; Dimitropoulou, E.; Frieß, U.; Richter, A.; Wagner, T.; Lampel, J.; Abuhassan, N.; et al. Intercomparison of NO2, O4, O3 and HCHO slant column measurements by MAX-DOAS and zenith-sky UV–visible spectrometers during CINDI-2. Atmos. Meas. Tech. 2020, 13, 2169–2208. [Google Scholar] [CrossRef]
- Schreier, S.F.; Richter, A.; Wittrock, F.; Burrows, J.P. Estimates of free-tropospheric NO2 and HCHO mixing ratios derived from high-altitude mountain MAX-DOAS observations at midlatitudes and in the tropics. Atmos. Chem. Phys. 2016, 16, 2803–2817. [Google Scholar] [CrossRef]
- Emeis, S.; Kalthoff, N.; Adler, B.; Pardyjak, E.; Paci, A.; Junkermann, W. High-resolution observations of transport and exchange processes in mountainous terrain. Atmosphere 2018, 9, 457. [Google Scholar] [CrossRef]
- Tomasi, E.; Giovannini, L.; Falocchi, M.; Zardi, D.; Antonacci, G. Preliminary pollutant dispersion modelling with CALMET and CALPUFF over complex terrain in the Bolzano Basin (IT). In Proceedings of the HARMO 2016—17th International Conference on Harmonisation within Atmospheric Dispersion Modelling for Regulatory Purposes, Budapest, Hungary, 9–12 May 2016; Ferenczi, Z., Bozo, L., Puskas, M.T., Eds.; Hungarian Meteorological Service: Budapest, Hungary, 2016; pp. 160–164. [Google Scholar]
- Haiden, T.; Kann, A.; Wittmann, C.; Pistotnik, G.; Bica, B.; Gruber, C. The integrated nowcasting through comprehensive analysis (INCA) system and its validation over the eastern Alpine region. Weather Forecast. 2011, 26, 166–183. [Google Scholar] [CrossRef]
- Hacker, J.; Draper, C.; Madaus, L. Challenges and opportunities for data assimilation in mountainous environments. Atmosphere 2018, 9, 127. [Google Scholar] [CrossRef]
- Chow, F.K.; Weigel, A.P.; Street, R.L.; Rotach, M.W.; Xue, M. High-resolution large-eddy simulations of flow in a steep Alpine valley. Part I: Methodology, verification, and sensitivity experiments. J. Appl. Meteorol. Climatol. 2006, 45, 63–86. [Google Scholar] [CrossRef]
- Skamarock, W.C. Evaluating mesoscale NWP models using kinetic energy spectra. Mon. Weather Rev. 2004, 132, 3019–3032. [Google Scholar] [CrossRef]
- Giovannini, L.; Antonacci, G.; Zardi, D.; Laiti, L.; Panziera, L. Sensitivity of simulated wind speed to spatial resolution over complex terrain. Energy Proced. 2014, 59, 323–329. [Google Scholar] [CrossRef]
- Shicker, I.; Seibert, P. Simulation of the meteorological conditions during a winter smog episode in the Inn Valley. Meteorol. Atmos. Phys. 2009, 103, 211–222. [Google Scholar] [CrossRef]
- Trini Castelli, S.; Morelli, S.; Anfossi, D.; Carvalho, J.; Zauli Sajani, S. Intercomparison of two models, ETA and RAMS, with TRACT field campaign data. Environ. Fluid Mech. 2004, 4, 157–196. [Google Scholar] [CrossRef]
- Balanzino, A.; Trini Castelli, S. Numerical experiments with RAMS model in highly complex terrain. Environ. Fluid Mech. 2018, 18, 357–381. [Google Scholar] [CrossRef]
- Wyngaard, J.C. Toward numerical modeling in the “terra incognita”. J. Atmos. Sci. 2004, 61, 1816–1826. [Google Scholar] [CrossRef]
- Chow, F.K.; Schar, C.; Ban, N.; Lundquist, K.A.; Schlemmer, L.; Shi, X. Crossing multiple gray zones in the transition from mesoscale to microscale simulation over complex terrain. Atmosphere 2019, 10, 274. [Google Scholar] [CrossRef]
- Muñoz-Esparza, D.; Sauer, J.A.; Linn, R.R. Limitations of one-dimensional mesoscale PBL parameterizations in reproducing mountain-wave flows. J. Atmos. Sci. 2016, 73, 2603–2614. [Google Scholar] [CrossRef]
- Goger, B.; Rotach, M.W.; Gohm, A.; Fuhrer, O.; Stiperski, I.; Holtslag, A.A.M. The impact of 3D effects on the simulation of turbulence kinetic energy structure in a major Alpine valley. Bound. Layer Meteorol. 2018, 168, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Łobocki, L. Surface-layer flux–gradient relationships over inclined terrain derived from a local equilibrium, turbulence closure model. Bound. Layer Meteorol. 2014, 150, 469–483. [Google Scholar] [CrossRef]
- Trini Castelli, S.; Ferrero, E.; Anfossi, D.; Ying, R. Comparison of turbulence closure models over a schematic valley in a neutral boundary layer. In Proceedings of the 13th Symposium on Boundary Layers and Turbulence, Dallas, TX, USA, 10–15 January 1999. [Google Scholar]
- Trini Castelli, S.; Ferrero, E.; Anfossi, D. Turbulence closures in neutral boundary layer over complex terrain. Bound. Layer Meteorol. 2001, 100, 405–419. [Google Scholar] [CrossRef]
- Ferrero, E.; Colonna, N. Nonlocal treatment of the buoyancy-shear-driven boundary layer. J. Atmos. Sci. 2006, 63, 2653–2662. [Google Scholar] [CrossRef]
- Canuto, V.; Howard, A.; Cheng, Y.; Dubovikov, M. Ocean turbulence, part II: Vertical diffusivities of momentum, heat, salt, mass and passive scalars. J. Phys. Oceanogr. 2002, 32, 240–264. [Google Scholar] [CrossRef]
- Gryanik, V.; Hartmann, J.; Raasch, S.; Schoroter, M. A refinement of the Millionschikov quasi-normality hypothesis for convective boundary layer turbulence. J. Atmos. Sci. 2005, 62, 2632–2638. [Google Scholar] [CrossRef]
- Colonna, N.M.; Ferrero, E.; Rizza, U. Nonlocal boundary layer: The pure buoyancy-driven and the buoyancy-shear-driven cases. J. Geophys. Res. Atmos. 2009, 114, 148–227. [Google Scholar] [CrossRef]
- Canuto, V. Turbulent convection with overshootings: Reynolds stress approach. Astrophys. J. 1992, 392, 218–232. [Google Scholar] [CrossRef]
- Ferrero, E.; Racca, M. The role of the non-local transport in modelling the shear-driven atmospheric boundary layer. J. Atmos. Sci. 2004, 61, 1434–1445. [Google Scholar] [CrossRef]
- Ferrero, E.; Alessandrini, S.; Vandenberghe, F. Assessment of planetary-boundary-layer schemes in the Weather Research and Forecasting model within and above an urban canopy layer. Bound. Layer Meteorol. 2018, 168, 289–319. [Google Scholar] [CrossRef]
- Cuxart, J. When can a high-resolution simulation over complex terrain be called LES? Front. Earth Sci. 2015, 3, 87. [Google Scholar] [CrossRef]
- Tomasi, E.; Giovannini, L.; Zardi, D.; de Franceschi, M. Optimization of Noah and Noah_MP land surface schemes in snow-melting conditions over complex terrain. Mon. Weather Rev. 2017, 145, 4727–4745. [Google Scholar] [CrossRef]
- Foster, C.S.; Crosman, E.T.; Horel, J.D. Simulations of a cold-air pool in Utah’s Salt Lake Valley: Sensitivity to land use and snow cover. Bound. Layer Meteorol. 2017, 164, 1–25. [Google Scholar] [CrossRef]
- Jiménez-Esteve, B.; Udina, M.; Soler, M.R.; Pepin, N.; Miró, J.R. Land use and topography influence in a complex terrain area: A high resolution mesoscale modelling study over the Eastern Pyrenees using the WRF model. Atmos. Res. 2018, 202, 49–62. [Google Scholar] [CrossRef]
- Massey, J.D.; Steenburgh, W.J.; Knievel, J.C.; Cheng, W.Y.Y. Regional soil moisture biases and their influence on WRF model temperature forecasts over the Intermountain West. Weather Forecast. 2016, 31, 197–216. [Google Scholar] [CrossRef]
- Ookouchi, Y.; Segal, M.; Kessler, R.C.; Pielke, R.A. Evaluation of soil moisture effects on the generation and modification of mesoscale circulations. Mon. Weather Rev. 1984, 112, 2281–2292. [Google Scholar] [CrossRef]
- Maggioni, V.; Houser, P.R. Soil moisture data assimilation. In Data Assimilation for Atmospheric, Oceanic and Hydrologic Applications; Park, S., Xu, L., Eds.; Springer: Cham, Switzerland, 2017; Volume 3, pp. 195–217. [Google Scholar]
- Chen, F.; Manning, K.W.; LeMone, M.A.; Trier, S.B.; Alfieri, J.G.; Roberts, R.; Tewari, M.; Niyogi, D.; Horst, T.W.; Oncley, S.P.; et al. Description and evaluation of the characteristics of the NCAR high-resolution land data assimilation system. J. Appl. Meteor. Climatol. 2007, 46, 694–713. [Google Scholar] [CrossRef]
- Giuseppe, F.D.; Cesari, D.; Bonafé, G. Soil initialization strategy for use in limited-area weather prediction systems. Mon. Weather. Rev. 2011, 139, 1844–1860. [Google Scholar] [CrossRef]
- Angevine, W.M.; Bazile, E.; Legain, D.; Pino, D. Land surface spinup for episode modeling. Atmos. Chem. Phys. 2014, 14, 8165–8172. [Google Scholar] [CrossRef]
- Maxwell, R.M.; Chow, F.K.; Kollet, S.J. The groundwater-land-surface-atmosphere connection: Soil moisture effects on the atmospheric boundary layer in fully-coupled simulations. Adv. Water Resour. 2007, 30, 2447–2466. [Google Scholar] [CrossRef]
- Rihani, J.F.; Chow, F.K.; Maxwell, R.M. Isolating effects of terrain and soil moisture heterogeneity on the atmospheric boundary layer: Idealized simulations to diagnose land-atmosphere feedbacks. J. Adv. Model. Earth Syst. 2015, 7, 915–937. [Google Scholar] [CrossRef]
- Zhong, J.; Lu, B.; Wang, W.; Huang, C.; Yang, Y. Impact of soil moisture on winter 2-m temperature forecast in Northern China. J. Hydrometeor. 2020, 21, 597–614. [Google Scholar] [CrossRef]
- Rummler, T.; Arnault, J.; Gochis, D.; Kunstmann, H. Role of lateral terrestrial water flow on the regional water cycle in a complex terrain region: Investigation with a fully coupled model system. J. Geophys. Res. Atmos. 2019, 124, 507–529. [Google Scholar] [CrossRef]
- Barlage, M.; Chen, F.; Tewari, M.; Ikeda, K.; Gochis, D.; Dudhia, J.; Rasmussen, R.; Livneh, B.; Ek, M.; Mitchell, K. Noah land surface model modifications to improve snowpack prediction in the Colorado Rocky Mountains. J. Geophys. Res. Atmos. 2010, 115, D22101. [Google Scholar] [CrossRef]
- Jin, J.; Miller, N.L.; Schlegel, N. Sensitivity study of four land surface schemes in the WRF Model. Adv. Meteor. 2010, 2010, 167436. [Google Scholar] [CrossRef]
- Hall, D.K.; Riggs, G.A.; Salomonson, V.V. MODIS/Terra Snow Cover 5-Min L2 Swath 500m, Version 5; NASA National Snow and Ice Data Center Distributed Active Archive Center: Boulder, CO, USA, 2006.
- Chen, F.; Kusaka, H.; Bornstein, R.; Ching, J.; Grimmond, C.S.B.; Grossman-Clarke, S.; Loridan, T.; Manning, K.W.; Martilli, A.; Miao, S.; et al. The integrated WRF/urban modelling system: Development, evaluation, and applications to urban environmental problems. Int. J. Climatol. 2011, 31, 273–288. [Google Scholar] [CrossRef]
- Ching, J.; Brown, M.; Burian, S.; Chen, F.; Cionco, R.; Hanna, A.; Hultgren, T.; McPherson, T.; Sailor, D.; Taha, H.; et al. National urban database and access portal tool. Bull. Amer. Meteor. Soc. 2009, 90, 1157–1168. [Google Scholar] [CrossRef]
- Goger, B.; Rotach, M.W.; Gohm, A.; Stiperski, I.; Fuhrer, O.; de Morsier, G. A new horizontal length scale for a three-dimensional turbulence parameterization in meso-scale atmospheric modeling over highly complex terrain. J. Appl. Meteorol. Climatol. 2019, 58, 2087–2102. [Google Scholar] [CrossRef]
- Rotach, M.W.; Gryning, S.E.; Tassone, C. A two-dimensional stochastic Lagrangian dispersion model for daytime conditions. Q. J. R. Meteorol. Soc. 1996, 122, 367–389. [Google Scholar] [CrossRef]
- Hanna, S. Applications in air pollution modeling. In Atmospheric Turbulence and Air Pollution Modelling; Nieuwstadt, F., van Dop, H., Eds.; Reidel: Dordrecht, The Netherlands, 1982; pp. 275–310. [Google Scholar]
- Trini Castelli, S.; Tinarelli, G.; Reisin, T.G. Comparison of atmospheric modelling systems simulating the flow, turbulence and dispersion at the microscale within obstacles. Environ. Fluid Mech. 2017, 17, 879–901. [Google Scholar] [CrossRef]
- Thomson, D.J. Criteria for the selection of stochastic models of particle trajectories in turbulent flows. J. Fluid Mech. 1987, 180, 529–556. [Google Scholar] [CrossRef]
- Luhar, A.K.; Britter, R.E. A random walk model for dispersion in inhomogeneous turbulence in a convective boundary layer. Atmos. Environ. 1989, 23, 1911–1924. [Google Scholar] [CrossRef]
- Flesch, T.K.; Wilson, J.D. A two-dimensional trajectory-simulation model for non-Gaussian, inhomogeneous turbulence within plant canopies. Bound. Layer Meteorol. 1992, 61, 349–374. [Google Scholar] [CrossRef]
- Monti, P.; Leuzzi, G. A closure to derive a three-dimensional well-mixed trajectory model for non-Gaussian, inhomogeneous turbulence. Bound. Layer Meteorol. 1996, 80, 311–331. [Google Scholar] [CrossRef]
- Wilson, J.D.; Flesch, T.K. Trajectory curvature as a selection criterion for valid Lagrangian stochastic dispersion models. Bound. Layer Meteorol. 1997, 84, 411–425. [Google Scholar] [CrossRef]
- Sawford, B.L. Rotation of trajectories in Lagrangian stochastic models of turbulent dispersion. Bound. Layer Meteorol. 1999, 93, 411–424. [Google Scholar] [CrossRef]
- Kurbanmuradov, O.; Sabelfeld, K. Lagrangian stochastic models for turbulent dispersion in the atmospheric boundary layer. Bound. Layer Meteorol. 2000, 97, 191–218. [Google Scholar] [CrossRef]
- Stein, A.F.; Lamb, D.; Draxler, R.R. Incorporation of detailed chemistry into a three-dimensional Lagrangian–Eulerian hybrid model: Application to regional tropospheric ozone. Atmos. Environ. 2000, 34, 4361–4372. [Google Scholar] [CrossRef]
- Alessandrini, S.; Ferrero, E. A hybrid Lagrangian–Eulerian particle model for reacting pollutant dispersion in non-homogeneous non-isotropic turbulence. Phys. A 2009, 388, 1375–1387. [Google Scholar] [CrossRef]
- Alessandrini, S.; Ferrero, E. A Lagrangian particle model with chemical reactions: Application in real atmosphere. Int. J. Environ. Pollut. 2011, 47, 97–107. [Google Scholar] [CrossRef]
- Kaplan, H. An estimation of a passive scalar variances using a one-particle Lagrangian transport and diffusion model. Phys. A 2014, 393, 1–9. [Google Scholar] [CrossRef]
- Ferrero, E.; Mortarini, L.; Alessandrini, S.; Lacagnina, C. Application of a bivariate gamma distribution for a chemically reacting plume in the atmosphere. Bound. Layer Meteorol. 2013, 147, 123–137. [Google Scholar] [CrossRef]
- Amicarelli, A.; Leuzzi, G.; Monti, P.; Alessandrini, S.; Ferrero, E. A stochastic Lagrangian micromixing model for the dispersion of reactive scalars in turbulent flows: Role of concentration fluctuations and improvements to the conserved scalar theory under non-homogeneous conditions. Environ. Fluid Mech. 2017, 17, 715–753. [Google Scholar] [CrossRef][Green Version]
- Ferrero, E.; Mortarini, L.; Alessandrini, S.; Lacagnina, C. A fluctuating plume model for pollutants dispersion with chemical reactions. Int. J. Environ. Pollut. 2012, 48, 3–12. [Google Scholar] [CrossRef]
- Garmory, A.; Richardson, E.S.; Mastorakos, E. Micromixing effects in a reacting plume by the stochastic fields method. Atmos. Environ. 2006, 40, 1078–1091. [Google Scholar] [CrossRef]
- Luhar, A.; Hibberd, M.; Borgas, M. A skewed meandering-plume model for concentration statistics in the convective boundary layer. Atmos. Environ. 2000, 34, 3599–3616. [Google Scholar] [CrossRef]
- Franzese, P. Lagrangian stochastic modeling of a fluctuating plume in the convective boundary layer. Atmos. Environ. 2003, 37, 1691–1701. [Google Scholar] [CrossRef]
- Mortarini, L.; Franzese, P.; Ferrero, E. A fluctuating plume model for concentration fluctuations in a plant canopy. Atmos. Environ. 2009, 43, 921–927. [Google Scholar] [CrossRef]
- Bisignano, A.; Mortarini, L.; Ferrero, E.; Alessandrini, S. Analytical offline approach for concentration fluctuations and higher order concentration moments. Int. J. Environ. Pollut. 2014, 5, 58–66. [Google Scholar] [CrossRef]
- Manor, A. A stochastic single particle lagrangian model for the concentration fluctuation in a plume dispersing inside an urban canopy. Bound. Layer Meteorol. 2014, 150, 327–340. [Google Scholar] [CrossRef]
- Ferrero, E.; Mortarini, L.; Purghè, F. A simple parameterization for the concentration variance dissipation in a Lagrangian single-particle model. Bound. Layer Meteorol. 2017, 163, 91–101. [Google Scholar] [CrossRef]
- Tinarelli, G.; Anfossi, D.; Brusasca, G.; Ferrero, E.; Giostra, U.; Morselli, M.G.; Moussafir, J.; Tampieri, F.; Trombetti, F. Lagrangian particle simulation of tracer dispersion in the lee of a schematic two-dimensional hill. J. Appl. Meteorol. 1994, 33, 744–756. [Google Scholar] [CrossRef]
- Alessandrini, S.; Ferrero, E.; Trini Castelli, S.; Anfossi, D. Influence of turbulent closure on the simulation of flow and dispersion in complex terrain. Int. J. Environ. Pollut. 2005, 24, 154–170. [Google Scholar] [CrossRef]
- Balanzino, A.; Pirovano, G.; Ferrero, E.; Causà, M.; Riva, G.M. Particulate matter pollution simulations in complex terrain. Int. J. Environ. Pollut. 2012, 48, 39–46. [Google Scholar] [CrossRef]
- Ferrero, E.; Trini Castelli, S.; Anfossi, D. Turbulence fields for atmospheric dispersion models in horizontally non-homogeneous conditions. Atmos. Environ. 2003, 37, 2305–2315. [Google Scholar] [CrossRef]
- Brusasca, G.; Tinarelli, G.; Anfossi, D. Particle model simulation of diffusion in low wind speed stable conditions. Atmos. Environ. 1992, 26, 707–723. [Google Scholar] [CrossRef]
- Oettl, D.; Almbauer, R.A.; Sturm, P.J. A new method to estimate diffusion in stable, low wind conditions. J. Appl. Meteorol. 2001, 40, 259–268. [Google Scholar] [CrossRef]
- Anfossi, D.; Alessandrini, S.; Trini Castelli, S.; Ferrero, E.; Oettl, D.; Degrazia, G. Tracer dispersion simulation in low wind speed conditions with a new 2-D Langevin equation system. Atmos. Environ. 2006, 40, 7234–7245. [Google Scholar] [CrossRef]
- Luhar, A.K.; Hurley, P.J. Application of a coupled prognostic model to turbulence and dispersion in light-wind stable conditions, with an analytical correction to vertically resolve concentrations near the surface. Atmos. Environ. 2012, 5, 56–66. [Google Scholar] [CrossRef]
- Luhar, A.K. Lagrangian particle modeling of dispersion in light winds. In Dispersion Lagrangian Modeling of the Atmosphere; Lin, J.C., Brunner, D., Gerbig, C., Stohl, A., Luhar, A., Webley, P., Eds.; American Geophysical Union: Washington, DC, USA, 2012; pp. 311–328. [Google Scholar]
- Pouliot, G.; Pierce, T.; Benjey, W.; O’Neill, S.M.; Ferguson, S.A. Wildfire emission modeling: Integrating bluesky and smoke. In Proceedings of the 14th International Emission Inventory Conference “Transforming Emission Inventories Meeting Future Challenges Today”, Las Vegas, NV, USA, 11–14 April 2005. [Google Scholar]
- Briggs, G.A. Plume rise predictions. In Lectures on Air Pollution and Environmental Impact Analyses. Workshop Proceedings; Haugen, D., Ed.; American Meteorological Society: Boston, Massachusetts, MA, USA, 1975; pp. 59–111. [Google Scholar]
- Weil, J.; Snyder, W.; Lawson, R., Jr.; Shipman, M. Experiments on buoyant plume dispersion in a laboratory convection tank. Bound. Layer Meteorol. 2002, 102, 367–414. [Google Scholar] [CrossRef]
- Morton, B.R.; Taylor, G.I.; Turner, J.S. Turbulent gravitational convection from maintained and instantaneous sources. Proc. Roy. Soc. London. 1956, A234, 1–23. [Google Scholar]
- Anfossi, D.; Ferrero, E.; Brusasca, G.; Marzorati, A.; Tinarelli, G. A simple way of computing buoyant plume rise in a Lagrangian stochastic model for airborne dispersion. Atmos. Environ. 1993, 27A, 1443–1451. [Google Scholar] [CrossRef]
- Webster, H.N.; Thomson, D.J. Validation of a Lagrangian model plume rise scheme using the Kincaid data set. Atmos. Environ. 2002, 36, 5031–5042. [Google Scholar] [CrossRef]
- Alessandrini, S.; Ferrero, E.; Anfossi, D. A new Lagrangian method for modelling the buoyant plume rise. Atmos. Environ. 2013, 77, 239–249. [Google Scholar] [CrossRef]
- Oettl, D.; Ferrero, E. A simple model to assess odour hours for regulatory purposes. Atmos. Environ. 2017, 155, 162–173. [Google Scholar] [CrossRef]
- Ferrero, E.; Alessandrini, S.; Anderson, B.; Tomasi, E.; Jiménez, P.; Meech, S. Lagrangian simulation of smoke plume from fire and validation using ground-based lidar and aircraft measurements. Atmos. Environ. 2019, 213, 659–674. [Google Scholar] [CrossRef]
- Thomson, D.J. A stochastic model for the motion of particle pairs in isotropic high-Reynolds-number turbulence, and its application to the problem of concentration variance. J. Fluid Mech. 1990, 210, 113–153. [Google Scholar] [CrossRef]
- Borgas, M.S.; Sawford, B.L. A family of stochastic models for particle dispersion in isotropic homogeneous stationary turbulence. J. Fluid Mech. 1994, 279, 69–99. [Google Scholar] [CrossRef]
- Pope, S. PDF methods for turbulent reactive flows. Prog. Energy Combust. Sci. 1985, 11, 119–192. [Google Scholar] [CrossRef]
- Cassiani, M.; Franzese, P.; Giostra, U. A PDF micromixing model of dispersion for atmospheric flow. Part I: Development of the model, application to homogeneous turbulence and to neutral boundary layer. Atmos. Environ. 2005, 39, 1457–1469. [Google Scholar] [CrossRef]
- Yee, E.; Chan, R.; Kosteniuk, P.R.; Chandler, G.M.; Biltoft, C.A.; Bowers, J.F. Incorporation of internal fluctuations in a meandering plume model of concentration fluctuations. Bound. Layer Meteorol. 1994, 67, 11–38. [Google Scholar] [CrossRef]
- Yee, E.; Wilson, D.J. A comparison of the detailed structure in dispersing tracer plumes measured in grid-generated turbulence with a meandering plume model incorporating internal fluctuations. Bound. Layer Meteorol. 2000, 94, 253–296. [Google Scholar] [CrossRef]
- Ferrero, E.; Oettl, D. An evaluation of a Lagrangian stochastic model for the assessment of odours. Atmos. Environ. 2019, 206, 237–246. [Google Scholar] [CrossRef]
- Ferrero, E.; Manor, A.; Mortarini, L.; Oettl, D. Concentration fluctuations and odor dispersion in Lagrangian models. Atmosphere 2020, 11, 27. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Giovannini, L.; Ferrero, E.; Karl, T.; Rotach, M.W.; Staquet, C.; Trini Castelli, S.; Zardi, D. Atmospheric Pollutant Dispersion over Complex Terrain: Challenges and Needs for Improving Air Quality Measurements and Modeling. Atmosphere 2020, 11, 646. https://doi.org/10.3390/atmos11060646
Giovannini L, Ferrero E, Karl T, Rotach MW, Staquet C, Trini Castelli S, Zardi D. Atmospheric Pollutant Dispersion over Complex Terrain: Challenges and Needs for Improving Air Quality Measurements and Modeling. Atmosphere. 2020; 11(6):646. https://doi.org/10.3390/atmos11060646
Chicago/Turabian StyleGiovannini, Lorenzo, Enrico Ferrero, Thomas Karl, Mathias W. Rotach, Chantal Staquet, Silvia Trini Castelli, and Dino Zardi. 2020. "Atmospheric Pollutant Dispersion over Complex Terrain: Challenges and Needs for Improving Air Quality Measurements and Modeling" Atmosphere 11, no. 6: 646. https://doi.org/10.3390/atmos11060646
APA StyleGiovannini, L., Ferrero, E., Karl, T., Rotach, M. W., Staquet, C., Trini Castelli, S., & Zardi, D. (2020). Atmospheric Pollutant Dispersion over Complex Terrain: Challenges and Needs for Improving Air Quality Measurements and Modeling. Atmosphere, 11(6), 646. https://doi.org/10.3390/atmos11060646





