Abstract
In this paper, the sea surface temperature (SST) based statistical seasonal forecast model (S4CAST) is utilized to examine the spatial and temporal prediction skill of Sahel heavy and extreme daily precipitation events. As in previous studies, S4CAST points out the Mediterranean Sea and El Niño Southern Oscillation (ENSO) as the main drivers of Sahel heavy/extreme daily rainfall variability at interannual timescales (period 1982–2015). Overall, the Mediterranean Sea emerges as a seasonal short-term predictor of heavy daily rainfall (1 month in advance), while ENSO returns a longer forecast window (up to 3 months in advance). Regarding the spatial skill, the response of heavy daily rainfall to the Mediterranean SST forcing is significant over a widespread area of the Sahel. Contrastingly, with the ENSO forcing, the response is only significant over the southernmost Sahel area. These differences can be attributed to the distinct physical mechanisms mediating the analyzed SST-rainfall teleconnections. This paper provides fundamental elements to develop an operational statistical-seasonal forecasting system of Sahel heavy and extreme daily precipitation events.
1. Introduction
The Sahel region is one of the most important observed climate change hotspots [1]. Increasingly unpredictable weather patterns associated with extreme rainfall events contribute to threatening the livelihoods of the Sahelian population [2,3], whose subsistence is highly dependent on rainfed agriculture [4,5].
Oceanic forcing is the dominant driver of the West African Monsoon (WAM) variability (e.g., [6,7]), while land-surface processes have an amplifying effect [8,9,10]. Oceans play an outstanding role in the climate system due, in part, to their large heat-storage capacity [11]. Energy is stored in the global oceans, to be subsequently released into the atmosphere via turbulent and radiative energy exchange at the sea surface. This process takes place at much longer timescales (seasonal to multi-decadal) than those typically associated with short-term weather prediction (1–10 days). In this context, several studies have shown the influence of sea surface temperatures (SSTs) on the WAM interannual variability, with El Niño-Southern Oscillation (ENSO) and the Mediterranean Sea playing a dominant role [12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Current state-of-the-art climate models are generally unable to properly reproduce tropical SST variability, owing to their systematic biases: the warm SST bias in the eastern tropical Atlantic [27,28], the biases in the link between surface wind stress and SST in the tropical Atlantic [29], the biases in the equatorial cold tongue and its impact on ENSO [30] and biases in tropical Pacific SSTs [31], among others. As a result, these biases hinder effective seasonal dynamical predictions of heavy and extreme daily precipitation events in West Africa [32,33,34,35].
Statistical methodologies based on SST predictors emerge as valuable alternatives and contribute to improve the predictability of monsoonal precipitation [36]. However, the predictability of rainfall characteristics such as extreme daily rainfall events has just started to be comprehensively documented. At interannual timescales, Diakhaté [37] (hereafter D19), addressed this question for the first time. They showed that Sahel heavy and extreme daily precipitation variability was mainly linked to ENSO and Mediterranean SST anomalies. During La Niña episodes, evidence was provided on the induced anomalous circulation over the Sahel with enhanced vertical destabilization (i.e., air convergence/divergence at lower/upper levels). Such conditions, together with the penetration of moisture-rich air from the Gulf of Guinea towards the Sahel, created a very favorable environment for deep convection and, thus, heavy and extreme rainfall occurrence. Regarding the Mediterranean, higher than usual SSTs were found to enhance evaporation and to strengthen the Sahara heat low (SHL), thus increasing the pressure gradient between the Sahara and Gulf of Guinea, in agreement with previous studies [21,34,38,39,40]. This increased meridional pressure gradient promoted a further northward penetration of the monsoonal flow from the Gulf of Guinea, in turn, feeding convergence over the Sahel. D19 also showed that the meridional circulation strengthened with changes in the SHL, combined with a large change of westerly flow from the tropical North Atlantic, which also increased moisture and heat transport into the Sahel [41]. Using a multi-linear regression model based on SSTs from these two basins (predictors), D19 found a significant skill for seasonal forecasting Sahel summer heavy and extreme daily rainfall, with up to four months forecasting windows. However, D19 analysis was based on spatial averages of daily rainfall. Therefore, the spatial distribution of heavy and extreme daily responses throughout the Sahel region and the amplitude of such signals were not specifically assessed. The present paper aims to fill this gap by using the novel Sea Surface temperature based Statistical Seasonal ForeCAST model (S4CAST; [36]). The paper is structured as follows: Section 2 describes the data and methods used. The main results of the paper are provided in Section 3. The main conclusions and a discussion conclude this article.
2. Data and Methodology
2.1. Predictor and Predictand Data Sets
The Climate Hazards Group Infrared Precipitation with Station Data (CHIRPS) were utilized to analyze daily rainfall for the period of 1982–2015. CHIRPs have a horizontal longitude-latitude resolution of 0.258° × 0.258° and integrate information from satellite and rain measurements over West Africa [42,43]. Daily August precipitation values were considered as an estimate of boreal summer monsoonal rainfall over the Sahel region (20° W–10° E, 10°–20° N). For each grid point, rainfall was stratified in terms of daily intensity. After removal of all precipitation events lower than 1 mm day−1, heavy and extreme daily events were considered as those above the daily 75th and 95th percentiles. The heavy category, therefore, includes extreme daily events. Thresholds were calculated over each Sahel grid-point individually. Subsequently, at each grid point, a time series was built with the total amount of rainfall for August of each year, which was obtained as a result of rainfall events belonging to the heavy or extreme categories, respectively. For this approach, we followed the definition of heavy and extreme daily rainfall provided by the Expert Team on Climate Change Detection and Indices (ETCCDI) without imposing any additional criterion on the duration of events. The final time series were standardized after a filter was applied using a Butterworth high-pass method with an 8-year cutoff period to keep the focus on interannual variability. The resultant variables were considered as predictands for the S4CAST model.
For the predictors, monthly SSTs from the NOAA Extended Reconstructed SST data set (ERSST) V5, with a resolution of 2.0° × 2.0° [44,45,46], were used. Three different domains for SST data were analyzed: (i) a global one without polar areas [180° W–180° E, 60° S–60° N], (ii) the Mediterranean Sea (16° E–38° E, 30°–40° N) and (iii) the Niño 3.4 region (170° W–120° W, 6° S–6° N). Predictor fields were standardized but not high-pass filtered, as interannual variability was already retained from predictands. Throughout the whole manuscript, the random phase test of Ebisuzaki [47] was used for the statistical hypothesis testing of correlation scores (p-value < 0.05). This consists to a non-parametric test designed to take into account the non-zero autocorrelation time series, a factor disregarded for instance in the regular Student’s t-test. It is based on resampling the phases of the Fourier transform of the original time series to build a probability distribution function against which the correlation of the original time series can be tested.
2.2. The Sea Surface Temperature Based Statistical Seasonal Forecast Model
The S4CAST is based on the maximum covariance analysis (MCA), a widely used methodology that is used to isolate patterns of maximum co-variability between two climate fields (e.g., [48,49,50]). The model performs the MCA on the covariance matrix calculated between two anomalous fields that are potentially related to each other. In the S4CAST configuration of this work, the forecast period corresponds to August (AUG) and the predictability of daily precipitation events (e.g., heavy, extreme) is analyzed considering lags from 0 (AUG) to 4 (April of the same year; APR). The temporal overlapping between the forecast period and the predictor is available by defining the monthly lags between both fields from monthly lag 0 (synchronous), which refers to the case in which the predictor and the predictand fields are taken at the same n-month period (cf. [34] for such application). As the predictions are based on historical data, all forecasts provided in this study are indeed hindcasts. It is also worth noting that the MCA works as a linear model, providing the time series (expansion coefficients) and their associated spatial patterns, which maximize co-variability, and must be interpreted in both positive and negative phases. In this framework, a unique (the leading) MCA mode is selected in order to isolate those modes of interannual SST variability that serve as potential seasonal predictors of heavy daily rainfall events. Note that the selection of additional modes of variability could improve the statistical forecast, but it likewise would obscure the identification of SST patterns and their associated teleconnection mechanisms. As a next step to evaluate predictability, S4CAST performs a leave-one-out cross-validated hindcast for each lag. As such, a linear regression model is built for each year being predicted, calculating the coefficients of the model with all the years in our database except the one that is predicted [51,52,53]. This methodology is particularly practical when handling periods of data of a few decades, in such a way that it is not necessary to separate consecutive time intervals for model training and validation [54].
To determine the model skill, Pearson correlation and root mean square error (RMSE) coefficients are considered. Respectively, these parameters provide a qualitative and quantitative measure of the estimate. Pearson correlation coefficients provide information about the co-variability (the sign of the response), ranging between 0 and 1, and the higher its value, the better the estimate. The RMSE measures the difference in magnitude between observation and forecast. Therefore, the lower its value, the better approach, whereas high values of RMSE indicate that the forecasts overestimate or underestimate the amplitude of the observations. Further information on the S4CAST can be found in Suárez-Moreno [36].
2.3. Teleconnection Mechanisms and Dynamics
To analyze the underlying physics of the identified teleconnection mechanisms, atmospheric data from the European Center for Medium-Range Weather Forecasts (ECMWF) ERA-Interim reanalysis were also utilized. ERA-Interim is provided at 0.75° horizontal resolution with 60 vertical atmospheric levels, from the surface up to 0.1 hPa [55]. The variables considered for the dynamical maps were: horizontal wind divergence at 200 hPa minus 850 hPa (DIV200/850) as an estimate of vertical air movement (positive values for air ascent, negative for subsidence); specific humidity at 850 hPa (q850) as an indicator of low level moisture availability, zonal and meridional winds at 850 hPa (u850, v850) and mean sea level pressure (mslp) to characterize the low-level atmospheric circulation.
3. Results
As mentioned in the first section, ENSO and the Mediterranean Sea were found to be the leading drivers of Sahel heavy daily rainfall variability at interannual timescales in D19. We first analyze the SST-forced response of Sahelian heavy daily rainfall events in August by applying the S4CAST model and using global SST anomalies as a predictor (Figure 1). The tropical eastern Pacific and the eastern Mediterranean are identified as the leading drivers of August Sahelian total rainfall (Figure 1g). This is consistent with Suárez-Moreno [26] and D19, as these SST variability patterns are identified at interannual timescales, and they appear highlighted for all rainfall indices (Figure 1a,c,e). However, while the Sahelian rainfall response is stronger for heavy and extreme daily rainfall events, which closely resemble the total response (Figure 1b,d), for moderate events (below 75th percentile), the response almost vanishes (Figure 1f). Accordingly, the atmospheric teleconnections between the tropical eastern Pacific and eastern Mediterranean to the Sahel explain better the interannual variability of heavy daily rainfall (which includes extreme events, above the 95th percentile) but not the moderate daily events (below the 75th percentile). For completeness, the expansion coefficient time series for global SSTs and Sahel rainfall is provided in Figure S1. Based on these findings, the present paper primarily focuses on heavy and extreme daily rainfall events. Indeed, these events are the most damaging and with the highest societal impacts. The S4CAST model is applied to evaluate the prediction of yearly contribution of heavy daily rainfall events over the Sahel during the peak of the Monsoon season (August). To this end, SSTs over the El Niño 3.4 region and the Mediterranean Sea are taken separately as predictors.
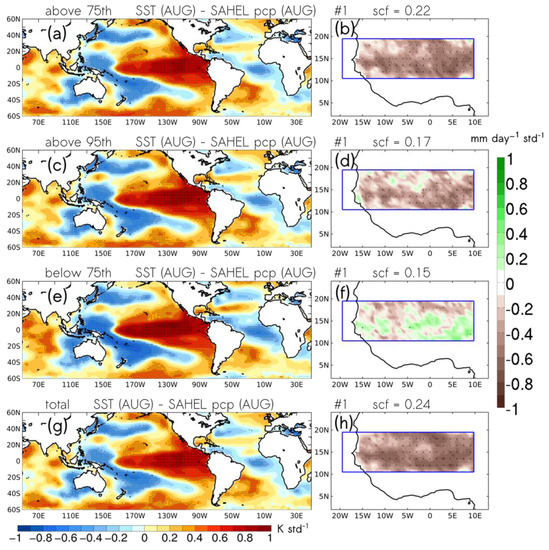
Figure 1.
Co-variability maps corresponding to the leading maximum covariance analysis (MCA) mode calculated between global SST anomalies (SSTA; 60° S–60° N) and different percentiles of anomalous Sahel (20° W–20° E; 10°–20° N) rainfall from the Chirps data set. (Left column) Homogeneous SSTA (K std−1) maps obtained by regression of sea surface temperature (SST) expansion coefficient U (see Figure S1) onto global SSTA. (Right Column) Heterogeneous maps of anomalous rainfall (mm day−1 std−1) obtained by regression of SST expansion coefficient U onto regional anomalous Sahelian rainfall. Co-variability maps are depicted for precipitation (a,b) above the 75th percentile, (c,d) above the 95th percentile, (e,f) below the 75th percentile and (g,h) total precipitation. The squared covariance fraction (scf) for each case is shown in figure titles. Stippling denotes 95% (0.05) statistical significance under a Monte Carlo test (1000 permutations).
3.1. Forecast Using SSTs over the Mediterranean Sea as Predictor
Figure 2 presents the cross-validated skill scores calculated from MCA between hindcasts and observations of anomalous Sahelian rainfall and Mediterranean SSTs, which are calculated in terms of Pearson correlation coefficients (Figure 2a) and RMSE (Figure 2b,c) at lag 0, and the tracking of their monthly-lagged progression back to lag 4 (April). Note that the difference between RMSE outcomes in the central and right columns of Figure 2 is explained by the fact that they are based on non-standardized vs. standardized predictor/predictand fields, respectively. Thus, the central column maps are dominated by standard deviation values, which are much higher over the south-western Sahel compared to the surrounding regions.
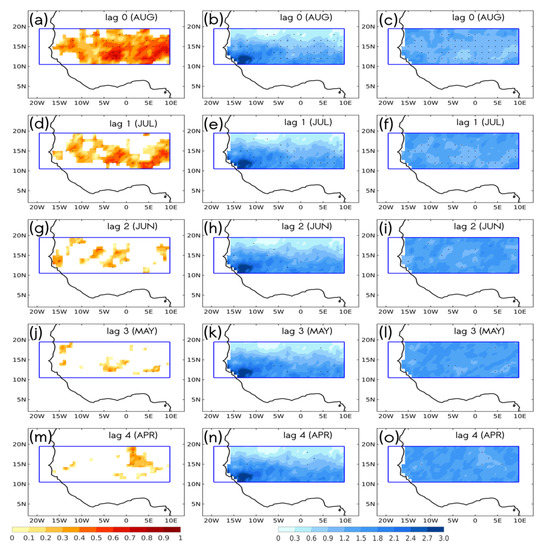
Figure 2.
Cross-validated skill scores calculated from MCA between forecasts and observations of anomalous Sahelian rainfall calculated in terms of (left column) Pearson correlation coefficients and (right column) root mean square error (RMSE). The analysis is based on the leading MCA calculated between the Eastern Mediterranean SSTA (16°–38° E; 30°–40° N) and the Sahel (20° W–20° E; 10°–20° N) rainfall above the 75th percentile (see details in the text). Cross-validated skill scores are shown for monthly lagged SSTA regarding August (AUG) precipitation: (a–c) AUG (lag 0), (d–f) JUL (lag 1), (g–i) JUN (lag 2), (j–l) MAY (lag 3) and (m–o) APR (lag 4). RMSE values in the middle (right) column are calculated from non-standardized (standardized) fields. Black stippled regions denote statistically significant values at 95% (0.05) according to a Monte Carlo test (1000 permutations).
Strong and significant values are observed in lag 0 and lag 1 in terms of correlation and RMSE (Figure 2a–f). From lag 2 and backward in time, we significantly lose predictive skill in terms of correlation (Figure 2g–o). Thus, the Mediterranean Sea emerges as a short-term (lag 1) seasonal predictor of heavy daily rainfall events in the Sahel. The fact that the Mediterranean variability is stronger during the summer months and has a much more reduced thermal inertia than the equatorial Pacific (due to its smaller size) may be behind this lack of predictive skill for lags 2 and beyond [21], a result not shown in D19 due to the applied methodology, which considered ENSO and MED together in the generated stepwise statistical seasonal model (cf. their Figure 8).
Figure 3 depicts the leading co-variability mode between Mediterranean SST anomalies and heavy daily rainfall events in the Sahel. The results correspond to lag 1 (JUL), for which certain predictability was found in terms of skill-scores (cf. Figure 2). The expansion coefficient time series is shown for the Mediterranean SST (blue bars) and Sahelian heavy daily rainfall (red line). A significant widespread warming of the Mediterranean (Figure 3b) is related to increased precipitation in the Sahel associated with heavy daily rainfall events (Figure 3c). Similar results were noted with extreme daily rainfall events (not shown). A significant SST warming is observed in the tropical Atlantic, which is liable to potentially induce drought conditions in the Sahel [22]. However, the signal does not appear to be robust enough to dampen the Mediterranean SST-forced response that was previously noted. By construction, the opposite SST-rainfall patterns shall also be considered. The associated square covariance fraction (scf) to this leading MCA mode is 0.58. For completeness, the same SST homogeneous maps and scfs as in Figure 3b are provided for all lags (0 to 4) in Figure S2.
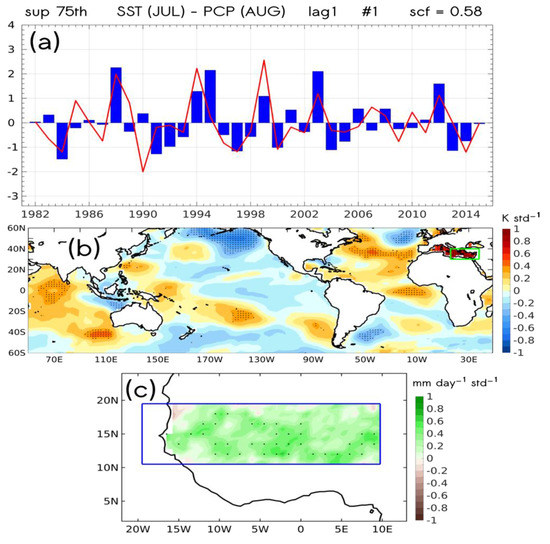
Figure 3.
Leading MCA mode calculated between the Eastern Mediterranean SSTA (16°–38° E; 30°–40° N) in JUL (lag 1) and the anomalous Sahel (20° W–20° E; 10°–20° N) rainfall above the 75th percentile in AUG. (a) Time series expansion coefficients for SST (U; blue bars) and rainfall (V; red line) for the leading JUL-AUG MCA mode. (b) Homogeneous SSTA (K std−1) map calculated by regression of SST expansion coefficient U onto global SSTA. Green contoured box denotes the region taken into account for MCA. (c) Heterogeneous map of anomalous rainfall (mm day−1 std−1) calculated by regression of SST expansion coefficient U onto regional anomalous Sahelian rainfall. Stippling denotes 95% (0.05) statistical significance under a Monte Carlo test (1000 permutations).
3.2. Forecast Using Niño 3.4 as Predictor
The Pearson correlation coefficients, as well as the RMSE skill-scores, were also evaluated with the Niño 3.4 forcing, by tracking the lagged progression from prediction lag 0 (August) to lag 4 (April) in Figure 4 (please note that only RMSE scores from standardized time series are provided). In contrast with the Mediterranean Sea, the response of August’s heavy daily rainfall is consistent within lags in terms of correlation coefficients up to lag 3 (Figure 4a–h), with the best estimate corresponding to lag 3 in terms of correlation and RMSE (Figure 4g,h). In this context, the response of August heavy daily rainfall appears significant along all the southern part of the Sahel box in terms of both metrics for lag 3. This, therefore, highlights El Niño 3.4 as a reliable predictor for the yearly contribution of heavy daily rainfall events during the peak of the WAM. Similar results were found for the extreme rainfall (not shown).
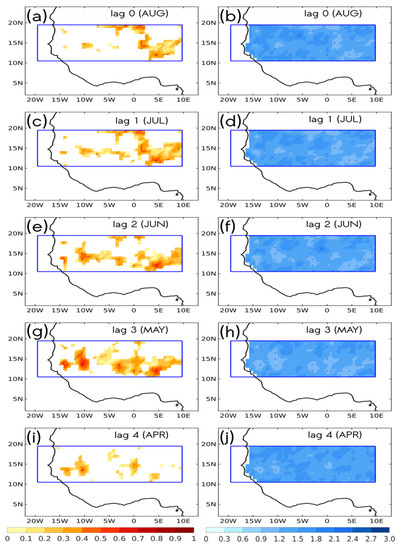
Figure 4.
As in Figure 2 but for the Niño 3.4 region (170°–120° W; 6° S–6° N) that is considered for MCA, and also only the RMSE from the standardized fields are represented. (a,b) AUG (lag 0), (c,d) JUL (lag 1), (e,f) JUN (lag 2), (g,h) MAY (lag 3) and (i,j) APR (lag 4)
Figure 5a shows the time series expansion coefficients for El Niño 3.4 SSTs (blue bars) and Sahel heavy daily precipitation (red line) anomalies, corresponding to their leading mode of co-variability at lag 3 (August for rainfall, May for SSTs), for which predictability was inferred (cf. Figure 4). The scf is 0.61. Figure 5b,c depict the spatial patterns for the leading co-variability mode between anomalous SSTs and heavy daily precipitation.
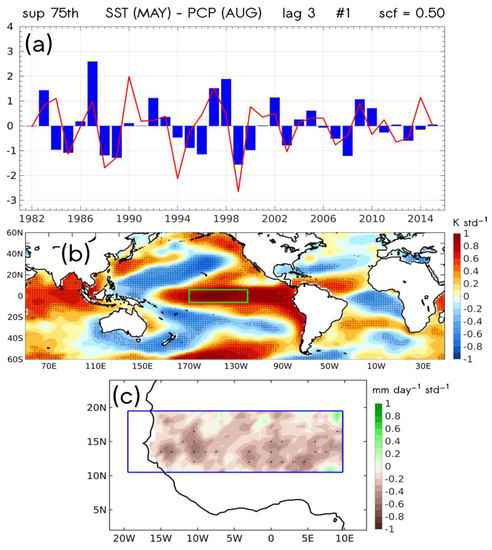
Figure 5.
As in Figure 3 but with the leading MCA mode calculated between SSTA in the Niño 3.4 region (170°–120° W; 6° S–6° N) in MAY (lag 3) and the anomalous Sahel rainfall above the 75th percentile in AUG. (a) Time series expansion coefficients for SST (U; blue bars) and rainfall (V; red line) for the leading JUL-AUG MCA mode. (b) Homogeneous SSTA (K std−1) map calculated by regression of SST expansion coefficient U onto global SSTA. Green contoured box denotes the region taken into account for MCA. (c) Heterogeneous map of anomalous rainfall (mm day−1 std−1) calculated by regression of SST expansion coefficient U onto regional anomalous Sahelian rainfall.
The fact that lag 3 Niño 3.4 SSTs provide the highest skill may be partly explained by the strong thermal inertia of tropical Pacific SSTs. Additionally, according to Figure S3, which depicts the homogeneous SST maps from lags 0–4, the worldwide patterns suggest that La Niña conditions promoting heavy Sahel precipitation appear to be decaying in time. Despite ENSO influence on the Sahel precipitation principally takes place during onset conditions, during the decay of some long-lasting La Niña events this signal has also been reported to be significant, which could be the case here [18].
3.3. Physical Mechanisms
To comprehensively analyze the dynamical mechanisms behind the statistical results provided so far, we present in Figure 6 the regression maps of the dynamical atmospheric fields described in Section 2.3 (August anomalies) onto the U expansion coefficients from the Mediterranean and ENSO lags depicting highest skill scores: lag 1-Mediterranean and lag 3-Niño3.4 (−1 sign to show La Niña conditions).
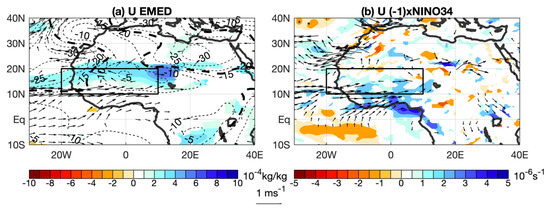
Figure 6.
Dynamical fields (Aug) regression onto the time series of the expansion coefficients for SST: (a) Mediterranean at lag 1 (Jul) and (b) Nino3.4 (−1 sign to show La Niña conditions) at lag 3 (May). In (a), the anomalies of specific humidity at 850 hPa (colors; kg kg−1), horizontal wind at 850 hPa in August (arrows; m s−1) and Sea Level Pressure (contours; 5 Pa interval); and in (b), the difference between horizontal wind divergence at 200 and 850 hPa (colors; s−1) and horizontal wind at 850 hPa in August (arrows; m s−1). In both panels, only significant anomalies are represented in colors and arrows based on 95% confidence interval using a Student’s t-test. For contours in (a) corresponding to the Sea Level Pressure anomaly, the significant threshold corresponds to the bold contours (solid (dashed) line for positive (negative) anomalies). The black boxes delimit the Sahel region.
According to Figure 6a, a warming of the eastern Mediterranean Sea may be responsible for enhanced evaporation into the air overlying the sea surface, thus inducing negative anomalies of mslp over the region. These mslp anomalies strengthen the sea level pressure gradient between the Gulf of Guinea and the Sahara, thus promoting a further penetration of the southwesterly monsoonal flow into the Sahel [34]. Other studies have suggested that for a warmer Mediterranean low-level moisture is transported by the mean flow across the Sahara to the south, feeding convergence over the Sahel to increase precipitation (e.g., [15,21]). However, in our case (Figure 6a), this effect is not evident and the moisture supply potentially increasing precipitation seems to be mainly advected from the Gulf of Guinea. Conversely, a Mediterranean cooling is known to disrupt the mechanisms aforementioned.
As for ENSO, Figure 6b shows than under La Niña conditions, the divergence of wind is increased in the upper levels, an indicator of vertical air destabilization and uplift. This is particularly evident in the southern Sahel area, where the highest prediction skill was found (Figure 4). Again, this mechanism is consistent with previous studies [34,D19]. As described by Rowell [14], deep convection is enhanced over a warmer eastern Tropical Pacific under El Niño conditions, transporting heat to the upper troposphere that triggers a stationary equatorial Kelvin wave to the east throughout the African–Atlantic sector and a Rossby wave to the west, resulting in anomalous subsidence over West Africa. The contrary (as is the case here) hold for La Niña.
When these two conditions are present at the same time, extreme precipitation may be further enhanced, as both ingredients for deep convection can interact with each other, for instance, through stronger latent heat release fluxes amplifying vertical destabilization and promoting deep organized convection. This is what was found in D19 (cf. their Figure 7), where both ENSO and Mediterranean (together) were identified as SST skillful predictors of Sahel heavy daily precipitation events.
3.4. Case Studies
In this section, we tested the use of the S4CAST to hindcast heavy daily rainfall during the monsoon peak (August) of specific years. In this context, we show two case studies for each oceanic predictor addressed in this study. The selection of the case studies was based on the skill-score time series of correlation, which were provided as outputs from the S4CAST model. Note that the rainfall signal should be evaluated focusing on regions where spatial skill scores were significant (cf. Figure 2d–f for the Mediterranean and Figure 4g,h for El Niño 3.4).
For the Mediterranean, we focused on 1994 and 2014, due to the significant values of correlation (green line in Figure 7a) relative to the whole period. Both hindcasts for 1994 and 2014 (Figure 7c,e, respectively) correctly estimated the anomalies of rainfall in the region. Nevertheless, the model underestimated the amplitude of the anomalies when compared with observations (Figure 7b,d). According to D19 (cf. their Figure 1), the year 1994 was marked by positive anomalies of total mean rainfall. Indeed, the 1994 rainy season was stated by some reports [56,57] as the wettest in 30 years across the Sahel. On year 2014, precipitation anomalies were negative, indicating a lower frequency of heavy daily precipitation events, a signal that our model was also able to replicate.
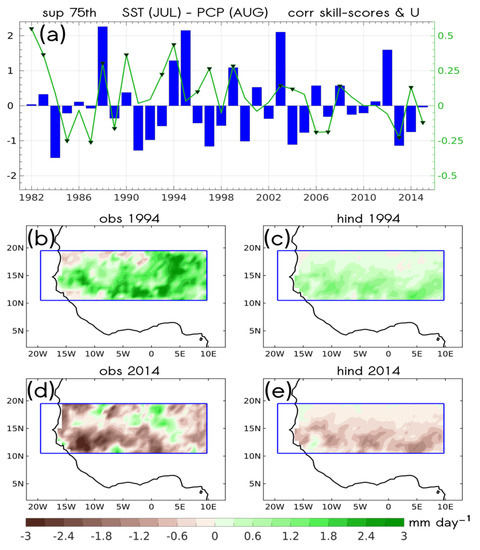
Figure 7.
Skill-score validation time series between the hindcasts and observations corresponding to the leading MCA mode between the Eastern Mediterranean SSTA (16°–38° E; 30°–40° N) in JUL (lag 1) and the anomalous Sahel (20° W–20° E; 10°–20° N) rainfall above the 75th percentile in AUG. (a) Validation time series (green line) in terms of Pearson correlation coefficients between maps of the observations and hindcasts for the regions of positive significant spatial skill scores (see Figure 2c). Significant values are denoted by green shaded triangles. Statistical significance is set at the 95% (0.05) level using the Monte Carlo method (1000 permutations). Time series expansion coefficients for SST (U; blue bars) denote the weight of the SSTA mode for each year. (b,c) Comparison between (b) observations and (c) hindcast for the 1994 case study. (d,e) Comparison between (d) observations and (e) hindcast for the 2014 case study.
Regarding the hindcasts associated with the El Niño 3.4 region as a predictor field, we show results corresponding to 1994 and 1997. The negative value for the expansion coefficient corresponding to 1994 (Figure 8a) indicates the sign reversal of the co-variability patterns with respect to what was shown in Figure 5b,c. Indeed, due to the linearity of the MCA, we expected the negative (positive) ENSO-like phase to be related to enhanced (diminished) heavy daily rainfall events, thus resulting in positive (negative) rainfall anomalies. Given that we found a La Niña-like pattern of 1994 as a reliable driver of heavy daily rainfall events resulting in positive rainfall anomalies (Figure 8b,c), by construction, El Niño must be associated with drought conditions due to the lack of such events, this being the situation for 1997 (Figure 8d,e). For both years, the sign of the hindcasted anomalies coincided with observations for the Sahel region. Nevertheless, For both 1994 and 1997, the model underestimated rainfall anomalies.
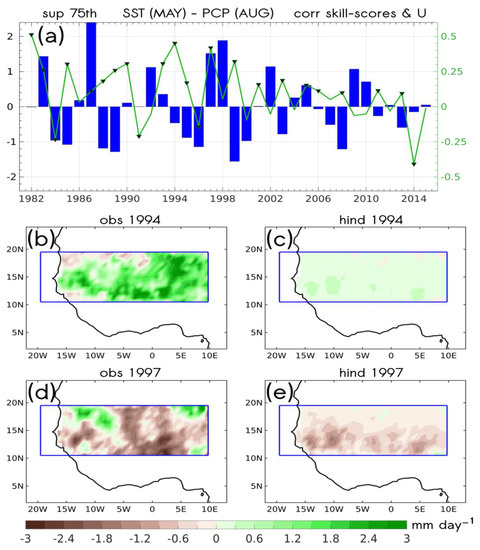
Figure 8.
As in Figure 7 but for the leading MCA mode between SSTA in the Niño 3.4 region (170°–120° W; 6° S–6° N) in MAY (lag 3), and the anomalous Sahel (20° W–20° E; 10°–20° N) rainfall above the 75th percentile in AUG (a). The case studies correspond to (b,c) 1994 and (d,e) 1997.
4. Discussion and Conclusions
In this paper, the novel Sea Surface temperature based Statistical Seasonal ForeCAST model (S4CAST; [36]) was utilized to exhaustively analyze the timing and spatial structure of the relation between Sahel heavy/extreme (75/95th percentile) daily precipitation events and skillful oceanic predictors identified in previous work: El Niño Southern Oscillation (ENSO) and the Mediterranean Sea [37]. To this aim, the NOAA Extended Reconstructed Sea Surface Temperature (SST) data set (ERSST), the Climate Hazards Group Infrared Precipitation with Station Data (CHIRPS) and the European Center for Medium-Range Weather Forecasts (ECMWF) ERA-Interim reanalysis were utilized for the period of 1982–2015.
For the Mediterranean (Figure 1, Figure 2 and Figure 3 and Figure 6), evidence was given that statistical prediction of heavy daily precipitation based on SSTs is possible up to one month in advance (predicting August precipitation in July) over a widespread area of the Sahel. These results are consistent with previous studies, as a warmer Mediterranean is known to foster humidity supply and convergence over vast Sahel areas during boreal summer [15,21,34,37]. On the contrary, colder SSTs over the Mediterranean are generally linked with a drier Sahel.
For ENSO (Figure 4, Figure 5 and Figure 6), results returned a longer forecast window of opportunity, up to three months in advance (predicting August precipitation in May), but constrained to the southernmost area of the Sahel. On the one hand, this spatial difference compared to the Mediterranean is due to the teleconnection mechanism involved, as El Niño’s impact over West Africa takes place via Kelvin and Rossby wave propagation, which act to increase subsidence over West Africa (with maximum values around the Gulf of Guinea coastline; [14,18,34]).
Finally, due to the approach undertaken in this study, ENSO and Mediterranean predictors of Sahel heavy and extreme daily precipitation were considered separately. This was done to isolate the signal of the spatial impact of each teleconnection and analyze its temporal predictability. Nevertheless, it must be noted that the prediction skill for predicting these precipitation events could improve by considering more additional Maximum Covariance Analysis modes than the leading ones or taking into account both predictors (ENSO and Mediterranean) together, as they may give feedback to each other (cf. [37]). For instance, during concomitant warmer Mediterranean SSTs and La Niña, large-scale enhanced moisture supply and vertical destabilization may be present over the Sahel, thus inducing deeper and better-organized convection owing to latent heat release processes.
In this paper, fundamental elements were provided to develop a skillful forecasting system of heavy and extreme daily precipitation events over West Africa, as shown in the analyzed case studies (Figure 7 and Figure 8). As a potential path for future research, the links between SST predictors and heavy daily precipitation events should be evaluated on a large ensemble of high-resolution Regional Climate Models, such as CORDEX-Africa.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4433/11/6/584/s1, Figure S1: Expansion coefficients time series for SST (U; blue bars) and rainfall (V; red line) corresponding to the leading MCA mode between global SSTA (60° S–60° N) and anomalous Sahel (20° W–20° E; 10–20° N) rainfall from Chirps dataset. The MCA is performed for different percentiles of precipitation: (a) above the 75th percentile; (b) above the 95th percentile; (c) below the 75th percentile and (d) total precipitation, Figure S2: Co-variability maps corresponding to the leading MCA mode calculated between SSTA over the Eastern Mediterranean Sea (EMED, 16–38° E; 30–40° N) and different percentiles of anomalous Sahel (20° W–20° E; 10–20° N) rainfall from Chirps dataset. (Left column) Homogeneous SSTA (K std−1) maps obtained by regression of SST expansion coefficient U (see Figure S1) onto EMED SSTA. (Right Column) Heterogeneous maps of anomalous rainfall (mm day−1 std−1) obtained by regression of SST expansion coefficient U onto regional anomalous Sahelian rainfall. Co-variability maps are depicted for precipitation (a,b) above the 75th percentile; (c,d) above the 95th percentile; (e,f) below the 75th percentile and (g,h) total precipitation. The squared covariance fraction (scf) for each case is shown in figure titles. Stippling denotes 95% (0.05) statistical significance under a Monte Carlo test (1000 permutations), Figure S3: As for Figure S2, but with SSTA over the Nino3.4 box (170–120° W; 6° S–6° N).
Author Contributions
M.D. led the calculations and writing of the article. R.S.-M. developed the S4CAST model, performed simulations and helped with the preparation of the article. I.G. and E.M. contributed to the conceptualization, writing, and revision of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research work was funded by the NERC/DFID Future Climate for Africa programme under the AMMA-2050 project, Grant NE/M020428/1, the EU H2020 project TRIATLAS (no. 817578) and the Spanish Ministry of Economy and Competitiveness (MINECO) project PRE4CAST (CGL2017-86415-R). Roberto Suárez-Moreno was supported by NSF award AGS-1734 760.
Acknowledgments
We are indebted to the Climate Hazards Group for providing the InfraRed Precipitation with Station data (CHIRPS; http://chg.geog.ucsb.edu/data/chirps/) the Met-Office Hadley Centre for the Sea Ice and Sea Surface Temperature dataset (HadISST; https://www.metoffice.gov.uk/hadobs/hadisst/) and the European Centre for Medium-Range Weather Forecasts for the ERA-Interim reanalysis (https://www.ecmwf.int/en/forecasts/datasets/reanalysis-datasets/era-interim). We also thank the two anonymous reviewers, whose pertinent comments and suggestions have contributed to improve this manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Turco, M.; Palazzi, E.; von Hardenberg, J.; Provenzale, A. Observed climate change hotspots. Geophys. Res. Lett. 2015, 42, 3521–3528. [Google Scholar] [CrossRef]
- Sultan, B.; Gaetani, M. Agriculture in West Africa in the twenty-first century Climate change and impacts scenarios, and potential for adaptation. Front. Plant Sci. 2016, 7, 1262. [Google Scholar] [CrossRef] [PubMed]
- Vischel, T.; Panthou, G.; Peyrillé, P.; Roehrig, R.; Quantin, G.; Lebel, T.; Wilcox, C.; Beucher, F.; Budiarti, M. Precipitation Extremes in the West African Sahel: Recent Evolution and Physical Mechanisms. In Tropical Extremes; Elsevier: Amsterdam, The Netherlands, 2019; pp. 95–138. [Google Scholar] [CrossRef]
- Batterbury, S.; Warren, A. The African Sahel 25 years after the great drought: Assessing progress and moving towards new agendas and approaches. Glob. Environ. Chang. 2001, 11, 1–8. [Google Scholar] [CrossRef]
- Mortimore, M.J.; Adams, W.M. Farmer adaptation, change and ‘crisis’ in the Sahel. Glob. Environ. Chang. 2001, 11, 49–57. [Google Scholar] [CrossRef]
- Folland, C.K.; Palmer, T.N.; Parker, D.E. Sahel rainfall and worldwide sea temperatures, 1901–1985. Nature 1986, 320, 602–607. [Google Scholar] [CrossRef]
- Rowell, D.P.; Folland, C.K.; Maskell, K.; Ward, M.N. Variability of summer rainfall over tropical North Africa (1906–92): Observations and modelling. Q. J. R. Meteor. Soc. 1995, 121, 669–704. [Google Scholar]
- Zeng, N.; Neelin, J.D.; Lau, K.M.; Tucker, C.J. Enhancement of interdecadal climate variability in the Sahel by vegetation interaction. Science 1999, 286, 1537–1540. [Google Scholar] [CrossRef]
- Wang, G.L.; Eltahir, E.A.B.; Foley, J.A.; Pollard, D.; Levis, S. Decadal variability of rainfall in the Sahel: Results from the coupled GENESIS-IBIS atmosphere–biosphere model. Clim. Dyn. 2004, 22, 625–637. [Google Scholar] [CrossRef]
- Kucharski, F.; Zeng, N.; Kalnay, E. A further assessment of vegetation feedback on decadal Sahel rainfall variability. Clim. Dyn. 2013, 40, 1453–1466. [Google Scholar] [CrossRef]
- Bjerknes, J. Atmospheric teleconnections from the equatorial Pacific. Mon. Weather Rev. 1969, 97, 163–172. [Google Scholar] [CrossRef]
- Janicot, S.; Harzallah, A.; Fontaine, B.; Moron, V. West African monsoon dynamics and eastern equatorial Atlantic and Pacific SST anomalies (1970–88). J. Clim. 1998, 11, 1874–1882. [Google Scholar] [CrossRef]
- Janicot, S.; Trzaska, S.; Poccard, I. Summer Sahel-ENSO teleconnection and decadal time scale SST variations. Clim. Dyn. 2001, 18, 303–320. [Google Scholar] [CrossRef]
- Rowell, D.P. Teleconnections between the tropical Pacific and the Sahel. Q. J. R. Meteor. Soc. 2001, 127, 1683–1706. [Google Scholar] [CrossRef]
- Rowell, D.P. The impact of Mediterranean SSTs on the Sahelian rainfall season. J. Clim. 2003, 16, 849–862. [Google Scholar] [CrossRef]
- Giannini, A.; Saravanan, R.; Chang, P. Oceanic forcing of Sahel rainfall on interannual to interdecadal time scales. Science 2003, 302, 1027–1030. [Google Scholar] [CrossRef] [PubMed]
- Giannini, A.; Saravanan, R.; Chang, P. Dynamics of the boreal summer African monsoon in the NSIPP1 atmospheric model. Clim. Dyn. 2005, 25, 517–535. [Google Scholar] [CrossRef]
- Joly, M.; Voldoire, A. Influence of ENSO on the West African monsoon: Temporal aspects and atmospheric processes. J. Clim. 2009, 22, 3193–3210. [Google Scholar] [CrossRef]
- Joly, M.; Voldoire, A. Role of the Gulf of Guinea in the inter-annual variability of the West African monsoon: What do we learn from CMIP3 coupled simulations? Int. J. Clim. 2010, 30, 1843–1856. [Google Scholar] [CrossRef]
- Fontaine, B.; Garcia-Serrano, J.; Roucou, P.; Rodriguez-Fonseca, B.; Losada, T.; Chauvin, F.; Janicot, S. Impacts of warm and cold situations in the Mediterranean basins on the West African monsoon: Observed connection patterns (1979–2006) and climate simulations. Clim. Dyn. 2010, 35, 95–114. [Google Scholar] [CrossRef]
- Gaetani, M.; Fontaine, B.; Roucou, R.; Baldi, M. Influence of the Mediterranean Sea on the West African monsoon: Intraseasonal variability in numerical simulations. J. Geophys. Res. 2010, 115, D24115. [Google Scholar] [CrossRef]
- Losada, T.; Rodríguez-Fonseca, B.; Janicot, S.; Gervois, S.; Chauvin, F.; Ruti, P. A multi-model approach to the Atlantic Equatorial mode: Impact on the West African monsoon. Clim. Dyn. 2010, 35, 29–43. [Google Scholar] [CrossRef]
- Mohino, E.; Rodríguez-Fonseca, B.; Mechoso, C.R.; Gervois, S.; Ruti, P.; Chauvin, F. Impacts of the tropical Pacific/Indian Oceans on the seasonal cycle of the West African monsoon. J. Clim. 2011, 24, 3878–3891. [Google Scholar] [CrossRef]
- Rodríguez-Fonseca, B.; Janicot, S.; Mohino, E.; Losada, T.; Bader, J.; Caminade, C.; Voldoire, A. Interannual and decadal SST-forced responses of the West African monsoon. Atmos. Sci. Lett. 2011, 12, 67–74. [Google Scholar] [CrossRef]
- Rodríguez-Fonseca, B.; Mohino, E.; Mechoso, C.R.; Caminade, C.; Biasutti, M.; Gaetani, M.; García-Serrano, J.; Vizy, E.K.; Cook, K.; Xue, Y.; et al. Variability and Predictability of West African Droughts. A review on the role of Sea Surface Temperature Anomalies. J. Clim. 2015, 28, 4034–4060. [Google Scholar] [CrossRef]
- Suárez-Moreno, R.; Rodríguez-Fonseca, B.; Barroso, J.A.; Fink, A.H. Interdecadal changes in the leading ocean forcing of Sahelian rainfall interannual variability: Atmospheric dynamics and role of multidecadal SST background. J. Clim. 2018, 31, 6687–6710. [Google Scholar] [CrossRef]
- Wahl, S.; Latif, M.; Park, W.; Keenlyside, N. On the tropical Atlantic SST warm bias in the Kiel Climate Model. Clim. Dyn. 2011, 36, 891–906. [Google Scholar] [CrossRef]
- Mohino, E.; Rodríguez-Fonseca, B.; Mechoso, C.R.; Losada, T.; Polo, I. Relationships among Intermodel Spread and Biases in Tropical Atlantic Sea Surface Temperatures. J. Clim. 2019, 32, 3615–3635. [Google Scholar] [CrossRef]
- Richter, I.; Xie, S.; Wittenberg, A.T.; Masumoto, Y. Tropical Atlantic biases and their relation to surface wind stress and terrestrial precipitation. Clim. Dyn. 2012, 38, 985–1001. [Google Scholar] [CrossRef]
- Vannière, B.; Guilyardi, E.; Madec, G.; Doblas-Reyes, F.J.; Woolnough, S. Using seasonal hindcasts to understand the origin of the equatorial cold tongue bias in CGCMs and its impact on ENSO. Clim. Dyn. 2013, 40, 963–981. [Google Scholar] [CrossRef]
- Xue, Y.; Chen, M.; Kumar, A.; Hu, Z.Z.; Wang, W. Predictions kill and bias of tropical Pacific sea surface temperatures in the NCEP Climate Forecast System version 2. J. Clim. 2013, 26, 5358–5378. [Google Scholar] [CrossRef]
- Richter, I.; Xie, S.P. On the origin of equatorial Atlantic biases in coupled general circulation models. Clim. Dyn. 2008, 31, 587–598. [Google Scholar] [CrossRef]
- Xu, Z.; Chang, P.; Richter, I.; Kim, W.; Tang, G. Diagnosing southeast tropical Atlantic SST and ocean circulation biases in the CMIP5 ensemble. Clim. Dyn. 2014, 43, 3123–3145. [Google Scholar] [CrossRef]
- Gómara, I.; Mohino, E.; Losada, T.; Dominguez, M.; Suarez-Moreno, R.; Rodriguez-Fonseca, B. Impact of dynamical regionalization on precipitation biases and teleconnections over West Africa. Clim. Dyn. 2018, 50, 4481–4506. [Google Scholar] [CrossRef]
- Steinig, S.; Harlaß, J.; Park, W.; Latif, M. Sahel rainfall strength and onset improvements due to more realistic Atlantic cold tongue development in a climate model. Sci. Rep. 2018, 8, 2569. [Google Scholar] [CrossRef]
- Suárez-Moreno, R.; Rodríguez-Fonseca, B. S4CAST v2.0: Sea surface temperature based statistical seasonal forecast model. Geosci. Model Dev. 2015, 8, 3971–4018. [Google Scholar] [CrossRef]
- Diakhaté, M.; Rodriguez-Fonseca, B.; Gómara, I.; Mohino, E.; Dieng, A.L.; Gaye, A.T. Oceanic Forcing on Interannual Variability of Sahel Heavy and Moderate Daily Rainfall. J. Hydrometeorol. 2019. [Google Scholar] [CrossRef]
- Rowell, D.P. Simulating SST teleconnections to Africa: What is the state of the art? J. Clim. 2013, 26, 5397–5418. [Google Scholar] [CrossRef]
- Peyrillé, P.; Lafore, J.P.; Redelsperger, J.L. An idealized two-dimensional framework to study the West African monsoon. Part I: Validation and key controlling factors. J. Atmos. Sci. 2007, 64, 2765–2782. [Google Scholar]
- Fontaine, B.; Monerie, P.A.; GaetRoweani, M.; Roucou, P. Climate adjustments over the African-Indian monsoon regions accompanying Mediterranean Sea thermal variability. J. Geophys. Res. 2011, 116, D23122. [Google Scholar] [CrossRef]
- Martin, E.R.; Thorncroft, C.D. The impact of the AMO on the West African monsoon annual cycle. Q. J. R. Meteorol. Soc. 2014, 140, 31–46. [Google Scholar] [CrossRef]
- Funk, C.C.; Peterson, P.J.; Landsfeld, M.F.; Pedreros, D.H.; Verdin, J.P.; Rowland, J.D.; Romero, B.E.; Husak, G.J.; Michaelsen, J.C.; Verdin, A.P. A quasi-global precipitation time series for drought monitoring. US Geol. Surv. Data Ser. 2014, 832, 1–12. [Google Scholar] [CrossRef]
- Funk, C.C.; Verdin, A.; Michaelsen, J.; Peterson, P.; Pedreros, D.; Husak, G. A global satellite-assisted precipitation climatology. Earth Syst. Sci. Data 2015, 7, 275–287. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W. Extended reconstruction of global sea surface temperatures based on COADS data (1854–1997). J. Clim. 2003, 16, 1495–1510. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W. Improved extended reconstruction of SST (1854–1997). J. Clim. 2004, 17, 2466–2477. [Google Scholar] [CrossRef]
- Smith, T.M.; Reynolds, R.W.; Peterson, T.C.; Lawrimore, J. Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880–2006). J. Clim. 2008, 21, 2283–2296. [Google Scholar] [CrossRef]
- Ebisuzaki, W. A method to estimate the statistical significance of a correlation when the data are serially correlated. J. Clim. 1997, 10, 2147–2153. [Google Scholar] [CrossRef]
- Bretherton, C.S.; Smith, C.; Wallace, J.M. An intercomparison of methods for finding coupled patterns in climate data. J. Clim. 1992, 5, 541–560. [Google Scholar] [CrossRef]
- Cherry, S. Singular value decomposition analysis and canonical correlation analysis. J. Clim. 1996, 9, 2003–2009. [Google Scholar] [CrossRef][Green Version]
- Widmann, M. One-dimensional CCA and SVD, and their relationship to regression maps. J. Clim. 2005, 18, 2785–2792. [Google Scholar] [CrossRef]
- Dayan, H.; Vialard, J.; Izumo, T.; Lengaigne, M. Does sea surface temperature outside the tropical Pacific contribute to enhanced ENSO predictability? Clim. Dyn. 2014, 43, 1311–1325. [Google Scholar] [CrossRef]
- Ter Braak, C.J.F.; Juggins, S. Weighted averaging partial least squares regression (WA-PLS): An improved method for reconstructing environmental variables from species assemblages. Hydrobiologia 1993, 269–270, 485–502. [Google Scholar] [CrossRef]
- Birks, H.J.B. The use of pollen analysis in the reconstruction of past climates: A review. In Climate and History: Studies in Past Climates and Their Impact on Man; Wigley, T.M.L., Ingram, M.J., Farmer, G., Eds.; Cambridge University Press: Cambridge, UK, 1981; pp. 111–138. [Google Scholar]
- Wang, B.; Xiang, B.; Li, J.; Webster, P.J.; Rajeevan, M.N.; Liu, J.; Ha, K.J. Rethinking Indian monsoon rainfall prediction in the context of recent global warming. Nat. Commun. 2015, 6, 7154. [Google Scholar] [CrossRef] [PubMed]
- Dee, D.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Con-figuration and performance of the data assimilation system. Q. J. R. Meteor. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- LeCompte, D.; Tinker, R.; Dionne, J.; Halpert, M.; Thiaw, W. Wettest Rainy Season in 30 Years across African Sahel; Special Climate Summary 94/2; NOAA: Washington, DC, USA, 1994; Available from the Climate Prediction Center Website. Available online: https://www.cpc.ncep.noaa.gov/products/assessments/assess_94/sahel.html (accessed on 9 April 2020).
- Nicholson, S.; Ba, M.; Kim, Y.J. Rainfall in the Sahel during 1994. J. Clim. 1996, 9, 1673–1680. [Google Scholar] [CrossRef][Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).