Effects of Model Coupling on Typhoon Kalmaegi (2014) Simulation in the South China Sea
Abstract
1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Best-Track Data
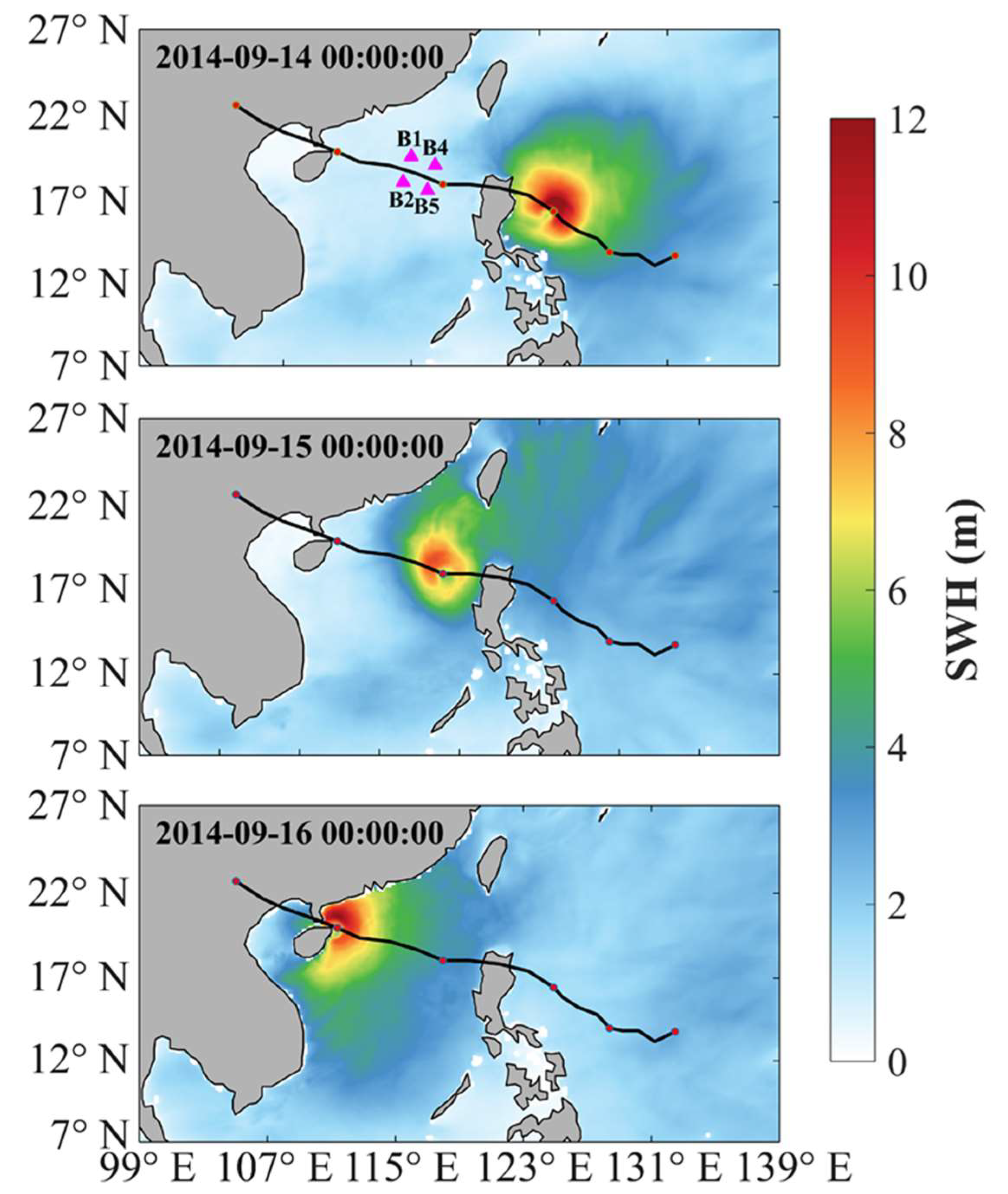
2.1.2. In-Situ Data
2.1.3. Satellite Data
2.1.4. Reanalysis and Model Data
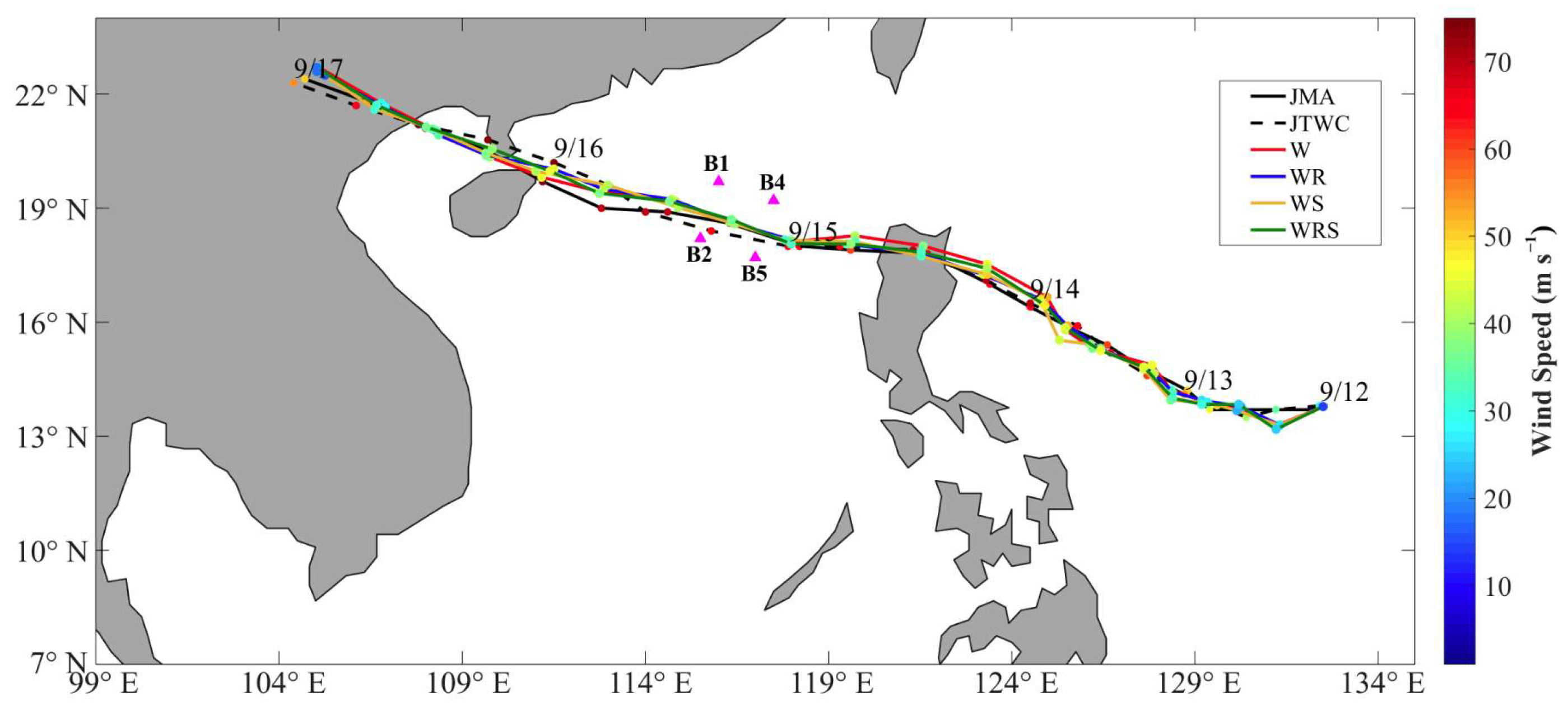
2.2. Model and Experimental Design
2.2.1. COAWST
2.2.2. Atmospheric Model
2.2.3. Oceanic Model
2.2.4. Wave Model
2.3. Sensitivity Tests
2.4. Evaluation of Model Performance
3. Results
3.1. Atmospheric Parameters
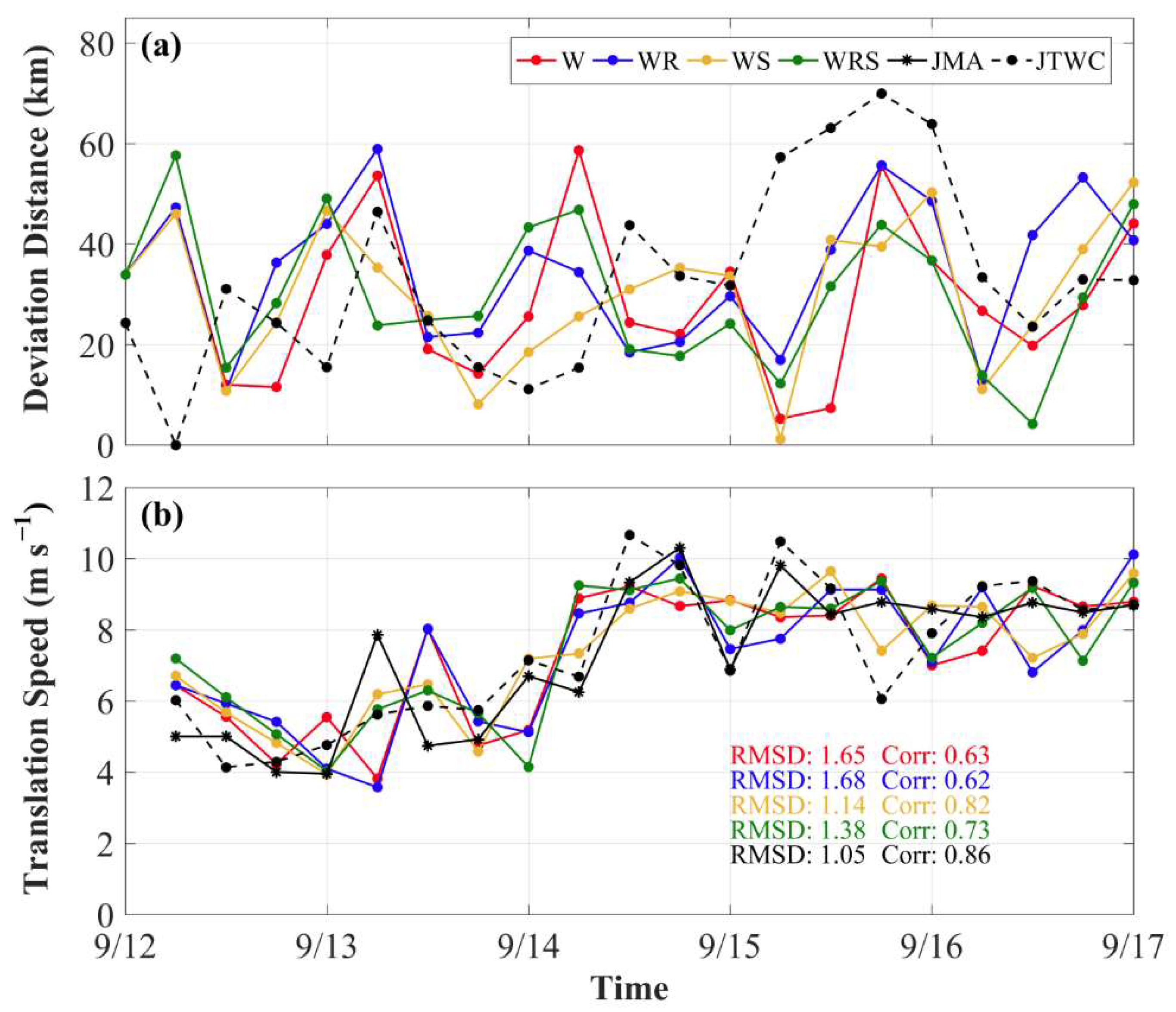
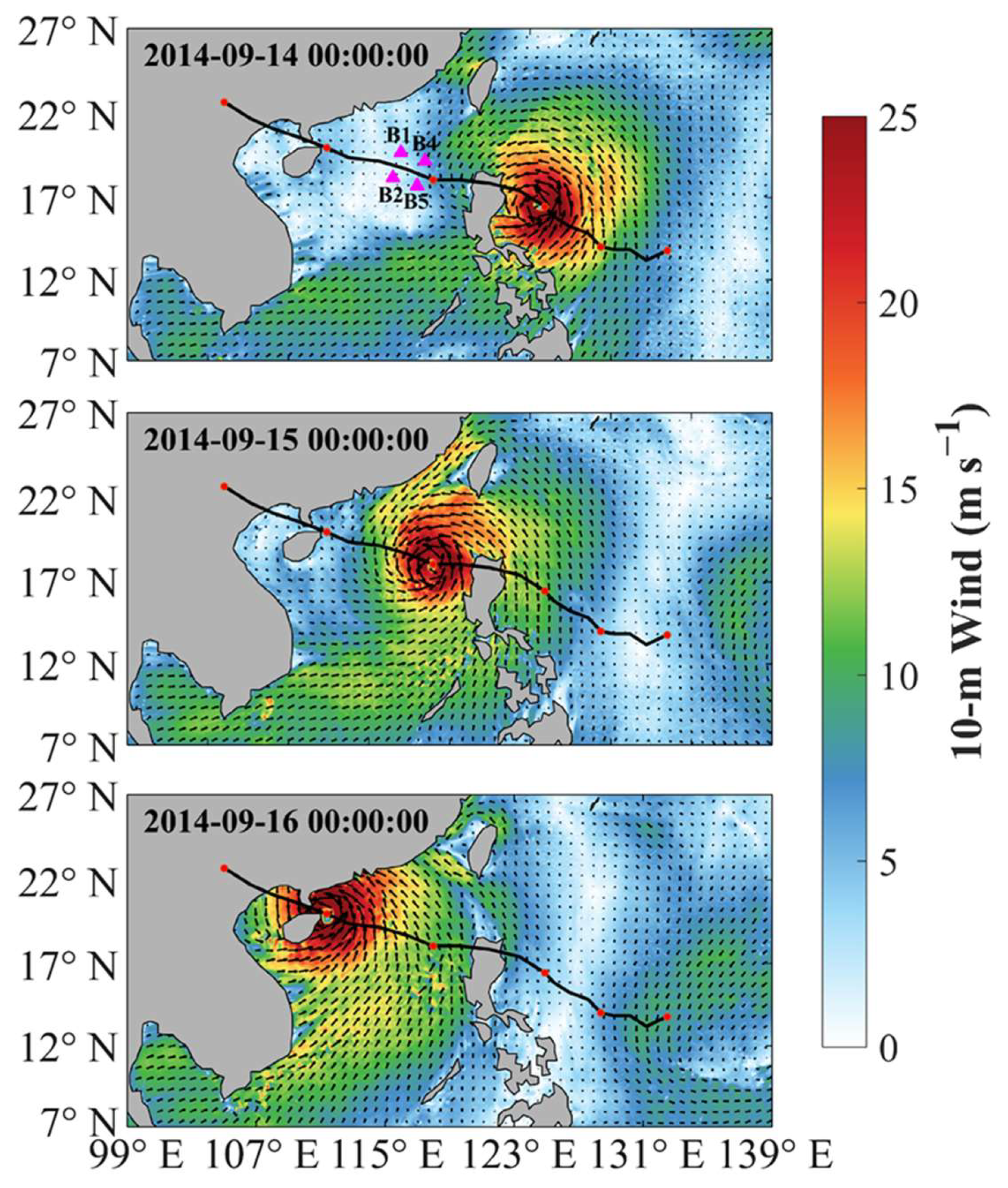
3.1.1. Typhoon Track and Intensity
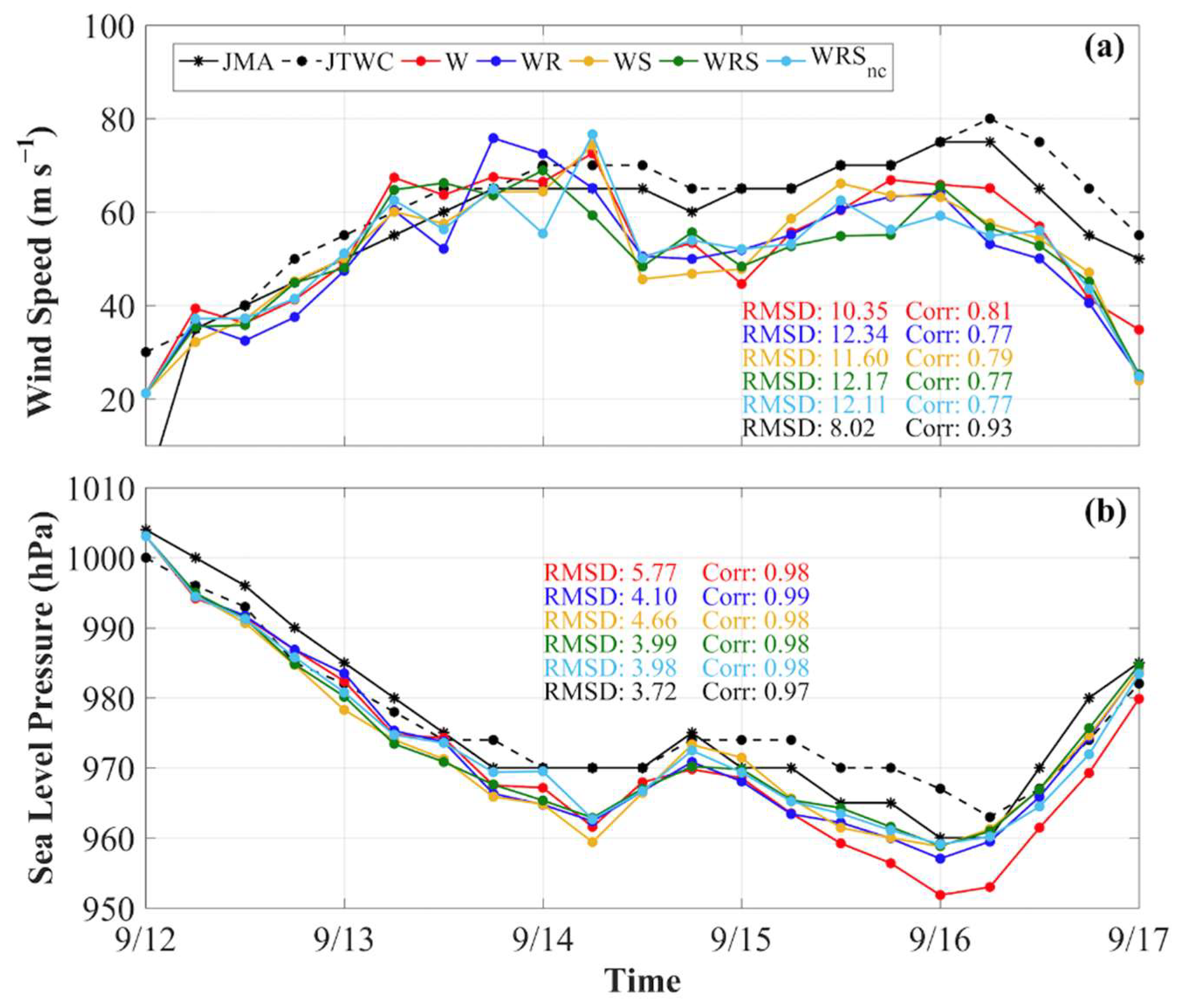
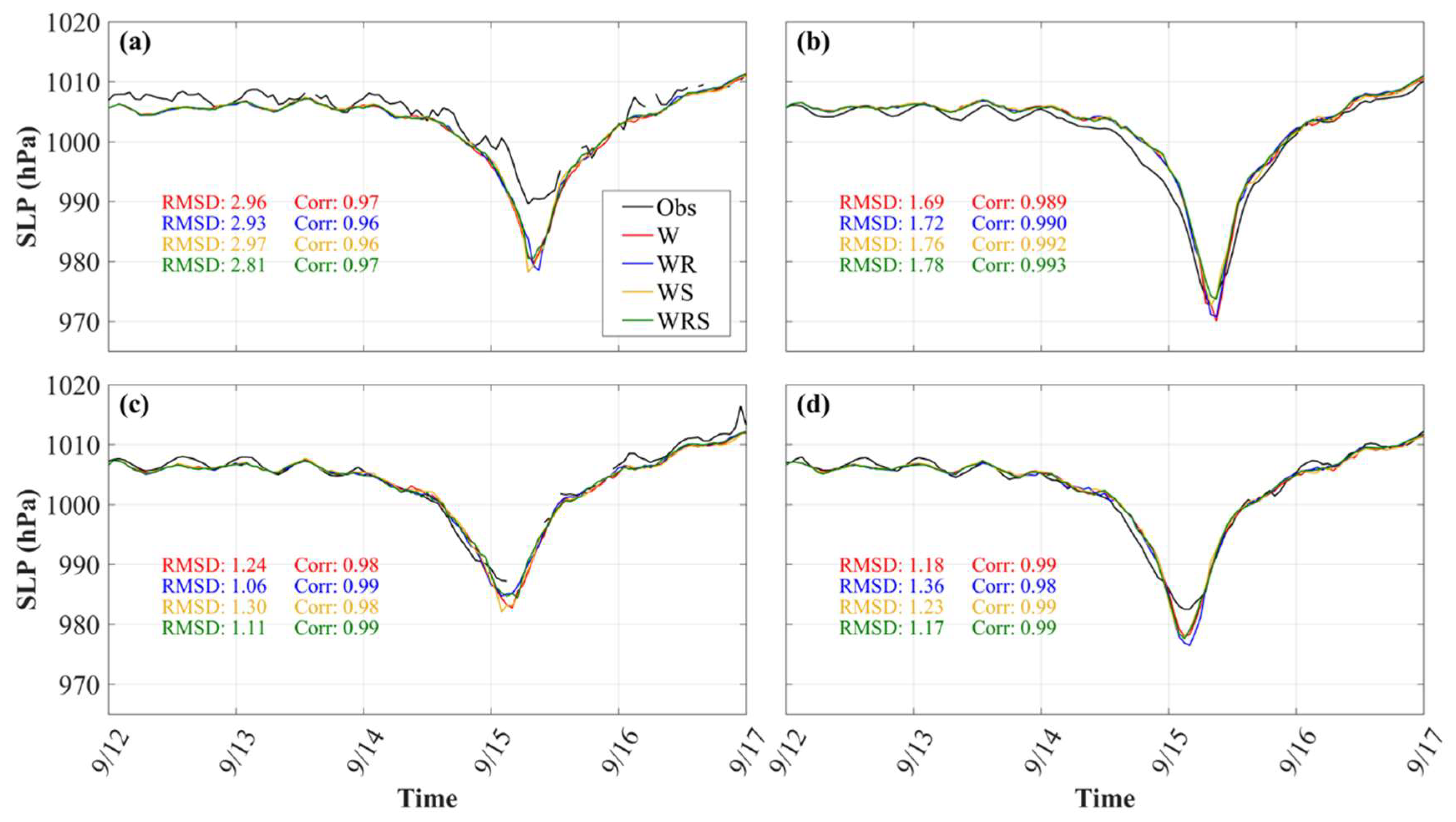
3.1.2. Sea Level Pressure
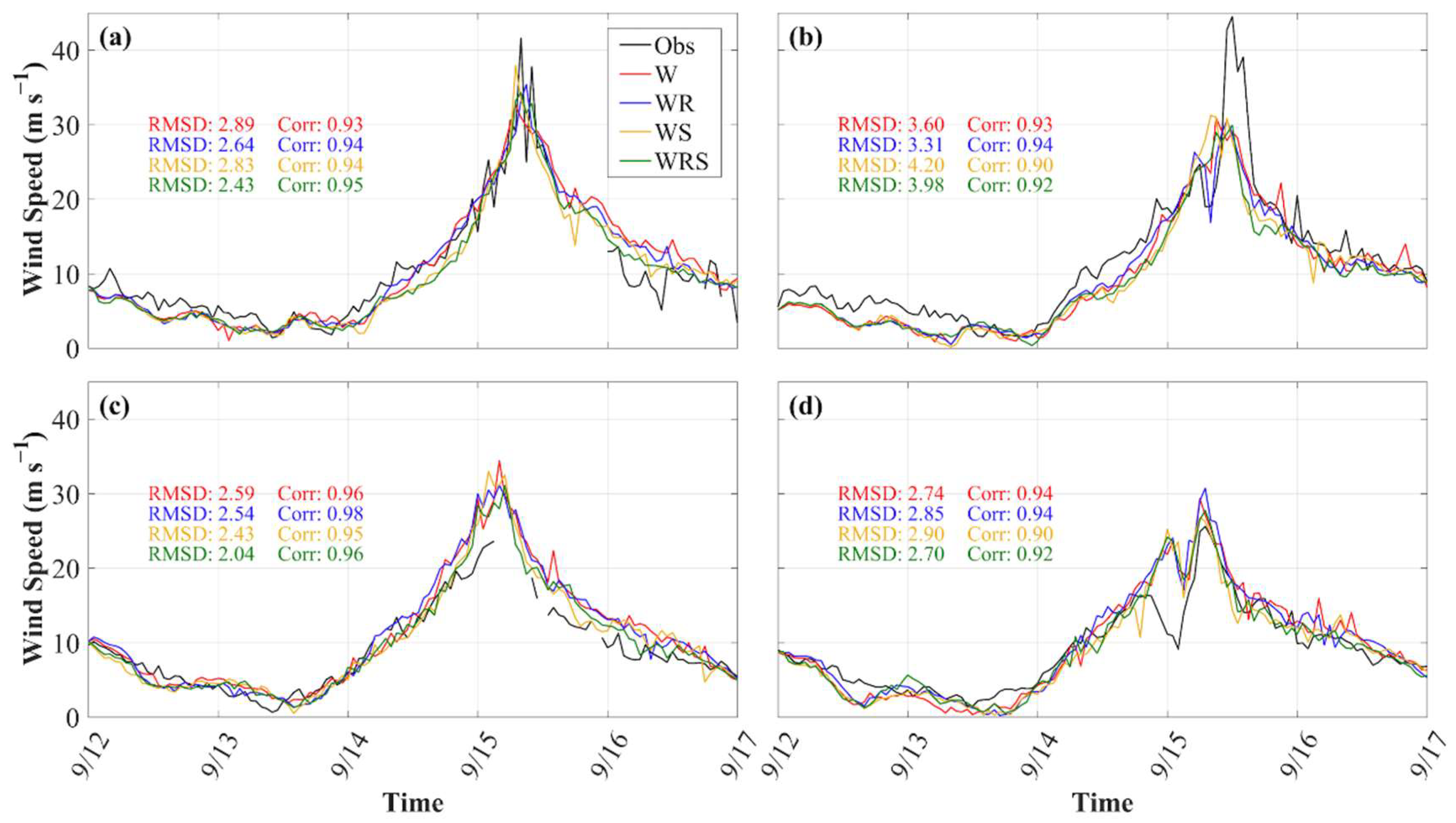
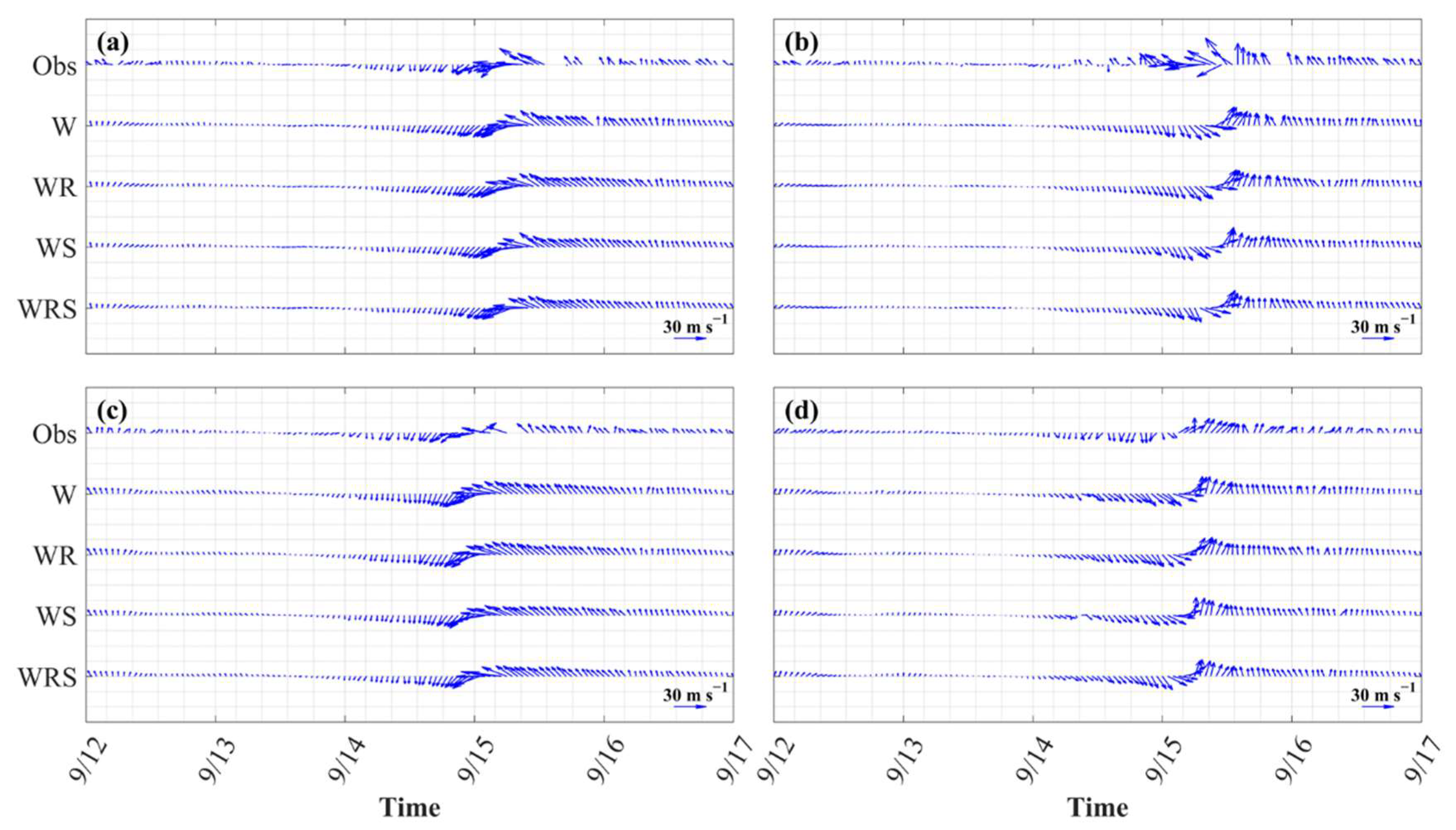
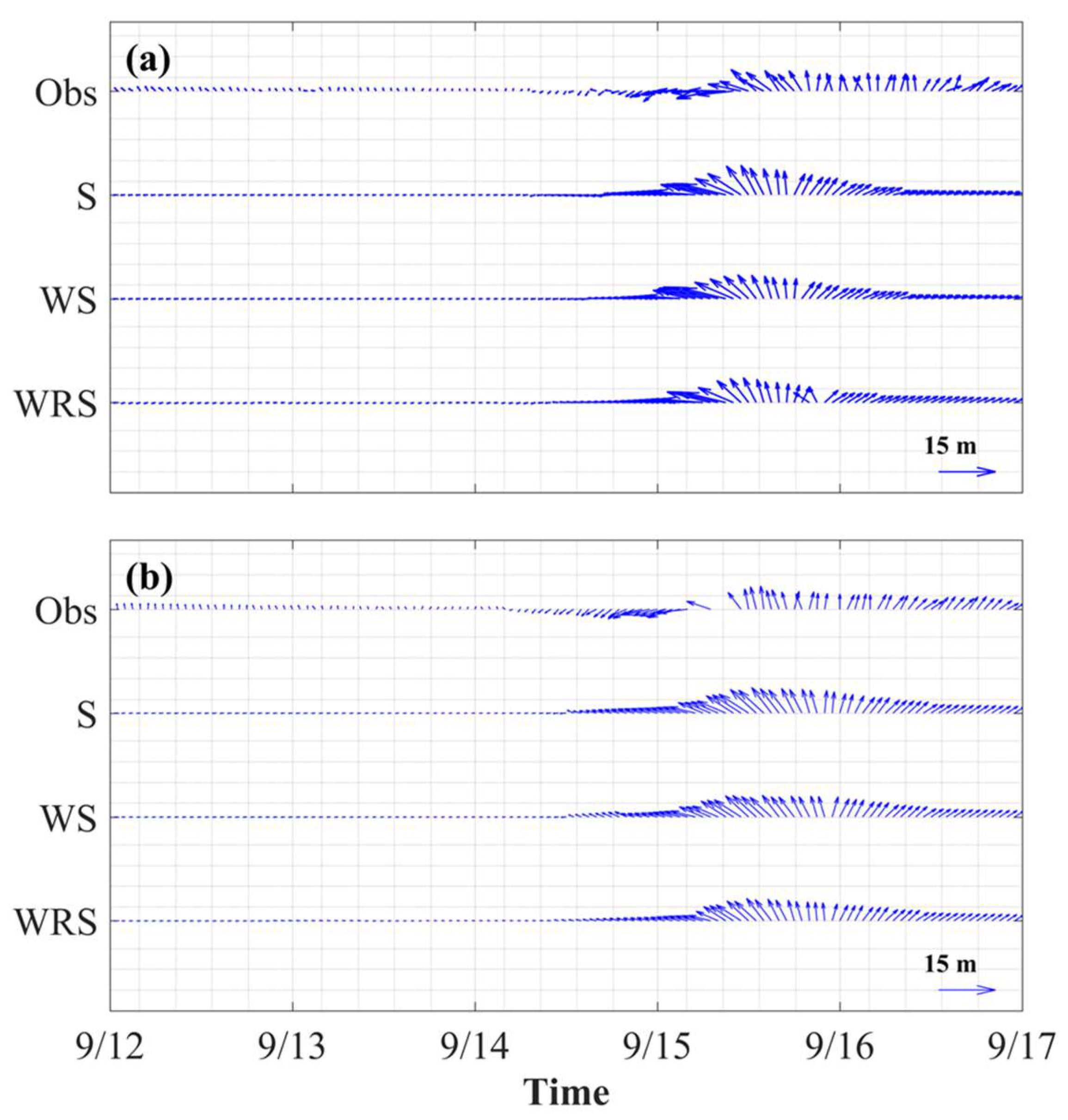
3.1.3. 10-m Wind
3.2. Oceanic Parameters
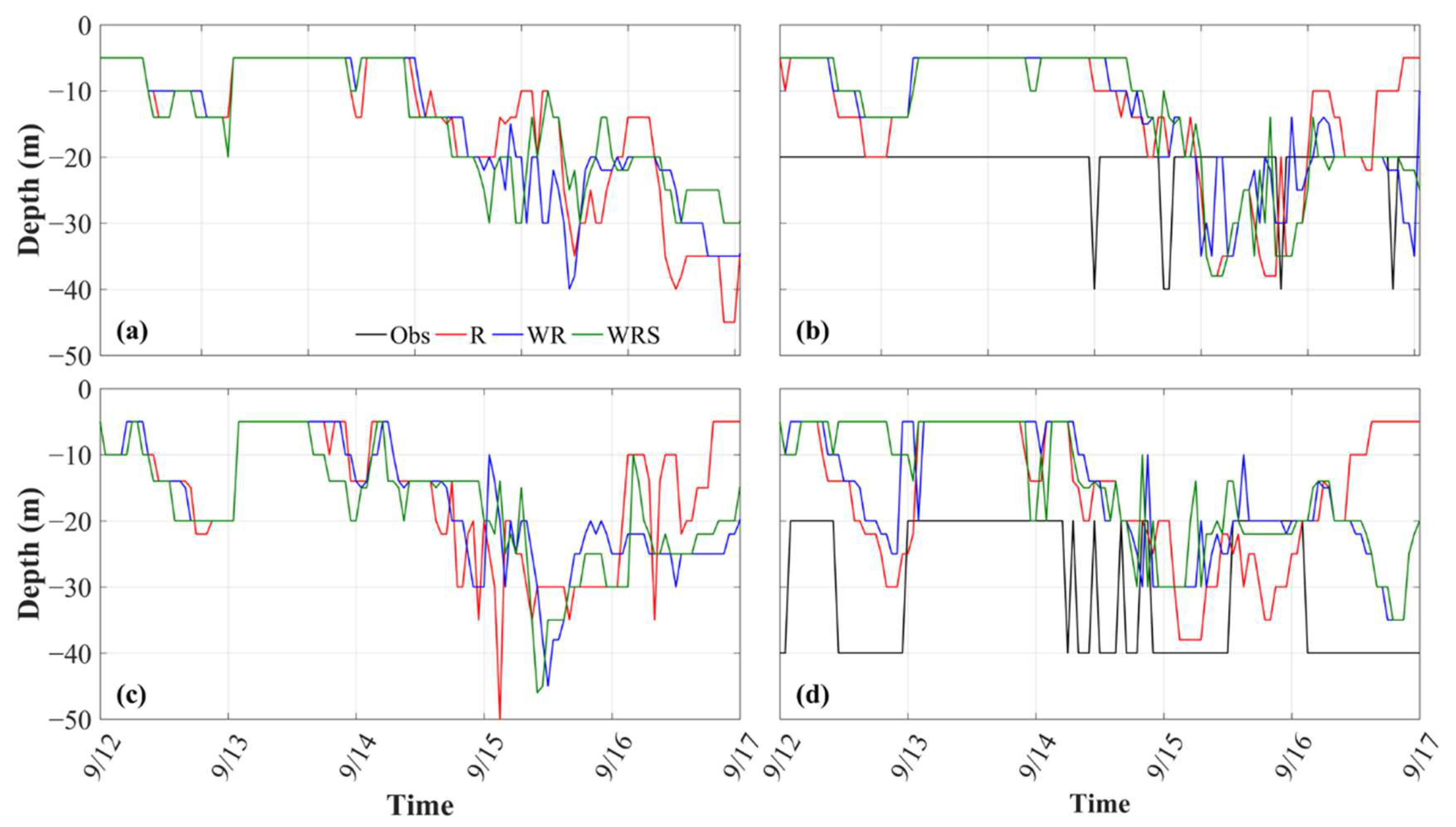
3.2.1. Ocean Current
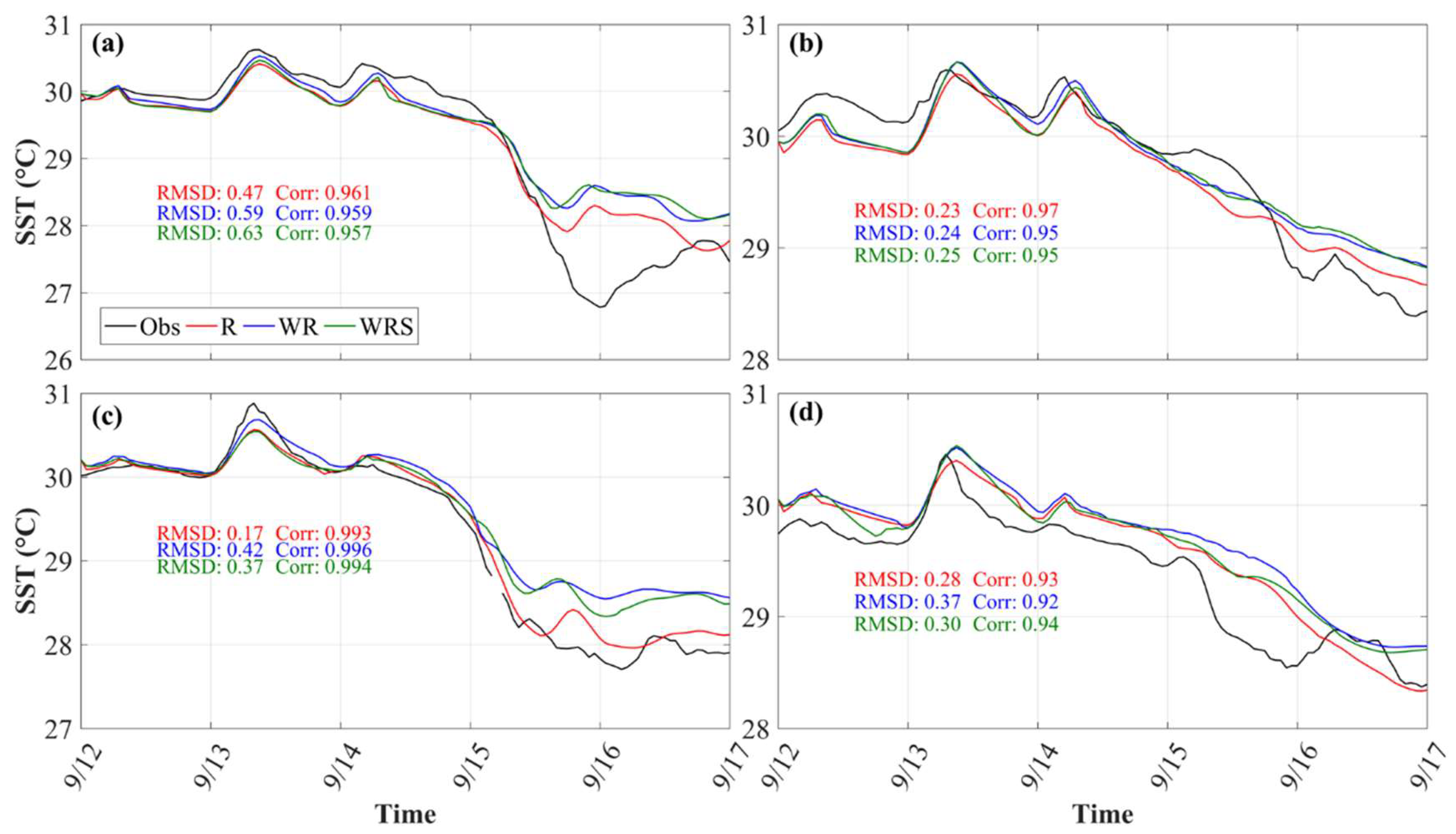
3.2.2. Sea Surface Temperature
3.2.3. Significant Wave Height
3.3. Skill Score
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Peduzzi, P.; Chatenoux, B.; Dao, H.; De Bono, A.; Herold, C.; Kossin, J.; Mouton, F.; Nordbeck, O. Global trends in tropical cyclone risk. Nat. Clim. Chang. 2012, 2, 289–294. [Google Scholar] [CrossRef]
- Emanuel, K. Will global warming make hurricane forecasting more difficult? Bull. Am. Meteorol. Soc. 2017, 98, 495–501. [Google Scholar] [CrossRef]
- Chang, Y.C.; Chen, G.Y.; Tseng, R.S.; Centurioni, L.R.; Chu, P.C. Observed near-surface flows under all tropical cyclone intensity levels using drifters in the northwestern Pacific. J. Geophys. Res. Ocean. 2013, 118, 2367–2377. [Google Scholar] [CrossRef]
- Brooks, D.A. The wake of Hurricane Allen in the western Gulf of Mexico. J. Phys. Oceanogr. 1983, 13, 117–129. [Google Scholar] [CrossRef]
- Wang, D.; Zhao, H. Estimation of phytoplankton responses to Hurricane Gonu over the Arabian Sea based on ocean color data. Sensors 2008, 8, 4878–4893. [Google Scholar] [CrossRef]
- Marks, F.; Shay, L.K. Landfalling Tropical Cyclones: Forecast Problems and Associated Research Opportunities. Bull. Am. Meteorol. Soc. 1998, 79, 305–323. [Google Scholar]
- Wu, R.; Zhang, H.; Chen, D.; Li, C.; Lin, J. Impact of Typhoon Kalmaegi (2014) on the South China Sea: Simulations using a fully coupled atmosphere-ocean-wave model. Ocean Model. 2018, 131, 132–151. [Google Scholar] [CrossRef]
- Price, J.F. Upper Ocean Response to a Hurricane. J. Phys. Ocean. 1981, 11, 153–175. [Google Scholar] [CrossRef]
- Bender, M.A.; Ginis, I.; Kurihara, Y. Numerical Simulations of Tropical Cyclone-Ocean Interaction With a High-Resolution Coupled Model. J. Geophys. Res. 1993, 98, 23245–23263. [Google Scholar] [CrossRef]
- Huang, P.; Sanford, T.B.; Imberger, J. Heat and turbulent kinetic energy budgets for surface layer cooling induced by the passage of Hurricane Frances (2004). J. Geophys. Res. 2009, 114, C12023. [Google Scholar] [CrossRef]
- Jullien, S.; Marchesiello, P.; Menkes, C.E.; Lefèvre, J.; Jourdain, N.C.; Samson, G.; Lengaigne, M. Ocean feedback to tropical cyclones: Climatology and processes. Clim. Dyn. 2014, 43, 2831–2854. [Google Scholar] [CrossRef]
- Riehl, H. A Model of Hurricane Formation. J. Appl. Phys. 1950, 21, 917. [Google Scholar] [CrossRef]
- Schade, L.R. Tropical Cyclone Intensity and Sea Surface Temperature. J. Atmos. Sci. 2000, 57, 3122–3130. [Google Scholar] [CrossRef]
- Yablonsky, R.M.; Ginis, I. Impact of a Warm Ocean Eddy’s Circulation on Hurricane-Induced Sea Surface Cooling with Implications for Hurricane Intensity. Mon. Weather Rev. 2013, 141, 997–1021. [Google Scholar] [CrossRef]
- Cangialosi, J.P. National Hurricane Center Forecast Verification—2018 Hurricane Season; National Hurricane Center: Miami, FL, USA; NOAA: Silver Spring, MD, USA, 2019.
- DeMaria, M.; Sampson, C.R.; Knaff, J.A.; Musgrave, K.D. Is tropical cyclone intensity guidance improving? Bull. Am. Meteorol. Soc. 2014, 95, 387–398. [Google Scholar] [CrossRef]
- Zambon, J.B.; He, R.; Warner, J.C. Investigation of hurricane Ivan using the Coupled Ocean–Atmosphere–Wave–Sediment Transport (COAWST) Model. Ocean Dyn. 2014, 64, 1535–1554. [Google Scholar] [CrossRef]
- Haghroosta, T.; Ismail, W.R. Typhoon activity and some important parameters in the South China Sea. Weather Clim. Extrem. 2017, 17, 29–35. [Google Scholar] [CrossRef]
- He, H.; Yang, J.; Wu, L.; Gong, D.; Wang, B.; Gao, M. Unusual growth in intense typhoon occurrences over the Philippine Sea in September after the mid-2000s. Clim. Dyn. 2017, 48, 1893–1910. [Google Scholar] [CrossRef]
- Liu, B.; Liu, H.; Xie, L.; Guan, C.; Zhao, D. A Coupled Atmosphere–Wave–Ocean Modeling System: Simulation of the Intensity of an Idealized Tropical Cyclone. Mon. Weather Rev. 2011, 139, 132–152. [Google Scholar] [CrossRef]
- Lengaigne, M.; Neetu, S.; Samson, G.; Vialard, J.; Krishnamohan, K.S.; Masson, S.; Jullien, S.; Suresh, I.; Menkes, C.E. Influence of air–sea coupling on Indian Ocean tropical cyclones. Clim. Dyn. 2019, 52, 577–598. [Google Scholar] [CrossRef]
- Chen, S.S.; Price, J.F.; Zhao, W.; Donelan, M.A.; Walsh, E.J. The CBLAST-Hurricane Program and the Next-Generation Fully Coupled Atmosphere–Wave–Ocean Models for Hurricane Research and Prediction. Bull. Am. Meteorol. Soc. 2007, 88, 311–318. [Google Scholar] [CrossRef]
- Chen, S.S.; Curcic, M. Ocean surface waves in Hurricane Ike (2008) and Superstorm Sandy (2012): Coupled model predictions and observations. Ocean Model. 2016, 103, 161–176. [Google Scholar] [CrossRef]
- Aijaz, S.; Ghantous, M.; Babanin, A.V.; Ginis, I.; Thomas, B.; Wake, G. Nonbreaking wave-induced mixing in upper ocean during tropical cyclones using coupled hurricane-ocean-wave modeling. J. Geophys. Res. Ocean. 2017, 122, 1–22. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Chu, P.C.; Guan, C.; Fu, H.; Chao, G.; Han, G.; Li, W. Impact of sea spray on the Yellow and East China Seas thermal structure during the passage of Typhoon Rammasun (2002). J. Geophys. Res. Ocean. 2017, 122, 7783–7802. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, X.; Wu, R.; Liu, F.; Yu, L.; Shang, X.; Qi, Y.; Wang, Y.; Song, X.; Xie, X.; et al. Ocean Response to Successive Typhoons Sarika and Haima (2016) Based on Data Acquired via Multiple Satellites and Moored Array. Remote Sens. 2019, 11, 2360. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Q. Directional spectra of hurricane-generated waves in the Gulf of Mexico. Geophys. Res. Lett. 2011, 38, L19608. [Google Scholar] [CrossRef]
- Bao, J.W.; Wilczak, J.M.; Choi, J.K.; Kantha, L.H. Numerical Simulations of Air–Sea Interaction under High Wind Conditions Using a Coupled Model: A Study of Hurricane Development. Mon. Weather Rev. 2000, 128, 2190–2210. [Google Scholar] [CrossRef]
- Wang, Y.; Kepert, J.D.; Holland, G.J. The Effect of Sea Spray Evaporation on Tropical Cyclone Boundary Layer Structure and Intensity. Mon. Weather Rev. 2001, 129, 2481–2500. [Google Scholar] [CrossRef]
- Liu, B.; Guan, C.; Xie, L.; Zhao, D. An Investigation of the Effects of Wave State and Sea Spray on an Idealized Typhoon Using an Air–Sea Coupled Modeling System. Adv. Atmos. Sci. 2012, 29, 391–406. [Google Scholar] [CrossRef]
- Zhao, B.; Qiao, F.; Cavaleri, L.; Wang, G.; Bertotti, L.; Liu, L. Sensitivity of typhoon modeling to surface waves and rainfall. J. Geophys. Res. Ocean. 2017, 122, 1702–1723. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Powell, M.D.; Pietrzak, J.D. Wind and waves in extreme hurricanes. J. Geophys. Res. Ocean. 2012, 117, C09003. [Google Scholar] [CrossRef]
- Rusu, L.; Guedes Soares, C. Modelling the wave-current interactions in an offshore basin using the SWAN model. Ocean Eng. 2011, 38, 63–76. [Google Scholar] [CrossRef]
- Donelan, M.A.; Dobson, F.W.; Smith, S.D.; Anderson, R.J. On the Dependence of Sea Surface Roughness on Wave Development. J. Phys. Oceanogr. 1993, 23, 2143–2149. [Google Scholar] [CrossRef]
- Tolman, H.L. A Third-Generation Model for Wind Waves on Slowly Varying, Unsteady, and Inhomogeneous Depths and Currents. J. Phys. Oceanogr. 1991, 21, 782–797. [Google Scholar] [CrossRef]
- Qiao, F.; Yuan, Y.; Yang, Y.; Zheng, Q.; Xia, C.; Ma, J. Wave-induced mixing in the upper ocean: Distribution and application to a global ocean circulation model. Geophys. Res. Lett. 2004, 31, L11303. [Google Scholar] [CrossRef]
- Craik, A.D.D.; Leibovich, S. A rational model for Langmuir circulations. J. Fluid Mech. 1976, 73, 401–426. [Google Scholar] [CrossRef]
- Wang, H.; Dong, C.; Yang, Y.; Gao, X. Parameterization of Wave-Induced Mixing Using the Large Eddy Simulation (LES) (I). Atmosphere (Basel) 2020, 11, 207. [Google Scholar] [CrossRef]
- Melville, W.K. The Role of Surface-Wave Breaking in Air-Sea Interaction. Annu. Rev. Fluid Mech. 1996, 28, 279–321. [Google Scholar] [CrossRef]
- Price, J.F.; Sanford, T.B.; Forristall, G.Z. Forced Stage Response to a Moving Hurricane. J. Phys. Oceanogr. 1994, 24, 233–260. [Google Scholar] [CrossRef]
- Warner, J.C.; Armstrong, B.; He, R.; Zambon, J.B. Development of a Coupled Ocean-Atmosphere-Wave-Sediment Transport (COAWST) Modeling System. Ocean Model. 2010, 35, 230–244. [Google Scholar] [CrossRef]
- Pianezze, J.; Barthe, C.; Bielli, S.; Tulet, P.; Jullien, S.; Cambon, G.; Bousquet, O.; Claeys, M.; Cordier, E. A New Coupled Ocean-Waves-Atmosphere Model Designed for Tropical Storm Studies: Example of Tropical Cyclone Bejisa (2013–2014) in the South-West Indian Ocean. J. Adv. Model. Earth Syst. 2018, 10, 801–825. [Google Scholar] [CrossRef]
- Doyle, J.D. Coupled Atmosphere–Ocean Wave Simulations under High Wind Conditions. Mon. Weather Rev. 2002, 130, 3087–3099. [Google Scholar] [CrossRef]
- Zhao, X.; Chan, J.C.L. Changes in Tropical Cyclone Intensity with Translation Speed and Mixed Layer Depth: Idealized WRF-ROMS Coupled Model Simulations. Q. J. R. Meteorol. Soc. 2017, 143, 152–163. [Google Scholar] [CrossRef]
- National Geophysical Data Center. 2-minute Gridded Global Relief Data (ETOPO2) v2. Available online: https://ngdc.noaa.gov/mgg/global/etopo2.html (accessed on 10 August 2019).
- Ricchi, A.; Miglietta, M.M.; Barbariol, F.; Benetazzo, A.; Bergamasco, A.; Bonaldo, D.; Cassardo, C.; Falcieri, F.M.; Modugno, G.; Russo, A.; et al. Sensitivity of a Mediterranean Tropical-Like Cyclone to Different Model Configurations and Coupling Strategies. Atmosphere (Basel) 2017, 8, 92. [Google Scholar] [CrossRef]
- Japan Meteorological Agency Tokyo-Typhoon Center Best-Track Data. Available online: https://www.jma.go.jp/jma/jma-eng/jma-center/rsmc-hp-pub-eg/besttrack.html (accessed on 2 July 2019).
- Joint Typhoon Warning Center Best-Track Data. Available online: http://www.usno.navy.mil/JTWC (accessed on 2 July 2019).
- Zhang, H.; Chen, D.; Zhou, L.; Liu, X.; Ding, T.; Zhou, B. Upper ocean response to typhoon Kalmaegi (2014). J. Geophys. Res. Ocean. 2016, 121, 6520–6535. [Google Scholar] [CrossRef]
- Remote Sensing Systems. Available online: http://www.remss.com (accessed on 25 July 2019).
- National Centers for Environmental Protection (NCEP) Final (FNL) Operational Global Analysis. Available online: http://rda.ucar.edu/datasets (accessed on 3 July 2019).
- HYbrid Coordinate Ocean Model (HYCOM). Available online: https://hycom.org/data/glbu0pt08/expt-91pt1 (accessed on 21 July 2019).
- WaveWatch III (WW3) Global Wave Model. Available online: https://coastwatch.pfeg.noaa.gov/erddap/griddap/ (accessed on 3 August 2019).
- Skamarock, W.C.; Klemp, J.B.; Dudhi, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3 (No. NCAR/TN-475+STR); University Corporation for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Model. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Booij, N.; Ris, R.C.; Holthuijsen, L.H. A third-generation wave model for coastal regions 1. Model description and validation. J. Geophys. Res. 1999, 104, 7649–7666. [Google Scholar] [CrossRef]
- Larson, J.; Jacob, R.; Ong, E. The Model Coupling Toolkit: A New Fortran90 Toolkit for Building Multiphysics Parallel Coupled Models. Int. J. High Perform. Comput. Appl. 2005, 19, 277–292. [Google Scholar] [CrossRef]
- Jones, P.W. A User’s Guide for SCRIP: A Spherical Coordinate Remapping and Interpolation Package; Los Alamos National Laboratory: Los Alamos, NM, USA, 1998.
- Carniel, S.; Benetazzo, A.; Bonaldo, D.; Falcieri, F.; Miglietta, M.; Ricchi, A.; Sclavo, M. Scratching beneath the surface while coupling atmosphere, ocean and waves: Analysis of a dense water formation event. Ocean Model. 2016, 58, 154–172. [Google Scholar] [CrossRef]
- Ricchi, A.; Miglietta, M.M.; Falco, P.P.; Benetazzo, A.; Bonaldo, D.; Bergamasco, A.; Sclavo, M.; Carniel, S. On the use of a coupled ocean-atmosphere-wave model during an extreme cold air outbreak over the Adriatic Sea. Atmos. Res. 2016, 172, 48–65. [Google Scholar] [CrossRef]
- Shan, H.X.; Dong, C.M. The SST–Wind Coupling Pattern in the East China Sea Based on a Regional Coupled Ocean–Atmosphere Model. Atmos.-Ocean 2017, 55, 230–246. [Google Scholar] [CrossRef]
- Charnock, H. Wind stress on a water surface. Q. J. R. Meteorol. Soc. 1955, 81, 639–640. [Google Scholar] [CrossRef]
- Taylor, P.K.; Yelland, M.J. The Dependence of Sea Surface Roughness on the Height and Steepness of the Waves. J. Phys. Oceanogr. 2001, 31, 572–590. [Google Scholar] [CrossRef]
- Kain, J.S. The Kain—Fritsch convective parameterization: An update. J. Appl. Meteorol. 2004, 43, 170–181. [Google Scholar] [CrossRef]
- Hong, S.Y.; Lim, J.O.J. The WRF Single-Moment 6-Class Microphysics Scheme (WSM6). J. Korean Meteorol. Soc. 2006, 42, 129–151. [Google Scholar]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the Winter Monsoon Experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Nakanishi, M.; Niino, H. An improved Mellor-Yamada Level-3 model: Its numerical stability and application to a regional prediction of advection fog. Bound.-Layer Meteorol. 2006, 119, 397–407. [Google Scholar] [CrossRef]
- Von Storch, H.; Langenberg, H.; Feser, F. A Spectral Nudging Technique for Dynamical Downscaling Purposes. Mon. Weather Rev. 2000, 128, 3664–3673. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient Inverse Modeling of Barotropic Ocean Tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Large, W.G.; McWilliams, J.C.; Doney, S.C. Oceanic vertical mixing: A review and a model with a nonlocal boundary layer parameterization. Rev. Geophys. 1994, 32, 363–403. [Google Scholar] [CrossRef]
- Zijlema, M.; Van Vledder, G.P.; Holthuijsen, L.H. Bottom friction and wind drag for wave models. Coast. Eng. 2012, 65, 19–26. [Google Scholar] [CrossRef]
- Kirby, J.T.; Chen, T.M. Surface waves on vertically sheared flows: Approximate dispersion relations. J. Geophys. Res. 1989, 94, 1013–1027. [Google Scholar] [CrossRef]
- Holthuijsen, L.H.; Herman, A.; Booij, N. Phase-decoupled refraction-diffraction for spectral wave models. Coast. Eng. 2003, 49, 291–305. [Google Scholar] [CrossRef]
- Komen, G.J.; Hasselmann, S.; Hasselmann, K. On the Existence of a Fully Developed Wind-Sea Spectrum. J. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Dong, C.; McWilliams, J.C.; Hall, A.; Hughes, M. Numerical simulation of a synoptic event in the Southern California Bight. J. Geophys. Res. 2011, 116, C05018. [Google Scholar] [CrossRef]
- Murphy, A.H. Climatology, Persistence, and Their Linear Combination as Standards of Reference in Skill Scores. Weather Forecast. 1992, 7, 692–698. [Google Scholar] [CrossRef]
- World Meteorological Organization. Guidelines for Converting between Various Wind Averaging Periods in Tropical Cyclone Conditions; World Meteorological Organization: Geneva, Switzerland, 2008. [Google Scholar]
- Barcikowska, M.; Feser, F.; von Storch, H. Usability of Best Track Data in Climate Statistics in the Western North Pacific. Mon. Weather Rev. 2012, 140, 2818–2830. [Google Scholar] [CrossRef]
- Emanuel, K. Contribution of tropical cyclones to meridional heat transport by the oceans. J. Geophys. Res. 2001, 106, 14771–14781. [Google Scholar] [CrossRef]
- Wu, R.; Li, C. Upper ocean response to the passage of two sequential typhoons. Deep. Res. Part I Oceanogr. Res. Pap. 2018, 132, 68–79. [Google Scholar] [CrossRef]
- Price, J.F.; Morzel, J.; Niiler, P.P. Warming of SST in the cool wake of a moving hurricane. J. Geophys. Res. 2008, 113, C07010. [Google Scholar] [CrossRef]
- Walker, N.D.; Leben, R.R.; Pilley, C.T.; Shannon, M.; Herndon, D.C.; Pun, I.-F.; Lin, I.I.; Gentemann, C.L. Slow translation speed causes rapid collapse of northeast Pacific Hurricane Kenneth over cold core eddy. Geophys. Res. Lett. 2014, 41, 7595–7601. [Google Scholar] [CrossRef]
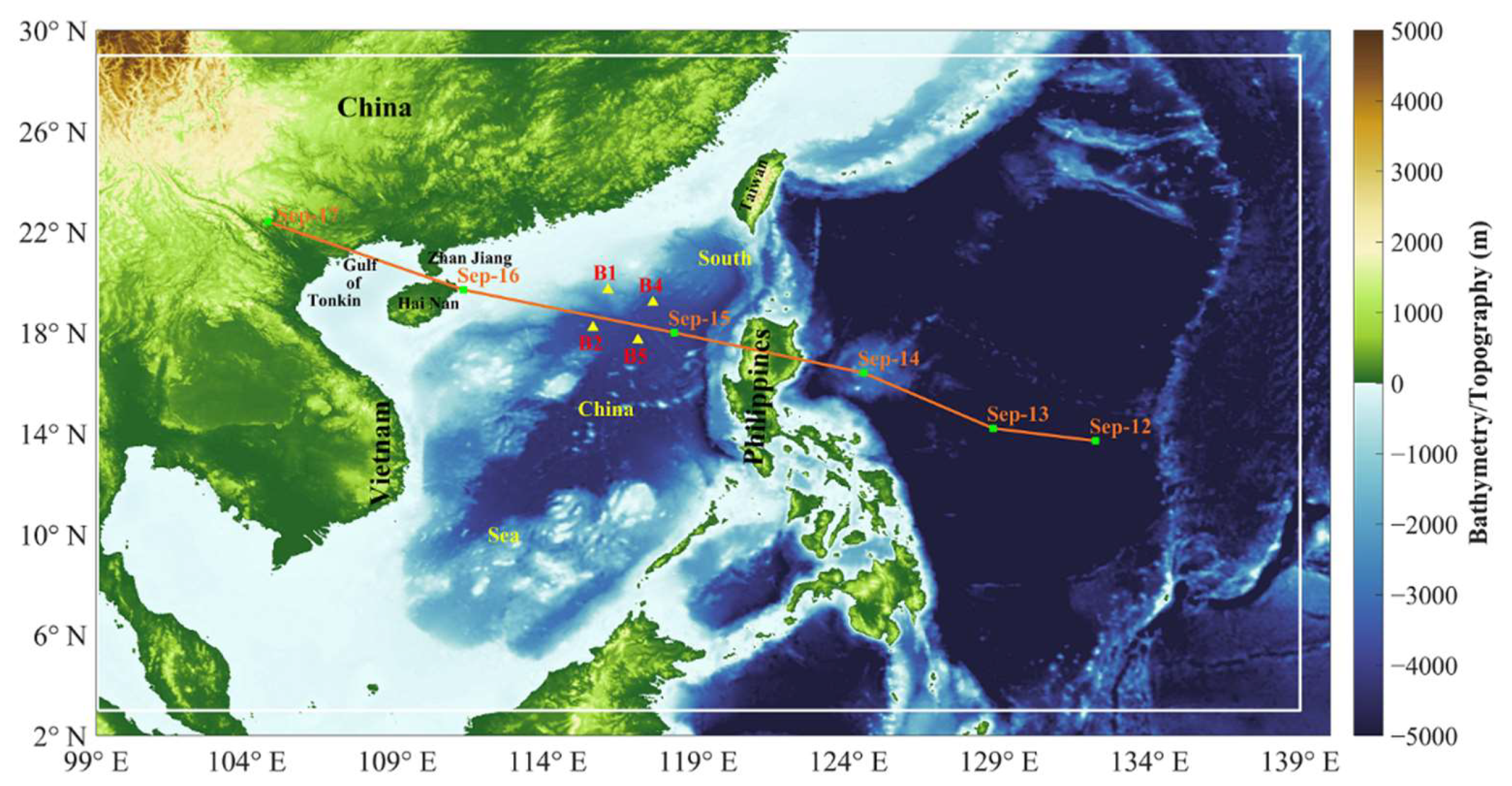

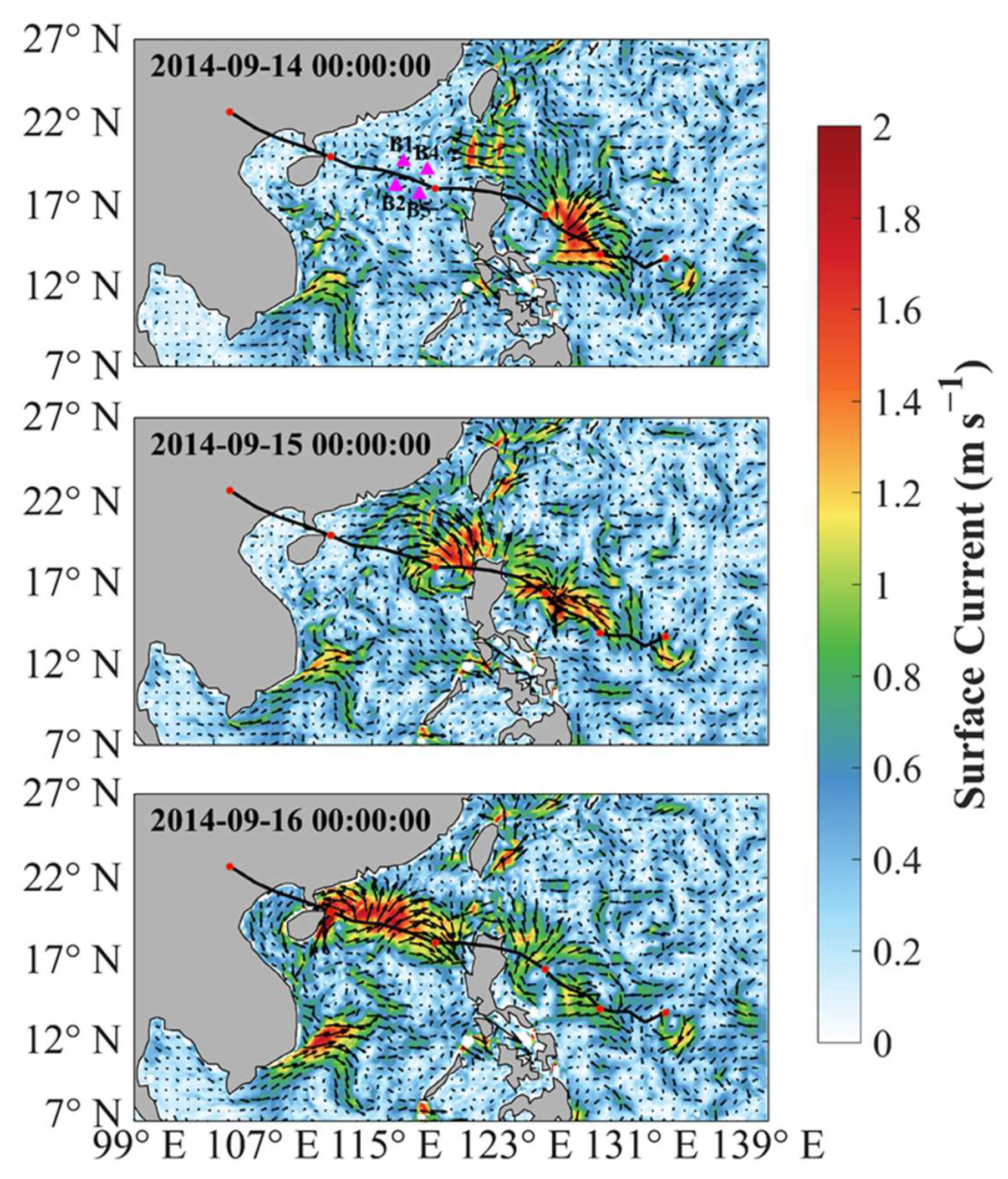
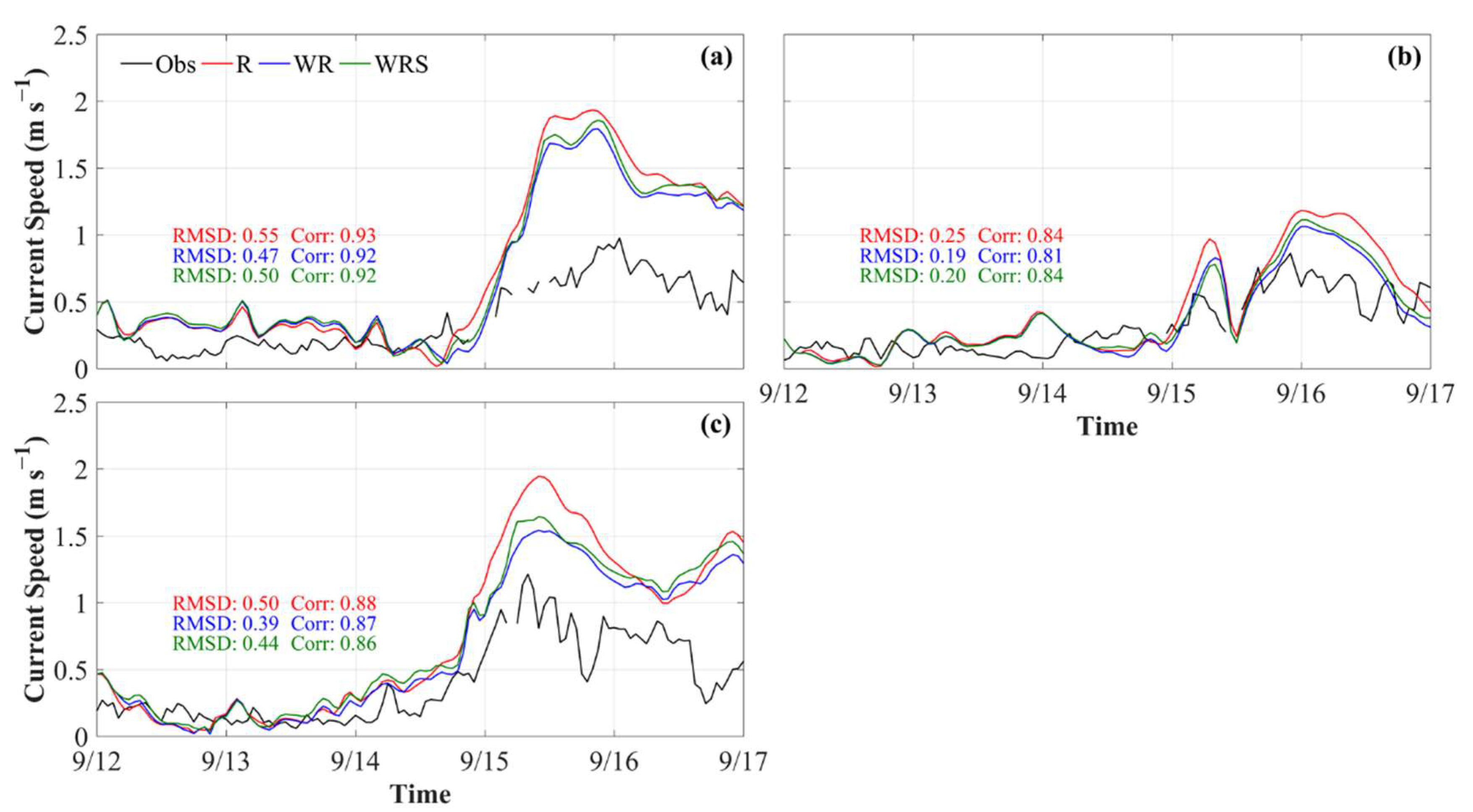
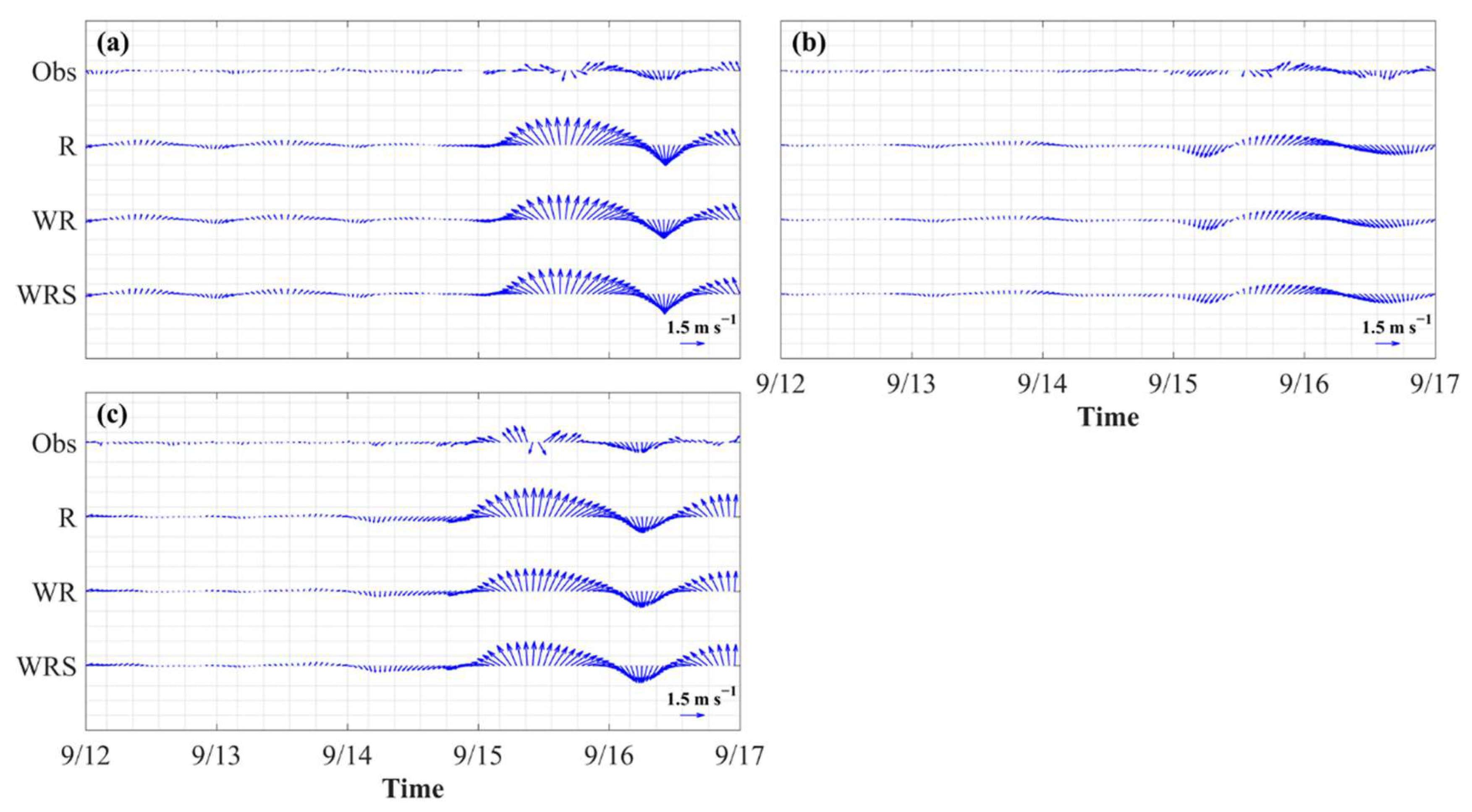
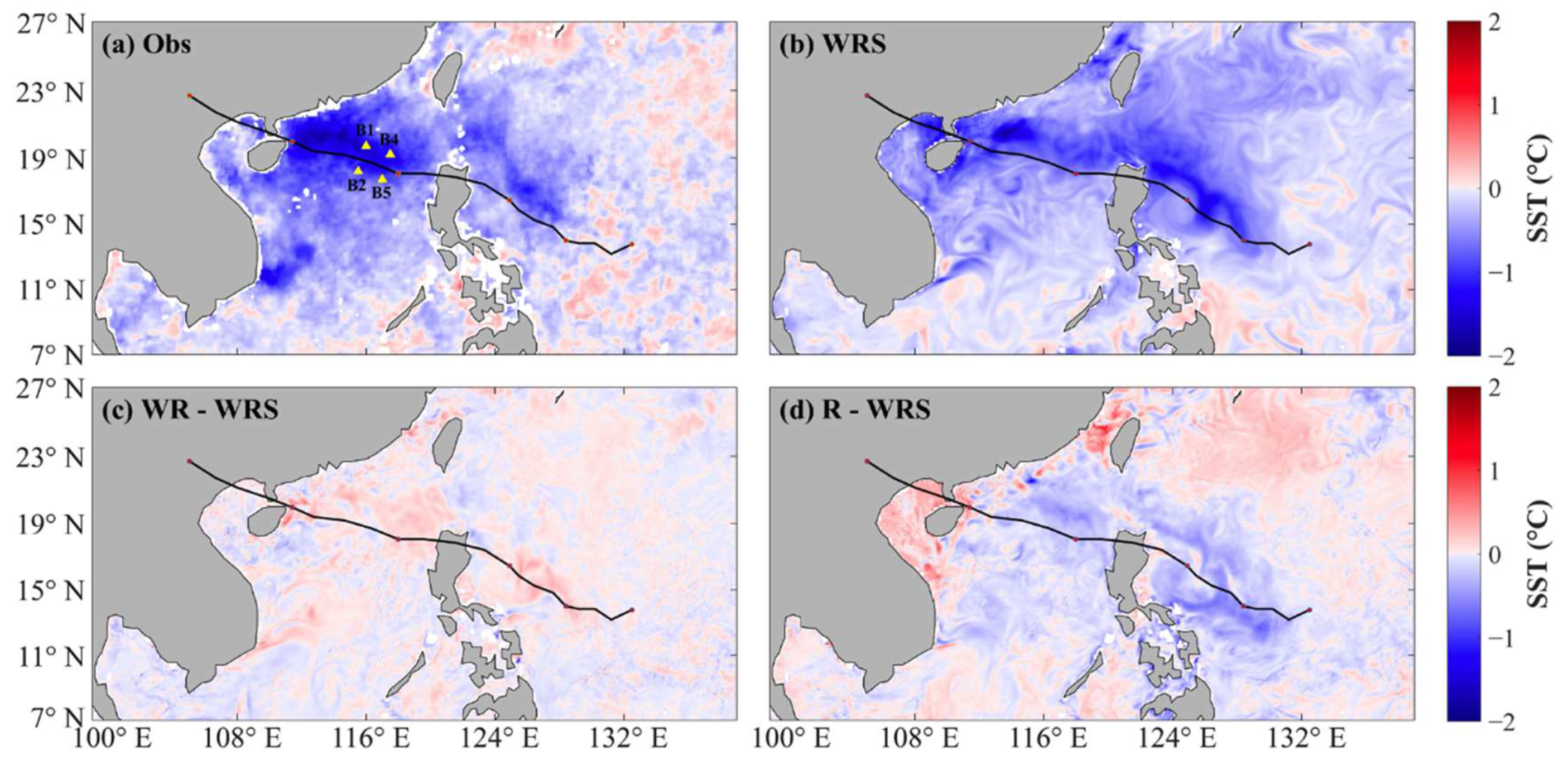

| Buoy | Longitude (°E) | Latitude (°N) | Water Depth (m) |
|---|---|---|---|
| 1 | 116.0 | 19.7 | 1630 |
| 2 | 115.5 | 18.2 | 3840 |
| 4 | 117.5 | 19.2 | 3690 |
| 5 | 117.0 | 17.7 | 3990 |
| Experiments | WRF | ROMS | SWAN |
|---|---|---|---|
| W | Yes | No | No |
| R | No | Yes | No |
| S | No | No | Yes |
| WR | Yes | Yes | No |
| WS | Yes | No | Yes |
| * WRS | Yes | Yes | Yes |
| Experiments | Wind | SLP | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSD | SSc | SSr | R2 | RMSD | SSc | SSr | |
| W | 0.9398 | 2.9551 | 0.0011 | −0.0949 | 0.9809 | 1.7682 | −0.0023 | −0.0337 |
| WR | 0.9501 | 2.8357 | 0.0120 | −0.0551 | 0.9813 | 1.7683 | −0.0018 | −0.0338 |
| WS | 0.9209 | 3.0884 | −0.0193 | −0.1211 | 0.9797 | 1.8160 | −0.0034 | −0.0696 |
| WRS | 0.9390 | 2.7859 | 0.0000 | 0.0000 | 0.9831 | 1.7151 | 0.0000 | 0.0000 |
| Experiments | SST | Current | ||||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSD | SSc | SSr | R2 | RMSD | SSc | SSr | |
| R | 0.9736 | 0.2888 | 0.0052 | 0.2923 | 0.8831 | 0.4348 | 0.0099 | −0.1703 |
| WR | 0.9698 | 0.4170 | −0.0012 | −0.0130 | 0.8683 | 0.3524 | −0.0074 | 0.0631 |
| WRS | 0.9687 | 0.4145 | 0.0000 | 0.0000 | 0.8744 | 0.3806 | 0.0000 | 0.0000 |
| Experiments | SWH | |||
|---|---|---|---|---|
| R2 | RMSD | SSc | SSr | |
| S | 0.9489 | 1.0466 | −0.0018 | −0.4104 |
| WS | 0.9488 | 0.8637 | −0.0019 | −0.1621 |
| WRS | 0.9506 | 0.7433 | 0.0000 | 0.0000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lim Kam Sian, K.T.C.; Dong, C.; Liu, H.; Wu, R.; Zhang, H. Effects of Model Coupling on Typhoon Kalmaegi (2014) Simulation in the South China Sea. Atmosphere 2020, 11, 432. https://doi.org/10.3390/atmos11040432
Lim Kam Sian KTC, Dong C, Liu H, Wu R, Zhang H. Effects of Model Coupling on Typhoon Kalmaegi (2014) Simulation in the South China Sea. Atmosphere. 2020; 11(4):432. https://doi.org/10.3390/atmos11040432
Chicago/Turabian StyleLim Kam Sian, Kenny T.C., Changming Dong, Hailong Liu, Renhao Wu, and Han Zhang. 2020. "Effects of Model Coupling on Typhoon Kalmaegi (2014) Simulation in the South China Sea" Atmosphere 11, no. 4: 432. https://doi.org/10.3390/atmos11040432
APA StyleLim Kam Sian, K. T. C., Dong, C., Liu, H., Wu, R., & Zhang, H. (2020). Effects of Model Coupling on Typhoon Kalmaegi (2014) Simulation in the South China Sea. Atmosphere, 11(4), 432. https://doi.org/10.3390/atmos11040432








