A Statistical Investigation of Mesoscale Precursors of Significant Tornadoes: The Italian Case Study
Abstract
1. Introduction
2. Materials and Methods
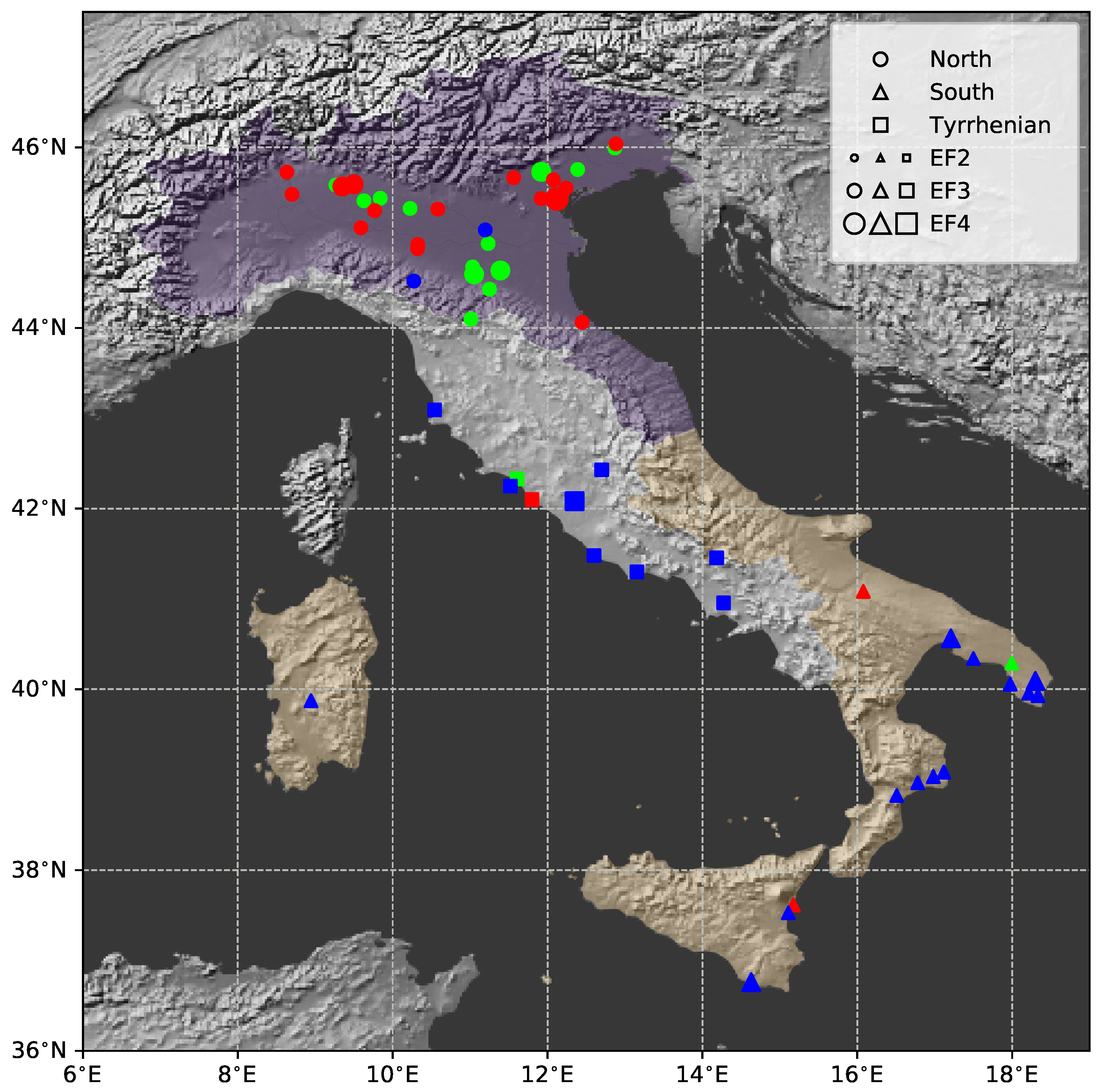
2.1. Records of Tornadoes
2.2. Reanalysis Datasets
2.3. Meteorological Parameters
- Wind shear (LLS, DLS). WS is computed as the magnitude of the vector representing the difference between the wind near the surface and at a fixed level in the air column. Two parameters are considered, the low-level shear (LLS) and the deep-level shear (DLS), representing the differences between the wind speed near the surface (1000 hPa) and at about 1 km and 6 km (900 hPa and 500 hPa, respectively). Although LLS and DLS are not calculated within the generally used 0–1km and 0–6 km layers, our different choice does not affect the results, also considering that all the analyzed tornadoes occur in flat regions (only one case is recorded above 300 m). It is important to highilight that previous studies [48,49] reveal that atmospheric reanalysis tends to underestimate the low-level shear compared to sounding observations.
- Updraft Maximum Vertical Velocity (WM). CAPE [50,51,52] represents the available potential energy. It is defined as , where z is the height, is the buoyancy force, is the Level of Free Convection, is the Equilibrium Level, and and are the virtual temperature of the air parcel and of the surrounding environment, respectively [23,53].The buoyancy produces the vertical acceleration of the air parcels: , where w is the vertical velocity component and t is time. In the reanalyses used in this work, CAPE is extracted from ECMWF, calculated as the maximum value among the air parcels lifted from different model levels below 350 hPa (MUCAPE). In this study, CAPE is expressed via the Updraft Maximum Vertical Velocity (WM), supposing that the buoyancy is the only active force according to the Parcel Theory: i.e., [23,53]. WM is computed at the same grid points and times as WS01 and WS06.
- Standardized values. To obtain comparable dimensionless indices, a standardization is applied. The generic index I is defined as , where X is the value of the parameter of interest (WM, LLS, or DLS). The mean value (climatological mean), as well as the standard deviation , are computed separately for each tornado, considering the 19 values of the parameter I at the same hour and calendar day when the tornado occurred for the years 2000–2018. Therefore, and have different values for each individual tornado, both for the ERA-5 and the ERA-Interim datasets.
2.4. Statistical Tools and Procedures
2.4.1. Homogeneity Tests
2.4.2. Conditional Probabilities
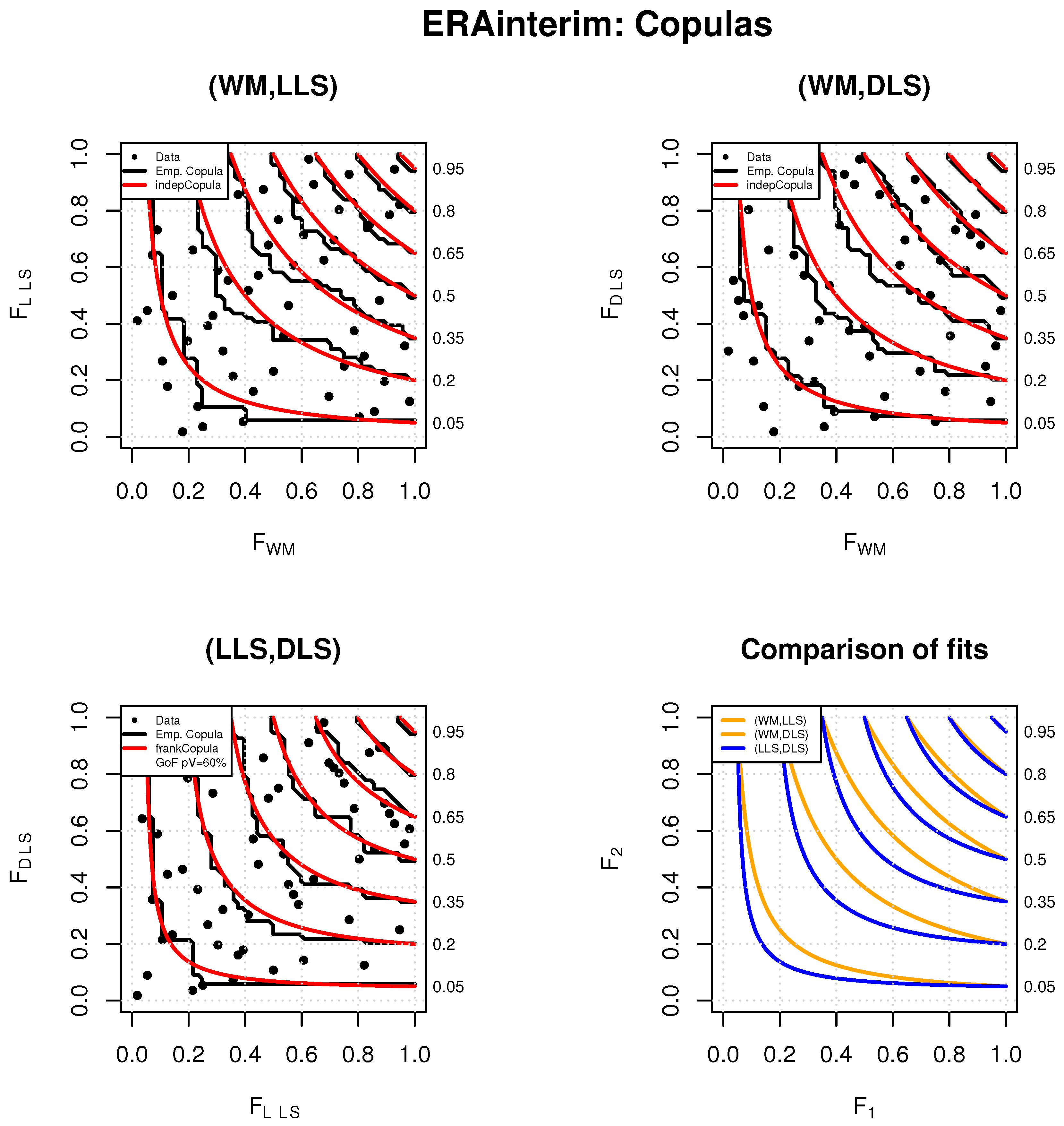
2.4.3. Multivariate Analysis via Copulas
3. Results
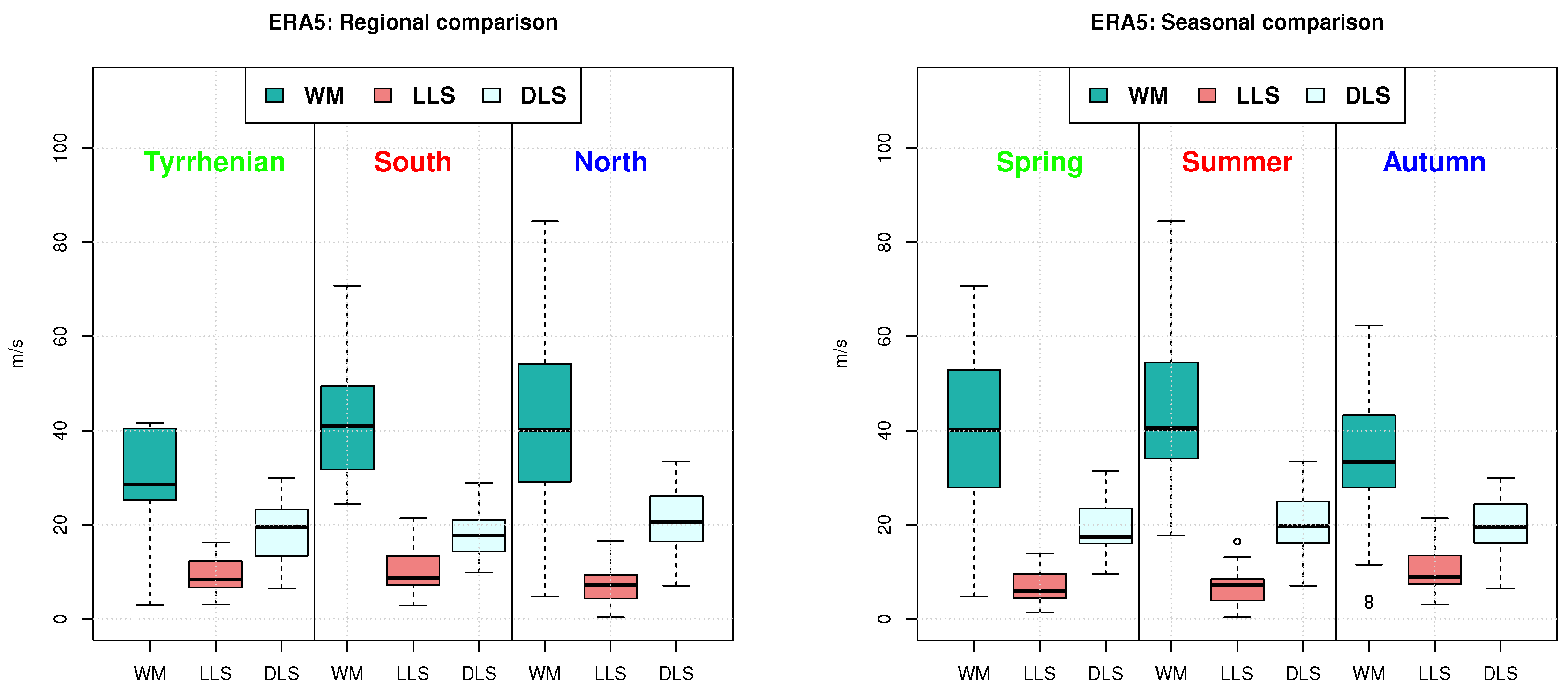
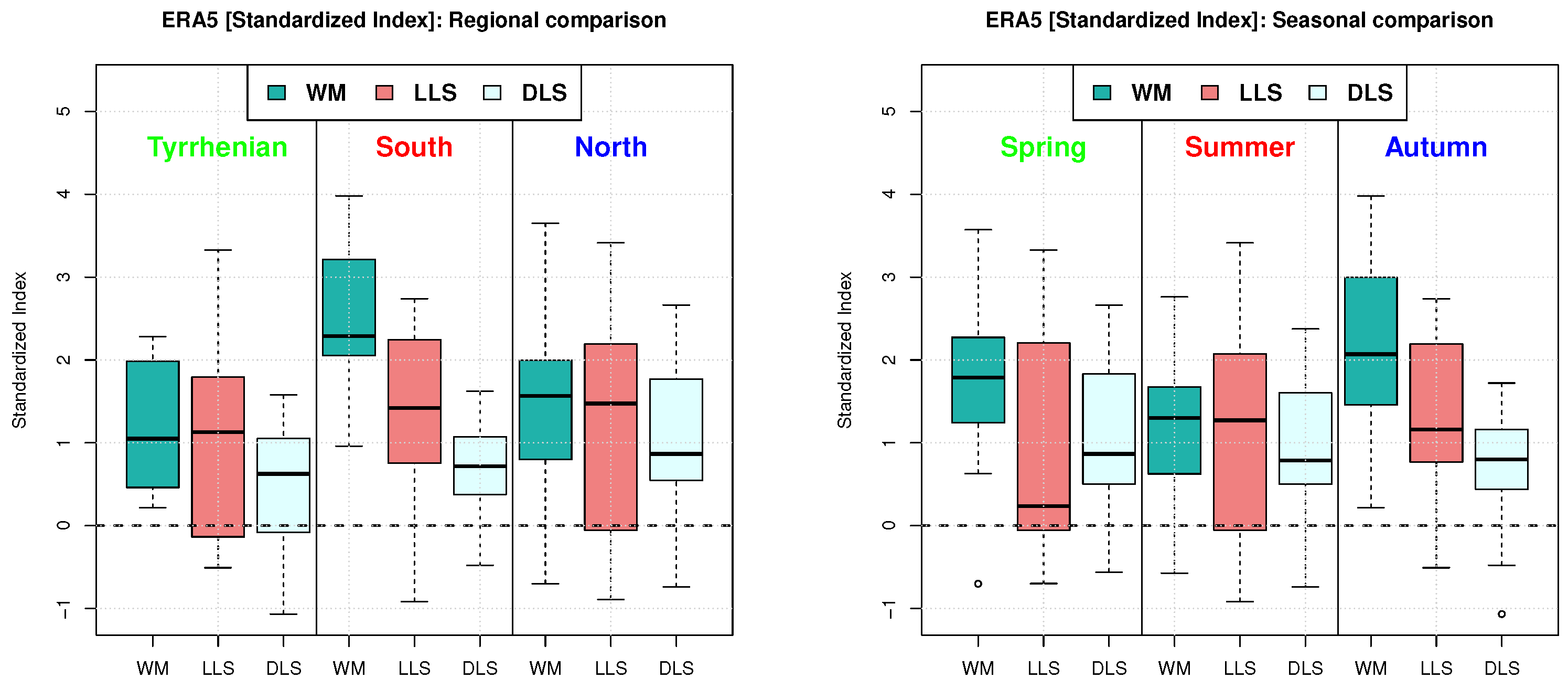
3.1. Relevance of Geographical and Seasonal Features
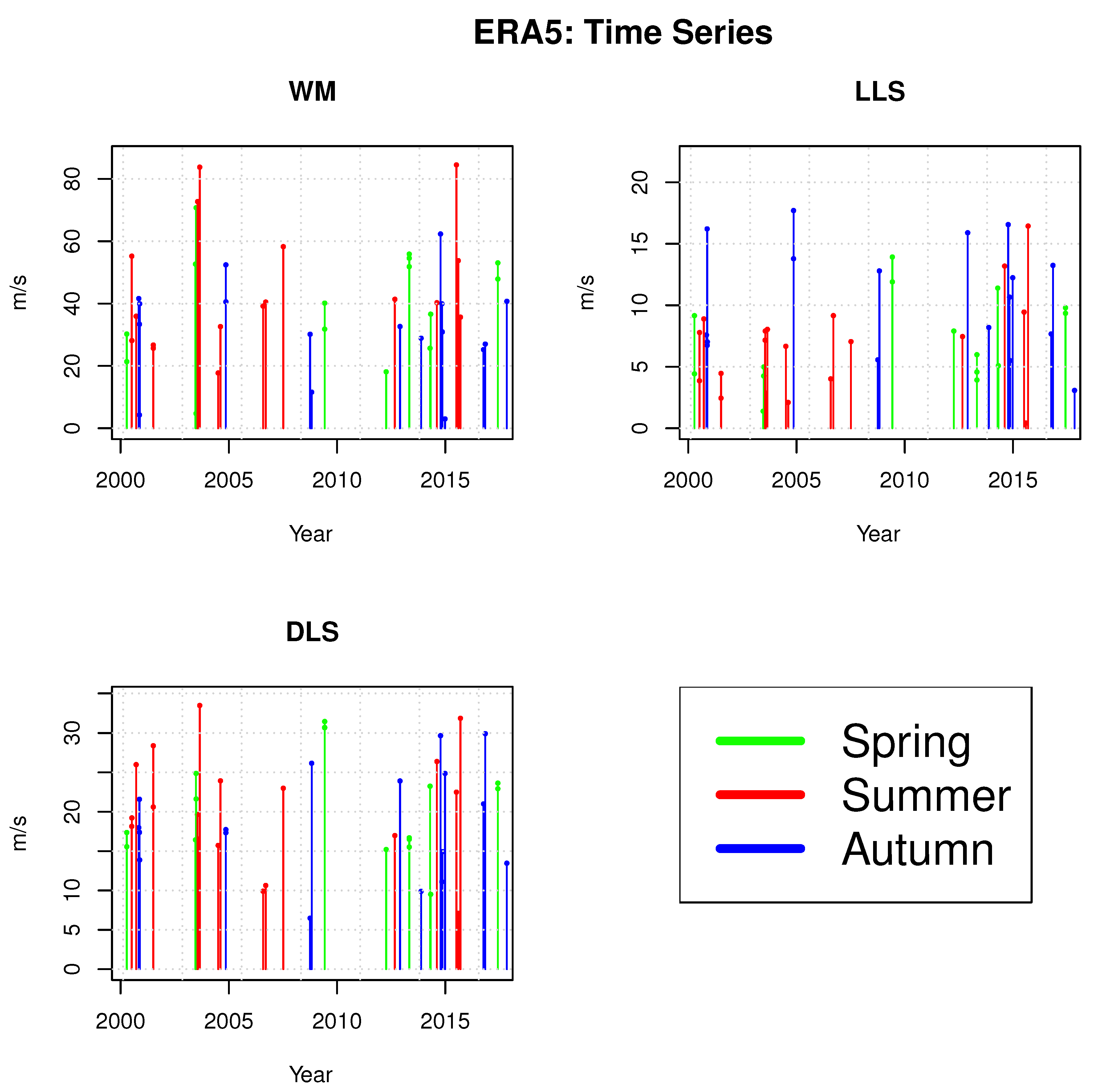
3.2. Evolution of WS and CAPE before a Tornado Occurrence
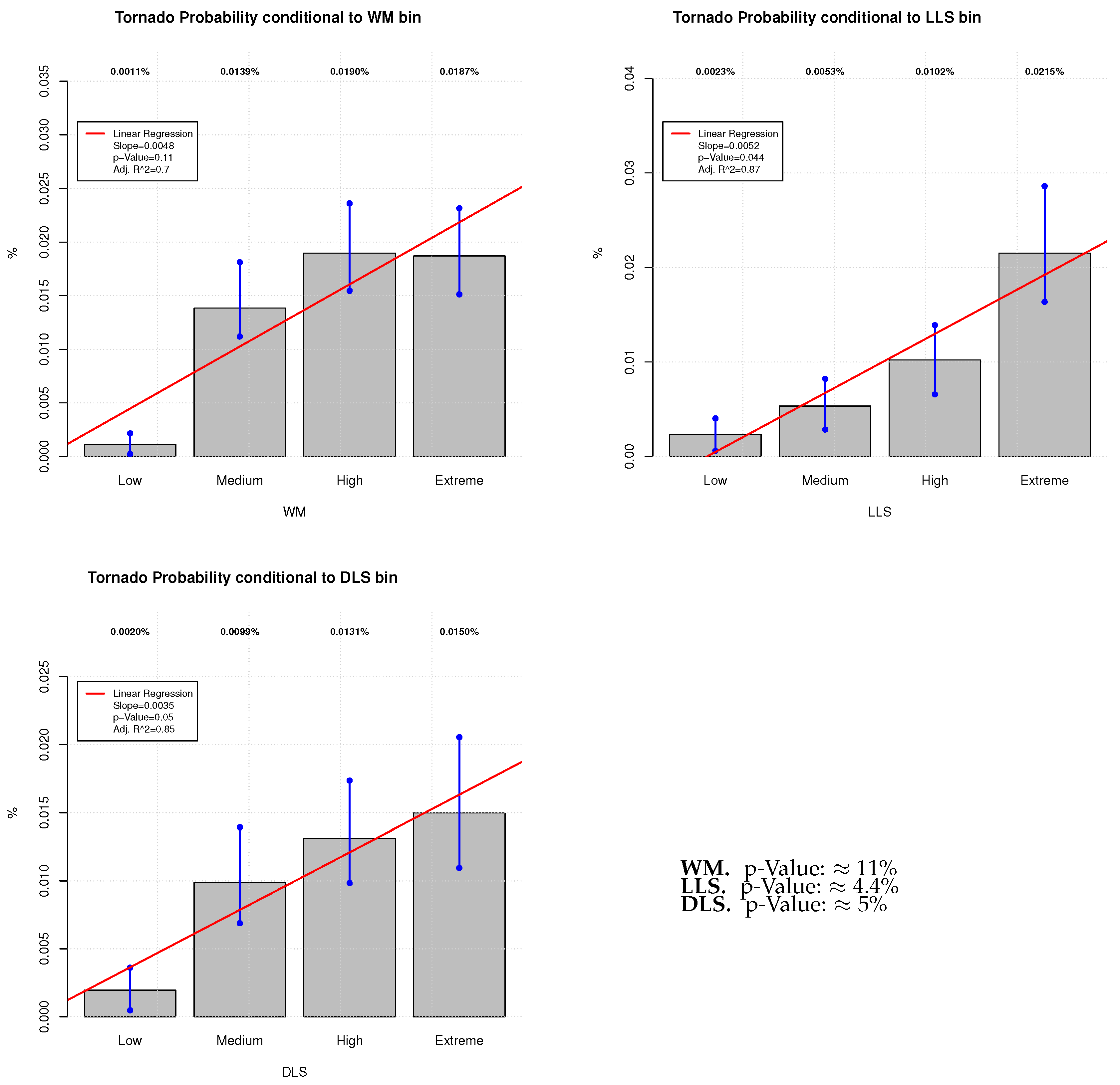
3.3. Conditional Probability of Tornado Occurrence
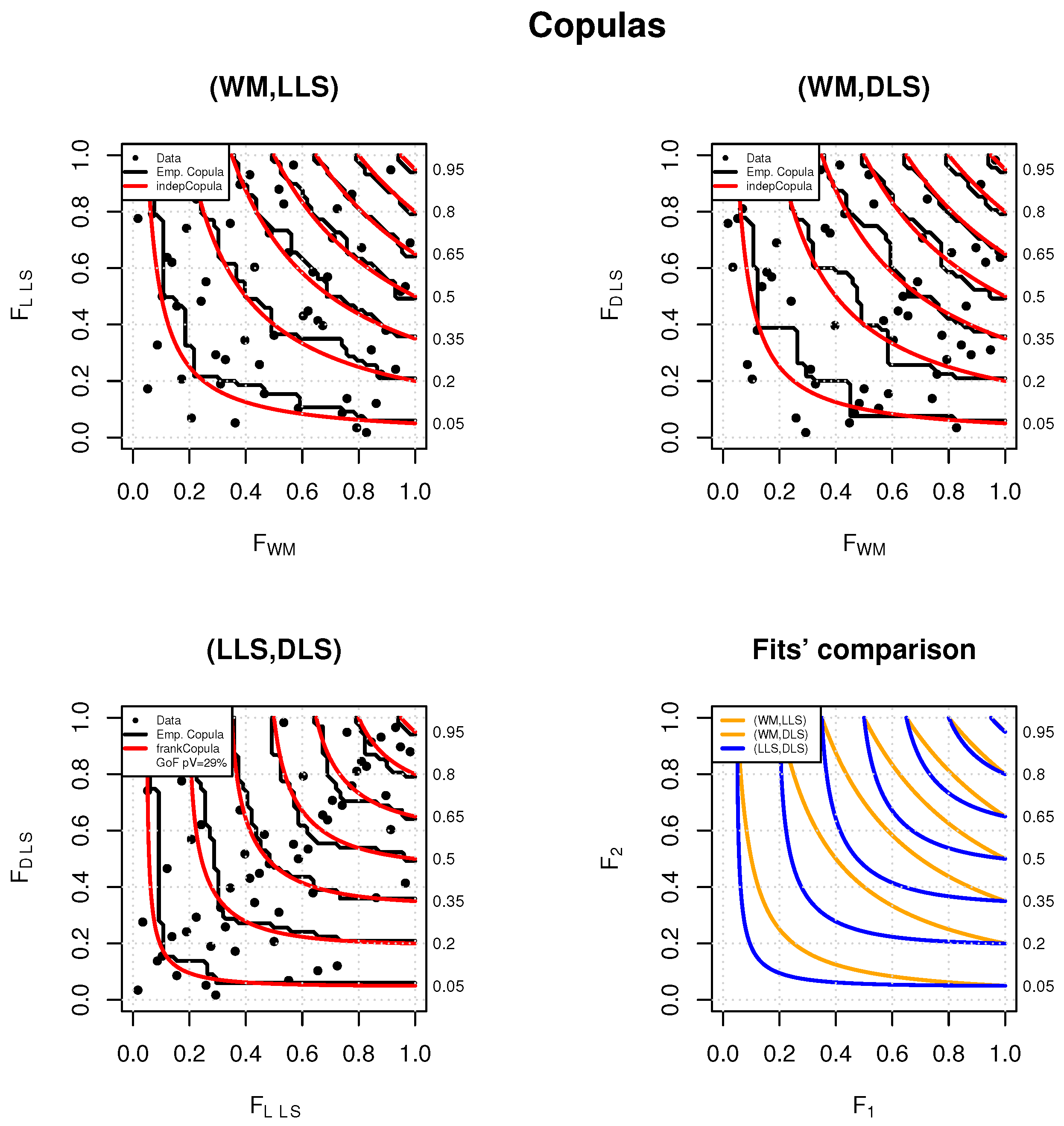
3.4. Multivariate Analysis of Tornado Occurrence
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| LLS | wind shear as the difference between the wind speed near the surface (1000 hPa) and at about 1 km (900 hPa) |
| DLS | wind shear as the difference between the wind speed near the surface and at about 6 km (500 hPa) |
| CAPE | convective available potential energy |
| WM | Updraft Maximum Vertical Velocity |
Appendix A. The Frank Family of Copulas
Appendix B. ERA-Interim Figures
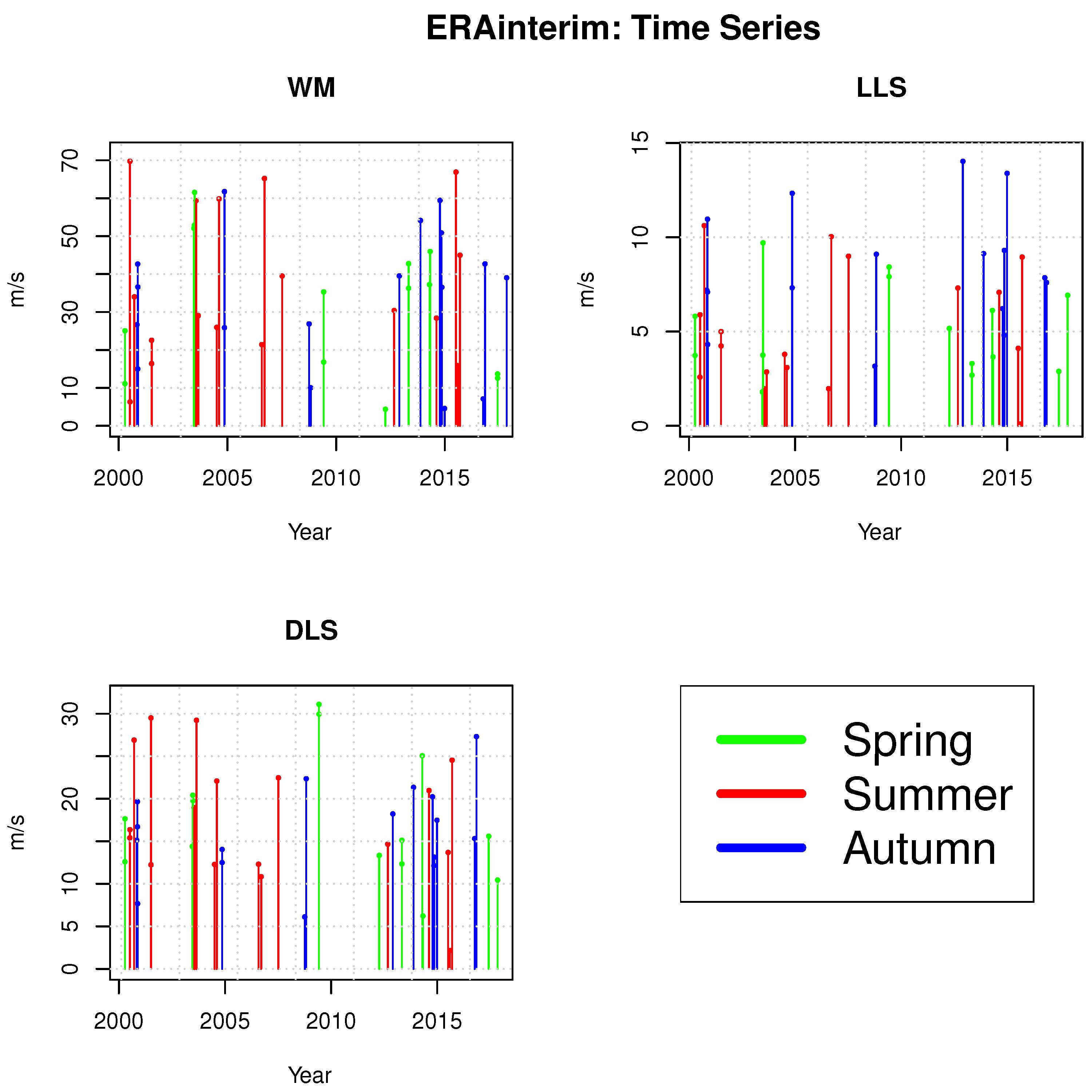
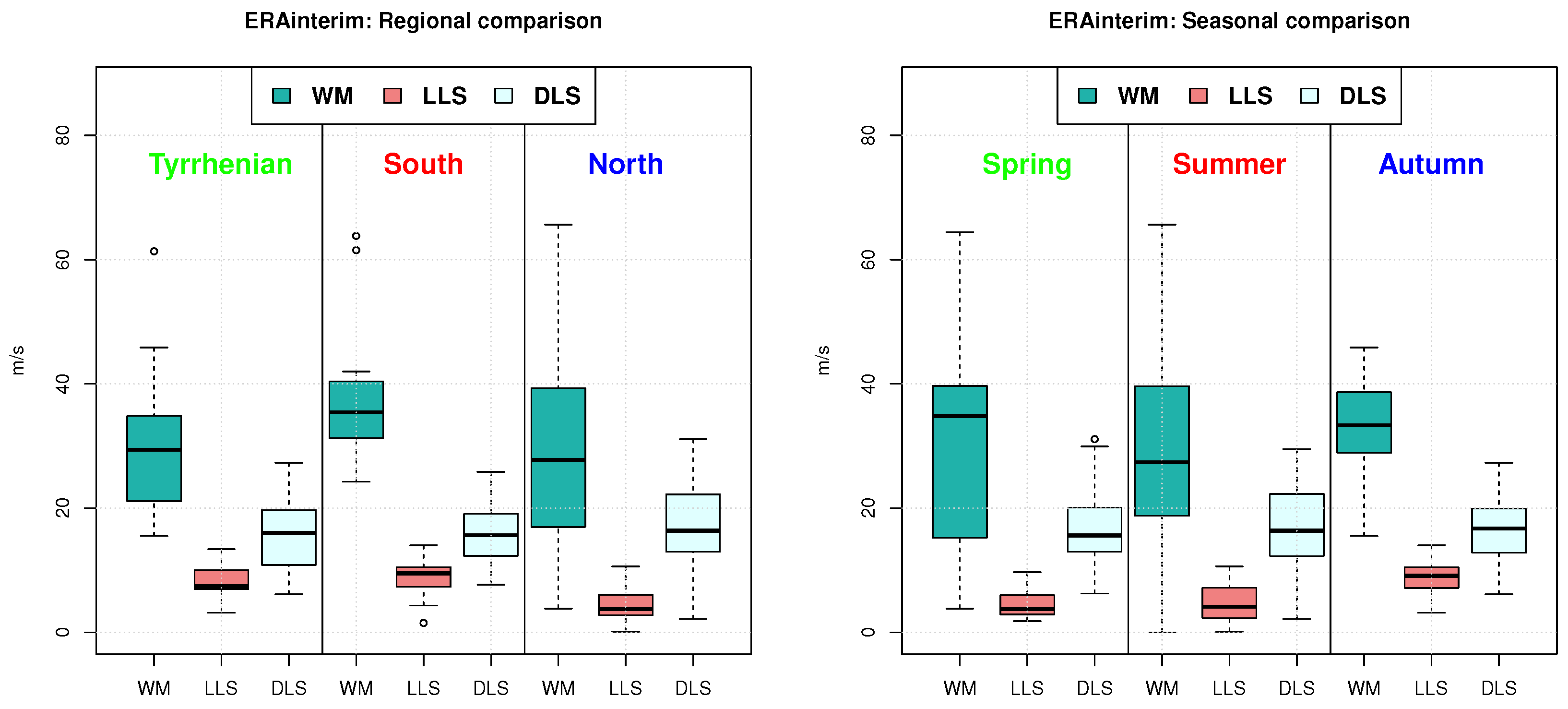
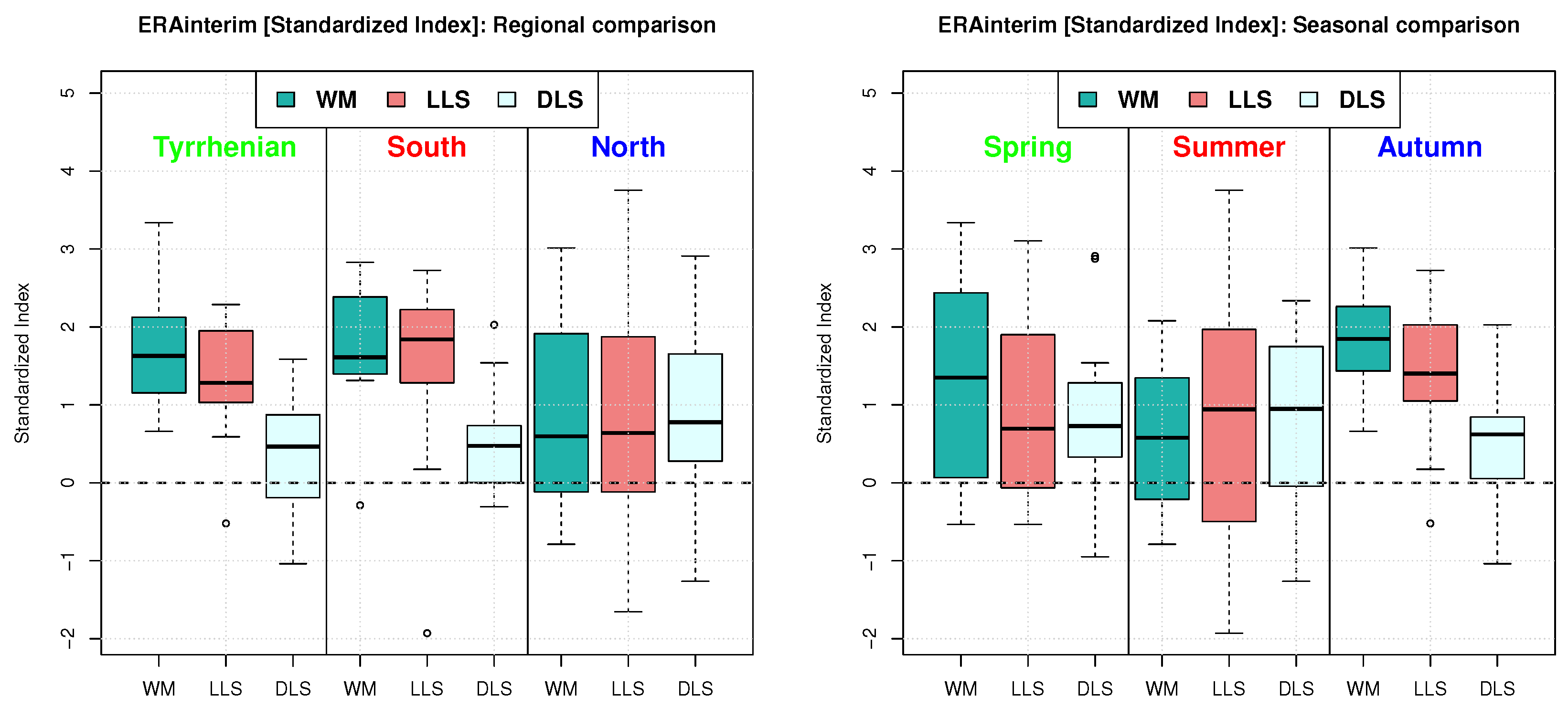
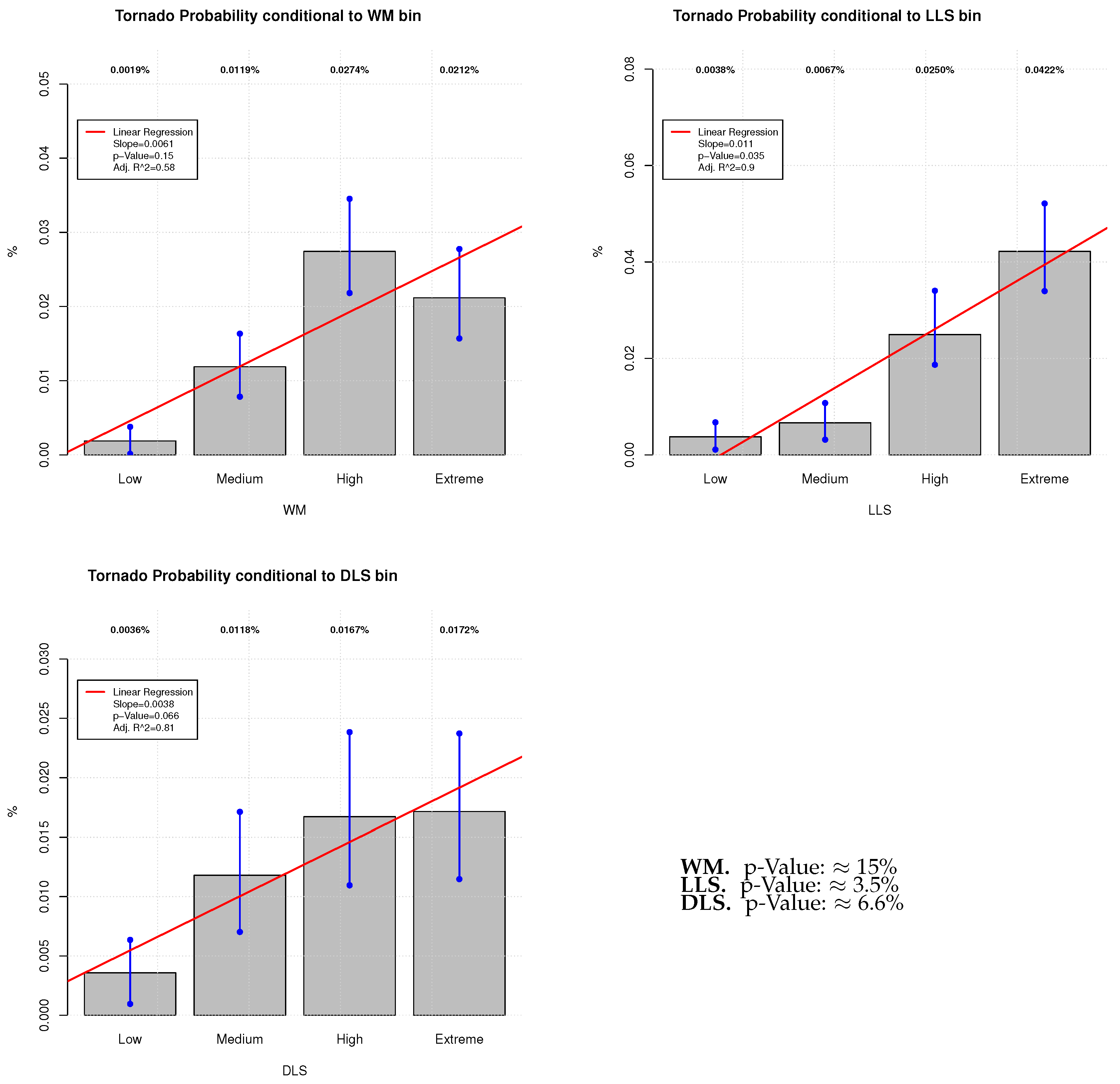
References
- Simmons, K.M.; Sutter, D.; Pielke, R. Normalized tornado damage in the United States: 1950–2011. Environ. Hazards 2013, 12, 132–147. [Google Scholar] [CrossRef]
- Antonescu, B.; Schultz, D.M.; Holzer, A.; Groenemeijer, P. Tornadoes in Europe: An Underestimated Threat. Bull. Am. Meteorol. Soc. 2017, 98, 713–728. [Google Scholar] [CrossRef]
- Brooks, H.E.; Lee, J.W.; Craven, J.P. The spatial distribution of severe thunderstorm and tornado environments from global reanalysis data. Atmos. Res. 2003, 67–68, 73–94. [Google Scholar] [CrossRef]
- Groenemeijer, P.; Kühne, T. A climatology of tornadoes in Europe: Results from the European severe weather database. Mon. Weather Rev. 2014, 142, 4775–4790. [Google Scholar] [CrossRef]
- Tippett, M.K.; Allen, J.T.; Gensini, V.A.; Brooks, H.E. Climate and Hazardous Convective Weather. Curr. Clim. Chang. Rep. 2015, 1, 60–73. [Google Scholar] [CrossRef]
- Palmieri, S.; Pulcini, A. Trombe d’aria sull’Italia. Riv. Meteorol. Aeronaut. 1978, 4, 263–277. [Google Scholar]
- Giaiotti, D.B.; Giovannoni, M.; Pucillo, A.; Stel, F. The climatology of tornadoes and waterspouts in Italy. Atmos. Res. 2007, 83, 534–541. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Matsangouras, I.T. An updated climatology of tornadoes and waterspout in Italy. Int. J. Climatol. 2018, 38, 3667–3683. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Arai, K.; Kusunoki, K.; Inoue, H.; Adachi, T.; Niino, H. Observational analysis of two waterspouts in northwestern Italy using an OPERA Doppler radar. Atmos. Res. 2020, 234, 104692. [Google Scholar] [CrossRef]
- Fujita, T.T. Proposed characterization of tornadoes and hurricanes by area and intensity. Satell. Mesometeorol. Res. Proj. 1971, 91, 42. [Google Scholar]
- Mahieu, P.; Wesolek, E. Tornado Rating in Europe with the Enhanced Fujita Scake (EF-Scale): Definition of Specific Damage Indicators for Accurate Tornado Ratings in Europe; Technical Report; KERAUNOS—Tornadoes and Severe Storms French Observatory: Nicosia, Cyprus, 2016. [Google Scholar] [CrossRef]
- Feuerstein, B.; Groenemeijer, P.; Dirksen, E.; Hubrig, M.; Holzer, A.M.; Dotzek, N. Towards an improved wind speed scale and damage description adapted for Central Europe. Atmos. Res. 2011, 100, 547–564. [Google Scholar] [CrossRef]
- Groenemeijer, P.; Holzer, A.M.; Hubrig, M.; Kühne, T.; Bock, L.; Soriano, J.d.D.; Gutiérrez-Rubio, D.; Kaltenberger, R.; van der Ploeg, B.; Strommer, G. The International Fujita (IF) Scale Tornado and Wind Damage Assessment Guide; Technical Report; ESSL: Munich, Germany, 2018. [Google Scholar]
- Meaden, J. Tornadoes in Britain: Their intensities and distribution in space and time. J. Meteorol. 1976, 1, 242–251. [Google Scholar]
- Brooks, H.; Doswell, C.A. Some aspects of the international climatology of tornadoes by damage classification. Atmos. Res. 2001, 56, 191–201. [Google Scholar] [CrossRef]
- Potter, S. Fine-Tuning Fujita: After 35 years, a new scale for rating tornadoes takes effect. Weatherwise 2007, 60, 64–71. [Google Scholar] [CrossRef]
- Miglietta, M.M.; Rotunno, R. An EF3 multivortex tornado over the Ionian region: Is it time for a dedicated warning system over Italy. Bull. Am. Meteorol. Soc. 2016, 97, 337–344. [Google Scholar] [CrossRef]
- Miglietta, M.; Mazon, J.; Rotunno, R. Numerical simulations of a tornadic supercell over the mediterranean. Weather Forecast. 2017, 32, 1209–1226. [Google Scholar] [CrossRef]
- Miglietta, M.; Mazon, J.; Motola, V.; Pasini, A. Effect of a positive sea surface temperature anomaly on a Mediterranean tornadic supercell. Sci. Rep. 2017, 7. [Google Scholar] [CrossRef]
- ARPAV. Temporali intensi di mercoledi 8 luglio in Veneto. In Relazione tornado sul Veneto; The Regional Environmental Protection Agency: Rome, Italy, 2015. [Google Scholar]
- Zanini, M.A.; Hofer, L.; Faleschini, F.; Pellegrino, C. Building damage assessment after the Riviera del Brenta tornado, northeast Italy. Nat. Hazards 2017, 86, 1247–1273. [Google Scholar] [CrossRef]
- Report2016. Il tornado di Pianiga, Dolo e Mira dell’8 luglio 2015. Available online: https://documenti.serenissimameteo.it/documents/tornado_8luglio2015_capitoli.pdf (accessed on 10 January 2020).
- Markowski, P.M.; Richardson, Y. Mesoscale Meteorology in Midlatitude; Wiley-Blackwell: Hoboken, NJ, USA, 2010. [Google Scholar]
- Brooks, H.E. Severe thunderstorms and climate change. Atmosp. Res. 2013, 123, 129–138. [Google Scholar] [CrossRef]
- Rotunno, R.; Klemp, J. On the Rotation and Propagation of Simulated Supercell Thunderstorms. J. Atmos. Sci. 1985, 42, 271–292. [Google Scholar] [CrossRef]
- Klemp, J. Dynamics Of Tornadic Thunderstorms. Ann. Rev. Fluid Mech. 1987, 19, 369–402. [Google Scholar] [CrossRef]
- Barnes, S.L. Some aspects of a severe, right-moving thunderstorm deduced from mesonet rawinsonde observations. Geophys. Fluid Dyn. 1970, 4, 147–158. [Google Scholar] [CrossRef]
- Schlesinger, R.E. A Three-Dimensional Numerical Model of an Isolated Deep Convective Cloud: Preliminary Results. J. Atmos. Sci. 1975, 32, 934–964. [Google Scholar] [CrossRef]
- Rotunno, R. On the Evolution of Thunderstorm Rotation. Mon. Weather Rev. 1981, 109, 577–586. [Google Scholar] [CrossRef]
- Markowski, P.M.; Richardson, Y.P. Tornadogenesis: Our current understanding, forecasting considerations, and questions to guide future research. Atmos. Res. 2009, 93, 3–10. [Google Scholar] [CrossRef]
- Weisman, M.L.; Rotunno, R. The Use of Vertical Wind Shear versus Helicity in Interpreting Supercell Dynamics. J. Atmos. Sci. 2000, 57, 1452–1472. [Google Scholar] [CrossRef]
- Markowski, P.M.; Richardson, Y.P. The Influence of Environmental Low-Level Shear and Cold Pools on Tornadogenesis: Insights from Idealized Simulations. J. Atmos. Sci. 2014, 71, 243–275. [Google Scholar] [CrossRef]
- Colquhoun, J.R.; Shepherd, D.J. An Objective Basis for Forecasting Tornado Intensity. Weather Forecast. 1989, 5, 35–50. [Google Scholar] [CrossRef]
- Thompson, R.L.; Edwards, R.; Hart, J.A. Close Proximity Soundings within Supercell Environments Obtained from the Rapid Update Cycle. Weather Forecast. 2003, 18, 1243–1261. [Google Scholar] [CrossRef]
- Dupilka, M.L.; Reuter, G.W. Forecasting Tornadic Thunderstorm Potential in Alberta Using Environmental Sounding Data. Part I: Wind Shear and Buoyancy. Weather Forecast. 2006, 21, 325–335. [Google Scholar] [CrossRef]
- Taszarek, M.; Brooks, H.E.; Czernecki, B. Sounding-Derived Parameters Associated with Convective Hazards in Europe. Mon. Weather Rev. 2017, 145, 1511–1528. [Google Scholar] [CrossRef]
- Grünwald, S.; Brooks, H. Relationship between sounding derived parameters and the strength of tornadoes in Europe and the USA from reanalysis data. Atmos. Res. 2011, 100, 479–488. [Google Scholar] [CrossRef]
- Púčik, T.; Groenemeijer, P.; Rýva, D.; Kolář, M. Proximity Soundings of Severe and Nonsevere Thunderstorms in Central Europe. Mon. Weather Rev. 2015, 143, 4805–4821. [Google Scholar] [CrossRef]
- Rodriguez, O.; Bech, J. Sounding-derived parameters associated with tornadic storms in Catalonia. Int. J. Clim. 2017, 38, 2400–2414. [Google Scholar] [CrossRef]
- Groenemeijer, P.; van Delden, A. Sounding-derived parameters associated with large hail and tornadoes in the Netherlands. Atmos. Res. 2007, 83, 473–487. [Google Scholar] [CrossRef]
- Thompson, R.L.; Smith, B.T.; Grams, J.S.; Dean, A.R.; Broyles, C. Convective Modes for Significant Severe Thunderstorms in the Contiguous United States. Part II: Supercell and QLCS Tornado Environments. Weather Forecast. 2012, 27, 1136–1154. [Google Scholar] [CrossRef]
- Craven, J.; Brooks, H. Baseline climatology of sounding derived parameters associated with deep, moist convection. Natl. Weather Dig. 2004, 28, 13–24. [Google Scholar]
- Rasmussen, E.N.; Blanchard, D.O. A Baseline Climatology of Sounding-Derived Supercell and Tornado Forecast Parameters. Weather Forecast. 1998, 13, 1148–1164. [Google Scholar] [CrossRef]
- Grams, J.S.; Thompson, R.L.; Snively, D.V.; Prentice, J.; Hodges, G.M.; Reames, L.J. A Climatology and Comparison of Parameters for Significant Tornado Events in the United States. Weather Forecast. 2012, 27, 106–123. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- ECMWF. Available online: https://confluence.ecmwf.int/display/CKB/ERA5%3A+data+documentation (accessed on 10 January 2020).
- ECMWF. Available online: https://confluence.ecmwf.int/display/CKB/ERA-Interim+known+issues (accessed on 10 January 2020).
- Gensini, V.A.; Mote, T.L.; Brooks, H.E. Severe-Thunderstorm Reanalysis Environments and Collocated Radiosonde Observations. J. Appl. Meteorol. Climatol. 2014, 53, 742–751. [Google Scholar] [CrossRef]
- Taszarek, M.; Brooks, H.E.; Czernecki, B.; Szuster, P.; Fortuniak, K. Climatological Aspects of Convective Parameters over Europe: A Comparison of ERA-Interim and Sounding Data. J. Clim. 2018, 31, 4281–4308. [Google Scholar] [CrossRef]
- Moncrieff, M.W.; Miller, M.J. The dynamics and simulation of tropical cumulonimbus and squall lines. Q. J. R. Meteorol. Soc. 1976, 102, 373–394. [Google Scholar] [CrossRef]
- Doswell, C.A.; Rasmussen, E.N. The Effect of Neglecting the Virtual Temperature Correction on CAPE Calculations. Weather Forecast. 1994, 9, 625–629. [Google Scholar] [CrossRef]
- Emanuel, K.A. Atmospheric Convection; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Holton, J.R. An Introduction to Dynamic Meteorology; Elsevier Academic Press: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Conover, W.J. Practical Nonparametric Statistics; John Wiley & Sons: New York, NY, USA, 1971. [Google Scholar]
- Neuhaeuser, M. Nonparametric Statistical Tests, A Computational Approach; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Corder, G.; Foreman, D. Nonparametric Statistics: A Step-by-Step Approach; Wiley: Hoboken, NJ, USA, 2014; ISBN 978-1118840313. [Google Scholar]
- Davison, A.C.; Hinkley, D.V. Bootstrap Methods and Their Application; Cambridge Series on Statistical and Probabilistic Mathematics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Nelsen, R. An Introduction to Copulas, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Joe, H. Dependence Modeling with Copulas; CRC Monographs on Statistics & Applied Probability; Chapman & Hall: London, UK, 2014. [Google Scholar]
- Durante, F.; Sempi, C. Principles of Copula Theory; CRC/Chapman & Hall: Boca Raton, FL, USA, 2015. [Google Scholar]
- Salvadori, G.; De Michele, C.; Kottegoda, N.; Rosso, R. Extremes in Nature. An Approach Using Copulas; Water Science and Technology Library Series; Springer: Dordrecht, The Netherlands, 2007; Volume 56, ISBN 978-1-4020-4415-1. [Google Scholar]
- Sklar, A. Fonctions de répartition à n dimensions et leurs marges. Publ. Inst. Stat. Univ. Paris 1959, 8, 229–231. [Google Scholar]
- Markowski, P.M.; Dotzek, N. A numerical study of the effects of orography on supercells. Atmos. Res. 2011, 100, 457–478. [Google Scholar] [CrossRef]
| ERA-5 | ||||
| Low | Medium | High | Extreme | |
| [15] | [14] | [14] | [14] | |
| WM | ||||
| LLS | ||||
| DLS | ||||
| ERA-Interim | ||||
| Low | Medium | High | Extreme | |
| [14] | [14] | [13] | [14] | |
| WM | ||||
| LLS | ||||
| DLS | ||||
| Regional Analysis | |||||||
| KS | AD | MW | |||||
| Region | ERA5 | ERAint. | ERA5 | ERAint. | ERA5 | ERAint. | |
| Tyr.-South | 14.30 | 24.59 | 2.10 | 7.03 | 1.70 | 7.74 | |
| WM | Tyr.-North | 5.70 | 80.88 | 4.80 | 67.24 | 4.20 | 69.62 |
| South-North | 27.70 | 0.99 | 25.50 | 1.73 | 92 | 4.12 | |
| Tyr.-South | 99.30 | 43.23 | 98.70 | 56.19 | 89.70 | 39.14 | |
| LLS | Tyr.-North | 45.70 | 0.39 | 45.30 | 0.32 | 27.30 | 0.37 |
| South-North | 27.70 | 0.06 | 11.80 | 0.01 | 8.60 | 0.01 | |
| Tyr.-South | 74.90 | 92.31 | 83.90 | 92.58 | 73.70 | 93.82 | |
| DLS | Tyr.-North | 75.20 | 79.59 | 62.10 | 70.94 | 44.50 | 51.39 |
| South-North | 26 | 46.31 | 24.50 | 33.06 | 20.70 | 26.64 | |
| Seasonal Analysis | |||||||
| KS | AD | MW | |||||
| Season | ERA5 | ERAint. | ERA5 | ERAint. | ERA5 | ERAint. | |
| Spring-Summer | 86.35 | 87.83 | 66.18 | 91.50 | 51.49 | 100 | |
| WM | Spring-Autumn | 20.68 | 25.62 | 23.03 | 13.24 | 27.29 | 74.25 |
| Summer-Autumn | 31.18 | 13.17 | 11.82 | 5.05 | 10.09 | 27.72 | |
| Spring-Summer | 83.08 | 67.56 | 69.92 | 56.88 | 60.74 | 94.47 | |
| LLS | Spring-Autumn | 5.69 | 0.06 | 2.20 | 0.02 | 2.38 | 0.02 |
| Summer-Autumn | 6.18 | 0.18 | 1.28 | 0.03 | 0.96 | 0.02 | |
| Spring-Summer | 93.18 | 67.56 | 91.55 | 70.01 | 75.81 | 91.71 | |
| DLS | Spring-Autumn | 63.24 | 96.53 | 61.28 | 85.21 | 100 | 90.49 |
| Summer-Autumn | 99.31 | 74.32 | 98.42 | 70.73 | 86.11 | 70.76 | |
| Actual Values | ||||
| ERA-Interim | ERA-5 | |||
| KS | AD | KS | AD | |
| WM | 0.0006% | 6.1 × 10−6% | 0.019% | 0.00057% |
| LLS | 0.18% | 0.82% | 3.8% | 2.6% |
| DLS | 3.9% | 4.6% | 6.4% | 1.1% |
| Standardised indices | ||||
| ERA-Interim | ERA-5 | |||
| KS | AD | KS | AD | |
| WM | 0.0082% | 0.00057% | 0.16% | 0.053% |
| LLS | 1.3% | 0.12% | 0.016% | 0.019% |
| DLS | 3.9% | 2.4% | 0.65% | 0.87% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ingrosso, R.; Lionello, P.; Miglietta, M.M.; Salvadori, G. A Statistical Investigation of Mesoscale Precursors of Significant Tornadoes: The Italian Case Study. Atmosphere 2020, 11, 301. https://doi.org/10.3390/atmos11030301
Ingrosso R, Lionello P, Miglietta MM, Salvadori G. A Statistical Investigation of Mesoscale Precursors of Significant Tornadoes: The Italian Case Study. Atmosphere. 2020; 11(3):301. https://doi.org/10.3390/atmos11030301
Chicago/Turabian StyleIngrosso, Roberto, Piero Lionello, Mario Marcello Miglietta, and Gianfausto Salvadori. 2020. "A Statistical Investigation of Mesoscale Precursors of Significant Tornadoes: The Italian Case Study" Atmosphere 11, no. 3: 301. https://doi.org/10.3390/atmos11030301
APA StyleIngrosso, R., Lionello, P., Miglietta, M. M., & Salvadori, G. (2020). A Statistical Investigation of Mesoscale Precursors of Significant Tornadoes: The Italian Case Study. Atmosphere, 11(3), 301. https://doi.org/10.3390/atmos11030301







