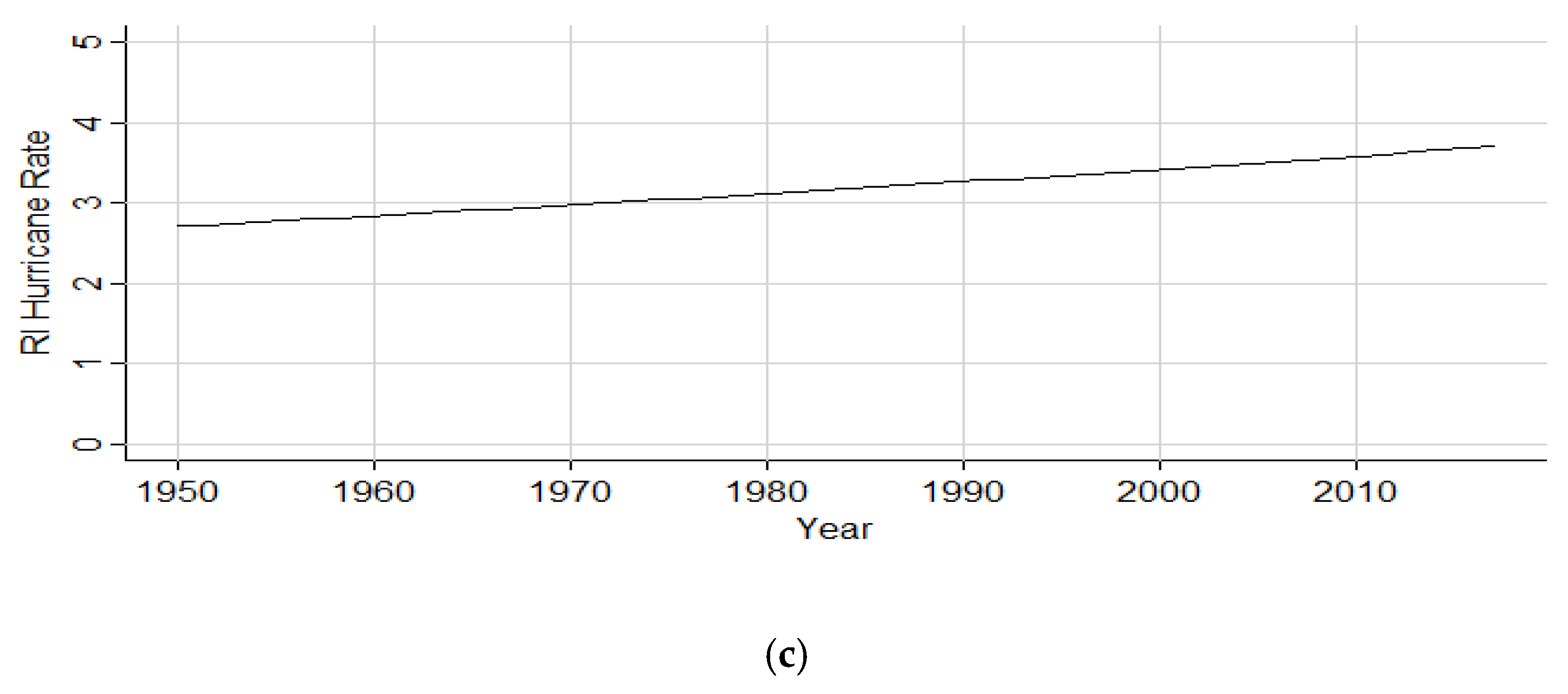1. Introduction
The scientific community’s ability to project tropical cyclone (TC) intensities and tracks has improved in recent years. However, the consistent variability within TC intensity and activity every season creates persistent barriers in formulating accurate predictions of TC paths and peak velocities [
1]. This is due to the range of severe hazards associated with these weather events, as well as the volatility that TCs are known to exhibit [
2]. One such example of TC changeability is a storm’s capacity to undergo rapid intensification (RI). RI is typically defined as a 30 knot (25 and 35) increase in the one-minute maximum sustained surface wind speed over a 24-h period [
3]. RI has recently become a main focus for researchers and policymakers in regard to TC hazards [
3].
The North Atlantic basin has historically been a very active TC genesis site. Thus, an in-depth investigation of RI in TCs tracking within the Atlantic is a necessity. The National Hurricane Center (NHC) and Statistical Hurricane Intensity Prediction Scheme (SHIPS) databases find that 31% of all TCs, 60% of all hurricanes, 83% of all major hurricanes (Category 3+ on the Saffir-Simpson Hurricane Wind Scale), and all of Categories 4 and 5 hurricanes undergo RI [
4]. Famously destructive storms, such as Camille (1969), Andrew (1992), Opal (1995), Mitch (1998), Charley (2004), Katrina (2005), Gustav (2008), Sandy (2012), and Harvey (2017) were shown to have undergone RI at some point within their life cycle [
4].
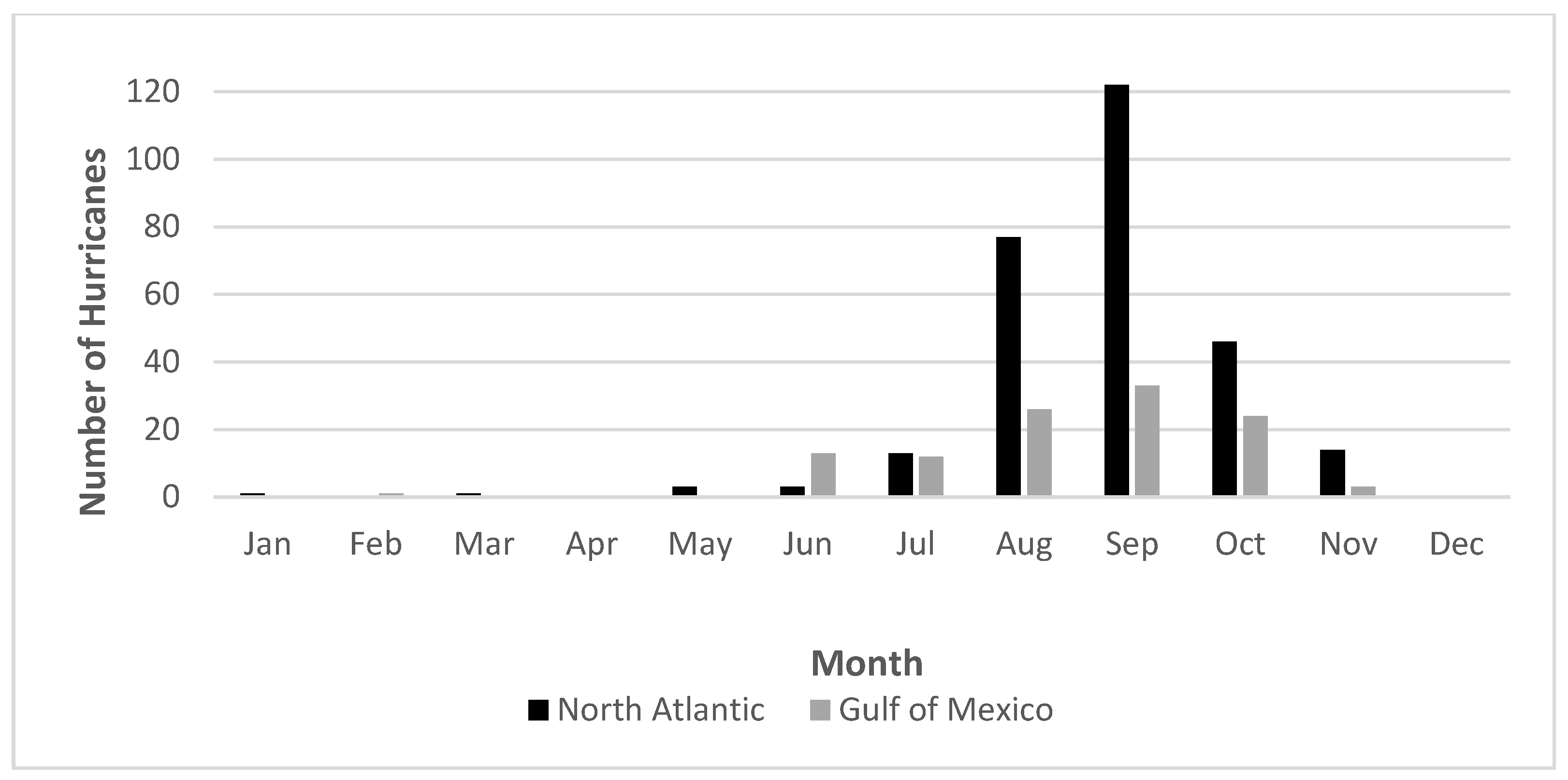
The seasonal RI distribution in the Atlantic basin follows the Atlantic seasonal hurricane distribution, with the highest RI occurrence in September [
5]. This is due to the increased likelihood of RI given the occurrence of more storms. From the years 1950 to 2014, the North Atlantic had a total of 988 TCs, and of these, 215 experienced at least one episode of RI. In relation to climate indices, RI is significantly correlated with the June–November El Niño southern oscillation (ENSO), main development region (MDR) sea surface temperatures, and the Atlantic warm pool (AWP) [
5]. It is also suggested that there are three main regions of maximum RI occurrence: the Gulf of Mexico and Western Caribbean Sea, the open ocean southeast and east of Florida, and the Western Tropical North Atlantic [
5,
6]. Xu and Wang (2014) discuss the dependence of TC intensification rates on storm intensity and size in the North Atlantic basin, concluding that the intensification rate is positively correlated with storm intensity and negatively correlated with storm size in terms of the radius of maximum wind.
Forecasting for Atlantic hurricane RI continues to present major challenges for researchers, climatologists, and meteorologists alike. The projections of RI are limited by two key issues: researchers lack a clear definition for RI, having varying thresholds for increasing wind speeds between 25 to 35 knots over a 24-h period, and researchers also differ in whether they utilize wind speed or minimum sea level pressure to measure RI. While these definitions are related, they are not synonymous with one another, therefore causing a lack of standardization in requirements for the measurement of RI [
4].
Current research suggests the warming climate may produce more intense TCs with a higher probability of undergoing RI during their life cycle [
3,
4,
5]. The increased likelihood of rapidly intensifying TCs necessitates the development of an RI climatology spanning the current North Atlantic record. While multiple studies have focused on the spatial origin patterns of RI, as well as potential forcing mechanisms that may be integral to the initiation of the RI process [
1,
3], [
5,
6,
7], there have been no studies dedicated to an analysis of the entire Atlantic basin record (1851 to 2017) with specific emphasis on possible trends in time, spatial clustering, and climatological characteristics per sub-basin. A comprehensive assessment of RI processes in the Atlantic basin can provide important information to researchers, thus allowing more accurate forecasts to be disseminated to potentially affected communities. This paper assesses temporal and spatial trends in RI hurricanes throughout the Atlantic Basin historical record as an in-depth statistical analysis to supplement the existing literature.
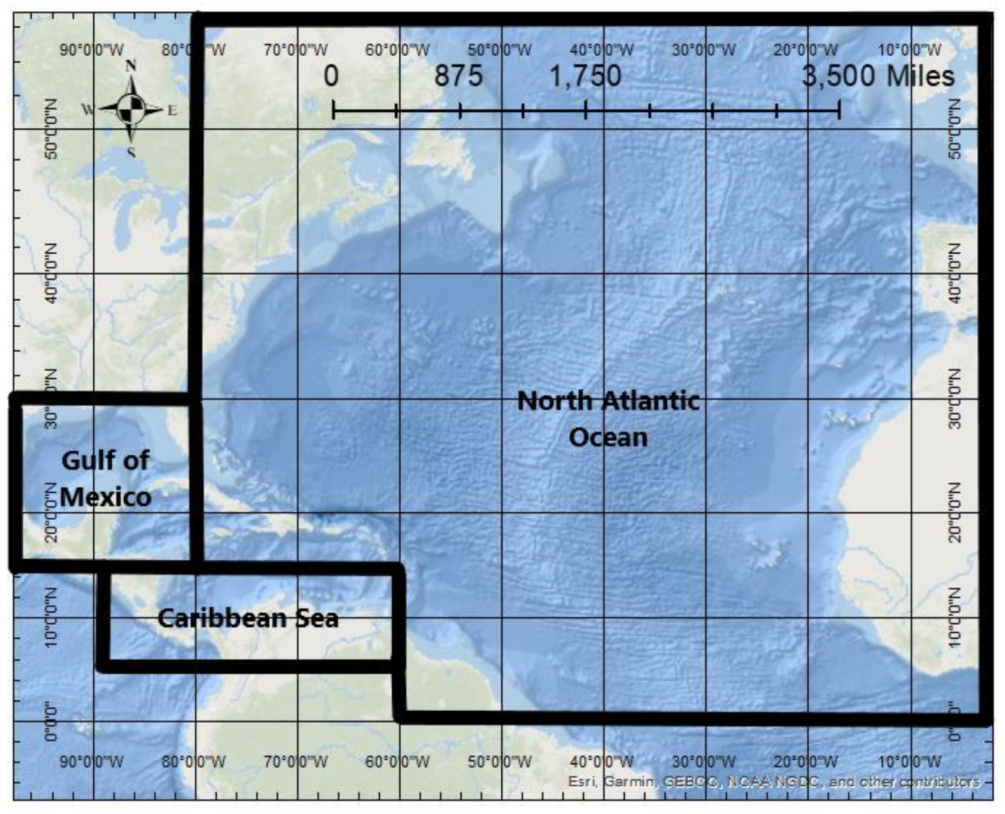
Figure 1 shows the study area and each delineated sub-basin.
The main objectives of this study are as follows:
To determine basin-wide and sub-basin frequency distributions and seasonality, with sub-basins organized into the North Atlantic, Gulf of Mexico, and Caribbean waterways (
Figure 1).
To examine potential trends in RI hurricane counts by utilizing a count time series regression model spanning the entire North Atlantic hurricane record (1851–2017) and shorter data subsets to assess possible data bias present in the trend.
To analyze spatiotemporal trends of storms that both originate and initiate their RI cycle within the Gulf of Mexico basin compared to those in the North Atlantic.
To examine spatiotemporal trends of storms that undergo more than one cycle of RI in their lifetime.
To explore spatial trends that may exist within the sub-basins in regard to RI hurricane origins, RI genesis, RI landfall, and RI lifetime maximum intensity (LMI) points.
4. Discussion and Concluding Remarks
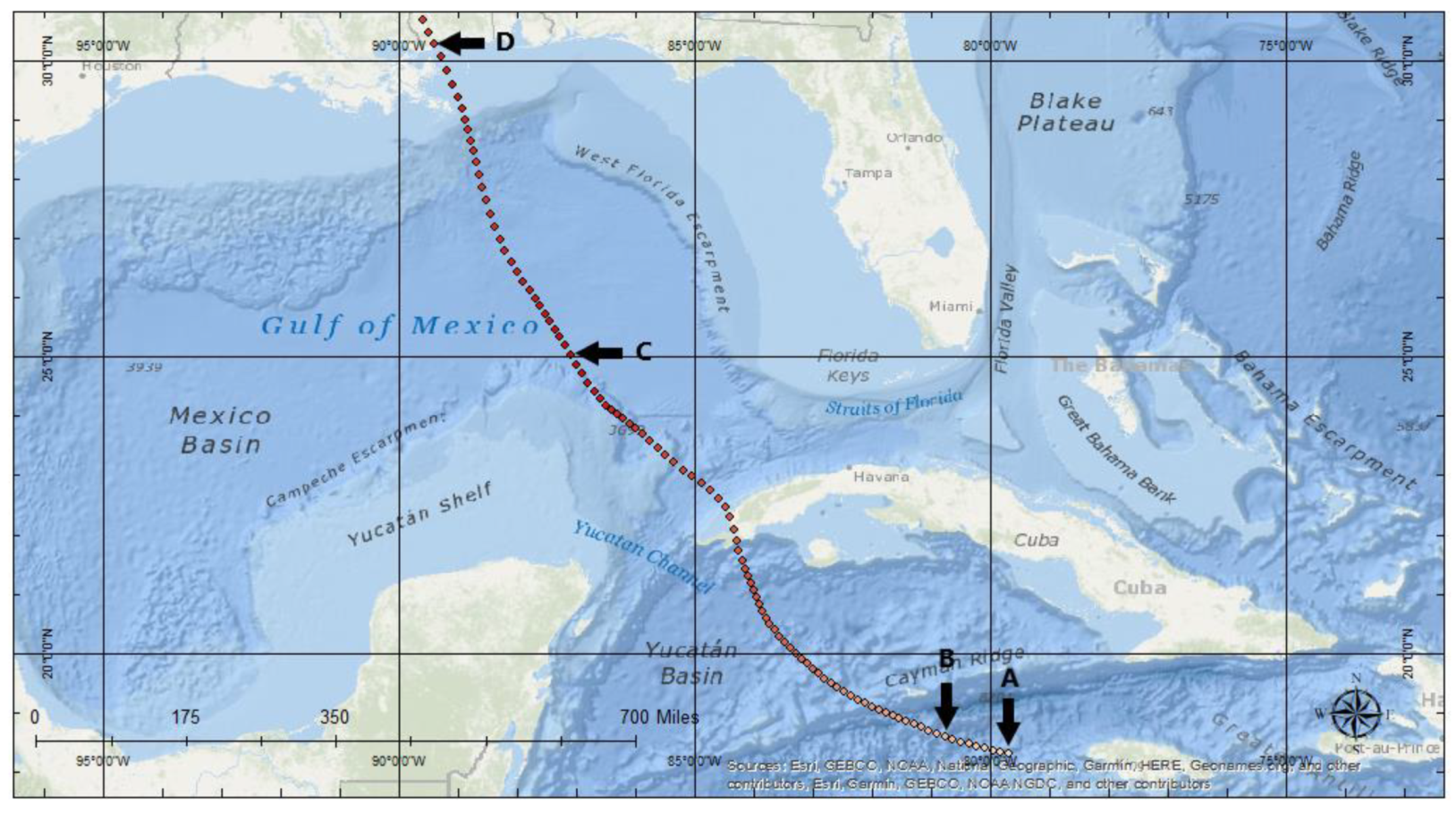
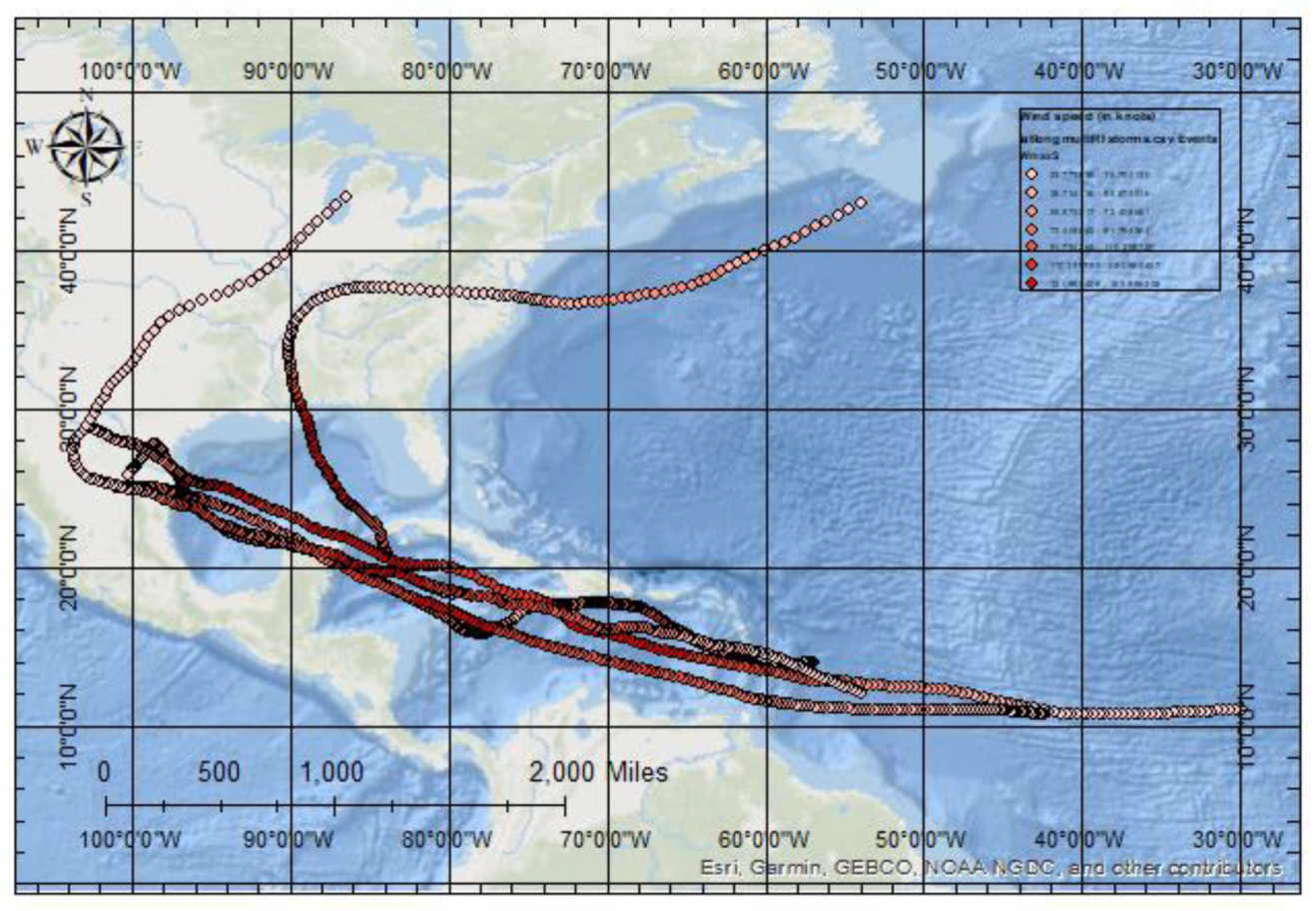
The seasonality and frequency of RI hurricanes in the Atlantic basin suggest that both geographical and environmental forcing processes are at play. The monthly RI hurricane distribution of the North Atlantic and Gulf of Mexico sub-basins generally follows a typical Atlantic hurricane season peak in August, September, and October. However, the sharp contrast between the singular September peak in the North Atlantic to the more consistent presence of RI hurricanes throughout the summer months of June, July, and August in the Gulf of Mexico indicates sub-basin variations. The Gulf of Mexico’s lesser, though steady, development of RI hurricanes shows a higher tendency for hurricanes to undergo the RI process within the sub-basin. Of further evidence in support of this idea is the five storms with four RI processes in their lifecycle that all tracked through the Gulf of Mexico and made landfall along the Gulf Coast.
Figure 18 depicts the tracks of these storms color-coded based on increasing intensity.
The high rate of RI storms within this sub-basin may be due to the more evenly distributed heating that the sub-basin receives throughout the summer months, as well as the higher temperatures the Gulf of Mexico is known to have in comparison to the North Atlantic. The Gulf of Mexico is also a more compact, shallower body of water, which allows for the hot water temperatures to occur during the entirety of the Boreal summer months.
Seventy-five percent of the storms initiating their first cycle of RI immediately following their origin within the North Atlantic sub-basin may be indicative of the involvement of larger atmospheric and oceanic forces. Although having a relatively small rate of occurrence (only 67 of the total number of storms), this result might suggest the existence of a triggering mechanism, such as proximity to the MDR, that could be the cause of an immediate RI onset, thus necessitating further analysis of the environmental determining factors that spur on RI events. These results are also varying from Tallapragada et al. [
22,
23] conclusions that most storms undergo RI at their origin. The present study shows that the majority of storms’ initial RI cycles were initiated at some point following the storm’s origin (83% of storms underwent RI at some other point in their cycle besides the origin of the storm). The higher windspeed values of RI storms in contrast with non-RI storms suggest, not surprisingly, that, on average, storms undergoing RI cycles tend to be more intense than storms that do not. Storms undergoing more than one cycle of RI within their lifetime were found to have an average LMI of 64.05 ms
−1 as compared to an average LMI of 48.27 ms
−1 for storms undergoing only one cycle of RI. This further corroborates the idea that the process of RI tends to spawn more intense and, thus, more dangerous, storms.
Upon sub-setting the data from 1980 on, it was found to have similar climatological results as the entirety of the record. The number of storms undergoing RI at some other point within their lifecycle besides their origin was found to be 129 of the 147 total storms from 1980 on (87.76% of the storms), which holds steady with the results of the entirety of the record that found 83% of storms underwent RI at some other point in their lifecycle besides their origin. Three of the five storms that underwent four cycles of RI occurred from 1980 on, and all five storms that underwent four cycles occurred from 1967 on where there was satellite data available. The monthly distribution also holds steady from 1980 on, showing a peak in August, September, and October, the highest of which still is September.
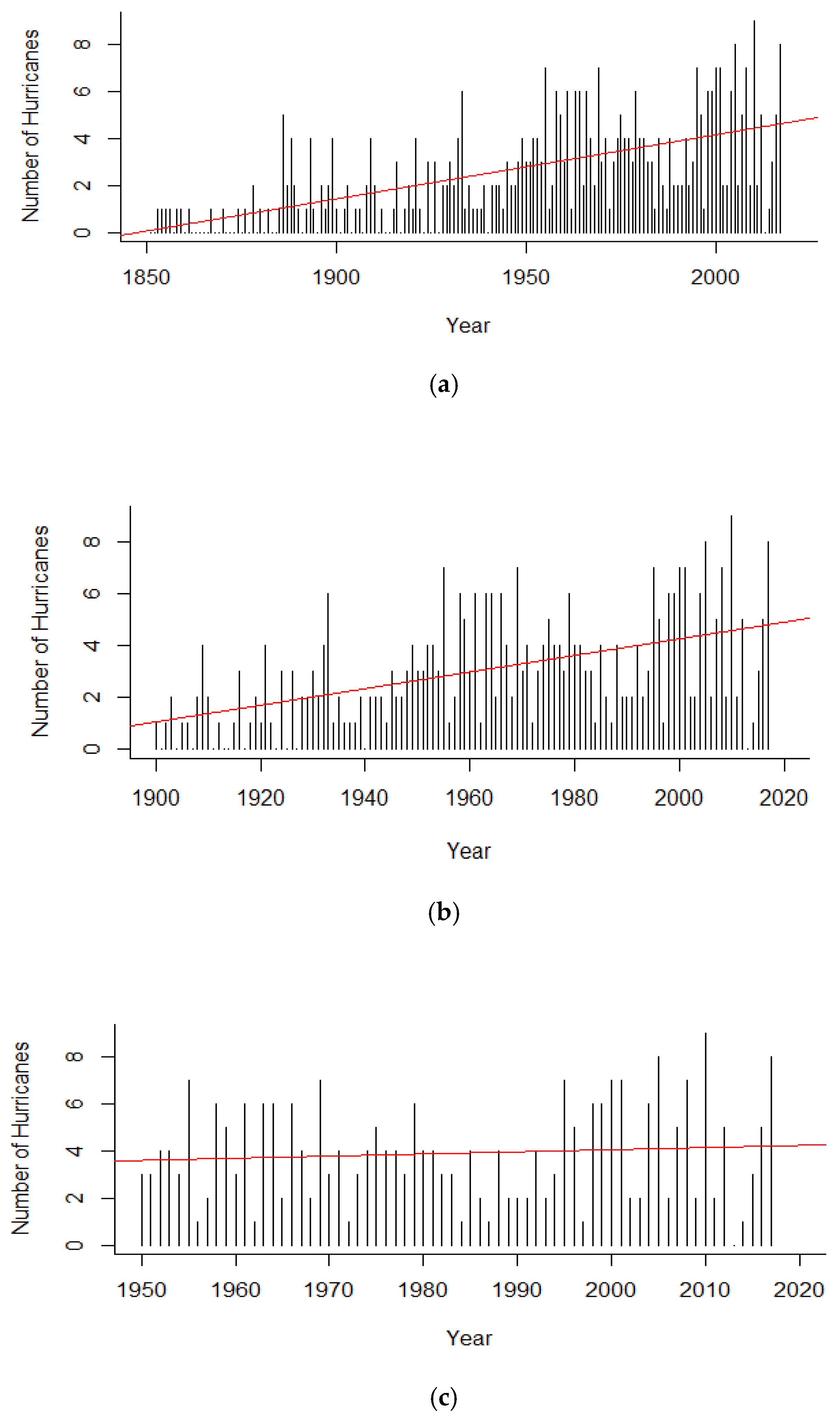
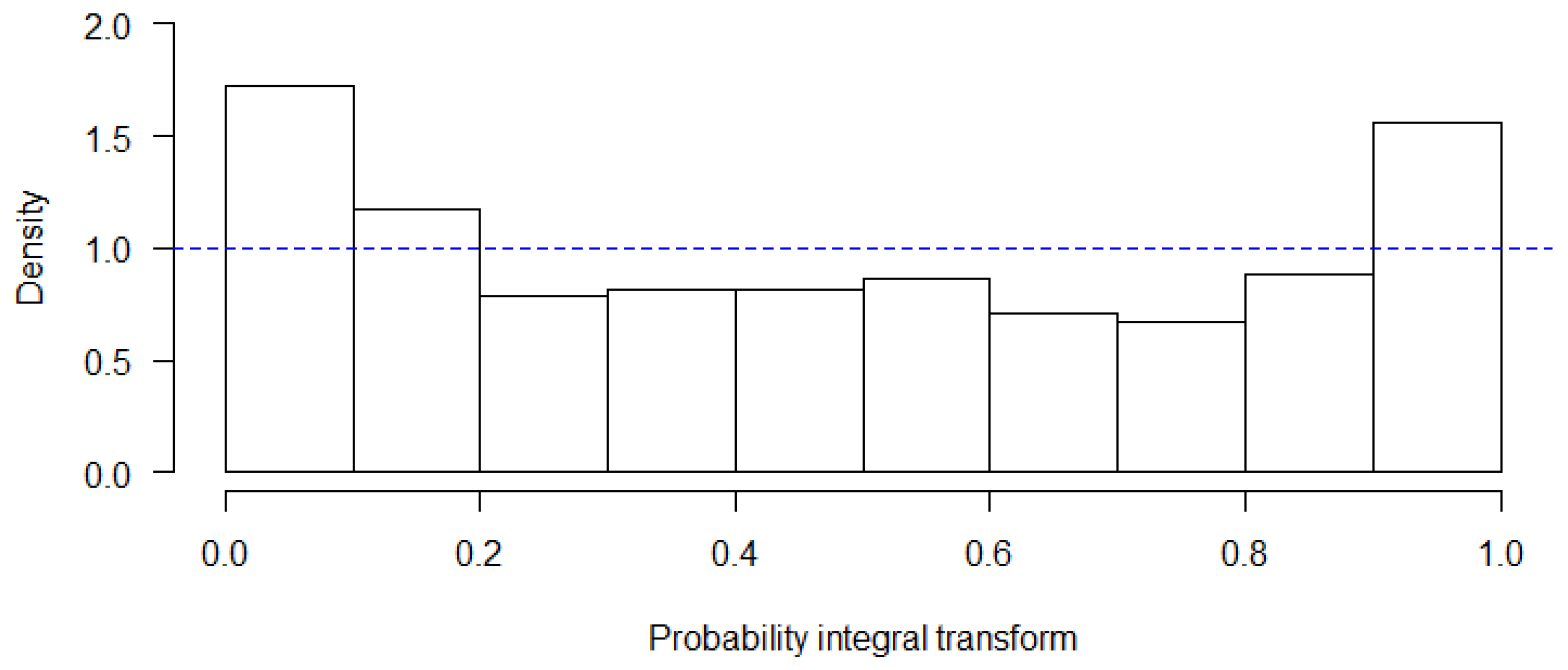
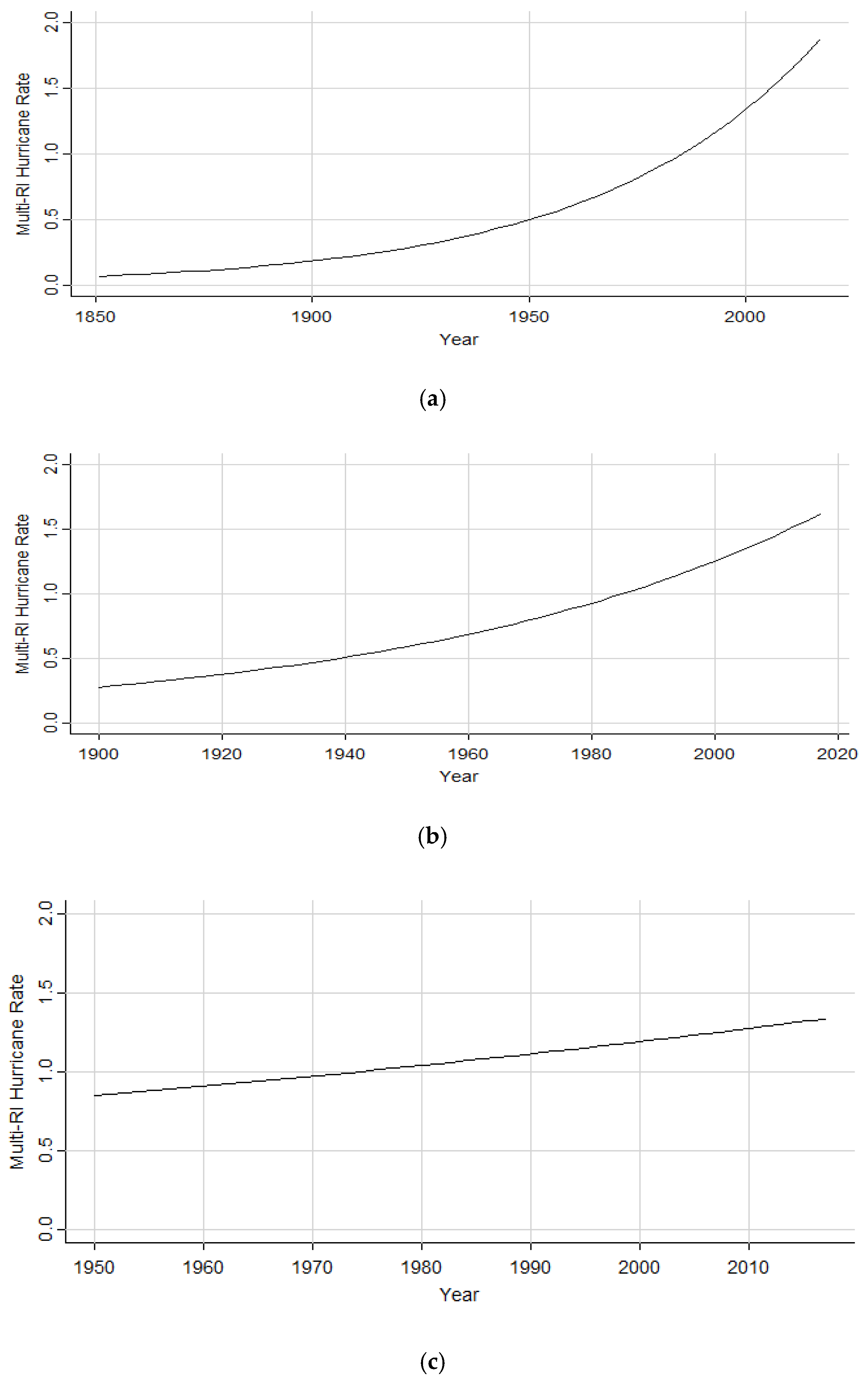
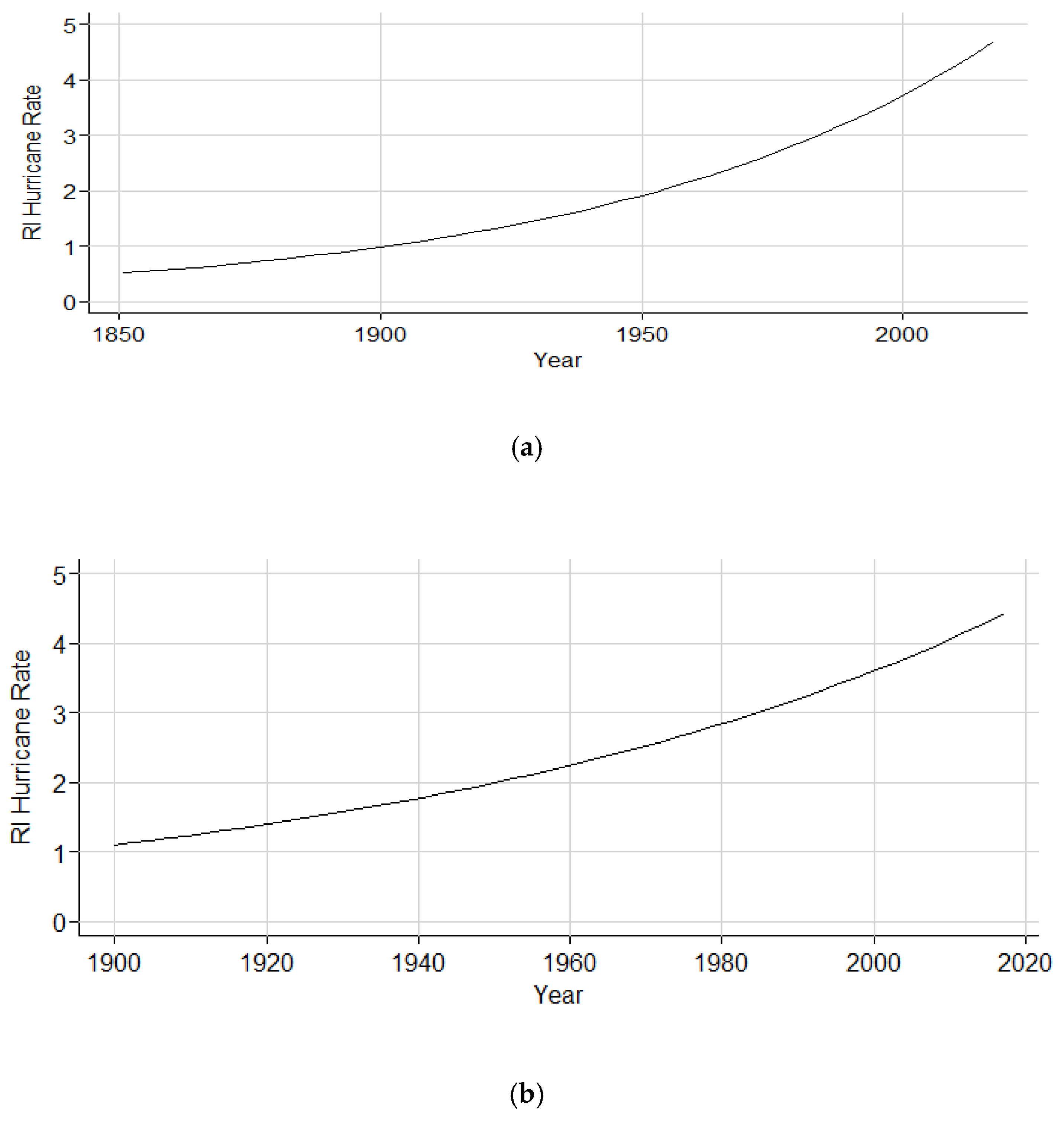
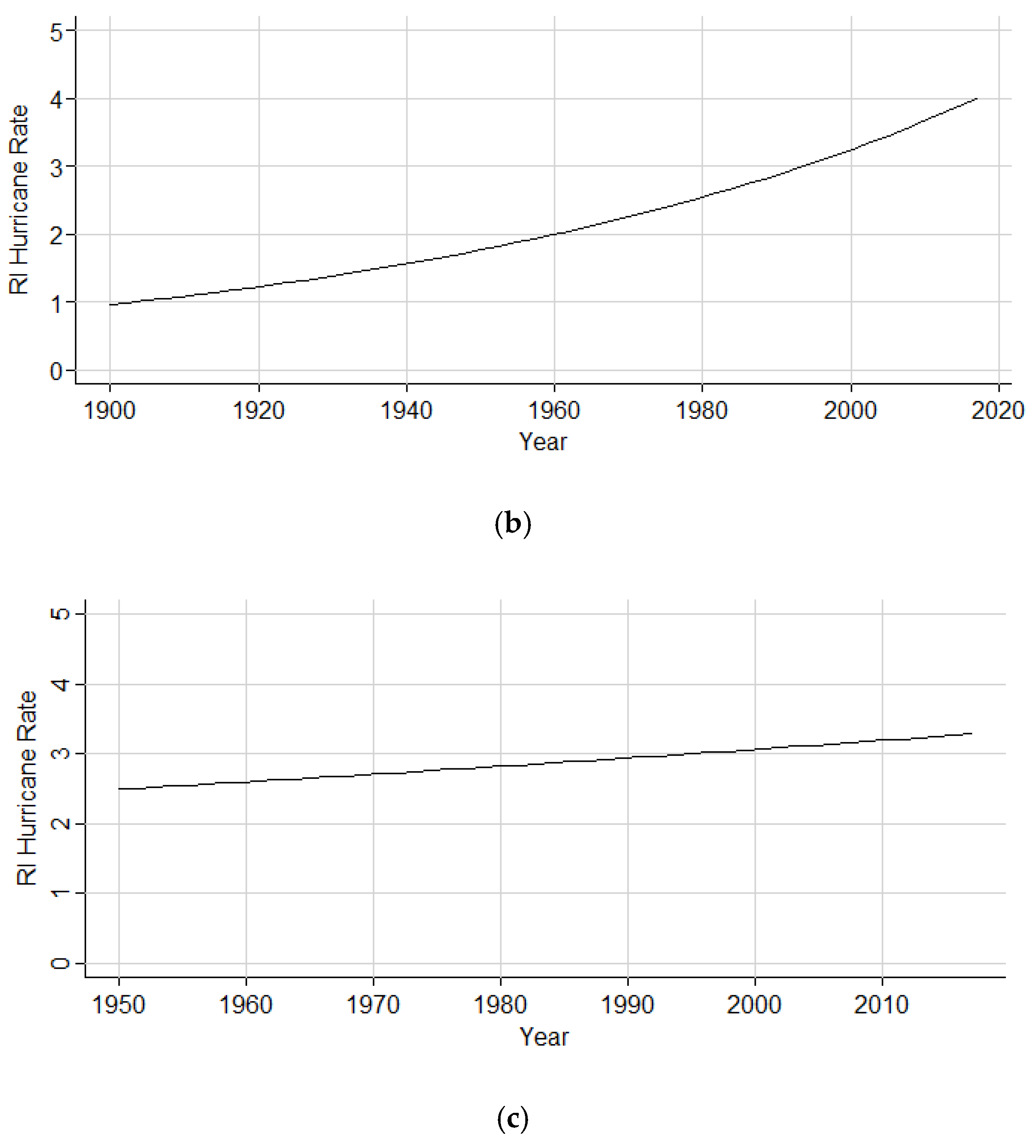
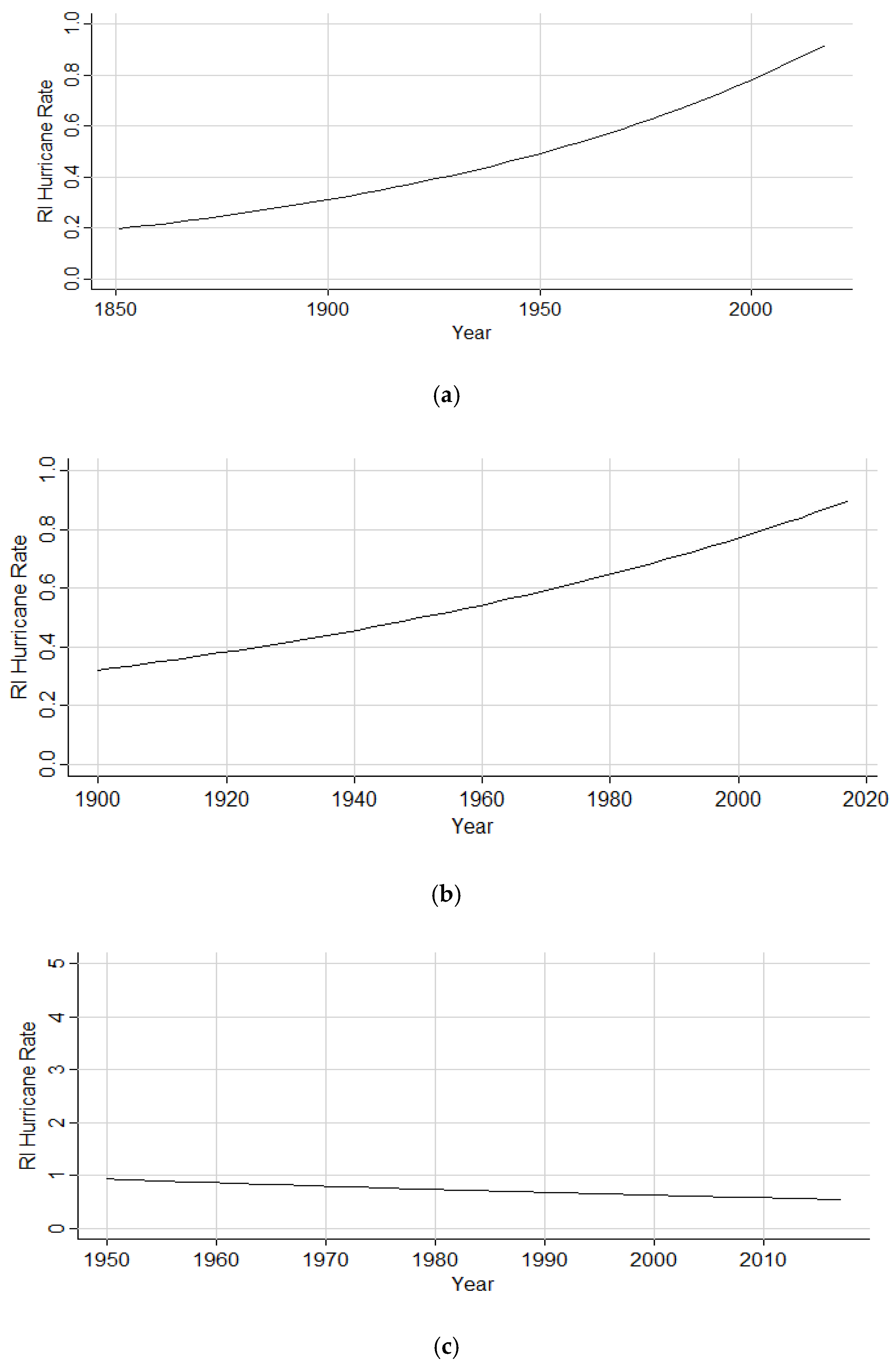
The GARCH model yields a positive increasing trend for RI hurricane counts in both the 1851–2017 and 1900–2017 subsets. The inconsistency in the CIs of the 1950–2017 subset may be illustrative of a false increasing trend from 1851 to 2017 based on missing storms from the earliest part of the HURDAT2 record. However, substantial advancements were made to the detection and cataloguing of hurricanes beginning in 1900 with the advent of wireless telegraph capabilities from ships [
24]. Thus, the trend seen in both 1851 to 2017 and 1900 to 2017 points to a legitimate significant increase over the record. The inconsistency of significance in the latter period’s trend could be related to the much shorter timeframe of data being analyzed, causing a smaller sample of data and, thus, a poorer estimate of the RI hurricane population parameter.
The use of the GARCH model is further supported by the Poisson regression analysis results in the North Atlantic sub-basin. Although the region shows factor increases for storms both originating and initiating RI, the chi-square p-value’s rejection of the null hypothesis suggests the Poisson distribution is not an appropriate model to describe storm patterns in the region. However, the positive increasing trend within both the GARCH and Poisson models supports a likely legitimate increase in RI hurricanes over time.
The factor increases of storms both originating and initiating RI within the Gulf of Mexico, and the steady rise in incidence rate ratios depicted in the graphics is indicative of consistent RI hurricane activity within the sub-basin. Although the Gulf of Mexico has substantially fewer events than the North Atlantic and Caribbean, the presence of RI storms within the basin has been not only steady but also slightly enhanced throughout time. The 0.7% factor decrease in the 1950 to 2017 subset of storms originating within the Gulf may speak to a decreasing trend but more than likely further illustrates the low frequency of storm originations for the basin in general. The 0.2% factor decrease of storms initiating RI within the Gulf of Mexico from the years 1950 to 2017 is an extremely low decline in activity and was also found to be an insignificant finding based on the p-value. Thus, an increase in Gulf of Mexico RI basin activity is still seen as the prominent finding. Similar to the consistent monthly distribution of RI events within the Gulf of Mexico during the summer months, the warm SSTs (sea surface temperatures) and shallower water of the sub-basin may play a role in this consistent activity, and warming waters in the region in response to anthropogenic climate change may correlate with the increasing trend.
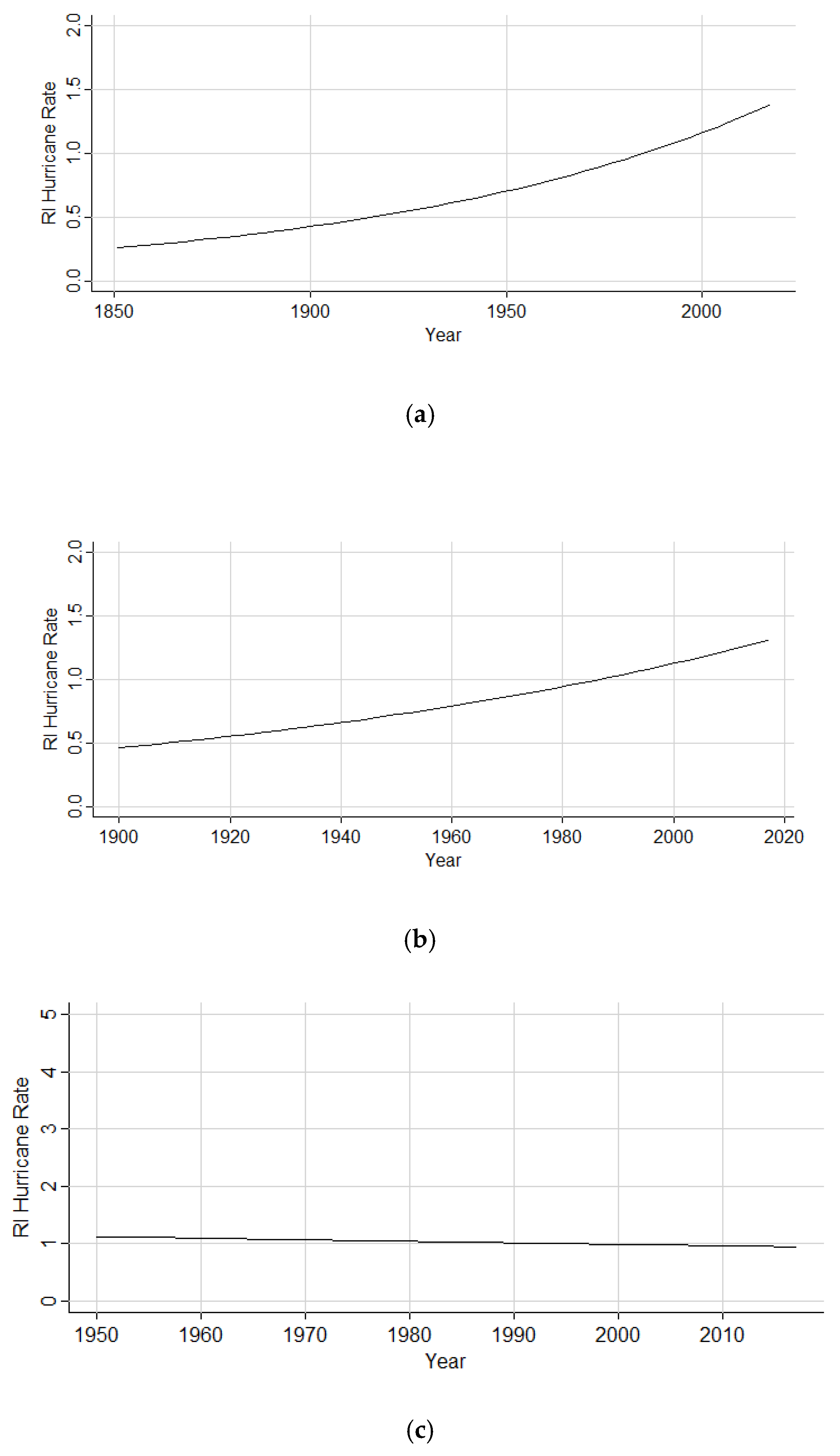
The Poisson regression results for multi-RI storms illustrate that, as time has progressed, more storms have begun to undergo more than one RI cycle during their lifetime. The consistent increase from all subsets of the data (1851 to 2017, 1900 to 2017, and 1950 to 2017) is further evidence in support of this upward trend of multi-RI events. These results may be indicative of changes in environmental fueling mechanisms, such as warmer SSTs (sea surface temperatures), conditions producing less vertical wind shear, or warmer air temperatures that allow for more evaporation and, thus, more precipitable water vapor.
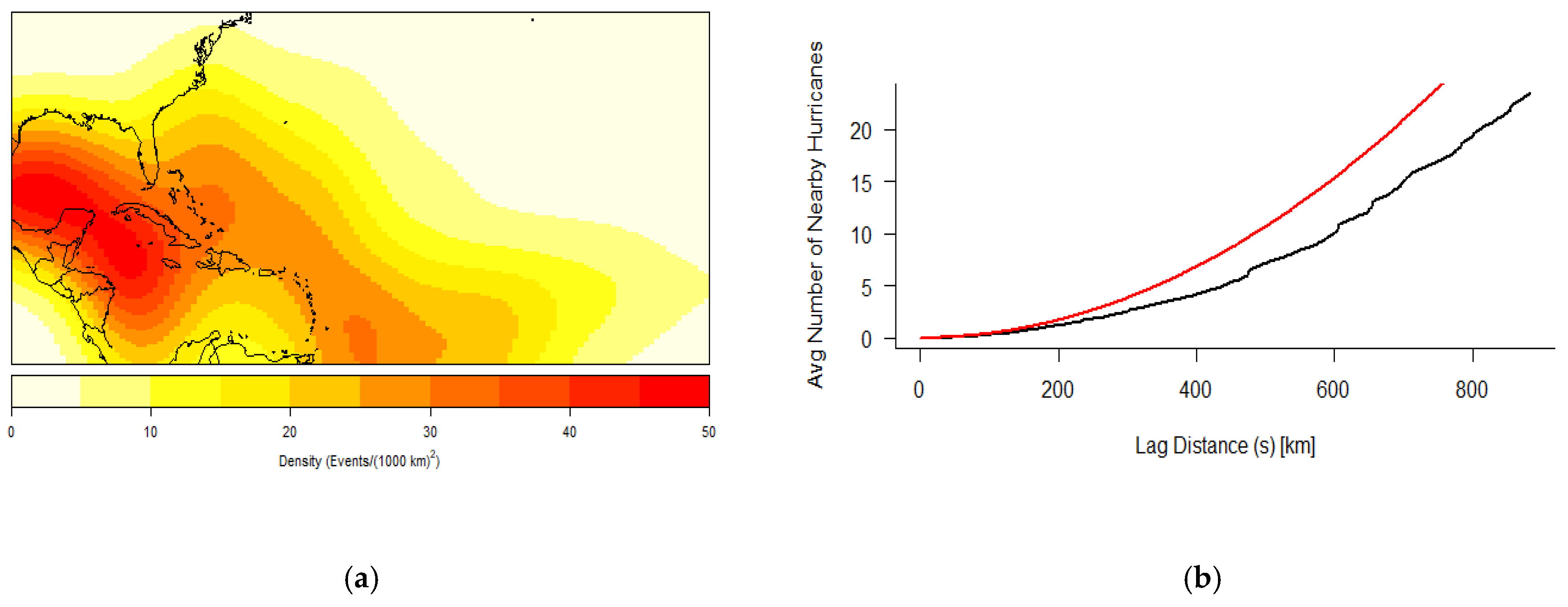
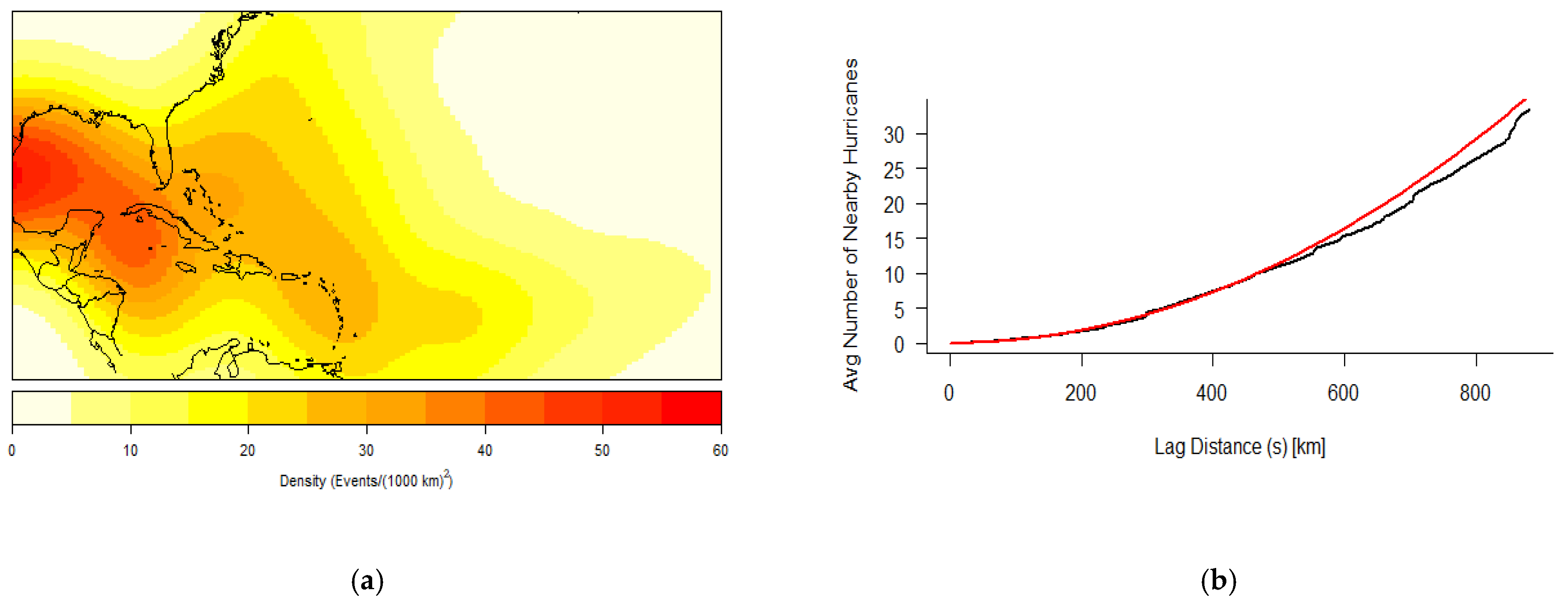
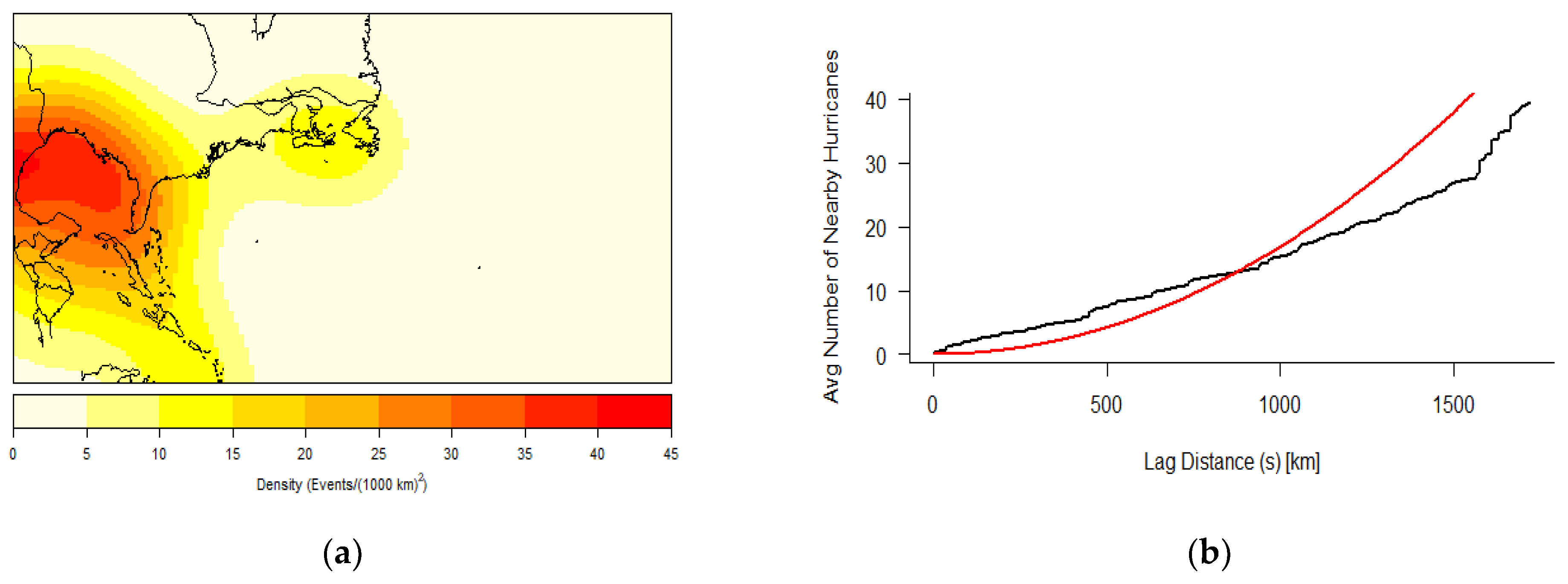
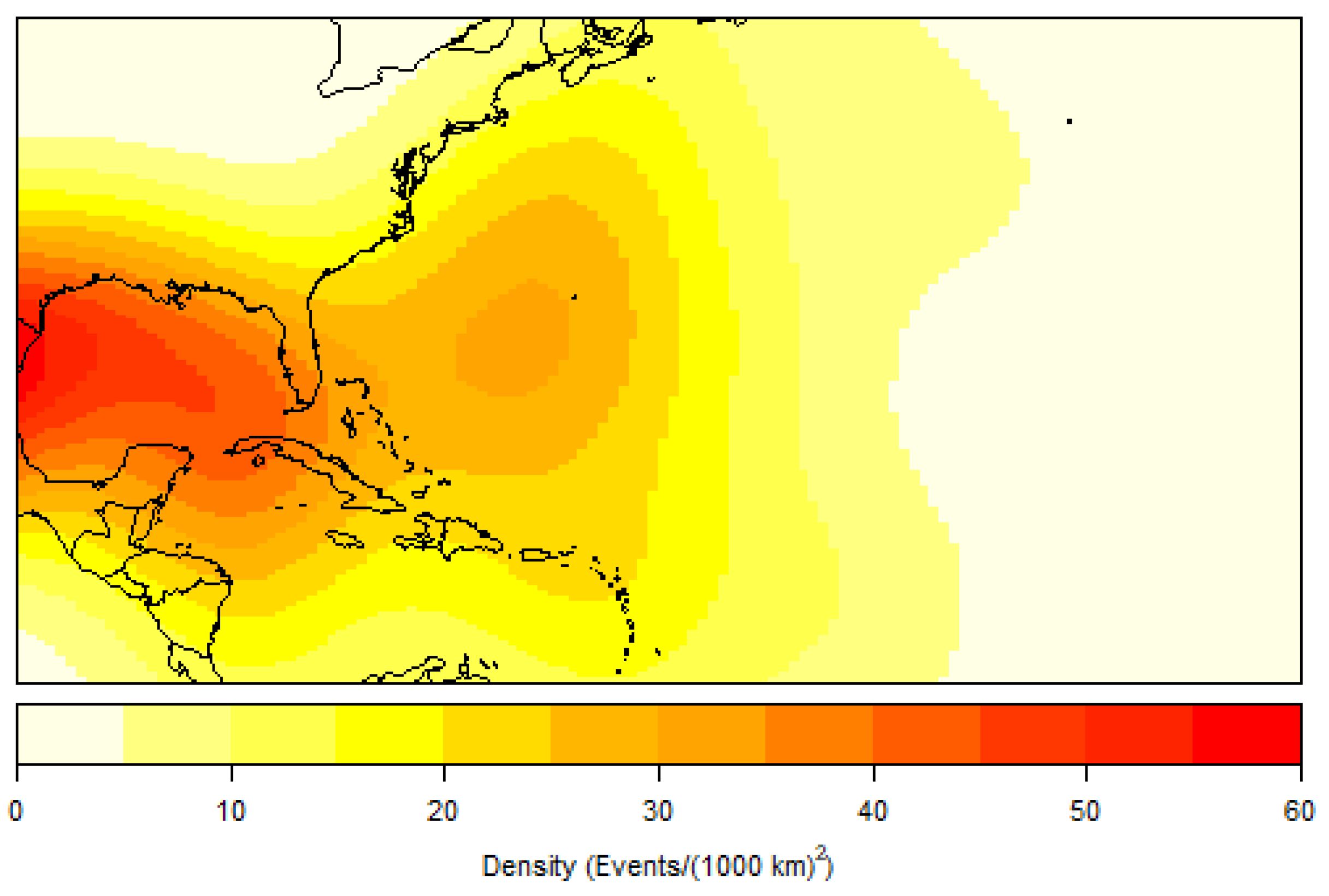
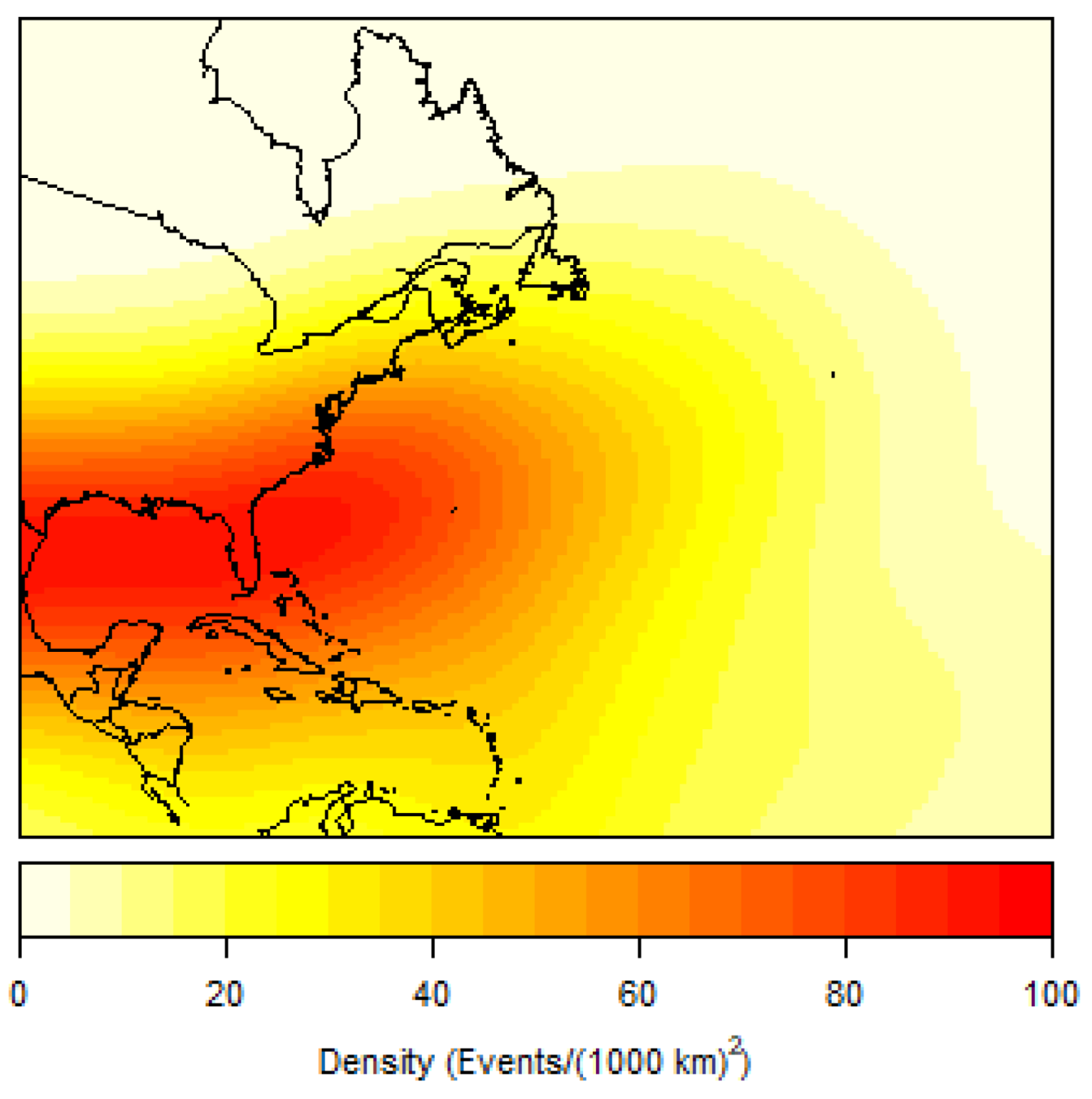
Spatial clustering appears to be centered around the Caribbean and Gulf of Mexico waterways, especially for the initiation of RI, the LMI of RI storms, and the landfall of these storms. Although the generalization of K results indicate a trend toward CSR the higher the lag distance, the presence of RI storms within these two sub-basins is noteworthy. RI storm origin points are clustered up to 150 km. This small lag distance indicates a weak patterning of points and supports the idea that an RI storm, like any hurricane, can develop at historically conducive areas in the basin. RI genesis points’ strong presence in the Caribbean and Gulf of Mexico may speak to the available heat and moisture of the area, though there is only a weak indication of clustering for these data. However, the initial RI completion points showing a trend toward the Gulf of Mexico is supported by a higher lag distance of 500 km. This indicates that RI storms not only have a likelihood of moving toward this sub-basin but also are spatially clustered there following the completion of their first cycle of RI. RI landfall points have the highest lag distance at 750 km, illustrating an even higher likelihood of clustering around the Gulf Coast, specifically Texas and Louisiana coastlines. Due to the available datapoints demonstrating that a large proportion of RI storms originate, travel, and make landfall within these geographical spaces, further investigation into common geographical features and environmental mechanisms that may allow for these storms to originate and mature is warranted.
The temporal cluster results indicate a significant likelihood of clustering within the Caribbean and Atlantic basins but not the Gulf of Mexico. The clustering within the North Atlantic and Caribbean is potentially linked to major atmospheric cycles like ENSO and the Atlantic multidecadal oscillation. These may help to explain the groupings of hurricanes in these regions and aid in future prediction capabilities for when RI might be more likely to be triggered within hurricanes. The lack of temporal hurricane clustering within the Gulf of Mexico is further evidence in support of the consistent presence of RI hurricanes within this sub-basin. This lack of clustering within the Gulf of Mexico coupled with the steady increasing trend shown in the Poisson regression results suggests that the Gulf of Mexico has seen consistent, yearly origins of RI hurricanes throughout the record of study (1851–2017).
The results of this study highlight two important findings. The first is that the Gulf of Mexico sees the consistent presence of RI hurricanes from year to year within the Boreal summer months. The second is that the process of RI is linked to the development of higher intensity storms. Thus, communities along the Gulf Coast should prepare to see consistent hurricanes that intensify quickly, mostly with little warning, and become highly intense hurricanes. In recent years, hurricanes such as Gustav (2008), Gordon (2012), and Harvey (2017)—all Gulf of Mexico rapid intensifiers that underwent RI right before they made landfall—have caught both forecasters and affected populations by surprise, resulting in billions of dollars’ worth of damages and a multitude of preventable deaths. Therefore, these results warrant a more focused investigation of the Gulf Coast area in both physical geography and population risk management perspectives. The levels of population preparedness, as well as the understanding of hurricanes and their associated hazards, of which RI is one, are important aspects to gauge in affected communities. Once a baseline of understanding is assessed, a proper education and preparedness curriculum can then be implemented by appropriate parties based on various community needs.
This research is part of a broader goal involving improvements to the predictions of TC paths and velocities to potentially decrease the number of lives lost and the cost of damage that these storms are known to cause. However, the focus on informing and aiding the public in their preparedness and understanding of these storms should be a top priority. It is a necessity to support affected populations in fully conceptualizing the dangers and risks of hurricanes and their hazards so that they can then increase their resiliency to such storms. Future research should aim to not only explain forcing mechanisms behind the RI process, as well as macro and mesoscale influences, but also to formulate effective communication approaches that would best relay proper preparedness strategies and information to communities most affected by these hazards.