Assessment of Open-path Spectrometer Accuracy at Low Path-integrated Methane Concentrations

Abstract

The accurate measurement of greenhouse gas emissions is a challenge for atmospheric science. Long-range open-path sensors are flexible enough to be applied to a variety of complex emission sources, and single devices are often used to measure both high and low path-integrated concentrations. As this technology develops, it is important to examine potential sources of inaccuracy. A GasFinder3 open-path laser was tested with a range of path-integrated concentrations from 11.7 to 182 ppm∙m CH₄ using certified standard gases. The measured path-integrated concentrations had a positive bias which was higher than 10% at low path-integrated concentrations (<50 ppm∙m) with a declining trend expected to be under 2% at 200 ppm∙m. A linear equation was used to correct the measured path-integrated concentrations to fit the expected values. After correction, the average bias was reduced to −0.36% and there was no relationship with path-integrated concentration. A relative bias less than ±3% was achieved above ca. 150 ppm∙m with or without calibration. Measurement campaigns may reduce error by increasing path lengths to maximize path-integrated concentration. When low path-integrated concentrations are expected, calibration over the expected range is beneficial.

1. Introduction

Measurements of CH₄ are a necessary component of research into greenhouse gas emissions and climate change. Long-range open-path sensors provide a unique solution to the measurement of emissions from large, heterogenous sources such as animal feeding operations, biogas facilities, or thawing permafrost and glacial margins [1,2,3]. Open-path sensors are also advantageous because they enable the use of path-switching, in which a single sensor is used to measure a series of paths in succession or based on wind direction. Path lengths vary depending on the size of the emission source, ranging from 10 to 300 m in the literature [3,4]. The primary unit of measurement for open-path sensors is a path-integrated concentration (in units of ppm∙m, or parts per million × metre), which is greatly affected by path length. For example, a concentration of 2 ppm measured in a path length of 10 m gives a path-integrated concentration of 20 ppm∙m, whereas the same concentration measured over a 100 m path results in 200 ppm∙m. Furthermore, most emission measurements require comparison of sensor paths upwind and downwind of a source, which are expected to have different concentrations. The ability to confidently resolve this concentration difference depends on measurement error. When designing an experimental layout, it would be helpful to understand the impact of path length and expected path-integrated concentration on measurement accuracy.

Open-path tunable diode lasers (OP-TDLs) have been widely accepted for open-path sensing applications, particularly in agriculture [5,6]. The instrument considered here is a new model of OP-TDL spectrometer (GasFinder3 (GF3), Boreal Laser Inc., Edmonton, Alberta) which aims to provide better accuracy and environmental stability than previous versions. The GF3 is available in high-range and low-range options, where the low-range version is designed to measure path-integrated concentrations over a large dynamic range, from 2 to 8500 ppm∙m.

For any new instrument, there is a need to understand the degree of accuracy under the conditions in which it is used. The path-integrated concentration recorded by GF3 is primarily assumed to be accurate based on a confidence factor (R²). The R² value indicates agreement between the absorption curves of the self-contained reference cell and the path being measured. An analysis of accuracy over a range of path-integrated concentrations has not been reported, especially at low path-integrated concentrations, which can be important for emissions measurement in agricultural settings where path-integrated concentrations are commonly below 200 ppm∙m.

Many applications of OP-TDLs involve a single device monitoring multiple paths. Differences in accuracy based on the measured path-integrated concentration could pose a challenge to experimental setups which switch between measuring short and long paths, for example, one source within a larger plume, or upwind and downwind concentrations around a source. Experimental site configurations often necessitate a wide range of path lengths; therefore it is important to closely examine the relationship between path-integrated concentration and accuracy. The purpose of this study is to experimentally evaluate the performance and bias of the GF3 sensor in measuring a range of low path-integrated CH₄ concentrations in laboratory conditions. These results will inform practitioners conducting field campaigns and help to reduce uncertainty in the measurement of CH₄, which is important for emission models and inventories.

2. Experiments

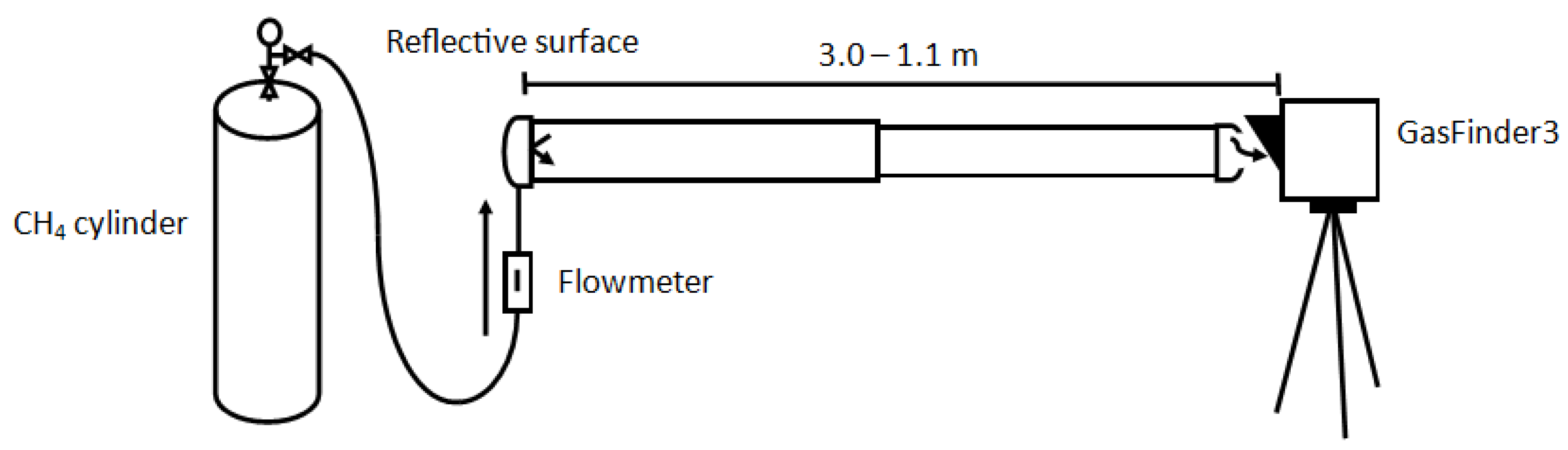
A single OP-TDL (GF3, Unit # CH4OP-30007) was used to sample fixed concentrations within a calibration chamber (Figure 1). This was one of the first GF3 sensors released by Boreal Laser, Inc. The sensor uses wavelength modulation spectroscopy. It has an integrated transmitter/receiver unit including a detector, a micro-computer, and a distributed feedback diode laser that operates in continuous wave output. The laser is thermally stabilized and is tuned to the 1654 nm absorption line for CH₄, which avoids interference from other gases including water vapour. The laser emits a beam through the air that is reflected and returned to the photodiode detector. To provide a reference waveform, another beam is emitted simultaneously through an onboard reference gas cell with 220 ppm∙m (5 cm length with a CH₄ concentration of 4,400 ppm). Additional details of the instrument design are provided in US patents 9,755,399B2 and 5,637,872.

The calibration chamber was composed of two to three 1 m length (total length = 3 m) sections of cylindrical polyvinyl chloride. One section had a smaller diameter (7.6 cm) than the others (10.2 cm), allowing the path length to be adjusted from 1.10 to 3.00 m. Rubber joints between sections were secured with steel straps. One end of the calibration chamber held a grey tape reflective surface (supplied by the laser manufacturer) used to return the infrared signal to the GF3 unit. This type of reflector provides reliable light return for path lengths up to 20 m and is suitable for the present application [7]. Path length was measured from the front of the GF3 unit to the reflective surface.

Tubing (6.35 mm inner diameter) at the reflective end of the calibration chamber allowed it to be filled with standard concentrations of CH₄. An open “window” (diameter = 2.5 cm) at one end was a passive outlet for CH₄ and kept the chamber at atmospheric pressure. The GF3 laser was positioned at the “window” end of the chamber, aimed at the reflector within.

Experimental trials were performed for 20 path-lengths ranging from 1.1 to 3.0 m (at 0.1 m intervals) at five CH₄ concentrations certified to ±1% analytical accuracy (10.6, 19.8, 30.6, 41.1, and 60.8 ppm). Therefore, a total of 100 path-integrated concentrations from 11.7 to 182 ppm∙m were observed. The five certified concentrations of CH₄ used in this study were supplied by Linde Canada Ltd. Standard gas was supplied to the calibration chamber at a rate of 7 L min⁻¹, and the chamber had a maximum volume of approximately 20 L. The measurement sequence involved flowing standard gas from a cylinder for 30 minutes to ensure stable concentrations, then incrementally shortening the path length from 3.0 to 1.1 m to obtain the range of path-integrated concentrations, and finally switching to a new standard gas cylinder and repeating the process. Measurements were done in order of increasing concentration, beginning with the 10.6 ppm standard and finishing with the 60.8 ppm standard.

Tests occurred in the laboratory during the daytime between July 13th and August 12th, 2016. The GF3 was given 30-60 minutes to stabilize after powering on before measurements were taken. Room temperature during trials was between 20 and 22 °C. Prior to using the GF3, the “Path Temperature” parameter was set to the nearest degree C. “Path Pressure” was set at 97.33 kPa, based on elevation. The operating parameters, light (Rx), and R², reported by the GF3 unit were maintained within the ideal operating range (Rx > 1000, R² > 95%) across all measurement periods.

At each combination of path length and CH₄ concentration, a period of 5 minutes was given for the calibration chamber concentration to stabilize, then a 3-minute period of data was recorded. The GF3 sampled the air at a rate of 0.5 Hz, with each sample containing 500 “sweeps” of the absorption feature. Each 3-minute measurement period consisted of 90 data points, for a total of n = 9000 (90 × 20 path-lengths × 5 [CH₄]) over the entire set of laboratory observations.

Bias was determined as the average difference, or error, in ppm∙m between the GF3 measurements and the prepared path-integrated concentrations [8]. Relative bias is the percentage of signal bias relative to the prepared path-integrated concentrations. Imprecision was defined as twice the standard deviation of the errors [8]. A linear calibration function was determined from the measured and expected path-integrated concentrations [9].

Potential sources of measurement error were considered and estimated. Independent, random errors included error in measuring the path length (±2 cm), error in standard gas concentration (each cylinder is certified to within ±1% and we used ±2% in calculations), error in air temperature (±2 °C), and error in laboratory pressure (±2 kPa). The latter two effects were calculated using the manufacturer provided correction curves for temperature and pressure. In addition, the potential error from ambient CH₄ concentrations mixing in the gap between the laser and the telescopic cylinder was considered by assuming the gap was either comprised entirely of ambient air (lower limit) or of gas from the cylinder (upper limit). The gap length was between 4 and 5 cm, and we used 5 cm in calculations (note: the gap is part of the measured path-length). For example, with a standard concentration of 30.6 ppm and path length of 3.0 m, the upper limit was 91.8 ppm∙m (0% error), while the lower limit was 90.36 ppm∙m (−1.6% error). Additional details are provided in Supplemental Materials. Errors were added in quadrature [10], and the upper and lower limits of the air gap error were considered separately.

3. Results

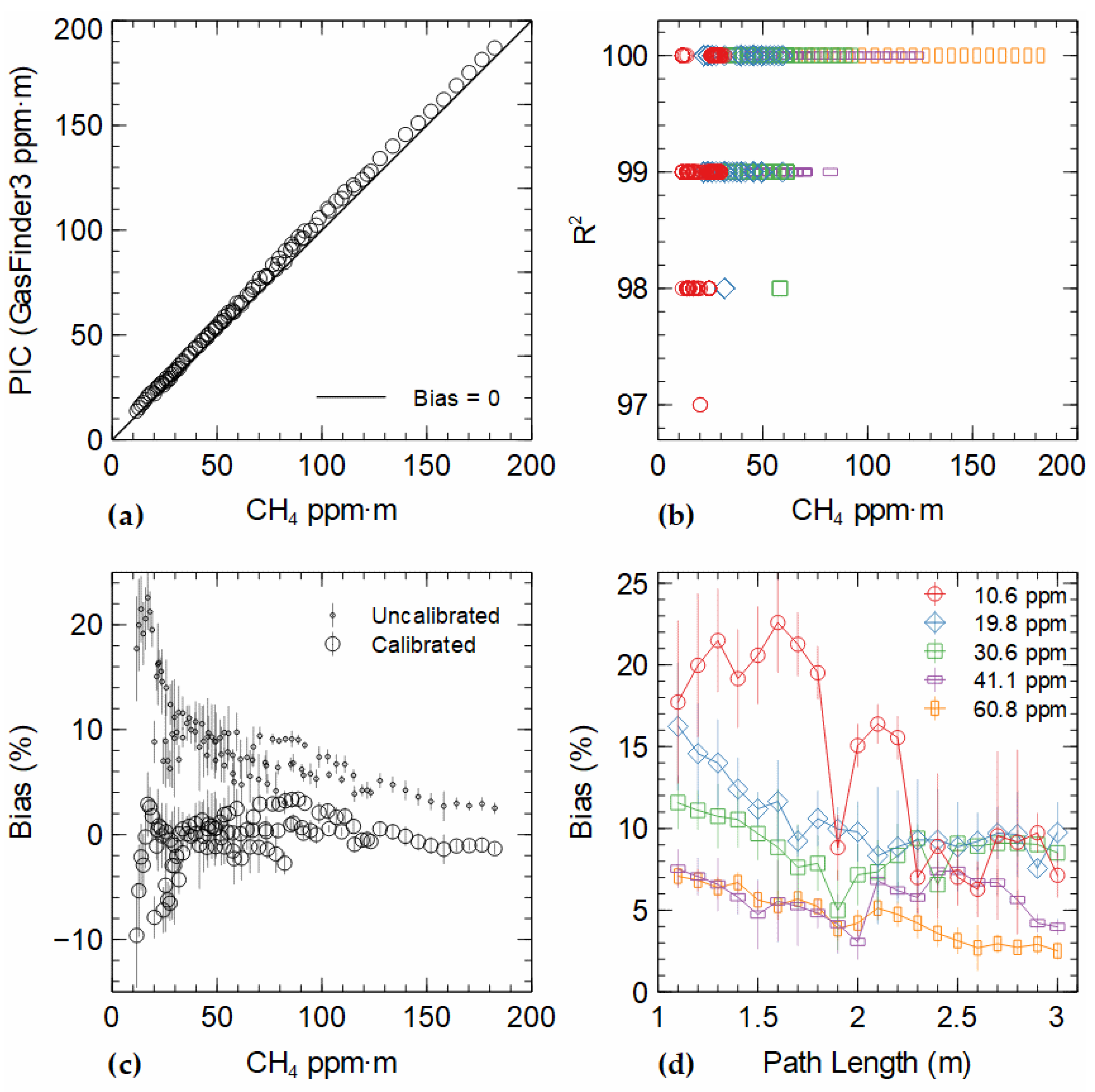
Among all observations (n = 9000), GF3 measurements showed a positive bias relative to expected concentrations. Figure 2a displays a transfer plot of path-integrated (ppm∙m) concentrations measured by the GF3 against those from certified CH₄ concentrations. Signal bias rose to a peak of approximately 7 ppm∙m between path-integrated concentrations of 88–102 ppm∙m. The lowest signal bias (1.57 ppm∙m) was seen at 24 ppm∙m, which represented a 6.5% error. The average signal bias was 4.67 ± 0.07 ppm∙m. The overall standard deviation of measurements was 0.41 ppm∙m on average, with a median of 0.37 ppm∙m (n = 100). The average relative bias across all path-integrated concentrations was 8.8% ± 0.1%. A relative bias greater than 10% was observed at low (<50 ppm∙m) path-integrated concentrations (Figure 2c,d). The total range was from 2.5% at 182 ppm∙m to 22.6% at 17 ppm∙m.

To correct the observed bias, a linear equation was used: C = 0.97793 × M − 2.8843 (r² = 0.9992), where C is the corrected and M is the measured ppm∙m value. After calibration, the relative bias averaged −0.36%; the relative bias over the range of path-integrated concentrations is shown in Figure 2c. Generally, bias was distributed above and below zero, with a narrowing spread as path-integrated concentration increased. Bias was often below −5% at path-integrated concentrations <28 ppm∙m, with the most negative value being −9.6% at 12 ppm∙m. The largest positive bias was 3.4% at 89 ppm∙m. As path-integrated concentration increased, the bias decreased to −0.99% at 176 ppm∙m.

Measurements were made with high confidence in the sample absorption spectrum. The average coefficient of determination between the sample and internal reference gas absorption spectra (waveforms)—reported by the GF3 as the R² output parameter—was 99.6 ± 0.6% (n = 9000), with all values between 97% and 100% (Figure 2b). At path-integrated concentrations <50 ppm∙m, average R² was 99.3% ± 0.7% (n = 3870); between 50 and 100 ppm∙m, R² was 99.8% ± 0.4% (n = 3870), and above 100 ppm∙m, R² was 100% (n = 1800). Thus, all data were measured with an acceptable level of confidence (considered to be >95% according to the manufacturer); however, there was a tendency for lower R² values at lower ppm∙m values (Figure 2b). This is consistent with reduced absorbance with less CH₄ in the sample path (lower concentrations and shorter path lengths).

Potential sources of measurement error are shown in

Table 1. Potential error contribution from uncertainty in measured path length, air gap in front of the laser, standard gas concentration, air temperature, and pressure. Error estimates are calculated for three path-lengths. Error related to a 5 cm air gap is calculated using ambient concentration of 1.8 ppm and the median standard gas concentration of 30.6 ppm (lower limit), while the upper limit assumes no ambient air mixed in the gap.

	Error Source
Path Length	Path Length	Air Gap		Standard Conc.	Temp.	Pressure	Total % Bias
	±0.02 m	lower	upper	±2%	±2 °C	±2 kPa	(range)
1.1 m	±1.8%	−4.2%	0%	±2%	±0.7%	±1.2%	−5.2% to 3.0%
2.0 m	±1.0%	−2.3%	0%	±2%	±0.7%	±1.2%	−3.5% to 2.6%
3.0 m	±0.7%	−1.6%	0%	±2%	±0.7%	±1.2%	−3.0% to 2.5%

. Three errors were independent of the measured path-length (accuracy of the standard gases, lab temperature, and pressure), while the other two error contributions were a function of path length (accuracy of measuring the path length, and the potential influence of an air gap). Four of the error sources were considered random as the measurement error could lead to either an over- or under-estimate (e.g., some of the five standard gas cylinders may have been above the certified concentration, while others may have been below). The error associated with an air gap, however, could only result in a negative error because the ambient CH₄ concentration was always less than the standard gas concentration. Error related to an air gap depends on the CH₄ concentration in the sample tube and path length. At 1.1 m path length, the potential error ranged from −4.8% to 3.0% at 10.6 ppm, and −5.3% to 3.0% at 60.8 ppm. At 3.0 m, the potential error ranged from −2.9% and −3.0% to 2.5% for the same concentrations. Summing the upper and lower values of each error source gives a range of potential bias, ranging from −5.2 to 3.0% at a 1.1 m pathlength, narrowing to −3.0% to 2.5% at 3.0 m path length (for a standard concentration of 30.6 ppm). Therefore, the potential error range was expected to be evenly distributed around zero, with a weak negative trend in the case of an air gap. After correction, the biases were generally within this error range when path-integrated concentrations were greater than 28 ppm∙m but were outside this range at lower ppm∙m values (Figure 2c).

4. Discussion

Before applying linear correction to measured path-integrated concentrations, the relative bias approached 2% at the highest path-integrated concentrations (around 182 ppm∙m). After correction, the bias approached −1% at the same path-integrated concentration. Thus, relative bias less than ±3% was achieved above ca. 150 ppm∙m with or without calibration. This may be acceptable in many applications, depending on emission source size, distance downwind, and other factors. At path-integrated concentrations less than 150 ppm∙m, the mean relative bias was considerably improved after applying linear calibration over the 11.7 to 182 ppm∙m range. Although the sensor had been calibrated prior to the experiment, path-integrated concentrations in this study are at the bottom 2% of the manufacturer’s calibration range of 2 to 8500 ppm∙m.

Low path-integrated concentrations were chosen because they are critical for many field studies. For example, path lengths in the 10 to 100 m range are often reported in agricultural emissions research, particularly for targeted measurements of biogas systems [1], manure management systems [11,12,13], or grazing cattle [14]. Where the research site permits, longer path lengths are used [2,15], which our data suggest would have lower bias. Another study used a higher range of path-integrated CH₄, from 529 to 2500 ppm∙m, to calibrate an OP-TDL and it was found to be accurate and in good agreement with another open-path spectrometer, but that study did not focus on measurements below the calibrated range [16]. Low path-integrated concentrations have also been shown to be relevant to long-term ecosystem monitoring and fugitive emission research [3,17].

Previous researchers have noted the importance of calibrating TDL spectrometers [9] and that inaccurate calibration may occur when the detector response from the sample path is much lower than the response from the reference path [18]. In our study, the lowest path-integrated concentrations (11.7 ppm∙m) were about 5% of the reference cell (220 ppm∙m). A linear calibration curve improved the fit with expected concentrations and greatly reduced bias, on average. The ability to resolve differences in concentration will depend on the standard deviation of measurements, which averaged 0.4 ppm∙m in this study, and could be reduced with longer averaging time (Supplemental Figure S1). The flexibility of path length (or using multiple paths of varying length) is a strength of OP-TDLs, but practitioners should be aware of potentially greater uncertainty at lower path-integrated concentrations (i.e., shorter paths). If accommodation cannot be made for measurement paths to contain ca. 200 ppm∙m CH₄, calibration over the expected range of low path-integrated concentrations is beneficial. Discussion with the manufacturer may be helpful to optimize the calibration and laser configuration over a lower ppm∙m range. Recognizing that the sensor technology and software are being constantly improved, further studies are recommended to evaluate performance of the GF3 and other instruments.

5. Conclusions

The experimental results suggest that accuracy of this GF3 open-path sensor was linked to the measured path-integrated concentration of CH₄ over a range of low path-integrated concentrations. A linear calibration curve was used to correct the measured values so that the remaining bias was small, on average (<0.4%), and was not related to path-integrated concentration. A relative bias less than ±3% was achieved above ca. 150 ppm∙m with or without calibration, e.g., at 182 ppm∙m, the bias was 2.5% before and −1% after calibration. The decreasing trend in uncorrected bias suggest it would be less than 1.5% at 200 ppm∙m. On the other hand, between 50 and 100 ppm∙m, uncorrected bias averaged 7.1% and was reduced to less than 0.5% after calibration. There was a tendency for greater bias when agreement between sample and reference absorption curves had an R² less than 100% (i.e., 97% to 99%), which occurred when the path-integrated concentration was <100 ppm∙m. Practitioners should be aware of potential increased measurement errors present at low path-integrated concentrations, and when R² is <100%. Calibration over the expected range of path-integrated concentrations is beneficial when low path-integrated concentrations are expected. Future research could evaluate effects of temperature and pressure, and could evaluate other sensors, to determine if the results are universal or instrument-dependent.