Sensitivity of Surface Fluxes in the ECMWF Land Surface Model to the Remotely Sensed Leaf Area Index and Root Distribution: Evaluation with Tower Flux Data
Abstract
1. Introduction
2. Data and Methods
2.1. Data
2.1.1. Tower Flux Data
2.1.2. Satellite Albedo and Leaf Area Index
2.2. CHTESSEL Model
2.3. Simulation Setup
2.4. Evaluation
3. Results
3.1. Comparison of LAI and Albedo
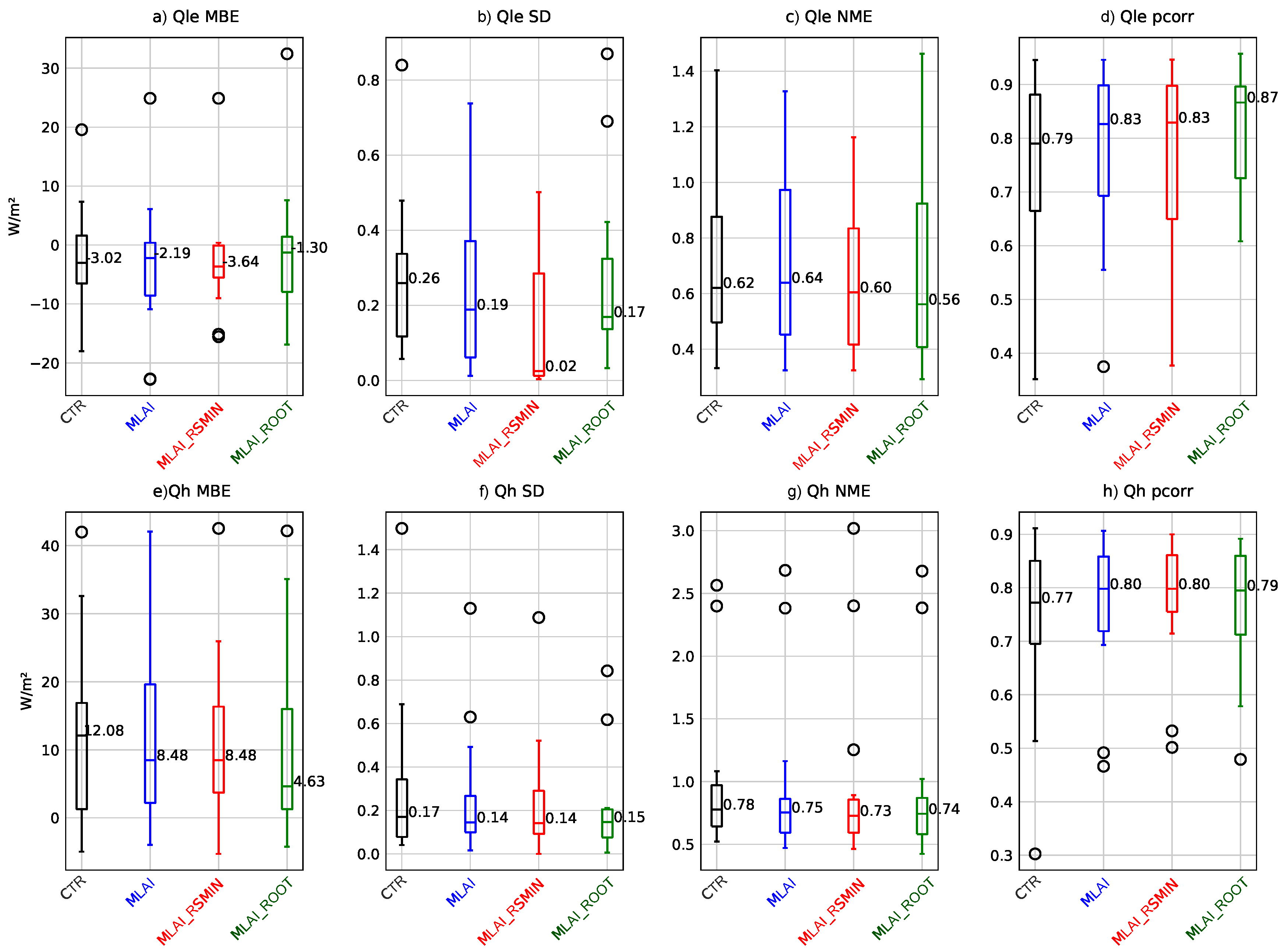
3.2. Fluxes Evaluation
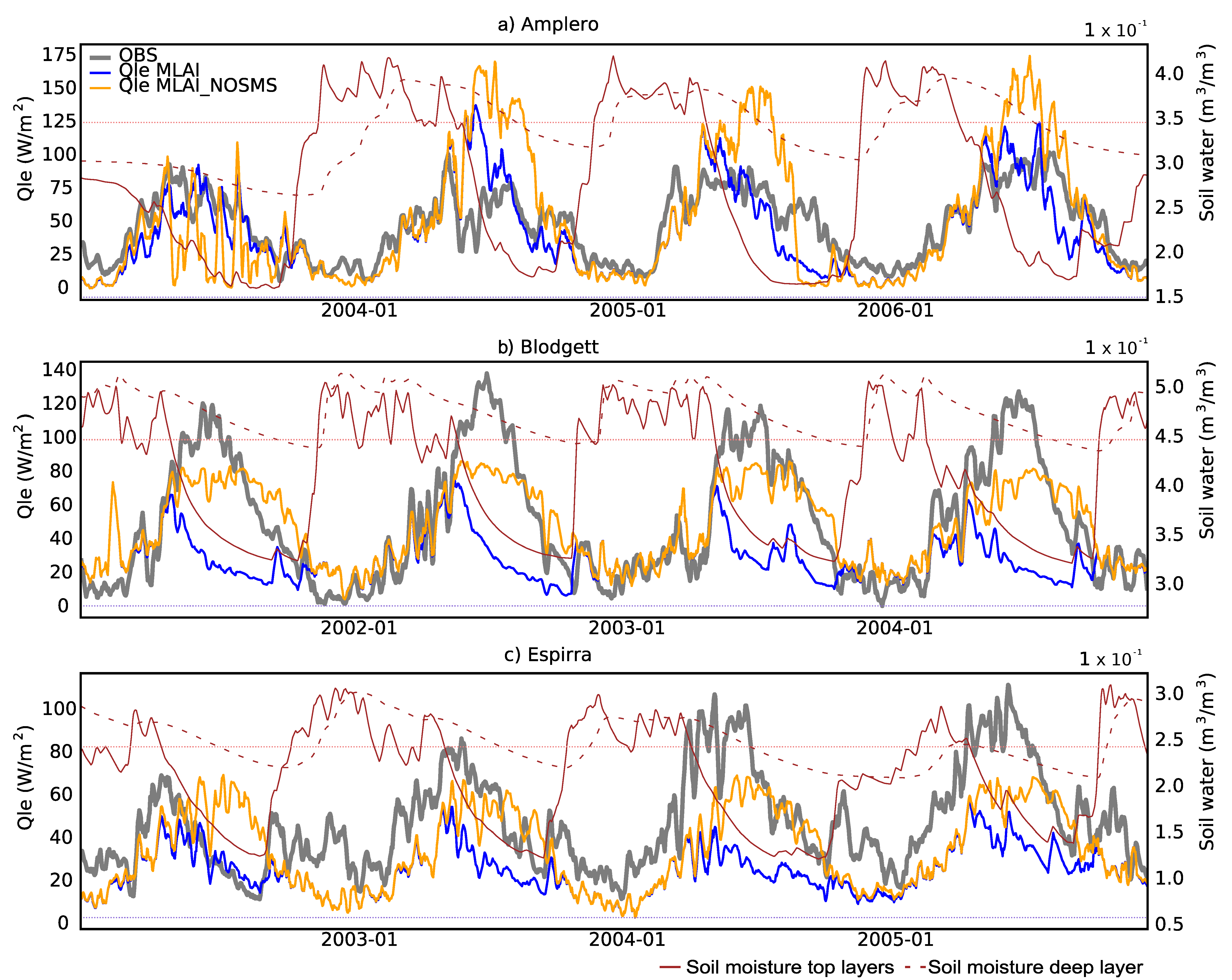
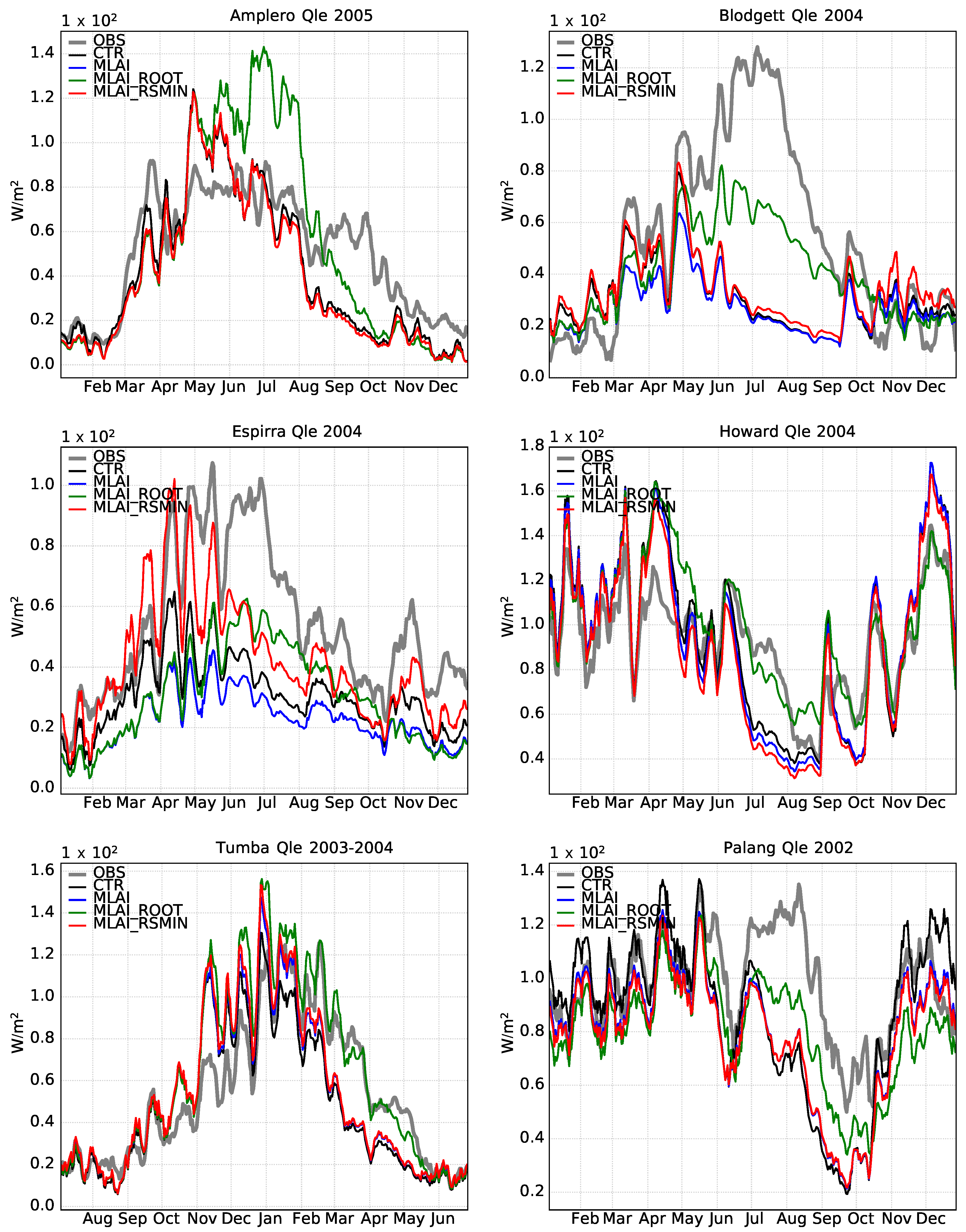
3.3. Soil Moisture Stress
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Carvalhais, N.; Forkel, M.; Khomik, M.; Bellarby, J.; Jung, M.; Migliavacca, M.; Mu, M.; Saatchi, S.; Santoro, M.; Thurner, M.; et al. Global covariation of carbon turnover times with climate in terrestrial ecosystems. Nature 2014, 514, 213–217. [Google Scholar] [CrossRef] [PubMed]
- Orth, R.; Seneviratne, S.I. Analysis of soil moisture memory from observations in Europe. J. Geophys. Res. Atmos. 2012, 117, 1–19. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.; Yamada, T.J.; Balsamo, G.; Berg, A.A.; Boisserie, M.; Dirmeyer, P.A.; Doblas-Reyes, F.J.; Drewitt, G.; Gordon, C.T.; et al. Contribution of land surface initialization to subseasonal forecast skill: First results from a multi-model experiment. Geophys. Res. Lett. 2010, 37, 1–6. [Google Scholar] [CrossRef]
- Koster, R.D.; Mahanama, S.P.; Yamada, T.J.; Balsamo, G.; Berg, A.A.; Boisserie, M.; Dirmeyer, P.A.; Doblas-Reyes, F.J.; Drewitt, G.; Gordon, C.T.; et al. The second phase of the global land-atmosphere coupling experiment: Soil moisture contributions to subseasonal forecast skill. J. Hydrometeorol. 2011, 12, 805–822. [Google Scholar] [CrossRef]
- Koster, R.D.; Walker, G.K. Interactive vegetation phenology, soil moisture, and monthly temperature forecasts. J. Hydrometeorol. 2015, 16, 1456–1465. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Corti, T.; Davin, E.L.; Hirschi, M.; Jaeger, E.B.; Lehner, I.; Orlowsky, B.; Teuling, A.J. Investigating soil moisture-climate interactions in a changing climate: A review. Earth-Sci. Rev. 2010, 99, 125–161. [Google Scholar] [CrossRef]
- Woodward, F.I. Vegetation-climate feedbacks in a greenhouse world. Philos. Trans. R. Soc. B Biol. Sci. 1998, 353, 29–39. [Google Scholar] [CrossRef]
- Denissen, J.M.; Teuling, A.J.; Reichstein, M.; Orth, R. Critical Soil Moisture Derived From Satellite Observations Over Europe. J. Geophys. Res. Atmos. 2020, 125, e2019JD031672. [Google Scholar] [CrossRef]
- Coenders-Gerrits, A.M.; Van Der Ent, R.J.; Bogaard, T.A.; Wang-Erlandsson, L.; Hrachowitz, M.; Savenije, H.H. Uncertainties in transpiration estimates. Nature 2014, 506, E1–E2. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Thornton, P.E.; Oleson, K.W.; Bonan, G.B. The partitioning of evapotranspiration into transpiration, soil evaporation, and canopy evaporation in a GCM: Impacts on land-atmosphere interaction. J. Hydrometeorol. 2007, 8, 862–880. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the global water cycle. Agric. For. Meteorol. 2014, 189–190, 115–117. [Google Scholar] [CrossRef]
- Liu, X.; Chen, F.; Barlage, M.; Niyogi, D. Implementing Dynamic Rooting Depth for Improved Simulation of Soil Moisture and Land Surface Feedbacks in Noah-MP-Crop. J. Adv. Model. Earth Syst. 2020, 12, 1–15. [Google Scholar] [CrossRef]
- Gentine, P.; Holtslag, A.A.; D’Andrea, F.; Ek, M. Surface and atmospheric controls on the onset of moist convection over land. J. Hydrometeorol. 2013, 14, 1443–1462. [Google Scholar] [CrossRef]
- Teuling, A.J.; Van Loon, A.F.; Seneviratne, S.I.; Lehner, I.; Aubinet, M.; Heinesch, B.; Bernhofer, C.; Grünwald, T.; Prasse, H.; Spank, U. Evapotranspiration amplifies European summer drought. Geophys. Res. Lett. 2013, 40, 2071–2075. [Google Scholar] [CrossRef]
- Vogel, M.M.; Orth, R.; Cheruy, F.; Hagemann, S.; Lorenz, R.; van den Hurk, B.J.; Seneviratne, S.I. Regional amplification of projected changes in extreme temperatures strongly controlled by soil moisture-temperature feedbacks. Geophys. Res. Lett. 2017, 44, 1511–1519. [Google Scholar] [CrossRef]
- Damour, G.; Simonneau, T.; Cochard, H.; Urban, L. An overview of models of stomatal conductance at the leaf level. Plant Cell Environ. 2010, 33, 1419–1438. [Google Scholar] [CrossRef] [PubMed]
- Sprintsin, M.; Chen, J.M.; Desai, A.; Gough, C.M. Evaluation of leaf-to-canopy upscaling methodologies against carbon flux data in North America. J. Geophys. Res. Biogeosci. 2012, 117, 1–17. [Google Scholar] [CrossRef]
- Balsamo, G.; Viterbo, P.; Beijaars, A.; van den Hurk, B.; Hirschi, M.; Betts, A.K.; Scipal, K. A revised hydrology for the ECMWF model: Verification from field site to terrestrial water storage and impact in the integrated forecast system. J. Hydrometeorol. 2009, 10, 623–643. [Google Scholar] [CrossRef]
- Boussetta, S.; Balsamo, G.; Beljaars, A.; Kral, T.; Jarlan, L. Impact of a satellite-derived leaf area index monthly climatology in a global numerical weather prediction model. Int. J. Remote Sens. 2013, 34, 3520–3542. [Google Scholar] [CrossRef]
- Best, M.J.; Abramowitz, G.; Johnson, H.R.; Pitman, A.J.; Balsamo, G.; Boone, A.; Cuntz, M.; Decharme, B.; Dirmeyer, P.A.; Dong, J.; et al. The plumbing of land surface models: Benchmarking model performance. J. Hydrometeorol. 2015, 16, 1425–1442. [Google Scholar] [CrossRef]
- Ukkola, A.M.; De Kauwe, M.G.; Pitman, A.J.; Best, M.J.; Abramowitz, G.; Haverd, V.; Decker, M.; Haughton, N. Land surface models systematically overestimate the intensity, duration and magnitude of seasonal-scale evaporative droughts. Environ. Res. Lett. 2016, 11. [Google Scholar] [CrossRef]
- Sungmin, O.; Dutra, E.; Orth, R. Robustness of process-based versus data-driven modeling in changing climatic conditions. J. Hydrometeorol. 2020, 21, 1929–1944. [Google Scholar] [CrossRef]
- Jarvis, P.G. The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1976, 273, 593–610. [Google Scholar] [CrossRef]
- Jacobs, C.M.; Van Den Hurk, B.J.; De Bruin, H.A. Stomatal behaviour and photosynthetic rate of unstressed grapevines in semi-arid conditions. Agric. For. Meteorol. 1996, 80, 111–134. [Google Scholar] [CrossRef]
- Boussetta, S.; Balsamo, G.; Beljaars, A.; Panareda, A.A.; Calvet, J.C.; Jacobs, C.; Van Den Hurk, B.; Viterbo, P.; Lafont, S.; Dutra, E.; et al. Natural land carbon dioxide exchanges in the ECMWF integrated forecasting system: Implementation and offline validation. J. Geophys. Res. Atmos. 2013, 118, 5923–5946. [Google Scholar] [CrossRef]
- Balsamo, G.; Agusti-Panareda, A.; Albergel, C.; Arduini, G.; Beljaars, A.; Bidlot, J.; Bousserez, N.; Boussetta, S.; Brown, A.; Buizza, R.; et al. Satellite and in situ observations for advancing global earth surface modelling: A review. Remote Sens. 2018, 10, 2038. [Google Scholar] [CrossRef]
- Zeng, X.; Dai, Y.J.; Dickinson, R.E.; Shaikh, M. The role of root distribution for climate simulation over land. Geophys. Res. Lett. 1998, 25, 4533–4536. [Google Scholar] [CrossRef]
- Desborough, C.E. The impact of root weighting on the response of transpiration to moisture stress in land surface schemes. Mon. Weather Rev. 1997, 125, 1920–1930. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Santhana Vannan, S.K.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G.; et al. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef]
- Haughton, N.; Abramowitz, G.; Pitman, A.J.; Or, D.; Best, M.J.; Johnson, H.R.; Balsamo, G.; Boone, A.; Cuntz, M.; Decharme, B.; et al. The plumbing of land surface models: Is poor performance a result of methodology or data quality? J. Hydrometeorol. 2016, 17, 1705–1723. [Google Scholar] [CrossRef]
- Haverd, V.; Cuntz, M.; Nieradzik, L.P.; Harman, I.N. Improved representations of coupled soil-canopy processes in the CABLE land surface model (Subversion revision 3432). Geosci. Model Dev. 2016, 9, 3111–3122. [Google Scholar] [CrossRef]
- Fang, H.; Wei, S.; Jiang, C.; Scipal, K. Theoretical uncertainty analysis of global MODIS, CYCLOPES, and GLOBCARBON LAI products using a triple collocation method. Remote Sens. Environ. 2012, 124, 610–621. [Google Scholar] [CrossRef]
- Sea, W.B.; Choler, P.; Beringer, J.; Weinmann, R.A.; Hutley, L.B.; Leuning, R. Documenting improvement in leaf area index estimates from MODIS using hemispherical photos for Australian savannas. Agric. For. Meteorol. 2011, 151, 1453–1461. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Weiss, M. Near real-time vegetation monitoring at global scale. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3473–3481. [Google Scholar] [CrossRef]
- Brown, L.A.; Meier, C.; Morris, H.; Pastor-Guzman, J.; Bai, G.; Lerebourg, C.; Gobron, N.; Lanconelli, C.; Clerici, M.; Dash, J. Evaluation of global leaf area index and fraction of absorbed photosynthetically active radiation products over North America using Copernicus Ground Based Observations for Validation data. Remote Sens. Environ. 2020, 247, 111935. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.P.; et al. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Wang, Z.; Schaaf, C.B.; Strahler, A.H.; Chopping, M.J.; Román, M.O.; Shuai, Y.; Woodcock, C.E.; Hollinger, D.Y.; Fitzjarrald, D.R. Evaluation of MODIS albedo product (MCD43A) over grassland, agriculture and forest surface types during dormant and snow-covered periods. Remote Sens. Environ. 2014, 140, 60–77. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, Z.; Li, Z.; Erb, A.; Schaaf, C.B. Evaluation of the global MODIS 30 arc-second spatially and temporally complete snow-free land surface albedo and reflectance anisotropy dataset. Int. J. Appl. Earth Obs. Geoinf. 2017, 58, 36–49. [Google Scholar] [CrossRef]
- Mahfouf, J.F. The Land Surface Scheme ISBA within the Meteo-France Climate Model ARPEGE. Part 1: Implementation and Preliminary Results. J. Clim. 1995, 8, 2039–2057. [Google Scholar] [CrossRef]
- Manzi, A.O.; Planton, S. Implementation of the ISBA parametrization scheme for land surface processes in a GCM - an annual cycle experiment. J. Hydrol. 1994, 155, 353–387. [Google Scholar] [CrossRef]
- Giard, D.; Bazile, E. Implementation of a new assimilation scheme for soil and surface variables in a global NWP model. Mon. Weather Rev. 2000, 128, 997–1015. [Google Scholar] [CrossRef]
- Dorman, J.L.; Sellers, P.J. A Global CLimatology of Albedo, Roughness Length and Stomatal Resistance for Atmospheric General Circulation Models as Represented by the Simple Biosphere Model (SiB). J. Appl. Meteorol. 1989, 28, 833–855. [Google Scholar] [CrossRef]
- Bonan, G.B. Comparison of two land surface process models using prescribed forcings. J. Geophys. Res. 1994, 99, 25803–25818. [Google Scholar] [CrossRef]
- Pitman, A. Description of the bare essentials of Surface transfer. Annu. Rev. Mater. Res. 1991, 32, 77–111. [Google Scholar]
- European Center for Medium range Weather Forecasts. IFS documentation CY46R1—Part IV: Physical Processes. 2019. Available online: https://www.ecmwf.int/en/elibrary/19308-part-iv-physical-processes (accessed on 15 December 2020).
- Cabelguenne, M.; Debaeke, P. Experimental determination and modelling of the soil water extraction capacities of crops of maize, sunflower, soya bean, sorghum and wheat. Plant Soil 1998, 202, 175–192. [Google Scholar] [CrossRef]
- Guswa, A.J. The influence of climate on root depth: A carbon cost-benefit analysis. Water Resour. Res. 2008, 44, 1–11. [Google Scholar] [CrossRef]
- Nielsen, D.C.; Vigil, M.F. Soil water extraction for several dryland crops. Agron. J. 2018, 110, 2447–2455. [Google Scholar] [CrossRef]
- Rodrigues, A.; Pita, G.; Mateus, J.; Kurz-Besson, C.; Casquilho, M.; Cerasoli, S.; Gomes, A.; Pereira, J. Eight years of continuous carbon fluxes measurements in a Portuguese eucalypt stand under two main events: Drought and felling. Agric. For. Meteorol. 2011, 151, 493–507. [Google Scholar] [CrossRef]
- Martens, B.; Schumacher, D.L.; Wouters, H.; Muñoz-Sabater, J.; Verhoest, N.E.; Miralles, D.G. Evaluating the land-surface energy partitioning in ERA5. Geosci. Model Dev. 2020, 13, 4159–4181. [Google Scholar] [CrossRef]
- Nogueira, M.; Boussetta, S.; Balsamo, G.; Albergel, C.; Trigo, I.F.; Johannsen, F.; Miralles, D.; Dutra, E. Upgrading land-cover and vegetation seasonality in the ECMWF coupled system: Verification with FLUXNET sites, METEOSAT satellite land surface temperatures and ERA5 atmospheric reanalysis. J. Geophys. Res. Atmos. 2020. in review. [Google Scholar]
- Ershadi, A.; McCabe, M.F.; Evans, J.P.; Chaney, N.W.; Wood, E.F. Multi-site evaluation of terrestrial evaporation models using FLUXNET data. Agric. For. Meteorol. 2014, 187, 46–61. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Dolman, H.; Field, C.; Grelle, A.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Albergel, C.; Dutra, E.; Bonan, B.; Zheng, Y.; Munier, S.; Balsamo, G.; de Rosnay, P.; Muñoz-Sabater, J.; Calvet, J.C. Monitoring and forecasting the impact of the 2018 summer heatwave on vegetation. Remote Sens. 2019, 11, 520. [Google Scholar] [CrossRef]
- Albergel, C.; Zheng, Y.; Bonan, B.; Dutra, E.; Rodríguez-Fernández, N.; Munier, S.; Draper, C.; De Rosnay, P.; Muñoz-Sabater, J.; Balsamo, G.; et al. Data assimilation for continuous global assessment of severe conditions over terrestrial surfaces. Hydrol. Earth Syst. Sci. 2020, 24, 4291–4316. [Google Scholar] [CrossRef]
- Boussetta, S.; Balsamo, G.; Dutra, E.; Beljaars, A.; Albergel, C. Assimilation of surface albedo and vegetation states from satellite observations and their impact on numerical weather prediction. Remote Sens. Environ. 2015, 163, 111–126. [Google Scholar] [CrossRef]
- Stöckli, R.; Rutishauser, T.; Dragoni, D.; O’Keefe, J.; Thornton, P.E.; Jolly, M.; Lu, L.; Denning, A.S. Remote sensing data assimilation for a prognostic phenology model. J. Geophys. Res. Biogeosci. 2008, 113, 1–19. [Google Scholar] [CrossRef]
- Egea, G.; Verhoef, A.; Vidale, P.L. Towards an improved and more flexible representation of water stress in coupled photosynthesis-stomatal conductance models. Agric. For. Meteorol. 2011, 151, 1370–1384. [Google Scholar] [CrossRef]
- Verhoef, A.; Egea, G. Modeling plant transpiration under limited soil water: Comparison of different plant and soil hydraulic parameterizations and preliminary implications for their use in land surface models. Agric. For. Meteorol. 2014, 191, 22–32. [Google Scholar] [CrossRef]
- Konings, A.G.; Williams, A.P.; Gentine, P. Sensitivity of grassland productivity to aridity controlled by stomatal and xylem regulation. Nat. Geosci. 2017, 10, 284–288. [Google Scholar] [CrossRef]
- Massmann, A.; Gentine, P.; Lin, C. When Does Vapor Pressure Deficit Drive or Reduce Evapotranspiration? J. Adv. Model. Earth Syst. 2019, 11, 3305–3320. [Google Scholar] [CrossRef]
- Pinto, C.A.; Nadezhdina, N.; David, J.S.; Kurz-Besson, C.; Caldeira, M.C.; Henriques, M.O.; Monteiro, F.G.; Pereira, J.S.; David, T.S. Transpiration in Quercus suber trees under shallow water table conditions: The role of soil and groundwater. Hydrol. Process. 2014, 28, 6067–6079. [Google Scholar] [CrossRef]
- Leonardini, G.; Anctil, F.; Abrahamowicz, M.; Gaborit, É.; Vionnet, V.; Nadeau, D.F.; Fortin, V. Evaluation of the Soil, Vegetation, and Snow (SVS) Land Surface Model for the Simulation of Surface Energy Fluxes and Soil Moisture under Snow-Free Conditions. Atmosphere 2020, 11, 278. [Google Scholar] [CrossRef]
- Stöckli, R.; Lawrence, D.M.; Niu, G.Y.; Oleson, K.W.; Thornton, P.E.; Yang, Z.L.; Bonan, G.B.; Denning, A.S.; Running, S.W. Use of FLUXNET in the Community Land Model development. J. Geophys. Res. Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Nogueira, M.; Albergel, C.; Boussetta, S.; Johannsen, F.; Trigo, I.F.; Ermida, S.L.; Martins, J.P.A.; Dutra, E. Role of vegetation in representing land surface temperature in the CHTESSEL (CY45R1) and SURFEX-ISBA (v8.1) land surface models: A case study over Iberia. Geosci. Model Dev. 2020, 13. [Google Scholar] [CrossRef]
- Orth, R.; Dutra, E.; Trigo, I.F.; Balsamo, G. Advancing land surface model development with satellite-based Earth observations. Hydrol. Earth Syst. Sci. 2017, 21, 2483–2495. [Google Scholar] [CrossRef]
| Station | Country | Latitude | Longitude | Plant Functional Type | Time Period |
|---|---|---|---|---|---|
| Amplero | Italy | 41.9041 | 13.6052 | Grassland | 2003–2006 |
| Blodgett | U.S. | 38.8953 | −120.633 | Evergreen needleleaf | 2000–2006 |
| Bugac | Hungary | 46.6917 | 19.6017 | Grassland | 2002–2006 |
| Espirra | Portugal | 38.6394 | −8.6018 | Evergreen broadleaf | 2001–2006 |
| Fort Peck | U.S. | 48.3077 | −105.102 | Grassland | 2000–2006 |
| Harvard | U.S. | 42.5378 | −72.1715 | Deciduous broadleaf | 1994–2001 |
| Hesse | France | 48.6742 | 7.0656 | Deciduous broadleaf | 1999–2006 |
| Howard | Australia | −12.4943 | 131.152 | Woody savannah | 2002–2005 |
| Howlandm | U.S. | 45.2041 | −68.7402 | Evergreen needleleaf | 1996–2004 |
| Hyytiala | Finland | 61.8474 | 24.2948 | Evergreen needleleaf | 2001–2004 |
| Kruger | South Africa | −25.0197 | 31.4969 | Savannah | 2002–2003 |
| Loobos | The Netherlands | 52.1679 | 5.744 | Evergreen needleleaf | 1997–2006 |
| Mopane | Botswana | −19.9165 | 23.5603 | Woody savannah | 1999–2001 |
| Palang | Indonesia | −2.345 | 114.036 | Evergreen broadleaf | 2002–2003 |
| Sylvania | U.S. | 46.242 | −89.3477 | Mixed forest | 2002–2005 |
| Tumbarumba | Australia | −35.6557 | 148.152 | Evergreen broadleaf | 2002–2005 |
| University of Michigan | U.S. | 45.5598 | −84.7138 | Deciduous broadleaf | 1999–2003 |
| Station | Vegetation Type | CTR | Optimal | Optimal |
|---|---|---|---|---|
| Amplero | L, short grass | 100 | 100 | 2 |
| Bugac | L, short grass | 100 | 175 | 0.5 |
| Fort Peck | L, short grass | 100 | 25 | 0.5 |
| Howard | L, tall grass | 175 | 125 | 2 |
| Kruger | L, tall grass | 100 | 300 | 2 |
| Mopane | L, tall grass | 175 | 300 | 1 |
| Blodgett | H, Evergreen needleleaf | 250 | 150 | 3 |
| Espirra | H, evergreen broadleaf | 240 | 75 | 3 |
| Harvard | H, deciduous broadleaf | 175 | 250 | 1 |
| Hesse | H, deciduous broadleaf | 175 | 175 | 2 |
| Howlandm | H, evergreen needleleaf | 250 | 275 | 0.5 |
| Hyytiala | H, evergreen needleleaf | 250 | 225 | 0.5 |
| Loobos | H, evergreen needleleaf | 250 | 150 | 2 |
| Palang | H, evergreen broadleaf | 240 | 275 | 2 |
| Sylvania | H, interrupted forest | 175 | 400 | 3 |
| Tumbarumba | H, evergreen broadleaf | 240 | 225 | 2 |
| University of Michigan | H, deciduous broadleaf | 175 | 400 | 3 |
| Simulation | Details |
|---|---|
| CTR | Control simulation with default CHTESSEL parametersand input LAI and Albedo |
| MALB | Same as CTR, but replacing the input albedo climatologywith the new high-resolution MODIS climatology |
| MLAI | Same as CTR, but replacing the input LAI climatologywith the new high-resolution MODIS climatology |
| MLAI_NOSMS | Same as MLAI, but removing the soil moisture stress function from the canopy resistance (setting ) when the soil moisture is above the wilting point in Equation (3) |
| MLAI_RSMIN | Same as MLAI, but selecting the optimal for each station from a set ofsimulations with varying between 25 and 500. |
| MLAI_ROOT | Same as MLAI, but using a uniform root distribution (Equation (5)) and selecting the optimal for each station from a set of simulations with of 0.5, 1, 2, and 3 m. |
| Station | Mean CTR | Mean MALB | RMSD MALB vs. CTR |
|---|---|---|---|
| Amplero | 0.16 | 0.15 | 0.03 |
| Blodgett | 0.13 | 0.1 | 0.02 |
| Bugac | 0.18 | 0.16 | 0.03 |
| Espirra | 0.16 | 0.14 | 0.02 |
| Fort Peck | 0.25 | 0.18 | 0.07 |
| Harvard | 0.11 | 0.13 | 0.03 |
| Hesse | 0.13 | 0.15 | 0.03 |
| Howard | 0.15 | 0.13 | 0.02 |
| Howlandm | 0.11 | 0.12 | 0.01 |
| Hyytiala | 0.12 | 0.11 | 0.02 |
| Kruger | 0.17 | 0.16 | 0.03 |
| Loobos | 0.17 | 0.11 | 0.07 |
| Mopane | 0.16 | 0.17 | 0.01 |
| Palang | 0.14 | 0.13 | 0.01 |
| Sylvania | 0.11 | 0.13 | 0.04 |
| Tumbarumba | 0.16 | 0.12 | 0.04 |
| University of Michigan | 0.11 | 0.13 | 0.03 |
| Median | 0.15 | 0.13 | 0.03 |
| Station | Mean CTR | Mean MLAI | Mean CGLS | RMSD MLAI vs. CTR | RMSD MODIS vs. CGLS |
|---|---|---|---|---|---|
| Amplero | 2.43 | 1.7 | 1.51 | 0.9 | 0.29 |
| Blodgett | 3.08 | 2.28 | 2.98 | 0.87 | 0.47 |
| Bugac | 1.93 | 0.92 | 1.04 | 1.04 | 0.17 |
| Espirra | 2.38 | 1.42 | 1.13 | 0.97 | 0.20 |
| Fort Peck | 0.89 | 0.35 | 0.34 | 0.54 | 0.08 |
| Harvard | 3.14 | 2.45 | 2.78 | 0.75 | 0.58 |
| Hesse | 2.35 | 2.66 | 2.27 | 1.65 | 0.52 |
| Howard | 1.76 | 1.55 | 1.58 | 0.28 | 0.47 |
| Howlandm | 3.08 | 2.40 | 2.83 | 1.04 | 0.82 |
| Hyytiala | 2.12 | 1.69 | 1.73 | 0.50 | 0.51 |
| Kruger | 1.76 | 0.98 | 0.93 | 0.80 | 0.16 |
| Loobos | 2.21 | 1.87 | 1.87 | 0.53 | 0.43 |
| Mopane | 1.59 | 0.87 | 0.65 | 0.73 | 0.25 |
| Palang | 5.59 | 4.42 | 4.01 | 1.20 | 0.40 |
| Sylvania | 2.63 | 1.73 | 2.24 | 0.91 | 0.62 |
| Tumbarumba | 3.60 | 4.31 | 3.09 | 0.83 | 0.72 |
| University of Michigan | 2.42 | 2.11 | 1.76 | 0.86 | 0.25 |
| Median | 2.38 | 1.73 | 1.76 | 0.86 | 0.43 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stevens, D.; Miranda, P.M.A.; Orth, R.; Boussetta, S.; Balsamo, G.; Dutra, E. Sensitivity of Surface Fluxes in the ECMWF Land Surface Model to the Remotely Sensed Leaf Area Index and Root Distribution: Evaluation with Tower Flux Data. Atmosphere 2020, 11, 1362. https://doi.org/10.3390/atmos11121362
Stevens D, Miranda PMA, Orth R, Boussetta S, Balsamo G, Dutra E. Sensitivity of Surface Fluxes in the ECMWF Land Surface Model to the Remotely Sensed Leaf Area Index and Root Distribution: Evaluation with Tower Flux Data. Atmosphere. 2020; 11(12):1362. https://doi.org/10.3390/atmos11121362
Chicago/Turabian StyleStevens, David, Pedro M. A. Miranda, René Orth, Souhail Boussetta, Gianpaolo Balsamo, and Emanuel Dutra. 2020. "Sensitivity of Surface Fluxes in the ECMWF Land Surface Model to the Remotely Sensed Leaf Area Index and Root Distribution: Evaluation with Tower Flux Data" Atmosphere 11, no. 12: 1362. https://doi.org/10.3390/atmos11121362
APA StyleStevens, D., Miranda, P. M. A., Orth, R., Boussetta, S., Balsamo, G., & Dutra, E. (2020). Sensitivity of Surface Fluxes in the ECMWF Land Surface Model to the Remotely Sensed Leaf Area Index and Root Distribution: Evaluation with Tower Flux Data. Atmosphere, 11(12), 1362. https://doi.org/10.3390/atmos11121362








