Numerical Study on the Influence of Weir Construction on Near-Surface Atmospheric Conditions
Abstract
1. Introduction
2. Data and Methodology
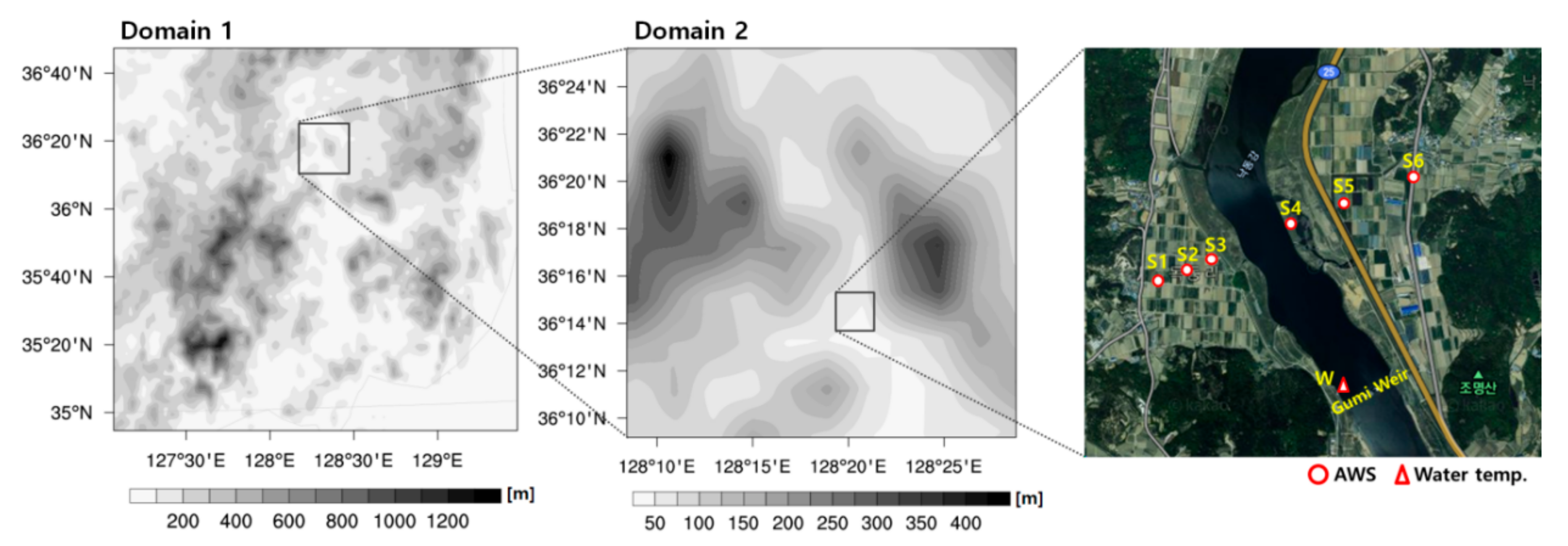
2.1. Model Configuration
2.2. Observation Site and Observation Dataset
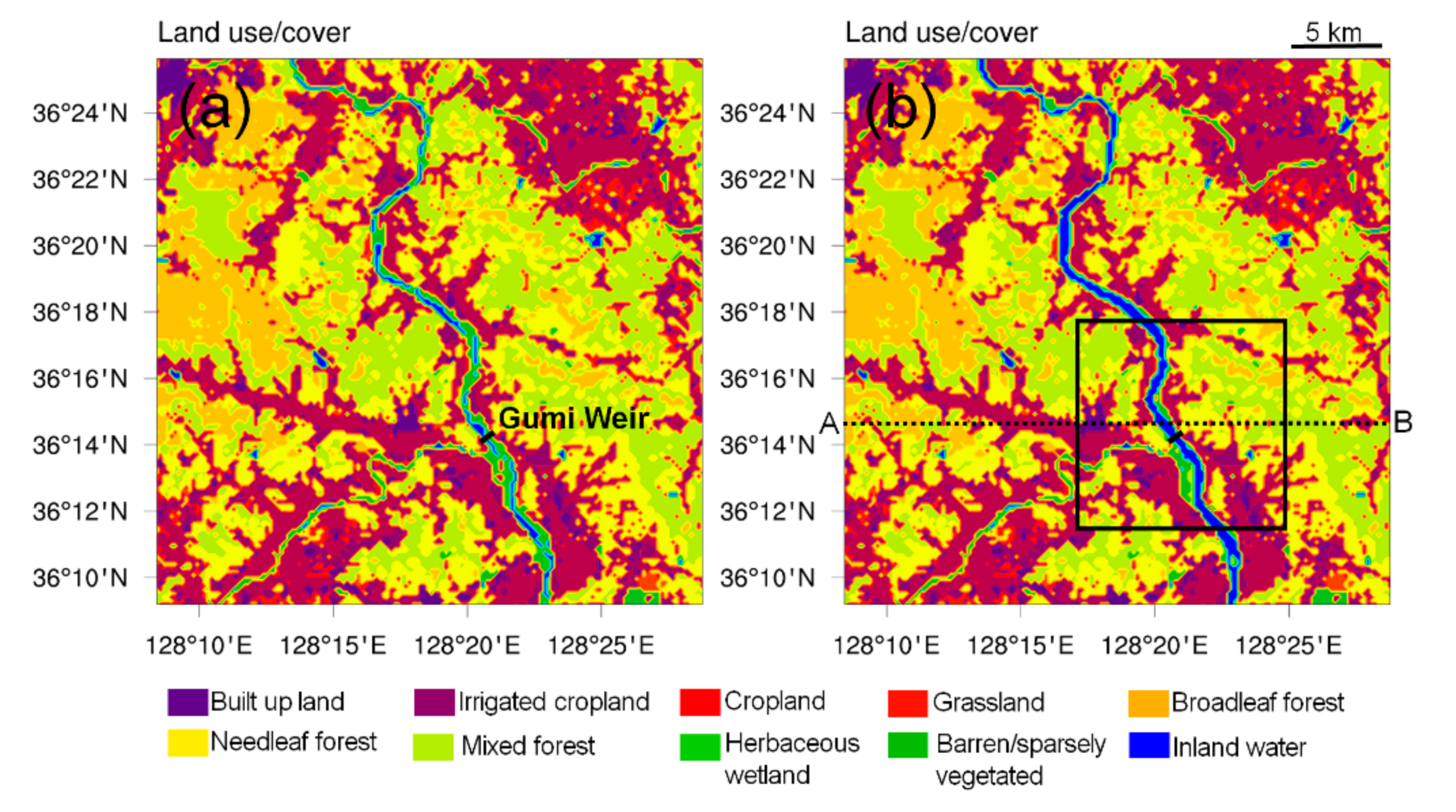
2.3. LULC Dataset of Weir Construction Scenarios
2.4. Study Cases
2.5. Paired t-Test
3. Results
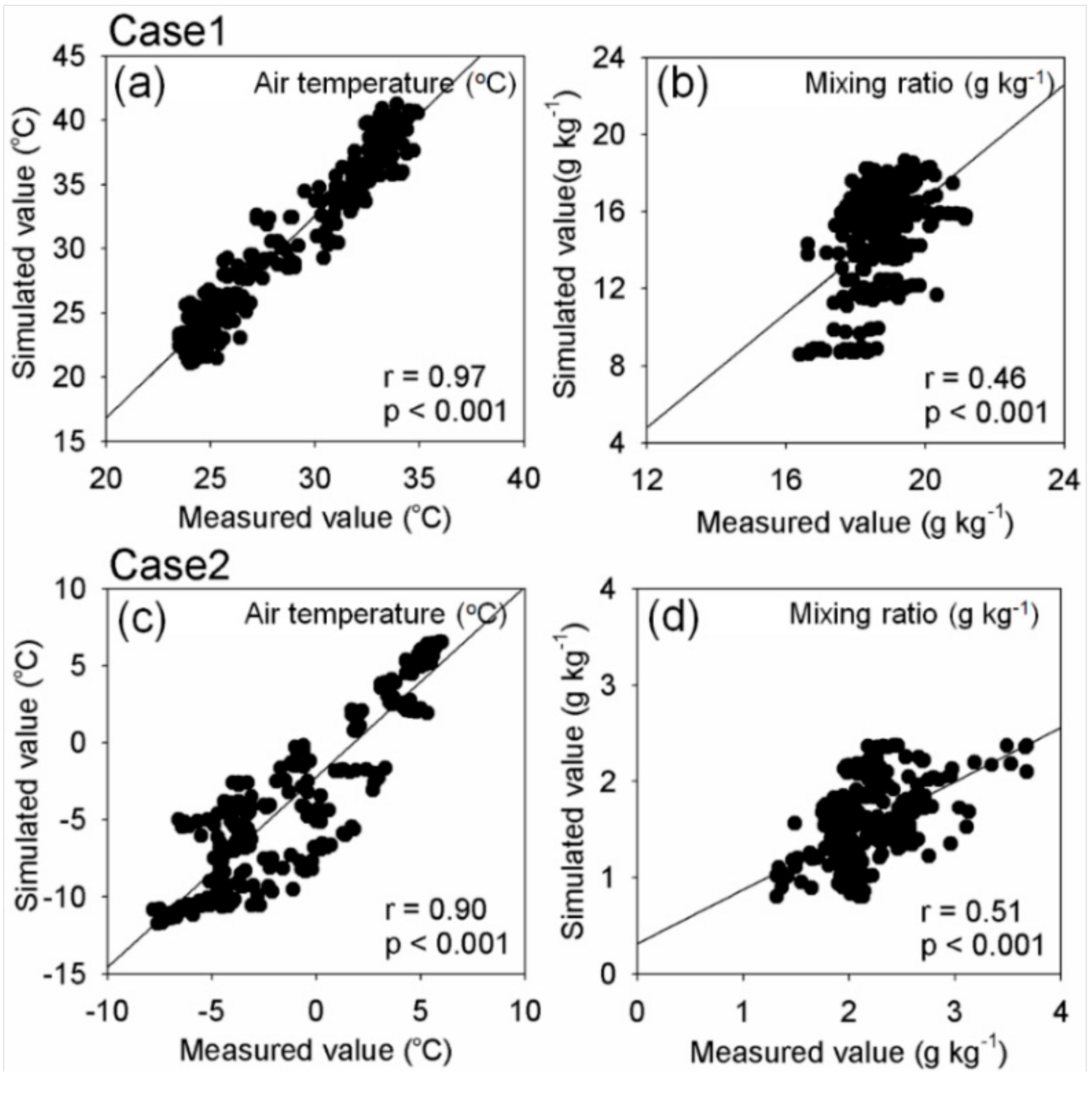
3.1. Model Evaluation
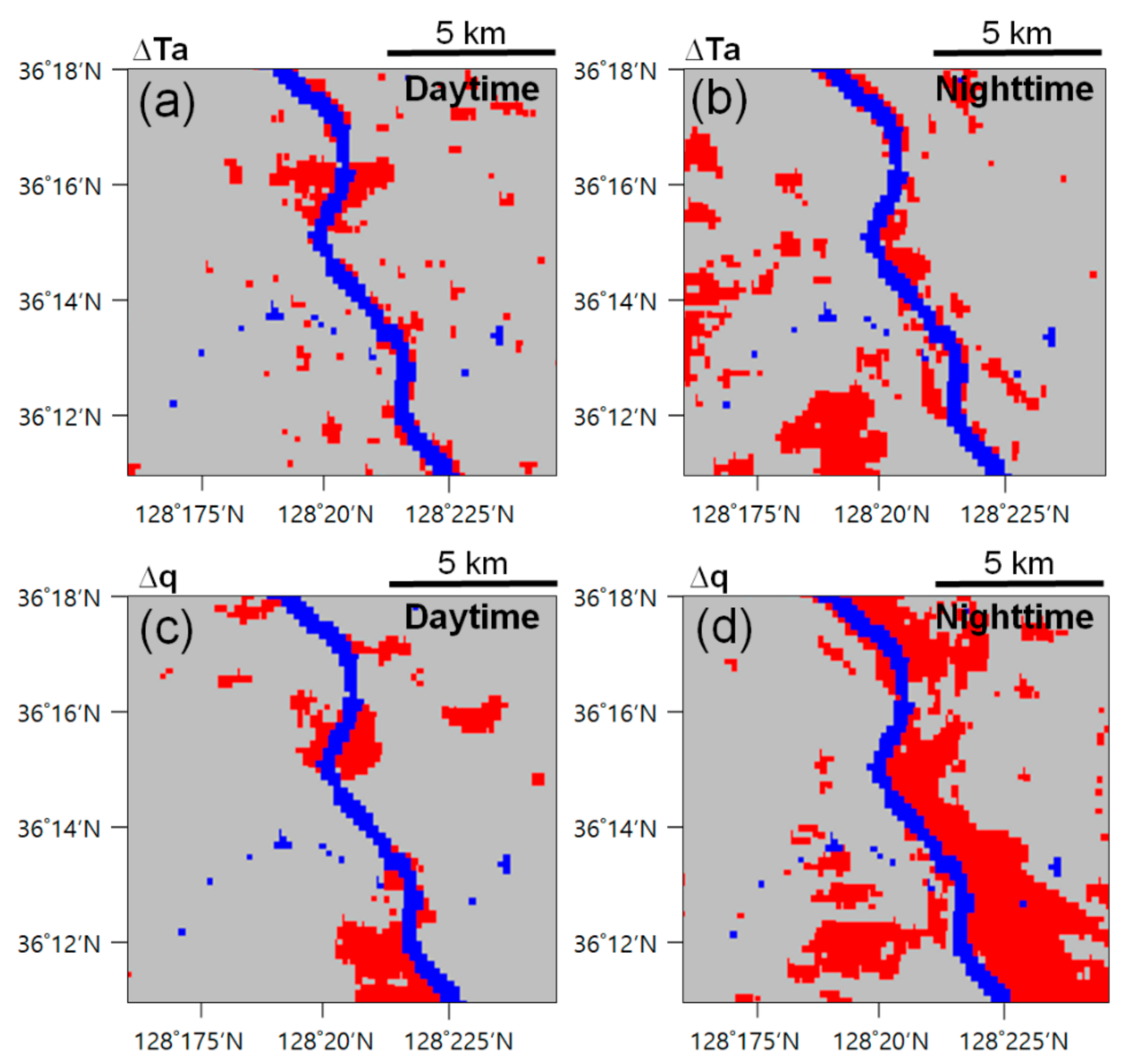
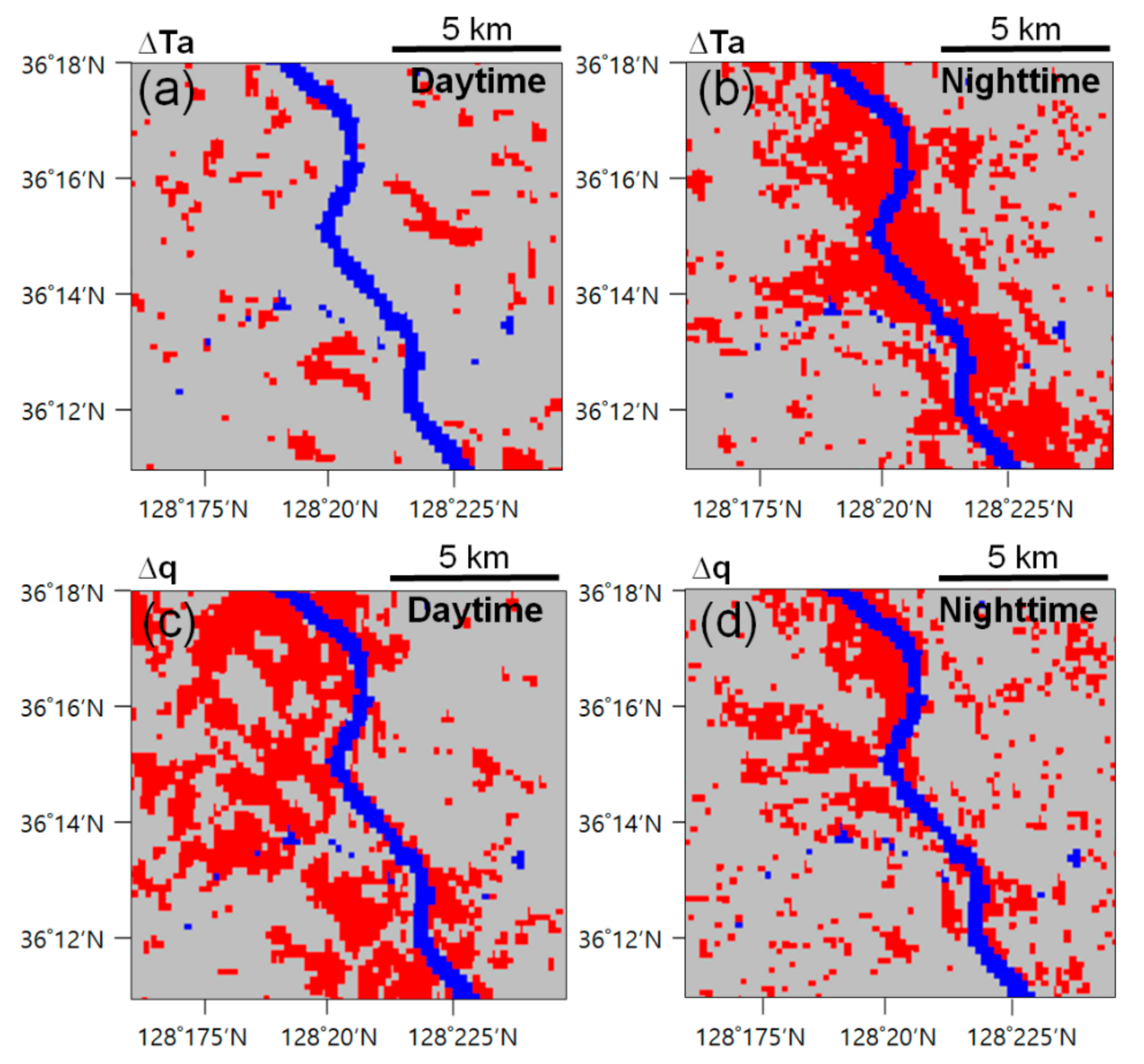
3.2. Changes of Meteorological Environment by Weir
3.3. Range of Affected Area
4. Discussion
5. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hohli, A.; Frenken, K. Evaporation from Artificial Lakes and Reservoirs; FAO-Aquastat: Rome, Italy, 2015; p. 10. [Google Scholar]
- Hogeboom, R.J.; Knook, L.; Hoekstra, A.Y. The blue water footprint of the world’s artificial reservoirs for hydroelectricity, irrigation, residential and industrial water supply, flood protection, fishing and recreation. Adv. Water Resour. 2018, 113, 285–294. [Google Scholar] [CrossRef]
- Lee, C.B. Changes of fog days and cloud amount by artificial lakes in Chuncheon. Asia-Pac. J. Atmos. Sci. 1981, 17, 18–26. [Google Scholar]
- Hong, S.G. Increase of the fogs in Andong due to the construction of Andong reservoir. Asia-Pac. J. Atmos. Sci. 1982, 18, 26–32. [Google Scholar]
- Stivari, S.M.; de Oliveira, A.P.; Karam, H.A.; Soares, J. Patterns of local circulation in the Itaipu Lake area: Numerical simulations of lake reeze. J. Appl. Meteorol. 2003, 42, 37–50. [Google Scholar] [CrossRef]
- Policarpo, C.; Salgado, R.; Costa, M.J. Numerical Simulations of Fog Events in Southern Portugal. Adv. Meteorol. 2017, 2017, 1–16. [Google Scholar] [CrossRef]
- Vogel, J.L.; Huff, F.A. Fog Effects Resulting from Power Plant Cooling Lakes. J. Appl. Meteorol. 1975, 14, 868–872. [Google Scholar] [CrossRef][Green Version]
- Brant, G.; Oliphant, A.J.; Blesius, L. Impacts of coastal advection fog on the surface radiation regime. AGUFM 2008, 2008, A51H-0206. [Google Scholar]
- Bates, G.T.; Giorgi, F.; Hostetler, S.W. Toward the Simulation of the Effects of the Great Lakes on Regional Climate. Mon. Weather. Rev. 1993, 121, 1373–1387. [Google Scholar] [CrossRef]
- Jeon, B.I.; Lee, Y.M. A change of local meteorological environment according to dam construction of Nakdong-River: II. Estimation using numerical model. J. Environ. Sci. 2002, 11, 281–288. [Google Scholar] [CrossRef]
- Samuelsson, P.; Kourzeneva, E.; Mironov, D. The impact of lakes on the European climate as simulated by a regional climate model. Boreal Environ. Res. 2010, 15, 113–129. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 2 (No. NCAR/TN-468+ STR). National Center for Atmospheric Research Boulder Co Mesoscale and Microscale Meteorology Div. 2005. Available online: https://apps.dtic.mil/dtic/tr/fulltext/u2/a487419.pdf (accessed on 9 December 2020).
- Byon, J.-Y.; Choi, Y.-J.; Seo, B.-K. Numerical Simulation of Local Circulation over the Daechung Lake Area by Using the Mesoscale Model. J. Korean Earth Sci. Soc. 2009, 30, 464–477. [Google Scholar] [CrossRef]
- Park, S.K.; Kim, J.H. A study on changes in local meteorological fields due to a change in land use in the lake Shihwa region using synthetic land cover data and high-resolution mesoscale model. Atmosphere 2011, 21, 405–414. [Google Scholar] [CrossRef]
- Cao, Q.; Yu, D.; Georgescu, M.; Han, Z.; Wu, J. Impacts of land use and land cover change on regional climate: A case study in the agro-pastoral transitional zone of China. Environ. Res. Lett. 2015, 10, 124025. [Google Scholar] [CrossRef]
- Yun, J.I.; Hwang, K.H.; Chung, H.H.; Shin, M.Y.; Lim, J.T.; Shin, J.C. Effects of an artificial lake on the local climate and the crop production in Suncheon area. Asia-Pac. J. Atmos. Sci. 1997, 33, 409–427. [Google Scholar]
- Catalano, F.; Moeng, C.-H. Large-Eddy Simulation of the Daytime Boundary Layer in an Idealized Valley Using the Weather Research and Forecasting Numerical Model. Bound. Layer Meteorol. 2010, 137, 49–75. [Google Scholar] [CrossRef]
- Moeng, C.-H.; Dudhia, J.; Klemp, J.; Sullivan, P. Examining Two-Way Grid Nesting for Large Eddy Simulation of the PBL Using the WRF Model. Mon. Weather Rev. 2007, 135, 2295–2311. [Google Scholar] [CrossRef]
- Talbot, C.; Bou-Zeid, E.; Smith, J. Nested Mesoscale Large-Eddy Simulations with WRF: Performance in Real Test Cases. J. Hydrometeorol. 2012, 13, 1421–1441. [Google Scholar] [CrossRef]
- Kang, M.; Lim, Y.-K.; Cho, C.; Kim, K.R.; Park, J.S.; Kim, B.-J. The Sensitivity Analyses of Initial Condition and Data Assimilation for a Fog Event using the Mesoscale Meteorological Model. J. Korean Earth Sci. Soc. 2015, 36, 567–579. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000; p. 771. [Google Scholar]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J. A Description of the Advanced Research WRF Version 3; NCAR Tech. Note NCAR/TN–4751 STR: Boulder, CO, USA, 2008; p. 113. [Google Scholar]
- Walters, D.; Boutle, I.; Brooks, M.; Melvin, T.; Stratton, R.; Vosper, S.B.; Wells, H.; Williams, K.; Wood, N.; Allen, T.; et al. The Met Office Unified Model Global Atmosphere 6.0/6.1 and JULES Global Land 6.0/6.1 configurations. Geosci. Model Dev. 2017, 10, 1487–1520. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land surface-hydrology model with the Penn State-NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Lim, K.-S.S.; Hong, S.-Y. Development of an Effective Double-Moment Cloud Microphysics Scheme with Prognostic Cloud Condensation Nuclei (CCN) for Weather and Climate Models. Mon. Weather Rev. 2010, 138, 1587–1612. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. Space Phys. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Chou, M.D.; Suarez, M.J. An efficient thermal infrared radiation parameterization for use in general circulation models. NASA Tech. Memo 1994, 104606, 1–85. [Google Scholar]
- Kang, J.H.; Suh, M.S.; Kwak, C.H. A Comparison of the Land Cover Data Sets over Asian Region: USGS, IGBP, and UMd. Atmosphere 2007, 17, 159–169. [Google Scholar]
- Ministry of Environment. Available online: Egis.me.go.kr/map/map.do?type=land (accessed on 17 September 2019).
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences; Academic Press: Cambridge, MA, USA, 2011; Volume 100. [Google Scholar]
- Sun, R.; Chen, L. How can urban water bodies be designed for climate adaptation? Landsc. Urban Plan. 2012, 105, 27–33. [Google Scholar] [CrossRef]
- Oke, T.R. Boundary Layer Climates; Routledge: London, UK, 1987. [Google Scholar]



| Domain1 | Domain2 | |
|---|---|---|
| Initial and boundary conditions | Local Data Assimilation and Prediction System (LDAPS) analysis data | |
| LULC dataset | 30 m horizontal resolution data (1.5 km) | |
| Horizontal resolution | 600 m (360 × 342) | 200 m (150 × 150) |
| Vertical resolution | 40 layers (up to 50 hPa) | |
| Turbulent fluxes | Yonsei University PBL [21] | Large Eddy Simulation [17,18,19,20] |
| Land surface model (LSM) | Noah LSM [25] | |
| Microphysics | WRF Double-Moment 6-class [26] | |
| Long-wave radiation | Rapid Radiative Transfer Model for GCMs [27] | |
| Shortwave radiation | Goddard short wave [28] | |
| Day | Night | ||||
|---|---|---|---|---|---|
| Max (m) | Mean (m) | Max (m) | Mean (m) | ||
| Case1 | Air temperature | 2000 | 234 | 1200 | 145 |
| Mixing ratio | 2400 | 341 | 4000 | 1059 | |
| Case2 | Air temperature | 565 | 19 | 4600 | 1100 |
| Mixing ratio | 3200 | 527 | 2600 | 361 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, M.; Kim, K.R.; Belorid, M. Numerical Study on the Influence of Weir Construction on Near-Surface Atmospheric Conditions. Atmosphere 2020, 11, 1337. https://doi.org/10.3390/atmos11121337
Kang M, Kim KR, Belorid M. Numerical Study on the Influence of Weir Construction on Near-Surface Atmospheric Conditions. Atmosphere. 2020; 11(12):1337. https://doi.org/10.3390/atmos11121337
Chicago/Turabian StyleKang, Misun, Kyu Rang Kim, and Miloslav Belorid. 2020. "Numerical Study on the Influence of Weir Construction on Near-Surface Atmospheric Conditions" Atmosphere 11, no. 12: 1337. https://doi.org/10.3390/atmos11121337
APA StyleKang, M., Kim, K. R., & Belorid, M. (2020). Numerical Study on the Influence of Weir Construction on Near-Surface Atmospheric Conditions. Atmosphere, 11(12), 1337. https://doi.org/10.3390/atmos11121337





