Abstract
This study proposes a climate service named Smart Climate Hydropower Tool (SCHT) and designed as a hybrid forecast system for supporting decision-making in a context of hydropower production. SCHT is technically designed to make use of information from state-of-art seasonal forecasts provided by the Copernicus Climate Data Store (CDS) combined with a range of different machine learning algorithms to perform the seasonal forecast of the accumulated inflow discharges to the reservoir of hydropower plants. The machine learning algorithms considered include support vector regression, Gaussian processes, long short-term memory, non-linear autoregressive neural networks with exogenous inputs, and a deep-learning neural networks model. Each machine learning model is trained over past decades datasets of recorded data, and forecast performances are validated and evaluated using separate test sets with reference to the historical average of discharge values and simpler multiparametric regressions. Final results are presented to the users through a user-friendly web interface developed from a tied connection with end-users in an effective co-design process. Methods are tested for forecasting the accumulated seasonal river discharges up to six months in advance for two catchments in Colombia, South America. Results indicate that the machine learning algorithms that make use of a complex and/or recurrent architecture can better simulate the temporal dynamic behaviour of the accumulated river discharge inflow to both case study reservoirs, thus rendering SCHT a useful tool in providing information for water resource managers in better planning the allocation of water resources for different users and for hydropower plant managers when negotiating power purchase contracts in competitive energy markets.
1. Introduction
Traditionally dominated by the use of fossil fuels, the global generation and supply of energy is one of the main causes for air and water pollution, damage to public health, land degradation, and wildlife and habitat losses [1]. Among the alternative energy sources to fossil fuels, hydropower stands out as a relatively stable renewable energy source that is technically accessible, economically competitive, and with a balanced impact on climate and human health [2,3,4,5]. Currently, hydropower accounts for more than 75% of the share of renewable energy sources used for electricity supply and approximately 17% of the global electricity supply share in 2015 [6]. Still, hydropower has a large exploitable potential for expansion worldwide [7], particularly in countries with either (or both) large elevation and large runoff [8].
One of the main challenges in hydropower production, though, pertains to the ability to forecast the seasonal hydropower potential in order to match the energy and water resources supply with the demand. Processes such as snow accumulation and melt, canopy interception, infiltration, soil storage, and baseflow all affect the runoff potential at seasonal scales; yet precipitation remains the main driver on the discharge that passes through the turbines in hydropower plants. Although highly flexible and with low costs to power ratio [9], seasonal hydropower potential production is strictly linked with future hydrometeorological conditions [10], which are often uncertain as the forecasting lead-time increases [11]. Long-term issues such as climate change and land cover change can potentially add another layer of uncertainty to seasonal hydropower potential production. For instance, in the Brazilian Amazon, it is estimated that climate change could lead to a decrease in hydropower potential ranging between −5.4 to −7.4% per month during the dry season, while when combined with the effects of land cover and land use changes (e.g., deforestation) it could lead to an increased interannual hydropower potential variability ranging between +50 to +69% [12]. In this context, hydrologic indexes can often be used as tools for supporting hydrometeorological-related decision-making water resources at the watershed level, not only at the seasonal scale but also under climate projections [13].
The integration of hydrometeorological forecasts into water management decision processes can potentially provide crucial information about future reservoir management conditions and potential hydropower production, allowing for better cost–benefit analysis when negotiating power purchase contracts in a competitive energy market [14,15]; yet, the consideration of seasonal forecasts variables in the context of hydropower decision-making is largely underestimated mainly due to the traditional risk averse nature of water managers [16]. During the past few decades, seasonal forecasting systems have consistently improved their ability in producing accurate hydrometeorological forecasts, mainly due to the larger availability of observation data, the improvement of the understanding and description of hydrometeorological processes, and the increased computational power allowing for more refined spatial and temporal representation of hydrometeorological variables [17,18]. Additional data pre-processing, such as bias-correction and downscaling, can further increase the quality of forecasted hydrometeorological variables [19,20]. Even if important advancements have been achieved at the sub-seasonal time horizon (i.e., a week to a month of forecast) [21,22,23,24,25], challenges remain for the seasonal lead-times (i.e., one to six months of forecast) [26,27,28], particularly in highly variable rainfall dominated catchments [29].
Machine learning techniques present themselves as an interesting tool for the seasonal forecasting of hydrometeorological variables due to their generalisation capability and relatively quick ability to generate simulations over an extended period of time [30]. In the context of decision-making of hydropower plants, processes such as inflow rates or potential energy trading can largely benefit from an enhanced and reliable seasonal energy forecast system [31]. In this context, machine learning algorithms have been successfully used for the seasonal forecasting of hydrometeorological processes since the late 90s [32,33,34,35,36]. Recently, Callegari et al. [37] have analysed the performance of a monthly river discharge forecasting model with a support vector regression (SVR) model in a European alpine area, concluding that although the SVR model delivers better forecasts than its simpler linear alternatives, long lead-time hydrological forecasting in Alpine catchments remains a challenge. Similarly, De Gregorio et al. [38] have used a SVR model for monthly river discharge forecasting with 1 month lead time over 300 alpine basins, in order to explore advantages and limits in an operational perspective, concluding that the SVR model shows better performances than the average of the previous 10 years in 94% of the cases, with a mean improvement of about 48% in root mean square error. Essenfelder and Giupponi [39] used a hybrid hydrologic-machine learning modelling framework to simulate the decision-making process of managing interbasin water transfer, concluding that machine learning can successfully simulate the complex water flow dynamics and be a useful instrument to support complex scenario analysis in watersheds subject to interbasin water transfers.
Exploiting the potential of machine learning for supporting decision-making in the context of water resources management and in particular of hydropower production, this paper presents an innovative web-cloud-based climate service named Smart Climate Hydropower Tool (SCHT). SCHT makes use of physically based hydrometeorological seasonal forecasts provided by the ECMWF’s operational seasonal forecast system 5 (SEAS5) [40] with a set of different machine learning algorithms (support vector regression—SVR, Gaussian processes—GP, long short-term memory—LSTM, non-linear autoregressive neural networks with exogenous inputs—NARX, and a deep-learning neural networks model—DL) to perform the seasonal forecast (i.e., 1 to 6 months) of the accumulated inflow discharges to the reservoir of an hydropower plant. The forecasts obtained from the different machine learning algorithms are compared against climatology, multiple linear regression, and persistence values. Methods are illustrated by simulating the seasonal inflow river discharges for two reservoirs, namely Betania and Guavio, and their river catchments, both located in Colombia, South America.
2. Material and Methods
2.1. Data
SCHT requires two main data categories to operate, namely, time series of observed hydrometeorological data from ground stations and hydrometeorological data from a seasonal forecast system. Further details pertaining to the data used by SCHT are shown in Table 1.

Table 1.
Summary of data used in the Smart Climate Hydropower Tool (SCHT).
Observed hydrometeorological data (i.e., precipitation, snowfall, temperature) from ground stations are used for training the machine learning forecast algorithms. Tabular hydrometeorological data are collected from publicly accessible hydrographic offices in Colombia [41], while additional data pertaining to the streamflow of rivers in the case study areas are also provided by Enel Green Power S.p.A. (not published data), the user of SCHT for the case studies described in this paper. Data on water volumes to the reservoirs are provided on a monthly scale. Data are collected as a time series from 1993 to present, being periodically updated with new data at the end of each month.
Hydrometeorological data, in particular precipitation data, are the main driver of runoff and the associated discharge that feed into the turbines of hydropower plants. Seasonal forecasting systems data can provide crucial data for projecting the potential hydropower production [17]. In this paper, we rely on the utilisation of seasonal forecast data provided by the Centro Euro-Mediterraneo sui Cambiamenti Climatici (CMCC) through the Copernicus Climate Change Service (C3S) Climate Data Store (CDS). In particular, we use seasonal forecasts at the monthly level on single levels from 2017 to present date, being periodically updated with new data at the end of each month. The variables of interest for our analysis are total precipitation and mean above ground air temperature, provided in grid multiband georeferenced format. The grid multiband georeferenced data are then spatially interpolated to the exact location of the observed hydrometeorological points by means of universal kriging interpolation method (e.g., [42]).
2.2. Machine Learning Techniques
SCHT utilises five different machine learning techniques to perform hydrometeorological seasonal forecasts, namely: support vector regression (SVR); Gaussian processes (GP); long short-term memory (LSTM); non-linear autoregressive neural networks with exogenous inputs (NARX), and a deep-learning neural networks model (DL). The input dataset to all five models is built from a two-step pre-processing phase, consisting of (i) selecting the seasonal forecast cells and hydrometeorological stations based on their spatial locations with regards to the basin contribution area of a particular reservoir and (ii) performing the feature selection of the input variables by means of a correlation matrix between the available input features and a tree-based ranking [43]. This pre-processing phase is fundamental to identify the meteorological stations and spatial grid cells from the seasonal forecast systems’ data that are more relevant for the reservoir of interest, and to remove potential redundancies coming from highly correlated spatial meteorological information. The resulting input training data for all five models are the same so as to maintain intra-model evaluation consistency. A general description of the input data utilised for calibrating/training the statistical methods and the machine learning techniques can be seen in Table 2.

Table 2.
Variable codes and related description of the data used for calibrating statistical methods and training the machine learning algorithms within SCHT.
The selected input data are then sequentially split between three distinct sets, namely training, validation, and test, following a proportion of 0.70:0.15:0.15, respectively. As the input data are a time series dataset, the sequential splitting, following the training, validation, and testing datasets order is done so as to avoid data leakage [44]. The training dataset is used to calibrate/train the machine learning models; the validation set is utilised as stopping criteria so as to avoid the overtraining or overfitting of the machine learning techniques, when applicable, and the test dataset is used as a way of verifying the accuracy of a trained model when stressed by new data, hence not being used during the training procedure. A k-fold cross-validation of 10 folds is performed for each model. In order to reduce the chances of the training procedure to get stuck into a local minimum (e.g., due to the initial weight values of the connections between neurons), about 1000 training attempts are performed for each model, each with a different random initialisation. The accuracy of the five machine learning techniques is compared against climatology, multiple linear regression, and persistence values, while their performance is intra-evaluated using the same model evaluation metrics, namely, root mean squared error (RMSE) [45]:
and the Nash–Sutcliffe model efficiency coefficient (NSE):
where Oi is the ith observation for a variable x, Ō is the mean value of observed data for a same variable x, Pi is the ith prediction for a same variable x, and n is the total number of observations.
Climatology, linear regression, and persistence are common, simple, and straightforward metrics to evaluate how the predictions of a certain model behave in comparison to observation records (e.g., [46]). RMSE and NSE are complimentary model evaluation metrics; while RMSE indicates how errors increase according to the variance of the frequency distribution of error magnitudes, NSE indicates how well the predictions are fitting the 1:1 line with respect to the observations [47]. RMSE values close to 0.0 indicate no error, while NSE values range between minus infinite and positive 1.0. A value of NSE = 1 means a perfect 1:1 predicted: observed fit, while NSE values between 0.0 and 1.0 are viewed as acceptable levels of performance.
2.2.1. Support Vector Regression (SVR)
SVR is a nonparametric machine learning technique that uses the principles of support vector machine (SVM) for classification and regression problems [48]. SVR is a supervised learning model, meaning that the learning algorithm analyse a target dataset for classification and regression analysis. The main goal of an SVR is to find a function that deviates from a certain range of target values by a difference no greater than a certain margin of tolerance (i.e., epsilon) for each training point. Non-linear SVR uses kernel functions to transform the input data into higher dimensional feature space so to make possible the linear separation between training points. An example of kernel functions include linear, polynomial, radial basis function (RBF), and sigmoid functions. The SVR model used in SCHT is built upon the Python module “scikit-learn” [49] and uses an epsilon-support vector regression and a radial basis function (RBF) kernel function for the learning process. Other parameters used for configuring the SVR model are: epsilon value for the epsilon-tube within which no penalty is associated in the training loss function is set to 0.01; RBF kernel coefficient is set to the inverse of the number of input features (variable depending on the case study), and the hard limit on iterations within the solver is set to infinite.
2.2.2. Gaussian Processes (GP)
GP is a nonparametric machine learning technique that relies on the concepts of multivariate Gaussian distribution to model the underlying probability distribution of a training dataset with respect to a set of target values [50]. As such, GP is a supervised learning method that can be used in regression, classification, and clustering problems [51]. GP assesses the probability of the potential solutions (i.e., functions) that fit to a given set of input training points, meaning that the resulting probability distribution represents the most probable range characterising the input data. By using a probabilistic approach, GP allows for the incorporation of a confidence interval of the predictions into the regression results. The distributions in GP is defined by two key elements, the mean value and the covariate matrix. While the mean describes the location in which the distribution is centred, the covariance matrix describes the shape of the distribution, ultimately controlling the characteristics of the potential solutions (i.e., functions). The covariance matrix is determined by its covariance function or the kernel of the GP. Common kernels for GP include linear, periodic, and RBF. The GP model used in SCHT is provided by the “kernlab” package in R and utilises a RBF kernel and the provided automatic routine, which relies on the hyperparameter estimation to calculate a good sigma value for the GP RBF function [52].
2.2.3. Long Short-Term Memory (LSTM)
LSTM is a type of recurrent neural network (RNN) designed to overcome the weakness of these type of models in memorising long-term sequences [53,54]. Differently from traditional recurrent neural networks models where a single internal state exists per neuron, an LSTM model has an additional state in which information can be stored and three gates used to optionally let information flow through the LSTM neurons [55]. The first gate (known as the forget gate) controls which elements of the LSTM neuron will be forgotten; the second gate (known as the input gate) controls which and how information updates the LSTM neuron state in the current time step; the third gate (known as the output gate) controls the information of the current LSTM neuron state that flows into the following LSTM neuron state [56]. The LSTM model developed for SCHT is build using the “tensorflow” [57] and “keras” [58] python libraries. The model is setup with a first single LSTM layer using a Swish activation function [59] followed by two dense hidden-layers using Swish activation functions and a rectified linear activation function (ReLU) at the output layer, hence allowing simulated values to be greater than the maximum observed values in the target dataset. A 12 month time-step (i.e., one year as the input data are at a monthly scale) is used for the LSTM model training, for all input variables. The stochastic gradient descent method “adam” is used as the optimiser algorithm. The model evaluates the RMSE of the model outputs with regards to the targets for both the training and validation datasets, for each training epoch, as a means of assessing the generalisation property of a trained LSTM model. As the training procedure of the LSTM model aims at reducing the error of the training dataset, a generalised LSTM model is expected to be capable of reproducing those error reductions also in an unbiased dataset (e.g., the validation dataset). In case the validation metrics do not improve for the validation dataset, early-stop is put in place, and the training procedure stops early stopping being put in place when 12 consecutive training epochs have been achieved with no improvement.
2.2.4. Non-Linear Autoregressive Neural Network, Exogenous Outputs (NARX)
Differently from traditional ANN and similarly to LSTM models, a NARX is a type of RNN model that accounts for feedback loops, which connects present with past decisions, essentially taking time and sequence into account, being a type of recurrent neural network. NARX and RNNs have been applied in several fields of research, such as hydrology, remote sensing, and image classification [33,60,61]. The model used in this study has been developed in R language and uses back-propagation as the supervised training technique and the Levenberg–Marquardt as the optimization algorithm [62]. The NARX model developed for SCHT evaluates the sum of squared errors (SSE) of the model outputs with regards to the targets for each training epoch as a way of assessing the generalization property of a trained model [63,64]. The developed NARX model runs in a multi-core configuration and provides an ensemble of trained models as a result, thus being suitable for probabilistic analysis. The input and target information are normalized by feature scaling before being processed by the model, while the initial number of hidden neurons per hidden layer is approximated as two-thirds of the summation of the number of neurons in the previous and next layers [65]. The model is setup as a two hidden-layers variant and using a Swish activation function [59] between hidden-layer nodes and a rectified linear (ReLU) activation unit function at the output layer, hence allowing simulated values to be greater than the maximum observed values in the target dataset. A 12 month time-step is used for the LSTM model training, for all input variables. Similar to the LSTM model, early-stopping is put in place when the number of consecutive epochs on which no improvement is observed on the validation dataset for 12 consecutive training epochs. The resulting NARX model consists of a single model, representing the best overall result after the training procedure.
2.2.5. Deep-Learning Neural Networks (DL)
DL is a variant of ANN models that includes the use of multilayer models that have the capability of learning from input data using a general-purpose learning procedure, resulting in potentially higher-level representation of the underlying data sources [66]. In this context, DL is able to learn from complex and high-dimensional data so as to infer robust and scalable results while minimizing the manual parameterisation of the model. Similar to ANN and RNN models, DL have been applied to several areas of research, including speech recognition, medical image analysis, and hydrology [67]. The DL model used in this study has been implemented using the R package H2O.ai [68]. The model is configured using the adaptive learning rate ADADELTA [69] for the stochastic gradient descent optimisation. The ADADELTA adaptive learning rate in H2O.ai requires two parameters to be set, namely rho and epsilon. These two parameters balance the global and local search for the minimum error and are setup with the values 0.95 and 1 × 10−8, respectively. The DL model structure is configured with a five hidden-layer depth dimension. Similar to the LSTM model, the early stopping criteria is setup to stop the training in case validation metrics do not improve by at least 1% for 12 consecutive training epochs.
2.3. Case Study Areas
Colombia has established its power market in 1995, driven primarily by the goal of increasing the reliability of energy supply in the domestic power system [70]. Due to lower-than-expected results in providing a reliable supply of energy along competitive outcomes, the original regulated energy market based on capacity payment was replaced in 2004 by a reliability market intended to ensure supply during tight hydrological conditions, often connected to El Niño phenomena [71]. In this context, private companies managed to enter the and establish themselves in the hydropower energy market in Colombia, and the selected case study areas are two large hydropower plants located in Colombia, namely Betania and Guavio, with a total combined capacity of 1790 MW, both managed by ENEL Greenpower Emgesa SA ESP society (see Figure 1). The Betania hydropower plant’s capacity is about 540.0 MW and has an average production of 2000 Gwh/year, being located in the Rio Magdalena catchment and counting with an upstream drainage area of about 13,000 km2. The Guavio hydropower plant, although having a smaller upstream drainage area of about 1500 km2, can produce approximately 2.3 times more energy than the Betania hydropower plant, having a capacity of roughly 1250 MW and an average annual production of 5500 Gwh/year. The climatological average of the monthly inflow river discharge to both reservoirs (calculated over the period spamming all the available data, i.e., from 1993 to 2019) are shown in Figure 1.
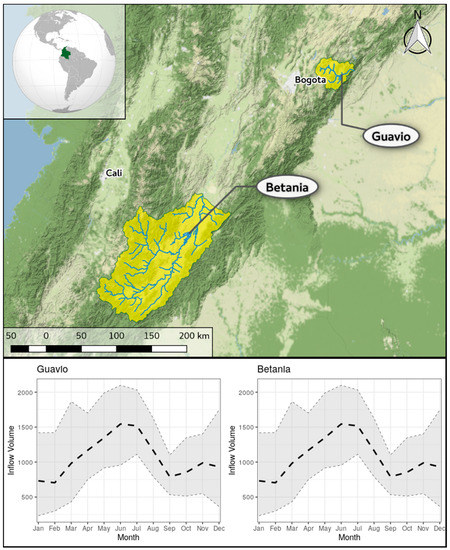
Figure 1.
Case study area and monthly reservoir river discharge, in Mm3, to the Guavio and Betania hydropower plants. The climatological average is highlighted as the black dashed line, while the monthly maximum and minimum values for each month during the period 1993–2019 are shown as the grey ribbon area.
Currently, forecasts of the seasonal inflow river discharges beyond currently available historical averages is still a challenge, and the potential added value of a seasonal forecast system is still unclear. In this context, having a reliable forecast of incoming volumes supports operational decision-making through planning the energy production accordingly. For each reservoir, the manager seeks to maximise the generation of energy constrained to future incoming water volumes, the potential withdrawals and outflows (e.g., ecological runoff), the current volume of water stored in the reservoir at the beginning of the month, and the energy market characteristics (e.g., energy price). As such, the information provided by SCHT can be used to assess potential financial costs for the producer when he needs to enter the energy market (i.e., buy/sell energy) or to cover missing revenues by accessing credit market, according to forecasted revenues from energy production in the incoming months.
2.4. SCHT as a Climate Service
Existing hydropower plants are managed to optimize both production and financial actions in the energy market. Since these facilities can be placed anywhere, it is necessary to develop a forecast workflow that can be easily adapted to a wide number of plants worldwide. SCHT considers a replicable and adaptable forecast workflow that ensures, in principle, the widest adaptability both to different geographic areas and temporal scales. One of the main advantages of the proposed methodology consists in the possibility of using globally available input features and data-driven forecast approaches that can be easily tuned for any combination of features. A schematic representation of SCHT as a climate service can be seen in Figure 2.
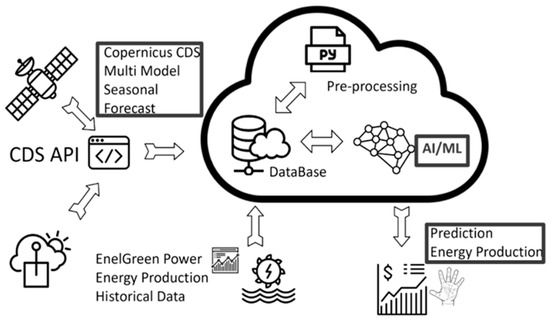
Figure 2.
Schematic representation of SCHT as a climate service.
SCHT (developed by GECOsistema srl within the context of the H2020 project “CLAR—Climate forecast enabled knowledge service” is an innovative web-cloud-based climate service that makes use of a set of machine learning methods for supporting decision-making in a context of hydropower production. As shown in Figure 2, SCHT utilises the state-of-the-art multi-model seasonal forecast data provided by the Copernicus Climate Change Service through the Climate Data Store, and historical hydrometeorological data pertaining to the case study area and provided by the user of the service. The data are stored in the cloud provided by the service, where it is pre-processed (e.g., feature selection and variable importance ranking, as described in the Material and Methods section) and passed to the machine learning model for performing the forecast of the accumulated water volumes inflow and the potential energy production. The service provides its final results as periodical monthly bulletins of inflow forecasts and historical data analysis related to the target variable (e.g., produced energy or related incoming discharge to one or more hydropower plants). These data are presented to the users through a user-friendly web interface, which is the result of a tied connection with end-users in an effective co-generation process, adding value to energy forecasts and ideally paving the road for highly scalability and replicability (e.g., development of similar services elsewhere).
SCHT targets energy producing companies and supports both their day-to-day management (operations) and their market (trading) activities. The service works as a technology-driven tool using a Software-As-A-Service (SaaS) business model. This business architecture counts on a continuous revenue flows: the target user accesses the web-based platform by paying an annual subscription fee with initial setup disbursement. To boost customers’ trust and put co-development in practice, SCHT can also offer tailored packages to multinational companies based on the number of plants that require the service. This business model flexibility boosts the client acquisition phases and allows differentiated revenue streams, while not excessively weighting on the costs associated to the service development and deployment.
SCHT is rooted in co-development with the target user, following the progressive shift on climate services from developer-centric perspectives towards climate adaptation and user-centric visions [72]. This approach works through two complementary channels: (i) the optimisation of energy production reducing the risks and costs associated with inefficient production; (ii) the improve existing operations, the service forecasts the energy volumes given changing short-terms climate conditions. When and if applied to multiple reservoirs, SCHT also provides information about the regional and global production of a given firm. The comprehensive picture highlights the existing risks and threats to the clients’ business model. Here, SCHT becomes a strategic feature for the intended user, assigning value to climate information.
3. Results and Discussion
This section presents the results of and the related discussion on the utilisation of the proposed machine learning model for the forecasting of accumulated river discharge inflow to the Guavio and Betania reservoirs. This section is divided in two sub-sections, where the first sub-section, named “Technical aspects of SCHT“, consists of presenting the technical results and discussion pertaining to the training and validation of the proposed machine learning models for forecasting the accumulated river discharge inflow, while the second sub-section, named “SCHT as a Climate Service” presents the discussion regarding the applicability of SCHT as a climate service and the potential benefits from its utilisation by hydropower managers.
3.1. Technical Aspects of SCHT
According to the proposed methodological framework, the methods and models considered in the present study can be grouped as follows:
- Group 1: Climatology, persistence, and multiple linear regression (MLR).This group includes the range of methods and models that are used as simple validation metrics for the more complex machine learning models.
- Group 2: Gaussian processes (GP) and support vector machine (SVM) models.This group includes the range of machine learning methods and models that do not use a validation dataset as a means for early stopping the training procedure.
- Group 3: Non-linear autoregressive neural networks (NARX), long short-term memory (LSTM), and deep-learning (DL) models.This group includes the range of machine learning methods and models that use a validation dataset as a means for early stopping the training procedure.
The validation dataset is used as during the training of a machine learning model in Group 3 so as to avoid the overfitting of the model to the training data. Two examples of a training process when using the validation dataset as a means for early stopping are shown in Figure 3.
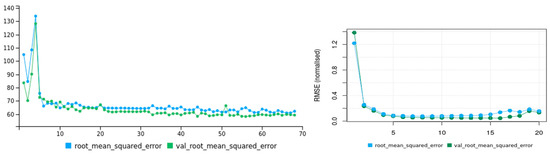
Figure 3.
Example of two training attempts of machine learning models from Group 3 that use the validation dataset as support information for early stopping. The x-axis represents training epochs. On the left, a training attempt of the long short-term memory (LSTM) model (y-axis indicates absolute root mean squared error (RMSE) values), and on the right, a training attempt of the non-linear autoregressive neural networks (NARX) model (y-axis indicates normalised RMSE values), both for one month lead-time forecasting at the Guavio reservoir.
As described in the material and methods sections, the evaluation of the accuracy of the training and testing metrics of the considered methods and models is done by means of the root mean squared error (RMSE) and the Nash–Sutcliffe model efficiency coefficient (NSE). Table 3 displays the numerical results of the model efficiency criteria considered in this study for both Betania and Guavio case studies. The results shown in Figure 4 and Figure 5, instead, depicts the mean model efficiency metrics results per model group, plus the climatological average results for reference.

Table 3.
Nash–Sutcliffe model efficiency coefficient (NSE) and RMSE results for the Betania and Guavio case studies, for all 6 forecast horizons.
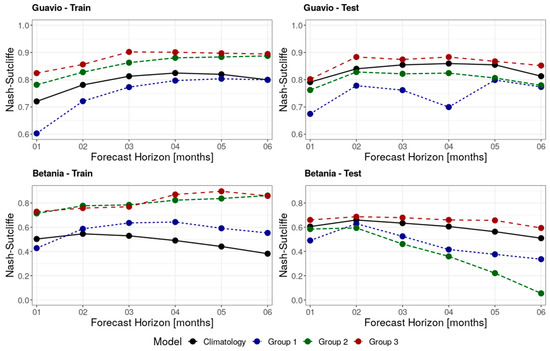
Figure 4.
Nash–Sutcliffe results of the machine learning models and validation metrics per group.
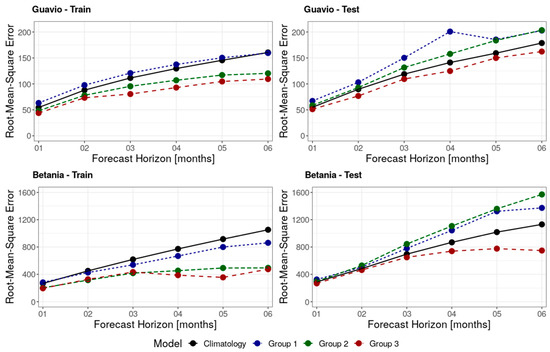
Figure 5.
Root mean squared error results of the machine learning models and validation metrics per group.
Given the results shown in Figure 4 and Figure 5, and Table 3, it is possible to verify that, as the forecast horizon increases, the forecasted results are subject to larger errors, both in the training and also in the test datasets, as shown by the generally increasing RMSE values. Interestingly, the NSE results indicate a less pronounced worsening of the results, while in some cases such as with the NARX or the Persistence models, the NSE results might increase as the forecast horizon increases. This contrasting behaviour is explained by two main factors: (i) the forecasted values are accumulated values spanning the forecast horizon and (ii) the NSE model efficiency coefficient is limited from minus infinity to +1, while the RMSE is not bounded. The first point explains why the RMSE increases as the forecast horizon increase, even if the NSE results do not follow the same pattern, as the scale of the forecasted values are different (e.g., average of approximately 1000 Mm3 for 1 month forecast and 6000 Mm3 for 6 months forecast for the Betania hydropower plant), while the second point explains the difference in behaviour between the two metrics, as the NSE values are in some sense normalised for the different scales of the target values.
The results shown in Table 3, Figure 4 and Figure 5 also indicate that, according to both the NSE and the RMSE model efficiency metrics, all the machine learning models belonging to Group 2 and Group 3 display better training results than both the climatological average and Group 1 models. The method from Group 1 that displays the best result when considering the training dataset is the MLR, which, however, generally behaves worse if compared to any other model from Groups 2 and 3, especially for longer forecast horizons (see Table 3). When considering the test dataset, Group 3 provides the most accurate forecasts with respect to the models in Group 1, in Group 2, and also with respect to climatology. In fact, for both case studies, the Group 3 models provide consistently better results than climatology. For the Betania case study, the skill of the models belonging to Group 3 with respect to climatology becomes more evident as the time horizon increases. Interestingly, the forecasting accuracy of the models belonging to Group 2 when considering the test dataset show an opposite behaviour with respect to climatology if compared to the training results, as the average results of Group 2 do not provide consistent better results than the climatological average for both NSE and RMSE (see Figure 4 and Figure 5). These results suggest that machine learning algorithms that make use of a complex and/or recurrent architecture can better simulate the temporal dynamic behaviour of the accumulated river discharge inflow to both the Guavio and Betania reservoirs.
In order to better understand the behaviour of the models in Group 3 with respect to climatology, the error histogram and the scatter plot distribution of observed versus forecasted values are analysed. These results are shown in Figure 6 and Figure 7. Figure 6 displays the error histogram of Group 3 models and climatology for a forecast horizon of 1 month for the Guavio reservoir, while Figure 7 displays the scatter plot of observed values versus forecasted values for the same models, time horizon, and case study.
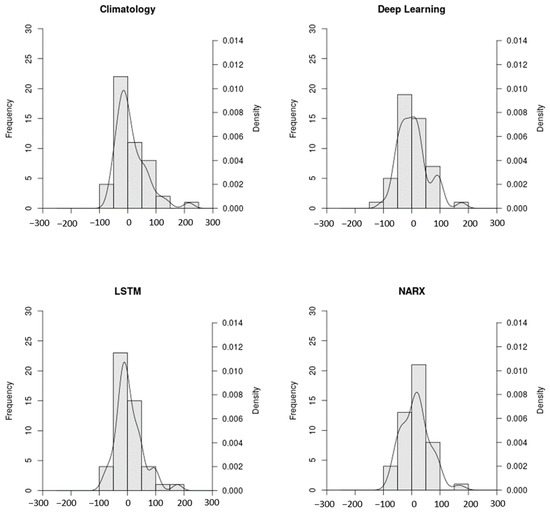
Figure 6.
Error histogram of Group 3 models and climatology for a forecast horizon of 1 month for the Guavio reservoir.
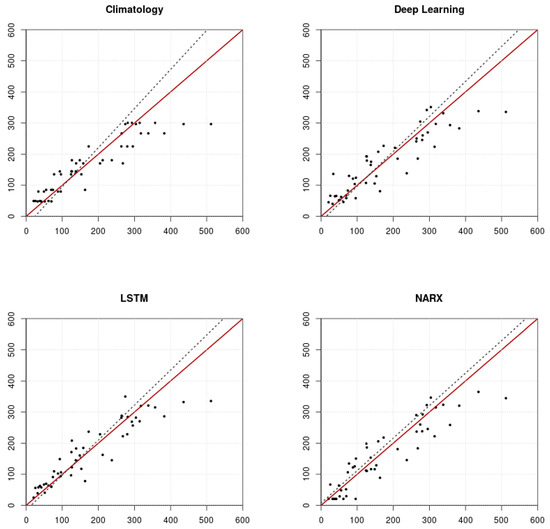
Figure 7.
Scatter plot (observed values on the x-axis and forecasted values on the y-axis) of Group 3 models and climatology for a forecast horizon of 1 month for the Guavio reservoir. The red line indicates a perfect fit of observed and forecasted values, while the black dashed line corresponds to the linear regression of the observed values given the forecasted values.
The results presented in Figure 6 and Figure 7 corroborate the findings that the models belonging to Group 3 (DL, NARX, LSTM) are the one with the best overall forecasting skill for predicting the accumulated river discharge inflow to both the Guavio and Betania reservoirs. However, it is not possible to define a model belonging to Group 3 as the one that presents the best overall forecasting skill. Hence, in order to evaluate the benefits for a potential user of the climate service SCHT, we proceed to evaluate the behaviour of the three best performing machine learning techniques as a unified model resulting from the averaging of the results of the models belonging to Group 3.
3.2. SCHT as a Climate Service
The models belonging to Group 3 can clearly provide more accurate estimates of the accumulated river discharge inflow to both the Guavio and Betania reservoirs with respect to more simple approaches, such as the climatological average, persistence analysis, and multiple linear regression. However, a question remains: what are the economic benefits that a user can get from using SCHT? To answer to this question, we evaluate the economic benefits of using the averaged results of the models in Group 3 with respect to the climatological average. Economic benefits are also evaluated in a scenario where a perfect forecast situation exists. Two forecasting scenarios are considered, as follows: a six months forecasting scenario for the Betania hydropower plant and a three month forecasting scenario for the Guavio hydropower plant. Both scenarios are set in the year 2019 and are issued in March. Moreover, we estimate that the Betania reservoir receives an accumulated river discharge inflow of approximately 12,770 Mm3/year, for an average production of 2000 Gwh/year, resulting in an estimated average production of 0.16 GWh/Mm3. Similarly, the Guavio reservoir receives an accumulated river discharge inflow of approximately 2048 Mm3/year, for an average production of 5500 Gwh/year, resulting in an estimated average production of 2.69 GWh/Mm3. For converting the units of energy production into an economic value, we use the mean electricity value for the residential sector in Colombia in 2019, a value of USD/kWh 0.14 [73], we assume a price volatility of USD/kWh ±0.01 during the simulation period. Moreover, we assume that the hydropower plant managers have perfect information about the energy prices during the forecasting period, meaning that the selling of energy occurs when marginal revenue is higher. Moreover, no forecasts regarding the market behaviour and/or the price volatility are considered, and the price volatility follows a linear trend throughout the simulation period. The results of this analysis are shown in Table 4.

Table 4.
Economic scenario analysis of the potential economic benefits of using SCHT with respect to climatological average forecasts.
As shown in Table 4, the scenario-based analysis of the potential economic benefits of using SCHT can improve seasonal forecast energy production with respect the climatological average. In fact, considering the designed scenario, the potential economic benefits of using SCHT can go up to approximately half a million US dollars for a combined forecast of a six month forecasting scenario for the Betania hydropower plant, and a three month forecasting scenario for the Guavio hydropower plant, given that the hydropower plant managers have access to perfect information regarding the future electricity values. Due to the latter, the potential economic benefits of SCHT are likely overestimated if compared against a real-life case situation. In any case, SCHT can increase the accuracy in forecasting the accumulated river discharge inflow to the reservoirs of the studies hydropower plants, information that is valuable for hydropower plants’ managers.
4. Conclusions
The Smart Climate Hydropower Tool (SCHT) is an innovative web-cloud-based service that implements a set of data-driven methods for river discharge forecast relying on a set of machine learning techniques. It is intended to better inform decision-makers in the hydropower energy production processes. The SCHT provides make use of historical and operational seasonal forecasts of hydrometeorological data to predict the accumulated seasonal river discharge into the reservoir of hydropower plants. The information generated by SCHT is relevant for both water resources management and financial planning. SCHT has been designed to be flexible and replicable, using data potentially available worldwide to foster application to virtually any hydropower plant, and is targeted to technicians and market traders. Here, we tested the applicability of SCHT as a climate service in two case study areas, namely the hydropower plants of Betania and Guavio, in Colombia, with annual energy production of 5500 and 2000 Gwh.
The results obtained from the implementation of SCHT suggest that the utilisation of machine learning algorithms that make use of complex and/or recurrent architecture provide the best temporal dynamic forecasting accuracy of the accumulated river discharge inflow to considered case studies. Moreover, the autoregressive neural networks, the long short-term memory, and the deep-learning models are all capable of proving better results than both the climatological average, persistence, and multiple linear regression for both case study areas and for the forecast horizons considered in this study. In fact, the improvement provided by SCHT with respect to the climatological average ranges from 6 to 14% for the accumulated inflow to the case study hydropower plants, while a perfect forecast ranges from 12 to 18%. In this sense, the results of SCHT can provide useful information for water resource managers in better planning the allocation of water resources for different users (e.g., irrigation for agriculture, human consumption, and generation of electricity) and hydropower plant managers (e.g., when negotiating power purchase contracts in a competitive energy market). Indeed, the scenario-based economic analysis of the potential economic benefits of using SCHT with respect to climatological average forecasts demonstrate that, for a considered forecasting period of 6 month and for the case studies covered in this study, the economic benefits of using SCHT are estimated around a figure of USD 750 per mM3 of increased accuracy in forecasting the accumulated inflow to the considered reservoirs.
Finally, we provide some recommendations for further developments in this field of research. Further studies could enhance the proposed methodology by considering a modelling chain for forecasting the water consumption for different uses during the forecast horizons, thus providing a better picture of the overall water balance of the reservoirs and enabling a better planning of the utilisation of water resources. Moreover, the incorporation of hydrological forecasts, groundwater dynamics, and the influence of the El Niño phenomena could also lead to better simulation results, particularly in what pertains to the longer horizon forecasts. Finally, SCHT methodology could be enhanced by incorporating an economic forecasting system of electricity prices in a competitive energy market, thus providing a more comprehensive and potentially more accurate picture of the possible economic gains from the utilisation of a similar climate service.
Author Contributions
A.H.E.: conceptualisation, methodology, validation, formal analysis, data curation, writing—original draft preparation, and writing—review and editing; F.L.: conceptualisation, writing—original draft preparation, and writing—review and editing; P.M. (Paolo Mazzoli): conceptualisation, methodology, validation, data curation, writing—review and editing, and supervision; S.B.: conceptualisation, methodology, and writing—review and editing; D.B.: conceptualisation and data curation; V.L.: conceptualisation and data curation; J.M.: conceptualisation, writing—review and editing, and supervision; P.M. (Paola Mercogliano): conceptualisation and data curation; F.d.V.: conceptualisation and data curation. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union’s Horizon 2020 research and innovation programme under the Gran Agreement No 730482 in the framework of CLARA Project.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Jacobson, M.Z. Review of solutions to global warming, air pollution, and energy security. Energy Environ. Sci. 2009, 2, 148–173. [Google Scholar] [CrossRef]
- Tahara, K.; Kojima, T.; Inaba, A. Evaluation of CO2 payback time of power plants by LCA. Energy Convers. Manag. 1997, 38 (Suppl. 1), 615–620. [Google Scholar] [CrossRef]
- Yüksel, I. Hydropower for sustainable water and energy development. Renew. Sustain. Energy Rev. 2010, 14, 462–469. [Google Scholar] [CrossRef]
- Edenhofer, O. Technical summary. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part A: Global and Sectoral Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Field, C.B., Barros, V.R., Dokken, D.J., Mach, K.J., Mastrandrea, M.D., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 35–94. [Google Scholar]
- Berga, L. The role of hydropower in climate change mitigation and adaptation: A review. Engineering 2016, 2, 313–318. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2019: Executive Summary. Available online: https://www.iea.org/reports/world-energy-outlook-2019 (accessed on 30 November 2020).
- Gernaat, D.E.H.J.; Bogaart, P.W.; van Vuuren, D.P.; Biemans, H.; Niessink, R. High-resolution assessment of global technical and economic hydropower potential. Nat. Energy 2017, 2, 821–828. [Google Scholar] [CrossRef]
- Zhou, Y.; Hejazi, M.; Smith, S.; Edmons, J.; Li, H.; Clarke, L.; Calvin, K.; Thomson, A. A comprehensive view of global potential for hydro-generated electricity. Energy Environ. Sci. 2015, 8, 2622–2633. [Google Scholar] [CrossRef]
- IRENA. Renewable Energy Techlogies: Cost Analysis Series, Hydropower. 2012. Available online: https://www.irena.org/publications/2012/Jun/Renewable-Energy-Cost-Analysis---Hydropower (accessed on 30 November 2020).
- Schaeffer, R.; Szklo, A.S.; de Lucena, A.F.; Borba, B.S.; Nogueira, L.P.; Fleming, F.P.; Troccoli, A.; Harrison, M.; Boulahya, M.S. Energy sector vulnerability to climate change: A review. Energy 2012, 38, 1–12. [Google Scholar] [CrossRef]
- Li, H.; Luo, L.; Wood, E.F.; Schaake, J. The role of initial conditions and forcing uncertainties in seasonal hydrologic forecasting. J. Geophys. Res. Atmos. 2009, 114, 1–10. [Google Scholar] [CrossRef]
- Arias, M.E.; Farinosi, F.; Lee, E.; Livino, A.; Briscoe, J.; Moorcroft, P.R. Impacts of climate change and deforestation on hydropower planning in the Brazilian Amazon. Nat. Sustain. 2020, 3, 430–436. [Google Scholar] [CrossRef]
- Sohoulande, C.D.D. Streamflow drought interpreted using SWAT model simulations of past and future hydrologic scenarios: Application to neches and trinity river basins, Texas. J. Hydrol. Eng. 2019, 24, 5019024. [Google Scholar] [CrossRef]
- Turner, S.W.D.; Bennett, J.C.; Robertson, D.E.; Galelli, S. Complex relationship between seasonal streamflow forecast skill and value in reservoir operations. Hydrol. Earth Syst. Sci. 2017, 21, 4841–4859. [Google Scholar] [CrossRef]
- Zapata, S.; Castaneda, M.; Garces, E.; Franco, C.J.; Dyner, I. Assessing security of supply in a largely hydroelectricity-based system: The Colombian case. Energy 2018, 156, 444–457. [Google Scholar] [CrossRef]
- Ahmad, S.K.; Hossain, F. Maximizing energy production from hydropower dams using short-term weather forecasts. Renew. Energy 2020, 146, 560–1577. [Google Scholar] [CrossRef]
- Gubler, S.; Sedlmeier, K.; Bhend, J.; Avalos, G.; Coelho, C.A.S.; Escajadillo, Y.; Jacques-Coper, M.; Martinez, R.; Schwierz, C.; de Skansi, M. Assessment of ECMWF SEAS5 seasonal forecast performance over South America. Weather Forecast 2020, 35, 561–584. [Google Scholar] [CrossRef]
- Block, P. Tailoring seasonal climate forecasts for hydropower operations. Hydrol. Earth Syst. Sci. 2011, 15, 1355–1368. [Google Scholar] [CrossRef]
- Bazile, R.; Boucher, M.A.; Perreault, L.; Leconte, R. Verification of ECMWF System 4 for seasonal hydrological forecasting in a northern climate. Hydrol. Earth Syst. Sci. 2017, 21, 5747–5762. [Google Scholar] [CrossRef]
- Anghileri, D.; Monhart, S.; Zhou, C.; Bogner, K.; Castelletti, A.; Burlando, P.; Zappa, M. The value of subseasonal hydrometeorological forecasts to hydropower operations: How much does preprocessing matter? Water Resour. Res. 2019, 55, 10159–10178. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal drought prediction: Advances, challenges, and future prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- Li, S.; Robertson, A.W. Evaluation of submonthly precipitation forecast skill from global ensemble prediction systems. Mon. Weather Rev. 2015, 143, 2871–2889. [Google Scholar] [CrossRef]
- Vitart, F. Madden—Julian Oscillation prediction and teleconnections in the S2S database. Q. J. R. Meteorol. Soc. 2017, 143, 2210–2220. [Google Scholar] [CrossRef]
- Yuan, X.; Roundy, J.K.; Wood, E.F.; Sheffield, J. Seasonal forecasting of global hydrologic extremes: System development and evaluation over GEWEX basins. Bull. Am. Meteorol. Soc. 2015, 96, 1895–1912. [Google Scholar] [CrossRef]
- Fan, F.M.; Pontes, P.R.M.; Buarque, D.C.; Collischonn, W. Evaluation of upper Uruguay river basin (Brazil) operational flood forecasts. RBRH 2017, 22. [Google Scholar] [CrossRef][Green Version]
- Long, Y.; Wang, H.; Jiang, C.; Ling, S. Seasonal inflow forecasts using gridded precipitation and soil moisture information: Implications for reservoir operation. Water Resour. Manag. 2019, 33, 3743–3757. [Google Scholar] [CrossRef]
- Morss, R.E.; Demuth, J.L.; Lazo, J.K. Communicating uncertainty in weather forecasts: A survey of the U.S. public. Weather Forecast 2008, 23, 974–991. [Google Scholar] [CrossRef]
- Doblas-Reyes, F.J.; Weisheimer, A.; Deque, M.; Keenlyside, N.; McVean, M.; Murphy, J.M.; Rogel, P.; Smith, D.; Palmer, T.N. Addressing model uncertainty in seasonal and annual dynamical ensemble forecasts. Q. J. R. Meteorol. Soc. 2009, 135, 1538–1559. [Google Scholar] [CrossRef]
- Wang, E.; Zhang, Y.; Luo, J.; Chiew, F.H.S.; Wang, Q.J. Monthly and seasonal streamflow forecasts using rainfall-runoff modeling and historical weather data. Water Resour. Res. 2011, 47, 1–13. [Google Scholar] [CrossRef]
- Teweldebrhan, A.; Burkhart, J.; Schuler, T.; Hjorth-Jensen, M. Coupled machine learning and the limits of acceptability approach applied in parameter identification for a distributed hydrological model. Hydrol. Earth Syst. Sci. Discuss. 2019, 24, 1–25. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Huppert, D.; Lettenmaier, D.P. Economic value of long-lead streamflow forecasts for columbia river hydropower. J. Water Resour. Plan. Manag. 2002, 128, 91–101. [Google Scholar] [CrossRef]
- Poff, N.L.; Tokar, S.; Johnson, P. Stream hydrological and ecological responses to climate change assessed with an artificial neural network. Limnol. Oceanogr. 1996, 41, 857–863. [Google Scholar] [CrossRef]
- Campolo, M.; Soldati, A.; Andreussi, P. Artificial neural network approach to flood forecasting in the River Arno. Hydrol. Sci. J. 2002, 48, 381–398. [Google Scholar] [CrossRef]
- Mutlu, E.; Chaubey, I.; Hexmoor, H.; Bajwa, S.G. Comparison of artificial neural network models for hydrologic predictions at multiple gauging stations in an agricultural watershed. Hydrol. Process. 2008, 22, 5097–5106. [Google Scholar] [CrossRef]
- Essenfelder, A.H. Short-Term Forecast of a River Flow Using Artificial Neural Networks; Federal University of Paraná: Parana, Brazil, 2009. [Google Scholar]
- Zhang, X.; Liang, F.; Yu, B.; Zong, Z. Explicitly integrating parameter, input, and structure uncertainties into Bayesian Neural Networks for probabilistic hydrologic forecasting. J. Hydrol. 2011, 409, 696–709. [Google Scholar] [CrossRef]
- Callegari, M.; Mazzoli, P.; De Gregorio, L.; Notarnicola, C.; Pasolli, L.; Petitta, M.; Pistocchi, A. Seasonal river discharge forecasting using support vector regression: A case study in the Italian Alps. Water 2015, 7, 2494–2515. [Google Scholar] [CrossRef]
- De Gregorio, L.; Callegari, M.; Mazzoli, P.; Bagli, S.; Broccoli, D.; Pistocchi, A.; Notarnicola, C. Operational river discharge forecasting with support vector regression technique applied to alpine catchments: Results, advantages, limits and lesson learned. Water Resour. Manag. 2018, 32, 229–242. [Google Scholar] [CrossRef]
- Essenfelder, A.H.; Giupponi, C. A coupled hydrologic-machine learning modelling framework to support hydrologic modelling in river basins under Interbasin Water Transfer regimes. Environ. Model. Softw. 2020, 131, 104779. [Google Scholar] [CrossRef]
- Johnson, S.J.; Stockdale, T.N.; Ferranti, L.; Balmaseda, M.A.; Molteni, F.; Magnusson, L.; Tietsche, S.; Decremer, D.; Weisheimer, A.; Balsamo, G.; et al. SEAS5: The new ECMWF seasonal forecast system. Geosci. Model Dev. 2019, 12, 1087–1117. [Google Scholar] [CrossRef]
- MINTIC. Caudales Medios Mensuales. Ministerio de Tecnologías de la Información y las Comunicaciones, 2020. Available online: https://www.datos.gov.co/Ambiente-y-Desarrollo-Sostenible/Caudales-Medios-Mensuales/45cv-fhv9 (accessed on 14 July 2019).
- Haylock, M.R.; Hofstra, N.; Klein Tank, A.M.G.; Klok, E.J.; Jones, P.D.; New, M. A European daily high-resolution gridded data set of surface temperature and precipitation for 1950–2006. J. Geophys. Res. Atmos. 2008, 113. [Google Scholar] [CrossRef]
- Gedeon, T.D. Data mining of inputs: Analysing magnitude and functional measures. Int. J. Neural Syst. 1997, 8, 209–218. [Google Scholar] [CrossRef]
- Bergmeir, C.; Hyndman, R.J.; Koo, B. A note on the validity of cross-validation for evaluating autoregressive time series prediction. Comput. Stat. Data Anal. 2018, 120, 70–83. [Google Scholar] [CrossRef]
- Sohoulande, C.D.D.; Martin, J.; Szogi, A.; Stone, K. Climate-driven prediction of land water storage anomalies: An outlook for water resources monitoring across the conterminous United States. J. Hydrol. 2020, 588, 125053. [Google Scholar] [CrossRef]
- Krysanova, V.; Donnelly, C.; Gelfan, A.; Gerten, D.; Arheimer, B.; Hattermann, F.; Kundzewicz, Z.W. How the performance of hydrological models relates to credibility of projections under climate change. Hydrol. Sci. J. 2018, 63, 696–720. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Binger, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Rasmussen, C.E. Gaussian processes in machine learning. In Revised Lectures, Proceedings of the Advanced Lectures on Machine Learning: ML Summer Schools, Canberra, Australia, 2–14 February 2003, Tübingen, Germany, 4–16 August 2003; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. [Google Scholar]
- Kim, H.-C.; Lee, J. Clustering based on gaussian processes. Neural Comput. 2017, 19, 3088–3107. [Google Scholar] [CrossRef] [PubMed]
- Karatzoglou, A.; Smola, A.; Hornik, K.; Zeileis, A. kernlab—An {S4} Package for Kernel Methods in {R.}. J. Stat. Softw. 2004, 11, 1–20. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Bengio, Y.; Simard, P.; Frasconi, P. Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Net. 2014, 5, 157. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of long short term memory networks and the hydrological model in runoff simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef]
- Allaire, J.J.; Tang, Y. Tensorflow: R Interface to ‘TensorFlow’. 2020. Available online: https://tensorflow.rstudio.com/ (accessed on 30 November 2020).
- Allaire, J.J.; Chollet, F. “keras: R Interface to ‘Keras’”. 2020. Available online: https://github.com/rstudio/keras (accessed on 30 November 2020).
- Ramachandran, P.; Zoph, B.; Le, Q.V. Swish: A self-gated activation function. Neural and Evolutionary Computing. arXiv 2017, arXiv:1710.05941v1. [Google Scholar]
- Heermann, P.D.; Khazenie, N. Classification of multispectral remote sensing data using a back-propagation neural network. IEEE Trans. Geosci. Remote Sens. 1992, 30, 81–88. [Google Scholar] [CrossRef]
- Giacinto, G.; Roli, F. Design of effective neural network ensembles for image classification purposes. Image Vis. Comput. 2001, 19, 699–707. [Google Scholar] [CrossRef]
- Essenfelder, A.H. Climate Change and Watershed Planning: Understanding the Related Impacts and Risks; Universita’ Ca’ Foscari Venezia: Venezia, Italy, 2017. [Google Scholar]
- Hsieh, W.W. Machine Learning Methods in the Environmental Sciences: Neural Networks and Kernels; Cambridge University Press: New York, NY, USA, 2009. [Google Scholar]
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Han, J. Application of Artificial Neural Networks for Flood Warning Systems; North Carolina State University: Raleigh, NC, USA, 2002. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Sit, M.; Demiray, B.Z.; Xiang, Z.; Ewing, G.J.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020. [Google Scholar] [CrossRef]
- LeDell, E.; Gill, N.; Aiello, S.; Fu, A.; Candel, A.; Click, C.; Kraljevic, T.; Nykodym, T.; Aboyoun, P.; Kurka, M.; et al. h2o: R Interface for the ‘H2O’ Scalable Machine Learning Platform. 2020. Available online: https://rdrr.io/cran/h2o/ (accessed on 30 November 2020).
- Zeiler, M.D. ADADELTA: An Adaptive Learning Rate Method. arXiv 2012, arXiv:1212.5701. [Google Scholar]
- Rudnick, H.; Velasquez, C. Learning from developing country power market experiences: The Case of Colombia. World Bank Policy Res. Work. Pap. 2019, 8771. [Google Scholar] [CrossRef]
- Morcillo, J.D.; Angulo, F.; Franco, C.J. Analyzing the hydroelectricity variability on power markets from a system dynamics and dynamic systems perspective: Seasonality and ENSO phenomenon. Energies 2020, 13, 2381. [Google Scholar] [CrossRef]
- Larosa, F.; Mysiak, J. Mapping the Landscape of Climate Services. Available online: https://iopscience.iop.org/article/10.1088/1748-9326/ab304d (accessed on 30 November 2020).
- McRae, S.; Wolak, F. Retail electricity pricing in Colombia and the efficient deployment of distributed Generation. Business 2019. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).