Estimation of PM2.5 Concentrations in New York State: Understanding the Influence of Vertical Mixing on Surface PM2.5 Using Machine Learning
Abstract
1. Introduction
2. Experiments
2.1. Datasets
2.1.1. Surface PM2.5 Observations
2.1.2. Meteorological Predictors
2.1.3. Aerosol Predictors
2.1.4. Geographic Predictors
2.1.5. Vertical Predictors
2.1.6. Data Processing
2.2. Model Configuration
- MLR model with set 1 predictors (MLR-1);
- MLR model and set 2 predictors (MLR-2);
- ANN model with set 1 predictors (ANN-1);
- ANN model with set 2 predictors (ANN-2).
2.3. Statistical Analysis
3. Results and Discussion
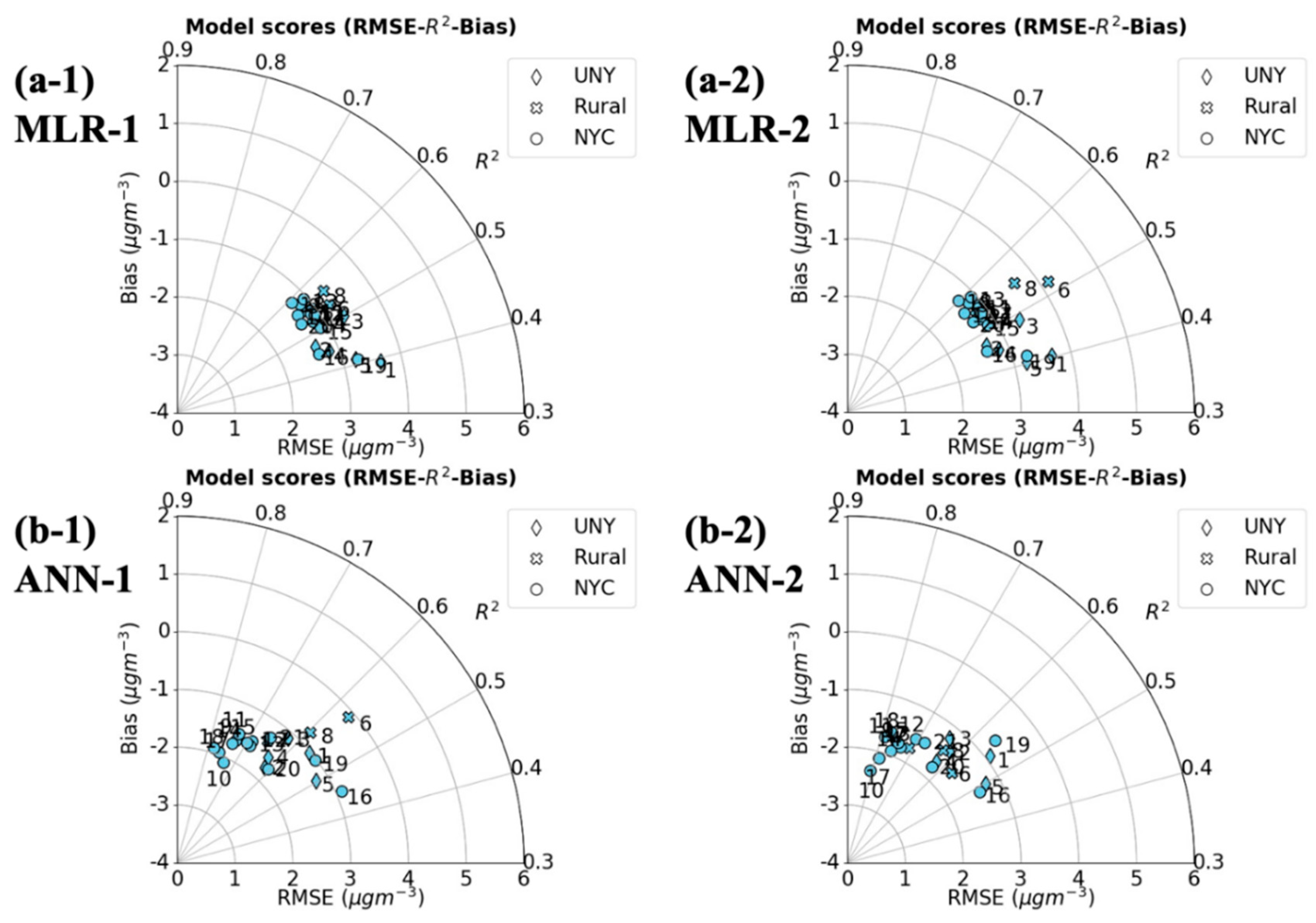
3.1. Model Performance
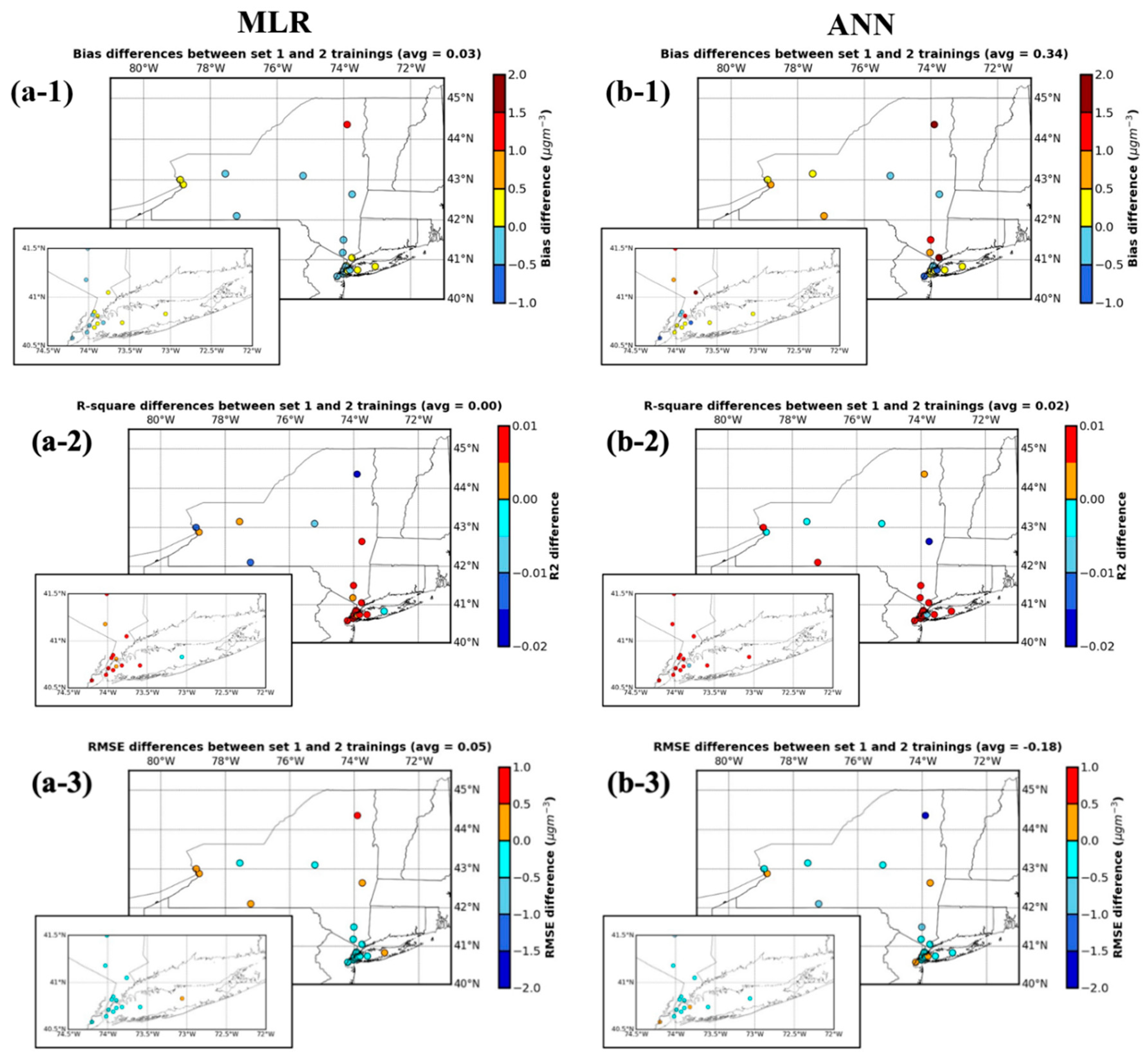
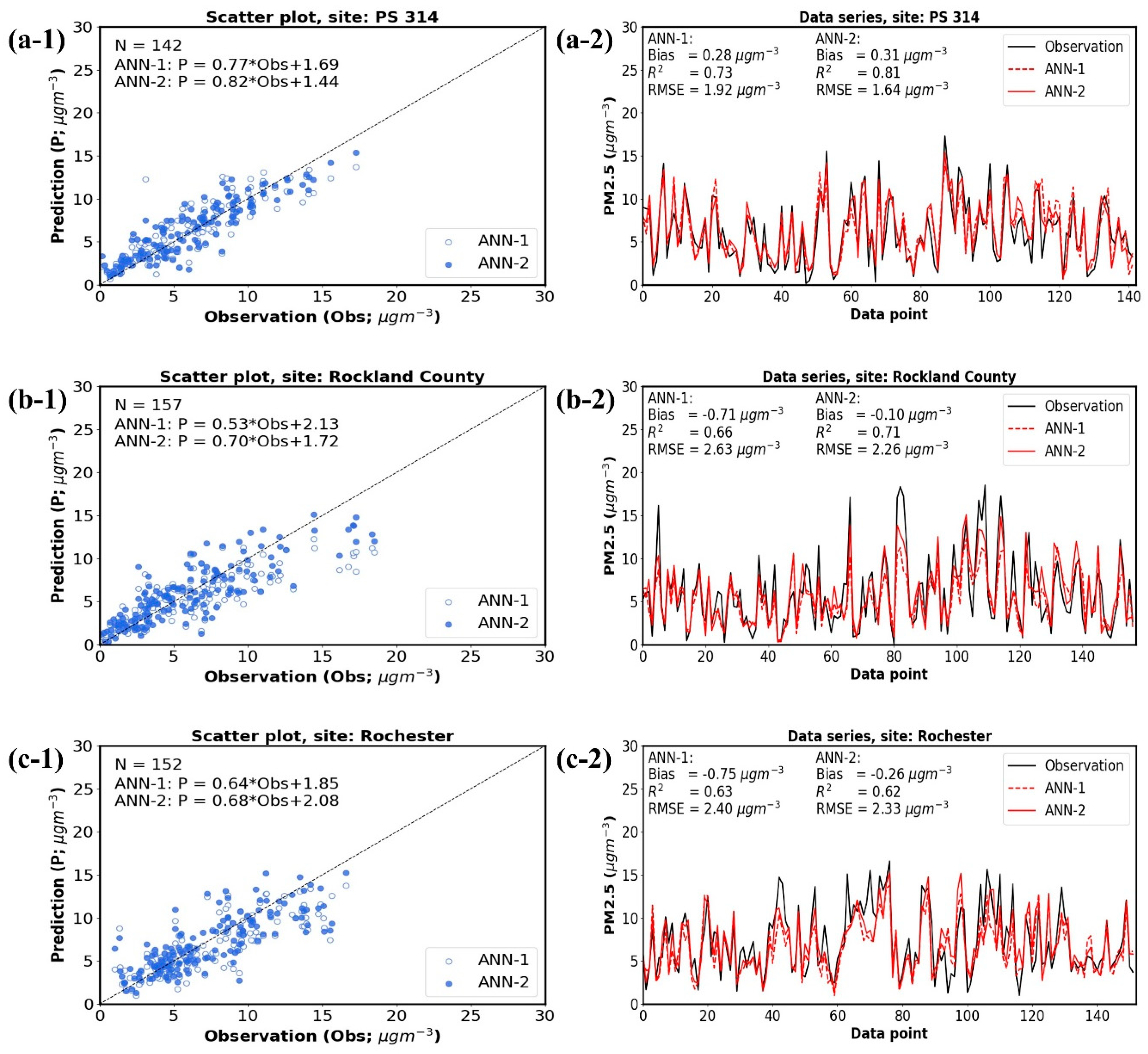
3.2. The Site-Variations of Model Performance
3.3. The Contributions of Predictors to Surface PM2.5 Concentrations
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
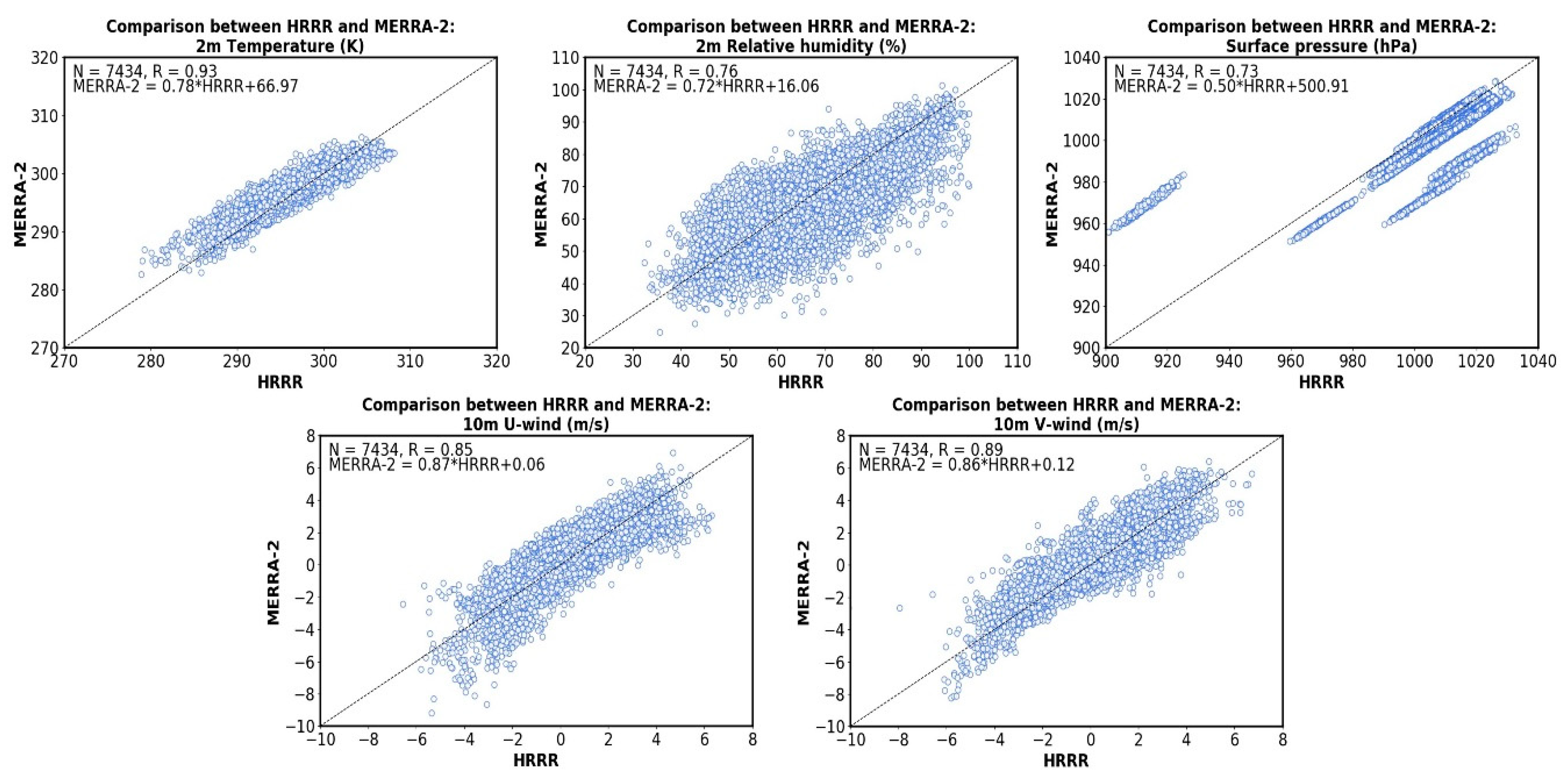
Appendix B
| U | V | RH | T | PBLH | PS | MERRA2_PM | Lat | Lon | VI | |
|---|---|---|---|---|---|---|---|---|---|---|
| U | ||||||||||
| V | −0.04 | |||||||||
| RH | −0.22 | 0.30 | ||||||||
| T | 0.17 | 0.24 | −0.14 | |||||||
| PBLH | 0.34 | −0.32 | −0.66 | 0.21 | ||||||
| PS | −0.23 | −0.10 | −0.19 | 0.32 | 0.08 | |||||
| MERRA2_PM | −0.03 | 0.26 | 0.19 | 0.39 | −0.12 | 0.16 | ||||
| Lat | 0.17 | 0.04 | 0.14 | −0.35 | −0.05 | −0.70 | −0.27 | |||
| Lon | −0.15 | −0.05 | −0.02 | 0.13 | 0.00 | 0.25 | 0.15 | −0.60 | ||
| VI | 0.10 | 0.00 | 0.11 | −0.20 | 0.04 | −0.54 | −0.18 | 0.62 | −0.21 | |
| Alt | 0.15 | 0.07 | 0.16 | −0.38 | −0.06 | −0.92 | −0.23 | 0.70 | −0.40 | 0.63 |
| Weekday | −0.01 | 0.08 | 0.03 | −0.03 | 0.00 | −0.03 | 0.08 | −0.01 | 0.01 | 0.00 |
| H-VWS | 0.14 | −0.26 | −0.18 | −0.32 | 0.22 | −0.02 | −0.13 | 0.03 | 0.01 | 0.02 |
| M-VWS | 0.18 | −0.22 | −0.19 | −0.20 | 0.20 | −0.08 | −0.24 | 0.07 | −0.04 | 0.04 |
| L-VWS | 0.14 | 0.35 | 0.25 | 0.06 | −0.28 | 0.02 | 0.16 | −0.09 | 0.07 | −0.11 |
| W_avg | 0.15 | 0.02 | −0.04 | 0.14 | 0.05 | 0.29 | 0.09 | −0.23 | −0.07 | −0.21 |
| AP_ratio | −0.01 | 0.00 | 0.02 | 0.00 | −0.01 | 0.00 | 0.04 | 0.00 | −0.01 | 0.00 |
| AOD | −0.08 | 0.24 | 0.27 | 0.31 | −0.10 | 0.15 | 0.61 | −0.30 | 0.20 | −0.26 |
| Obs_PM | 0.06 | 0.38 | 0.19 | 0.49 | −0.16 | 0.04 | 0.57 | −0.05 | −0.05 | −0.12 |
| Alt | Weekday | H-VWS | M-VWS | L-VWS | W_avg | AP_ratio | AOD | |||
| U | ||||||||||
| V | ||||||||||
| RH | ||||||||||
| T | ||||||||||
| PBLH | ||||||||||
| PS | ||||||||||
| MERR2A_P | ||||||||||
| M | ||||||||||
| Lat | ||||||||||
| Lon | ||||||||||
| VI | ||||||||||
| Alt | ||||||||||
| Weekday | 0.00 | |||||||||
| H-VWS | 0.01 | −0.01 | ||||||||
| M-VWS | 0.06 | −0.05 | 0.22 | |||||||
| L-VWS | −0.11 | −0.04 | −0.11 | 0.08 | ||||||
| W_avg | −0.27 | 0.01 | −0.01 | 0.04 | 0.21 | |||||
| AP_ratio | 0.00 | −0.01 | 0.01 | 0.02 | 0.01 | 0.00 | ||||
| AOD | −0.23 | 0.09 | −0.15 | −0.20 | 0.14 | 0.07 | 0.00 | |||
| obs_PM | −0.09 | 0.02 | −0.22 | −0.26 | 0.13 | 0.06 | 0.03 | 0.40 |
Appendix C
| Label | Name | ID Number | Bias (µg m−3) | R-Squared | RMSE (µg m−3) | |||
|---|---|---|---|---|---|---|---|---|
| Set 1 | Set 2 | Set 1 | Set 2 | Set 1 | Set 2 | |||
| 1 | Albany | 360010005 | −1.93 | −2.01 | 0.39 | 0.40 | 3.63 | 3.66 |
| 2 | Buffalo | 360290005 | 0.37 | 0.45 | 0.47 | 0.47 | 2.64 | 2.66 |
| 3 | Tonawanda II | 360291014 | 0.67 | 0.72 | 0.50 | 0.49 | 3.33 | 3.37 |
| 4 | Rochester | 360551007 | −0.51 | −0.53 | 0.45 | 0.45 | 2.83 | 2.83 |
| 5 | Utica | 360652001 | 1.19 | 1.12 | 0.41 | 0.40 | 3.22 | 3.21 |
| 6 | Whiteface Mountain | 360310003 | 2.36 | 3.47 | 0.54 | 0.52 | 3.22 | 4.13 |
| 7 | Rockland County | 360870005 | −0.18 | −0.19 | 0.55 | 0.56 | 2.83 | 2.82 |
| 8 | Pinnacle State Park | 361010003 | −2.64 | −3.06 | 0.56 | 0.55 | 3.29 | 3.65 |
| 9 | Bronx | 360050112 | 0.32 | 0.32 | 0.58 | 0.58 | 2.83 | 2.82 |
| 10 | PS 314 | 360470052 | 1.11 | 1.08 | 0.56 | 0.57 | 2.68 | 2.65 |
| 11 | PS 274 | 360470118 | 1.08 | 1.09 | 0.55 | 0.56 | 2.95 | 2.93 |
| 12 | Esienhower Park | 360590005 | 0.49 | 0.52 | 0.55 | 0.56 | 2.91 | 2.89 |
| 13 | IS 143 | 360610115 | −0.93 | −0.92 | 0.58 | 0.59 | 2.94 | 2.92 |
| 14 | Division St. | 360610134 | −0.40 | −0.41 | 0.52 | 0.53 | 2.83 | 2.80 |
| 15 | CCNY | 360610135 | −0.64 | −0.64 | 0.50 | 0.51 | 2.88 | 2.86 |
| 16 | Newburgh | 360710002 | 0.69 | 0.65 | 0.45 | 0.46 | 2.65 | 2.63 |
| 17 | Maspeth | 360810120 | 0.84 | 0.84 | 0.54 | 0.55 | 2.88 | 2.87 |
| 18 | Queens | 360810124 | −0.74 | −0.76 | 0.59 | 0.60 | 2.74 | 2.72 |
| 19 | FKILL | 360850111 | −1.06 | −1.06 | 0.41 | 0.42 | 3.26 | 3.25 |
| 20 | Holtsville | 361030009 | 1.03 | 1.09 | 0.54 | 0.54 | 2.64 | 2.67 |
| 21 | White Plain | 361192004 | −0.59 | −0.52 | 0.54 | 0.54 | 2.91 | 2.88 |
Appendix D
| Label | Name | ID Number | Bias (µg m−3) | R-Squared | RMSE (µg m−3) | |||
|---|---|---|---|---|---|---|---|---|
| Set 1 | Set 2 | Set 1 | Set 2 | Set 1 | Set 2 | |||
| 1 | Albany | 360010005 | −1.42 | −1.52 | 0.57 | 0.55 | 2.97 | 3.07 |
| 2 | Buffalo | 360290005 | −0.12 | 0.66 | 0.62 | 0.62 | 2.24 | 2.61 |
| 3 | Tonawanda II | 360291014 | 0.23 | 0.37 | 0.62 | 0.64 | 2.88 | 2.79 |
| 4 | Rochester | 360551007 | −0.75 | −0.26 | 0.63 | 0.62 | 2.40 | 2.33 |
| 5 | Utica | 360652001 | 0.51 | 0.12 | 0.50 | 0.50 | 2.79 | 2.75 |
| 6 | Whiteface Mountain | 360310003 | −2.99 | −1.16 | 0.57 | 0.57 | 3.89 | 2.38 |
| 7 | Rockland County | 360870005 | −0.71 | −0.10 | 0.66 | 0.71 | 2.63 | 2.26 |
| 8 | Pinnacle State Park | 361010003 | −2.60 | −1.80 | 0.60 | 0.63 | 3.22 | 2.55 |
| 9 | Bronx | 360050112 | −0.60 | 0.72 | 0.73 | 0.75 | 2.35 | 2.24 |
| 10 | PS 314 | 360470052 | 0.28 | 0.31 | 0.73 | 0.81 | 1.92 | 1.64 |
| 11 | PS 274 | 360470118 | 1.25 | 1.28 | 0.73 | 0.79 | 2.47 | 2.27 |
| 12 | Esienhower Park | 360590005 | 0.21 | 0.34 | 0.69 | 0.71 | 2.47 | 2.44 |
| 13 | IS 143 | 360610115 | 0.13 | −0.16 | 0.69 | 0.74 | 2.38 | 2.20 |
| 14 | Division St. | 360610134 | −0.87 | −0.56 | 0.74 | 0.76 | 2.27 | 2.07 |
| 15 | CCNY | 360610135 | −0.98 | −1.01 | 0.70 | 0.75 | 2.40 | 2.25 |
| 16 | Newburgh | 360710002 | −1.74 | −0.70 | 0.46 | 0.49 | 3.10 | 2.59 |
| 17 | Maspeth | 360810120 | 0.14 | 0.14 | 0.76 | 0.79 | 2.05 | 1.89 |
| 18 | Queens | 360810124 | −0.83 | −1.36 | 0.78 | 0.78 | 2.09 | 2.38 |
| 19 | FKILL | 360850111 | −1.15 | −2.00 | 0.54 | 0.57 | 2.97 | 3.32 |
| 20 | Holtsville | 361030009 | −0.39 | −0.21 | 0.61 | 0.62 | 2.25 | 2.21 |
| 21 | White Plain | 361192004 | −0.88 | 0.73 | 0.66 | 0.68 | 2.71 | 2.46 |
Appendix E
| Site | U | V | RH | T | PBLH (10−3) | PS (10−4) | MERRA2_PM | Lat | Lon | VI | Alt |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MLR-1 | |||||||||||
| PS 314 | 0.088 | 0.246 | 0.012 | 0.437 | −1.587 | 3.611 | 0.277 | 1.025 | 0.068 | −5.370 | 0.007 |
| Rochester | 0.101 | 0.248 | 0.009 | 0.424 | −1.556 | 3.568 | 0.289 | 0.982 | 0.075 | −4.764 | 0.007 |
| Rockland County | 0.114 | 0.236 | 0.012 | 0.431 | −1.586 | 3.444 | 0.277 | 1.018 | 0.055 | −4.851 | 0.006 |
| MLR-2 | |||||||||||
| PS 314 | 0.109 | 0.264 | 0.012 | 0.437 | −1.678 | 3.269 | 0.271 | 1.005 | 0.063 | −5.298 | 0.006 |
| Rochester | 0.122 | 0.271 | 0.010 | 0.427 | −1.689 | 3.239 | 0.283 | 0.959 | 0.071 | −4.715 | 0.006 |
| Rockland County | 0.137 | 0.257 | 0.013 | 0.430 | −1.690 | 3.040 | 0.272 | 0.997 | 0.052 | −4.790 | 0.006 |
| Site | Weekday | AOD | H-VWS | M-VWS | L-VWS | W_avg | AP_ratio | ||||
| MLR-1 | |||||||||||
| PS 314 | −0.008 | 1.342 | |||||||||
| Rochester | −0.008 | 1.062 | |||||||||
| Rockland County | −0.004 | 1.111 | |||||||||
| MLR-2 | |||||||||||
| PS 314 | −0.015 | 1.357 | 91.666 | −118.698 | −83.530 | 0.625 | 0.009 | ||||
| Rochester | −0.015 | 1.080 | 105.872 | −105.617 | −102.905 | 0.452 | 0.007 | ||||
| Rockland County | −0.012 | 1.125 | 88.544 | −117.948 | −100.918 | 0.945 | 0.010 | ||||
References
- Pope, I.C.; Burnett, R.T.; Thun, M.J.; Calle, E.E.; Krewski, D.; Ito, K.; Thurston, G.D. Lung cancer, cardiopulmonary mortality, and long-term exposure to fine particulate air pollution. J. Am. Med. Assoc. 2002, 287, 1132–1141. [Google Scholar] [CrossRef] [PubMed]
- Pope, C.A.; Burnett, R.T., III; Thurston, G.D.; Thun, M.J.; Calle, E.E.; Krewski, D.; Godleski, J.J. Cardiovascular Mortality and Long-Term Exposure to Particulate Air Pollution: Epidemiological Evidence of General Pathophysiological Pathways of Disease. Circulation 2004, 1, 71–77. [Google Scholar] [CrossRef] [PubMed]
- Apte, J.S.; Marshall, J.D.; Cohen, A.J.; Brauer, M. Addressing Global Mortality from Ambient PM2.5. Environ. Sci. Technol. 2015, 49, 8057–8066. [Google Scholar] [CrossRef] [PubMed]
- Franklin, M.; Zeka, A.; Schwartz, J. Association between PM2.5 and all-cause and specific-cause mortality in 27 US communities. J. Expo. Sci. Environ. Epidemiol. 2007, 17, 279–287. [Google Scholar] [CrossRef]
- Behera, S.N.; Sharma, M. Reconstructing Primary and Secondary Components of PM2.5 Composition for an Urban Atmosphere. Aerosol Sci. Technol. 2010, 44, 983–992. [Google Scholar] [CrossRef]
- Edney, E.O.; Kleindienst, T.E.; Jaoui, M.; Lewandowski, M.; Offenberg, J.H.; Wang, W.; Claeys, M. Formation of 2-methyltetrols and 2-methylglyceric acid in secondary organic aerosol from laboratory irradiated isoprene/NOX/SO2/air mixtures and their detection in ambient PM2.5 samples collected in the eastern United States. Atmos. Environ. 2005, 39, 5281–5289. [Google Scholar] [CrossRef]
- Lonati, G.; Ozgen, S.; Giugliano, M. Primary and secondary carbonaceous species in PM2.5 samples in Milan (Italy). Atmos. Environ. 2007, 41, 4599–4610. [Google Scholar] [CrossRef]
- Wang, Y.; Zhuang, G.; Tang, A.; Yuan, H.; Sun, Y.; Chen, S.; Zheng, A. The ion chemistry and the source of PM2.5 aerosol in Beijing. Atmos. Environ. 2005, 39, 3771–3784. [Google Scholar] [CrossRef]
- Yu, S.; Mathur, R.; Schere, K.; Kang, D.; Pleim, J.; Young, J.; Tong, D.; Pouliot, G.; McKeen, S.A.; Rao, S.T. Evaluation of real-time PM2.5 forecasts and process analysis for PM2.5 formation over the eastern United States using the Eta-CMAQ forecast model during the 2004 ICARTT study. J. Geophys. Res. 2008, 113, D06204. [Google Scholar] [CrossRef]
- Dawson, J.P.; Adams, P.J.; Pandis, S.N. Sensitivity of PM2.5 to climate in the Eastern US: A modeling case study. Atmos. Chem. Phys. 2007, 7, 4295–4309. [Google Scholar] [CrossRef]
- Tai, A.P.K.; Mickley, L.J.; Jacob, D.J. Correlations between fine particulate matter (PM2.5) and meteorological variables in the United States: Implications for the sensitivity of PM2.5 to climate change. Atmos. Environ. 2010, 44, 3976–3984. [Google Scholar] [CrossRef]
- Tran, H.N.Q.; Mölders, N. Investigations on meteorological conditions for elevated PM2.5 in Fairbanks, Alaska. Atmos. Res. 2011, 99, 39–49. [Google Scholar] [CrossRef]
- Wang, J.; Ogawa, S. Effects of Meteorological Conditions on PM2.5 Concentrations in Nagasaki, Japan. Int. J. Environ. Res. Public Health 2015, 12, 9089–9101. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Zhang, X.; Gong, D.; Quan, W.; Zhao, X.; Ma, Z.; Kim, S.-J. Evolution of surface O3 and PM2.5 concentrations and their relationships with meteorological conditions over the last decade in Beijing. Atmos. Environ. 2015, 108, 67–75. [Google Scholar] [CrossRef]
- Chen, Y.; An, J.; Wang, X.; Sun, Y.; Wang, Z.; Duan, J. Observation of wind shear during evening transition and an estimation of submicron aerosol concentrations in Beijing using a Doppler wind lidar. J. Meteor. Res. 2017, 31, 350–362. [Google Scholar] [CrossRef]
- Li, Z.; Guo, J.; Ding, A.; Liao, H.; Liu, J.; Sun, Y.; Wang, T.; Xue, H.; Zhang, H.; Zhu, B. Aerosol and boundary-layer interactions and impact on air quality. Nat. Sci. Rev. 2017, 4, 810–833. [Google Scholar] [CrossRef]
- Yang, Y.; Yim, S.H.L.; Haywood, J.; Osborne, M.; Chan, J.C.S.; Zeng, Z.; Cheng, J.C.H. Characteristics of heavy particulate matter pollution events over Hong Kong and their relationships with vertical wind profiles using high-time-resolution Doppler lidar measurements. J. Geophys. Res. Atmos. 2019, 124, 9609–9623. [Google Scholar] [CrossRef]
- Zhang, J.; Rao, S.T. The Role of Vertical Mixing in the Temporal Evolution of Ground-Level Ozone Concentrations. J. Appl. Meteor. 1999, 38, 1674–1691. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, J.; Yang, Y.; Wang, Y.; Yim, S.H.L. Vertical Wind Shear Modulates Particulate Matter Pollutions: A Perspective from Radar Wind Profiler Observations in Beijing, China. Remote Sens. 2020, 12, 546. [Google Scholar] [CrossRef]
- Hu, J.; Chen, J.; Ying, Q.; Zhang, H. One-year simulation of ozone and particulate matter in China using WRF/CMAQ modeling system. Atmos. Chem. Phys. 2016, 16, 10333–10350. [Google Scholar] [CrossRef]
- Saide, P.E.; Carmichael, G.R.; Spak, S.N.; Gallardo, L.; Osses, A.E.; Mena-Carrasco, M.A.; Pagowski, M. Forecasting urban PM10 and PM2.5 pollution episodes in very stable nocturnal conditions and complex terrain using WRF–Chem CO tracer model. Atmos. Environ. 2011, 45, 2769–2780. [Google Scholar] [CrossRef]
- Eeftens, M.; Beelen, R.; de Hoogh, K.; Bellander, T.; Cesaroni, G.; Cirach, M.; Declercq, C.; Dėdelė, A.; Dons, E.; De Nazelle, A.; et al. Development of Land Use Regression Models for PM2.5, PM2.5 Absorbance, PM10 and PMcoarse in 20 European Study Areas; Results of the ESCAPE Project. Environ. Sci. Technol. 2012, 46, 11195–11205. [Google Scholar] [CrossRef] [PubMed]
- Hoek, G.; Beelen, R.; de Hoogh, K.; Vienneau, D.; Gulliver, J.; Fischer, P.; Briggs, D. A review of land-use regression models to assess spatial variation of outdoor air pollution. Atmos. Environ. 2008, 42, 7561–7578. [Google Scholar] [CrossRef]
- Chu, Y.; Liu, Y.; Li, X.; Liu, Z.; Lu, H.; Lu, Y.; Mao, Z.; Chen, X.; Li, N.; Ren, M.; et al. A Review on Predicting Ground PM2.5 Concentration Using Satellite Aerosol Optical Depth. Atmosphere 2016, 7, 129. [Google Scholar] [CrossRef]
- Liu, Y.; Sarnat, J.A.; Kilaru, V.; Jacob, D.J.; Koutrakis, P. Estimating Ground-Level PM2.5 in the Eastern United States Using Satellite Remote Sensing. Environ. Sci. Technol. 2005, 39, 3269–3278. [Google Scholar] [CrossRef] [PubMed]
- Van Donkelaar, A.; Martin, R.V.; Spurr, R.J.D.; Burnett, R.T. High-Resolution Satellite-Derived PM2.5 from Optimal Estimation and Geographically Weighted Regression over North America. Environ. Sci. Technol. 2015, 49, 10482–10491. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: Multiple regression approach. J. Geophys. Res. 2009, 114, D14205. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S.A. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: 2. A neural network approach. J. Geophys. Res. 2009, 114, D20205. [Google Scholar] [CrossRef]
- Reid, C.E.; Jerrett, M.; Petersen, M.L.; Pfister, G.G.; Morefield, P.E.; Tager, I.B.; Raffuse, S.M.; Balmes, J.R. Spatiotemporal Prediction of Fine Particulate Matter During the 2008 Northern California Wildfires Using Machine Learning. Environ. Sci. Technol. 2015, 49, 3887–3896. [Google Scholar] [CrossRef]
- Engel-Cox, J.A.; Holloman, C.H.; Coutant, B.W.; Hoff, R.M. Qualitative and quantitative evaluation of MODIS satellite sensor data for regional and urban scale air quality. Atmos. Environ. 2004, 38, 2495–2509. [Google Scholar] [CrossRef]
- Weber, S.A.; Engel-Cox, J.A.; Hoff, R.M.; Prados, A.I.; Zhang, H. An improved method for estimating surface fine particle concentrations using seasonally adjusted satellite aerosol optical depth. J. Air Waste Manag. Assoc. 2010, 60, 574–585. [Google Scholar] [CrossRef] [PubMed]
- Xu, Y.; Ho, H.C.; Wong, M.S.; Deng, C.; Shi, Y.; Chan, T.-C.; Knudby, A. Evaluation of machine learning techniques with multiple remote sensing datasets in estimating monthly concentrations of ground-level PM2.5. Environ. Pollut. 2018, 242, 1417–1426. [Google Scholar] [CrossRef] [PubMed]
- Xue, T.; Zheng, Y.; Tong, D.; Zheng, B.; Li, X.; Zhu, T.; Zhang, Q. Spatiotemporal continuous estimates of PM2.5 concentrations in China, 2000–2016: A machine learning method with inputs from satellites, chemical transport model, and ground observations. Environ. Int. 2019, 123, 345–357. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Brauer, M.; Raffuse, S.; Henderson, S.B. Machine Learning Approach to Estimate Hourly Exposure to Fine Particulate Matter for Urban, Rural, and Remote Populations during Wildfire Seasons. Environ. Sci. Technol. 2018, 52, 13239–13249. [Google Scholar] [CrossRef] [PubMed]
- Emami, F.; Masiol, M.; Hopke, P.K. Air pollution at Rochester, NY: Long-term trends and multivariate analysis of upwind SO2 source impacts. Sci. Total Environ. 2018, 612, 1506–1515. [Google Scholar] [CrossRef] [PubMed]
- Rattigan, O.V.; Felton, H.D.; Bae, M.-S.; Schwab, J.J.; Demerjian, K.L. Multi-year hourly PM2.5 carbon measurements in New York: Diurnal, day of week and seasonal patterns. Atmos. Environ. 2010, 44, 2043–2053. [Google Scholar] [CrossRef]
- Rattigan, O.V.; Civerolo, K.L.; Felton, H.D.; Schwab, J.J.; Demerjian, K.L. Long Term Trends in New York: PM2.5 Mass and Particle Components. Aerosol Air Qual. Res. 2015, 16, 191–1203. [Google Scholar] [CrossRef]
- Squizzato, S.; Masiol, M.; Rich, D.Q.; Hopke, P.K. PM2.5 and gaseous pollutants in New York state during 2005–2016: Spatial variability, temporal trends, and economic influences. Atmos. Environ. 2018, 183, 209–224. [Google Scholar] [CrossRef]
- Bari, A.; Dutkiewicz, V.A.; Judd, C.D.; Wilson, L.R.; Luttinger, D.; Husain, L. Regional sources of particulate sulfate, SO2, PM2.5, HCL, HNO3, HONO and NH3 in New York, NY. Atmos. Environ. 2003, 37, 2837–2844. [Google Scholar] [CrossRef]
- Qin, Y.; Kim, E.; Hopke, P.K. The concentrations and sources of PM2.5 in metropolitan New York City. Atmos. Environ. 2006, 40, 312–332. [Google Scholar] [CrossRef]
- DeGaetano, A.T.; Doherty, O.M. Temporal, spatial and meteorological variations in hourly PM2.5 concentration extremes in New York City. Atmos. Environ. 2004, 38, 1547–1558. [Google Scholar] [CrossRef]
- Dutkiewicz, V.A.; Das, M.; Husain, L. The relationship between regional SO2 emissions and downwind aerosol sulfate concentrations in the Northeastern US. Atmos. Environ. 2000, 34, 1821–1832. [Google Scholar] [CrossRef]
- Dutkiewicz, V.A.; Qureshi, S.; Khan, A.R.; Ferraro, V.; Schwab, J.; Demerjian, K.; Husain, L. Sources of fine particulate sulfate in New York. Atmos. Environ. 2004, 38, 3179–3189. [Google Scholar] [CrossRef]
- Dutkiewicz, V.A.; Husain, L.; Roychowdhury, U.K.; Demerjian, K.L. Impact of Canadian wildfire smoke on air quality at two rural sites in NY State. Atmos. Environ. 2011, 45, 2028–2033. [Google Scholar] [CrossRef]
- Hung, W.-T.; Lu, C.-H.S.; Shrestha, B.; Lin, H.-C.; Lin, C.-A.; Grohan, D.; Hong, J.; Ahmadov, R.; James, E.; Joseph, E. The impacts of transported wildfire smoke aerosols on surface air quality in New York State: A case study in summer 2018. Atmos. Environ. 2020, 227, 117415. [Google Scholar] [CrossRef]
- Roger, H.M.; Ditto, J.C.; Gentner, D.R. Evidence for impacts on surface-level air quality in the northeastern US from long-distance transport of smoke from North American fires during the Long Island Sound Tropospheric Ozone Study (LISTOS) 2018. Atmos. Chem. Phys. 2020, 20, 671–682. [Google Scholar] [CrossRef]
- Wu, Y.; Arapi, A.; Huang, J.; Gross, B.; Moshary, F. Intra-continental wildfire smoke transport and impact on local air quality observed by ground-based and satellite remote sensing in New York City. Atmos. Environ. 2018, 187, 266–281. [Google Scholar] [CrossRef]
- Zu, K.; Tao, G.; Long, K.; Goodman, J.; Valberg, P. Long-range fine particulate matter from the 2002 Quebec forest fires and daily mortality in Greater Boston and New York City. Air Qual. Atmos. Health 2016, 9, 213–221. [Google Scholar] [CrossRef]
- Alexander, C.R.; Weygandt, S.S.; Smirnova, T.G.; Benjamin, S.; Hofmann, P.; James, E.P.; Koch, D.A. High Resolution Rapid Refresh (HRRR): Recent enhancements and evaluation during the 2010 convective season. In Proceedings of the 25th Conference on Severe Local Storms, Denver, CO, USA, 12 October 2010. [Google Scholar]
- Cao, C.; Deluccia, F.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the VIIRS onboard the S-NPP satellite. IEEE Trans. Geosci. Remote Sens. 2013, 99. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Climate 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Colarco, P.; da Silva, A.; Chin, M.; Diehl, T. Online simulations of global aerosol distributions in the NASA GEOS-4 model and comparisons to satellite and ground-based aerosol optical depth. J. Geophys. Res. 2010, 115, D14207. [Google Scholar] [CrossRef]
- Buchard, V.; Randles, C.A.; da Silva, A.M.; Darmenov, A.; Colarco, P.R.; Govindaraju, R.; Ferrare, R.; Hair, J.; Beyersdorf, A.J.; Ziemba, L.D.; et al. The MERRA-2 Aerosol Reanalysis, 1980 Onward. Part II: Evaluation and Case Studies. J. Climate 2017, 30, 6851–6872. [Google Scholar] [CrossRef] [PubMed]
- Randles, C.A.; da Silva, A.M.; Buchard, V.; Colarco, P.R.; Darmenov, A.; Govindaraju, R.; Smirnov, A.; Holben, B.; Ferrare, R.; Hair, J.; et al. The MERRA-2 Aerosol Reanalysis, 1980 Onward. Part I: System description and data assimilation evaluation. J. Climate 2017, 30, 6823–6850. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Obata, K.; Miura, T.; Yoshioka, H.; Huete, A.R.; Vargas, M. Spectral Cross-Calibration of VIIRS Enhanced Vegetation Index with MODIS: A Case Study Using Year-Long Global Data. Remote Sens. 2016, 8, 34. [Google Scholar] [CrossRef]
- Géron, A. Hands-on Machine Learning with Scikit-Learn and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems; O’Reilly Media: Sebastopol, CA, USA, 2017; ISBN 978-1491962299. [Google Scholar]
- Hornik, K.; Stinchcombe, M.; White, H. Multilayer feedforward networks are universal approximators. Neural Netw. 1989, 2, 359–366. [Google Scholar] [CrossRef]
- LeCun, Y.; Bottou, L.; Bengio, Y.; Haffner, P. Gradient-Based Learning Applied to Document Recognition. Proc. IEEE 1998, 86, 2278–2324. [Google Scholar] [CrossRef]
- Fletcher, D.; Goss, E. Forecasting with neural networks: An application using bankruptcy data. Inf. Manag. 1993, 24, 159–167. [Google Scholar] [CrossRef]
- Chollet, F. Deep Learning with Python; Manning Publications Co.: Greenwich, CT, USA, 2017; ISBN 9781617294433. [Google Scholar]
- Sammut, C.; Webb, G.I. Encyclopedia of Machine Learning; Springer Publishing Company: New York, NY, USA, 2011; ISBN 9780387301648. [Google Scholar]
- Watson, G.; Telesca, D.; Reid, C.; Pfister, G.; Jerrett, M. Machine learning models accurately model ozone exposure during wildfire events. Environ. Pollut. 2019, 254. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- McGovern, A.; Lagerquist, R.; Gagne, D.J.; Jergensen, G.E.; Elmore, K.L.; Homeyer, C.R.; Smith, T. Making the Black Box More Transparent: Understanding the Physical Implications of Machine Learning. Bull. Amer. Meteor. Soc. 2019, 100, 2175–2199. [Google Scholar] [CrossRef]
- Pal, S.; Davis, K.J.; Lauvaux, T.; Browell, E.V.; Gaudet, B.J.; Stauffer, D.R.; Obland, M.D.; Choi, Y.; DiGangi, J.P.; Feng, S.; et al. Observations of greenhouse gas changes across summer frontal boundaries in the eastern United States. J. Geophys. Res. Atmos. 2020, 125, e2019JD030526. [Google Scholar] [CrossRef]

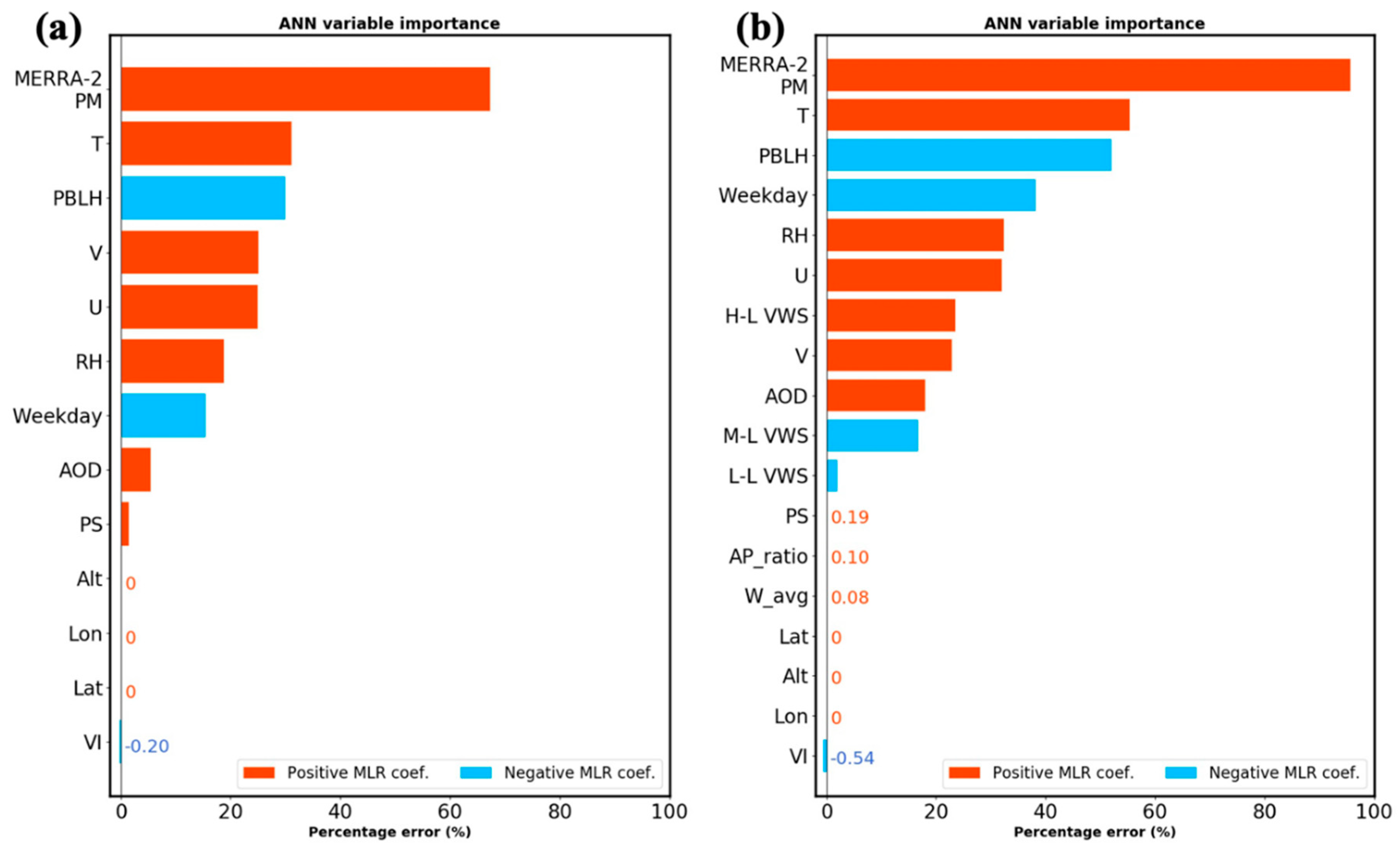
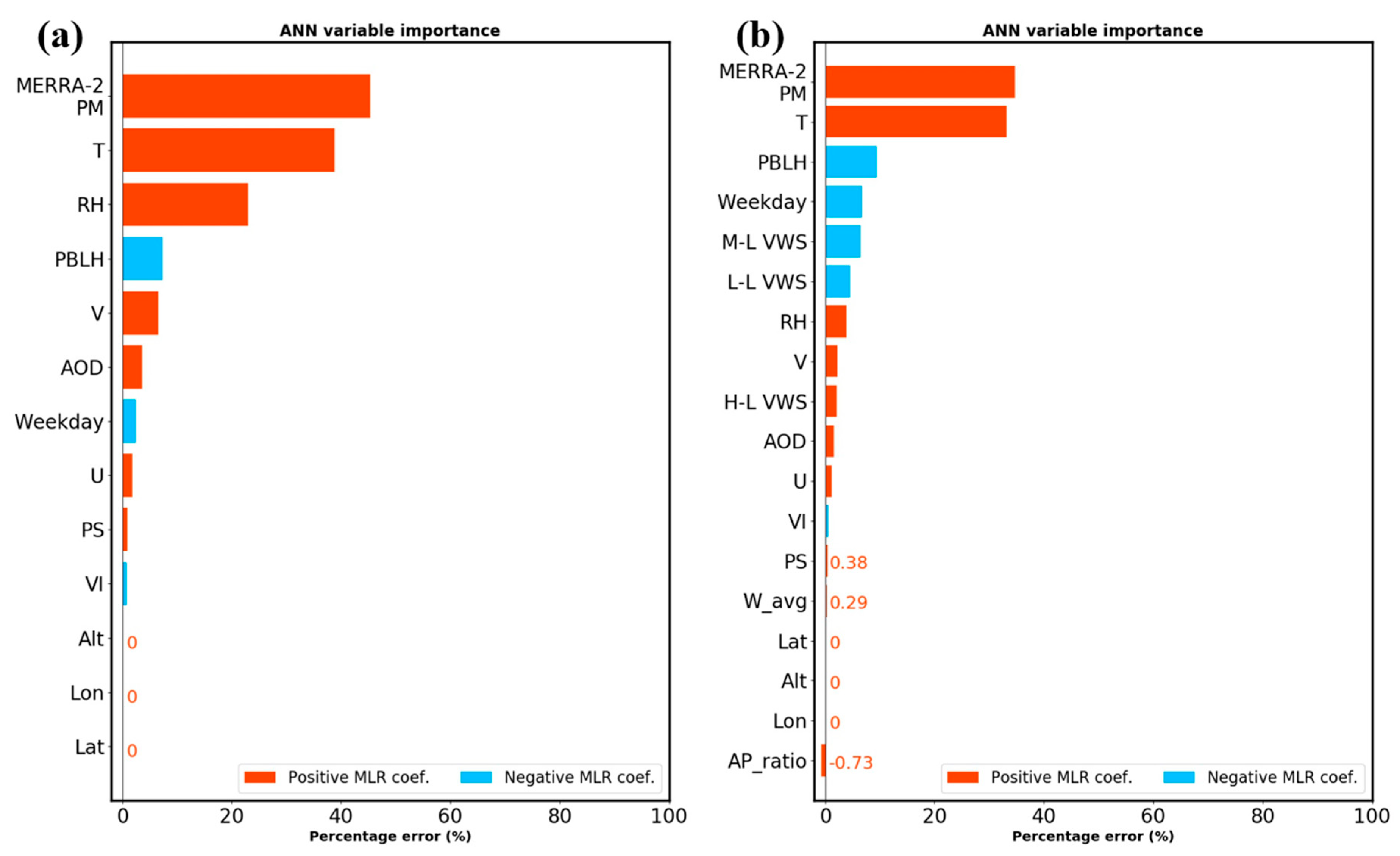
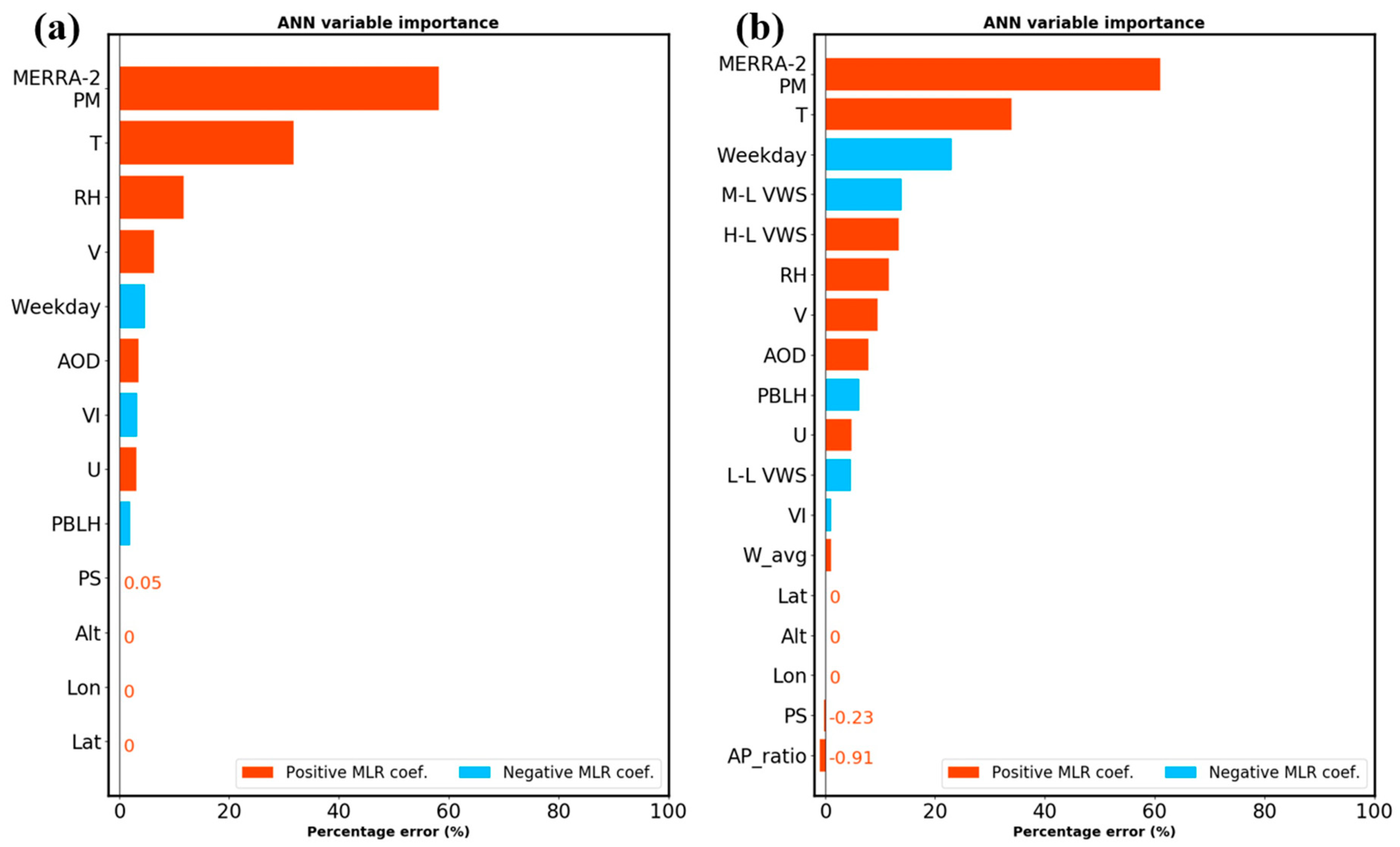
| Variable | Source | Level | Spatial Resolution | Temporal Resolution |
|---|---|---|---|---|
| Target | ||||
| PM2.5 observation (µg m−3) | EPA AQS 1 | Surface | Hourly | |
| Meteorological predictors | ||||
| Surface pressure (Pa) | HRRR 2 | Surface | 3 km | 3-hourly |
| Temperature (K) | HRRR | 2 m a.g.l. | 3 km | 3-hourly |
| Relative humidity (%) | HRRR | 2 m a.g.l. | 3 km | 3-hourly |
| U-component of horizontal wind (m s−1) | HRRR | 10 m a.g.l. | 3 km | 3-hourly |
| V-component of horizontal wind (m s−1) | HRRR | 10 m a.g.l. | 3 km | 3-hourly |
| Planetary boundary layer height (m) | HRRR | 3 km | 3-hourly | |
| Aerosol predictors | ||||
| Aerosol optical depth | VIIRS 3 | Total column | 0.25° × 0.25° | Daily |
| PM2.5 concentration (µg m−3) | MERRA-2 4 | Surface | 0.5° × 0.625° | Hourly |
| Geographic predictors | ||||
| Latitude | EPA AQS | |||
| Longitude | EPA AQS | |||
| Altitude (m) | EPA AQS | |||
| Vegetation index | VIIRS 5 | Surface | 0.05° × 0.05° | Monthly |
| Weekday | Daily | |||
| Vertical predictors | ||||
| Wind shear (s−1) | HRRR | Surface—850 hPa 850—700 hPa 700—500 hPa | 3 km | 3-hourly |
| Average vertical velocity (Pa s−1) | HRRR | Surface—500 hPa | 3 km | 3-hourly |
| Ratio of AOD change rate to PM change rate | VIIRS | 0.25° × 0.25° | Daily | |
| EPA AQS | Daily | |||
| Label | Name | ID Number | Latitude | Longitude | Altitude (m) | Type |
|---|---|---|---|---|---|---|
| 1 | Albany | 360010005 | 42.64 | −73.75 | 7 | UNY |
| 2 | Buffalo | 360290005 | 42.88 | −78.81 | 185 | UNY |
| 3 | Tonawanda II | 360291014 | 43 | −78.9 | 182 | UNY |
| 4 | Rochester * | 360551007 | 43.15 | −77.55 | 137 | UNY |
| 5 | Utica | 360652001 | 43.1 | −75.22 | 139 | UNY |
| 6 | Whiteface Mountain | 360310003 | 44.36 | −73.9 | 599 | Rural |
| 7 | Rockland County | 360870005 | 41.18 | −74.03 | 140 | Rural |
| 8 | Pinnacle State Park * | 361010003 | 42.1 | −77.21 | 507 | Rural |
| 9 | Bronx | 360050112 | 40.81 | −73.89 | 20 | NYC |
| 10 | PS 314 | 360470052 | 40.64 | −74.02 | 26 | NYC |
| 11 | PS 274 | 360470118 | 40.69 | −73.93 | 18 | NYC |
| 12 | Esienhower Park | 360590005 | 40.74 | −73.59 | 27 | NYC |
| 13 | IS 143 | 360610115 | 40.85 | −73.93 | 0 | NYC |
| 14 | Division St. | 360610134 | 40.71 | −73.99 | 17 | NYC |
| 15 | CCNY | 360610135 | 40.82 | −73.95 | 45 | NYC |
| 16 | Newburgh | 360710002 | 41.5 | −74.01 | 127 | NYC |
| 17 | Maspeth | 360810120 | 40.73 | −73.89 | 31 | NYC |
| 18 | Queens * | 360810124 | 40.74 | −73.82 | 25 | NYC |
| 19 | FKILL | 360850111 | 40.58 | −74.2 | 3 | NYC |
| 20 | Holtsville | 361030009 | 40.83 | −73.06 | 45 | NYC |
| 21 | White Plain | 361192004 | 41.05 | −73.76 | 64 | NYC |
| Model | Bias (µg m−3) | R-Squared | RMSE (µg m−3) |
|---|---|---|---|
| MLR-1 | 0.03 ± 1.14 | 0.51 ± 0.06 | 2.96 ± 0.26 |
| MLR-2 | 0.06 ± 1.31 | 0.52 ± 0.06 | 3.01 ± 0.39 |
| ANN-1 | −0.63 ± 0.99 | 0.65 ± 0.09 | 2.59 ± 0.45 |
| ANN-2 | −0.29 ± 0.88 | 0.67 ± 0.10 | 2.42 ± 0.37 |
| Model | Bias (µg m−3) | R-Squared | RMSE (µg m−3) |
|---|---|---|---|
| Rural sites | |||
| MLR-1 | −0.15 ± 2.04 | 0.55 ± 0.01 | 3.11 ± 0.20 |
| MLR-2 | 0.07 ± 2.67 | 0.54 ± 0.02 | 3.53 ± 0.54 |
| ANN-1 | −2.10 ± 1.00 | 0.61 ± 0.04 | 3.25 ± 0.51 |
| ANN-2 | −1.02 ± 0.70 | 0.64 ± 0.06 | 2.40 ± 0.12 |
| NYC sites | |||
| MLR-1 | 0.09 ± 0.80 | 0.53 ± 0.05 | 2.85 ± 0.16 |
| MLR-2 | 0.10 ± 0.80 | 0.54 ± 0.05 | 2.84 ± 0.15 |
| ANN-1 | −0.42 ± 0.76 | 0.68 ± 0.09 | 2.42 ± 0.33 |
| ANN-2 | −0.19 ± 0.89 | 0.71 ± 0.09 | 2.31 ± 0.38 |
| UNY sites | |||
| MLR-1 | −0.04 ± 1.09 | 0.45 ± 0.04 | 3.13 ± 0.35 |
| MLR-2 | −0.05 ± 1.12 | 0.44 ± 0.04 | 3.15 ± 0.36 |
| ANN-1 | −0.31 ± 0.70 | 0.59 ± 0.05 | 2.66 ± 0.29 |
| ANN-2 | −0.13 ± 0.76 | 0.58 ± 0.05 | 2.71 ± 0.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hung, W.-T.; Lu, C.-H.; Alessandrini, S.; Kumar, R.; Lin, C.-A. Estimation of PM2.5 Concentrations in New York State: Understanding the Influence of Vertical Mixing on Surface PM2.5 Using Machine Learning. Atmosphere 2020, 11, 1303. https://doi.org/10.3390/atmos11121303
Hung W-T, Lu C-H, Alessandrini S, Kumar R, Lin C-A. Estimation of PM2.5 Concentrations in New York State: Understanding the Influence of Vertical Mixing on Surface PM2.5 Using Machine Learning. Atmosphere. 2020; 11(12):1303. https://doi.org/10.3390/atmos11121303
Chicago/Turabian StyleHung, Wei-Ting, Cheng-Hsuan (Sarah) Lu, Stefano Alessandrini, Rajesh Kumar, and Chin-An Lin. 2020. "Estimation of PM2.5 Concentrations in New York State: Understanding the Influence of Vertical Mixing on Surface PM2.5 Using Machine Learning" Atmosphere 11, no. 12: 1303. https://doi.org/10.3390/atmos11121303
APA StyleHung, W.-T., Lu, C.-H., Alessandrini, S., Kumar, R., & Lin, C.-A. (2020). Estimation of PM2.5 Concentrations in New York State: Understanding the Influence of Vertical Mixing on Surface PM2.5 Using Machine Learning. Atmosphere, 11(12), 1303. https://doi.org/10.3390/atmos11121303





