Numerical Modeling of Formation and Rise of Gas and Dust Cloud from Large Scale Commercial Blasting
Abstract
1. Introduction
2. Numerical Models for Describing the Gas and Dust Cloud
2.1. A numerical Model of Fireball Formation (Eulerian Model)
2.2. Numerical Model of the Rising Thermal (Navier–Stokes LES Code)
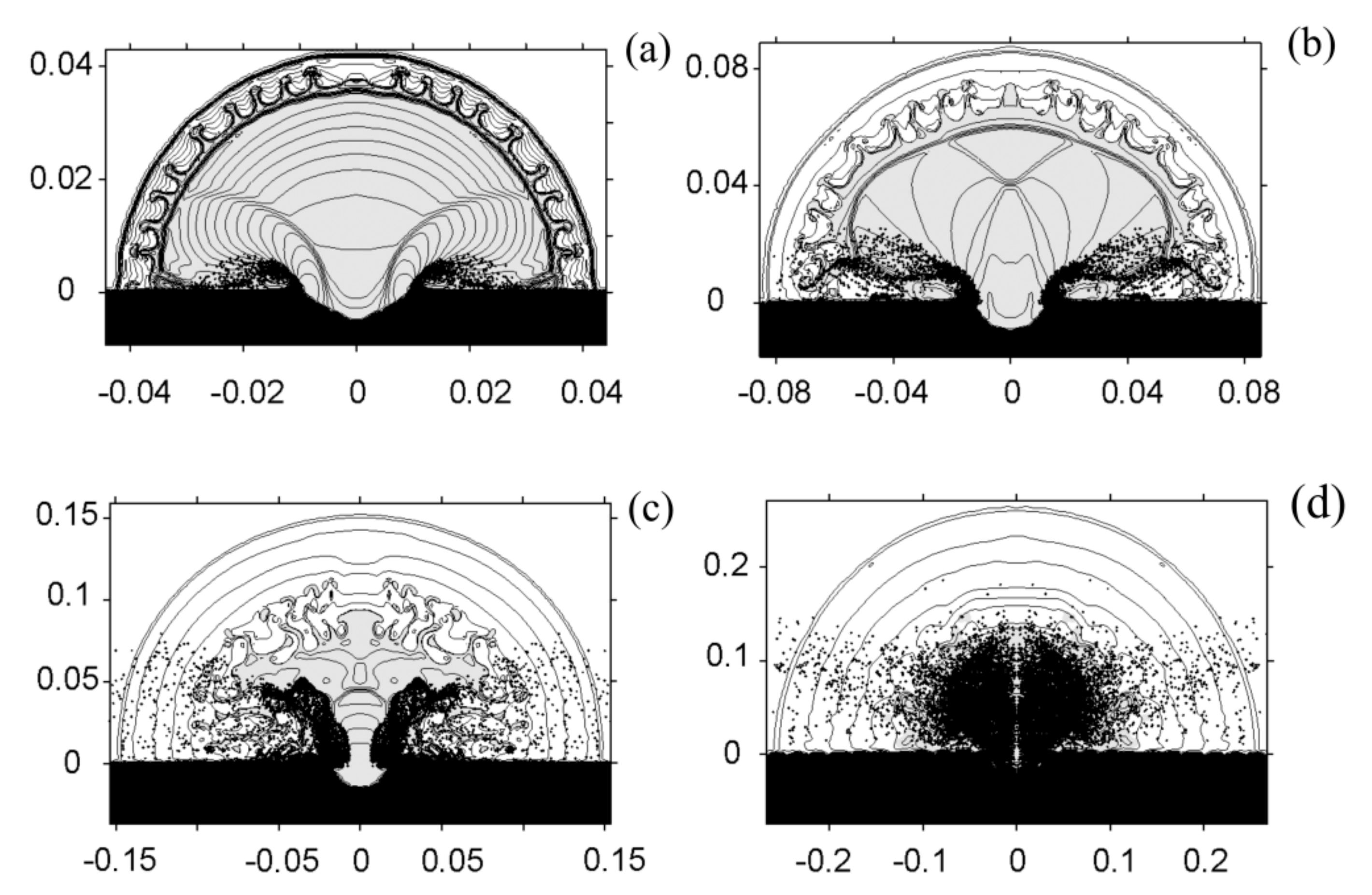
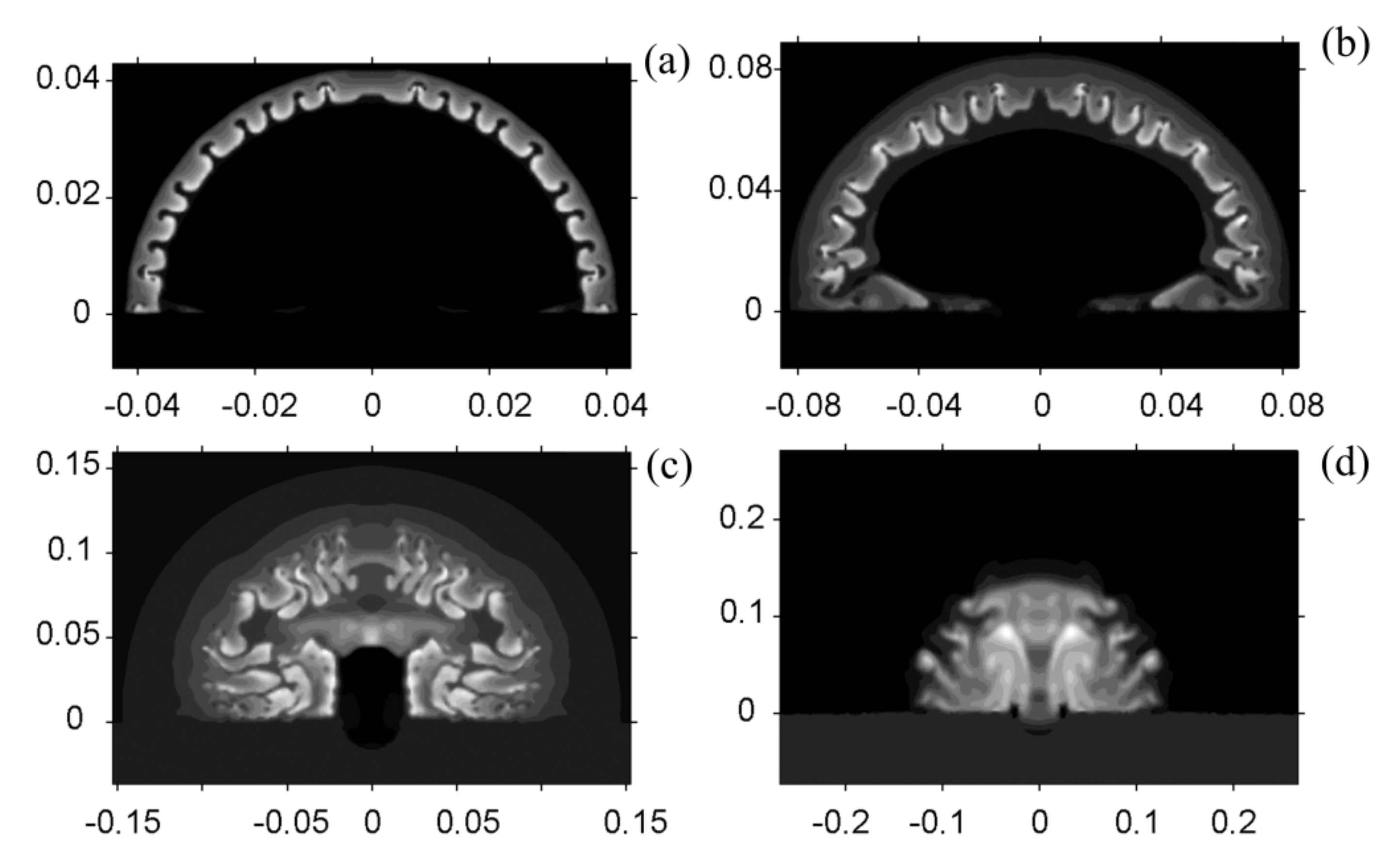
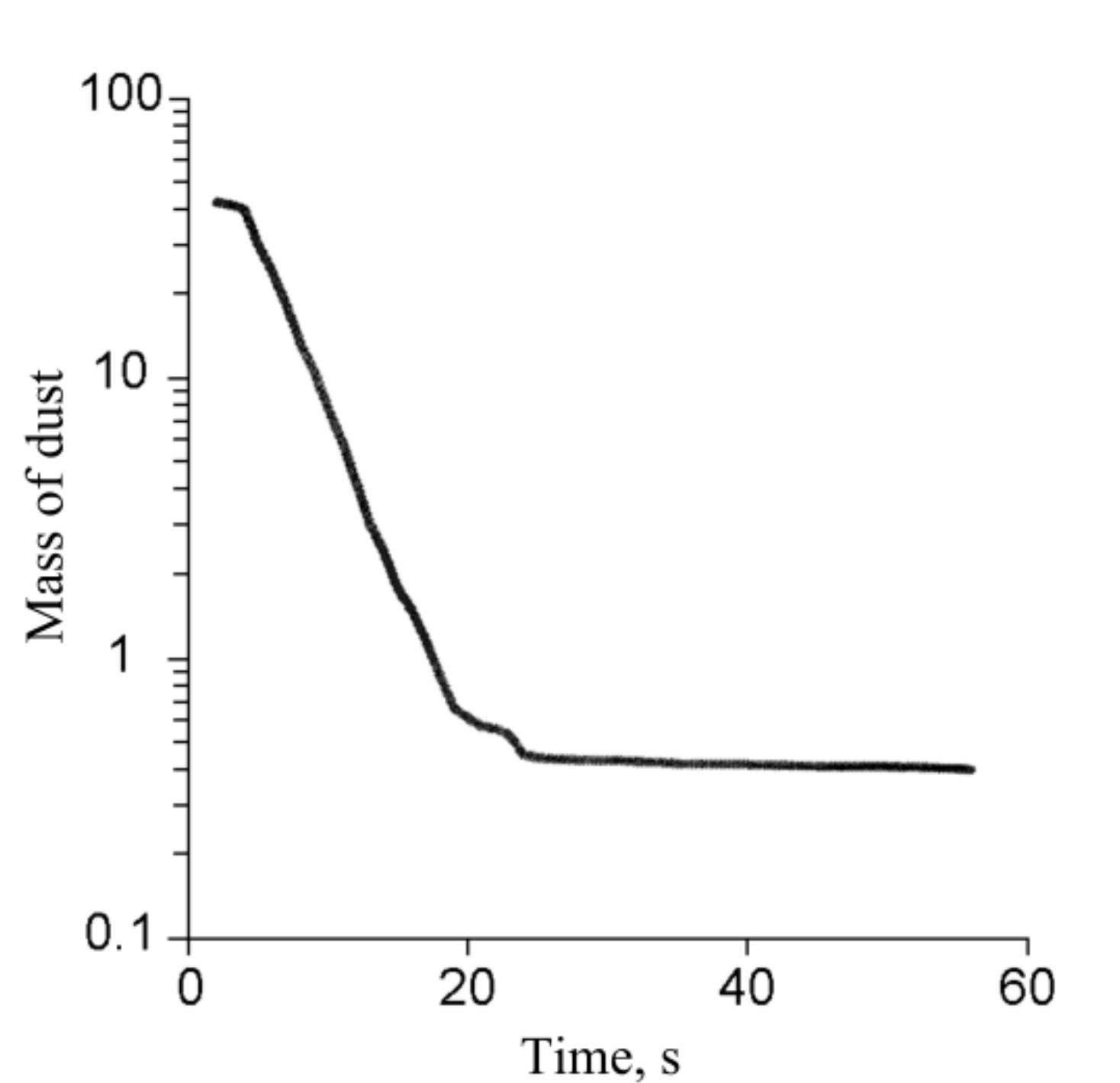
3. Modeling the Gas and Dust Cloud Initiated by a 500 t TNT Explosion
4. The Gas and Dust Cloud Rise Initiated by a TNT Explosion
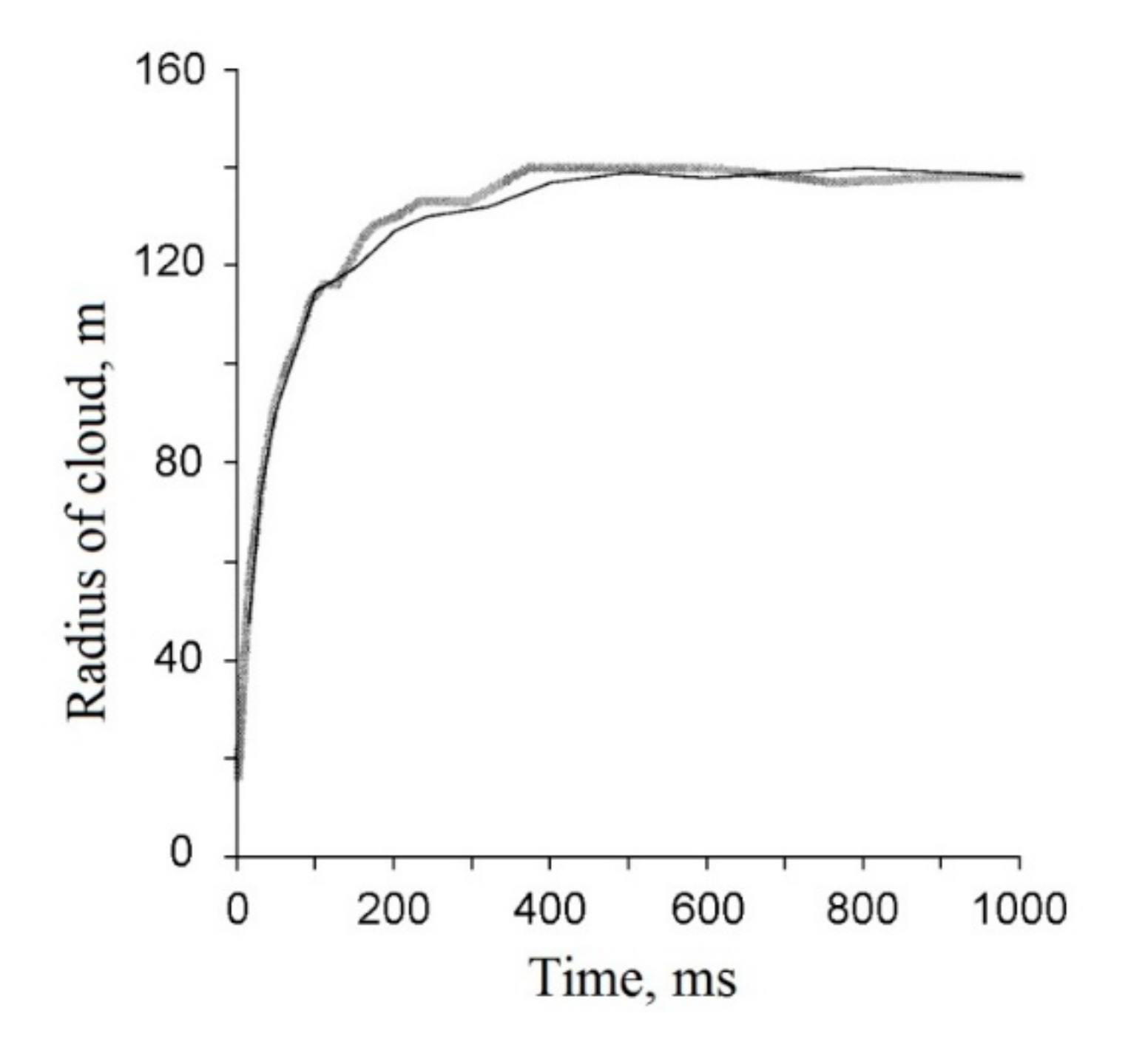
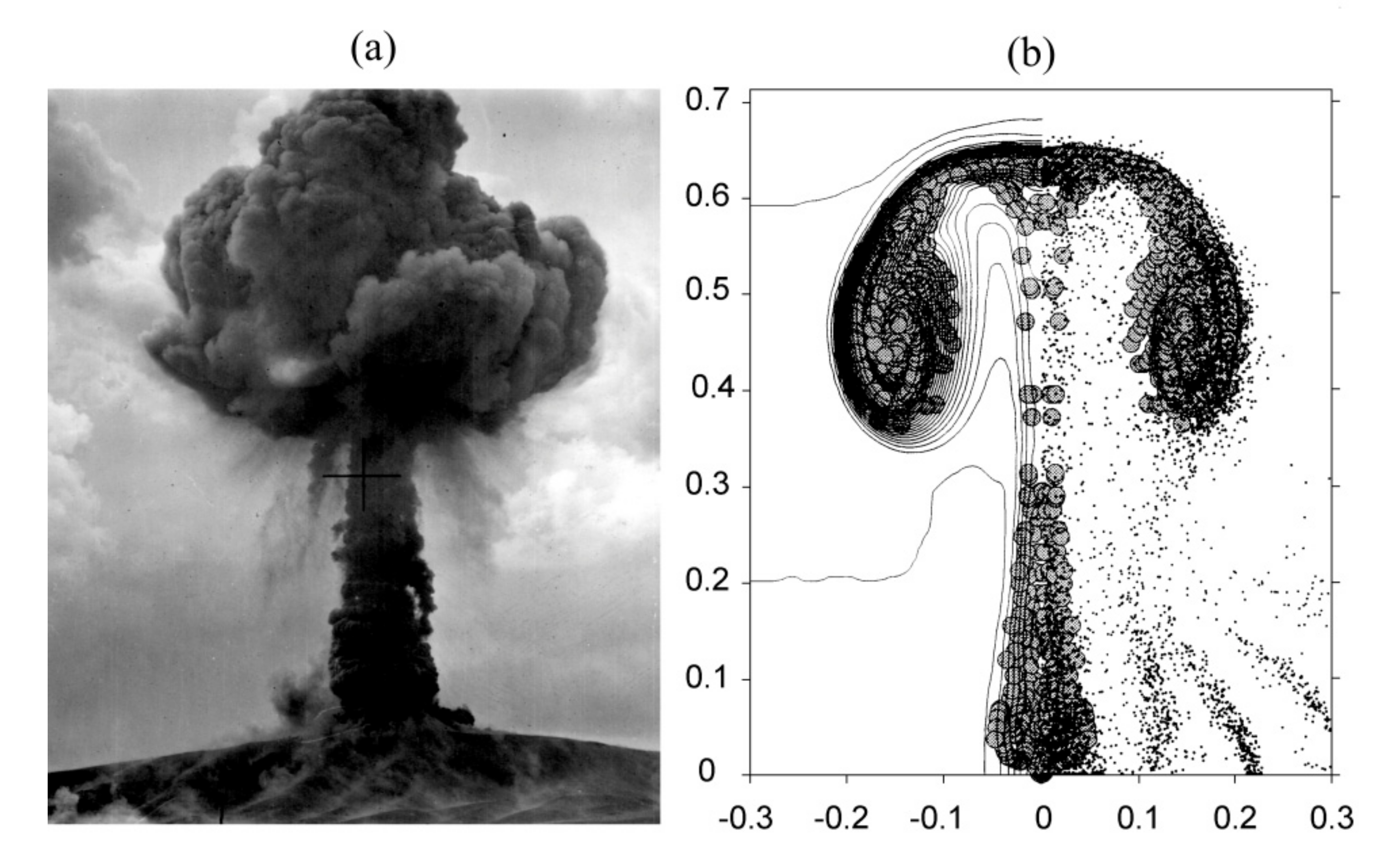
4.1. The Rise of the Thermal Initiated by a 500 t TNT Explosion
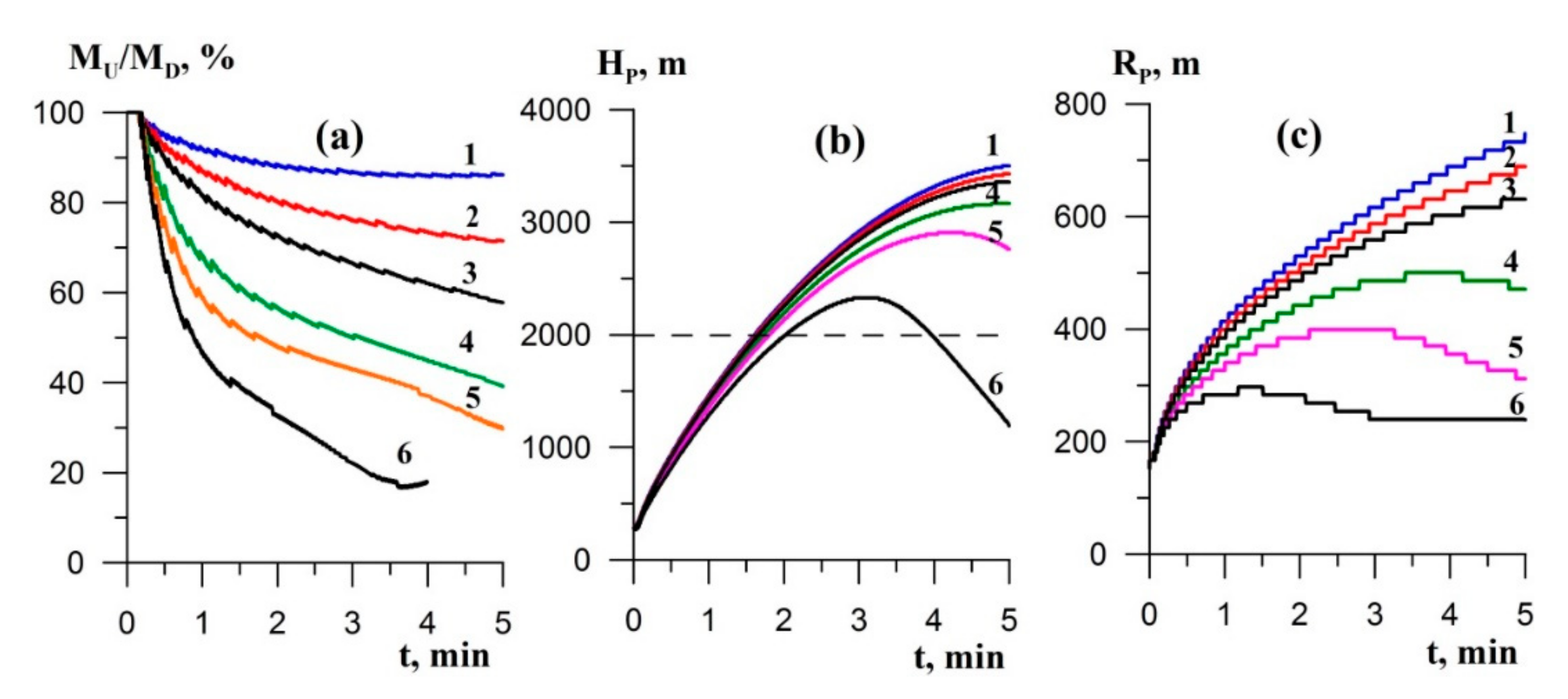
4.2. The Gas and Dust Cloud Rise Initiated by 1–1000 t TNT Explosion
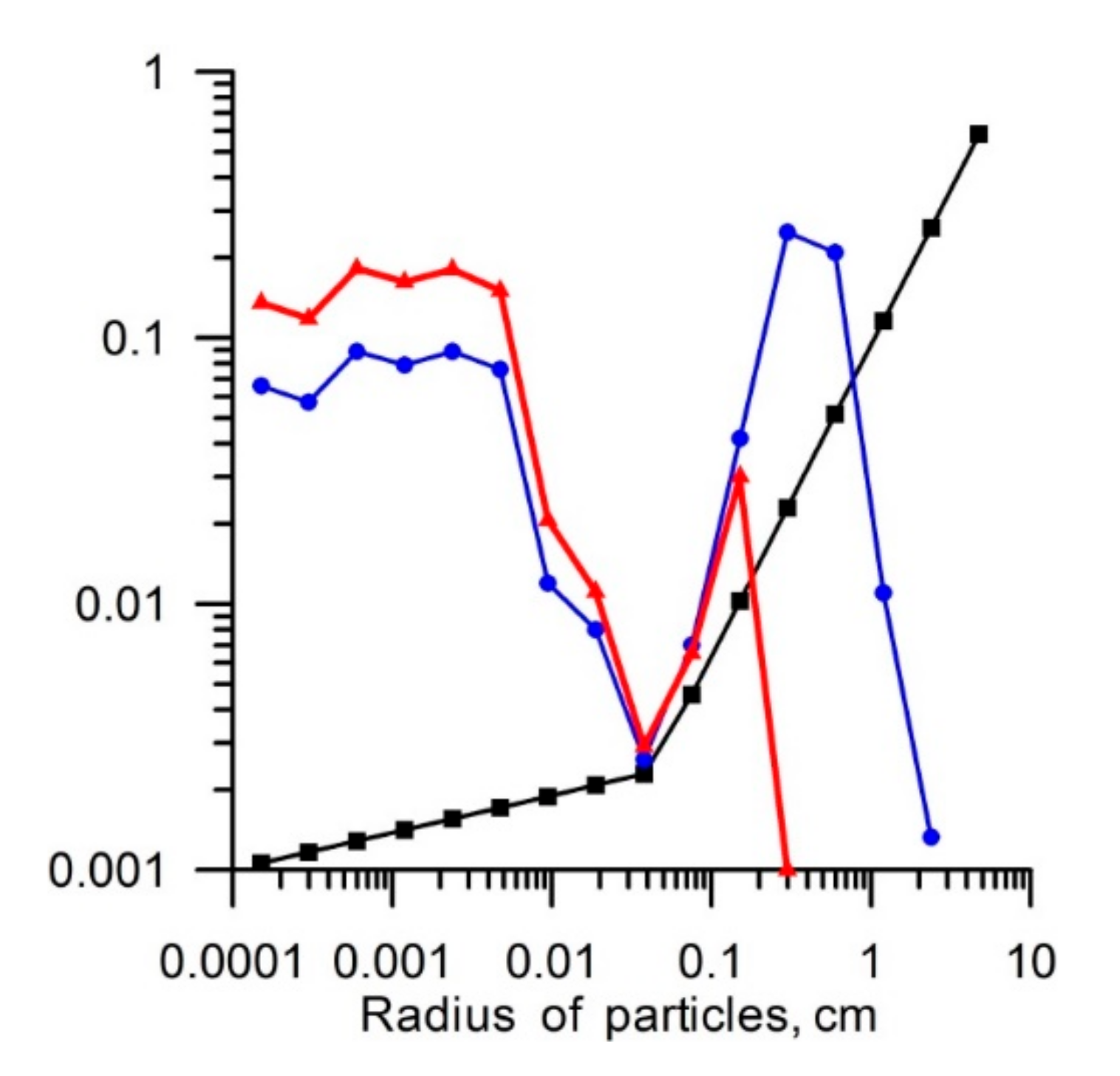
5. The Size Distribution of Dust Particles
6. Discussion of Results and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Trubetskoy, K.N.; Galchenko, Y.P. Methodology for estimating promising development paradigm for mineral mining and processing industry. J. Min. Sci. 2015, 51, 407–415. [Google Scholar] [CrossRef]
- Viktorov, S.D. The explosive destruction of the rock is the basis of progress in mining. Min. Inf. Anal. Bull. 2015, 1, 63–75. (In Russian) [Google Scholar]
- Patra, A.K.; Gautam, S.; Kumar, P. Emissions and human health impact of particulate matter from surface mining operation—A review. Environ. Technol. Innov. 2016, 5, 233–249. [Google Scholar] [CrossRef]
- Ministry of Natural Resources of Russia. State Report: On the State and Protection of the Environment of the Russian Federation in 2018; NPP “Kadastr”, Ministry of Natural Resources of Russia: Moscow, Russia, 2019; p. 844. Available online: https://www.mnr.gov.ru/docs/o_sostoyanii_i_ob_okhrane_okruzhayushchey_sredy_rossiyskoy_federatsii/gosudarstvennyy_doklad_o_sostoyanii_i_ob_okhrane_okruzhayushchey_sredy_rossiyskoy_federatsii_v_2018_/ (accessed on 30 August 2020). (In Russian)
- Rout, T.K.; Masto, R.E.; Padhy, P.K.; Ram, L.C.; George, J.; Joshi, G. Heavy metals in dusts from commercial and residential areas of Jharia coal mining town. Environ. Earth Sci. 2014, 73, 347–359. [Google Scholar] [CrossRef]
- Gautam, S.; Kumar, P.; Patra, A.K. Occupational exposure to particulate matter in three Indian opencast mines. Air Qual. Atmos. Health 2014, 9, 143–158. [Google Scholar] [CrossRef]
- Csavina, J.; Field, J.; Taylor, M.P.; Gao, S.; Landázuri, A.; Betterton, E.A.; Sáez, A.E. A review on the importance of metals and metalloids in atmospheric dust and aerosol from mining operations. Sci. Total Environ. 2012, 433, 58–73. [Google Scholar] [CrossRef]
- Barrows, A.; Cathey, S.; Petersen, C. Marine environment microfiber contamination: Global patterns and the diversity of microparticle origins. Environ. Pollut. 2018, 237, 275–284. [Google Scholar] [CrossRef]
- Zhang, Z.X. Rock Fracture and Blasting. Theory and Applications; Elsevier, Butterworth-Heinemann: Amsterdam, The Netherlands, 2016; p. 528. [Google Scholar]
- Michailov, O.Y.; Tarasenko, J.V. Golden jubilee of the iron ore giant of Russia. Gorn. Zhurnal 2017, 5, 15–18. (In Russian) [Google Scholar]
- Silva, J.; Worsey, T.; Lusk, B. Practical assessment of rock damage due to blasting. Int. J. Min. Sci. Technol. 2018, 29, 379–385. [Google Scholar] [CrossRef]
- Beresnevich, P.V.; Mikhailov, V.A.; Filatov, S.S. Aerology Quarries: Reference Book; Nedra: Moscow, Russia, 1990; 280p. (In Russian) [Google Scholar]
- Roy, S.; Adhikari, G.R.; Singh, T.N. Development of emission factors for quantification of blasting dust at surface. J. Environ. Prot. 2010, 1, 346–361. [Google Scholar] [CrossRef]
- Adushkin, V.V.; Spivak, A.A.; Soloviev, S.P.; Pernik, L.M.; Kishkina, S.B. Environmental consequences of mass chemical blasting in open pits. Geoekologiya 2000, 6, 554–563. (In Russian) [Google Scholar]
- Monjezi, M.; Shahriar, K.; Dehghani, H.; Namin, F.S. Environmental impact assessment of open pit mining in Iran. Environ. Earth Sci. 2008, 58, 205–216. [Google Scholar] [CrossRef]
- Fişne, A.; Kuzu, C.; Hüdaverdi, T. Prediction of environmental impacts of quarry blasting operation using fuzzy logic. Environ. Monit. Assess. 2010, 174, 461–470. [Google Scholar] [CrossRef] [PubMed]
- Adushkin, V.V.; Weidler, P.G.; Dubovskoi, A.N.; Pernik, L.M.; Popel, S.I.; Friedrich, F. Properties of nano- and microparticles emitted into the environment from open-pit mining of iron deposits. Geol. Ore Depos. 2010, 52, 373–380. [Google Scholar] [CrossRef]
- Ugarov, A.A.; Ismagilov, R.I.; Badtiev, B.; Borisov, I.I. State-of-the art and future considerations on drilling-and-blasting system at plants of Metalloinvest. Gorn. Zhurnal 2017, 5, 102–106. [Google Scholar] [CrossRef]
- Zvyagintseva, A.V.; Sazonova, S.A.; Kulneva, V.V. Analytical monitoring of the harmful effects at the Lebedinsky Mining and Processing Plant (Lebedinsky GOK) on the environment and improvement of environmental protection measures. Inf. Technol. Build. Soc. Econ. Syst. 2020, 1, 92–99. (In Russian) [Google Scholar]
- Sairanen, M.; Rinne, M.; Selonen, O. A review of dust emission dispersions in rock aggregate and natural stone quarries. Int. J. Min. Reclam. Environ. 2017, 32, 196–220. [Google Scholar] [CrossRef]
- Silvester, S.; Lowndes, I.S.; Hargreaves, D. A computational study of particulate emissions from an open pit quarry under neutral atmospheric conditions. Atmos. Environ. 2009, 43, 6415–6424. [Google Scholar] [CrossRef]
- Joseph, G.; Lowndes, I.S.; Hargreaves, D. A computational study of particulate emissions from Old Moor Quarry, UK. J. Wind. Eng. Ind. Aerodyn. 2018, 172, 68–84. [Google Scholar] [CrossRef]
- Torno, S.; Toraño, J.; Menendez, M.; Gent, M. CFD simulation of blasting dust for the design of physical barriers. Environ. Earth Sci. 2010, 64, 73–83. [Google Scholar] [CrossRef]
- Reed, W.R. Significant Dust Dispersion Models for Mining Operations; NIOSH-Publications Disseminations: Cincinnati, OH, USA, 2005; p. 27. [Google Scholar]
- Belotserkovskiy, O.M.; Andrushchenko, V.A.; Shevelev, Y.D. Dynamics of Spatial Vortex Flows in an Inhomogeneous Atmosphere: Computational Experiment; Yanus: Moscow, Russia, 2000; p. 456. (In Russian) [Google Scholar]
- Shuvalov, V. Multi-dimensional hydrodynamic code SOVA for interfacial flows: Application to the thermal layer effect. Shock Waves 1999, 9, 381–390. [Google Scholar] [CrossRef]
- Shuvalov, V.; Artem’Eva, N.; Kosarev, I. 3D hydrodynamic code sova for multimaterial flows, application to Shoemakerlevy 9 comet impact problem. Int. J. Impact Eng. 1999, 23, 847–858. [Google Scholar] [CrossRef]
- Andreyev, S.G.; Babkin, A.V.; Baum, F.A.; Imkhovik, N.A.; Kobylkin, I.F.; Kolpakov, V.I.; Ladov, S.V.; Odintsov, V.A.; Orlenko, L.P.; Okhitin, V.N.; et al. Explosion Physics, 3rd ed.; Fizmatlit: Moscow, Russia, 2004; Volume 1, p. 823. (In Russian) [Google Scholar]
- Andreyev, S.G.; Babkin, A.V.; Baum, F.A.; Imkhovik, N.A.; Kobylkin, I.F.; Kolpakov, V.I.; Ladov, S.V.; Odintsov, V.A.; Orlenko, L.P.; Okhitin, V.N.; et al. Explosion Physics, 3rd ed.; Fizmatlit: Moscow, Russia, 2004; Volume 2, p. 648. (In Russian) [Google Scholar]
- Vasil’yev, A.A.; Zhdan, S.A. Parameters of a shock wave in the explosion of a cylindrical explosive charge in air. Fiz. Goreniya Vzryva 1981, 17, 99–105. (In Russian) [Google Scholar]
- Kuznetsov, N.M. Thermodynamic Functions and Shock Adiabats of Air at High Temperatures; Mashinostroyeniye: Moscow, Russia, 1965; p. 465. (In Russian) [Google Scholar]
- Tompson, S.L.; Lauson, H.S. Improvements in the Chart D Radiation-Hydrodynamic CODE III: Revised Analytic Equation of State; Report SC-RR-71 0714; Sandia National Laboratory: Albuquerque, NM, USA, 1974; p. 121.
- Teterev, A.V. Cratering model of asteroid and comet impact on a planetary surface. Int. J. Impact Eng. 1999, 23, 921–932. [Google Scholar] [CrossRef]
- Nigmatulin, R.I. Dynamics of Multiphase Media; Hemisphere Publishing Corporation: New York, NY, USA, 1990; Volume 2, p. 507. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Course of theoretical physics. In Fluid Mechanics, 2nd ed.; Pergamon Press: Oxford, UK, 1987; Volume 6, p. 554. [Google Scholar]
- Zatevakhin, M.A.; Kuznetcov, A.E.; Nikulin, D.A.; Strelets, M.K. Numerical simulation of the process of levitation of a system of high-temperature turbulent thermals in an inhomogeneous compressible atmosphere. High Temp. 1994, 32, 42–55. [Google Scholar]
- Harlow, F.H.; Welch, J.E. Numerical calculation of time-dependent viscous incompressible flow of fluid with free surface. Phys. Fluids 1965, 8, 2182. [Google Scholar] [CrossRef]
- Viecelly, J.A. A computing method for incompressible flows bounded by moving walls. J. Comp. Phys. 1971, 8, 119–143. [Google Scholar] [CrossRef]
- Lesier, M.; Metais, O. New trends in large-eddy simulations of turbulence. Annu. Rev. Fluid Mech. 1996, 28, 45–82. [Google Scholar] [CrossRef]
- Hazins, V.M. Approach in Problems on floating up of high temperature thermals in stratified atmosphere. High Temp. 2010, 48, 402–410. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Anderson, D.A.; Tannehill, J.C.; Pletcher, R.H. Computational Fluid Mechanics and Heat Transfer; Hemisphere Publishing Corporation: New York, NY, USA, 1984; p. 599. [Google Scholar]
- Sreekantha, B.; Anand, S.; Ikkurthi, V.R.; Chaudhury, P.; Sapra, B.K.; Mayya, Y.S.; Chaturvedi, S. Evolution of particle metrics in a buoyant aerosol cloud from explosive releases. Aerosol Sci. Technol. 2020, 54, 656–667. [Google Scholar] [CrossRef]
- Ivanov, B.A.; Bazilevskiy, A.T. On the fragment-size distribution of ejecta of impact craters. In Proceedings of the Lunar and Planetary Science XIV, Houston, TX, USA, 14–18 March 1983; pp. 345–346. [Google Scholar]
- Brode, H.L. The Blast Wave in Air Resulting from a High Temperature, High Pressure Sphere of Air (U); RAND Corporation: Santa Monica, CA, USA, 1956; Available online: https://www.rand.org/pubs/research_memoranda/RM1825.html (accessed on 30 August 2020).
- Rozhdestvenskiy, V.B.; Khristoforov, B.D.; Yur’yev, V.L. Influence of the Rayleigh-Taylor instability on the radiation characteristics of an explosive explosion in air. Prikl. Mekhanika Tekhnicheskaya Fiz. 1989, 5, 107–114. (In Russian) [Google Scholar] [CrossRef]
- State Standard 4401-81: Standart Atmosphere: Parameters; Izdatel’stvo Standartov: Moscow, Russia, 1982; p. 181. Available online: https://files.stroyinf.ru/Data2/1/4294823/4294823872.pdf (accessed on 30 August 2020). (In Russian)
- Church, H. Cloud Rise from High-Explosives Detonations; Office of Scientific and Technical Information (OSTI): Albuquerque, NM, USA, 1969. [Google Scholar]
- Kansa, E.J. Time-Dependent Buoyant Puff Model for Explosive Sources; Technical Report UCRL-ID-128733; Lawrence Livermore National Laboratory: Livermore, CA, USA, 1997.
- Spidell, M.T.; Gordon, J.M.; Pitz, J.; Gross, K.C.; Perram, G.P. High speed radiometric measurements of IED detonation fireballs. SPIE Def. Secur. Sens. 2010, 7668, 76680. [Google Scholar] [CrossRef]
- Morton, B.R.; Taylor, G.I.; Turner, J.S. Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 234, 1–23. [Google Scholar] [CrossRef]
- Gualtieri, C.; Angeloudis, A.; Bombardelli, F.; Jha, S.; Stoesser, T. On the values for the turbulent Schmidt number in environmental flows. Fluids 2017, 2, 17. [Google Scholar] [CrossRef]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khazins, V.M.; Shuvalov, V.V.; Soloviev, S.P. Numerical Modeling of Formation and Rise of Gas and Dust Cloud from Large Scale Commercial Blasting. Atmosphere 2020, 11, 1112. https://doi.org/10.3390/atmos11101112
Khazins VM, Shuvalov VV, Soloviev SP. Numerical Modeling of Formation and Rise of Gas and Dust Cloud from Large Scale Commercial Blasting. Atmosphere. 2020; 11(10):1112. https://doi.org/10.3390/atmos11101112
Chicago/Turabian StyleKhazins, Valery M., Valery V. Shuvalov, and Sergey P. Soloviev. 2020. "Numerical Modeling of Formation and Rise of Gas and Dust Cloud from Large Scale Commercial Blasting" Atmosphere 11, no. 10: 1112. https://doi.org/10.3390/atmos11101112
APA StyleKhazins, V. M., Shuvalov, V. V., & Soloviev, S. P. (2020). Numerical Modeling of Formation and Rise of Gas and Dust Cloud from Large Scale Commercial Blasting. Atmosphere, 11(10), 1112. https://doi.org/10.3390/atmos11101112



