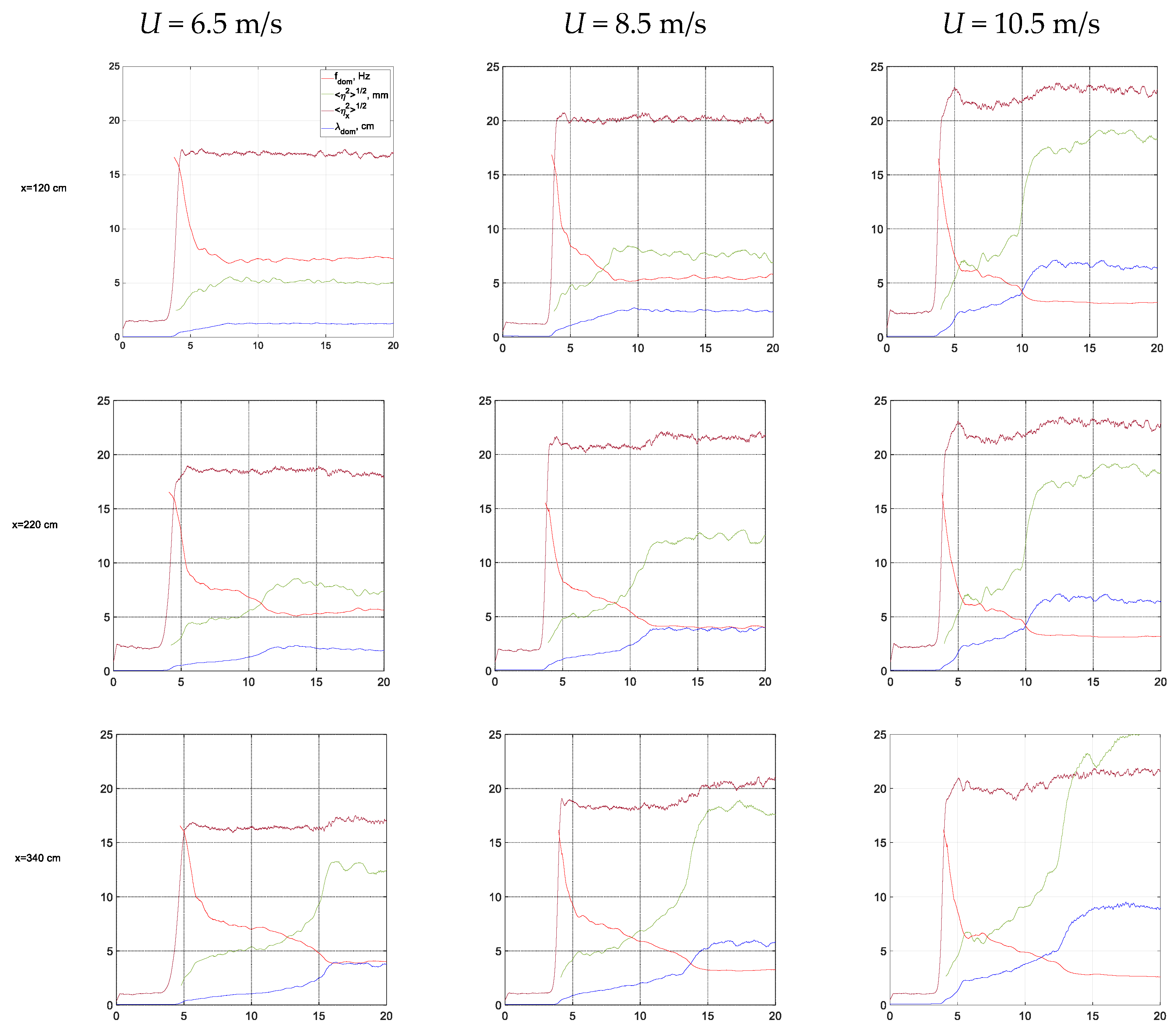
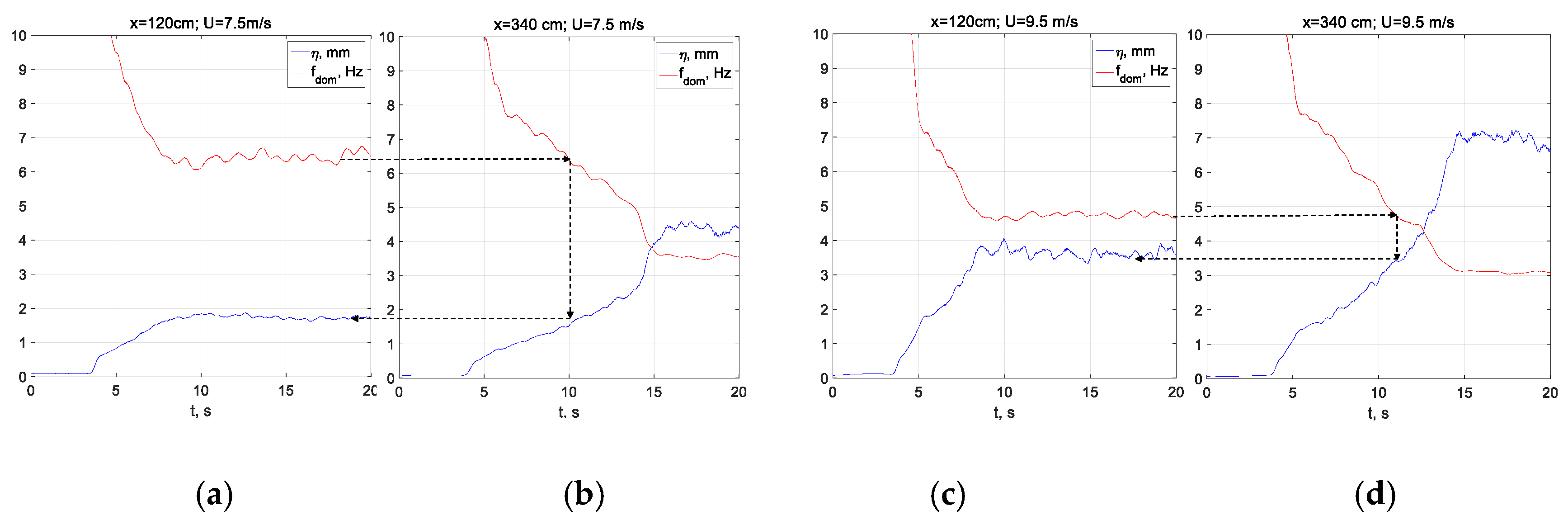
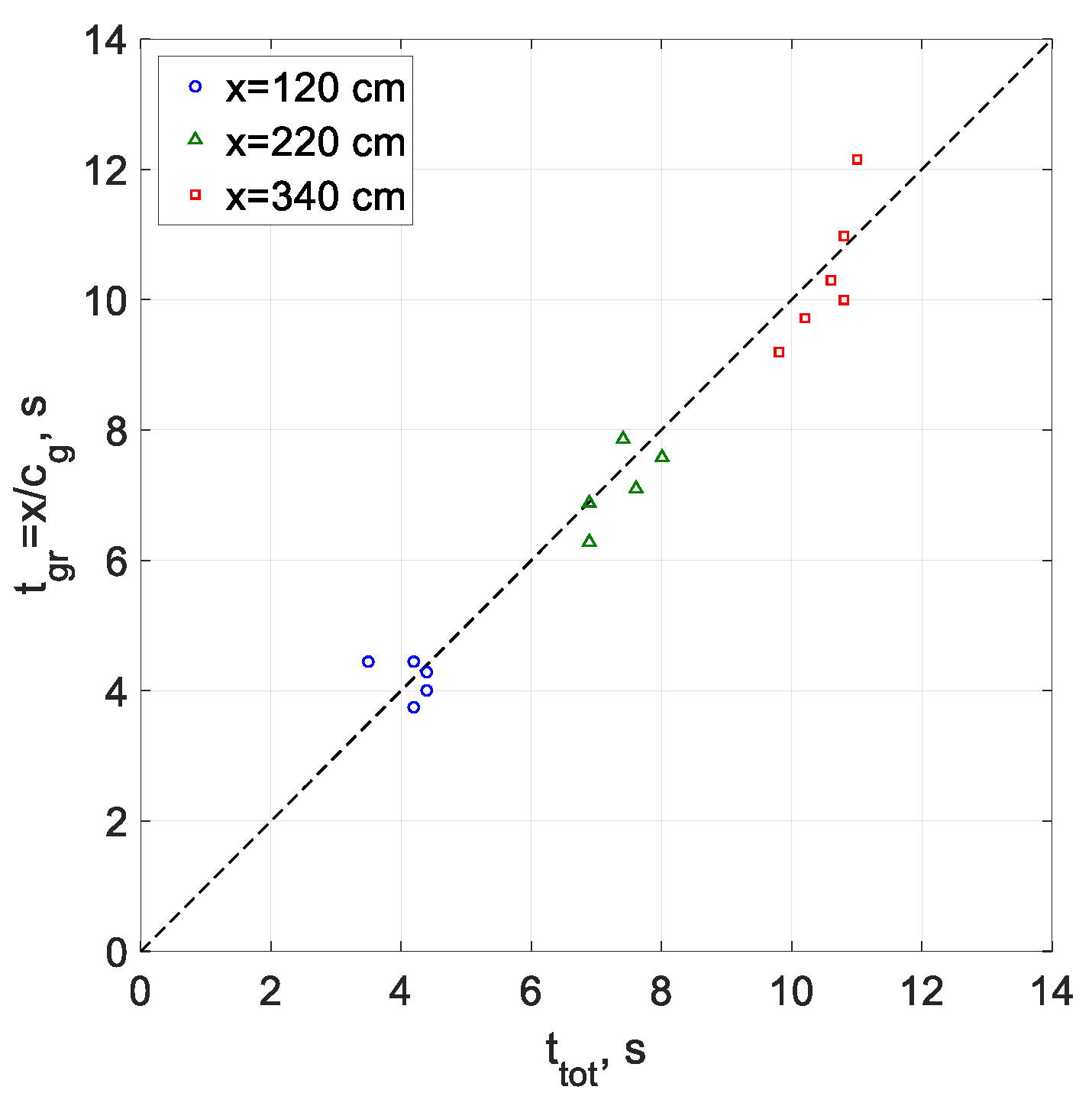
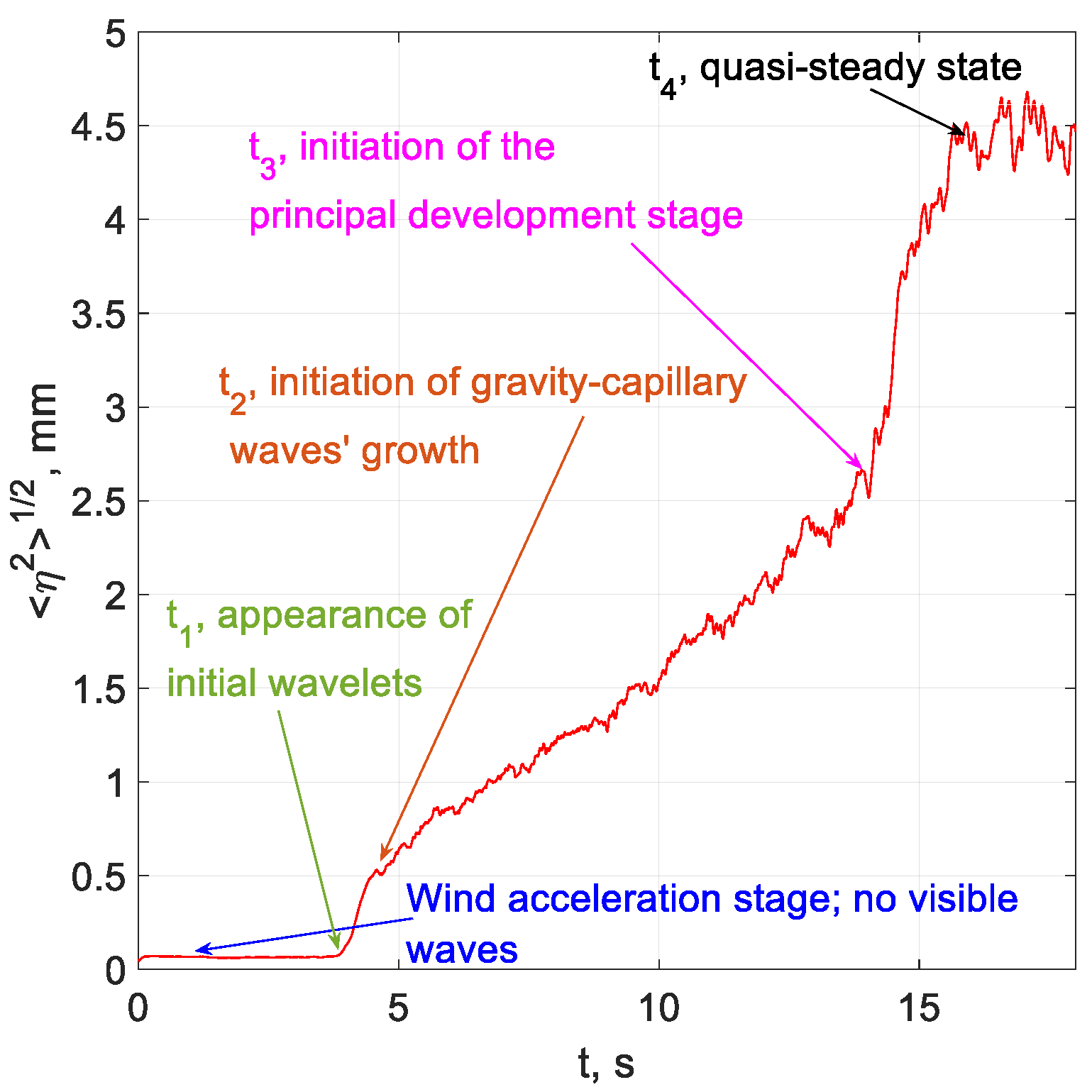
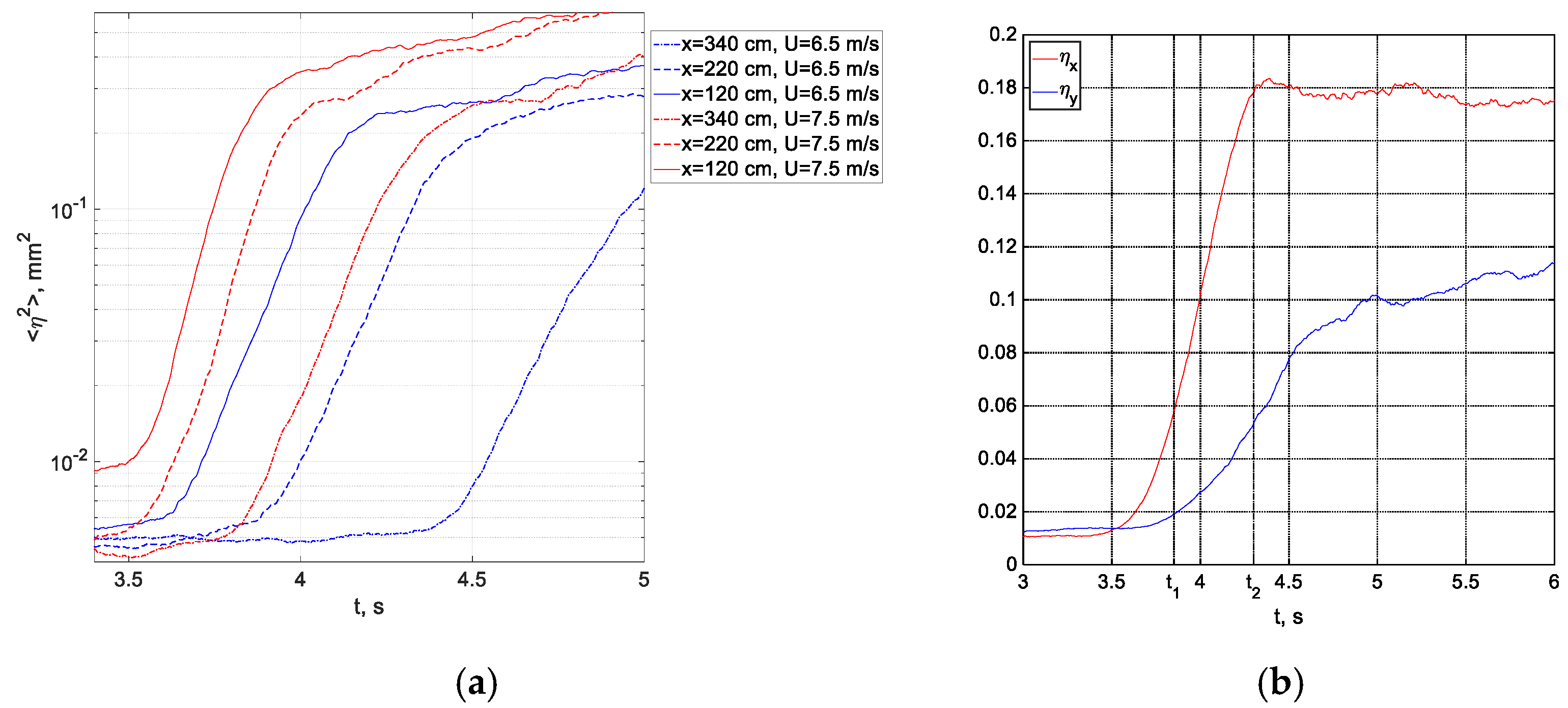
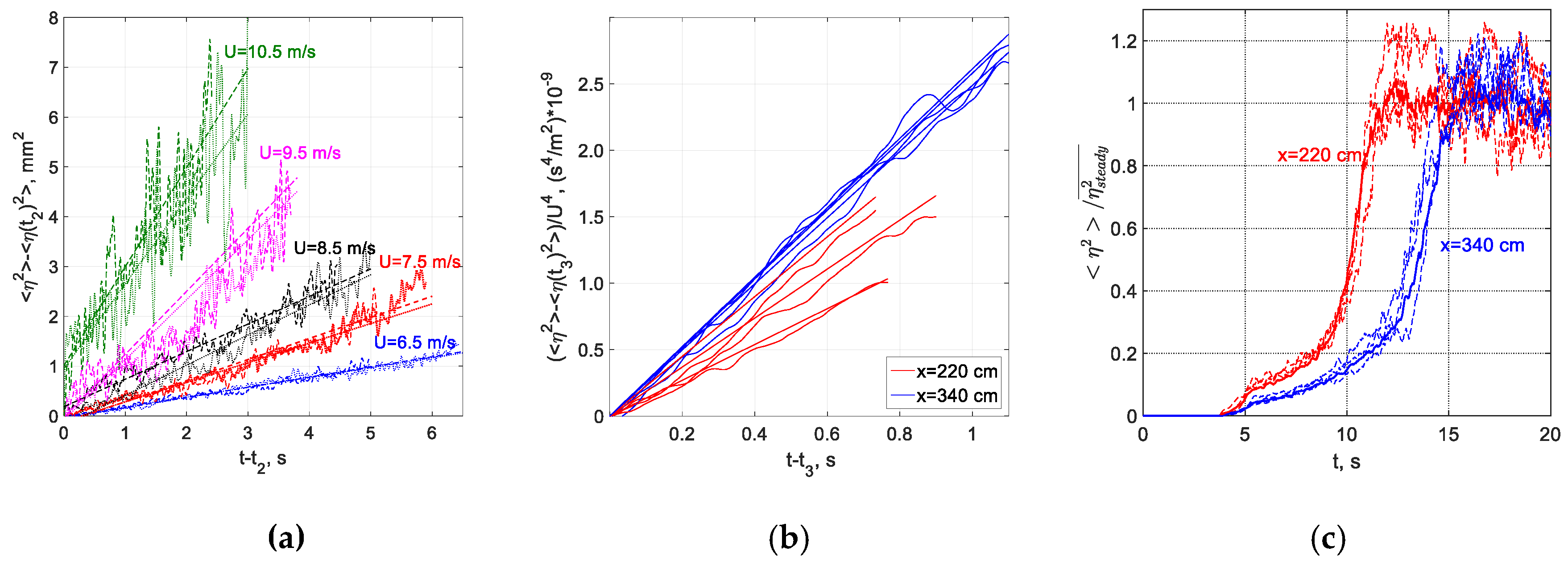
3.1. Characterization of the Air Flow above Wind Waves: Mean Velocity Profiles and Vertical Distributions of Reynolds Stresses
The interfacial shear stress
and thus the friction velocity
are usually determined in field as well as in laboratory experiments by performing measurements in the airflow. An accurate measurement of
is of crucial importance for the comparison of data obtained under various experimental conditions and for the evaluation of predictions of the theoretical models. The structure of the mean flow above the air-water interface is analogous to that of the turbulent flow above a stationary rough surface so that the logarithmic turbulent velocity profile
U(
z) outside the viscous sublayer is usually represented as:
where
= 0.41 is the von Karman constant and
z0 is the characteristic roughness. The drift velocity induced by the wind
Us at the local mean water surface
z = 0 should be accounted for and subtracted from the measured mean wind velocity
U(
z) in Equation (4) [
33,
51]. Both the friction velocity
and the roughness
z0 can be determined by fitting the measured velocity profile to Equation (4).
Alternatively, the friction velocity can be estimated by application of the eddy correlation method [
4]. To this end, instantaneous turbulent velocity fluctuations
u′ and
w′ in the horizontal (with wind) and vertical directions are measured by an X-hot-film probe. A profile of the turbulent Reynolds shear stress
extrapolated to the mean water surface elevation defines the friction velocity
(
z ). Values of the friction velocity in air
determined by thermal anemometry were reported by [
33,
68,
69], among others.
In [
53], measurements of instantaneous surface elevation and mean air velocity turbulent velocity fluctuation profiles were performed at seven fetches (1.0 m ≤
x ≤ 3.4 m) and at six different blower settings corresponding to the maximum wind velocities
Umax in the test section ranging from 5.5 to 11.2 m/s. No significant variation of
Umax was detected; deviations from the mean value along the test section did not exceed a few percentage points. Therefore, the average for all the fetch values of
Umax were used as the reference velocity. At each fetch and wind speed, the data acquisition was initiated only after the stationary wind and wave conditions, as well as the constant temperature, were attained.
To get accurate values of the friction velocity, the density of the measuring locations was higher closer to the air-water interface. At each measuring location and airflow rate, the sampling of X-hot-film data at the rate of 120 Hz continued for at least 5 minutes (min) to accumulate a sufficient amount of data for statistical analysis. Sensitivity to the sampling frequency was checked by performing experiments where the hot-film data were sampled at the rate of 1200 Hz/channel. No significant effect of the sampling frequency on the statistical turbulent flow parameters was detected. At each blower setting, the hot-film calibration was repeated after the completion of measurements at all elevations. In the Pitot-tube measurements of the vertical mean air velocity profiles, the vertical positions ranged from 1 mm to 130 mm relative to the highest wave crest, with the sampling duration at each point being 1 min.
The mean velocity distributions for two representative fetches (
x = 260 cm and
x = 240 cm) are presented in
Figure 2. Additional experimental data on the vertical air velocity profiles can be found in [
51,
53]. Coles [
70] showed that for solid stationary surfaces, starting from
(approximately about 20% of the turbulent boundary layer thickness), the profile is no longer of logarithmic form, and is affected by the flow in the outer (‘wake’) layer. Thus, the boundary layer thickness over the mean water surface
δ (taken here as the elevation where the mean velocity attains 99% of its maximum value) was chosen in
Figure 2 as a parameter to normalize the elevation over the mean water surface. The values of
δ range from about 50 mm at shorter fetches to about 80–90 mm at
x = 340 cm; the variation of
δ with wind velocity at each fetch is insignificant. The advantage offered by the automatic experimental procedure made possible air velocity measurements at about 100 vertical positions. For lower wind velocities and thus lower wave crests, measurements were performed quite close to the water surface. Since waves grow with the fetch
x and with the wind velocity
Umax, the lowest measuring location had to be shifted upward (relative to the mean water level) accordingly. It is possible to distinguish in the profiles plotted in
Figure 2 between two regions. The lower part of each profile, up to about 0.4
δ, i.e., for maximum elevations not exceeding about 15 mm for lower fetches to about 30 mm at the far end of the test section, is linearly fitted and exhibits logarithmic velocity distribution, while above this region, deviation from the fit can be noticed [
70,
71]. When the log fit is performed on the whole set of data that extends to the outer part of the boundary layer, the resulting slope of the line is somewhat different, and the values of
and
z0 resulting from such a fit are less accurate. The logarithmic fit curves for a given
Umax at panels in
Figure 2 have similar slopes. The same observation holds for additional fetches, as shown in [
53]. In view of Equation (4), this indicates that the friction velocity
does not vary notably with fetch. The vertical shift of the profiles with
x and with
Umax implies that the effective surface roughness
z0 in the present experiments generally increases with fetch and with the wind velocity.
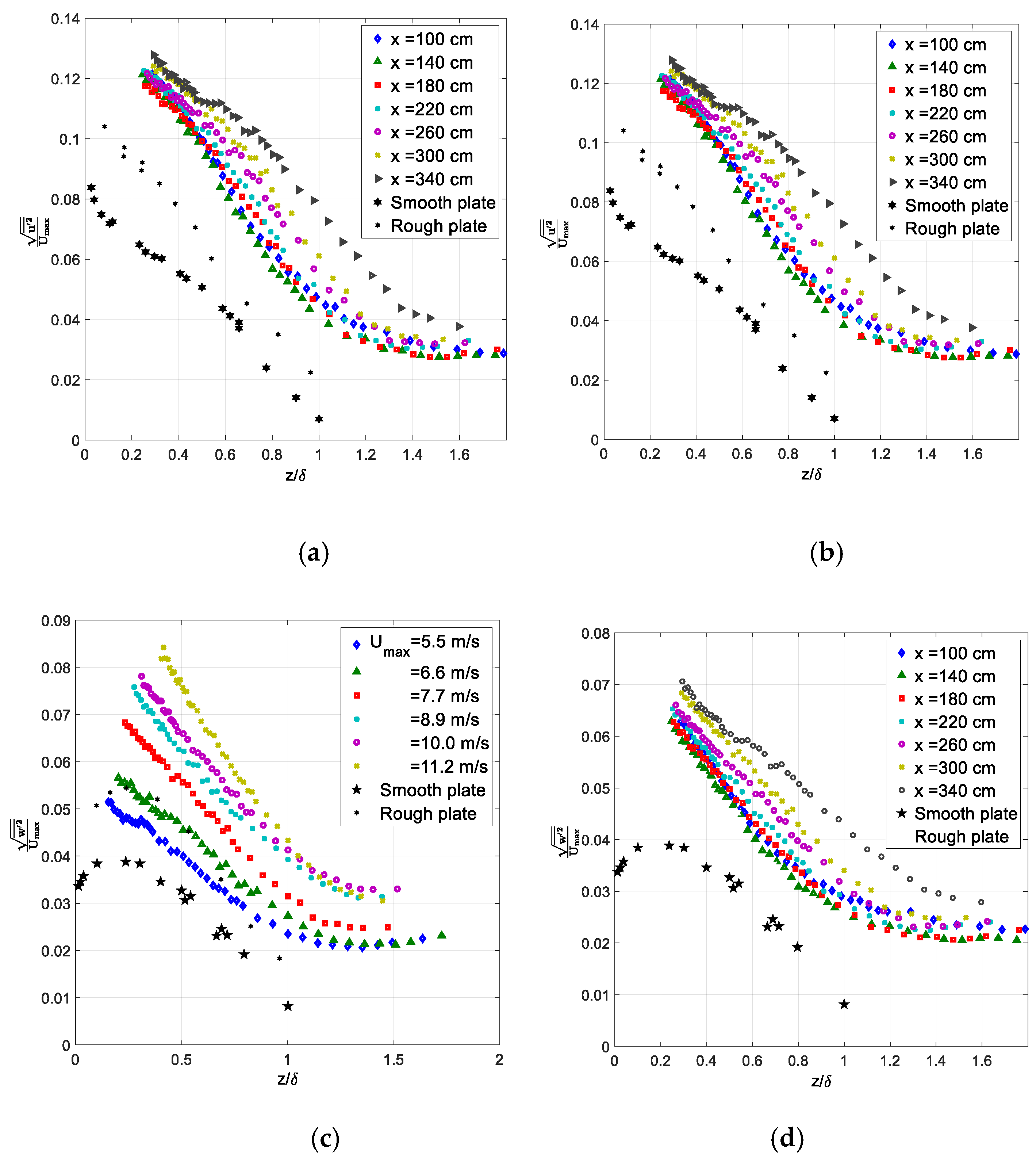
The vertical profiles of the root mean square (RMS) values of the deviations of the instantaneous velocity components from the local mean values in both longitudinal (
u′) and vertical (
w′) directions measured with an X-type hot-film anemometer are presented in
Figure 3. The effect of the wind velocity in the test section represented by
Umax is studied in panels (
a) and (
c) for a fixed fetch
x = 300 cm. In
Figure 3b,d, the profiles of the normalized by
Umax RMS values of two components of the turbulent fluctuations are plotted for various fetches, and a constant value of
Umax = 7.7 m/s are plotted. Those results are related to the classical measurements of turbulent flow over a solid surface in
Figure 3a,c. Here, the corresponding vertical profiles of turbulent velocity fluctuations measured in turbulent boundary layer over a smooth plate by Klebanoff [
72] and over a rough plate by Corrsin and Kistler [
73] (see also Hinze [
74]) are presented as well; those measurements were performed at comparable free stream air velocities.
As in
Figure 2, the distance
z from the mean surface level is normalized by the boundary layer thickness
δ. The values of the normalized turbulent velocity fluctuations
u′ and
w’ in
Figure 3 exhibit qualitative and to some extent quantitative similarity, with those in the turbulent boundary layer over a solid surface, although they are generally somewhat higher even than those in the flow over a rough rigid plate. The difference can be mainly attributed to the higher turbulent level in our wind tunnel, as can be seen from comparison of the turbulent intensities outside the boundary layer. Due to the limitations imposed by water waves, measurements were mostly made at somewhat higher elevations. Note also that in closer vicinity to the interface, the RMS values of the velocity fluctuations as
z tends to zero over a solid surface vanish, while over the waves, they remain finite due to the orbital wave motion at the air-water interface.
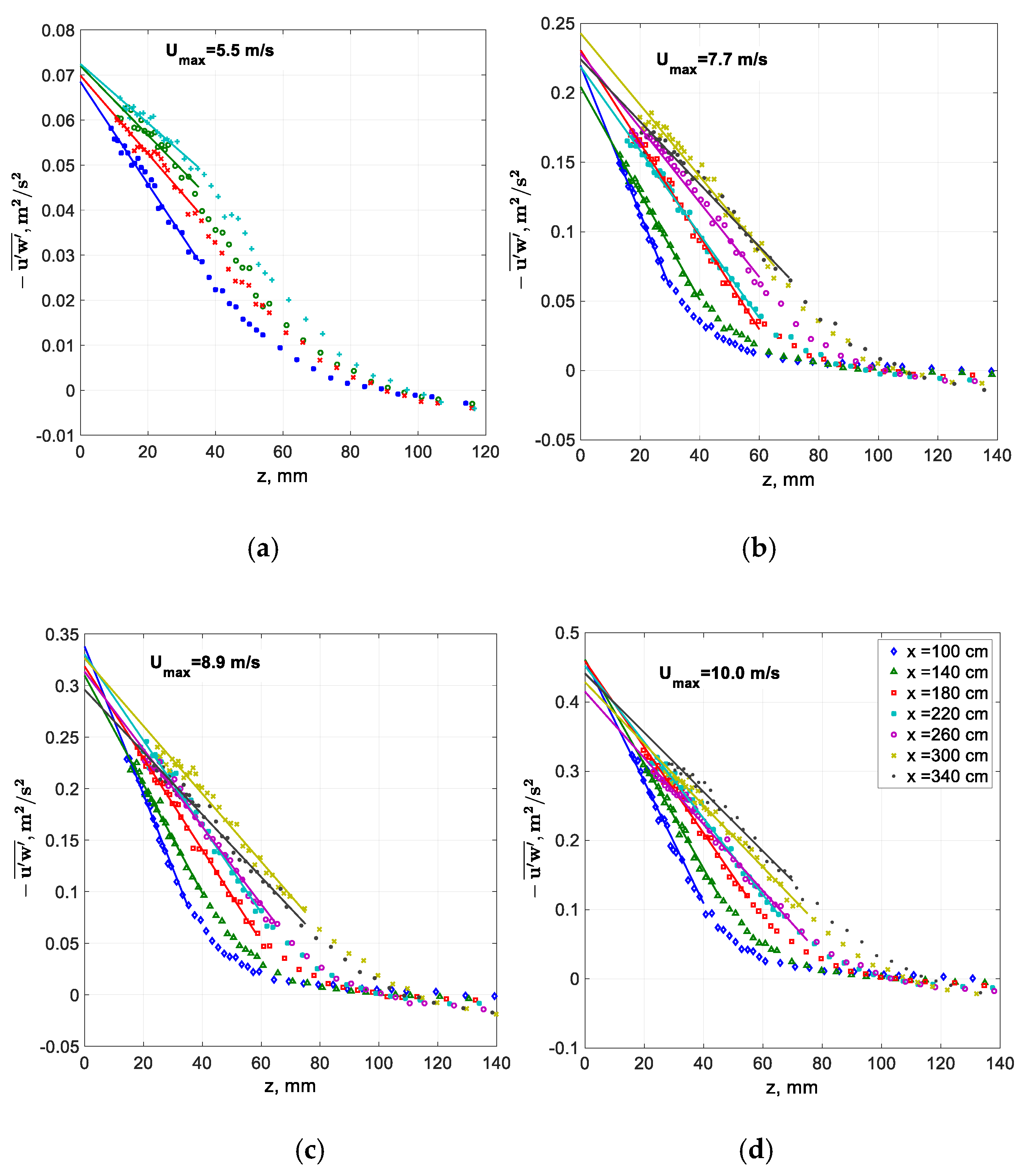
Measurements of the Reynolds shear stresses
allow the direct evaluation of the friction velocity
(the so-called eddy correlation method). The measured variation of the Reynolds shear stress
with height is presented in
Figure 4 for four wind velocities
Umax; additional data can be found in [
53]. The vertical profiles of the Reynolds stress are affected by the mean pressure gradient [
52]. The pressure drop over the test section is quite modest, ranging from a few Pascals for low flow rates to about 20 Pa for
Umax ≈ 9 m/s. The Reynolds shear stresses within the boundary layer vary linearly with elevation for all wind flow rates and fetches, vanishing in the central part of the test section, and changing sign with approach to the roof of the channel. The data points within the boundary layer were linearly fitted, with fits extrapolated to the mean water level
z = 0. The limiting value of the Reynolds shear stress at
z = 0 can be seen as the squared value of the friction velocity
(the so-called eddy correlation method). The very limited scatter of the limiting values of
extrapolated to
z = 0 in each frame of
Figure 4 indicates that the values of the friction velocity measured by the eddy correlation method in the present experiments are practically independent of fetch. However, the interfacial shear stress increases notably with the wind velocity.
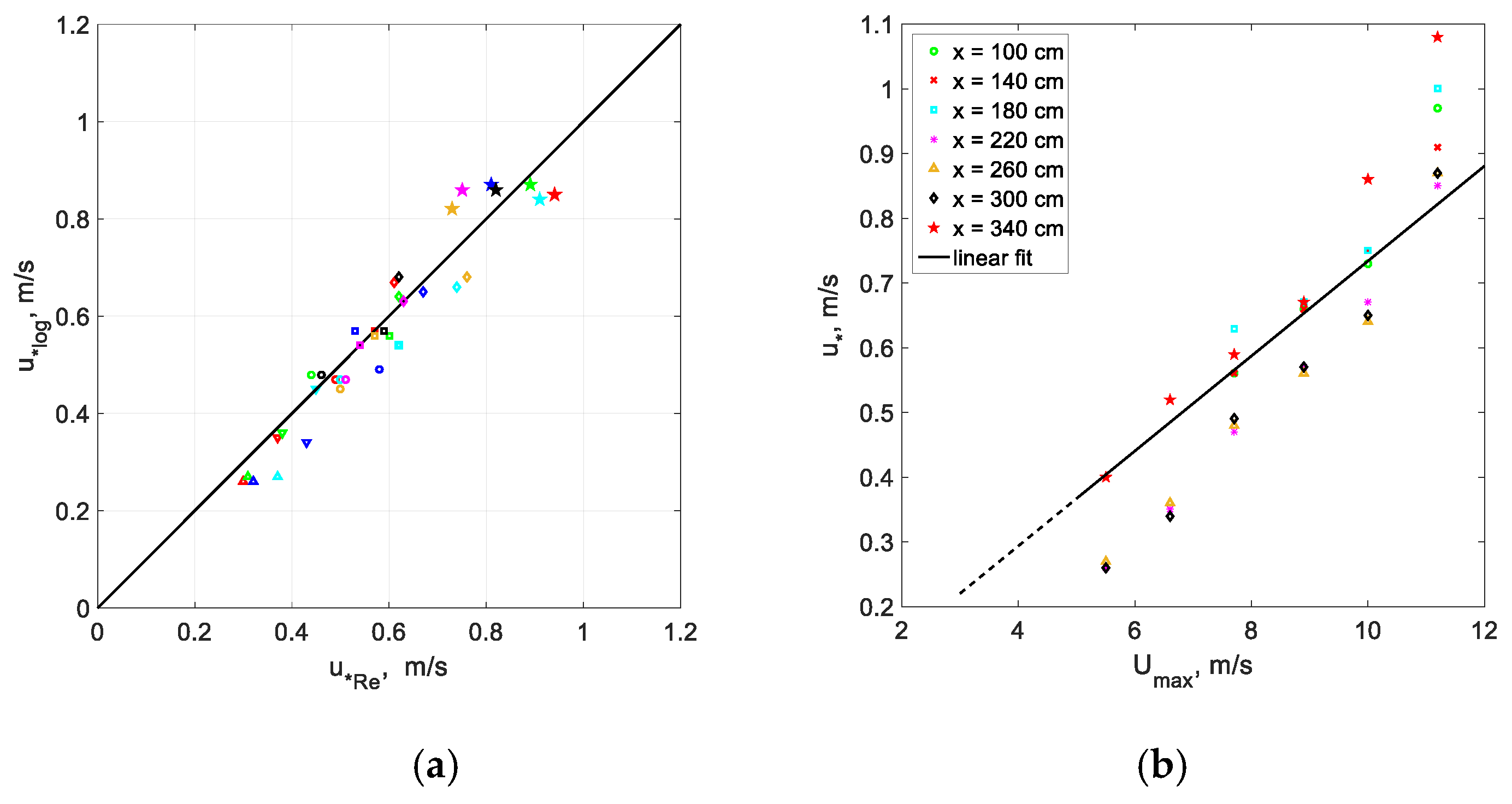
The eddy correlation method for the determination of the shear stress is considered more reliable as compared to determination of
from the velocity profiles, as presented in
Figure 2 and in the application of Equation (4), since the Reynolds stress is measured directly. However, thermal anemometry is more complicated and time consuming; thus, the measurements in [
53] were carried out for a limited set of parameters. To validate the accuracy of both approaches, the friction velocities estimated from the logarithmic fit of mean velocity profiles and the values derived by application of the eddy correlation method are compared in
Figure 5a for all fetches and wind flow rates.
It is obvious from
Figure 5a that these two independent methods yield very similar results, with the scatter within about 5–10% and data points spread at both sides of the 45° line. Thus, it is demonstrated that estimating the values of
from the logarithmic fit of the mean wind velocity profile that contains a sufficiently large number of data points close to the air-waterinterface can serve as a reliable method for the determination of the friction velocity. However, it should be stressed that measurements should be restricted to elevation satisfying the condition
z/δ < 0.4.
As can be seen in
Figure 5b, the values of
do not depend notably on the location along the test section (with a possible exception of very short fetches), and are roughly proportional to
Umax. The fit in this figure corresponds to the relation
= 0.73
Umax. These results are in agreement with [
51]. An attempt has been made to examine the effect of the surface drift velocity,
Us, on the values of
and
z0, by substituting
U(
z) –
Us instead of the mean velocity
U(z) in
Figure 1a. The measurements of
Us were performed in [
51] using particle tracking velocimetry and demonstrated that the drift velocity constitutes about 3% of
Umax. However, this modification had only a minor effect on
and
z0 that did not cause deviation exceeding 2–3% for
, and practically did not affect the effective roughness. The values of the effective water surface roughness,
z0, that were also retrieved from those fitted velocity profiles as shown in
Figure 2, as well as more details on the measurements of friction velocity are presented in [
53].
3.2. Statistical Parameters of Waves under Steady Wind Forcing
Measurements of the principal statistical parameters of wind waves were carried out in Zavadsky et al. [
75] at eight fetches (100 cm ≤
x ≤ 380 cm). The blower operated at nine airflow rates, resulting in the maximum wind velocities in the test section in the range 3.3 m/s ≤
Umax ≤ 12.3 m/s and friction velocities 0.17 m/s ≤
≤ 1.28 m/s. At each fetch and wind velocity
Umax, the instantaneous variation of the surface elevation was continuously recorded for 90 min at the sampling rate 120 Hz, thus enabling the accumulation of very large ensembles of experimental data.
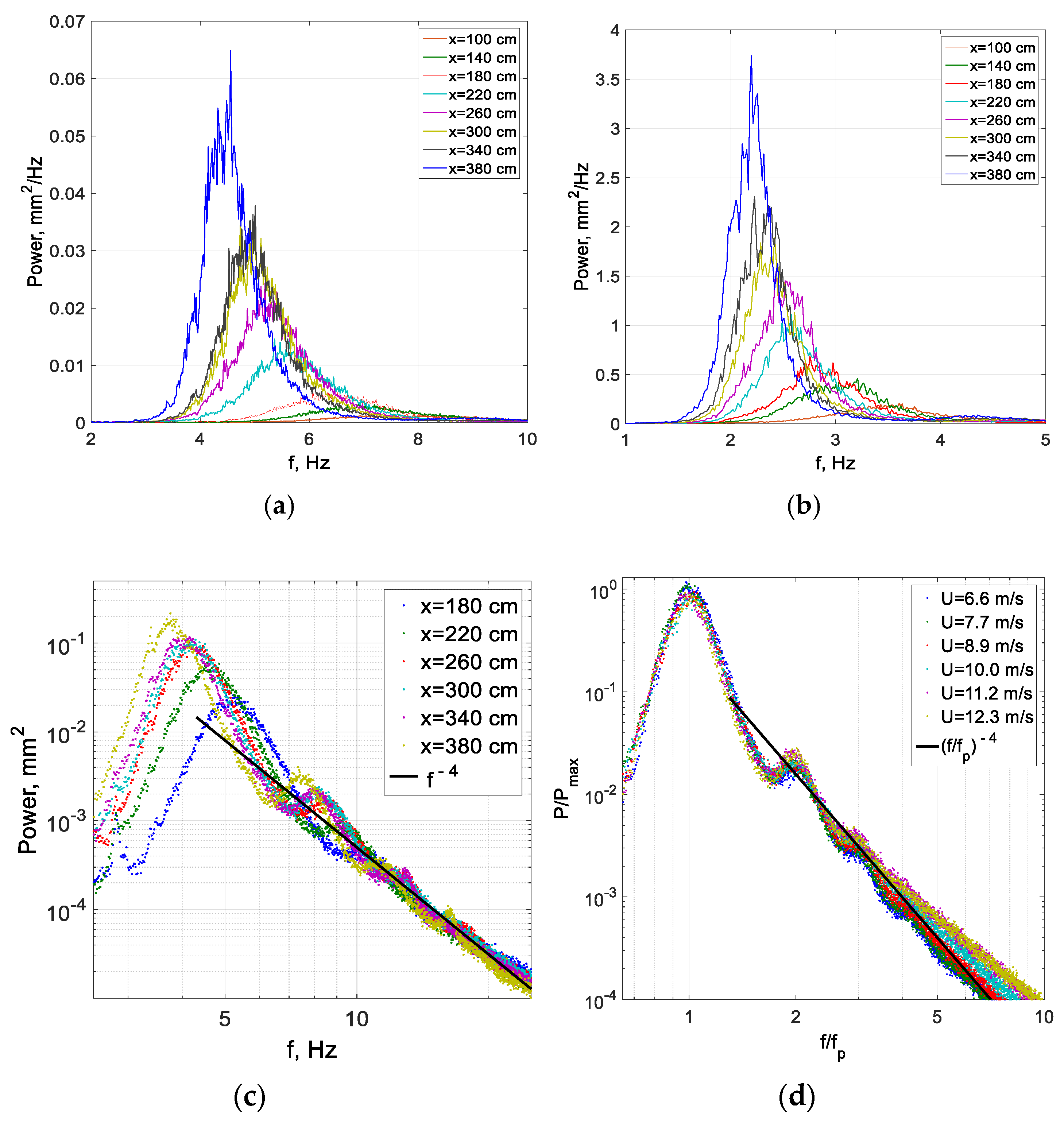
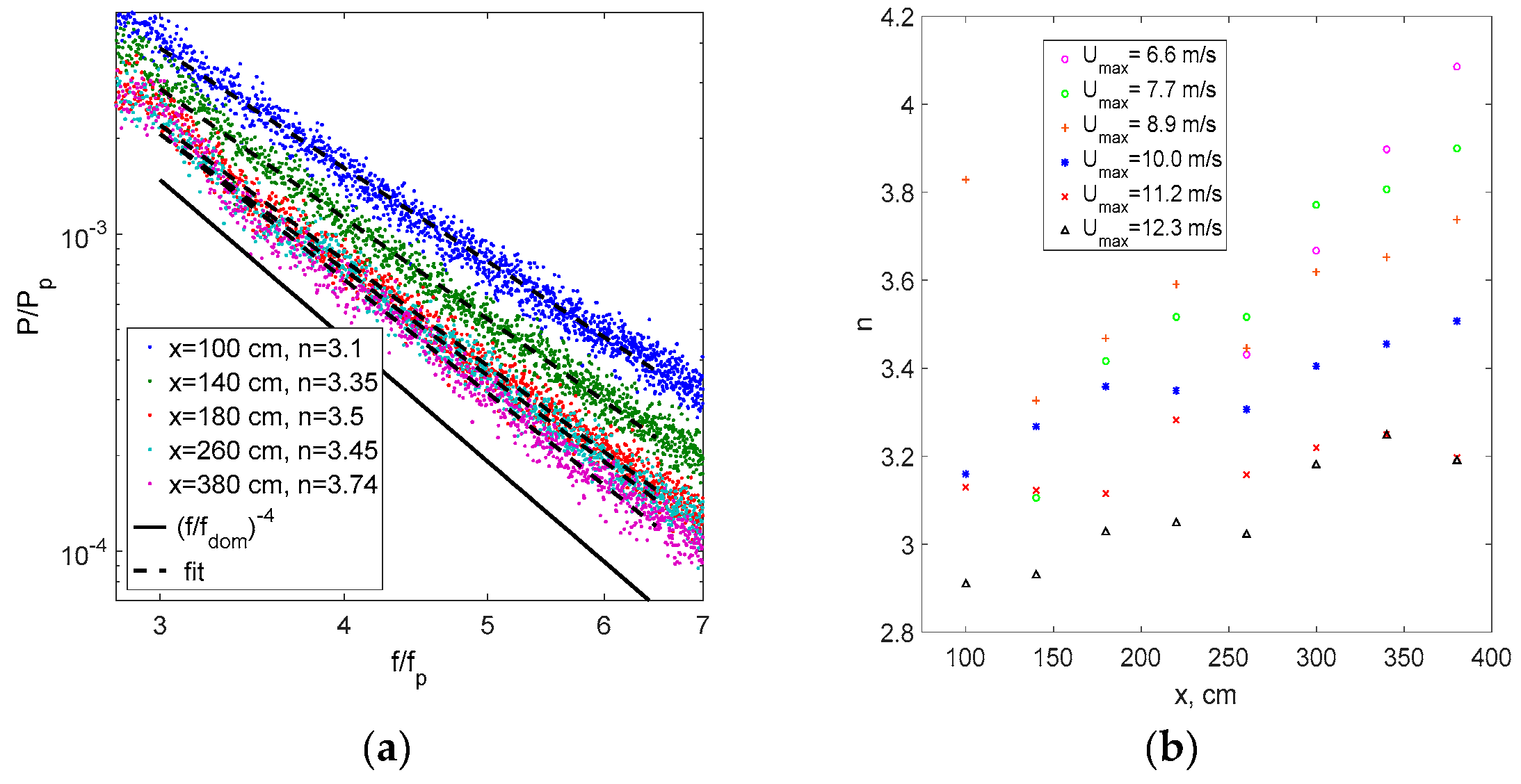
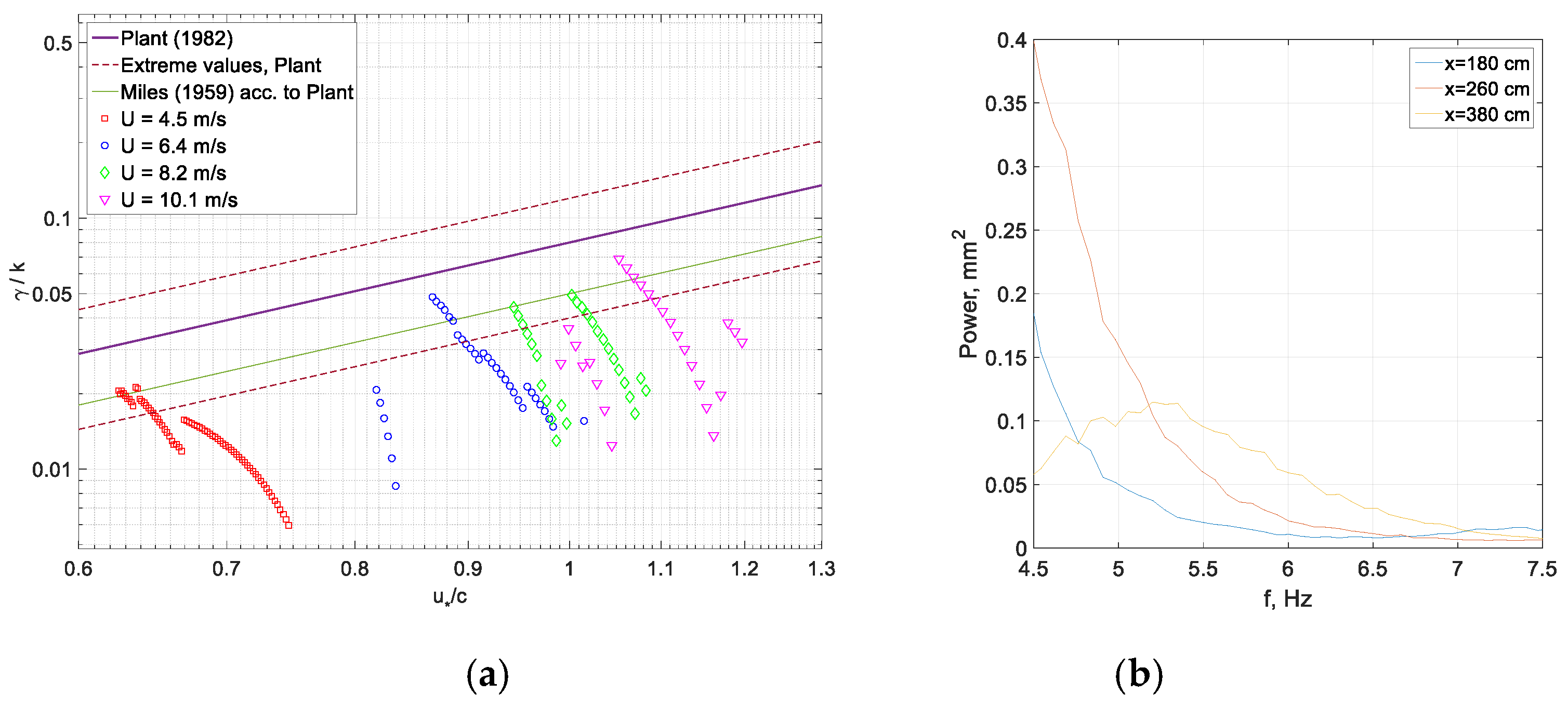
The power spectra of the surface elevation variation with time,
η(
t), were calculated by dividing each record into windows that contained 8192 points (duration of each window about 70 s), with 50% overlap, resulting in 94 segments for each fetch and airflow rate. The variation with fetch of the surface elevation power spectra averaged over all windows is presented in
Figure 6a,b for two representative airflow rates.
It is obvious from these panels in
Figure 6 that at each flow rate, the total wave energy increases along the channel, while the peak frequency decreases with fetch; therefore, both the horizontal and vertical axes of the two panels of
Figure 6 are scaled differently. A comparison of the panels in
Figure 6a,b also demonstrates downshifting of the peak frequency at a given fetch with increasing wind speed. These results are in agreement with [
51]. The characteristic frequency of the wind-wave field can be defined either as the frequency at the spectral peak,
fp, or as the dominant frequency,
fdom, based on the spectral moments:
As mentioned in the Introduction, the zero-th moment m0 defines the characteristic wave amplitude Note that in Equation (5), the integration is carried out over the free waves’ domain only; this domain for each spectrum, ωmin < ω < ωmax, is taken within ±60% of the peak frequency.
Since
fdom is an integral value and thus less prone to variations in the experimentally estimated wave power spectra; it is a more robust quantity at each fetch and airflow rate. However, the frequency of the spectral peak
fp is a physical and visual parameter that is more intuitively straightforward than
fdom, and therefore is usually chosen as the characteristic of the wave field. To mitigate the scatter in the power spectra as seen in
Figure 6, the value of
fp is defined as the frequency of the peak of the parabolic fit performed within about ±0.3 Hz around the maximum values in the experimentally determined spectra. The comparison of the values of
fdom and
fp carried out in [
75] demonstrated that although the difference between these two parameters is small,
fdom is consistently larger than
fp due to the greater contribution of higher frequencies in the computation of the spectral moments
m1, as shown in Equation (5), with the slope of the linear fit of 0.96.
The surface elevation power spectra are now examined in greater detail in
Figure 6c,d. In
Figure 6c, the spectra obtained at several selected fetches at a constant air flow rate are plotted in a logarithmic scale as a function of the dimensional frequency, whereas in
Figure 6d, the power spectra are normalized by their peak values and plotted for several wind velocities as a function of
f/fp. The lines corresponding to the power law:
with
n = 4 are also plotted in
Figure 6c,d.
The spectra in the panels c and d of
Figure 6 are characterized by peaks at the second and the third harmonics of the peak frequency
fp; at low wind velocities, even weaker peaks corresponding to the fourth harmonic can be identified. Those peaks signify the contribution of nonlinear bound waves. At frequencies exceeding the third or the fourth harmonics of
fp, the peaks associated with bound waves cannot be distinguished; those frequencies correspond to the so-called quasi-saturated high-frequency tail. The normalized power spectra of the surface elevation for a range of wind flow rates in
Figure 6d seem to collapse on a single curve for
f < 3
fp.
The tail behavior is only in qualitative agreement with that corresponding to
n = 4; a notable spread of the tail slope is clearly visible in
Figure 6d. Therefore, a closer look at the power-law dependence on the frequency of the high-frequency ‘tail’ of the spectra is presented in
Figure 7a. The linear fit range 3 <
f/fp < 6 was chosen in this figure, as the spectra in this part are free of noticeable higher harmonic peaks, which can affect the slope. The power
n that defines the exponent in the power law shown in Equation (6) is defined by the slope of the fit. The values of
n are usually somewhat above
n = 3 and remain mostly below
n = 4; they decrease with wind velocity and have a tendency to increase with fetch. At the largest wind velocity, the measured value of
n is the lowest, and is close to the theoretical prediction of
n = 17/6, which equals approximately 2.83, for purely capillary waves [
76], it increases with fetch from
n = 3.1 for
x = 100 cm to
n = 3.74 for the longest fetch,
x = 380 cm.
The measured characteristic wave parameters can be presented as relations among dimensionless groups. For steady wind forcing, those parameters depend on fetch only. The friction velocity
is the quantity directly related to momentum transfer from air to water, and as stated in
Section 3.1, for a given airflow rate in the test section, it is essentially independent of fetch. The characteristic wave amplitude can be represented either by the RMS value of the surface elevation
, or based on the zero spectrum momentum,
. The definition based on the spectral momentum seems to be advantageous as it contains free wave components only, which is in agreement with most nonlinear wind-wave theories; see e.g., [
49]. The comparison of
and
for all experimental conditions demonstrates that wave energy is mainly contained in the spectral range around the peak frequency; the values of
are smaller than the corresponding RMS values of the surface elevation by less than about 3%.
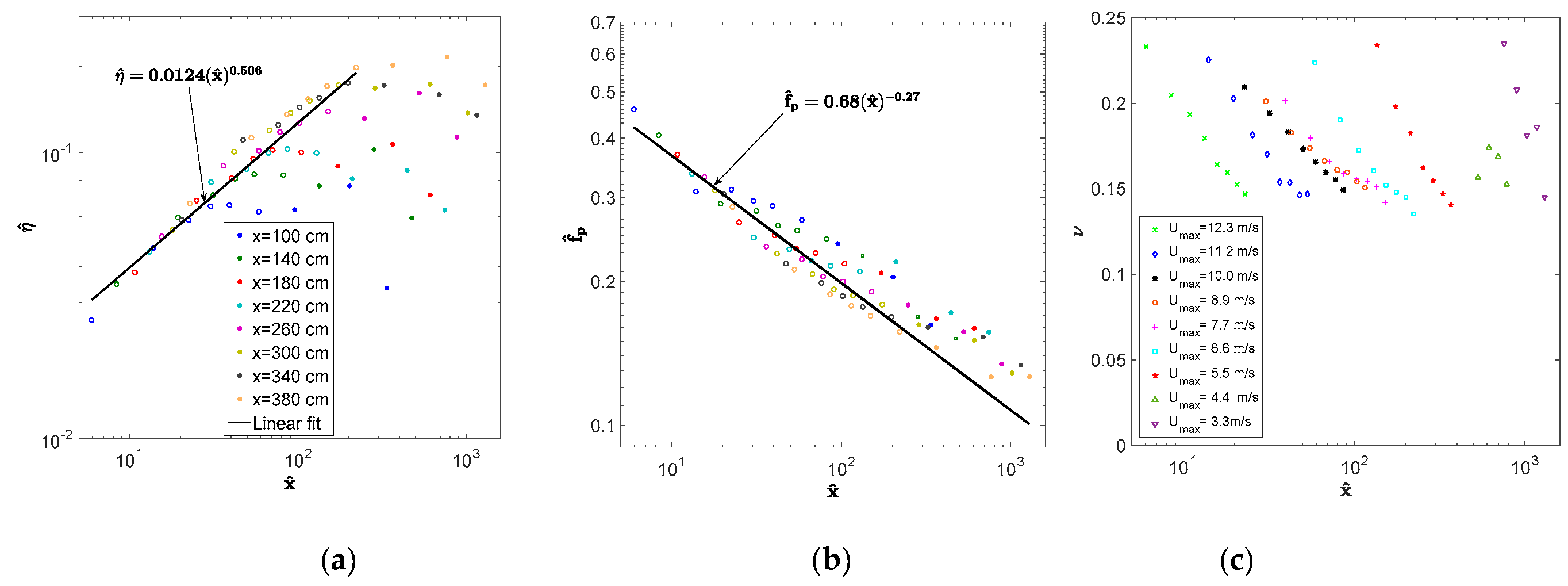
In view of the relations shown in Equations (1) and (2), the characteristic amplitude and the peak frequency can be presented in dimensionless form as
and
, where the dimensionless fetch
=
. Note that for a given dimensional distance from the inlet
x, the dimensionless fetch
decreases with
, and thus with the increased airflow rate in the tank. The dependencies of the dimensionless amplitudes
and dimensionless peak frequencies
on the dimensionless fetch
are plotted in
Figure 8a,b.
The majority of points (denoted by open symbols) in panels a and b in
Figure 8 fit a linear dependence in log–log coordinates, and thus exhibit power-law behavior. The dimensionless frequency
decreases with the dimensionless fetch as
, while the dimensionless wave amplitudes
grow as
. The scatter of data represented by open symbols around the fit line can be attributed in part to local variations in the friction velocities. The power dependencies presented in
Figure 8a,b are in agreement with the wind-wave channel measurements at a comparable range of dimensionless fetches by Mitsuyasu [
77] and Mitsuyasu and Honda [
78], who suggested the following relations:
Similar results were obtained in field measurements by the JONSWAP group [
79] and by Kahma [
80]. The points in
Figure 6a,b that do not fit the general trend and are marked by filled symbols correspond to lower wind velocities and thus higher dimensionless fetches
. The peak frequencies at lower wind velocities mostly exceed 5 Hz at all fetches; the frequencies of the corresponding short waves are strongly affected by Doppler shift due to the surface drift current [
51]. The effect of the drift current that is mostly pronounced at low airflow rates seems to cause the deviation from the power law of the energy growth and peak frequency variation along the test section; therefore, these values were not included in the data fits in
Figure 6. The relation between the dimensionless wave amplitude
and peak frequency
can be obtained from the linear fits in
Figure 6:
This result differs somewhat from the generally accepted −3/2 power law
Hs = BTs−3/2 proposed by Toba [
81] that is based on extensive empirical data; here,
Hs is the significant wave height, and
Ts is defined by the peak frequency.
The dimensionless spectral width ν defined by the spectral moments in Equation (5) as:
is an integral characteristic of the shape of the free-wave part of the power spectrum at lower frequencies around
fp. The values of ν calculated for all wind velocities in the present experiment are plotted in
Figure 8c as a function of the dimensionless fetch
. For each
Umax, the spectral width decreases with
x, the rate of decrease is higher at lower fetches and wind velocities. The values of the spectral width vary from about ν = 0.25 to ν = 0.145; they become nearly constant around
ν = 0.17 for higher fetches and stronger winds. Thus, the process of the evolution of wind-wave spectra with fetch is characterized by a decrease in both the peak frequency
fp and the spectral width ν.
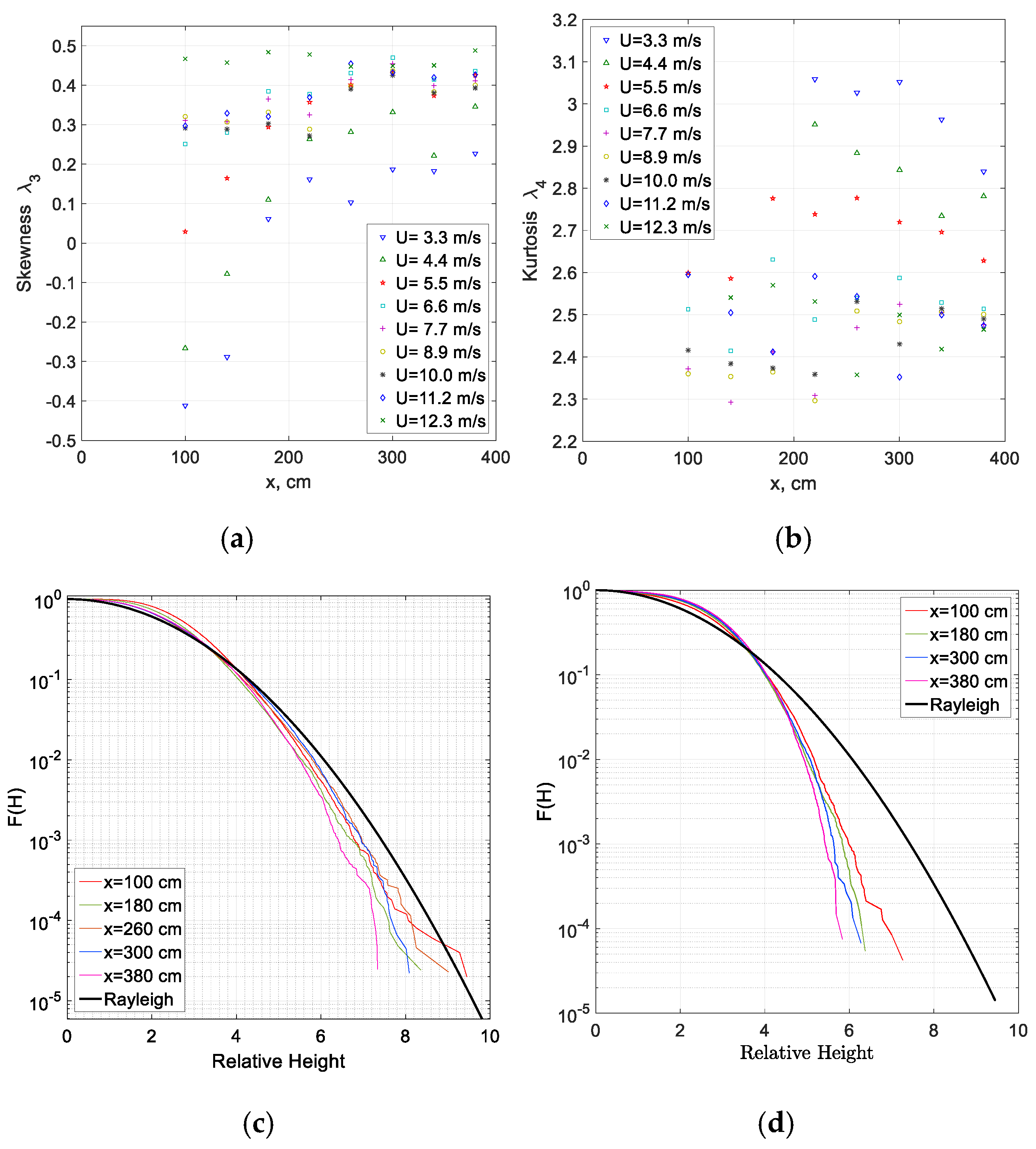
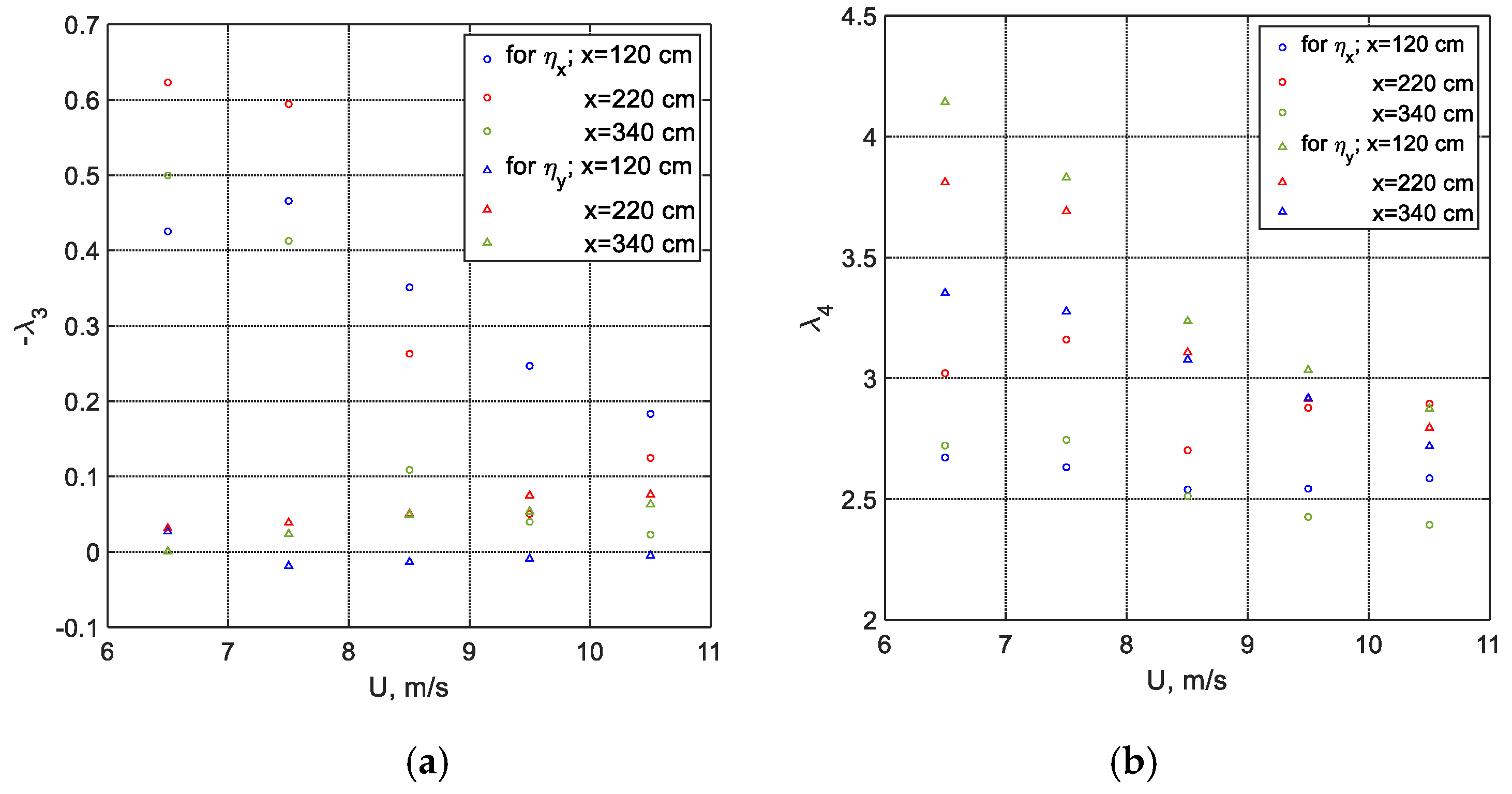
The deviation of the surface elevation behavior in a random wind-wave field from Gaussianity is examined in
Figure 9. The lack of exact Gaussianity can be characterized by coefficients of skewness,
λ3, and kurtosis,
λ4, which is defined as:
for normally distributed random variables,
λ3 = 0 and
λ4 = 3. The values of
λ3 and
λ4 calculated from the measured data for all cases are plotted in
Figure 9a,b.
The skewness coefficient
λ3 is plotted in
Figure 9a. It characterizes the vertical wave asymmetry and is positive for all records except for very short fetches and the lowest wind velocities, where the wave heights are extremely small (usually less than 1 mm). The measured values of skewness tend to increase with fetch and with wind velocity, attaining values close to 0.5 at larger fetches and wind velocities. Positive values of
λ3 characterize an essentially nonlinear wave field where the crest heights exceed those of troughs due to the contribution of the second-order bound waves that cause an effective increase in wave crests and decrease in troughs [
82]. The kurtosis coefficient characterizes the deviation of wave height probability distribution from Gaussian. The values of
λ4 plotted in
Figure 9b are below the Gaussian limit of three for all wind velocities and at all fetches, except for the low wind velocity at moderate fetches, where it is somewhat higher. For wind velocities exceeding about 7 m/s, the kurtosis coefficient seems to be nearly constant at
λ4 ≈ 2.4–2.6 and essentially independent of both the fetch and the wind velocity. These values of
λ4 indicate a relative deficit of large-amplitude waves in the distribution. The values of kurtosis presented in
Figure 9(b) are in qualitative agreement with the experimental results of Shemer et al. [
82] obtained for mechanically generated unidirectional random waves at comparable values of the spectral width
ν. However, they disagree with the results of wind-wave simulations by Annenkov and Shrira [
83] based on the Zakharov equation, which obtained
λ4 > 3.
The relatively low probability of very steep waves in the present experiments, as suggested by the results of
Figure 9b, is further validated by plotting the probability distribution of the wave height along the flume, as shown in
Figure 9c. The results presented for the extreme values of the airflow rate in these experiments are also representative for all other wind velocities. For linear narrow-band Gaussian waves, the wave heights
H follow the Rayleigh exceedance distribution [
84]:
Longuet-Higgins [
85] also has shown that nonlinearities can cause the deviation of surface elevation distributions
F(
H) from the Gaussian statistics. Numerous laboratory experiments, in situ measurements, and numerical simulations indeed support this conclusion (see, e.g., [
82,
86,
87] and the references therein).
The exceedance distributions obtained in the present experiments are compared in
Figure 9c,d with the Rayleigh distribution. Each individual wave height was calculated as the difference between the maximum and minimum between two consecutive positive zero crossings. Note that the statistics in those panels is based on ensembles that contain more than 10
4 individual waves. For all experimental conditions, notable deviations from the Rayleigh distribution are indeed clearly visible in those panels. For the Rayleigh distribution, the significant wave height
Hs ≈ 4
. The probability of small and moderate waves with heights
H <
Hs, is higher in
Figure 9c,d than that corresponding to the Rayleigh distribution. However, the probability of waves higher than
Hs is overestimated by Equation (10). These deviations from the Rayleigh distribution are stronger for the higher wind velocity in
Figure 9d as compared to the weaker wind case in
Figure 9c. No dependence of the measured
F(
H) on fetch can be clearly identified in those panels. Few extreme waves recorded at the low wind flow rate in
Figure 9c appear exclusively at short fetches characterized by vanishing wave heights. Extremely steep (the so-called freak) waves are usually defined as waves with heights exceeding 2
Hs or 8
. Thus, it follows from the present results that the probability of such waves is considerably overestimated by the Rayleigh distribution; those waves are totally absent in all ensembles accumulated at the high wind velocity, as shown in
Figure 9d.
The asymmetry of wind waves was further investigated by Zavadski and Shemer [
88]. The positive values of the skewness coefficient
λ3 in
Figure 9a indicate asymmetry relative to the horizontal axis. The asymmetry of individual waves relative to the vertical axis can be characterized in terms of the distances between a successive wave crest, trough, and the next crest [
89]. However, this approach is applicable mainly for the characterization of individual two-dimensional waves; it is ill-suited to describe the statistically representative asymmetry of random wind waves. Elgar [
90] and Elgar and Guza [
91] demonstrated that the asymmetry
A relative to the vertical axis is related to the imaginary part of the frequency bispectrum of the surface elevation variation in time,
η(
t). They showed that the imaginary part of the bispectrum can be presented by the Hilbert transform
H(
η(
t)), and that the asymmetry
A can be seen as the normalized skewness of
H(
η(
t)):
where the overbar denotes time averaging.
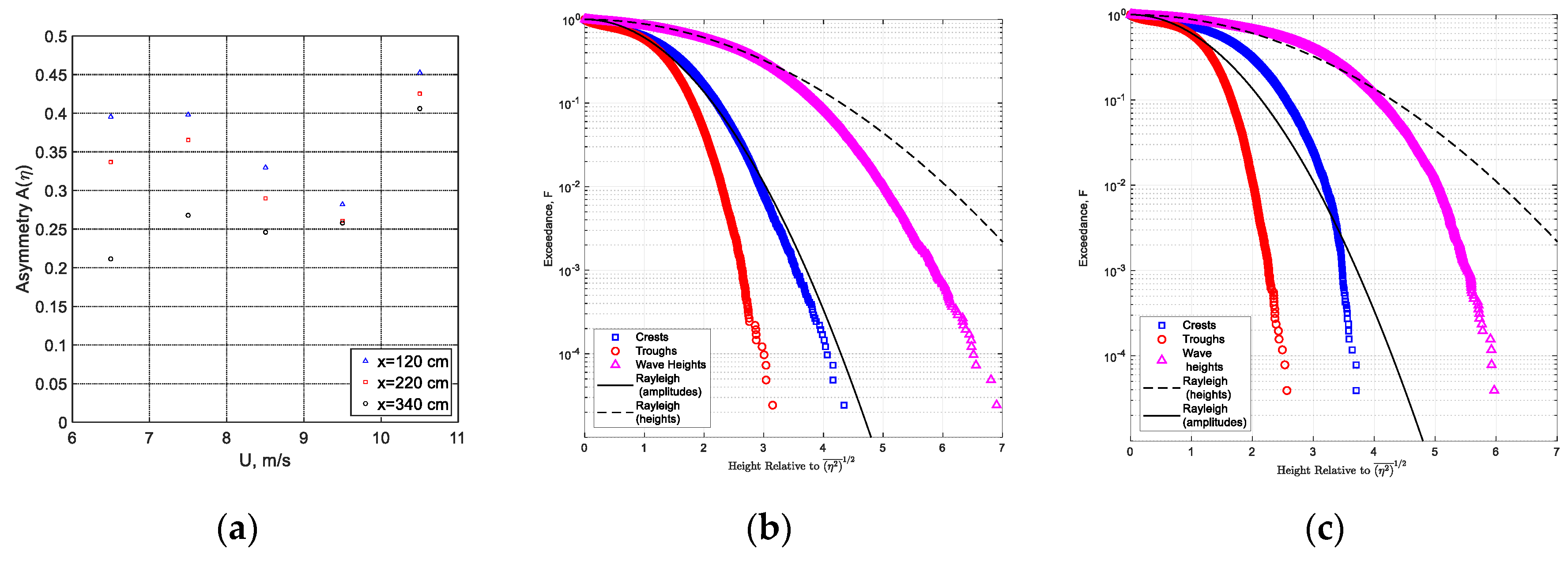
The asymmetry of the surface elevation calculated using Equation (11) is plotted in
Figure 10a for several fetches and wind velocities. The positive values of
A(
η) correspond to the forward face of the wave being steeper, on average, than the rear slope. For a given wind velocity, the asymmetry decreases with fetch.
In addition to wave heights, the exceedance of probability distributions for crest heights and trough depths were also computed in [
88]. The crest and trough parameters were calculated as local maxima and local minima between two consecutive positive zero crossings. In those experiments, the total sampling duration was about 3 h at each fetch and wind velocity, allowing to record ensembles containing the number of individual waves (0.3–0.8 × 10
5) that are even larger than those used for computing statistics in
Figure 9. Therefore, probability distribution tails could be accurately estimated.
For linear narrow-band Gaussian waves, the version of Equation (11) for the wave crests
ηc and troughs
ηt for the Rayleigh exceedance distributions is:
The measured exceedance distributions for crests, troughs, and wave heights are plotted in
Figure 10b,c for two representative cases. All the measured exceedance distributions of
and
deviate notably from the Rayleigh shape. As in
Figure 9c,d, the probability of extremely steep (rogue) waves, with heights exceeding
by a factor of eight, is below the Rayleigh prediction by orders of magnitude in all cases. The probability of extremely high crests exceeding 4
is vanishingly small compared to that corresponding to the Rayleigh distribution. However, the probability of very high crests is by orders of magnitude larger than that of very deep troughs. Therefore, the vertical asymmetry due to nonlinear bound waves is well pronounced, resulting in significant skewness,
λ3. Additional data and a comparison of results with some theoretical distributions that account for nonlinear effects are presented in [
88]. It is shown there that the nonlinear exceedance distributions still overestimate the probability of very steep waves.
3.3. Coupling between Waves and Airflow
Surface current is created due to the shear stress induced by the wind blowing over the water surface, as well as due to waves’ nonlinearity; the water surface velocity provides the boundary condition for the forcing wind. To assess the effect of the drift current on the wind waves’ parameters, measurements of the surface water velocity were performed in [
51] using particle tracking velocimetry (PTV). Small light-weighted paper disks dispensed a few millimeters above the water surface through a long dry pipe served as tracers and were imaged by a video camera. Water velocity was measured at several fetches up to
x = 410 cm from the entrance to the test section; at each fetch and wind velocity, about 350–400 were used. Special care was taken to provide adequate illumination; for details, see [
66]. The 640 × 480-pixel camera imaged a 15-cm long area at the rate of 60 fps. The recorded video clips allowed monitoring each particle’s trajectory and calculating each particle’s velocity components along and across the imaged section. Two surface velocity components,
Us and
Vs, were tracked across all the frames of appearance using the PTV processing software. While the PTV-derived mean values of the crosswind surface velocity
Vs were found to be close to zero, as expected (
Figure 2), the along-wind component
Us can be quite significant, and was found to constitute about 3% of the maximum wind velocity in the test section,
Umax. Note that the values of the water surface velocity have been subtracted from the measured air velocities
U(
z) while performing the fit according to Equation (4). The logarithmic velocity profiles plotted in
Figure 2 account for this adjustment; however, the importance of this correction proved to be mostly negligible.
The presence of water surface drift may be more substantial for the sufficiently short slow-propagating gravity–capillary waves. In an absence of current, the radian frequency
ω = 2
πf is related to the wave number
k by the gravity–capillary dispersion relation:
where
σ is the water–air surface tension. The shear current close to the water surface can affect the dispersion relation due to the Doppler shift. To evaluate this effect, the wave phase velocity (celerity) of short waves,
c =
ω/k, was measured directly using two consecutive probes, thus allowing determining the wave number from independently measured wave celerities and frequencies. Each frequency component of the spectrum was examined separately. The celerity for each frequency for which the cross-correlation between the two gauge outputs was sufficiently high was determined by calculating the complex cross-spectrum of the two wave gauges’ output. The ensemble of measured values of
c determined at the local peak frequency
fp at numerous fetches and wind flow rates was compared to the celerities of the corresponding gravity–capillary waves calculated based on Equation (14),
cgc. The obtained results were fitted to an empirical dispersion relation of the form:
Subsequently, an empirical dispersion relation in Equation (15) was suggested in [
88] with coefficients
a = 0.006 m and
b = −2.2·10
−5 m, which are somewhat different from those in [
51]. The relation in [
90] was obtained using a different approach; it fits the data of [
51] well, but covers a wider range of wave numbers: 20 m
−1 <
k < 150 m
−1. This relation is in agreement with results reported elsewhere regarding the presence of the wind-induced shear flow [
28,
92]. More details on experiments that resulted in the empirical dispersion relation in Equation (15) are given in [
51,
88].
Contrary to studies in which wave-related properties in the airflow were investigated over deterministic mechanically generated waves, the turbulent flow over a naturally evolving random wind-wave field is considered here. While the records of the surface elevation show quasi-periodic behavior with the local dominant typical frequency, air velocity components
u(
t) and
w(
t) exhibit high-frequency fluctuations that are typical for turbulent flow. The frequency spectra of
u(
t) and
w(
t) exhibit peaks at the same frequency
fp as in the spectra of
η(
t); however, the velocity fluctuations spectra are notably wider than those of
η; their amplitudes remain significant for the whole range of frequencies [
53]. While the turbulent fluctuations in
u and
w are modulated by wind waves at frequencies close to
fp, even near the air-water interface and in the presence of steep and relatively narrow-band wind waves, the fluctuations in both velocity components and the surface elevation variation are not closely related. The relation between water waves and air velocity fluctuations weakens further at higher elevations, shorter fetches, or lower wind flow rates.
To extract the quantitative relations between various random parameters in the absence of fixed frequency and phase references, cross-spectral analysis was applied. The extent of similarity between two time-dependent signals
f(
t) and
g(
t) at various radian frequencies
ω can be characterized by the cross-correlation coefficient
rfg(
ω) calculated as the absolute value of the normalized cross-spectrum Γ
fg(ω) [
93]. The phase shift
θfg(
ω) between the two signals
f(
t) and
g(
t) at frequency
ω is defined as the argument of the corresponding component of the complex cross-spectrum value at this frequency,
Sfg(
ω), so that
θfg is positive when
f leads
g, and negative otherwise. Apparently, it only makes sense to consider the phase shift between the signals at frequencies where they are sufficiently well correlated, as represented by the value of
rfg(
ω).
The records accumulated in [
53] were divided into windows containing 1024 data points for each signal, corresponding to the window length of about 8 s (frequency resolution of about 0.12 Hz), with 50% overlap. About 70 independent estimates of the cross-spectra were obtained from the available records for each sensor location and airflow rate; the averaged over all windows cross-spectra were computed at all flow conditions and for different measuring locations.
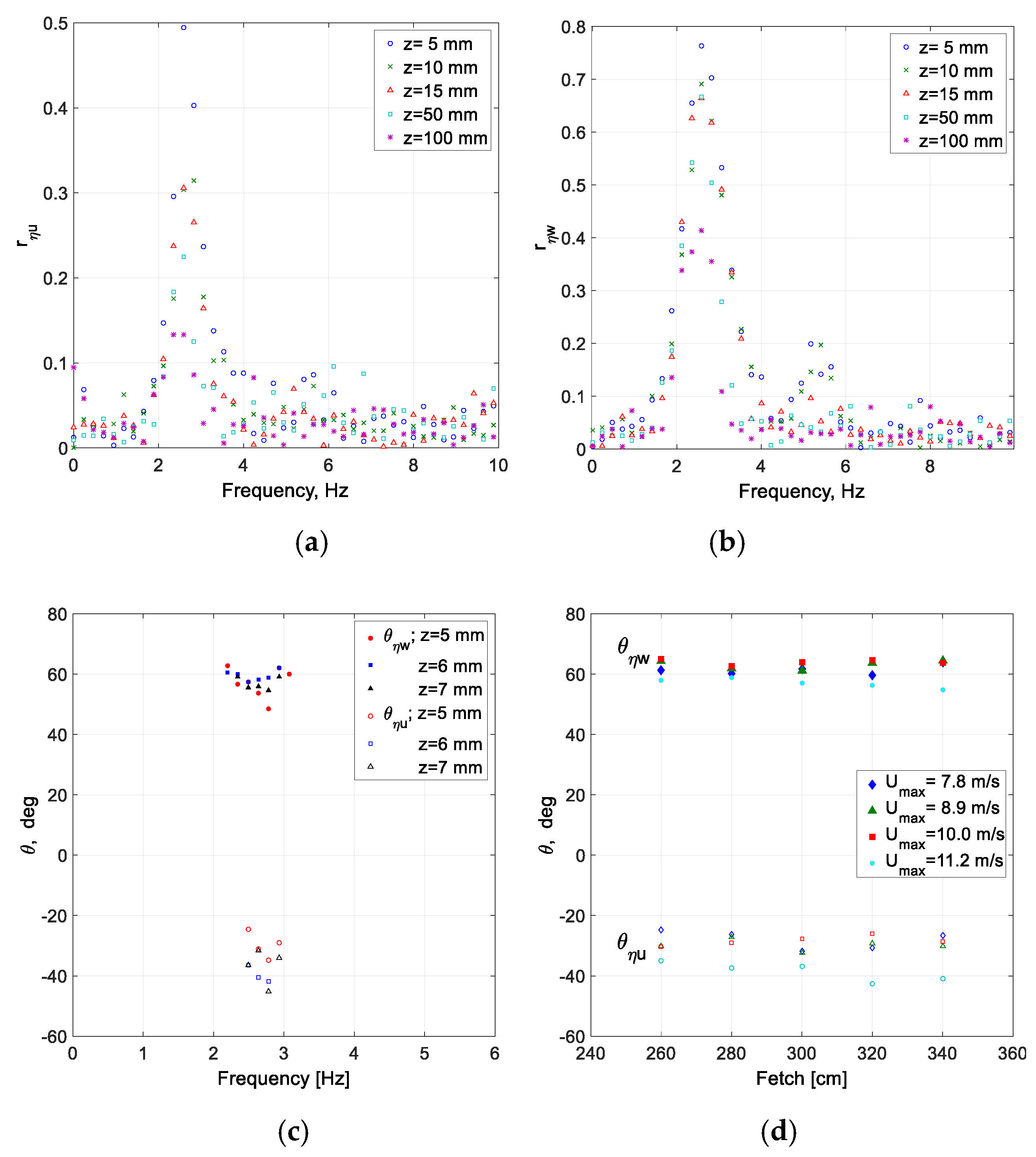
The cross-correlation coefficients between the fluctuating parts of the two velocity components,
u and
w, and the surface elevation at wind velocities below
Umax = 7.7 m/s and fetches shorter than 220 cm were too low to enable extracting meaningful information. The cross-correlation coefficients between the horizontal velocity fluctuations
u at a number of vertical locations and the surface elevation,
rηu are presented at fetch
x = 260 cm and wind velocity
Umax = 11.2 m/s in
Figure 11a.
Figure 11b depicts the corresponding cross-correlation coefficient for the vertical velocity component,
rηw, at
x = 340 cm. In both panels, a well-defined peak around the fundamental wave frequency
fp is observed; the values of
fp decrease with fetch. The maximum of the cross-correlation coefficient with the surface elevation is notably higher for the vertical velocity fluctuations as compared to the horizontal ones. This difference in the correlation level stems from the fact that the wave-induced fluctuations of velocity fluctuations in airflow above water have similar amplitudes in the longitudinal and vertical directions, whereas the velocity fluctuations in the horizontal direction due to the background turbulence not related to the underlying wave field are significantly higher than the vertical ones. The values of the correlation coefficients decay with height. Secondary peaks in the frequency dependence of the cross-correlation coefficient can be noticed at the second harmonic of the peak wave frequency, and to some extent even at the third harmonic. These secondary peaks indicate that velocity fluctuations in air are also affected by higher-order bound wave harmonics.
The resulting phase shifts
θηu and
θηw for
Umax = 11.2 m/s and two fetches,
x = 260 cm and
x = 340 cm, are presented in
Figure 11c. For each velocity component, the phase shifts relative to the surface elevation are clustered in tight “clouds”. The larger scatter in the
θηu “cloud” as compared to that of
θηw can be attributed to the lower correlation level of the longitudinal velocity component with the surface elevation variation, as compared to
rηw, as seen in
Figure 11a,b. The measured phase shifts seem to be independent of elevation. For both fetches in
Figure 11c, the average phase shift between
η and the longitudinal velocity fluctuations is close to −30°, and between
η and
w, it is close to 60°.
Figure 11d demonstrates that similar results are obtained for other wind velocities and fetches.
The results of
Figure 11c,d can be seen as phase shifts between the wave-coherent velocity fluctuations in air and the water surface elevation
η. The phase shift that is close to 90° between the two velocity components results in a vanishing phase-coherent shear Reynolds stress. To validate this conclusion, an attempt was made in [
53] to examine directly the correlation between the surface elevation
η(
t) and the fluctuating instantaneous contributions to the Reynolds shear stress, −
u′w′(
t). Even for the longest fetch and highest wind velocity employed in that study, and thus the longest and highest wind waves, no significant correlation between those two time series has been found; the correlation coefficient was small at all frequencies, including the vicinity of
fp. Thus, it seems that not only do the the wave-induced velocity fluctuations in air not contribute to the mean Reynolds shear stress, there is also no detectable wave-induced time-dependent variation of
with the phase of the dominant wave.
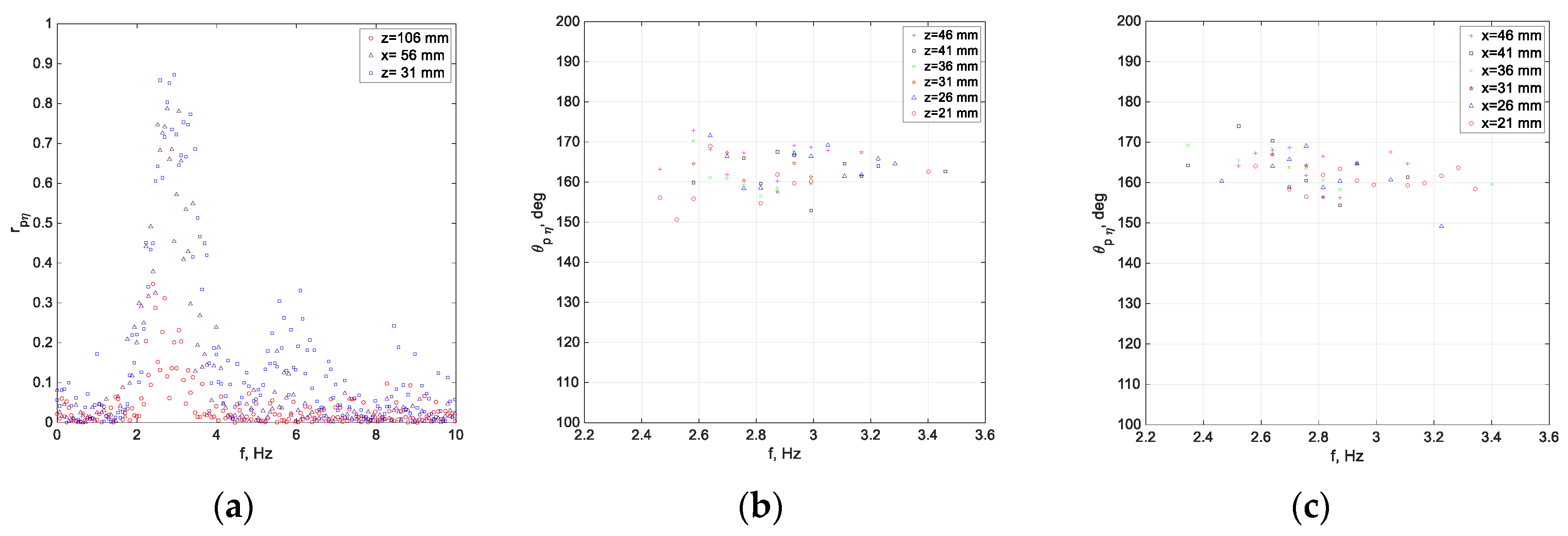
Measurements of the fluctuations of the static pressure in the airflow above the water surface were made in [
51] using the static pressure probe described in [
52]. Some representative results showing the dependence on frequency of the cross-correlation coefficients between the static pressure fluctuations in air and the water surface elevation,
rpη, are given in [
51] for several elevations above the mean water surface
z. The values of
rpη are generally quite small for most frequencies, the correlation between surface elevation and pressure variations becoming significant around the peak frequency
fp and only sufficiently close to the air-water interface. Note that for lower wind velocities in the test section and thus smaller wind-wave amplitudes, the wave-coherent pressure fluctuations were correspondingly weaker, rendering the less reliable results on cross-coherence between air pressure fluctuations and the surface elevation variations. The dependence on frequency of the cross-correlation coefficient between air pressure and
η strongly resembles the shape of wave frequency spectra, cf.
Figure 6. Close to the air-water interface, significant correlation seems to exist also at frequencies corresponding to the second, and to some extent, even to the third harmonic of
fp, thus reflecting the contribution of bound waves to wave-coherent air pressure fluctuations.
The phase difference values between pressure fluctuations and surface elevation were obtained from the complex pressure–surface elevation cross-spectra for those frequencies only at which significant correlation was detected (defined as
rpη > 0.6). The dependence of
θpη on frequency (around the peak frequency at about 3 Hz) is presented in
Figure 12b,c for two fetches and the highest wind flow rate in experiments. For all experimental conditions at which significant correlation between pressure and surface elevation fluctuations was detected, the values of
θpη were smaller than 180° and showed no notable variations with
z or with fetch. Thee phase angles of pressure fluctuations presented in
Figure 12a,b are in good agreement with the results reported in [
9,
31,
94].
The RMS values of the pressure fluctuations in each record were extrapolated to the undisturbed water surface level, and used in [
51] as characterizing the magnitude of wave-coherent pressure fluctuations at the local dominant wave frequency for each airflow rate in the test section, while the values of
θpη represented their phases. Those results allowed estimating the form drag
τform [
4,
5,
13], the amount of work being done by pressure on the water surface, and the growth rate of the wave energy at the dominant frequency. Detailed results are given in [
51].
3.4. The Two-Dimensional Features of the Wind-Wave Field
Measurements of wind-generated waves, such as described above, are mostly based on wave gauges that provide information on the temporal variation of the surface elevation at the sensor location. However, the wind-wave field is never unidirectional. The diverse approaches that have been applied in attempts to extract information on the two-dimensional structure of the wave field were briefly reviewed in [
66]. To this end, two essentially different methods described in
Section 2 were used in our studies to gain information on the 2D spatial structure of wind waves: stereo video imaging and the laser slope gauge (LSG). Due to improvements in computational power and computational algorithms, the application of stereo video imaging in field experiments with cameras either installed on offshore platforms or on a moving vessel expanded significantly in recent years. The comparison of video imaging results with those obtained using a standard instrumentation that was carried out in those experiments provided evidence that at open sea scales, stereo wave imaging is effective to retrieve data on medium-to-short wavelengths; see [
17] and additional references therein. Stereo video imaging, similarly to alternative optical methods of reconstruction of the instantaneous water surface shape, requires considerable computational resources that currently limit their effective spatial resolution and the overall duration of continuous imaging. The question of accuracy of the surface shape obtained using stereo imaging not yet been fully resolved.
In [
66], stereo video imaging was applied in a small-scale laboratory facility to study the two-dimensional structure of the wind-wave field under controlled conditions. Fast video recording enables extracting both the temporal and spatial information. The application of various instruments under identical forcing conditions enabled the verification of reliability and determination of the limitations of the applied methods. Details of the verification procedure, various sources of errors, and estimates of accuracy of the stereo video imaging reconstruction process are given in [
66]. For stereo imaging of the wind-wave field, all other sensors were removed, and the video images were acquired in a separate set of experiments at three fetches,
x = 110 cm,
x = 220 cm, and
x = 340 cm, and three wind speeds,
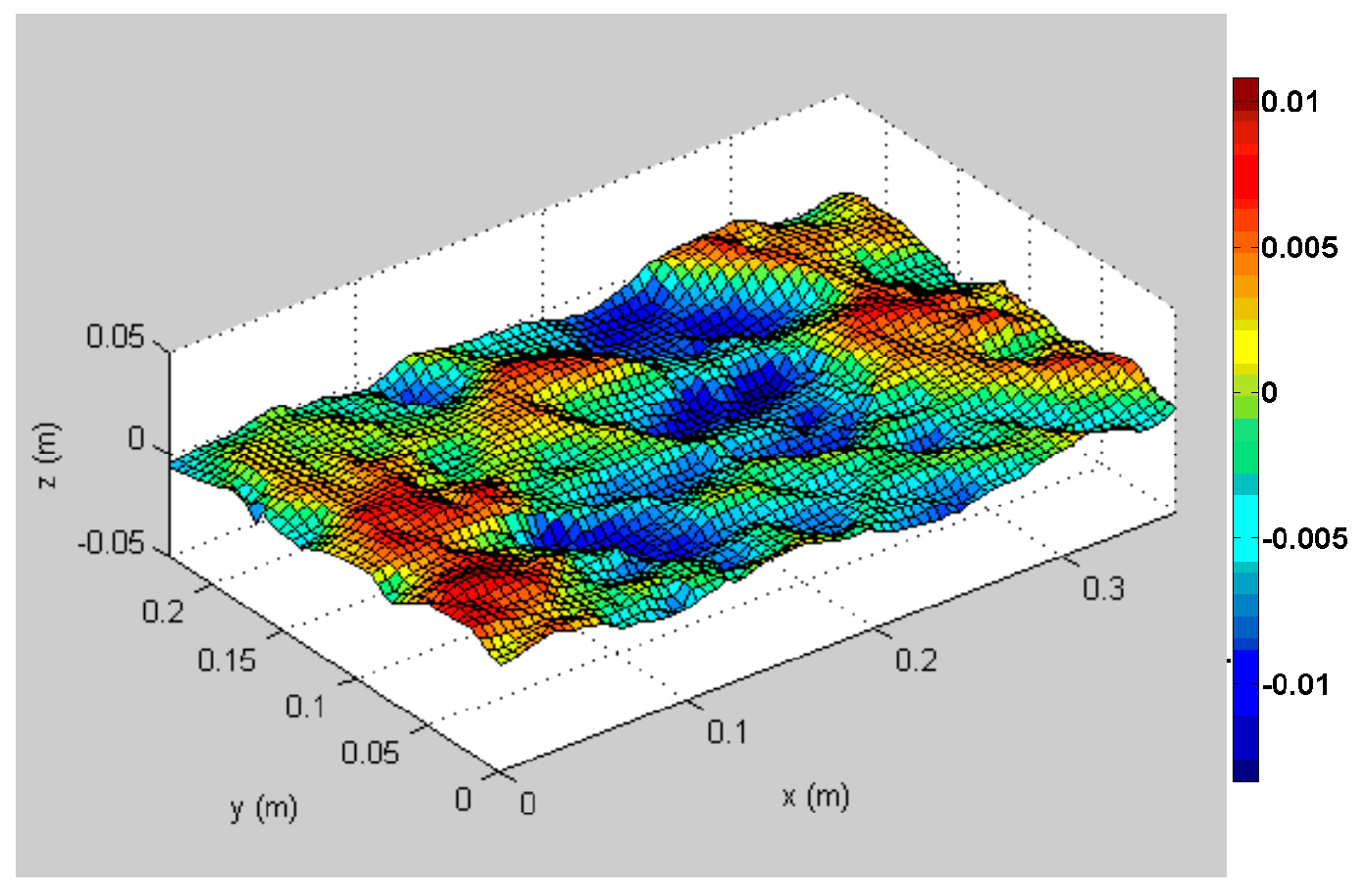
Umax = 6.5 m/s, 8.5 m/s, and 10.5 m/s. A typical reconstructed “snapshot” representing the instantaneous surface elevation in the surface area that is common to both cameras is presented in
Figure 13.
Surface elevation variation with time at a fixed location,
η(
x,
y,
t), can be retrieved from the sequence of reconstructed 3D surfaces, as shown in
Figure 13. The root mean square (RMS) values of the surface elevation
were computed at all wind velocities and fetches from a time series taken from the virtual wave gauges located across the central part of the reconstructed images. These records were compared in [
66] with the wave-gauge results at an identical wind velocity and fetch (but not acquired simultaneously with the video imaging). Comparison of the two signals indicated that they have comparable wave heights and dominant frequencies; the records derived from the stereo imaging were usually somewhat noisier. Taking the wave gauge results as a reference, the stereo imaging method overestimates
by up to 30% at low wind velocities and thus small wave amplitudes; however, for stronger winds and longer fetches resulting in the surface elevation fluctuations exceeding 5 mm, the relative error was reduced to under 15%. In view of the inaccuracy of stereo imaging of low-amplitude waves, frequency spectra of the surface elevation variation obtained by the stereo imaging and by the wave gauge were compared in [
66] only for the moderate and high wind forcing and at longer fetches. Although not identical, the spectra obtained by different techniques exhibit similarity in all examined cases, in particular within about 30% of the peak frequency. Away from the spectral peak, and thus for much smaller wave amplitudes, the frequency spectra derived from sequences of reconstructed stereo video records become less reliable. Thus, it transpires that at the currently available resolution, stereo imaging is capable of providing information on the gross features of the wave field, while more fine details may be inaccurate.
Thus, the major advantage offered by the stereo imaging over alternative measuring methods is its ability to characterize the global structure of the wind-wave field. This advantage was exploited in [
66] to assess the spatial coherence of the wave field applying the spatial autocovariance function in the along-wind and crosswind directions, which is defined as:
respectively, as a quantitative parameter. The autocovariance function
was computed along the imaged area for constant values of the spanwise coordinate
y; the reference value of
x was taken at the right (upwind) end of the image. The resulting values of
were averaged over various
y coordinates in the central part of the image, and then over all the reconstructed surfaces. Similarly, in computations of the autocovariance function in the crosswind direction,
the averaging was first performed over different constant values of
x within the reconstructed surface elevation map; subsequent averaging was carried out over the whole set of the instantaneous reconstructed surfaces.
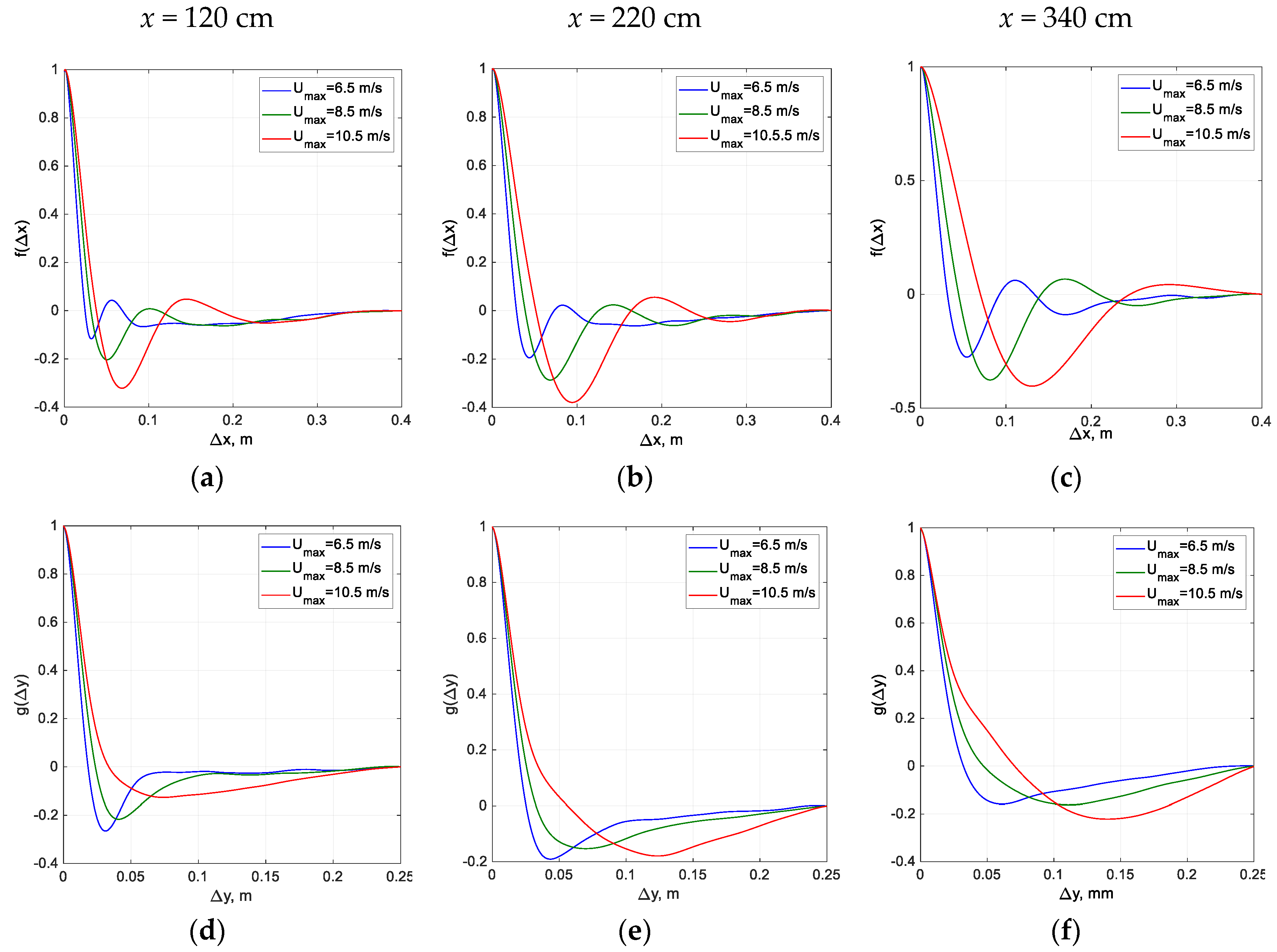
The computed autocovariance functions
and
for different fetches
x and wind velocities
Umax are plotted in
Figure 14. In all examined cases, the autocovariance functions decay fast and effectively attain zero after the second local minimum. In analogy with the autocovariance function for a deterministic monochromatic wave, the values of ∆
x at the first local minimum in all the panels of
Figure 14 may be seen as corresponding to one-half of the local dominant wavelength
λd. Since the wave field is spatially inhomogeneous and the characteristic wavelengths
λd increase with the fetch for each wind velocity, the autocovariance functions
f(∆
x) were computed by direct integration without invoking the Fourier transform that implies periodicity. The estimated wavelengths range from 7 cm to 27 cm, which according to the dispersion relation in Equation (15) correspond to dominant frequencies ranging from 2.4 Hz to 4.7 Hz.
The locations of minima and maxima of the autocovariance functions in the crosswind direction,
g(∆
y), plotted in
Figure 14d–f do not differ notably from those in panels a to c of that Figure, although the functions
g(∆
y) decay faster (as emphasized by the different horizontal scales adopted for
f(∆
x) and
g(∆
y)). The functions
f(∆
x) and
g(Δ
y) effectively vanish at distances comparable to the dominant wavelength, indicating that the spatial variations of the surface elevation become statistically independent at relatively short distances. Those short correlations lengths in both along-wind and crosswind directions are in accordance with the snapshot in
Figure 13 that shows short-crested and three-dimensional wind waves in the present experiments.
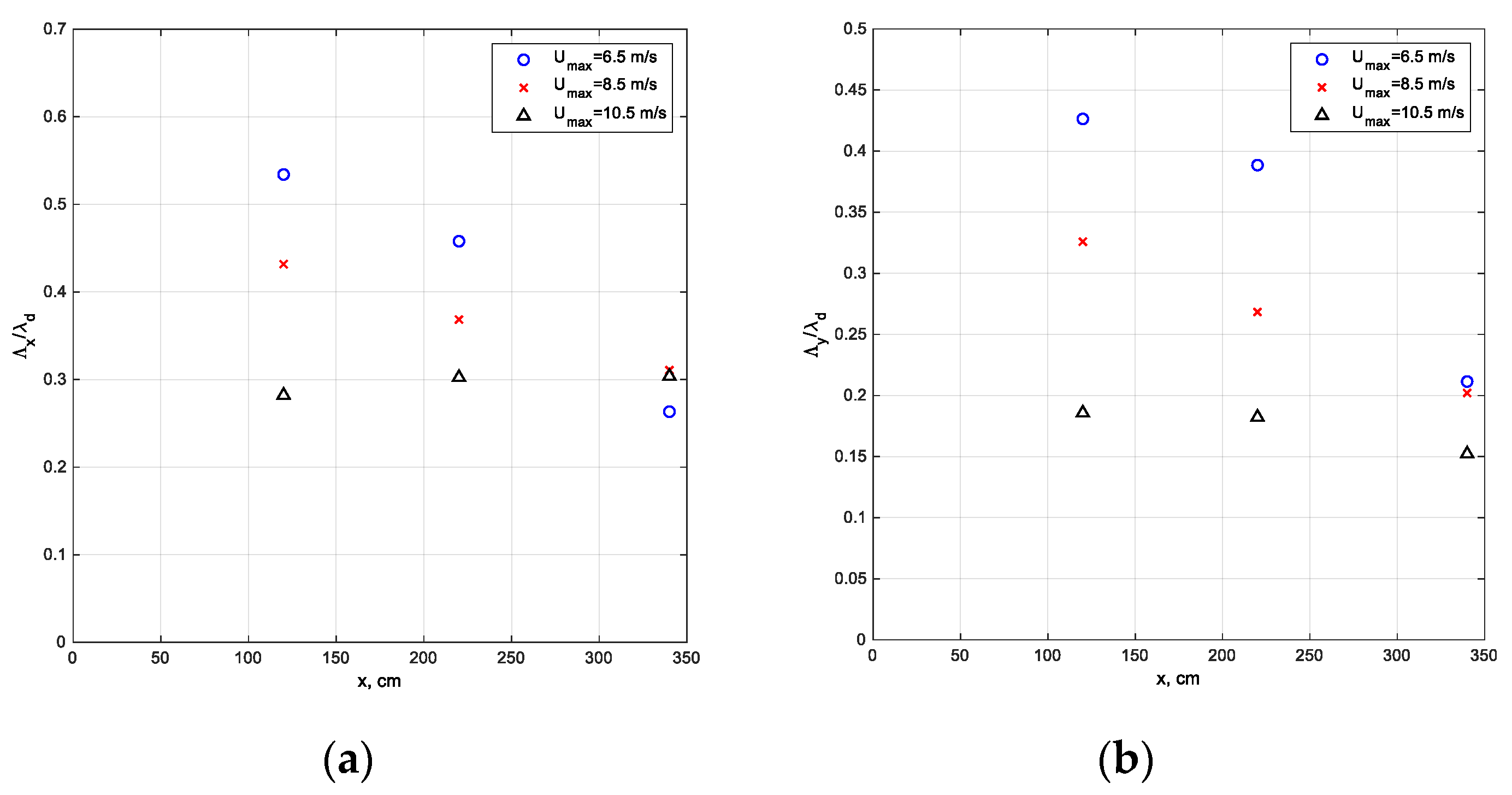
Integral length scales that characterize the spatial extent of coherence of the wind-wave field can in downwind,
Λx, and crosswind,
Λy, directions can be defined as:
respectively. Both integral length scales
Λx and
Λy normalized by the local characteristic scale of wind waves,
λd, are plotted in
Figure 15. The dominant wind-wave lengths
λd were determined for each fetch and wind velocity from the dominant frequency
fd using the empirical dispersion relation shown in Equation (15). The results of
Figure 15 demonstrate that the normalized integral scales
Λx and
Λy are notably smaller than unity. This implies that although the wind waves propagate in a relatively narrow channel with mean wind velocity directed along the test section, the waves cease to be coherent at distances much shorter than the dominant wavelength
λd. Since for all wind velocities and fetches, the dominant wavelengths remain smaller than the channel width, the waves in the central part of the test section are thus essentially unaffected by the presence of sidewalls. In view of results presented in
Figure 15b, the data taken along the lines
y = const. that are separated by more than about 5 cm can be considered as statistically independent.
To complete the discussion on wind waves’ coherence, the temporal autocovariance function was defined in analogy with Equation (16) as:
and computed from wave gauge measurements, laser slope gauge, and stereo video imaging [
66]. The wave gauge-derived absolute values of
h(∆
t) at the first minimum are significantly larger than the corresponding values of
f(∆
x). The fact that the wavenumber spectrum is wider than the frequency spectrum (approximately by a factor of two for pure gravity waves) contributes to this difference. Moreover, a fetch-limited wave field is statistically stationary, but spatially inhomogeneous. The spatial variation of the wind-wave field over the expanse of the image causes an additional decrease in the autocovariance function
f(∆
x). The temporal autocovariance functions retrieved from the virtual wave gauge at a single point of the reconstructed surfaces from stereo imaging and the corresponding autocovariance function calculated from the measurements carried out by a real wave gauge yielded close locations of the first local minima. The temporal correlation estimated by all measurement methods vanishes for time delays ∆
t of the order of the corresponding wave period.
An attempt was made in [
66] to compute the directional wave spectra
S(
k,θ), in which
k = (
kx2+
ky2)
1/2 is the wavenumber and
θ = tan
−1(
ky/
kx) defines the wave vector angle using sequences of the three-dimensional instantaneous water surfaces reconstructed from stereo video imaging. Then, the resulting power spectra were averaged over the whole set of reconstructed surfaces, as shown in
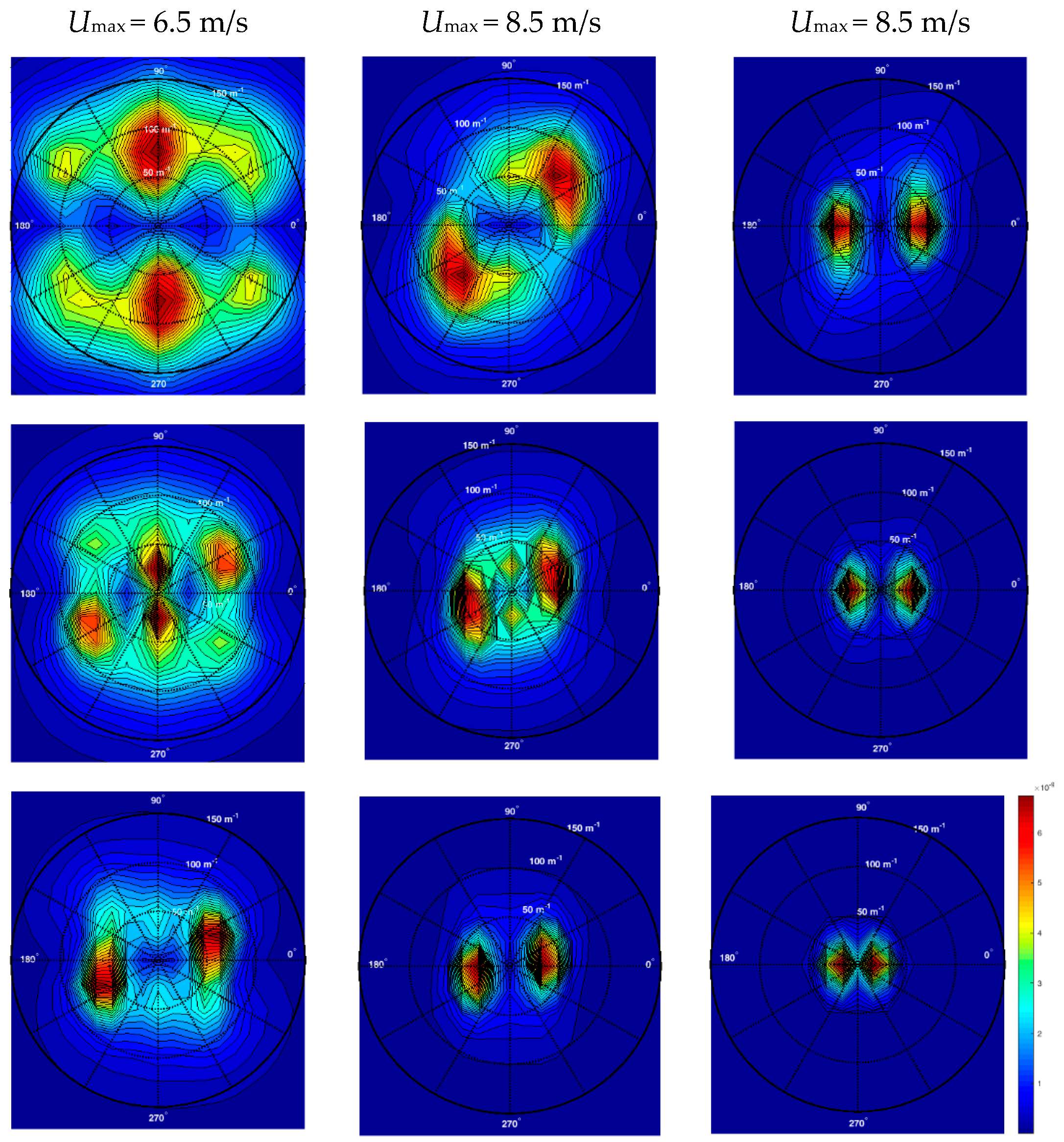
Figure 13. The spectra at all fetches and for all wind velocities are presented in
Figure 16. The directional ambiguity that is common to all instantaneous spatial images can be resolved in most cases, since the direction of wind is from right to left.
At low wind velocities and shorter fetches, the wave amplitudes are small; the corresponding spectra are characterized by the presence of waves in the crosswind direction. Thus, the question of directional ambiguity remains open for those cases; most probably, waves propagating in both positive and negative
y directions are present. The direction of the dominant wave for moderate winds deviates slightly to the left of the wind direction; this may suggest that the reconstruction procedure for low elevations introduces directional inaccuracy. However, Caulliez and Collard [
95], who performed reconstruction of the decimeter-scale water–wave surface based on the simultaneous imaging of the wave slopes in two perpendicular directions, also report on asymmetry in the directional spectra at early stages of wind waves’ evolution. Deviations of the wave propagation direction from that of the wind were observed in field experiments [
96]. As waves grow and become longer at high wind speeds and larger fetches, the asymmetry of the spectra disappears; the contours of the directional spectra are at 180° (the wind direction). The wave numbers associated with the dominant waves in those cases are in general agreement with the results obtained from the autocorrelation function, the relative error being within about 15%. At highest wind velocity and the longest fetch, the wavelength is overestimated in the spectral representation; this is apparently due to insufficient image size, which in this case becomes comparable with the wavelength. The spectra are characterized by directional spreading of up to 60° around the wind direction and thus represent an essentially three-dimensional and short-crested wave field.
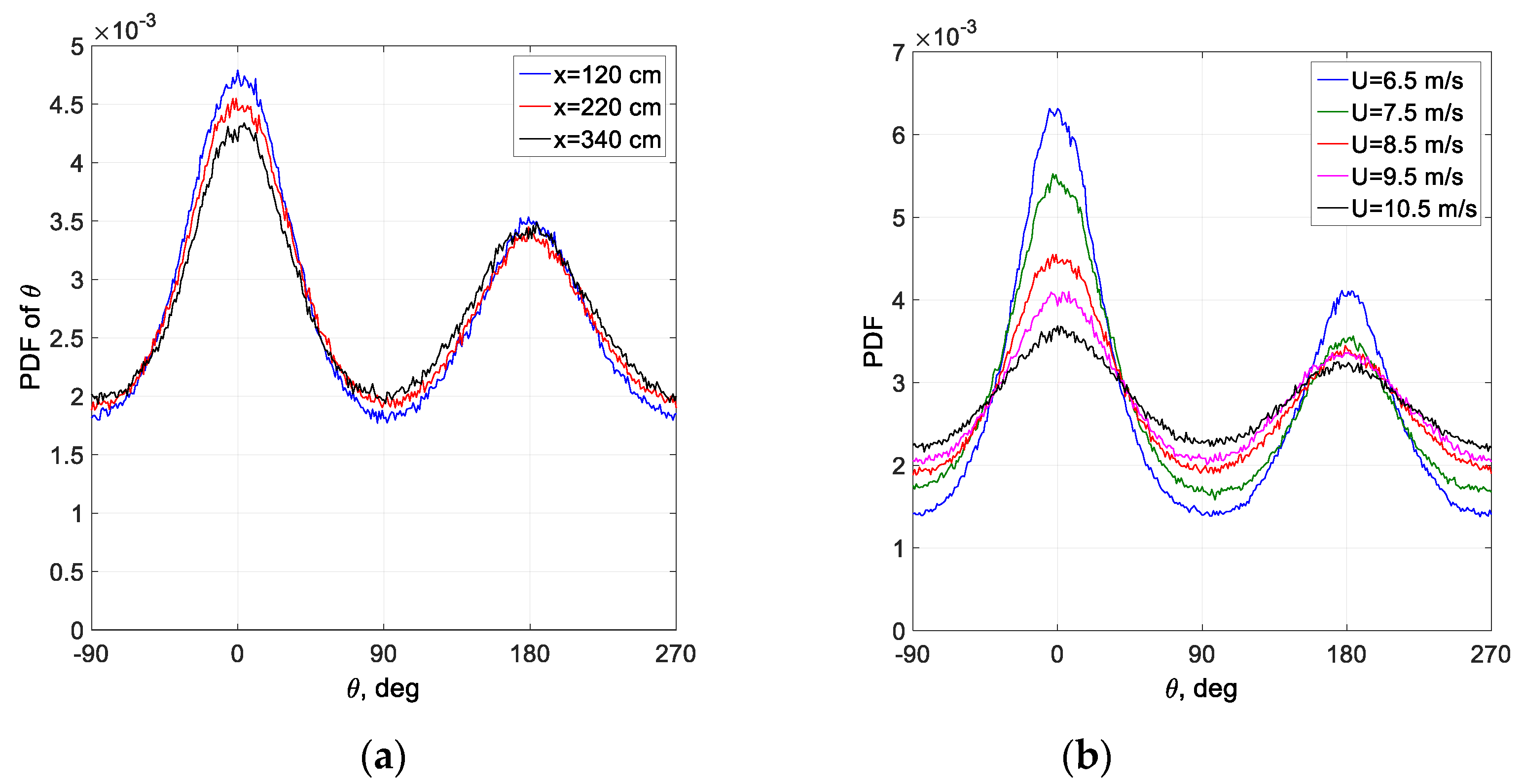
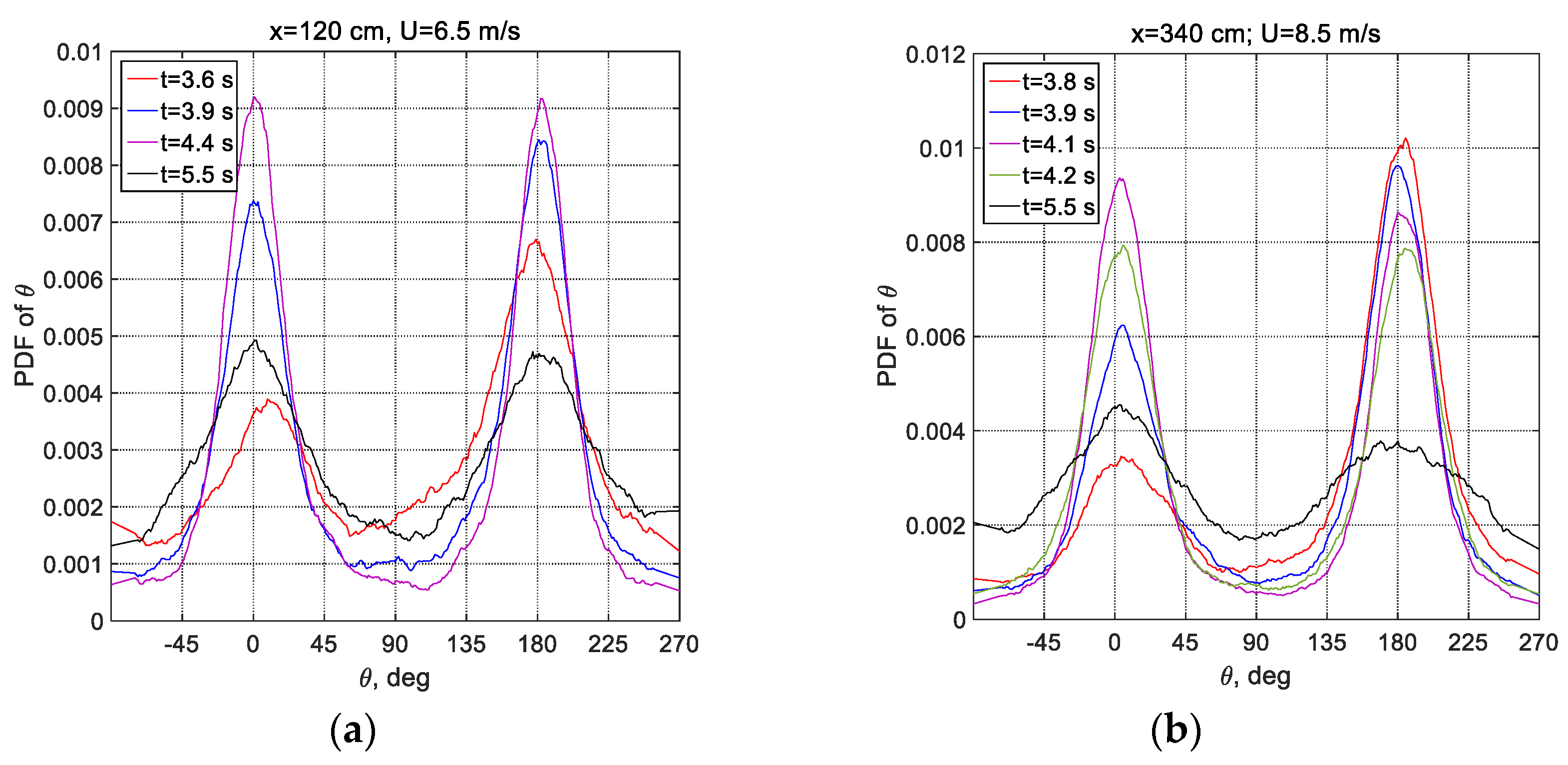
A different experimental approach that sheds light on the three-dimensional structure of wind waves is based on application of the laser slope gauge (LSG). Temporal records of the variation of the instantaneous surface slope components provided by LSG allow characterizing the direction of the vector normal to the instantaneous surface shape at the measuring location. The projection of the vector normal to the surface on the horizontal plane allows determining the azimuthal angle of the instantaneous slope,
θ = tan
−1(
ηy/
ηx). The probability distribution functions of the instantaneous azimuthal angles are presented in
Figure 17a for three fetches and a single wind velocity
Umax = 8.5 m/s, and in
Figure 17b for the fetch
x = 220 cm and different wind velocities. All the probability distribution functions plotted in
Figure 17 are nearly symmetric around the channel axis. The directional spreading is essential; the probability of the azimuthal angle in the crosswind direction (
θ = ± 90°) is significant. All the curves in
Figure 17 have two distinctive peaks at
θ = 0° and
θ = 180
°; the prevailing direction of the waves is aligned with that of the wind. The probability that the azimuthal angle
θ = 0° that is obtained for a forward-leaning slope is notably lower than that of the rear inclination. This front–back asymmetry of the wave shape based on the LSG measurements observed in
Figure 17 is in agreement with the asymmetry
A(
η) of the surface elevation measured by a wave gauge, as plotted in
Figure 10a. The probability distributions of the slope inclination direction in
Figure 17a do not vary notably with fetch; similar behavior was obtained for all other wind velocities. The effect of the wind velocity on the variability of the slope direction is much more noticeable, as shown in
Figure 17b. The probability distribution functions of the azimuthal angle
θ become flatter, and the probability of the instantaneous slope in the crosswind direction increases for stronger winds.
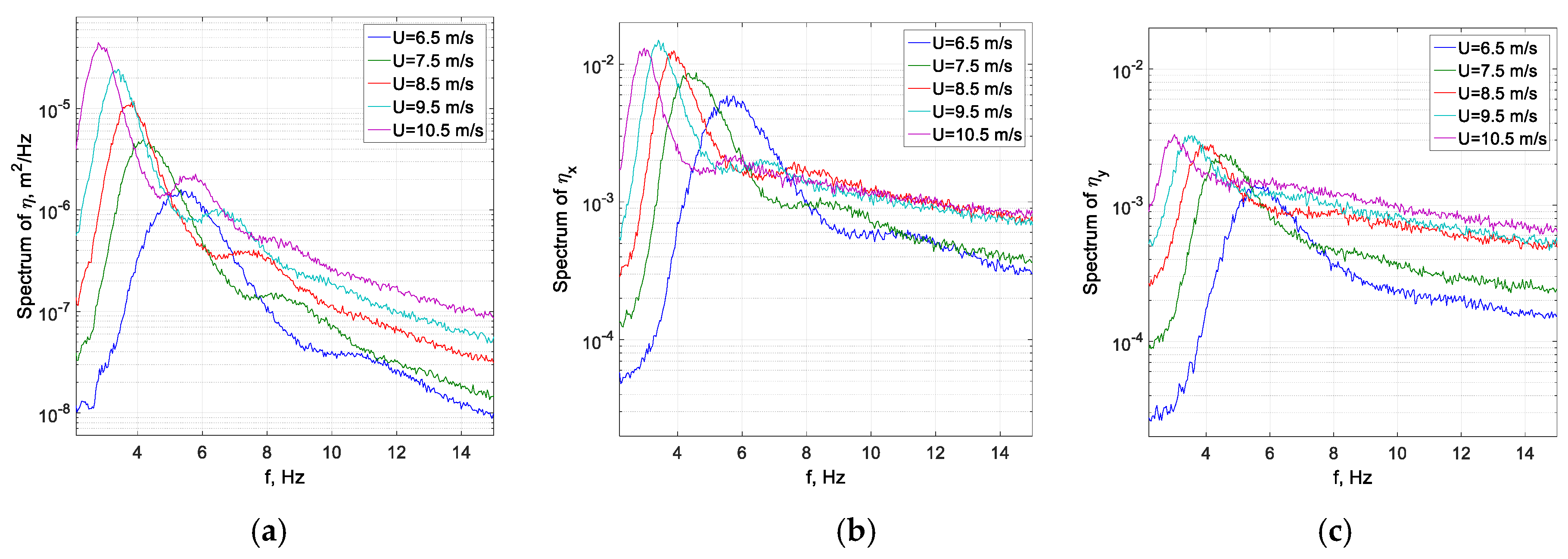
The measured by LSG temporal dependencies of downwind ∂
η/∂x(
t) and crosswind ∂
η/∂y(
t) slope components allow comparing their frequency spectra with those of the surface elevation
η(
t). Such a comparison is carried out in
Figure 18 for the fetch
x = 220 cm and different wind velocities
Umax. The power spectra of
η(
t) are also plotted in this figure for comparison. As in the spectra of
η(
t) (
Figure 6), the total power of the slope components spectra increases with
Umax. Apart from the principal peak at
fp, the slope spectra are characterized by secondary peaks representing bound waves; those secondary peaks seem to be less prominent in the spectra of ∂
η/∂y. The peak frequencies decrease with the wind velocity.
For all wind velocities, the peak frequencies
fp of the slope components do not differ much from those of the surface elevation spectra. Nevertheless, it can be noticed that the values of
fp of the downwind surface slope spectra in
Figure 18b exceed somewhat those of the surface elevation spectra in
Figure 18a. This can be attributed to the fact that the power of the downwind surface slope, ∂
η/∂x(
t), is proportional to (
akx)
2, in which
kx is the longitudinal component of the wave vector, rather than of the wave amplitude squared,
a2. The peak frequencies of the crosswind surface slope ∂
η/∂y(
t) do not differ significantly from the peak frequencies of ∂
η/∂x(
t). Contrary to the surface elevation spectra, the spectral intensities of the slope components in the peak region seem to be only weakly dependent on
U, in particular for longer fetches. At the same fetch and wind velocity, the power of the downwind slope component around
fp exceeds significantly that of the corresponding crosswind component; however, at frequencies exceeding 10 Hz, they become comparable. Thus, it appears that short wind waves in the capillary range may not have a preferred propagation direction.
The high frequency part of the power spectra of the surface slope components ∂
η/∂x and ∂
η/∂y can be presented by the power law shown in Equation (6), similarly to the surface elevation
η; see
Figure 7b. The slope exponents corresponding to the power law fit of all the tails of the spectra of ∂
η/∂x and ∂
η/∂y are summarized in
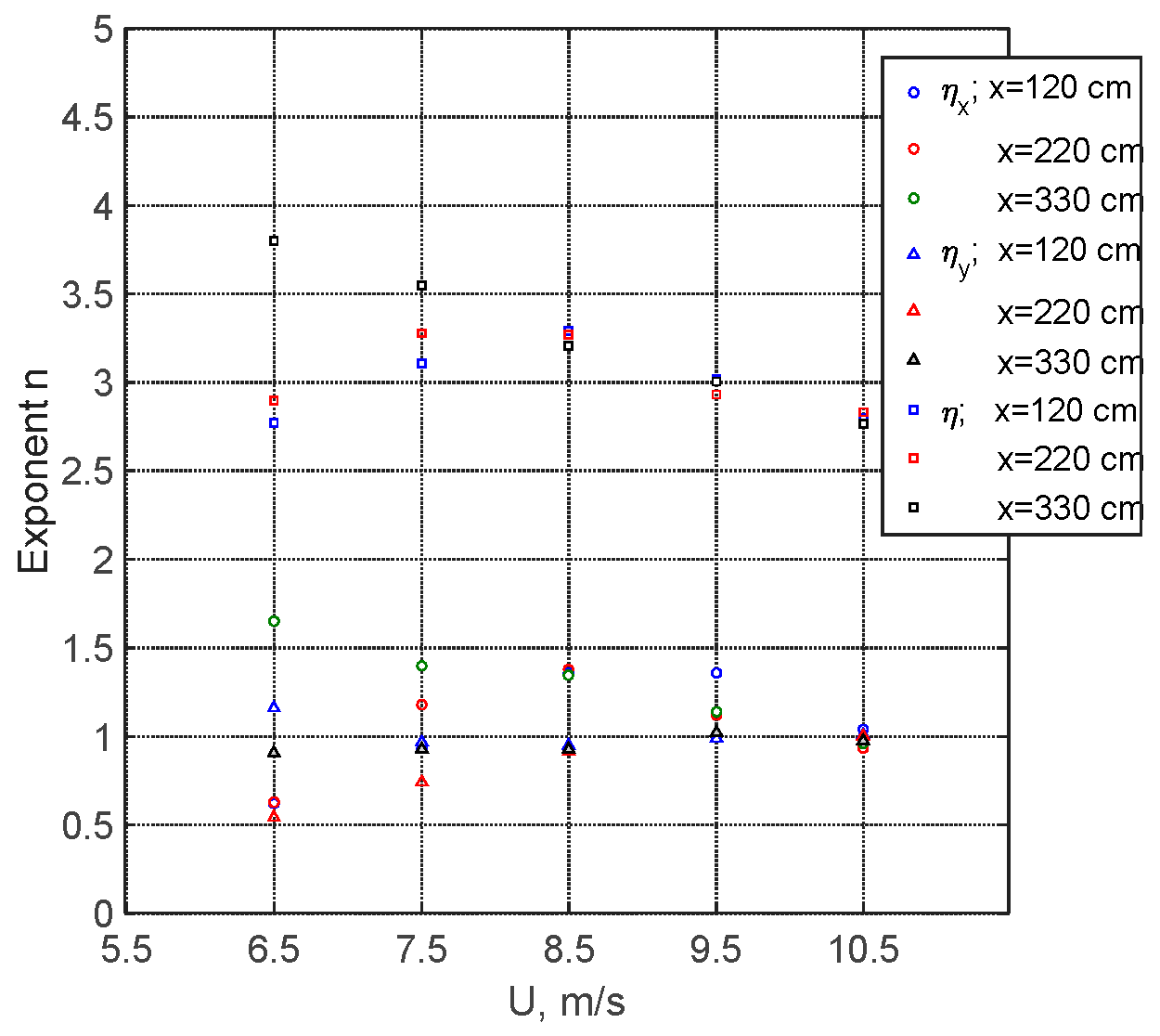
Figure 19 for all the fetches and wind velocities employed in [
88]. The exponents obtained in those experiments for the surface elevation spectra are also plotted for comparison. At lower wind velocities and shorter fetches, wave amplitudes are quite small; therefore, the results exhibit considerable scatter. For all the cases considered, the exponents of the spectral tail of
η are close to
n = 3, which is in agreement with
Figure 7b for this frequency range. The spectral tail slope exponents for both downwind ∂
η/∂x and crosswind ∂
η/∂y surface slope components do not differ significantly, and with increasing wind velocity, seem to converge to a value close to unity.
As noticed above, at each frequency
f, the ratio of the spectral component powers of the surface slope ∂
η/∂x and of the surface elevation
η is
k2(
f). It follows from the linear dispersion relation for gravity-capillary waves shown in Equation (14) that at frequencies exceeding about 10 Hz, the contribution of the surface tension term in Equation (14) becomes dominant; thus,
k ~ ω2/3, and one can expect
–
nη = 4/3. The difference between exponents in
Figure 19 apparently exceeds this value. This discrepancy can be understood in view of the fact that the frequencies of short wind waves are affected by Doppler shift, which is induced by the shear stress and Stokes drift current, as discussed in
Section 3.3 in relation to the empirical dispersion relation shown in Equation (15).
Similarly to the results presented in
Figure 9a,b, the deviation from the Gaussianity of the surface slope components can be characterized by their higher statistical moments. The skewness coefficient of both LSG-measured surface slope components,
and
, provides quantitative estimates of wave slope asymmetry about the along-wind and crosswind axes. The normalized values of the skewness of the downwind component of the surface slope,
ηx, characterize the vertical wave asymmetry, and the vertical asymmetry associated with the slope
A(
ηx) =
is obtained from measurements that are independent of those used to compute asymmetry
A(
η) according to Equation (12) and as plotted in
Figure 10a. The variation of
with wind velocity and fetch is presented in
Figure 20 together with the skewness coefficients,
. Negative values of slope skewness are associated with shorter and thus steeper forward wave faces. The absolute values of
are small (|
| < 0.1), thus indicating that waves are on average vertically symmetric in the crosswind direction.
The front–rear wave asymmetry characterized by the skewness of the surface slope,
A(∂
η/∂x), decreases as the waves grow larger with fetch, which is in agreement with the behavior of
A(
η) in
Figure 10a. The vertical wave asymmetry determined from the skewness of the surface slope decreases with the wind velocity
U. The asymmetry magnitudes
A(
η) are of the same order as those in
A(∂
η/∂x), although they are somewhat different. The dependence of
A(∂
η/∂x) on wind velocity is more pronounced than that of
A(
η). Additional results on the statistical parameters of wind waves and the discussion of those findings can be found in [
75,
88].