North Sea Wave Database (NSWD) and the Need for Reliable Resource Data: A 38 Year Database for Metocean and Wave Energy Assessments
Abstract
1. Introduction
Gap in Knowledge
2. Materials and Methods
2.1. Modelling Inputs
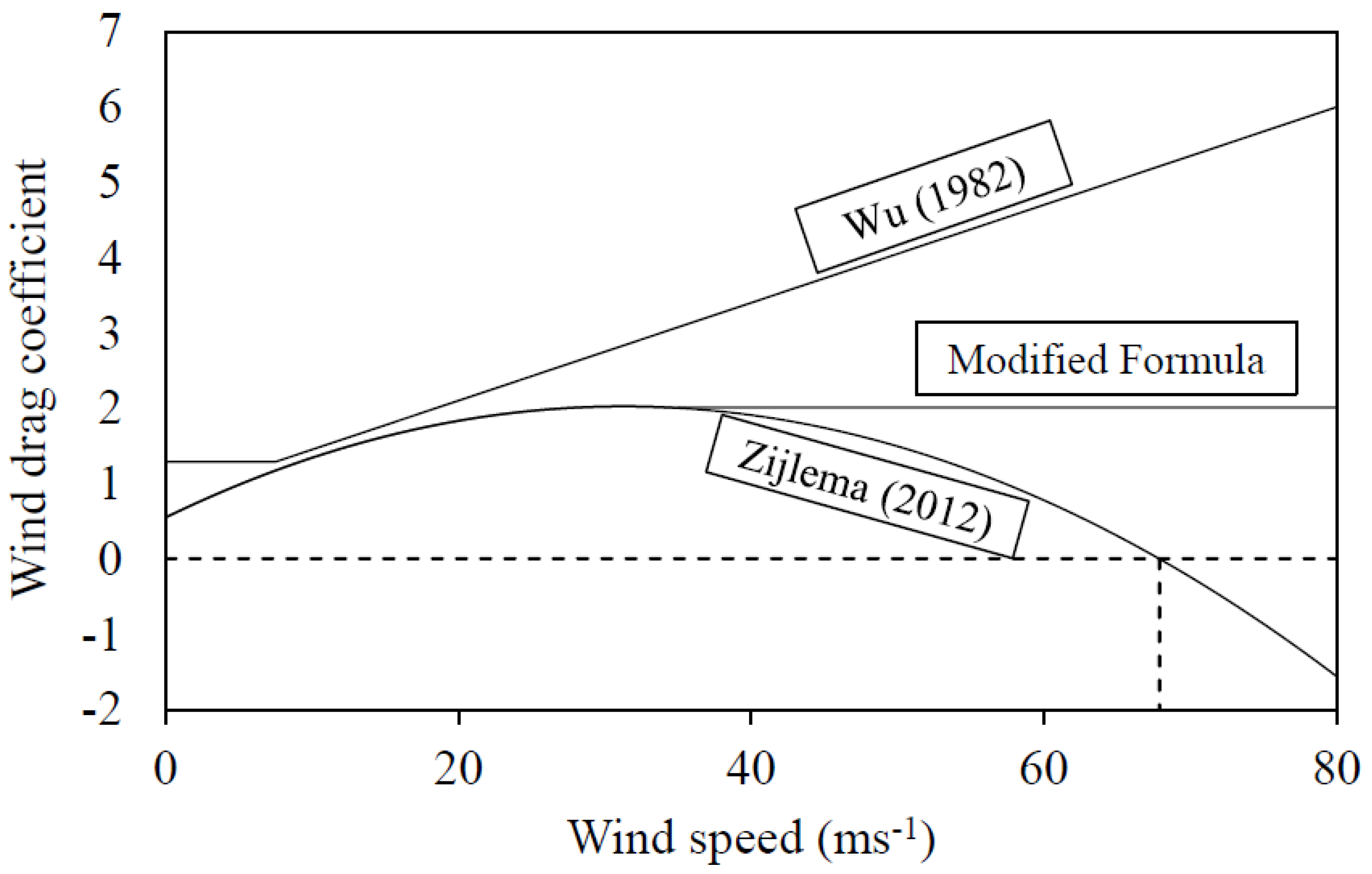
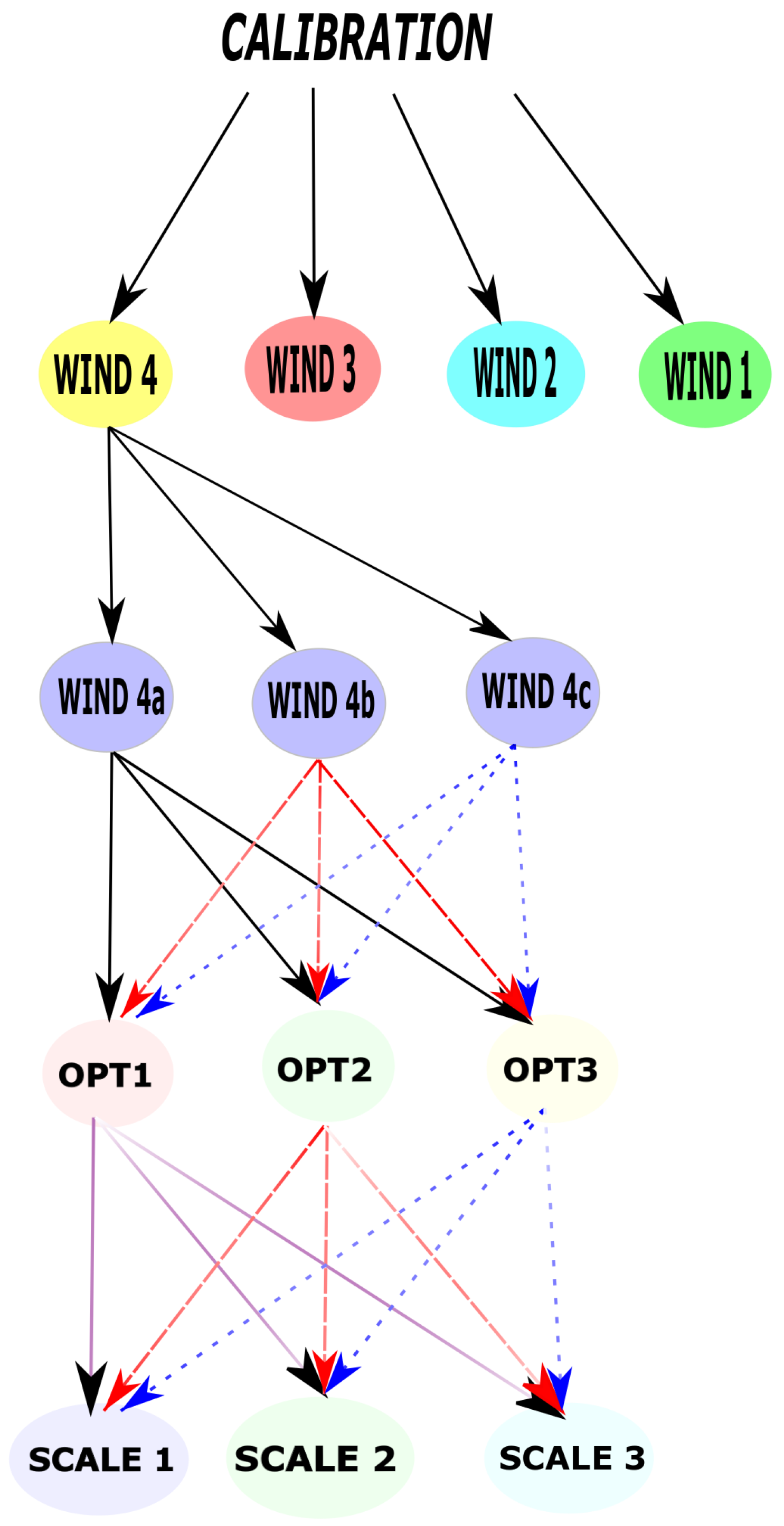
2.2. Calibration Parametrisation
3. Results and Analysis
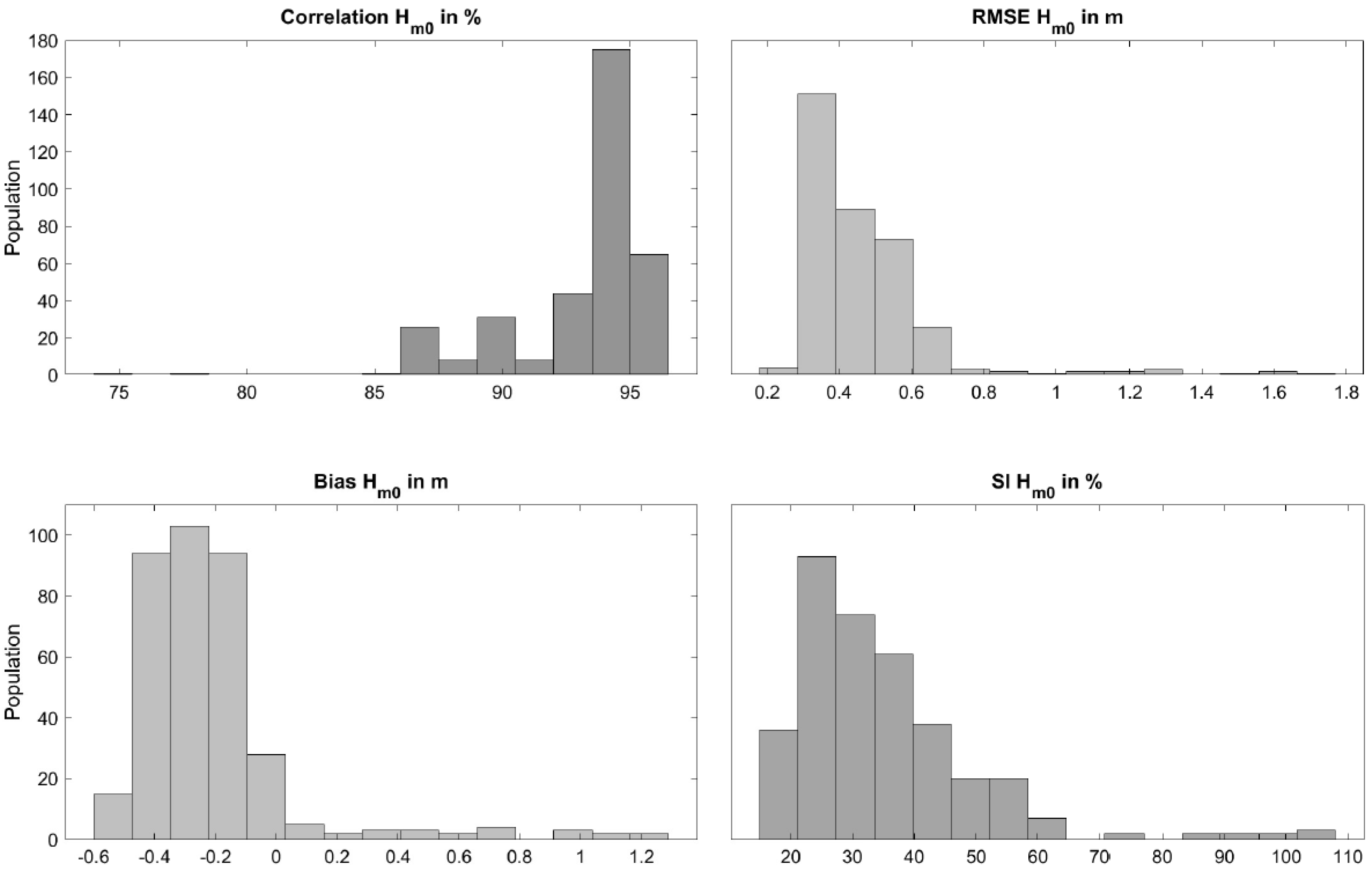
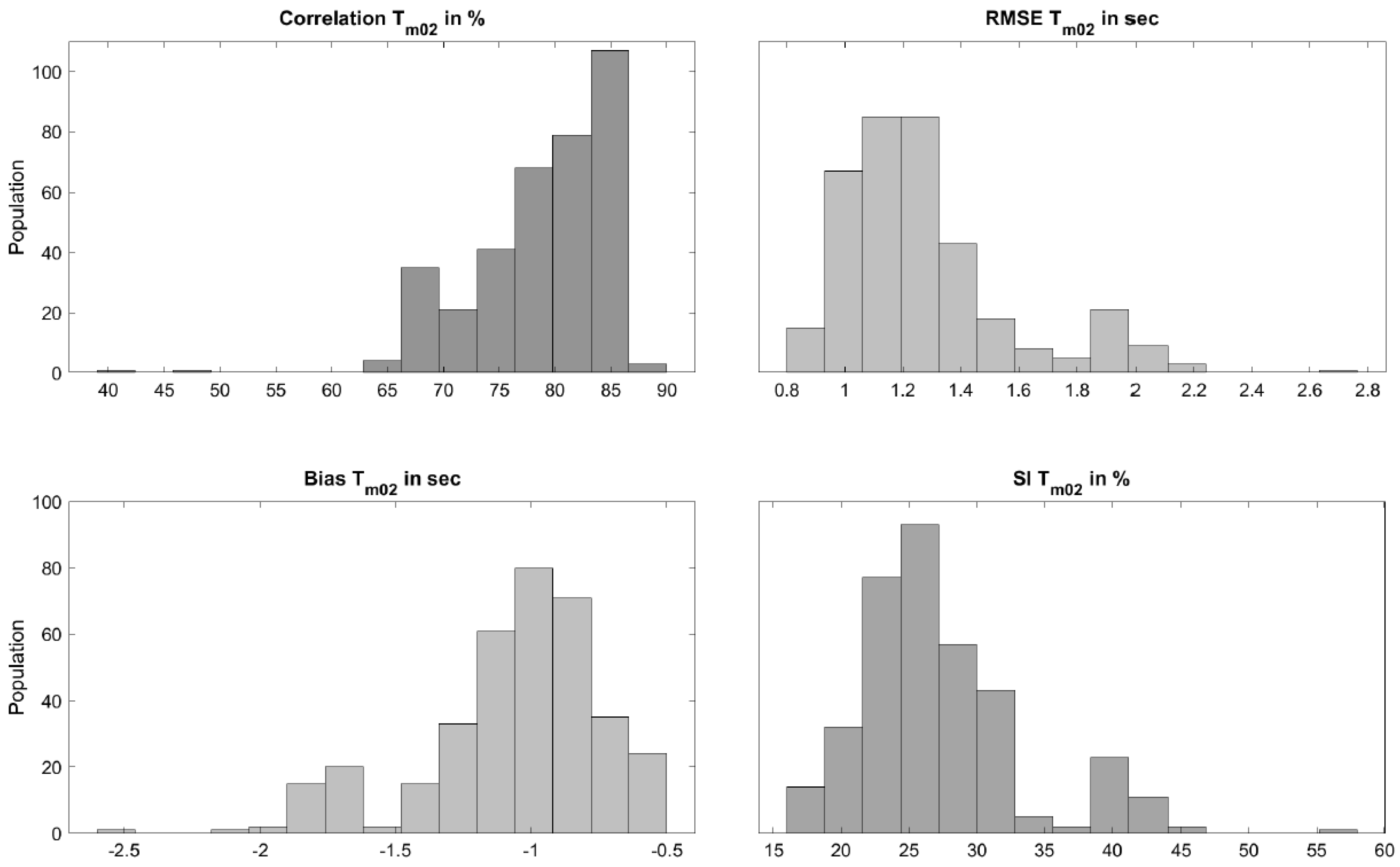
3.1. Calibration
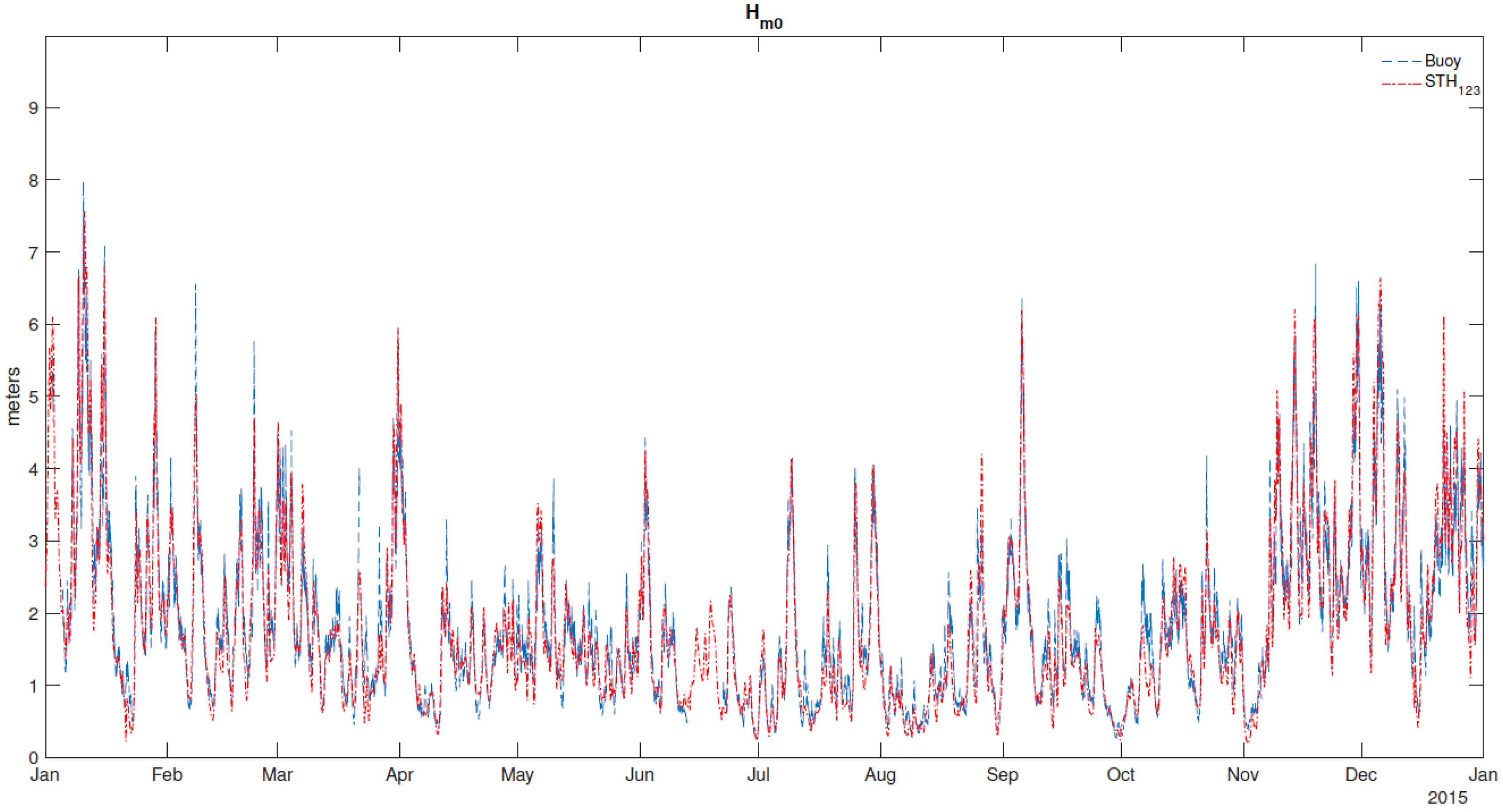
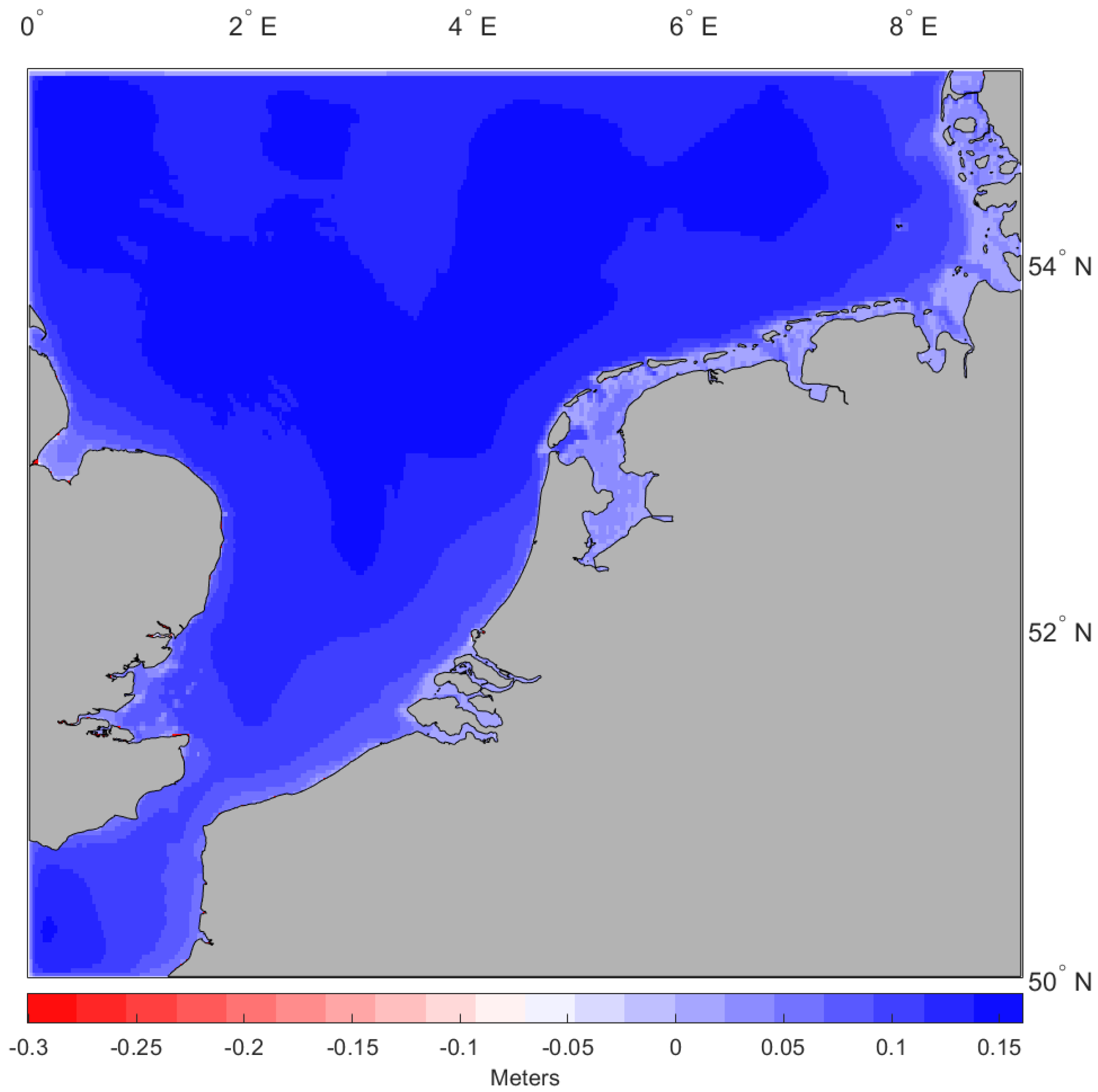
3.2. Validation
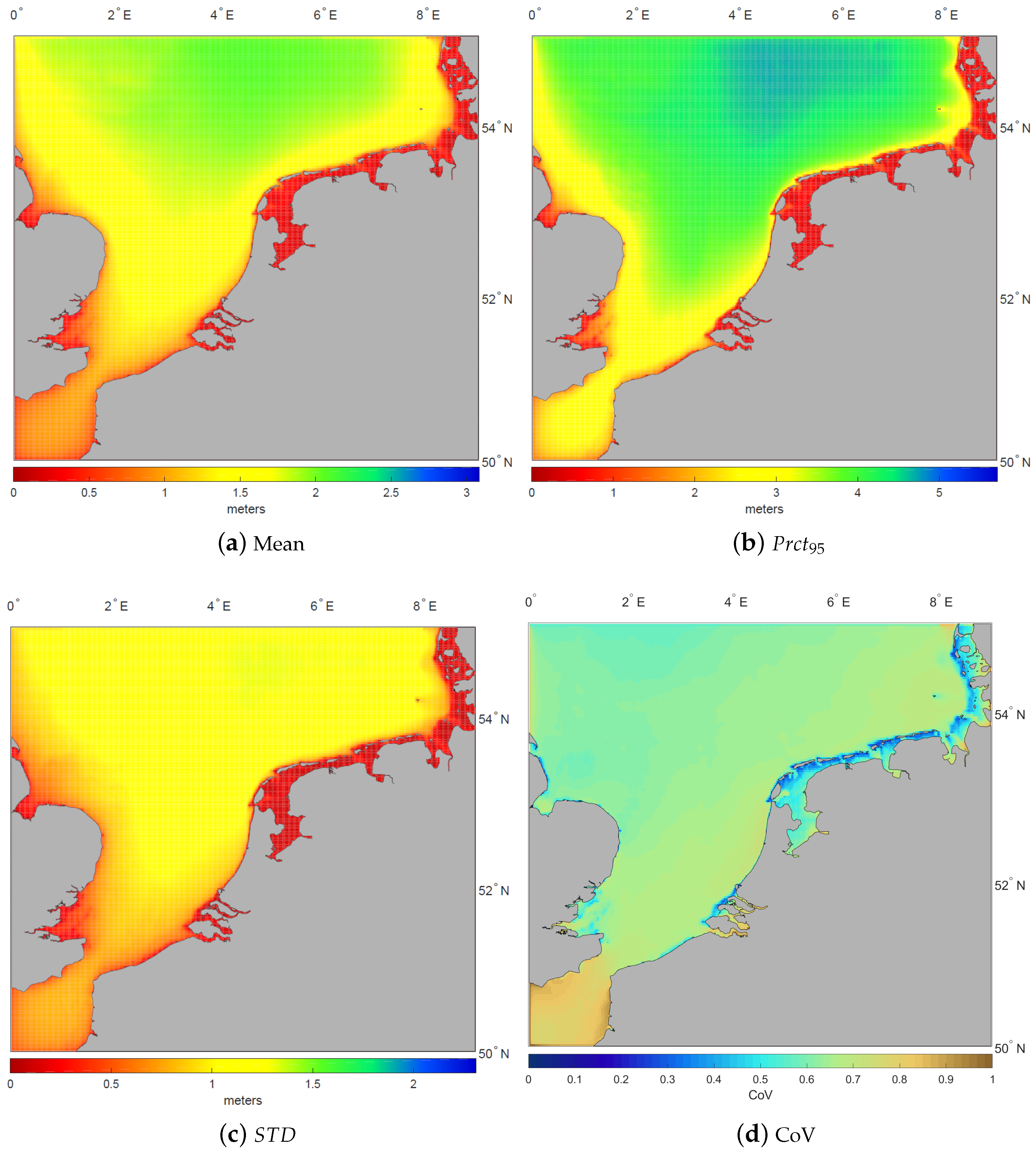
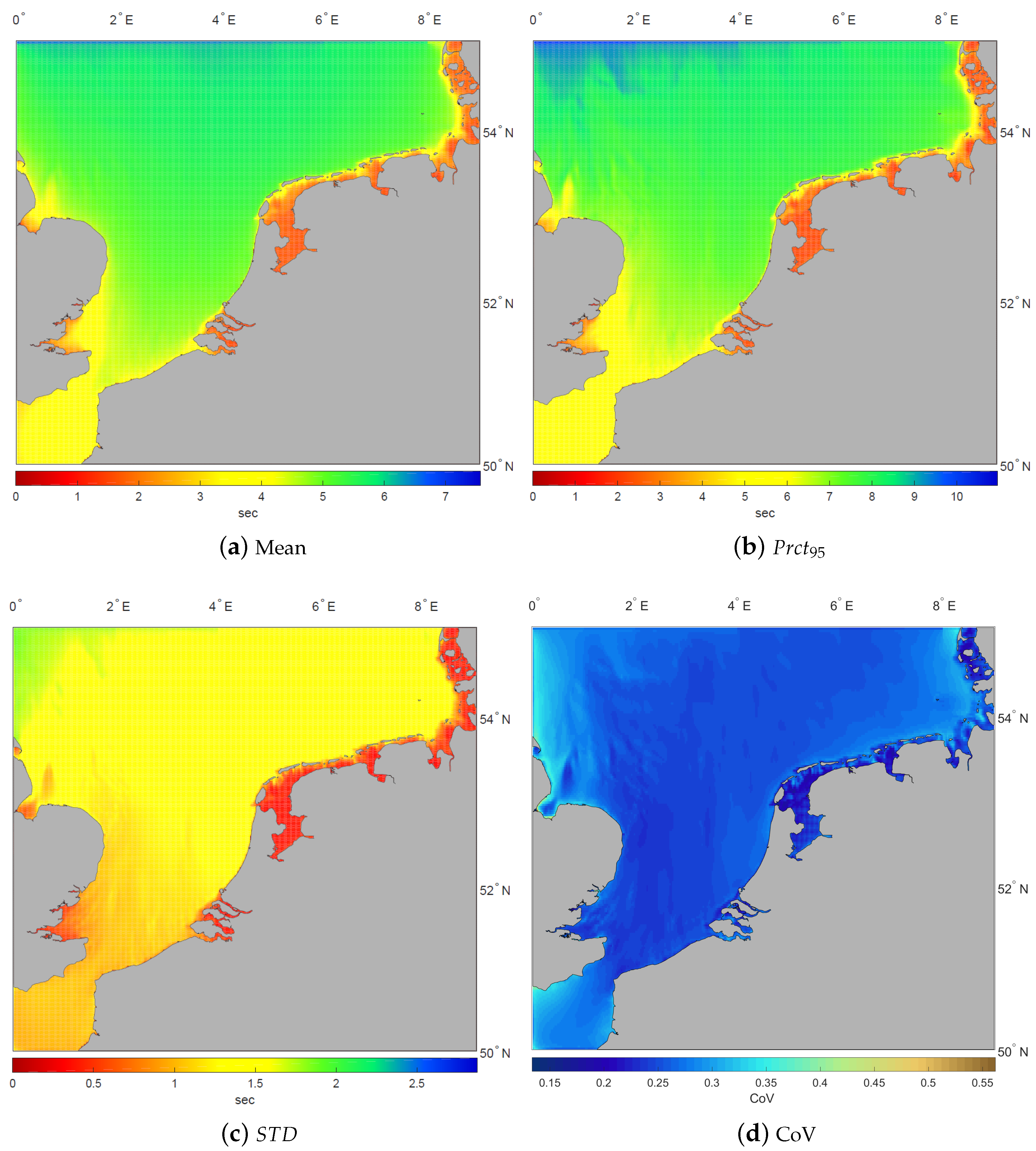
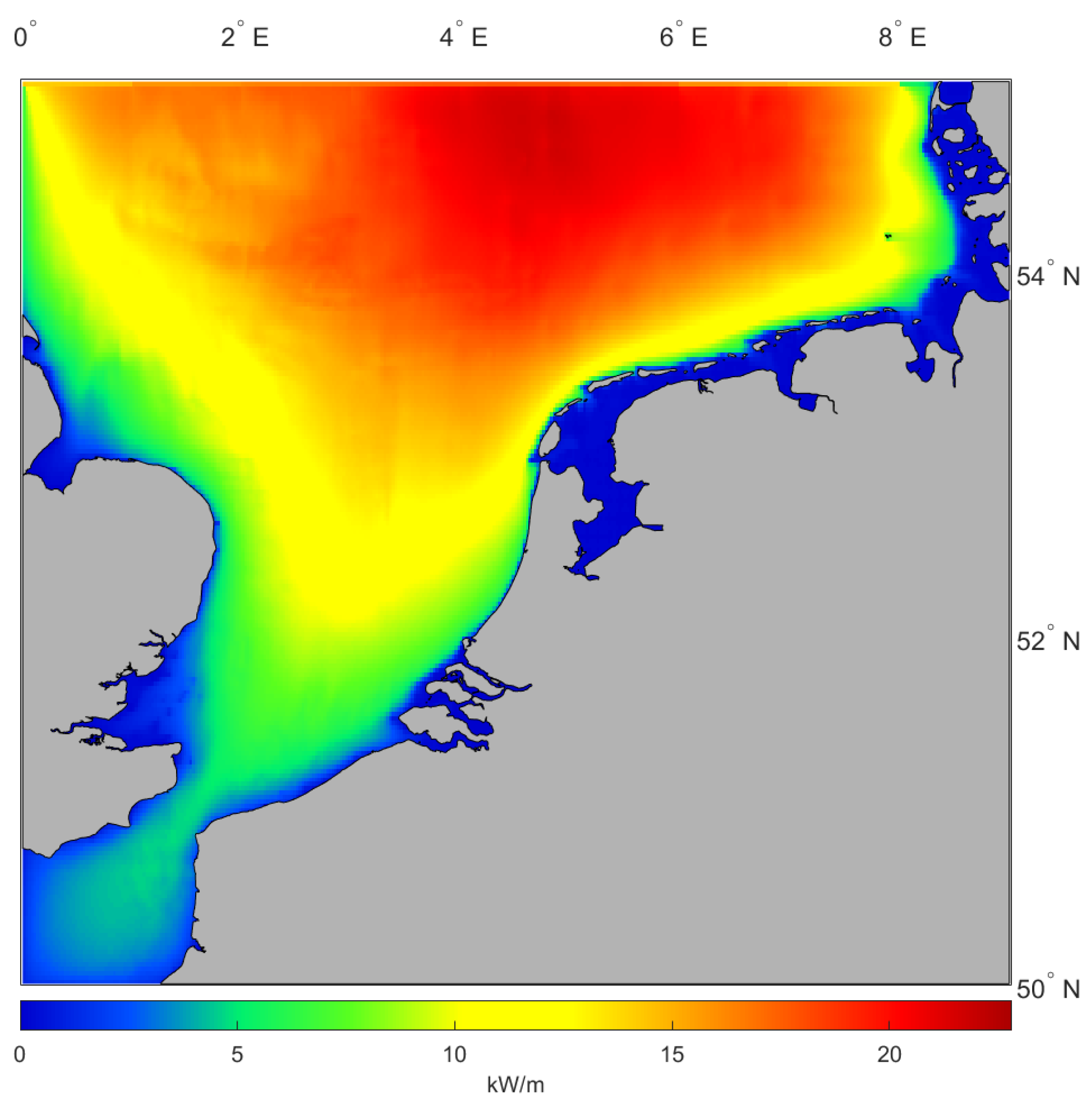
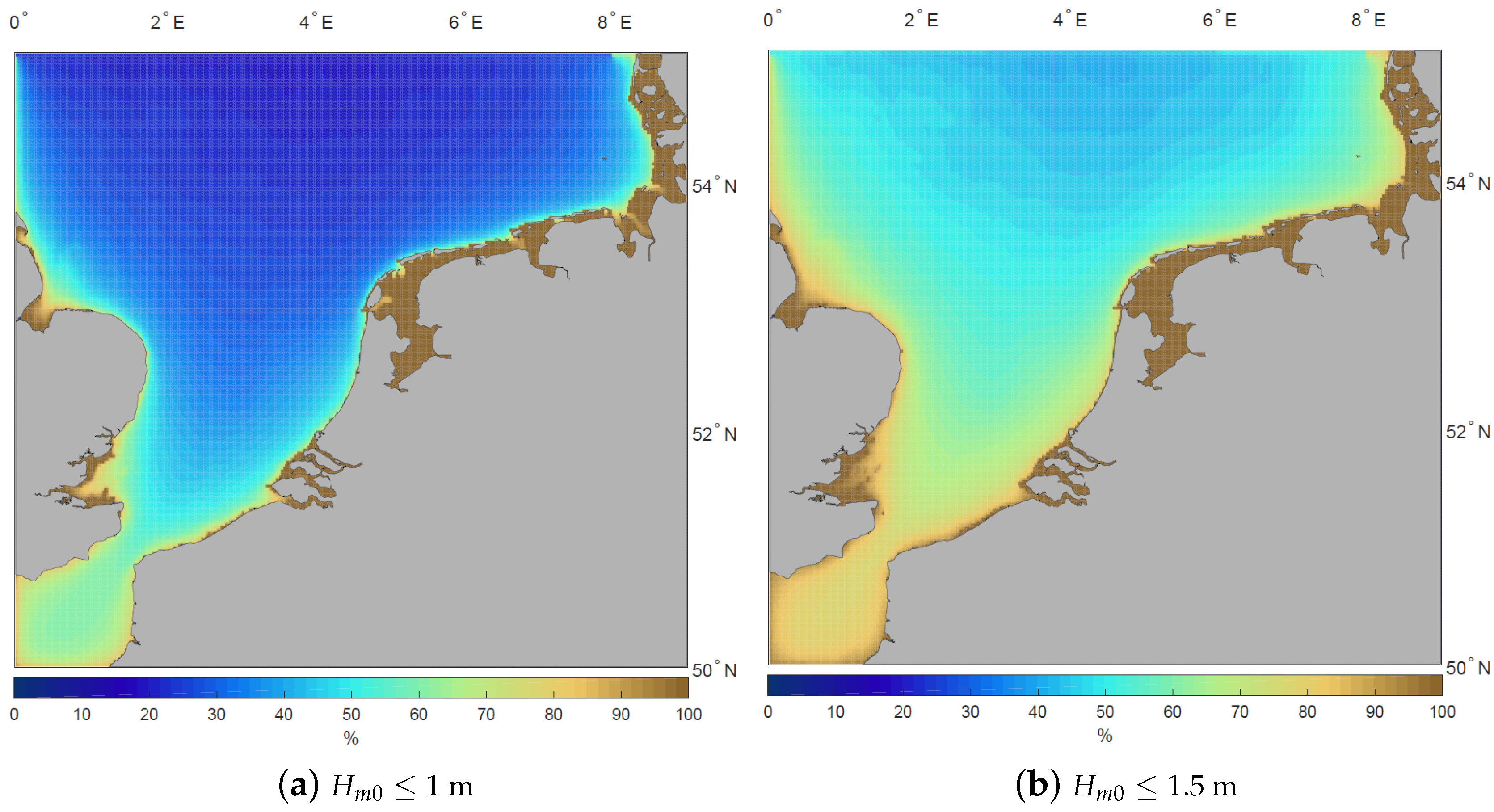
4. Metocean Resource Assessment with the North Sea Wave Database (NSWD)
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Exponential growth | |
| wave steepness coefficient | |
| direction | |
| longitude | |
| Water density | |
| angular frequency | |
| latitude | |
| Non-dimensional Wind | |
| A | linear growth |
| c | energy propagation |
| wind drag coefficient | |
| cumulative dissipation | |
| centimetres | |
| Coefficient of Variation | |
| CSN | Climatological Standard Normals |
| Mean wave direction | |
| E | action density |
| f | frequency |
| Significant wave height | |
| Maximum significant wave height | |
| g | gravitational acceleration |
| local dissipation | |
| m | Meters |
| Maintenance and operation | |
| MPI | Model Performance Index |
| NWM | Numerical Wave Models |
| Peak wave direction | |
| Percentile value | |
| R | Correlation coefficient |
| Root Mean Square Error | |
| Observed changes | |
| , s | seconds |
| Scatter Index | |
| wind input | |
| triads | |
| Quadruplet interactions | |
| Whitecapping | |
| bottom friction | |
| depth breaking | |
| t | time |
| Mean Zero Crossing period | |
| Average wave period | |
| Maximum of average wave period | |
| wave energy converters | |
| Wind speed at 10 meter height | |
| Reference Wind |
References
- Caires, S.; Groeneweg, J.; Sterl, A. Past and Futures Changes in the North Sea Extreme Waves. ICCE 2008, 19, 7666. [Google Scholar]
- Lavidas, G.; Agarwal, A.; Venugopal, V. Marine Activities Dependence on Offshore Climatic Conditions. In Energy in Transportation (EinT), ASHRAE; Deligkiozi, I., Ed.; ASHRAE: Athens, Greece, 2016; pp. 29–36. [Google Scholar]
- Agarwal, A. A Long-Term Analysis of the Wave Climate in the North East Atlantic and North Sea. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 2015. [Google Scholar]
- Reguero, B.; Losada, I.J.; Mendez, J.F. A recent increase in global wave power as a consequence of oceanic warming. Nat. Commun. 2019, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Chawla, A.; Spindler, D.M.; Tolman, H.L. Validation of a thirty year wave hindcast using the Climate Forecast System Reanalysis winds. Ocean. Model. 2013, 70, 189–206. [Google Scholar] [CrossRef]
- Reguero, B.; Losada, I.; Méndez, F. A global wave power resource and its seasonal, interannual and long-term variability. Appl. Energy 2015, 148, 366–380. [Google Scholar] [CrossRef]
- Caires, S.; Sterl, A. 100-year return value estimates for ocean wind speed and significant wave height from the ERA-40 data. J. Clim. 2005, 18, 1032–1048. [Google Scholar] [CrossRef]
- Galanis, G.; Chu, P.C.; Kallos, G.; Kuo, Y.H.; Dodson, C.T.J. Wave height characteristics in the north Atlantic ocean: A new approach based on statistical and geometrical techniques. Stoch. Environ. Res. Risk Assess. 2012, 26, 83–103. [Google Scholar] [CrossRef]
- Bailey, B.H.; McDonald, S.L.; Bernadett, D.W.; Markus, M.J.; Elsholz, K.V. Wind Resource Assessment Handbook: Fundamentals for Conducting a Successful Monitoring Program; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 1997.
- World Bank. Best Practice Guidelines for Mesoscale Wind Mapping Projects for the World Bank; Technical Report; World Bank: Washington, DC, USA, 2010. [Google Scholar]
- Ingram, D.; Smith, G.H.; Ferriera, C.; Smith, H. Protocols for the Equitable Assessment of Marine Energy Converters; Technical Report; Institute of Energy Systems, University of Edinburgh, School of Engineering: Edinburgh, UK, 2011. [Google Scholar]
- Smith, H.; Maisondieu, C. Resource Assessment for Cornwall, Isles of Scilly and PNMI; Technical Report; University of Exeter and Ifremer: Exeter, UK, 2014. [Google Scholar]
- Lavidas, G.; Venugopal, V.; Friedrich, D. Wave energy extraction in Scotland through an improved nearshore wave atlas. Int. J. Mar. Energy 2017, 17, 64–83. [Google Scholar] [CrossRef]
- World Meteorological Organization. WMO Guidelines on the Calculation of Climate Normals; Technical Report; World Meteorological Organization: Geneva, Switzerland, 2017. [Google Scholar]
- Cavaleri, L.; Sclavo, M. The calibration of wind and wave model data in the Mediterranean Sea. Coast. Eng. 2006, 53, 613–627. [Google Scholar] [CrossRef]
- Vinoth, J.; Young, I.R. Global Estimates of Extreme Wind Speed and Wave Height. J. Clim. 2011, 24, 1647–1665. [Google Scholar] [CrossRef]
- Cavaleri, L.; Bertotti, L.; Pezzutto, P. Accuracy of altimeter data in inner and coastal seas. Ocean Sci. 2019, 15, 227–233. [Google Scholar] [CrossRef]
- WAMDI, G. The WAM Model-a Third Generation Ocean Wave Prediction Model. Phys. Oceanogr. 1988, 18, 1775–1810. [Google Scholar]
- Lavidas, G.; Venugopal, V. Application of numerical wave models at European coastlines: A review. Renew. Sustain. Energy Rev. 2018, 92, 489–500. [Google Scholar] [CrossRef]
- Rijkswaterstaat. Ministry of Infrastructure and Water Management. Available online: https://www.rijkswaterstaat.nl (accessed on 21 March 2019).
- Larsén, X.G.; Kalogeri, C.; Galanis, G.; Kallos, G. A statistical methodology for the estimation of extreme wave conditions for offshore renewable applications. Renew. Energy 2015, 80, 205–218. [Google Scholar] [CrossRef]
- Dodet, G.; Bertin, X.; Taborda, R. Wave climate variability in the North-East Atlantic Ocean over the last six decades. Ocean Model. 2010, 31, 120–131. [Google Scholar] [CrossRef]
- Delft, T. SWAN Scientific and Technical Documentation Cycle III Version 41.01; Technical Report; Delft University of Technology: Delft, The Netherlands, 2014. [Google Scholar]
- Amante, C.; Eakins, B. ETOPO1 1 Arc-Minute Global Relief Model: Procedures, Data Sources and Analysis; NOAA Technical Memorandum NESDIS NGDC-24; NOAA: Silver Spring, MD, USA, 2014. [Google Scholar]
- Wessel, P.; Smith, W.H.F. A Global Self-consistent, Hierarchical, High-resolution Shoreline Database. J. Geophys. Res. 1996, 101, 8741–8743. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Akpinar, A.; Ponce de León, S. An assessment of the wind re-analyses in the modelling of an extreme sea state in the Black Sea. Dyn. Atmos. Ocean. 2016, 73, 61–75. [Google Scholar] [CrossRef]
- Stopa, J.E.; Cheung, K.F. Intercomparison of wind and wave data from the ECMWF Reanalysis Interim and the NCEP Climate Forecast System Reanalysis. Ocean. Model. 2014, 75, 65–83. [Google Scholar] [CrossRef]
- Lavidas, G.; Venugopal, V.; Friedrich, D. Sensitivity of a numerical wave model on wind re-analysis datasets. Dyn. Atmos. Ocean. 2017, 77, 1–16. [Google Scholar] [CrossRef]
- Agarwal, A.; Venugopal, V.; Harrison, G.P. The assessment of extreme wave analysis methods applied to potential marine energy sites using numerical model data. Renew. Sustain. Energy Rev. 2013, 27, 244–257. [Google Scholar] [CrossRef]
- National Oceanic and Atmospheric Administration (NOAA), WaveWatchIII. Available online: https://polar.ncep.noaa.gov/waves/wavewatch/ (accessed on 14 September 2019).
- Ponce de León, S.; Bettencourt, J.; Van Vledder, G.P.; Doohan, P.; Higgins, C.; Guedes Soares, C.; Dias, F. Performance of WAVEWATCH-III and SWAN Models in the North Sea. In Proceedings of the 37th International Conference on Ocean, Madrid, Spain, 17–22 June 2018. [Google Scholar] [CrossRef]
- Kamranzad, B.; Mori, N. Future wind and wave climate projections in the Indian Ocean based on a super-high-resolution MRI-AGCM3.2S model projection. Clim. Dyn. 2019. [Google Scholar] [CrossRef]
- Rogers, W.E.; Babanin, A.V.; Wang, D.W. Observation-Consistent Input and Whitecapping Dissipation in a Model for Wind-Generated Surface Waves: Description and Simple Calculations. J. Atmos. Ocean. Technol. 2012, 29, 1329–1346. [Google Scholar] [CrossRef]
- Komen, G.; Hasselmann, S.; Hasselmann, K. On the Existence of a Fully Developed Wind-Sea Spectrum.pdf. Phys. Oceanogr. 1984, 14, 1271–1285. [Google Scholar] [CrossRef]
- Janssen, P.A. Quasi-Linear theory of Wind-Wave Generation applied to wave forecasting. J. Phys. Oceanogr. 1991, 6, 1631–1642. [Google Scholar] [CrossRef]
- van der Westhuysen, A.J.; Zijlema, M.; Battjes, J. Nonlinear saturation-based whitecapping dissipation in SWAN for deep and shallow water. Coast. Eng. 2007, 54, 151–170. [Google Scholar] [CrossRef]
- Zieger, S.; Babanin, A.V.; Erick Rogers, W.; Young, I.R. Observation-based source terms in the third-generation wave model WAVEWATCH. Ocean Model. 2015. [Google Scholar] [CrossRef]
- Hwang, P.A. A Note on the Ocean Surface Roughness Spectrum. J. Atmos. Ocean. Technol. 2011, 28, 436–443. [Google Scholar] [CrossRef]
- Fan, Y.; Lin, S.J.; Held, I.M.; Yu, Z.; Tolman, H.L. Global Ocean Surface Wave Simulation Using a Coupled Atmosphere–Wave Model. J. Clim. 2012, 25, 6233–6252. [Google Scholar] [CrossRef]
- Ardhuin, F.; Rogers, E.; Babanin, A.V.; Filipot, J.F.; Magne, R.; Roland, A.; van der Westhuysen, A.; Queffeulou, P.; Lefevre, J.M.; Aouf, L.; et al. Semiempirical Dissipation Source Functions for Ocean Waves. Part I: Definition, Calibration, and Validation. J. Phys. Oceanogr. 2010, 40, 1917–1941. [Google Scholar] [CrossRef]
- Janssen, P.A. Wave-induced Stress and drag of air flow over sea waves. J. Phys. Oceanogr. 1988, 19, 745–754. [Google Scholar] [CrossRef]
- Zijlema, M.; van Vledder, G.P.; Holthuijsen, L. Bottom friction and wind drag for wave models. Coast. Eng. 2012, 65, 19–26. [Google Scholar] [CrossRef]
- Rijkswaterstaat. Open Data Rijkswaterstaat Waterdienst. 2018. Available online: https://bignieuws.nl/open-data-rijkswaterstaat/ (accessed on 10 February 2019).
- Lavidas, G. Wave Energy Resource Modelling and Energy Pattern Identification Using a Spectral Wave Model. Ph.D. Thesis, University of Edinburgh, School of Engineering, Edinburgh, UK, 2016. [Google Scholar]
- Katsouris, G.; Savenije, L.B. Offshore Wind Access 2017; Technical Report December 2016; Energy Centre Netherlands (ECN): Petten, The Netherlands, 2017. [Google Scholar]
- Lavidas, G.; Agarwal, A.; Venugopal, V. Availability and Accessibility for Offshore Operations in the Mediterranean Sea. J. Waterw. Port Coast. Ocean. Eng. 2018, 144, 1–13. [Google Scholar] [CrossRef]
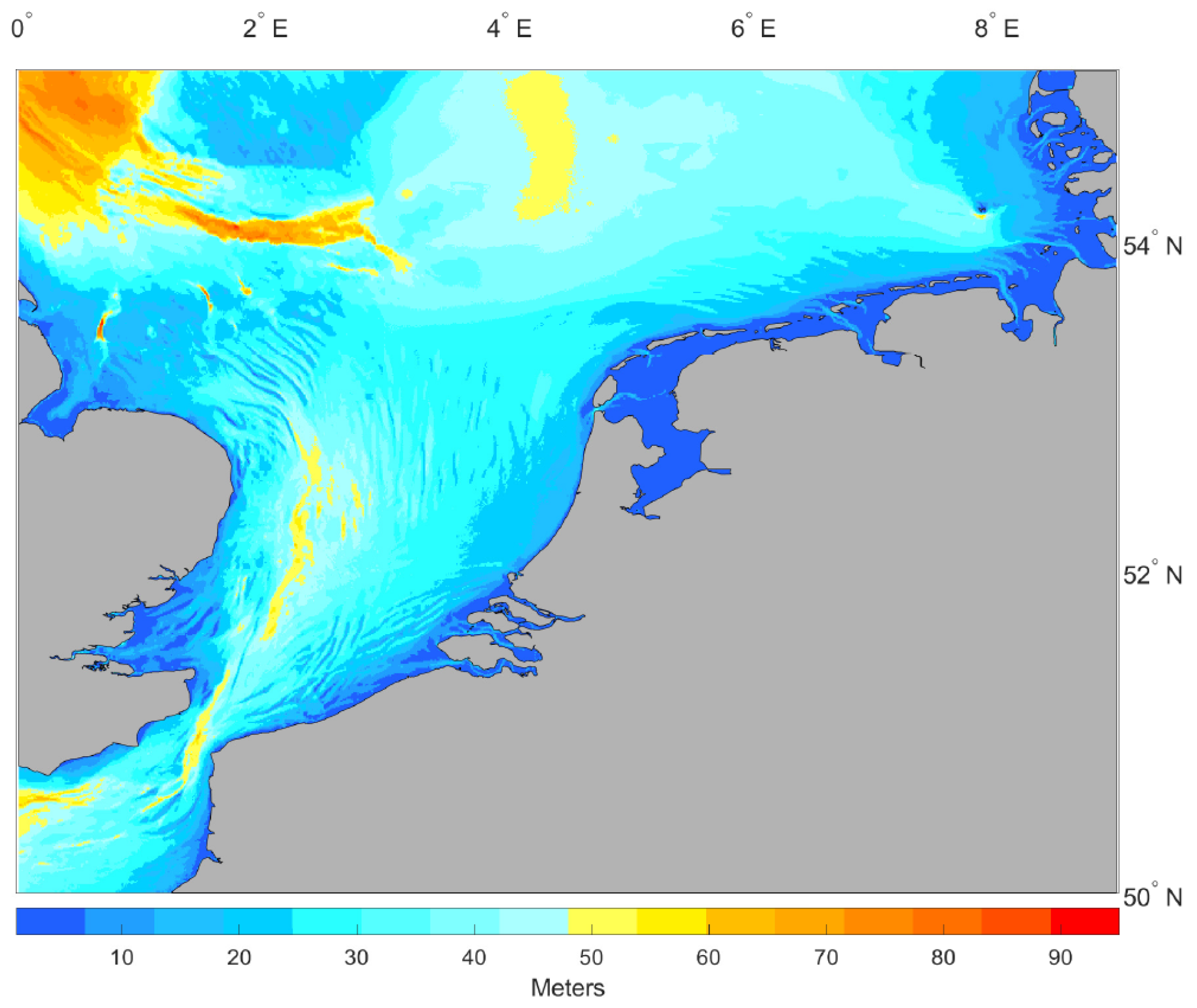
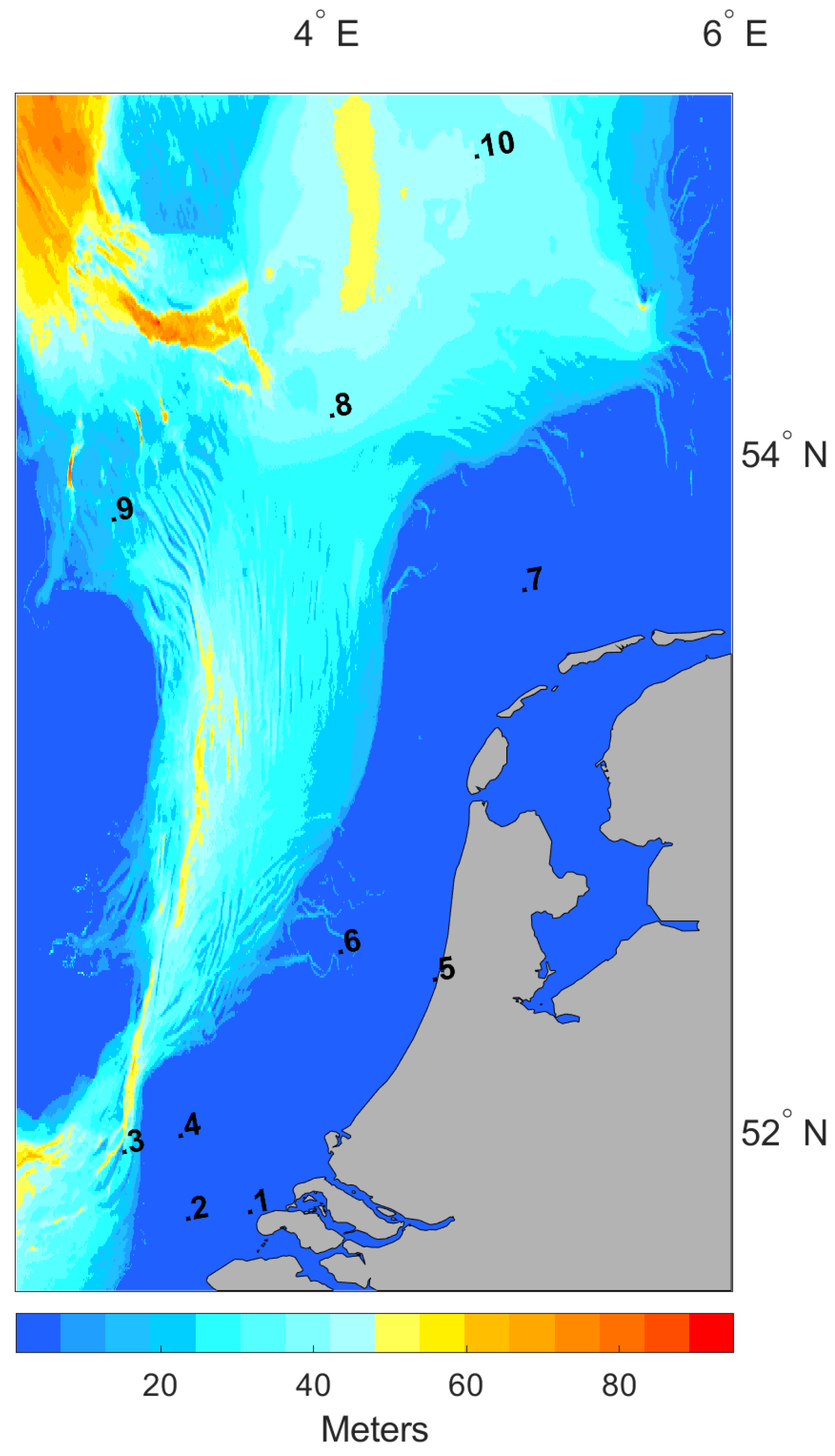
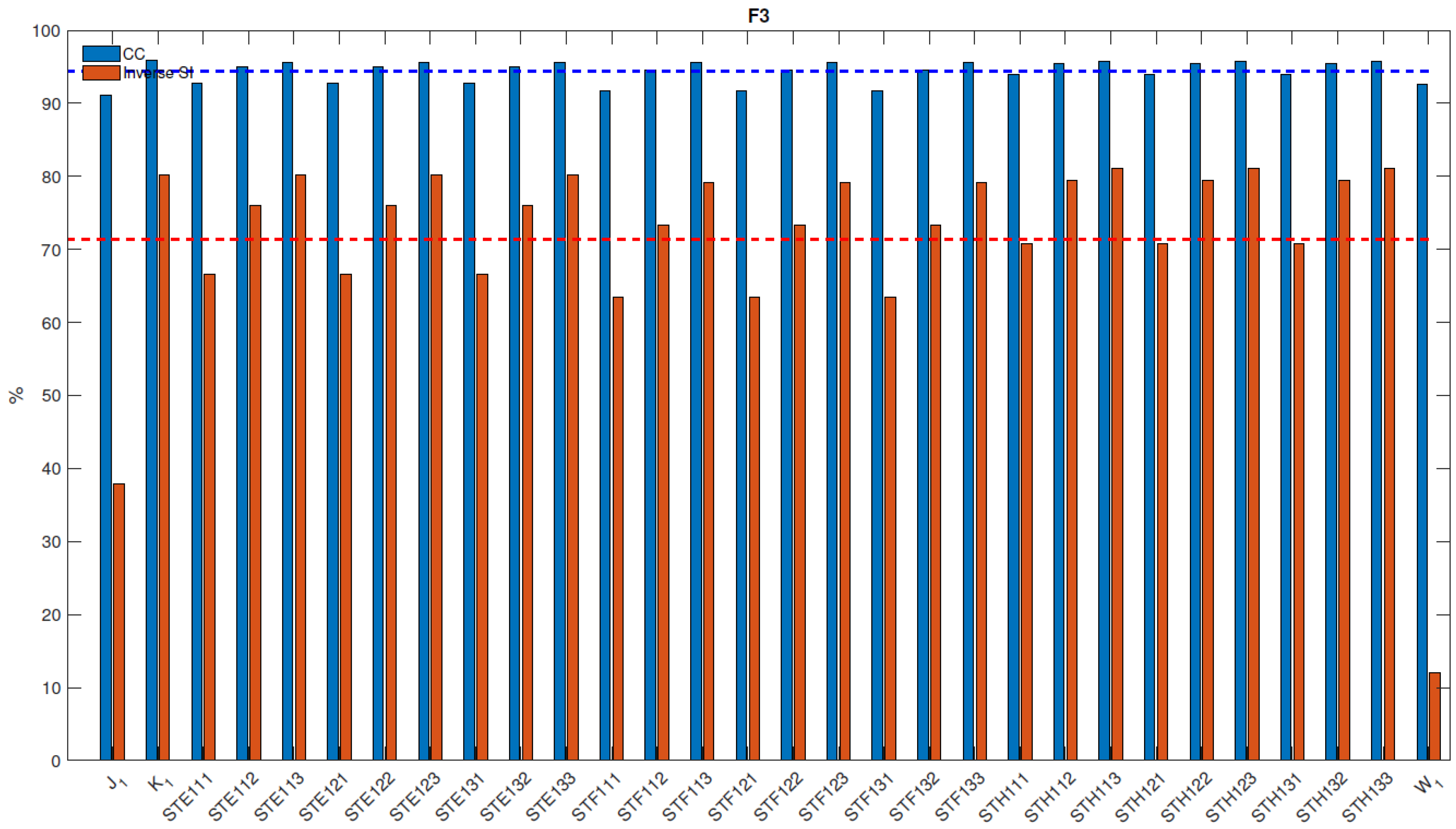
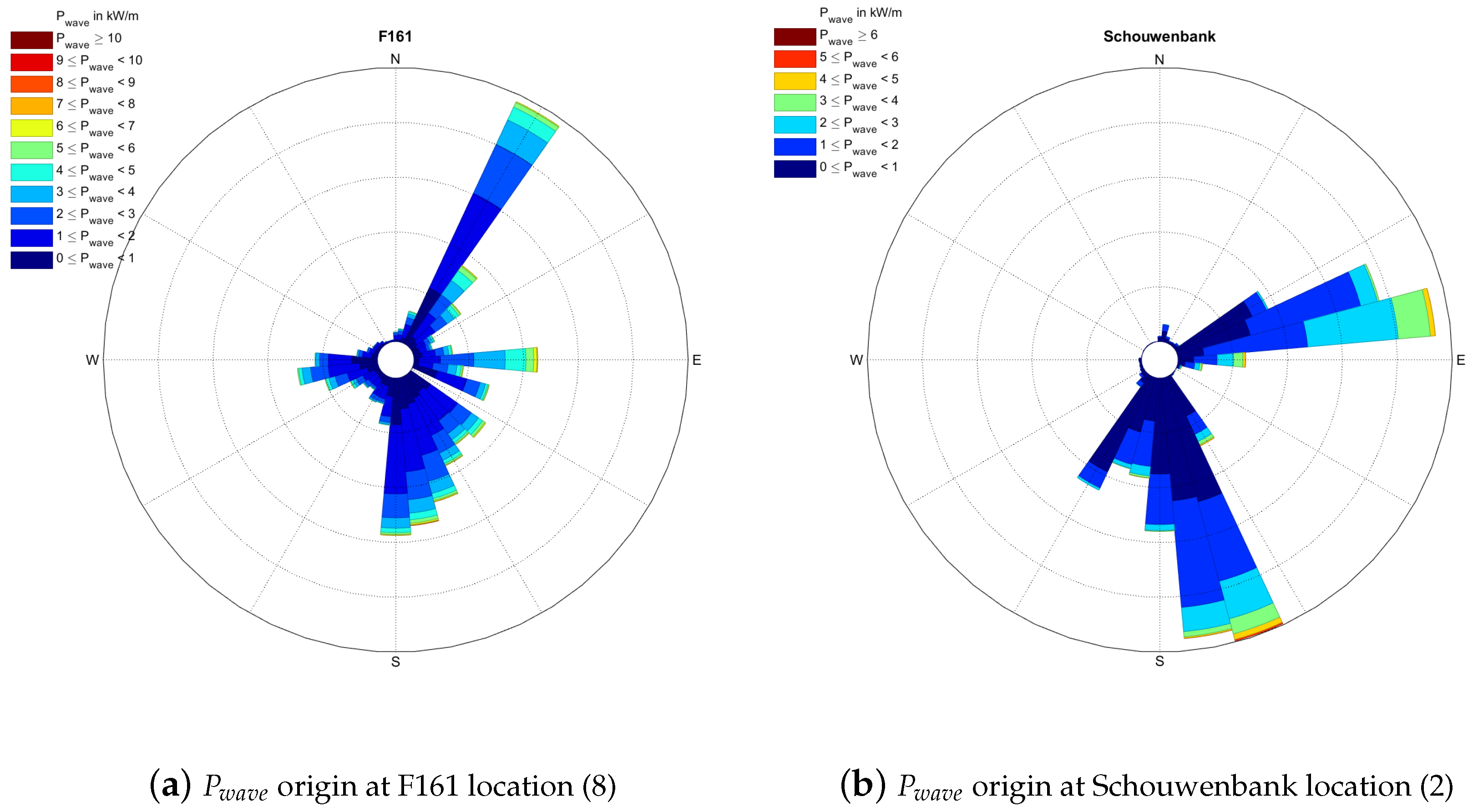
| In-Situ (Buoy) | Longitude () | Latitude () | Map Number | Data Availability |
|---|---|---|---|---|
| Brouwershavensegat | 3.61 | 51.76 | 1 | 69% |
| Schouwenbank | 3.31 | 51.74 | 2 | 63% |
| Eurogeul DWE | 3 | 51.94 | 3 | 64% |
| Europlatform 3 | 3.27 | 51.99 | 4 | 71% |
| IJgeulstroompaal 1 | 4.51 | 52.46 | 5 | 67% |
| IJmuiden Munitiestort 2 | 4.05 | 52.55 | 6 | 73% |
| L91 | 4.96 | 53.61 | 7 | 65% |
| F161 | 4.01 | 54.11 | 8 | 68% |
| J61 | 2.95 | 53.81 | 9 | 76% |
| F3 platform | 4.72 | 54.85 | 10 | 94% |
| RMSE | Bias (m) | SI | RMSE | Bias (s) | SI | |||
|---|---|---|---|---|---|---|---|---|
| Brouwershavensegat | 90% | 0.36 | −0.17 | 37% | 76% | 1.15 | −0.90 | 28% |
| Europlatform 3 | 94% | 0.46 | −0.24 | 35% | 82% | 1.30 | −1.16 | 28% |
| Eurogeul DWE | 94% | 0.46 | −0.23 | 34% | 82% | 1.19 | −1.04 | 28% |
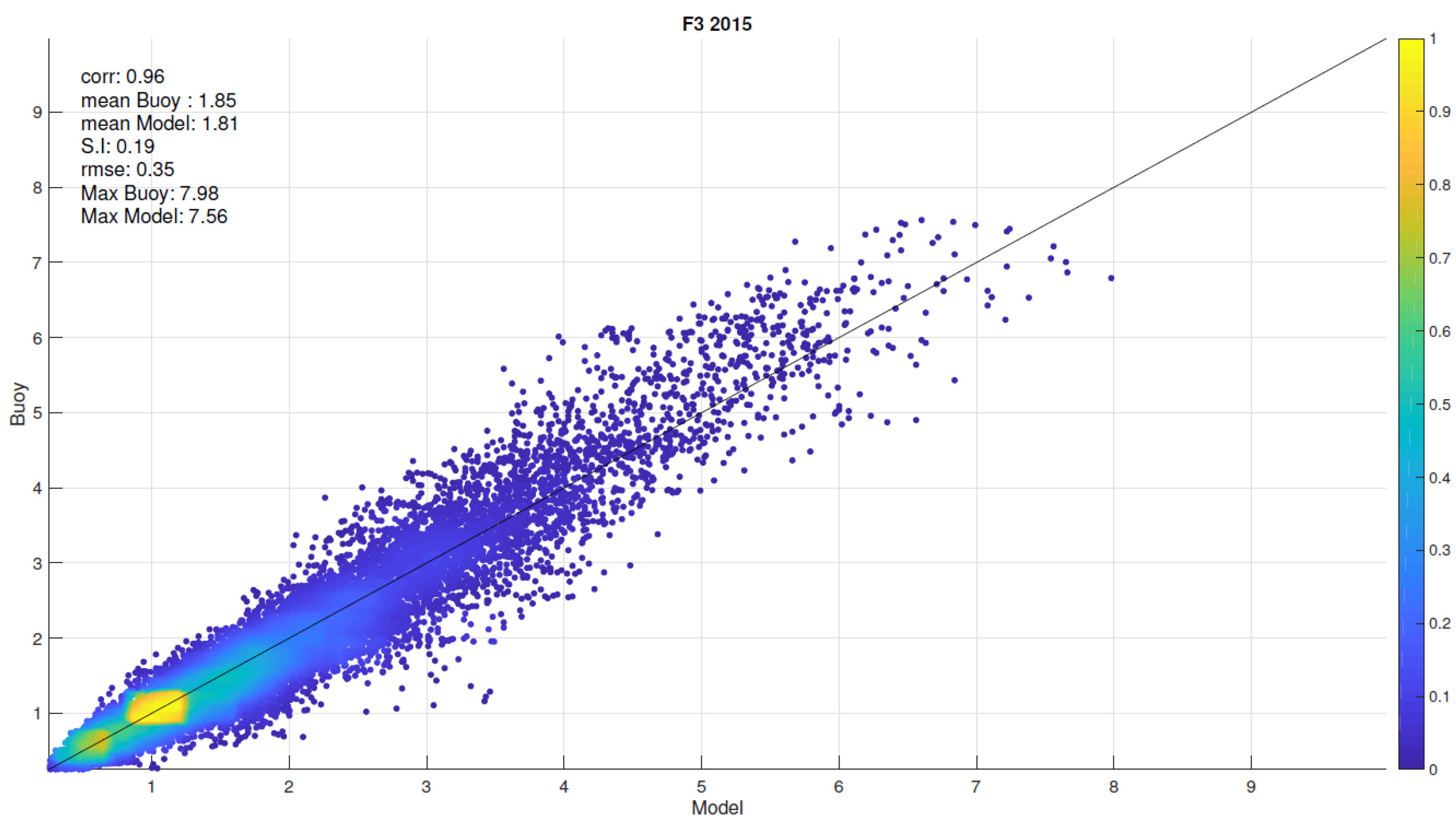
| F3 platform | 94% | 0.53 | −0.17 | 28% | 78% | 1,07 | −0.68 | 20% |
| F161 | 95% | 0.50 | −0.14 | 29% | 78% | 1,26 | −0.99 | 24% |
| Ijgeulstroompaal 1 | 94% | 0.50 | −0.32 | 41% | 81% | 1,11 | −0.88 | 25% |
| Ijmuiden Munitiestort 2 | 94% | 0.45 | −0.24 | 35% | 81% | 1,19 | −1.01 | 26% |
| J61 | 94% | 0.47 | −0.18 | 32% | 79% | 1.07 | −0.78 | 22% |
| L91 | 96% | 0.42 | −0.10 | 28% | 82% | 1.44 | −1.20 | 27% |
| Schouwenbank | 93% | 0.43 | -0.21 | 35% | 79% | 1.24 | −1.09 | 28% |
| R | 93.95% | 95.51% | 95.77% | 93.95% | 95.51% | 95.77% | 93.95% | 95.51% | 95.77% |
| RMSE | 0.54 | 0.38 | 0.35 | 0.54 | 0.38 | 0.35 | 0.54 | 0.38 | 0.35 |
| Bias (m) | −0.37 | −0.18 | −0.04 | −0.37 | −0.18 | −0.04 | −0.37 | −0.18 | −0.04 |
| SI | 29.19% | 20.50% | 18.96% | 29.19% | 20.50% | 18.96% | 29.19% | 20.50% | 18.96% |
| Maxima (m) | 6.31 | 7.03 | 7.56 | 6.31 | 7.03 | 7.56 | 6.31 | 7.03 | 7.56 |
| Brouwershavensegat | Europlatform 3 | Eurogeul DWE | |||||||||||||
| 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | |
| R | 92.05% | 89.19% | n/a | 91.50% | 91.61% | 93.23% | 92.80% | n/a | 94.33% | 93.56% | 93.55% | 92.59% | n/a | 94.35% | 93.42% |
| RMSE (m) | 0.27 | 0.27 | n/a | 0.32 | 0.27 | 0.34 | 0.35 | n/a | 0.42 | 0.34 | 0.36 | 0.36 | n/a | 0.42 | 0.36 |
| MPI | 99.22% | 99.28% | n/a | 99.24% | 99.31% | 99.04% | 98.98% | n/a | 98.91% | 99.07% | 98.96% | 98.95% | n/a | 98.90% | 99.01% |
| Bias (m) | 0.08 | 0.11 | n/a | 0.15 | 0.10 | 0.11 | 0.12 | n/a | 0.22 | 0.11 | 0.15 | 0.15 | n/a | 0.23 | 0.13 |
| SI | 29.38% | 32.92% | n/a | 32.18% | 30.55% | 27.53% | 29.83% | n/a | 31.11% | 28.32% | 29.90% | 32.43% | n/a | 31.88% | 29.16% |
| Max buoy (m) | 5.17 | 4.04 | n/a | 4.00 | 4.59 | 5.22 | 4.69 | n/a | 4.76 | 5.74 | 5.06 | 4.88 | n/a | 5.25 | 5.57 |
| Max SWAN (m) | 3.89 | 3.24 | n/a | 3.52 | 3.53 | 6.40 | 6.04 | n/a | 5.04 | 5.62 | 6.53 | 6.08 | n/a | 5.02 | 5.62 |
| F161 | F3 | Ijgeulstroompaal 1 | |||||||||||||
| 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | |
| R | 92.17% | 93.35% | n/a | 93.19% | 91.92% | 92.17% | 93.49% | 94.92% | 95.93% | 94.96% | 92.61% | 90.93% | n/a | 95.26% | 91.32% |
| RMSE (m) | 0.66 | 0.68 | n/a | 0.71 | 0.62 | 0.69 | 0.70 | 0.51 | 0.53 | 0.48 | 0.27 | 0.25 | n/a | 0.28 | 0.28 |
| MPI | 98.83% | 98.78% | n/a | 98.75% | 98.72% | 98.78% | 98.74% | 98.65% | 98.57% | 98.70% | 99.15% | 99.24% | n/a | 99.08% | 99.13% |
| Bias (m) | 0.43 | 0.45 | n/a | 0.46 | 0.38 | 0.49 | 0.51 | 0.29 | 0.32 | 0.27 | 0.00 | 0.04 | n/a | 0.05 | −0.02 |
| SI | 43.67% | 43.61% | n/a | 48.53% | 42.89% | 44.09% | 43.79% | 30.21% | 28.67% | 27.98% | 25.37% | 29.40% | n/a | 23.29% | 28.46% |
| buoy (m) | 6.78 | 7.56 | n/a | 5.61 | 5.62 | 7.84 | 9.52 | 7.58 | 7.98 | 7.47 | 5.29 | 3.51 | n/a | 5.25 | 6.27 |
| SWAN (m) | 8.13 | 8.19 | n/a | 6.64 | 6.24 | 7.94 | 9.40 | 8.02 | 7.88 | 8.28 | 4.69 | 3.72 | n/a | 4.60 | 4.12 |
| Ijmuiden Munitiestort 2 | J61 | L91 | |||||||||||||
| 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | |
| R | 93.27% | 90.12% | 94.33% | 94.20% | 93.50% | n/a | n/a | n/a | 90.55% | 87.39% | n/a | n/a | n/a | 96% | n/a |
| RMSE (m) | 0.32 | 0.31 | 0.33 | 0.39 | 0.32 | n/a | n/a | n/a | 0.68 | 0.66 | n/a | n/a | n/a | 0.29 | n/a |
| MPI | 98.95% | 99.05% | 99.04% | 98.88% | 98.91% | n/a | n/a | n/a | 98.84% | 98.98% | n/a | n/a | n/a | 99% | n/a |
| Bias (m) | 0.12 | 0.13 | 0.10 | 0.18 | 0.11 | n/a | n/a | n/a | 0.43 | 0.41 | n/a | n/a | n/a | −0.10 | n/a |
| SI | 26.63% | 30.85% | 27.51% | 30.11% | 28.25% | n/a | n/a | n/a | 45.15% | 49.39% | n/a | n/a | n/a | 19 % | n/a |
| buoy (m) | 6.25 | 5.42 | 6.18 | 5.58 | 4.81 | n/a | n/a | n/a | 6.24 | 6.58 | n/a | n/a | n/a | 6.24 | n/a |
| SWAN (m) | 6.49 | 3.84 | 5.75 | 5.08 | 5.64 | n/a | n/a | n/a | 6.06 | 6.85 | n/a | n/a | n/a | 6.70 | n/a |
| Schouwenbank | |||||||||||||||
| 2012 | 2013 | 2014 | 2015 | 2016 | |||||||||||
| R | 86.01% | 79.35% | n/a | 85.76% | 81.07% | ||||||||||
| RMSE (m) | 0.47 | 0.43 | n/a | 0.45 | 0.48 | ||||||||||
| MPI | 98.90% | 98.83% | n/a | 98.83% | 98.91% | ||||||||||
| Bias (m) | −0.19 | −0.06 | n/a | −0.11 | −0.14 | ||||||||||
| SI | 33.65% | 36.06% | n/a | 31.62% | 36.85% | ||||||||||
| buoy (m) | 6.28 | 4.76 | n/a | 5.47 | 5.46 | ||||||||||
| SWAN (m) | 5.72 | 4.00 | n/a | 4.26 | 5.12 | ||||||||||
| Brouwershavensegat | Europlatform 3 | Eurogeul DWE | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | |
| R | 77.47% | 73.09% | n/a | 78.95% | 79.33% | 82.19% | 78.57% | n/a | 85.61% | 85.57% | 83.87% | 79.13% | n/a | 86.07% | 84.71% |
| RMSE (s) | 0.66 | 0.63 | n/a | 0.61 | 0.65 | 0.71 | 0.70 | n/a | 0.65 | 0.61 | 0.65 | 0.63 | n/a | 0.57 | 0.60 |
| MPI | 96.50% | 96.49% | n/a | 96.83% | 96.88% | 96.42% | 96.14% | n/a | 96.25% | 96.48% | 96.22% | 95.93% | n/a | 96.31% | 96.42% |
| Bias (s) | −0.28 | −0.25 | n/a | −0.18 | −0.27 | −0.41 | −0.37 | n/a | −0.35 | −0.45 | −0.28 | −0.27 | n/a | −0.24 | −0.29 |
| SI | 16.17% | 15.65% | n/a | 15.05% | 15.81% | 15.55% | 15.54% | n/a | 14.05% | 13.33% | 14.61% | 14.56% | n/a | 12.89% | 13.63% |
| Max buoy (s) | 15.80 | 7.20 | n/a | 7.00 | 7.40 | 7.70 | 7.80 | n/a | 7.80 | 8.10 | 7.80 | 7.90 | n/a | 7.60 | 7.60 |
| Max SWAN (s) | 8.15 | 7.13 | n/a | 7.08 | 6.52 | 8.30 | 7.78 | n/a | 7.12 | 7.64 | 8.41 | 7.74 | n/a | 6.99 | 7.54 |
| F161 | F3 | Ijgeulstroompaal 1 | |||||||||||||
| 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | |
| R | 85.28% | 85.84% | n/a | 86.36% | 87.56% | 84.91% | 87.03% | 84.15% | 89.19% | 87.72% | 80.12% | 73.68% | n/a | 84.77% | 80.12% |
| RMSE (s) | 0.63 | 0.66 | n/a | 0.65 | 0.63 | 0.62 | 0.59 | 0.68 | 0.59 | 0.61 | 0.62 | 0.69 | n/a | 0.64 | 0.69 |
| MPI | 96.26% | 96.22% | n/a | 96.03% | 95.82% | 95.93% | 95.90% | 95.92% | 95.97% | 96.12% | 96.60% | 96.34% | n/a | 96.62% | 96.24% |
| Bias (s) | 0.16 | 0.16 | n/a | 0.14 | 0.14 | −0.03 | −0.02 | −0.02 | 0.02 | 0.02 | −0.11 | −0.22 | n/a | −0.15 | −0.29 |
| SI | 13.19% | 13.58% | n/a | 13.76% | 13.43% | 11.90% | 11.38% | 13.49% | 11.38% | 11.94% | 14.52% | 16.96% | n/a | 14.59% | 16.14% |
| Max buoy (s) | 8.70 | 9.50 | n/a | 7.70 | 7.90 | 9.00 | 10.50 | 9.50 | 9.40 | 9.50 | 7.90 | 8.30 | n/a | 7.90 | 8.20 |
| Max SWAN (s) | 9.05 | 9.27 | n/a | 8.57 | 7.88 | 9.44 | 10.11 | 11.60 | 9.20 | 9.94 | 8.07 | 8.24 | n/a | 7.22 | 6.89 |
| Ijmuiden Munitiestort 2 | J61 | L91 | |||||||||||||
| 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | 2012 | 2013 | 2014 | 2015 | 2016 | |
| R | 82.05% | 74.51% | 80.00% | 84.78% | 85.24% | n/a | n/a | n/a | 74.60% | 78.24% | 57.79% | n/a | n/a | n/a | n/a |
| RMSE (s) | 0.65 | 0.69 | 0.70 | 0.62 | 0.65 | n/a | n/a | n/a | 0.90 | 0.82 | 1.01 | n/a | n/a | n/a | n/a |
| MPI | 95.97% | 95.89% | 96.37% | 96.06% | 95.73% | n/a | n/a | n/a | 95.94% | 96.08% | 96.13% | n/a | n/a | n/a | n/a |
| Bias (s) | −0.28 | −0.33 | −0.30 | −0.25 | −0.34 | n/a | n/a | n/a | −0.43 | −0.38 | −0.02 | n/a | n/a | n/a | n/a |
| SI | 14.22% | 15.85% | 15.82% | 13.75% | 14.48% | n/a | n/a | n/a | 17.11% | 15.86% | 21.19% | n/a | n/a | n/a | n/a |
| Max buoy (s) | 8.40 | 9.20 | 9.30 | 7.80 | 8.00 | n/a | n/a | n/a | 10.20 | 9.70 | 13.00 | n/a | n/a | n/a | n/a |
| Max SWAN (s) | 8.54 | 7.99 | 8.64 | 7.31 | 7.76 | n/a | n/a | n/a | 9.13 | 8.20 | 9.21 | n/a | n/a | n/a | n/a |
| Schouwenbank | |||||||||||||||
| R | 71.84% | 55.96% | n/a | 76.13% | 73.53% | ||||||||||
| RMSE (s) | 1.11 | 1.10 | n/a | 1.04 | 1.08 | ||||||||||
| MPI | 96.12% | 95.35% | n/a | 96.00% | 95.96% | ||||||||||
| Bias (s) | −0.86 | −0.78 | n/a | −0.83 | −0.85 | ||||||||||
| SI | 22.74% | 23.08% | n/a | 21.52% | 22.45% | ||||||||||
| Max buoy (s) | 9.00 | 10.10 | n/a | 8.60 | 8.20 | ||||||||||
| Max SWAN (s) | 7.79 | 6.92 | n/a | 6.82 | 7.33 | ||||||||||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lavidas, G.; Polinder, H. North Sea Wave Database (NSWD) and the Need for Reliable Resource Data: A 38 Year Database for Metocean and Wave Energy Assessments. Atmosphere 2019, 10, 551. https://doi.org/10.3390/atmos10090551
Lavidas G, Polinder H. North Sea Wave Database (NSWD) and the Need for Reliable Resource Data: A 38 Year Database for Metocean and Wave Energy Assessments. Atmosphere. 2019; 10(9):551. https://doi.org/10.3390/atmos10090551
Chicago/Turabian StyleLavidas, George, and Henk Polinder. 2019. "North Sea Wave Database (NSWD) and the Need for Reliable Resource Data: A 38 Year Database for Metocean and Wave Energy Assessments" Atmosphere 10, no. 9: 551. https://doi.org/10.3390/atmos10090551
APA StyleLavidas, G., & Polinder, H. (2019). North Sea Wave Database (NSWD) and the Need for Reliable Resource Data: A 38 Year Database for Metocean and Wave Energy Assessments. Atmosphere, 10(9), 551. https://doi.org/10.3390/atmos10090551







