Optical Energy Variability Induced by Speckle: The Cases of MERLIN and CHARM-F IPDA Lidar
Abstract
1. Introduction
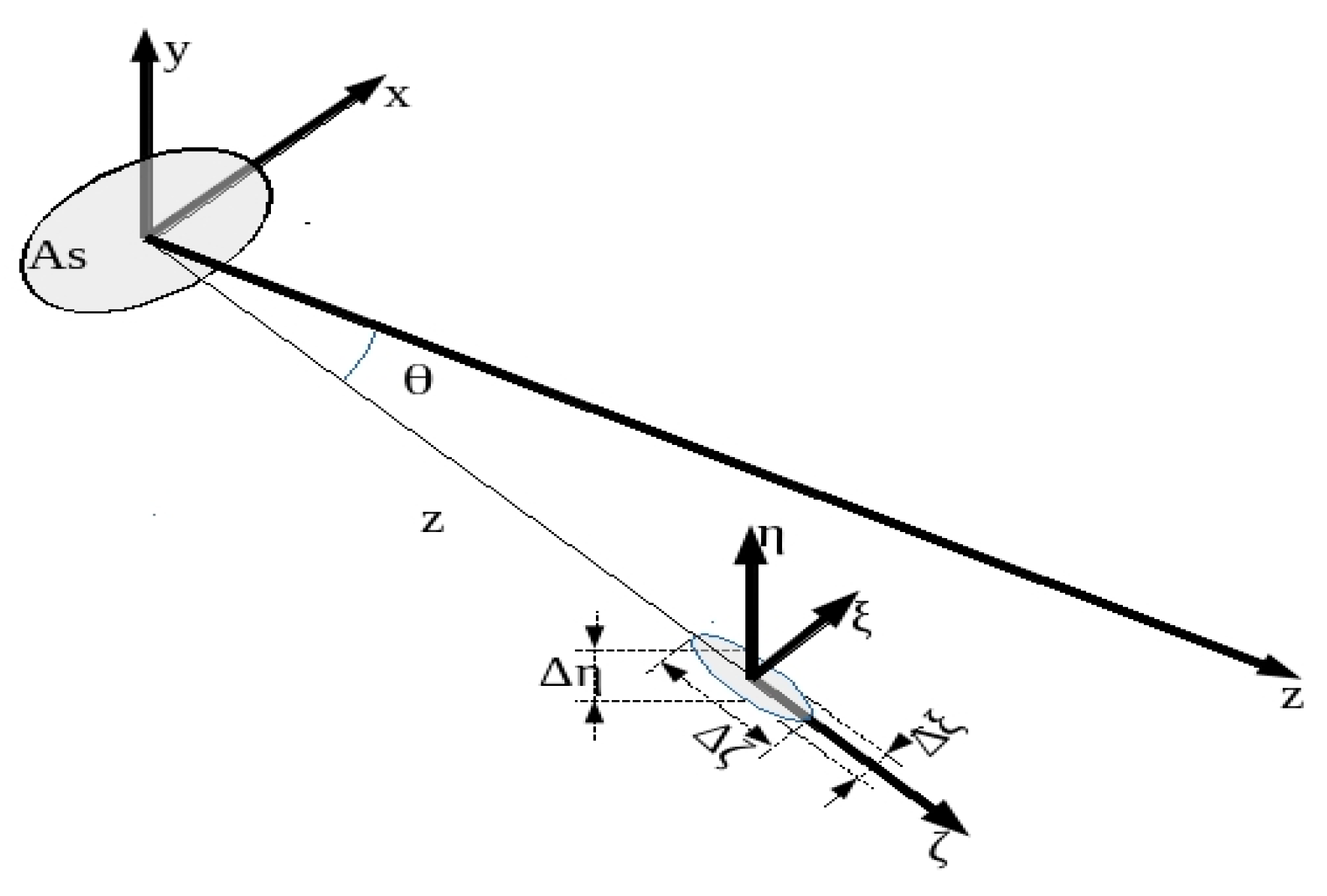
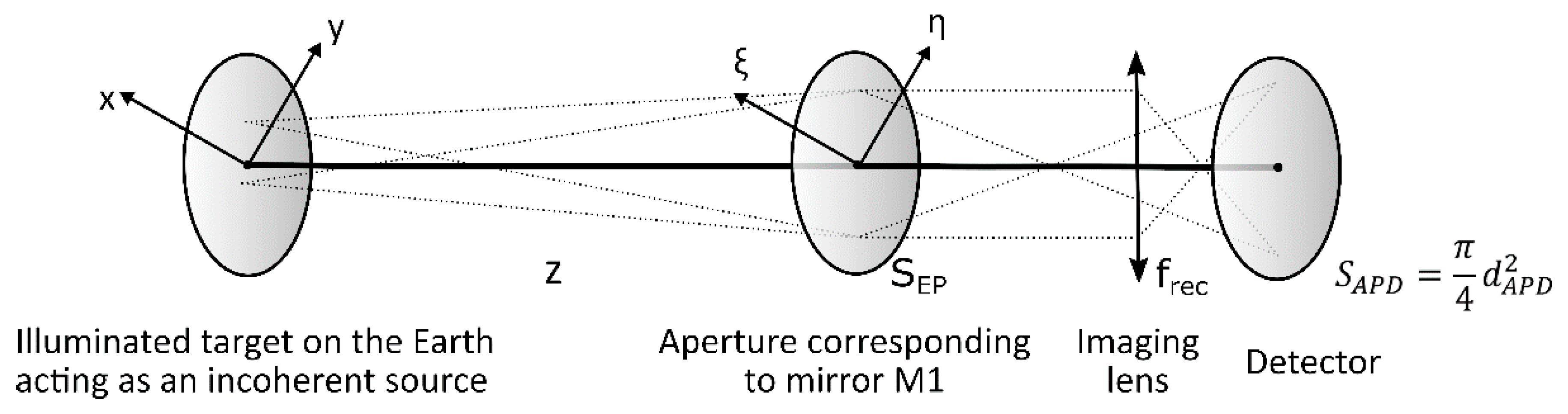
2. The Parameters Which Determines the Speckle Contribution to XCH4 SNR and Their Values for Merlin and Charm-F
2.1. How Does Speckle Contribute to Signal-to-Noise Ratio on XCH4 Measurements?
2.2. MERLIN and CHARM-F Data Sets
3. Speckle Contributions to Signal-to-Noise Ratio on MERLIN or CHARM-F XCH4 Measurements
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Speckle Theory
References
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M.; et al. Carbon and Others, Biogeochemical Cycles. In Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-n., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Midgley, V.B., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013; pp. 465–570. [Google Scholar]
- Ehret, G.; Bousquet, P.; Pierangelo, C.; Alpers, M.; Millet, B.; Abshire, J.B.; Bovensmann, H.; Burrows, J.P.; Chevallier, F.; Ciais, P.; et al. MERLIN: A French-German Space Lidar Mission Dedicated to Atmospheric Methane. Remote Sens. 2017, 9, 1052. [Google Scholar] [CrossRef]
- Kiemle, C.; Quatrevalet, M.; Ehret, G.; Amediek, A.; Fix, A.; Wirth, M. Sensitivity studies for a space-based methane lidar mission. Atmos. Meas. Tech. 2011, 4, 2195–2211. [Google Scholar] [CrossRef]
- Pierangelo, C.; Millet, B.; Esteve, F.; Alpers, M.; Ehret, G.; Flamant, P.; Berthier, S.; Gibert, F.; Chomette, O.; Edouart, D.; et al. MERLIN (Methane Remote Sensing Lidar Mission): An Overview. ILRC 27 EPJ Web Conf. 2016, 119, 26001. [Google Scholar] [CrossRef]
- Bousquet, P.; Pierangelo, C.; Bacour, C.; Marshall, J.; Peylin, P.; Ayar, P.V.; Ehret, G.; Bréon, F.M.; Chevallier, F.; Crevoisier, C.; et al. Error Budget of the MEthane Remote LIdar missioN and Its Impact on the Uncertainties of the Global Methane Budget. JGR Atmos. 2018, 123, 766–785. [Google Scholar] [CrossRef]
- Bode, M.; Alpers, M.; Millet, B.; Ehret, G.; Flamant, P. MERLIN: An integrated path differential absorption (IPDA) lidar for global methane remote sensing. In Proceedings of the International Conference on Space Optics—ICSO, Tenerife, Canari Island, Spain, 6–10 October 2014. [Google Scholar]
- Amediek, A.; Ehret, G.; Fix, A.; Wirth, M.; Büdenbender, C.; Quatrevalet, M.; Kiemle, C.; Gerbig, C. CHARM-F a new airborne integrated-path differential-absorption lidar for carbon dioxide and methane observations: Measurement performance and quantification of strong point source emissions. Appl. Opt. 2017, 56, 5182–5197. [Google Scholar] [CrossRef] [PubMed]
- Ingmann, P.; Bensi, P.; Durand, D. Six Candidate Earth Explorer Core Missions—Reports for Assessment: A-SCOPE—Advanced Space Carbon and climate Observation of Planet Earth; Clissold, P., Ed.; ESA Communication Production Office: Noordwijk, The Netherlands, 2008. [Google Scholar]
- Caron, J.; Durand, Y. Operating wavelengths optimization for a spaceborne lidar measuring atmospheric CO2. Appl. Opt. 2009, 48, 5413–5422. [Google Scholar] [CrossRef]
- NASA, Active Sensing of CO2 Emissions over Nights, Days, and Seasons (ASCENDS) Mission. NASA Science Definition and Planning Workshop Report. Available online: https://cce.nasa.gov/ascends (accessed on 10 September 2019).
- Ehret, G.; Kiemle, C.; Wirth, M.; Amediek, A.; Fix, A.; Houweling, S. Space-borne remote sensing of CO2, CH4, and N2O by integrated path differential absorption lidar: A sensitivity analysis. Appl. Phys. B 2008, 90, 593. [Google Scholar] [CrossRef]
- Amediek, A.; Fix, A.; Wirth, M.; Ehret, G. Development of an OPO system at 1.57 μm for integrated path DIAL measurement of atmospheric carbon dioxide. Appl. Phys. B 2008, 92, 295. [Google Scholar] [CrossRef]
- Abshire, J.B.; Riris, H.; Allan, G.R.; Weaver, C.J.; Mao, J.; Sun, X.; Hasselbrack, W.E.; Kawa, S.R.; Biraud, S. Pulsed airborne lidar measurements of atmospheric CO2 column absorption. Tellus B Chem. Phys. Meteorol. 2010, 62, 770–783. [Google Scholar] [CrossRef]
- Riris, H.; Numata, K.; Li, S.; Wu, S.; Ramanathan, A.; Dawsey, M.; Mao, J.; Kawa, R.; Abshire, J.B. Airborne measurements of atmospheric methane column abundance using a pulsed integrated-path differential absorption lidar. Appl. Opt. 2012, 51, 8296–8305. [Google Scholar] [CrossRef]
- Refaat, T.F.; Ismail, S.; Nehrir, A.; Hair, J.; Crawford, J.; Leifer, I.; Shuman, T. Performance evaluation of a 1.6-μm methane DIAL system from ground, aircraft and UAV platforms. Opt. Express 2013, 21, 30415–30432. [Google Scholar] [CrossRef] [PubMed]
- Abshire, J.B.; Ramanathan, A.; Riris, H.; Mao, J.; Allan, G.R.; Hasselbrack, W.E.; Weaver, C.J.; Browell, E.V. Airborne measurements of CO2 column concentration and range using a pulsed direct detection IPDA lidar. Remote Sens. 2014, 6, 443–469. [Google Scholar] [CrossRef]
- Refaat, T.F.; Singh, U.N.; Yu, J.; Petros, M.; Ismail, S.; Kavaya, M.J.; Davis, K.J. Evaluation of an airborne triple-pulsed 2 μm IPDA lidar for simultaneous and independent atmospheric water vapor and carbon dioxide measurements. Appl. Opt. 2015, 54, 1387–1398. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Petros, M.; Singh, U.N.; Refaat, T.F.; Reithmaier, K.; Remus, R.; Johnson, W. An airborne 2-μm double-pulsed direct-detection lidar instrument for atmospheric CO2 column measurements. J. Atmos. Ocean. Technol. 2017, 34, 385–400. [Google Scholar] [CrossRef]
- Singh, U.N.; Refaat, T.F.; Ismail, S.; Davis, K.; Kawa, S.R.; Menzies, R.; Petros, M. Feasibility study of a space-based high pulse energy 2 μm CO2 IPDA lidar. Appl. Opt. 2017, 56, 6531. [Google Scholar] [CrossRef] [PubMed]
- Abshire, J.B.; Ramanathan, A.K.; Riris, H.; Allan, G.R.; Sun, X.; Hasselbrack, W.E.; Mao, J.; Wu, S.; Chen, J.; Numata, K.; et al. Airborne measurements of CO2 column concentrations made with a pulsed IPDA lidar using a multiple-wavelength-locked laser and HgCdTe APD detector. Atmos. Meas. Tech. 2018, 11, 2001–2025. [Google Scholar] [CrossRef]
- Wagner, G.A.; Plusquellic, D.F. Multi-frequency differential absorption LIDAR system for remote sensing of CO2 and H2O near 1.6 μm. Opt. Express. 2018, 26, 19420–19434. [Google Scholar] [CrossRef] [PubMed]
- Wagner, G.A.; Plusquellic, D.F. Ground-based, integrated path differential absorption LIDAR measurement of CO2, CH4, and H2O near 1.6 μm. Appl. Opt. 2016, 55, 6292–6310. [Google Scholar] [CrossRef]
- Spiers, G.D.; Menzies, R.T.; Jacob, J.; Christensen, L.E.; Phillips, M.W.; Choi, Y.; Browell, E.V. Atmospheric CO2 measurements with a 2 μm airborne laser absorption spectrometer employing coherent detection. Appl. Opt. 2011, 50, 2098–2111. [Google Scholar] [CrossRef]
- Menzies, R.T.; Spiers, G.D.; Jacob, J.C. Airborne laser absorption spectrometer measurements of atmospheric CO2 column mole fractions: Source and sink detection and environmental impacts on retrievals. J. Atmos. Ocean. Technol. 2014, 31, 404–421. [Google Scholar] [CrossRef]
- Sakaizawa, D.; Kawakami, S.; Nakajima, M.; Sawa, Y.; Matsueda, H. Ground-based demonstration of a CO2 remote sensor using a 1.57 μm differential laser absorption spectrometer with direct detection. J. Appl. Remote Sens. 2010, 4, 043548. [Google Scholar] [CrossRef]
- Sakaizawa, D.; Kawakami, S.; Nakajima, M.; Tanaka, T.; Morino, I.; Uchino, O. An airborne amplitude-modulated 1.57 μm differential laser absorption spectrometer: Simultaneous measurement of partial column-averaged dry air mixing ratio of CO2 and target range. Atmos. Meas. Tech. 2013, 6, 387–396. [Google Scholar] [CrossRef]
- Du, J.; Zhu, Y.; Li, S.; Zhang, J.; Sun, Y.; Zang, H.; Liu, D.; Ma, X.; Bi, D.; Liu, J.; et al. Double-pulse 1.57 μm integrated path differential absorption lidar ground validation for atmospheric carbon dioxide measurement. Appl. Opt. 2017, 56, 7053–7058. [Google Scholar] [CrossRef] [PubMed]
- Queißer, M.; Burton, M.; Fiorani, L. Differential absorption lidar for volcanic CO2 sensing tested in an unstable atmosphere. Opt. Express 2015, 23, 6634–6644. [Google Scholar] [CrossRef] [PubMed]
- Fiorani, L.; Santoro, S.; Parracino, S.; Nuvoli, M.; Minopoli, C.; Aiuppa, A. Volcanic CO2 detection with a DFM/OPA-based lidar. Opt. Lett. 2015, 40, 1034–1036. [Google Scholar] [CrossRef] [PubMed]
- Dainty, J.C. Laser Speckle and Related Phenomena; Springer science & business Media: Berlin, Germany, 1975. [Google Scholar]
- Goodman, J.W. Statistical Optics; John Wiley & Sons: Hoboken, NJ, USA, 1985. [Google Scholar]
- Ohtsubo, J.; Asakura, T. Velocity measurement of a diffuse object by using time-varying speckles. Opt. Quantum Electron. 1976, 8, 523–529. [Google Scholar] [CrossRef]
- Ostberg, K. Differential Absorption Lidar: Effects of Speckle Noise; Research Inst of National Defence Stockholm: Stockholm, Sweden, 1979. [Google Scholar]
- Flamant, P.H.; Menzies, R.T.; Kavaya, M.J. Evidence for speckle effects on pulsed CO2 lidar signal returns from remote targets. Appl. Opt. 1984, 23, 1412–1417. [Google Scholar] [CrossRef]
- Murty, S.R. Aerosol speckle effects on atmospheric pulsed lidar backscattered signals. Appl. Opt. 1989, 28, 875–878. [Google Scholar] [CrossRef]
- MacKerrow, E.P.; Schmitt, M.J. Measurement of integrated speckle statistics for CO2 lidar returns from a moving, nonuniform, hard target. Appl. Opt. 1997, 36, 6921–6937. [Google Scholar] [CrossRef]
- Nelson, D.H.; Walters, D.L.; MacKerrow, E.P.; Schmitt, M.J.; Quick, C.R.; Porch, W.M.; Petrin, R.R. Wave optics simulation of atmospheric turbulence and reflective speckle effects in CO2 lidar. Appl. Opt. 2000, 39, 1857–1871. [Google Scholar] [CrossRef]
- Chen, J.R.; Numata, K.; Wu, S.T. Error reduction methods for integrated-path differential-absorption lidar measurements. Opt. Express. 2012, 20, 15589–15609. [Google Scholar] [CrossRef] [PubMed]
- Refaat, T.F.; Singh, U.N.; Petros, M.; Remus, R.; Yu, J. Self-calibration and laser energy monitor validations for a double-pulsed 2-μm CO2 integrated path differential absorption lidar application. Appl. Opt. 2015, 54, 7240–7251. [Google Scholar] [CrossRef] [PubMed]
- Fix, A.; Quatrevalet, M.; Amediek, A.; Wirth, M. Energy calibration of integrated path differential absorption lidars. Appl. Opt. 2018, 57, 7501–7514. [Google Scholar] [CrossRef] [PubMed]
- Wenyi, H.; Jiqiao, L.; Yadan, Z.; Junfa, D.; Xiuhua, M.; Shiguang, L.; Junxuan, Z.; Xiaopeng, Z.; Weibiao, C. Analysis of energy monitoring for a double-pulsed CO2 integrated path differential absorption lidar at 1.57 μm. Appl. Opt. 2019, 58, 616–625. [Google Scholar] [CrossRef]
- Jacquinet-Husson, N.; Armante, R.; Scott, N.A.; Chedin, A.; Crépeau, L.; Boutammine, C.; Bouhdaoui, A.; Crevoisier, C.; Capelle, V.; Boonne, C.; et al. The 2015 edition of the GEISA spectroscopic database. J. Mol. Spectrosc. 2016, 327, 31–72. [Google Scholar] [CrossRef]
- Delahaye, T.; Maxwell, S.E.; Reed, Z.D.; Lin, H.; Hodges, J.T.; Sung, K.; Devi, V.; Warneke, T.; Tran, H. Precise methane absorption measurements in the 1.64 μm spectral region for the MERLIN mission. J. Geophys. Res. Atmos. 2016, 121, 7360–7370. [Google Scholar] [CrossRef] [PubMed]
- Delahaye, T.; Ghysels, M.; Hodges, J.T.; Sung, K.; Armante, R.; Tran, H. Measurement and modeling of air-broadened methane absorption in the MERLIN spectral region at low temperatures. J. Geophys. Res. Atmos. 2019, 124, 3556–3564. [Google Scholar] [CrossRef]
- Nicodemus, F.E. Directional Reflectance and Emissivity of an Opaque Surface. Appl. Opt. 1965, 4, 767–775. [Google Scholar] [CrossRef]
- McClain, S.C.; Bartlett, C.L.; Pezzaniti, J.L.; Chipman, R.A. Depolarization measurements of an integrating sphere. Appl. Opt. 1995, 34, 152–154. [Google Scholar] [CrossRef] [PubMed]
- Tellier, Y.; Pierangelo, C.; Wirth, M.; Gibert, F.; Marnas, F. Averaging bias correction for the future space-borne methane IPDA lidar mission MERLIN. Atmos. Meas. Tech. 2018, 11, 5865–5884. [Google Scholar] [CrossRef]
- Lowenthal, S.; Joyeux, D. Speckle Removal by a Slowly Moving Diffuser Associated with a Motionless Diffuser. J. Opt. Soc. Am. 1971, 61, 847–851. [Google Scholar] [CrossRef]
- Singh Mehta, D.; Naik, D.; Singh, R.; Takeda, M. Laser speckle reduction by multimode optical fiber bundle with combined temporal, spatial, and angular diversity. Appl. Opt. 2012, 51, 1894–1904. [Google Scholar] [CrossRef] [PubMed]
- Mandel, L.; Wolf, E. Coherence Properties of Optical Fields. Rev. Mod. Phys. 1965, 37, 231–287. [Google Scholar] [CrossRef]
- Loudon, R. The Quantum Theory of Light; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Wang, Q. Discussion on the fully developed speckle field. Optik 2013, 124, 2948–2950. [Google Scholar] [CrossRef]
- Li, Q.; Chiang, F. Three-dimensional dimension of laser speckle. Appl. Opt. 1992, 31, 6287–6291. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Symbol | MERLIN | CHARM-F |
|---|---|---|---|
| Distance between ground and receiver | z | 506.3 km | 8.5 km |
| Instrument speed relative from Earth | v | 7.6 km/s | 0.2 km/s |
| ON wavelength | λon | 1645.5518 nm | 1645.555 nm |
| OFF wavelength | λoff | 1645.8460 nm | 1645.860 nm |
| Polarization of the emitted beam | P | 1 | 1 |
| FWHM laser pulse energy density spectrum | dνl | 60 MHz | 50 MHz |
| Beam full divergence at e−2 at transmitter telescope output | divbeam | 0.18125 mrad | 3 to 6 mrad |
| Length of elliptical entrance pupil | LM1 | 0.7325 m | 0.06 m |
| Width of elliptical entrance pupil | lM1 | 0.69 m | 0.06 m |
| Obscuration of M1 by M2 | OM2 | 0.03% | 0.00% |
| Focal length of reception optics | frec | 0.4704 m | 0.0303 m |
| Avalanche photo-diode diameter | dAPD | 200 μm | 200 μm |
| Spectral filter width | Lfilter | 2 nm | 2 nm |
| Sampling frequency | νsample | 75 MHz = 1/13.3 ns | 100 MHz = 1/10.0 ns |
| Quantity | Symbol | MERLIN | CHARM-F |
|---|---|---|---|
| Diameter at e−2 for energy distribution on ground | de2G = z divbeam | 91.8 m | 25.5–51.0 m |
| Diameter of the FOV on ground | dfov = z dAPD/frec | 215.3 m | 56.1 m |
| Effective size of the entrance pupil | SEP = π/4 LM1 lM1 (1-OM2) | 3850.5 cm2 | 28.2 cm2 |
| Speckle Characteristics | Symbol | MERLIN | CHARM-F |
|---|---|---|---|
| Effective surface on ground for laser fluxes | Sefflas ~ π/4 de2G2 | 6618.7 m2 | 510.7–2042.8 m2 |
| Effective surface on ground for solar flux | Seffsun = π/4 dfov2 | 36406.4 m2 | 2471.8 m2 |
| Coherence surface for laser fluxes | Sclas = 4/π (λ/divbeam)2 | 105 mm2 | 0.38–0.096 mm2 |
| Coherence surface for solar flux | Scsun = 4/π (λ × frec/dAPD)2 | 19 mm2 | 0.079 mm2 |
| Characteristic time for sun light | τcsun = 1/(Lfilter × c/λ2) | 4.52 10−3 ns | 4.52 10−3 ns |
| Number of spatial speckles for laser fluxes | Mslas = 1 + SEP/Sclas | 3668 | 7440–29449 |
| Number of spatial speckles for solar flux | Mssun = 1 + SEP/Scsun | 20267 | 35786 |
| Number of temporal speckles for laser fluxes | Mtlas = 1 | 1 | 1 |
| Number of temporal speckles for solar flux | Mtsun = 1 + δtdis/τcsun | 296–2951 | 222–2213 |
| MERLIN | CHARM-F | MERLIN | CHARM-F | ||
|---|---|---|---|---|---|
| SNRPon/Poff | 61 | 86 | RREPon/Poff | 1.6% | 1.2% |
| SNRPsun | 3470–10948 | 3986–12585 | RREPsun | 0.0% | 0.0% |
| SNREon/Poff | 43 | 59 | RREEon/Eoff | 2.3% | 1.7% |
| SNRsn | <49 | about 3000 | RREsn | >2.0% | 0.0% |
| MERLIN | CHARM-F | |
|---|---|---|
| Noise for one shot | 60 ppb | 41 ppb |
| Noise for a 7s average | 5 ppb | 3 ppb |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cassé, V.; Gibert, F.; Edouart, D.; Chomette, O.; Crevoisier, C. Optical Energy Variability Induced by Speckle: The Cases of MERLIN and CHARM-F IPDA Lidar. Atmosphere 2019, 10, 540. https://doi.org/10.3390/atmos10090540
Cassé V, Gibert F, Edouart D, Chomette O, Crevoisier C. Optical Energy Variability Induced by Speckle: The Cases of MERLIN and CHARM-F IPDA Lidar. Atmosphere. 2019; 10(9):540. https://doi.org/10.3390/atmos10090540
Chicago/Turabian StyleCassé, Vincent, Fabien Gibert, Dimitri Edouart, Olivier Chomette, and Cyril Crevoisier. 2019. "Optical Energy Variability Induced by Speckle: The Cases of MERLIN and CHARM-F IPDA Lidar" Atmosphere 10, no. 9: 540. https://doi.org/10.3390/atmos10090540
APA StyleCassé, V., Gibert, F., Edouart, D., Chomette, O., & Crevoisier, C. (2019). Optical Energy Variability Induced by Speckle: The Cases of MERLIN and CHARM-F IPDA Lidar. Atmosphere, 10(9), 540. https://doi.org/10.3390/atmos10090540





