A Numerical Study of Aerosol Effects on Electrification with Different Intensity Thunderclouds
Abstract
1. Introduction
2. Model Description
2.1. Cloud Model
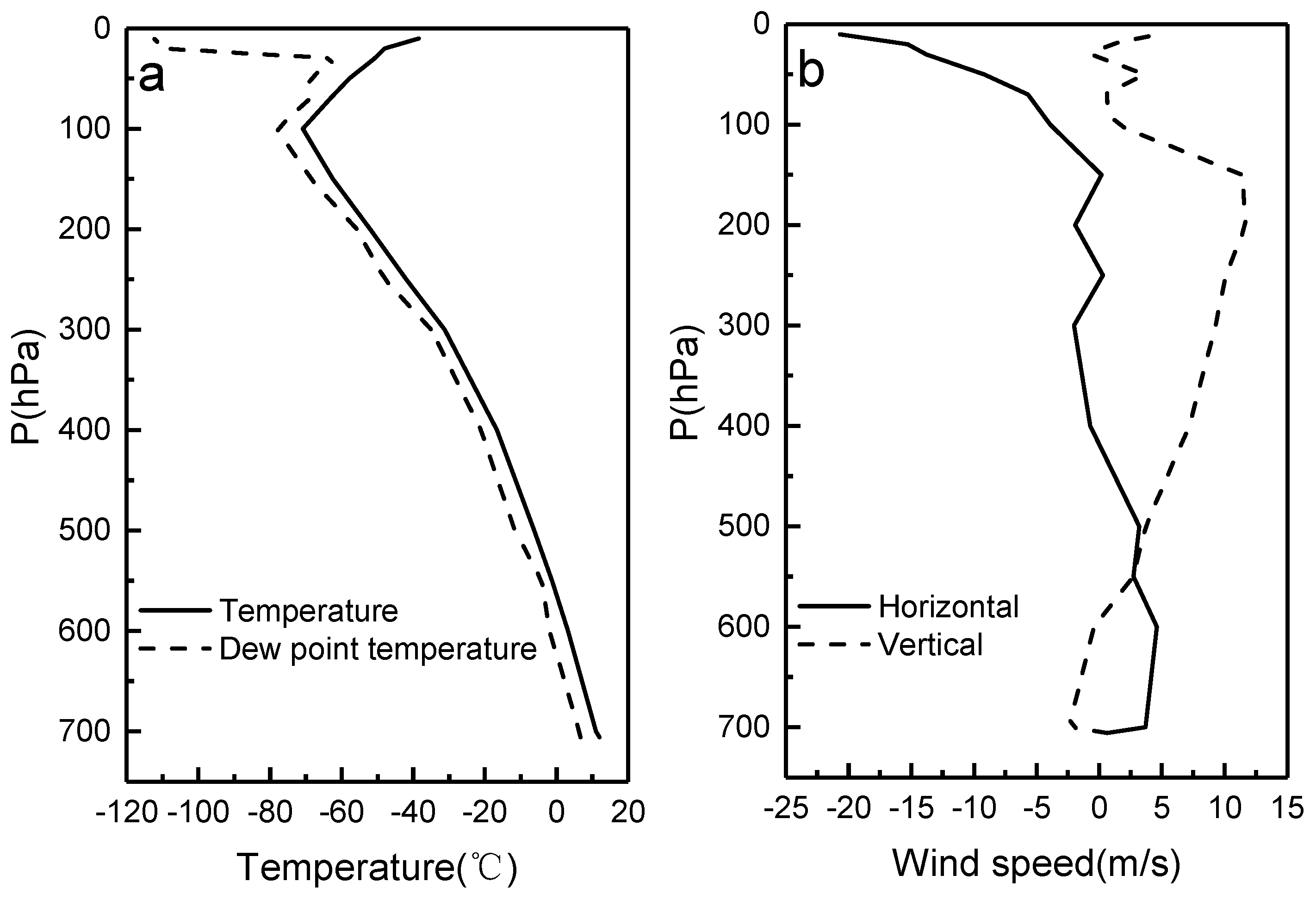
2.2. Model Initialization and Method in Numerical Experiments
3. Results
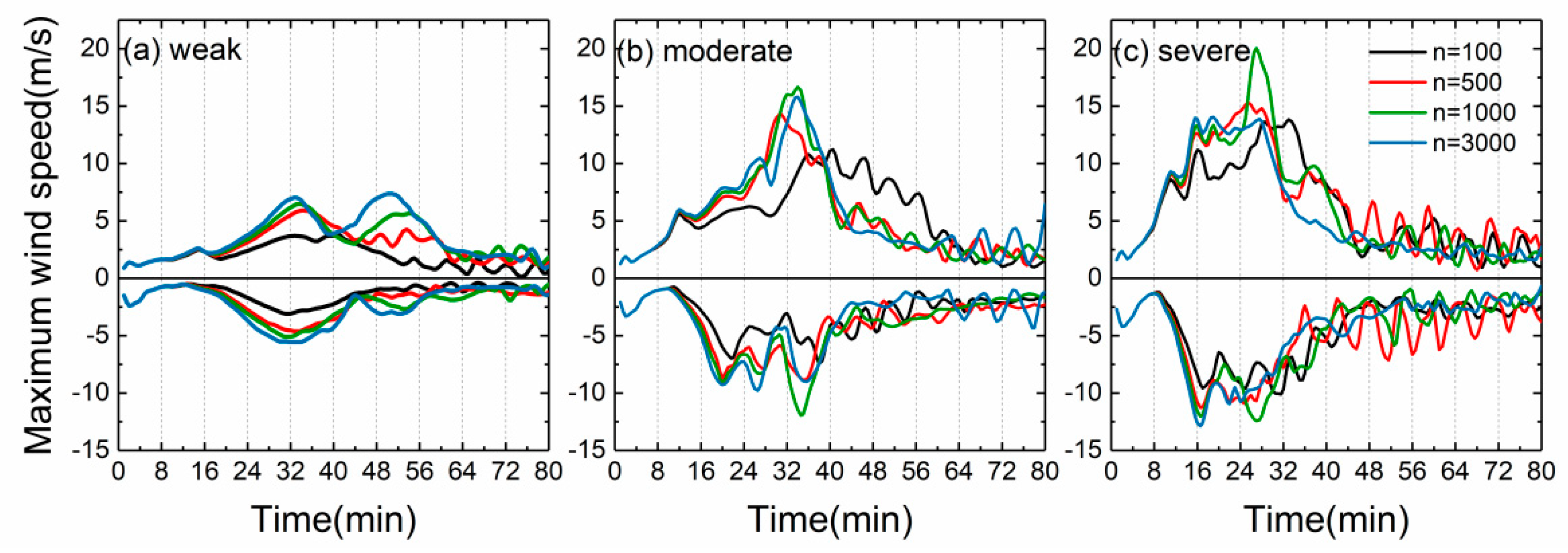
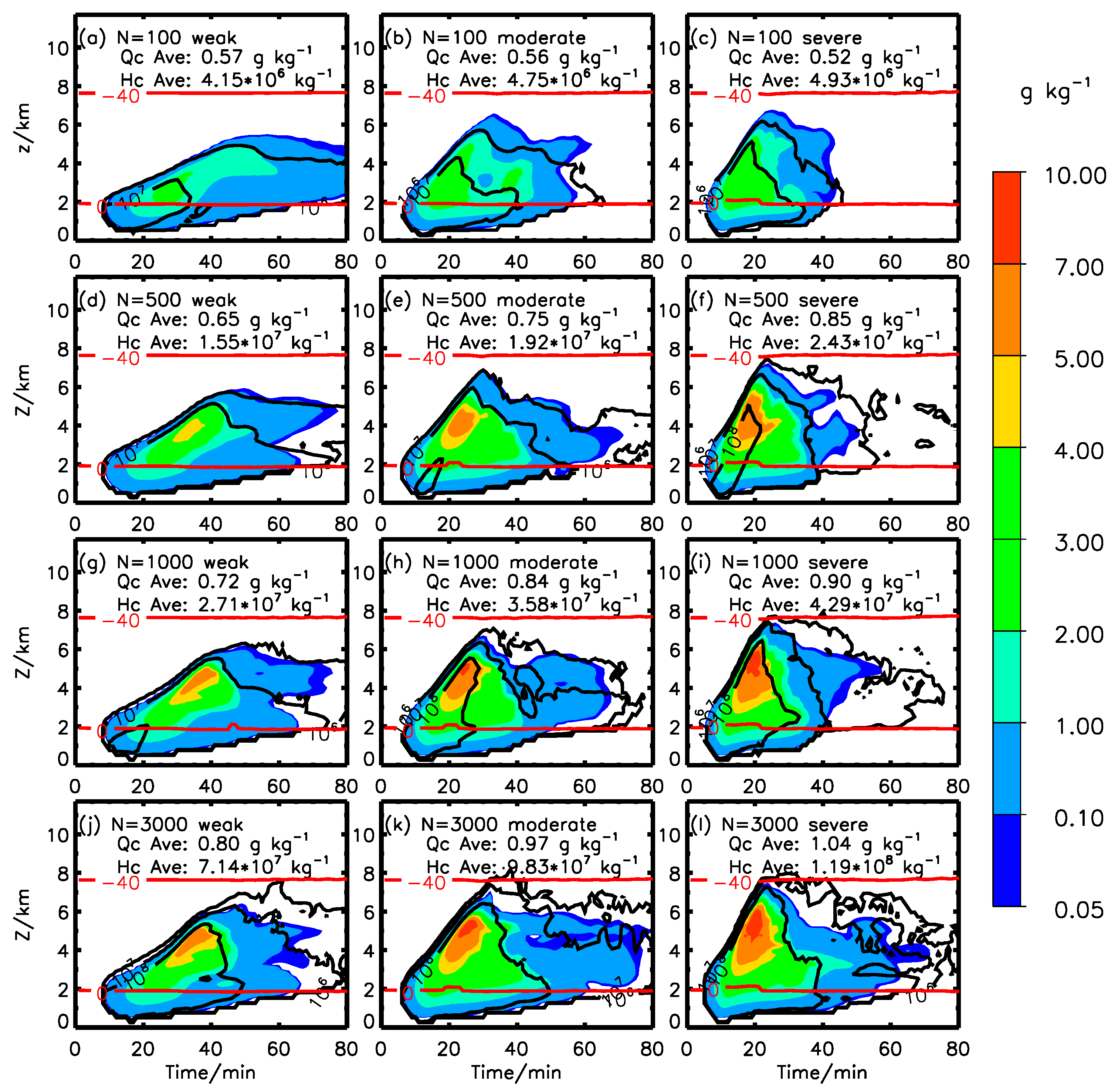
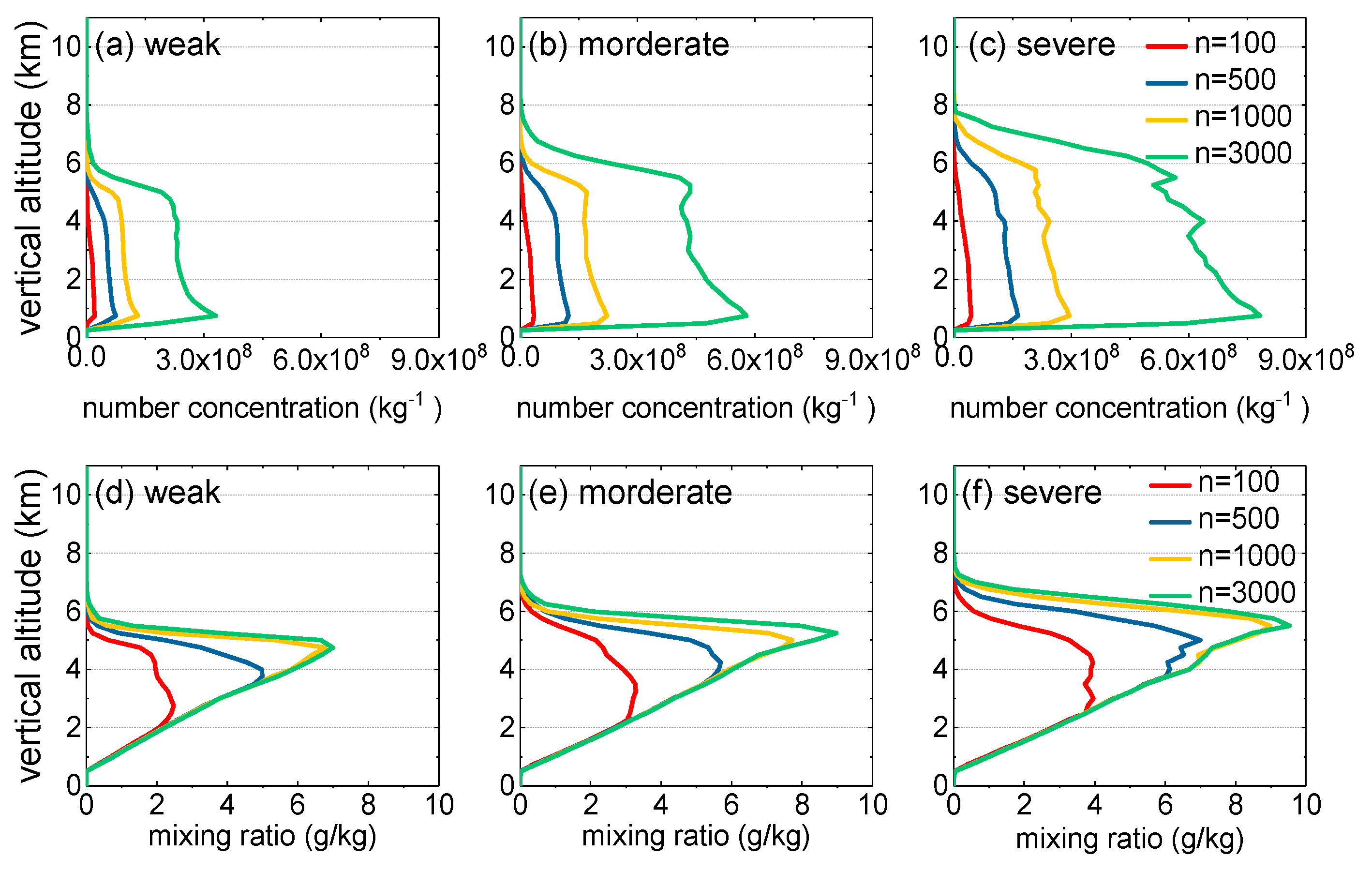
3.1. Dynamic and Microphysical Processes
3.2. Charging Rate
3.3. Electrification Charge Structure
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Latham, D. Lightning flashes from a prescribed fire-induced cloud. J. Geophys. Res. Atmos. 1991, 96, 17151–17157. [Google Scholar] [CrossRef]
- Lyons, W.A.; Uliasz, M.; Nelson, T.E. Large Peak Current Cloud-to-Ground Lightning Flashes during the Summer Months in the Contiguous United States. Mon. Weather Rev. 1998, 126, 2217–2233. [Google Scholar] [CrossRef]
- Murray, N.D.; Orville, R.E.; Huffines, G.R. Effect of pollution from Central American fires on cloud-to-ground lightning in May 1998. Geophys. Res. Lett. 2000, 27, 2249–2252. [Google Scholar] [CrossRef]
- Lang, T.J.; Rutledge, S.A. Cloud-to-ground lightning downwind of the 2002 Hayman forest fire in Colorado. Geophys. Res. Lett. 2006, 33, L03804. [Google Scholar] [CrossRef]
- Altaratz, O.; Koren, I.; Yair, Y.; Price, C. Lightning response to smoke from Amazonian fires. Geophys. Res. Lett. 2010, 37, 363–372. [Google Scholar] [CrossRef]
- Logan, T. Anomalous Lightning Behavior during the 26–27 August 2007 Northern Great Plains Severe Weather Event. J. Geophys. Res. Atmos. 2018, 123, 1771–1784. [Google Scholar] [CrossRef]
- Williams, E.; Rosenfeld, D.; Madden, N.; Gerlach, J.; Gears, N.; Atkinson, L.; Dunnermann, N.; Frostom, G.; Antonio, M.; Biazon, B. Contrasting convective regimes over the Amazon: Implications for cloud electrification. J. Geophys. Res. 2002, 107, 1–19. [Google Scholar] [CrossRef]
- Williams, E.; Stanfill, S. The physical origin of the land–ocean contrast in lightning activity. Comptes Rendus Phys. 2002, 3, 1277–1292. [Google Scholar] [CrossRef]
- Rosenfeld., D.; Lensky., I.M. Satellite–Based Insights into Precipitation Formation Processes in Continental and Maritime Convective Clouds. Bull. Am. Meteorol. Soc. 1998, 79, 2457–2476. [Google Scholar] [CrossRef]
- Zheng, Y.; Rosenfeld, D. Linear relation between convective cloud base height and updrafts and application to satellite retrievals. Geophys. Res. Lett. 2015, 42, 6485–6491. [Google Scholar] [CrossRef]
- Zheng, Y. The oretical understanding of the linear relationship between convective updrafts and cloud-base height for shallow cumulus clouds. Part I: Maritime conditions. J. Atmos. Sci. 2019, 76, 2539–2558. [Google Scholar] [CrossRef]
- Rosenfeld, D.; Lohmann, U.; Raga, G.B.; O’Dowd, C.D.; Kulmala, M.; Fuzzi, S.; Andreae, M.O. Flood or drought: how do aerosols affect precipitation? Science 2008, 321, 1309–1313. [Google Scholar] [CrossRef] [PubMed]
- Mitzeva, R.; Saunders, C.; Tsenova, B. Parameterisation of non-inductive charging in thundercloud regions free of cloud droplets. Atmos. Res. 2006, 82, 102–111. [Google Scholar] [CrossRef]
- Shi, Z.; Tan, Y.B.; Tang, H.Q.; Sun, J.; Yang, Y.; Peng, L.; Guo, X.F. Aerosol effect on the land-ocean contrast in thundercloud electrification and lightning frequency. Atmos. Res. 2015, 164, 131–141. [Google Scholar] [CrossRef]
- Kar, S.K.; Liou, Y.A.; Ha, K.J. Aerosol effects on the enhancement of cloud-to-ground lightning over major urban areas of South Korea. Atmos. Res. 2009, 92, 80–87. [Google Scholar] [CrossRef]
- Stallins, J.A.; Bentley, M.L.; Ashley, W.S.; Mulholland, J.A. Weekend–weekday aerosols and geographic variability in cloud-to-ground lightning for the urban region of Atlanta, Georgia, USA. Reg. Environ. Chang. 2013, 13, 137–151. [Google Scholar] [CrossRef]
- Naccarato, K.P.; Jr, O.P.; Pinto, I.R.C.A. Evidence of thermal and aerosol effects on the cloud-to-ground lightning density and polarity over large urban areas of Southeastern Brazil. Geophys. Res. Lett. 2003, 30, 1–3. [Google Scholar] [CrossRef]
- Pinto, I.R.C.A.; Jr, O.P.; Gomes, M.A.S.S.; Ferreira, N.J. Urban effect on the characteristics of cloud-to-ground lightning over Belo Horizonte-Brazil. Ann. Geophys. 2004, 22, 697–700. [Google Scholar] [CrossRef]
- Tan, Y.B.; Peng, L.; Shi, Z.; Chen, H.R. Lightning flash density in relation to aerosol over Nanjing (China). Atmos. Res. 2016, 174, 1–8. [Google Scholar]
- Wang, Q.; Li, Z.; Guo, J.; Zhao, C.; Cribb, M. The climate impact of aerosols on the lightning flash rate: is it detectable from long-term measurements? Atmos. Chem. Physic 2018, 18, 12797–12816. [Google Scholar] [CrossRef]
- Mansell, E.R.; Ziegler, C.L. Aerosol Effects on Simulated Storm Electrification and Precipitation in a Two-Moment Bulk Microphysics Model. J. Atmos. Sci. 2013, 70, 2032–2050. [Google Scholar] [CrossRef]
- Zhao, P.; Yan, Y.; Hui, X. The effects of aerosol on development of thundercloud electrification: A simulation study in Weather Research and Forecasting (WRF) model. Atmos. Res. 2015, 153, 376–391. [Google Scholar] [CrossRef]
- Zhao, P.; Yin, Y.; Xiao, H. The effects of aerosol on development of thundercloud electrification: A electrification and lightning discharges during thunderclouds. J. Geophys. 2017, 60, 3041–3050. [Google Scholar]
- Fan, J.; Zhang, R.; Li, G.; Tao, W.K.; Li, X. Simulations of cumulus clouds using a spectral microphysics cloud-resolving model. J. Geophys. Res. Atmos. 2007, 112, 1–14. [Google Scholar] [CrossRef]
- Wang, C. A modeling study of the response of tropical deep convection to the increase of cloud condensation nuclei concentration: 1. Dynamics and microphysics. J. Geophys. Res. Atmos. 2005, 110, D21211. [Google Scholar] [CrossRef]
- Li, G.; Yuan, W.; Zhang, R. Incorporation of a two-moment bulk microphysics scheme to the WRF model to investigate aerosol-cloud interaction. J. Geophys. Res. Atmos. 2008, 113, D15. [Google Scholar] [CrossRef]
- Tao, W.K.; Li, X.; Khain, A.; Matsui, T.; Lang, S.; Simpson, J. Role of atmospheric aerosol concentration on deep convective precipitation: Cloud-resolving model simulations. J. Geophys. Res. Atmos. 2007, 112, 24. [Google Scholar] [CrossRef]
- Bjorn, S.; Graham, F. Untangling aerosol effects on clouds and precipitation in a buffered system. Nature 2009, 461, 607–613. [Google Scholar]
- Shi, Z.; Tan, Y.; Liu, Y.; Liu, J.; Luan, J. Effects of relative humidity on electrification and lightning discharges in thunderclouds. Terr. Atmos. Ocean. Sci. 2018, 29, 695–708. [Google Scholar] [CrossRef]
- Carrió, G.G.; Cotton, W.R. On the buffering of CCN impacts on wintertime orographic clouds: An idealized examination. Atmos. Res. 2014, 137, 136–144. [Google Scholar] [CrossRef]
- Hu, Z. Numerical simulation of microprocesses in cumulonimbus clouds (I) microphysical model. Acta Meteorol. Sin. 1987, 45, 467–484. [Google Scholar]
- Yin, Y.; Levin, Z.; Reisin, T.G.; Tzivion, S. The effects of giant cloud condensation nuclei on the development of precipitation in convective clouds—a numerical study. Atmos. Res. 2000, 53, 91–116. [Google Scholar] [CrossRef]
- Fletcher, N.H. The Physics of Rainclouds; Cambridge University Press: Cambridge, UK, 1962. [Google Scholar]
- Sun, A.; Chun, H.Y.; Baik, J.J.; Yan, M. Influence of Electrification on Microphysical and Dynamical Processes in a Numerically Simulated thundercloud. J. Appl. Meteorol. 2002, 41, 1112–1127. [Google Scholar] [CrossRef]
- Cooper, W.A. A method of detecting contact ice nuclei using filter samples. In Proceedings of the Cloud Physics Conference preprints, Clermont-Ferrand, France, 15–19 July 1980; pp. 665–668. [Google Scholar]
- Mossop, S.C. Production of secondary ice particles during the growth of graupel by riming. Q. J. R. Meteorol. Soc. 1976, 102, 45–57. [Google Scholar] [CrossRef]
- Ziegler, C.L.; Macgorman, D.R.; Dye, J.E.; Ray, P.S. A model evaluation of noninductive graupel-ice charging in the early electrification of a mountain thundercloud. J. Geophys. Res. Atmos. 1991, 96, 12833–12855. [Google Scholar] [CrossRef]
- Mansell, E.R.; Macgorman, D.R.; Ziegler, C.L.; Straka, J.M. Charge structure and lightning sensitivity in a simulated multicell thundercloud. J. Geophys. Res. Atmos. 2005, 110, D12. [Google Scholar] [CrossRef]
- Gardiner, B.; Lamb, D.; Pitter, R.L.; Hallett, J.; Saunders, C.P.R. Measurements of initial potential gradient and particle charges in a Montana summer thundercloud. J. Geophys. Res. Atmos. 1985, 90, 6079–6086. [Google Scholar] [CrossRef]
- Pereyra, R.G.; Avila, E.E.; Castellano, N.E.; Saunders, C.P. A laboratory study of graupel charging. J. Geophys. 2000, 105, 20803–20812. [Google Scholar] [CrossRef]
- Tan, Y.; Tao, S.; Liang, Z.; Zhu, B. Numerical study on relationship between lightning types and distribution of space charge and electric potential. J. Geophys. Res. Atmos. 2014, 119, 1003–1014. [Google Scholar] [CrossRef]
- Tan, Y.; Tao, S.; Zhu, B. Fine-resolution simulation of the channel structures and propagation features of intracloud lightning. Geophys. Res. Lett. 2006, 33, L09809. [Google Scholar] [CrossRef]
- Marwitz, J.D. The Structure and Motion of Severe Hailstorms. Part III: Severely Sheared Storms. J. Appl. Meteorol. 1972, 11, 189–201. [Google Scholar] [CrossRef]
- Williams, E.R.; Zhang, R.; Rydock, J. Mixed-Phase Microphysics and Cloud Electrification. J. Atmos. Sci. 1991, 48, 2195–2203. [Google Scholar] [CrossRef]
- Deng, M.; Yin, Y.; Zhao, P. Effects of cloud condensation nuclei concentration on the electrification of thundercloud: A numerical simulation. Chin. J. Atmos. Sci. 2017, 41, 106–120. [Google Scholar]
- Rosenfeld, D. TRMM observed first direct evidence of smoke from forest fires inhibiting rainfall. Geophys. Res. Lett. 1999, 26, 3105–3108. [Google Scholar] [CrossRef]
- Lynn, B.; Khain, A.; Rosenfeld, D.; Woodley, W.L. Effects of aerosols on precipitation from orographic clouds. J. Geophys. Res. Atmos. 2007, 112, D10. [Google Scholar] [CrossRef]
- Liu, J.; Tan, Y.; Shi, Z.; Wang, M.; Yu, M.; Zheng, T. A numerical study of the effects of aerosol on microphysical process and electrification in thunderclouds. Clim. Environ. Res. 2018, 23, 758–768. [Google Scholar]
- Muhlbauer, A.; Lohmann, U. Sensitivity Studies of the Role of Aerosols in Warm-Phase Orographic Precipitation in Different Dynamical Flow Regimes. J. Atmos. Sci. 2008, 65, 2522–2542. [Google Scholar] [CrossRef]
- Rosenfeld, D.; L Woodley, W. Closing the 50-year circle: From cloud seeding to space and back to climate change through precipitation physics. Cloud Syst. Hurric. Trop. Rainfall Meas. Mission (Trmm), Meteor. Monogr 2003, 51, 59–80. [Google Scholar]
- Andreae, M.O.; Rosenfeld, D.; Artaxo, P.; Costa, A.A.; Frank, G.P.; Longo, K.M.; Silva-Dias, M.A.F. Smoking Rain Clouds over the Amazon. Science 2004, 303, 1337–1342. [Google Scholar] [CrossRef] [PubMed]
- Tan, Y.B.; Ma, X.; Xiang, C.Y.; Xia, Y.L.; Zhang, X. A numerical study of the effects of aerosol on electrification and lightning discharges during thunderclouds. Chin. J. Geophys. 2017, 60, 431–442. [Google Scholar]
- Khain, A.; Rosenfeld, D.; Pokrovsky, A. Simulating convective clouds with sustained supercooled liquid water down to −37.5 °C using a spectral microphysics model. Geophys. Res. Lett 2001, 28, 3887–3890. [Google Scholar] [CrossRef]
- Yang, H.; Xiao, H.; Hong, Y.C. A numerical study of aerosol effects on cloud microphysical processes of hailstorm clouds. Atmosphere. 2011, 102, 432–443. [Google Scholar] [CrossRef]
- Miller, K.; Gadian, A.; Saunders, C.; Latham, J.; Christian, H. Modelling and observations of thundercloud electrification and lightning. Atmos. Res. 2001, 58, 89–115. [Google Scholar] [CrossRef]
- Tan, Y.B.; Shi, Z.; Chen, Z.L.; Peng, L.; Yang, Y.; Guo, X.F.; Chen, H.R. A numerical study of aerosol effects on electrification of thunderclouds. J. Atmos. Sol. Terr. Phys. 2015, 154, 210–214. [Google Scholar]
- Macgorman, D.R.; Rust, W.D.; Krehbiel, P.; Rison, W.; Bruning, E.; Wiens, K. The electrical structure of two supercell storms during steps. Mon. Wea. Rev 2005, 133, 2583–2607. [Google Scholar] [CrossRef]
- Kuhlman, K.M.; Ziegler, C.L.; Mansell, E.R.; Macgorman, D.R.; Straka, J.M. Numerically simulated electrification and lightning of the 29 June 2000 steps supercell storm. Mon. Weather Rev. 2006, 134, 85–121. [Google Scholar] [CrossRef]
- Teller, A.; Levin, Z. The effects of aerosols on precipitation and dimensions of subtropical clouds: a sensitivity study using a numerical cloud model. Atmos. Chem. Phys. 2006, 6, 67–80. [Google Scholar] [CrossRef]
- Barahona, D.; Nenes, A. Parameterization of cirrus cloud formation in large-scale models: Homogeneous nucleation. J. Geophys. Res. Atmos. 2008, 113, D11. [Google Scholar] [CrossRef]
- Demott, P.J.; Mccluskey, C.S.; Petters, M.; Suski, K.J.; Levin, E.J.; Hill, T.C.J.; Atwood, S.A.; Schill, G.P.; Rocci, K.; Boose, Y. Aerosol and Cloud-Nucleating Particle Observations during an Atmospheric River Event. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 14–18 December 2015. [Google Scholar]


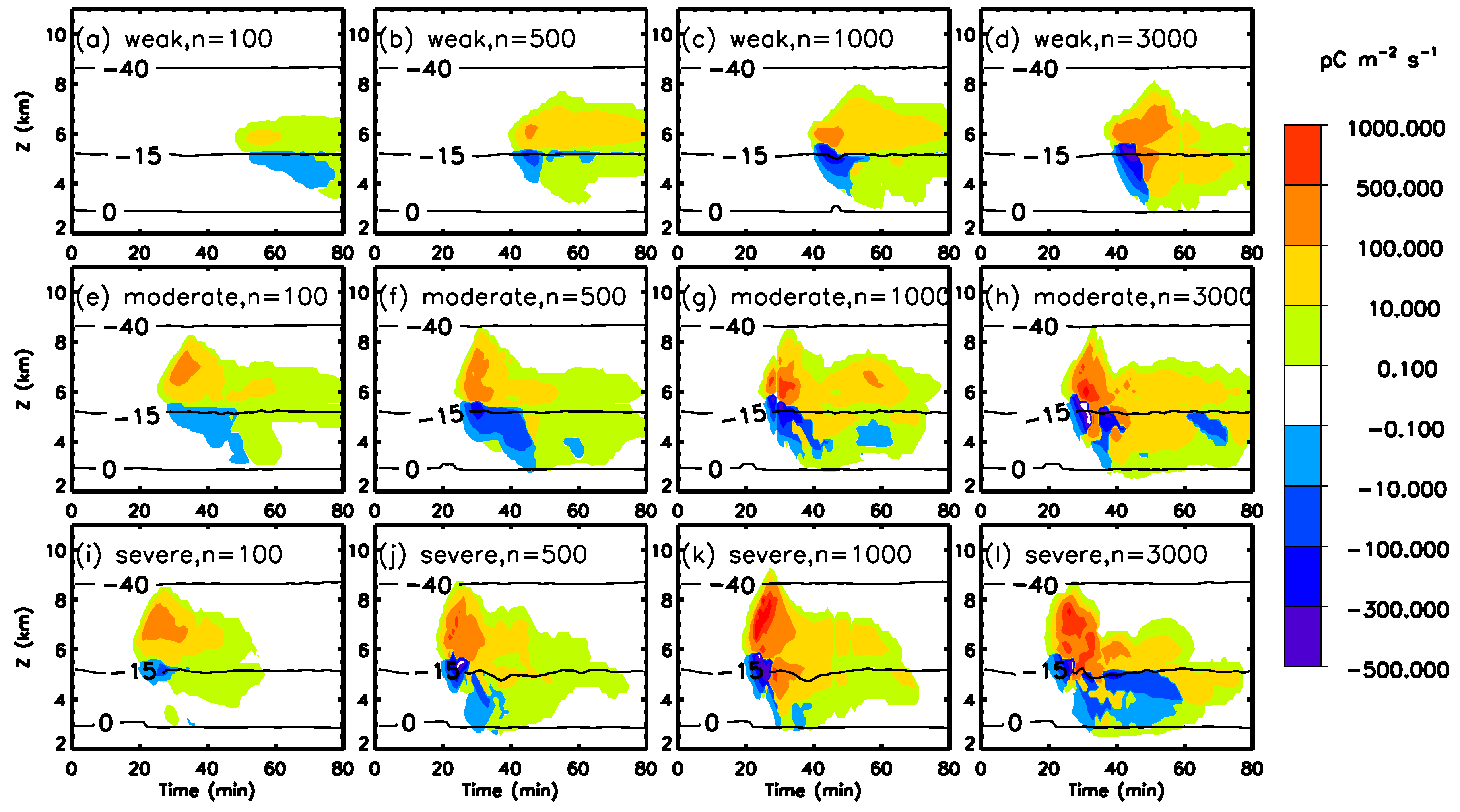

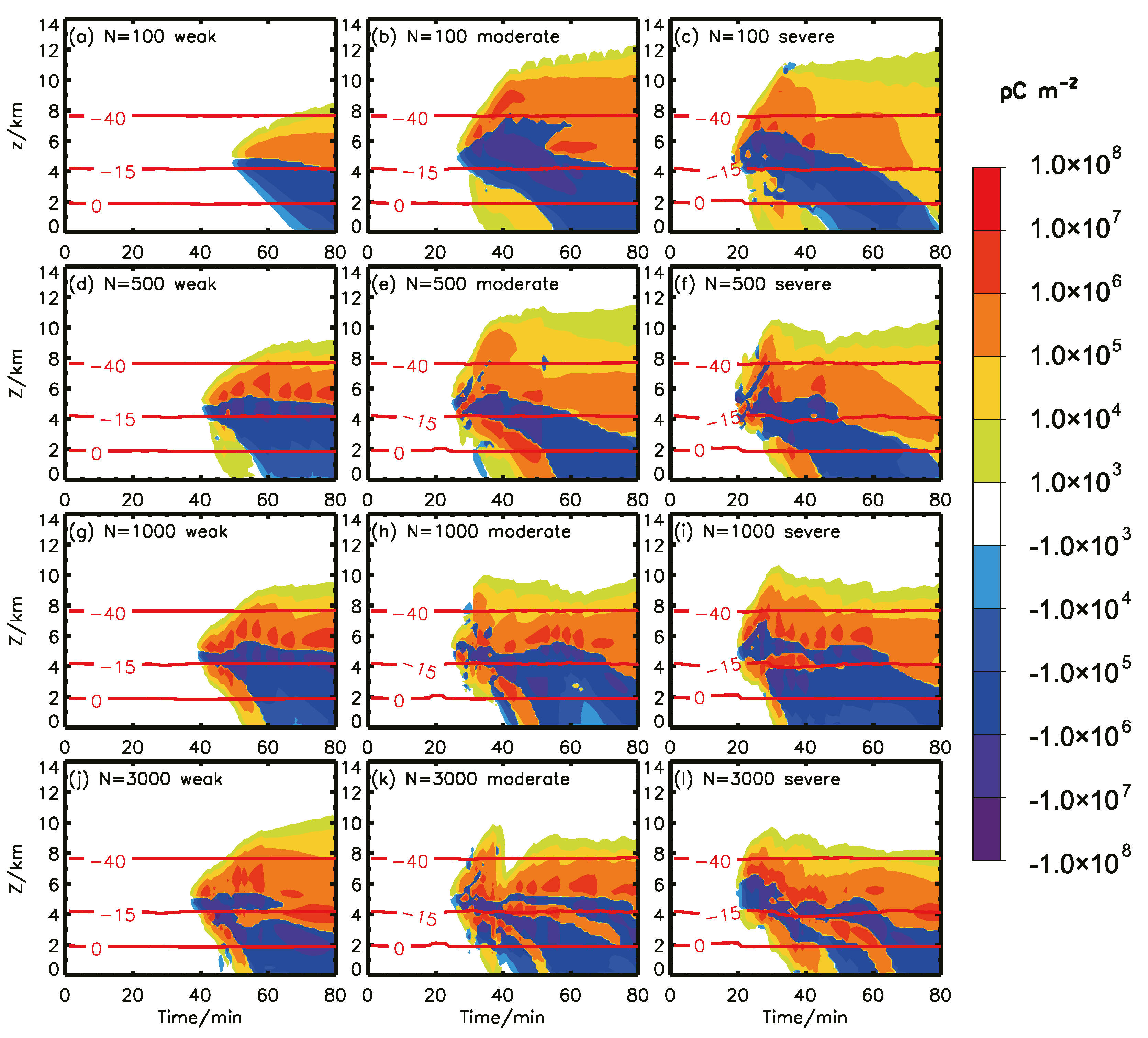
| Thundercloud Intensity | N0 (cm−3) | Non-Inductive Charging Rate (pC m−2 s−1) | Inductive Charging Rate (pC m−2 s−1) | ||
|---|---|---|---|---|---|
| Max | Min | Max | Min | ||
| Weak | 100 | 3.10 | −20.79 | 2.37 | −0.56 |
| 500 | 43.48 | −155.31 | 6.83 | −25.13 | |
| 1000 | 297.19 | −374.77 | 75.56 | −44.80 | |
| 3000 | 481.56 | −464.36 | 224.40 | −198.30 | |
| Moderate | 100 | 8.94 | −240.22 | 9.12 | −2.15 |
| 500 | 261.38 | −438.90 | 121.72 | −29.56 | |
| 1000 | 481.86 | −923.66 | 77.80 | −62.35 | |
| 3000 | 715.30 | −1397.86 | 225.38 | −117.65 | |
| Severe | 100 | 26.94 | −468.03 | 10.13 | −14.63 |
| 500 | 561.99 | −738.28 | 114.41 | −193.66 | |
| 1000 | 595.90 | −1724.95 | 110.53 | −58.34 | |
| 3000 | 597.50 | −1289.69 | 121.72 | −37.67 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Z.; Li, L.; Tan, Y.; Wang, H.; Li, C. A Numerical Study of Aerosol Effects on Electrification with Different Intensity Thunderclouds. Atmosphere 2019, 10, 508. https://doi.org/10.3390/atmos10090508
Shi Z, Li L, Tan Y, Wang H, Li C. A Numerical Study of Aerosol Effects on Electrification with Different Intensity Thunderclouds. Atmosphere. 2019; 10(9):508. https://doi.org/10.3390/atmos10090508
Chicago/Turabian StyleShi, Zheng, LuYing Li, YongBo Tan, HaiChao Wang, and ChunSun Li. 2019. "A Numerical Study of Aerosol Effects on Electrification with Different Intensity Thunderclouds" Atmosphere 10, no. 9: 508. https://doi.org/10.3390/atmos10090508
APA StyleShi, Z., Li, L., Tan, Y., Wang, H., & Li, C. (2019). A Numerical Study of Aerosol Effects on Electrification with Different Intensity Thunderclouds. Atmosphere, 10(9), 508. https://doi.org/10.3390/atmos10090508





