4.1. Observed Stress Estimates
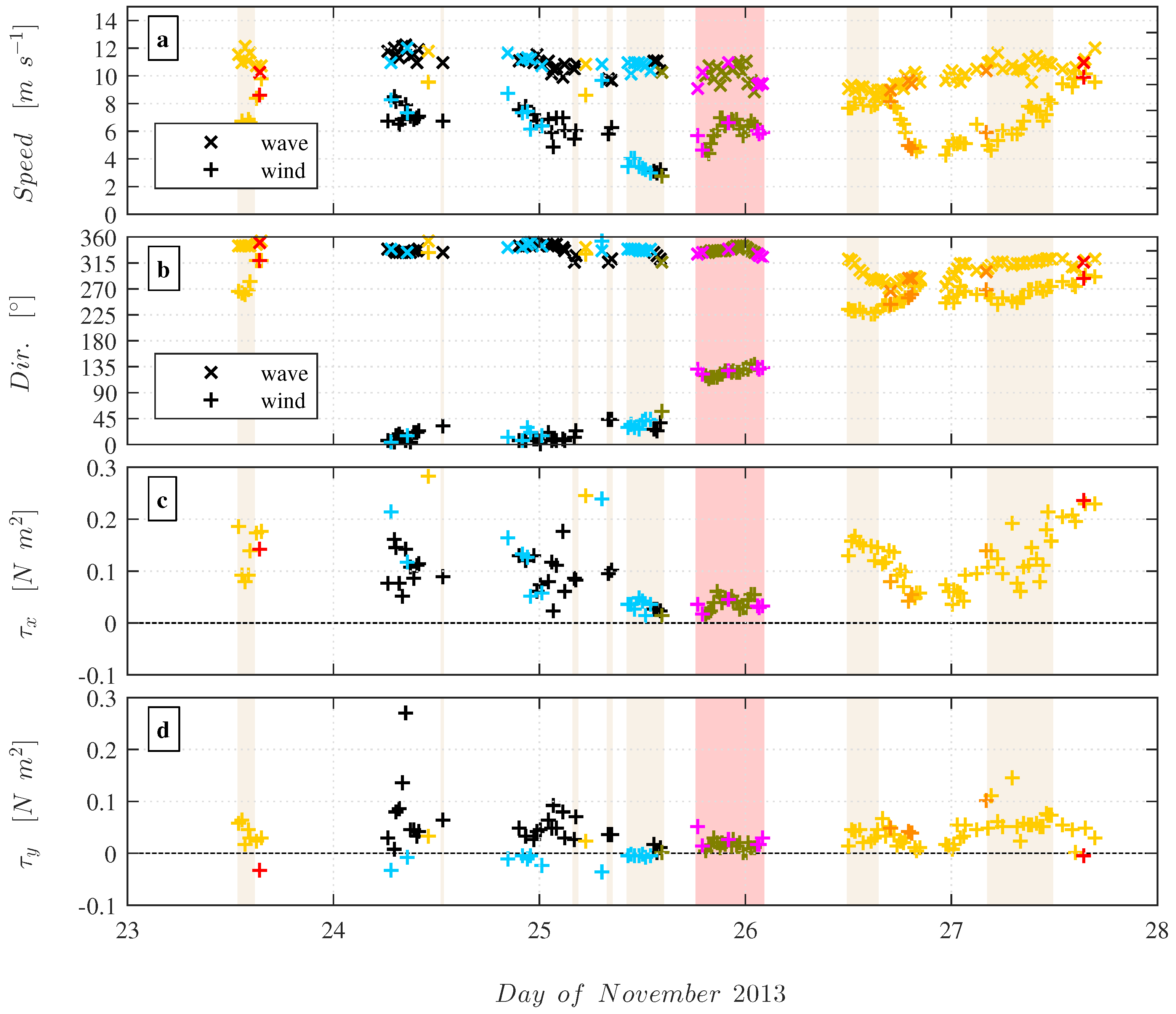
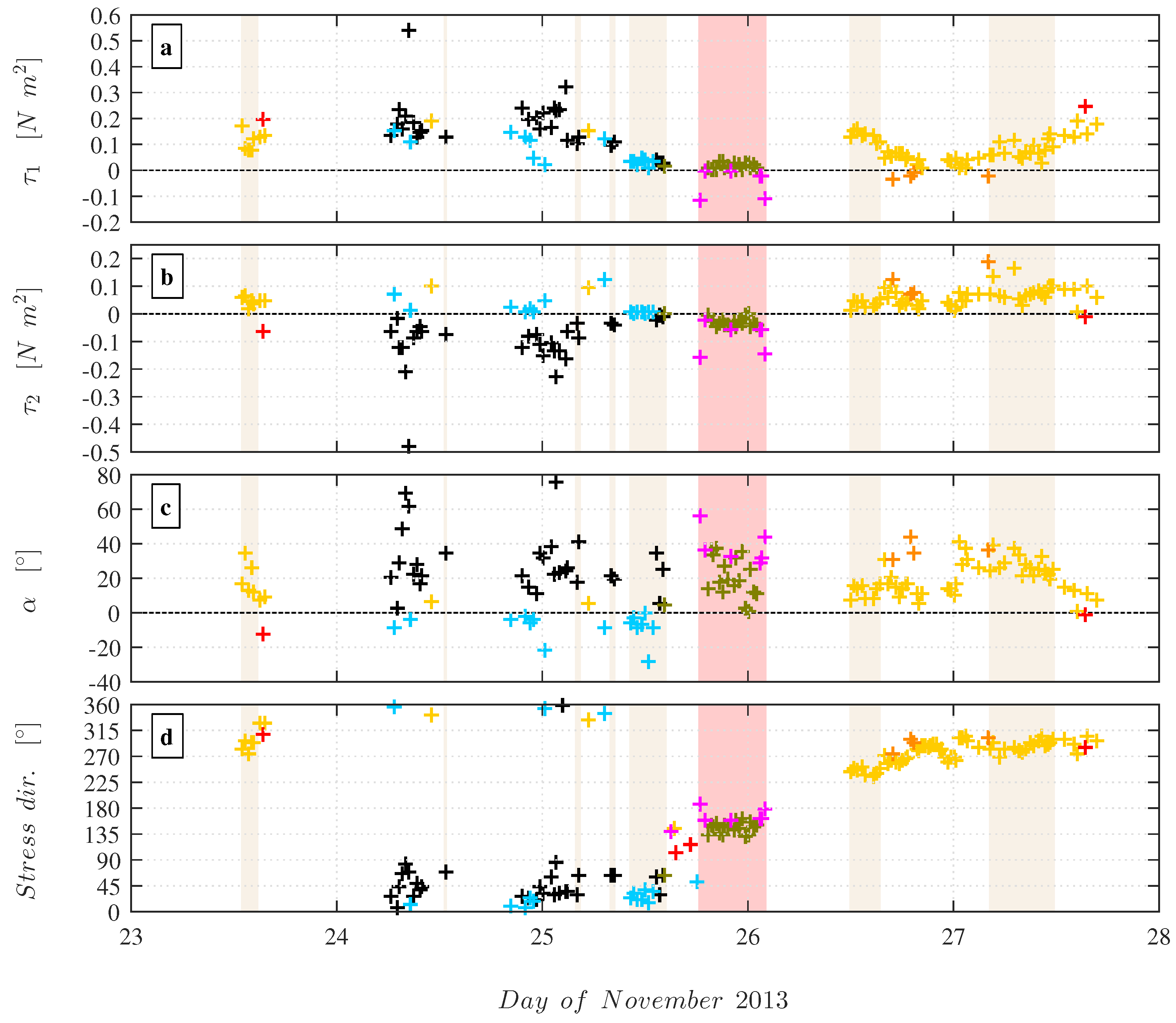
Figure 4 shows the time series of the wind speed and wave phase speed, the wind and wave direction and the along-wind and cross-wind wind stress measured in the orthogonal coordinate system. The color of the data points corresponds to seven observed combinations of the wind stress components
and
, which are presented in
Section 4.2. Time periods associated with cross-swell and counter-swell situations are indicated by the light grey and dark grey shading, respectively.
As expected from the rotation of the recorded wind vector into the streamwise wind, the along-wind stress () was found to be positive for all data runs. Cross-wind stresses () were positive (negative) when the stress off-wind angle was located to the right (left) of the horizontal wind vector. The majority of the data runs recorded after 26 November were associated with a positive cross-wind stress. The magnitude of the cross-wind stress was found to be generally smaller than the along-wind stress, resulting from the rotation of the wind vector into the streamwise wind. However, the stress magnitude of both and was comparable and close to zero for data runs that are associated with cross-swell and counter-swell cases on 25 November and with wind-following swell cases before midnight on 26 November.
Figure 5 shows the magnitude of the corresponding wind stress components,
and
, the off-wind angle
and the stress direction. Positive values of
were found for the majority of the data runs. This is regularly observed when winds blow over slower propagating short locally wind-generated waves, which extracts momentum from the wind and leads to further formation and growth of the wind-generated waves [
20,
24]. Negative values of
, both during the counter-swell period on 25 November and also for some of the wind-following swell cases on 26 November, are associated with situations in which the wind speed decreases quickly so that the locally wind-generated waves temporarily travel faster than the wind [
20]. Based on the possible combinations of the wind stress direction relative to the wind and swell wave directions, the stress component aligned with the swell wave direction (
) can acquire differed signs. The stress component
is positive when both the off-wind angle
and the relative angle
between the wind and the swell waves have the same sign, and
. If the two angles have opposite signs and
,
becomes negative. The stress component
is always negative for counter-swell cases in which the swell waves are dragging the wind. This different directions of
are illustrated in
Figure 6 (
Section 4.2). Similar to the behavior of the wind stress components in the orthogonal coordinate frame,
and
reached values close to zero on 25 November and before midnight on 26 November. Corresponding estimates of the off-wind angle
between the wind and the stress vector were found to exhibit a large scatter. This is commonly observed in open ocean conditions when the wind is blowing over a swell dominated sea. Based on the sign of the off-wind angle, the stress direction is orientated to either the right or left of the wind direction.
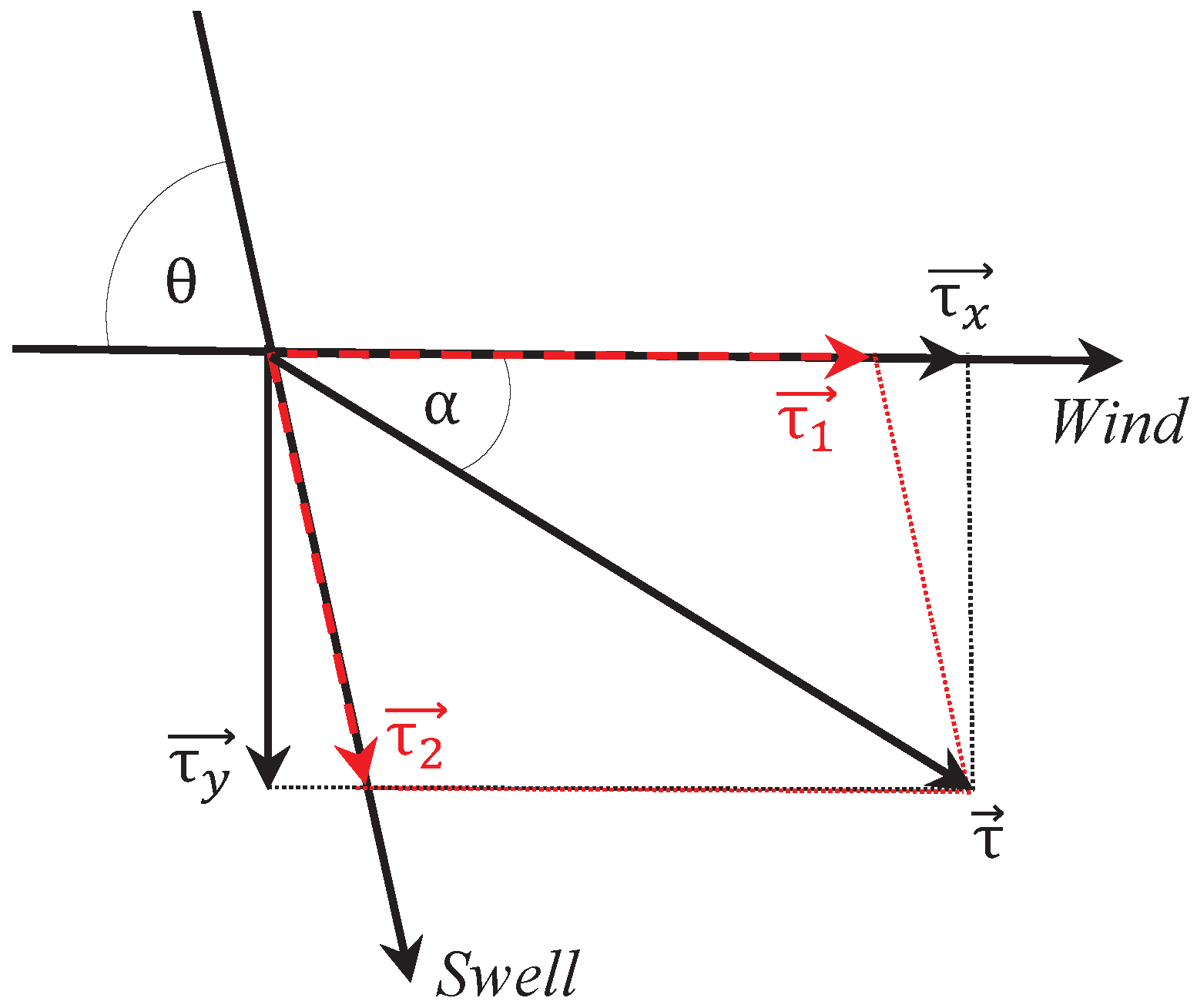
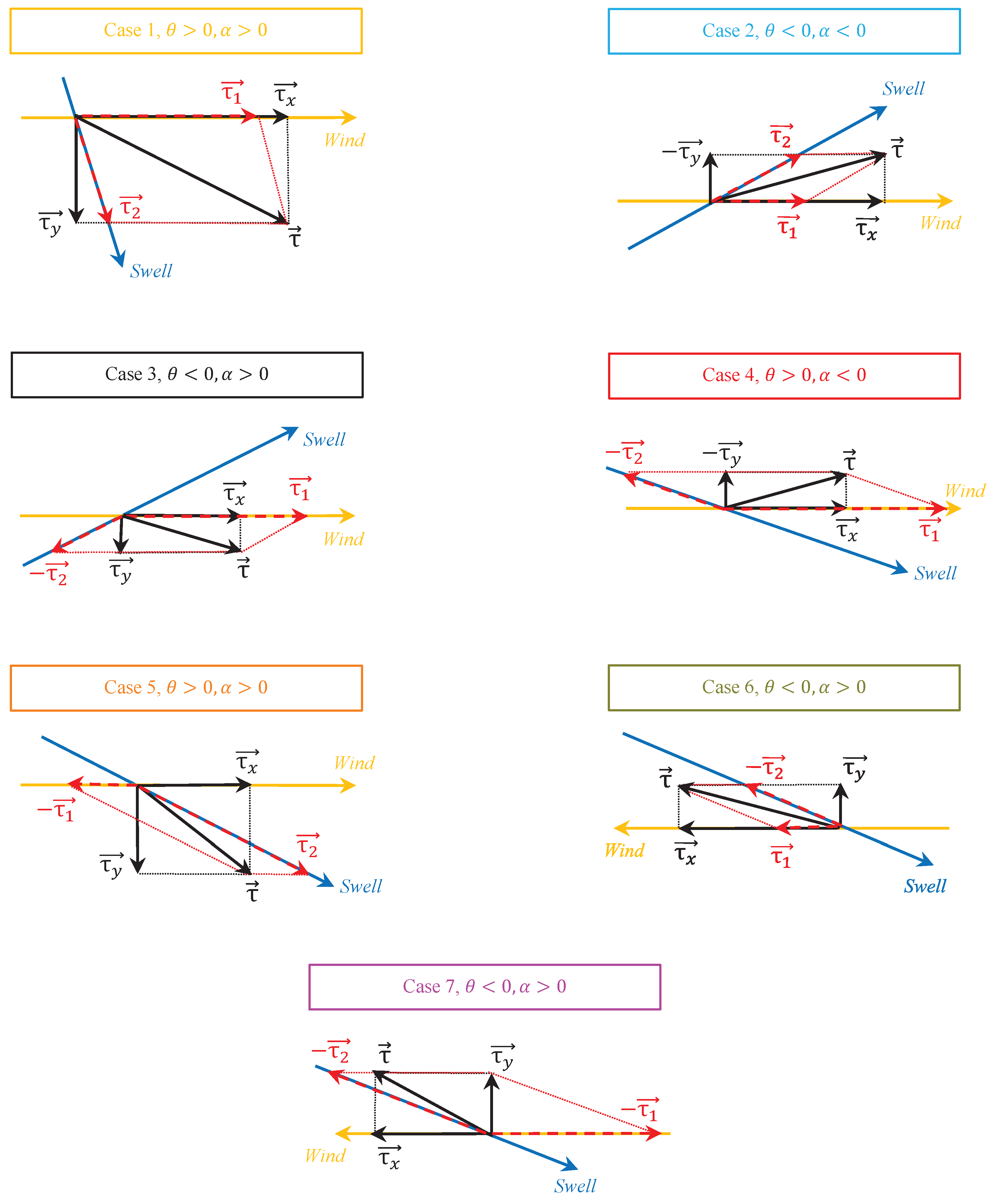
4.2. Schematic Representation of the Observed Stress Vector Components
Based on the signs of the relative angle
and the off-wind angle
, we identified seven idealized combinations of the stress vector direction relative to the wind and swell direction within our dataset.
Figure 6 shows a schematic representation of each combination, along with its corresponding stress vector components. For the remainder of this paper, we refer to the identified combinations as “cases”, as shown by different marker edge colors in
Figure 4,
Figure 5,
Figure 6,
Figure 7,
Figure 8 and
Figure 9. Cases 1–5 are associated with wind-following and cross-swell, where
.
The stress vector arrangement of Case 1 is typical for situations with moderate to strong winds [
20], in which
and
. Both
and
are positive and the resulting stress vector is situated in the acute angle created by the wind and swell propagation direction, to the right of the wind vector. Consequently, the corresponding stress vector components
and
can only be positive. This case was observed at the beginning and from the second half of the deployment period (data runs shown in yellow). The inverted situation, Case 2, occurs when
and
. In this case, the cross-wind stress
is negative while
and
remain positive. This situation was observed during 24–26 November (data runs shown in blue).
The stress vector arrangement in Case 3 is typically observed when weak to moderate winds blow over strong swell that travels approximately into the wind direction and faster than the wind [
20]. This case is associated with
and
, and the stress vector is situated to the right of the wind vector in an obtuse angle created by the wind direction and the direction opposite to the direction of the swell waves.
,
and
are positive, while
is negative and pointing in the direction opposite to the swell propagation direction. This case occurred during 24–25 November (data runs in black). Similar to this case is the inverted situation, Case 4, in which
and
. Here,
and
are positive while
and
are negative and the resulting wind stress vector is situated to the left of the wind vector in an obtuse angle created by the wind direction and the direction opposite to the swell propagation. This case was sporadically observed throughout the deployment period (data runs shown in red).
Case 5 is associated with a decaying wind regime where the locally wind-generated waves travel faster than the wind and thereby exert a drag on the lower meters of atmospheric surface layer. The wind conditions for Case 5 require that the wind is not only strong enough so that
, but also weak enough to satisfy
[
20]. This case has similarities with Case 1 and is characterized by
and
, but the wind stress vector is situated in an obtuse angle created by the swell propagation direction and the opposite wind direction. Within the analyzed dataset, we identified four data runs that fall into this category (data runs shown in orange). Case 6 is associated with a counter-swell situations where
and
, with
,
and
being positive. The stress vector is situated in the acute angle between the wind direction and the direction opposite to the swell propagation direction, and
is negative due to wave drag which extracts energy from the atmospheric surface layer [
20]. Case 7 is associated with a decaying wind regime where short wind-generated waves travel faster than the wind, i.e.,
and
are negative. The net stress vector is therefore situated in the obtuse angle between the direction opposite to the swell propagation and the direction opposite to the wind direction. Cases 6 and 7 were both observed on 25 November (data runs in olive and magenta, respectively). Among our seven cases, Cases 1–4 and Case 6 are typically observed during swell conditions and were previously reported by Geernaert et al. [
3], Rieder et al. [
4], Rieder and Smith [
5], Grachev and Fairall [
6] and Grachev et al. [
20].
4.3. Stress Direction and Stress Magnitude
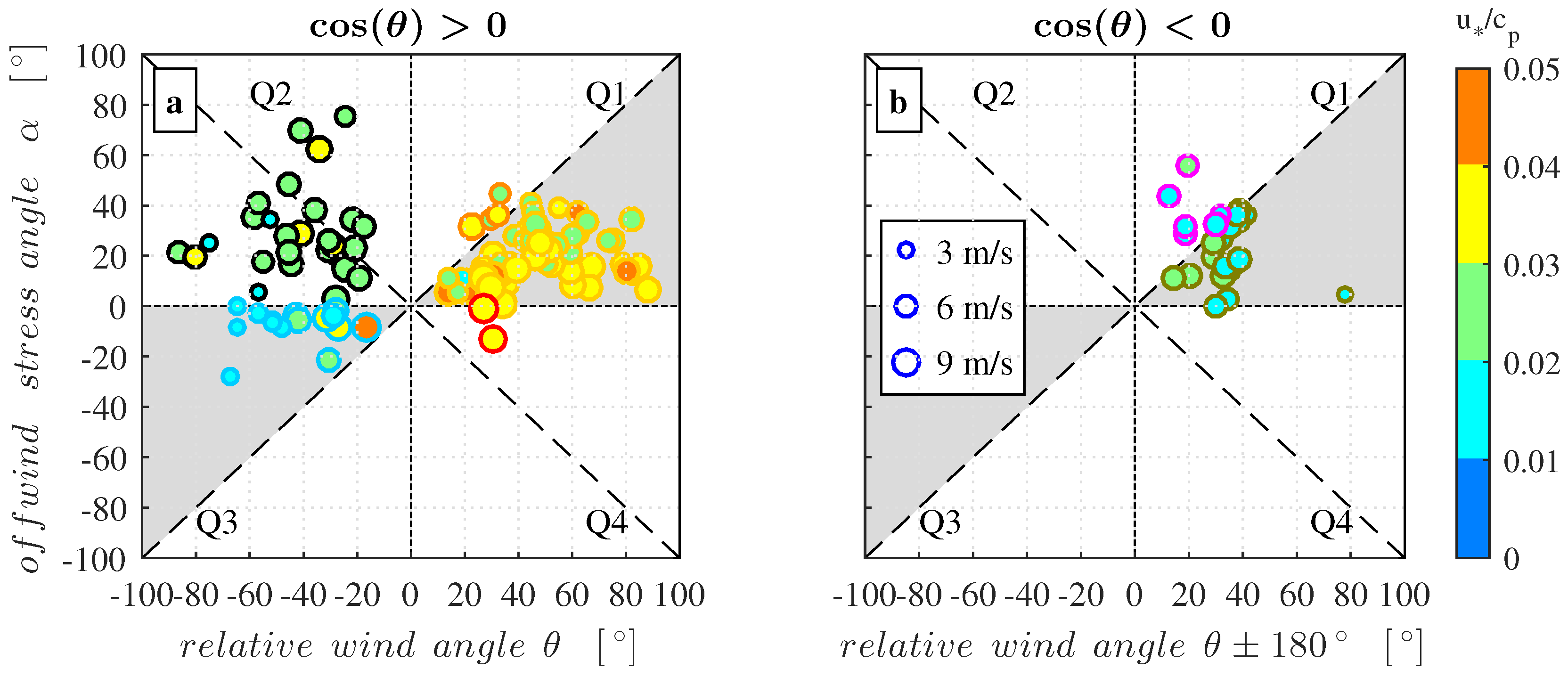
To visualize the direction of the stress vector relative to the wind and swell direction, the off-wind angle
between the stress vector and the wind vector is plotted against the relative angle
between the wind and the swell direction in
Figure 7. The marker color indicates the wave age, while the marker edge color follows the coding for the different cases given in
Figure 6. In general, data points that are aligned with the abscissa, i.e.,
, correspond to runs where the stress angle is aligned with the wind direction. Data points that are located along the dashed diagonal line in Quadrant Q1 and Quadrant Q3 are associated with a wind stress vector that points in the swell propagation direction.
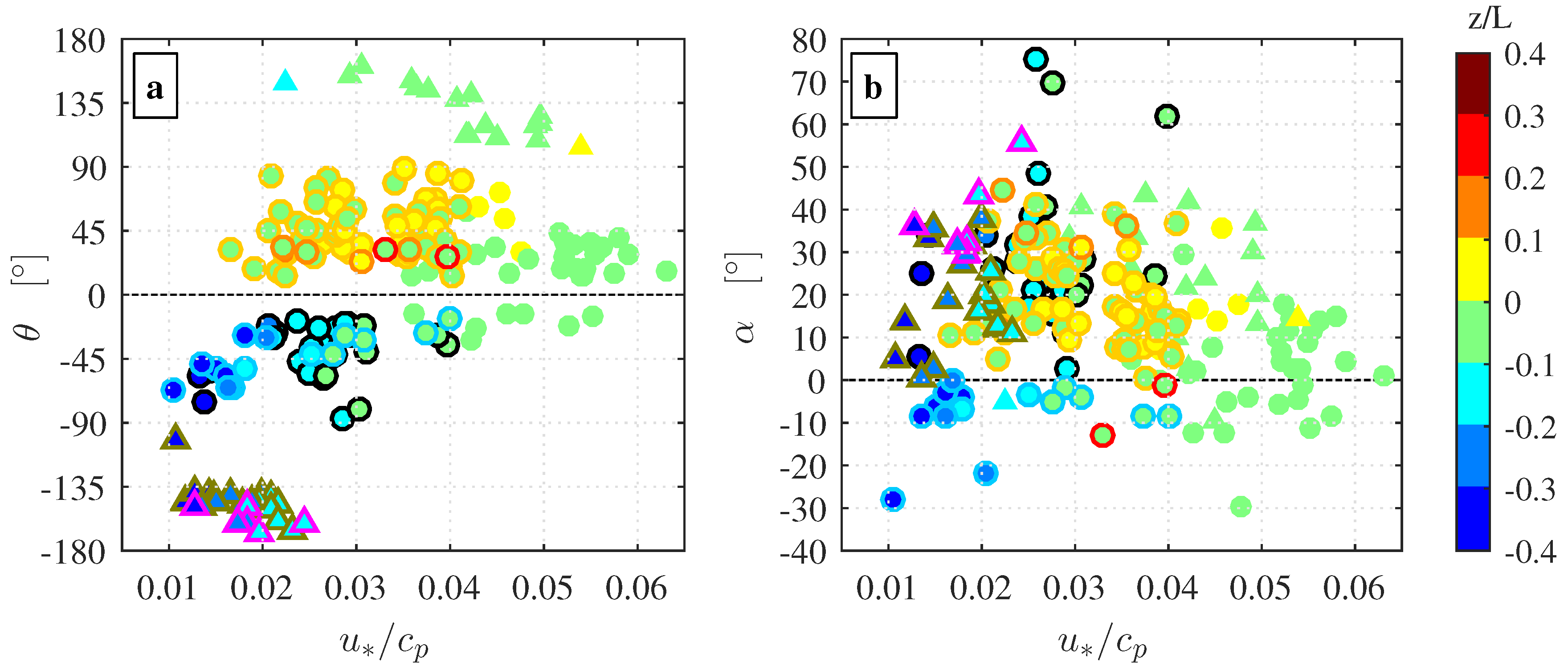
The different cases presented in
Figure 6 are distributed as follows: (i) data points situated within the shaded areas in Quadrants Q1 and Q3 of
Figure 7a correspond to Cases 1 and 2; (ii) data points situated in Quadrants Q3 and Q4 of
Figure 7a correspond to Cases 3 and 4, respectively, while data points outside the shaded area in Quadrant Q1 correspond to Case 5; and (iii) the data points situated in the shaded area of
Figure 7b correspond to Case 6, while those points outside this area belong to Case 7. Notably, the majority of the data runs are associated with a wind stress vector that is deviating from the mean wind direction. We found that 46% of the data runs for which
and 54% of the cases for which
have an off-wind angle that is larger than 20°. Moreover, the data exhibit a dependency on both the inverse wave age parameter and on the wind speed. For example, data points for Cases 1 and 5 (
Figure 7a, Quadrant Q1), associated with mixed seas and strong winds (
,
7–10 m s
−1), have off-wind angles below 20°, while larger off-wind angles are found for data runs associated with a swell dominated sea state and moderate winds (
,
4–7 m s
−1). Furthermore, most of the data runs associated with Cases 3, 6 and 7 clearly have off-wind angles larger than 20°. Many of the counter-swell runs appear to be closely aligned with the opposite swell direction.
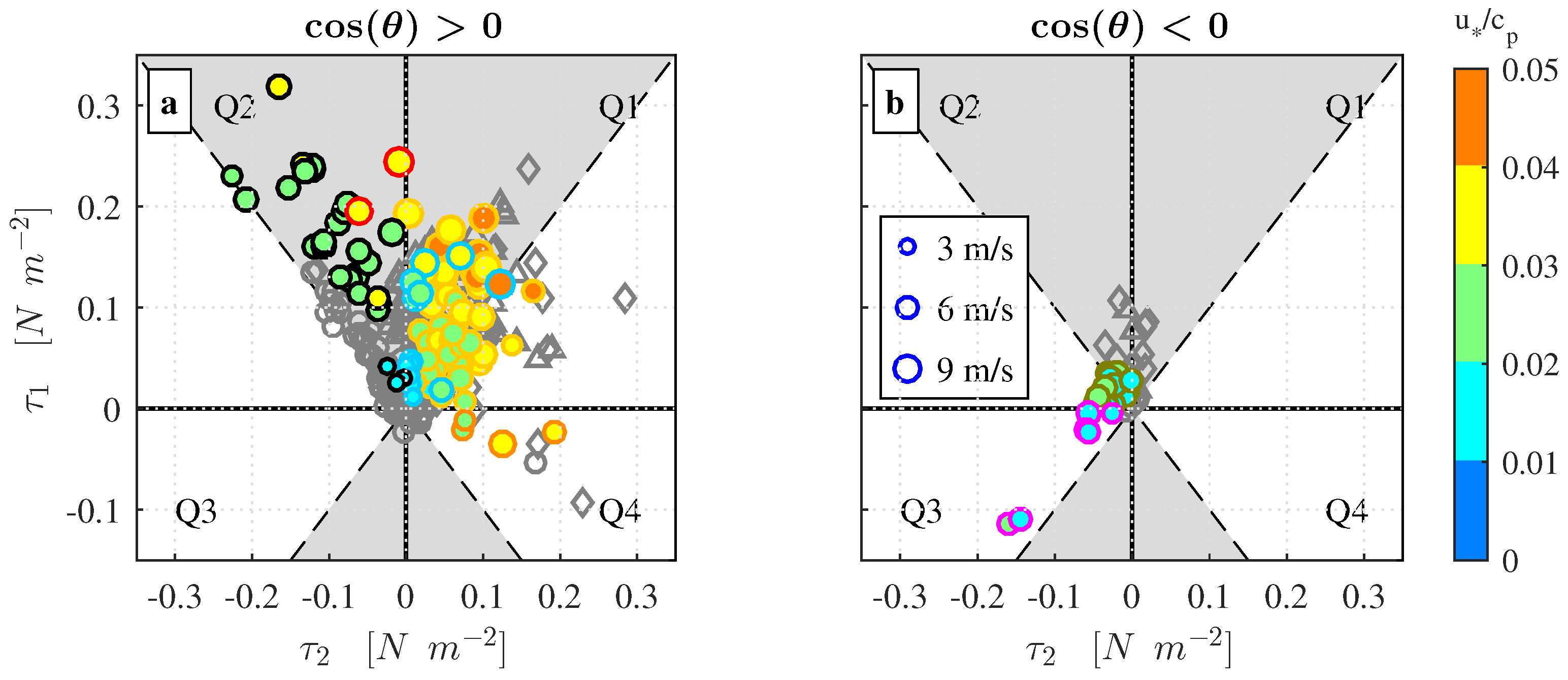
The size of the off-wind angle
is directly related to the magnitude of the stress vector components. A comparison between the wind stress aligned with the wind (
) and the swell waves direction (
) is shown in
Figure 8. The majority (77%) of the data runs associated with wind-following and cross-swell conditions (
) are located within the shaded area in the upper two quadrants of
Figure 8a. These data are typically observed for situations where
, belonging to Cases 1 and 2 in Quadrant Q1, and to Cases 3 and 4 in Quadrant Q2. Note that the seemingly elongated behavior of the data points in Quadrant Q2 is a result of self-correlation in the solutions of Equation (
4). As stated by Grachev et al. [
20], this self-correlation can affect the relative positions of the data points within this quadrant but it cannot change the signs of
and
. Data runs with stress vector component
are located in the white area of Quadrants Q1 (
, Case 1) and Q4 (
, Case 5). These data account for approximately 23% of the presented data for which
, whereof approximately 80% (18% of the presented data for which
) have a stress vector that is situated within ±20° of the swell direction. For counter-swell cases (
Figure 8b), data associated with the typically observed Case 6 are located in Quadrant Q2, while data belonging to Case 7 are located in Quadrant Q3. We observed that 66% of the counter-swell runs were associated with a stress vector for which
(white area of Quadrants Q2 and Q3). The stress vector was situated within ±20° to the opposite swell propagation direction in 58% of the counter-swell runs.
A dependency on both inverse wave age and wind speed is apparent in
Figure 8a. The data are mainly distributed in diagonal bands with an inverse wave age parameter that is increasing with increasing wind speed and wind stress. For wind-following and cross-swell data runs associated with
, the lowest values of
and
are associated with strong swell, i.e.,
, and wind speeds below 5 m s
−1 (cyan data points). The highest stress estimates are found for wind speeds exceeding 8 m s
−1 over a sea mixed with both swell and locally wind-generated waves (orange data points). Unexpectedly, we found that 12 of the 20 data runs which have a stress vector aligned within ±20° of the swell direction were recorded in wind speeds of about 5 m s
. The remaining eight data runs were recorded in wind speeds up to 8 m s
−1. If an interaction between the swell waves and the atmospheric surface layer would affect the wind stress direction, we would have expected that a stress vector alignment towards the swell propagation direction would occur for wind speeds much lower than 5 m s
−1.
In counter-swell conditions, the wind is blowing against the waves which increases the surface drag [
27,
45]. Consequently, the wind stress estimates are expected to be higher than that of the wind-following swell conditions. Nonetheless, our stress estimates recorded during the counter-swell period (
Figure 8b) were found to be unexpectedly low. These data runs were recorded during strong swell and wind speeds ranging 4–7 m s
−1. The low wind stress values recorded during the counter-swell period would suggest that the atmospheric surface layer at the measurement height was decoupled from the sea surface, so that wind stress was not influenced by the waves. This hypothesis will be further discussed in
Section 4.6.
To provide a reference for the stress estimates presented in this study, data reported in Grachev et al. [
20] (their Figures 11–13) are also shown in
Figure 8. These data consist of three
RP FLIP datasets collected by NOAA/ETL and WHOI during the San Clemente Ocean Probing Experiment (SCOPE) in 1993, the Marine Boundary Layer II (MBL II) experiment in 1995 and the Coastal Ocean Probing Experiment (COPE) in 1995 (cf. Grachev and Fairall [
6], Grachev et al. [
20]). Although the Marstein data were recorded in a coastal area and only 1.2 km from shore, the stress estimates associated with
exhibit a good resemblance with the three
RP FLIP datasets that were collected 15 km (SCOPE), 50 km (MBL II) and 20 km (COPE) off the US west coast. For wind-following and cross-swell cases (
Figure 8a), the magnitude of the Marstein and
RP FLIP wind stress components in Quadrants Q1 and Q4 are comparable, and both datasets consist of cases where
. Marstein data in Quadrant Q2 were found to be slightly shifted upward compared to the
RP FLIP datasets, conceivable due to higher values of
or due to the self-correlation in the solution of Equation (
4). For counter-swell cases (
Figure 8b), the wind stress magnitudes of the Marstein data are generally comparable to the
RP FLIP data runs. Nonetheless, the majority of the counter-swell cases in the Marstein dataset are associated with a wind stress vector that is situated within ±20° to the opposite swell propagation direction, i.e.,
. In contrast, the counter-swell cases of the three
RP FLIP data are clearly associated with a wind stress vector that is more closely aligned with the wind direction vector, i.e.,
; data located within the shaded area of the Quadrant Q2. Note that the
RP FLIP data runs in Quadrant Q1, i.e.,
, correspond to “forbidden” cases as a result of measurement inaccuracies [
20].
4.4. Stress Direction and Stability
The relative angle
between the wind and the swell is shown as a function of inverse wave age and the stability parameter
in
Figure 9a. To show the decreasing range of
with increasing inverse wave age parameter, and thus increasing wind speed, this figure also includes data runs associated with a complex wind sea, i.e., short locally wind-generated waves are superimposed on top of longer swell waves such that
. These data runs are shown without marker edge color and were otherwise excluded from the data analysis. From the data runs included in the analysis, approximately 70% of the wind-following and cross-swell cases for which
were recorded during near-neutral stratifications, i.e.,
(green and yellow circles with marker edge color). Unstable stratifications (
) occurred only during periods with strong swell (
), and include all analyzed counter-swell cases. Interestingly, unstable stratification is almost exclusively associated with negative values of
. Moreover, it appears that
has a relationship with
for wind-following and cross-swell cases during unstable stratification, where the relative angle between the wind and the swell wave direction increases with decreasing inverse wave age (cyan and blue circles).
Figure 9b shows the off-wind angle (
) as function of the inverse wave age parameter and the stability parameter. Similar to the angle
, the off-wind angle exhibit a wide range over wave ages related to swell dominated and mixed seas (
). The range of
decreases with increasing inverse wave age parameter and wind speed, as reported by, e.g., Drennan et al. [
45] and Li et al. [
38]. We notice that approximately 87% of the data runs used in our analysis (markers with edge color) have positive off-wind angles. In contrast to the relative angle
between the wind and swell direction, both positive and negative off-wind angles are associated with unstable stratification. No clear dependency between
and
could be identified in the present dataset. Nonetheless, all data runs belonging to Cases 2 and 4 (data points with blue and red edge colors, respectively) are associated with values of
and the off-wind angles range between
and 0°. Data runs recorded over a complex wind sea (
) are also associated with
. It remains ambiguous if negative values of
and
at the buoy’s deployment site generally are associated with a negative stability parameter (either unstable or near-neutral stratification), or if these observations are a result of the limited number of performed measurements. It also remains unclear why data runs belonging to Cases 2 and 4 only have small negative off-wind angles. These data runs are related to moderate winds (3–5 m s
−1) that blow over a strong cross-swell during an unstable stratification (
, cyan and blue markers), and moderate to strong winds of 6–9 m s
−1 that blow over a wind-following swell in near-neutral conditions (green markers with edge color). The small off-wind angles suggest that the stress vector is roughly aligned with the wind direction and that, contrary to the remaining data, the swell waves have little or no influence on the wind stress direction. For example, data runs with both
and
(cyan and blue markers) were found to have a lower wave steepness (
0.02–0.03) than the remaining cross-swell and wind-following swell cases (
0.03–0.06) (not shown). We speculate that the small off-wind angles associated with Cases 2 and Case 4 could result from a combination of an unstable stratification and a low wave steepness. The low wave steepness might reduce the amount of swell wave-induced dynamic pressure perturbations at the sea surface, which contributes to the form stress (cf. Högström et al. [
46]). Simultaneously, the upward transport of the pressure perturbations (due to vertical displacement of the air by the swell waves) into the lower meters of the atmospheric surface layer is effectively reduced by the unstable stratification. Support for this speculation can be found in
Figure 8a. Stress estimates for Case 2 associated with
(cyan data points) are located close to the ordinate axis, i.e.,
. This indicates that the wind stress component
, which is aligned with the swell wave direction, is negligible for these data runs. The wind stress would thus mainly be supported by the component
, and this would explain the observed small off-wind angles for Case 2. Moreover, the results in
Section 4.6 indicate that these data runs might be associated with a land-footprint and the formation of an internal boundary layer. It is reasonable to assume that the surface roughness of the land is higher than the surface roughness of the swell waves. A higher surface roughness will increase the shear stress and thus contribute to an increase of
(Equation (
7)). Therefore, a land-footprint might also contribute to keep the wind stress vector aligned with the wind direction.
4.5. Spectral Description of the Wind Stress and Wave Direction
The deviation of the stress vector from the wind direction can be further examined from the spectral description of the wind stress direction. For this, we followed the approach of Rieder et al. [
4] and computed the off-wind angle between the stress vector and the wind vector as a function of frequency:
where
and
are the real parts of the vertical momentum flux cospectra in the along-wind and cross-wind direction, respectively. The resulting off-wind angles were then binned by logarithmic averaging over uniformly spaced “log10” frequency bands. The corresponding net-stress directions were obtained as a function of frequency by adding the mean wind direction to the binned off-wind angles of
. The net-stress direction can be compared with the directional wave spectra to highlight interdependencies between the wind stress and the waves at different frequencies.
Data for the peak and mean wave directions were recorded by the Wavescan buoy. However, the directional wave spectra that were computed by the buoy’s internal data processing unit were not stored. To obtain estimates of the wave directions at different frequencies, we used the IMU accelerometer data and applied a modified PUV-approach, as described by Flügge et al. [
35]. It is emphasized that the computed directional wave spectra are only estimates and can, on average, differ from the “true” wave directions by up to 20° [
35]. Nonetheless, peak and mean wave directions computed by the modified PUV-approach were found to be in relatively good agreement with the corresponding wave direction data from the Wavescan buoy (not shown). We are therefore confident that the wave direction spectra computed by the modified PUV-approach are reliable.
To minimize errors in the wind stress directions computed with Equation (
8), stress direction estimates of successive data runs were averaged together. This requires that the relative angle
between the wind and the swell direction exhibits only small variations between successive data runs [
4]. Within the present dataset, we identified four time periods in which the variation of
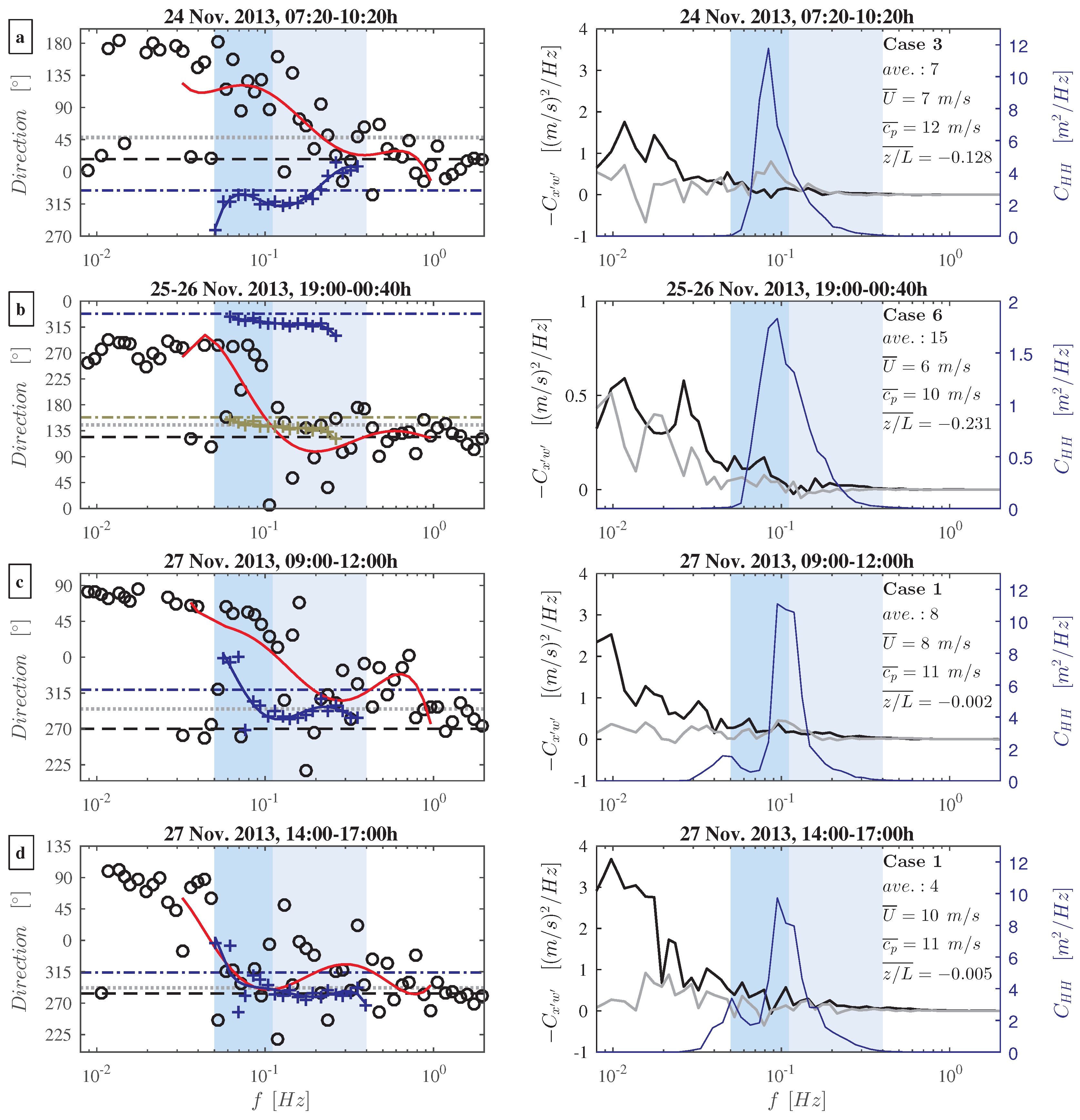
between successive data runs is smaller than 8°. Estimates of the wind stress and the wave direction as function of frequency for these four time periods are shown in the left column of
Figure 10. To better visualize the turning of the wind stress and wave directions, a fifth-order least-square-fit polynomial is drawn through both the stress and wave direction data (cf. Rieder et al. [
4]) over the frequency range of 0.03–1 Hz, which corresponds to wave periods between 1 and 30 s. We found that a fifth-order fit is most suitable to display the change of the wind stress direction in our data. Note that three data points in
Figure 10b and four data points in
Figure 10c, corresponding to frequencies below
0.06 Hz and directions below 180° and 320°, respectively, were excluded from the calculation of the fifth-order polynomial fit in order to remove artifacts resulting from the fitting procedure. The right column of
Figure 10 shows the corresponding heave variance spectra and the along-wind and cross-wind cospectra for each time period.
Figure 10 also gives the numbers of averaged data runs and the corresponding mean values of the wind speed recorded at the sonic anemometer, the wave phase speed and the stability parameter at the measurement height.
Figure 10a shows estimates of the wind stress and wave directions for a 3 h period on 24 November. This time period consists of data runs belonging to Case 3 (
Figure 6), which had a mean net-wind stress directed 30° to the right of the mean wind direction. The wave field contained waves with periods between 3 and 20 s and the average relative angle between the wind and the waves,
was −44°, i.e., to the left of the mean wind direction. Short waves with
Hz and the corresponding wind stress directions were roughly aligned with the mean wind direction. This supports our assumption made in
Section 2 that the short waves approximately propagate into the mean wind direction. For
0.25 Hz, the wave direction turned counter-clockwise with decreasing frequency (
), while the corresponding estimates of the wind stress direction turned clockwise (
). Although we only have a limited amount of data, it can be speculated that the turning of the waves and wind stress into opposite directions at frequencies larger than 0.25 Hz might indicate that only short waves with periods lower than 5 s are concurrent with the wind stress in situations associated with Case 3.
Estimates of the wind stress and wave directions for a 5.5 h counter-swell period corresponding to Case 6 are shown in
Figure 10b. For convenience, the opposite wave directions and the mean value of the opposite average wave direction are shown in olive green. The net-wind stress was orientated 22° to the right of the mean wind direction, in between the mean wind direction and the direction opposite to the average wave direction. The relative angle between the mean wind and the average wave direction was −145°, while the relative angle between the mean wind and the opposite average wave direction was 35°. Waves with periods between 4 and 16 s were present during the counter-swell period, and the shortest waves at
Hz were aligned close to the mean wind direction. The wave direction was slightly turning clockwise with decreasing frequency and the longest swell waves at
Hz were closely aligned with the average wave direction. Estimates of the wind stress direction are scattered around the mean wind direction within the frequency band of the locally wind-generated waves. The fifth-order polynomial fit indicates that the wind stress was orientated to the left of the mean wind direction within most of this frequency band. Within the swell wave frequency band, the wind stress turned clockwise, i.e., to the right of the mean wind direction, with decreasing frequency.
Estimates of the wind stress and wave direction for the typically observed Case 1 are presented in
Figure 10c,d, which show estimates for two different 3 h time periods on 27 November. During the first time period (
Figure 10c), the wave field contained waves with periods between 3 and 20 s and the average wave direction was 49° to the right of the mean wind direction. The mean net-wind stress direction had an angle of 25° to the right of the mean wind direction and was thus situated between the mean wind and average wave direction (
Figure 6, Case 1). Many of the locally generated short wind waves at
0.1–0.2 and
Hz appear to have been roughly aligned with the mean wind direction. Waves with frequencies of 0.1–0.2 Hz seem to have a slightly different propagation direction concurrent with the net-wind stress. Nonetheless, the estimated wave directions within this frequency band might be uncertain due to limitations in the modified PUV-approach [
35]. Estimates of the wind stress direction are situated between the mean wind and the average wave direction in the frequency range of 0.2–0.35 Hz, which is similar to the observations presented by Rieder et al. [
4]. Wind stress directions appears to have been more aligned towards the average wave direction for frequencies of 0.35–0.8 Hz. This might indicate the existence of non-stationary processes at the measurement site, as well as residual noise from incomplete motion correction. The estimates of both the wind stress direction and the wave direction turned clockwise within the swell wave frequency band. The fifth-order polynomial fit suggests that the turning of the wind stress direction started at a slightly higher frequency (
Hz) than the turning of the wave direction. Consequently, the relative angle
between the wind and the swell waves was larger for shorter swell waves and decreased with decreasing frequency for longer swell waves.
During the second period on 27 November (
Figure 10d), the average wind speed increased and was close to the phase speed of the waves. The peak wave direction became more aligned with the mean wind direction as
decreased to 30°. Moreover, the angle between the mean wind and the net-wind stress direction decreased to 8°, and the net-wind stress direction was thus closely aligned with the mean wind direction. In comparison to the first period on 27 November, the direction for most of the locally wind-generated waves became co-directional with the mean wind direction. The corresponding estimates of the wind stress direction in this frequency band were found to be scattered around the mean wind and the average wave direction. The fifth-order polynomial fit suggests that wind stress had a tendency to be directed towards the average wave direction for
Hz. Within the swell wave frequency band, the estimates of the wind stress and the wave direction were found to be in reasonable agreement.
Common for all four time periods in
Figure 10 is a change of the wave direction with decreasing frequency and a corresponding change of the wind stress direction, particularly in the swell wave frequency band. This is illustrated in
Figure 10a–c where a clear clockwise turning of the wind stress direction can be seen in this frequency band. Moreover, the fifth-order polynomial fit in
Figure 10b–d appear to resemble the turning of the waves, which is similar to the findings in Rieder et al. [
4]. This suggests an interdependency between the wind stress and the swell waves, i.e., the direction of the wind stress in at the buoy’s deployment site is influenced by the swell waves despite its vicinity to the coast. Support for this observation can found from by the respective heave variance spectra and the along-wind and cross-wind cospectra in the right column of
Figure 10. It is reasonable to assume that any interdependency between the wind stress and the surface gravity waves can only take place within the frequency band of the wave field, i.e., all frequencies covered by the respective heave variance spectra. The along-wind and cross-wind cospectra show that the spectral energy of the wind stress was negligible at frequencies corresponding to the locally wind-generated waves, i.e.,
0.2 Hz in all four time periods. The spectral energy of the wind stress is increasing with decreasing frequency and a pronounced increase in the spectral energy of the wind stress is first visible within the swell wave frequency band. This implies that an interdependency between the wind stress and the wave field must occur in the swell wave frequency band because the wind stress has not sufficient energy at higher frequencies to influence the wind stress. The influence of swell waves on the wind stress direction in the open ocean was previously reported by Geernaert et al. [
3], Rieder et al. [
4], Rieder and Smith [
5], Grachev and Fairall [
6] and Grachev et al. [
20].
Interestingly, it appears that the clockwise turning of the wind stress and waves direction was out of phase during the first time period on 27 November (
Figure 10c). We expected to see a similar behavior in the turning of the wind stress and wave direction, as shown in
Figure 10d, due to the almost similar conditions during the two time periods. An explanation for the differences between these two time periods might be related to the increased spectral energy at the peak wave frequency in the cross-wind cospectra seen in
Figure 10a (Case 3) and
Figure 10c (Case 1). A corresponding increase in spectral energy in the cross-wind cospectra is absent during the second time period of 27 November (
Figure 10d). We speculate that the larger angle between the mean wind and the average wave direction in the first time period led to a slightly increased cross-wind stress around the peak wave frequency, which is situated at the transition between the frequency range of the wind-generated and the swell waves (
Figure 10c). The air-flow close to the sea surface might have felt the most energetic swell waves (at the peak wave frequency) that were travelling at a cross-wind angle relative to the mean wind direction (
). The stress direction in
Figure 10c suggests that the turning of the wind stress occurred at the peak wave frequency, while the turning of the swell wave direction occurred at slightly lower frequencies. In the second time period of 27 November (
Figure 10d), the relative angle between the mean wind direction and the peak wave direction decreased to
, and the wind stress directions within the swell wave frequency band were situated between the mean wind and the average wave direction. We further hypothesize that the cross-directional forcing of the most energetic swell waves on the air flow might not have been strong enough to influence the wind stress direction at the peak wave frequency. Nonetheless, the wind stress estimates in
Figure 10d suggest that the stress direction did undergo a clockwise tuning which occurred at the lowest swell wave frequency,
Hz. At this frequency, the corresponding heave variance spectra exhibit an additional small spectral peak. We suggest that the longest swell waves, which were propagating at an angle of ∼80° and ∼50° to the mean wind direction and average wave direction, respectively, have contributed to the clockwise tuning of the wind stress direction in the second period of 27 November.
4.6. Case Study-Counter-Swell Period
The comparison between the Marstein dataset and the three datasets collected aboard
RP FLIP (
Section 4.3,
Figure 8) shows that our wind stress estimates are in good agreement with open ocean wind stress measurements, except for the counter-swell period. When winds blow against the waves, the wind stress is expected to be higher than in the wind-following swell conditions [
27,
45]. Nonetheless, the wind stress recorded at Marstein was found to be unexpectedly low during the counter-swell period. In this section, we attempt to provide an explanation for this seemingly paradoxical observation.
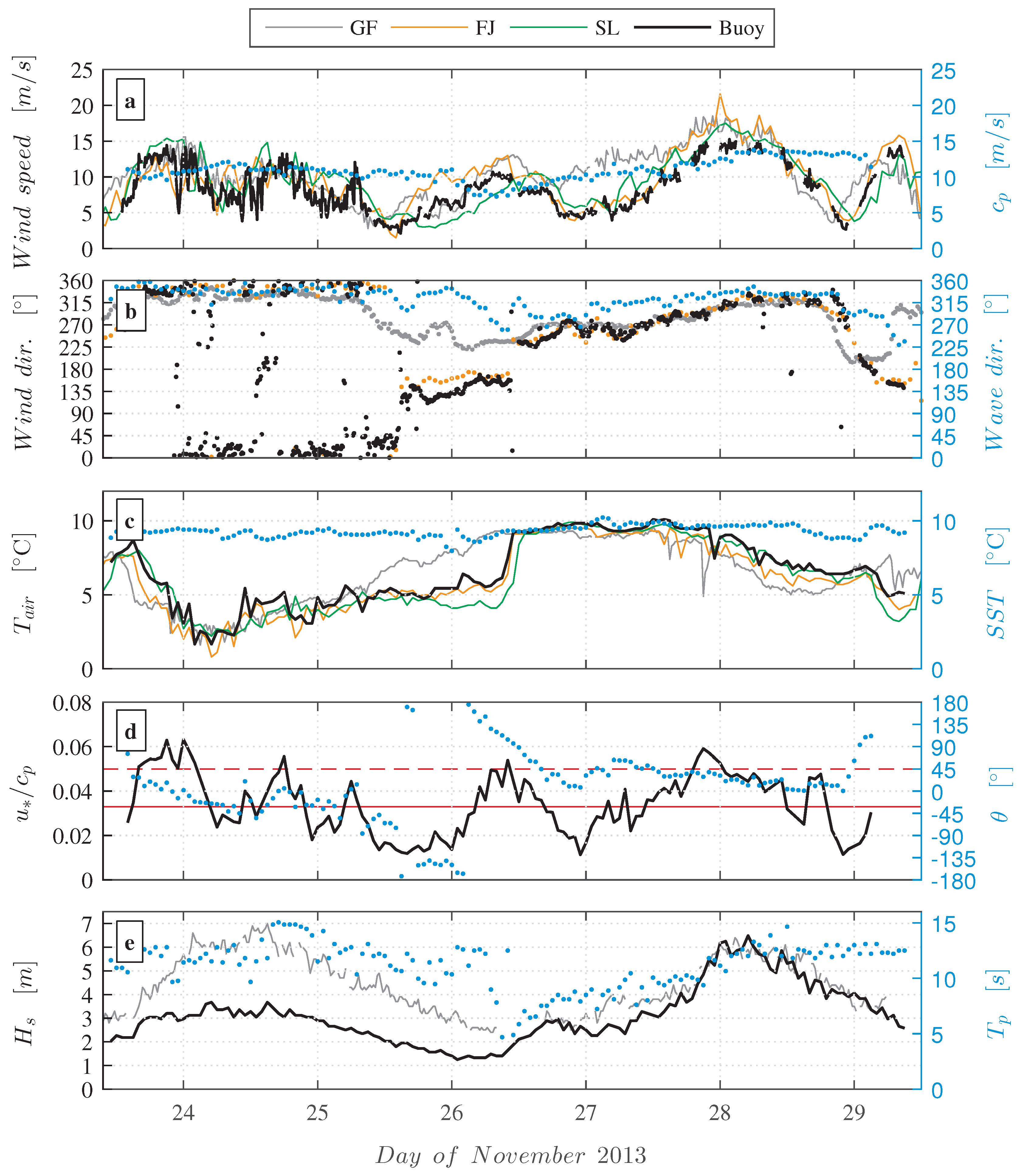
During the first two days of the buoy’s deployment period, the wind was blowing from a northwest to northerly direction (
Figure 3b). On the morning of 25 November, the wind direction changed clockwise towards a northeasterly direction (25–45°) for a period of approximately 5 h, before a sudden shift in wind direction towards southeasterly (115–145°) occurred. The southeasterly winds prevailed for a period of 19 h in which the wind slowly turned more southerly, before the occurrence of a new sudden (clockwise) shift towards southwest on 26 November. The two distinct shifts in wind direction are clearly visible in
Figure 3b, and were also recorded at the Fedje met-station (orange dots in
Figure 3b). Moreover, the second shift in wind direction on 26 November was accompanied by a distinct increase in air temperature, which increased by approximately 4 °C and reached the same value as the sea surface temperature. Interestingly, no sudden shifts in wind direction or air temperature were recorded at the Gullfaks C oil platform in the North Sea. The wind direction at Gullfaks turned gradually counter-clockwise from northwesterly to southwesterly on 25 November, and the air temperature gradually increased by approximately 4 °C between 25 and 26 November (grey dots and line in
Figure 3b,c). The sudden changes in wind direction, in combination with the sudden increase in air temperature, suggest that local boundary layer processes were affecting the WaveScan buoy’s deployment site 1.2 km offshore.
Figure 3a,b shows that the turning of the wind to a north-easterly direction on 25 November is accompanied by a drop in wind speed from 10 to 5 m s
−1. During the 5 h period with north-easterly winds, the wind speed decreased further to approximately 3 m s
−1. Note that the sudden change towards a south-westerly wind direction occurred at this wind speed, which was the lowest recorded wind during the deployment period.
We hypothesize that the temperature difference between the land and the sea, in combination with the low wind speed and the unstable atmospheric stratification, led to the onset of a land breeze circulation. Winds blowing towards the sea near the ground would extended the lower part of the land boundary layer further offshore, where the cool air would warm and raise upward. If the wind direction is reversed higher up, the wind would extend the marine atmospheric boundary layer over the coastal areas of the land, where the warmer air would cool and sink downward. The land breeze would thus lead to a mixing between the marine atmospheric boundary layer and the land boundary layer.
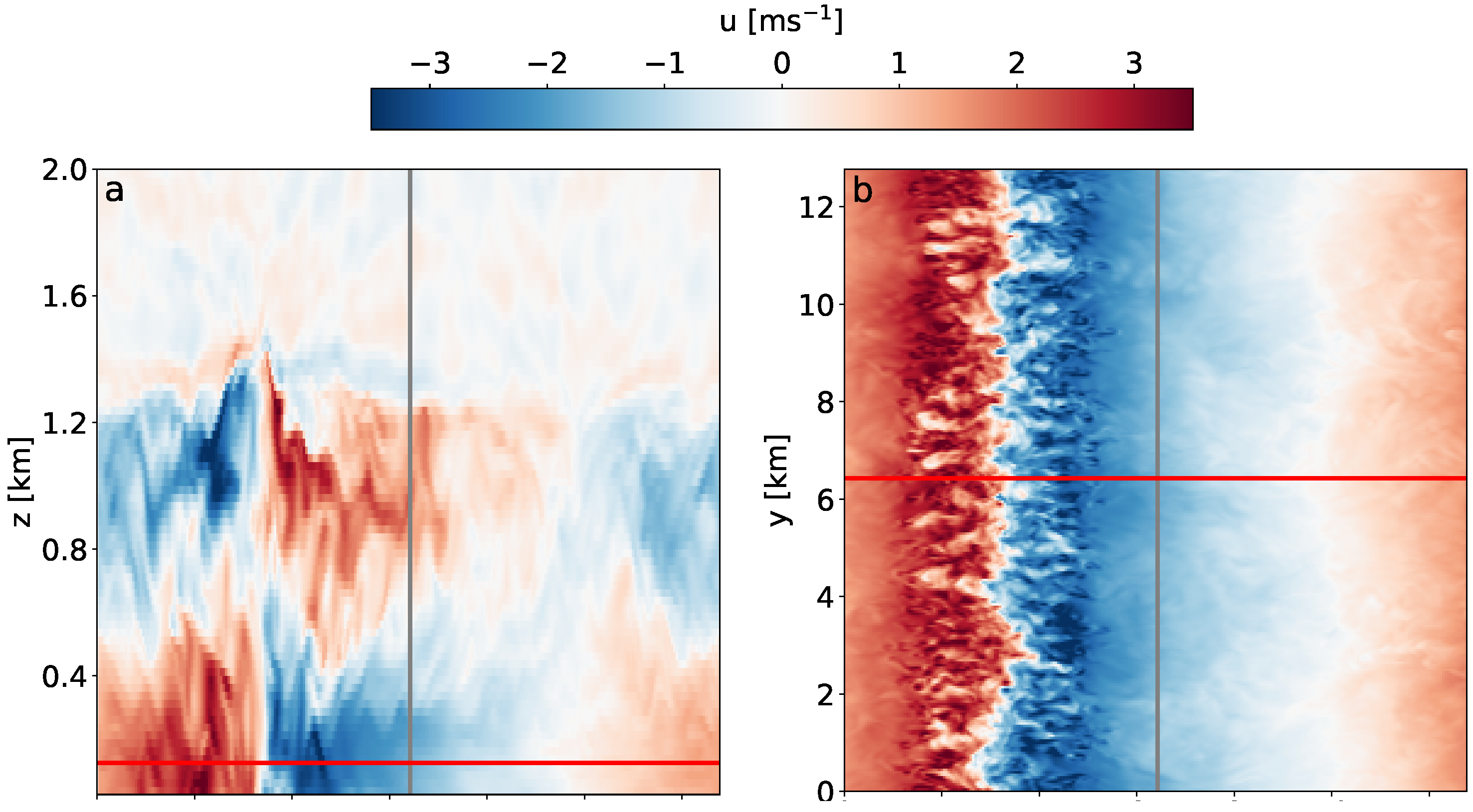
In a first attempt to evaluate the hypothesis that the southeasterly winds during the counter-swell period were associated with a land breeze circulation caused by the temperature gradient between the warmer sea and the colder land, we performed an idealized LES simulation with PALM (Parallelized Large-Eddy Simulation Model) [
47]. The simplistic setup consisted of a north–south oriented coastline that separates a surface with a constant temperature of 10 °C to the west (sea) from one with 0 °C to the east (land). The simulation was initialized without background wind and run for 12 h. For more details on the PALM model in general, and the specific setup used for this study, the reader is referred to
Appendix A.
Figure 11 presents a snapshot from the LES simulations after 6 h modelling time. It shows the development of a land-breeze circulation with easterly winds of about 300 m depth that reaches nearly 3 km offshore. The highest wind speeds of around 3 m s
−1 are found at a distance of 2 km from the coast, very close to the offshore distance of the buoy in our study. How far the mixed boundary layer extends offshore typically depends on the strength of the land breeze, the atmospheric stability and on fetch limitations. The results of our LES simulation indicate that our measurement site 1.2 km offshore is well inside the potential reach of a land breeze circulation, and thus our measurements might have been performed within a mixed boundary layer rather than in a pure marine atmospheric boundary layer during the counter-swell period with prevailing southeasterly winds.
Nonetheless, even within a mixed boundary layer, increased wind stress is expected when the wind is blowing against the waves. Given that the observed wind stress was low during the counter-swell period, we further hypothesize that the mixed boundary layer was decoupled from the undulating sea surface. The mixed boundary layer might have acted as an internal (transition) boundary layer that was situated between the wave boundary layer and the marine or land atmospheric boundary layer higher up. Turbulence generation due to shear stress and wave stress (
Section 2), and hence the exchange of momentum from the atmosphere to the ocean, might only have occurred within a shallow wave boundary layer up to 3 m above the sea surface (cf. Cifuentes-Lorenzen et al. [
21]), thus leaving the internal boundary layer decoupled from the wave boundary layer.
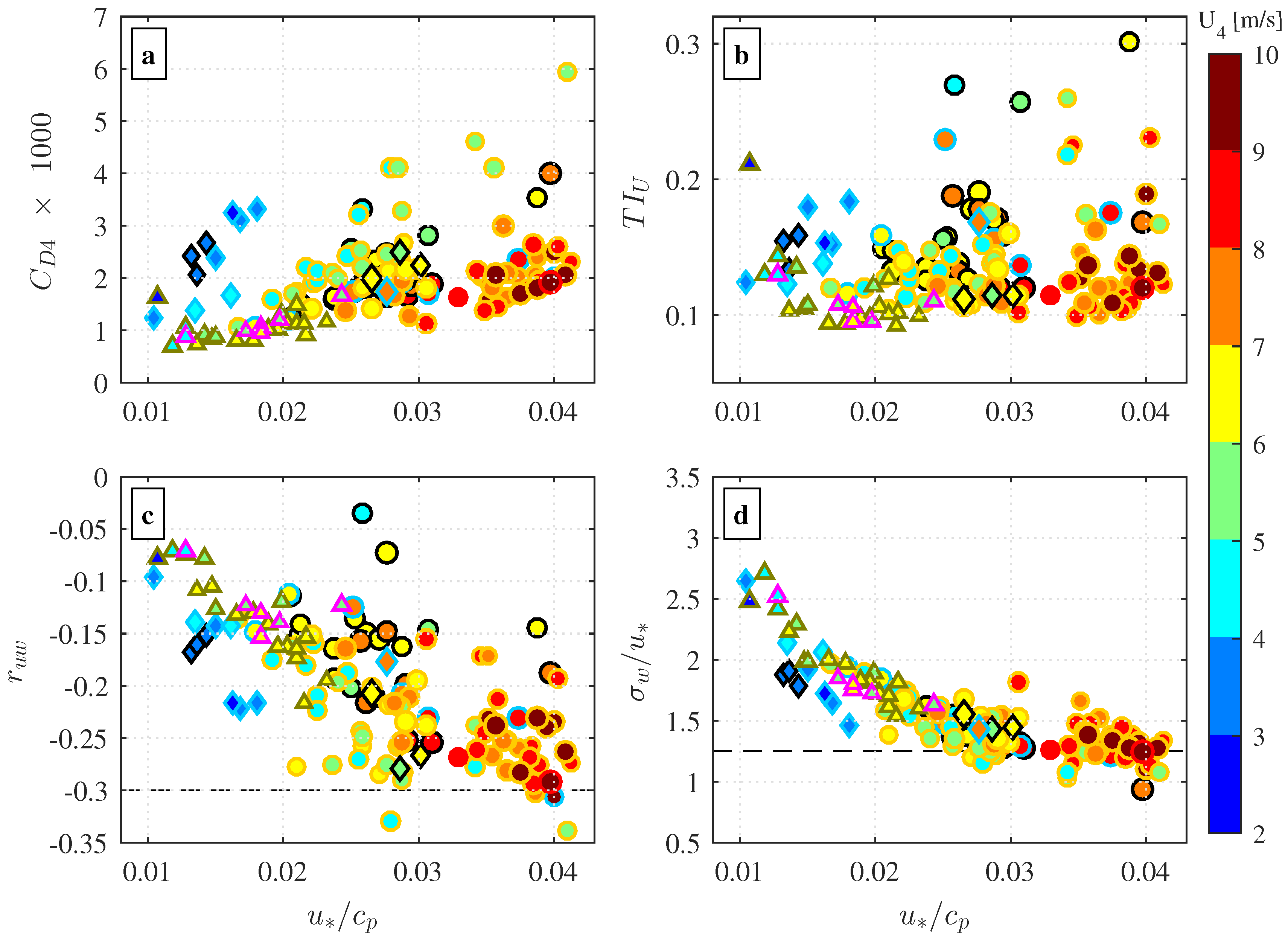
Within a decoupled internal boundary layer, one would expect only low turbulence generation and thus only weak wind stress. An indication for this can be seen in
Figure 12, which shows the drag coefficients, the turbulence intensities for the along-wind component, the correlation coefficients between
u and
w and the normalized vertical velocity standard deviations, computed for the measurement height of 4 m above the sea surface. The drag coefficients in
Figure 12a reveal the presence of three wind regimes during the buoy’s deployment period: (1) a regime for winds blowing from open ocean directions and associated with wind-following and cross-swell (shown as circles); (2) a regime for winds blowing over land towards the sea from northeasterly directions and associated with cross-swell (shown as diamonds); and (3) a regime for winds blowing over land towards the sea from southeasterly directions and associated with counter-swell (shown as triangles). The first wind regime (circles) exhibits the typically observed dependency of the drag coefficient on the inverse wave age parameter and wind speed (cf. Edson et al. [
25], Smedman et al. [
48]). This dependency is expected, as higher winds will increase the sea surface roughness and thus the wind stress. The second regime is characterized by high drag coefficients, especially for wind speeds below 5 m s
−1 (cyan and blue diamonds) where the drag coefficients appear to be much higher compared to the other two wind regimes. Moreover, turbulence intensities for wind speeds below 5 m s
−1, both for horizontal and vertical velocity components, were found to be equal or higher than the turbulence intensities recorded in the other two wind regimes. Note that the Case 2 data runs with wind speeds below 5 m s
−1 (cyan and blue diamonds with blue edge color) are associated with low off-wind angles (
Figure 9). We therefore suggest that data runs associated with northeasterly winds had a land-footprint and that the deployment site, in fact, was situated within a mixed boundary layer. This is similar to recent findings presented by Grachev et al. [
11]. The third wind regime succeeded the second wind regime and is clearly distinguished from the other two wind regimes by low drag coefficients and low turbulence intensities (triangles). If the boundary layer was fully coupled with the sea surface, we would expect that these data runs have high drag coefficients and turbulence intensities, resulting from enhanced wind drag on waves travelling in the opposite wind direction and from enhanced shear stress due to land-footprints. However, the analyzed data clearly show reduced drag coefficients and turbulence intensities for counter-swell cases. This suggests that shear turbulence generation processes at the measurement height of 4 m were either suppressed or absent, which supports our hypothesis of a decoupling between the undulating sea surface and the atmospheric boundary layer. Although the wind stress estimates recorded during the counter-swell period were small and therefore subject to measurement errors, the data indicate that the wind stress component aligned with the wind direction (
) was close to zero for most of the presented counter-swell runs. The corresponding wind stress component aligned with the (opposite) swell direction (
) was found to be slightly larger. In the absence of sufficient turbulent shear production, i.e.,
, the wind stress vector has to align itself towards the opposite swell wave propagation direction, i.e.,
. This explains why the wind stress direction for the majority (58%) of the counter-swell cases was situated within ±20° to the opposite swell propagation direction (
Figure 7 and
Figure 8).
The mechanism behind a decoupling between the sea surface and the atmosphere during counter-swell remains ambiguous. A decoupling between the ocean and the atmosphere would likely occur in wind-following and cross-swell situations with strong background swell and weak winds. Such a situation was reported by Smedman et al. [
49,
50], where fast travelling swell waves transported momentum from the ocean to the atmosphere, thus counteracting the downward transport of momentum from the atmosphere to the ocean. However, the opposite directions between the wind and the swell waves during counter-swell will always lead to an enhanced wind stress, and thus transport of momentum from the atmosphere to the ocean. Another mechanism could be related to negative values of
, i.e., data runs associated with Case 7. In these situations, the short wind-generated waves travel faster than the wind and transfer momentum to the atmosphere. During periods of decreasing weak winds with low shear turbulence production, the upward transport of momentum from the short waves could counteract the weak downward transport of momentum from the atmosphere to the ocean. However, as the wind generates the short waves, the sea state will adapt itself after a short period of time so that this special situation cannot last long. Therefore, it seems unlikely that air–sea interaction processes could be responsible for a decoupling between the atmosphere and the ocean during counter-swell.
Nonetheless, we noticed that the last hour before the onset of the counter-swell period was characterized by a wind stress vector arrangement corresponding to Case 3 (
Figure 6), in which
and
(
Figure 5). Negative values of
indicate that the swell waves travel faster than the wind and thus transfer momentum upward into the atmosphere. The net-momentum transport
across the air–sea interface depends on the magnitude of the stress components
and
, and on the shear stress
(Equation (
5)). The three Case 3 data runs that were recorded directly before the onset of the counter-swell period are located near the center of the coordinate system in
Figure 8 (cyan markers with black edge color). The stress estimates are closely aligned to the
line, which indicates that both stress components might have counteracted each other so that
(Equation (
6)). Therefore, only the shear stress close to the sea surface would have controlled the exchange of momentum across the air–sea interface. As these data runs are associated with wind speeds close to 3 m s
−1, an unstable atmospheric stratification and a low wave steepness (not shown), it is reasonable to assume that the shear stress was low prior to the onset of the counter-swell period. Such a situation would support the onset of a land breeze circulation and the establishment of an internal boundary layer (with land-footprints) that could have been decoupled from the sea surface.
For all three wind regimes, we found that the correlation coefficients
decreased and the normalized vertical velocity standard deviation
increased with decreasing inverse wave age (
Figure 12c,d). The dashed lines in
Figure 12c,d indicate the respective constant values observed for neutral conditions over land [
51,
52]. The deviation of our data from the constant values is related to atmospheric stratification (not shown), but also implies a wave age dependency [
52]. This would suggest that the Monin–Obukhov similarity theory is no longer valid for data runs that were recorded during strong swell, such as reported in several studies (cf. Edson et al. [
25], Högström et al. [
26], Drennan et al. [
36,
45], Smedman et al. [
50]). The lower values for data runs associated with northeasterly winds (diamonds) provide another indication for the presence of a land-footprint in data runs associated with northeasterly winds. Counter-swell cases (triangles) are expected to follow the Monin–Obukhov similarity theory [
45]. However, the deviation of the counter-swell data points from the land-based constants suggest that the Monin–Obukhov similarity theory was not valid in this wind regime.
Interestingly, the counter-swell values for the drag coefficients,
and
,have some similarities with observations over wind-following and cross-swell reported by Smedman et al. [
49,
50]. They describe a period in which winds below 3 m s
−1 blew over swell waves with
and
, and reported an average 10-m drag coefficient of
, a low kinematic momentum flux (
) in the lowest 100–200 m, a constant wind speed up to 500 m and high turbulence intensities. They further reported a reduction of
from
to values between
and 0, and an increase of the normalized velocity standard deviations,
, from
to 3. These observations were attributed to the presence of “inactive turbulence” that was “imported” from the upper part of the boundary layer into the surface layer by pressure transport. Smedman et al. [
50] argued that a downward transfer of momentum took place in a shallow surface layer just above the undulating sea surface, and that this downward transfer was counteracted by an upward transfer of momentum produced by pressure fluctuations of the swell waves. Consequently, the net-momentum transport was close to zero, thus leaving only “inactive turbulence” to explain their observation of high turbulence intensities.
Despite the similarities between our values for the drag coefficients,
and
, and those reported by Smedman et al. [
50], we only observed low turbulence intensities during the counter-swell period. This indicates that shear generation of turbulence was either suppressed or absent during this period. Unfortunately, since turbulence and wind speed were not observed at higher levels, a more detailed investigation of the boundary layer structure cannot be performed. Nonetheless, we speculate that those similarities can be an indication that Monin–Obukhov similarity theory might not be sufficient to describe the complex interaction between the land and the ocean in the coastal zone (cf. Yang et al. [
53,
54]).