Spatial Predictability of Heavy Rainfall Events in East China and the Application of Spatial-Based Methods of Probabilistic Forecasting
Abstract
1. Introduction
2. Data and Methods
2.1. Model Configuration
2.2. Ensemble Design
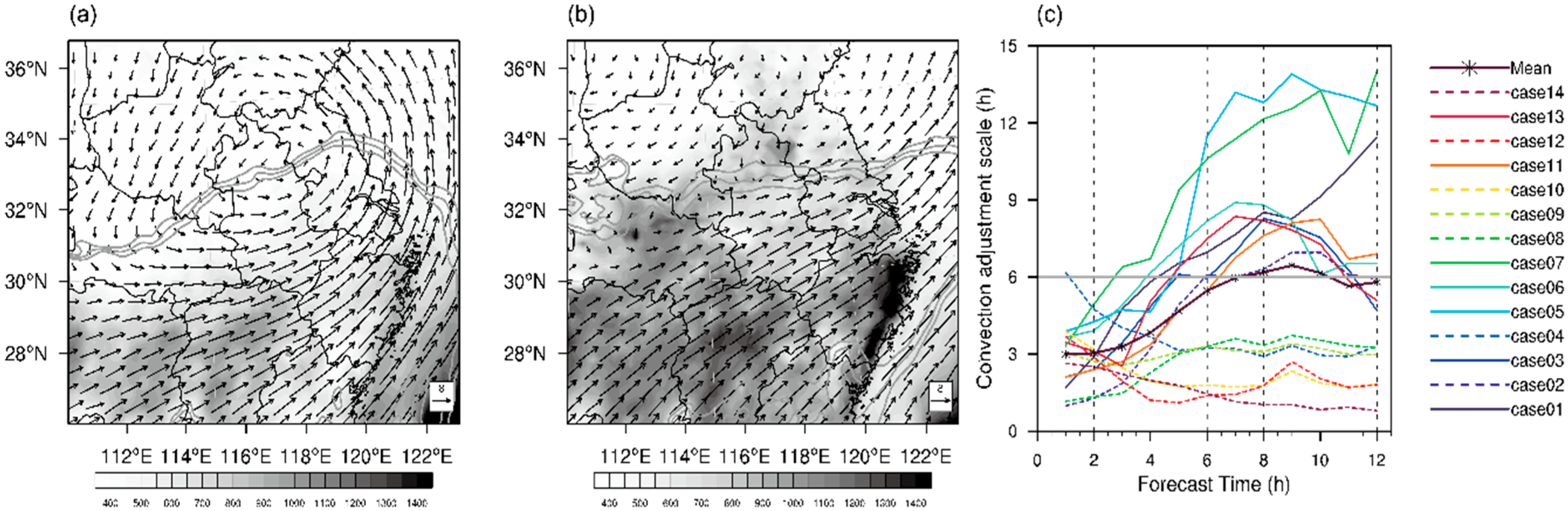
2.3. Selection and Classification of Cases
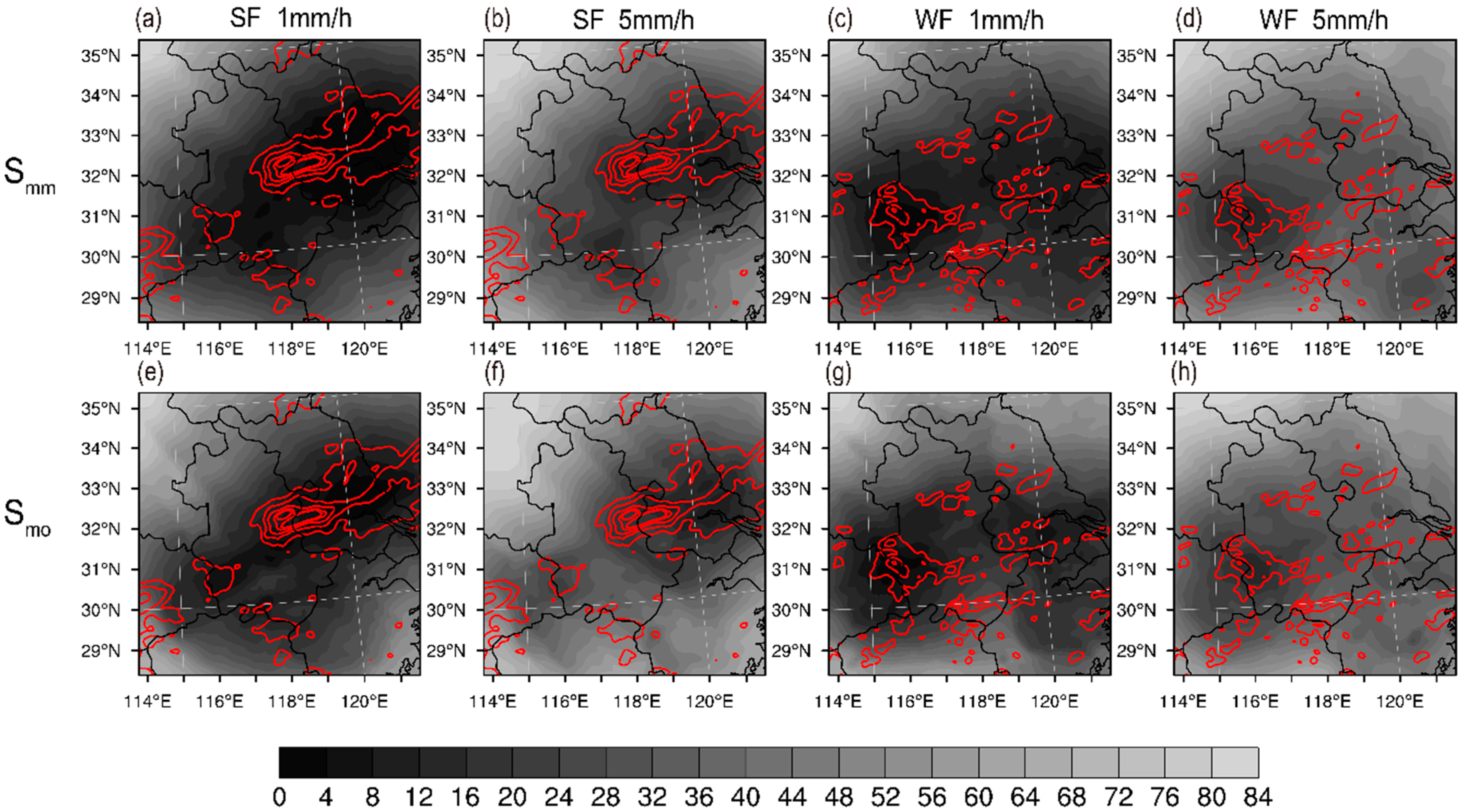
2.4. Location-Dependent Agreement Scale
2.5. Probability Generation Methods
2.6. Verification
2.6.1. Fractions Brier Score (FBS)
2.6.2. Area Under Curve (AUC) Score
3. Results
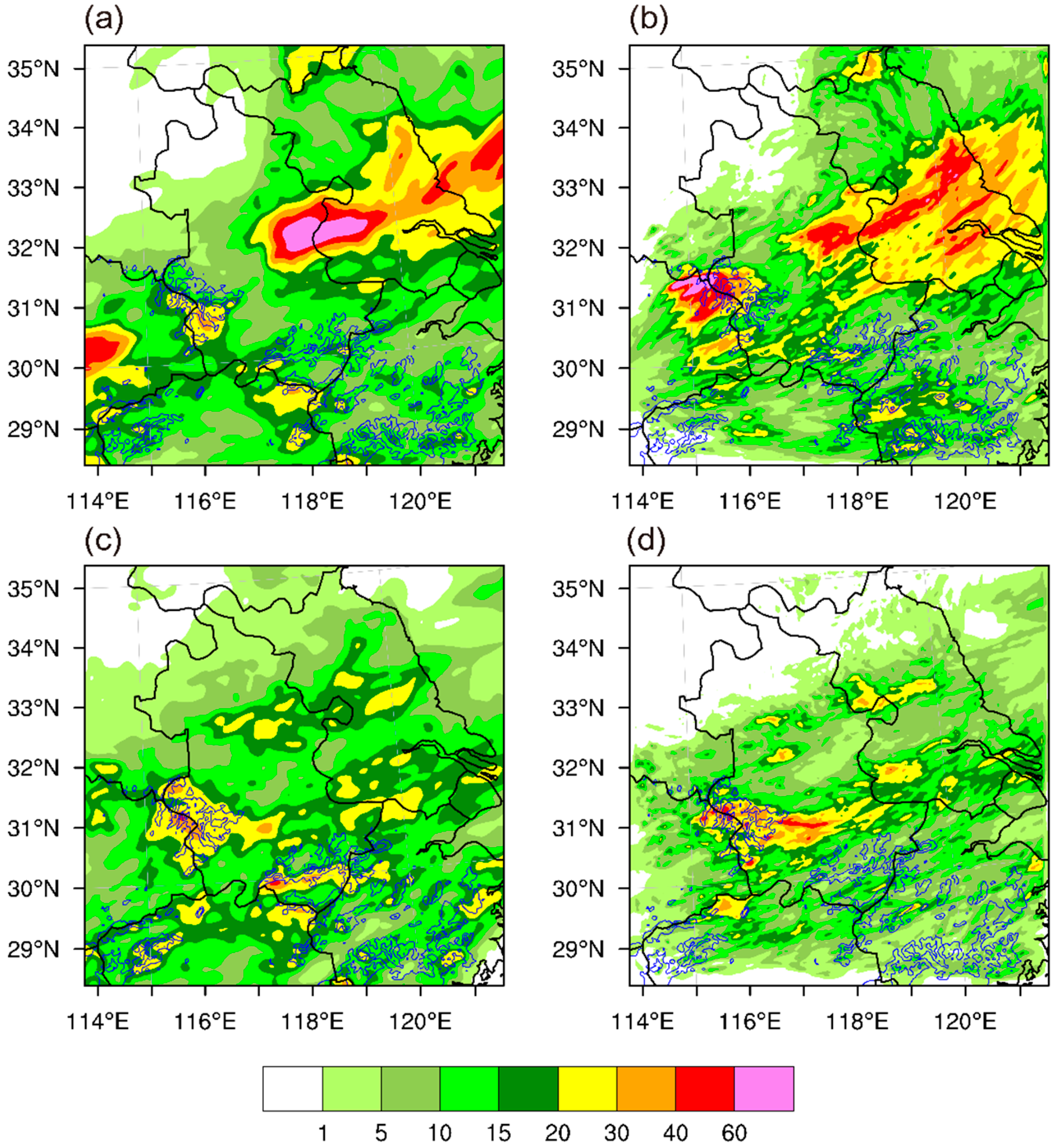
3.1. Overview of Heavy Rainfall Events
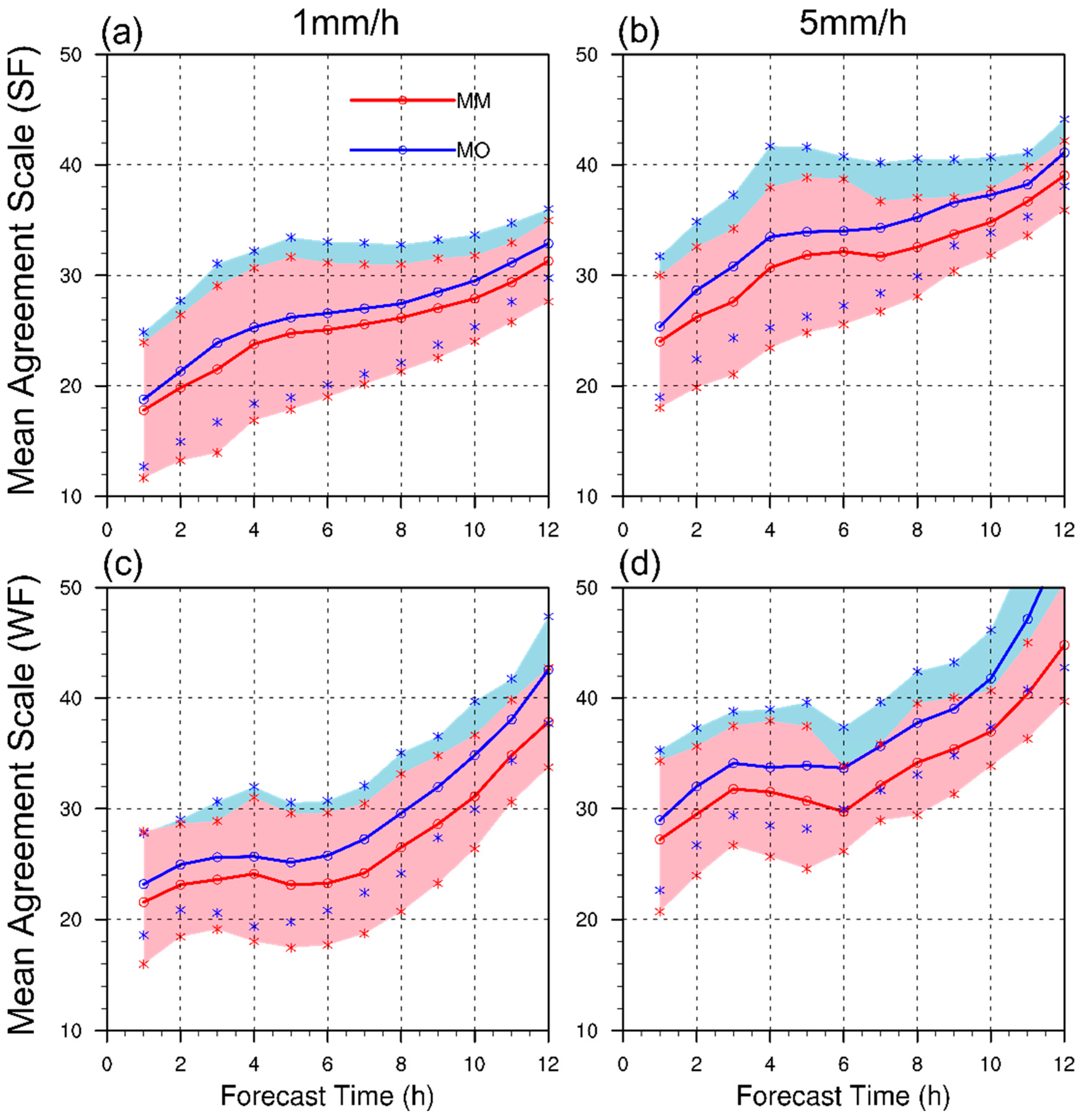
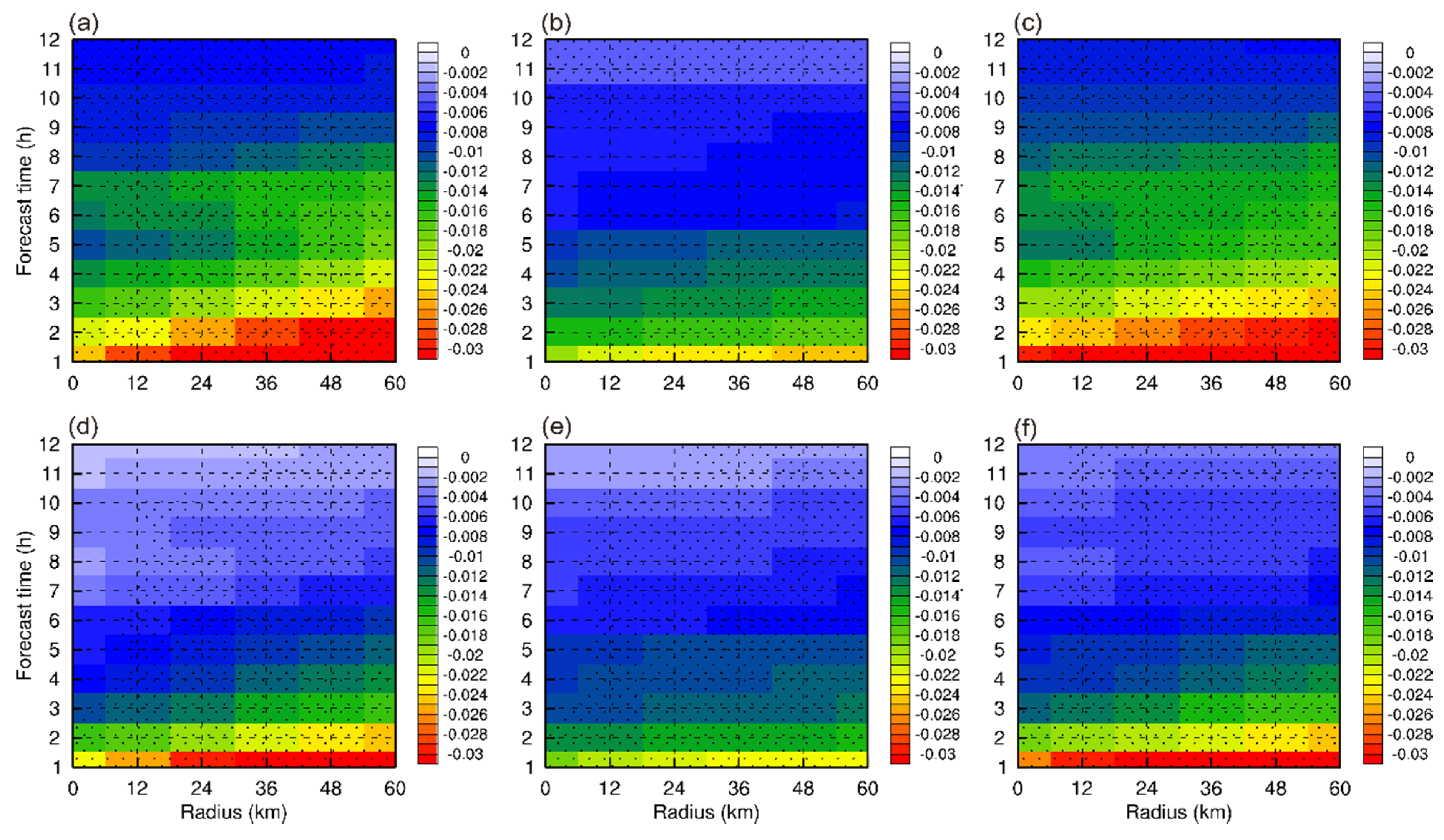
3.2. Spatial Predictability and Spread–Skill Relationship
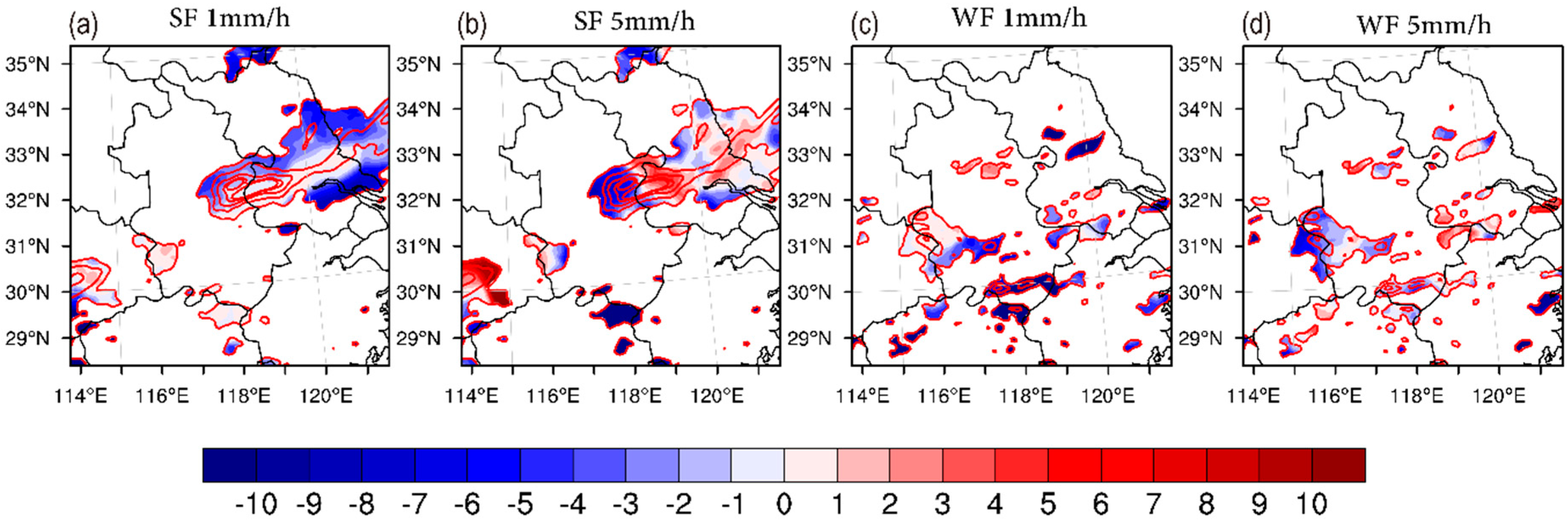
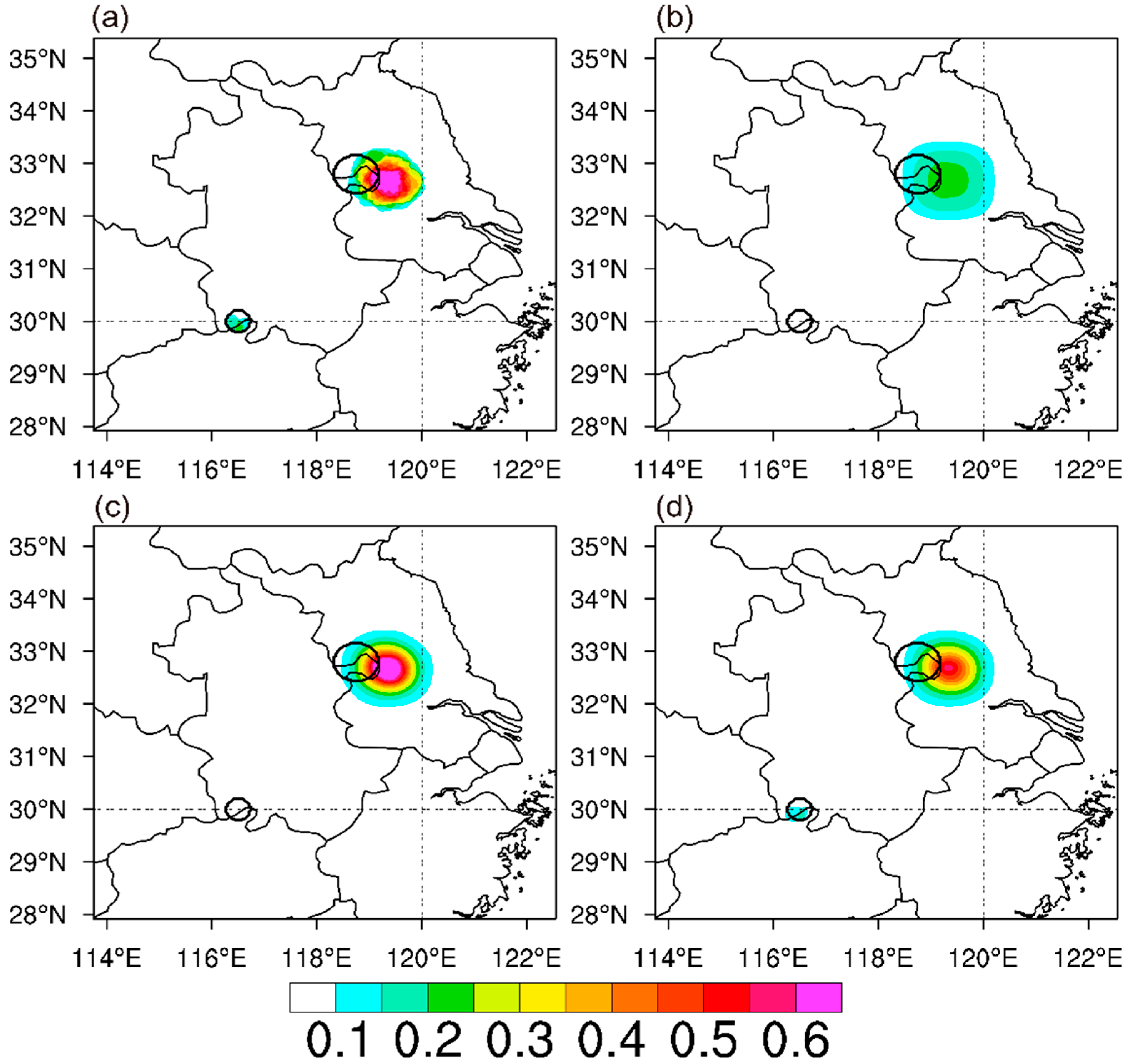
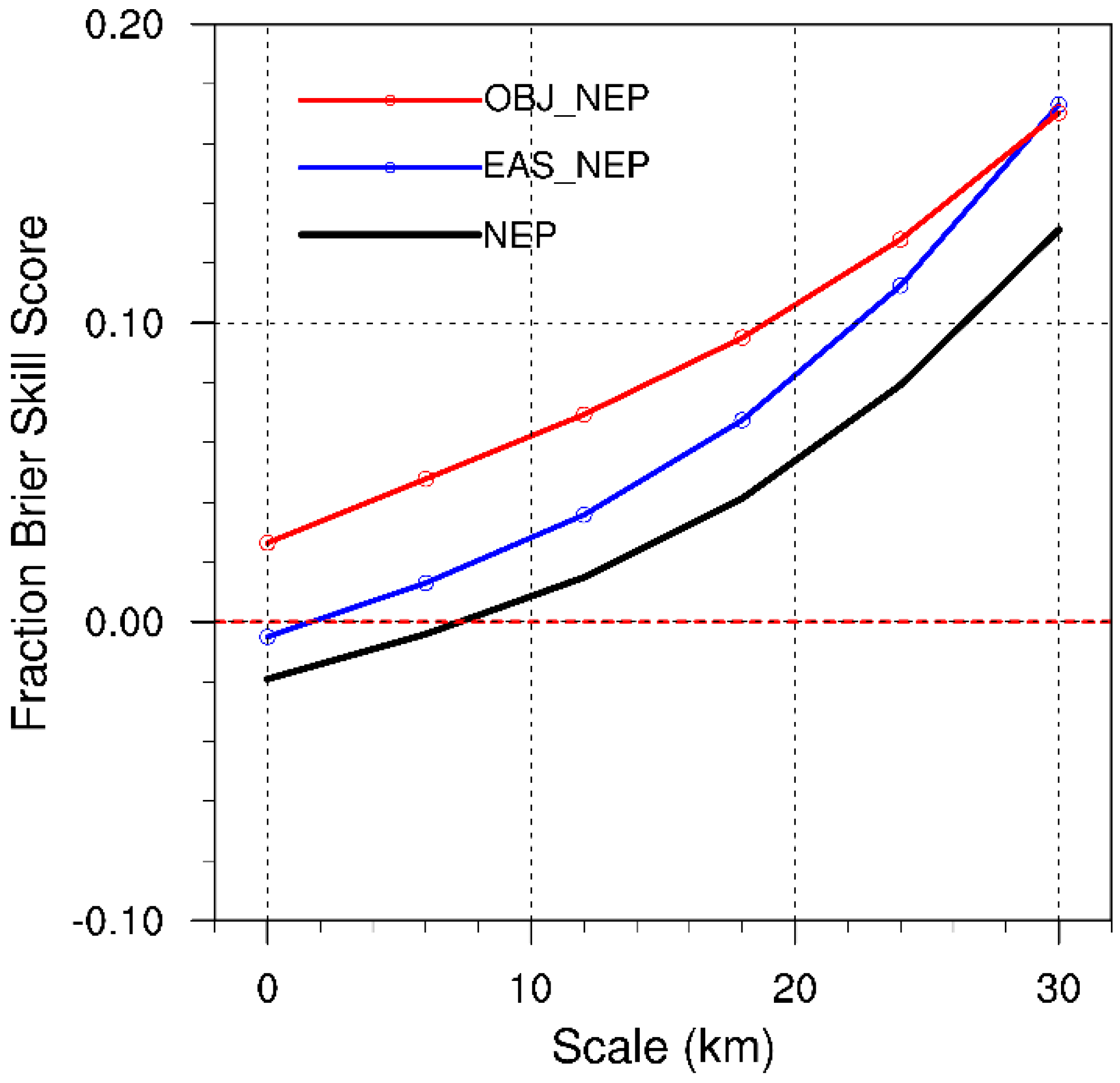
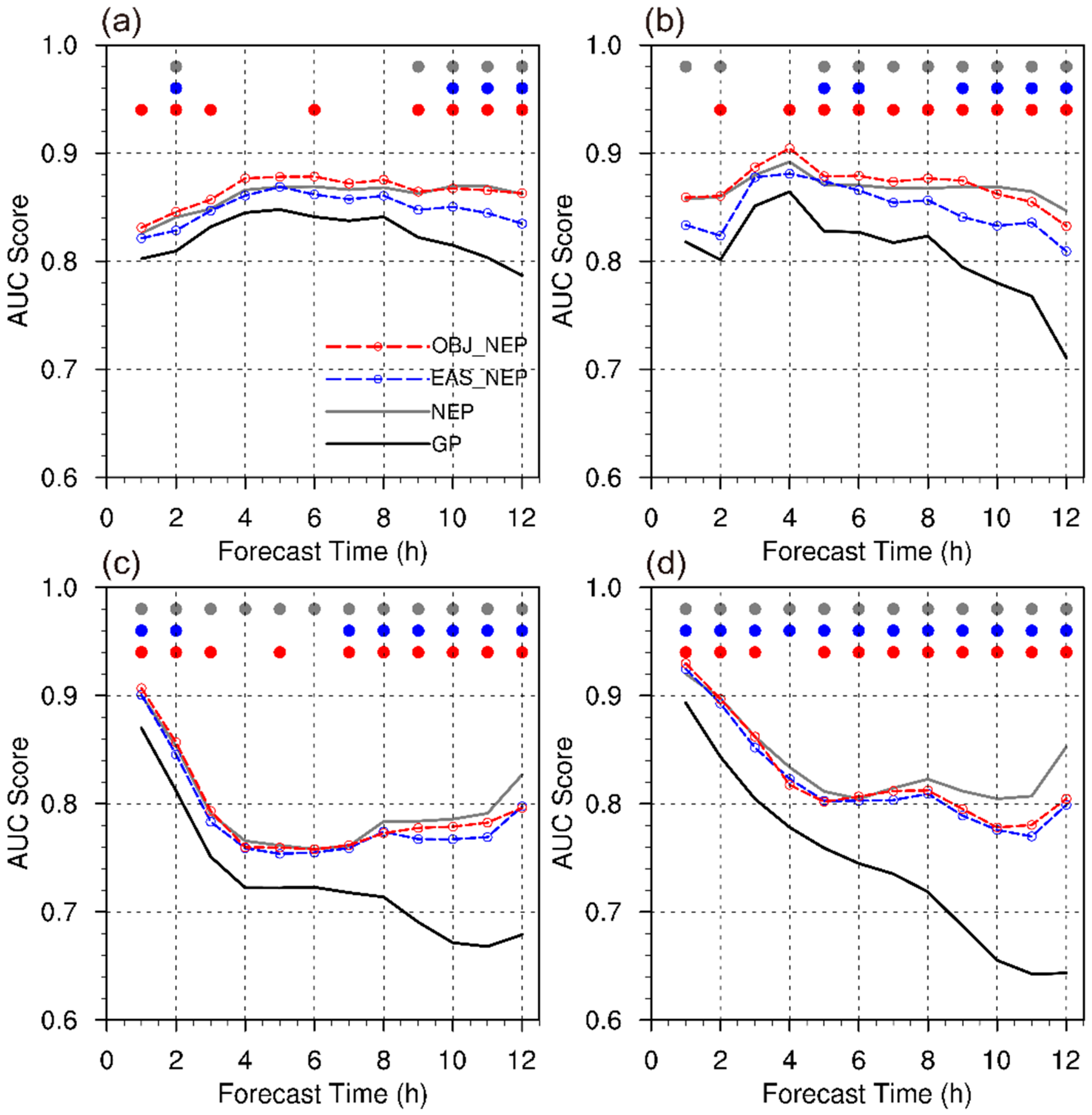
3.3. Verification of Probability Forecasts
3.3.1. Idealized Experiment
3.3.2. WRF-EnKF CSEF Experiment
4. Discussion and Conclusions
- (1)
- Using the convective adjustment timescale proposed by Done et al. [60] to distinguish convective regimes as strong forcing (SF) and weak forcing (WF) events over the YHRV;
- (2)
- (3)
- Offering a new probabilistic forecast approach using an object-based method, fully considering regime-dependent predictability;
- (4)
- Verifying the effectiveness of the new probabilistic forecast approach in both idealized and true events using the fraction Brier score (FBS) and area under curve (AUC) score.
Author Contributions
Funding
Conflicts of Interest
References
- Peralta, C.; Ben Bouallègue, Z.; Theis, S.E.; Gebhardt, C.; Buchhold, M. Accounting for initial condition uncertainties in COSMO-DE-EPS. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef]
- Nuissier, O.; Joly, B.; Vié, B.; Ducrocq, V. Uncertainty of lateral boundary conditions in a convection-permitting ensemble: A strategy of selection for Mediterranean heavy precipitation events. Nat. Hazards Earth Syst. Sci. 2012, 12, 2993. [Google Scholar] [CrossRef]
- Harnisch, F.; Keil, C. Initial Conditions for Convective-Scale Ensemble Forecasting Provided by Ensemble Data Assimilation. Mon. Weather Rev. 2015, 143, 1583–1600. [Google Scholar] [CrossRef]
- Caron, J.-F. Mismatching Perturbations at the Lateral Boundaries in Limited-Area Ensemble Forecasting: A Case Study. Mon. Weather Rev. 2013, 141, 356–374. [Google Scholar] [CrossRef]
- Tennant, W. Improving initial condition perturbations for MOGREPS-UK. Q. J. R. Meteorol. Soc. 2015, 141, 2324–2336. [Google Scholar] [CrossRef]
- Vié, B.; Nuissier, O.; Ducrocq, V. Cloud-Resolving Ensemble Simulations of Mediterranean Heavy Precipitating Events: Uncertainty on Initial Conditions and Lateral Boundary Conditions. Mon. Weather Rev. 2011, 139, 403–423. [Google Scholar] [CrossRef]
- Bouttier, F.; Vié, B.; Nuissier, O.; Raynaud, L. Impact of Stochastic Physics in a Convection-Permitting Ensemble. Mon. Weather Rev. 2012, 140, 3706–3721. [Google Scholar] [CrossRef]
- Zhang, F.; Bei, N.; Rotunno, R.; Snyder, C.; Epifanio, C.C. Mesoscale Predictability of Moist Baroclinic Waves: Convection-Permitting Experiments and Multistage Error Growth Dynamics. J. Atmos. Sci. 2007, 64, 3579–3594. [Google Scholar] [CrossRef]
- Selz, T.; Craig, G.C. Upscale Error Growth in a High-Resolution Simulation of a Summertime Weather Event over Europe. Mon. Weather Rev. 2015, 143, 813–827. [Google Scholar] [CrossRef]
- Surcel, M.; Zawadzki, I.; Yau, M.K. A Study on the Scale Dependence of the Predictability of Precipitation Patterns. J. Atmos. Sci. 2015, 72, 216–235. [Google Scholar] [CrossRef]
- Sun, Y.Q.; Zhang, F. Intrinsic versus Practical Limits of Atmospheric Predictability and the Significance of the Butterfly Effect. J. Atmos. Sci. 2016, 73, 1419–1438. [Google Scholar] [CrossRef]
- Zhang, X. Multiscale Characteristics of Different-Source Perturbations and Their Interactions for Convection-Permitting Ensemble Forecasting during SCMREX. Mon. Weather Rev. 2019, 147, 291–310. [Google Scholar] [CrossRef]
- Romine, G.S.; Schwartz, C.S.; Berner, J.; Fossell, K.R.; Snyder, C.; Anderson, J.L.; Weisman, M.L. Representing Forecast Error in a Convection-Permitting Ensemble System. Mon. Weather Rev. 2014, 142, 4519–4541. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Romine, G.S.; Smith, K.R.; Weisman, M.L. Characterizing and Optimizing Precipitation Forecasts from a Convection-Permitting Ensemble Initialized by a Mesoscale Ensemble Kalman Filter. Weather Forecast. 2014, 29, 1295–1318. [Google Scholar] [CrossRef]
- Dey, S.R.A.; Plant, R.S.; Roberts, N.M.; Migliorini, S. Assessing spatial precipitation uncertainties in a convective-scale ensemble. Q. J. R. Meteorol. Soc. 2016, 142, 2935–2948. [Google Scholar] [CrossRef]
- Chen, X.; Yuan, H.; Xue, M. Spatial spread–skill relationship in terms of agreement scales for precipitation forecasts in a convection-allowing ensemble. Q. J. R. Meteorol. Soc. 2018, 144, 85–98. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Sobash, R.A. Generating Probabilistic Forecasts from Convection-Allowing Ensembles Using Neighborhood Approaches: A Review and Recommendations. Mon. Weather Rev. 2017, 145, 3397–3418. [Google Scholar] [CrossRef]
- Wang, X.; Bishop, C.H. A Comparison of Breeding and Ensemble Transform Kalman Filter Ensemble Forecast Schemes. J. Atmos. Sci. 2003, 60, 1140–1158. [Google Scholar] [CrossRef]
- Wang, X.; Bishop, C.H.; Julier, S.J. Which Is Better, an Ensemble of Positive–Negative Pairs or a Centered Spherical Simplex Ensemble? Mon. Weather Rev. 2004, 132, 1590–1605. [Google Scholar] [CrossRef]
- Wang, Y.; Tascu, S.; Weidle, F.; Schmeisser, K. Evaluation of the Added Value of Regional Ensemble Forecasts on Global Ensemble Forecasts. Weather Forecast. 2012, 27, 972–987. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, J.; Zhi, X.; Wang, Y. A Comparison of ETKF and Downscaling in a Regional Ensemble Prediction System. Atmosphere 2015, 6, 341–360. [Google Scholar] [CrossRef]
- Weidle, F.; Wang, Y.; Smet, G. On the Impact of the Choice of Global Ensemble in Forcing a Regional Ensemble System. Weather Forecast. 2016, 31, 515–530. [Google Scholar] [CrossRef]
- Gilleland, E.; Ahijevych, D.; Brown, B.G.; Casati, B.; Ebert, E.E. Intercomparison of Spatial Forecast Verification Methods. Weather Forecast. 2009, 24, 1416–1430. [Google Scholar] [CrossRef]
- Mittermaier, M.; Roberts, N.; Thompson, S.A. A long-term assessment of precipitation forecast skill using the Fractions Skill Score. Meteorol. Appl. 2013, 20, 176–186. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X. Object-Based Evaluation of a Storm-Scale Ensemble during the 2009 NOAA Hazardous Weather Testbed Spring Experiment. Mon. Weather Rev. 2013, 141, 1079–1098. [Google Scholar] [CrossRef]
- Roberts, N.M.; Lean, H.W. Scale-Selective Verification of Rainfall Accumulations from High-Resolution Forecasts of Convective Events. Mon. Weather Rev. 2008, 136, 78–97. [Google Scholar] [CrossRef]
- Mittermaier, M.; Roberts, N. Intercomparison of Spatial Forecast Verification Methods: Identifying Skillful Spatial Scales Using the Fractions Skill Score. Weather Forecast. 2010, 25, 343–354. [Google Scholar] [CrossRef]
- Dey, S.R.A.; Leoncini, G.; Roberts, N.M.; Plant, R.S.; Migliorini, S. A Spatial View of Ensemble Spread in Convection Permitting Ensembles. Mon. Weather Rev. 2014, 142, 4091–4107. [Google Scholar] [CrossRef]
- Clark, A.J.; Gao, J.; Marsh, P.T.; Smith, T.; Kain, J.S.; Correia, J.; Xue, M.; Kong, F. Tornado Pathlength Forecasts from 2010 to 2011 Using Ensemble Updraft Helicity. Weather Forecast. 2013, 28, 387–407. [Google Scholar] [CrossRef]
- Zhu, K.; Yang, Y.; Xue, M. Percentile-based neighborhood precipitation verification and its application to a landfalling tropical storm case with radar data assimilation. Adv. Atmos. Sci. 2015, 32, 1449–1459. [Google Scholar] [CrossRef]
- Blake, B.T.; Carley, J.R.; Alcott, T.I.; Jankov, I.; Pyle, M.E.; Perfater, S.E.; Albright, B. An Adaptive Approach for the Calculation of Ensemble Gridpoint Probabilities. Weather Forecast. 2018, 33, 1063–1080. [Google Scholar] [CrossRef]
- Dey, S.R.A.; Roberts, N.M.; Plant, R.S.; Migliorini, S. A new method for the characterization and verification of local spatial predictability for convective-scale ensembles. Q. J. R. Meteorol. Soc. 2016, 142, 1982–1996. [Google Scholar] [CrossRef]
- Davis, C.; Brown, B.; Bullock, R. Object-Based Verification of Precipitation Forecasts. Part I: Methodology and Application to Mesoscale Rain Areas. Mon. Weather Rev. 2006, 134, 1772–1784. [Google Scholar] [CrossRef]
- Davis, C.A.; Brown, B.G.; Bullock, R.; Halley-Gotway, J. The Method for Object-Based Diagnostic Evaluation (MODE) Applied to Numerical Forecasts from the 2005 NSSL/SPC Spring Program. Weather Forecast. 2009, 24, 1252–1267. [Google Scholar] [CrossRef]
- Gallus, W.A. Application of Object-Based Verification Techniques to Ensemble Precipitation Forecasts. Weather Forecast. 2010, 25, 144–158. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, F. Impacts of Mountain–Plains Solenoid on Diurnal Variations of Rainfalls along the Mei-Yu Front over the East China Plains. Mon. Weather Rev. 2012, 140, 379–397. [Google Scholar] [CrossRef]
- Ding, Y.; Chan, J.C. The East Asian summer monsoon: An overview. Meteorol. Atmos. Phys. 2005, 89, 117–142. [Google Scholar]
- Luo, Y.; Qian, W.; Zhang, R. Gridded hourly precipitation analysis from high-density rain gauge network over the Yangtze-Huai rivers basin during the 2007 Meiyu season and comparison with CMORPH. J. Hydrometeorol. 2013, 14, 1243–1258. [Google Scholar] [CrossRef]
- Martin, W.J.; Xue, M. Sensitivity Analysis of Convection of the 24 May 2002 IHOP Case Using Very Large Ensembles. Mon. Weather Rev. 2006, 134, 192–207. [Google Scholar] [CrossRef][Green Version]
- Li, H.; Cui, X.; Zhang, D.-L. Sensitivity of the initiation of an isolated thunderstorm over the Beijing metropolitan region to urbanization, terrain morphology and cold outflows. Q. J. R. Meteorol. Soc. 2017, 143, 3153–3164. [Google Scholar] [CrossRef]
- Keil, C.; Heinlein, F.; Craig, G.C. The convective adjustment time-scale as indicator of predictability of convective precipitation. Q. J. R. Meteorol. Soc. 2014, 140, 480–490. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X.; Carley, J.R.; Wicker, L.J.; Karstens, C. A comparison of multiscale GSI-based EnKF and 3DVar data assimilation using radar and conventional observations for midlatitude convective-scale precipitation forecasts. Mon. Weather Rev. 2015, 143, 3087–3108. [Google Scholar] [CrossRef]
- Flack, D.L.A.; Gray, S.L.; Plant, R.S.; Lean, H.W.; Craig, G.C. Convective-Scale Perturbation Growth across the Spectrum of Convective Regimes. Mon. Weather Rev. 2018, 146, 387–405. [Google Scholar] [CrossRef]
- Skamarock, W.C.; Klemp, J.B.; Dudhia, J.; Gill, D.O.; Barker, D.M.; Duda, M.G.; Huang, X.-Y.; Wang, W.; Powers, J.G. A Description of the Advanced Research WRF Version 3, NCAR Technical Note; National Center for Atmospheric Research: Boulder, CO, USA, 2008. [Google Scholar]
- Grasso, L.; Lindsey, D.T.; Lim, K.-S.S.; Clark, A.; Bikos, D.; Dembek, S.R. Evaluation of and Suggested Improvements to the WSM6 Microphysics in WRF-ARW Using Synthetic and Observed GOES-13 Imagery. Mon. Weather Rev. 2014, 142, 3635–3650. [Google Scholar] [CrossRef]
- Grell, G.A.; Dévényi, D. A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys. Res. Lett. 2002, 29, 38-1–38-4. [Google Scholar] [CrossRef]
- Hong, S.-Y.; Noh, Y.; Dudhia, J. A New Vertical Diffusion Package with an Explicit Treatment of Entrainment Processes. Mon. Weather Rev. 2006, 134, 2318–2341. [Google Scholar] [CrossRef]
- Mlawer, E.J.; Taubman, S.J.; Brown, P.D.; Iacono, M.J.; Clough, S.A. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. D Atmos. 1997, 102, 16663–16682. [Google Scholar] [CrossRef]
- Chou, M.-D.; Suarez, M.J. A solar radiation parameterization (CLIRAD-SW) for atmospheric studies. NASA Tech. Memo. 1999, 15, 48. [Google Scholar]
- Whitaker, J.S.; Hamill, T.M. Ensemble Data Assimilation without Perturbed Observations. Mon. Weather Rev. 2002, 130, 1913–1924. [Google Scholar] [CrossRef]
- Hagedorn, R.; Hamill, T.M.; Whitaker, J.S. Probabilistic Forecast Calibration Using ECMWF and GFS Ensemble Reforecasts. Part I: Two-Meter Temperatures. Mon. Weather Rev. 2008, 136, 2608–2619. [Google Scholar] [CrossRef]
- Hagedorn, R.; Buizza, R.; Hamill, T.M.; Leutbecher, M.; Palmer, T.N. Comparing TIGGE multimodel forecasts with reforecast-calibrated ECMWF ensemble forecasts. Q. J. R. Meteorol. Soc. 2012, 138, 1814–1827. [Google Scholar] [CrossRef]
- Johnson, A.; Wang, X. A Study of Multiscale Initial Condition Perturbation Methods for Convection-Permitting Ensemble Forecasts. Mon. Weather Rev. 2016, 144, 2579–2604. [Google Scholar] [CrossRef]
- Gasperoni, N.A.; Xue, M.; Palmer, R.D.; Gao, J. Sensitivity of Convective Initiation Prediction to Near-Surface Moisture When Assimilating Radar Refractivity: Impact Tests Using OSSEs. J. Atmos. Ocean. Technol. 2013, 30, 2281–2302. [Google Scholar] [CrossRef]
- Madaus, L.E.; Hakim, G.J. Constraining Ensemble Forecasts of Discrete Convective Initiation with Surface Observations. Mon. Weather Rev. 2017, 145, 2597–2610. [Google Scholar] [CrossRef]
- Anderson, J.L.; Anderson, S.L. A Monte Carlo Implementation of the Nonlinear Filtering Problem to Produce Ensemble Assimilations and Forecasts. Mon. Weather Rev. 1999, 127, 2741–2758. [Google Scholar] [CrossRef]
- Tong, M.; Xue, M. Ensemble Kalman Filter Assimilation of Doppler Radar Data with a Compressible Nonhydrostatic Model: OSS Experiments. Mon. Weather Rev. 2005, 133, 1789–1807. [Google Scholar] [CrossRef]
- Zhang, F.; Snyder, C.; Sun, J. Impacts of Initial Estimate and Observation Availability on Convective-Scale Data Assimilation with an Ensemble Kalman Filter. Mon. Weather Rev. 2004, 132, 1238–1253. [Google Scholar] [CrossRef]
- Liu, J.Y.; Tan, Z.M.; Zhang, Y. Study of the three types of torrential rains of different formation mechanism during the Meiyu period. Acta Meteorol. Sin. 2012, 70, 452–466. [Google Scholar]
- Done, J.M.; Craig, G.C.; Gray, S.L.; Clark, P.A.; Gray, M.E.B. Mesoscale simulations of organized convection: Importance of convective equilibrium. Q. J. R. Meteorol. Soc. 2006, 132, 737–756. [Google Scholar] [CrossRef]
- Done, J.M.; Craig, G.C.; Gray, S.L.; Clark, P.A. Case-to-case variability of predictability of deep convection in a mesoscale model. Q. J. R. Meteorol. Soc. 2012, 138, 638–648. [Google Scholar] [CrossRef]
- Flack, D.L.A.; Plant, R.S.; Gray, S.L.; Lean, H.W.; Keil, C.; Craig, G.C. Characterisation of convective regimes over the British Isles. Q. J. R. Meteorol. Soc. 2016, 142, 1541–1553. [Google Scholar] [CrossRef]
- Surcel, M.; Zawadzki, I.; Yau, M.K.; Xue, M.; Kong, F. More on the Scale Dependence of the Predictability of Precipitation Patterns: Extension to the 2009–13 CAPS Spring Experiment Ensemble Forecasts. Mon. Weather Rev. 2017, 145, 3625–3646. [Google Scholar] [CrossRef]
- Schwartz, C.S.; Kain, J.S.; Weiss, S.J.; Xue, M.; Bright, D.R.; Kong, F.; Thomas, K.W.; Levit, J.J.; Coniglio, M.C.; Wandishin, M.S. Toward Improved Convection-Allowing Ensembles: Model Physics Sensitivities and Optimizing Probabilistic Guidance with Small Ensemble Membership. Weather Forecast. 2010, 25, 263–280. [Google Scholar] [CrossRef]
- Brier, G.W. The Statistical Theory of Turbulence and the Problem of Diffusion in the Atmosphere. J. Atmos. Sci. 1950, 7, 283–290. [Google Scholar] [CrossRef]
- Wandishin, M.S.; Mullen, S.J. Multiclass ROC Analysis. Weather Forecast. 2009, 24, 530–547. [Google Scholar] [CrossRef]
- Marzban, C. The ROC Curve and the Area under It as Performance Measures. Weather Forecast. 2004, 19, 1106–1114. [Google Scholar] [CrossRef]
- Chen, Y.; Chan, Y.; Chen, T.; He, H. Characteristics analysis of warm-sector rainstorms over the middle-lowers reaches of the Yangtze River. Meteorol. Mon. 2016, 42, 724–731. (In Chinese) [Google Scholar]
- Hohenegger, C.; Schar, C. Atmospheric Predictability at Synoptic Versus Cloud-Resolving Scales. Bull. Am. Meteorol. Soc. 2007, 88, 1783–1794. [Google Scholar] [CrossRef]
- Nielsen, E.R.; Schumacher, R.S. Using Convection-Allowing Ensembles to Understand the Predictability of an Extreme Rainfall Event. Mon. Weather Rev. 2016, 144, 3651–3676. [Google Scholar] [CrossRef]
- Klasa, C.; Arpagaus, M.; Walser, A.; Wernli, H. On the Time Evolution of Limited-Area Ensemble Variance: Case Stud. with the Convection-Permitting Ensemble COSMO-E. J. Atmos. Sci. 2019, 76, 11–26. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhuang, X.; Zhu, H.; Min, J.; Zhang, L.; Wu, N.; Wu, Z.; Wang, S. Spatial Predictability of Heavy Rainfall Events in East China and the Application of Spatial-Based Methods of Probabilistic Forecasting. Atmosphere 2019, 10, 490. https://doi.org/10.3390/atmos10090490
Zhuang X, Zhu H, Min J, Zhang L, Wu N, Wu Z, Wang S. Spatial Predictability of Heavy Rainfall Events in East China and the Application of Spatial-Based Methods of Probabilistic Forecasting. Atmosphere. 2019; 10(9):490. https://doi.org/10.3390/atmos10090490
Chicago/Turabian StyleZhuang, Xiaoran, Haonan Zhu, Jinzhong Min, Liu Zhang, Naigen Wu, Zhipeng Wu, and Shiqi Wang. 2019. "Spatial Predictability of Heavy Rainfall Events in East China and the Application of Spatial-Based Methods of Probabilistic Forecasting" Atmosphere 10, no. 9: 490. https://doi.org/10.3390/atmos10090490
APA StyleZhuang, X., Zhu, H., Min, J., Zhang, L., Wu, N., Wu, Z., & Wang, S. (2019). Spatial Predictability of Heavy Rainfall Events in East China and the Application of Spatial-Based Methods of Probabilistic Forecasting. Atmosphere, 10(9), 490. https://doi.org/10.3390/atmos10090490



