Projections of Alpine Snow-Cover in a High-Resolution Climate Simulation
Abstract
1. Introduction
- Do kilometer–scale regional climate simulations provide an added value in terms of snow cover representation in Alpine terrain?
- How is Alpine snow cover expected to change by the end of the 21st century based on high resolution regional climate simulations?
2. Data and Methods
2.1. Model Data
2.2. Observational Data
- First, measured snow depth data were converted to SWE using a snow density model based on methods presented by Martinec and Rango [25]. This model describes accumulation and densification of the snowpack layer by layer. Here, we used a recalibrated version of their original model using data from over 10,000 snow profiles presented in Jonas et al. [26].
- Then, for each day, the station data was detrended allowing non-linear SWE profiles.
- Next, the detrended SWE values were interpolated to the model orography using a 3-dimensional Gaussian filter weighting approach described in Jrg-Hess et al. [27]. Optimized filter widths were identified using a leave-one-out validation approach.
- Finally, a subgrid scaling was applied to account for the influence of topography on snow distribution and redistribution in mountainous terrain. To this end, slope- and aspect-dependent correction functions were trained using a set of high-resolution snow depth maps from airborne lidar acquisitions in the European Alps as presented in Grünewald et al. [28], and applied at a 25 m spatial resolution.
2.3. Methods
3. Results
3.1. Evaluation of Snow Water Equivalent
3.1.1. Seasonal Mean Snow Water Equivalent
3.1.2. Annual Cycle of Snow Water Equivalent
3.1.3. Height Profile of Snow Water Equivalent
3.2. Climate Change Signal of Alpine Snow Water Equivalents
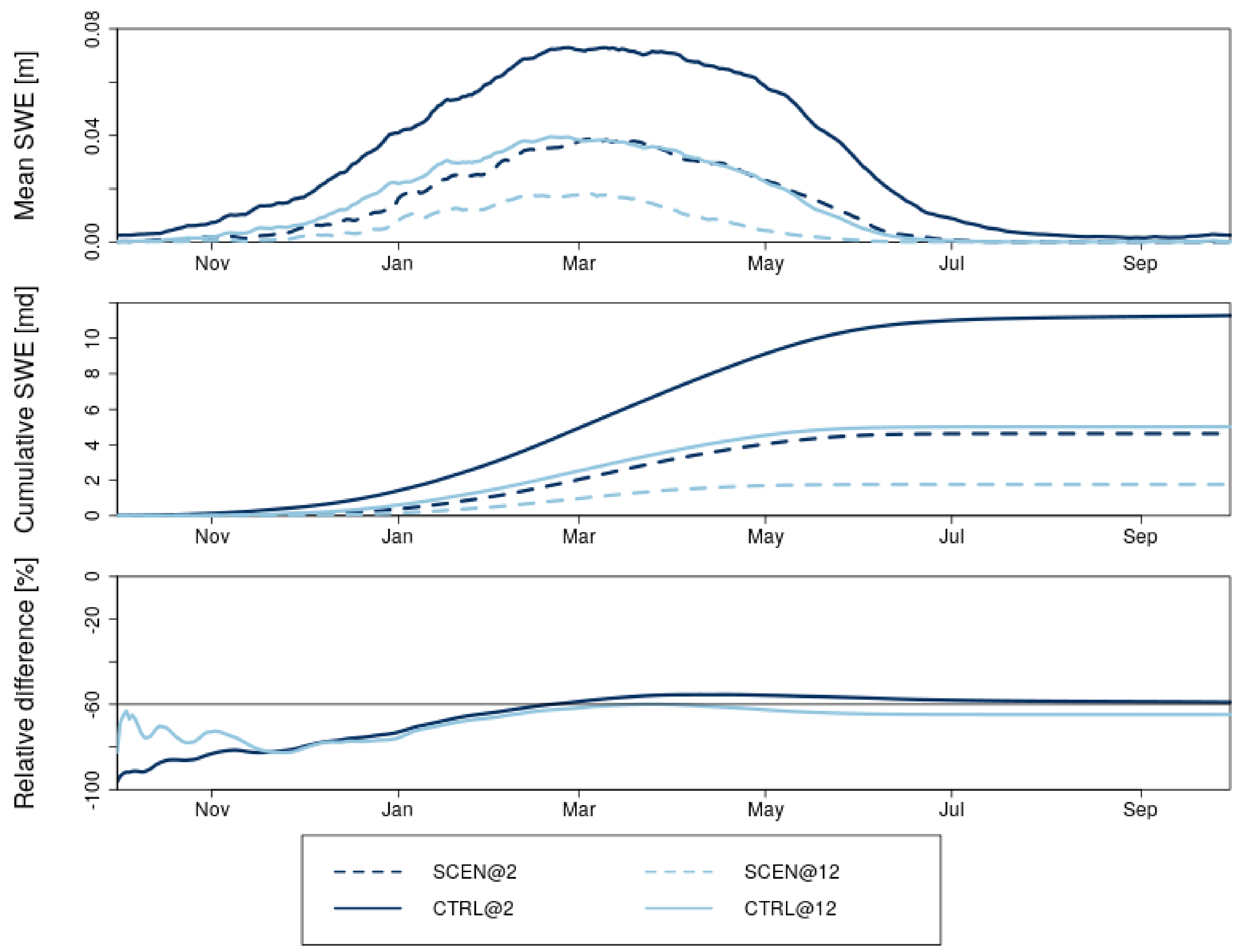
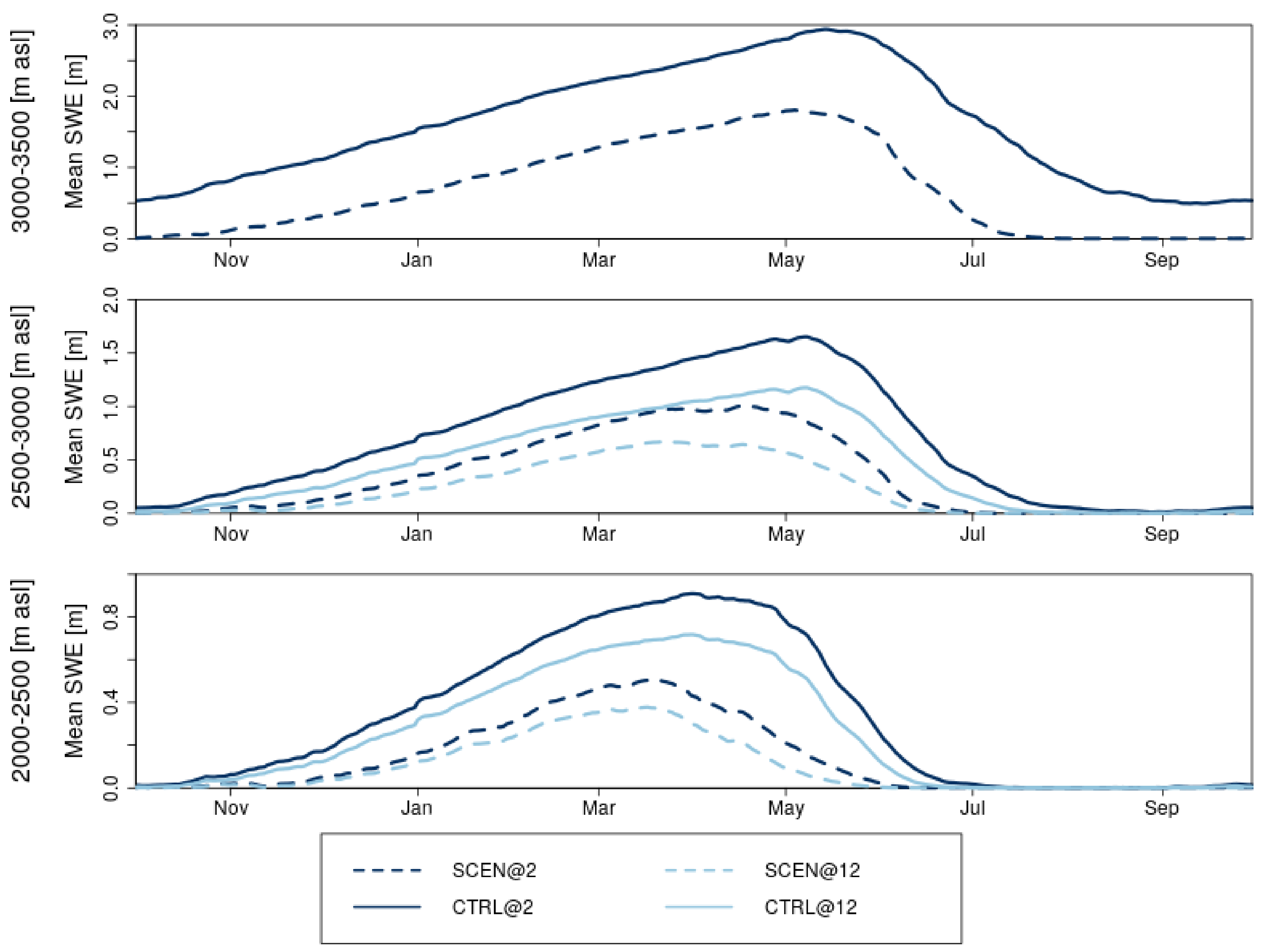
3.2.1. Annual Cycle of Snow Water Equivalent in a Warmer Climate
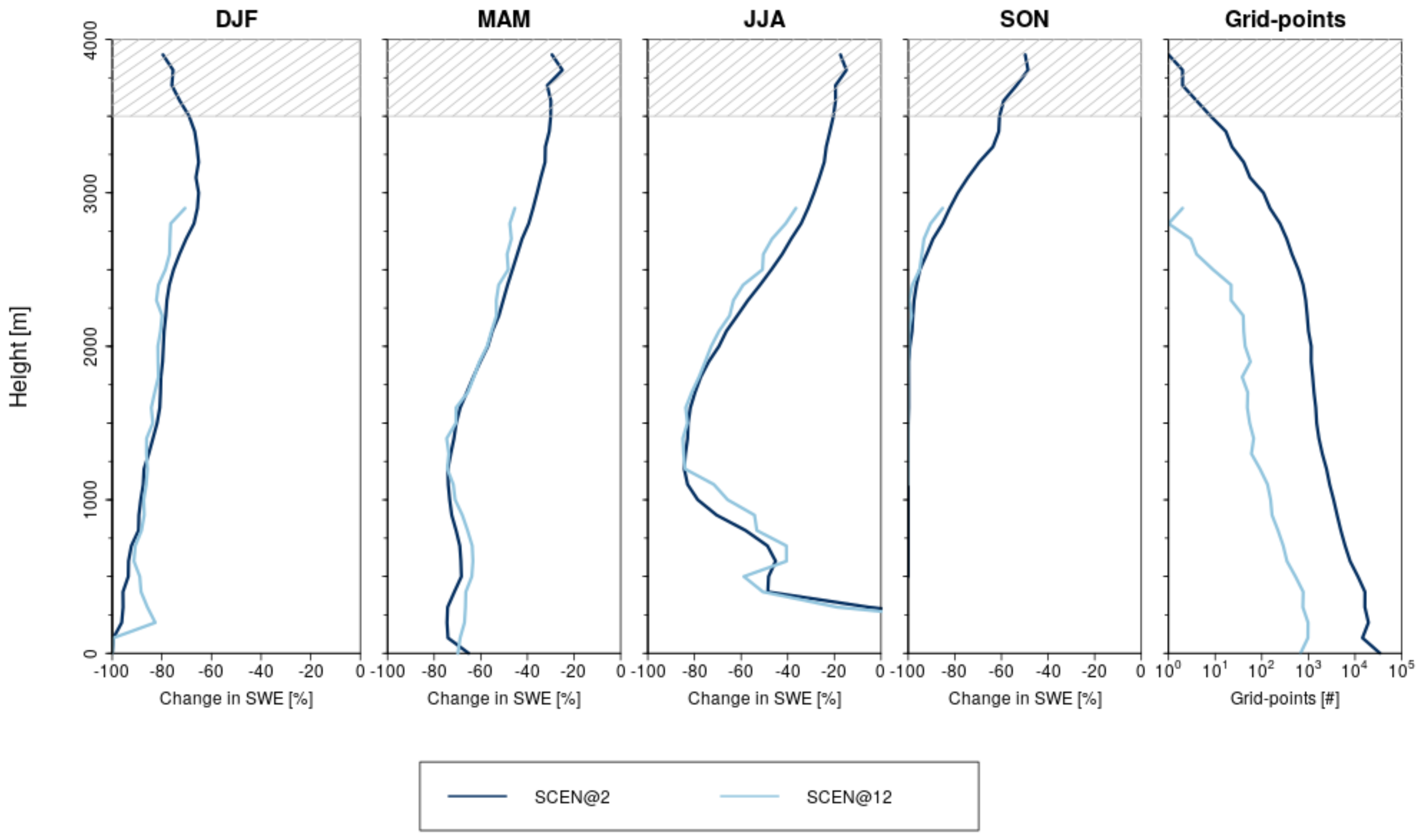
3.2.2. Projected Changes in the Vertical Profile of Snow Water Equivalent
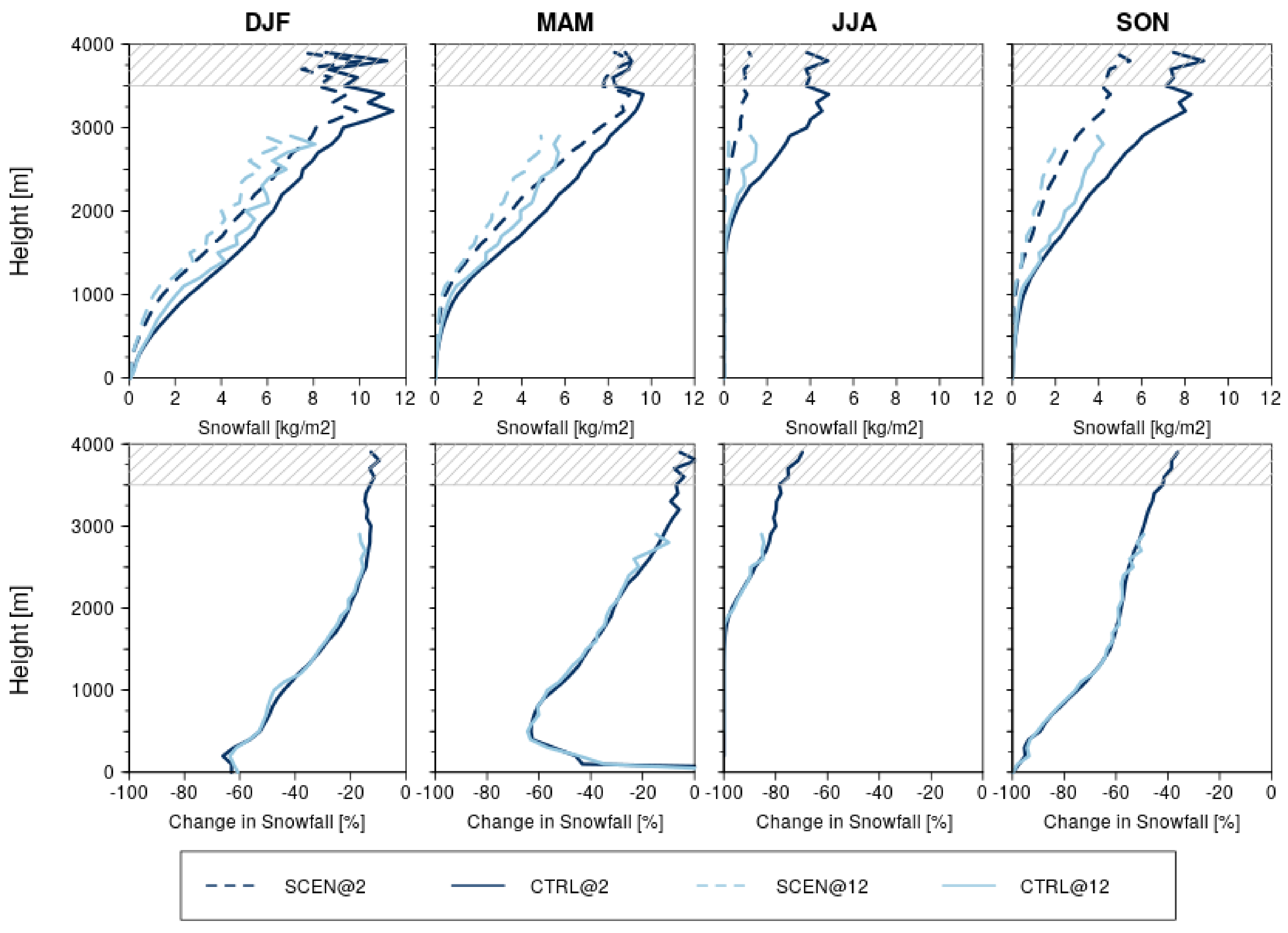
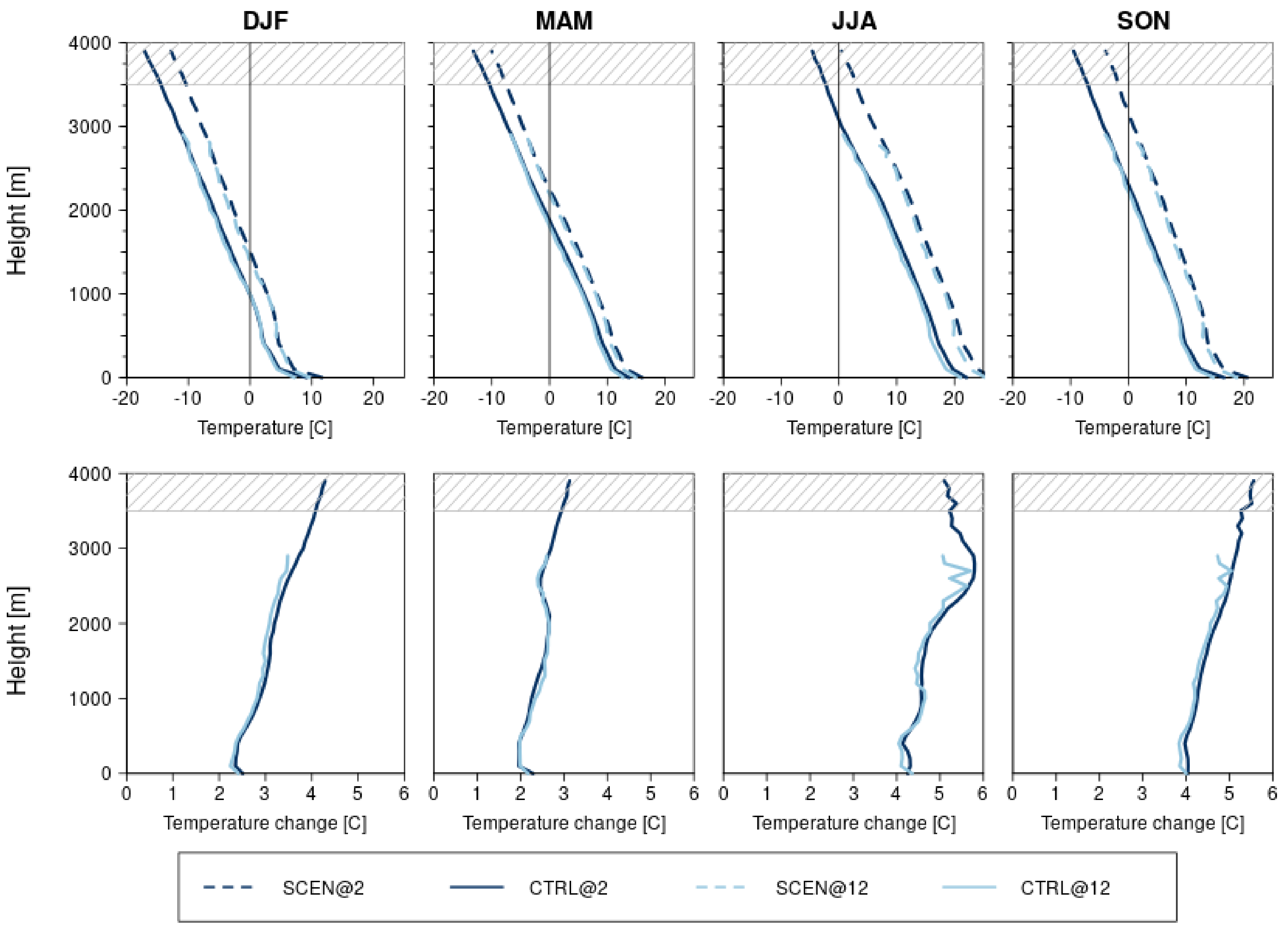
3.3. Projected Changes in the Vertical Profile of Temperature and Snowfall
3.4. Discussion
4. Conclusions
- High resolution climate simulations are a promising tool to improve the simulation of Alpine snow cover. They clearly outperform simulations with grid spacings of 12 km and 50 km in representing the annual cycle of SWE. Also, thanks to the better representation of topography, the high resolution simulations can represent snow cover on high elevation levels where snow may be present even during the summer months.
- Under climate change, Alpine snow cover amounts are expected to drop by 60% in the high resolution simulation. This result is in line with the literature and simulations with larger grid spacing (12 km). However, the high resolution climate simulation allows to analyse changes above 3000 m asl, where a loss of perennial snow cover can be expected.
- Overall, the high-resolution climate model approach is especially promising for regions with complex topography and at high elevations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stocker, T.F.; Qin, D.; Plattner, G.K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M.; et al. Climate Change 2013: The Physical Science Basis; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- Laternser, M.; Schneebeli, M. Long-term snow climate trends of the Swiss Alps (1931–99). Int. J. Climatol. 2003, 23, 733–750. [Google Scholar] [CrossRef]
- Scherrer, S.C.; Appenzeller, C.; Laternser, M. Trends in Swiss Alpine snow days: The role of local-and large-scale climate variability. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Beniston, M.; Keller, F.; Koffi, B.; Goyette, S. Estimates of snow accumulation and volume in the Swiss Alps under changing climatic conditions. Theor. Appl. Climatol. 2003, 76, 125–140. [Google Scholar] [CrossRef]
- Steger, C.; Kotlarski, S.; Jonas, T.; Schär, C. Alpine snow cover in a changing climate: A regional climate model perspective. Clim. Dyn. 2013, 41, 735–754. [Google Scholar] [CrossRef]
- Scherrer, S.; Ceppi, P.; Croci-Maspoli, M.; Appenzeller, C. Snow-albedo feedback and Swiss spring temperature trends. Theor. Appl. Climatol. 2012, 110, 509–516. [Google Scholar] [CrossRef]
- Marchand, P.J. Life in the Cold: An Introduction to Winter Ecology; UPNE: Hanover, NH, USA, 2014. [Google Scholar]
- Elsasser, H.; Abegg, B.; Buerki, R. Climate change and winter sports: Environmental and economic threats. Geogr. Bull. 2006, 38, 26. [Google Scholar]
- Swiss Federal Office of Energy SFOE. Hydropower; SFOE: Bern, Switzerland, 2018. [Google Scholar]
- Voigt, T.; Füssel, H.M.; Gärtner-Roer, I.; Huggel, C.; Marty, C.; Zemp, M. Impacts of Climate Change on Snow, Ice, and Permafrost in Europe: Observed Trends, Future Projections, and Socio-Economic Relevance; European Topic Centre on Air and Climate Change: Bilthoven, The Netherlands, 2010. [Google Scholar]
- Ban, N.; Schmidli, J.; Schär, C. Evaluation of the convection-resolving regional climate modeling approach in decade-long simulations. J. Geophys. Res. Atmos. 2014, 119, 7889–7907. [Google Scholar] [CrossRef]
- Ban, N.; Schmidli, J.; Schär, C. Heavy precipitation in a changing climate: Does short-term summer precipitation increase faster? Geophys. Res. Lett. 2015, 42, 1165–1172. [Google Scholar] [CrossRef]
- Kendon, E.J.; Roberts, N.M.; Senior, C.A.; Roberts, M.J. Realism of rainfall in a very high-resolution regional climate model. J. Clim. 2012, 25, 5791–5806. [Google Scholar] [CrossRef]
- Coppola, E.; Sobolowski, S.; Pichelli, E.; Raffaele, F.; Ahrens, B.; Anders, I.; Ban, N.; Bastin, S.; Belda, M.; Belusic, D.; et al. A first-of-its-kind multi-model convection permitting ensemble for investigating convective phenomena over Europe and the Mediterranean. Clim. Dyn. 2017, 1–32. [Google Scholar] [CrossRef]
- Dutra, E.; Kotlarski, S.; Viterbo, P.; Balsamo, G.; Miranda, P.M.; Schär, C.; Bissolli, P.; Jonas, T. Snow cover sensitivity to horizontal resolution, parameterizations, and atmospheric forcing in a land surface model. J. Geophys. Res. Atmos. 2011, 116, D21109. [Google Scholar] [CrossRef]
- Rasmussen, R.; Liu, C.; Ikeda, K.; Gochis, D.; Yates, D.; Chen, F.; Tewari, M.; Barlage, M.; Dudhia, J.; Yu, W.; et al. High-resolution coupled climate runoff simulations of seasonal snowfall over Colorado: A process study of current and warmer climate. J. Clim. 2011, 24, 3015–3048. [Google Scholar] [CrossRef]
- Kotlarski, S.; Bosshard, T.; Lüthi, D.; Pall, P.; Schär, C. Elevation gradients of European climate change in the regional climate model COSMO-CLM. Clim. Chang. 2012, 112, 189–215. [Google Scholar] [CrossRef]
- Steppeler, J.; Doms, G.; Schättler, U.; Bitzer, H.; Gassmann, A.; Damrath, U.; Gregoric, G. Meso-gamma scale forecasts using the nonhydrostatic model LM. Meteorol. Atmos. Phys. 2003, 82, 75–96. [Google Scholar] [CrossRef]
- Doms, G.; Förstner, J. Development of a kilometer-scale NWP-system: LMK. COSMO Newsl. 2004, 4, 159–167. [Google Scholar]
- Baldauf, M.; Seifert, A.; Förstner, J.; Majewski, D.; Raschendorfer, M.; Reinhardt, T. Operational Convection-Scale Numerical Weather Prediction with the COSMO Model: Description and sensitivities. Mon. Weather Rev. 2011, 139, 3887–3905. [Google Scholar] [CrossRef]
- Tiedtke, M. A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon. Weather. Rev. 1989, 117, 1779–1800. [Google Scholar] [CrossRef]
- Doms, G.; Förstner, J.; Heise, E.; Herzog, H.; Mironov, D.; Raschendorfer, M.; Reinhardt, T.; Ritter, B.; Schrodin, R.; Schulz, J.P.; et al. A Description of the Nonhydrostatic Regional COSMO Model. Part II: Physical Parameterization; Deutscher Wetterdienst: Offenbach, Germany, 2011. [Google Scholar]
- Stevens, B.; Giorgetta, M.; Esch, M.; Mauritsen, T.; Crueger, T.; Rast, S.; Salzmann, M.; Schmidt, H.; Bader, J.; Block, K.; et al. Atmospheric component of the MPI-M Earth System Model: ECHAM6. J. Adv. Model. Earth Syst. 2013, 5, 146–172. [Google Scholar] [CrossRef]
- Giorgi, F. Thirty Years of Regional Climate Modeling: Where Are We and Where Are We Going next? J. Geophys. Res. 2019, 124, 5696–5723. [Google Scholar] [CrossRef]
- Martinec, J.; Rango, A. Indirect evaluation of snow reserves in mountain basins. IAHS Publ. 1991, 205, 111–119. [Google Scholar]
- Jonas, T.; Marty, C.; Magnusson, J. Estimating the snow water equivalent from snow depth measurements in the Swiss Alps. J. Hydrol. 2009, 378, 161–167. [Google Scholar] [CrossRef]
- Jörg-Hess, S.; Griessinger, N.; Zappa, M. Probabilistic forecasts of snow water equivalent and runoff in mountainous areas. J. Hydrometeorol. 2015, 16, 2169–2186. [Google Scholar] [CrossRef]
- Grünewald, T.; Bühler, Y.; Lehning, M. Elevation dependency of mountain snow depth. Cryosphere 2014, 8, 2381–2394. [Google Scholar] [CrossRef]
- Hüsler, F.; Jonas, T.; Riffler, M.; Musial, J.P.; Wunderle, S. A satellite-based snow cover climatology (1985–2011) for the European Alps derived from AVHRR data. Cryosphere 2014, 8, 73–90. [Google Scholar] [CrossRef]
- Bales, R.; Dressler, K.; Imam, B.; Fassnacht, S.; Lampkin, D. Fractional snow cover in the Colorado and Rio Grande basins, 1995–2002. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Fassnacht, S.; Dressler, K.; Bales, R. Snow water equivalent interpolation for the Colorado River Basin from snow telemetry (SNOTEL) data. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Fassnacht, S.; Dressler, K.; Hultstrand, D.; Bales, R.; Patterson, G. Temporal inconsistencies in coarse-scale snow water equivalent patterns: Colorado River Basin snow telemetry-topography regressions. Pirineos 2012, 165–185. [Google Scholar] [CrossRef]
- Hantel, M.; Hirtl-Wielke, L.M. Sensitivity of Alpine snow cover to European temperature. Int. J. Climatol. 2007, 27, 1265–1275. [Google Scholar] [CrossRef]
- Hantel, M.; Maurer, C.; Mayer, D. The snowline climate of the Alps 1961–2010. Theor. Appl. Climatol. 2012, 110, 517–537. [Google Scholar] [CrossRef]
- Kuhn, M.; Helfricht, K.; Ortner, M.; Landmann, J.; Gurgiser, W. Liquid water storage in snow and ice in 86 Eastern Alpine basins and its changes from 1970–97 to 1998–2006. Ann. Glaciol. 2016, 57, 11–18. [Google Scholar] [CrossRef][Green Version]
- Frei, P.; Kotlarski, S.; Liniger, M.A.; Schär, C. Snowfall in the Alps: Evaluation and projections based on the EURO-CORDEX regional climate models. Cryosphere 2018, 2018, 1–24. [Google Scholar] [CrossRef]
- Heim, C. Daily Temperature Variability in Convection-Resolving Climate Simulations. Master’s Thesis, IAC ETHZ, Zurich, Switzerland, 2015. [Google Scholar]
- Santer, B.D.; Wigley, T.M.; Mears, C.; Wentz, F.J.; Klein, S.A.; Seidel, D.J.; Taylor, K.E.; Thorne, P.W.; Wehner, M.F.; Gleckler, P.J.; et al. Amplification of surface temperature trends and variability in the tropical atmosphere. Science 2005, 309, 1551–1556. [Google Scholar] [CrossRef]
- Kotlarski, S.; Lüthi, D.; Schär, C. The elevation dependency of 21st century European climate change: An RCM ensemble perspective. Int. J. Climatol. 2015, 35, 3902–3920. [Google Scholar] [CrossRef]
- Brogli, R.; Kröner, N.; Sørland, S.L.; Lüthi, D.; Schär, C. The Role of Hadley Circulation and Lapse-Rate Changes for the Future European Summer Climate. J. Clim. 2019, 32, 385–404. [Google Scholar] [CrossRef]
- Winter, K.J.P.M.; Kotlarski, S.; Scherrer, S.C.; Schär, C. The Alpine snow-albedo feedback in regional climate models. Clim. Dyn. 2017, 48, 1109–1124. [Google Scholar] [CrossRef]
- Kendon, E.J.; Roberts, N.M.; Fowler, H.J.; Roberts, M.J.; Chan, S.C.; Senior, C.A. Heavier summer downpours with climate change revealed by weather forecast resolution model. Nat. Clim. Chang. 2014, 4, 570. [Google Scholar] [CrossRef]
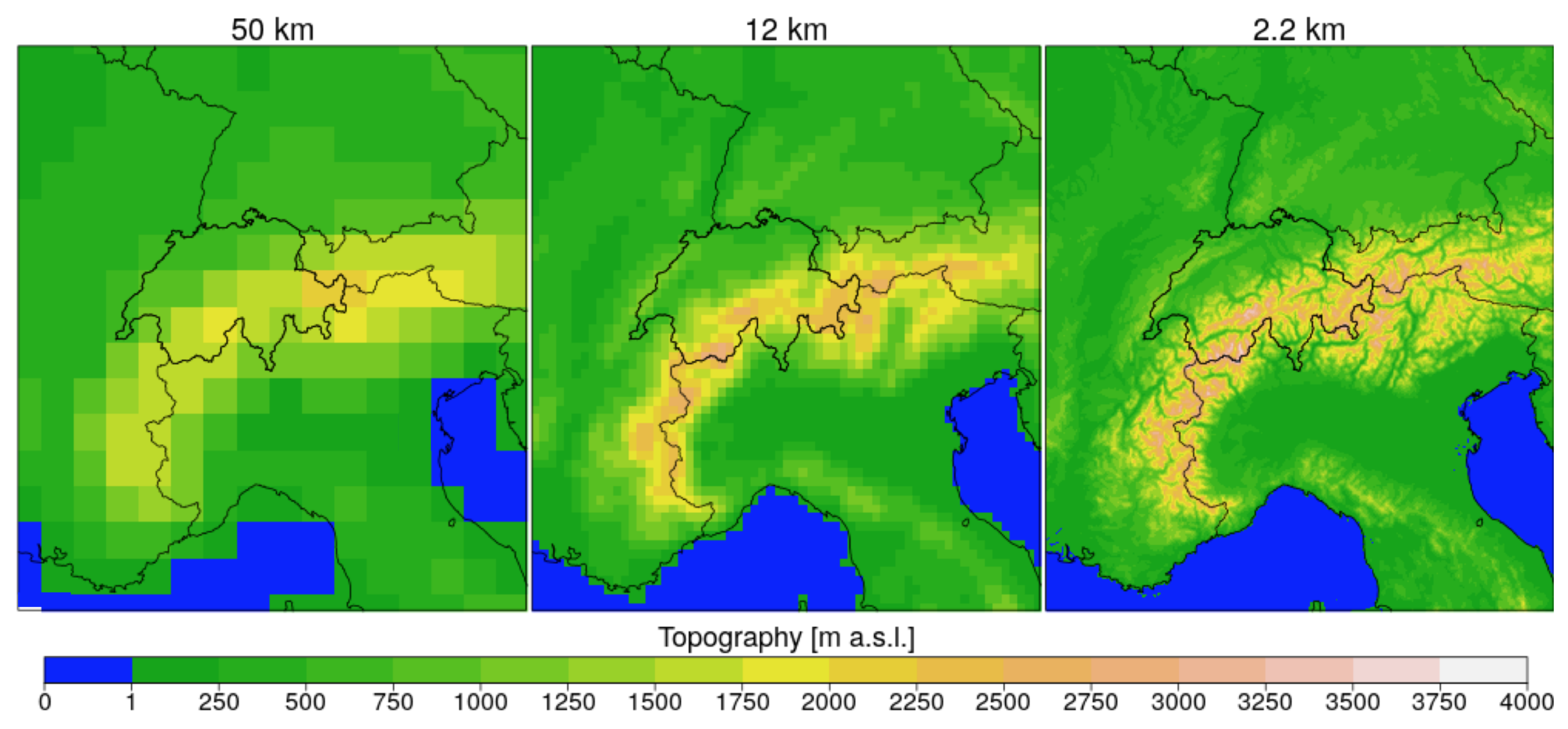

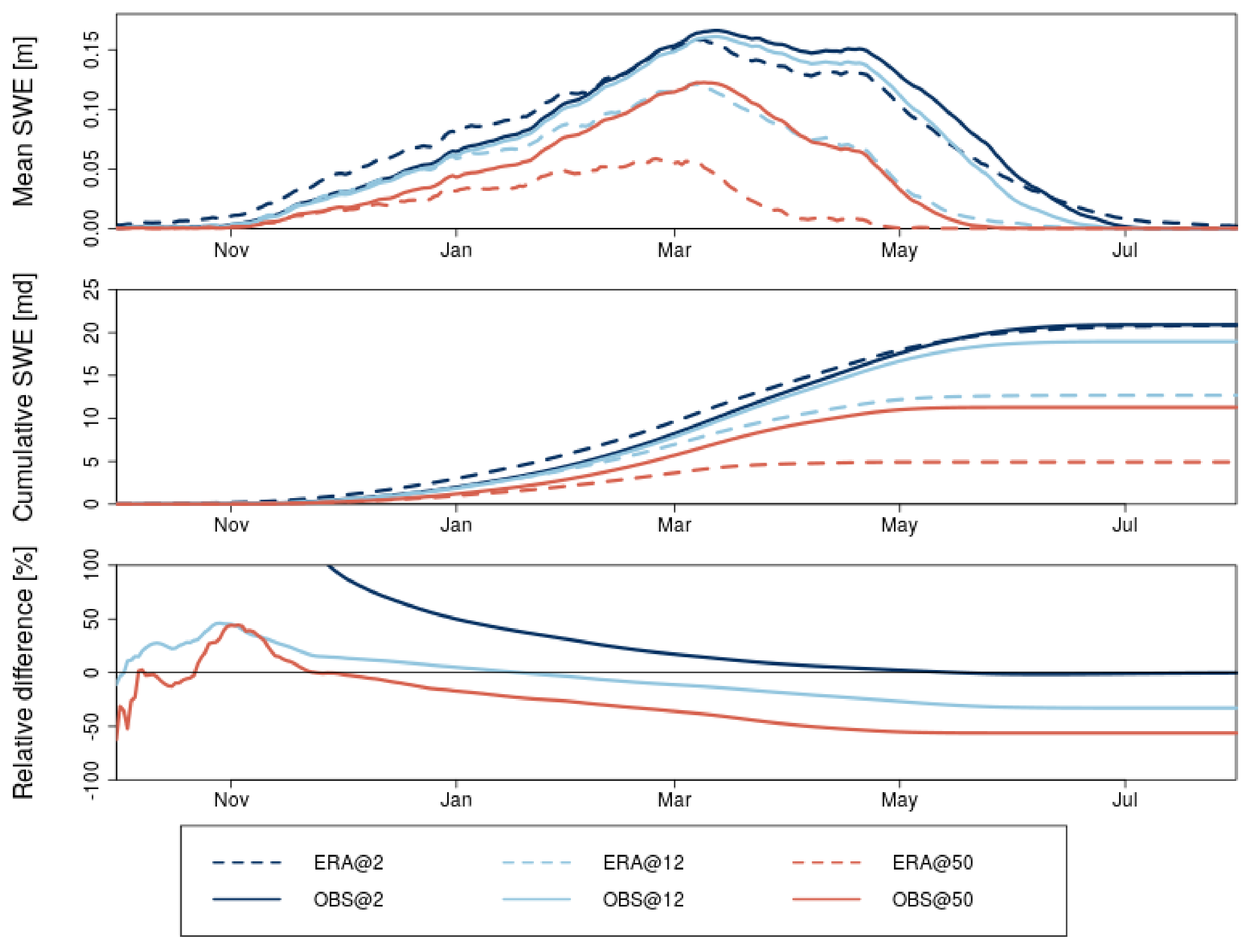
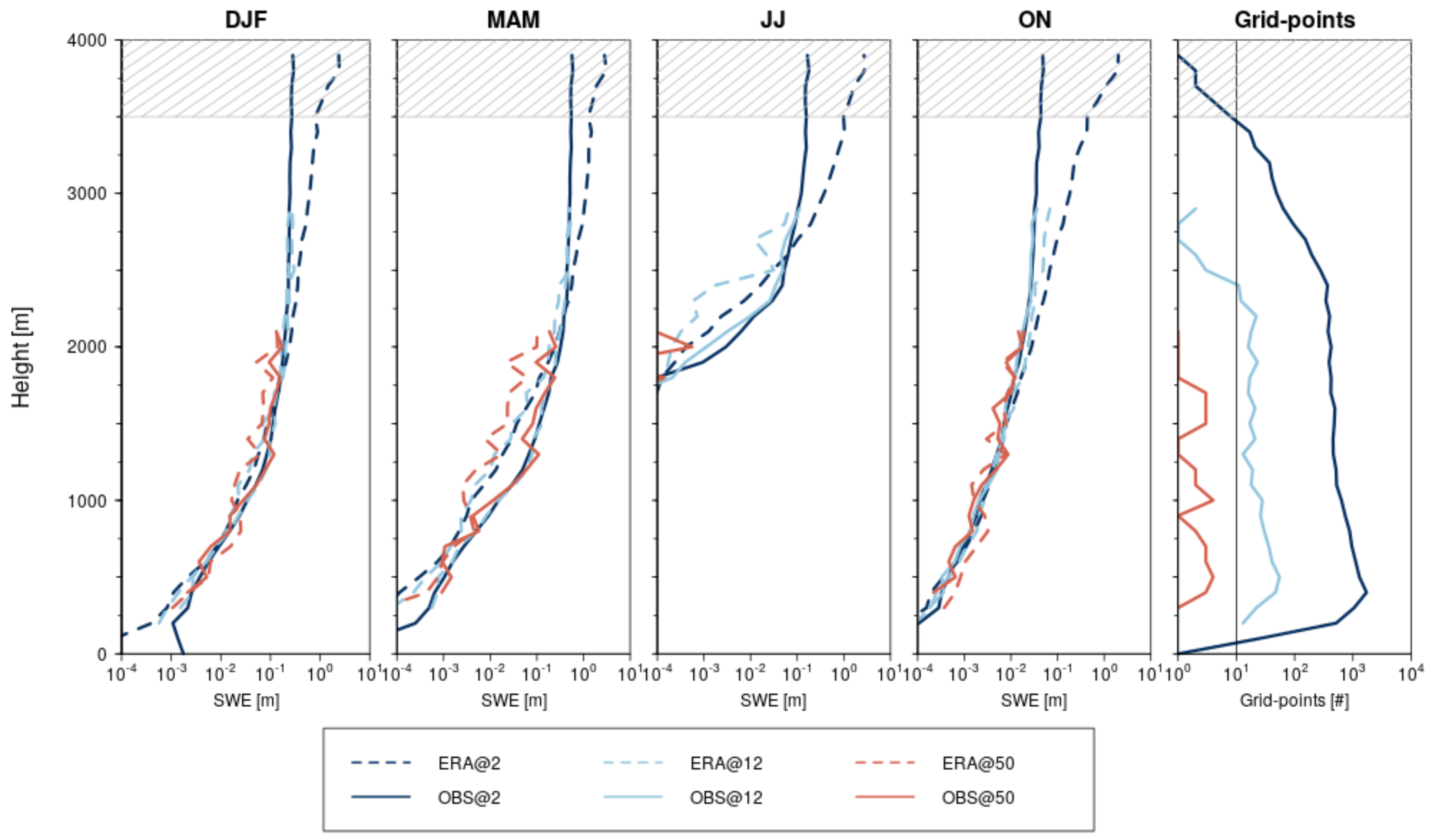
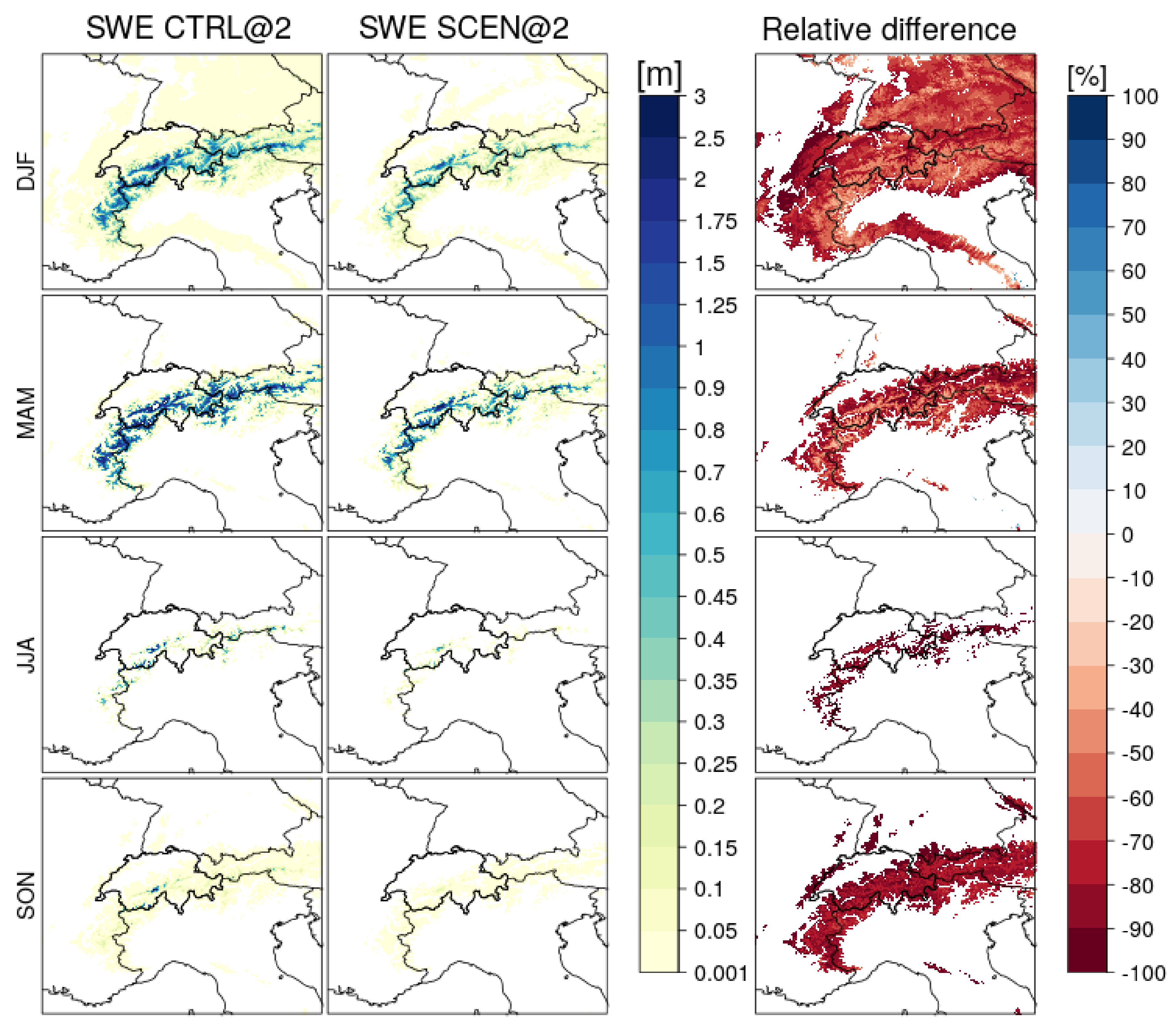
| Model Run | Period | Time | Driving Data | (km) | (s) | Deep Convection | # Grid Points in Analysis Area | # Grid Points above 2000 m | Highest Grid Point (m asl) |
|---|---|---|---|---|---|---|---|---|---|
| ERA@50 | Evaluation | 1998–2007 | Era-Interim | 50 | 300 | Tiedtke | 651 (31 × 25) | 2 | 2102 |
| ERA@12 | Evaluation | 1998–2007 | Era-Interim | 12 | 90 | Tiedtke | 7676 | 188 | 2958 |
| CTRL@12 | Control | 1991–2000 | MPI-ESM-LR | (101 × 76) | |||||
| SCEN@12 | Scenario | 2081–2090 | MPI-ESM-LR (RCP8.5) | ||||||
| ERA@2 | Evaluation | 1998–2007 | ERA@12 km | 2.2 | 20 | Explicit | 161,236 | 6796 | 3944 |
| CTRL@2 | Control | 1991–2000 | CTRL@12 km | (466 × 346) | |||||
| SCEN@2 | Scenario | 2081–2090 | SCEN@12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lüthi, S.; Ban, N.; Kotlarski, S.; Steger, C.R.; Jonas, T.; Schär, C. Projections of Alpine Snow-Cover in a High-Resolution Climate Simulation. Atmosphere 2019, 10, 463. https://doi.org/10.3390/atmos10080463
Lüthi S, Ban N, Kotlarski S, Steger CR, Jonas T, Schär C. Projections of Alpine Snow-Cover in a High-Resolution Climate Simulation. Atmosphere. 2019; 10(8):463. https://doi.org/10.3390/atmos10080463
Chicago/Turabian StyleLüthi, Samuel, Nikolina Ban, Sven Kotlarski, Christian R. Steger, Tobias Jonas, and Christoph Schär. 2019. "Projections of Alpine Snow-Cover in a High-Resolution Climate Simulation" Atmosphere 10, no. 8: 463. https://doi.org/10.3390/atmos10080463
APA StyleLüthi, S., Ban, N., Kotlarski, S., Steger, C. R., Jonas, T., & Schär, C. (2019). Projections of Alpine Snow-Cover in a High-Resolution Climate Simulation. Atmosphere, 10(8), 463. https://doi.org/10.3390/atmos10080463






